-
In high-energy nuclear physics, productions of prompt photons and photon-associated jets with high transverse momentum are valuable observations of the short-distance dynamics of quarks and gluons [1]. Because the prompt photon is precisely calculable by perturbative quantum chromodynamics (pQCD) at higher order corrections and carries no color charge like other gauge bosons, it has been widely regarded as an optimal probe of the initial state of collisions [2-6], as well as an excellent tag of an inversive parton (jet) to quantify the mechanisms of jet quenching in ultrarelativistic heavy-ion collisions [7-14]. In the past few years, the ATLAS [15-17] and CMS [18-20] collaborations have made many measurements on isolated prompt photon and
$ \gamma $ +jet productions in proton-proton, proton-nucleus, and nucleus-nucleus collisions. The isolated photon's nuclear modification factor depending on the photon transverse energy$ E_{\rm T}^{\gamma} $ measured in most central Pb-Pb collisions has large uncertainty, it also shows centrality dependence at limited$ E_{\rm T}^{\gamma} $ intervals [7].$ \gamma $ +jet events have been discussed to extend the study of the tomography of quark-gluon plasma (QGP) created in heavy-ion collisions. For instance, the distribution of photon plus jet transverse momentum imbalance$\left( x_{j\gamma}=p_{\rm T}^{\rm jet}/\right. $ $ \left. p_{\rm T}^{\gamma}\right) $ indicates that most of the jet's initial energy would be damped and deposited in most central Pb+Pb collisions [20]. In this study, we employ the productions of isolated photons and photon+jet in p+A collisions to probe the initial-state cold nuclear matter (CNM) effects.In elementary hadron-hadron collisions, with pQCD, the cross-section of the leading particle (and jet) could in general be expressed as a convolution of the parton distribution functions (PDFs), hard partonic cross-section, and fragmentation functions (FFs) if applicable. The PDF for a parton i from the free proton
$ (f_i^p(x, Q^2)) $ is nonperturbative in the frame of the QCD collinear factorization theorem [21, 22] and its evolution in the scale$ Q^2 $ can be depicted as the DGLAP equations [23-25]. In p+A collisions, PDFs in the nuclear environment should be modified owing to different CNM effects, such as shadowing, anti-shadowing, the EMC effect, and Fermi motion [26]. It is expected that the QCD factorization theorem may hold for nuclei as a good approximation, and we can replace the PDF in a free proton$ (f_i^p(x, Q^2)) $ with the nuclear PDF (nPDF)$ (f_i^A(x, Q^2)) $ to effectively include different CNM effects to study hard processes in p+A collisions.In the past three decades, our understanding of global fits of nPDFs have been regularly enriched by the growing experimental results of the fixed-target deep inelastic scattering (DIS) and low-mass Drell-Yan (DY) dilepton measurements [27-29], as well as the theoretical predictions from leading order (LO) up to next-to-next-to-leading order (NNLO) [30-33]. In the DSSZ framework [34], the global analysis for the nPDFs is presented as the ratio of parton distributions in a proton of a nucleus and in a free proton,
$ R_i^A(x, Q^2)=f_i^A(x, Q^2)$ $/f_i^p(x, Q^2) $ , evolving at the initial scale$ Q_0 = 1~{\rm GeV} $ . The DSSZ analysis not only uses the$ l^\pm/\mu- $ DIS datasets and p$ + $ A DY datasets, but also first includes the inclusive pion production in the deuteron and gold collisions at PHENIX to constrain the nuclear gluon PDF. EPPS16 [35] is an extension of the previous EPS09 framework [36] with the additional experimental data from proton-lead collisions at the LHC [37-39] for the first time. It offers a less biased and flavor-dependent fitting analysis for nuclear PDFs. Following the CTEQ global PDF fitting framework [31, 40, 41], nCTEQ15 [42] describes the nuclear dependence of nPDFs at next-to-leading order (NLO) on different nuclei, including Pb. nIMParton [43] is a global analysis based on two datasets of nuclear DIS data, which either only contains isospin-scalar nuclei or all nuclear data. The difference between the fitting functions obtained by these two datasets is in the shadowing (small x region) effects. In addition, Fermi motion, the off-shell effect, nucleon swelling, and parton-parton recombination are considered together in the nIMParton framework. Other parameterizations of nPDFs have also been proposed [44-48], and so far, owing to the lack of sufficient experimental data, limited constraints and large uncertainties appear in the nuclear gluon distribution, especially in the small-x and large-$ Q^2 $ region, and the nuclear quark distribution at large x for all sets of nPDFs.In this work, we study the isolated prompt photon and
$ \gamma+ $ jet productions in proton-lead collisions at LHC energy$ \sqrt{s_{NN}}=8.16 $ TeV using the JETPHOX NLO pQCD software [1, 49, 50] with updated proton PDFs$ - $ CT14 parametrization [41]. The nPDF parametrizations (DSSZ, EPPS16, nCTEQ15) are performed at NLO accuracy and the nIMParton is based on LO calculations with parton-parton recombination. These four sets of nPDF parameterizations have been utilized in obtaining the photon and photon-associated jet cross-sections in p+A collisions. We calculate the nuclear modification factors$ R_{\rm pPb} $ for isolated photon production as a function of transverse momentum$ p_{\rm T}^{\gamma} $ and pseudo-rapidity$ \eta^\gamma $ at both forward and backward rapidity regions, the forward-backward asymmetry$ Y_{\rm pPb}^{\rm asym} $ for isolated photon production as a function of$ p_{\rm T}^{\gamma} $ , and the nuclear modification factors$ R_{\rm pPb} $ for$ \gamma+ $ jet production as a function of$ \eta_{\gamma \rm Jet} $ at limited$ p_{\rm T}^{\rm avg} $ intervals. We address the quantification of dominant Bjorken x regions detected under different specific rapidity and transverse momentum ranges.The remainder of this paper is organized as follows: in Section 2, we describe our pQCD predictions of prompt-photon-associated-jet inclusive cross-sections in proton-proton collisions at 8 TeV. In Section 3, we discuss the nuclear modification of isolated prompt photon productions at both forward and backward regions at
$ 8.16 $ TeV. In Section 4, the CNM effects on photon$ + $ jet productions are studied at different transverse momentum intervals at$ 8.16 $ TeV. Finally, we summarize this work in Section 5. -
High-
$ p_{\rm T} $ prompt photons mainly arise from two possible mechanisms in hadronic collisions, produced directly in the hard sub-processes referred to as "direct" photons or fragmented from an energetic parton. We consider that the NLO-inclusive cross-section for the production of prompt photons with transverse momentum$ p_{\rm T}^{\gamma} $ is given by the sum of the fragmentation and direct contributions, written as [1, 50],$ \begin{split} \sigma\left(p_{\rm T}^{\gamma}\right)=&\hat{\sigma}^D\left(p_{\rm T}^{\gamma};\mu;M;M_F\right)\\ &+\sum\limits_k\int_0^1\frac{{\rm d}z}{z}\hat{\sigma}^F\left(p_{\rm T}^{\gamma}/z;\mu;M;M_F\right)D_k^{\gamma}\left(z;M_F\right), \end{split} $

(1) where
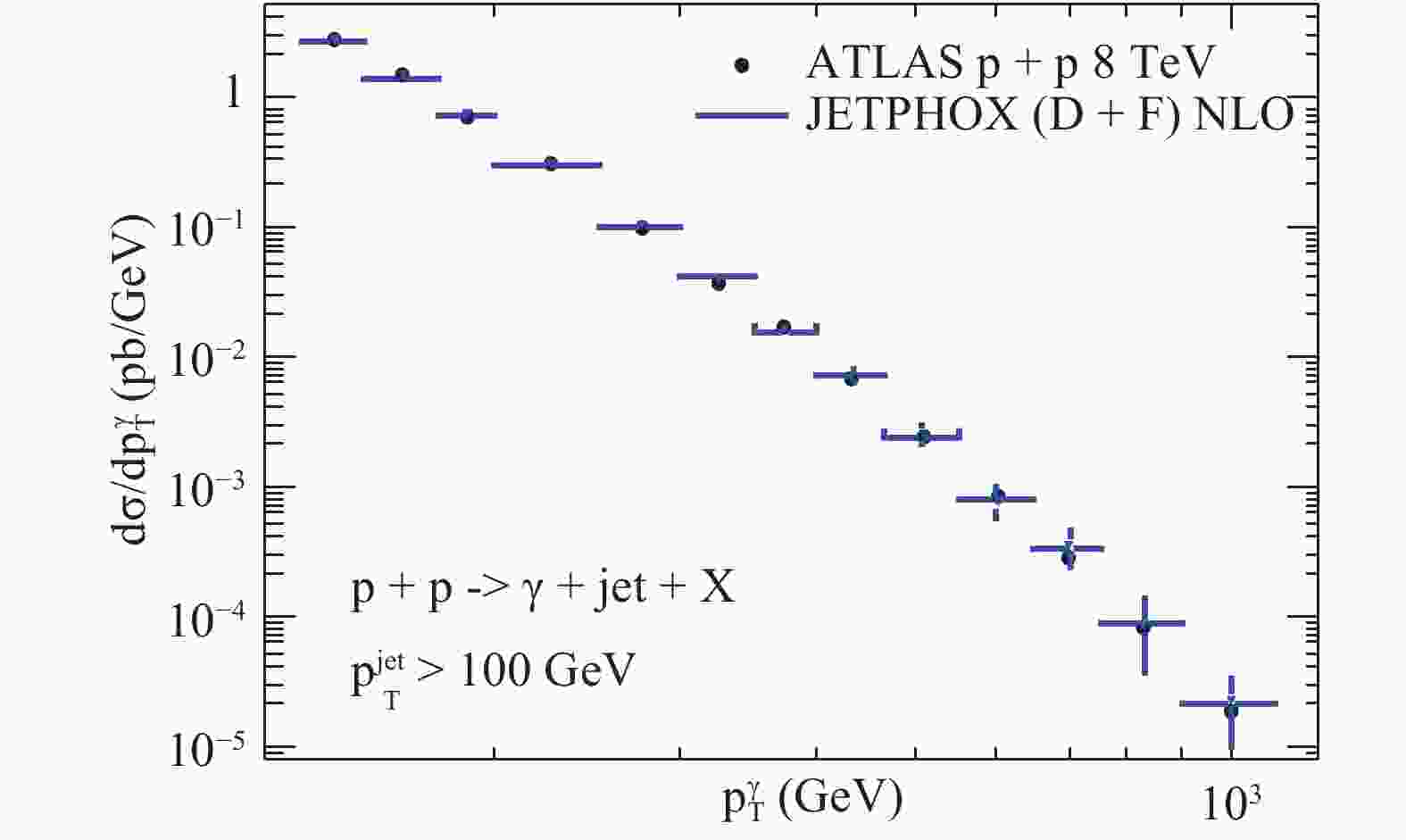
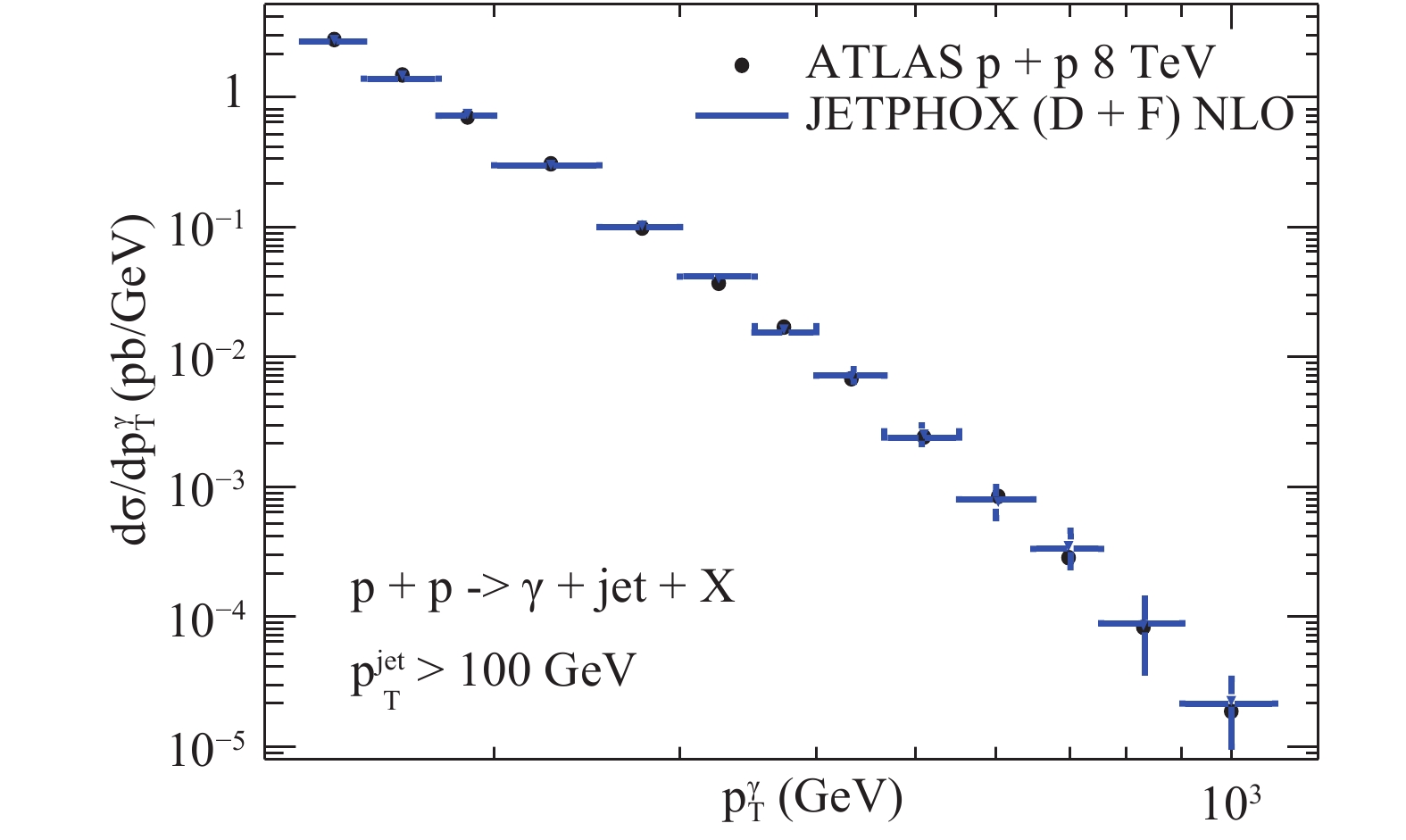
$ \mu $ is the renormalization scale,$ M $ is the initial state factorization scale, and$ M_F $ is an arbitrary final state fragmentation scale. The contribution$ \hat{\sigma}^F $ denotes the partonic cross-section for producing a parton convoluted with the PDF of the incoming proton, and$ D_k^{\gamma} $ is the fragmentation function of a parton$ k $ (quarks, anti-quarks, and gluon) into a photon.$ \hat{\sigma}^D $ includes the partonic cross-section for producing a direct photon and the corresponding PDFs. Experimentally, there are also secondary photons originated from hadron decay during the collisions, and therefore an isolation cut would be applied for the substantial production of photons. A photon is isolated if the amount of deposited hadronic transverse energy$ E_{\rm T} $ is not more than a specific upper limit$ E_{\rm T}^{\rm iso} $ in a fixed radius$ R_{\rm iso}=\sqrt{(\eta-\eta_\gamma)^2+(\phi-\phi_\gamma)^2} $ in pseudo-rapidity and azimuthal angle around the photon direction. This restriction on the yields of isolated photons could not only reject the secondary decay photons, but also reduce the contribution from fragmentation processes. In the following, we focus on the production of isolated photons and isolated photon-tagged jets in hadronic collisions.We calculate isolated photon and jet productions in proton-proton collisions at 8 TeV using the JETPHOX NLO pQCD program [1, 49, 50] with CT14 nPDFs [41] in accordance with the ATLAS experiment [16]. The isolated energy cut for a photon has been set as
$ E_{ \rm T}^{ \rm iso}<6 $ GeV, and the isolated cone of radius in the pseudo-rapidity and azimuthal angle plane is$ R_{\rm cone}=0.4 $ . Moreover, photons are selected if their transverse momentum$ p_{\rm T}^{\gamma}>130 {\rm GeV} $ and$ |\eta^{\gamma}|<2.37 $ , except for$ 1.37<|\eta^{\gamma}|<1.56 $ . Jets are reconstructed by the anti-$ k_{t} $ algorithm with cone size$ R=0.6 $ and$ p_{\rm T}^{\rm jet}>100 {\rm GeV} $ and$ |\eta^{\rm jet}|<4.4 $ . In Fig. 1, we calculate the differential cross-section$ {\rm d}\sigma/{\rm d}p_{\rm T}^{\gamma} $ up to$ p_{\rm T}^{\gamma}=1 $ TeV in proton-proton collisions at$ \rm 8 $ TeV, and our theoretical predication shows good agreement with the ATLAS experimental results. -
The inclusive cross-section for the isolated photon production in proton-nucleus collisions could be evaluated by using nPDFs as substitutes for free-nucleon PDFs in the collinear factorization framework as stated above, which could effectively include different CNM effects.
In our calculations, we obtain the nPDFs
$ f_i^A(x, Q^2) $ by multiplying the CT14 PDFs [41] with a flavor- and scale-dependent factor$ R_i^A(x, Q^2) $ taken from four different parameterizations, DSSZ [34], EPPS16 [35], nCTEQ15 [42], and nIMParton [43]. These four parameterizations for the nPDFs are similar, in that they categorize CNM effects with Bjorken x region into shadowing, anti-shadowing, EMC effect, and so on, but differ in the specific formalisms and parameters for describing the CNM effects and the input experimental data used in the global fits. DSSZ, nCTEQ15, and EPPS16 could be convoluted in the expression for calculating the photon production at NLO, because they are also quantified in the NLO pQCD framework. The LO results for photon production are applied with nIMParton parameterization to maintain the consistency of the analysis.The nuclear modification factors in proton+lead collisions are defined as:
$ R_{\rm pPb}=\frac{{\rm d}\sigma^{\rm pPb}/{\rm d}p_{\rm T}}{\langle N_{\rm coll}\rangle {\rm d}\sigma^{\rm pp}/{\rm d}p_{\rm T}} $

(2) with
$ \langle N_{\rm coll}\rangle $ representing the number of binary nucleon-nucleon collisions by the Glauber model [51].Now we can make our theoretical predictions for the isolated prompt photon production in p
$ + $ p and p$ + $ Pb collisions at the very forward rapidity region$ \rm 3<\eta^{\gamma}<4 $ at$ \rm \sqrt{s_{NN}}=8.16 $ TeV with ATLAS isolated cuts for photons [16], along with the photon transverse momentum constrained in the range$ 40~{\rm GeV}<p_{\rm T}^{\gamma}<300~{\rm GeV} $ . We display the nuclear modification ratio$ R_{\rm pPb}^{\gamma} $ as a function of$ p_{\rm T}^{\gamma} $ in the upper panel of Fig. 2. The momentum fraction carried by the initial parton from the incoming particle can be approximately estimated to LO as$ x_{1, 2}= $ $\displaystyle\frac{p_{\rm T}}{\sqrt{s_{NN}}}\left({ e}^{\pm y_1}+{e}^{\pm y_2}\right) $ , where$ x_1\left(x_p\right) $ is the initial parton coming from the proton in the$ +z $ direction,$ x_2(x_{\rm pb}) $ is the initial parton coming from lead in the$ -z $ direction in$ \rm p+Pb $ collisions, and$ y_{1, 2} $ is the rapidity of$ \gamma $ and the associated jet respectively. The estimated average Bjorken$ \langle x_{\rm Pb}\rangle $ has been defined as the event's average value of Bjorken$ x_{\rm Pb} $ in the JetPhox simulation. In the bottom panel of Fig. 2, we show the estimation of the parton's average momentum fraction off-nucleus based on NLO results in JETPHOX. We have checked that$ \langle x_{\rm Pb}\rangle $ for the nPDF parameterizations vary slightly from each other. We can see that the average Bjorken$ \langle x_{\rm Pb}\rangle $ is lower than 0.055 at the very forward rapidity region, which represents the shadowing effect dominating the CNM effects. Moreover, the average Bjorken$ \langle x_{\rm Pb}\rangle $ has a positive linear dependence with$ p_{\rm T}^{\gamma} $ expected in its LO estimation.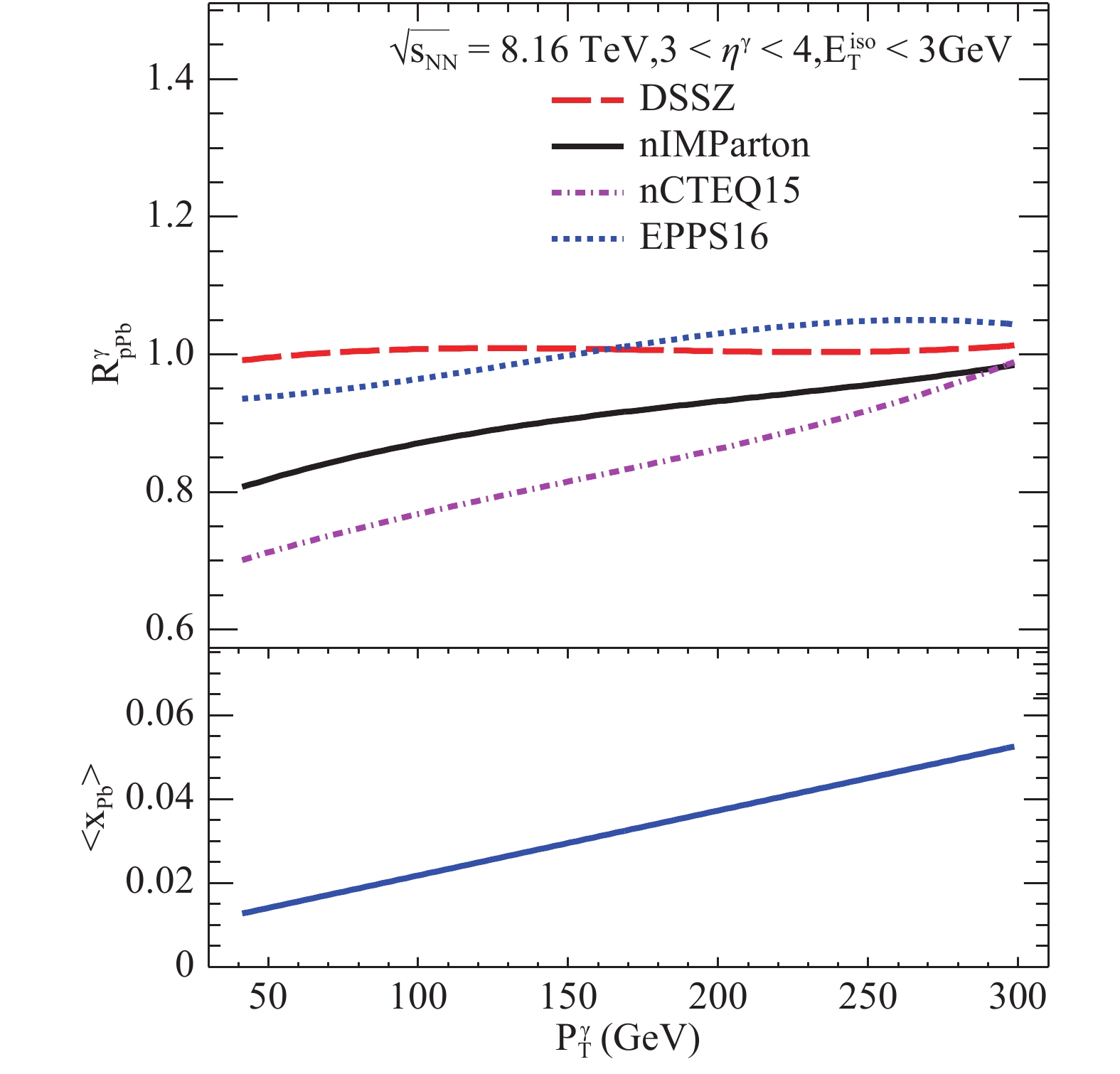
Figure 2. (color online) (Upper) Comparison between the nuclear modification ratios
$R_{\rm pPb}$ for p-Pb collisions at$\sqrt{s}$ = 8.16 TeV and$\rm 3 < \eta^{\gamma} < 4$ using the nCTEQ15, EPPS16, DSSZ, and nIMParton nuclear modifications and the CT14 free-proton PDFs. (Bottom) Corresponding average Bjorken$\langle x_{\rm Pb}\rangle$ as function of$ p_{\rm T}^{\gamma}$ .In Fig. 2, we see that the shadowing effect of DSSZ is unremarkable on the suppression of isolated photon production in p
$ + $ Pb collisions when the average Bjorken$ \langle x_{\rm Pb}\rangle<0.055 $ . We also notice that DSSZ's$ R_{\rm pPb}^{\gamma}(p_{\rm T}^{\gamma}) $ shows a very weak$ p_{\rm T}^{\gamma} $ dependence, which means its shadowing effect is nearly independent of the photon's transverse momentum in DSSZ at the forward rapidity region. Meanwhile the other three parameterizations' shadowing effects decrease with$ p_{\rm T}^{\gamma} $ increasing upon$ 3<\eta^{\gamma}<4 $ . Additionally, we observe that the shadowing of the brand-new nPDF parametrization, nIMParton, is only weaker than that of nCTEQ15 in our discussion.In Fig. 3, a similar phenomenon of the positively linear correlation between
$ \langle x_{\rm Pb}\rangle $ and$ p_{\rm T}^{\gamma} $ has been shown at backward rapidity$ -4<\eta^{\gamma}<-3 $ . However, the estimated average Bjorken$ \langle x_{\rm Pb}\rangle $ ranges from 0.25 to 0.8, which mostly correspond to the EMC effect. We could go a little further to distinguish the EMC maxima of the four different parameterizations from each nuclear modification factor's extreme point. For example, nIMParton's EMC minimum appears at$ p_{\rm T}^{\gamma}=150 $ GeV and the corresponding average Bjorken is located around$ \langle x_{\rm Pb}\rangle=0.5 $ , which is the lowest in our results. We further investigate the correlations between$ x_{\rm Pb} $ and$ p_{\rm T}^{\gamma} $ at both forward and backward rapidities to NLO, as shown in Fig. 4. We observe the broadening of Bjorken$ x_{\rm Pb} $ at a specific$ p_{\rm T}^{\gamma} $ interval owing to higher corrections, and the spreading of$ x_{\rm Pb} $ at small$ p_{\rm T}^{\gamma} $ is rather wider. Additionally, we can see a very dense statistics cluster around the low$ p_{\rm T}^{\gamma} $ in our Monte-Carlo simulation, because of the possibility distribution of the hard subprocesses for the photon production following double-logarithmic declining with the photon transverse momentum.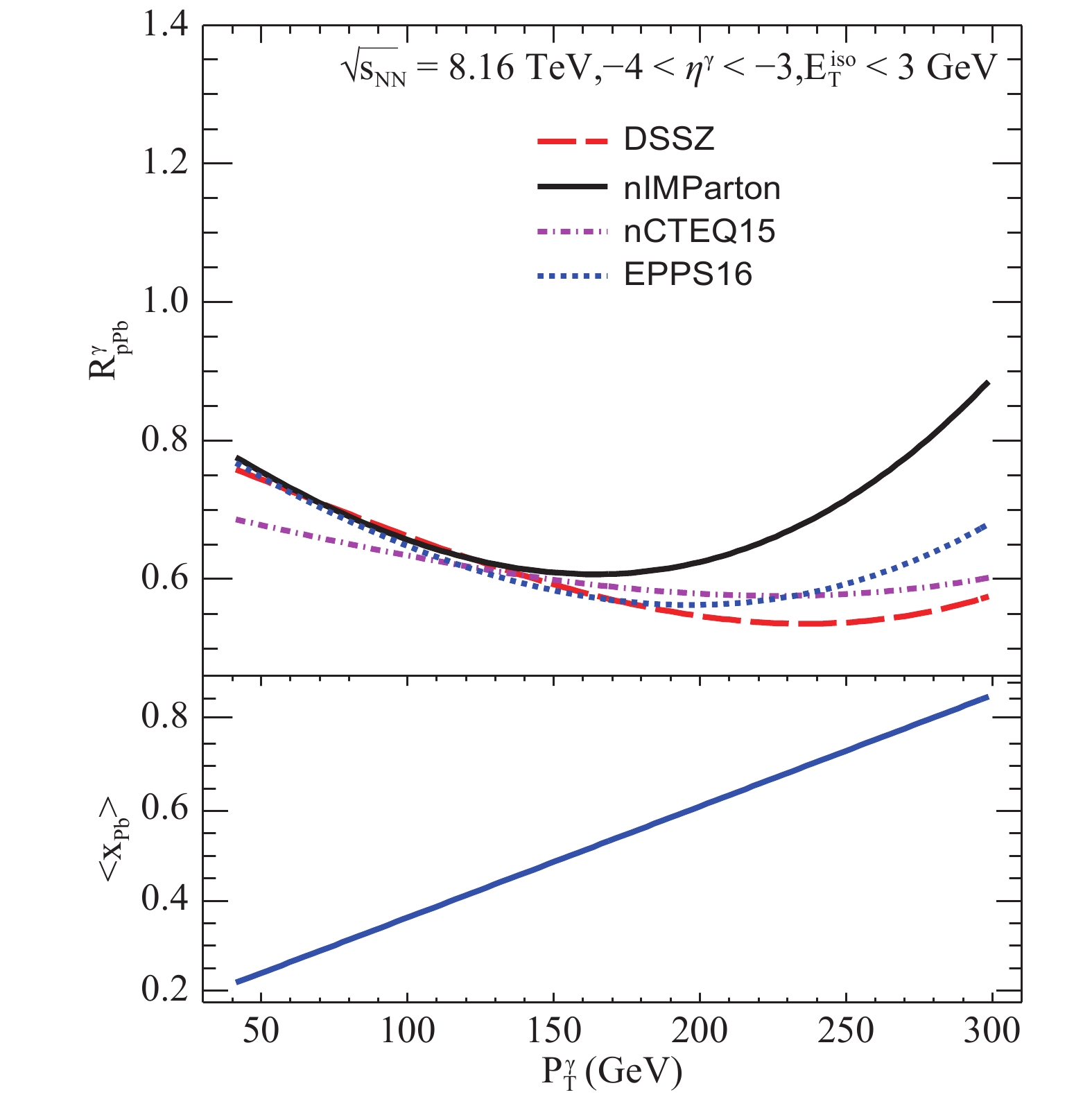
Figure 3. (color online) Same as Fig. 2, except at backward rapidity
$\rm -4 < \eta^{\gamma} < -3$ .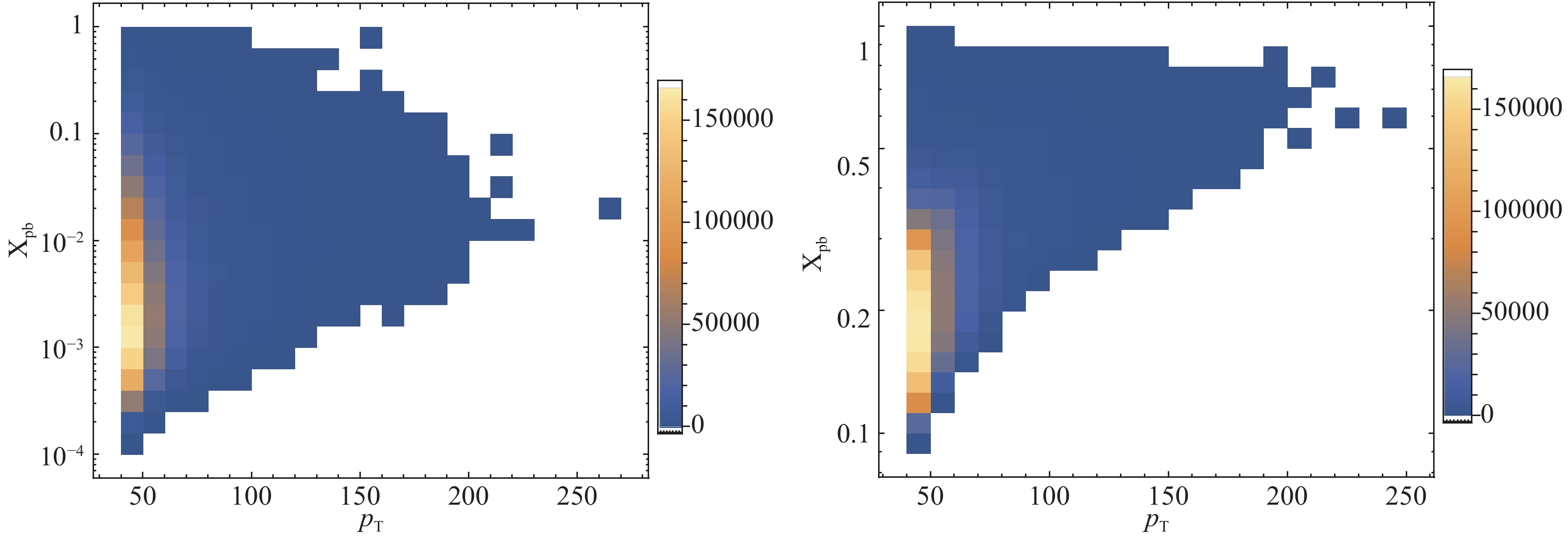
Figure 4. (color online) (Left) NLO fluctuations at forward rapidity
$ \rm 3<\eta^{\gamma}<4 $ ; (Right) NLO fluctuations at backward rapidity$ -4<\eta^{\gamma}<-3 $ .Noting that the nuclear modification factor is sensitive to the nPDF and p+p baseline [52], we may calculate the ratio of the photon production at forward and backward rapidity; this could eliminate the large uncertainty in the free-nucleon PDFs, which could be used to probe the CNM effects with less arbitrariness [12-14]. We define the forward-backward yield asymmetry as:
$ Y_{\rm p Pb}^{\rm asym}=\frac{{\rm d}\sigma/{\rm d}p_T({\rm p+Pb} \rightarrow \gamma+X)|_{\eta\in[\eta_1, \eta_2]}}{{\rm d}\sigma/{\rm d}p_{\rm T}({\rm p+Pb} \rightarrow \gamma+X)|_{\eta\in[-\eta_2, -\eta_1]}} . $

(3) Our predictions of the forward-to-backward yield asymmetries
$ Y_{\rm pPb}^{\rm asym} $ for the isolated prompt photon production in p+Pb collisions at$ \rm \sqrt{s}=8.16 $ TeV and$ \rm 3 < |\eta^{\gamma}| < $ 4 are shown in Fig. 5. As a result of the symmetry of the colliding system, there is nearly no forward-to-backward yield asymmetry observed in proton-proton collisions.$ Y_{\rm pPb}^{\rm asym} $ is larger than one in p+Pb collisions, which means the photon production suffers more suppression in the backward-rapidity region. Overall, the EMC effect reduces the photon production more effectively than the shadowing effect does. Moreover, we notice that the value of$ Y_{\rm pPb}^{\rm asym} $ starts decreasing to one with all parameterizations owing to the decreasing of the EMC effect at relatively high$ p_{\rm T}^{\gamma} $ . This manifestation seems less obvious in nCTEQ15, as its EMC maximum is close to the highest boundary of$ p_{\rm T}^{\gamma} $ and our approximate curve fitting.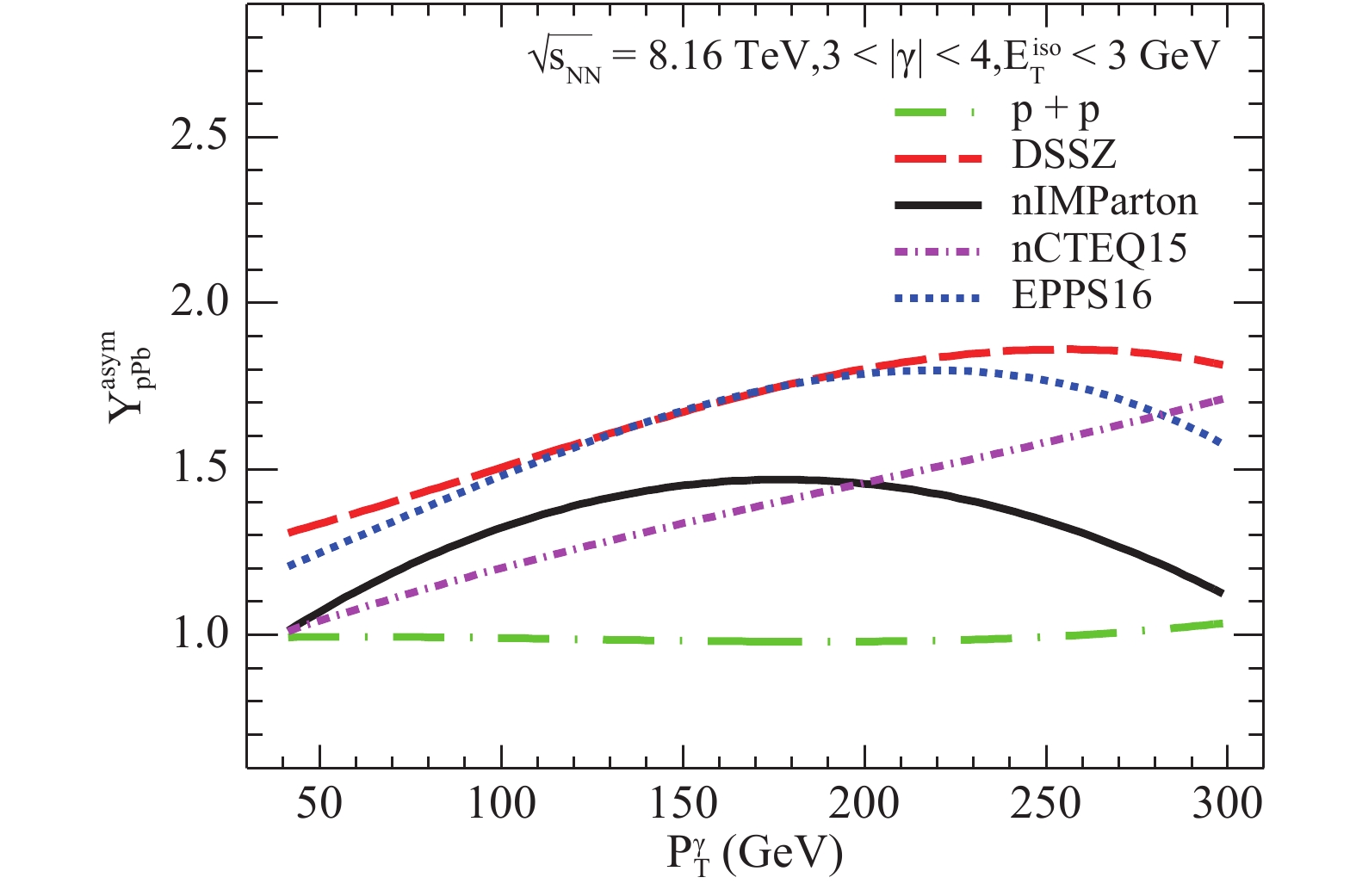
Figure 5. (color online) Comparison between the forward-to-backward asymmetry
$\rm Y_{asym}$ for p-Pb collisions at$\sqrt{s_{NN}}$ = 8.16 TeV and$\rm 3 < \eta^{\gamma} < 4$ using the nCTEQ15, EPPS16, DSSZ, and nIMParton nuclear modifications and the CT14 free-proton PDFs.In order to further explore the impact of input nuclear modifications on the cross-section of isolated prompt photon productions in proton-nucleus collisions, we further discuss the isolated photon's nuclear modification factor
$ R_{\rm pPb}^{\gamma}(\eta^{\gamma}) $ as a function of the photon's rapidity$ \eta^{\gamma} $ at both forward and backward rapidities. The Fig. 6 shows a growing suppression of the photon productions from DSSZ, EPPS16, nIMParton, and nCTEQ15 at forward pseudo-rapidity, which quantitatively appears in accordance with the$ R_{\rm pPb}^{\gamma}(p_{\rm T}^{\gamma}) $ at$ p_{\rm T}^{\gamma}=50~{\rm GeV} $ owing to the highest statistics at the lowest-$ p_{\rm T}^{\gamma} $ region in the Monte-Carlo simulations exhibited above in Fig. 2. However,$ R_{\rm pPb}^{\gamma}(\eta^{\gamma}) $ shows very weak$ \eta^{\gamma} $ dependence, because the variation of Bjorken$ x_{\rm Pb} $ is at the magnitude of$ 10^{-3} $ in the$ 3<\eta^{\gamma}<4 $ region, shown at the bottom of Fig. 6. Combining the results of$ R_{\rm pPb} $ evolved with$ p_{\rm T}^{\gamma} $ and$ \eta^{\gamma} $ , the suppression pattern of isolated photons could be quantitatively analyzed through$ \langle x_{\rm Pb}\rangle $ at both forward and backward rapidities. In Fig. 7, the nuclear modification factors using the four different nPDFs all show a nearly positive linear relation with$ \eta^{\gamma} $ , the values of which agree with$ R_{\rm pPb}^{\gamma}(p_{\rm T}^{\gamma}) $ through the average Bjorken$ \langle x_{\rm Pb}\rangle $ , as shown in Fig. 7 and Fig. 3, respectively. The nCTEQ15 parameterization gives a stronger suppression than the others, which could be confirmed in the prediction of$ R_{\rm pPb}^{\gamma}\left(p_{\rm T}^{\gamma}\right) $ at the low-$ p_{\rm T}^{\gamma} $ region in Fig. 3.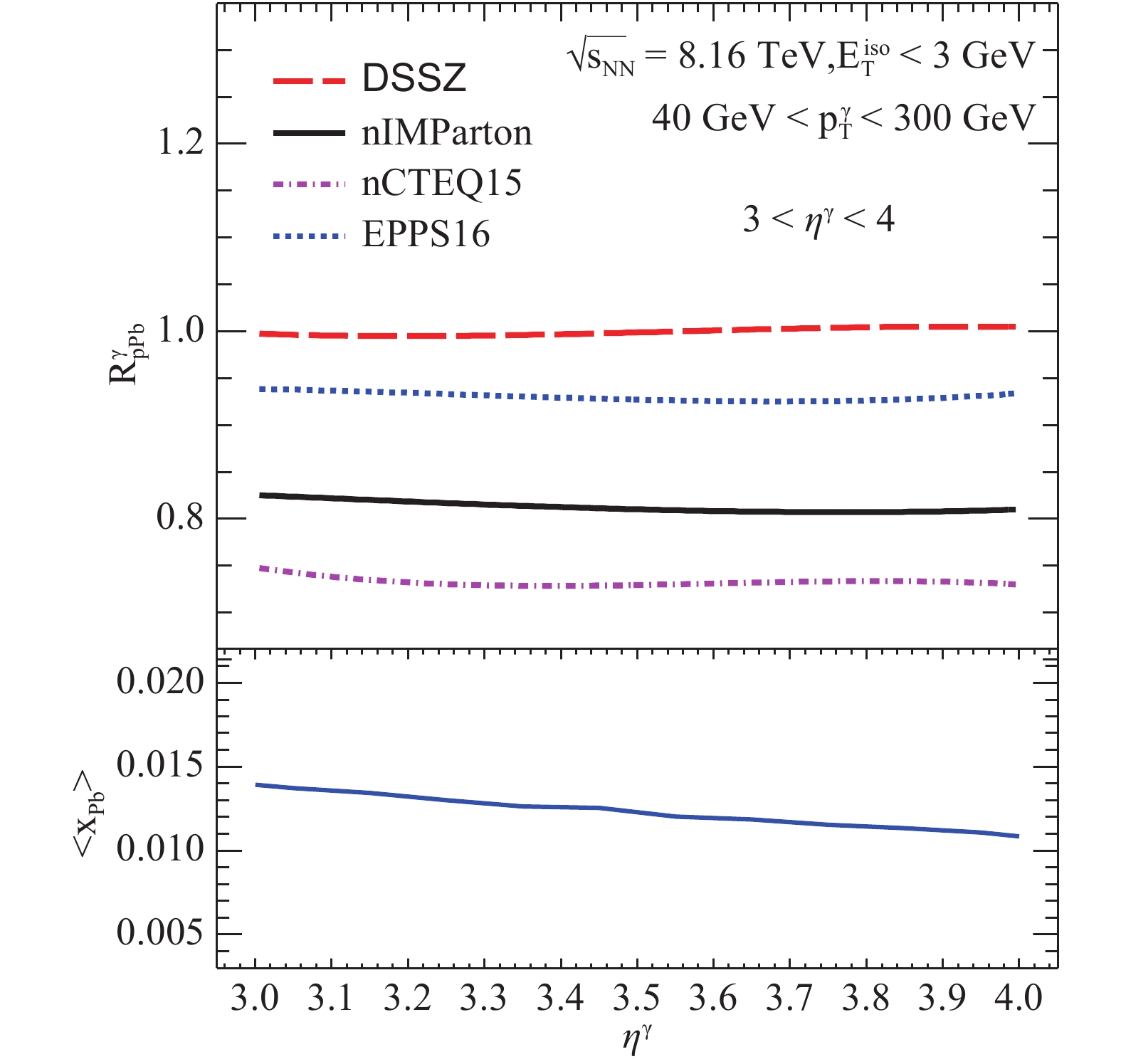
Figure 6. (color online) Same as Fig. 2, but as a function of photon rapidity
$\eta^{\gamma}$ .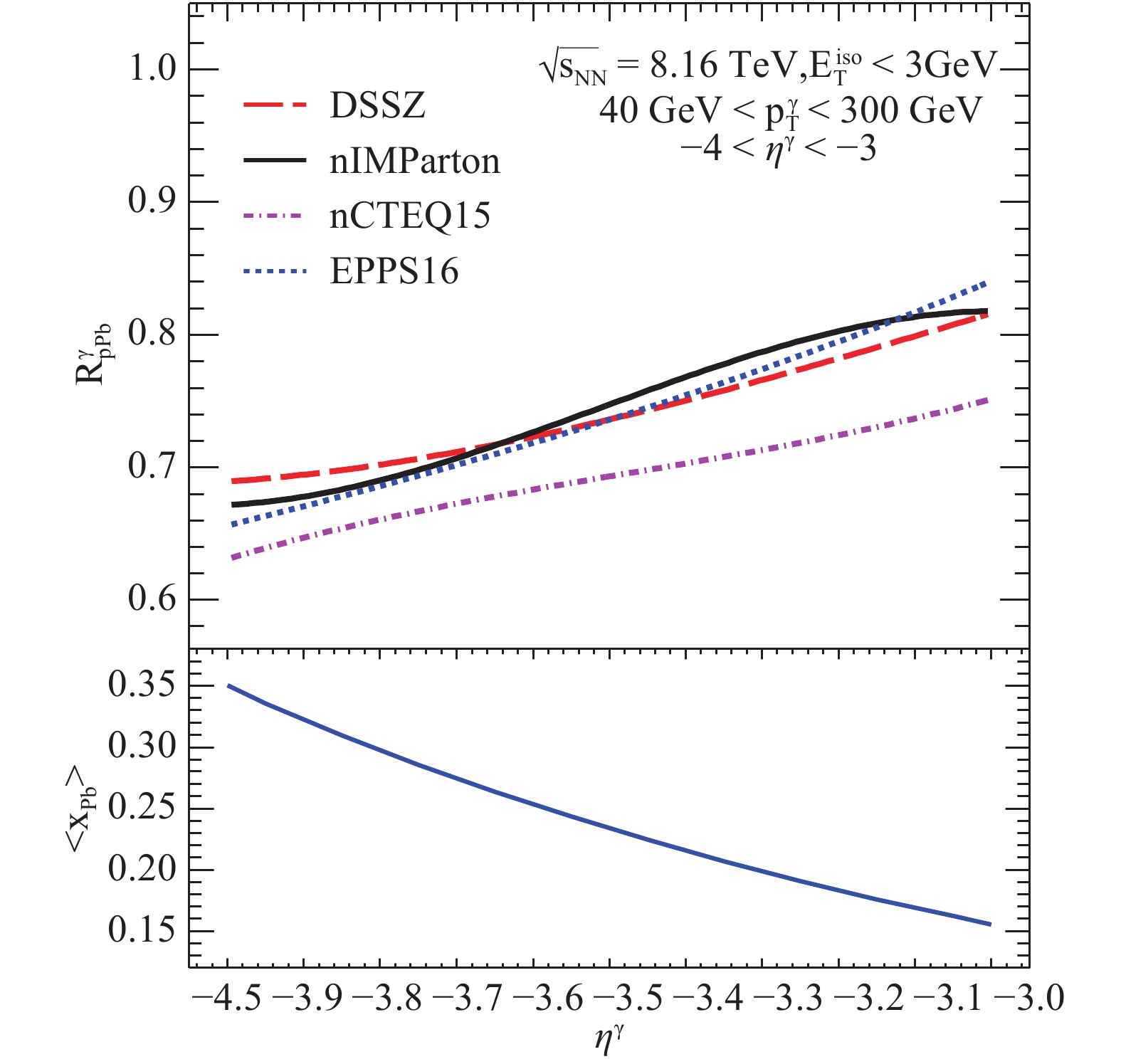
Figure 7. (color online) Same as Fig. 2, but as a function of photon rapidity
$\eta^{\gamma}$ . -
As compared to isolated photon production, the isolated-photon-associated jet production in p+A reactions has more leverage power to access CNM effects in a wider kinematic region owing to its exclusive property. To understand the nuclear modifications for isolated-prompt-photon-associated jet productions, one usually estimates the momentum fractions of the initial-state partons at LO to evaluate the contribution to CNM effects by the final-state kinematics, namely
$ x_{1, 2} $ defined above. In the following, we are enlightened by the work on dijets production in the CMS collaboration [53], and provide the$ \gamma $ +jet pseudo-rapidity$ \eta_{\gamma \rm jet}=\displaystyle\frac{1}{2}(\eta_\gamma+\eta_{\rm Jet}) $ distributions of a photon-tagged jet in a specific range of their average transverse momentum$ p_{\rm T}^{\rm avg}=\displaystyle\frac{1}{2}\left(p_{\rm T}^{\gamma}+p_{\rm T}^{\rm Jet}\right) $ . As$ \eta_{\gamma\rm jet} $ would be equal to$ \displaystyle\frac{1}{2}\ln(x_{\rm p}/x_{\rm Pb}) $ in the center-of-mass frame when two partons collide with each other at LO, the NLO simulation would give rise to complicated correlations between$ x_{\rm Pb} $ ($ x_{\rm p} $ ) and$ \eta_{\gamma\rm jet} $ , describing the nuclear matter's influence, as shown in Fig. 8. We also compute the correlations between$ x_{\rm Pb}/x_{\rm p} $ and$ \eta_{\gamma\rm Jet} $ in the interval of 115 GeV$ <p_{\rm T}^{\rm avg}< $ 4000 GeV in Fig. 8. It is shown though at NLO accuracy, that both distributions of$ x_{\rm Pb} $ and$ x_{\rm p} $ over$ \eta_{\gamma\rm jet} $ are rather wide, when the ratio$ x_{\rm Pb}/x_{\rm p} $ at NLO is rather narrow and centered at values at LO with very high statistics.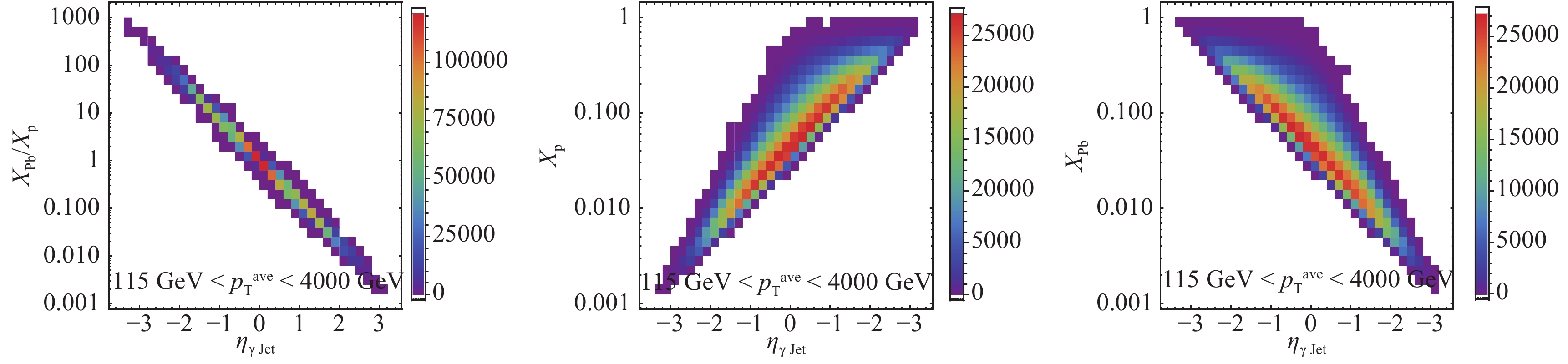
Figure 8. (color online) Correlation between
$ x_{\rm Pb}/x_{\rm p} $ (Left),$ x_{\rm p} $ (Middle),$ x_{\rm Pb} $ (Right), and$ \gamma+ $ jet pseudo-rapidity$ \eta_{\gamma\rm jet} $ .In Fig. 9, we notice that there are tiny shifts in
$ \displaystyle\frac{<x_2>}{<x_1>} $ as a function of$ \rm\eta_{\gamma jet} $ caused by nuclear matter. Based on the relation between$ \rm \eta_{\gamma Jet} $ and$ \langle x_{\rm Pb}\rangle $ , we could assess the predominant regions of$ \rm \eta_{\gamma Jet} $ for different CNM effects. The$ \gamma+ $ jet production is sensitive to shadowing ($ \rm \eta_{\gamma Jet}> $ $1.6 $ ), anti-shadowing ($ -0.2<\rm\eta_{\gamma Jet}<1.6 $ ), and EMC effects ($ \rm \eta_{\gamma Jet}<-0.2 $ ) in the$ 150<p_{\rm T}^{\rm avg}<200 $ interval, shown by the black line in Fig. 10. The average Bjorken$ \langle x_{\rm Pb}\rangle $ shows a nearly negative log-linear relation with$ \rm \eta_{\gamma Jet} $ , and becomes globally higher when the$ p_{\rm T}^{\rm avg} $ interval increases.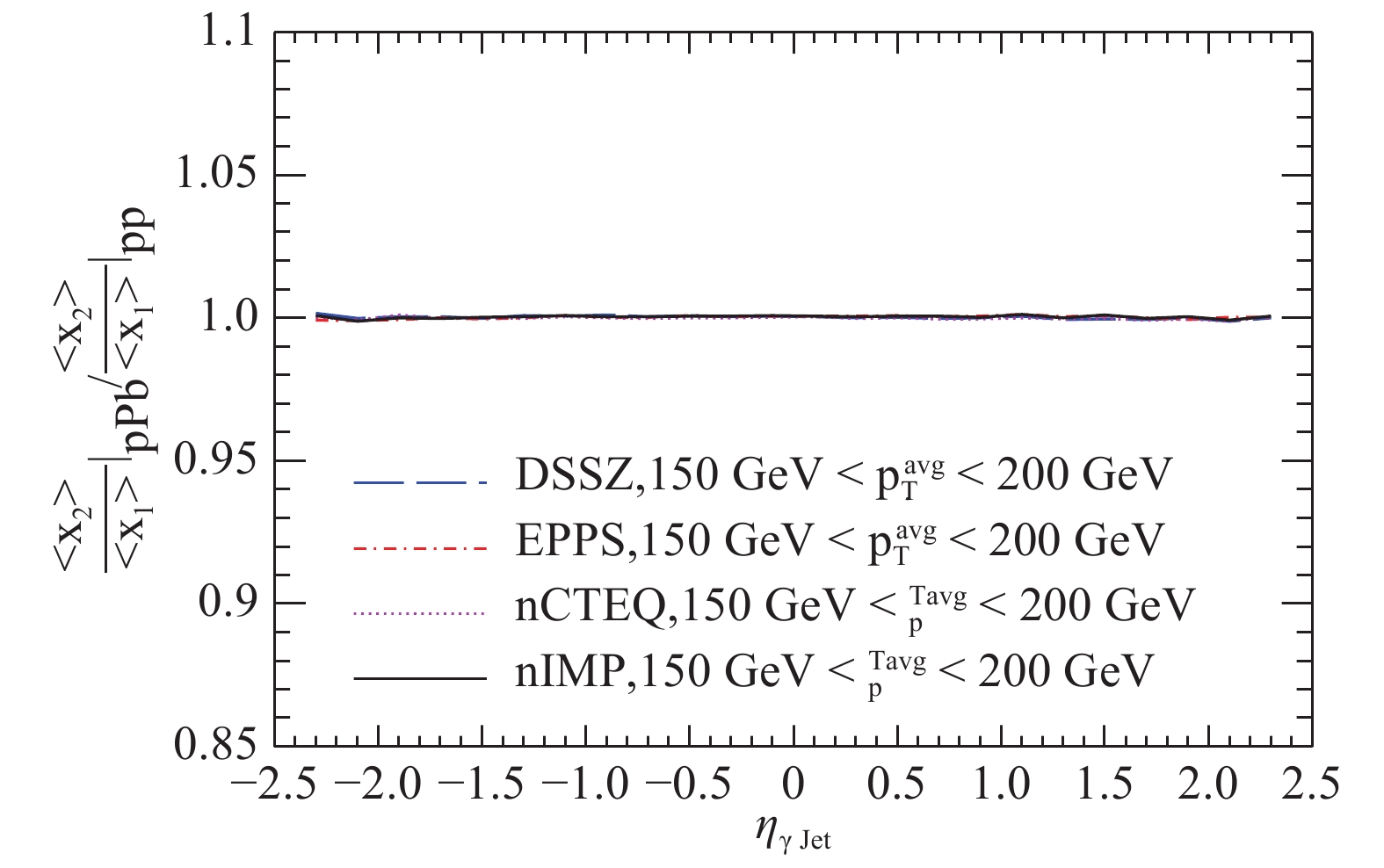
Figure 9. (color online) Ratio of
$\langle x_2\rangle/\langle x_1\rangle$ in p$+$ Pb and p$+$ p collisions as a function of$\rm\eta_{\gamma jet}$ , considering different CNM effects descriptions.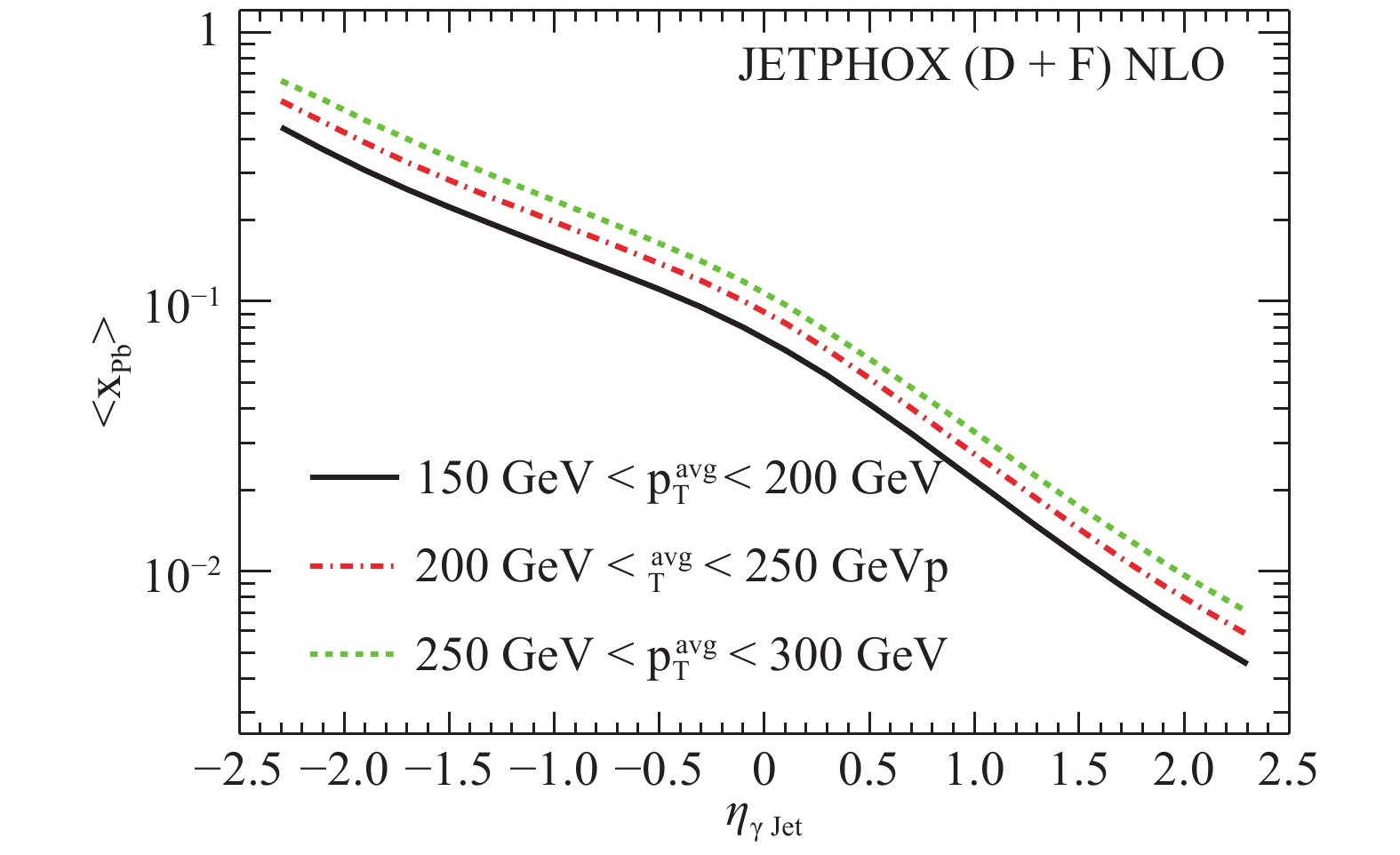
Figure 10. (color online) Mean Bjorken x of the parton from the lead ion
$x_{\rm Pb}$ obtained from JetPhox as a function of$\rm\eta_{\gamma jet}$ in different$\gamma+$ jet events'$p_{\rm T}^{\rm avg}$ intervals.Furthermore, we discuss the nuclear modification factor for
$ \gamma+ $ jet production as a function of$ \rm \eta_{\gamma jet} $ at 115 GeV$ <p_{\rm T}^{\rm avg}< $ 4000 GeV, shown in Fig. 11, and 200 GeV$ <p_{\rm T}^{\rm avg}< $ 250 GeV, shown in Fig. 12. We have roughly estimated that the nuclear modification factor is sensitive to shadowing when$ \rm \eta_{\gamma jet}>1.6 $ and is sensitive to the EMC effect when$ \rm \eta_{\gamma jet}<-0.2 $ . In the total average transverse momentum interval (115 GeV$ <p_{\rm T}^{\rm avg}<$ $ 4000 $ GeV), we found that nIMParton offers the strongest shadowing effect, EPPS16 has the most predominant anti-shadowing effect and EMC effect, and the effects shown by DSSZ are between those of nIMParton and EPPS16. Meanwhile, nCTEQ15 provides a nearly constant suppression when$ \rm \eta_{\gamma jet} $ varies. When the average transverse momentum interval is limited to 200 GeV$ <p_{\rm T}^{\rm avg}<$ 250 GeV, the shadowing of nCTEQ15 starts to restore, and it remains flattened at small$ \rm \eta_{\gamma jet} $ and large average Bjorken$ \langle x_{\rm Pb}\rangle $ . The shadowing of nIMParton and EPPS16 becomes more damped, EPPS16 has a clearer anti-shadowing peak, and nIMParton and DSSZ begin to reveal anti-shadowing peaks. DSSZ provides the strongest EMC suppression in this situation. It is emphasized that by leveraging the rapidity and transverse momentum of both photon and jets with measured$ p_{\rm T}^{\rm avg} $ and$ \rm \eta_{\gamma jet} $ , we can access CNM effects in a wide regime and also allocate different kinematics precisely, where the differences among varieties of nPDF sets may be investigated more effectively.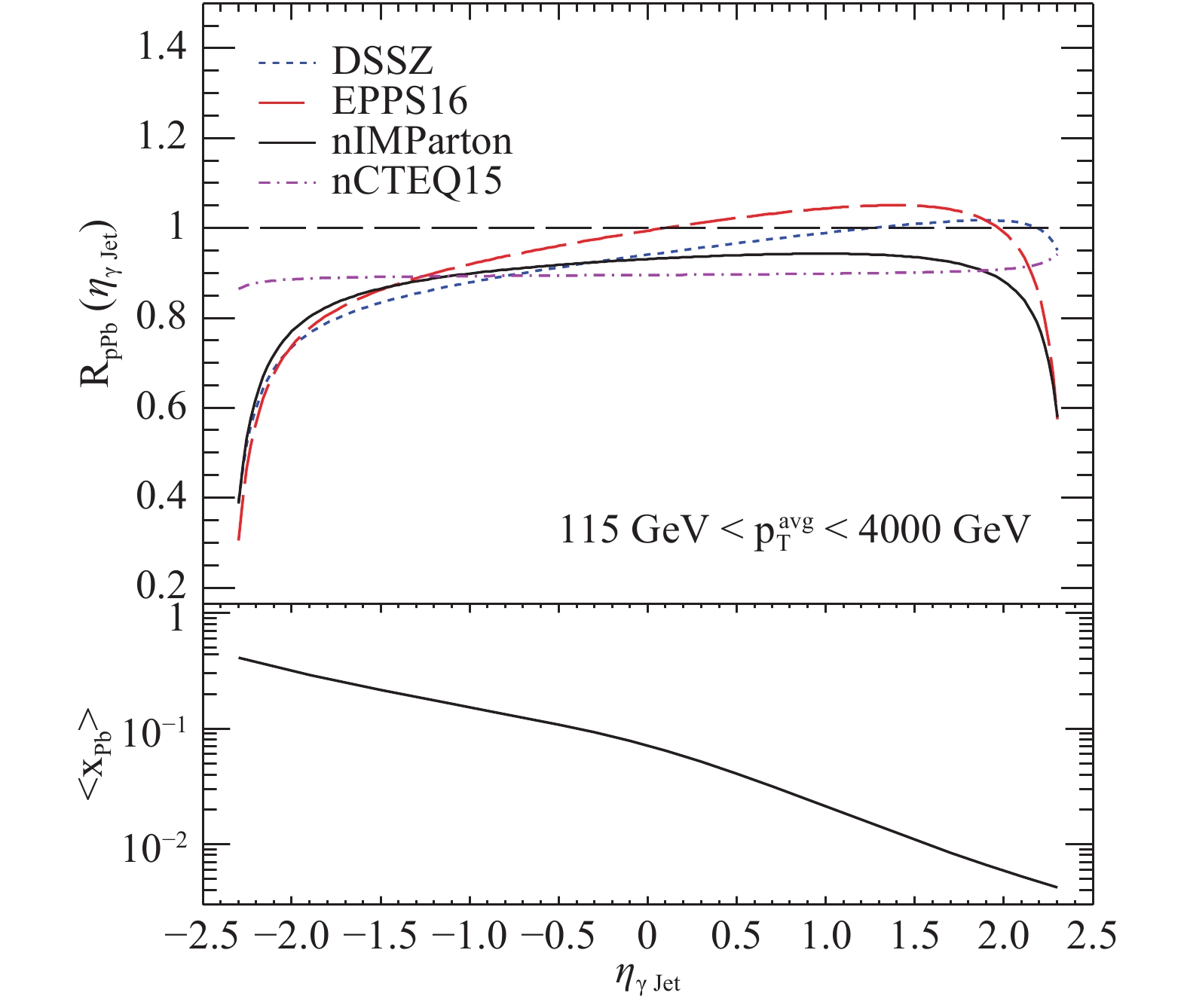
Figure 11. (color online) (Upper) Nuclear modification factor for
$\gamma+$ jet production as a function of$\rm\eta_{\gamma jet}$ at 115 GeV$ <p_{\rm T}^{\rm avg}<$ 4000 GeV. The NLO pQCD calculation is based on JetPhox with nCTEQ15, EPPS16, DSSZ, and nIMParton as the nPDFs. (Bottom) Corresponding average Bjorken$\langle x_{\rm Pb}\rangle$ as function of$\rm \eta^{\gamma Jet}$ .
Figure 12. (color online) Same as Fig. 11, except for at 200 GeV
$<p_ {\rm{T}}^{\rm{avg}}<250$ GeV -
We calculate the productions of isolated prompt photon and
$ \gamma + $ jet in p+A with CNM effects from four sets of nPDF parameterizations, i.e., DSSZ, EPPS16, nCTEQ15, and nIMParton, by utilizing the NLO pQCD approach (nIMParton at LO) at LHC$ 8.16 $ TeV. We present the nuclear modification ratio of isolated prompt photon$ R_{\rm pA}^{\gamma}(p_{\rm T}^{\gamma}) $ and$ R_{\rm pA}^{\gamma}(\eta^{\gamma}) $ , and that the find shadowing effect and EMC effects dominate at the very forward- and backward-rapidity regions, respectively. The prompt photon nuclear modification ratio shows weak rapidity dependence in the forward region and varies linearly in the backward-rapidity region. The production of the isolated photon associated with jet gives us the leveraged power to study the tomography of CNM, and the CNM effects of$ \gamma $ +jet productions could be intuitively presented in the constrained rapidity$ \rm\eta_{\gamma jet} $ and average transverse momentum$ p_{\rm T}^{\rm avg} $ region in our discussion. In terms of sensitivity, comparisons of the CNM contribution of four different nPDF parameterizations have been exhibited, and nCTEQ15 shows peculiar results compared to the others, which could extend our understanding of the constraints of different nPDF descriptions. It is noted that the nPDF parametric form (nIMParton) proposed by the Institute of Modern Physics in China has been applied for the first time to investigate hard processes in ultrarelativistic heavy-ion collisions, with a comparison against the predictions of three other mainstream nPDF groups.
Probing cold nuclear matter effects with the productions of isolated-${\gamma} $ and ${\gamma} $ +jet in p+Pb collisions at ${\sqrt{{s}_{{NN}}}}= $ 8.16 TeV
- Received Date: 2019-01-19
- Available Online: 2019-04-01
Abstract: We investigate cold nuclear matter (CNM) effects on the productions of isolated prompt photons and







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

























 DownLoad:
DownLoad: