-
The pseudo-spin symmetry (PSS), first discovered in spherical nuclei [1, 2] and later in deformed nuclei [3, 4], corresponds to the quasi-degeneracy of two single-particle orbits
$ (n, l , j = l+1/2) $ and ($ n -1, l+2 $ ,$ j = l+3/2 $ ), namely the pseudo-spin partners$ j_\gtrless = \tilde l \pm 1/2 $ with$ \tilde l = l+1 $ . Since the discovery of PSS, intensive efforts have been devoted to exploring the origin and conservation condition of PSS in the past decades [5-11]. Until the end of last century, the PSS was recognized as a relativistic symmetry [5]. The conservation condition of PSS is that the sum of the scalar$ S(r) $ and vector$ V(r) $ potentials in the single-particle Dirac equation equals to zero, i.e.,$ V(r)+S(r) = 0 $ [5]. Subsequently, it was demonstrated that the exact PSS can be deduced with the condition$ {\rm d}(V+S)/{\rm d}r = 0 $ [8], and further, a new relativistic model that fulfils this condition with bound single-particle states was proposed in Ref. [12]. Moreover, it became well-known that the orbital angular momentum$ \tilde l $ is indeed the one of the lower components of the Dirac spinors [5]. Thereafter, the PSS was also tested in deformed nuclei [13] and resonant states [14, 15] within the relativistic frame. Furthermore, the conservation condition leads to rather precisely preserved spin symmetry (SS) in the anti-nucleon spectra, which indeed shares the origin with the PSS in nuclear single particle spectra [16]. As revealed by the conservation conditions, both the PSS and SS reflect an important aspect of nuclear dynamics, which benchmarks our understanding of the nuclear structure properties.Over the past few decades, worldwide rapid development of the radioactive ion beam (RIB) facilities and detector systems has brought about the revolution in nuclear physics and largely enriched our knowledge of the atomic nucleus, ranging from the stable nucleus to the one far from its stability valley. When approaching the neutron/proton drip lines, unexpected characteristic structures, such as new magic numbers, can arise [17]. For example, the neutron magicity
$ N = 16 $ is observed in the drip-line doubly magic nucleus 24O [18]. More recently, new magicities at$ N = 32 $ and$ N =34 $ in calcium isotopes were implied by experimental evidence, such as the rather high excitation energy of the$ 2_1^+ $ state and high precision mass measurements [19-24]. The occurrence of new magicities at$ N = 32 $ and$ N =34 $ was further supported by the ab-initio calculations [25, 26], shell model [23, 27], and some energy density functions with the tensor force [28–30]. Specifically it was suggested that the nuclear tensor force may play a role in the occurrence of the$ N = 32 $ magicity in 52Ca [30]. Most recently, the opening of$ N = 34 $ magicity was considered to be related to the emergence of the bubble-like structure in the predicted doubly magic drip line nucleus 48Si [31] that generally leads to certain PSS violation [7, 8, 32, 33]. This inspired our interests to explore the restoration of PSS in the relevant nuclei, particularly with the$ N = 32 $ and$ N =34 $ isotones.Relativistically, the description of nuclear dynamics in the ground state can be achieved with the meson exchange diagram of nuclear force [34], following the spirit of density-functional theory [35, 36]. This leads to the well-known covariant density-functional (CDF) theory, including its main branches - the relativistic mean field (RMF) [33, 37-40] and relativistic Hartree-Fock (RHF) [30, 31, 41–48] theories, which have provided successful descriptions of nuclear structure properties for nuclei in the entire nuclear chart. Aiming at the
$ N = 32 $ and$ N =34 $ isotones, we restrict ourselves within the RHF theory, as the presence of Fock terms has brought significant improvements in numerous aspects, including the self-consistent description of shell evolution [47, 49–51], nuclear tensor force [49, 51-54], appropriate restoration of PSS [10, 30, 47, 48, 55], nuclear spin-isospin excitations [56, 57],$ \beta $ -decay properties [58], etc. Particularly, with the RHF Lagrangian PKA1 [48], in which the$ \pi $ - and$ \rho $ -tensor couplings are taken into account, the new magicities of$ N = 32 $ and$ N =34 $ in 52, 54Ca can be well reproduced, consistently with the experimental evidence and other theoretical calculations. Thus far, the RHF-PKA1 is the only covariant density functional that can interpret self-consistently the occurrence of both new magicities$ N = 32 $ and$ N =34 $ .In present work, we will focus on the restoration of PSS along the isotonic chains of
$ N = 32 $ and$ N =34 $ and the physics behind, by adopting the RHF calculations with the Lagrangian PKA1. The contents are organized as follows. In Section 2, the general formalism of the radial Dirac equation and the corresponding Schrödinger-like equation is provided. In Section 3, the restoration of PSS along the$ N = 32 $ and$ N =34 $ isotonic chains is studied, taking the proton pseudo-spin doublet ($ \pi2s_{1/2} $ ,$ \pi1d_{3/2} $ ) as an example, and the physics is discussed in detail. Finally, a brief summary is provided in Section 4. -
Spherical symmetry is assumed for the
$ N = 32 $ and$ N =34 $ isotones in this study. Some of the selected isotones are potentially deformed, however, the restriction of spherical symmetry is applied for simplicity and convenience in revealing the physics of the PSS violation and restoration. With the assumption of spherical symmetry, similar systematics of violation and restoration of the PSS are found for both$ N = 32 $ and$ N =34 $ isotones, and following the similar density evolutions, the mechanism is clarified.For a spherical nucleus, the Dirac spinor of the nucleon is expressed as follows,
$ \begin{align} \psi ( r) = & \dfrac{1}{r} \begin{pmatrix} i G (r) {\cal Y}_{j m }^{l }(\vartheta,\varphi) \\ -F (r) {\cal Y}_{j m }^{l '}(\vartheta,\varphi) \end{pmatrix}, \end{align} $

(1) where
$ G(r) $ and$ F(r) $ denote the radial wave functions for the upper and lower components, respectively, and$ {\cal Y}_{jm}^l $ is the spherical spinor with angular momentum$ j $ and the projection$ m $ . For the orbital angular momenta$ l $ and$ l' $ of the upper and lower components,$ l+l' = 2j $ holds true. As mentioned above, pseudo-spin partners share the orbital angular momentum$ l' $ of the lower component.In the RHF approach, restricted to the spherical symmetry, the variation of the RHF energy functional [59] leads to the radial Dirac equations, i.e., the relativistic Hartree-Fock equations as follows,
$ \begin{split} E G(r) =& - \Big[\dfrac{\rm d}{{\rm d}r} - \dfrac{\kappa}{r} - \Sigma_T(r)\Big] F(r) \\&+ \big[\Sigma_0(r) + \Sigma_S(r)\big] G(r) + Y(r), \end{split} \tag{2a} $

(2a) $ \begin{split} EF(r) =& + \Big[\dfrac{\rm d}{{\rm d}r} + \dfrac{\kappa}{r} + \Sigma_T(r)\Big] G(r) \\&+ \big[\Sigma_0(r) - \Sigma_S(r)-2M\big] F(r) + X(r),\end{split} \tag{2b} $

(2b) where
$ E $ is the single-particle energy,$ \kappa = j+1/2 $ for$ j = l-1/2 $ and$ -(j+1/2) $ for$ j = l+1/2 $ , and$ \Sigma_0 $ ,$ \Sigma_S $ and$ \Sigma_T $ are the vector, scalar, and tensor self-energies contributed by the Hartree and rearrangement terms [41, 44, 47, 48, 59]. Differently from the RMF theory, the inclusion of Fock terms leads to the non-local integral terms$ Y $ and$ X $ [41, 59], and the radial Dirac equation becomes an integro-differential expression. To avoid the complexity in solving the integro-differential equation, the non-local integral term$ Y $ is localized as$ \begin{align} Y_G(r) \equiv & \dfrac{Y(r) G(r)}{G^2(r) + F^2(r)}, & Y_F(r) \equiv & \dfrac{Y(r) F(r)}{G^2(r) + F^2(r)}, \end{align} $

(3) The term
$ X $ is likewise localized with equivalent local potentials$ X_G $ and$ X_F $ [41]. Thus, the radial Dirac equation (2) can be expressed as,$ \Big[\dfrac{{\rm d}}{{\rm d}r} - \dfrac{\kappa}{r} - \Sigma_T - Y_F\Big]F - \big[\Delta - E\big]G = 0, \tag{4a} $

(4a) $ \Big[\dfrac{{\rm d}}{{\rm d}r} + \dfrac{\kappa}{r} + \Sigma_T + X_G\Big]G + \big[V - E\big]F = 0, \tag{4b} $

(4b) where
$ \Delta \equiv \Delta^D + Y_G $ with$ \Delta^D \equiv \Sigma_S + \Sigma_0 $ , and$ V \equiv V^D + X_F $ with$ V^D\equiv \Sigma_0 - \Sigma_S - 2M $ .Since the PSS is tightly related to the lower component of the Dirac spinor, it is convenient in general to derive a Schrödinger-like equation for the
$ F $ component [8, 10], which can be expressed as,$ \begin{align} &\dfrac{1}{V^D - E} \dfrac{{\rm d}^2}{{\rm d}r^2} F + \dfrac{1}{V^D-E} \big[V_{\rm PCB} + \hat{\cal{V}}^D + \hat{\cal{V}}^E \big] F = E F, \end{align} $

(5) where the pseudo centrifugal barrier
$ V_{\rm PCB} $ , and the Hartree ($ \hat{\cal V}^D $ ) and Fock ($ \hat{\cal V} ^E $ ) terms read as,$ \begin{align} &V _{\rm PCB} = - \dfrac{\kappa(\kappa - 1)}{r ^2}, \end{align} $

(6) $ \begin{align} &\hat{\cal{V}}^D = V_1^D \dfrac{{\rm d}}{{\rm d}r} + V_2^D + V^D_{\rm{PSO}} + V_\Delta, \end{align} $

(7) $ \begin{align} &\hat{\cal{V}}^E = V_1^E \dfrac{{\rm d}}{{\rm d}r} + V_2^E + V^E_{\rm{PSO}}. \end{align} $

(8) In the Hartree (
$ \hat{\cal V}^D $ ) and Fock ($ \hat{\cal V}^E $ ) terms, the relevant terms read as,$ \begin{align} &V_1^D = -\dfrac{1}{\Delta-E} \dfrac{{\rm d}\Delta^D}{{\rm d}r}, \end{align} $

(9) $ \begin{align} &V_2^D = \dfrac{ \Sigma_T }{\Delta-E} \dfrac{{\rm d}\Delta^D}{{\rm d}r} - \dfrac{{\rm d}\Sigma_T}{{\rm d}r} - \Sigma_T^2, \end{align} $

(10) $ \begin{align} &V_{\rm{PSO}}^D = \dfrac{\kappa}{r} \Big[\dfrac{1}{\Delta-E} \dfrac{{\rm d}\Delta^D}{{\rm d}r}- 2 \Sigma_T \Big], \end{align} $

(11) $ \begin{align} &V_{\Delta} = \Delta ^D (V ^D - E), \end{align} $

(12) $ \begin{align} &V_1^E = -\dfrac{1}{\Delta-E} \dfrac{{\rm d}Y_G}{{\rm d}r} + X_G - Y_F, \end{align} $

(13) $ \begin{split} V_2^E =& \dfrac{1}{\Delta-E} \dfrac{{\rm d}Y_G}{{\rm d}r} \Sigma_T + \dfrac{1}{\Delta-E} \dfrac{{\rm d}\big(\Delta^D+Y_G\big)}{{\rm d}r} Y_F \\ & - \dfrac{{\rm d}Y_F}{{\rm d}r} - \Sigma_T \big[X_G+Y_F\big] - X_G Y_F \\& + (V^D - E) Y_G + X_F (\Delta - E), \end{split} $

(14) $ \begin{align} V_{\rm{PSO}}^E = \dfrac{\kappa}{r} \Big[\dfrac{1}{\Delta-E} \dfrac{{\rm d}Y_G}{{\rm d}r} - X_G - Y_F\Big], \end{align} $

(15) where
$ V_{\rm{PSO}} $ corresponds to the pseudo-spin orbital (PSO) potential. Similarly to Ref. [10], the following integral is introduced to evaluate the contributions from various channels to the single-particle energy$ E $ ,$ \begin{align} \dfrac{1}{\int_0^\infty F^2 {\rm d}r} \int_0^\infty \dfrac{F \hat{O} F}{V^D - E} {\rm d}r, \end{align} $

(16) where
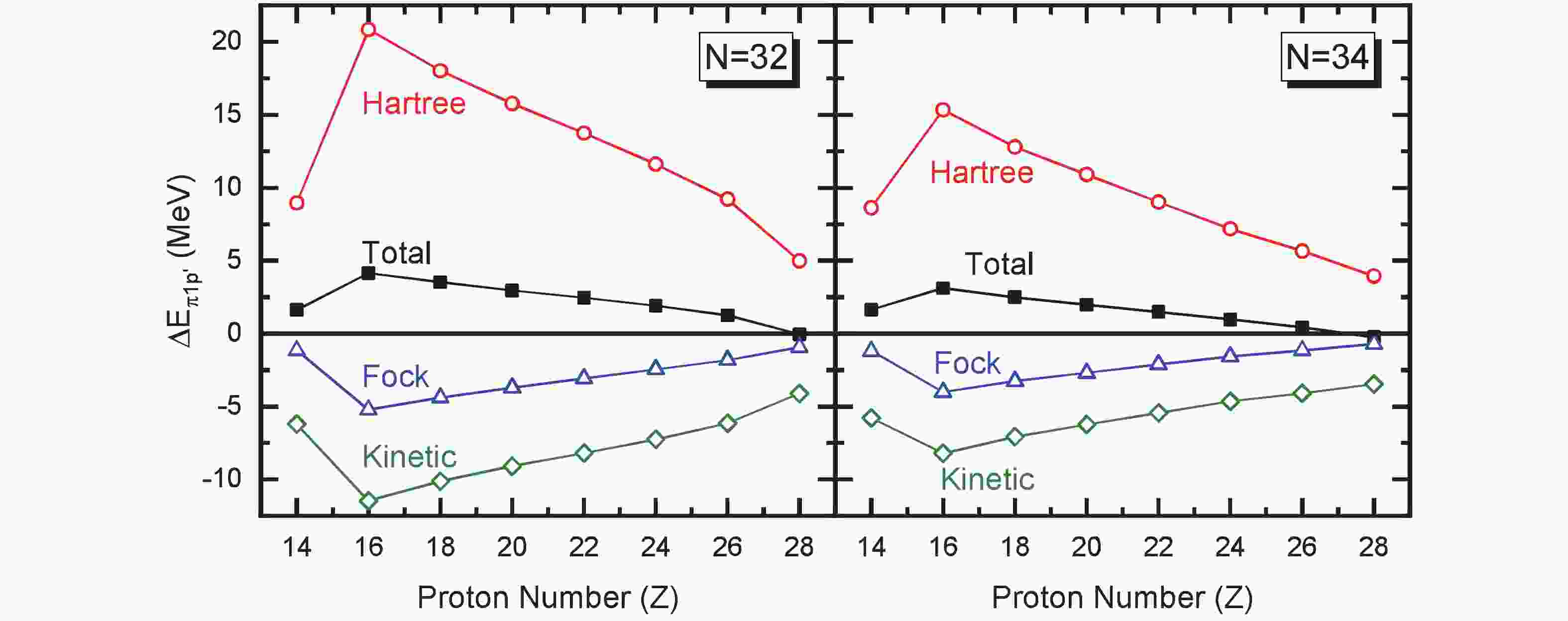
$ \hat O $ represents the operator in different channels. Specifically, the kinetic term (see Fig. 3) corresponds to$ \hat O = {\rm d}^2/{\rm d}r^2 + V_{\rm PCB} $ .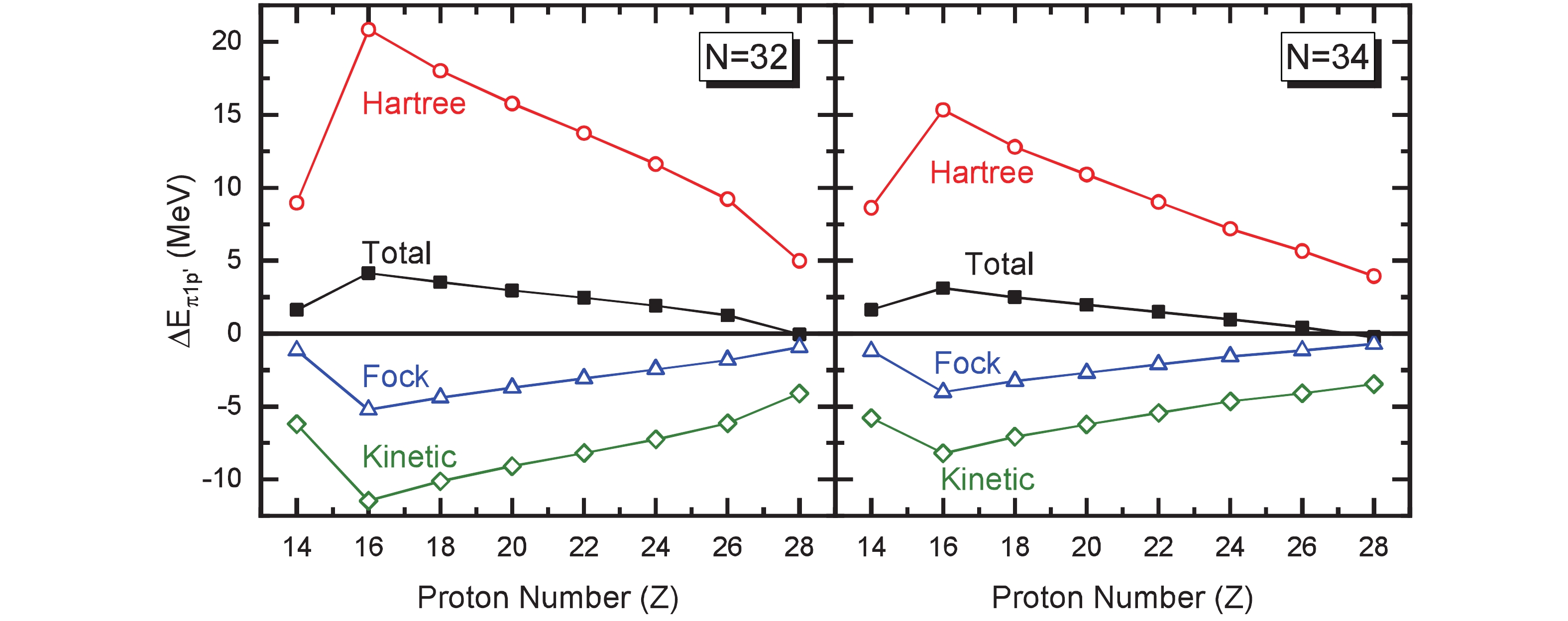
Figure 3. (color online) Contributions to the pseudo-spin orbital splittings
$\Delta E_{\pi1p'}$ along the isotonic chains of$N = 32$ (left panel) and$N = 34$ (right panel), including the total and the ones from the Kinetic, Hartree, and Fock terms. The results are extracted from the calculations of RHF with PKA1 plus finite-range pairing force Gogny D1S. -
In this study, we focus on the even-even
$ N = 32 $ and N =$ 34 $ isotones from Si ($ Z = 14 $ ) to Ni ($ Z = 28 $ ). The calculations are performed within the relativistic Hartree-Fock (RHF) scheme by imposing spherical symmetry to all selected nuclei. The RHF mean fields are evaluated by the covariant density-functional with Fock terms PKA1 [48], which takes the one-pion exchange and$ \rho $ -tensor couplings into account using the Fock terms and interprets successfully the new magicities$ N = 32 $ and$ N =34 $ in calcium [30]. Moreover, with the presence of Fock terms, the important ingredient of nuclear force—tensor force is naturally included [52, 53].For the open-shell isotones, pairing correlations are handled with the BCS approximation, and the pairing force is adopted as the finite-range Gogny D1S [60] to have a natural energy cutoff. Although some isotones such as
$ ^{48}{\rm Si} $ are located at the neutron drip line, the BCS pairing with the finite-range pairing force Gogny D1S can still provide reasonable evaluation for the structure properties of the relevant exotic nuclei due to the predicted magicities [31]. In fact, the calculations with the Bogoliubov pairing [40, 61-65], by the relativistic Hartree-Fock-Bogoliubov (RHFB) theory [47], present similar systematics of the PSS restoration along the selected isotonic chains. Such consistency is not very surprising. Because of the predicted neutron and proton magic shells in 48Si [31], little continuum effect is involved, which indeed plays an essential role in other exotic nuclei, such as for the halo formation [62-65]. In contrast, localization of the non-local integral terms [see Eq.(3)] fails in solving the RHFB equation directly, which is instead solved by expanding the quasi-particle wave functions on the Dirac Woods-Saxon basis [47, 66]. Technically, it is more convenient and straightforward to understand the physics in the PSS restoration under the BCS scheme.Figure 1 shows the proton (
$ \pi $ ) single-particle energies along the isotonic chains of$ N = 32 $ and$ N =34 $ from silicon to nickel, and the results are obtained by the RHF theory with PKA1 plus the finite-range pairing force Gogny D1S. Fig. 1 shows that single-particle energies monotonously increase with respect to the proton number Z, except the$ \pi2s_{1/2} $ orbits, which become more strongly bound from silicon to sulphur. As a consequence of the abnormal behavior of$ \pi2s_{1/2} $ , the sub-shell$ Z = 14 $ , the new magic shell confirmed experimentally in 34Si [67] and predicted theoretically in 48Si [31], is quenched significantly, leading to the emergence of a remarkable sub-shell$ Z = 16 $ in 48S ($ N = 32 $ ) and less remarkable one in$ ^{50}{\rm S} $ ($ N = 34 $ ), deduced from the distinct violation of PSS for the doublet$ (\pi2s_{1/2}, \pi1d_{3/2}) $ . Subsequently from sulphur to nickel, the PSO splitting between$ \pi2s_{1/2} $ and$ \pi1d_{3/2} $ monotonously decreases with the proton number, eventually presenting appropriate restoration of the PSS at 60, 62Ni.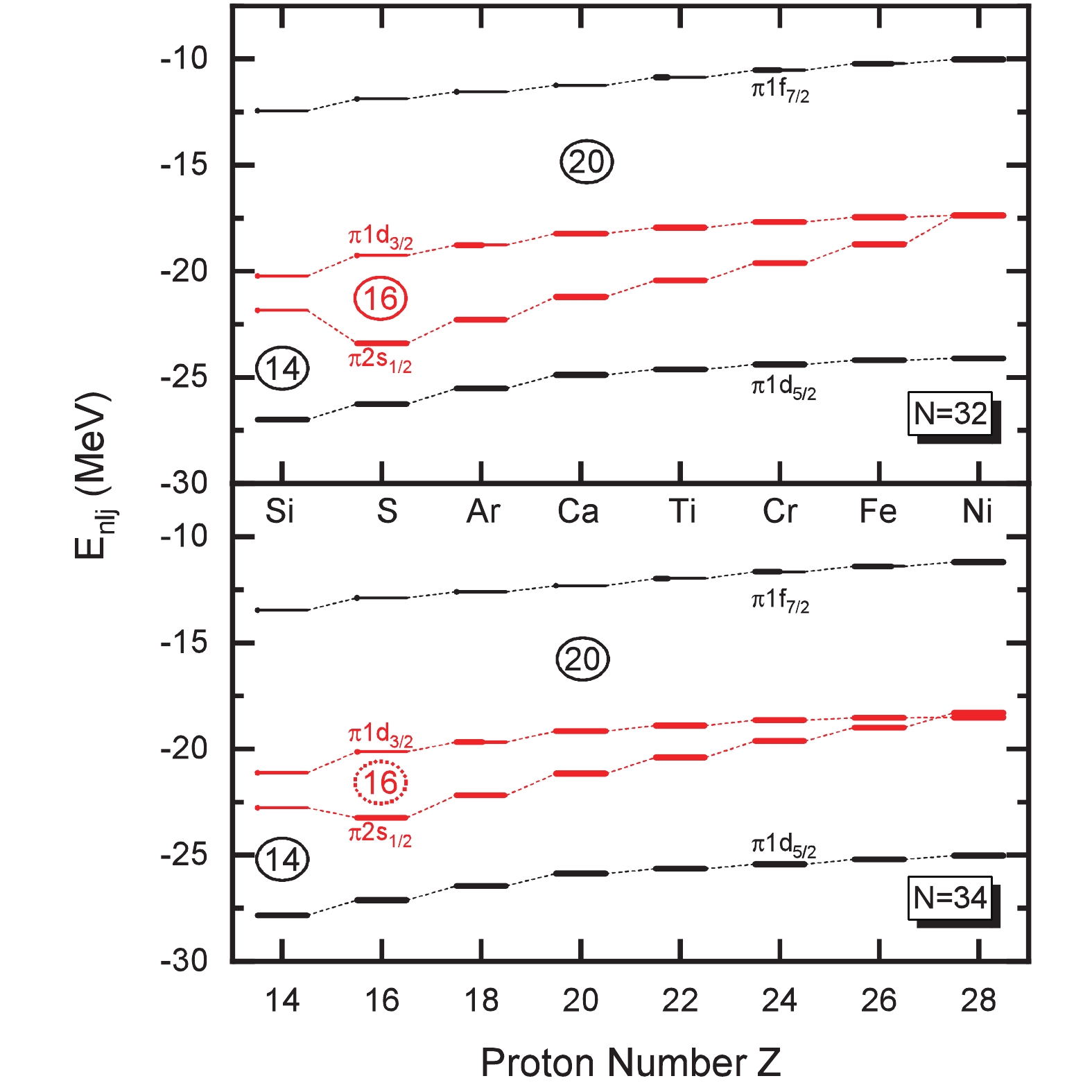
Figure 1. (color online) Proton single-particle energies of N = 32 (upper panel) and N = 34 (lower panel) isotones from Si to Ni, where the thick bars denote occupation probabilities. The results are extracted from the calculations of RHF with PKA1 [48], in which the pairing correlations are considered with the BCS approximation and the finite-range pairing force Gogny D1S [60].
As seen from Fig. 1 shows that the proton valence orbits for the selected isotones are the pseudo-spin partners
$ (\pi2s_{1/2}, \pi1d_{3/2}) $ and$ \pi1f_{7/2} $ , which contain the$ j = l-1/2 $ and$ j = l+1/2 $ orbits. For the neutron valence orbits, mainly the spin partners$ \nu2p $ and the state$ \nu1f_{5/2} $ , of the single-particle configuration is slightly changed because of the pairing effects in some open-shell isotones. Thus, it is naturally expected that the tensor force might play a role in PSS restoration due to its characteristic nature – the spin dependence [30, 47, 49, 52, 68]. Starting from the Dirac equation (2), Fig. 2 shows the evolution of pseudo-spin orbital splittings of the doublets$(\pi2s_{1/2}, $ $ \pi1d_{3/2}) $ , denoted as$ \Delta E_{\pi1p'} = E_{\pi1d_{3/2}} - E_{\pi2s_{1/2}} $ , along the$ N = 32 $ and$ N =34 $ isotonic chains. Distinctive PSS violation is found in both$ N = 32 $ and$ N =34 $ isotones of sulphur, while towards nickel the PSS becomes well restored, even leading to the inversion of$ sd $ orbits. With the relativistic formalism proposed in Ref. [52] and implemented in Ref. [53], the contributions from the tensor force components, which are naturally introduced by the Fock terms, are extracted and depicted with open symbols in Fig. 2. Being consistent with the nature of the tensor force and the systematics of the proton configurations shown in Fig. 1, the tensor contributions to the pseudo-spin orbit splitting$ \Delta E_{\pi1p'} $ are weakened when approaching the spin-saturated proton$ Z = 20 $ , namely 52,54Ca. Afterwards, such effects tend to be enhanced as protons become spin-unsaturated. Nevertheless, the tensor force cannot account for the overall systematics of the PSS restoration along both isotonic chains, which only partially interprets the evolution of$ \Delta E_{\pi1p'} $ from calcium to nickel.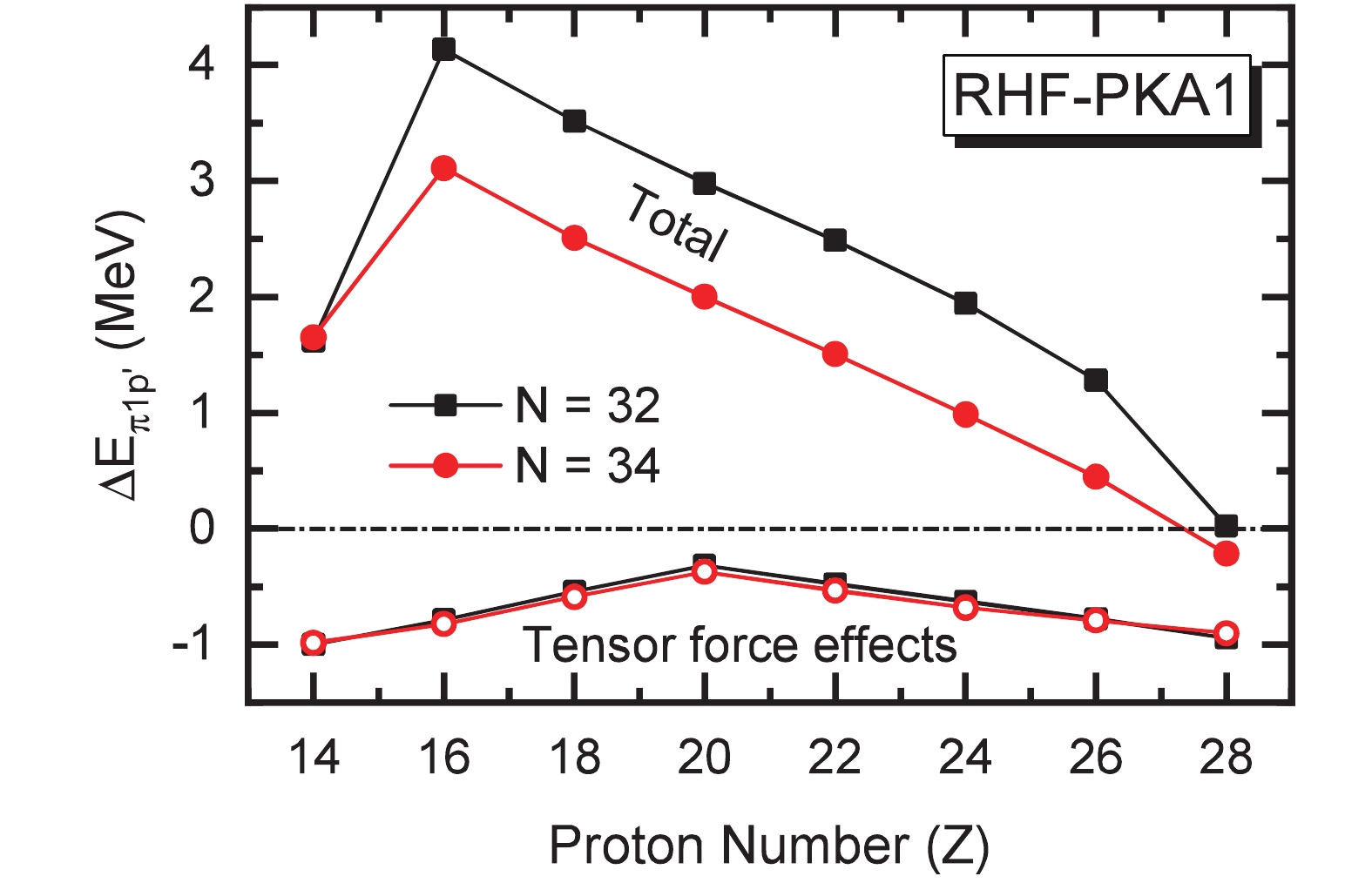
Figure 2. (color online) Evolution of pseudo-spin orbit splitting
$\Delta E_{\pi 1p'} = E_{\pi2s_{1/2}}- E_{\pi1d_{3/2}}$ along the isotonic chains of$N = 32$ and$N = 34$ , where open symbols represent contributions from tensor forces. The results are extracted from the calculations of RHF with PKA1 and finite-range pairing force Gogny D1S.To better understand the overall evolution of
$ \Delta E_{\pi1p'} $ along both isotonic chains in Fig. 2, particularly for the distinct violation of PSS at sulphur, the radial Dirac equation is reduced into a Schrödinger-like equation for the lower component of the Dirac spinor, as the authors did in Eq. (5) of Refs. [8, 10]. This can provide quantitative evaluation of the contributions to$ \Delta E_{\pi1p'} $ from various channels. In practice, the contributions are detailed as the kinetic, Hartree, and Fock terms, and the obtained results are given in Fig. 3, showing similar systematics for$ N = 32 $ (left panel) and$ N =34 $ (right panel) isotones. Fig. 3 shows that the overall evolution of$ \Delta E_{\pi1p'} $ , including the distinct violation at sulphur, is largely determined by the Hartree terms, which are partially canceled by the kinetic and Fock terms. Such results are not surprising, since the tensor force, that contributes via the Fock terms, does not play the expected role. The PSS as a relativistic symmetry originates from the large cancellation between the strong scalar and vector fields, namely$ V+S = 0 $ [5] or$ {\rm d}(V+S)/{\rm d}r = 0 $ [8]. Although with the presence of Fock terms, the situation becomes more complicated in the RHF theory [10], the Lorentz covariance remains and the opposite behaviors between Hartree and Fock terms in Fig. 3 are simply due to the opposite sign from the anti-commutation relation of Fermions.From Fig. 3 interprets the overall systematics of
$ \Delta E_{\pi1p'} $ quite well. Meanwhile, the puzzle remains regarding why the distinct PSS violation appears from silicon to sulphur for both$ N = 32 $ and$ N =34 $ isotones. In further exploration, Fig. 4 shows the proton density profiles of silicon, sulphur, calcium, chromium, and nickel, as well as the mean field potentials$ \Delta ^D = \Sigma_S+\Sigma_0 $ whose radial derivatives together with$ \kappa $ -quantities dominate the strength of pseudo-spin orbital couplings. The proton density profiles of 46,48Si are distinctly central-depressed, because the$ \pi2s_{1/2} $ orbits are empty, as shown in Fig. 1. Such semi-bubble structure, as a quantum effect, can be reduced by correlations beyond the mean field. For instance, if the$ s $ -state is close enough to the last occupied one, the pairing correlations [69-72], as well as the multi-reference framework beyond mean field [73, 74], may lead to a substantially occupied$ s $ -state that can wash out the central depletion. The sizes of the energy gaps$ Z = 14 $ in 46,48Si (see Fig. 1) are large enough to assess the prediction of a bubble-like structure. With the$ \pi2s_{1/2} $ orbits are fully occupied in 48,50S, the density profiles become distinctly central-bumped. Consequently, the mean field potentials$ \Delta^D $ in 48,50S are deepened remarkably. Although the Coulomb repulsion is considerably enhanced from silicon to sulphur, the deepened mean field potential leads to a deeper bound$ \pi 2s_{1/2} $ in sulphur, as seen in Fig. 1, because the$ s $ orbits, without the blocking of centrifugal repulsion, can strongly couple with the interior region of$ \Delta^D $ . In contrast, the$ \pi 1d_{3/2} $ orbits in 48,50S, with strong centrifugal repulsion, are less bound than in 46,48Si. Thus, the pseudo-spin orbital splitting$ \Delta E_{\pi 1p'} $ is significantly enlarged from silicon to sulphur.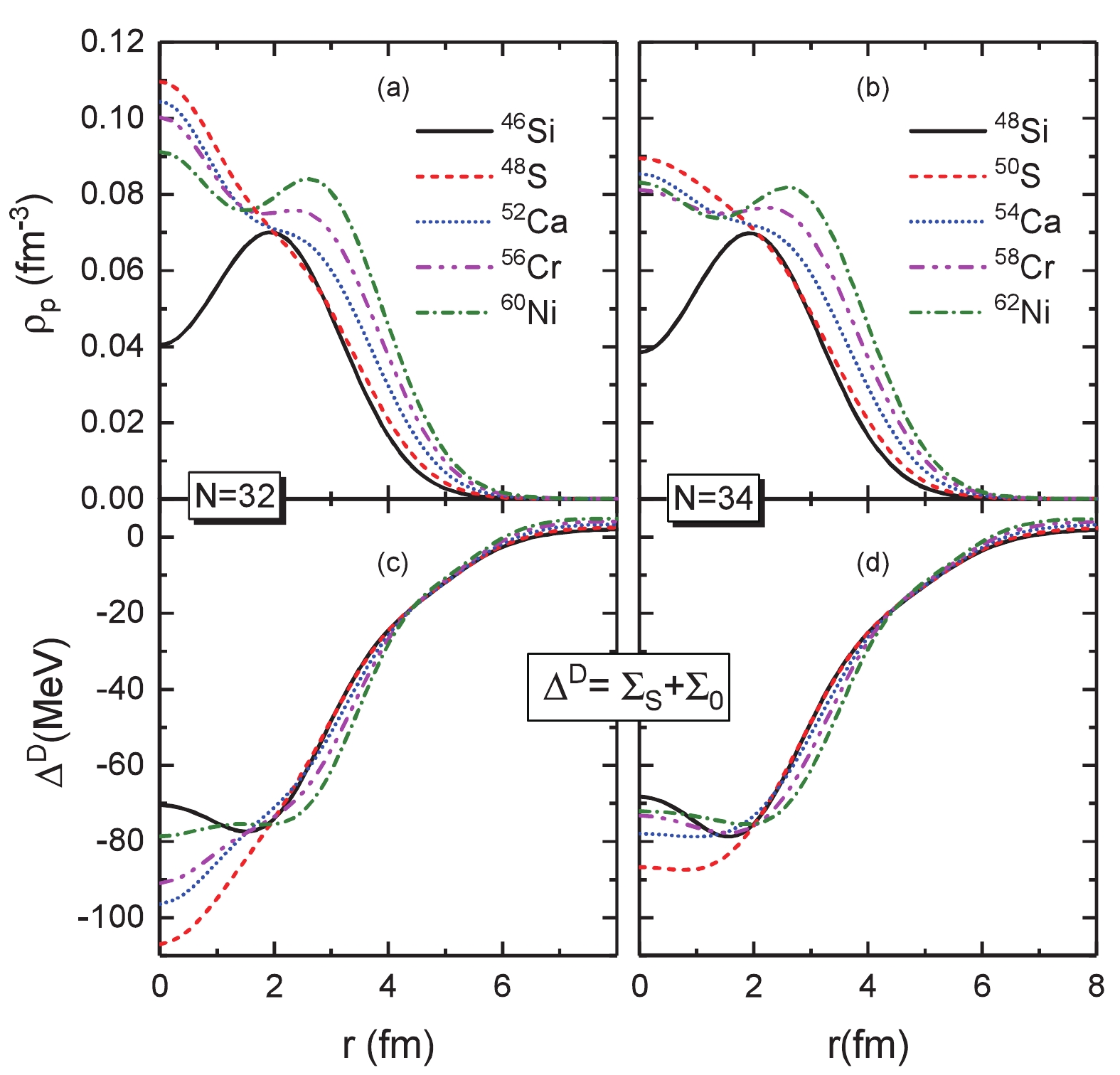
Figure 4. (color online) Proton densities [plots (a,b)] and mean field potential
$\Delta^D = \Sigma_S + \Sigma_0$ [plots (c, d)] of the selected$N = 32$ (left panels) and$N = 34$ (right panels) isotones. The results are extracted from the calculations of RHF with PKA1 with finite-range pairing force Gogny D1S.Referring to the conservation condition of the PSS, i.e.,
$ {\rm d}[V(r)+S(r)]/{\rm d}r = 0 $ , the evolution of$ \Delta E_{\pi1p'} $ from silicon to sulphur can be well understood. As shown in Fig. 4 (c), the mean field potential$ \Delta ^D $ in 46Si is consistently central-bumped with the proton semi-bubble structure [see plot (a)], which provides an cancellation to the derivative$ {\rm d} \Delta^D /{\rm d}r $ at the edge of the potential well. In contrast, with two more protons occupying the$ \pi 2s_{1/2} $ orbit, the proton density in 48S becomes central-bumped and the potential$ \Delta^D $ is consistently central-depressed, which presents distinct enhancement of the derivative$ {\rm d} \Delta^D / {\rm d}r $ . Thus, the PSO potential, which is proportional to the derivative$ {\rm d}\Delta^D/{\rm d}r $ , is increased, leading to distinctly enlarged PSO splitting$ \Delta E_{\pi1p'} $ from 46Si to 48S. To a lesser extent, a similar situation can be found in the N = 34 isotones 48Si and 50S, see Figs. 4(b) and (d). After sulphur, the valence protons gradually occupy the$ \pi1d_{3/2} $ and$ 1f_{7/2} $ orbits, and the density profiles become increasingly less central-bumped and the mean field potential$ \Delta^D $ becomes increasingly central-flat, leading to eventually well-restored PSS at nickel. Additionally, within the RMF theory, a more realistic condition, i.e.,$ V_{\rm PCB}>>V_{\rm PSO} $ , was proposed to guarantee the approximate PSS conservation in nuclei [8]. While within the RHF theory, the situation is largely changed and this condition is not fulfilled any more due to the complicated non-local mean field induced by the Fock terms [10], which has likewise been tested for the selected isotones. -
In this study, the restoration of the pseudo-spin symmetry (PSS) along the
$ N = 32 $ and N = 34 isotonic chains, as well as the driving mechanism, is studied by applying the relativistic Hartree-Fock calculations with the PKA1 and BCS approximation for the pairing correlations with the finite range pairing force Gogny D1S. In both$ N = 32 $ and$ N =34 $ isotones, a distinct violation of PSS appears from silicon to sulphur for the proton pseudo-spin doublets$ (\pi2s_{1/2}, \pi1d_{3/2}) $ , which opens the sub-shell$ Z = 16 $ in 48S. From sulphur to nickel the PSS becomes increasingly restored, leading to the inversion of$ sd $ orbits at nickel. The effects of the tensor force introduced naturally via the Fock terms can only partially interpret the restoration of the PSS from calcium to nickel, while this fails for the overall systematics along both isotonic chains. By reducing radial Dirac equation into the Schrödinger-like equation, further investigation illustrates that the overall systematics of the restoration of the PSS can be well described by the contributions of Hartree terms. Moreover, the analysis of the proton density profiles and relevant mean field potentials indicate that the PSS violation at sulphur can be attributed to dramatic changes of the bubble-like density profiles in silicon to the central-bumped ones in sulphur. Moreover, afterwards the PSS restoration can be self-consistently interpreted by increasingly central-flat density profiles from sulphur to nickel, along with consistent changes in the mean field potentials.
Restoration of pseudo-spin symmetry in N = 32 and N = 34 isotonesdescribed by relativistic Hartree-Fock theory
- Received Date: 2019-02-26
- Accepted Date: 2019-05-06
- Available Online: 2019-07-01
Abstract: The restoration of pseudo-spin symmetry (PSS) along the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: