-
The shell effect is one of the basic pillars of nuclear structure [1]. Ten nuclei with double magic numbers act as the cornerstone in the whole nuclear diagram [2]. They can play important roles in understanding nuclear structure properties [3]. The nature of the single-particle state is also important for nuclear structure studies [4]. The shell effect can be studied by measuring the ground-state binding energy with high-precision mass-measurement technology [5]. With the progress made by radioactive beams, people have found surprising evidence that closed-shell nuclei may lose their magicity in regions of extreme isospin imbalance, which gives a strong impetus to study the nuclei around tin isotopes [6].
Tin isotopes have a magic number of protons (Z = 50) and two tin isotopes have neutron magic numbers (
$ ^{100} $ Sn$ _{50} $ and$ ^{132} $ Sn$ _{82} $ ) [2]. The latter is essential for the extension of the theoretical approach to heavier and richer neutron systems.$ ^{132} $ Sn is particularly important as it is currently the only region for which spectroscopic information can be obtained around a heavy, neutron-rich nucleus with doubly closed shells away from stability [7]. The$ ^{132} $ Sn nucleus has been studied intensively both experimentally and theoretically over the last two decades [8]. It has a single-particle structure, which can provide the starting point to explore the shell evolution of neutron-rich nuclei beyond the N = 82 shell closure [9].In the theoretical discussions of Ref. [10], they calculated the
$ \Delta^{(3)} $ values along the Sn isotope chain by using density functional theory (DFT) under the SLy4 parameter with different pairing forces. They also calculated the N = 81 and 83 isotone chains. The results showed that when the assumed shapes of these nuclei were spherical,$ \Delta^{(3)} $ remained unchanged as the number of protons increased, indicating that the shape polarization effect needed to be considered. With the deformed shape obtained self-consistently,$ \Delta^{(3)} $ were two nearly parallel descending lines when the number of protons increased. The explanation for this was that the deformation effects caused by single particles or holes are similar. For N = 83 isotones, in which abnormal staggering was found (increasing with proton number), no satisfactory results were obtained. In Ref. [11], they showed that odd-even staggering (OES) can be reproduced by using realistic interactions in the shell model framework.We would like to test whether the abnormal OES behavior of binding energies in nuclei around N = 82 can be described in Skyrme DFT. The interplay of the mean-field forces and pairing forces will be investigated. More sets of Skyrme forces are used, to test the sensitivity of the mean-field potentials. The density dependence of the pairing interaction will be investigated in more details, with different approximations of pairing correlations. Thus, some combinations of the Skyrme and pairing forces may give reasonable descriptions of the mass OES in tin isotopes and abnormal behavior of OES around
$ ^{132} $ Sn. Hopefully, a more reasonable choice of pairing force might be determined.The present paper is structured as follows. We introduce the basic concepts in Sec. 2. In Sec. 3, we provide the calculations and analysis of three different pairing forces using Skyrme DFT. Conclusions are drawn in Sec. 4.
-
DFT of nuclei has extensive applications in low-energy nuclear physics [12, 13]. For a clear presentation, we repeat the formulations in the literature, related to the calculations done in this work.
To describe the system of fermions, the two-body Hamiltonian in terms of annihilation and creation operators
$ (c, c^{\dagger}) $ [14] is often used, as,$ H = \sum\limits_{n_{1}n_{2}}e_{n_{1}n_{2}}c_{n_{1}}^{\dagger}c_{n_{2}} +\frac{1}{4}\sum\limits_{n_{1}n_{2}n_{3}n_{4}} \bar{\nu}_{n_{1}n_{2}n_{3}n_{4}}c_{n_{1}}^{\dagger}c_{n_{2}}^{\dagger}c_{n_{3}}c_{n_{4}}, $

(1) where
$ \bar{\nu}_{n_{1}n_{2}n_{3}n_{4}} = \langle n_{1}n_{2}|V|n_{3}n_{4}-n_{4}n_{3}\rangle $ is the anti-symmetrized two-body matrix element.In the Hartree-Fock-Bogoliubov (HFB) approximation, the ground-state wave function
$ |\Phi\rangle $ is the quasi-particle vacuum$ \alpha_{k}|\Phi\rangle = 0 $ , in which$ (\alpha,\alpha^{\dagger}) $ are the quasi-particle operators, connected to the particle operators with the Bogoliubov transform$ \alpha_{k} = \sum\limits_{n}(U_{nk}^{\ast}c_{n}+V_{nk}^{\ast}c_{n}^{\dagger}),\; \; \; \; \alpha_{k}^{\dagger} = \sum\limits_{n}(V_{nk}c_{n}+U_{nk}c_{n}^{\dagger}), $

(2) rewritten in matrix form as
$ \left( {\begin{array}{*{20}{c}} \alpha \\ {{\alpha ^{\dagger} }} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{U^{\dagger} }}&{{V^{\dagger} }}\\ {{V^T}}&{{U^T}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} c\\ {{c^{\dagger} }} \end{array}} \right).$

(3) The generalized quasi-particle densities are formed by the particle density
$ \rho $ and the pairing tensor$ \kappa $ , as$ \begin{array}{l} \rho_{nn'} = \langle\Phi|c_{n'}^{\dagger}c_{n}|\Phi\rangle = (V^{\ast}V^{T})_{nn'},\\ \kappa_{nn'} = \langle\Phi|c_{n'}c_{n}|\Phi\rangle = (V^{\ast}U^{T})_{nn'}. \end{array} $

(4) The expectation of the Hamiltonian can be calculated as the function
$ E[\rho,\kappa] = \frac{\langle\Phi|H|\Phi\rangle}{\langle\Phi|\Phi\rangle} = {\rm Tr}\left[\left(e+\frac{1}{2}\Gamma\right)\rho\right]-\frac{1}{2}{\rm Tr}[\Delta\kappa^{\ast}], $

(5) where
$ \begin{split} \Gamma_{n_{1}n_{3}} =& \sum\limits_{n_{2}n_{4}}\bar{\nu}_{n_{1}n_{2}n_{3}n_{4}}\rho_{n_{4}n_{2}}, \\ \Delta_{n_{1}n_{2}} =& \frac{1}{2}\sum\limits_{n_{3}n_{4}}\bar{\nu}_{n_{1}n_{2}n_{3}n_{4}}\kappa_{n_{3}n_{4}}. \end{split} $

(6) Thus, the HFB equation is obtained as the variation of the energy with respect to
$ \rho $ and$ \kappa $ ,$ \left( {\begin{array}{*{20}{c}} {e + \Gamma - \lambda }&\Delta \\ { - {\Delta ^ * }}&{ - {{(e + \Gamma )}^ * } + \lambda } \end{array}} \right)\left( {\begin{array}{*{20}{c}} U\\ V \end{array}} \right) = E\left( {\begin{array}{*{20}{c}} U\\ V \end{array}} \right), $

(7) where
$ \lambda $ is the Fermi energy, acting as the Lagrange multiplier, to maintain the required average number of particles.The energy of the nucleus is the integral of the Hamiltonian density
$ {\cal{H}} (r) $ in space,$ E = \int{\rm{d}}^{3}r\,{\cal{H}}(r)\; . $

(8) The Hamiltonian density consists of the kinetic energy, potential energy
$ \chi_{t} $ , and pairing term$ \tilde{\chi}_{t} $ :$ {\cal{H}}[\rho,\kappa] = \frac{\hbar^{2}}{2m}\tau(r) +\sum\limits_{t = 0,1}\chi_{t}(r) +\sum\limits_{t = 0,1}\tilde{\chi}_{t}(r), $

(9) where the density of the kinetic energy is
$ \tau(r) $ , and the symbol$ t = 0,1 $ means isoscalar and isovector, respectively [14].For the Skyrme DFT, the particle-hole part usually has the form
$ \begin{split} \chi_{t}({{r}}) =& C_{t}^{\rho\rho}\rho_{t}^{2}+C_{t}^{\rho\tau}\rho_{t}\tau_{t}+C_{t}^{J^{2}}{\mathbb{J}}_{t}^{2}\\ &+C_{t}^{\rho\Delta\rho}\rho_{t}\Delta\rho_{t}+C_{t}^{\rho\nabla J}\rho_{t}\nabla\cdot{{J}}_{t}, \end{split} $

(10) where
$ \rho_{t} $ ,$ \tau_{t} $ , and$ {{J}}_{t}(t = 0,1) $ can be expressed with the density matrix$ \rho_{t}({{r}}\sigma,{{r}}'\sigma') $ . The coupling constants are simply real numbers, except for$ C_{t}^{\rho\rho} = C_{t0}^{\rho\rho}+C_{tD}^{\rho\rho}\rho_{0}^{\gamma}, $

(11) as the traditional density-dependence one.
In the particle–particle channel, we use
$ \delta $ pairing interactions. The pairing force has the following form [15]:$ V(r_{1},r_{2}) = V_{0}\left[1-\eta\left(\frac{\rho}{\rho_{0}}\right)^{\gamma}\right]\delta(r_{1}-r_{2})\; , $

(12) where
$ V_{0} $ is the pairing strength for neutrons (n) or protons (p),$ \eta $ and$ \gamma $ are parameters (in our calculations$ \gamma $ = 1), the total density is$ \rho $ , and$ \rho_{0} $ is the saturation density fixed at 0.16 fm$ ^{-3} $ .Due to the choice of
$ \eta $ , one can obtain different types of pairing, including mixed, volume and surface pairing. When$ \eta = 0 $ , it is the volume pairing force, which indicates no obvious density dependence, acting in the nuclear volume. When$ \eta $ = 1, it is the surface interaction, which is very sensitive to the nuclear surface. When$ \eta $ = 0.5, it is mixed pairing, which is the combination of the two previous types of pairing [15]. We also take$ \eta = 0.25 $ and 0.75 to test the sensitivity of the control parameter$ \eta $ in more detail, although these two values are quite unusual in the literature.The Lipkin-Nogami (LN) method modifies the energy E by an extra second-order Kamlah correction [16],
$ E\rightarrow E-\lambda_{2}\langle\Delta\hat{N}^{2}\rangle\; , $

(13) where
$ \langle\Delta\hat{N}^{2}\rangle = \langle\hat{N}^{2}\rangle-\langle\hat{N}\rangle^{2} $ . However, the coefficient$ \lambda_{2} $ can be derived from the following formula [16–18]:$ \lambda_{2} = \frac{G_{{\texttt{eff}}}}{4}\frac{{\rm Tr}'(1-\rho)\kappa {\rm Tr}'\rho\kappa-2{\rm Tr}(1-\rho)^{2}\rho^{2}} {[{\rm Tr}\rho(1-\rho)]^{2}-2{\rm Tr}\rho^{2}(1-\rho)^{2}}\; , $

(14) where the effective strength
$ G_{{\texttt{eff}}} = -\dfrac{\bar{\Delta}^2}{E_{{\texttt{pair}}}} $ is evaluated from the pairing energy$ E_{{\texttt{pair}}} = -\frac{1}{2}{\rm{Tr}}\Delta\kappa, $

(15) and the average pairing gap
$ \bar{\Delta} = \frac{{\rm{Tr}}\Delta\rho}{{\rm{Tr}}\rho}. $

(16) The projection on the good particle number (the particle number operator
$ \hat{Z} $ corresponds to the eigenstates of protons, and$ \hat{N} $ to the eigenstates of neutrons) can be obtained from the Bogoliubov wave function, and the projection operators can be written as an integrals over the gauge angles [19],$ \hat{P}_{N} = \frac{1}{2\pi}\int_{0}^{2\pi}{\rm d}\phi_{N}{\rm e}^{{\rm i}\phi_{N}(\hat{N}-N)}\; , $

(17) where the neutron number projection is represented by N. For the intrinsic wavefunction with well-defined "number parity", the integral interval in the above equation can be reduced to
$ [0,\pi] $ . Furthermore, the above integral can be calculated as the sum using the Fomenko expansion [20],$ \hat{P}_{N} = \frac{1}{M}\sum\limits_{m = 1}^{M}{\rm e}^{{\rm i}\phi_{N,\; m}(\hat{N}-N)},\; \;\;\; \; \phi_{N,\; m} = \frac{\pi}{M}m, $

(18) where M is the total number of points. To reduce the influence caused by the singularity, which appears at
$ \dfrac{\pi}{2} $ and causes the occupation probability to become 0.5 accidentally, we are restricted to using an odd number for M, which we choose to be 19 for both protons and neutrons.The number of protons Z has a similar expression. Through a wave function
$ |\Psi\rangle $ we can obtain the N and Z eigenstates$ |\Phi(N,Z)\rangle = \hat{P}_{N}\hat{P}_{Z}|\Psi\rangle \; . $

(19) In the HFB wave function
$ |\Psi\rangle $ ,$ \hat{P}_{N}\hat{P}_{Z} $ can be used to build a wave function with a definite particle number and calculate the expected energy:$ E^{N}[\rho,\kappa] = \frac{\langle\Phi|H P^{N}|\Phi\rangle}{\langle\Phi|P^{N}|\rangle} = \frac{\int {\rm d}\phi\langle\Phi|H{\rm e}^{{\rm i}\phi(\hat{N}-N)}|\Phi\rangle} {\int {\rm d}\phi\langle\Phi|{\rm e}^{{\rm i}\phi(\hat{N}-N)}|\Phi\rangle}\; . $

(20) The wave function
$ |\Psi\rangle $ is determined by solving the HFB equation, and this process is called the projection after variation (PAV).The energy of an odd nucleus is related to the polarization effect of the nuclear shape and single-particle structure caused by quasi-particle blocking [21]. There are several ways to evaluate the empirical OES, such as three-, four-, and five-point formulas [21-24]. The following formula is the simplest three-point formula to study the gap parameter
$ \Delta^{(3)} :$ $ \Delta^{(3)}(N) = \frac{\pi_{A+1}}{2}[B(N-1,Z)-2B(N,Z)+B(N+1,Z)]\; . $

(21) $ B(N,Z) $ represents the binding energy of the$ (N,Z) $ nucleus and$ \pi_{A} = (-1)^{A} $ is the number parity. This second-order variance in binding energies is centered at the odd-N nuclei for neutron OES. In the current paper, the OES simply refers to the gap parameter calculated from the above three-point formula. -
We would like to study the effect of pairing correlations on various observables of nuclei near
$ ^{132} $ Sn in the nuclear chart. We choose Skyrme energy density functionals with SLy4 [25], SkM* [26], and Universal Nuclear Energy Density Function (UNEDF) [27-29] parameters together with different pairing forces using the code HFBTHO(V3.00) [30]. A total of 20 major harmonic-oscillator shells are chosen as the basis and a 60 MeV cutoff is used as the pairing window in all calculations.In UNEDF families, the mixed pairing force within the HFBLN approximation is used and the pairing strength has been fitted systematically. We use the default choice of pairing force for the UNEDF parameters. For the DFT with SLy4 and SkM* forces, the neutron pairing strength has been fitted to the empirical pairing gap of 1.245 MeV in
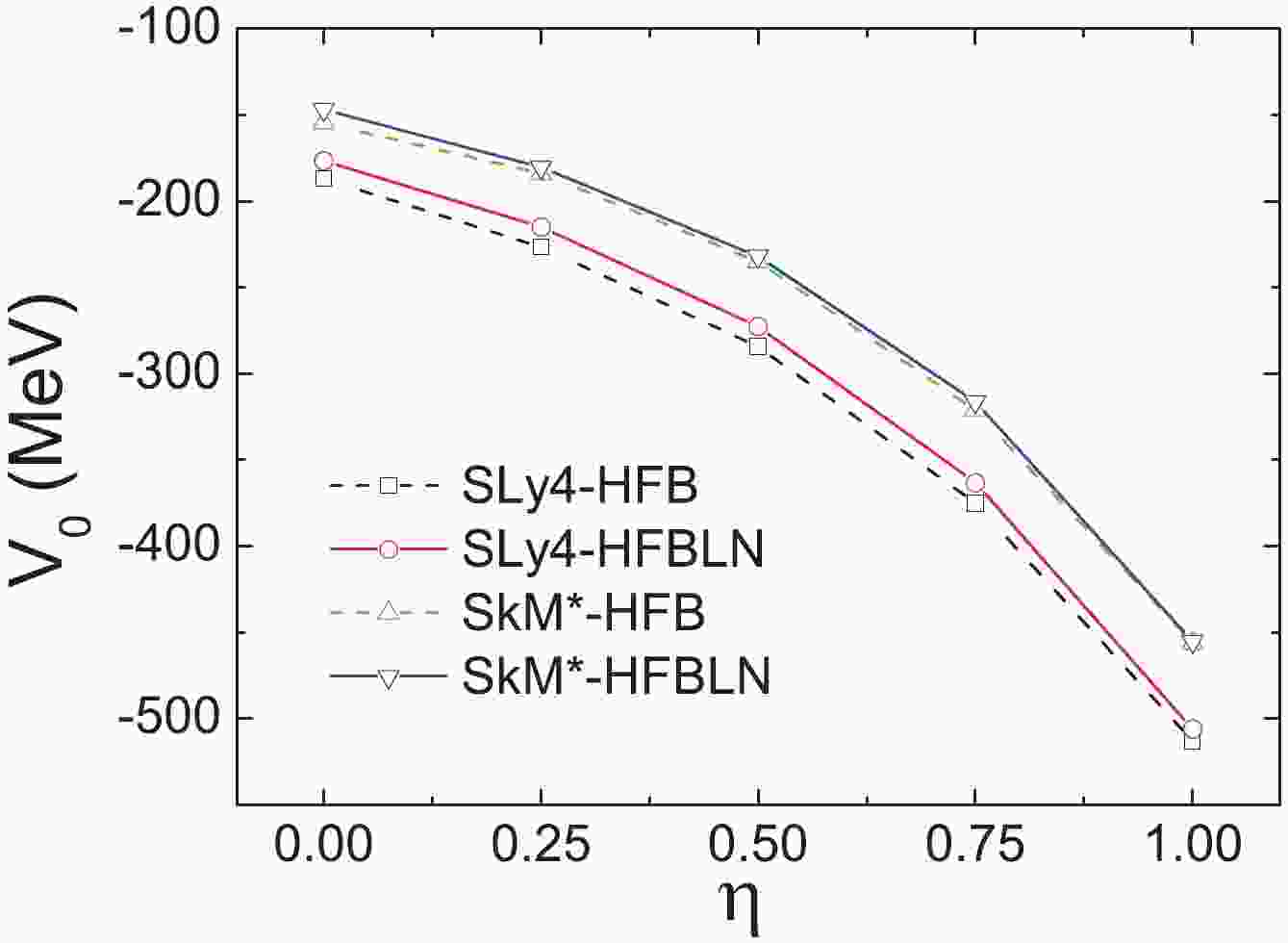
$ ^{120} $ Sn, and the proton pairing strength is equal to the neutron one, the same choice as made in Ref. [10].In Fig. 1, the resulting pairing strength is shown against the control parameter
$ \eta $ in the HFB and HFBLN approximations. The curves of the SLy4 and SkM* forces have a relatively similar trend. In addition, it is seen that a larger pairing strength is required for the SLy4 parameter, when fitting to the same pairing gap, reflecting the differences between these two mean-field potentials.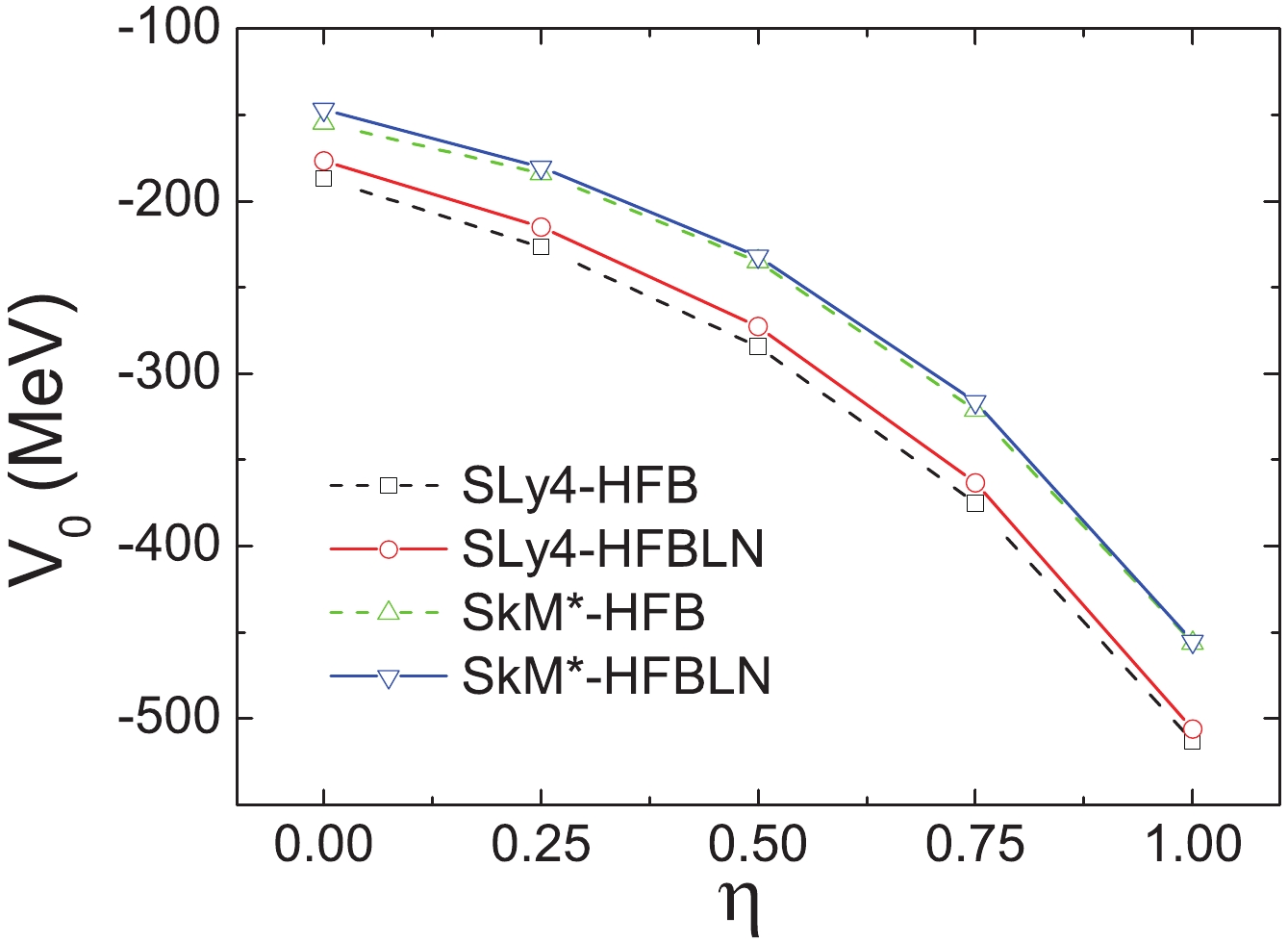
Figure 1. (color online) Pairing strength
$ V_0 $ as a function of the parameter$ \eta $ . The strength$ V_0 $ was adjusted, so as to reproduce the neutron gap 1.245 MeV in$ ^{120} $ Sn.When
$ \eta $ is close to 0, the pairing tends to happen equivalently in the nuclear volume, and when it is close to 1, the pairing tends to peak at the nuclear surface. It is seen that for$ \eta $ between the values of 0.0 and 0.5, the absolute value of the pairing strength$ V_0 $ increases nearly linearly. However, for$ \eta = 0.75 $ to 1.00, there is a sudden increase in the pairing strength. The surface pairing requires a much larger strength$ V_0 $ to produce the same pairing gap as the volume or mixed pairing. -
The calculated average neutron pairing gaps of tin isotopes are shown in Fig. 2, starting from
$ ^{120} $ Sn. The strengths of the pairing forces have been fitted to the empirical pairing gap of$ ^{120} $ Sn, thus the starting points of all these curves are the same. It is seen that for neutron numbers between 70 and 82, which are in the same major shells, the calculated pairing gaps from different pairing forces agree with each other quite well. However, the deviations become immediately obvious for nuclei with neutron numbers larger than 82. The variance of the calculated neutron pairing gaps becomes large after the N = 82 shell closure, indicating that larger uncertainties occur for the$ N = 83 $ nuclei than for the$ N = 81 $ nuclei.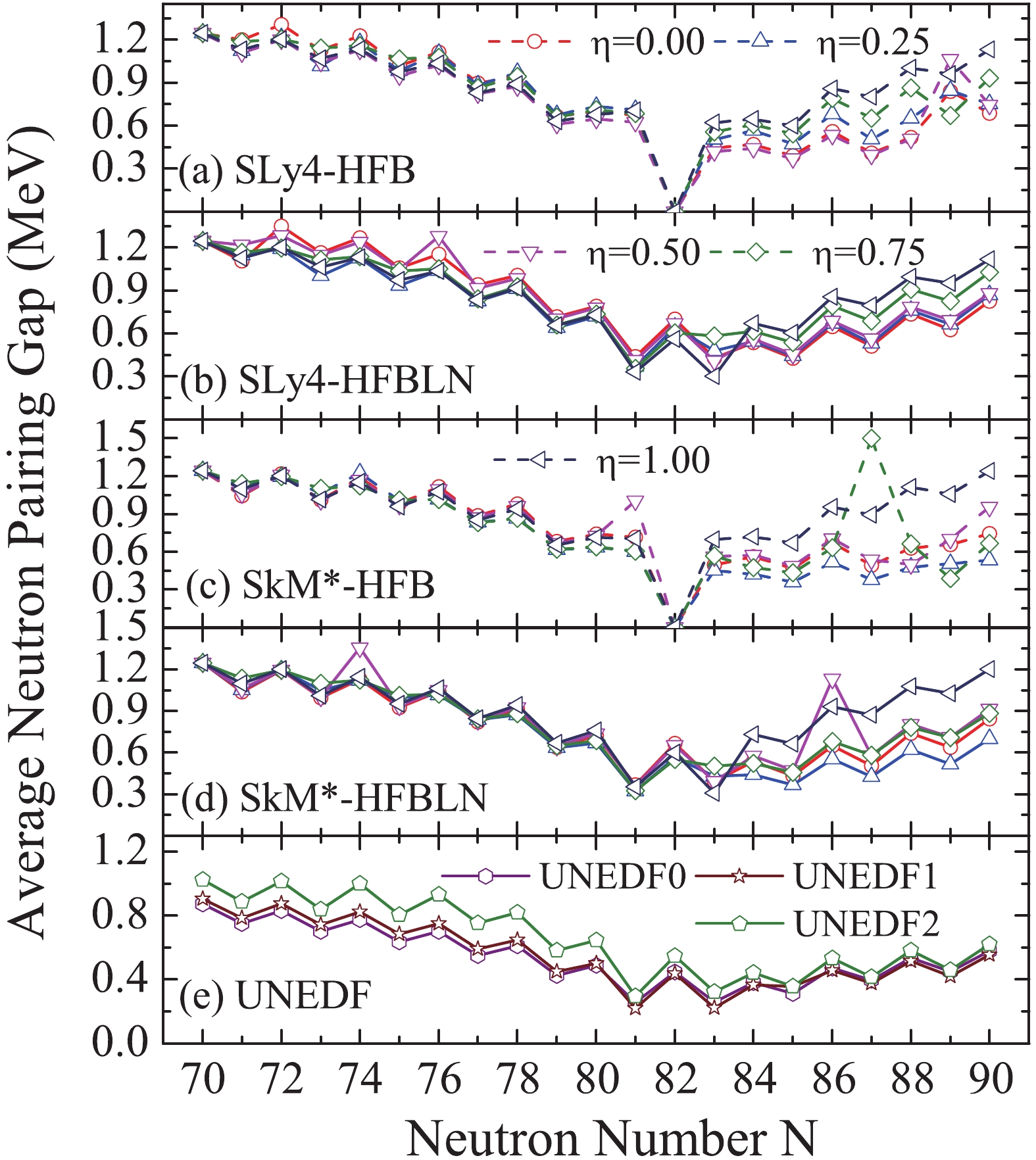
Figure 2. (color online) Calculated average neutron pairing gaps of tin isotopes. Results of different choices of
$ \eta $ in the pairing force are shown. Panels (a–b) and (c–d) were calculated under the SLy4 and SkM$ ^{*} $ parameters, respectively. Panel (e) shows the results calculated under the UNEDF parameters.This might be the reason that the current form of pairing force in Eq. (12) is still too simplified, compared to the form of particle-hole channel, which cannot give a universal description of pairing correlations for nuclei even in different major shells. One may need to renormalize the pairing forces in different regions in the nuclear chart.
When the neutron number is larger than 82, it seems that with a larger value of
$ \eta $ in Eq. (12), the pairing gap tends to be larger, especially for$ \eta = 1.00 $ , which is the surface pairing force. For neutron numbers less than 82, the resulting gaps from using the surface pairing force are similar to or sometimes even smaller than those of others. The pairing gap disappears at the magic number N = 82 in the HFB approximation, whereas it is still large in the HFBLN approximation because the force of gauge symmetry is broken.The trends of these curves in Fig. 2 under different Skyrme forces are similar, and the variations with the change of
$ \eta $ value with SkM* force are larger than those with SLy4 force. For the UNEDF parameter sets, the mixed pairing force ($ \eta = 0.5 $ ) together with the HFBLN approximation is used. The neutron pairing gaps given by different sets of UNEDF series are similar, and smaller than those by SkM* and SLy4 forces.We then calculated the mass OES
$ \Delta^{(3)} $ of the odd-N in the tin isotope chain, as shown in Fig. 3. The curve of experimental OES is fairly flat for neutron numbers between 69 and 79, and suddenly drops around the magic number$ N = 82 $ . All the calculations can roughly reproduce the trend of the experimental OES. It is seen that the OES from the three-point formula is different from the average pairing gap shown in Fig. 2. Compared to the HFB approximation, the calculated OES is closer to the data in HFBLN approximation. The results given by the SkM* force agree better with the data than those given by the SLy4 force. The OES results given by the UNEDF parameters are smaller than those by other calculations.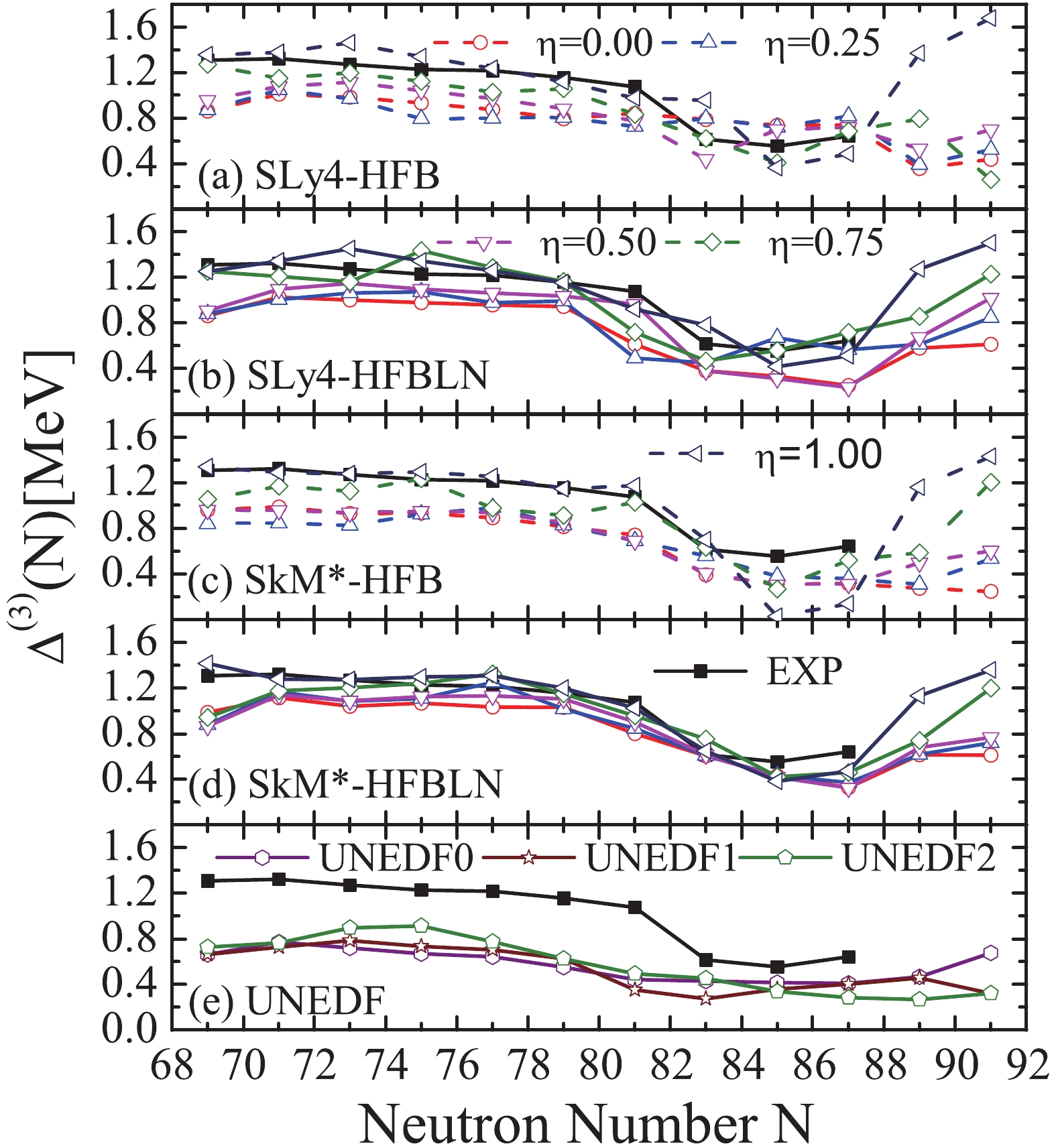
Figure 3. (color online) As in Fig. 2, but for the mass OES of the odd-N tin isotopes. The experimental data are also shown.
The results of the OES become smaller than the experimental data when the value of
$ \eta $ decreases, although all these pairing forces can produce similar neutron pairing gaps for$ N = 70\sim80 $ as shown in Fig. 2. It appears that for$ \eta = 0.75 $ and 1.00, which close to the surface extreme, the results are close to experimental data. The OES calculated by using$ \eta = 0.75 $ and 1.00 is explicitly larger than others at neutron number 89 and 91, where the experimental values are missing currently. The surface pairing usually leads to a stronger OES, which might be the reason that pairing force affect the single particle orbitals around the Fermi level mostly, near the region of nuclear surface in the coordinate space. -
We then study whether or not the abnormal behavior of OES around
$ ^{132} $ Sn can be reproduced, by using different Skyrme force and different treatment of the pairing. The results by the UNEDF DFT are shown first, in Fig. 4, together with the experimental data. It is seen that for the experimental OES of the neutron hole (N = 81 isotones) decrease with the proton number, and the experimental one of the neutron particle (N = 83 isotones) increase with the proton number.
Figure 4. (color online) OES of the N = 81 and 83 isotones. Experimental OES is in panel (a), and the results by UNEDF parameters are given in (b–d).
The choice of mixed pairing together with the HFBLN approximation has been made for all the UNEDF parameters.
$ \Delta^{(3)} $ as given by the UNEDF0 parameter decreases for both the N = 81 and 83 isotones. Using the UNEDF1 and UNEDF2 parameters can reproduce the systematics of the experimental data. However, similarly to in Fig. 3, the staggering calculated by these UNEDF DFTs is explicitly smaller than the OES from the experimental data.We also use the SLy4 and SkM* DFT, as shown in Fig. 5. In this figure, it seen that although the
$ \Delta^{(3)} $ given by these two Skyrme forces are explicitly different, they both show a decreasing trend of neutron OES with an increase in the number of protons. Thus, the systematics of the N = 83 isotone are not reproduced by these two DFTs.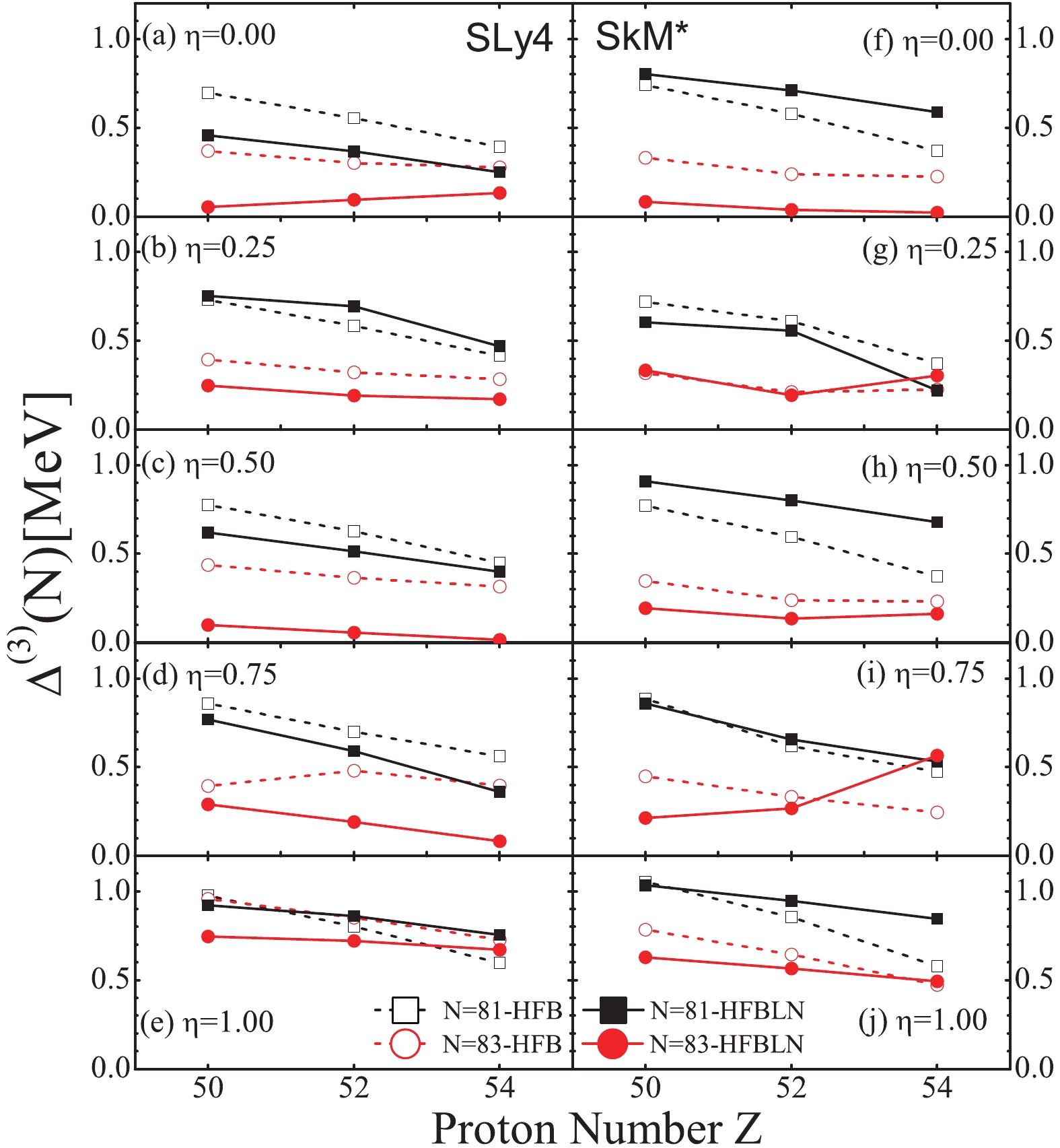
Figure 5. (color online) As in Fig. 4, but for OES calculated by the Skyrme DFT with SLy4 and SkM* parameters, as shown in panels (a–e) and (f–j), respectively. In the plot, the results using different choices of
$ \eta $ in the pairing force are given.Using the same Skyrme force, the
$ \Delta^{(3)} $ trends with different pairing force forms are similar. With increasing$ \eta $ in the pairing force, the OES increases, as already seen in Fig. 3 of the previous subsection. When$ \eta = 0.75 $ and 1.0, the staggering of the N = 81 isotone is quite close to the behavior of the experimental data. Comparing the results of HFB and HFBLN, we found that the$ \Delta^{(3)} $ given by HFBLN decreased more slowly as the number of valence protons increased than that calculated by HFB.The particle number projection after the convergence of the HFBLN approximation (PLN) can be used as an efficient way to describe the pairing correlation [13], especially for near-closed-shell nuclei [6]. The results of OES by PLN calculations are shown in Fig. 6. The OES from PLN calculations with larger
$ \eta $ in the pairing force is also larger, in general, but the systematics of OES by PLN are different from those of HFBLN in Fig. 5.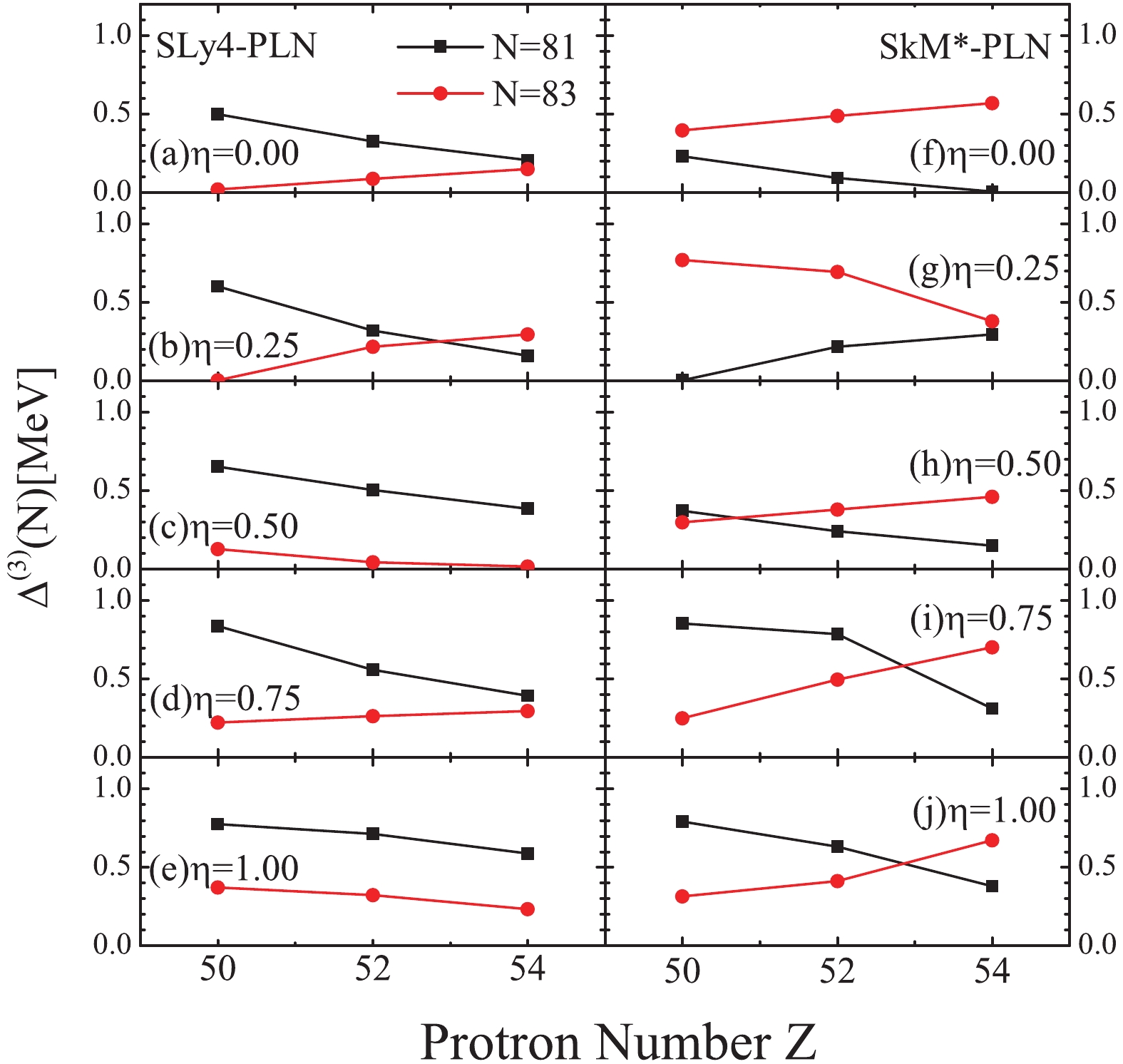
Figure 6. (color online) As in Fig. 5, but for OES given by PLN calculations with SLy4 and SkM* DFT.
Most of these calculations show decreasing OES of the N = 81 isotone against proton number, which is similar to those given by HFBLN calculations. For the N = 83 isotone, in various sets of PLN calculations, the neutron OES increases with proton number, capturing similar behavior to the experimental OES. In particular, the OES in N = 83 isotones given by the SkM* force become close to the experimental OES, for most cases. Thus, the systematics of OES can be improved by the PLN approach. Of course, discrepancies between the experimental data still exist.
For the N = 81 and 83 isotones, whether the deformation configuration and energy level filling are reasonable may play a crucial role in the
$ \Delta^{(3)} $ calculation. In our calculations, the deformations are obtained by the variational principle in the DFT approach. The resulted deformations are given in Fig. 7.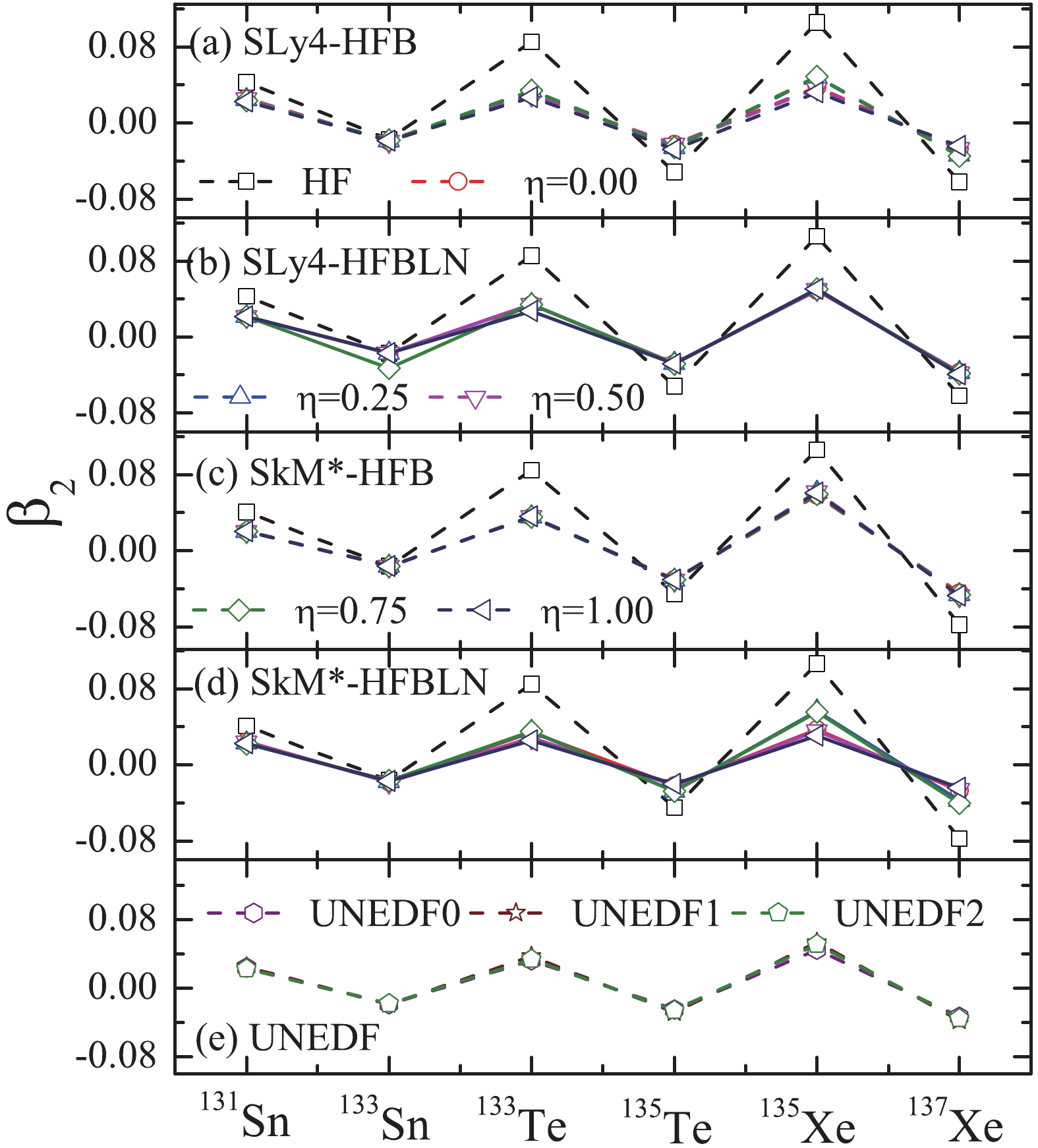
Figure 7. (color online) The
$ \beta_{2} $ deformation values of odd-A nuclei, calculated self-consistently under Skyrme energy DFT with SLy4, SkM$ ^{*} $ , and UNEDF parameters.It can be seen that the
$ \beta_{2} $ deformation values for N = 81 isotones are positive and the$ \beta_{2} $ deformation values of N = 83 isotones are negative, and that both become larger as the number of protons increases. With different Skyrme forces, the deformation values are basically the same. The$ \beta_{2} $ deformation values calculated by HF are larger than the$ \beta_{2} $ deformation values calculated by both HFB and HFBLN. The pairing correlation tends to reduce the deformation. Using different pairing force gives nearly the same result.As these nuclei are around the
$ N = 82 $ shell closure, their deformations are close to zero. The effect of shape fluctuation could have a large impact on their binding energies, as discussed in Refs. [31-33]. It is expected that such a beyond-mean field effect could potentially improve the OES systematics, and this requires further study. -
In this work, we focused on the study of the mass OES behavior around tin isotopes in the DFT framework. The OES,
$ \Delta^{(3)} $ , is extracted from the three-point formula of binding energies in the current work. For the Skyrme force, we choose SkM*, SLy4, and the UNEDF family. For the pairing force, by tuning$ \eta $ as the control parameter, we use mixed-, surface-, and volume-type force, and the other two pairing forces intermediate between the volume and surface force. Different treatments of pairing correlations, including HFB, HFBLN, and PLN approximations, are tested. The strength of the pairing force in SkM* and SLy4 DFT is fixed to the same empirical pairing gap of$ ^{120} $ Sn.It is found that, in tin isotopes with neutron numbers less than 82, the average pairing gaps by different pairing forces are nearly the same. However, variances occur when the neutron number is larger than 82, and the average gap tends to be larger if the pairing interaction is close to the limit of surface pairing.
Thus, the uncertainties in the neutron pairing gap of
$ N = 83 $ are larger than those of$ N = 81 $ . This also indicates that the form of pairing force used in this work is too simple to give a universal description across the nuclear chart, and one may need to readjust the pairing strength in different nuclear regions.The pairing forces in the UNEDF parameters were fixed systematically to experimental data during the fitting procedure. The mixed pairing together with the HFBLN approximation were used with their original parameters. It is seen that the average gaps given by the UNEDF parameters are smaller than those given by the SkM* and SLy4 DFT.
The mass OES of the tin isotopes has been studied. The systematics of the calculated OES in Skyrme DFT are generally similar to the data. When the pairing is more active at the surface, a larger mass of OES is obtained, and vice versa. The surface pairing is quite close to or slightly larger than the experimental OES. It appears that the results given by the pairing force with
$ \eta = 0.75 $ are also close to the data, whereas those given by other pairing forces are smaller. The mass OES of tin isotopes given by the UNEDF parameters is also smaller than the experimental one.In experiments, it was found that around
$ ^{132} $ Sn isotopes, the OES in N = 81 isotones decreases with proton number, whereas it increases in N = 83 isotones; thus, abnormal OES was indicated. In all calculations, a decrease in OES in N = 81 isotones is obtained. However, it is difficult to reproduce the increase in OES in N = 83 isotones in the HFB or HFBLN approximation.The increasing OES in N = 83 isotones is only obtained by several cases, e.g., UNEDF1 and 2. It appears that UNEDF1 and 2 can give good systematics of the mass OES, but the staggering is smaller than the experimental one. Thus, one can enhance the strength of the pairing force to improve the description of OES, but because all the parameters of the UNEDF families are fitted systematically, the calculations of other observables may become poor.
From the results of OES in tin isotopes and the OES around
$ ^{132} $ Sn, it is seen that the OES systematics are influenced by both the mean-field and pairing forces. The OES given by the SkM* force agrees more closely with the experimental data than that given by the SLy4 force. By changing the density dependence of the pairing force by tuning the parameter$ \eta $ , the trend of the OES does not change significantly, but stronger staggering is obtained if the pairing is more favored at the nuclear surface.It is also found that in most cases, the OES given by the HFBLN approximation is closer to the experimental data than that given by the HFB approximation. We attempted PLN calculations for SkM* and SLy4 DFT as well. After treatment of the particle number projection, the OES systematics can be changed significantly. It is found that the calculated systematics of OES in N = 83 isotones become close to the experimental ones for several cases, especially for the SkM* DFT. It appears that such abnormal OES can be produced for various combinations of Skyrme and pairing forces. This might be further evidence that restoration of symmetry can improve the mean-field calculations.
As we take the mass OES as the only observable in this study, it might be difficult to determine the most preferable pairing force in the Skyrme DFT. A 50/50 balance of volume and surface pairing forces is commonly adopted in the literature. Sometimes, the mixed pairing force produces OES closer to that by volume pairing, which is often smaller than the experimental OES. Surface pairing usually leads to a much larger OES, but it can be larger than the experimental one. Thus, one can tune the ratio between the volume and surface pairing to obtain a good reproduction of the mass OES. For many cases in this study, a lower ratio of volume pairing and larger ratio of surface pairing (
$ \eta = 0.75 $ ) could lead to good agreement. For nuclei around$ ^{132} $ Sn, the shapes are close to spherical and thus the effect of shape fluctuations could be large, but this is not included in this work. Thus, it can be expected that the OES can be improved after the inclusion of such beyond-mean-field calculations, and future study is needed.
Abnormal odd-even staggering behavior around 132Sn studied by density functional theory
- Received Date: 2020-01-23
- Accepted Date: 2020-04-14
- Available Online: 2020-09-01
Abstract: In this work, we have performed Skyrme density functional theory (DFT) calculations of nuclei around 132Sn to study whether the abnormal odd-even staggering (OES) behavior of binding energies around N = 82 can be reproduced. With the Skyrme forces SLy4 and SkM*, we tested the volume- and surface-type pairing forces and also the intermediate between these two pairing forces, in the Hartree-Fock-Bogoliubov (HFB) approximation with or without the Lipkin-Nogami (LN) approximation or particle number projection after the convergence of HFBLN (PLN). The Universal Nuclear Energy Density Function (UNEDF) parameter sets are also used. The trend of the neutron OES against the neutron number or proton number does not change significantly by tuning the density dependence of the pairing force. Moreover, for the pairing force that is favored more at the nuclear surface, a larger mass OES is obtained, and vice versa. It appears that the combination of volume and surface pairing can give better agreement with the data. In the studies of the OES, a larger ratio of surface to volume pairing might be favored. Additionally, in most cases, the OES given by the HFBLN approximation agrees more closely with the experimental data. We found that both the Skyrme and pairing forces can influence the OES behavior. The mass OES calculated by the UNEDF DFT is explicitly smaller than the experimental one. The UNEDF1 and UNEDF2 forces can reproduce the experimental trend of the abnormal OES around 132Sn. The neutron OES of the tin isotopes given by the SkM* force agrees more closely with the experimental one than that given by the SLy4 force in most cases. Both SLy4 and SkM* DFT have difficulties in reproducing the abnormal OES around 132Sn. Using the PLN method, the systematics of OES are improved for several combinations of Skyrme and pairing forces.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: