Heavy flavor quenching and flow: the roles of initial condition, pre-equilibrium evolution, and in-medium interaction

1. Introduction

• 1. Introduction
• 2. Production, energy loss, and hadronization of heavy quarks
•      2.1 Initial production of heavy quarks
•      2.2 In-medium evolution of heavy quarks
•      2.3 Hadronization of heavy quarks
• 3. Nuclear modification of heavy flavor mesons
• 4. Summary

Relativistic heavy-ion collisions provide a unique opportunity to study nuclear matter under conditions of extreme density and temperature. It is now generally acknowledged that color-deconfined QCD matter, known as Quark-Gluon Plasma (QGP), has been produced in high-energy nuclear collisions at the Relativistic Heavy-Ion Collider (RHIC) and the Large Hadron Collider (LHC) [1]. The QGP behaves like a strongly interacting fluid, as revealed by the large anisotropic collective flow of hadrons emitted in these energetic heavy-ion collisions [2-4]. The collective flow has been successfully explained by relativistic hydrodynamic simulation with small values in the shear-viscosity-to-entropy-density ratio ($\eta/s$) [5-8].

More evidence of quark-gluon degrees of freedom inside the QGP is jet quenching [9-11]. Energetic quarks and gluons produced in the primordial stage of nuclear collisions lose energy while traversing the hot and dense nuclear matter before fragmenting into hadrons. The study of energetic jets and hadrons and their medium modification in heavy-ion collisions provides a valuable means of probing the QGP properties, such as the jet transport coefficient inside the QGP [12]. Much effort has been devoted to understanding the nuclear modification of jets, such as single inclusive hadron/jet suppression [12-16], di-hadron/jet correlations [17-21], photon/Z-triggered hadron/jet correlations [22-27], and other differential substructures of full jets [28-32]. Among the hard probes, heavy quarks are of particular interest since their flavors are conserved when interacting with QGP. Thus, they can probe the traversed nuclear medium cleanly [33, 34]. At low $p_{{T}}$, heavy quarks may probe the color potential of the QGP [35]; at intermediate $p_{{T}}$, heavy flavor hadron chemistry can help extend our knowledge of the hadronization process of jet partons [36-40]; at high $p_{{T}}$, heavy quarks can probe directly the mass hierarchy of parton energy loss inside a thermalized QGP medium [41, 42].

Various transport models have been developed to study heavy quark dynamics in heavy-ion collisions. Some models only include the collisional energy loss of heavy quarks by assuming the large mass approximation [43-45]; others also consider radiative energy loss and medium-induced gluon emission, which are important for high $p_{{T}}$ heavy quarks [46-56]. While various models have been built on rather different assumptions about the heavy-quark-medium interaction, many provide reasonable descriptions of experimental data on heavy quarks. In Ref. [57], it is shown that a factor of 2 difference remains in the heavy quark transport coefficient when different transport models are tuned to describe the same data. Note that this discrepancy mainly originates from different energy-loss mechanisms, and the uncertainties could be much larger if the effects of using different medium profiles and hadronization models are included. To obtain a clear picture of heavy flavor production and medium modification, it is important to understand the systematic uncertainties engendered by various model components, such as the initial heavy quark spectrum, the assumptions of heavy-quark-medium interaction in the pre-equilibrium stage, heavy quark energy loss and hadronization mechanisms, the geometry and flow of the QGP, as well as the temperature dependence of the heavy-quark transport coefficient. Some of these aspects have been investigated in earlier studies [57-61]. In this work, we extend such studies and perform a systematic investigation on the uncertainties from all the above-mentioned sources using the state-of-the-art Langevin-hydrodynamics model that incorporates both the collisional and radiative energy losses of heavy quarks through a dynamical QGP medium [50, 51]. By combining with the up-to-date fragmentation-coalescence hadronization approach [40], we analyze the nuclear modification factor ($R_{{AA}}$) and elliptic flow coefficient ($v_2$) of heavy mesons and compare them to experimental data obtained at the RHIC and the LHC.

The paper is organized as follows. In Sec. 2, we review the production, energy loss, and hadronization of heavy quarks within our advanced Langevin-hydrodynamics framework coupled to a hybrid fragmentation-coalescence hadronization model. In Sec. 3, we present our numerical results for D meson suppression and elliptic flow, together with their dependence on the initial heavy quark spectrum, the energy loss and hadronization mechanisms, the pre-equilibrium temperature profile of the medium, the flow of the medium, and the temperature dependence of the heavy quark diffusion coefficient. A summary is given in Sec. 4.

2. Production, energy loss, and hadronization of heavy quarks

• 1. Introduction
• 2. Production, energy loss, and hadronization of heavy quarks
•      2.1 Initial production of heavy quarks
•      2.2 In-medium evolution of heavy quarks
•      2.3 Hadronization of heavy quarks
• 3. Nuclear modification of heavy flavor mesons
• 4. Summary

2.1 Initial production of heavy quarks

• 1. Introduction
• 2. Production, energy loss, and hadronization of heavy quarks
•      2.1 Initial production of heavy quarks
•      2.2 In-medium evolution of heavy quarks
•      2.3 Hadronization of heavy quarks
• 3. Nuclear modification of heavy flavor mesons
• 4. Summary

Because of their large masses, heavy quarks are mainly produced via hard scatterings in the primordial stage of relativistic heavy-ion collisions. This allows us to use a Monte-Carlo (MC) Glauber model to determine the spatial distribution for the production vertices of heavy quarks and use the perturbative QCD (pQCD) approach to calculate their initial momentum spectra. In this work, we use the Fixed-Order-Next-to-Leading-Log (FONLL) framework [62-64] to calculate the initial heavy quark spectra, if not otherwise specified. Within this framework, we apply the CT14NLO [65] parton distribution function (PDF) for the free proton and the EPPS16 [66] parametrization for PDF in nuclei to take into account the nuclear shadowing effect. We will investigate the systematic uncertainties between using these FONLL spectra and the Leading-Order (LO) pQCD spectra [67] in the next section. The nuclear shadowing effect on heavy flavor observables will also be discussed.

2.2 In-medium evolution of heavy quarks

• 1. Introduction
• 2. Production, energy loss, and hadronization of heavy quarks
•      2.1 Initial production of heavy quarks
•      2.2 In-medium evolution of heavy quarks
•      2.3 Hadronization of heavy quarks
• 3. Nuclear modification of heavy flavor mesons
• 4. Summary

During their propagation through the QGP fireball, heavy quarks lose energy via both quasi-elastic scatterings with thermal light partons in-medium and the inelastic medium-induced gluon emission [9, 68]. In this work, we utilize the following modified Langevin equation [50] that simultaneously incorporates these two processes to describe the time evolution of the energy and momentum of heavy quarks while they traverse the QGP:

In the above equation, the first two terms on the right-hand side are inherited from the classical Langevin equation, representing the drag force and thermal random force experienced by a heavy quark while it diffuses inside a thermal medium due to multiple scatterings. For a minimal model, we assume that the thermal force $\vec{\xi}$ does not depend on the heavy quark momentum and satisfies the correlation relation of a white noise $\langle\xi^{i}(t)\xi^{j}(t^{\prime})\rangle = \kappa\delta^{ij}\delta(t-t^{\prime})$, where $\kappa$ is the momentum diffusion coefficient of heavy quarks and is related to the spatial diffusion coefficient via $D_{\rm{s}}\equiv T/[M\eta_{D}(0)] = 2T^{2}/\kappa$ if the fluctuation-dissipation relation $\eta_{D}(p) = \kappa/(2TE)$ is respected.

Apart from the above two terms acquired from the quasi-elastic scatterings, a third term $\vec{f_{g}} = -{\rm d}\vec{p}_{g}/{\rm d}t$ is introduced to describe the recoil force exerted on heavy quarks while they emit medium-induced gluons, with $\vec{p}_{g}$ being the momentum of the emitted gluons. The probability of gluon radiation during the time interval $(t,t+\Delta t)$ is related to the average number of radiated gluons in $\Delta t$ as

On the condition that the chosen $\Delta t$ is sufficiently small, the average number $\langle N_{g}(t,\Delta t)\rangle$ is less than 1 and can be interpreted as a probability. In this study, the gluon distribution function in Eq. (2) is taken from the higher-twist energy loss calculation [69-71]:

where x is the fractional energy of the emitted gluon taken from the parent heavy quark, $k_\perp$ is the transverse momentum of the gluon, $\alpha _{\rm{s}}$ is the strong coupling which runs with $k_\perp^2$, $P(x)$ is the $Q\rightarrow Qg$ splitting function, and $\tau _{f} = 2Ex(1-x)/(k_{\perp}^{2}+x^{2}M^{2})$ is the gluon formation time with E and M being the energy and mass of heavy quarks. Note that the multiplicative term at the end of Eq. (3) is known as the “dead cone factor” that characterizes the mass dependence of the radiative energy loss of hard partons. In Eq. (3), $\hat q$ is the gluon transport coefficient and may be related to the quark diffusion coefficient via $\hat q = 2\kappa C_{A}/C_{F}$. Thus, in this modified Langevin model, there is only one free parameter that we choose to be the dimensionless quantity $D_{\rm{s}}(2\pi T)$.

When simulating the radiative energy loss of heavy quarks, a lower cut-off energy of the radiated gluon $\omega _{0} = \pi T$ is imposed to mimic the balance between the gluon emission and absorption processes around the thermal scale. Below $\omega _{0}$, gluon radiation is disabled and the evolution of heavy quarks at low energy is entirely controlled by quasi-elastic scatterings. In other words, $x\in [\pi T/E,1]$ is used when calculating the gluon radiation probability in Eq. (2). This allows an approximate thermal equilibration of heavy quarks after a sufficiently long evolution although the exact fluctuation-dissipation relation cannot be assured due to the lack of the gluon absorption process [50].

To calculate heavy-quark energy loss within a realistic QGP medium, we couple this improved Langevin approach to a hydrodynamic model that provides the temperature profiles of the QGP fireball. In this work, we use two hydrodynamic models – (2+1)-dimensional Vishnew [72-74] and (3+1)-dimensional CLVisc [75, 76] to calculate heavy-quark observables. The Glauber model is used to calculate the initial entropy/energy-density distributions for these hydrodynamic simulations. The starting time of the hydrodynamic evolution $\tau_{\rm hydro} = 0.6$ fm and the shear-viscosity-to-entropy-density-ratio $\eta/s = 0.08$ are fixed to provide the satisfactory soft-hadron spectra observed at RHIC and the LHC. At every time step, each heavy quark is first boosted into the local rest frame of the fluid cell through which it propagates. In this frame, the energy and momentum of the heavy quark are updated based on our improved Langevin equation. Then, the heavy quark is boosted back to the global center-of-momentum frame from which it streams to the next time step. Unless otherwise specified, the starting time $\tau_0$ for heavy-quark-medium interaction is set at $\tau_0 = 0.6$ fm, which means that we assume free-streaming for heavy quarks before $\tau_0$. However, the uncertainties of heavy flavor observables due to different choices of $\tau_0$ and different assumptions about the medium's temperature profiles before $\tau_0$ will be explored later in this work.

2.3 Hadronization of heavy quarks

• 1. Introduction
• 2. Production, energy loss, and hadronization of heavy quarks
•      2.1 Initial production of heavy quarks
•      2.2 In-medium evolution of heavy quarks
•      2.3 Hadronization of heavy quarks
• 3. Nuclear modification of heavy flavor mesons
• 4. Summary

When the local temperature of the hydrodynamic medium drops to $T_{\rm{c}} = 160$ MeV, we switch-off the interaction between heavy quarks and the medium. Then the heavy quarks are converted into heavy flavor hadrons by applying our up-to-date hybrid fragmentation-coalescence model [40].

Typically, fragmentation dominates at a high transverse momentum and the heavy-light-quark-coalescence dominates at a low transverse momentum. The momentum-dependent coalescence probability is determined by the wavefunction overlap between the free constituent quark states and the hadronic bound states and can be expressed as the Wigner function [77]. For the coalescence of two quarks into a meson, the Wigner function reads:

where $\vec{r}$ and $\vec{q}$ are the relative position and momentum between the two quarks in their center of momentum frame. The statistics factor $g_M$ represents the ratio of the spin-color degrees of freedom between the final-state meson and the initial-state quarks. For instances, it is 1/36 for the $D^0$ ground state but 1/12 for $D^{*0}$. In this work, the simple harmonic oscillator potential is assumed for the meson wavefunction $\phi_M$, with the oscillator frequency $\omega$ as the single parameter of this coalescence model. To coalesce three quarks into a baryon, we first combine two quarks and then their center-of-momentum with the third quark. Following Ref. [40], we include both s and p-wave hadronic states, which cover all major charmed hadron species reported by the Particle Data Group (PDG) [78]. This is essential for understanding the observed charmed hadron chemistry – $\Lambda_c/D^0$ and $D_{\rm s}/D^0$ ratios – at RHIC and the LHC [40].

The above Wigner functions are used to calculate the probabilities for heavy quarks to coalesce with thermal light quarks into all possible hadrons when they cross the QGP boundary. Light quarks are assumed to follow the thermal distribution in the local rest frame of the expanding QGP. Based on these probabilities, we use the Monte-Carlo method to determine which specific coalescence channels heavy quarks take to become hadrons. For heavy quarks that do not coalesce, we implement a Pythia simulation [79] to fragment them into hadrons. The above-mentioned model parameter $\omega$ is determined for the total coalescence probability of a zero momentum charm quark to be 1 since it is kinematically forbidden to fragment. This yields $\omega = 0.24$ GeV after including all s and p-wave charmed hadron states.

3. Nuclear modification of heavy flavor mesons

• 1. Introduction
• 2. Production, energy loss, and hadronization of heavy quarks
•      2.1 Initial production of heavy quarks
•      2.2 In-medium evolution of heavy quarks
•      2.3 Hadronization of heavy quarks
• 3. Nuclear modification of heavy flavor mesons
• 4. Summary

In this section, we present the numerical results of the nuclear modification of heavy flavor mesons in heavy-ion collisions at RHIC and the LHC. Particularly, we investigate in detail how these observables depend on different model ingredients, such as the initial heavy quark spectrum, the starting time of the heavy-quark-medium interaction, the temperature profile of the medium in the pre-equilibrium stage, the energy loss and hadronization mechanisms of heavy quarks, the flow of medium, and the temperature dependence of the heavy quark transport coefficient.

In this work, we focus on the two most common heavy flavor observables: the nuclear modification factor $R_{{AA}}$ and the elliptic flow coefficient $v_2$ that quantify the overall energy loss of heavy quarks and the asymmetry of heavy quark energy loss in different directions within the fireball. They are defined as follows:

where $N_{\rm{coll}}$ is the average number of binary collisions in a given centrality bin of AA collisions, and $\langle \ldots \rangle$ denotes the average over the final-state charmed hadrons observed in our simulations. In this work, we employ smooth hydrodynamic profiles. Therefore, x-z defines the event plane and x-y defines the transverse plane of AA collisions. The effects of event-by-event fluctuations on heavy flavor observables have been studied in our earlier work [80, 81], and were found to be small.

With the above setups, we calculate the D meson $R_{{AA}}$ and $v_{2}$ in 10-40% Au-Au collisions at $\sqrt{s_{{NN}}} = 200$ GeV and 30-50% Pb-Pb collisions at $\sqrt{s_{{NN}}} = 5.02$ TeV, and compare the results to STAR data at RHIC [82, 83] and ALICE and CMS data at the LHC [83-85].

First, we investigate how the D meson $R_{{AA}}$ and $v_2$ are affected by the initial heavy quark spectrum. In Fig. 1, we compare the results from four different setups by using the LO spectra with and without the nuclear shadowing effect and the FONLL spectra with and without the nuclear shadowing effect. The diffusion coefficient of heavy quarks is set as $D_{\rm{s}}(2\pi T) = 3$ at RHIC and 4 at the LHC in order to reasonably describe the experimental data on $R_{{AA}}$. The smaller diffusion coefficient at RHIC than at the LHC can be understood as the stronger average jet-medium interaction at RHIC due to its lower average medium temperature [12]. As mentioned earlier, the starting time of heavy-quark-medium interaction is set as $\tau_0 = 0.6$ fm for this comparison.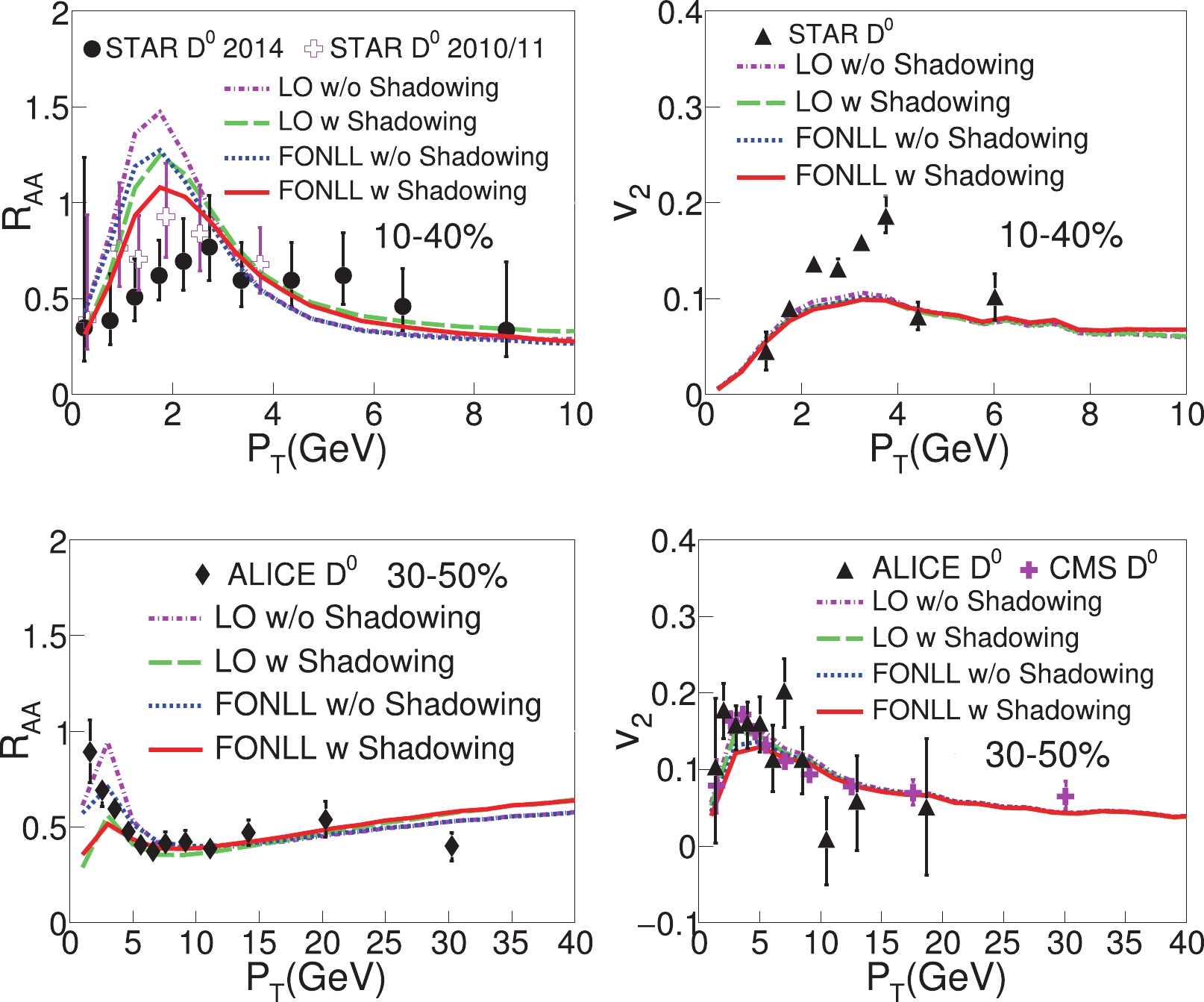

Figure 1

Figure 1.  (color online) Effects of initial heavy quark spectrum on D meson $R_{{AA}}$ (left-hand panels) and $v_2$ (right-hand panels) at RHIC (upper panels) and the LHC (lower panels).

DownLoad: Full-Size Img PowerPoint

As shown in the left panels of Fig. 1, without the nuclear shadowing effect, using the FONLL spectrum leads to a smaller $R_{{AA}}$ at low$p_{{T}}$ than using the LO spectrum (13% smaller at RHIC and 25% smaller at the LHC), while no apparent difference is observed at high $p_{{T}}$. This is consistent with the findings in Ref. [58] since the FONLL spectrum is lower than the LO spectrum below $p_{{T}}\sim 5$ GeV, but they converge above $5$ GeV. The inclusion of the nuclear shadowing effect significantly suppresses the initial spectrum of charm quarks in AA collisions at low $p_{{T}}$ compared to that in pp collisions (15% at RHIC and 27% at the LHC when the EPPS16 parameterization is applied within the FONLL framework), while at high $p_{{T}}$ the spectrum is slightly enhanced (anti-shadowing). This effect is reflected directly in the result for D meson $R_{{AA}}$. For elliptic flow $v_2$ in the right-hand panels of Fig. 1 we can see that different spectra yield a negligible effect on the D meson $v_2$ at RHIC. At the LHC, using the FONLL spectrum yields a $v_2$ that is approximately 19% smaller than that using the LO spectrum below $p_{{T}}\sim 5$ GeV. For the rest of our work, we will use the FONLL spectrum combined with the EPPS16 parametrization of nuclear shadowing in our calculations.

To date, we know little about jet-medium interactions in the pre-equilibrium stage of heavy-ion collisions. In most literature, energetic particles are assumed to stream freely during this stage until the thermalized QGP forms (e.g. $\tau _{0} = 0.6$ fm). However, as shown in Refs. [86, 87], the interactions during this stage could be strong. Therefore, it is worth quantifying the possible uncertainties in jet-quenching observables from different model assumptions for the pre-equilibrium stage.

In Fig. 2, we first compare two different starting times, $\tau_0$, for heavy-quark-medium interactions (0.6 fm vs. 1.2 fm). To determine the pure effect of different starting times on the D meson $v_2$, we first adjust the diffusion coefficient for the two choices of $\tau_0$ to yield a similar D meson $R_{{AA}}$, as shown in the left-hand panels of Fig. 2. Due to the shorter evolution time of heavy quarks within the QGP, using a later starting time for heavy-quark-medium interaction (i.e., $\tau_0 = 1.2$ fm) requires an approximately 35% smaller diffusion coefficient $D_{\rm{s}}$, which means a greater coupling strength between heavy quarks and the QGP to reproduce suppression that equals that when using the starting time of $\tau_0 = 0.6$ fm. With the same D meson $R_{{AA}}$, a larger D meson $v_2$ is observed at low $p_{{T}}$ in the right-hand panels for $\tau_0 = 1.2$ fm compared to $\tau_0 = 0.6$ (8% larger at RHIC and 24% at the LHC). This is because shifting more interaction to later stages of the QGP evolution, when the anisotropic medium flow is stronger, allows low $p_{{T}}$ (near-thermal) heavy quarks to pick up more $v_2$ from the nuclear medium.

Figure 2

Figure 2.  (color online) Effects of the starting time $\tau_0$ of heavy-quark-medium interactions on D meson $R_{{AA}}$ (left-hand panels) and $v_2$ (right-hand panels) at RHIC (upper panels) and the LHC (lower panels).

DownLoad: Full-Size Img PowerPoint

To further investigate how different assumptions for heavy-quark-medium interaction in the pre-equilibrium stage affect heavy quark observables, we extend the above study beyond the free-streaming hypothesis for heavy quarks before $\tau_0$. We compare different modelings of the temperature profiles of the pre-equilibrium stage before the thermalized QGP forms. For heavy quark evolution in the pre-equilibrium stage ($0<\tau<\tau_0$), we still utilize the modified Langevin dynamics [Eq. (1)] in the same way as during the QGP phase ($\tau>\tau_0$) on condition that the temperature profile of the background medium is provided. As illustrated in Fig. 3, four different scenarios are used for the temperature profile of the medium before $\tau_0$ (0.6 fm): (1) $T(\tau) = 0$ – free-streaming, (2) $T(\tau) = T(\tau _{0})(\tau/\tau_0)$ – a linear increase from 0 to $\tau_0$, (3) $T(\tau) = T(\tau_0)$ – constant temperature before $\tau_0$, and (4) $T(\tau) = T(\tau _{0})(\tau_0/\tau)^{1/3}$ – Bjorken evolution profiles before $\tau_0$.

Figure 3

Figure 3.  (color online) Effects of different temperature profiles of the pre-equilibrium stage on D meson $R_{{AA}}$ (left-hand panels) and $v_2$ (right-hand panels) at RHIC (upper panels) and the LHC (lower panels).

DownLoad: Full-Size Img PowerPoint

In Fig. 2, similarly to the previous study we adjust the diffusion coefficients for these different model setups to provide a similar D meson $R_{{AA}}$ in the left-hand panels of Fig. 3. One can see that a larger $D_{\rm{s}}$ or weaker heavy-quark-medium coupling strength is required when a higher average medium temperature is modeled for the pre-equilibrium stage. After the D meson $R_{{AA}}$ is fixed, we can see from the right-hand panels that different assumptions of the pre-equilibrium temperature profiles give rise to a different elliptic flow $v_2$ of D mesons. The free-streaming assumption yields a $v_2$ that is approximately 39% (19%) larger than the constant temperature and Bjorken evolution profiles at low $p_{{T}}$ at RHIC (the LHC). The elliptic flow $v_2$ for the linear increasing temperature profile lies in the middle. Very little effect is observed in the high $p_{{T}}$ regime. This is consistent with the findings in Fig. 2: a stronger heavy-quark-medium interaction at a later time results in a larger $v_2$ (after tuning the model parameter to describe $R_{{AA}}$). Our results are qualitatively consistent with the result in Ref. [60], though the effect found in our study is quantitatively smaller, especially at high $p_{{T}}$. Keeping in mind the above uncertainties from the pre-equilibrium stage, we now turn to explore the effects arising from other model ingredients using the free-streaming hypothesis before $\tau_0 = 0.6$ fm in the rest of this work.

The energy loss of heavy quarks inside the QGP is the main cause for the nuclear modification of D mesons in heavy-ion collisions. Therefore, it is crucial to understand the detailed energy loss mechanism for heavy quarks in QGP. In Fig. 4, we observe how collisional and radiative energy losses contribute to the D meson $R_{{AA}}$ and $v_2$, individually. The diffusion coefficient of charm quarks is set as $D_{\rm{s}}(2\pi T) = 3$ at RHIC and 4 at the LHC such that our model provides a reasonable description of the experimental data after the inclusion of both the collisional and radiative energy loss mechanisms.

Figure 4

Figure 4.  (color online) Effects of collisional vs. radiative energy loss mechanisms on D meson $R_{{AA}}$ (left-hand panels) and $v_2$ (right-hand panels) at RHIC (upper panels) and the LHC (lower panels).

DownLoad: Full-Size Img PowerPoint

From $R_{{AA}}$ (left-hand panels) and $v_2$ (right-hand panels) in Fig. 4, we observe that collisional energy loss dominates heavy quark evolution at low $p_{{T}}$ while radiative energy loss dominates at high $p_{{T}}$. For D meson $R_{{AA}}$, the crossing point is around 5 GeV at RHIC and around 7 GeV at the LHC. The difference in this crossing point at RHIC and the LHC is mainly caused by different initial charm quark spectra and different QGP flow velocities at these two colliding energies. One can also see that neither collisional nor radiative mechanism alone is sufficient to describe the $p_{{T}}$ dependence of D meson observables.

In Fig. 5 we present contributions from different hadronization mechanisms – fragmentation vs. coalescence – to the heavy-meson observables at RHIC and the LHC. The parameter settings used here are the same as those applied in Fig. 4 above. In the left-hand panels for $R_{{AA}}$, one observes that the coalescence mechanism dominates the D meson yield up to $p_{{T}}\sim 5$ GeV, while fragmentation dominates above that. The coalescence mechanism combines low $p_{{T}}$ charm quarks with thermal light quarks into D mesons, this results in the bump structure in their $R_{{AA}}$ around 2 GeV. Meanwhile, as shown in the right-hand panels, coalescence also enhances the D meson $v_2$ since it adds the larger momentum space anisotropy of thermal light quarks to charm quarks when forming D mesons. At both RHIC and the LHC, introducing the coalescence mechanism is crucial for providing a reasonable description of the D meson observables up to $p_{{T}}\sim 10$ GeV.

Figure 5

Figure 5.  (color online) Effects of different hadronization mechanisms on D meson $R_{{AA}}$ (left-hand panels) and $v_2$ (right-hand panels) at RHIC (upper panels) and the LHC (lower panels).

DownLoad: Full-Size Img PowerPoint

Apart from reliably modeling heavy quark energy loss and hadronization in QGP, the medium profile is also a crucial ingredient for describing the D meson observables in heavy-ion collisions. There are two aspects of medium property: geometry and radial flow. Within our Langevin-hydrodynamics model, one may switch-off the impact of QGP flow on heavy quark evolution by solving the Langevin equation in the center-of-momentum frame of heavy-ion collisions instead of the local rest frame of the fluid. This enables us to investigate the individual contributions to the D meson observables from medium geometry and flow .

In Fig. 6, we compare the results for the D meson $R_{{AA}}$ and $v_{2}$ with and without switching on the QGP flow. The diffusion coefficient is again set as $D_{\rm{s}}(2\pi T) = 3$ (4) at RHIC (the LHC). In the left-hand panels, one can see that the QGP flow accelerates charm quarks and thus strongly enhances the D meson yield (thus the $R_{{AA}}$) from intermediate to high $p_{{T}}$ ($2\sim 10$ GeV), and meanwhile the D meson yield (thus $R_{{AA}}$) decreases at very low $p_{{T}}$. In the right-hand panels, one can see that the effect of QGP flow on the D meson $v_2$ is also quite significant. At low $p_{{T}}$, the anisotropic flow of the QGP is the dominant source for the D meson $v_2$. The impact of medium flow decreases with $p_{{T}}$ and diminishes around 20 GeV. At high $p_{{T}}$, the anisotropic geometry of QGP becomes the dominant origin of the D meson $v_2$ since high $p_{{T}}$ charm quarks lose different amounts of energy when propagating along different paths through the QGP medium. The above results clearly suggest that, when performing heavy and light flavor jet quenching calculations, one should use a realistic hydrodynamic simulation of the QGP evolution that is tuned to describe soft-bulk observables, otherwise, the results may not be reliable.

Figure 6

Figure 6.  (color online) Effects of QGP flow on D meson $R_{{AA}}$ (left-hand panels) and $v_2$ (right-hand panels) at RHIC (upper panels) and the LHC (lower panels).

DownLoad: Full-Size Img PowerPoint

In the end, we explore how the different temperature dependencies of the diffusion coefficient $D_{\rm{s}}$ affect heavy-quark observables in heavy-ion collisions. Reference [88] has shown that the linear dependence of $D_{\rm{s}}(2\pi T)$ on the medium temperature T is a reasonable approximation, as suggested by the lattice QCD calculation and the phenomenological extraction from the model-to-data comparison. In this study, we assume the parameterized form for the diffusion coefficient $D_{\rm{s}}(2\pi T) = a+bT$ and vary the slope parameter b as 0, 7, and 14 GeV^-1. The parameter a is adjusted for our model to provide a reasonable description of the D meson $R_{{AA}}$ at RHIC and the LHC, as shown in the left-hand panels of Fig. 7. With such setups, we compare the results by using three different parameterizations of $D_{\rm{s}}(2\pi T)$: constant (3 at RHIC and 4 at the LHC), $2+(7{\;\rm{GeV}}^{-1})T$, and $(14{\;\rm{GeV}}^{-1})T$.

Figure 7

Figure 7.  (color online) Effects of the temperature dependence of the diffusion coefficient $D_{\rm{s}}(2\pi T)$ on D meson $R_{{AA}}$ (left-hand panels) and $v_2$ (right-hand panels) at RHIC (upper panels) and the LHC (lower panels).

DownLoad: Full-Size Img PowerPoint

In the right-hand panels of Fig. 7, we show the effect of different temperature dependencies of $D_{\rm{s}}$ on the D meson $v_2$ using the above linear approximation. One can see that the effect is negligible at RHIC. At the LHC, it is within 12% at low $p_{{T}}$ and becomes invisible above approximately 8 GeV. It is noted that if one applies a much greater enhancement to the heavy-quark-medium interaction at low temperatures (near $T_{\rm{c}}$) [44, 89], one may observe a larger increase of elliptic flow $v_2$ for D mesons consequent to more energy loss being shifted to a later time in the QGP evolution. However, in the linear approximation of $D_{\rm{s}}(2\pi T)$ vs. T, the effect on the D meson $v_2$ is very limited.

4. Summary

• 1. Introduction
• 2. Production, energy loss, and hadronization of heavy quarks
•      2.1 Initial production of heavy quarks
•      2.2 In-medium evolution of heavy quarks
•      2.3 Hadronization of heavy quarks
• 3. Nuclear modification of heavy flavor mesons
• 4. Summary

We have conducted a systematic study on heavy flavor suppression and flow in heavy-ion collisions at RHIC and the LHC. Using the state-of-the-art Langevin-hydrodynamics framework coupled to the up-to-date hybrid coalescence-fragmentation hadronization model, we have investigated in detail how various components of the heavy quark model contribute to the heavy meson $R_{{AA}}$ and $v_2$ observed in high-energy nuclear collisions.

Our study shows that the energy-loss mechanism, hadronization-mechanism, and medium properties are the most essential factors for correctly describing the heavy flavor observables in heavy-ion collisions. While collisional energy loss dominates the D meson $R_{{AA}}$ up to $p_{{T}} = 5\sim 7$ GeV, radiative energy loss dominates at a higher $R_{AA}$. Neither the collisional nor radiative component alone is sufficient to provide the correct $p_{{T}}$ dependence for the nuclear modification of heavy flavors. The coalescence mechanism in heavy quark hadronization is crucial for describing the D meson $R_{{AA}}$ and $v_2$ up to $p_{{T}} \sim 10$ GeV, beyond which fragmentation dominates. We have also investigated the individual contributions of two major components of the QGP – geometry and radial flow – on the D meson spectra and flow. The result clearly shows that radial flow has a significant effect on both the $R_{{AA}}$ and $v_2$ of D mesons below $p_{{T}}\sim 10$ GeV. However, at higher $p_{{T}}$, $R_{{AA}}$ is mainly determined by the average temperature of the medium and $v_2$ is mostly driven by the geometric anisotropy of the medium.

In our work, we also performed a systematic estimation of the uncertainties in D meson suppression and flow due to different implementations of the initial heavy quark spectra, heavy-quark-medium interaction in the pre-equilibrium stage, and heavy quark diffusion coefficient. While different assumptions for the above aspects have little effect in the high $p_{{T}}$ regime, they do introduce noticeable uncertainties at low $p_{{T}}$. Applying different initial charm quark spectra (FONLL vs. LO) may yield a difference of up to 25% in $R_{{AA}}$ and a 19% difference in $v_2$ for D mesons. The inclusion of the nuclear shadowing effect can reduce the $R_{{AA}}$ up to 27% at low $p_{{T}}$. Delaying the heavy-quark-medium interaction to a later time can increase the D meson $v_2$ when the model is tuned to describe the same $R_{{AA}}$. This effect has been demonstrated consistently from three different perspectives in this work. (1) Delaying the starting time of the heavy-quark-medium interaction from 0.6 fm to 1.2 fm can increase the low $p_{{T}}$ D meson $v_2$ by up to 24%. (2) The free-streaming assumption in the pre-equilibrium stage obtains a $v_2$ up to 39% larger than that obtained by assuming constant temperature and Bjorken evolution profiles for the pre-equilibrium stage. (3) With the linear assumption for the temperature dependence of the heavy quark diffusion coefficient $D_{\rm{s}}(2\pi T)$, one may obtain a $v_2$ up to 12% larger when increasing the heavy-quark-medium interaction at low temperature. However, all these effects become negligible when the D meson $p_{{T}}$ is above 10 GeV. These uncertainties should be considered carefully when interpreting heavy quark phenomenology or using heavy quarks to probe QGP properties in relativistic heavy-ion collisions.

We are grateful to Weiyao Ke for the discussions.

References