-
In recent years, the gauge/gravity duality has been successfully used with strongly coupled systems in condensed matter physics, yielding an important branch of the holographic approach, which is now known as AdS/CMT duality [1]. It is well known that the instability of AdS black holes is essential for explaining the abundant phase structure of condensed matter systems at boundary. Especially, spontaneous breaking of
$ U(1) $ gauge symmetry in the bulk region yields novel black holes with scalar hair, which provides a novel picture for the condensation of superconductivity [2-4]. In contrast, spontaneous breaking of translational invariance yields spatially modulated modes for black holes, which is holographically dual to the formation of charge density waves (CDWs) [5-16]. For high$ T_c $ superconductors, the CDW phase is also known as the pseudo-gap phase and is critical for understanding high$ T_c $ superconductivity [17].Typically, a holographic CDW is formed over an AdS-RN background with translational symmetry. The basic idea is to add unstable terms to the action, such that the
$ BF $ bound of AdS black holes is violated below some value of the Hawking temperature. As a result, the ordinary AdS-RN background becomes unstable and flows to a new configuration, which exhibits a periodic structure along a spatial direction, yielding CDWs. In this paper, we investigate the instability of AdS-RN black holes without translational invariance. In the AdS/CMT duality, a bulk geometry without translational invariance should be constructed for obtaining finite direct current (DC) conductivity for the dual system. If the translational symmetry is preserved, the momentum is conserved, allowing the DC to flow without relaxation, yielding infinite conductivity. This does not happen in practical situations. In the holographic framework, there are two ways to break the translational symmetry by hand (for a brief review, see [18]). One approach is to construct a lattice manifestly by introducing spatially modulated sources in the bulk region [19-23]. However, in this framework, it is very challenging to explore low temperature effects, owing to the numerical difficulties associated with solving partial differential equations (PDEs) [24]. An alternative approach is to introduce the momentum dissipation by linear axion fields, helical lattices, or Q-lattices, which may be called "homogeneous lattices" [25-37]. In these models, although the translation symmetry is broken, the equations of motion are still ordinary differential equations (ODEs) and can be numerically solved even in the zero temperature limit. Remarkably, in this framework, a novel metal/insulator transition has been observed [25], which makes it plausible for studying quantum critical phenomena in the holographic setup with lattices [31].Therefore, it is very desirable to construct holographic CDWs over a lattice background rather than over a background with translational symmetry. This observation provided the main motivation for this work. First, we investigate the instability of AdS black holes with homogeneous lattices, using the perturbation analysis tools. We determine the unstable region in the configuration space in the presence of axion fields and Q-lattices. We demonstrate that the presence of the linear axion field always suppresses the instability of AdS-RN black holes. However, in the Q-lattice framework, we find that in the low temperature limit, the unstable region becomes the smallest near the critical region of the metal/insulator transition. This novel phenomenon is reminiscent of the role of the holographic entanglement entropy, which signals the occurrence of a quantum phase transition.
The remainder of this paper is organized as follows. In Section II, we introduce the holographic model for CDWs and briefly review the instability of AdS-RN black holes. In Section III, we analyze the instability of black holes with momentum relaxation owing to the linear axion fields. Then, we focus on the instability of the Q-lattice background in Section IV. Our results and conclusions are given in Section V.
-
In this section, we introduce a holographic model without a lattice structure in four dimensional spacetime, in which the gravity is coupled to a dilaton field and two massless
$ U(1) $ gauge fields. In the subsequent secitons, we impose a lattice structure based on this setup. The action is given by$ S = \frac{1}{2\kappa^2}\int {\rm d}^4 x \sqrt{-g} \ {{\cal{L}}_1}, $

(1) where
$\begin{aligned}[b] {{\cal{L}}_1} =& R-\frac{1}{2}\left ( \nabla \Phi \right )^2-V\left ( \Phi \right ) \\&-\frac{1}{4}Z_{A}(\Phi )F^2 -\frac{1}{4} Z_{B}(\Phi )G^2 \\&-\frac{1}{2} Z_{AB}(\Phi )FG, \end{aligned}$

(2) with
$ F = dA $ and$ G = dB $ . Two gauge fields A and B correspond to two global$ U(1) $ symmetries on the boundary. We will treat gauge field B as the electromagnetic field and will consider its transport properties. The real dilaton field$ \Phi $ will be viewed as the order parameter of the translational symmetry breaking. We propose that functions$ V,\ Z_A, $ $ Z_{B}, \ Z_{AB} $ should have the following forms:$ \begin{aligned}[b] \;\; V ( \Phi ) =& -\frac{1}{L^{2}} + \frac{1}{2}m_{s}^{2}\Phi ^{2}, \\ Z_{A}(\Phi ) =& 1-\frac{\beta }{2} L^2 \Phi^2,\\ Z_{B}(\Phi ) =& 1,\\ Z_{AB}(\Phi ) =& \frac{\gamma }{\sqrt{2}} L \Phi. \end{aligned} $

(3) In the above setup, two important terms are introduced. One is the
$ \beta $ -term, which is essential for inducing the instability of AdS-RN black holes for forming CDWs. The other$ \gamma $ -term is not essential and just drives the tip of the unstable dome deviating from$ k_c = 0 $ .The equations of motion are given by
$ \begin{aligned}[b] R_{\mu \nu }-T_{\mu \nu }^{\Phi }-T_{\mu \nu }^{A }-T_{\mu \nu }^{B }-T_{\mu \nu }^{AB } =& 0, \\ \nabla ^{2} \Phi -\frac{1}{4}Z_{A}' F^2 -\frac{1}{4}Z_{B}' G^2 -V' =& 0, \\ \nabla_{\mu }(Z_A F^{\mu \nu }+Z_{AB} G^{\mu \nu }) =& 0, \\ \nabla_{\mu }(Z_B G^{\mu \nu} +Z_{AB} F^{\mu \nu } ) =& 0, \end{aligned} $

(4) where
$ \begin{aligned}[b] T_{\mu \nu }^{\Phi } =& \frac{1}{2} \nabla_{\mu }\Phi \nabla_{\nu }\Phi +\frac{1}{2}V g_{\mu \nu }, \\ T_{\mu \nu }^{A } =& \frac{Z_{A}}{2} \left(F_{\mu \rho }F^{\rho }_{\nu }- \frac{1}{4} g_{\mu \nu }F^2\right), \\ T_{\mu \nu }^{B } =& \frac{Z_{B}}{2} \left(G_{\mu \rho }G^{\rho }_{\nu }- \frac{1}{4} g_{\mu \nu }G^2\right), \\ T_{\mu \nu }^{AB } =& Z_{AB} \left(G_{ (\mu | \rho | }F^{\rho }_{\nu )}- \frac{1}{4} g_{\mu \nu }GF\right). \end{aligned} $

(5) The equations of motion admit a planar AdS-RN black hole as a solution, with translational symmetry along both the x and y directions, which is given as
$ \begin{aligned}[b] {\rm d}s^{2} =& \frac{1}{z^2}\left[-(1-z)p(z){\rm d}t^{2}+\frac{{\rm d}z^{2}}{(1-z)p(z)}+{\rm d}x^{2} +{\rm d}y^{2}\right], \\ A_t =& \mu(1-z), \;\;\ \Phi = 0, \ \;\; B = 0, \end{aligned} $

(6) where
$ p(z) = 4 \left(1+z+z^2-\dfrac{\mu^2 z^3}{16} \right) $ , and$ \mu $ is the chemical potential of gauge field A. In this system of coordinates, the black hole horizon is located at$ z = 1 $ , and the AdS boundary is at$ z = 0 $ . The Hawking temperature of the black hole is simply given by$ T/ \mu = (48-\mu^2)/(16 \pi \mu) $ . Throughout this paper, we set the AdS radius to$ l^2 = 6L^2 = 1/4 $ . Without loss of generality, two coupling constants are$ \beta = -94 $ and$ \gamma = 16.4 $ .In the instability analysis of AdS black holes, the key point is that, in the zero temperature limit, the near horizon geometry of AdS-RN black holes will be
$ AdS_2 \times R^2 $ . Once the$ BF $ bound of$ AdS_2 $ is violated, the near horizon geometry becomes unstable and flows to a new solution as the infrared fixed point, which is characterized by the appearance of spatially modulated modes in the bulk region. Such analogous instability remains at a finite temperature for AdS-RN black holes (for details we refer to [5]). Specifically, we consider the following perturbations for examining the instability of electrically charged AdS-RN black holes:$ \begin{aligned}[b] \delta \Phi =& \phi (z) \cos (k x), \\ \delta B =& b_{t} (z) \cos (k x). \end{aligned} $

(7) The instability of the background is signaled by the existence of non-trivial solutions to the perturbation equations of
$ \delta \Phi $ and$ \delta B $ , which spontaneously break the translational symmetry along the x direction. Taking the AdS-RN as the background and substituting (7) into the equations of motion (4), we obtain two coupled linear differential equations for$ \phi (z) $ and$ b_{t} (z) $ . We impose the regular boundary condition at the horizon,$ z = 1 $ . While near the AdS boundary$ z = 0 $ , we can expand$ \phi(z) $ and$ b_t(z) $ as$ \begin{aligned}[b]\phi (z) \approx & \phi _{s} z^{3-\Delta _{\phi }} +\phi _{o} z^{\Delta _{\phi}}+\cdots, \\ b_{t}(z) \approx & b_{s} z^{2-\Delta _{B}} + b_{o}z^{\Delta _{B}-1}+\cdots, \end{aligned} $

(8) where
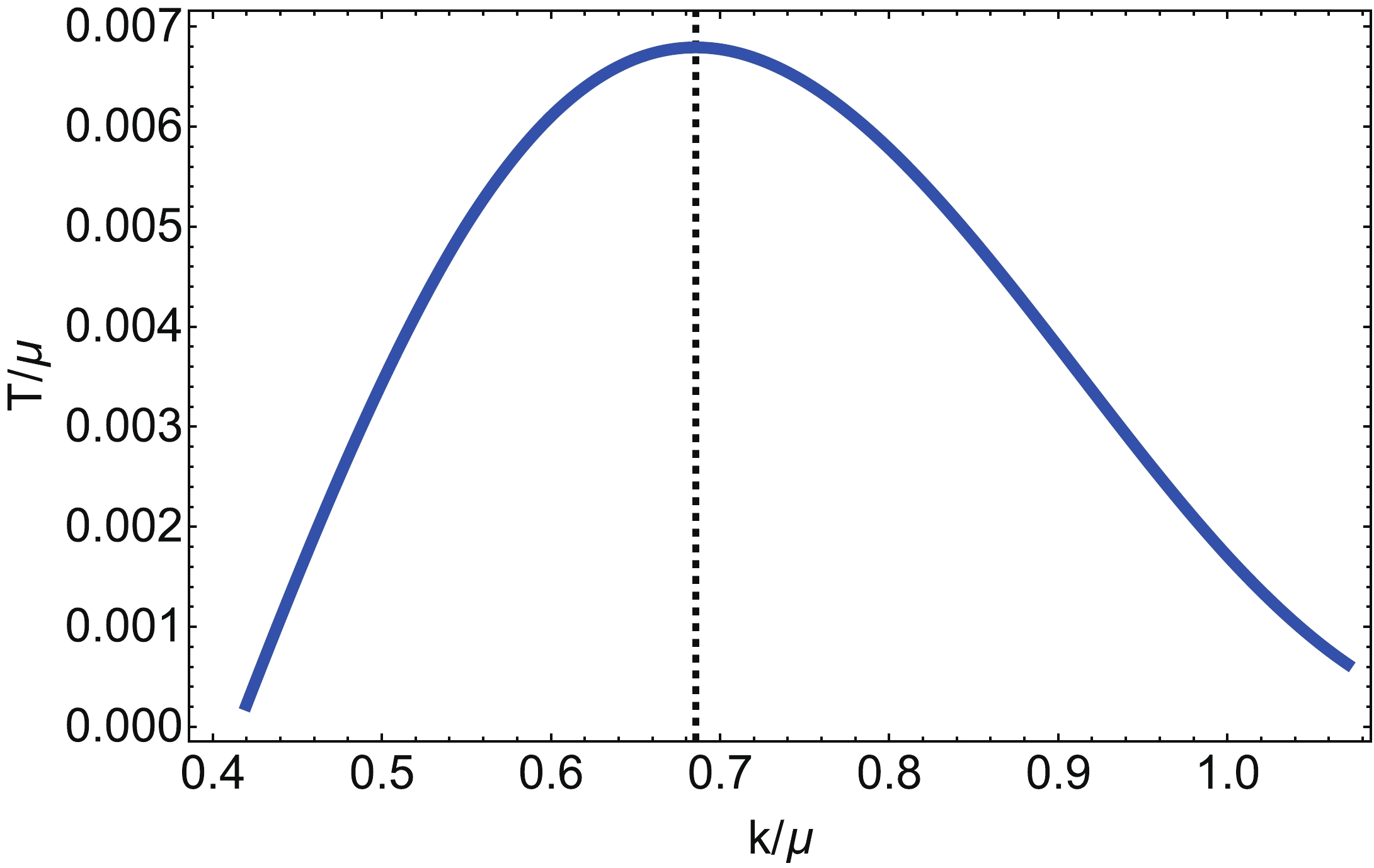
$ \Delta _{\phi } = 3/2 +\sqrt{9/4+m_{s }^2 l^2} $ and$ \Delta _{B } = 2 $ . We turn off the source terms, namely$ \phi_s = b_s = 0 $ . Whether there exist non-trivial solutions to these equations depends on the wave number k as well as the Hawking temperature of the black hole background. For illustration, we set the dilaton mass$ m_{s}^{2} = -2/l^2 = -8 $ . In Fig. 1, we plot the critical temperature as a function of the wave number. Clearly, the curve is bell shaped, with a dome-like unstable region. The highest critical temperature is$ T_{\rm max}/ \mu \approx 0.0068 $ , for the wave number$ k_c/ \mu \approx 0.6856 $ . Within the dome, the AdS-RN black hole becomes unstable, and the charge density of gauge field B becomes spatially modulated. -
In this section, we consider the instability of black holes without translational invariance by adding axion fields into the above action, which becomes
$ S = \frac{1}{2\kappa^2}\int {\rm d}^4 x \sqrt{-g} \ ({{\cal{L}}_1}+{\cal{L}}_{\rm axions}), $

(9) with
$ {{\cal{L}}_1} $ given by (2), and$ {\cal{L}}_{\rm axions} = -\frac{1}{2}\sum\limits_{a = 1}^{2}(\nabla \chi _{a} )^2, $

(10) where
$ \chi _{a} $ are two real, massless scalar fields. This model allows a very simple but exact solution with momentum relaxation, which is given as$ \begin{aligned}[b] {\rm d}s^{2} =& \frac{1}{z^2}\left[-(1-z)U(z){\rm d}t^{2}+\frac{{\rm d}z^{2}}{(1-z)U(z)}+{\rm d}x^{2} +{\rm d}y^{2}\right], \\ A_t =& \mu(1-z),\;\;\; \chi _{1} = \alpha x ,\;\;\; \chi _{2} = \alpha y ,\;\;\; \Phi = 0, \;\;\;\ B = 0, \end{aligned} $

(11) where
$ U(z) = 4+4z -\frac{1}{2}(\alpha^{2} -8)z^{2} -\frac{1}{4} \mu^{2} z^{3} $ . The Hawking temperature of the black hole is given by$ T/ \mu = $ $ (48-\mu^2-2\alpha^{2} )/(16 \pi \mu) $ . The axion fields introduce momentum relaxation in both the x and y directions, leading to a finite DC conductivity [27]. Here, we are concerned with its impact on the instability of the background. Without loss of generality, we turn to the same perturbations as in (7). To find the critical temperature, we do not need to solve the perturbation equations directly. Instead, we extract the mass terms from the perturbation equations of$ \delta \Phi $ and$ \delta B $ , which form a matrix. The matrix elements are functions of the wave number k as well as the temperature T. Above the critical temperature, all the eigenvalues of this matrix are always positive for arbitrary k, implying the system is stable with respect to perturbations. As the temperature decreases, the critical temperature is signaled by one of the eigenvalues of the matrix becoming zero for some special k. This corresponds to the critical temperature, because the mass terms become negative and violate the BF bound of black holes as the temperature further decreases, indicating the system instability, such that non-trivial solutions to the perturbation equations exist. Such an eigenvalue problem of mass terms has been studied in detail previously [21, 28]. The left panel in Fig. 2 shows the critical temperature versus the wave number$ k/\mu $ and the amplitude of axion fields$ \alpha/ \mu $ . It is obvious that, with increase in the amplitude$ \alpha/ \mu $ , the unstable region becomes smaller, indicating that the instability of the black hole is suppressed by the presence of the axion field. We also plot the highest critical temperature$ T_{\rm max}/ \mu $ and the corresponding wave number$ k_c/ \mu $ as a function of$ \alpha/ \mu $ , as illustrated by the middle and right panels of Fig. 2. We notice that$ k_c/ \mu $ grows linearly with large$ \alpha/ \mu $ , while$ T_{\rm max} / \mu $ drops down quickly with$ \alpha/ \mu $ . This phenomenon is similar to what was observed for other holographic models [38].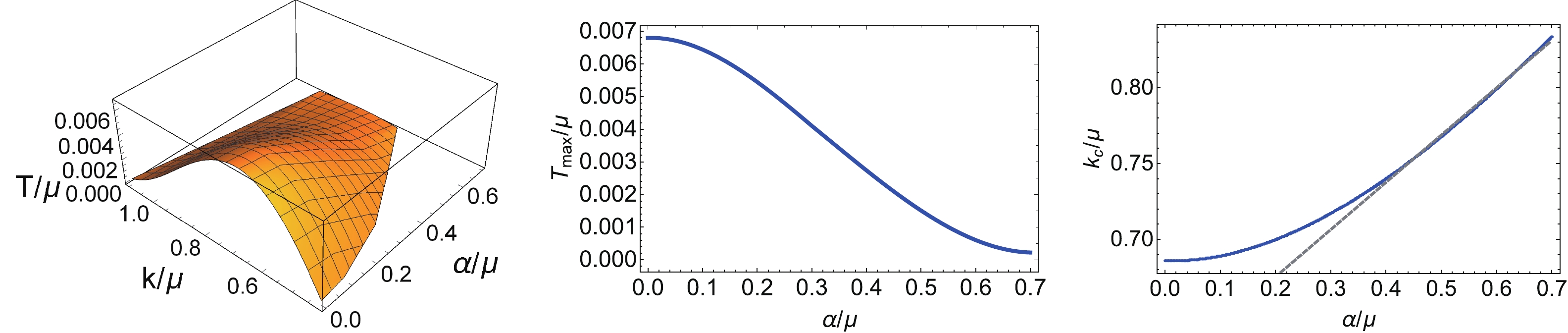
Figure 2. (color online) Left: critical temperature versus the wave number
$ k / \mu $ and the amplitude of the axion field$ \alpha/ \mu $ . Middle: maximal critical temperature$ T_{\rm max}/ \mu $ versus the amplitude of the axion field$ \alpha/ \mu $ . Right: the wave number$ k_c $ versus the amplitude of the axion field$ \alpha/ \mu $ . -
In this section, we consider the instability of black holes with the Q-lattice [26]. Now, the action becomes
$ S = \frac{1}{2\kappa^2}\int {\rm d}^4 x \sqrt{-g} \ ({{\cal{L}}_1}+{\cal{L}}_{Q}), $

(12) with
$ {{\cal{L}}_1} $ from (2) and$ {\cal{L}}_{Q} = -(\left | \nabla \Psi \right |^{2} + m_{q} \left | \Psi \right |^{2} ), $

(13) where
$ \Psi $ is a complex scalar field. Then, the Einstein equations become$ R_{\mu \nu }-T_{\mu \nu }^{\Phi }-T_{\mu \nu }^{A }-T_{\mu \nu }^{B }-T_{\mu \nu }^{AB } -T_{\mu \nu }^{\Psi} = 0, $

(14) with
$ T_{\mu \nu }^{\Phi } $ $ T_{\mu \nu }^{A } $ ,$ T_{\mu \nu }^{B } $ ,$ T_{\mu \nu }^{AB } $ from (4) and$ T_{\mu \nu }^{\Psi} = \nabla_{\mu }\Psi \nabla_{\nu }\Psi ^{*} + \frac{1}{2} m_{q}^{2}\left | \Psi \right |^{2} g_{\mu \nu }. $

(15) In addition, we have the equation of motion for
$ \Psi $ :$ ( \nabla ^{2} - m_{q})\Psi = 0. $

(16) We consider the following ansatz for the electrically charged AdS-RN black hole on the Q-lattice:
$ \begin{aligned}[b] {\rm d}s^{2} =& \frac{1}{z^2}\left[-(1-z)p(z)U{\rm d}t^{2}+\frac{{\rm d}z^{2}}{(1-z)p(z)U}+ V_1 {\rm d}x^{2} + V_2 {\rm d}y^{2}\right], \\ A_t =& \mu(1-z)a,\;\; \Psi = {\rm e}^{{\rm i}k_q x} z^{3-\Delta_q }\psi ,\;\; \ \Phi = 0,\;\; \ B = 0, \end{aligned} $

(17) with
$ \Delta_q = 3/2 \pm(9/4 + m_{q}^2 l^2) $ . We set the mass of the scalar field to$ m_{q}^{2} = -8 $ . Note that U,$ V_1 $ ,$ V_2 $ ,$ \psi $ , and a are functions of the radial coordinate z only. The Hawking temperature is$ T/ \mu = (48-\mu^2)/(16 \pi \mu) $ . If one sets$ U = V_1 = V_2 = a = 1 $ and$ \psi = 0 $ , we return to the standard AdS-RN black hole. For the non-trivial Q-lattice solution, the boundary conditions at$ z = 0 $ are given by$ U = V_1 = V_2 = a = 1,\;\;\; \ \psi = \lambda ,\;\;\; \ \Phi = 0,\;\;\; \ B = 0, $

(18) and we consider the regular boundary condition for the horizon. As a result, a typical black hole solution for the Q-lattice is characterized by three scale invariant parameters, which are
$ T/ \mu $ ,$ \lambda/ \mu $ , and$ k_q/ \mu $ .One remarkable feature of these Q-lattice backgrounds is that they exhibit a novel metal/insulator transition when the lattice parameters
$ \lambda/ \mu $ and$ k_q/ \mu $ are adjusted in the low temperature limit [25]; the phase diagrams for metal/insulator phases for Q-lattice backgrounds have been studied in Refs. [28, 31]. For a given background, the DC conductivity can be expressed in terms of the horizon data as$ \sigma _{\rm DC} = \left(\sqrt{\frac{V_{2}}{V_{1}}}+\frac{\mu ^{2}a^{2}\sqrt{V_{1}V_{2}}}{k_q^{2} \psi^{2} }\right )|_{z = 1}. $

(19) Throughout this paper, we identify the metallic phase and the insulating phase by evaluating Eq. (19) around
$ T/\mu = 0.001 $ . The quantum critical line is given by$ \partial _{T} \sigma _{\rm DC} = 0 $ . In Fig. 3, we demonstrate the phase diagram for the Q-lattice system.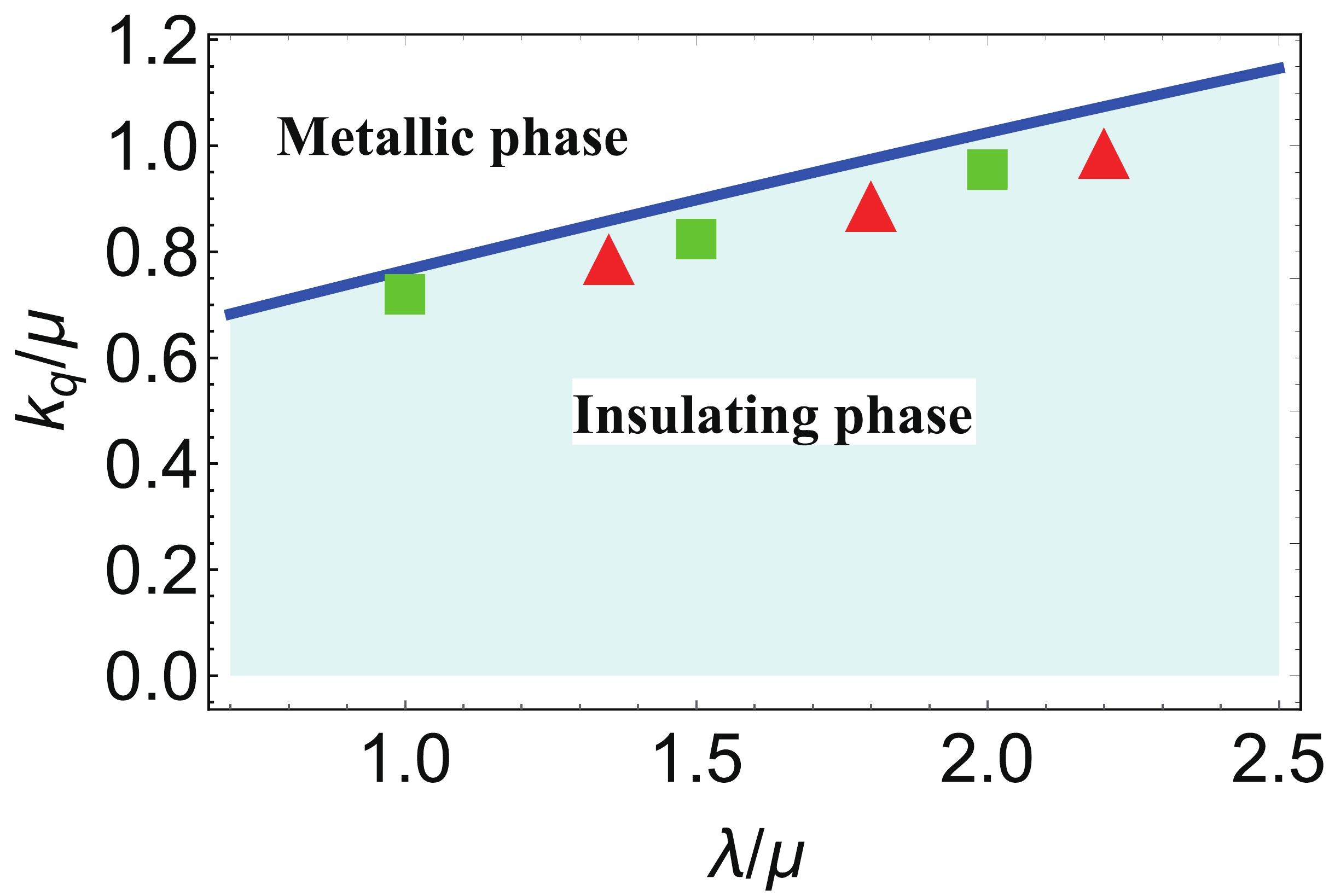
Figure 3. (color online) The phase diagram for the Q-lattice system at temperature
$ T/\mu = 0.001 $ . The red triangles stand for the valleys of the highest critical temperatures$ T_{\rm max}/\mu $ when varying$ \lambda/ \mu $ at fixed$ k_q/ \mu $ . The green squares stand for the valleys of the highest critical temperatures$ T_{\rm max} /\mu $ when varying$ k_q/ \mu $ at fixed$ \lambda/ \mu $ .Now, we focus on the instability of these black holes with lattices. We consider the same perturbations as in (7). In Fig. 4, we plot the unstable region of the background for different values of
$ \lambda/ \mu $ , for the wave number of the Q-lattice$ k_q/\mu $ fixed at$ k_q/ \mu = 0.8 $ and$ k_q/\mu = 0.9 $ . The region below each curve is the unstable region, in which spatially modulated modes with the wave number$ k/\mu $ may emerge. In contrast to the results observed for the axion model in the previous section, we found here that the unstable region does not change monotonously with the lattice parameter anymore. To our surprise, we found that the unstable region shrinks with increase in$ \lambda/\mu $ at first but widens again later. To present these findings in a more transparent manner, we mark the highest critical temperature$ T_{\rm max}/\mu $ with a red dot on each curve and denote the corresponding wave number as$ k_c/\mu $ . Then, we plot$ T_{\rm max}/\mu $ and$ k_c/\mu $ as functions of the lattice amplitude$ \lambda/ \mu $ , and the result is shown in Fig. 5. Clearly,$ T_{\rm max}/\mu $ reaches a minimum and then rises up again with increase in$ \lambda/ \mu $ . Going back to the phase diagram of the Q-lattice, we find that the turning points are quite close to the critical line for the metal/insulator transition. To check this, we also plot the unstable region of the background for different values of$ k_q/ \mu $ , while fixing the lattice amplitude$ \lambda/ \mu $ , and the result is shown in Fig. 6. Correspondingly,$ T_{\rm max}/\mu $ and$ k_c/\mu $ as functions of the wave number$ k_q/ \mu $ are plotted in Fig. 7. Again, we find that the turning points of$ T_{\rm max}/\mu $ are quite close to the critical line, as marked in Fig. 3. Since the curve with the minimal value of$ T_{\rm max}/\mu $ encloses the smallest region of instability, as illustrated in Fig. 4, we conclude that the black hole background in the vicinity of the metal/insulator transition is the most stable solution under the perturbations of spatially modulated modes given by (8).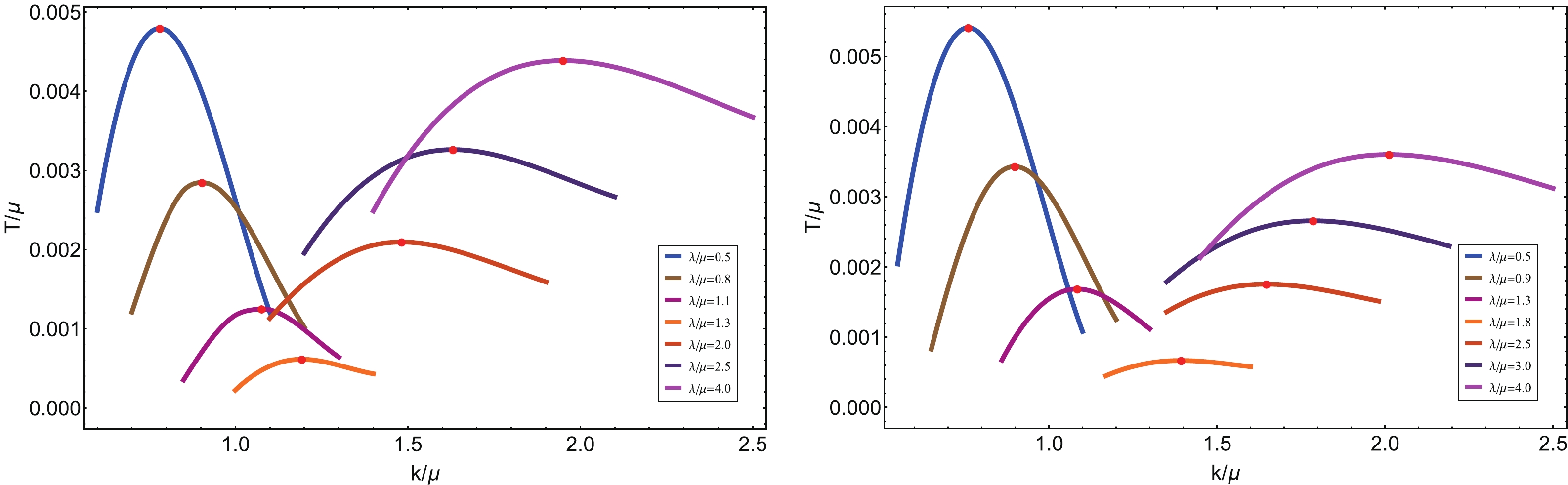
Figure 4. (color online) The unstable region of the background for different values of
$ \lambda/ \mu $ , for the wave number of the Q-lattice$ k_q $ fixed at$ k_q/ \mu = 0.8 $ (left) and$ k_q/\mu = 0.9 $ (right). The red dots mark the highest critical temperature for each curve, for the corresponding wave number$ k_c/ \mu $ .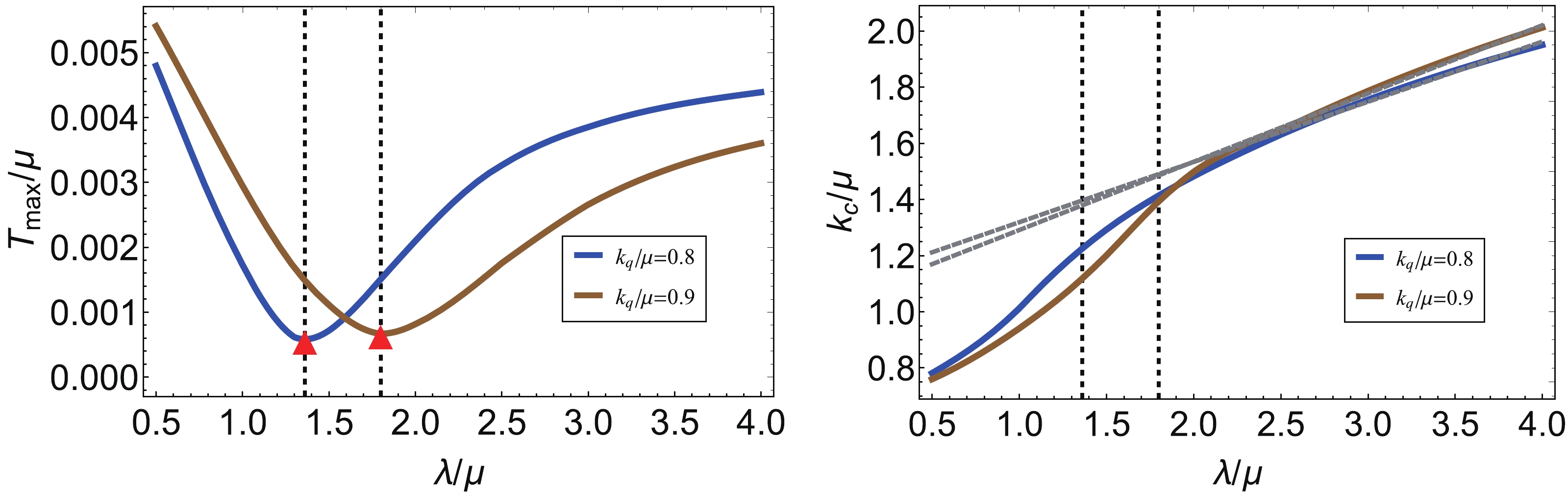
Figure 5. (color online) Maximal critical temperature
$ T_{\rm max}/\mu $ and wave number$ k_c/\mu $ versus the lattice amplitude$ \lambda/ \mu $ , for wave numbers$ k_q/ \mu = 0.8 $ and$ k_q/\mu = 0.9 $ .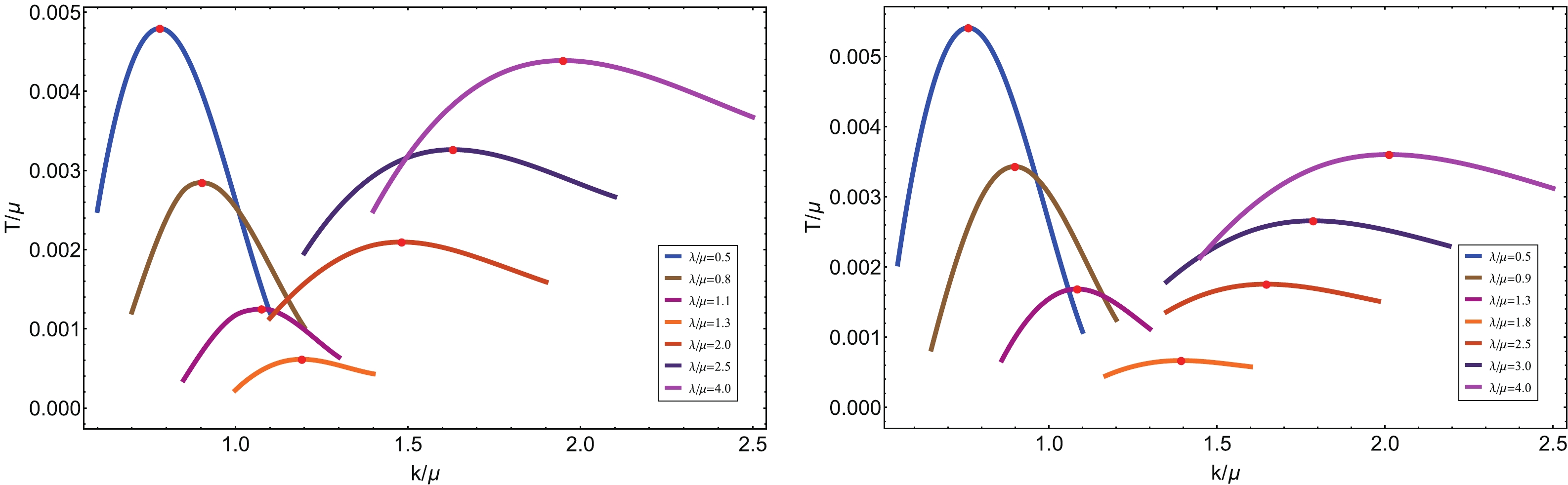
Figure 6. (color online) The unstable region of the background for different values of
$ k_q/ \mu $ , for the lattice amplitude$ \lambda/ \mu $ fixed at$ \lambda/ \mu = 1 $ (left) and$ \lambda/\mu = 2 $ (right). The red dots mark the highest critical temperature for each curve, for the corresponding wave number$ k_c/ \mu $ .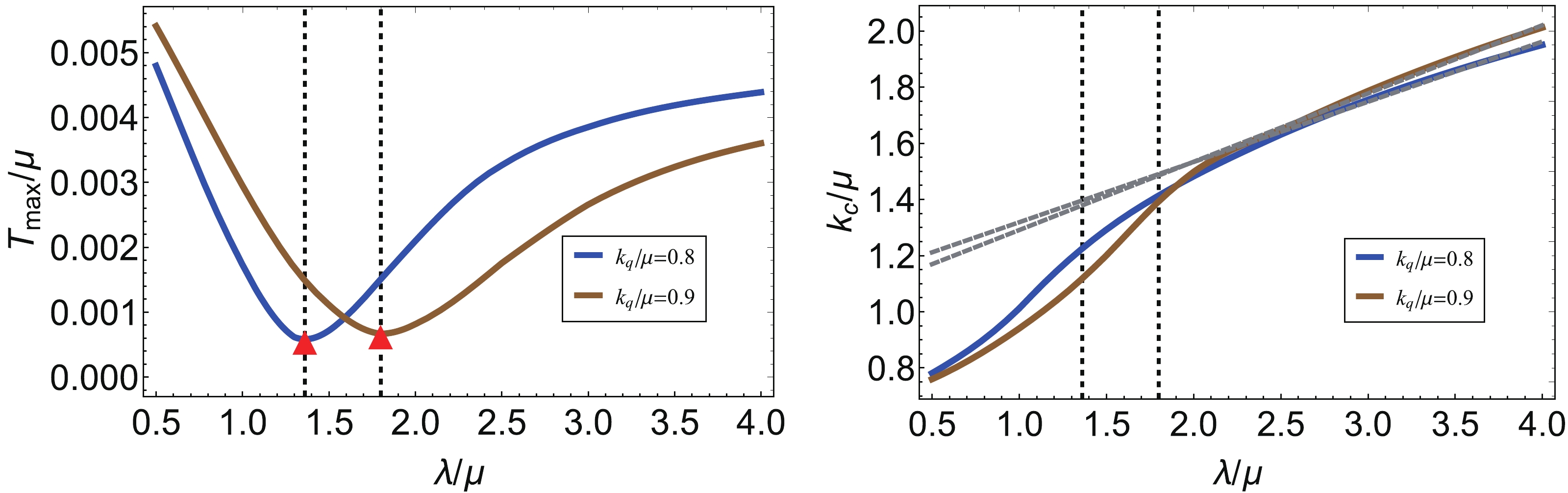
Figure 7. (color online) Maximal critical temperature
$ T_{\rm max}/\mu $ and wave number$ k_c/\mu $ versus the lattice wave number$ k_q/ \mu $ , for amplitudes$ \lambda/ \mu = 1 $ and$ \lambda/ \mu = 2 $ .First of all, it is quite interesting to compare the change in
$ T_{\rm max}/ \mu $ for CDWs with that of superconductivity with the change in the Q-lattice parameters; this was previously addressed in [28]. We find that the critical temperature of superconductivity is always suppressed by the presence of the Q-lattice. When the lattice effect is sufficiently strong, the critical temperature of superconductivity drops down to zero, such that the superconducting phase disappears. However, for CDWs, the critical temperature increases again with increases in the values of the lattice parameters, which means the background becomes more unstable and it is easier to form a new background with CDWs. This difference may be understood based on the phase diagram of the Q-lattice background, as shown in Fig. 3. For large$ \lambda/\mu $ , the dual system falls into a deep insulating phase. Therefore, it is more difficult to induce superconductivity over such insulating phases. On the contrary, the CDW phase itself is an insulating phase. Thus, such a background dual to a deep insulating phase assists in the formation of CDWs.This phenomenon indicates that the instability of the background might be useful for characterizing the occurrence of quantum phase transitions. It is well known that, in the absence of ordinary order parameters, it is very difficult to diagnose quantum phase transitions. Previously, a role for the holographic entanglement entropy in diagnosing quantum phase transitions has been suggested in a series of papers [31, 33, 39]. The holographic entanglement entropy or its derivative with respect to system parameters exhibits a peak or a valley in the vicinity of the critical region. Here, we found that
$ T_{\rm max}/ \mu $ of CDWs exhibits a similar behavior as the entanglement entropy. Physically, it implies that the system becomes rather stable with respect to the perturbations with spatially modulated modes near the critical point of a quantum phase transition in the zero temperature limit. Intuitively, this can be explained as follows. The formation of CDWs over a fixed background results from a thermodynamic phase transition. Near the critical point of a quantum phase transition, the system becomes long-range correlated, such that the effects of thermal perturbations are suppressed, yielding a more stable background with the lowest$ T_{\rm max}/ \mu $ .Finally, we comment on the commensurability of these black holes with lattices, which involves comparing the wave number of the CDW, namely
$ k_c/ \mu $ , with the wave number of the corresponding lattice. We plot$ k_c/ \mu $ as a function of the lattice amplitude$ \lambda/ \mu $ in Fig. 5 and as a function of the wave number of the Q-lattice$ k_q/ \mu $ in Fig. 7. We find that$ k_c/ \mu $ grows linearly with the amplitude of the Q-lattice$ \lambda/ \mu $ for large$ \lambda/ \mu $ . However, it decreases with the wave number of the Q-lattice$ k_q/ \mu $ for large$ k_q/ \mu $ . No manifest effect or phenomenon is observed for$ k_c/ \mu = k_q/ \mu $ . The commensurability seems absent in this setup, similar to the result observed in [38]. -
In this paper, we have investigated the instability of black holes with momentum relaxation. We found that the presence of linear axion fields suppresses the instability of AdS-RN black holes. The wave number
$ k_c/ \mu $ of spatially modulated modes grows linearly with the axion field$ \alpha/ \mu $ for large$ \alpha/ \mu $ . More importantly, in the Q-lattice framework, we have demonstrated that, in the zero temperature limit, the unstable dome is the smallest near the critical region of the metal/insulator transition. The highest critical temperature$ T_{\rm max}/\mu $ displays a valley near the critical points of the metal/insulator transition. This novel phenomenon is reminiscent of the behavior of the holographic entanglement entropy during quantum phase transitions. We conjecture that any instability of the background leading to a thermodynamic phase transition would be greatly suppressed in the critical region of a quantum phase transition, since in this region, the system becomes long-range correlated. The commensurate effect is absent in both models with homogeneous lattices, similar to the results obtained in [39].In this paper, we have only presented the perturbation analysis for a fixed background, for justifying the instability of this background. To explicitly construct a new background with both lattices and CDWs, one needs to go beyond the perturbation analysis and solve all the equations of motion numerically, which are PDEs rather than ODEs. It is completely plausible to obtain such solutions at normal temperatures, as suggested by [5, 6]. However, as we mentioned in the introduction, finding numerical solutions becomes rather difficult in the zero temperature limit. Our analysis of the instability of black holes, presented in this paper, sheds light on the construction of CDW backgrounds with the Q-lattice in the zero temperature limit, since the critical temperature and the unstable region have been manifestly disclosed at extremely low temperatures.
The phase diagram for high
$ T_c $ superconductivity exhibits a very rich structure, with many universal features. Currently, it is still challenging to exactly duplicate this phase diagram in the holographic approach. Based on our current work, one may further introduce a complex scalar field as the order parameter of superconductivity and consider the condensation of superconductivity owing to the$ U(1) $ gauge symmetry breaking. Then, it will be quite interesting to investigate the relationship between CDWs and superconductivity for such a lattice background. -
We are very grateful to Peng Liu, Yuxuan Liu, Chao Niu, Jianpin Wu, and Zhuoyu Xian for helpful discussions and former collaborations on building holographic lattices.
Instability of AdS black holes with lattices
- Received Date: 2020-09-02
- Available Online: 2021-02-15
Abstract: Anti-de Sitter (AdS) black holes with lattices are essential for optical conductivity studies in the holographic approach. We investigate the instability of these black holes that can result in the holographic description of charge density waves. In the presence of homogeneous axion fields, we show that the instability of AdS-Reissner-Nordström (AdS-RN) black holes is always suppressed. However, in the presence of Q-lattices, we find that the unstable region becomes the smallest in the vicinity of the critical region for the metal/insulator phase transition. This novel phenomenon is reminiscent of the behavior of the holographic entanglement entropy during quantum phase transitions.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: