-
Heavy ion collisions (HICs) provide crucial insights into the features of the nuclear equation of state (EOS) and the in-medium
$ NN $ cross sections for a wide range of densities, temperatures, and neutron-proton asymmetries. However, the transient states of compressed/expanded nuclear matter during a reaction, such as the pressure and density, cannot be directly measured due to the spatial-temporal scale of reaction systems, which is beyond the capability of measurement. To extract the EOS or in-medium$ NN $ cross sections, the transport models used to simulate the HICs are indispensable.Many transport codes have been developed to extract the isospin asymmetric nuclear EOS and in-medium
$ NN $ cross sections [1-21]. However, the model dependences of the constraints of symmetry energy [22-32] and in-medium$ NN $ cross sections [33-38] become apparent as different conclusions could be drawn from the same data. This situation led to the idea of a systematic comparison and evaluation of transport codes under controlled conditions [39-42]. Previous studies in this direction were dedicated to the comparison of transport model predictions for Au+Au collisions [39], and for benchmarking the treatment of nucleon-nucleon collisions and Pauli blocking [40] and$ \Delta $ production [41] in box calculations with the cascade mode. Comparisons of the mean field have been performed in box calculations with the Vlasov mode [42]. Currently, the observed differences in the reaction path and corresponding observables mainly result from differences in the initialization of the systems and in the treatment of Pauli blocking effects. The latter, i.e., Pauli blocking, describes the statistical ability to populate the final states in a fermionic system in the gain (loss) term of the transport equation, and it is crucial for simulating the low-intermediate energy HICs in transport models.The Pauli blocking algorithms in the Boltzmann-Uehling-Uhlenbeck (BUU) approach and quantum molecular dynamics (QMD) approach are different. In the BUU approach, Pauli blocking may be improved by increasing the number of test particles to infinity. In the QMD approach, a fixed width of Gaussian wave packet is used to represent a nucleon. This leads to a strong fluctuation, which is important in physics for describing cluster formation and multifragmentation, but underestimates the Pauli blocking effect as in Ref. [40]. Consequently, one can expect that the successful
$ NN $ collision rate could be overestimated in the transport codes, and thus, the extracted model dependent in-medium$ NN $ cross sections deviate from their real values. Moreover, owing to the difficulties in the descriptions of Pauli blocking in the QMD approach, different Pauli blocking algorithms have been developed in QMD codes [40]. Thus, studying the theoretical uncertainties in the transport model calculations is a consensus for reliably extracting the related physics and improving the reliability of models.The goal of this work is to learn the systematic deviation of the Pauli blocking ratio compared to the analytical values and evaluate the uncertainties of nuclear stopping power caused by different Pauli blocking algorithms in the simulations of HICs, which are mainly used to extract the in-medium
$ NN $ cross sections. All the calculations are performed within the framework of the improved QMD model (ImQMD) [3, 43-45], but the Pauli blocking algorithms are replaced by three typical algorithms.The paper is organized as follows: In Sec. II, we briefly describe the three typical Pauli blocking algorithms in the market and the in-medium
$ NN $ cross sections we try to analyze. In Sec. III, the successful/attempted collision rates and Pauli blocking ratios obtained with different Pauli blocking algorithms in the nuclear matter, the finite nucleus, and the HICs are presented and discussed. Furthermore, a simple discussion on the influence of in-medium$ NN $ cross sections on the stopping power is also presented. We do not compare the model calculations with the data for extracting the real values of in-medium$ NN $ cross sections in this work, because the Pauli blocking algorithms still need to be improved. A summary and outlook are given in Sec. IV. -
In this section, we only mention the three typical Pauli blocking algorithms that are directly related to the Uehling-Uhlenbeck factor in the transport equation, and the in-medium
$ NN $ cross sections that we used. There are also some efforts to improve the Pauli blocking in the transport codes by adding additional constraints [10, 35, 46, 47], but we do not discuss those in this work. More details about the mean field potential and the treatment of nucleon-nucleon collision in the ImQMD model can be found in Refs. [3, 43-45]. -
In the QMD type models, each nucleon is represented by a Gaussian wave packet,
$ \psi_i({{r}}) = \frac{1}{(2\pi\sigma_r^2)^{3/4}}{\rm e}^{{\textstyle -\frac{({{r}}-{{r}}_{i})^2}{4\sigma_r^2}}+{\rm i}{{r}}\cdot {{p}}_{i}/\hbar},\ i = 1, \cdots, A $

(1) where
$ \sigma_r $ and${{r}}_{i}$ are the width and centroid of the wave packet, respectively. Its Wigner density reads$ f_{W,i}({{r}},{{p}}) = \frac{1}{(\pi\hbar)^{3}}{\rm e}^{\textstyle -\frac{({{r}}-{{r}}_{i})^2}{2\sigma_r^2}-\frac{({{p}}-{{{p}}_{i}})^2}{2\sigma_p^2}}, $

(2) where
$ \sigma_r\sigma_p = \hbar/2 $ . The Wigner density expresses the probability density of the simultaneous values of${{r}}$ and${{p}}$ for the ith nucleon. When Eq. (2) is integrated with respect to${{p}}$ , the correct probability in coordinate space$ |\psi_i({{r}})|^2 $ is given; if we integrate Eq. (2) with respect to${{r}}$ , the correct probability in momentum space$|C_i({{p}})|^2$ can also be verified [3].In the treatment of the collision of
$ i+j\to i'+j' $ at a certain time step in the code, the positions of particle i and j are kept the same before and after the collision, i.e.,${{r}}_i = {{r}}'_{i}$ ,${{r}}_j = {{r}}'_{j}$ , while the momenta of particles i and j are changed, i.e.,$ p_i+p_j\to p'_i+p'_j $ . Thus, the probability of the final state$ p'_i $ occupied by other nucleons, i.e.,$ P(p'_i) $ , can be calculated based on$\sum_{j\ne i} f_{W,j}({{r}},{{p}})$ in the phase-space cell around$ p'_i $ . In the following discussions, we briefly mention the methods of the calculation of$ P(p'_i) $ , such as PB-Wigner, PB-Husimi, and PB-HSP, which are adopted in the different QMD codes. -
For the PB-Wigner algorithm, the probability of the final state
$ p'_i $ being occupied by other particles is expressed as$P_\tau(p'_i) = P_\tau({{r}}_i, {{p}}'_i)$ ,$\begin{aligned}[b] P_{\tau}({{r}}_i,{{p}}'_i) =& \frac{1}{2/h^3}\sum_{j\in\tau, j\ne i} f_{W,j}({{r}}_i,{{p}}'_i)\\ =& 4\sum_{j\in\tau(j\neq i)}^{A} \exp \left[-\frac{({{r}}_{i}-{{r}}_{j})^{2}}{2\sigma_{r}^{2}}\right]\times \exp\left[-\frac{({{p}}'_{i}-{{p}}_{j})^{2}}{2\sigma_{p}^{2}}\right], \end{aligned}$

(3) with
$ \tau = n $ or p. The factor$ 2/h^3 $ results from consideration of the spin in the phase-space cell.$ P_\tau(p'_i) $ could be larger than 1, because of the fluctuation and the semi-classical transport equation. If the occupation probability$P_\tau({{r}}_i,{{p}}'_i)$ is larger than$ 1 $ , the occupation probability$P_\tau({{r}}_i,{{p}}'_i)$ is replaced by$\min{(P_\tau({{r}}_i,{{p}}'_i),1)}$ . The PB-Wigner method is used in ImQMD [3, 43-45], IQMD-BNU [8], JAM [11, 12], JQMD [13, 14], and UrQMD [6, 15, 35]. In the ImQMD and UrQMD models, additional criteria are also adopted to enhance the Pauli blocking ratio [35, 43], but for convenience, the effect will not be discussed in this paper. -
In the PB-Husimi algorithm, the probability of the final state
$ p'_i $ being occupied by other particles is expressed according to the Husimi function [48]. The Husimi function ensured to have a good property as probability in the AMD model [48], and the distribution is broader than the Wigner function. In detail, the Husimi phase-space distribution function, i.e.,$f_H({{r}},{{p}})$ , in the QMD is related to the Wigner phase-space distribution$f_W({{r}},{{p}})$ as in Refs. [49, 50],$ f_{H,i}({{r}},{{p}}) = \int W({{r}},{{p}} \, \vert {{r}}',{{p}}') f_{W,i}({{r}}',{{p}}') {\rm{d}} {{r}}' {\rm{d}} {{p}}', $

(4) with
$ W({{r}},{{p}} \, \vert {{r}}',{{p}}') = \frac{1}{(\pi\hbar)^{3}} \exp \left[ -\frac{({{r}}'-{{r}})^2}{2\sigma_{r}^{2}}- \frac{({{p}}'-{{p}})^2}{2\sigma_{p}^{2}} \right]. $

(5) By using Eqs. (4) and (5), we obtain the Husimi phase-space distribution function as follows:
$ f_{H,i}({{r}},{{p}}) = \frac{1}{h^{3}} \exp \left[ -\frac{({{r}}-{{r}}_{i})^2}{4\sigma_{r}^{2}}- \frac{({{p}}-{{p}}_{i})^2}{4\sigma_{p}^{2}} \right]. $

(6) Thus, the occupation probability at
${{p}} = {{p}}'_i$ and${{r}} = {{r}}_i$ can be obtained as$P_\tau(p'_i) = P_{\tau}({{r}}_i,{{p}}'_i)$ ,$ \begin{aligned}[b] P_{\tau}({{r}}_i,{{p}}'_i) =& \frac{1}{2/h^3}\sum\limits_{j\in\tau, j\ne i} f_{H,j}({{r}}_i,{{p}}'_i)\\ =& \frac{1}{2}\sum\limits_{j\in\tau(j\neq i)}^{A} \exp \left[-\frac{({{r}}_{i}-{{r}}_{j})^{2}}{4\sigma_{r}^{2}}\right]\times \exp\left[-\frac{({{p}}'_{i}-{{p}}_{j})^{2}}{4\sigma_{p}^{2}}\right]. \end{aligned}$

(7) Similarly, if the occupation probability
$P_{\tau}({{r}}_i,{{p}}'_i)$ is larger than$ 1 $ ,$P_{\tau}({{r}}_i,{{p}}'_i) = \min{(P_{\tau}({{r}}_i,{{p}}'_i),1)}$ . -
In the PB-HSP algorithm, the occupation probability
$P_{\tau}({{r}}_i,{{p}}'_i)$ is calculated as$P_\tau(p'_i) = P_{\tau}({{r}}_i,{{p}}'_i)$ :$ P_{\tau}({{r}}_i,{{p}}'_i) = \sum\limits_{j\in\tau(j\neq i)}^{A} (O_{ij}^{(x)}/\frac{4}{3}\pi R_{x}^{3}) (O_{ij}^{(p)}/\frac{4}{3}\pi R_{p}^{3}), $

(8) where,
$ O_{ij}^{(x)}(O_{ij}^{(p)}) $ is the volume of the overlap region of hard spheres with the radius$ R_{x}(R_{p}) $ of nucleons i and j in coordinate (momentum) space. As the volume of the overlap region of hard spheres is used, we simply name it HSP.$ O_{ij}^{(x)} $ is calculated by$ O_{ij}^{(x)} = \left\{ {\begin{array}{*{20}{l}} {0{\mkern 1mu} ,}&{L_{ij}^{(x)} \geqslant 2{R_x}}\\ {\dfrac{4}{3}\pi R_x^3 - \pi L_{ij}^{(x)}\left[ {R_x^2 - \dfrac{1}{3}{{(\dfrac{{L_{ij}^{(x)}}}{2})}^2}} \right],}&{L_{ij}^{(x)} < 2{R_x}} \end{array}} \right. $

(9) where
$L_{ij}^{(x)} = |{{r}}_i-{{r}}_j|$ . By replacing$ L_{ij}^{(x)} $ with$L_{ij}^{(p)} = |{{p}}'_i-{{p}}_j|$ and$ R_x $ with$ R_p $ , one can obtain$ O_{ik}^{(p)} $ . Here, we take$ R_{x} $ = 3.367 fm,$ R_{p} $ = 112.5 MeV/c as in Ref. [40]. This method corresponds to the uniform phase-space density distribution in coordinate and momentum space, i.e., one nucleon occupies the phase-space cell with the size$ \dfrac{4}{3}\pi R_{x}^{3}\cdot \dfrac{4}{3}\pi R_{p}^{3} = \dfrac{h^{3}}{2} $ . Similarly, if the occupation probability$P_\tau({{r}}_i,{{p}}'_i)$ is larger than$ 1 $ , the occupation probability should be replaced by$\min (P_\tau({{r}}_i,{{p}}'_i),1)$ . The PB-HSP method is adopted in QMD [46], LQMD [9], and TuQMD [10, 47]① -
In ImQMD, the isospin dependent
$ NN $ cross sections and the differential cross sections in free space are taken from Ref. [51]. The in-medium$ NN $ cross sections in the ImQMD model are named$\sigma^{\rm med}_{\rm QMD}$ , and$\sigma^{\rm med}_{\rm QMD} = R*\sigma^{\rm free}$ , where the medium correction factor$R = (1+ \eta(E_{\rm beam})\rho / $ $ \rho_0)$ . Here, we want to stress that the model dependent$\sigma^{\rm med}_{\rm QMD}$ is not exactly the same as in true$\sigma^{\rm med}$ , and we will show it in the nuclear matter calculations in Sec. IIIA. -
In this section, we first evaluate the Pauli blocking algorithms in nuclear matter in cascade mode, and then in the finite nucleus and HICs. Finally, the uncertainties of different Pauli blocking algorithms on the stopping power and in-medium
$ NN $ cross sections are presented and discussed. -
During the HICs, various effects interplay and propagate during the reaction process; thus, it is hard to evaluate the Pauli blocking only in the HICs. To disentangle the interplay between mean field and
$ NN $ collisions, we first analyze the nucleon number distribution of the final state${{p}}'_i$ , i.e.,${\rm d}N/{\rm d}p'$ , and the occupation probability of the final state${{p}}'_i$ , i.e.,$ P_\tau(p'_i) $ in the cascade mode, i.e., without mean-field potential, in the nuclear matter.To simulate the nuclear matter, a box with imposed periodic boundary conditions is adopted. The periodic boundary conditions are the same as those in Ref. [40], i.e., the dimensions of the cubic box are
$ L_{\alpha} $ = 20 fm,$ \alpha\equiv x,y,z $ , and the position of the center of the box is ($ L_x/2, L_y/2, L_z/2 $ ). The box is initialized with a finite temperature in uniform nuclear matter. The density is$ \rho = 0.16 $ fm$ ^{-3} $ and the isospin asymmetry equals zero, which corresponds to 1280 nucleons (640 neutrons + 640 protons) in the box. In coordinate space, the positions of nucleons are initialized randomly from$ 0 $ to$ L_{\alpha} $ . In momentum space, the momenta of nucleons are initialized according to the Fermi-Dirac distribution,$ f = 1/\{1+ $ exp$ [(\epsilon - \mu)/T]\} $ , with$ \epsilon = p^{2}/2m $ , nucleon mass m = 938 MeV/$ c^2 $ , chemical potential$ \mu $ = 36.84 MeV, and temperature T = 5 MeV. The$ NN $ collision cross sections are set as 40 mb.In Figs. 1(a), (b) and (c), we present
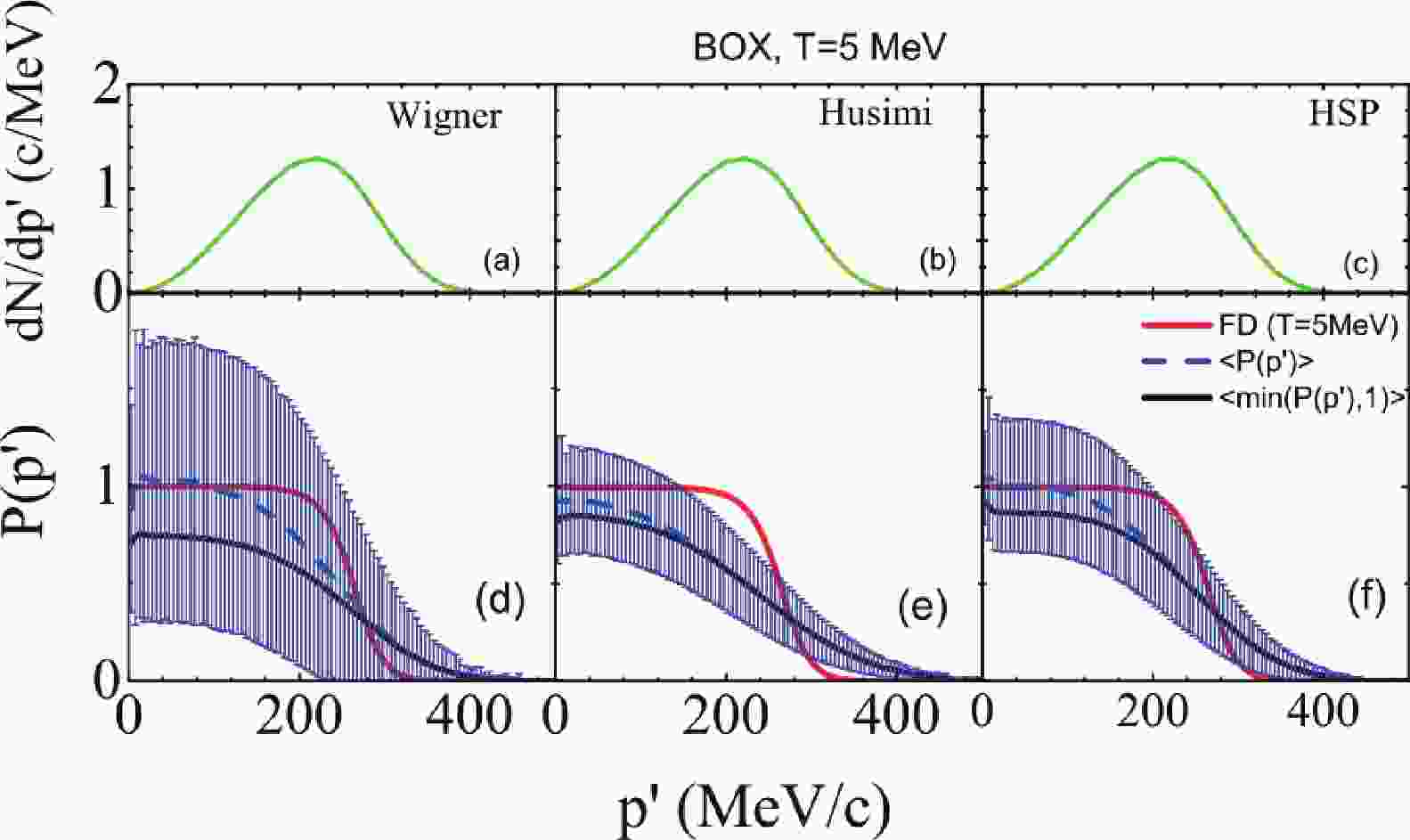
${\rm d}N/{\rm d}p'$ after the evolution of the first time step, i.e., at$ t = 1 $ fm/c, to understand how many nucleons participate in the$ NN $ collisions at a certain momentum. The reason why we choose the first time step, i.e., t = 1 fm/c, is that the momentum space distribution at the first time step is still governed by the initialized Fermi-Dirac distribution. Thus, one can evaluate the Pauli blocking algorithms by comparing the occupation probability with the Fermi-Dirac distribution. The observed differences in the distribution reflect the accuracy of different treatments of Pauli blocking. Panels (a), (b), and (c) are for the cases of PB-Wigner, PB-Husimi, and PB-HSP, respectively. A total of 10,000 events are performed at T = 5 MeV. The${\rm d}N/{\rm d}p'$ of PB-Wigner, PB-Husimi, and PB-HSP are almost the same, because the momenta of nucleons in the initial state are sampled within the same Fermi-Dirac distribution and only one time step is considered.${\rm d}N/{\rm d}p'$ increases with momentum, reaches a maximum around 220 MeV/c, and then decreases.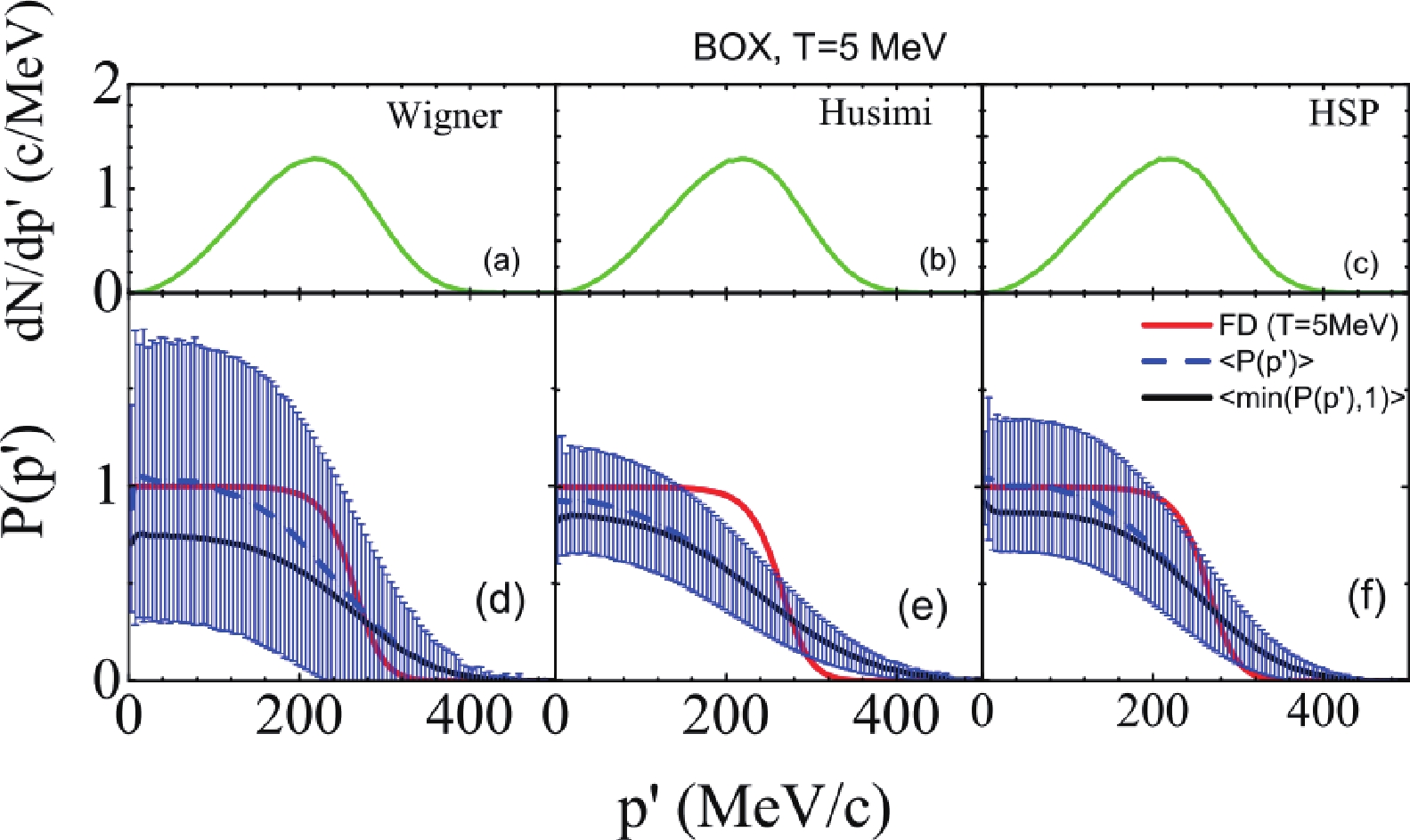
Figure 1. (color online) Panels (a), (b), and (c) are the momentum distributions of the final state of nucleon-nucleon collisions at t = 1 fm/c. Panels (d), (e), and (f) are the occupation probabilities for different Pauli blocking algorithms, i.e., PB-Wigner, PB-Husimi, and PB-HSP, respectively. Red lines denote the analytical values of occupation probability (see text for more details).
Figures 1(d), (e), and (f) show the occupation probability for the Pauli blocking algorithms of PB-Wigner, PB-Husimi, and PB-HSP, respectively. The mean values of the occupation probability, i.e.,
$ \langle P(p')\rangle $ , and their standard deviations, i.e.$ \langle (P(p')-\langle P(p')\rangle)^2 \rangle^{1/2} $ , are shown as blue curves and blue error bars. The actual averaged occupation probabilities used in the ImQMD calculations, i.e.,$ \langle $ min$ (P(p'),1)\rangle $ , are shown as black curves. The actual occupation probability$ \langle $ min$ (P(p'),1) \rangle $ is always slightly lower than$ \langle P(p')\rangle $ due to the truncation of$ P(p') $ by using min$ (P(p'),1) $ . The red lines are the analytical values of occupation probability, i.e., the Fermi-Dirac occupation probability. Among these three Pauli blocking algorithms, PB-Husimi has the smallest standard deviations due to the large width in Eq. (7). Furthermore, all the algorithms used in the QMD codes deviate from the theoretical values as discussed in Ref. [40]. It underestimates the Pauli blocking probability in the lower momentum region and overestimates the blocking probability in the high momentum region due to the strong fluctuation.To quantitatively evaluate the Pauli blocking algorithms, we present the attempted collision rate
$\dfrac{{\rm d}N^{\rm att.}_{\rm coll}}{{\rm d}t}$ , successful collision rate$\dfrac{{\rm d}N^{\rm suc.}_{\rm coll.}}{{\rm d}t}$ , and Pauli blocking ratio$R_{\rm block}$ as a function of temperature in Figs. 2(a) and (b), respectively. Here,$R_{\rm block}$ is defined as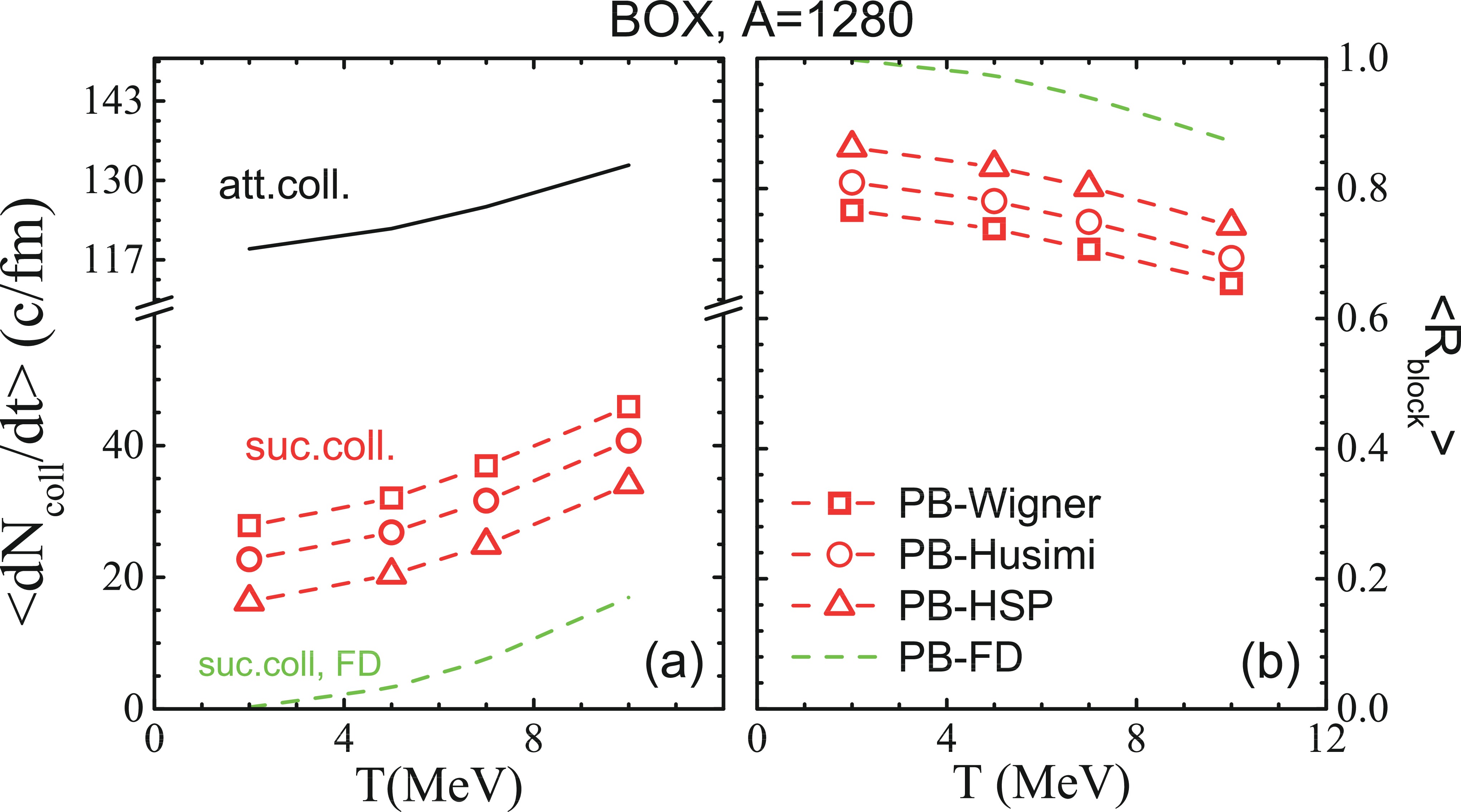
Figure 2. (color online) Panel (a): Averaged attempted collision rate
$\left\langle\dfrac{{\rm d}N^{\rm att.}_{\rm coll.}}{{\rm d}t}\right\rangle$ and successful collision rate$\left\langle\dfrac{{\rm d}N^{\rm suc.}_{\rm coll.}}{{\rm d}t}\right\rangle$ as functions of temperature. The red lines with different symbols are from different Pauli blocking algorithms. Panel (b): Averaged blocking ratio$\langle R_{\rm block}\rangle$ for different Pauli blocking (see text for more details).$ R_{\rm block} = 1-\frac{{\rm d}N^{\rm suc.}_{\rm coll.}}{{\rm d}t}\Bigg/\frac{{\rm d}N^{\rm att.}_{\rm coll.}}{{\rm d}t}. $

(10) The temperature T is from 2 MeV to 10 MeV, which corresponds to the low-intermediate energy HICs. The black line is the result for the averaged attempted collision rate, which is calculated by an analytical formula as in Ref. [40], i.e.,
$ \left\langle \frac{{\rm d}N^{\rm att.}_{\rm coll.}}{{\rm d}t}\right\rangle = \frac{1}{2}A\rho\langle v_{\rm rel}\sigma^{\rm med}\rangle. $

(11) Here, A is the nucleon number,
$ \rho $ is the density,$ v_{\rm rel} $ is the relative velocity between two colliding nucleons,$\sigma^{\rm med}$ is the in-medium$ NN $ cross section, and$ \sigma^{\rm med} = 40 $ mb. Equation (11) corresponds to the case of no Pauli blocking. As illustrated in Fig. 2(a), the analytical values of averaged attempted collision rate (black line) increase with increasing temperature.The red lines with different symbols in Fig. 2(a) are the averaged successful collision rates obtained with PB-Wigner (squares), PB-Husimi (circles), and PB-HSP (triangles). The green line represents the result of the Pauli blocker, which is fixed to the initialized Fermi-Dirac distribution for given temperatures, i.e., PB-FD. It is used for evaluating how well the Pauli blocking algorithms is in the nuclear matter. Similar to the results in Ref. [40], the averaged successful collision rates from PB-Wigner, PB-Husimi, and PB-HSP are larger than the analytical successful collision rates from PB-FD. Among these, the results from PB-HSP are closer to those of PB-FD than the others.
In Fig. 2(b), we plot the averaged blocking ratios
$\langle R_{\rm block}\rangle$ as a function of T, which are calculated over the time interval 60-140 fm/c and from 200 events. The values of$\langle R_{\rm block}\rangle$ from different Pauli blocking algorithms decrease with increasing temperature. Furthermore, the$\langle R_{\rm block}\rangle$ obtained with PB-Wigner, PB-Husimi, and PB-HSP are smaller by approximately 13%-25% than the analytical values, i.e.,$\langle R_{\rm block}\rangle$ obtained with PB-FD. This means that the different Pauli blocking algorithms used in the transport codes overestimate the successful collision rate. Thus, to obtain the same successful collision rate from the Pauli blocking algorithms adopted in QMD and from the analytical Pauli blocking, one can imagine that$\sigma^{\rm med}_{\rm QMD}$ is smaller than its true values, i.e.,$\sigma^{\rm med}_{\rm QMD} < \sigma^{\rm med}$ . For example, at$ T = 10 $ MeV,$\sigma^{\rm med}_{\rm QMD}/\sigma^{\rm med}\approx $ 37-50% (or,$\sigma^{\rm med}\approx 2\sim 2.7 \sigma^{\rm med}_{\rm QMD}$ ) for the selected three Pauli blocking algorithms based on Eqs. (10) and (11). -
One should notice that the Pauli blocking effect in the nuclear matter is not exactly the same as that in the finite size system due to the boundary effect. Thus, we further check it in a finite nucleus where the mean-field potential is also considered for binding the nucleons together. In the following calculations, the interaction parameter set of SkM* is adopted.
As a test of Pauli blocking in the finite nucleus, Fig. 3(a) shows the successful
$ NN $ collision rate as a function of radial distance r, i.e.,$\left\langle \dfrac{{\rm d}N^{\rm suc.}_{\rm coll.}}{{\rm d}t {\rm d}r}\right\rangle$ from 1000 events, in$ ^{124}{\rm{Sn}} $ . The lines with different colors represent the results obtained with PB-Wigner (black line), PB-Husimi (red line), and PB-HSP (green line), respectively. Similar to the calculations in nuclear matter, the values of$\left\langle \dfrac{{\rm d}N^{\rm suc.}_{\rm coll.}}{{\rm d}t {\rm d}r}\right\rangle$ are obtained at 1 fm/c, and the values of$\left\langle \dfrac{{\rm d}N^{\rm suc.}_{\rm coll.}}{{\rm d}t}\right\rangle$ are approximately 0.9-1.6 c/fm. Among the three kinds of Pauli blocking, the calculation with PB-HSP gives the smallest successful collision rate. The differences in successful collision rate between the three kinds of Pauli blocking cannot be as clearly observed as in the nuclear matter. The reasons are: 1) the finite system has a small nucleon number, and 2) the density distribution is a kind of Woods-Saxon form, which leads to more nucleons with low momentum distribution of the initial nuclei.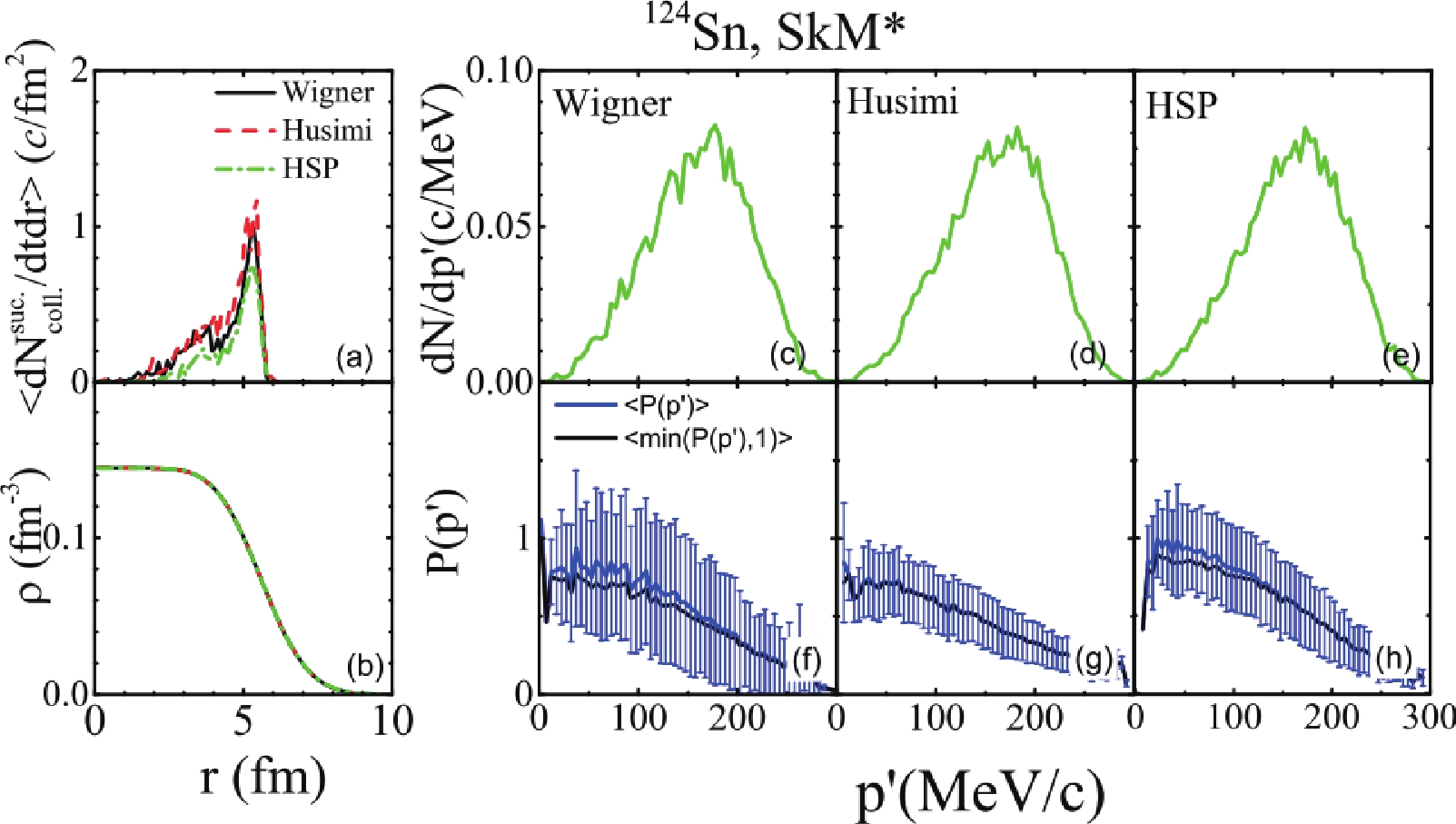
Figure 3. (color online) Panel (a): Successful collision rates as functions of radial distance for
$^{124}$ Sn. Panel (b): Density distribution of$^{124}$ Sn. Panels (c), (d), and (e): Momentum distribution of scattered nucleons. Panels (f), (g), and (h): Occupation probability. They correspond to different Pauli blocking algorithms, i.e., PB-Wigner, PB-Husimi, and PB-HSP, respectively (see the text for details).In addition, most of the successful
$ NN $ collisions occur at approximately r = 5.2 fm, which is close to the surface of the nucleus as found in the density distribution plots in panel (b). This can be mainly attributed to the defects of the Pauli blocking algorithms in the QMD models, because the system only evolves by one time step. Some ad hoc methods to overcome this defect are presented in Refs. [46, 47], but a consistent improvement of Pauli blocking near the surface of the nucleus or reaction system is still a theoretical challenge.Panels (c), (d), and (e) show
${\rm d}N/{\rm d}p'$ of the final state of$ NN $ collisions in different Pauli blocking algorithms, i.e., PB-Wigner, PB-Husimi, and PB-HSP, respectively, and it clearly illustrates the importance of Pauli blocking within the Fermi momentum. The mean values of occupation probability$ \langle P(p')\rangle $ and mean actual occupation probability$ \langle $ min$ (P(p'),1) \rangle $ at 1 fm/c are shown by the blue and black curves in panels (f)-(h), respectively. Similar to the finding in the nuclear matter, there is also$ \langle\min(P(p'),1) \rangle \leqslant \langle P(p')\rangle $ in the finite nucleus. The standard deviation of the occupation probability$ P(p') $ is indicated by blue error bars, and it shows that PB-Wigner has the largest fluctuation among the three Pauli blocking algorithms. The values obtained with PB-HSP are closer to 1 at low momentum than those of the other two algorithms. -
Nuclear stopping governs the amount of dissipated energy under the competition between the mean field potential and nucleon-nucleon collisions, and can be measured by the ratio between transverse and longitudinal components of kinematical observables [52-54]. For example, the ratio of the variances of the transverse rapidity distribution to that of the longitudinal rapidity distributions of emitted particles, which is named as
$ vartl $ [53],$ vartl = \frac{\langle y_{t}^{2}\rangle}{\langle y_{z}^{2}\rangle}. $

(12) The energy-based isotropy ratio
$ R_E $ [52] and the momentum-based isotropy ratio$ R_{p} $ [54] are also used in experiments to measure the stopping power. These quantities measure the transfer of momentum from the entrance direction to the transverse direction, and thus, they are closely related to the successful$ NN $ collision rate. Therefore, a study of the nuclear stopping observable can provide an insight into the in-medium$ NN $ cross sections and Pauli blocking effects.Before discussing the stopping power in HICs, we first present the free
$ NN $ cross sections [51] used in the ImQMD calculations and the corresponding mean attempted collision rate in Figs. 4(a) and (b), respectively. As shown in panel (a), both the cross sections of nn/pp (black line) and np (red line) decrease with beam energy. In more detail, in the ImQMD model, we also set$\sigma^{\rm free}_{nn/pp} = 60$ mb and$\sigma^{\rm free}_{np} = 180$ mb at$p_{\rm lab} < 0.3$ GeV/c (or$E_{\rm lab} < 50$ MeV) to avoid the spurious low energy$ NN $ collisions in the nuclear medium. Figure 4(b) shows the mean attempted collision rate by nucleons, i.e.,$\langle \rho v_{\rm rel}\sigma^{\rm free}_{NN} \rangle$ , for nn/pp and np, in the uniform nuclear matter with$ \rho = 0.16 $ fm$ ^{-3} $ . The mean attempted collision rate for np decreases with increasing beam energy, while the mean attempted collision rate for nn/pp first decreases and then increases at$E_{\rm lab} > \sim 100$ MeV. This is different to the behaviors in Fig. 2, where a constant$ NN $ cross section of$ 40 $ mb is used. Thus, one may expect that the stopping power may weakly depend on the beam energy or decrease with increasing beam energy if$\sigma^{\rm free}_{nn/pp,np}$ is used and Pauli blocking is switched off in the model.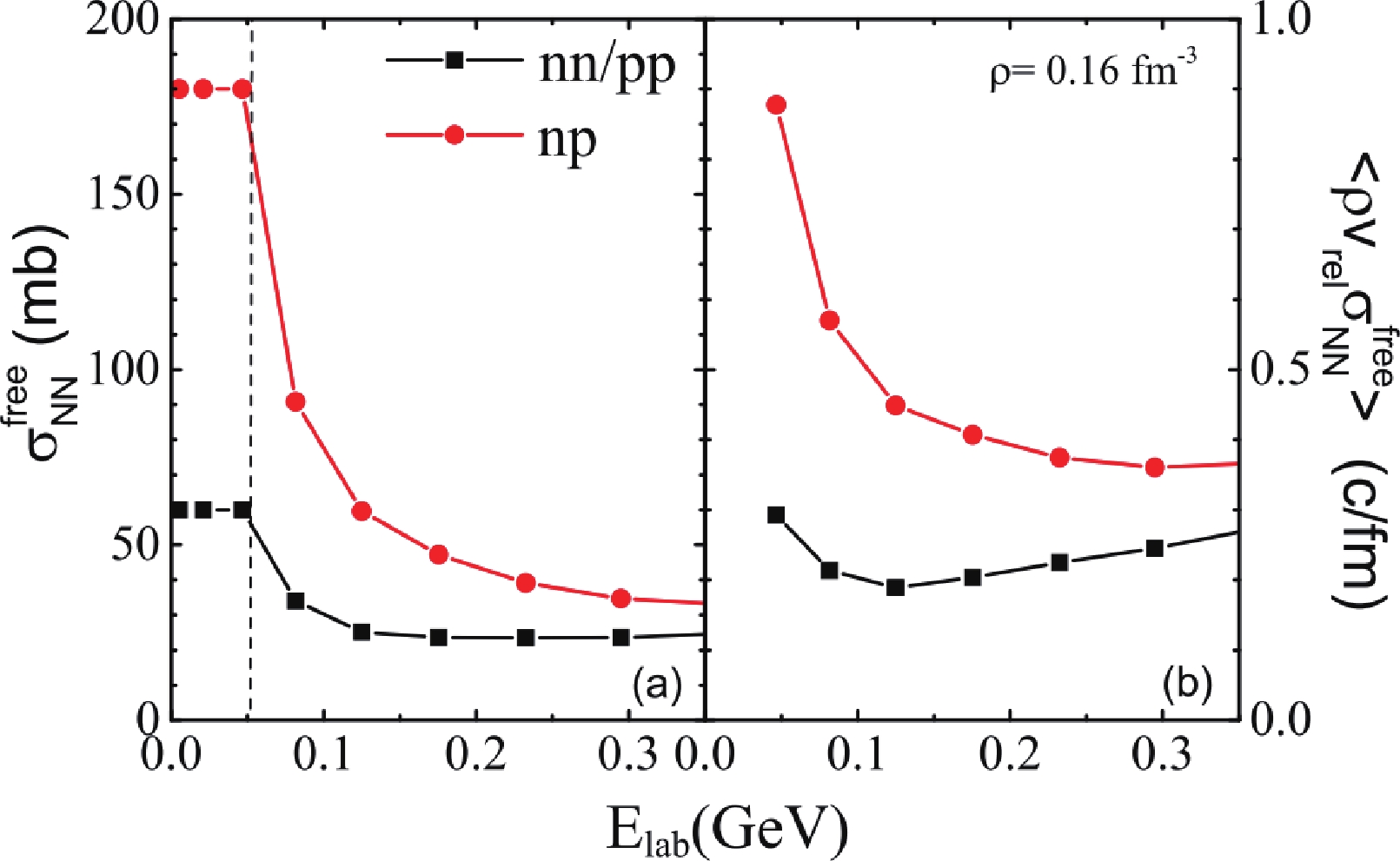
Figure 4. (color online) Panel (a): Cross section of nn/pp and np used in the ImQMD model. Panel (b): Mean attempted collision rate obtained with the free
$NN$ cross sections in nuclear matter.However, the Pauli blocking effect is indispensable for low-intermediate energy HICs. In Fig. 5(a), the averaged blocking ratios
$\langle R_{\rm block}\rangle$ as a function of beam energy for$\rm ^{112}Sn+^{124}Sn$ at b = 1 fm are presented. The values of$\langle R_{\rm block}\rangle$ are obtained over the time interval 0-400 fm/c and 10,000 events. The black lines with different symbols are the results obtained with PB-Wigner (squares), PB-Husimi (circles), and PB-HSP (triangles), in the case of$\sigma^{\rm free}$ being adopted in the ImQMD calculations. The values of$\langle R_{\rm block}\rangle$ obtained with PB-Husimi and PB-HSP are almost same, but PB-Wigner results in the largest$\langle R_{\rm block}\rangle$ among the three kinds of Pauli blocking algorithms. It is opposite to the finding in the nuclear matter, and can be understood from the reaction dynamics. At the early stage of reaction, the weakest Pauli blocking algorithm observed in the nuclear matter calculations, i.e., PB-Wigner, results in more$ NN $ collisions than PB-Husimi or PB-HSP. More$ NN $ collisions provide a larger repulsion for nucleons during the compressed stage, and make the system expand to a larger momentum space than that with fewer$ NN $ collisions. Thus, the successful collision rates for PB-Wigner become smaller than those for PB-Husimi or PB-HSP after the compression stage. Consequently, the largest$\langle R_{\rm block}\rangle = $ $ \left\langle 1-\dfrac{{\rm d}N^{\rm suc.}_{\rm coll.}}{{\rm d}t}\Biggr/\dfrac{{\rm d}N^{\rm att.}_{\rm coll.}}{{\rm d}t}\right\rangle$ values for PB-Wigner are obtained by averaging over the time interval 0-400 fm/c. This effect becomes obvious at high beam energy where the$ NN $ collisions are more frequent than low beam energies.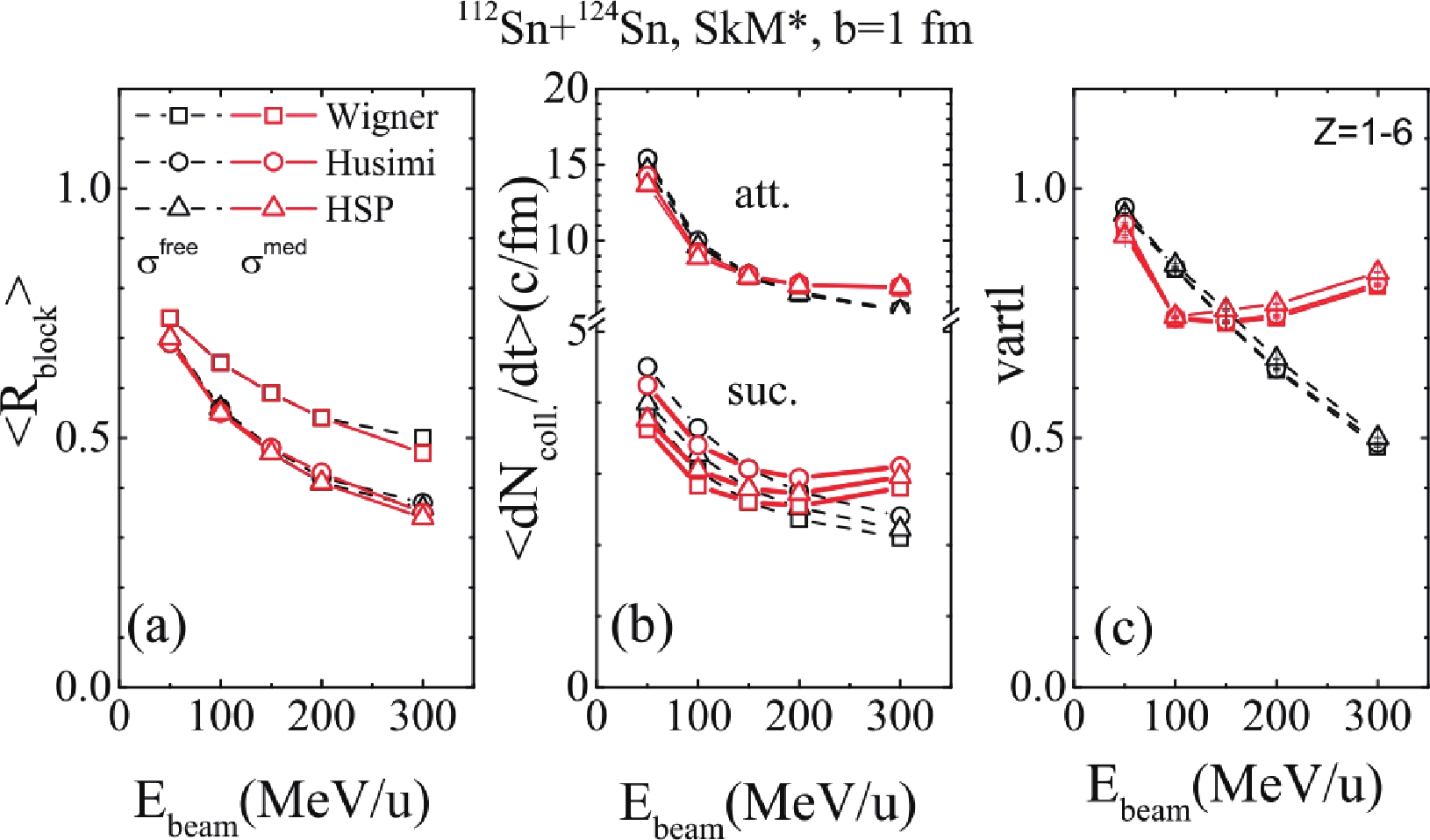
Figure 5. (color online) (a)
$\langle R_{\rm block}\rangle$ as a function of beam energy; (b) the mean attempted$NN$ and successful$NN$ collision rates as a function of beam energy; (c)$vartl$ as a function of beam energy. The different symbols are for different Pauli blocking, and the different colors are for different in-medium cross sections.To explore the uncertainties of the theoretical predictions on stopping power by using different Pauli blocking algorithms, we present the averaged attempted and successful collision rates, i.e.,
$\left\langle \dfrac{{\rm d}N^{\rm att.}_{\rm coll.}}{{\rm d}t}\right\rangle$ and$\left\langle \dfrac{{\rm d}N^{\rm suc.}_{\rm coll.}}{{\rm d}t}\right\rangle$ , as a function of beam energy in Fig. 5(b). The values of$\left\langle \dfrac{{\rm d}N^{\rm att.}_{\rm coll.}}{{\rm d}t}\right\rangle$ and$\left\langle \dfrac{{\rm d}N^{\rm suc.}_{\rm coll.}}{{\rm d}t}\right\rangle$ are obtained over the time interval 0-400 fm/c and from 10,000 events, and they decrease with increasing beam energy. The values of$\left\langle \dfrac{{\rm d}N^{\rm suc.}_{\rm coll.}}{{\rm d}t}\right\rangle$ are in the range 2-5 c/fm, and the different Pauli blocking algorithms lead to approximately 11%-15% difference in$\left\langle \dfrac{{\rm d}N^{\rm suc.}_{\rm coll.}}{{\rm d}t}\right\rangle$ . The difference in$\left\langle \dfrac{{\rm d}N^{\rm suc.}_{\rm coll.}}{{\rm d}t}\right\rangle$ between the PB-Wigner and the other two methods is not as large as that in panel (a), because$\langle R_{\rm block}\rangle$ is calculated by the formula$\langle R_{\rm block} \rangle = \left\langle 1-\dfrac{{\rm d}N^{\rm suc.}_{\rm coll.}}{{\rm d}t}\Biggr/\dfrac{{\rm d}N^{\rm suc.}_{\rm coll.}}{{\rm d}t}\right\rangle$ , which is different from$1-\left\langle \dfrac{{\rm d}N^{\rm suc.}_{\rm coll.}}{{\rm d}t}\right\rangle\Biggr/\left\langle \dfrac{{\rm d}N^{\rm suc.}_{\rm coll.}}{{\rm d}t}\right\rangle$ .The values of
$ vartl $ obtained from the different methods of Pauli blocking are presented in Fig. 5(c). In these calculations,$ vartl $ is calculated from the rapidity distribution of charged particles$ Z = 1-6 $ weighted by their charge number to weaken the defect on the cluster formation mechanism at low-intermediate energy HICs. Our calculations show that the values of$ vartl $ weakly depend on the Pauli blocking algorithms we used owing to the small number of successful collision rates, as shown in panel (b). Furthermore, the calculations with$ \sigma^{free} $ predict that the values of$ vartl $ decrease with increasing beam energy. This behavior is opposite to the observation in experiments [53] where$ vartl $ increases with increasing beam energy for Au+Au at$E_{\rm beam} > 100$ MeV/u. This difference illustrates that the in-medium correction on the$ NN $ cross sections is needed. -
To test the effect of in-medium
$ NN $ cross sections on stopping power, we simply take$\sigma^{\rm med}_{\rm QMD}$ as$\sigma^{\rm med}_{\rm QMD} = $ $ (1+\eta(E_{\rm beam})\rho/\rho_0)\sigma^{\rm free}$ in the code. For$E_{\rm beam}\leqslant 100$ MeV,$ \eta $ is set as -0.2. At$E_{\rm beam} = $ 150, 200, and 300 MeV,$ \eta = $ 0.0, 0.2, and 0.8, respectively. The red lines with symbols in panels (a), (b), and (c) are the results obtained with$\sigma^{\rm med}_{\rm QMD}$ . As illustrated in Fig. 5(a), the values of$\langle R_{\rm block}\rangle$ weakly depend on the correction of the in-medium$ NN $ cross sections. However, as shown in panel (b), the in-medium$ NN $ cross sections reduce the attempted and successful collision rates by$ \sim $ 7% at$E_{\rm beam}\leqslant 100$ MeV and enhance the attempted and successful collision rates by$ >7 $ % at$E_{\rm beam} > 100$ MeV. Consequently, as in panel (c), the values of$ vartl $ are suppressed at$E_{\rm beam}\leqslant 100$ MeV/u, and enhanced at$E_{\rm beam} > 100$ MeV/u.However, one should bear in mind that even the disappeared sensitivity is found among the results obtained with the three PB methods in HIC simulations, the improvements to the PB method are still necessary. The reasons are as follows: 1) all PB methods underestimate the Pauli blocking ratio by approximately 13%-25% in nuclear matter calculations, in which analytical values are used to evaluate the accuracy of the PB method. For a finite nucleus at T=0 MeV, the successful collision rates are not blocked to zero. This means that the three PB methods are not good enough. 2) For the Pauli blocking ratios in HICs, we need to know the analytical values of Pauli blocking. Currently, we do not know the analytical values, and thus do not know how much they deviate from the true values and whether the deviations are too large to neglect. A reliable extraction of the in-medium
$ NN $ cross section by comparing HIC data with transport model calculations must require an accuracy method to treat the Pauli blocking in the simulation of HICs. The improvement of Pauli blocking is still in progress. -
In summary, we first evaluate the different Pauli blocking algorithms in the nuclear matter in cascade mode, i.e., only with
$ NN $ collisions. Our calculations show that the averaged occupation probabilities obtained with PB-Husimi and PB-HSP are closer to the analytical values than those obtained with PB-Wigner, but all three algorithms used in the QMD codes underestimate the Pauli blocking ratio by 13%-25% at$ T\leqslant 10 $ MeV. This underestimation may lead to the extracted in-medium$ NN $ cross sections from QMD type models being smaller than the true in-medium$ NN $ cross sections. For example, at T = 10 MeV,$\sigma^{\rm med} = 2\sim2.7\sigma^{\rm med}_{\rm QMD}$ , in the case of obtaining the same successful collision rate as in its analytical values.Furthermore, we evaluate the different Pauli blocking algorithms in the finite nucleus, in which both mean field potential and
$ NN $ collisions are included. For the finite nucleus, the Pauli blocking ratios are in the range of 69%-83% for different Pauli blocking algorithms owing to the defects of Pauli blocking in the QMD model. The spurious$ NN $ collision mainly occurs around the surface of the finite nucleus. There have been some efforts to improve the Pauli blocking, especially near the surface of the nucleus or the reaction system, but consistent treatment is still a big challenge for the many-body transport theory.By using the Pauli blocking algorithms currently in the market, the uncertainties of different Pauli blocking algorithms on the excitation function of stopping power in HICs are discussed. Our finding is that the uncertainties of stopping power with different Pauli blocking are less than 5%. If one would like to produce the behaviors of the
$ vartl $ increasing with beam energy, a strong enhancement of in-medium$ NN $ cross sections is needed. Nevertheless, for obtaining the true values of in-medium$ NN $ cross sections by comparing the HIC data with the transport model calculations, a refined Pauli blocking algorithm must be developed in the future. -
The authors are thankful for the helpful discussions with Dr. Yongjia Wang and Dr. D. Cozma on the Pauli blocking algorithms.
Theoretical uncertainties on the extraction of in-medium NN cross sections by different Pauli blocking algorithms
- Received Date: 2021-03-09
- Available Online: 2021-07-15
Abstract: Three typical Pauli blocking algorithms in quantum molecular dynamics type models are investigated in the nuclear matter, the nucleus, and heavy ion collisions. In nuclear matter, the blocking ratios obtained with the three algorithms are underestimated by 13%-25% compared to the corresponding analytical values. For a finite nucleus, spurious collisions occur around the surface of the nucleus owing to the defects of the Pauli blocking algorithms. In the simulations of heavy ion collisions, the uncertainty of stopping power arising from the different Pauli blocking algorithms is less than 5%. Furthermore, the in-medium effects of nucleon-nucleon (NN) cross sections on the nuclear stopping power are discussed. Our results show that the transport model calculations with free NN cross sections result in the stopping power decreasing with beam energy when the beam energy is less than 300 MeV/u. To increase or decrease the values of the stopping power, the transport model calculations need enhanced or suppressed model dependent in-medium NN cross sections that are expected to be smaller than the true in-medium NN cross sections.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: