-
The universe is in a stage of accelerated expansion, which can be described by a negative pressure system [1]. Two sources of negative pressure are considered to drive this expansion: the cosmological constant and quintessence dark energy. Inspired by the thermodynamics of anti-de Sitter (AdS) black holes (BHs) against the background of the variable cosmological constant Λ, Kastor
$ et\; al. $ and Dolan proposed a scenario to investigate BH thermodynamics in the extended phase space. If Λ is given the meaning of thermodynamic pressure P, the BH mass is naturally explained by thermodynamic enthalpy [2–4].Based on this approach, various BH phase transitions have been advanced to AdS space-time. The phase transition of small-large BHs occurs in charged AdS BH systems, and it is similar to the van der Waals (vdW) fluid system in classical thermodynamics. In Ref. [5], Kubiznak
$ et\; al. $ calculated the universal constant and critical exponents of the Reissner-Nordström (RN) AdS BH and vdW systems, observing that these key parameters are consistent. Wei$ et\; al. $ provided a universal formula of normalized scalar curvature$ R_{\rm N} $ in the Ruppeiner geometry approach suitable for classical and BH systems and observed that the specific values of the critical exponent of$ R_{\rm N} $ of RN AdS BHs and vdW fluids are identical [6, 7]. Hence, the difference in the critical behavior between the BH and vdW systems can be used to prove the deviation of the BH phase transition from the vdW phase transition. Some relevant thermodynamic studies on different charged BHs in extended phase space are reported in Refs. [8–14].Considering RN AdS BH coupling with quintessence dark energy, the phase transition characteristics of BH become interesting. Li showed the effect of quintessence dark energy on the critical behavior of RN AdS BHs [15]. Compared with the standard vdW phase transition, the universal constant has a significant difference and noticeably changes with the values of BH parameters, but the critical exponents retain the standard value. Toledo
$ et\; al. $ investigated the thermal behaviors of RN AdS BHs with cloud of strings and quintessence dark energy, observing that the critical point exhibited an analogous phenomenon. [16]. We believe that the reason for this phenomenon is that the thermal behavior of quintessence has not been fully considered.As a candidate to explain the accelerated expansion of the universe, quintessence dark energy can provide a pressure similar to the cosmological constant. The pressure
$ P_{\rm q} $ is related to the state parameter$ \omega_{\rm q} $ and the energy density$ \rho_{\rm q} $ of quintessence, satisfying$ P_{\rm q} \equiv \omega_{\rm q}\rho_{\rm q} $ [17, 18]. Based on the assumption that the energy tensor of the perfect fluid satisfies the linearity and additivity, Kiselev derived the solution of a spherically-symmetric BH in the$ \omega_{\rm q} $ range of quintessence dark energy ($ -1 < \omega_{\rm q} < -1/3 $ ) [19]. Because Kiselev's model is simple and feasible, most thermodynamic studies based on the coexistence of dark energy and BHs introduce quintessence using this approach, including reseach related to critical behavior [15, 16, 20–22].In contrast to the research considering Λ as the phase transition pressure of AdS BHs, we abandon the discussion of BH phase transitions in AdS space-time. We focus on the thermal characteristics of the interaction between quintessence dark energy and BHs. One of the reasons for this consideration is that combining the thermal behavior of quintessence with BH thermodynamics is easy. Using the practice of constructing the extended phase space with the
$ \Lambda-P $ relation, we can naturally construct the "quintessential" phase space using the state equation of quintessence.The paper is organized as follows. In Sec. II, we briefly review the solution of a BH surrounded by dark energy quintessence. In Sec. III, we construct the BH thermodynamics in the quintessential phase space and investigate the
$ P_{\rm q}-\upsilon $ critical behavior. Sec. IV provides our conclusions and discussion. -
With the condition of additivity and linearity in the energy momentum tensor, Kiselev derived the quintessential matter field equation and obtained a static spherically-symmetric charged BH solution [19]. We briefly review this work in this section. The general metric of the spherically symmetric static gravitational field is
$ \begin{equation} {\rm d}s^2={\rm e}^{\rm \nu}{\rm d}t^2-{\rm e}^{\rm \lambda}{\rm d}r^2-r^2({\rm d}\theta^2+{\rm sin}^2\theta{\rm d}\phi^2), \end{equation} $

(1) where ν and λ are functions of r. The Einstein equations are expressed as
$ \begin{eqnarray} &2T_{\rm t}^{\rm \; t}=-{\rm e}^{\rm -\lambda}\Big(\frac{1}{r^2}-\frac{\lambda'}{r}\Big)+\frac{1}{r^2}, \end{eqnarray} $

(2) $ \begin{eqnarray} &2T_{\rm r}^{\rm \; r}=-{\rm e}^{\rm -\lambda}\Big(\frac{1}{r^2}+\frac{\nu'}{r}\Big)+\frac{1}{r^2}, \end{eqnarray} $

(3) $ \begin{eqnarray} &2T_{\rm \theta}^{\rm \; \theta}=2T_{\rm \phi}^{\rm \; \phi}=-\frac{1}{2}{\rm e}^{\rm -\lambda}\Big(\nu''+\frac{\nu'^2}{2}+\frac{\nu'-\lambda'}{r}-\frac{\nu'\lambda'}{2}\Big). \end{eqnarray} $

(4) The energy-momentum tensor of the quintessence can be expressed as
$ \begin{eqnarray} T_{\rm t}^{\rm \; t}=T_{\rm r}^{\rm \; r}=\rho_{\rm q},\; \; \; T_{\rm \theta}^{\rm \; \theta}=T_{\rm \phi}^{\rm \; \phi}=-\frac{1}{2}\rho_{\rm q}(3\omega_{\rm q}+1), \end{eqnarray} $

(5) where
$ \rho_{\rm q} $ and$ \omega_{\rm q} $ are the energy density and state parameters of quintessence, respectively. By using$ \lambda=-{\rm ln}(1+f) $ , the energy-momentum tensor of the quintessence can be rewritten as$ \begin{eqnarray} T_{t}^{\; t}=T_{r}^{\; r}=-\frac{1}{2r^2}(f+rf'), \end{eqnarray} $

(6) $ \begin{eqnarray} T_{\rm \theta}^{\rm \; \theta}=T_{\rm \phi}^{\rm \; \phi}=-\frac{1}{4r}(2f'+rf''). \end{eqnarray} $

(7) Using Eqs. (5) and (7), we can observe that f satisfies the linear equation
$ \begin{equation} (3\omega_{\rm q}+1)f+3(\omega_{\rm q}+1)rf'+r^2f''=0, \end{equation} $

(8) with two solutions in the following form:
$ \begin{eqnarray} \; \; \; \; \; \; \; \; \; \; \; \; f_{\rm q}=\frac{c}{r^{3\omega_{\rm q}+1}},\; \; \; \; \; f_{\rm BH}=-\frac{r_{g}}{r}, \end{eqnarray} $

(9) where c and
$r_{g}$ are the normalization factors. Because the additivity and linearity are considered to be satisfied,$f_{\rm BH-q}=f_{\rm BH}+f_{\rm q}$ is also considered a solution of the above equation. We can observe that there are two coexisting forms between the quintessence and BHs: non interacting form ($ f_{\rm q} $ and$f_{\rm BH}$ ) and interacting form ($f_{\rm BH-q}$ ). We can predict that the non interacting form contains a scenario similar to the cosmological constant, that is, when$ f_{\rm q} $ has a larger scale evolution characteristic than$f_{\rm BH}$ . Our paper focuses on the interacting form$f_{\rm BH-q}$ . Substituting the first solution of quintessence into Eq. (5), we obtain$ \rho_{\rm q} $ as$ \begin{equation} \rho_{\rm q}=\frac{c}{2}\frac{3\omega_{\rm q}}{r^{3(\omega_{\rm q}+1)}}. \end{equation} $

(10) To ensure that
$ \rho_{\rm q} $ is always greater than zero, c should be consistent with$ \omega_{\rm q} $ in sign. It is well known that dark energy is divided into three types according to the scope of$ \omega_{\rm q} $ :● Case 1 asymptotically flat:
$ -1/3<\omega_{\rm q}<0 $ .● Case 2 quintessence dark energy:
$ -1<\omega_{\rm q}<-1/3 $ .● Case 3 phantom dark energy:
$ \omega_{\rm q}<-1 $ .The metric of exact spherically-symmetric solutions for the Einstein equations describing BHs interacting with the quintessential matter is expressed as
$ \begin{equation} {\rm d}s^2=f(r){\rm d}t^2-f(r)^{-1}{\rm d}r^2-r^2({\rm d}\theta^2+{\rm \sin}^2\theta{\rm d}\phi^2), \end{equation} $

(11) where
$ f(r) $ is the metric potential, which can be expressed as [19]$ \begin{equation} f(r)=1-\frac{2M}{r}-\sum\limits_{n}\Big(\frac{r_n}{r}\Big)^{3\omega_n+1}, \end{equation} $

(12) where M is the BH mass,
$r_{n}$ is the dimensional normalization constant, and$\omega_{n}$ is the quintessential state parameter. From this expression, we can obtain the metric for RN BH interacting with quintessence or the Schwarzschild one if the BH charge$ Q=0 $ ; we obtain$ \begin{equation} f(r)_{\rm q}=1-\frac{2M}{r}+\frac{Q^2}{r^2}-\Big(\frac{r_{\rm q}}{r}\Big)^{3\omega_{\rm q}+1}. \end{equation} $

(13) -
Assuming
$ r_{\rm q}^{3\omega_{\rm q}+1} \equiv kc $ $ (k>0) $ , Eq. (13) can be rewritten as$ \begin{equation} f(r)_{\rm q}=1-\frac{2M}{r}+\frac{Q^2}{r^2}-\frac{kc}{r^{3\omega_{\rm q}+1}}. \end{equation} $

(14) The mass M can be expressed with the horizon radius
$ r+ $ as$ \begin{equation} M=\frac{r_+}{2}+\frac{Q^2}{2r_+}-\frac{kc}{2r_+^{3\omega_{\rm q}}}. \end{equation} $

(15) The Hawking temperature can be obtained as
$ \begin{equation} T=\frac{f'(r_+)_{\rm q}}{4\pi}=\frac{1}{4\pi r_+}\Bigg(1-\frac{Q^2}{r_+^2}+\frac{3\omega_{\rm q}kc}{r_+^{3\omega_{\rm q}+1}}\Bigg). \end{equation} $

(16) The entropy is
$ \begin{equation} S=\int_{0}^{r_+}\frac{1}{T}\Big(\frac{\partial M}{\partial r_+}\Big){\rm d}r_+=\pi r_+^2. \end{equation} $

(17) With the newly thermodynamic quantities defined from quintessence, the conventional first law of BH thermodynamics is
$ \begin{equation} {\rm d}M=T{\rm d}S+\Phi{\rm d}Q+\mathcal{C}{\rm d}c, \end{equation} $

(18) where
$ \mathcal{C} $ is the physical quantity conjugate to the parameter c. The quantity related to quintessence introduced in this manner can make the first law consistent with the Smarr relation. The physical quantities from Eq. (15) are given by$ \begin{equation} \Phi=\; \Bigg(\frac{\partial M}{\partial Q}\Bigg)_{S,c}=\; \frac{Q}{r_+}, \end{equation} $

(19) $ \begin{equation} \mathcal{C}=\; \Bigg(\frac{\partial M}{\partial c}\Bigg)_{S,Q}=-\frac{k}{2r_+^{3\omega_{\rm q}}}. \end{equation} $

(20) Additionally, the conventional Smarr relation is
$ \begin{equation} M=2TS+\Phi Q+(1+3\omega_{\rm q})\mathcal{C}c. \end{equation} $

(21) It is possible that a significant component of the energy density of the universe has an equation of state different from those of matter, radiation, or cosmological constant (Λ), i.e., quintessence dark energy [23]. It is a dynamical, slowly-evolving, spatially inhomogeneous component with negative pressure [24]. Based on this concept, we assume that the interaction between the BH and quintessence causes the BH to obtain pressure, which is related to the pressure of quintessence. Using Eq. (10) and restoring the discarded
$ 4\pi $ , the equation of state of quintessence with ideal fluid properties is$ \begin{equation} P_{\rm q}=\frac{c}{8\pi}\frac{3\omega_{\rm q}^2}{r^{3(\omega_{\rm q}+1)}}. \end{equation} $

(22) Note that for theoretical analysis, we do not limit
$ \omega_{\rm q} $ to the range of dark energy$ (-1,-1/3) $ ; therefore, the sign of c is not required, and the pressure$ P_{\rm q} $ in the quintessential phase space can be any real number. Hence, the following relationship can be easily derived:$ \begin{equation} {\rm d}c=\frac{8\pi r^{3(\omega_{\rm q}+1)}}{3\omega_{\rm q}^2}{\rm d}P_{\rm q}. \end{equation} $

(23) Using the above equation, we can popularize the conventional first law of BH thermodynamics (18) and conventional Smarr relation (21) to the quintessential phase space:
$ \begin{equation} {\rm d}M=T{\rm d}S+\Phi{\rm d}Q+V_{\rm q}{\rm d}P_{\rm q}, \end{equation} $

(24) $ \begin{equation} M=2TS+\Phi Q+(1+3\omega_{\rm q})V_{\rm q}P_{\rm q}, \end{equation} $

(25) where
$ V_{\rm q} $ is the conjugate quantity of the pressure$ P_{\rm q} $ , satisfying$ \begin{equation} V_{\rm q}=\frac{8\pi r^{3(\omega_{\rm q}+1)}}{3\omega_{\rm q}^2}\mathcal{C}=\frac{4\pi kr_+^3}{3\omega_{\rm q}^2}. \end{equation} $

(26) Note that
$ V_{\rm q} $ can return to the general thermodynamic volume$ V=\frac{4}{3}\pi r_+^3 $ if the free parameter$ k = \omega_{\rm q}^2 $ . Furthermore, the Smarr relation in the quintessential phase space can return to the extended phase space if$ \omega_{\rm q} = -1 $ . -
In the previous subsection, we use the equation of state of quintessence to construct the quintessential phase space. The first law of BH thermodynamics and Smarr relation in this scenario are derived. Next, we investigate
$ P_{\rm q}-\upsilon $ criticality under the framework of the quintessential phase space.Utilizing Eqs. (16) and (22), the equation of state of a BH can be expressed as
$ \begin{equation} P_{\rm q}=\frac{\omega_{\rm q}}{k}\Bigg(\frac{T}{2r_+}-\frac{1}{8\pi r_+^2}+\frac{Q^2}{8\pi r_+^4}\Bigg). \end{equation} $

(27) According to the critical conditions
$ \Big(\dfrac{{\partial P}}{{\partial r_{+}}}\Big)=\Big(\dfrac{{\partial^2 P}}{{\partial r_{+}^2}}\Big)=0 $ , the critical thermodynamic quantities of the RN BH in this scenario can be obtained:$ \begin{aligned}[b] r_{\rm qc}=&\sqrt{6}Q,\; \quad\; \; T_{\rm qc}=\frac{1}{3\sqrt{6}\pi Q},\\ P_{\rm qc}=&\frac{\omega_{\rm q}}{k}\frac{1}{96\pi Q^2}. \end{aligned} $

(28) The sign consistency between
$ \omega_{\rm q} $ and c makes$ P_{\rm q} $ and$ P_{\rm qc} $ have such characteristics, that is, the occurrence of this phase transition does not depend on whether the pressure provided by quintessence is positive or negative. For dark energy ($ -1<\omega_{\rm q} <-1/3 $ ), this phase transition can occur during the accelerating expansion of the universe caused by negative pressure provided by quintessence. The universal constant$ \varepsilon \equiv {P_{\rm c}\upsilon_{\rm c}}/{T_{\rm c}} $ can be expressed as$ \begin{equation} \varepsilon_{\rm q} = \frac{{P_{\rm qc}\upsilon_{\rm qc}}}{{T_{\rm qc}}} = \frac{\omega_{\rm q}}{k}\frac{3}{8}. \end{equation} $

(29) where
$ \upsilon_{\rm qc} $ is the specific volume, satisfying$ \upsilon_{\rm qc}=2r_{\rm qc} $ [5]. We set the absolute value of universal constant of a standard vdW-type phase transition as$ 3/8 $ . Judging from the universal constant, the ratio$ \omega_{\rm q}/k $ can make the phase transition far from the standard vdW-type. Using reduced parameter space, we investigate the phase transition characteristics near the critical point. The equation of state Eq. (27) is restructured as$ \begin{equation} p_{\rm q} = \frac{3}{8}\frac{\tau}{\nu}-\frac{2}{\nu^2}+\frac{1}{3\nu^4}, \end{equation} $

(30) where
$ \begin{equation} p_{\rm q}=\frac{P_{\rm q}}{P_{\rm qc}}, \; \; \; \tau=\frac{T}{T_{\rm qc}}, \; \; \; \nu=\frac{\upsilon}{\upsilon_{\rm qc}}. \end{equation} $

(31) We observe that Eq. (30) and Ref. [7] (Eq. (93)) are identical, indicating that the phase transition of RN BH in the quintessential phase space has the same critical exponents and critical behavior of normalized scalar curvature
$R_{\rm N}$ as the standard vdW-type phase transition, and more importantly, it is independent of$ \omega_{\rm q} $ and k.Furthermore, the Gibbs free energy of an RN BH in the quintessential phase space can be expressed as
$ \begin{equation} G=M-TS=\frac{3Q^2}{4r_+}+\frac{r_+}{4}-\frac{(2+3\omega_{\rm q})p_{\rm q}r_+^3}{144Q^2\omega_{\rm q}}. \end{equation} $

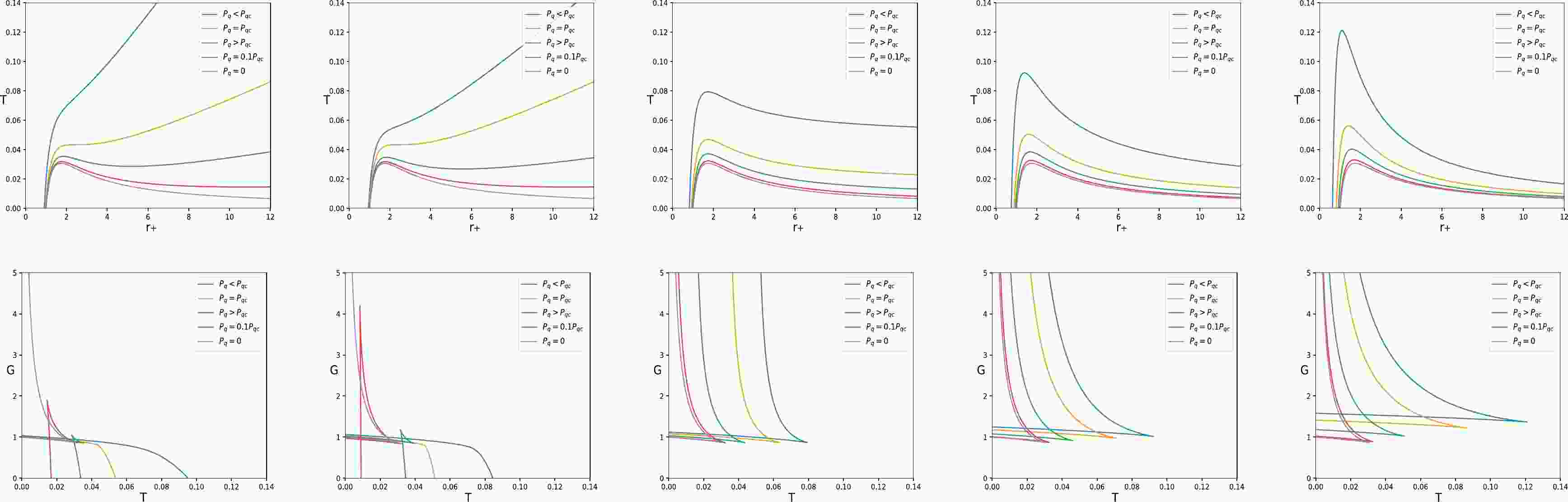
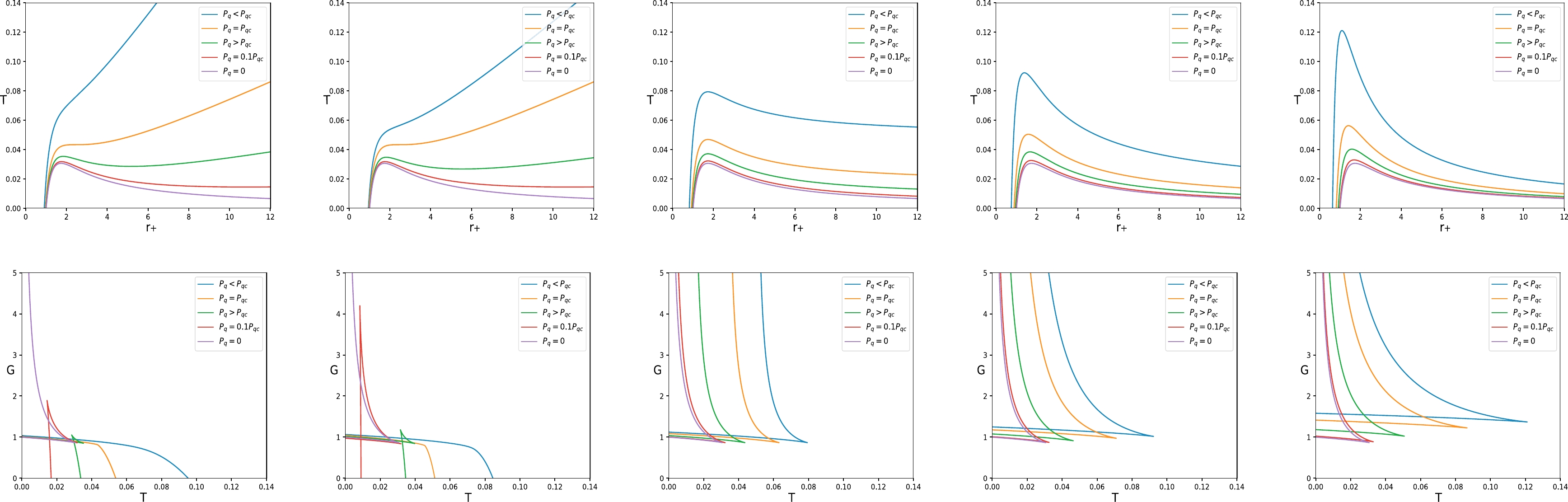
(32) We can observe that the value of the free parameter k does not affect the behavior of the Gibbs free energy. For dark energy (
$ -1<\omega_{\rm q} <-1/3 $ ), T as a function of$ r_{+} $ and G as a function of T are depicted in Fig. 1. The typical swallowtail behavior of Gibbs function is retained only when$ \omega_{\rm q} $ is less than$ -2/3 $ value, which corresponds to the vdW-type phase transition in$ T-r_{+} $ plane. The atypical swallowtail behavior (the swallowtail surrounded by$ T=0 $ ) always exists, which corresponds to a distinctive process in the$ T-r_{+} $ plane. The distinctive process is caused by the repulsive force provided by quintessence with negative pressure as the leading force in the later stage, which is exhibited as the temperature being depressed. It differs significantly from the scenario in which gravity dominates in the late stage of the extended phase space. -
When the free parameter k is fixed to
$ \omega_{\rm q}^2 $ , the thermodynamic volume is consistent with that in the extended phase space, implying that the pressure of the BH system in this case can be directly composed of these two parts. In this scenario, the equation of state in the quintessential phase space is$ \begin{equation} P_{\rm q}=\frac{1}{\omega_{\rm q}}\Bigg(\frac{T}{2r_+}-\frac{1}{8\pi r_+^2}+\frac{Q^2}{8\pi r_+^4}\Bigg). \end{equation} $

(33) In Ref. [5], the equation of state in the extended phase space is expressed as
$ \begin{equation} P_{\rm \Lambda}=\frac{T}{2r_+}-\frac{1}{8\pi r_+^2}+\frac{Q^2}{8\pi r_+^4}. \end{equation} $

(34) Hence, we can obtain the equation of state after the combination:
$ \begin{equation} P_{\rm tot}=\Bigg(1-\frac{1}{\omega_{\rm q}}\Bigg)\Bigg(\frac{T}{2r_+}-\frac{1}{8\pi r_+^2}+\frac{Q^2}{8\pi r_+^4}\Bigg). \end{equation} $

(35) Therefore, the critical thermodynamic quantity is
$ \begin{eqnarray} r_{\rm c}=\sqrt{6}Q,\; T_{\rm c}=\frac{1}{3\sqrt{6}\pi Q},\; P_{\rm totc}=\frac{1}{96\pi Q^2}\Bigg(1-\frac{1}{\omega_{\rm q}}\Bigg). \end{eqnarray} $

(36) That is, we can obtain the critical universal constant as
$ \begin{equation} \varepsilon_{\rm q} = \frac{3}{8}\Bigg(1-\frac{1}{\omega_{\rm q}}\Bigg). \end{equation} $

(37) If the dark energy case
$ -1<\omega_{\rm q} <-1/3 $ ,$ \varepsilon_{\rm tot} $ is within$ {3}/{4} < \varepsilon_{\rm tot} < {3}/{2} $ , which remains greater than the standard value$ 3/8 $ of vdW-type phase transition. Based on Eqs. (26) and (35),$ P_{\rm tot} $ as a function of V is depicted in Fig. 2. The increase in$ \omega_{\rm q} $ noticeably moves the isotherm upward, that is, the system pressure is increased. The features of vdW-type phase transition can be observed on the$ P_{\rm tot}-V $ plane with different$ \omega_{\rm q} $ values, implying that, in the context of AdS space-time, gravity is the leading force in the later stage, which is different from the case only quintessence dark energy exists.
Figure 2. (color online)
$ P_{\rm q} $ as a function of V. The BH charge is taken as$ Q = 1 $ and the quintessence state parameter$ \omega_{\rm q} = -1, -5/6, $ $ -2/3, -1/2, -1/3 $ .We can easily observe that the reduced equation of state has the same form as Eq. (27); therefore, this phase transition is still a second-order phase transition.
-
When the free parameter k is fixed to
$ 1 $ , Eq. (16) becomes the general form of coupling quintessence, in which the direct coupling between non-relativistic matter and quintessence is not considered. The equation of state in the quintessential phase space can be expressed as$ \begin{equation} P_{\rm q}=\omega_{\rm q}\Bigg(\frac{T}{2r_+}-\frac{1}{8\pi r_+^2}+\frac{Q^2}{8\pi r_+^4}\Bigg). \end{equation} $

(38) When the general thermodynamic volume V is used as the variable, we adjust the pressure in the quintessential phase when combining the pressure of the two phase spaces, which does not break the first law of thermodynamics and Smarr relation. Using Eqs. (26) and (38), we can obtain
$ \begin{equation} V_{\rm q}P_{\rm q}=VP'_{\rm q}\rightarrow P'_{\rm q}=\frac{V_{\rm q}P_{\rm q}}{V}=\frac{k}{\omega_{\rm q}^2}P_{\rm q}, \end{equation} $

(39) and the combined pressure
$ P_{\rm tot} $ is$ \begin{equation} P_{\rm tot}=P_{\rm \Lambda}-\frac{k}{\omega_{\rm q}^2}P_{\rm q}. \end{equation} $

(40) The equation of state after combination can yield an expression similar to Eq. (35):
$ \begin{equation} P_{\rm tot}=P_{\rm \Lambda}-\frac{1}{\omega_{\rm q}^2}P_{\rm q}=\Bigg(1-\frac{1}{\omega_{\rm q}}\Bigg)\Bigg(\frac{T}{2r_+}-\frac{1}{8\pi r_+^2}+\frac{Q^2}{8\pi r_+^4}\Bigg). \end{equation} $

(41) We observe that the combination of the quintessential and extended phase spaces is not regulated by the free parameter k, which means that coupling between non-relativistic matter and quintessence does not affect the thermodynamic characteristics of the RN BH system.
-
The thermodynamic properties of an RN BH in the quintessential phase space are revealed in this analysis. When RN BH is surrounded by the thermal quintessence, the quintessence exerts a pressure
$ P_{\rm q} $ the event horizon in spherically symmetric BH, which leads to the discussion of the BH thermodynamics in the quintessential phase space. For an RN BH interacting with quintessence, we use the equation of the state of quintessence to obtain the first law of BH thermodynamics and Smarr relation in the quintessential phase space and investigate the critical behavior of this thermodynamic system. We observe that the conjugate quantity$ V_{\rm q} $ of the pressure$ P_{\rm q} $ is often not equal to the thermodynamic volume V. A phase transition occurs during the evolution of an RN BH in the quintessential phase space, and its similarity to the standard vdW-type phase transition depends on the ratio$ \omega_{\rm q}/k $ in terms of the universal constant. From the perspective of critical exponents and critical behavior of normalized scalar curvature$R_{\rm N}$ , the phase transition is typically a second-order phase transition, which is the same as the standard vdW-type phase transition. We believe that the existence of this phase transition results in strange critical phenomena mentioned in the introduction when an RN AdS BH surrounded by quintessence dark energy is considered in the extended phase space.The
$ T-r_{+} $ and$ G-T $ diagrams show that, if$ -1<\omega_{\rm q}<-2/3 $ , the features of vdW-type phase transition emerge, including typical equal area and typical swallowtail behaviors. If$ -2/3<\omega_{\rm q}<-1/3 $ , the features of vdW-type phase transition completely lost, a distinctive phase transition occupied and an atypical swallowtail behavior (the swallowtail surrounded by$ T = 0 $ ) replaces the typical swallowtail behavior, which is caused by the depression of quintessence with negative pressure. This effect increases with the increase in the state parameter$ \omega_{\rm q} $ .We further discuss the combination of RN BHs in the quintessential and extended phase spaces under two simple cases. Constructing the combination based on the general thermodynamic volume
$ V=(4/3)\pi r^3 $ , the form of the equation of state has consistency and is not controlled by the free parameter k. We observe that the universal constant$ \varepsilon_{\rm tot} $ is within$ {3}/{4} < \varepsilon_{\rm tot} < {3}/{2} $ if$ \omega_{\rm q} $ is within$ -1<\omega_{\rm q}<-2/3 $ . The interaction with quintessence dark energy causes the universal constant of RN AdS BHs to be larger than the standard vdW-type phase transition, but the phase transition grade is still of second-order. These results suggest that the quintessential phase space must be constructed with the pressure from quintessence to improve the thermodynamic research of AdS BHs involving quintessence dark energy, and it can be used as a new probe to explore BH thermodynamics.
Thermodynamics of black holes in the quintessential phase space
- Received Date: 2022-08-13
- Available Online: 2023-01-15
Abstract: Considering that the negative pressure of the accelerated expansion of the universe results from the cosmological constant or the dark energy quintessence, we use the dark energy quintessence to construct the "quintessential" phase space. In contrast to the previous discussion in which the cosmological constant is considered as the black hole (BH) phase transition pressure, in this analysis, we believe that the pressure results from quintessence. The characteristics of critical behavior, Gibbs free energy, and temperature behavior in quintessential phase space are investigated. We observe that the phase transition belongs to van der Waals phase transition within





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: