-
Quantum chromodynamics (QCD) is a fundamental theory describing strong interaction that exhibits two fascinating nonperturbative features: confinement and dynamical chiral symmetry breaking (DCSB). These features govern properties of QCD bound states–hadrons. At finite temperature, a heat bath affects the dynamics and hence properties of hadrons, e.g., hadron masses and decay constants. At high temperature, the hadron matter undergoes phase transitions: deconfinement and chiral restoration; and a new state of matter, i.e., quark-gluon plasma (QGP), may form [1, 2]. Studies on QCD phase transition have become both experimental and theoretical frontiers [3–10].
At finite temperature, thermal modifications may occur for hadron properties, e.g., mass, size, and structure. Among mesons, pion π is of particular importance. This pion has a twofold role: the Goldstone mode of DCSB and the quark-antiquark bound state embodying confinement. The temperature dependence of its properties is critical to understand the QCD phase transitions. Moreover, its chiral partner, i.e., the scalar meson σ, plays also an important role. In vacuum, a sizable π-σ mass splitting can be observed. However, they tend to degenerate in a heat bath, which indicates chiral symmetry restoration.
The properties of light mesons at finite temperature have attracted much attention. Many approaches have been proposed in recent years, e.g., lattice QCD [11, 12], chiral perturbation theory (ChPT) [13, 14], Nambu–Jona-Lasinio (NJL) model [15, 16], Polyakov-loop-extended NJL model [17–19], functional renormalization group [20, 21], and others [22–26]. The QCD's Dyson-Schwinger equations (DSE) is a nonperturbative and Poincaré covariant framework capable of simultaneously describing confinement and DCSB. It has been widely used to study hadron properties in both vacuum and media [3, 27–34]. Mesons, the two-body bound states, correspond to the poles of the scattering matrices between quarks and antiquarks at zero temperature. Thus, the bound-state equation, i.e., the homogenous Bethe-Salpeter equation (BSE), is defined by the on-shell condition. However, at finite temperature, the situation is different. Mesons in a heat bath may dissociate [35]. In such a case, the poles may be smeared and become peaks with finite widths. Consequently, the homogenous BSE cannot be well defined any more. Moreover, to solve the homogenous BSE, one needs analytically continued quark propagators as input. The analytical continuation is difficult for the quark propagators defined on the Matsubara frequencies in the imaginary-time formalism of the thermal field theory.
In the DSE framework, the screening masses of pion and sigma meson at finite temperature were studied with a simplified approximation [36]. However, studies on pole masses and spectral widths of pion and sigma meson at finite temperature with a realistic approximation are still missing. Therefore, in this study, we analyzed the spectral functions of mesonic correlation functions to study properties of pseudoscalar and scalar mesons at finite temperature according to previous results [33, 34]. The imaginary-time correlation functions were computed with the solutions of the quark gap equation and inhomogeneous BSE. For solving them, we adopted the so-called rainbow-ladder (RL) truncation, which approximates the quark-gluon vertex as the bare one and the BSE kernel as the one-gluon-exchange form. The RL truncation is the leading symmetry-preserving approximation, which can realize the twofold role of pion, i.e., the quark-antiquark bound state and the Goldstone boson [37–39].
In Sec. II, we describe the gap equation of the quark propagator at finite temperature and study the chiral phase transition. In Sec. III, we analyze the relationship between thermal properties of π and σ and chiral symmetry restoration. We also extend the analysis by studying the cases of kaon and
$ s\bar{s} $ pseudoscalar meson. In Sec. IV, we present a brief summary and perspectives. -
The quark gap equation at finite temperature was described in Refs. [3, 5]; it reads
$ S\left({\omega}_{n}, \vec{p}\right)^{-1} = Z_{2}\left({\rm i} \vec{\gamma} \cdot \vec{p}+{\rm i} \gamma_{4} {\omega}_{n}+Z_{m} m\right) + \Sigma({\omega}_{n}, \vec{p})\,, $

(1) with the self-energy in the rainbow approximation
$ \Sigma\left({\omega}_{n}, \vec{p}\right) = \frac{4}{3} Z_{1} T {\textstyle\sum} \int_l \frac{{\rm d}^{3} q}{(2 \pi)^{3}} g^{2} D_{\mu \nu}\left(k_{\Omega}\right) \gamma_{\mu} S\left({\omega}_{l}, \vec{q}\right) \gamma_{\nu} \,,\quad $

(2) where
$ {\omega}_{l}=(2 l+1) \pi T $ are the fermionic Matsubara frequencies; m is the current quark mass, which defines the chiral limit for$ m = 0 $ ;$ Z_{1,2,m} $ are the quark-gluon vertex, quark wave function, and mass renormalization constants, respectively; and$ {\textstyle\sum} \displaystyle\int_l $ represents the summation of Matsubara frequencies and three-dimensional integral.$ D_{\mu \nu}\left(k_{\Omega}\right) $ is the dressed-gluon propagator which has the form$ \begin{array}{*{20}{l}} g^{2} D_{\mu \nu}\left(k_{\Omega}\right)=P_{\mu \nu}^{T} \mathcal{D}\left(k_{\Omega}^{2}\right)+P_{\mu \nu}^{L}\mathcal{D}\left(k_{\Omega}^{2}+m_{g}^{2}\right), \end{array} $

(3) where the gluon momentum
$ k_{\Omega}:=\left({\omega}_{n}-{\omega}_{l}, \vec{p}-\vec{q}\right) $ , the gluon Debye mass$ m_g^2=(16 / 5) T^{2} $ [3, 32, 40–43], and$ \mathcal{D} $ denotes the interaction kernel. Note that the temperature breaks the Euclidean$ O(4) $ symmetry, and thus the gluon tensor structure breaks into transverse and longitudinal parts:$ P_{\mu \nu}^{T} :=\left\{\begin{array}{ll}{0,\; \quad\qquad\qquad} {\mu \text { and/or } \nu=4}, \\ {\delta_{i j}-\dfrac{k_{i} k_{j}}{k^{2}},\quad\quad} {\mu, \nu=i, j=1,2,3},\end{array}\right. $

(4) $ P_{\mu \nu}^{L} :=\delta_{\mu \nu}-\frac{k_{\mu} k_{\nu}}{k^{2}} - P_{\mu \nu}^{T}. $

(5) The interaction kernel must be specified. In general, phenomenological models are adopted [30, 44]. According to the modern DSE and lattice QCD, the gluon mass scale is the most important feature of the interaction kernel. This means that a realistic model must be finite and saturated in the infrared region. In this study, we used the simplified form of the Qin-Chang model [44]:
$ \mathcal{D}\left(k_{\Omega}^{2}\right)=\xi \frac{8 \pi^{2}}{\omega^{4}} {\rm e}^{-k_{\Omega}^{2} / \omega^{2}}\,, $

(6) which have two parameters, i.e., the strength ξ and width ω, for characterizing the interaction. Herein, we set
$\xi\omega=(0.82~ \mathrm{GeV})^{3}$ with$ \omega=0.5 $ GeV. Given that the simplified model has no ultraviolet tail, the renormalization procedure can be skipped.The solution of the gap equation, i.e., the dressed quark propagator, can be decomposed as follows:
$ \begin{array}{*{20}{l}} S\left({\omega}_{n}, \vec{p}\right)^{-1}= {\rm i}\vec{\gamma} \cdot \vec{p} A +{\rm i} \gamma_{4} {\omega}_{n} C + B\,, \end{array} $

(7) where
$ A,B,C $ are scalar functions depending on the Matsubara frequency$ \omega_n^2 $ and spatial momentum$ \vec{p}^2 $ . With the solution for the fully dressed-quark propagator, we studied the chiral phase transition and obtained the (pseudo-) critical temperature$T_{\rm c}$ . The corresponding order parameter is the chiral condensate. In the chiral limit, we have$ -\langle\bar{\psi} \psi\rangle_{0} = N_{c}T \operatorname{tr}_{D}{\textstyle\sum} \int_n \frac{{\rm d}^{3} p}{(2 \pi)^{3}} S\left(\omega_{n},\vec{p}\right). $

(8) Herein, the integral simply converges because the interaction model is ultraviolet-free. However, if a nonzero current quark mass is involved, Eq. (8) diverges and does not provide a well-defined chiral condensate. Hence, we introduce a subtraction procedure and define the chiral condensate as
$ -\langle\bar{\psi} \psi\rangle=N_{c}T\operatorname{tr}_{D} {\textstyle\sum} \int_n\frac{{\rm d}^{3} p}{(2 \pi)^{3}}\left[S\left(\omega_{n},\vec{p}\right)-S_{0}\left(\omega_{n},\vec{p}\right)\right], $

(9) and chiral susceptibility
$ \begin{equation} \chi_m(T)=-\frac{\partial}{\partial m}\langle\bar{\psi} \psi\rangle, \end{equation} $

(10) with
$ S_{0}\left(\omega_{n},\vec{p}\right) $ being the free quark propagator. It should be emphasized that the subtraction procedure only works for the simplified interaction model, although the correct$T_{\rm c}$ can be extracted through it [45]. However, this subtraction has residuals at high temperature. An accurate high temperature behavior requires a more strict definition of chiral condensate [46]. More general discussions are available in Refs. [47–52].In this study, we set the current quark masses as
$ \begin{array}{*{20}{l}} m_{u/d} = 4.8\ \text{MeV} \text{ and } m_{s} = 116\ \text{MeV}, \end{array} $

(11) by fitting the pseudoscalar mesons in vacuum (
$ m_\pi = $ 0.135 GeV and$ m_K = 0.495\ \text{GeV} $ ). Accordingly, we obtained the leptonic decay constants ($ f_{\pi} =0.095\ \text{GeV} $ and$ f_{K} =0.110\ \text{GeV} $ ), which were consistent with the empirical values. In the following discussion, we only analyze the chiral condensate of light quarks. For the case of strange quarks, see Refs. [3, 50, 53], for instance.At zero temperature, we obtain the chiral condensate
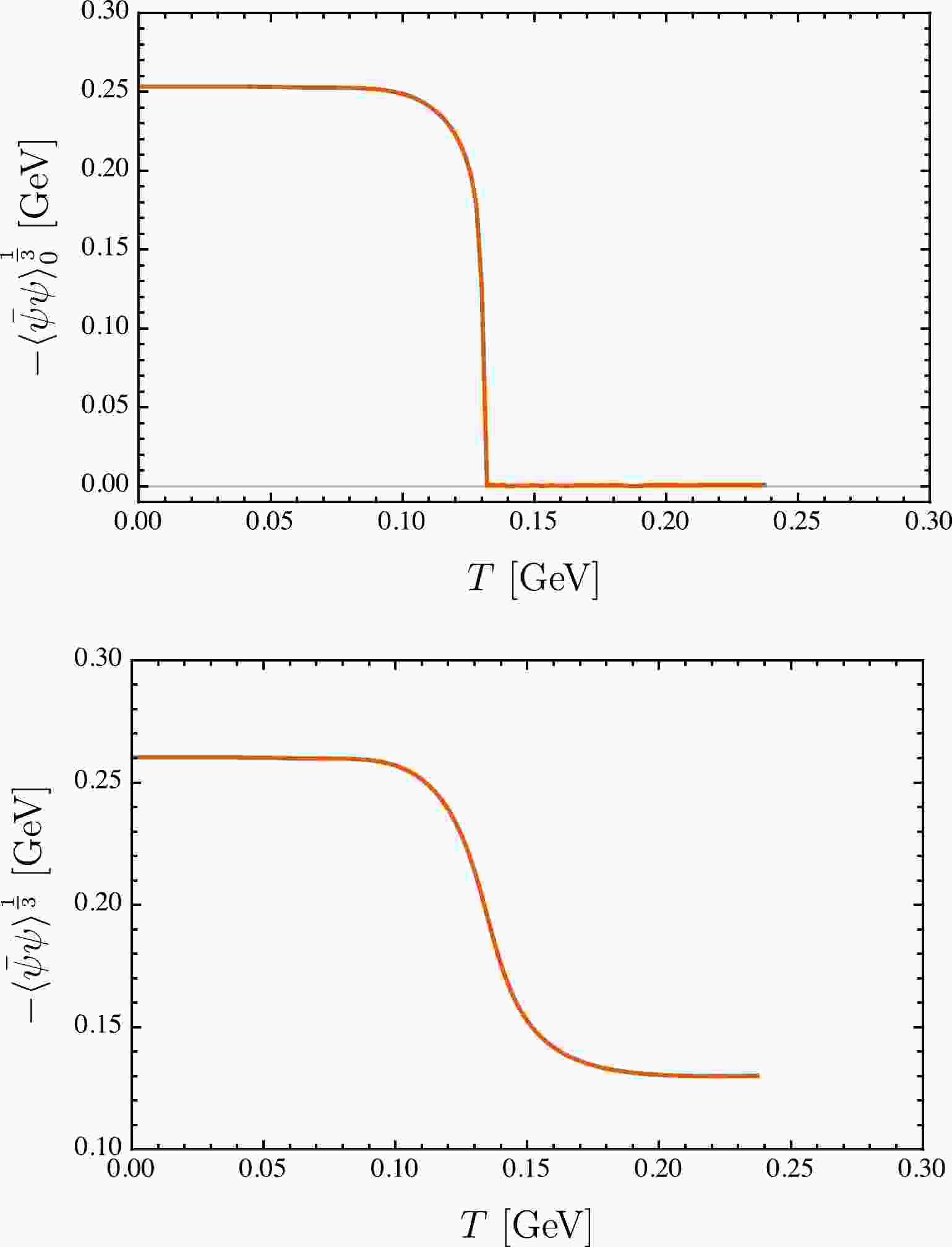
$ -\langle\bar{\psi} \psi\rangle=(0.26\ \text{GeV})^3 $ , which is consistent with the Gell-Mann-Oakes-Renner (GMOR) relation [54]:$ f_\pi^2 m_\pi^2 = - 2 m_{u/d} \langle\bar{\psi} \psi\rangle. $

(12) With increasing temperature, the chiral condensate in the chiral limit gradually decreases and completely vanishes when
$ T > 0.131 $ GeV. The evolution behavior is shown in Fig. 1 for both the case with finite current quark masses and the chiral limit. In other words, the chiral symmetry is partially restored at finite temperature. The complete restoration of chiral symmetry is a phase transition with critical temperature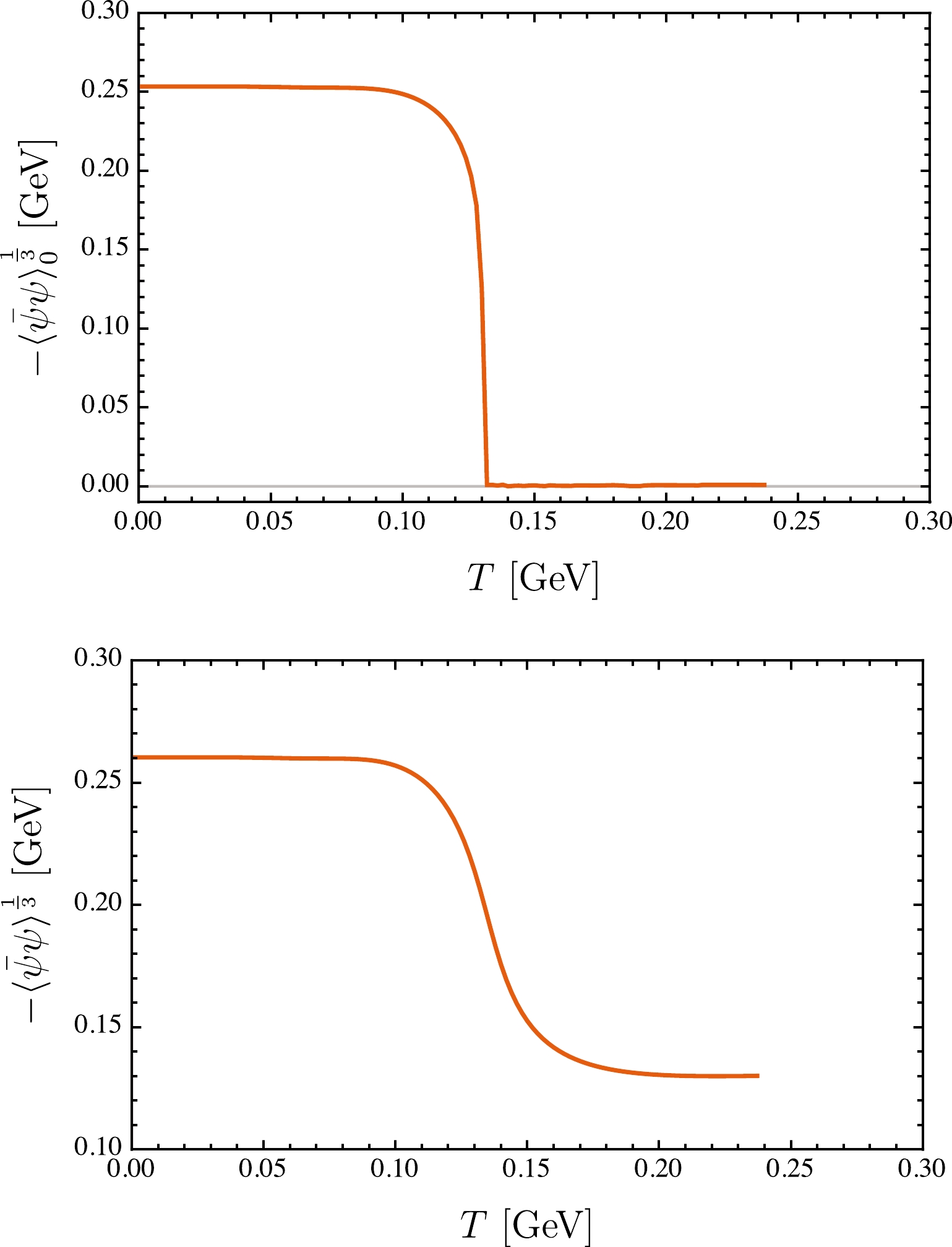
Figure 1. (color online) Thermal evolution behaviors of the chiral condensate in and beyond the chiral limit. Upper panel:
$ m_{u/d}=0 $ MeV; lower panel:$ m_{u/d}=4.8 $ MeV.$ \begin{array}{*{20}{l}} T_{\rm c}\sim 0.131\ \text{GeV}\,, \end{array} $

(13) which is consistent with the result in the chiral limit extrapolated by the latest lattice simulations:
$T_{\rm c}=$ 0.132 GeV [55]. However, beyond the chiral limit, e.g.,$ m_{u/d}= $ 4.8 MeV, the phase transition of chiral symmetry restoration becomes a crossover (see the lower panel in Fig. 1). For such a case, the definition of the pseudo-critical temperature, i.e.,$T_{\rm pc}$ , is not unique. For instance,$T_{\rm pc}$ can be the temperature of the maximum chiral susceptibility [50, 53, 56] or the inflection point of the chiral condensate [57, 58]. By studying the chiral susceptibility maximum, which is shown in Fig. 2, we can obtain the pseudo-critical temperature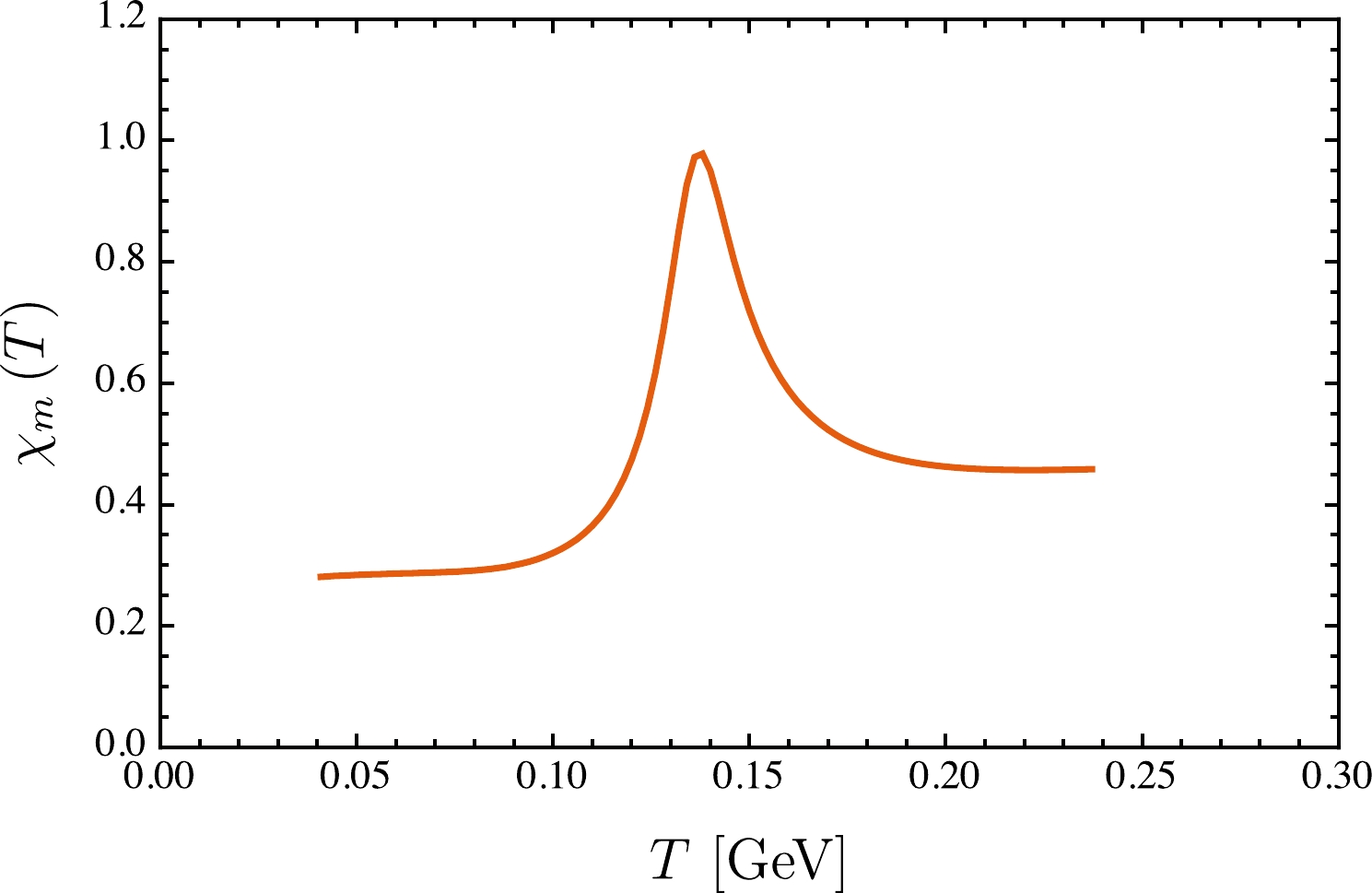
Figure 2. (color online) Thermal evolution behavior of the chiral susceptibility beyond the chiral limit; for this plot,
$ m_{u/d} = $ 4.8 MeV.$ \begin{array}{*{20}{l}} T_{\rm pc}\sim 0.137\ \text{GeV} \end{array} $

(14) which is slightly lower than the recently reported result of lattice simulations with physical current quark mass:
$T_{\rm c}=0.156\ \text{GeV}$ [59]. -
In the previous section, the quark gap equation was solved to study the chiral restoration at finite temperature, and the (pseudo-)critical temperatures were obtained. Next, we investigate the properties of mesons, especially pion, in the neighborhood of
$T_{\rm c,pc}$ . In vacuum, mesons can be solved by the homogeneous BSE, a counterpart of the Schrödinger's equation. However, as mentioned in the introduction, it may be ill-defined at finite temperature. In this study, we applied previous reported results [33, 34, 60] to extract meson properties from correlation functions.In terms of Green functions, the Euclidean mesonic correlation function can be defined as [33]

where
$ P_4=2n\pi T $ , with$ n \in \mathbb{Z} $ , is the bosonic Matsubara frequencies, and$ \vec{P} $ is the total spatial momentum; gray circular blobs and black dots denote dressed$ \Gamma_H $ and bare$ \gamma_H $ vertices, respectively; the subscript H specifies$ J^P $ as a quantum number with$ \gamma_H \in \{ \mathbf{I}, \gamma_5, \gamma_\mu, \gamma_5\gamma_\mu, \cdots \} $ . The dressed vertices can be solved by the inhomogeneous BSE, which reads
where the dressed quark propagators are fed with the solution of the quark gap equation, and K denotes the two-particle irreducible quark-antiquark scattering kernel.
In the rainbow-ladder approximation, the inhomogeneous BSE for the dressed vertices can be expressed as
$ \begin{aligned}[b]& \Gamma_{H}\left(P_4; \omega_n, \vec{p}\right)\\=&Z_{H} \gamma_{H}-Z_{1} \sum\int_l \frac{{\rm d}^{3} \vec{q}}{(2 \pi)^{3}} g^{2} D_{\mu \nu}\left(k_\Omega\right)\\ & \times \frac{\lambda_{a}}{2} \gamma_{\mu} S\left(\omega_l, \vec{q}\right) \Gamma_{H}\left(P_4;\omega_l, \vec{q}\right) S\left(\omega_l+P_4, \vec{q}\right) \frac{\lambda_{a}}{2} \gamma_{v}\,, \end{aligned} $

(17) where
$ \omega_n $ and$ \vec{p} $ are the relative Matsubara frequencies and spatial momenta between two quarks, respectively, and the total spatial momenta of the vertices are$ \vec{P}=0 $ , given that we can utilize the rest frame to extract observables without loss of generality. Because all momenta are Euclidean and real, we need no information about quark propagators on the complex plane. With the solutions of the quark gap equation and inhomogeneous BSE, all ingredients in Eq. (15) are available; consequently, the correlation functions can be computed.Observables are encoded in the spectral functions of correlation functions. The key to obtain observables is twofold: a well-defined spectral representation to bridge the spectral and correlation functions; a reliable method to extract the spectral functions from this representation. First, in the rest frame, the correlation functions only depend on the Matsubara frequencies
$ P_4 $ which are discrete. With polynomial interpolations of quark propagators, we can solve the vertices for$ P_4 \in \mathbb{R} $ by using the inhomogeneous BSE, i.e., Eq. (17). Inserting the solution into Eq. (15), we obtain the correlation functions on the whole real axis. We tested several interpolation schemes for quark propagators and found that the produced correlation functions remain mostly unchanged. In other words, the procedure is accurate and robust. As we will see, this could make our further analysis more convenient.The correlation functions have a formal integral representation as
$ \Pi_{H}\left(P_4^{2}\right)=\int_{0}^{\infty} \frac{{\rm d} \omega^{2}}{2 \pi} \frac{\rho_{H}(\omega)}{\omega^{2}+P_4^{2}} - (\text {subtraction})\,, $

(18) where
$ \rho_H(\omega) $ is the spectral function. For the pseudoscalar (scalar) channel, in the non-interacting limit, the spectral function has an asymptotic behavior at large ω as [61, 62]$ \rho(\omega)\rightarrow \frac{3}{4\pi}\omega^2 \,. $

(19) Given that the spectral integral generates a quadratic divergence, an appropriate subtraction is required.
According to Ref. [33], we introduce a discrete transform for correlation functions as (the subscript H has been suppressed)
$ \begin{aligned}[b] \hat{\Pi}\left(P_4^{2}\right) := & \frac{\Pi(s^{2})}{(s^{2}-s_1^{2})(s^{2}-s_2^{2})}\\ &+\frac{\Pi(s_1^{2})}{(s_1^{2}-s^{2})(s_1^{2}-s_2^{2})}+\frac{\Pi(s_2^{2})}{(s_2^{2}-s^{2})(s_2^{2}-s_1^{2})}\,. \end{aligned} $

(20) where
$ s=P_4, s_1=P_4+\Delta, s_2=P_4+2\Delta $ , and Δ is a positive constant. Then, the transformed correlation functions have a well-defined spectral representation:$ \hat{\Pi}\left(P_4^{2}\right)=\int_{0}^{\infty} \frac{{\rm d} \omega^{2}}{2 \pi} \frac{\rho(\omega)}{\left(\omega^{2}+s^{2}\right)\left(\omega^{2}+s_1^2\right)\left(\omega^{2}+s_2^{2}\right)}. $

(21) In principle, the choice of the constant Δ does not affect the extracted spectral functions. However, in the numerical calculations, a large Δ could produce
$ \hat{\Pi}\left(P_4^{2}\right) $ with a small magnitude, which may involve sizable relative errors. Meanwhile, for a small Δ, the transform involves small denominators and thus unstable numerical differences. In this study, we set$\Delta = 0.8\pi – 4\pi T_{\rm max}$ , where$ T_{\rm max}=0.2 $ GeV is the highest temperature in the analysis.Inserting the non-interacting spectral function into the spectral representation given by Eq. (21), we obtain the non-interacting correlation function as
$ \hat{\Pi}^{\text{asy}}\left(P_4^{2}\right)=\frac{3}{4\pi}\int_{0}^{\infty} \frac{{\rm d} \omega^{2}}{2 \pi} \frac{\omega^2}{\left(\omega^{2}+s^{2}\right)\left(\omega^{2}+s_1^2\right)\left(\omega^{2}+s_2^{2}\right)}. $

(22) By comparing the numerical results of
$ \hat{\Pi}_\pi(P_4^2) $ and$ \hat{\Pi}^{\text{asy}}(P_4^2) $ , we can intuitively see how the interaction is modified by a heat bath. The comparison is presented in Fig. 3. Note that the transformed correlation functions$ \hat{\Pi}_\pi $ are almost identical to that in vacuum when$ T<0.1 $ GeV. With temperature increasing, the infrared behavior (i.e.,$ P_4<1 $ GeV) of$ \hat{\Pi}_\pi $ gradually decreases. This means that the low-energy interaction is weakened by a heat bath. Moreover, it can be seen that the thermal effect is significantly strong in the neighborhood of$ T\sim 0.13 $ GeV, which coincides with the pseudo-critical temperature$T_{\rm pc}$ of chiral phase crossover. Therefore, it is expected that the thermal evolution of meson properties, especially π and σ, may strongly signal chiral phase transition or crossover.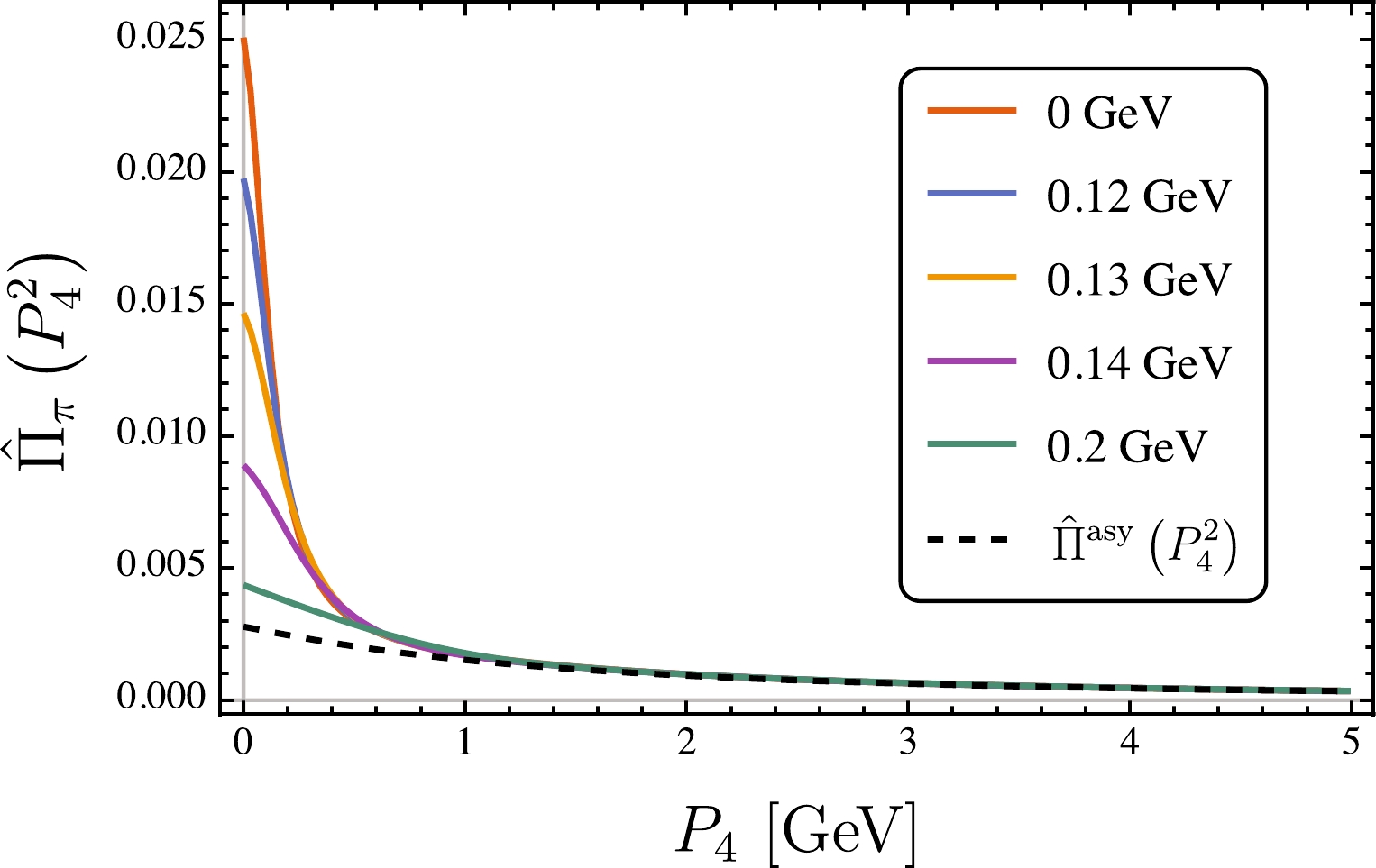
Figure 3. (color online) Correlation function of pion at different temperatures; for this plot, the current quark mass was set as
$ m_{u/d}=4.8 $ MeV.To obtain more information on mesons, such as the mass and width, we still need to explicitly reconstruct spectral functions using Eq. (21). Although the reconstruction is an ill-posed problem, many numerical methods are available on the market, e.g., the maximum entropy method (MEM), which has been widely used [63–65]. In this study, we adopted MEM with the asymptotic spectral function as the default model. First, we found that a peak appeared in the low-energy region of the extracted spectral functions, which is absent for the non-interacting spectral function. This peak encodes information on the interaction. For increasing temperature, the peaks became lower and broader, and eventually disappeared. For instance, the thermal evolution behavior for pion spectral functions is shown in Fig. 4.
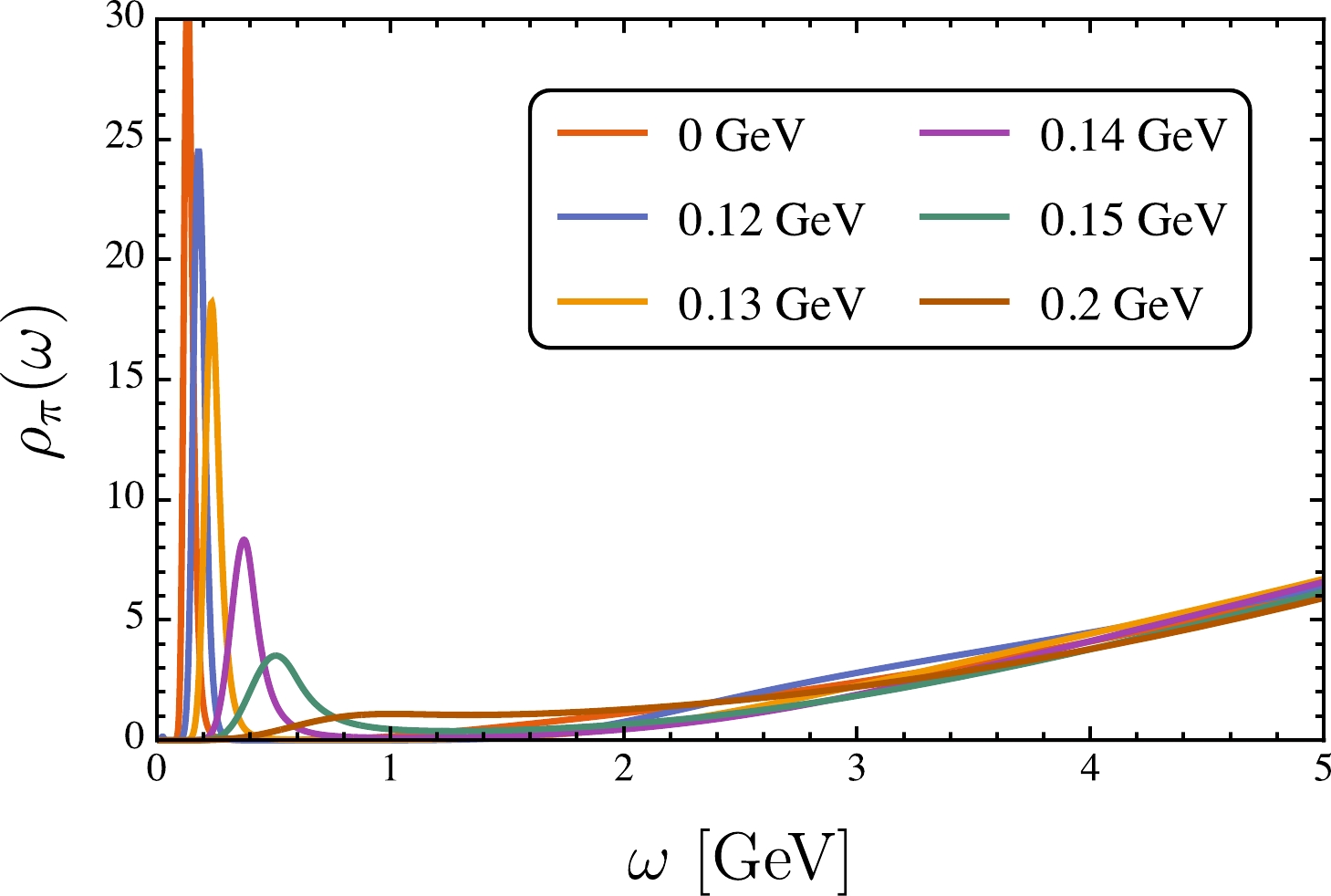
Figure 4. (color online) Extracted pion spectral functions at different temperatures; for this plot, the current quark mass was set as
$ m_{u/d} = 4.8 $ MeV.To isolate the peak for analyzing meson properties, we can define the interacting spectral function as
$ \begin{array}{*{20}{l}} \hat{\rho}(\omega) = {\rho}(\omega) - {\rho}^{\rm asy}(\omega)\,. \end{array} $

(23) Then, the location of the peak corresponds to the meson mass, and the full width at half maximum (FWHM) to the decay width. The ratio of width to mass, denoted by R, can reflect whether a meson has been reliably defined. If the width is comparable to the mass, the peak can be hardly defined as a bound state. In the rest of this section, we analyze how the masses and the widths of the chiral partner, i.e., π and σ, evolve with temperature, and discuss how the thermal properties of the Goldstone boson connect to chiral phase transition or crossover. In our framework, the width of bound state in vacuum is zero. However, for numerical reasons, a bit of width is left. Hence, in the actual calculations, we also subtracted the width at zero temperature to eliminate numerical artifacts.
Let us first consider the case in the chiral limit. On the basis of the Goldstone theorem at finite temperature [35], the pion spectral function
$ \rho_\pi(\omega) $ should have a zero mass peak with vanishing width, which corresponds to massless pion, i.e.,$ \begin{array}{*{20}{l}} \rho_\pi(\omega) \propto \delta(\omega) + {\rm regular\; term}\,. \end{array} $

(24) Accordingly, the pseudoscalar correlation function has a pole at
$ P_4 = 0 $ . The massless pion remains unchanged below the critical temperature, i.e.,$T < T_{\rm c}$ . However, given that the chiral symmetry is completely restored above the critical temperature, i.e.,$T > T_{\rm c}$ , the zero mass peak for pion should shift. Moreover, properties of the chiral partner, i.e., π and σ, must be identical owing to the chiral symmetry. The numerical results are presented in Fig. 5 and confirm the aforementioned analysis. For$T > T_{\rm c}$ , the pion mass exhibits an increasing trend. It seems that pion can survive far above the critical temperature. However, it was found that the ratio of width to mass increases very rapidly after the chiral phase transition. This means that the pion cannot be considered as a well-defined bound state any more. We analyzed the evolution of the ratio versus temperature and found that the steepest ascent point$ T_d $ , which defines the pion dissociation temperature, coincides with$T_{\rm c}$ . The result is shown as the lower panel in Fig. 5. The pion dissociation temperature$ T_d $ is also called the Mott temperature, in which the pion is not considered a bound state. In this sense, the pion dissociation can intuitively signal the deconfinement phase transition because the quarks and antiquarks can be released from bound states [66]. Thus, our results suggest that the chiral and deconfinement phase transitions occur at the same temperature. This conclusion is consistent with the analysis of quark spectral properties [67, 68]. However, note that there are several ways to define the deconfinement temperature, e.g., the Polyakov loop [69, 70], dual quark condensate [71], or strange quark number susceptibility [72]. The deconfinement temperature may vary depending on its definition. It is an ongoing hot debate whether the chiral and deconfinement transitions are the same or different transitions.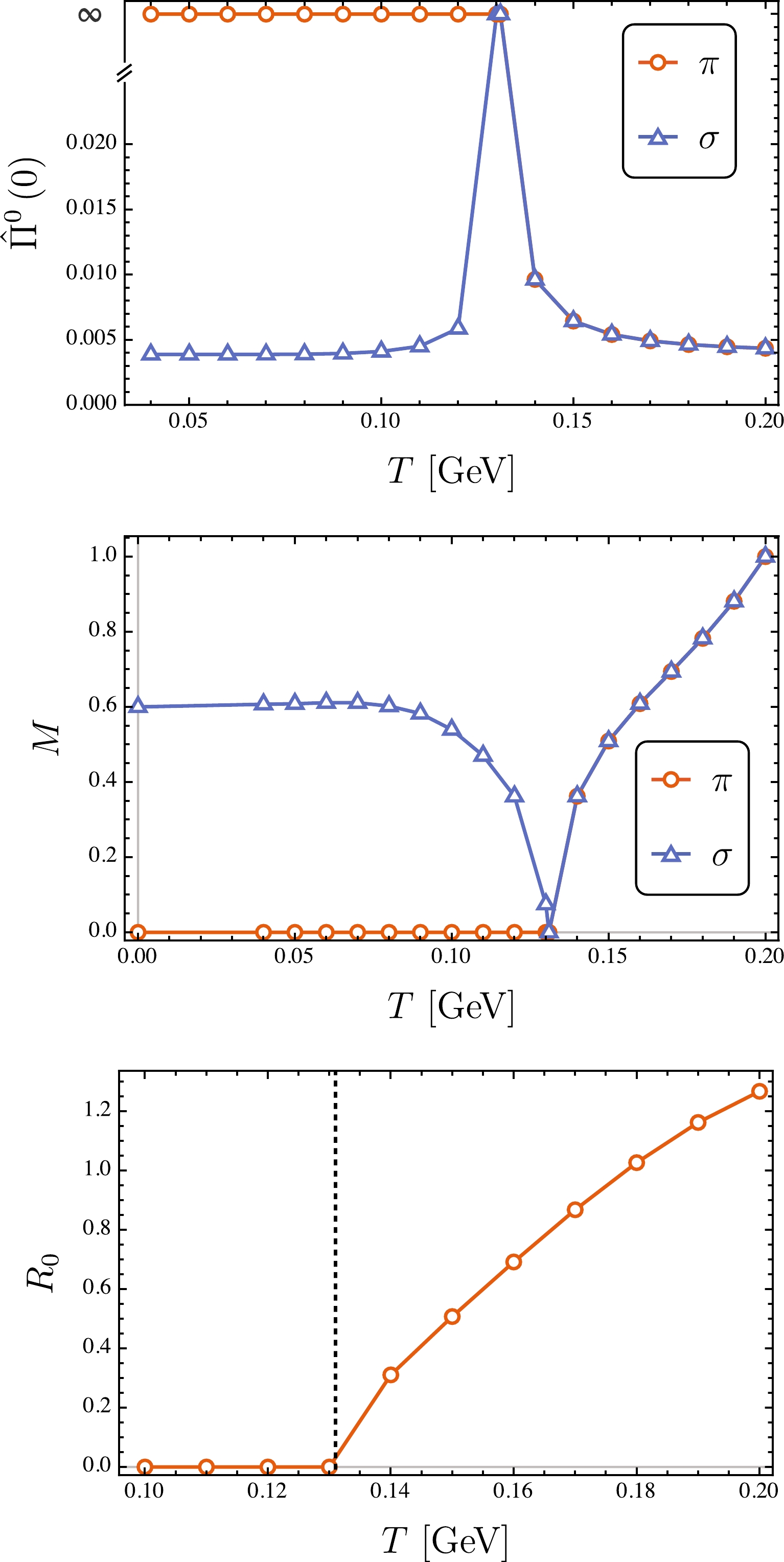
Figure 5. (color online) Upper panel: Pseudoscalar and scalar correlation functions at
$ P_4=0 $ and different temperatures; middle panel: Peak locations of pseudoscalar and scalar spectral functions at different temperatures; lower panel: Ratios of width to mass for pseudoscalar peaks at different temperatures, where the vertical line indicates the steepest ascent temperature. Here, the calculations were performed at the chiral limit.Next, we discuss the case beyond the chiral limit, i.e.,
$ m_{u/d} = 4.8 $ MeV. It is generally believed that, once a small current quark mass is involved, the chiral symmetry is no longer exact, and the pion becomes slightly massive according to the GMOR relation. It is expected that the pion has a finite width at finite temperature. The disappearing of a massless pion can be easily read out from the divergence-free correlation functions (see for instance the upper panel in Fig. 6). For increasing temperature, the difference between pseudoscalar and scalar correlation functions decreases but does not eventually vanish in the asymptotic limit because the chiral symmetry is explicitly broken by the finite current quark mass. For$ T\lesssim m_\pi $ , the masses of π and σ increase and decrease, respectively. They become very close at high temperature, e.g.,$ T>0.15 $ GeV. The evolution behaviors of the π and σ masses versus temperature are shown as the middle panel of Fig. 6. These results are consistent with those obtained by ChPT and holography QCD, which point out a slight positive shift of pion mass at low temperature [13, 26, 35]. Herein, we also include the behavior of the effective quark mass, which is defined as the Euclidean quark mass [56]:
Figure 6. (color online) Upper panel: Pseudoscalar and scalar correlation functions at
$ P_4=0 $ and different temperatures; middle panel: Peak locations of pseudoscalar and scalar spectral functions at different temperatures; lower panel: Ratios of width to mass for pseudoscalar peaks at different temperatures, where the vertical line indicates the steepest ascent temperature. Here, the calculations were performed beyond the chiral limit, i.e.,$ m_{u/d} = 4.8 $ MeV.$ \begin{equation} M_{E}\equiv \left\{p^{2} \mid p^{2}>0,\ p^{2}=B\left(\omega_{0}^{2},\vec{p}^{2}\right)/A\left(\omega_{0}^{2},\vec{p}^{2}\right)\right\}. \end{equation} $

(25) At
$ T\approx 0.14 $ GeV,$ M_\pi\approx 2M_E $ , which intuitively suggests that the pion has no bounding energy and cannot be considered as a bound-state. Note that, because of the fact that the dressed-quark mass function is dependent on$ \omega_n $ and$ \vec{p} $ ,$ M_E $ is simply a effective mass scale, not a free quark mass.As mentioned above, for the chiral phase crossover, the definition of pseudo-critical temperature is not unique. Based on the discussion on the chiral limit, we again studied the pion dissociation by analyzing its ratio of width to mass versus temperature. Thus, we could define the pseudo-critical temperature as the pion dissociation temperature, i.e.,
$ \begin{array}{*{20}{l}} T_{\rm pc} := T_d^\pi \,. \end{array} $

(26) The results are shown as the lower panel in Fig. 6, from which we obtained that
$T_{\rm pc} = T_{d}^\pi = 0.142$ GeV. This value is slightly higher than that defined by the maximum point of the chiral susceptibility. Considering that numerical uncertainties may exist in the reconstruction of spectral functions, the deviation is negligible. In other words, the pion dissociation can effectively signal a phase transition.To complete our discussion, we also studied kaon and fictitious pseudoscalar
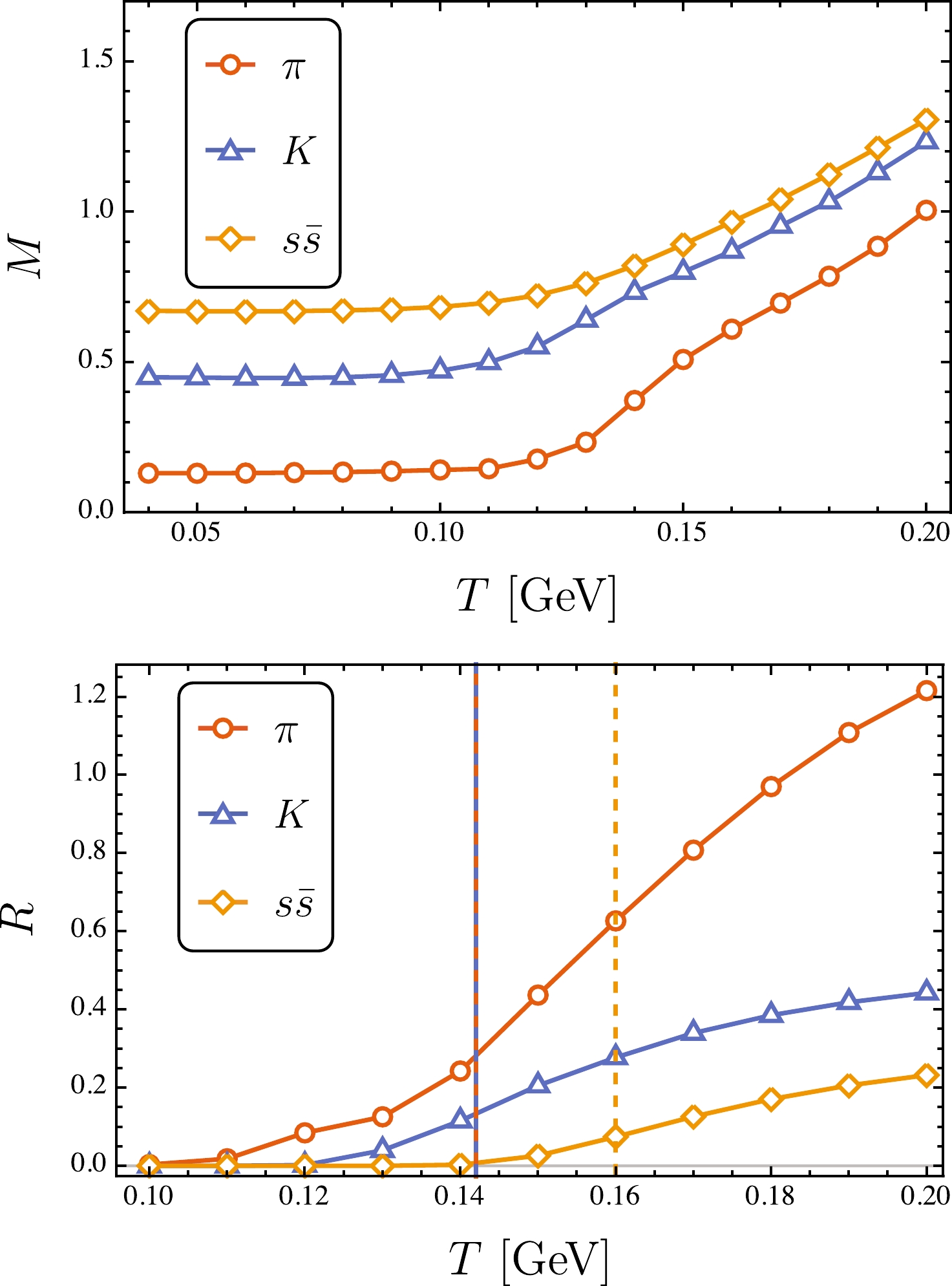
$ s\bar{s} $ . It should be emphasized that the RL approximation cannot handle physical η and$ \eta^\prime $ ; their analysis requires the consideration of the unquench effect of gluon as well as the flavor mixing effect. If we use a Bethe-Salpeter kernel, which is specifically optimized for η and$ \eta^\prime $ , it is possible to calculate their thermal properties within our framework [73]. In this study, the analysis of fictitious$ s\bar{s} $ was conducted to show the effect of the current-quark mass. At low temperature, all modes remain almost untouched. For increasing temperature, their masses gradually increase, but the increasing behaviors are smoother for heavier modes. The comparison for all modes is shown as the upper panel in Fig. 7. The lower panel of the same figure shows the ratios of width to mass for all modes at different temperatures. The vertical lines indicate the corresponding dissociation temperatures, i.e.,$ T_d^K \approx T_d^\pi = 0.142 $ GeV and$ T_d^{s\bar{s}} \approx 1.14 T_d^\pi = 0.160 $ GeV. This suggests that bound states of heavy quarks may survive after the chiral restoration crossover (for similar results, see, e.g., Ref. [34] and references therein). -
In summary, we studied QCD phase transitions, i.e., chiral symmetry restoration and deconfinement, at finite temperature and zero chemical potential. We mainly focused on the thermal properties of pseudoscalar mesons, e.g., π, K, and pseudoscalar
$ s\bar{s} $ , owing to their twofold roles as bound states and Goldstone modes. The meson properties were extracted by reconstructing spectral functions from Euclidean mesonic correlation functions that can be computed with the self-consistent solutions of the rainbow-ladder truncated BSE and DSE. In this study, we combined the developed nonperturbative DSE framework and an advanced numerical algorithm. Our critical temperature in the chiral limit is consistent with state-of-the-art lattice QCD simulations, which makes our parameters more realistic and results more reliable than previous calculations.At the chiral limit, for increasing temperature, the chiral symmetry is restored via a phase transition at
$T_{\rm c} \sim 0.131$ GeV. For$T < T_{\rm c}$ , the pion is always massless as the Goldstone boson of DCSB. The comparison between the evolution behaviors of pseudoscalar and scalar correlation functions versus temperature indicates gradual chiral restoration. Moreover, the pion dissociates at the critical temperature. The pion dissociation temperature, denoted by$ T_d^\pi $ , can be considered as the critical temperature of both chiral symmetry restoration and deconfinement. Beyond the chiral limit, the pseudo-critical temperature was obtained at the maximum point of the chiral susceptibility, i.e.,$T_{\rm pc} = 0.137$ GeV. Considering that the definition of$T_{\rm pc}$ is not unique, it is suggested that$ T_d^\pi $ can serve as an alternative option. For the physical current quark mass,$ T_d^\pi = 0.142 $ GeV, which is consistent with the value obtained by analyzing the chiral susceptibility. Finally, we analyzed thermal properties of kaon and$ s\bar{s} $ . It was found that π and K dissociate almost simultaneously, but heavier$ s\bar{s} $ can survive at higher temperature.The above results can be improved by using a sophisticated truncation scheme beyond the RL approximation [74]. In addition, the above analysis can be extended to the QCD phase diagram on temperature and chemical potential plane. In-medium meson properties can serve as a powerful tool to identify phase structures and reveal phase properties.
-
We would like to pay tribute to Hong-Shi Zong, a great mentor and close friend who passed away in March 2021. We are also grateful for helpful discussion with Heng-Tong Ding, Hai-Tao Shu and Shi-Yang Chen.
Chiral symmetry restoration and properties of Goldstone bosons at finite temperature
- Received Date: 2022-03-21
- Available Online: 2023-03-15
Abstract: We study chiral symmetry restoration by analyzing thermal properties of QCD's(pseudo-) Goldstone bosons, especially the pion. The meson properties are obtained from the spectral densities of mesonic imaginary-time correlation functions. To obtain the correlation functions, we solve the Dyson-Schwinger equations and the inhomogeneous Bethe-Salpeter equations in the leading symmetry-preserving rainbow-ladder approximation. In chiral limit, the pion and its partner sigma degenerate at the critical temperature






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: