Simple model for cluster radioactivity half-lives in trans-lead nuclei

I. INTRODUCTION

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
•      A Cluster radioactivity half-lives
•      B Semi-empirical formulas
• III. RESULTS AND DISCUSSION
• IV. SUMMARY

Cluster radioactivity refers to a decay process that lies between α decay and spontaneous fission [1−5]. It involves the emission of particles from the nucleus that are heavier than α particles but lighter than the lightest fission fragments [6−8]. This type of decay is commonly known as heavy ion radioactivity. In 1980, cluster radioactivity in heavy nuclei was first predicted by Sandulescu, Poenaru, and Greiner [9]. In 1984, Rose and Jones first observed the phenomenon of cluster radioactivity with the emission of $^{14}\rm{C}$ from $^{223}\rm{Ra}$ [10]. Subsequently, Gales et al. [11] and Price et al. [12] definitively confirmed the presence of this distinctive manifestation of radioactivity via experimental investigations. Shortly thereafter, a multitude of clusters heavier than $^{14}\rm{C}$ were discovered in trans-lead nuclei, encompassing $^{20} \rm{O}$, $^{23} \rm{F}$, $^{22,24-26} \rm{Ne}$, $^{28,30} \rm{Mg}$, and $^{32,34} \rm{Si}$ [13, 14], and these observations highlighted the occurrence of cluster radioactivity, particularly in cases where the daughter nuclei are the doubly magic nucleus $^{208} \rm{Pb}$ or its neighboring isotopes [15−19]. This portends that the shell effect plays a vital role in the emission of clusters from heavy nuclei.

To comprehend and explain the phenomenon of cluster radioactivity, numerous researchers have proposed diverse theoretical approaches and/or models, which can be broadly classified into two groups: α-like models [5, 20−32] and fission-like models [33−48]. For α-like models, similar to the tunneling theory of α decay [49−51], the process is generally regarded as a non-adiabatic process. It is assumed that the cluster is preformed in the parent nucleus before penetrating the barrier with a certain cluster formation probability, which is determined by the overlapping district between the parent and daughter nucleus before the available radioactive decay energy $Q_c$ of the cluster penetrates the barrier. For example, Ren et al. [32] systematically calculated the half-life of cluster radioactivity using a microscopic density-dependent model (DDCM) with the renormalized M3Y nucleon-nucleon interaction, considering the dependence of the preformation probability of clusters on the number of charges. Subsequently, Ni et al. [5] extended the generalized density-dependent cluster model (GDDCM) to study cluster radioactivity by numerically constructing the microscopic cluster-daughter potential [20−23]. For fission-like models, the cluster is considered to form during the adiabatic rearrangement process of the parent nucleus. During this process, the atomic nucleus continuously deforms until it reaches the fission configuration after crossing the potential barrier. For example, Santhosh et al. [52] considered a simple power-law interpolation in the Coulomb and proximity potential (CPPM) model and calculated the probability of cluster formation as the probability of penetration through the interior of the potential barrier. Poenaru et al. [37] used two models of analytic super-asymmetric fission (ASAF) and the universal formula (UNIV) to calculate the half-lives of cluster radioactivity and α decay within superheavy nuclei [39−42]. Furthermore, the phenomenon of cluster radioactivity has been extensively investigated using various empirical formulas, such as a unified formula for α decay and cluster radioactivity proposed by Ni et al. [53], a three-parameter model-independent formula proposed by Balasubramaniam et al. [54], and the universal decay law (UDL) formula proposed by Qi et al. [55, 56]. These formulas can clearly elucidate this bizarre decay mode and provide a reliable theoretical basis for future research.

In 2020, based on the Wentzel-Kramers-Brillouin (WKB) approximation and Bohr–Sommerfeld quantization condition, Bayrak [57] proposed a new simple model (HOPM) to study the favored α decay half-lives of 263 nuclei. In this model, there is only one adjustable parameter, that is, the depth of the nucleus potential $V_0$ obtained by fitting the experimental α decay half-lives. Since α decay, cluster radioactivity, and proton radioactivity are analogously described by the quantum mechanical effect. Whether this model can be extended to research on cluster radioactivity is a highly interesting topic. Meanwhile, the cluster preformation probability $P_c$ is key to calculating cluster radioactivity half-lives. In 1988, Blendowske and Walliser [58] found that $P_c$ is related to the α preformation probability $P_\alpha$ via $\log_{10}P_c= \dfrac{A_c-1}{3}\log_{10}P_\alpha$, where $A_c$ is the mass number of the emitted cluster. Recently, Wang et al. [59] modified this relationship between $P_c$ and $P_\alpha$ to $\log_{10}P_c=\dfrac{A_c-1}{3}\log_{10}P_\alpha+ c'$, where $c'$ is an adjustable parameter. Based on these two aspects, considering the modified preformation probability $P_c$, we extend HOPM to systematically study the cluster radioactivity half-lives of 28 trans-lead nuclei. The calculated results reproduce the experimental data well.

This article is organized as follows. A brief introduction to the theoretical framework for the cluster radioactivity half-lives in HOPM and semi-empirical formulas is presented in Sec. II, detailed numerical results and the discussion are given in Sec. III, and a summary is presented in Sec. IV.

II. THEORETICAL FRAMEWORK

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
•      A Cluster radioactivity half-lives
•      B Semi-empirical formulas
• III. RESULTS AND DISCUSSION
• IV. SUMMARY

A Cluster radioactivity half-lives

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
•      A Cluster radioactivity half-lives
•      B Semi-empirical formulas
• III. RESULTS AND DISCUSSION
• IV. SUMMARY

The cluster radioactivity half-life $T_{1/2}$ is generally calculated using [32]

where $\hbar$ is the reduced Plank constant, and Γ is the cluster radioactivity width, which can be expressed as follows in the framework of HOPM [57]:

where $\mu=m_d m_c/(m_d+m_c)\approx\ A_d A_c M_{\rm nuc}/(A_d+A_c)$ is the reduced mass of the cluster-daughter nucleus system, with $A_d$ as the mass number of the daughter nucleus and $M_{\rm nuc}=931.5 \,{\rm MeV}/c^2$ as the nuclear mass unit, $P_c$ is the preformation probability, $F_c$ denotes the knocking frequency of the emitted cluster in the potential barrier, and $S_c$ denotes the action integral. They can be expressed as

where r represents the distance between the centers of the cluster and daughter nuclei, $k(r)=\sqrt{\dfrac{2\mu}{\hbar^2}(V(r)-Q_c)}$ is the wave number, with $V(r)$ and $Q_c$ as the total interaction potential and cluster radioactivity decay energy, respectively, and $r_1$ and $r_2$ denote the classical turning points and satisfy the condition $V(r_1)=V(r_2)=Q_c$. The decay energy $Q_c$ is obtained using [60]

where $B(A_c,Z_c)$, $B(A_d,Z_d)$, and $B(A,Z)$ are the binding energies of the emitted cluster, daughter nucleus, and parent nucleus, respectively, taken from AME2020 [61] and NUBASE2020 [62], with $Z_c$, $Z_d$, and Z as the proton numbers of the emitted cluster, daughter nucleus, and parent nucleus, respectively, and A is the mass number of the parent nucleus.

The total interaction potential $V(r)$ between the emitted cluster and daughter nucleus includes the nuclear potential $V_N(r)$, Coulomb potential $V_c(r)$, and centrifugal potential $V_l(r)$. It can be expressed as

In this study, we choose $V_N(r)$ in the modified harmonic oscillator form, as in [57],

where $V_0$ and $V_1$ are the parameters of the depth and diffusivity of the nuclear potential, respectively. The Coulomb potential $V_C$ is taken as the potential of a uniformly charged sphere with radius R, which can be expressed as [57]

where ${\rm e}^2=1.4399652 \; {\rm MeV \cdot fm}$ is the square of the electronic elementary charge, and R is the sharp radius, which is chosen via a semi-empirical formula in terms of mass number, $R=r_0(A_d^{1/3}+A_c^{1/3})$, with $r_0=1.2249$ [63]. The centrifugal potential can be generally expressed as $V_l(r)=\dfrac{\hbar^2\,l\,(l+1)}{2\mu\,r^2}$, where l is the orbital angular momentum taken away by the emitted cluster. Previous studies [30, 59] have shown that the influence of l on the half-lives of cluster radioactivity is negligible. Furthermore, to simplify this model, we ignore the centrifugal contribution in this study. Then, the total interaction potential $V(r)$ can be further written as [57]

where $C_0=\dfrac{3Z_c\,Z_d\,{\rm e}^2}{2R}$, $C_1=\dfrac{Z_c\,Z_d\,{\rm e}^2}{2R^3}$, and $C_2=Z_c\,Z_d{\rm e}^2$. Using the condition $V(r_1)=V(r_2)=Q_c$, we obtain $r_1=\sqrt{\dfrac{Q_c+V_0-C_0}{V_1-C_1}}$ and $r_2=\dfrac{C_2}{Q_c}$.

Based on the principles of classical and quantum mechanics, the Bohr-Sommerfeld quantization condition can reduce the freedom of the system, which is also a vital application of the WKB approximation [64]. In this study, we use this condition to reduce the degrees of freedom in the interaction between the daughter nucleus and the emitted cluster. It is expressed as [65, 66]

where $G_c$ is the global quantum number, obtained using the relationship $G_c = \dfrac{G_\alpha A_c}{4}$ [66], where $G_\alpha$ is the global quantum number of α decay, which is determined using the Wildermuth quantum rule and expressed as [65]

Then, the relationship between $V_0$ and $V_1$ can be expressed as

with the integral conditions $C_0<(Q_c+V_0)$ and $C_1< V_1$.

Based on Ref. [58], we choose the depth of the nuclear potential between the emitted cluster and daughter nucleus $V_0$ as $V_0=25A_c \; {\rm MeV}$. Using Eq. (12), the normalization factor $F_c$ and action integral $S_c$ can be further written as

Therefore, the cluster radioactivity half-life $T_{1/2}$ can be expressed as

B Semi-empirical formulas

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
•      A Cluster radioactivity half-lives
•      B Semi-empirical formulas
• III. RESULTS AND DISCUSSION
• IV. SUMMARY

1   UDL-formula

In 2009, based on the microscopic mechanism of charged particle emission within α-like R-matrix theory, Qi et al. [56] proposed the UDL, which can be given by

where $\mathcal{A}=A_cA_d/(A_c+A_d)$ is the reduced mass of the emitted cluster-daughter nucleus system, measured in units of nucleon mass. The adjustable parameters are $a=0.4314$, $b=-0.3921$, and $c=-32.7044$.

2   MBM-formula

In 2004, Balasubramaniam et al. [54] proposed a model-independent formula (MBM) with three parameters by considering the characteristics of exotic cluster decays. It can be expressed as

where ${\eta=(A_d-A_c)/A}$ and $\eta_{z}=(Z_d-Z_c)/Z$ represent the mass and charge asymmetry, respectively. The adjustable parameters are $a=10.603$, $b=78.027$, and $c=-80.669$.

3   TAM-formula

In 2013, Tavares et al. [67] presented a novel approach (TAM) for estimating the cluster radioactivity half-lives of translead parent nuclei. It can be given by

where the adjustable parameters are $a=12.8717$, $b= -5.1222$, $c=-4.6496$, and $d=-73.3326$.

III. RESULTS AND DISCUSSION

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
•      A Cluster radioactivity half-lives
•      B Semi-empirical formulas
• III. RESULTS AND DISCUSSION
• IV. SUMMARY

Cluster preformation probability $P_c$ can be considered as the overlap between the actual ground state configuration and the configuration of clusters coupled to sub-states. In 1988, Blendowske and Walliser [58] first found the relationship between the cluster preformation probability $P_c$ and mass of the emitted cluster $A_c$ as $\log_{10}P_c=\dfrac{A_c-1}{3}\log_{10}P_\alpha$. To further show this relationship, we plot $-\log_{10}P_c$ versus $\dfrac{A_c-1}{3}$ for even-even and odd-A parent nuclei in Figs. 1 and 2, respectively. $P_c$ is extracted using the relevant experimental data in Eq. (15) and listed in the third column of Table 1. From these figures, we can see that $-\log_{10}P_c$ and $\dfrac{A_c-1}{3}$ exhibit a clear linear relationship but have intercepts. This conclusion aligns with that of Wang et al. [59], although the value of $P_c$ is obtained using different models.

Figure 1

Figure 1.  (color online) Negative of the logarithm of the preformation penetrability $-\log_{10}P_c$ versus $(A_c-1)/3$ for e-e nuclei.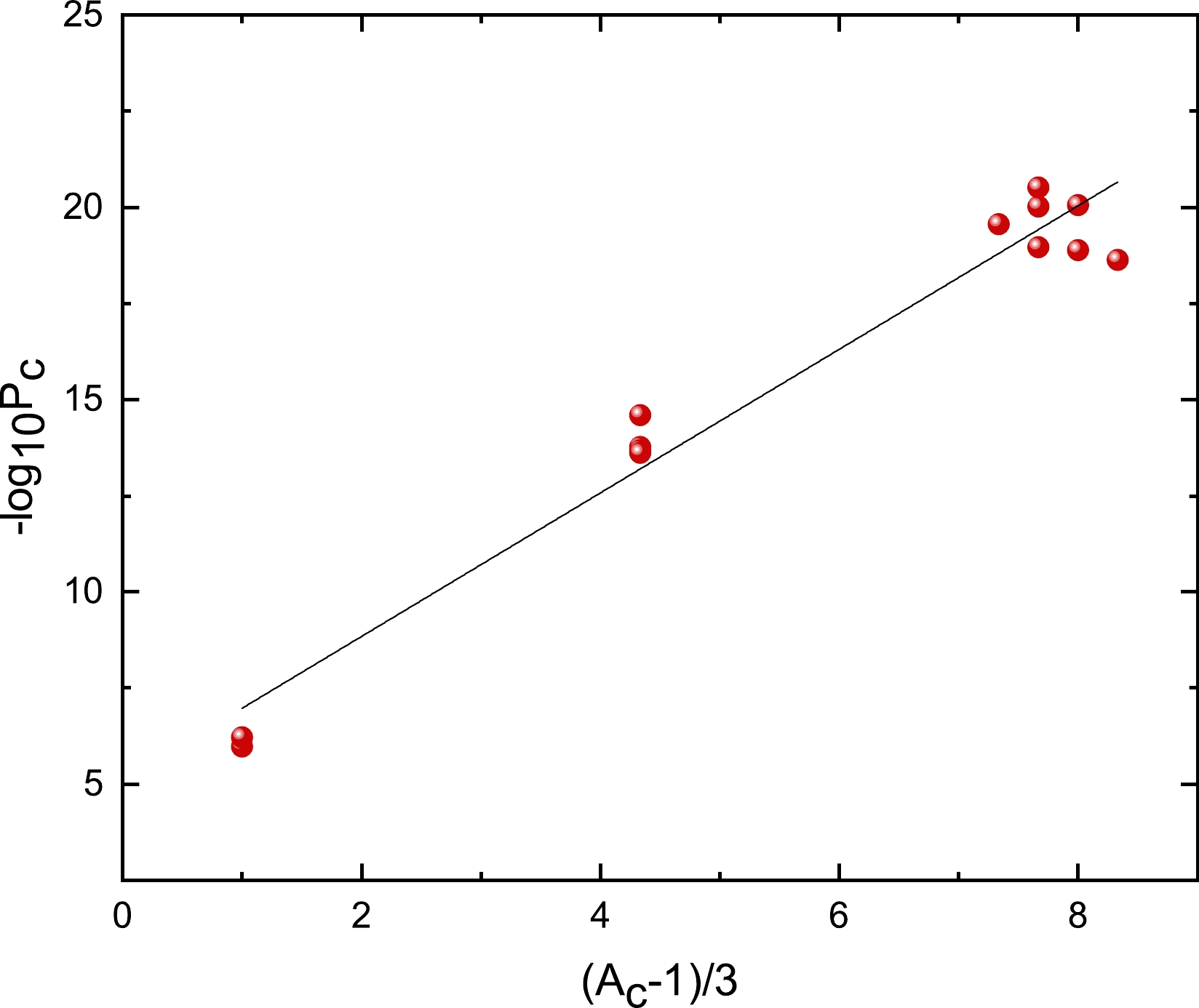

DownLoad: Full-Size Img PowerPoint

Figure 2

Figure 2.  (color online) Same as Fig. 1, but for odd-A nuclei.

DownLoad: Full-Size Img PowerPoint

Table 1

Table 1.  Comparison of experimental cluster radioactivity half-lives with those calculated using different theoretical models and/or formulas in logarithmic form. The values of $Q_c$ and the experimental cluster radioactivity half-lives are taken from Refs. [4, 59, 68, 69].

Decay	${Q_c}$/MeV	$P_c$	${\rm{log}}_{10}T_{1/2}^{\rm{{Exp}}}$	${\rm{log}}_{10}T_{1/2}^{\rm{{HOPM}}}$	${\rm{log}}_{10}T_{1/2}^{\rm{{UDL}}}$	${\rm{log}}_{10}T_{1/2}^{\rm{{MBM}}}$	${\rm{log}}_{10}T_{1/2}^{\rm{{TAM}}}$
				Even-even nuclei
$^{212}$Po$\to ^{208}$Pb+$^{4}$He	8.95	$1.908\times10^{-6}$	−6.52	−5.397	−13.120	−17.348	−20.213
$^{214}$Po$\to ^{210}$Pb+$^{4}$He	7.833	$1.461\times10^{-6}$	−3.78	−2.773	−9.922	−12.978	−15.912
$^{238}$Pu$\to ^{234}$U+$^{4}$He	5.590	$7.900\times10^{-8}$	9.59	9.330	4.513	−0.138	1.025
$^{222}$Ra$\to ^{208}$Pb+$^{14}$C	33.05	$3.207\times10^{-13}$	11.22	11.266	10.070	12.225	12.351
$^{224}$Ra$\to ^{210}$Pb+$^{14}$C	30.54	$8.606\times10^{-14}$	15.92	15.395	15.368	15.998	16.926
$^{226}$Ra$\to \; ^{212}$Pb+$^{14}$C	28.21	$1.369\times10^{-14}$	21.19	19.867	20.913	19.941	21.708
$^{228}$Th$\to ^{208}$Pb+$^{20}$O	44.72	$3.629\times10^{-16}$	20.72	21.239	21.973	22.228	21.972
$^{230}$U$\to \; ^{208}$Pb+$^{22}$Ne	61.40	$1.603\times10^{-18}$	19.57	18.874	20.712	21.335	23.002
$^{230}$Th$\to ^{206}$Hg+$^{24}$Ne	57.57	$1.859\times10^{-19}$	24.64	24.147	25.733	25.854	25.867
$^{232}$U$\to \; ^{208}$Pb+$^{24}$Ne	62.31	$5.190\times10^{-19}$	20.40	20.353	20.587	22.258	21.955
$^{234}$U$\to ^{210}$Pb+$^{24}$Ne	58.83	$1.593\times10^{-19}$	25.25	24.690	26.492	25.317	26.076
$^{234}$U$\to ^{208}$Pb+$^{26}$Ne	59.47	$1.094\times10^{-19}$	25.88	26.297	26.902	26.320	25.302
$^{234}$U$\to ^{206}$Hg+$^{28}$Mg	74.13	$8.637\times10^{-22}$	25.14	24.594	25.738	25.941	26.010
$^{236}$U$\to ^{208}$Hg+$^{28}$Mg	71.69	$2.254\times10^{-21}$	27.58	27.450	29.612	27.811	28.628
$^{236}$Pu$\to ^{208}$Pb+$^{28}$Mg	79.67	$7.260\times10^{-22}$	21.67	21.048	20.640	22.817	22.378
$^{238}$Pu$\to ^{210}$Pb+$^{28}$Mg	75.91	$5.719\times10^{-22}$	25.70	24.975	26.260	25.417	26.085
$^{236}$U$\to ^{206}$Hg+$^{30}$Mg	72.51	$2.815\times10^{-21}$	27.58	28.686	25.472	28.462	25.561
$^{238}$Pu$\to ^{208}$Pb+$^{30}$Mg	77.00	$3.978\times10^{-22}$	25.67	25.926	29.533	25.903	27.734
$^{238}$Pu$\to ^{206}$Hg+$^{32}$Si	91.19	$1.479\times10^{-23}$	25.28	25.246	25.723	25.626	24.983
$^{242}$Cm $\to ^{208}$Pb+$^{34}$Si	96.53	$3.549\times10^{-23}$	23.15	24.636	22.374	24.468	22.941
				Odd-A nuclei
$^{213}$Po$\to ^{209}$Pb+$^{4}$He	8.54	$1.052\times10^{-6}$	−5.37	−4.379	−12.024	−15.843	−18.733
$^{215}$At$\to ^{211}$Bi+$^{4}$He	8.178	$6.108\times10^{-7}$	−4.00	−3.244	−10.574	−14.388	−16.937
$^{221}$Fr$\to \; ^{207}$Tl+$^{14}$C	31.32	$1.687\times10^{-14}$	14.52	13.941	12.640	14.61	14.732
$^{221}$Ra$\to ^{207}$Pb+$^{14}$C	32.40	$2.071\times10^{-14}$	13.39	12.900	11.450	13.138	13.484
$^{223}$Ra$\to ^{209}$Pb+$^{14}$C	31.83	$2.529\times10^{-15}$	15.25	13.847	12.564	14.004	14.507
$^{225}$Ac$\to ^{211}$Bi+$^{14}$C	30.48	$2.390\times10^{-14}$	17.34	16.913	16.605	16.238	17.761
$^{231}$Pa$\to ^{208}$Pb+$^{23}$F	51.84	$2.755\times10^{-20}$	26.02	25.257	24.982	24.699	24.077
$^{231}$Pa$\to ^{207}$Tl+$^{24}$Ne	60.42	$9.430\times10^{-21}$	23.38	22.773	22.253	23.585	23.276
$^{233}$U$\to \; ^{209}$Pb+$^{24}$Ne	60.50	$3.036\times10^{-21}$	24.82	23.721	23.622	23.815	24.073
$^{235}$U$\to ^{211}$Pb+$^{24}$Ne	57.36	$1.093\times10^{-19}$	27.42	27.877	29.168	26.697	27.946
$^{233}$U$\to \; ^{208}$Pb+$^{25}$Ne	60.75	$8.759\times10^{-21}$	24.82	24.804	23.864	24.971	23.729
$^{235}$U$\to ^{210}$Pb+$^{25}$Ne	57.83	$1.294\times10^{-19}$	27.42	28.573	28.919	27.071	27.434
$^{235}$U$\to \; ^{209}$Pb+$^{26}$Ne	58.11	$2.305\times10^{-19}$	27.45	29.476	29.398	27.598	26.99

DownLoad: CSV

Show Table

In the following, based on the modified form of $P_c$ of Wang et al. [59], i.e., $\log_{10}P_c=\dfrac{A_c-1}{3}\log_{10}P_\alpha+c'$, and fitting the $P_c$ listed in the third column of Table 1, we obtain $P_\alpha=0.0195$ and $c'=-5.1330$ for even-even parent nuclei and $P_\alpha=0.0136$ and $c'=-5.1022$ for odd-A parent nuclei. The values of $P_\alpha$ are close to those of previous studies [2, 4, 30, 63, 70]. It is crucial to emphasize that the cluster preformation probability $P_c$ exhibits a strong dependence on the corresponding model. As a result, $P_c$ can vary considerably over several orders of magnitude [2, 4, 30, 59, 63, 70]. Recently, Delion [47] derived a universal analytical relationship that represents the logarithm of the reduced width squared as a fragmentation potential, which is based on a simple model of Coulomb interactions, including a shifted harmonic oscillator potential. Furthermore, the relationship between the logarithmical form of preformation probability (spectroscopic factor) $\log_{10}P_c$ and the fragmentation potential $V_{\rm frag}$ is linear, where $V_{\rm frag}$ can be expressed as

As a verification, we plot the logarithm of the modified form $P_c$ versus the fragmentation potential $V_{\rm frag}$ for even-even and odd-A parent nuclei in Fig. 3 (a) and (b), respectively. As shown in this figure, there is a clear linear relationship between $\log_{10}P_c$ and $V_{\rm frag}$. This linear relationship may be model-independent.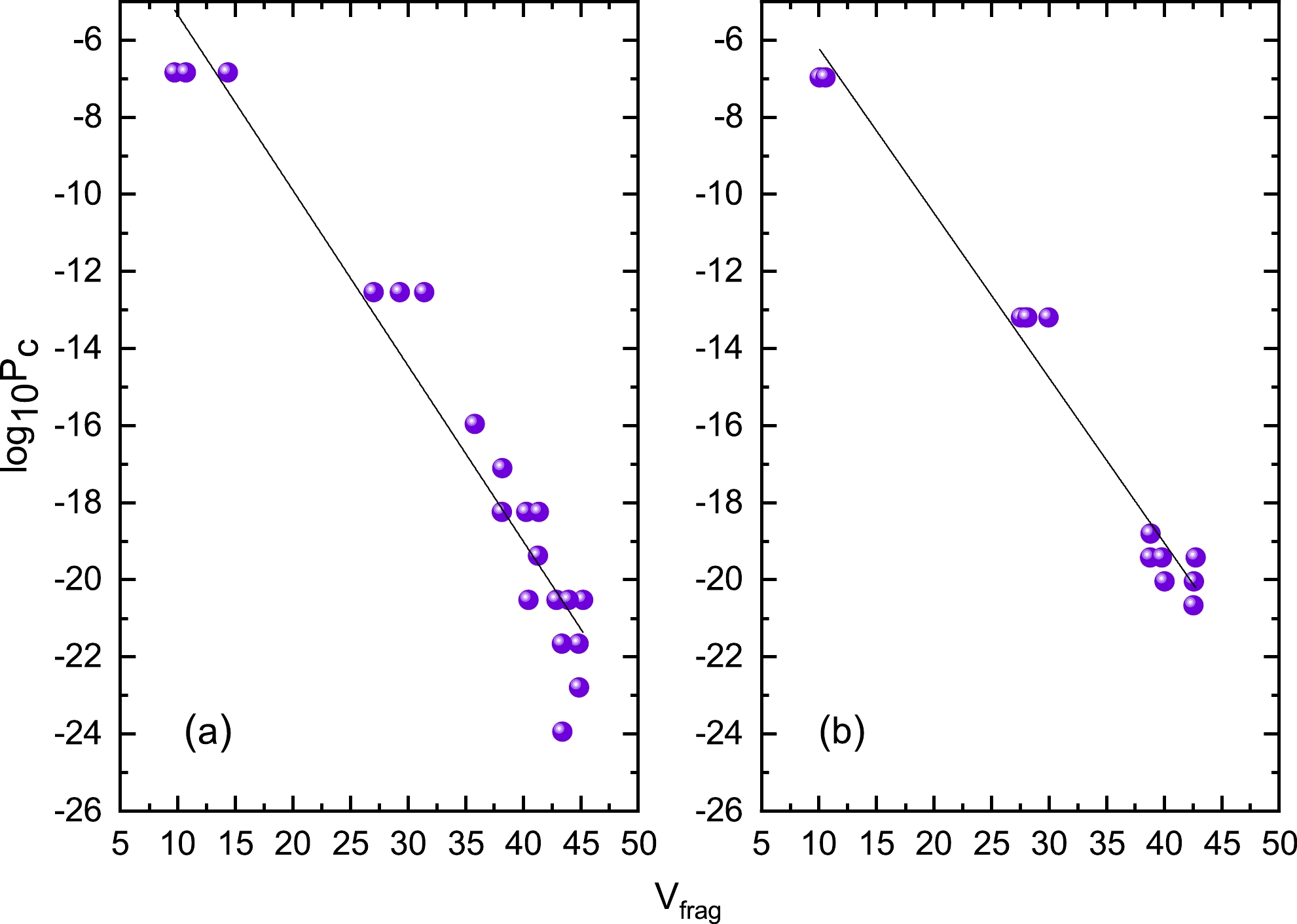

Figure 3

Figure 3.  (color online) Logarithm of the preformation penetrability $\log_{10}P_c$ versus the fragmentation potential $V_{\rm frag}$. (a) and (b) present the cases of e-e and odd-A parent nuclei, respectively.

DownLoad: Full-Size Img PowerPoint

Immediately after, using the modified form of $P_c$ with a certain slope $\log_{10}P_\alpha$ and intercept $c'$, we calculate the corresponding $P_c$ of each emitted cluster. Based on the obtained $P_c$, we systematically calculate the cluster radioactivity half-lives of 28 trans-lead nuclei using Eq. (15). For comparison, UDL [56], MBM [54], and TAM [67] are also used. The detailed results are presented in Table 1. In this table, the first and second columns contain the decay process and cluster radioactivity decay energy $Q_c$, respectively. The last five columns are the experimental cluster radioactivity half-lives and those calculated using HOPM, UDL [56], MBM [54], and TAM [67] in logarithmic form, denoted as ${\rm{log}}_{10}T_{1/2}^{\rm{{Exp}}}$, ${\rm{log}}_{10}T_{1/2}^{\rm{{HOPM}}}$, ${\rm{log}}_{10}T_{1/2}^{\rm{{UDL}}}$, ${\rm{log}}_{10}T_{1/2}^{\rm{{MBM}}}$, and ${\rm{log}}_{10}T_{1/2}^{\rm{{TAM}}}$, respectively. It can be easily seen from this table that the calculations from HOPM are essentially consistent with the experimental data.

To intuitively compare the experimental and calculated data, we plot the differences between the experimental cluster radioactivity half-lives and those calculated using different formulas in logarithmic form in Fig. 4. In this figure, the pink sphere, green upward triangle, blue downward triangle, and purple five-pointed star represent the results obtained using HOPM, UDL, MBM, and TAM, respectively. As shown in this figure, compared with the other calculated results, the cluster radioactivity half-lives obtained from our study are generally consistent with the experimental data, and the deviations between the experimental and calculated data are within $\pm 1.0$. To further quantitatively compare the experimental cluster radioactivity half-lives with the results of HOPM, UDL, MBM, and TAM, the standard deviation σ is employed, which is defined as

Figure 4

Figure 4.  (color online) Comparison of the differences between the experimental cluster radioactivity half-lives and those calculated using the UDL, MBM, TAM, and HOPM in logarithmic form.

DownLoad: Full-Size Img PowerPoint

where $\log_{10}{T^{\rm{exp}}_{1/2_i}}$ and $\log_{10}{T^{\rm{cal}}_{1/2_i}}$ denote the logarithmic form of the experimental and calculated cluster radioactivity half-lives for the i-th nucleus, respectively. The σ values for 28 trans-lead nuclei using HOPM, UDL, MBM, and TAM are listed in Table 2. As shown in this table, σ is 0.696 of HOPM for even-even nuclei, which is smaller than the results from UDL, MBM, and TAM, which are 1.423, 1.025, and 1.369, respectively. For odd-A nuclei, the σ of HOPM, MBM, and TAM are 0.978, 0.758, and 0.787, respectively, which are smaller than the results from MBM with 1.651. σ is 0.818 of HOPM for the total nuclei, which is better than the results obtained using UDL, MBM, and TAM formulas, which are 1.510, 0.930, and 1.176, respectively. It is further shown that HOPM and the modified preformation probability are reliable and can reproduce the calculated cluster radioactivity half-life well.

Table 2

Table 2.  Standard deviation σ between the experimental data and those calculated using $\rm{HOPM}$, UDL [56], MBM [54], and TAM [67].

Model	$\rm{HOPM}$	$\rm{UDL}$	$\rm{MBM}$	$\rm{TAM}$
even-even(n=17)	$0.696$	$1.423$	$1.025$	$1.369$
odd-A(n=11)	$0.978$	$1.651$	$0.758$	$0.787$
total(n=28)	$0.818$	$1.510$	$0.930$	$1.176$

DownLoad: CSV

Show Table

Considering the good agreement between the cluster radioactivity experimental half-lives and calculated values within HOPM, we further extend this model to predict the cluster radioactivity half-lives of 51 possible cluster radioactive candidates whose cluster radioactivities are energetically allowed or observed but not yet quantified in NUBASE2020 [62]. For comparison, UDL, MBM, and TAM are also used. The detailed predictions are given in Table 3. In this table, the first and second columns are same as in Table 1, and the last four columns are the predicted cluster radioactivity half-lives obtained using HOPM, UDL, MBM, and TAM in logarithmic form, denoted as${\rm{log}}_{10}T_{1/2}^{\rm{{HOPM}}}$, ${\rm{log}}_{10}T_{1/2}^{\rm{{UDL}}}$, ${\rm{log}}_{10}T_{1/2}^{\rm{{MBM}}}$, and ${\rm{log}}_{10}T_{1/2}^{\rm{{TAM}}}$, respectively. As shown in Table 3, our predictions are in good agreement with those of UDL, MBM, and TAM formulas.

Table 3

Table 3.  Predicted half-lives for possible cluster radioactive nuclei. The values of $Q_c$ and the experimental cluster radioactivity half-lives are taken from Ref. [68].

	$Q_{c}$/MeV	${\rm{log}}_{10}T_{1/2}^{\rm{{Exp}}}$	${\rm{log}}_{10}T_{1/2}^{\rm{{HOPM}}}$	${\rm{log}}_{10}T_{1/2}^{\rm{{UDL}}}$	${\rm{log}}_{10}T_{1/2}^{\rm{{MBM}}}$	${\rm{log}}_{10}T_{1/2}^{\rm{{TAM}}}$
$^{219}$Rn$\to \; ^{205}$Hg+$^{14}$C	28.10	−	18.996	19.079	19.747	20.437
$^{220}$Rn$\to \; ^{206}$Hg+$^{14}$C	28.54	−	17.496	17.941	18.986	19.496
$^{221}$Fr$\to \; ^{206}$Hg+$^{15}$N	34.12	−	18.477	21.554	21.322	24.244
$^{223}$Ra$\to \; ^{205}$Hg+$^{18}$O	40.30	−	24.087	26.453	24.993	27.337
$^{225}$Ra$\to \; ^{211}$Pb+$^{14}$C	29.47	−	18.021	17.827	17.752	19.052
$^{225}$Ra$\to \; ^{205}$Hg+$^{20}$O	40.48	−	27.119	28.284	27.008	27.030
$^{226}$Ra$\to \; ^{206}$Hg+$^{20}$O	40.82	−	25.582	27.455	26.585	26.456
$^{223}$Ac$\to \; ^{208}$Pb+$^{15}$N	39.47	$>$14.76	15.213	12.938	14.503	16.607
$^{227}$Ac$\to \; ^{207}$Tl+$^{20}$O	43.09	−	22.805	23.942	23.941	23.630
$^{229}$Ac$\to \; ^{206}$Hg+$^{23}$F	48.35	−	25.524	28.921	27.925	27.246
$^{226}$Th$\to \; ^{208}$Pb+$^{18}$O	45.73	$>$16.76	16.870	18.136	18.955	20.501
$^{226}$Th$\to \; ^{212}$Po+$^{14}$C	30.55	$>$15.36	16.893	17.545	16.268	18.338
$^{227}$Th$\to \; ^{209}$Pb+$^{18}$O	44.20	−	19.902	21.003	20.685	22.750
$^{228}$Th$\to \; ^{206}$Hg+$^{22}$Ne	55.74	−	23.863	27.481	25.832	28.240
$^{229}$Th$\to \; ^{209}$Pb+$^{20}$O	43.40	−	24.282	24.644	23.805	23.973
$^{229}$Th$\to \; ^{205}$Hg+$^{24}$Ne	57.83	−	24.953	25.327	25.584	25.539
$^{231}$Th$\to \; ^{207}$Hg+$^{24}$Ne	56.25	−	27.142	28.126	27.127	27.567
$^{231}$Th$\to \; ^{206}$Hg+$^{25}$Ne	56.80	−	27.696	27.911	27.414	26.851
$^{232}$Th$\to \; ^{208}$Hg+$^{24}$Ne	54.67	$>$29.2	28.245	31.121	28.705	29.682
$^{232}$Th$\to \; ^{206}$Hg+$^{26}$Ne	55.91	$>$29.2	28.993	30.378	29.099	28.014
$^{227}$Pa$\to \; ^{209}$Bi+$^{18}$O	45.87	−	22.082	19.167	19.003	21.097
$^{229}$Pa$\to \; ^{207}$Tl+$^{22}$Ne	58.96	−	23.053	23.303	23.157	25.037
$^{230}$U$\to \; ^{208}$Pb+$^{22}$Ne	61.39	$>$18.2	18.885	20.729	21.344	23.014
$^{230}$U$\to \; ^{206}$Pb+$^{24}$Ne	61.35	$>$18.2	21.410	22.346	23.001	23.061
$^{232}$U$\to \; ^{204}$Hg+$^{28}$Mg	74.32	$>$22.26	24.304	25.592	25.734	25.812
$^{233}$U$\to \; ^{205}$Hg+$^{28}$Mg	74.23	$>$27.59	25.835	25.657	25.834	25.906
$^{235}$U$\to \; ^{211}$Pb+$^{24}$Ne	57.36	$>$27.65	27.877	29.168	26.696	27.947
$^{235}$U$\to \; ^{210}$Pb+$^{25}$Ne	57.68	$>$27.65	28.781	29.412	27.211	27.536
$^{235}$U$\to \; ^{207}$Hg+$^{28}$Mg	72.43	$>$28.45	27.936	28.446	27.221	27.821
$^{235}$U$\to \; ^{206}$Hg+$^{29}$Mg	72.48	$>$28.45	29.043	29.025	27.825	27.766
$^{236}$U$\to \; ^{212}$Pb+$^{24}$Ne	55.95	$>$26.27	28.726	31.816	28.069	29.797
$^{236}$U$\to \; ^{210}$Pb+$^{26}$Ne	56.69	$>$26.27	30.267	32.107	28.981	28.818
$^{236}$U$\to \; ^{208}$Hg+$^{28}$Mg	70.73	$>$26.27	28.600	31.255	28.545	29.695
$^{236}$U$\to \; ^{206}$Hg+$^{30}$Mg	72.27	$>$26.27	28.974	29.947	28.644	27.994
$^{238}$U$\to \; ^{208}$Hg+$^{30}$Mg	69.46	−	32.594	34.783	30.914	31.141
$^{231}$Np$\to \; ^{209}$Bi+$^{22}$Ne	61.90	−	23.797	21.375	21.179	23.289
$^{233}$Np$\to \; ^{209}$Bi+$^{24}$Ne	62.16	−	24.926	22.366	22.642	22.990
$^{235}$Np$\to \; ^{207}$Tl+$^{28}$Mg	77.10	−	23.691	22.816	24.201	23.941
$^{237}$Np$\to \; ^{207}$Tl+$^{30}$Mg	74.79	$>$27.57	27.227	27.530	27.129	26.287
$^{237}$Pu$\to \; ^{209}$Pb+$^{28}$Mg	77.73	−	24.409	23.489	24.135	24.257
Continued on next page

DownLoad: CSV

Show Table

Table 3

Table 3-continued from previous page
	$Q_{c}$/MeV	${\rm{log}}_{10}T_{1/2}^{\rm{{Exp}}}$	${\rm{log}}_{10}T_{1/2}^{\rm{{HOPM}}}$	${\rm{log}}_{10}T_{1/2}^{\rm{{UDL}}}$	${\rm{log}}_{10}T_{1/2}^{\rm{{MBM}}}$	${\rm{log}}_{10}T_{1/2}^{\rm{{TAM}}}$
$^{237}$Pu$\to \; ^{208}$Pb+$^{29}$Mg	77.45	−	25.811	24.514	24.949	24.534
$^{237}$Pu$\to \; ^{205}$Hg+$^{32}$Si	91.46	−	26.548	25.170	25.429	25.319
$^{239}$Pu$\to \; ^{209}$Pb+$^{30}$Mg	75.08	−	29.614	28.790	27.295	26.941
$^{239}$Pu$\to \; ^{205}$Hg+$^{34}$Si	90.87	−	29.203	26.824	26.849	25.849
$^{237}$Am$\to \; ^{209}$Bi+$^{28}$Mg	79.85	−	27.032	22.058	23.016	23.128
$^{239}$Am$\to \; ^{207}$Tl+$^{32}$Si	94.50	−	26.223	22.648	24.139	23.667
$^{241}$Am$\to \; ^{207}$Tl+$^{34}$Si	93.96	$>$24.41	27.512	24.130	25.507	24.132
$^{240}$Cm$\to \; ^{208}$Pb+$^{32}$Si	97.55	−	21.854	20.310	22.866	22.095
$^{241}$Cm$\to \; ^{209}$Pb+$^{32}$Si	95.39	−	25.359	23.191	24.070	23.902
$^{243}$Cm$\to \; ^{209}$Pb+$^{34}$Si	94.79	−	27.971	24.770	25.472	24.415
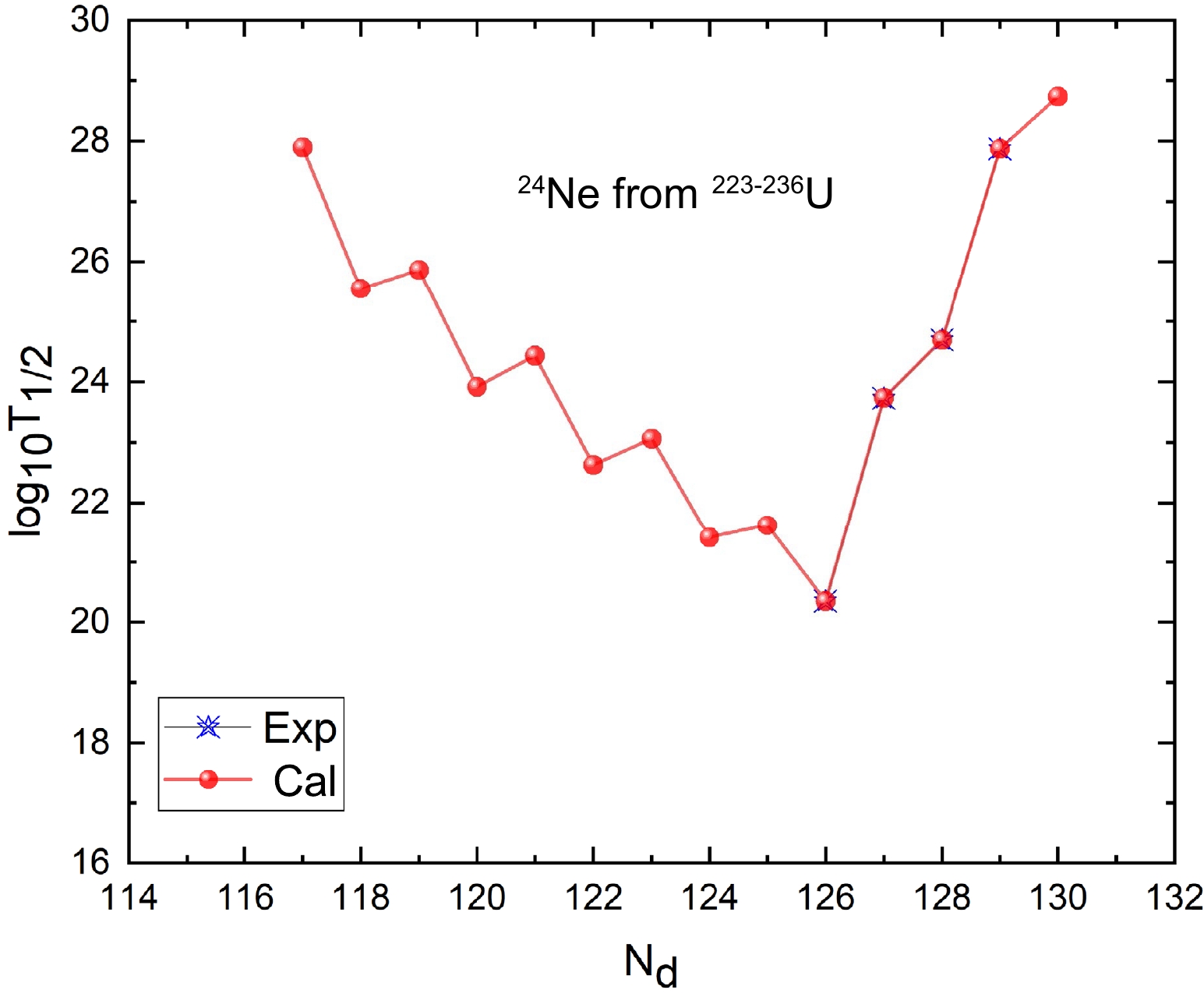
$^{244}$Cm$\to \; ^{210}$Pb+$^{34}$Si	93.17	−	27.849	27.059	26.433	25.825

DownLoad: CSV

Show Table

As is well known, cluster radioactivity is closely related to the shell effect, which has prompted widespread interest in the field of nuclear physics [68, 71, 72]. To verify the shell effect in the cluster radioactivity process, we calculate the cluster radioactivity half-lives of the emitter cluster $\rm{^{14}C}$ from $\rm{^{216-229}Ra}$ isotopes and $\rm{^{24}Ne}$ from $\rm{^{223-226}U}$ isotopes, which give the daughters $\rm{^{202-215}Pb}$ and $\rm{^{199-212}Pb}$. The detailed calculated results are listed in Table 4. In this table, the first and fourth columns, second and fifth columns, and third and sixth columns denote the decay process, decay energy $Q_c$, and calculated cluster radioactivity half-lives in logarithmic form, respectively. As shown in Table 4, the shortest value of the cluster radioactivity half-life occurs when daughter nuclei are the doubly magic $\rm{^{208}Pb}$ (Z = 82, N = 126). Meanwhile, the relationship between the experimental and calculated cluster radioactivity half-lives in logarithmic form and the daughter neutron number for the cluster $\rm{^{14}C}$ from $\rm{^{216-229}Ra}$ isotopes and $\rm{^{24}Ne}$ from $\rm{^{223-236}U}$ isotopes is plotted in Figs. 5 and 6, respectively. From these two figures, we can find the minimum logarithmic half-life of the double magic kernel $\rm {^ {208} Pb}$(Z=82, N=126). Consequently, this confirms that neutron shell closure plays a crucial role in cluster radioactivity [68, 71, 72]. We hope that these predicted half-lives will be useful for identifying new cluster emissions of the trans-tin region in future measurements.

Table 4

Table 4.  Calculated cluster radioactivity half-lives for the emission of $\rm{^{14}C}$ from various isotopes of $\rm{^{216-229}Ra}$ and the emission of $\rm{^{24}Ne}$ from various isotopes of $\rm{^{223-236}U}$. The values of $Q_c$ are taken from Refs. [27, 68].

	$Q_{c}$/MeV	${\rm{log}}_{10}T_{1/2}^{\rm{{HOPM}}}$	Decay	$Q_{c}$/MeV	${\rm{log}}_{10}T_{1/2}^{\rm{{HOPM}}}$
$^{216}$Ra$\to ^{202}$Pb+$^{14}$C	26.21	24.035	$^{223}$U$\to \; ^{199}$Pb+$^{24}$Ne	57.02	27.900
$^{217}$Ra$\to ^{203}$Pb+$^{14}$C	27.65	21.498	$^{224}$U$\to ^{200}$Pb+$^{24}$Ne	57.91	25.544
$^{218}$Ra$\to \; ^{204}$Pb+$^{14}$C	28.74	18.633	$^{225}$U$\to ^{201}$Pb+$^{24}$Ne	58.59	25.860
$^{219}$Ra$\to ^{205}$Pb+$^{14}$C	30.14	16.663	$^{226}$U$\to ^{202}$Pb+$^{24}$Ne	59.21	23.913
$^{220}$Ra$\to ^{206}$Pb+$^{14}$C	31.04	14.450	$^{227}$U$\to ^{203}$Pb+$^{24}$Ne	59.76	24.432
$^{221}$Ra$\to ^{207}$Pb+$^{14}$C	32.4	12.900	$^{228}$U$\to ^{204}$Pb+$^{24}$Ne	60.29	22.626
$^{222}$Ra$\to ^{208}$Pb+$^{14}$C	33.05	11.266	$^{229}$U$\to ^{205}$Pb+$^{24}$Ne	60.93	23.060
$^{223}$Ra$\to ^{209}$Pb+$^{14}$C	31.83	13.847	$^{230}$U$\to ^{206}$Pb+$^{24}$Ne	61.35	21.410
$^{224}$Ra$\to ^{210}$Pb+$^{14}$C	30.54	15.395	$^{231}$U$\to ^{207}$Pb+$^{24}$Ne	62.21	21.616
$^{225}$Ra$\to ^{211}$Pb+$^{14}$C	29.47	18.021	$^{232}$U$\to ^{208}$Pb+$^{24}$Ne	62.31	20.353
$^{226}$Ra$\to ^{212}$Pb+$^{14}$C	28.2	19.887	$^{233}$U$\to ^{209}$Pb+$^{24}$Ne	60.49	23.733
$^{227}$Ra$\to ^{213}$Pb+$^{14}$C	27.34	22.379	$^{234}$U$\to ^{210}$Pb+$^{24}$Ne	58.83	24.690
$^{228}$Ra$\to ^{214}$Pb+$^{14}$C	26.1	24.562	$^{235}$U$\to ^{211}$Pb+$^{24}$Ne	57.36	27.877
$^{229}$Ra$\to ^{215}$Pb+$^{14}$C	25.06	27.795	$^{236}$U$\to ^{212}$Pb+$^{24}$Ne	55.94	28.740

DownLoad: CSV

Show Table

Figure 5

Figure 5.  (color online) Plot of calculated ${\rm{log}}_{10}T_{1/2}$ versus the neutron number of daughter nuclei for the emission of the cluster $\rm{^{14}C}$ from Ra isotopes. The red circles and dark blue stars represent the calculated and experimental half-lives, respectively.

DownLoad: Full-Size Img PowerPoint

Figure 6

Figure 6.  (color online) Plot of calculated ${\rm{log}}_{10}T_{1/2}$ versus the neutron number of daughter nuclei for the emission of the cluster $\rm{^{24}Ne}$ from U isotopes. The red circles and dark blue stars represent the calculated and experimental half-lives, respectively.

DownLoad: Full-Size Img PowerPoint

IV. SUMMARY

• I. INTRODUCTION
• II. THEORETICAL FRAMEWORK
•      A Cluster radioactivity half-lives
•      B Semi-empirical formulas
• III. RESULTS AND DISCUSSION
• IV. SUMMARY

In summary, based on the WKB approximation and Bohr–Sommerfeld quantization condition and considering a modified preformation probability$P_c$, we verify that the linear relationship between $\log_{10}P_c$ and $V_{\rm frag}$is model-independent and extend HOPM to systematically study the cluster radioactivity half-lives of 28 trans-lead nuclei. The results are in good agreement with the experimental data. In addition, we also extend HOPM to predict the cluster radioactivity half-lives of 51 possible cluster radioactive candidates whose cluster radioactivities are energetically allowed or observed but not yet quantified in NUBASE2020. The predicted results are reasonably consistent with those obtained using UDL, MBM, and TAM. Furthermore, the shell effect in the cluster radioactivity process is verified by predicting the emitter cluster $\rm{^{14}C}$ from $\rm{^{216-229}Ra}$ isotopes and $\rm{^{24}Ne}$ from $\rm{^{223-236}U}$ isotopes, which may guide future experiments.

References