-
An extra
$ U(1)_{L_\mu-L_\tau} $ gauge symmetry extension of the standard model (SM) is anomaly-free and naturally breaks lepton flavour universality (LFU) because the$ U(1)_{L_\mu-L_\tau} $ gauge boson couples only to$ \mu(\tau) $ and not to e. The model was originally formulated by He, Joshi, Lew, and Volkas [1]. Thereafter, this type of$ U(1)_{L_\mu-L_\tau} $ model has been modified from its minimal version, and many variants have been proposed in the context of different phenomenological purposes, such as the muon$ g-2 $ anomaly [2−10], dark matter (DM) puzzle [8−18], and$ b \to s\mu^+\mu^- $ anomaly [19−30].In this study, we combine the muon
$ g-2 $ anomaly and DM observables and examine the$ U(1)_{L_\mu-L_\tau} $ breaking phase transition (PT), gravitational wave (GW) signatures, and exclusion of the LHC direct searches in an extra$ U(1)_{L_\mu-L_\tau} $ gauge symmetry extension of the SM. The model was proposed by one of the authors in [10], in which the new particles include vector-like leptons ($ E_1,\; E_2,\; N $ ), the$ U(1)_{L_\mu-L_\tau} $ breaking scalar S, and the gauge boson$ Z' $ , as well as the dark matter candidate$ X_I $ and its heavy partner$ X_R $ . When the PT is of first-order, the GW can be generated and detected in current and future GW experiments, such as LISA [31], Taiji [32], TianQin [33], Big Bang Observer (BBO) [34], DECi-hertz Interferometer GW Observatory (DECIGO) [34], and Ultimate-DECIGO (U-DECIGO) [35]. In addition, the null results of the LHC direct searches can exclude some parameter space achieving a first-order PT (FOPT). -
Under the local
$ U(1)_{L_\mu-L_\tau} $ , the second (third) generation left-handed lepton doublet and right-handed singlet,$ L_\mu $ ,$ \mu_R $ , ($ L_\tau $ ,$ \tau_R $ ), are charged with charge 1 (–1). To obtain the mass of$ U(1)_{L_\mu-L_\tau} $ gauge boson$ Z' $ , a complex singlet scalar$ {\cal{S}} $ is required to break the the$ U(1)_{L_\mu-L_\tau} $ symmetry. Another complex singlet scalar X with$ U(1)_{L_\mu-L_\tau} $ charge is introduced, whose lighter component may be a candidate of DM. In addition, we add vector-like lepton doublet fields ($E''_{L,R}$ ) and singlet fields ($ E'_{L,R} $ ), which mediate the X interactions to the muon lepton, and contribute to the muon$ g-2 $ . The quantum numbers of these fields under the gauge group$S U(3)_C\times S U(2)_L\times U(1)_Y\times U(1)_{L_\mu-L_\tau}$ are listed in Table 1.SU(3) $ _c $ 

SU(2) $ _L $ 

U(1) $ _Y $ 

U(1) $ _{L_\mu-L_\tau} $ 

X 1 1 $ 0 $ 

$ q_x $ 

$ {\cal{S}} $ 

1 1 $ 0 $ 

$ -2q_x $ 

$E''_{L,R}$ 

1 2 $ -1/2 $ 

$ 1-q_x $ 

$ E'_{L,R} $ 

1 1 $ -1 $ 

$ 1-q_x $ 

Table 1.
$ U(1)_{L_\mu-L_\tau} $ quantum numbers of the new fields.The Lagrangian is written as follows:
$ \begin{aligned}[b] {\cal{L}} =& {\cal{L}}_{\rm SM} -{1 \over 4} Z'_{\mu\nu} Z^{\prime\mu\nu} + g_{Z'} Z'^{\mu}(\bar{\mu}\gamma_\mu \mu + \bar{\nu}_{\mu_L}\gamma_\mu\nu_{\mu_L} \\&- \bar{\tau}\gamma_\mu \tau - \bar{\nu}_{\tau_L} \gamma_\mu\nu_{\tau_L})+ \bar{E''} (i \not D ) E''+ \bar{E'} (i \not D ) E'\\&+ (D_\mu X^\dagger) (D^\mu X) + (D_\mu {\cal{S}}^\dagger) (D^\mu {\cal{S}}) -V + \mathcal{L}_{\rm Y}. \end{aligned} $

(1) Here,
$ Z'_{\mu\nu}=\partial_\mu Z'_\nu-\partial_\nu Z'_\mu $ is the field strength tensor,$ D_\mu $ is the covariant derivative, and$ g_{Z'} $ is the gauge coupling constant of the$ U(1)_{L_\mu-L_\tau} $ . V and$ \mathcal{L}_{\rm Y} $ denote the scalar potential and Yukawa interactions, respectively.The scalar potential V containing the SM Higgs parts can be given by
$ \begin{aligned}[b] V =& -\mu_{h}^2 (H^{\dagger} H) - \mu_{S}^2 ({\cal{S}}^{\dagger} {\cal{S}}) + m_X^2 (X^{\dagger} X) + \left[\mu X^2 {\cal{S}} + \rm h.c.\right] \\ &+ \lambda_H (H^{\dagger} H)^2 + \lambda_S ({\cal{S}}^{\dagger} {\cal{S}})^2 + \lambda_X (X^{\dagger} X)^2 + \lambda_{SX} ({\cal{S}}^{\dagger} {\cal{S}})(X^{\dagger} X) \\ &+ \lambda_{HS}(H^{\dagger} H)({\cal{S}}^{\dagger} {\cal{S}}) + \lambda_{HX}(H^{\dagger} H)(X^{\dagger} X) \end{aligned} $

(2) with
$ \begin{aligned}[b]& H=\left(\begin{array}{c} G^+ \\ \dfrac{1}{\sqrt{2}}\,(h_1+v_h+{\rm i}G) \end{array}\right)\,,\\& {\cal{S}}={1\over \sqrt{2}} \left( h_2+v_S+ {\rm i}\omega\right) \,,\\& X={1\over \sqrt{2}} \left( X_R+{\rm i}X_I\right) \,. \end{aligned} $

(3) Here,
$ v_h=246 $ GeV and$ v_S $ are vacuum expectation values (VeVs) of H and$ {\cal{S}} $ , respectively, and the X field has no VeV. One can determine the mass parameters$ \mu^{2}_{h} $ and$ \mu^{2}_{S} $ of Eq. (2) by the potential minimization conditions,$ \begin{aligned}[b] \begin{split} &\quad \mu_{h}^2 = \lambda_H v_h^2 + {1 \over 2} \lambda_{HS} v_S^2,\\ &\quad \mu_{S}^2 = \lambda_S v_S^2 + {1 \over 2} \lambda_{HS} v_h^2.\\ \end{split} \end{aligned} $

(4) After
$ {\cal{S}} $ acquires the VeV, the μ term makes the complex scalar X split into two real scalar fields ($ X_R $ ,$ X_I $ ), and their masses are$ \begin{aligned}[b] &m_{X_R}^2 = m_X^2 + {1 \over 2} \lambda_{HX} v_H^2 + {1 \over 2}\lambda_{SX} v_S^2 + \sqrt{2} \mu v_S\\ &m_{X_I}^2 = m_X^2 + {1 \over 2} \lambda_{HX} v_H^2 + {1 \over 2}\lambda_{SX} v_S^2 - \sqrt{2} \mu v_S. \end{aligned} $

(5) After the
$ U(1)_{L_\mu-L_\tau} $ is broken, there is still remnant$ Z_2 $ symmetry, which guarantee the lightest component$ X_I $ to be a candidate of DM.The
$ \lambda_{HS} $ and$ \lambda_{HX} $ terms will lead to the couplings of the 125 GeV Higgs (h) and DM. To suppress the stringent constraints from the DM direct detection and indirect detection experiments, we simply assume that the$ hX_IX_I $ coupling is absent, that is,$ \lambda_{HX}=0 $ and$ \lambda_{HS}=0 $ . Thus, the 125 GeV Higgs h is purely from$ h_1 $ and the extra CP-even Higgs S is purely from$ h_2 $ . Their masses are given by$ \begin{array}{*{20}{l}} m_h^2=2\lambda_H v_h^2,\; \; \; m_S^2=2\lambda_S v_S^2. \end{array} $

(6) After
$ {\cal{S}} $ acquires VeV, the$ U(1)_{L_\mu-L_\tau} $ gauge boson$ Z' $ obtains a mass,$ \begin{array}{*{20}{l}} m_Z' = 2g_Z' \mid q_x\mid v_S. \end{array} $

(7) The Yukawa interactions
$ \mathcal{L}_{\rm Y} $ can be written as$ \begin{aligned}[b] -\mathcal{L}_{\rm Y,mass} =& m_1 \overline{E'_L} E'_R + m_2 \overline{E''_L} E''_R + \kappa_{1} \overline{\mu_R} X E'_L+ \kappa_{2} \overline{L_\mu} X E''_R \\ & + \sqrt{2}y_1 \overline{E^"_L} H E'_R + \sqrt{2}y_2 \overline{E^"_R} H E'_L\\& +\frac{\sqrt{2}m_\mu}{v} \overline{L_\mu}H \mu_R + {\rm h.c.}. \end{aligned} $

(8) After electroweak symmetry breaking, the vector-like lepton masses are given by
$ \begin{array}{*{20}{l}} M_E = \begin{pmatrix} m_1 & y_2 v_h \\ y_1 v_h & m_2 \end{pmatrix}. \end{array} $

(9) By making a bi-unitary transformation with the rotation matrices for the right-handed fields and the left-handed fields,
$ \begin{array}{*{20}{l}} U_L = \begin{pmatrix} c_L & -s_L \\ s_L & c_L \end{pmatrix}, \quad U_R = \begin{pmatrix} c_R & -s_R \\ s_R & c_R \end{pmatrix}, \end{array} $

(10) where
$ c_{L,R}^2 + s_{L,R}^2 = 1 $ , we can diagonalize the mass matrix for the vector-like lepton,$ \begin{array}{*{20}{l}} U_L^\dagger M_E U_R = \mathrm{diag}\left(m_{E_1}, m_{E_2}\right). \end{array} $

(11) $ E_1 $ and$ E_2 $ are the mass eigenstates of charged vector-like leptons, and the mass of the neutral vector-like lepton N is$ \begin{array}{*{20}{l}} m_{N}=m_2=m_{E_2} c_L c_R+m_{E_1} s_L s_R. \end{array} $

(12) $ E_1 $ and$ E_2 $ can mediate$ X_R $ and$ X_I $ interactions to muon lepton,$ \begin{aligned}[b] -\mathcal{L}_{\rm X} \supset & \frac{1}{\sqrt{2}}(X_R+ {\rm i} X_I)[\bar{\mu}_R (\kappa_1 c_L E_{1L} -\kappa_1 s_L E_{2L}) \\&+ \bar{\mu}_L (\kappa_2 s_R E_{1R} + \kappa_2 c_R E_{2R})] + {\rm h.c.}\, , \end{aligned} $

(13) and have the couplings to the 125 GeV Higgs,
$ \begin{aligned}[b] -\mathcal{L}_{\rm h} \supset& \frac{m_{E_1}(c_L^2 s_R^2 +c_R^2 s_L^2)-2m_{E_2}s_L c_L s_R c_R}{v_h}\; h\bar{E}_1E_1,\\ &+\frac{m_{E_2}(s_L^2 c_R^2 +c_L^2 s_R^2)-2m_{E_1}s_L c_L s_R c_R}{v_h}\; h\bar{E}_2E_2. \end{aligned} $

(14) -
We fix
$ m_h= $ 125 GeV,$ v_h= $ 246 GeV,$ q_x=-1 $ ,$ \lambda_{HS}=0 $ , and$ \lambda_{HX}=0 $ and take$ g_{Z'} $ ,$ m_{Z'} $ ,$ \lambda_X $ ,$ \lambda_{SX} $ ,$ m_S $ ,$ m_{X_R} $ ,$ m_{X_I} $ ,$ m_{E_1} $ ,$ m_{E_2} $ ,$ s_L $ ,$ s_R $ ,$ \kappa_1 $ , and$ \kappa_2 $ as the free parameters. To maintain the perturbativity, we conservatively choose$ \begin{aligned}[b] &\mid\lambda_{SX}\mid\leq 4\pi,\; \;\; \mid\lambda_X\mid\leq 4\pi,\\ &-\frac{1}{2}\leq\kappa_1 \leq \frac{1}{2},\;\; \; -\frac{1}{2}\leq\kappa_2 \leq \frac{1}{2}, \end{aligned} $

(15) and take the mixing parameters
$ s_L $ and$ s_R $ as$ -\frac{1}{\sqrt{2}} \leq s_L \leq \frac{1}{\sqrt{2}}, \; \; -\frac{1}{\sqrt{2}} \leq s_R \leq \frac{1}{\sqrt{2}}. $

(16) The mass parameters are scanned over in the following ranges:
$ \begin{aligned}[b] & 60\; {\rm GeV} \leq m_{X_I} \leq 500\; {\rm GeV},\; \; \; m_{X_I} \leq m_{X_R} \leq 500 \; {\rm GeV},\\ &m_{X_I} \leq m_{E_1} \leq 500 \; {\rm GeV},\; \; \; m_{X_I} \leq m_{E_2} \leq 500 \; {\rm GeV},\\ & 100 \; {\rm GeV} \leq m_{Z'} \leq 500 \; {\rm GeV},\; \; \; 100 \; {\rm GeV} \leq m_{S} \leq 500 \; {\rm GeV}. \end{aligned} $

(17) The mass of neutral vector-like lepton N is a function of
$ m_{E_1} $ ,$ m_{E_2} $ ,$ s_L $ , and$ s_R $ , and$ m_{X_I}<m_N $ is imposed. We require 0$ <g_{Z'}/m_{Z'}\leq $ (550 GeV)$ ^{-1} $ to be consistent with the bound of the neutrino trident process [36].The potential stability in Eq. (2) requires the following condition:
$ \begin{aligned}[b] &\lambda_H \geq 0 \,, \quad \lambda_S \geq 0 \,,\quad \lambda_X \geq 0 \,,\quad \\ & \lambda_{HS} \geq - 2\sqrt{\lambda_H \,\lambda_{S}} \,, \quad \lambda_{HX} \geq - 2\sqrt{\lambda_H \,\lambda_{X}} \,,\\& \lambda_{SX} \geq - 2\sqrt{\lambda_S \,\lambda_{X}} \,, \\& \sqrt{\lambda_{HS}+2\sqrt{\lambda_H \,\lambda_S}} \sqrt{\lambda_{HX}+ 2\sqrt{\lambda_H \,\lambda_{X}}} \sqrt{\lambda_{SX}+2\sqrt{\lambda_S\,\lambda_{X}}} \\ &+ 2\,\sqrt{\lambda_H \lambda_S \lambda_{X}} + \lambda_{HS} \sqrt{\lambda_{X}} + \lambda_{HX} \sqrt{\lambda_S} + \lambda_{SX} \sqrt{\lambda_H} \geq 0 \,. \end{aligned} $

(18) The one-loop diagrams with the vector-like lepton can give additional corrections to the oblique parameters (
$ S,\; T,\; U $ ), which can be calculated as in Refs. [37−39]. Taking the recent fit results of Ref. [40], we use the following values of S, T, and U:$ \begin{array}{*{20}{l}} S=-0.01\pm 0.10,\; \; T=0.03\pm 0.12,\; \; U=0.02 \pm 0.11, \end{array} $

(19) with the correlation coefficients
$ \begin{array}{*{20}{l}} \rho_{ST} = 0.92,\; \; \rho_{SU} = -0.80,\; \; \rho_{TU} = -0.93. \end{array} $

(20) The one-loop diagrams of the charged vector-like leptons
$ E_1 $ and$ E_2 $ can contribute to the$ h\to \gamma\gamma $ decay, and the bound of the diphoton signal strength of the 125 GeV Higgs is imposed [40],$ \begin{array}{*{20}{l}} \mu_{\gamma\gamma}= 1.11^{+0.10}_{-0.09}. \end{array} $

(21) In the model, the dominant corrections to the muon
$ g-2 $ are from the one-loop diagrams with the vector-like leptons ($ E_1,\; E_2) $ and scalar fields ($ X_R $ and$ X_I $ ), which are approximately calculated as in Refs. [41−43]$ \begin{aligned}[b] \Delta a_\mu =&\frac{1}{32\pi^2}m_\mu \left(\kappa_1 c_L \kappa_2 s_R H(m_{E_1},m_{X_R})\right.\\&-\kappa_1 s_L \kappa_2 c_R H(m_{E_2},m_{X_R}) \\ &\left. +\kappa_1 c_L \kappa_2 s_R H(m_{E_1},m_{X_I})-\kappa_1 s_L \kappa_2 c_R H(m_{E_2},m_{X_I}) \right), \end{aligned} $

(22) where the function
$ H(m_{f},m_{\phi})=\frac{m_f}{m_{\phi}^2}\frac{(r^2-4r+2\log{r}+3)}{(r-1)^3} $

(23) with
$ r=\dfrac{m_f^2}{m_{\phi}^2} $ . The combined average for the muon$ g-2 $ with Fermilab E989 [44] and Brookhaven E821 [45] is obtained, and the difference from the SM prediction becomes$ \begin{array}{*{20}{l}} \Delta a_\mu=a_\mu^{\rm exp}-a_\mu^{\rm SM}=(25.1\pm5.9)\times10^{-10}, \end{array} $

(24) which shows a
$ 4.2\sigma $ discrepancy from the SM. Very recently, on August 10, 2023, the E989 experiment at Fermilab released an update regarding the measurement from Run-2 and Run-3 [46]. The new combined value yields a deviation of$ \begin{array}{*{20}{l}} \Delta a_\mu=a_\mu^{\rm exp}-a_\mu^{\rm SM}=(24.9\pm4.8)\times10^{-10}, \end{array} $

(25) which leads to a
$ 5.1\sigma $ discrepancy. The recent lattice calculation [47] and the experiment determination [48] of the hadron vacuum polarization contribution to the muon$ g-2 $ point the value closer to the SM prediction, and hence, the tension relaxes to a low sigma level.If kinematically allowed, the DM pair-annihilation processes includes
$ X_IX_I \to \mu^+\mu^-,\; Z'Z',\; SS $ . In addition, a small mass splitting between the DM and the other new particles ($ E_1,\; E_2,\; N $ ,$ X_R $ ) can lead to coannihilation. The Planck collaboration reported the relic density of cold DM in the universe,$ \Omega_{c}h^2 = 0.1198 \pm 0.0015 $ [49], and the theoretical prediction of the model is calculated by$ \textsf{micrOMEGAs-5.2.13} $ [50].After imposing the constraints of theory, oblique parameters, and diphoton signal data of the 125 GeV Higgs, we project the samples accommodating the DM relic density and muon
$ g-2 $ anomaly within$ 2\sigma $ ranges in Fig. 1. From Fig. 1 , we find that the correct DM relic density can be obtained for most of the parameter region of$\min(m_{E_1},\; m_{E_2},\; m_N,\; m_{X_R})-m_{X_I} < 350$ GeV and –400 GeV$ < \min(m_{Z'},m_S) - m_{X_I}< $ 400 GeV. The DM relic density is mainly produced via the DM pair-annihilation processes$ X_IX_I \to \; Z'Z',\; SS $ for the region of$\min(m_{Z'},m_S) < m_{X_I}$ , coannihilation processes for the region of$ \min(m_{E_1},\; m_{E_2},\; m_N,\; m_{X_R}) $ close to$ m_{X_I} $ , and$ X_IX_I \to \mu^+\mu^- $ for the region of both$ \min(m_{E_1},\; m_{E_2},\; m_N, m_{X_R})>m_{X_I} $ and$ \min(m_{Z'},m_S) > m_{X_I} $ . However, once the explanation of the muon$ g-2 $ anomaly is simultaneously required, most of the region of$\min (m_{E_1},\; m_{E_2},\; m_N,\; m_{X_R}) > m_{X_I}$ and$\min(m_{Z'},m_S) > m_{X_I}$ is ruled out. This is because the muon$ g-2 $ anomaly favors small interactions between the vector-like leptons and muon mediated by$ X_I $ , and thus, the$ X_IX_I \to \mu^+\mu^- $ process fails to produce the correct DM relic density.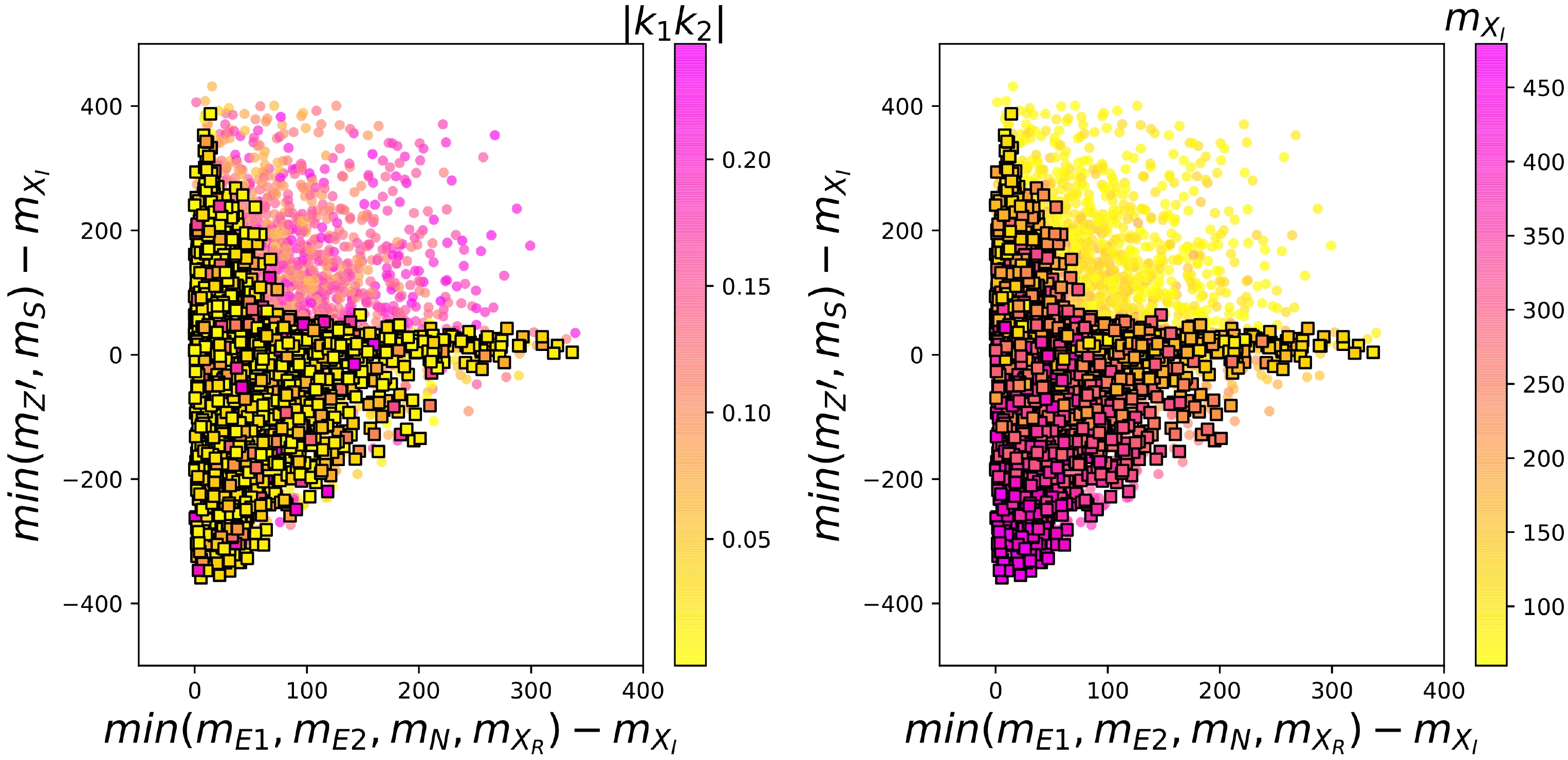
Figure 1. (color online) Surviving samples explaining the DM relic density and muon
$ g-2 $ anomaly while satisfying the constraints from theory, oblique parameter, and 125 GeV Higgs diphoton signal. The circles and squares are excluded and allowed by the DM relic data.$ X_I $ does not couple to the SM quark, and its couplings to the muon lepton and vector-like leptons are restricted by the muon$ g-2 $ anomaly. Therefore, the model can accommodate the bound from the DM direct detection naturally. -
At high temperatures, the global minimum of the finite-temperature effective potential is at the origin, that is,
$S U(2)_L\times U(1)_Y\times U(1)_{L_\mu-L_\tau}$ is unbroken. When the temperature drops, the potential changes and at some point develops a minimum at non-vanishing field values. The PT between the unbroken and the broken phase can proceed in basically two different ways. In a FOPT, at the critical temperature$ T_C $ , the two degenerate minima will be at different points in the field space, typically with a potential barrier in between. For a second-order (cross-over) transition, the broken and symmetric minimum are not degenerate until they are at the same point in the field space. In this study, we focus on a first-order$ U(1)_{L_\mu-L_\tau} $ breaking PT. -
To examine PT, we first take
$ h_1 $ ,$ h_2 $ , and$ X_r $ as the field configurations, and obtain the field dependent masses of the scalars (h, S,$ X_R $ ,$ X_I $ ), Goldstone boson ($ G,\; \omega,\; G^{\pm} $ ), gauge boson, and fermions. The field dependent masses of the scalars are as follows:${\hat m}^2_{h,S,X_R} ={\rm{eigenvalues}} ( {\widehat{{\mathcal{M}}^2_P}} )\ ,$

(26) $ {\hat m}^2_{G,\omega,X_I} ={\rm{eigenvalues}} ( {\widehat{\mathcal{M}^2_A}}) \ , $

(27) $ \begin{array}{*{20}{l}} {\hat m}^2_{G^\pm} = \lambda_H h_1^2 - \lambda_H v_h^2 \ , \end{array} $

(28) with
$ \begin{aligned}[b] \widehat{\mathcal{M}^2_P}_{11} &=3 \lambda_{H} h^2_1 - \lambda_{H} v_h^2\\ \widehat{\mathcal{M}^2_P}_{22} &=- \lambda_S v_S^2 + 3 \lambda_S h_2^2 + { \lambda_{SX} \over 2} X_r^2\\ \widehat{\mathcal{M}^2_P}_{33} &=m_X^2+\sqrt{2}\mu h_2 + { \lambda_{SX} \over 2} h_2^2 + 3 \lambda_X X_r^2\\ \widehat{\mathcal{M}^2_P}_{23} &=\widehat{\mathcal{M}^2_P}_{32}=\sqrt{2} \mu X_r + \lambda_{SX} h_2 X_r \\ \widehat{\mathcal{M}^2_P}_{12} &=\widehat{\mathcal{M}^2_P}_{21}=\widehat{\mathcal{M}^2_P}_{13} =\widehat{\mathcal{M}^2_P}_{31}=0\\ \widehat{\mathcal{M}^2_A}_{11} &= \lambda_{H} h^2_1 - \lambda_{H} v_h^2\\ \widehat{\mathcal{M}^2_A}_{22} &=- \lambda_{S} v_S^2 + \lambda_S h^{2}_{2}+ { \lambda_{SX} \over 2} X_r^{2}\\ \widehat{\mathcal{M}^2_A}_{33} &=m_X^2-\sqrt{2} \mu h_2 + \lambda_X X^{2}_{r}+ { \lambda_{SX} \over 2} h_2^{2}\\ \widehat{\mathcal{M}^2_A}_{23} &=\widehat{\mathcal{M}^2_A}_{32}=-\sqrt{2} \mu X_r\\ \widehat{\mathcal{M}^2_A}_{12} &=\widehat{\mathcal{M}^2_A}_{21}=\widehat{\mathcal{M}^2_A}_{13}=\widehat{\mathcal{M}^2_A}_{31}=0. \end{aligned} $

(29) The field dependent masses of the gauge boson are
$ {\hat m}^2_{W^\pm} = {1\over 4} g^2 h^{2}_{1}, \quad {\hat m}^2_{Z} = {1\over 4} (g^2+g'^2) h^{2}_{1}, $

(30) $ {\hat m}^2_{\gamma}=0 , \quad {\hat m}^2_{Z'} = q_x^2 g_{Z'}^2 (4h^{2}_{2}+X^2_{r}), $

(31) The field dependent masses of the vector-like lepton are
$ \widehat{\mathcal{M}}^2_{E_1,E_2,\mu} ={\rm{eigenvalues}} ( \widehat{\mathcal{M}_E}\widehat{\mathcal{M}_E}^T ) $

(32) with
$ \begin{array}{*{20}{l}} && \widehat{\mathcal{M}_E}= \begin{pmatrix} m_1 & \quad y_2 h_{1} & \quad \kappa_1 X_r\\ y_1 h_{1} & \quad m_2 & \quad 0\\ 0 & \quad \kappa_2 X_r & \quad \dfrac{m_{\mu} h_1}{v_h} \end{pmatrix} . \end{array} $

(33) For the quarks of the SM, we only consider the top quark,
$ \widehat{\mathcal{M}^2_{t}} =y_t^2 h_1^2 $

(34) with
$ y_t=m_t/v_h $ .To examine the
$ U(1)_{L_\mu-L_\tau} $ breaking PT, we need to study the thermal effective potential$V_{\rm eff}$ in terms of the classical fields ($ h_1,h_2,X_r $ ), which is composed of four parts:$ \begin{aligned}[b] V_{\rm eff} (h_1,h_2,X_r,T)=&V_{0}(h_1,h_2,X_r) + V_{\rm CW}(h_1,h_2,X_r) \\&+ V_{\rm CT}(h_1,h_2,X_r) + V_{T}(h_1,h_2,X_r,T)\\& + V_{\rm ring}(h_1,h_2,X_r,T). \end{aligned} $

(35) $ V_{0} $ is the tree-level potential,$V_{\rm CW}$ is the Coleman-Weinberg (CW) potential [51],$V_{\rm CT}$ is the counter term,$ V_{T} $ is the thermal correction [52], and$V_{\rm ring}$ is the resummed daisy corrections [53, 54]. In this study, we calculate$V_{\rm eff}$ in the Landau gauge.The tree-level potential
$ V_0 $ in terms of the classical fields ($ h_1,h_2,X_r $ ) from Eq. (2) is as follows:$ \begin{aligned}[b] V_0(h_1,h_2,X_r)=& -\frac{\mu_h^2}{2} h_1^2 - \frac{\mu_S^2}{2} h_2^2 + \frac{m_X^2}{2} X_r^2 + \frac{\mu}{\sqrt{2}} h_2 X_r^2\\ &+\frac{\lambda_H}{4} h_1^4 + \frac{\lambda_S}{4} h_2^4 + \frac{\lambda_X}{4} X_r^4 + \frac{\lambda_{SX}}{4} X_r^2 h_2^2 . \end{aligned} $

(36) The CW potential in the
$ \overline{\rm MS} $ scheme at 1-loop level has the form [51]$ \begin{aligned}[b] V_{\rm CW}(h_{1},h_{2},X_r) =& \sum\limits_{i} (-1)^{2s_i} n_i\frac{ {\hat m}_i^4 (h_{1},h_{2},X_r)}{64\pi^2}\\&\times\left[\ln \frac{ {\hat m}_i^2 (h_{1},h_{2},X_r)}{Q^2}-C_i\right] \; \ , \end{aligned} $

(37) where
$ i=h,S,X_R,X_I,G,\omega,G^\pm,W^\pm,Z,Z',t,E_1,E_2,\mu $ , and$ s_i $ is the spin of particle i. Q is a renormalization scale, and we take$ Q=m_S $ . Constant$ C_i =\dfrac{3}{2} $ for scalars or fermions and$ C_i = \dfrac{5}{6} $ for gauge bosons.$ n_i $ is the number of degree of freedom,$ \begin{aligned}[b] &n_h=n_S=n_{X_R}=n_{X_I}=n_G=n_{\omega}=1\\ &n_{G^\pm}=2,\; \; n_{W^\pm}=6,\; n_{Z}=n_{Z'}=3\\ &n_{t}=12,\; \; n_{E_1}=n_{E_2}=n_{\mu}=4. \end{aligned} $

(38) With
$V_{\rm CW}$ being included in the potential, the minimization conditions of the scalar potential and CP-even mass matrix will be shifted slightly. To maintain these relations, the counter terms$V_{\rm ct}$ should be added,$ \begin{aligned}[b] V_{\rm CT}=&\delta m_1^2 h_{1}^2+\delta m_2^2 h_{2}^2 + \delta m_X^2 X_r^2 + \delta \lambda_H h_{1}^4+\delta \lambda_{S} h_{2}^4\\ & +\delta \lambda_X X_{r}^4 + \delta \mu X_r^2 h_2 +\delta \lambda_{SX} h_2^2 X_r^2. \end{aligned} $

(39) The relevant coefficients are determined by
$ \begin{aligned}[b]& \frac{\partial V_{\rm CT}}{\partial h_{1}} = -\frac{\partial V_{\rm CW}}{\partial h_{1}}\;, \quad \frac{\partial V_{\rm CT}}{\partial h_{2}} = -\frac{\partial V_{\rm CW}}{\partial h_{2}},\; \\& \frac{\partial V_{\rm CT}}{\partial X_r} = -\frac{\partial V_{\rm CW}}{\partial X_r}, \end{aligned} $

(40) $ \begin{aligned}[b]& \frac{\partial^{2} V_{\rm CT}}{\partial h_{1}\partial h_{1}} = - \frac{\partial^{2} V_{\rm CW}}{\partial h_{1}\partial h_{1}}\;, \quad \frac{\partial^{2} V_{\rm CT}}{\partial h_{2}\partial h_{2}} = - \frac{\partial^{2} V_{\rm CW}}{\partial h_{2}\partial h_{2}}\;,\\& \frac{\partial^{2} V_{\rm CT}}{\partial X_{r}\partial X_{r}} = - \frac{\partial^{2} V_{\rm CW}}{\partial X_{r}\partial X_{r}}\;,\quad \frac{\partial^{2} V_{\rm CT}}{\partial h_{1}\partial h_{2}} = - \frac{\partial^{2} V_{\rm CW}}{\partial h_{1}\partial h_{2}}\;,\\& \frac{\partial^{2} V_{\rm CT}}{\partial h_1\partial X_r} = - \frac{\partial^{2} V_{\rm CW}}{\partial h_1\partial X_r}\;, \quad \frac{\partial^{2} V_{\rm CT}}{\partial h_2\partial X_r} = - \frac{\partial^{2} V_{\rm CW}}{\partial h_2\partial X_r}\;, \quad \end{aligned} $

(41) which are evaluated at the EW minimum of
$ \{ h_{1}=v_h, h_{2}=v_S, X_r=0 \} $ on both sides. As a result, the VeVs of$ h_{1} $ ,$ h_{2} $ ,$ X_r $ and the CP-even mass matrix will not be shifted. We verify that the following relations hold true$ \frac{\partial^{2} V_{\rm CW}}{\partial h_{1}\partial h_{2}} =0\;, \quad \frac{\partial^{2} V_{\rm CW}}{\partial h_{1}\partial X_{r}} =0\;. $

(42) For the left seven equations, eight parameters need to be fixed, and thus, one renormalization constant is left for determination. We choose to use
$ \delta m_1^2 $ ,$ \delta m_2^2 $ ,$ \delta m_X^2 $ ,$ \delta \lambda_H $ ,$ \delta \lambda_{S} $ ,$ \delta \lambda_X $ ,$ \delta \lambda_{SX} $ , and set$ \delta \mu=0 $ . It is a well-known problem that the second derivative of the CW potential in the vacuum suffers from logarithmic divergences originating from the vanishing Goldstone masses. To avoid the problems with infrared divergent Goldstone contributions, we simply remove the Goldstone corrections in the renormalization conditions following the approaches of [55, 56]. This is simply a change of renormalization conditions, and the shift it causes in the potential shape is negligible.The thermal contributions
$ V_T $ to the potential can be written as [52]$ V_{\rm th}(h_{1},h_{2},X_r,T) = \frac{T^4}{2\pi^2}\, \sum\limits_i n_i J_{B,F}\left( \frac{ {\hat m}_i^2(h_{1},h_{2},X_r)}{T^2}\right)\;, $

(43) where
$ i=h,S,X_R,X_I,G,\omega,G^\pm,W^\pm,Z,Z',t,E_1,E_2,\mu $ , and the functions$ J_{B,F} $ are$ J_{B,F}(y) = \pm \int_0^\infty\, {\rm d} x\, x^2\, \ln\left[1\mp {\rm exp}\left(-\sqrt{x^2+y}\right)\right]. $

(44) Finally, the thermal corrections with resumed ring diagrams are given [53, 54].
$ \begin{aligned}[b] V_{\rm ring}\left(h_{1},h_{2},X_r, T\right) =&-\frac{T}{12\pi }\sum\limits_{i} n_{i}\Big[ \left( \bar{M}_{i}^{2}\left(h_{1},h_{2},X_r,T\right) \right)^{\frac{3}{2}}\\&-\left( {\hat m}_{i}^{2}\left(h_{1},h_{2},X_r,T\right) \right)^{\frac{3}{2}}\Big] , \end{aligned} $

(45) where
$ i=h,S,X_R,X_I,G,\omega,G^\pm,W^\pm_L,Z_L,Z'_L,\gamma_L $ .$ W^\pm_L,~ Z_L, Z'_L $ , and$ \gamma_L $ are the longitudinal gauge bosons with$n_{W^\pm_L}=2, n_{Z_L}=n_{Z'_L}=n_{\gamma_L}=1$ . The thermal Debye masses$\bar{M}_{i}^{2}\left(h_{1},h_2, X_r, T\right)$ for the CP-even and CP-odd scalar fields are the eigenvalues of the full mass matrix,$ \begin{array}{*{20}{l}} \bar{M}_{i}^{2}\left( h_{1},h_{2},X_r,T\right) ={\rm eigenvalues} \left[\widehat{\mathcal{M}_{X}^2}\left( h_{1},h_{2},X_r\right) +\Pi _{X}(T)\right] , \end{array} $

(46) where
$ \Pi_X $ ($ X=P,A $ ) are given by$ \begin{aligned}[b] (\Pi_{P,A})_{11} =& \left[{9g^2\over 2} + {3g'^2\over 2} + 12y_t^2 + 4(y_2^2+y_1^2) +12 \lambda_{H} \right] {T^2 \over 24} \\ (\Pi_{P,A})_{22} =& \left[8 \lambda_S + 2 \lambda_{SX} + 24q_x^2 g^2_{Z'} \right] {T^2 \over 24} \\ (\Pi_{P,A})_{33} =& \left[8 \lambda_X + 2 \lambda_{SX} + 6q_x^2 g^2_{Z'} + 2\kappa_1^2+4\kappa_2^2 \right] {T^2 \over 24} \\ (\Pi_{P,A})_{12} =&(\Pi_{P,A})_{21} =(\Pi_{P,A})_{13} =(\Pi_{P,A})_{31} \\ =&(\Pi_{P,A})_{32} =(\Pi_{P,A})_{23} =0. \end{aligned} $

(47) The thermal Debye mass of
$ G^{\pm} $ is$ \begin{array}{*{20}{l}} \bar{M}_{G^+G^-}^{2}\left( h_{1},h_{2},X_r,T\right) = \lambda_H h_1^2 - \lambda_H v_h^2 +\Pi _{P11}. \end{array} $

(48) The Debye masses of longitudinal gauge bosons are
$ \begin{aligned}[b] \bar{M}_{W^{\pm}_L}^2 \left( h_{1},h_{2},X_r,T\right)=& {1 \over 4} g^2 h^2_1 + {11\over 6} g^2 T^2, \\ \bar{M}_{Z_L,\gamma_L}^{2}\left( h_{1},h_{2},X_r,T\right) =&\frac{1}{8}\left(g^2+g'^2\right)\left(h_1^2+\frac{22}{3}T^2\right) \pm \frac{1}{2}\Delta, \end{aligned} $

$ \begin{aligned}[b] \bar{M}_{Z'_L}^2\left( h_{1},h_{2},X_r,T\right) =& q_x^2 g_{Z'}^2 (4h^{2}_{2}+X^2_{r})\\& + {1\over 6} g^2_{Z'} T^2 \left[12-12q_x+ 16q_x^2\right], \end{aligned} $

(49) with
$ \Delta=\sqrt{\left[\dfrac{1}{4}\left(g^2-g'^2\right)\left(h_1^2+\dfrac{22}{3}T^2\right)\right]^2+\dfrac{1}{4}g^2 g'^2 h_1^2} $ .In Fig. 2, we display the scatter plots achieving FOFP and accommodating the DM relic density, muon
$ g-2 $ anomaly, and various constraints mentioned previously. We observe that the strength of FOPT is sensitive to the parameter$ \lambda_S $ . As$ \lambda_S $ decreases, the the critical temperature$ T_C $ tends to decrease, and the strength of FOPT tends to increase. We choose two benchmark points (BPs) to show how the PT happens. The input parameters of BP1 and BP2 are listed in Table 2, and their phase histories are presented in Fig. 3 on the field configurations versus temperature plane. For BP1 and BP2, the potential minima at any temperatures always locate at$ \langle X_r\rangle $ =0. As the universe cools, a FOPT takes place during which$ h_2 $ acquires a nonzero VeV and the other two fields remain zero. As the temperature continues to decrease,$ h_1 $ starts to develop a nonzero VeV during the second PT, which is of second-order. Finally, the observed vacuum is obtained at the present temperature.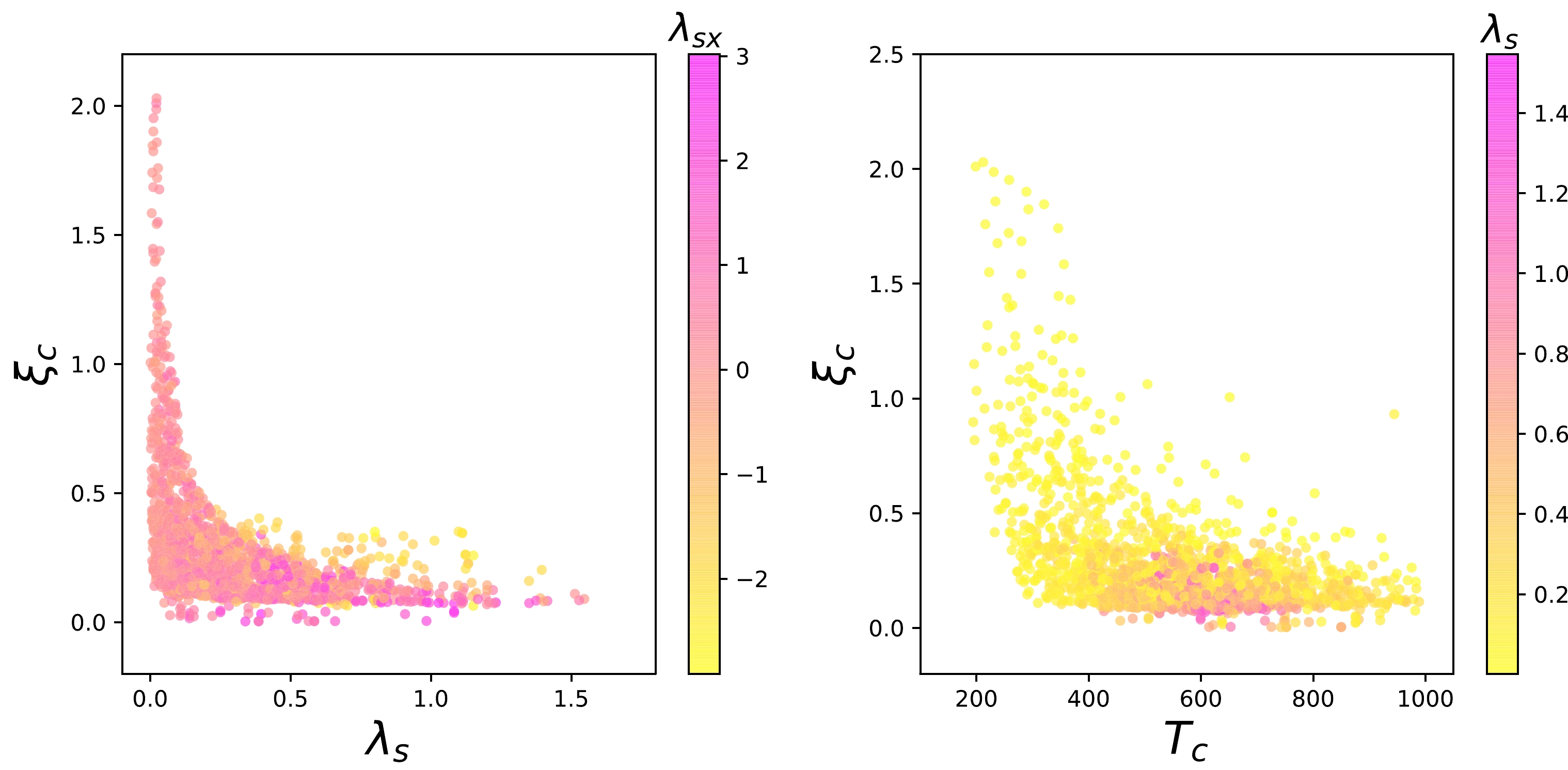
Figure 2. (color online) Surviving samples achieving FOFP and accommodating the DM relic density, muon
$ g-2 $ anomaly, and various constraints mentioned previously.$ \xi_C=\dfrac{<h_2>}{T_C} $ denotes the strength of the$ U(1)_{L_\mu-L_\tau} $ breaking FOPT at the critical temperature$ T_C $ .$\lambda_{SX}$ 

$\lambda_{X}$ 

$\lambda_{s}$ 

$k_{1}k_{2}$ 

$s_L$ 

$s_R$ 

$g_Z\prime$ 

$m_{X_I}$ /GeV

$ {BP1}$ 

0.298 1.478 0.067 0.0061 0.113 0.254 0.481 302.9 $ {BP2}$ 

0.304 0.337 0.017 −0.0164 −0.280 −0.374 0.319 319.2 $m_{X_R}$ /GeV

$m_{E_1}$ /GeV

$m_{E_2}$ /GeV

$m_Z\prime$ /GeV

$m_S$ /GeV

$ {BP1}$ 

410.2 357.4 454.6 308.4 117.1 $ {BP2}$ 

331.4 363.8 469.0 312.3 91.6 Table 2. Input parameters for BP1 and BP2.
-
As the
$ U(1)_{L_\mu-L_\tau} $ gauge boson$ Z' $ does not couple to quarks,$ Z' $ is rather difficult to produce at the LHC. Vector-like leptons are mainly a pair produced at the LHC via the electroweak processes mediated by the SM gauge bosons, and$ E_{1,2} \to \mu X_I $ and$ N\to \nu_\mu X_I $ are the main decay modes of vector-like leptons. Thus, we employ the ATLAS analysis of$2\ell+E_T^{\rm miss}$ with 139 fb$ ^{-1} $ integrated luminosity data to restrict our model [57], which is implemented in the$ \textsf{MadAnalysis5} $ [58−60] assuming a 95% confidence level for the exclusion limit. The simulations for the samples are performed using${\mathrm{MG5}}\_{\mathrm{aMC-3.3.2}}$ [61] with$\mathrm{PYTHIA8}$ [62] and$\mathrm{Delphes-3.2.0}$ [63].In Fig. 4, we employ the ATLAS analysis of
$2\ell+E_T^{\rm miss}$ at the LHC to restrict the parameter space, which has been satisfied by the DM relic density, muon$ g-2 $ , FOPT, and various constraints discussed above. Fig. 4 indicates that the DM mass is allowed to be as low as 100 GeV when the value of$\min(m_{E_1},\; m_{E_2})-m_{X_I}$ is small. This is because the muon from the vector-like lepton decay has soft energy, and its detection efficiency is decreased at the LHC. As the DM mass increases, the value of$\min(m_{E_1},\; m_{E_2})-m_{X_I}$ increases, and the lightest charged vector-like lepton is allowed to have a larger mass. -
Stochastic GWs are produced during a FOPT via bubble collision, sound waves in the plasma, and magneto-hydrodynamics turbulence. As most of the PT energy is pumped into the surrounding fluid shells, making sound waves the dominant contribution to GWs, we will focus on the GW spectrum from the sound waves in the plasma.
The sound wave spectra can be expressed as functions of two FOPT parameters β and α,
$ \frac{\beta}{H_n}=T\frac{{\rm d} (S_3(T)/T)}{{\rm d} T}\Big|_{T=T_n}\; ,\; \; \; \; \alpha=\frac{\Delta\rho}{\rho_R}=\frac{\Delta\rho}{\pi^2 g_{\ast} T_n^4/30}\;. $

(50) Here,
$ H_n $ is the Hubble parameter at the nucleation temperature$ T_n $ , and$ g_{\ast} $ is the effective number of relativistic degrees of freedom. β characterizes the approximate inverse time duration of the strong first-order PT, and α is defined as the vacuum energy released from the PT normalized by the total radiation energy density$ \rho_R $ at$ T_n $ .The GW spectrum from the sound waves can be expressed by [64]
$ \begin{aligned}[b] \Omega_{ \rm{sw}}h^{2} = & 2.65\times10^{-6}\left( \frac{H_{n}}{\beta}\right)\left(\frac{\kappa_{v} \alpha}{1+\alpha} \right)^{2} \left( \frac{100}{g_{\ast}}\right)^{1/3} v_w \\ &\times \left(\frac{f}{f_{sw}} \right)^{3} \left( \frac{7}{4+3(f/f_{ \rm{sw}})^{2}} \right) ^{7/2} \Upsilon(\tau_{sw})\ , \end{aligned} $

(51) where
$ v_w $ is the wall velocity, and we take$ v_w=c_s=\sqrt{1/3} $ , with$ c_s $ being the sound velocity.$f_{sw}$ is the present peak frequency of the spectrum,$ f_{sw} \ = \ 1.9\times10^{-5}\frac{1}{v_w}\left(\frac{\beta}{H_{n}} \right) \left( \frac{T_{n}}{100 \rm{GeV}} \right) \left( \frac{g_{\ast}}{100}\right)^{1/6} \rm{Hz} \,. $

(52) $ \kappa_{v} $ is the fraction of latent heat transformed into the kinetic energy of the fluid [65],$ \kappa_v \simeq \frac{\alpha^{2/5}} {0.017 + (0.997 + \alpha)^{2/5}}. $

(53) The suppression factor of Eq. (51) [66],
$ \Upsilon(\tau_{sw})=1-\frac{1}{\sqrt{1+2\tau_{sw}H_n}}, $

(54) appears due to the finite lifetime
$ \tau_{sw} $ of the sound waves [67, 68],$ \tau_{sw}=\frac{\tilde{v}_W(8\pi)^{1/3}}{\beta \bar{U}_f}, \; \;\; \bar{U}^2_f=\frac{3}{4}\frac{\kappa_v\alpha}{1+\alpha}. $

(55) We calculate GW spectra for thousands of parameter points accommodating the muon
$ g-2 $ , DM relic density, and exclusion limits of the LHC direct searches, and find that all the peak strengths are below the sensitivity curve of BBO. Approximately 10% of the survived points can generate U-DECIGO sensitive gravitational wave, including BP1 and BP2. These points favor a small$ \lambda_S $ for which the strength of FOPT tends to have a large value. The GW spectra of BP1 and BP2 are shown along with expected sensitivities of various future interferometer experiments in Fig. 5. The lowest peak frequency is 0.003 HZ from BP1, and the highest peak frequency is 0.2 HZ from BP2. -
We study an extra
$ U(1)_{L_\mu-L_\tau} $ gauge symmetry extension of the standard model by considering the dark matter, muon$ g-2 $ anomaly,$ U(1)_{L_\mu-L_\tau} $ breaking PT, GW spectra, and bound from the direct detection at the LHC. The following conclusions were drawn. (i) A joint explanation of the dark matter relic density and muon$ g-2 $ anomaly rules out the region where both$\min(m_{E_1}, m_{E_2},m_N,m_{X_R})$ and$\min(m_{Z'},m_S)$ are much larger than$ m_{X_I} $ . (ii) A first-order$ U(1)_{L_\mu-L_\tau} $ breaking PT can be achieved in the parameter space explaining the DM relic density and muon$ g-2 $ anomaly simultaneously, and the corresponding gravitational wave spectra can reach the sensitivity of U-DECIGO. (iii) The mass spectra of the vector-like leptons and dark matter are stringently restricted by the direct searches at the LHC.
U(1)Lμ-Lτ breaking phase transition, muon g–2, dark matter, collider, and gravitational wave
- Received Date: 2023-09-20
- Available Online: 2024-02-15
Abstract: Combining the dark matter and muon






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

























 DownLoad:
DownLoad: