-
Since Becquerel's first discovery of spontaneous radioactivity over a century ago, scientists have discovered various forms of nuclear decay and reaction, which includes α decay [1–12], beta decay [13], fragmentation reactions [14, 15], heavy-ion collisions [16–19], etc. [20–25]. Two-proton (
$ 2p $ ) radioactivity that involves the emission of two protons was observed around the proton drip line, and a novel exotic decay mode was discovered above. The study of$ 2p $ radioactivity can provide valuable insights into information on nuclear structure, such as the sequence of particle energies, wave function of emitted two protons, spin, parity, and the effect of deformation and so on [26–31]. Then,$ 2p $ radioactivity became one of the hot topics in nuclear physics [32–36]. In the 1960s, Zel'dovich [37] and Goldansky [38] made the first prediction of$ 2p $ radioactivity independently. At the same time, Goldansky tried to identify potential candidates for$ 2p $ radioactivity and coined the term "two-proton radioactivity" [38, 39]. Subsequently, the extremely short-lived$ 2p $ radioactivity, i.e., not true$ 2p $ radioactivity ($ {Q}_{2p}>0 $ and$ {Q}_{p}>0 $ , where$ {Q}_{2p} $ and$ {Q}_{p} $ are the released energy of$ 2p $ radioactivity and single-proton emission, respectively), was observed through a series of ground-state emitters in an experiment before 2002, such as$ ^{6}{\rm{Be}}$ [40],$ ^{12}{\rm{O}}$ [41–44], and$ ^{16}{\rm{Ne}}$ [45]. With the development of experimental radioactive beam facilities and new detection technology,$ ^{45}{\rm{Fe}}$ was confirmed as the first true$ 2p $ radioactivity ($ {Q}_{2p}>0 $ and$ {Q}_{p}<0 $ ) nucleus in the experiments by Pfützner et al. [46] at GSI (Germany) and Giovinazzo et al. [47] at GANIL (France) in 2002, respectively. Later on,$ ^{19}{\rm{Mg}}$ [48],$ ^{48}{\rm{Ni}}$ [49], and$ ^{54}{\rm{Zn}}$ [50] were found as true$ 2p $ radioactivity nuclei in different experiments.To date, various models and/or approaches have been proposed to describe the emission mechanism of
$ 2p $ radioactivity and determine its typical half-life. In general, these models and/or approaches can be divided into three main types: the three-body model where the emitted two protons from the parent nucleus may be an isotropic emission with no angular correlation [51–55], the simultaneous versus sequential decay model [38, 56], and the simplified theoretical models where the two protons released from the parent nucleus exhibit a strong correlation as a result of the proton-proton pairing effect, which includes the direct decay model [57–62] and diproton model [63]. In the former, Grigorenko considered$ 2p $ radioactivity as a three-body problem [55] based on the hyperspherical harmonics method, and Rotureau et al. investigated$ 2p $ radioactivity in the framework of the shell model embedded in the continuum [64]. In the latter, Lvarez-Rodríguez et al. described that the simultaneous versus sequential decay is possible when the two-body resonance energy and width are both small and the effective barrier is very thick [56]. In 2017, Gonalves et al. treated the$ 2p $ emission process as 2He cluster and calculated half-lives of 2p emitters using the effective liquid drop model (ELDM) [65]. In 2020, Cui et al. studied the$ 2p $ radioactivity of nuclei in the ground state using a generalized liquid drop model (GLDM) [66]. Soon after, Liu et al. [67] systematically analyzed$ 2p $ radioactivity based on the Gamow-like model [68, 69]. In 2021, considering the effect of deformation, Santhosh proposed the Coulomb and proximity potential model for deformed nuclei (CPPMDN) to systemtically calculate the$ 2p $ radioactivity half-life [30]. At the same time, the two-potential approach with Skyrme-Hartree-Fock (TPASHF), the unified fission model (UFM), and the phenomenological model with a screened electrostatic barrier (SEB) were proposed to study$ 2p $ radioactivity half-life by Pan et al. [34], Xing et al. [36] and Zou et al. [35], respectively. Their calculated results could reproduce the experimental data well. However, there is no agreement on whether the two protons are simultaneously emitted as two independent protons or as a "diproton emission" similar to the emission of a 2He-like cluster from the mother nucleus. Furthermore, some empirical and/or semi-empirical formulas can successfully reproduce the$ 2p $ radioactivity half-life, such as Liu's two-parameter empirical formula [70] and the four-parameter empirical formula proposed by Sreeja et al. [71].In 2020, Bayrak proposed a novel and simple model to calculate the half-lives of 263 favored α decay nuclei utilizing the Wentzel-Kramers-Brillouin (WKB) approximation and the Bohr-Sommerfeld quantization condition [72]. There is only one adjustable parameter:
$ V_0 $ , i.e., the depth of nuclear potential determined by fitting the experimental α decay half-lives in this model. Recently, Zhu et al. successfully extended this model to the aspect of cluster radioactivity [73]. Considering that the$ 2p $ radioactivity process could share the same mechanism of the tunneling effect with α decay and cluster radioactivity, whether this model can be extended to study$ 2p $ radioactivity is an interesting question. To this end, we extend this simple model to systematically study the half-lives of$ 2p $ radioactivity and try to improve this model while considering the effect of deformation. The results show that the theoretical values are consistent with the experimental data. Meanwhile, we use this improved model to predict the half-lives of some possible$ 2p $ radioactivity candidates whose 2p radioactivity is energetically allowed or observed but not yet quantified in NUBASE2020 [74].This article is organized as follows. In Section II, the theoretical framework for the simple model is concisely described. The calculations and discussion are presented in Section III. Finally, a brief summary is given in Section IV.
-
The
$ 2p $ radioactivity half-life$ {T}_{1/2} $ is defined as [75]$ {T}_{1/2} = \frac{\hbar{\rm{ln2}}}{\Gamma}, $

(1) where
$ \hbar $ represents the reduced Plank constant. The$ 2p $ radioactivity width Γ can be expressed as follows:$ \Gamma={{S}_{2p}}{F}\frac{\hbar^{2}}{4\mu}{{\rm exp}{(-2P)}}, $

(2) where
$ \mu={m}_{d}{m}_{2p}/({m}_{d}+{m}_{2p})\approx 938.3\times 2\times{A}_{d}/A $ MeV$ /c^{2} $ is the reduced mass with$ {m}_{d} $ and$ {m}_{2p} $ as the masses of the daughter nucleus and the emitted two protons, respectively, and$ {A}_{d} $ and A are the mass numbers of the daughter nucleus and parent nucleus, respectively [67].$ {S}_{ 2p} $ represents the preformation factor for$ 2p $ radioactivity. It can be obtained by using the cluster overlap approximation [76], which can be expressed as$ {S}_{ 2p}=G_1^2[ A /(A -2)]^{2n}\chi^2, $

(3) where
$ G_1^2=(2n)!/[2^{2n}(n!)^2] $ [77], with$ n\approx (3Z)^{1/3}-1 $ [78] being the average principal proton oscillator quantum number, where Z is the proton number of the parent nucleus. The parameter$ \chi^2=0.0143 $ was determined by fitting the experimental half-lives [66]. The normalization factor F [75] and action integral P can be expressed as$ F=\frac{1}{\int_{0}^{r_1}{\rm d}r\dfrac{1}{2k(r)}}, $

(4) $ P=\int_{r_1}^{r_2}{\rm d}r{k(r)}, $

(5) where
$ k(r)=\sqrt{\dfrac{2\mu}{\hbar^2}(V_{2p}(r)-Q_{2p})} $ is the wave number in the barrier region of the total interaction potential. r represents the distance between the centers of the emitted two protons and daughter nucleus.$ {Q_{2p}} $ is the released energy of$ 2p $ radioactivity. The classical turning points$ r_1 $ and$ r_2 $ satisfy the conditions$ V_{2p}(r_1)=V_{2p}(r_2)=Q_{2p} $ .The total interaction potential
$ V_{2p}(r) $ between the emitted two protons and daughter nucleus, including nuclear potential$ V_{N}(r) $ , Coulomb potential$ V_{C}(r) $ , and centrifugal potential$ V_{l}(r) $ , is written as [79]$ V_{2p}(r)=V_{N}(r)+V_{C}(r)+V_{l}(r). $

(6) In this study, we chose
$ V_{N}(r) $ as the modified harmonic oscillator form [72]. This can be expressed as follows:$ V_{N}(r)=-V_{0}+V_{1}r^{2}, $

(7) where
$ V_{0} $ and$ V_{1} $ are the depth and diffusivity of the nuclear potential, respectively.For the Coulomb potential
$ V_{C}(r) $ in$ 2p $ radioactivity, we choose the potential as a uniformly charged sphere with radius R, denoted as$ \ V_{C}(r)=\left\{\begin{array}{ll} \dfrac{\ Z_{2p}Z_{d}e^{2}}{2R}\left(3-\dfrac{r^{2}}{{R}^2}\right) ,&r\le r_{1},\\ \ \dfrac{Z_{2p}Z_{d}e^{2}}{r} ,&r>r_{1}, \end{array}\right. $

(8) where
$ e^{2}=1.4399652 $ $ {\rm{MeV\cdot}}{\rm{fm}}$ is the square of the electronic elementary charge and$ R=r_{0}(A_{2p}^{1/3}+A_{d}^{1/3}) $ . Here,$ r_0 $ ,$ A_{2p} $ ,$ Z_{2p} $ , and$ Z_{d} $ are the effective nuclear radius parameter, mass number of the emitted two protons, and proton numbers of the emitted two protons and daughter nucleus, respectively. In this study,$ r_0=1.28 $ fm was taken from Ref. [80].The centrifugal potential
$ V_{l}(r) $ can be written as$ V_{l}(r)=\frac{\hbar^{2} l( l+1)}{2\mu r^{2}}, $

(9) where l is the orbital angular momentum taken away by the emitted two protons. In this work, considering all known
$ 2p $ radioactivity nuclei in the experiment having$ l=0 $ , then$ V_{l}(r)=0 $ . Therefore, the total interaction potential$ V_{2p}(r) $ can be expressed as$ V_{2p}(r)=\left\{\begin{array}{*{20}{l}} { C_{0}-V_{0}+(V_{1}-C_{1})r^{2} ,}&{r\le r_{1},}\\ {\dfrac{C_{2}}{r} ,}&{r>r_{1}, }\end{array}\right. $

(10) where
$ C_{0}=\dfrac{3Z_{2p}Z_{d}e^{2}}{2R} $ ,$ C_{1}=\dfrac{Z_{2p}Z_{d}e^{2}}{2R^{3}} $ , and$ C_{2}=Z_{2p}Z_{d}e^{2} $ . Using the condition$ V_{2p}(r_1)=V_{2p}(r_2)=Q_{2p} $ , we can obtain$r_1=\sqrt{({Q_{2p}+V_{0}-C_{0}})/({V_{1}-C_{1}})}$ and$ r_2=\dfrac{C_{2}}{Q_{2p}} $ [72]. The turning points explicitly depend on the effective potential parameters$ V_0 $ and$ 2p $ radioactivity energy$ {Q_{2p}} $ . Taking$ ^{67}{\rm{Kr}}$ as an example, we plot total interaction potential$ V_{2p}(r) $ given by Eq. (10) as a function of the distance r between the centers of the emitted two protons and daughter nucleus in Fig. 1.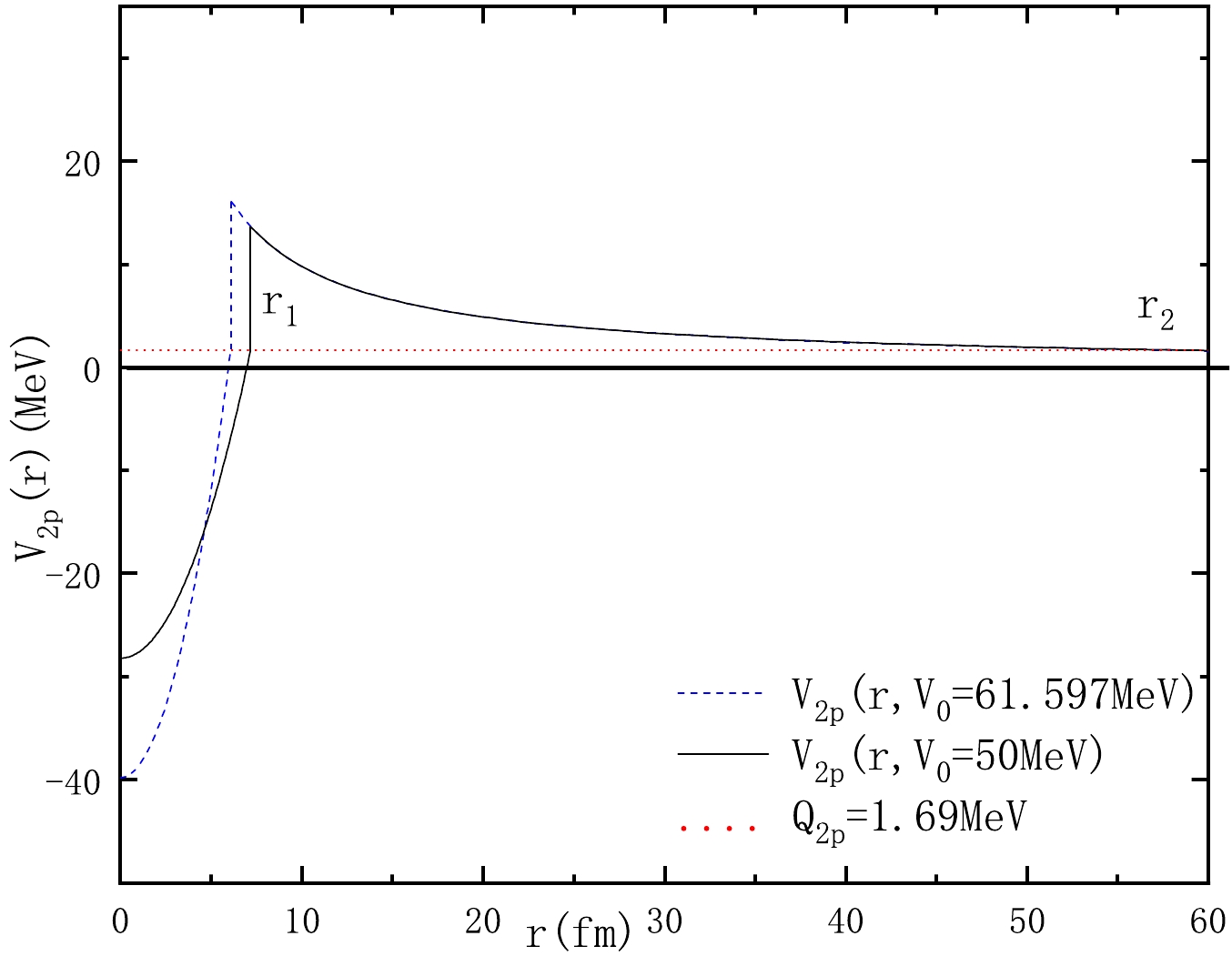
Figure 1. (color online) Total interaction potential
$V_{2p}(r)$ in terms of the different potential depths shown as a function of the distance r between the centers of the emitted two protons and daughter nucleus for the$^{67}{\rm{Kr}}\rightarrow ^{65}{\rm Se}+2p+Q_{2p}$ system with$Q_{2p}=1.69\, {\rm{ MeV}}$ .The Bohr-Sommerfeld quantization condition can reduce the freedom of the system, which is also a vital application of the WKB approximation [81, 82]. In this work, we use this condition to reduce the degrees of freedom of the total potential describing the interaction between emitted two protons and daughter nucleus. The formula for this condition can be expressed as
$ \int_{0}^{r_1}{\rm d}r{k(r)}=(G-l+1)\frac{\pi}{2}. $

(11) Here, the global quantum number
$ G=2n_r+l $ in Eq. (11) is dependent on the Wildermuth quantum rule, with$ n_r $ and l representing the radial and angular momentum quantum numbers, respectively [83]. We chose$G=2, 3, \;4,\; 5$ corresponding to the$ 2\hbar\omega $ ,$ 3\hbar\omega $ ,$ 4\hbar\omega $ , and$ 5\hbar\omega $ oscillator shell depending on the individual nuclei for$ 2p $ radioactivity [84]. The relationship between$ V_0 $ and$ V_1 $ can be expressed as$ V_1=C_1+\frac{\mu}{2\hbar^2}\left(\frac{Q_{2p}+V_0-C_0}{1+G}\right)^2, $

(12) with the integral conditions
$ Q_{2p}+V_0>C_0 $ and$ V_1>C_1 $ . Based on the above, we can analytically obtain the normalization factor F and action integral P, which can be expressed as$ F=\frac{4}{\pi}\sqrt{\frac{2\mu}{\hbar^2}(V_1-C_1)}, $

(13) $ \begin{aligned}[b] P=\;& \sqrt{\frac{2\mu}{\hbar^2}}{\frac{C_2}{\sqrt{Q_{2p}}}} \Bigg(\arccos\sqrt{\frac{Q_{2p}r_1}{C_2}}\\ &-\sqrt{\frac{Q_{2p}r_1}{C_2}-\left({\frac{Q_{2p}r_1}{C_2}}\right)^2} \Bigg). \end{aligned} $

(14) Therefore, the logarithm of
$ 2p $ radioactivity half-lives can be obtained by$ {\rm{log}}_{10}{T_{1/2}}=A+B/\sqrt{Q_{2p}}, $

(15) where A and B can be expressed as
$ A={\rm log}_{10}\left(\frac{\pi\hbar ln2}{P}\frac{1+{G}}{Q_{2p}+{V_0}-{C_0}}\right), $

$ \begin{aligned}[b] B=\;&{2C_2{{\rm{log}}_{10}}(e)\sqrt{\frac{2\mu}{\hbar^2}}}\Bigg(\arccos\sqrt{\frac{Q_{2p}r_1}{C_2}} \\& -\sqrt{\frac{Q_{2p}r_1}{C_2}-\left({\frac{Q_{2p}r_1}{C_2}}\right)^2} \Bigg). \end{aligned} $

(16) Considering the substantial impact of deformation on nuclear structure, especially for two-proton emitters characterized by non-spherical shapes[23, 30] with the additional term
$ a_{\beta}\left| \beta_{2}\right| $ , the newly proposed model can calculate the$ 2p $ radioactivity half-lives [85]. The deformation values$ \beta_{2} $ are taken from Möller et al. [86]. This can be written as$ {\rm{log}}_{10}{T_{1/2}}=A+B/\sqrt{Q_{2p}}+a_{\beta}\left| \beta_{2}\right|. $

(17) -
In 2019, based on the effective liquid drop model (ELDM), Sreeja et al. proposed an empirical formula to calculate the half-lives of
$ 2p $ radioactivity [71]. This can be expressed as$ {\rm{log}}_{10}{T_{1/2}}=((a\times l)+b)Z_d^{0.8} Q_{2p}^{-1/2}+((c\times l)+d), $

(18) where
$ a=0.1578 $ ,$ b=1.9474 $ ,$ c=-1.8795 $ , and$ d= -24.847 $ denote the adjustable parameters, which are determined by fitting the calculated results of the ELDM [71]. -
In 2021, based on the Geiger-Nuttall law and experimental data, Liu et al. proposed a two-parameter empirical formula to study
$ 2p $ radioactivity half-lives [70]. This can be formulated as$ {\rm{log}}_{10}{T_{1/2}}=a(Z_d^{0.8}+l^{ 0.25}) Q_{2p}^{-1/2} +b, $

(19) where the adjustable parameters
$ a=2.032 $ and$ b= -26.832 $ , respectively [70]. -
Based on the Wentzel-Kramers-Brillouin approximation and Bohr-Sommerfeld quantization condition, we extend a simple phenomenological model proposed by Bayrak to systematically study the half-lives of favored
$ 2p $ radioactivity for nuclei with$ 4<Z<36 $ . In this model, there are two adjustbale parameters$ V_0 $ and$ a_{\beta} $ : the depth of nuclear potential and coefficient of effect for deformation, respectively. Based on the experimental data of the true$ 2p $ radioactivity nuclei using the genetic algorithm, we obtain the optimal adjustable parameters$ V_0=61.597 $ $ {\rm{MeV}}$ and$ a_{\beta}=-1.250 $ . Due to the formula$ V_0 = 25A_{2p} $ $ {\rm{MeV}}$ based on Ref. [87], we can judge that the value of$ V_0 $ is reasonable. Using this model, we systematically calculate the favored$ 2p $ radioactivity half-lives. The detailed calculations are presented in Table 1. In this table, the first three columns represent the$ 2p $ radioactive parent nuclei,$ 2p $ radioactivity released energy$ Q_{2p} $ , and the experimental data of the$ 2p $ radioactivity half-lives$ \log_{10}T_{1/2}^{\rm{exp}} $ , respectively. The fourth to fourteenth columns are calculated data of the$ 2p $ radioactivity half-lives by using our model with Eqs. (15) and (17), Gamow-like model (GLM), generalized liquid drop model (GLDM), four-parameter empirical formula by Sreeja et al., two-parameter empirical formula by Liu et al., ELDM, TPASHF, SEB, UFM, and CPPMDN, respectively. The last column gives the logarithm of errors between the experimental half-lives of$ 2p $ radioactivity and the calculated ones with our model$(\log_{10}{HF}={\log_{10}T_{1/2}^{\rm{exp}}} -{\log_{10}T_{1/2}^{\rm{Cal}}})$ . From this table, it can be seen that for the true$ 2p $ radioactivity nuclei$ ^{19}{\rm{Mg}}$ ,$ ^{45}{\rm{Fe}}$ ,$ ^{48}{\rm{Ni}}$ ,$ ^{54}{\rm{Zn}}$ , and$ ^{67}{\rm{Kr}}$ , most of the$ \log_{10}{HF} $ values are between –1 and 1. This means that our calculated half-lives differs by approximately one order of magnitude from the experimental value. In particular, for$ ^{45}{\rm{Fe}}$ ($ Q_{2p}=1.15{{\rm{MeV}}} $ ) and$ ^{48}{\rm{Ni}}$ ($ Q_{2p}=1.31{{\rm{MeV}}} $ ), the values of$ \log_{10}{HF} $ are –0.06 and –0.09, respectively. For the not true$ 2p $ radioactivity nuclei$ ^{6}{\rm{Be}}$ ,$ ^{12}{\rm{O}}$ , and$ ^{16}{\rm{Ne}}$ , the values of$ \log_{10}{HF} $ are relatively large. Clearly, the calculated half-lives of 16Ne and 67Kr nuclei show significant improvement when the effects of deformation are considered, compared to calculations without deformation. This shows that our improved formula is effective.Nuclei $ Q_{2p} $ /MeV

$ \log_{10}T_{1/2}^{\rm{exp}} $ 

$ \log_{10}T_{1/2} $ (s)

$ \log_{10}{\textit{HF}} $ 

Cal1 Cal2 GLM GLDM Sreeja Liu ELDM TPASHF SEB UFM CPPMDN 6Be 1.37 [40] −20.30 [40] −20.24 −20.24 −19.70 −19.37 −21.95 −23.81 −19.97 − −19.86 −19.41 −21.91 −0.06 12O $ 1.64 $ [41]

$-20.20 $ [41]

$ -18.50 $ 

$ -18.50 $ 

$ -18.04 $ 

$ -19.71 $ 

$ -18.47 $ 

$ -20.17 $ 

$ -18.27 $ 

− $ -17.70 $ 

$ -18.45 $ 

$ -20.90 $ 

$ -1.70 $ 

1.82 [38] −20.94 [38] −18.74 −18.74 −18.30 −19.46 −18.79 −20.52 − − −18.03 −18.69 −21.22 −2.20 $ 1.79 $ [43]

$ -20.10 $ [43]

$ -18.70 $ 

$ -18.70 $ 

$ -18.26 $ 

$ -19.43 $ 

$ -18.74 $ 

$ -20.46 $ 

− − $ -17.98 $ 

$ -18.65 $ 

$ -21.17 $ 

$ -1.40 $ 

1.80 [44] −20.12 [44] −18.71 −18.71 −18.73 −19.44 −18.76 −20.48 − − −18.00 −18.66 −21.19 −1.41 16Ne 1.33 [38] −20.64 [38] −16.52 −17.07 −16.23 −16.45 −15.94 −17.53 − − −15.47 −16.49 −18.01 −3.57 $ 1.40 $ [45]

$ -20.38 $ [45]

$ -16.71 $ 

$ -17.26 $ 

$ -16.43 $ 

$ -16.63 $ 

$ -16.16 $ 

$ -17.77 $ 

$ -16.60 $ 

− $ -15.71 $ 

$ -16.68 $ 

$ -18.25 $ 

$ -3.12 $ 

19Mg $ 0.75 $ [48]

$ -11.40 $ [48]

$ -11.77 $ 

$ -12.07 $ 

$ -11.46 $ 

$ -11.79 $ 

$ -10.66 $ 

$ -12.03 $ 

$ -11.72 $ 

$ -11.00 $ 

$ -10.58 $ 

$ -11.77 $ 

$ -11.96 $ 

$ 0.67 $ 

45Fe $ 1.10 $ [46]

$ -2.40 $ [46]

$ -1.85 $ 

$ -1.85 $ 

$ -2.09 $ 

$ -2.23 $ 

$ -1.25 $ 

$ -2.21 $ 

− $ -2.1 $ 

$ -2.32 $ 

$ -1.94 $ 

$ -2.76 $ 

$ -0.55 $ 

1.14 [47] −2.07 [47] −2.33 −2.33 −2.58 −2.71 −1.66 −2.64 − −2.43 −2.67 −2.43 −2.36 0.26 $ 1.15 $ [49]

$ -2.55 $ [49]

$ -2.49 $ 

$ -2.49 $ 

$ -2.74 $ 

$ -2.87 $ 

$ -1.80 $ 

$ -2.79 $ 

$ -2.43 $ 

$ -2.53 $ 

$ -2.78 $ 

$ -2.6 $ 

$ -2.53 $ 

$ -0.06 $ 

1.21[88] −2.42 [88] −3.11 −3.11 −3.37 −3.50 −2.34 −3.35 − −3.15 −3.24 −3.23 −3.15 0.69 48Ni 1.29 [89] −2.52 [89] −2.22 −2.22 −2.59 −2.62 −1.61 −2.59 − −2.17 −2.55 −2.29 −2.17 −0.30 $ 1.35 $ [49]

$ -2.08 $ [49]

$ -2.83 $ 

$ -2.83 $ 

$ -3.21 $ 

$ -3.24 $ 

$ -2.13 $ 

$ -3.13 $ 

− $ -2.79 $ 

$ -3.00 $ 

$ -2.91 $ 

$ -2.79 $ 

$ 0.75 $ 

$ 1.31 $ [90]

$ -2.52 $ [90]

$ -2.43 $ 

$ -2.43 $ 

$ -2.80 $ 

$ -2.83 $ 

$ -1.80 $ 

$ -2.77 $ 

$ -2.36 $ 

$ -2.38 $ 

− $ -2.5 $ 

$ -2.38 $ 

$ -0.09 $ 

54Zn $ 1.28 $ [91]

$ -2.76 $ [91]

$ -1.25 $ 

$ -1.59 $ 

$ -0.93 $ 

$ -0.87 $ 

$ -0.10 $ 

$ -1.01 $ 

− $ -1.45 $ 

$ -1.31 $ 

$ -0.52 $ 

$ -1.45 $ 

$ -1.17 $ 

$ 1.48 $ [50]

$ -2.43 $ [50]

$ -3.28 $ 

$ -3.62 $ 

$ -3.01 $ 

$ -2.95 $ 

$ -1.83 $ 

$ -2.81 $ 

$ -2.52 $ 

$ -2.59 $ 

$ -2.81 $ 

$ -2.61 $ 

$ -2.59 $ 

$ 1.19 $ 

67Kr $ 1.69 $ [92]

$ -1.70 $ [92]

$ -0.75 $ 

$ -1.08 $ 

$ -0.76 $ 

$ -1.25 $ 

$ 0.31 $ 

$ -0.58 $ 

$ -0.06 $ 

$ -1.06 $ 

$ -0.95 $ 

$ -0.54 $ 

$ -1.06 $ 

$ -0.62 $ 

Table 1. Comparisons between the experimental
$ 2p $ radioactivity half-lives and calculated ones using eleven different theoretical models and/or empirical formulas. The experimental$ 2p $ radioactivity half-lives in logarithmic form$ \log_{10}T_{1/2}^{\rm{exp}} $ and experimental$ 2p $ released energy$ Q_{2p} $ were extracted from the corresponding references. The deformation values$ \beta_{2} $ were taken from Möller et al. [87].To intuitively compare these results, Fig. 2 plots the differences between the experimental and calculated data by using different theoretical models and/or empirical formulas, i.e., our model with Eq. (17), GLM, GLDM, ELDM, TPASHF, SEB, UFM, CPPMDN, and empirical formulas proposed by Sreeja et al. and Liu et al.. It is evident from this figure that the values of
${\log_{10}T_{1/2}^{\rm{exp}}}- {\log_{10}T_{1/2}^{\rm{cal}}}$ for the true$ 2p $ radioactivity nuclei ($ ^{19}{\rm{Mg}}$ ,$ ^{45}{\rm{Fe}}$ ,$ ^{48}{\rm{Ni}}$ ,$ ^{54}{\rm{Zn}}$ , and$ ^{67}{\rm{Kr}}$ ) are basically within$ \pm 1 $ , which means that our model can reproduce the experimental half-lives accurately. Nevertheless, regarding the not true radioactivity nuclei ($ ^{6}{\rm{Be}}$ ,$ ^{12}{\rm{O}}$ , and$ ^{16}{\rm{Ne}}$ ), the experimental data cannot be reproduced properly, especially for$ ^{16}{\rm{Ne}}$ , with a reported$Q_{2p}=1.33 ~ {{\rm{MeV}}}$ and$Q_{2p}=1.40 $ MeV. We can observe that there is a difference of more than two orders of magnitude between the experimental and calculated half-lives in several nuclei. This may account for the imperfection of early detection technologies and radioactive beam equipment. Meanwhile, we plot the logarithm$ 2p $ radiactivity half-lives of$ ^{12}{\rm{O}}$ ,$ ^{45}{\rm{Fe}}$ , and$ ^{48}{\rm{Ni}}$ nuclei as a function of$ Q_{2p} $ using the$ 2p $ radioactivity formula with Eq. (17) in Fig. 3. There is clearly a linear correlation between the logarithm half-lives and the releasd energy$ Q_{2p} $ . In addition, it is worth noting that some studies suggested that nuclear deformation effects or collective mechanisms will influence the$ 2p $ radioactive half-life to some extent [55]. At the same time, because the original model is a two-body model for calculating the half-lives of α decay, it only considers two-body problems. When we treat the emitted two protons as a 2He cluster, it may lead to some loss of detailed structural information, such as the core and valence protons of$ 2p $ radioactivity [64]. We will consider addressing this issue in future work.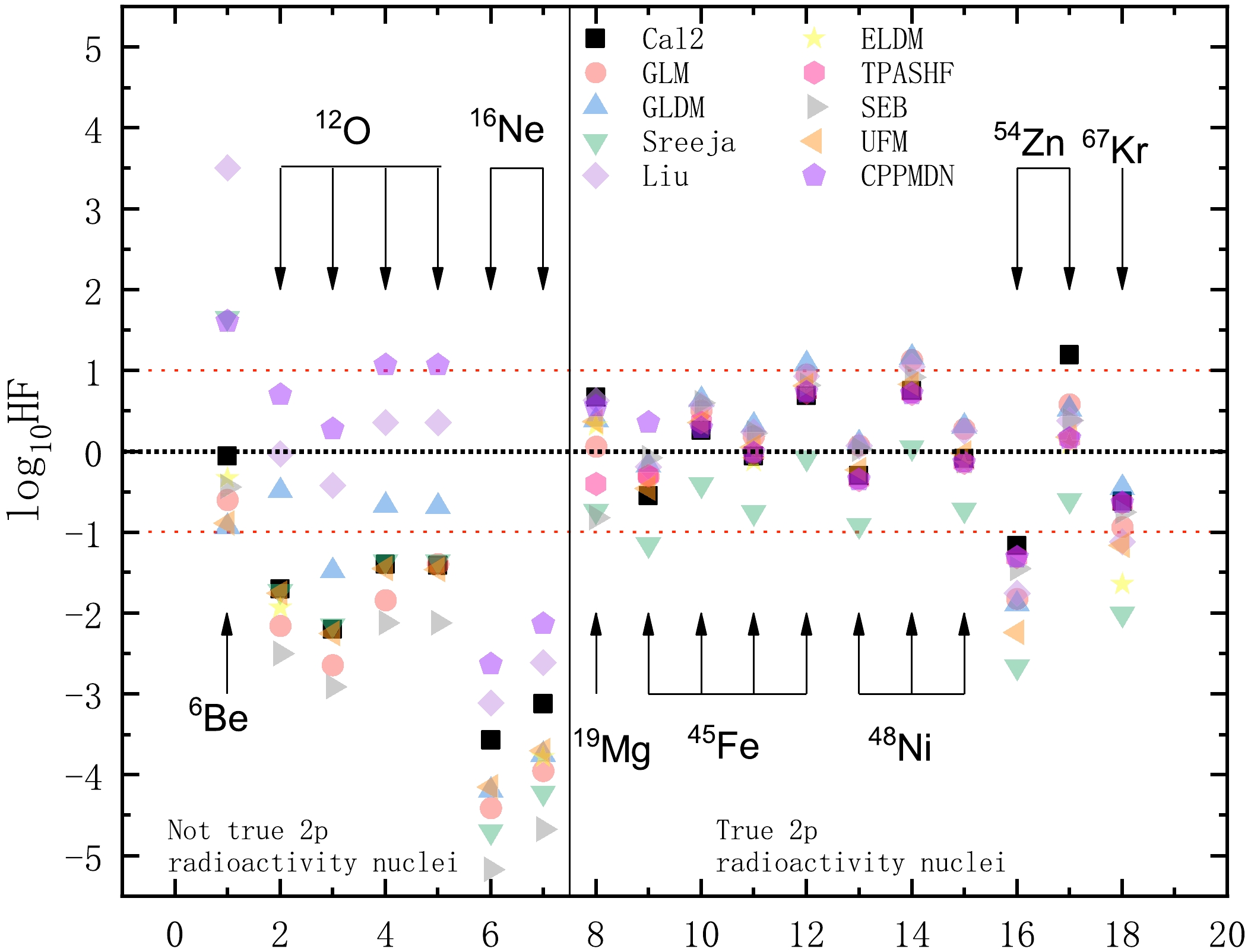
Figure 2. (color online) Deviations between the experimental
$2p$ radioactivity half-lives and calculated ones with different theoretical models and/or empirical formulas.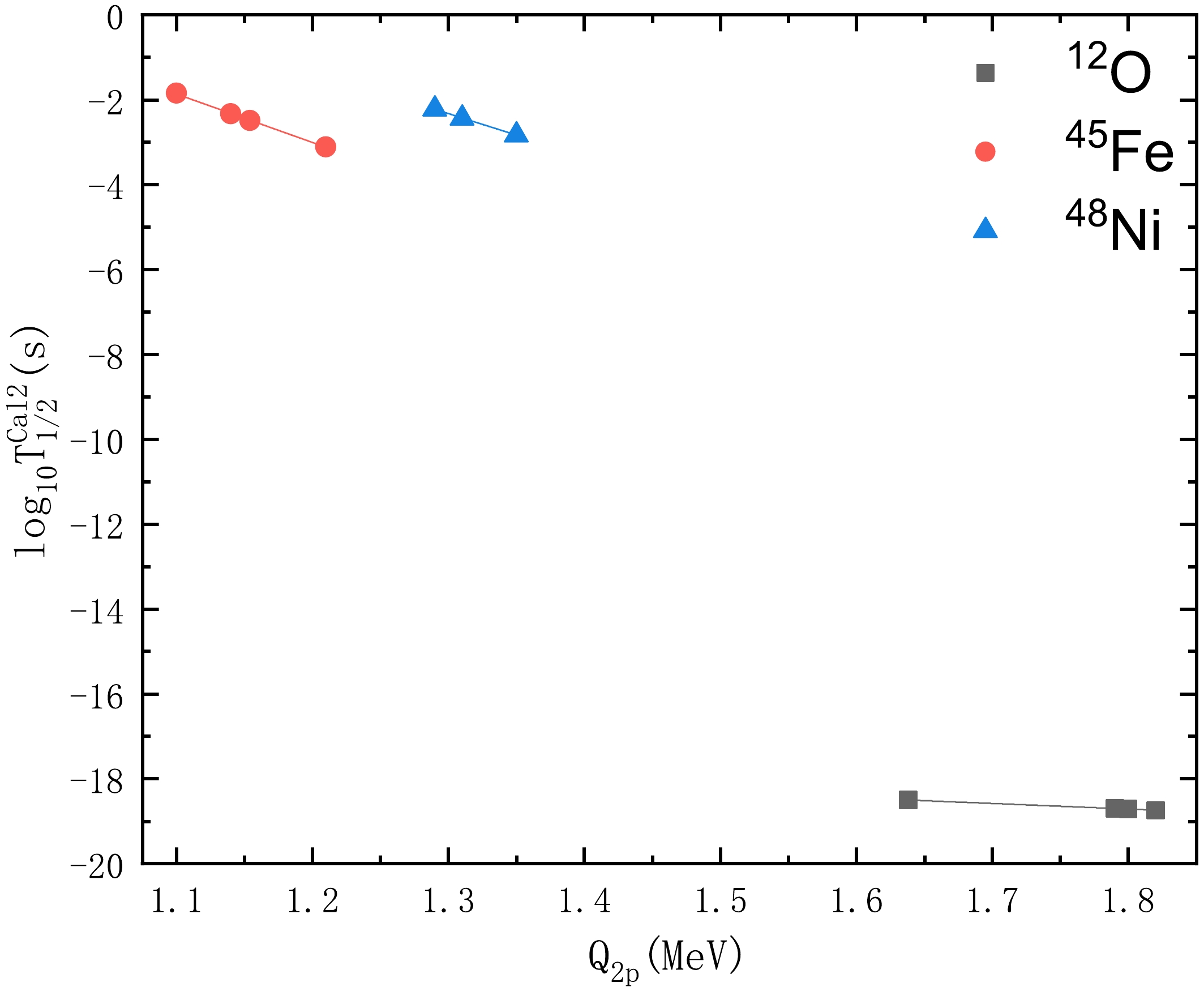
Figure 3. (color online) Linear relation between the calculated logarithmic
$2p$ radioactivity half-lives and released energy$Q_{2p}$ .The standard deviation σ, quantifying the difference between the experimental data and the calculated ones, can be defined as
$ \sigma = \sqrt{\sum{({\rm{log}}_{10}{T_{1/2}^{\rm{cal}}}-{\rm{log}}_{10}{T_{1/2}^{\rm{exp}}})^2}/n} \; , $

(20) where
$ {\rm{log}}_{10}{T_{1/2}^{\rm{exp}}} $ and$ {\rm{log}}_{10}{T_{1/2}^{\rm{cal}}} $ are the logarithmic forms of the experimental and calculated$ 2p $ radioactivity half-lives, respectively. n is the number of nuclei involved in$ 2p $ radioactivity cases. In the following, we calculate the standard deviation σ values between the experimental data and calculated ones by using our model with Eq. (15), Eq. (17), GLM, GLDM, ELDM, TPASHF, SEB, UFM, CPPMDN, four-parameter empirical formula by Sreeja, and two-parameter empirical formula by Liu. All of the calculated results are listed in Table 2. From this table, we can clearly see that the standard deviation of our improved model is 0.683, which is better than those of GLM, GLDM, ELDM, SEB, UFM, Sreeja's empirical formula, and Liu's empirical formula results (0.809, 0.818, 1.166, 0.815, 0.754, 0.736, and 0.867, respectively). In particular, the σ values for the true$ 2p $ radioactivity nuclei within our model decreased by$({0.809-0.683})/{0.809}$ =15.7% relative to the Gamow-like model. This indicates that the half-lives calculated by our model can reproduce the experimental data well.Model Cal1 Cal2 GLM GLDM Sreeja Liu ELDM TPASHF SEB UFM CPPMDN σ $ 0.710 $ 

$ 0.683 $ 

$ 0.809 $ 

$ 0.818 $ 

$ 1.166 $ 

$ 0.815 $ 

$ 0.754 $ 

$ 0.581 $ 

$ 0.736 $ 

$ 0.867 $ 

$ 0.592 $ 

Table 2. Standard deviations σ between the experimental data and calculated ones using different theoretical models and empirical formulas for the true
$ 2p $ radioactivity.Encouraged by the good agreement between the experimental
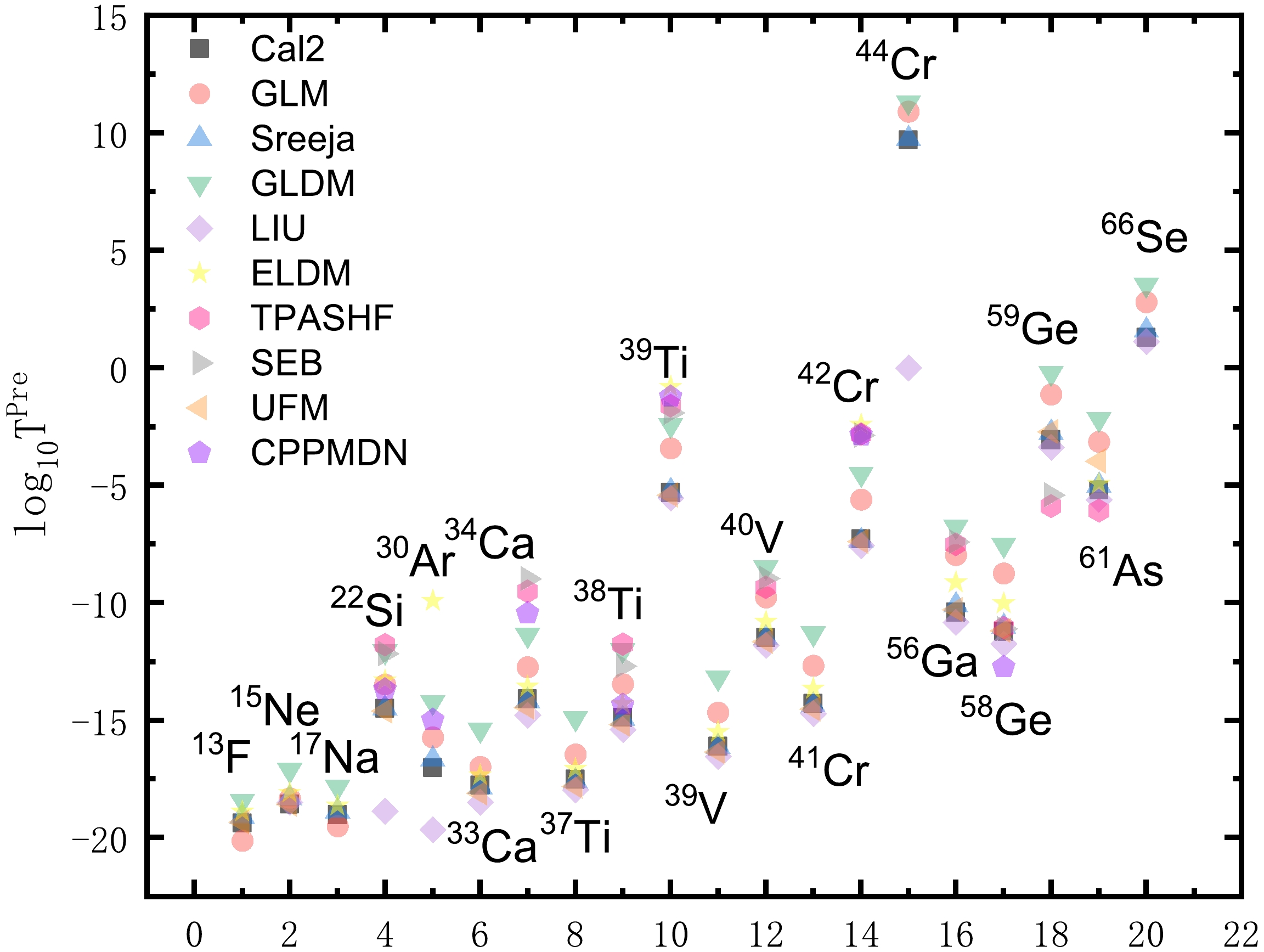
$ 2p $ radioactivity half-lives and the calculated ones in our model, this model is used to predict the half-lives of some possible$ 2p $ radioactivity candidates. For some potential$ 2p $ radioactivity candidates, the deformation value$ \beta_{2} $ remained undetermined within the study of Möller et al. [86]. Thus, we provisionally assign the deformation value$ \beta_{2}=0 $ . The predicted results are listed in Table 3. In this table, the first and second columns show the predicted$ 2p $ radioactivity parent nuclei and$ 2p $ radioactivity released energy$ Q_{2p} $ , with values taken from the latest evaluated atomic mass table of NUBASE2020 [74]. The third and fourth columns show the predicted half-lives of$ 2p $ radioactivity candidates using our model with Eqs. (15) and (17). The fifth to thirteenth columns represent the predicted half-lives values calculated by Liu, Sreeja, GLM, GLDM, ELDM, TPASHF, SEB, UFM, and CPPMDN, respectively. Taking$ ^{22}{\rm{Si}}$ as an example, our predicted value is –14.50, which is also consistent with the predictions of other models and/or empirical formulas. It is evident that our calculated values are all within the same order of magnitude. To intuitively compare these results, we plot the differences of each predicted value in Fig. 4. In this figure, the black square, red circle, blue upward triangle, green downward triangle, purple diamond, yellow star, pink hexagon, gray right triangle, orange left triangle, and violet pentagon represent the logarithmic form of predicted half-life values of our work, Liu, Sreeja, GLM, GLDM, ELDM, TPASHF, SEB, UFM, and CPPMDN, respectively. From this figure, it is evident that the predicted 2p radioactivity half-lives by our model show consistency with those calculated by GLM, GLDM, and UFM. These predicted results of possible$ 2p $ radioactivity candidates will be helpful in the search for new candidates in future experiments.Nuclei $ Q_{2p} $ (MeV)

$ \log_{10}T_{1/2} $ (s)

Cal1 Cal2 GLM GLDM Sreeja Liu ELDM TPASHF SEB UFM CPPMDN 13F $ 3.09 $ 

$ -19.39 $ 

$ -19.39 $ 

$ -20.13 $ 

$ -18.42 $ 

$ -19.10 $ 

− $ -18.89 $ 

− − $ -19.33 $ 

− 15Ne $ 2.52 $ 

$ -18.58 $ 

$ -18.58 $ 

$ -18.76 $ 

$ -17.11 $ 

$ -18.32 $ 

$ -18.48 $ 

$ -18.08 $ 

− − $ -18.57 $ 

− 17Na $ 3.57 $ 

$ -19.01 $ 

$ -19.01 $ 

$ -19.51 $ 

$ -17.83 $ 

$ -18.87 $ 

− $ -18.63 $ 

− − $ -18.95 $ 

− 22Si $ 1.58 $ 

$ -14.50 $ 

$ -14.50 $ 

$ -13.48 $ 

$ -12.05 $ 

$ -14.50 $ 

$ -18.87 $ 

$ -13.32 $ 

$ -11.78 $ 

$ -12.17 $ 

$ -14.61 $ 

$ -13.70 $ 

30Ar $ 3.42 $ 

$ -16.67 $ 

$ -17.02 $ 

$ -15.74 $ 

$ -14.22 $ 

$ -16.67 $ 

$ -19.66 $ 

$ -9.91 $ 

− − − $ -14.99 $ 

33Ca $ 5.13 $ 

$ -17.72 $ 

$ -17.76 $ 

$ -16.98 $ 

$ -15.40 $ 

$ -17.85 $ 

$ -18.48 $ 

$ -17.35 $ 

− − $ -18.11 $ 

− 34Ca $ 2.51 $ 

$ -14.09 $ 

$ -14.09 $ 

$ -12.74 $ 

$ -11.35 $ 

$ -14.18 $ 

$ -14.78 $ 

$ -13.56 $ 

$ -9.51 $ 

$ -8.99 $ 

$ -14.46 $ 

$ -10.44 $ 

37Ti $ 5.40 $ 

$ -17.38 $ 

$ -17.52 $ 

$ -16.46 $ 

$ -14.91 $ 

$ -17.59 $ 

$ -17.96 $ 

$ -17.07 $ 

− − $ -17.81 $ 

− 38Ti $ 3.24 $ 

$ -14.73 $ 

$ -14.88 $ 

$ -13.45 $ 

$ -12.02 $ 

$ -14.95 $ 

$ -15.38 $ 

$ -14.30 $ 

$ -11.77 $ 

$ -12.70 $ 

$ -15.18 $ 

$ -14.35 $ 

39Ti $ 1.06 $ 

$ -5.19 $ 

$ -5.32 $ 

$ -3.43 $ 

$ -2.43 $ 

$ -5.24 $ 

$ -5.55 $ 

$ -0.81 $ 

$ -1.62 $ 

$ -1.91 $ 

$ -5.41 $ 

$ -1.23 $ 

39V $ 4.21 $ 

$ -15.85 $ 

$ -16.12 $ 

$ -14.67 $ 

$ -13.19 $ 

$ -16.13 $ 

$ -16.54 $ 

$ -15.49 $ 

− − $ -16.34 $ 

− 40V $ 2.14 $ 

$ -11.26 $ 

$ -11.49 $ 

$ -9.77 $ 

$ -8.50 $ 

$ -11.50 $ 

$ -11.80 $ 

$ -10.80 $ 

$ -9.34 $ 

$ -8.97 $ 

$ -11.66 $ 

− 41Cr $ 3.33 $ 

$ -14.04 $ 

$ -14.28 $ 

$ -12.68 $ 

$ -11.29 $ 

$ -14.37 $ 

$ -14.72 $ 

$ -13.66 $ 

− − $ -14.53 $ 

− 42Cr $ 1.48 $ 

$ -7.14 $ 

$ -7.29 $ 

$ -5.60 $ 

$ -4.50 $ 

$ -7.37 $ 

$ -7.56 $ 

$ -2.43 $ 

$ -2.83 $ 

$ -2.87 $ 

$ -7.40 $ 

$ -2.86 $ 

44Cr $ 0.50 $ 

$ 9.70 $ 

$ 9.70 $ 

$ 10.91 $ 

$ 11.31 $ 

$ 9.73 $ 

− − − − − − 56Ga $ 2.82 $ 

$ -10.16 $ 

$ -10.40 $ 

$ -7.96 $ 

$ -6.76 $ 

$ -10.11 $ 

$ -10.83 $ 

$ -9.14 $ 

$ -7.51 $ 

$ -7.41 $ 

$ -10.30 $ 

− 58Ge $ 3.23 $ 

$ -10.99 $ 

$ -11.21 $ 

$ -8.74 $ 

$ -7.51 $ 

$ -11.01 $ 

$ -11.73 $ 

$ -10.02 $ 

$ -11.06 $ 

$ -11.10 $ 

$ -11.19 $ 

$ -12.73 $ 

59Ge $ 1.60 $ 

$ -2.88 $ 

$ -3.07 $ 

$ -1.13 $ 

$ -0.22 $ 

$ -2.77 $ 

$ -3.37 $ 

− $ -5.88 $ 

$ -5.41 $ 

$ -2.73 $ 

− 61Ge $ 1.98 $ 

$ -5.04 $ 

$ -5.21 $ 

$ -3.15 $ 

$ -2.16 $ 

$ -5.02 $ 

$ -5.61 $ 

$ -4.95 $ 

$ -6.07 $ 

− $ -3.97 $ 

− 66Se $ 1.39 $ 

$ 1.58 $ 

$ 1.30 $ 

$ 2.79 $ 

$ 3.54 $ 

$ 1.59 $ 

$ 1.12 $ 

− − − − − -
In this work, considering the preformation factor
$ {S}_{2p} $ and deformation parameter$ \beta_{2} $ , based on the Wentzel-Kramers-Brillouin approximation, Bohr-Sommerfeld quantization condition, and Bayrak's model, the half-lives of$ 2p $ radioactivity nuclei with$ 4<Z<36 $ were systematically investigated. The calculated results can effectively reproduce the experimental data. In addition, we also predicted the half-lives of potential$ 2p $ radioactivity candidates and compared them with the results obtained from GLM, GLDM, ELDM, TPASHF, SEB, UFM, CPPMDN, and the empirical formulas proposed by Liu and Sreeja. These calculations revealed that our predicted values are in good agreement with each other. These predicted values can also serve as theoretical references for future experimental studies.
A simple model for two-proton radioactivity
- Received Date: 2024-04-22
- Available Online: 2024-10-15
Abstract: In this work, considering the preformation factor of the emitted two protons in parent nucleus





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: