-
Nuclear structure of atomic nuclei in the region with
$ Z > $ 82 and$ N \leq $ 126 has attracted significant attention in recent years [1−4]. The systematics of isomers in this region have been extensively examined; for example,$ 8^{+} $ [5−12], as well as$ 9^{-} $ and/or$ 10^{-} $ isomers [5−8] have been observed in Po-Rn-Ra isotopes. These observations pro-vide a good experimental ground for testing residual interactions between valence nucleons in theoretical models.The
$ 8^{+} $ isomers in the even-even Po-Rn-Ra nuclei with$ N = 122-126 $ can be understood as seniority isomers, where the angular momentum is attributed to two unpaired nucleons occupying the$ \pi h_{9/2} $ orbit, i.e., illustrating the conservation of seniority two [11, 13]. In the seniority scheme, the$ 0^{+}_1 $ state of a semimagic even-even nucleus is typically described as a seniority-zero state, and low-lying excited states are suggested to have seniority two [14]. The seniority structure for a high-j orbit has been identified in various nuclear regions [15]. Several distinct experimental features have been observed [13]. The energy spacing between the$ 0^{+} $ and$ 2^{+} $ states is large, and the energies of the$ 4^{+} $ ,$ 6^{+} $ , and subsequent seniority-two states are close to each other. The isomer with$ I = 2j - 1 $ represents the state of maximum angular momentum within the seniority-two configuration space. The electric quadrupole reduced transition probability, denoted as$ B(E2) $ , from$ 2^{+}_1 $ to$ 0^{+}_1 $ state exhibits a downward parabolic trend as the number of nucleons occupying a high-j orbit increases, reaching a maximum at half occupancy of the orbit. Conversely, the$ B(E2) $ value for transitions conserving seniority follows an upward parabolic trajectory as the number of nucleons in high-j orbit increases, reaching a minimum when half of the orbit is filled.However, as the number of valence nucleons (or holes) increases, collective motions start to emerge in atomic nuclei due to the residual proton-neutron interaction. Hence, the low-lying states of these nuclei may not be adequately described solely by the seniority scheme [2]. This is particularly evident in the case of Po-Rn-Ra isotopes with
$ N < 126 $ , where the presence of seniority-like states and collective modes in low-lying states has been suggested [13]. The experimental measurement of$ B(E2; 2_1^{+} \rightarrow 0_1^{+}) $ and theoretical calculations within the BCS-based QRPA propose the emergence of collectivity in$ ^{208,210} {\rm{Rn}}$ and$ ^{206} {\rm{Po}}$ [16]. The lifetimes of$ 4_1^{+} $ states in$ ^{204,206} {\rm{Po}}$ were measured in Ref. [1], with the derived$ B(E2; 4_1^{+} \rightarrow 2_1^{+}) $ values indicating the development of collective behavior in the$ 4_1^{+} $ states of Po isotopes with$ N \leq 124 $ . In recent studies, the lifetime of$ 6_1^{+} $ state in$ ^{206} {\rm{Po}}$ was measured, with the obtained$ B(E2; 6_1^{+} \rightarrow 4_1^{+}) $ values suggesting that$ 6_1^{+} $ state behaves as a seniority-two state [3].The nucleus
$ ^{206} {\rm{Rn}}$ , with$ N = 120 $ , can be crucial in elucidating the nature of the transition from single-particle seniority-type excitations to collective excitations. The level structure of$ ^{206} {\rm{Rn}}$ was investigated long time ago. In Ref. [17],$ ^{206} {\rm{Rn}}$ was produced by$ \beta^+ $ decay, and the level scheme was enriched up to 2269.9 keV. Furthermore, the half-life of the$ 8^{+} $ isomer was measured to be 6.3(24) ns. In Ref. [18],$ ^{206} {\rm{Rn}}$ was produced by a fusion reaction, and the level scheme was enriched up to 4130 keV, and the half-life of$ 8^{+} $ isomer was measured to be 19(3) ns. It is worth mentioning that several γ rays were observed in the study conducted in Ref. [17]. However, they were not observed in the reasearch reported in Ref. [18]. -
The experiment was performed at the China Institute of Atomic Energy (CIAE) in Beijing. A
$ ^{14} {\rm{N}}$ beam with an energy of 78 MeV was delivered by the HI-13 tandem accelerator. Excited states of$ ^{206} {\rm{Rn}}$ were populated via$ ^{197} {\rm{Au}}$ ($ ^{14} {\rm{N}}$ , 5n) fusion reaction. Furthermore,$ ^{206} {\rm{Rn}}$ nucleus is a by-product, and$ ^{197} {\rm{Au}}$ target with a thickness of 10 mg/cm2 is used as backing material in the$ ^{100} {\rm{Mo}}$ ($ ^{14} {\rm{N}}$ ,$ xn $ ) fusion-evaporation reaction, where a 0.5 mg/cm2 foil of$ ^{100} {\rm{Mo}}$ is used as the target. Given that$ ^{100} {\rm{Mo}}$ target used in this experiment is relatively thin and$ ^{197} {\rm{Au}}$ backing is much thicker,$ ^{14} {\rm{N}}$ +$ ^{197} {\rm{Au}}$ fusion reaction occurs easily. Furthermore,$ ^{207} {\rm{Rn}}$ nucleus was produced via$ ^{197} {\rm{Au}}$ ($ ^{14} {\rm{N}}$ , 4n) reaction, and its level scheme was significantly extended [19]. Similarly,$ ^{206} {\rm{Rn}}$ nucleus has been well populated. In the present experiment, an array composed of nine BGO-Compton-suppressed HPGe detectors, two low-energy photon (LEP) HPGe detectors, and one clover detector was used to detect γ rays. The Compton-suppressed HPGe detector has an energy resolution of 2.0−2.5 keV for the 1332.5-keV γ ray from$ ^{60} $ Co, while a planar HPGe detector has an energy resolution of 0.6−0.7 keV for 121.78-keV γ rays from$ ^{152} $ Eu. The positions of the detectors were as follows: three HPGe detectors and one clover detector were placed at approximately 90° with respect to the beam direction, two HPGe detectors were placed at approximately 40°, four HPGe detectors were placed at approximately 140°, and two LEP HPGe detectors were placed at approximately 120°. A total of$84\,\times $ $ 10^6 $ γ-γ coincident events were acquired, from which a symmetric γ-γ matrix was generated. The data were analyzed using RADWARE software [20]. The details of the experimental setup have been reported in a previous study [21].Meanwhile, a directional correlation (DCO) from oriented states matrix was created by sorting the data from the detectors at approximately 40° and 140° on one axis and the data from the detectors at approximately 90° on the other axis. DCO ratios [22], which distinguish quadrupole and dipole transitions for unknown transitions, were obtained from spectra by gating on either known quadrupole or dipole transitions. In the present array geometry, a DCO ratio of approximately 1.0 corresponds to stretched quadrupole transitions [23] and approximately 0.6 corresponds to pure dipole transitions when gating on a quadrupole transition.
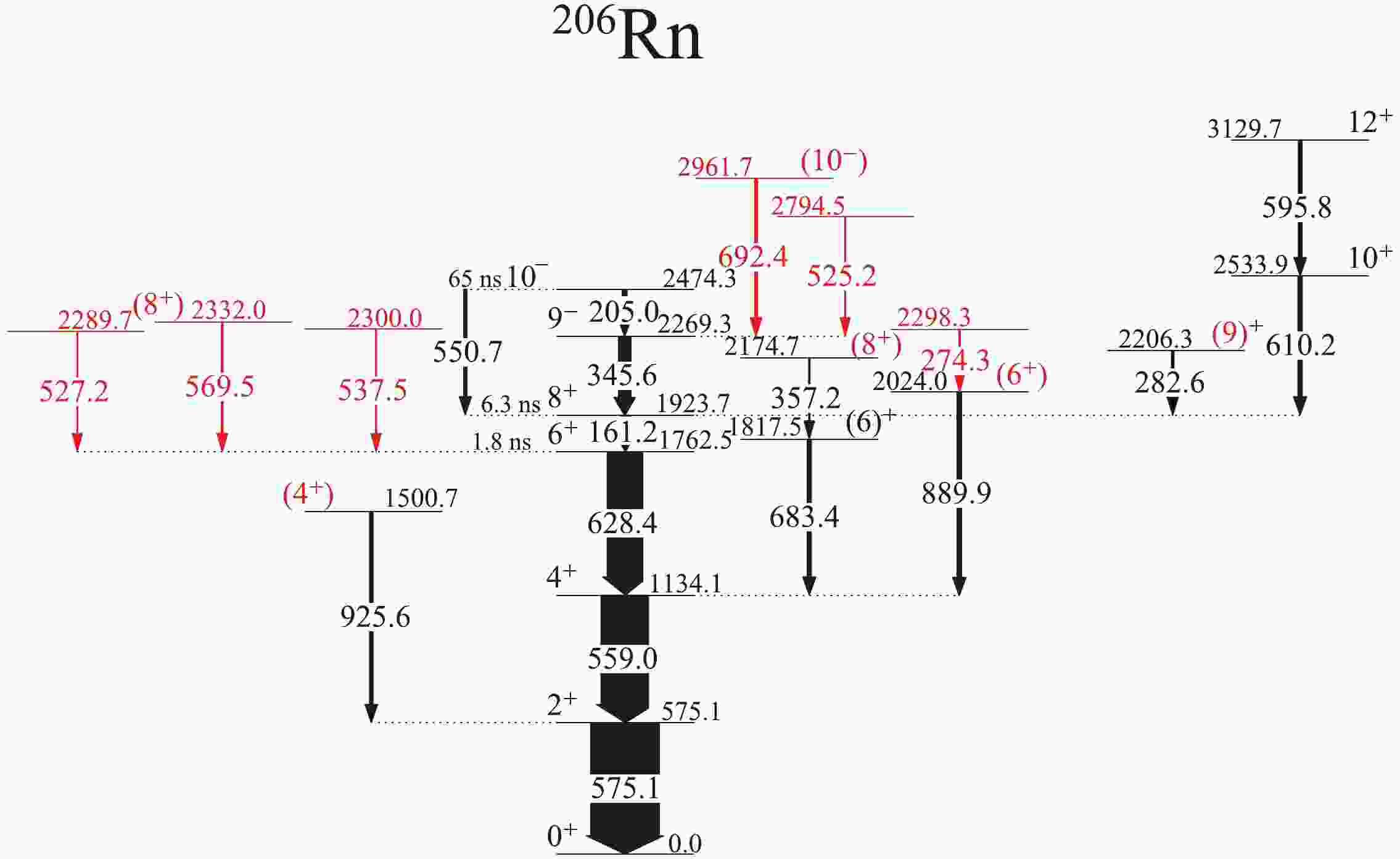
The partial level scheme of
$ ^{206} {\rm{Rn}}$ obtained in the present experiment is shown in Fig. 1. The observed coincidence relationships, intensity balances, and energy sums determined the placement of γ-rays in the level scheme. The energies, relative intensities, and DCO ratios of γ rays, as well as the energies and spin-parities of levels, are summarized in Table 1. In this experiment, the connecting transitions exceeding the 205.0-keV transition in Ref. [18] were difficult to observe, while the other transitions, previously reported [17, 18], were verified by the present data. Additionally, six new transitions in the level scheme (denoted by red arrows in Fig. 1) were added based on γ -γ coincidence analysis. Typical prompt γ -γ coincidence spectra for$ ^{206} {\rm{Rn}}$ are shown in Figs. 2 and 3. In the following, the extensions and corrections for the levels, when compared with the previous study, will be discussed.
Figure 1. (color online) Partial level scheme of
$ ^{206} {\rm{Rn}}$ established in the present study. New transitions and levels are denoted in red. The level and transition energies are provided in keV. The arrow widths are related to the observed γ-ray intensities. Furthermore, the half-lives in Refs. [17, 18] for the isomeric states are indicated.${E}_\gamma$ a /keV

${I}_\gamma$ (relative) b

${R}_{\mathrm{DCO} }$ c

${E}_i$ /keV

${E}_f$ /keV

${J}_i^{\pi}$ 

${J}_f^{\pi}$ 

161.2(3) 14.9(6) 0.82(12) 1923.7 1762.5 8+ 6+ 205.0(4) 6.7(3) 0.69(9) 2474.3 2269.3 10− 9− 274.3*(6) 0.9(1) − 2298.3 2024.0 − (6+) 282.6(4) 2.3(1) 0.66(9) 2206.3 1923.7 (9)+ 8+ 345.6(2) 18.0(6) 0.64(7) 2269.3 1923.7 9− 8+ 357.2(6) 1.5(1) 0.94(12) 2174.7 1817.5 (8+) (6)+ 525.2*(8) 2.3(3) − 2794.5 2269.3 − 9− 527.2*(8) 3.3(3) − 2289.7 1762.5 − 6+ 537.5*(7) 1.3(1) − 2300.0 1762.5 − 6+ 550.7(6) 4.4(2) 0.97(11) 2474.3 1923.7 10− 8+ 559.0(2) 70(2) 0.95(6) 1134.1 575.1 4+ 2+ 569.5*(7) 2.4(2) 1.08(13) 2332.0 1762.5 8+ 6+ 575.1(2) 100(3) 1.00(6) 575.1 0 2+ 0+ 595.8(9) 4.8(4) 1.13(15) 3129.7 2533.9 12+ 10+ 610.2(5) 6.1(5) 1.01(14) 2533.9 1923.7 10+ 8+ 628.4(2) 52(3) 1.00(9) 1762.5 1134.1 6+ 4+ 683.4(4) 5.8(3) 0.98(10) 1817.5 1134.1 (6)+ 4+ 692.4*(5) 4.3(2) 0.66(13) 2961.7 2269.3 (10−) 9− 889.9(5) 6.3(3) 0.92(9) 2024.0 1134.1 (6+) 4+ 925.6(6) 4.9(2) 0.96(16) 1500.7 575.1 (4+) 2+ a The asterisks denote newly identified γ−ray transitions and excited states. b Intensities of transitions are normalized to the 575.1 keV transition. c DCO ratios gated by quadrupole transitions. Table 1. γ-ray energies, relative intensities, measured DCO ratios, initial and final level energies, and initial as well as final spins of transitions in
$^{206}{\rm{Rn}}$ .
Figure 2. (color online) Spectra of γ rays for
$ ^{206} {\rm{Rn}}$ gated on the (a) 575.1 keV, (b) 559.0 keV, (c) 628.4 keV, (d) 161.2 keV, and (e) 889.9 keV transitions. Peaks with parentheses denote contamination. Specifically, contaminated peaks labeled with A, B, C, D, E, and F in the spectra originate from the contaminations of$ ^{109} {\rm{In}}$ [21],$ ^{197} {\rm{Au}}$ [25],$ ^{110} {\rm{Cd}}$ [26],$ ^{207} {\rm{Rn}}$ [19],$ ^{109} {\rm{Cd}}$ [27], and$ ^{110} {\rm{In}}$ [28], respectively. The peak at 629 keV in the 628.4-keV gated spectrum is difficult to attribute to a nucleus.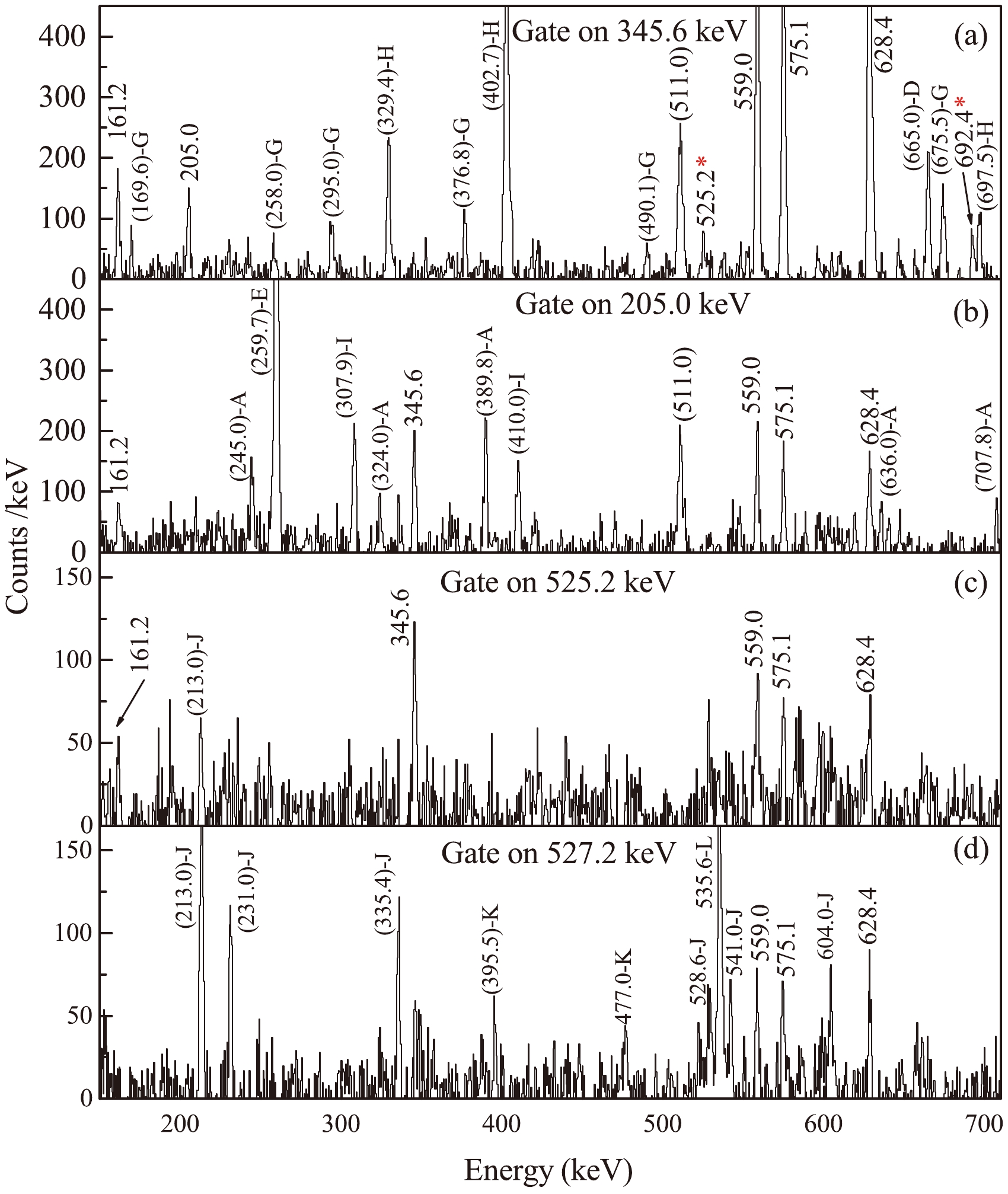
Figure 3. (color online) Spectra of γ rays for
$ ^{206} {\rm{Rn}}$ gated on the (a) 345.6 keV, (b) 205.0 keV, (c) 525.2 keV, and (d) 527.2 keV transitions. Peaks with parentheses denote contamination. Contaminated peaks labeled with G, H, D, A, E, I, J, K, and L in the spectra originate from the contaminations of$ ^{106} {\rm{Ag}}$ [29],$ ^{207} {\rm{At}}$ [30],$ ^{207} {\rm{Rn}}$ [19],$ ^{109} {\rm{In}}$ [21],$ ^{109} {\rm{Cd}}$ [27],$ ^{107} {\rm{Ag}}$ [31],$ ^{108} {\rm{In}}$ [28],$ ^{206} {\rm{Po}}$ [32], and$ ^{100} {\rm{Mo}}$ [33], respectively.The 925.6-keV γ ray, which feeds the 2+ state, was observed in the current study and in the previous study [17] (with an energy of approximately 926.5 keV), but not in Ref. [18]. Similarly, as shown in Fig. 2, the 683.4, 889.9, 357.2, and 282.6 keV transitions (with energies of
$ \approx $ 684, 890.6, 356.0, and 282.6 keV in the previous study [17]) were also observed in this experiment. The DCO ratio of 925.6 keV transition is approximately 0.96, corresponding to a quadrupole transition. Therefore, the spin-parity of the 1500.7 keV state, deexcited by the 925.6 keV γ ray, was proposed to be 4+. In fact, it was suggested as a 4+ based solely on IBA calculations in Ref. [17]. However, a spin of J = (2,3) for 1500.7-keV state was proposed in NNDC [24], with a comment noting that the absence of a direct feeding from the 6+ level at 1763 keV, which is populated in$ ^{206} $ Fr ε decay, would argue against a 4+ assignment. The 889.9-keV transition, deexciting the 2024.0-keV level, has been tentatively assigned an$ E2 $ nature, following the DCO information. Accordingly, the level has been tentatively assigned a spin-parity of 6+. There was no spin-parity assignment for this level, identified as$ \approx $ 2024.9 keV, in the previous study [17]. Similarly, the spin-parity of 2174.7-keV level, deexcited by 357.2-keV transition, was also not assigned in the previous study. Based on the DCO ratio of 357.2 keV transition, the 2174.7-keV level was proposed as 8+ in the present study. The spin-parity of 2206.3-keV level (2206.9 keV in previous study), deexcited by the 282.6 keV transition, was assigned to be (7-9)+ in the previous study [17]. In the present experiment, the 282.6-keV transition is a dipole transition based on its DCO ratio. Additionally, a comparison with neighboring nuclear systems reveals the presence of 9+ states (decaying to 8+ states via γ transitions) in both$ ^{204} {\rm{Po}}$ [8] and$ ^{206} {\rm{Po}}$ [7] nuclei, while no 7+ states are observed. Therefore, the spin-parity of the 2206.3 keV level has been suggested to be 9+.A new 274.3-keV transition is visible in the coincidence spectra gated on the 575.1, 559.0, and 889.9 keV transitions in Figs. 2(a), 2(b), and 2(e), respectively. Therefore, this transition is placed as shown in Fig. 1. Given the low statistics of this transition, the DCO ratio is difficult to obtain; the spin-parity of the 2298.3-keV level has not been assigned. Two new transitions of 537.5 and 569.5 keV are identified in coincidence with the 575.1, 559.0, and 628.4 keV γ rays, as shown in Figs. 2(a)−2(c). Given that there is no coincidence between the two transitions, they were placed above the 1762.5 level. The 569.5-keV transition from the 2332.0-keV state has been identified as a quadrupole transition based on its DCO ratio, and the state has been tentatively assigned a spin-parity of 8+. The DCO ratio of the 537.5 keV transition cannot be obtained because of low statistics. A new 692.4-keV transition is placed above the 2269.3-keV level based on its coincidence relationships, as demonstrated in Figs. 2(a)−2(d) and 3(a). The spin-parity of the 2961.7-keV state, deexcited by this transition, has been tentatively assigned to be 10
$ ^{-} $ based on DCO information and systematics.Two transitions with energies of 525.2 and 527.2 keV are in coincidence with the 575.1,559.0, and 628.4 keV transitions, as demonstrated in Figs. 2(a)−2(c), 3(c), and 3(d). However, the transitions with energies of about 527.8 and 525.5 keV, deexcited from the 3362 and 3888 keV levels respectively, were tentatively identified in a previous study [18]. However, as mentioned earlier, the connecting transitions above the 205.0-keV transition (deexcited from 2474.3 keV) were difficult to observe in the current experiment. Furthermore, as demonstrated in Figs. 2(d), 3(a), 3(c), and 3(d), the 525.2 keV transition is also in coincidence with 161.2- and 345.6-keV transitions, whereas the 527.2-keV transition is not in coincidence with the 161.2- and 345.6-keV transitions. As observed from the 205.0-keV gated spectrum in Fig. 3(b), the absence of peaks at energies of 525.2 and 527.2 keV indicates that the 525.2- and 527.2-keV transitions do not coincide with the 205.0-keV transition. Consequently, we tentatively placed these two transitions as shown in Fig. 1 (denoted in red).
-
To interpret the experimental level structure in
$ ^{206} {\rm{Rn}}$ , we performed the full configuration shell-model calculation with a monopole and multipole optimized effective interaction based on the PBPKH [34] interaction. The PBPKH interaction was initially derived for the single-particle space of$ Z = $ 58−114 and$ N = $ 100−164 shells. However, due to the significantly expansive dimension of the configuration space, our calculations have been constrained to the single-particle space of$ Z = $ 82−114 and$ N = $ 100−126 shells, i.e., the proton orbits,$ 0h_{9/2} $ ,$ 1f_{7/2} $ ,$ 0i_{13/2} $ and the neutron orbits,$ 1f_{5/2} $ ,$ 2p_{3/2} $ ,$ 2p_{1/2} $ ,$ 0i_{13/2} $ , above the$ ^{182} $ Pb core. The dimension of$ M = 0 $ configuration space is$ \sim 3.5 \times 10^8 $ . The calculation was performed by NuShellX [35] and Bigstick [36, 37] codes. The single-particle configurations obtained from our shell-model calculation, along with the level energies, are presented in Table 2. Given that the configuration mixing is important in$ ^{206} {\rm{Rn}}$ , the top two configurations with the highest proportions in the wave function for each state are listed in Table 2. We also calculate the reduced electric quadrupole and magnetic dipole transition probabilities,$ B(E2) $ and$ B(M1) $ , for which we consider the standard effective charges$ (e_{\pi},e_{\nu}) = (1.5e,0.5e) $ and effective g factors$(g_{l\pi},\;g_{l\nu},\;g_{s\pi},\;g_{s\nu}) = (1.1\mu_{\rm N},\;-0.1\mu_{\rm N},\;5.586\mu_{\rm N}\times0.7, -3.826 \mu_{\rm N}\times0.7 )$ . The effective charges and g-factors used are similar to those employed in Refs. [38, 39].${J}^{\pi}$ (ħ)

${E} _\mathrm{exp}$ /keV

${E } _\mathrm{cal}$ /keV

Wave function (π $ \otimes $ ν)

Probability $ 0_{1}^{+} $ 

0 0 4 0 0 $\otimes $ 4 2 0 14

21.83% 4 0 0 $\otimes $ 2 4 0 14

21.42% $ 2_{1}^{+} $ 

575.1 648 4 0 0 $\otimes $ 4 2 0 14

18.85% 4 0 0 $\otimes $ 2 4 0 14

17.67% $ 2_2^{+} $ 

− 1062 4 0 0 $\otimes $ 4 2 0 14

16.56% 4 0 0 $\otimes $ 3 3 0 14

14.62% $ 4_{1}^{+} $ 

1134.1 1118 4 0 0 $\otimes $ 3 3 0 14

21.31% 4 0 0 $\otimes $ 2 4 0 14

14.35% $ 4_{2}^{+} $ 

1500.7 1330 4 0 0 $\otimes $ 3 3 0 14

23.50% 4 0 0 $\otimes $ 2 4 0 14

19.43% $ 6_{1}^{+} $ 

1762.5 1707 4 0 0 $\otimes $ 2 4 0 14

24.76% 4 0 0 $\otimes $ 4 2 0 14

22.85% $ 6_{2}^{+} $ 

1817.5 1801 4 0 0 $\otimes $ 3 3 0 14

32.52% 4 0 0 $\otimes $ 4 2 0 14

13.93% $ 6_{3}^{+} $ 

2024.0 1846 4 0 0 $\otimes $ 4 2 0 14

23.28% 4 0 0 $\otimes $ 2 4 0 14

17.85% $ 7_{1}^{+} $ 

− 2097 4 0 0 $\otimes $ 2 4 0 14

23.90% 4 0 0 $\otimes $ 4 2 0 14

22.06% $ 8_{1}^{+} $ 

1923.7 1773 4 0 0 $\otimes $ 4 2 0 14

26.81% 4 0 0 $\otimes $ 2 4 0 14

25.06% $ 8_{2}^{+} $ 

2174.1 2310 4 0 0 $\otimes $ 2 4 0 14

25.16% 4 0 0 $\otimes $ 4 2 0 14

15.80% $ 8_{3}^{+} $ 

2332.0 2483 4 0 0 $\otimes $ 2 4 0 14

19.97% 4 0 0 $\otimes $ 4 2 0 14

18.71% $ 9_{1}^{+} $ 

2206.3 2514 4 0 0 $\otimes $ 2 4 0 14

27.55% 4 0 0 $\otimes $ 4 2 0 14

14.08% $ 10_{1}^{+} $ 

2533.7 2291 4 0 0 $\otimes $ 4 2 0 14

26.26% 4 0 0 $\otimes $ 2 4 0 14

21.61% $ 12_{1}^{+} $ 

3129.7 2616 4 0 0 $\otimes $ 2 4 0 14

45.61% 4 0 0 $\otimes $ 4 2 0 14

18.11% $ 9_{1}^{-} $ 

2269.3 2213 4 0 0 $\otimes $ 3 4 0 13

23.50% 4 0 0 $\otimes $ 5 2 0 13

17.51% $ 10_{1}^{-} $ 

2474.3 2491 3 0 1 $\otimes $ 2 4 0 14

17.56% 3 0 1 $\otimes $ 4 2 0 14

11.76% $ 10_{2}^{-} $ 

2961.7 2863 4 0 0 $\otimes $ 3 4 0 13

18.98% 4 0 0 $\otimes $ 3 3 1 13

16.37% Table 2. Level energies and single-particle configurations obtained from our shell-model calculation. Only the top two configurations with the highest proportions in the wave function for each state are listed. The fourth column represents the occupation of π(
$ h_{9/2} $ $ f_{7/2} $ $ i_{13/2} $ )$\otimes $ ν($ f_{5/2} $ $ p_{3/2} $ $ p_{1/2} $ $ i_{13/2} $ ) configuration.Additionally, the nucleon-pair approximation (NPA) of the shell model [40−42] has been employed for a more comprehensive understanding of the low-lying structure of
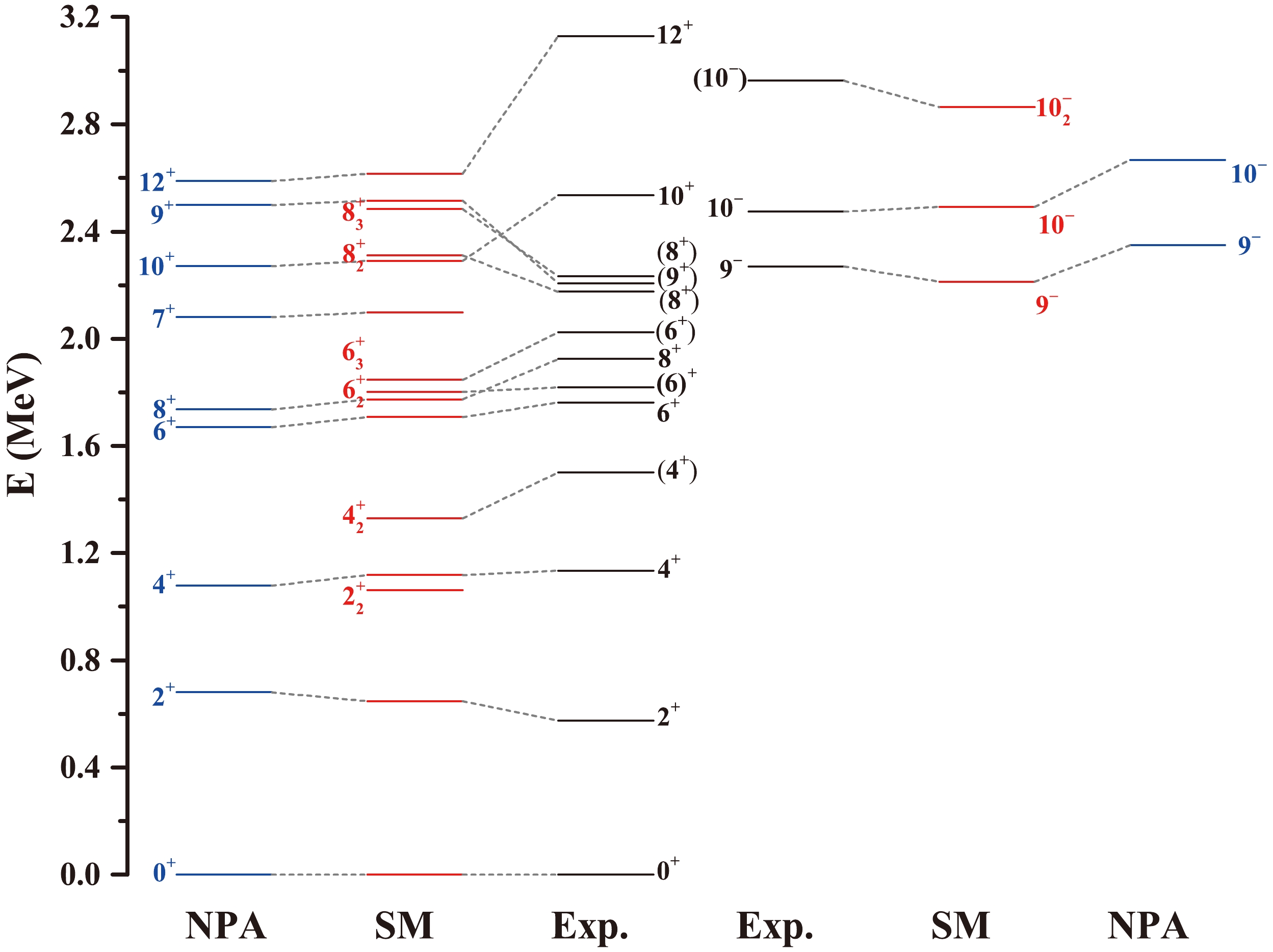
$ ^{206} {\rm{Rn}}$ . The single-particle space and effective interaction are the same as those used in the shell-model calculation. The building blocks of the NPA are collective nucleon pairs with good spin and parity, such as S and D pairs (i.e., collective pairs with spin and parity$ I^{\pi} = 0^+ $ and$ 2^+ $ , respectively). The NPA has been demonstrated to be an efficient approximation for low-lying states of nearly-spherical and transitional nuclei [43], and recently it has been further developed to describe deformed nuclei [44−46]. The detailed theoretical framework of NPA can be found in Ref. [43]. In the NPA calculation presented in this study, we incorporate the high-spin even-parity G, I, and K pairs (i.e., collective pairs with$ I^{\pi} = 4^+,6^+ $ , and$ 8^+ $ , respectively), as well as the odd-parity L and M pairs (i.e.,$ I^{\pi} = 9^- $ and$ 10^- $ , respectively), in addition to considering the transitional$ SD $ pairs. The comparison of the energy levels between shell-model and NPA calculations and experimental data is presented in Fig. 4. As shown in Fig. 4, the level energies obtained by both the shell model and NPA are in agreement with the experimental data, with discrepancies of approximately 100 keV for certain states with the exception of$ J^{\pi} = $ $ 12^{+} $ . -
First, let us begin our discussion with the results of the even-parity states in
$ ^{206} {\rm{Rn}}$ obtained from the shell model. For the level energies of$ 0_1^+ $ ,$ 2_1^+ $ ,$ 4_1^+ $ ,$ 6_1^+ $ , and$ 8_1^+ $ states, the shell-model calculation is in good agreement with the experimental data. The top two single-particle configurations with the highest proportions in$ 0_1^{+} $ and$ 2_1^{+} $ states are π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^4_{5/2}p^2_{3/2}) $ and π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^2_{5/2}p^4_{3/2}) $ . For the$ 4_1^{+} $ state, the configurations are π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^3_{5/2}p^3_{3/2}) $ and π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^2_{5/2}p^4_{3/2}) $ . The former configuration implies the occurrence of a neutron excitation from$ p_{3/2} $ to$ f_{5/2} $ . The configurations for the$ 6_1^{+} $ state are π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^2_{5/2}p^4_{3/2}) $ and π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^4_{5/2} $ $ p^2_{3/2}) $ , and those for the$ 8_1^{+} $ state are π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^4_{5/2} $ $ p^2_{3/2}) $ and π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^2_{5/2}p^4_{3/2}) $ . The dominant configurations in the$ 6_1^{+} $ and$ 8_1^{+} $ states do not exhibit the situation in the$ 4_1^{+} $ state, where$ 1f_{5/2} $ and$ 2p_{3/2} $ orbitals each occupy three neutrons. It is important to note that a measurement of the g-factor for the$ 8^{+} $ isomer in$ ^{206} {\rm{Rn}}$ , as reported in Ref. [5], supports$\pi (h^2_{9/2})_{8^+}$ configuration. This indicates the coupling of angular momentum$ J = 8$ from two unpaired protons on$ 0h_{9/2} $ orbital. Furthermore,$ B(E2) $ values, along with the corresponding half-lives, obtained from experimental data and our calculation, are listed in Table 3. Although the calculated half-lives of$ 6_1^{+} $ and$ 8_1^{+} $ states differ from the experimental data by nearly one order of magnitude, our calculations indicate that these two states have relatively long half-lives, suggesting their isomeric nature.${J} _i^{\pi}$ 

$ \rightarrow $ 

${J} _f^{\pi}$ (ħ)

$ \delta E_{\mathrm{expt}} $ a /MeV

$ B(E2)_{\mathrm{SM}} $ 

$ e^2 $ fm4

$ B(E2)_{\mathrm{NPA}} $ 

$ e^2 $ fm4

$ [T_{1/2}]_{\mathrm{expt}} $/ns 

$ [T_{1/2}]_{\mathrm{SM}} $ /ns

$ [T_{1/2}]_{\mathrm{NPA}} $ /ns

$2 _1^{+} $ 

$ \rightarrow $ 

$0 _1^{+} $ 

− 575 502 − − − $4 _1^{+} $ 

$ \rightarrow $ 

$2 _1^{+} $ 

− 187 214 − − − $6 _1^{+} $ 

$ \rightarrow $ 

$4 _1^{+} $ 

0.6284 37.1 9.10 1.8(13) [17] 0.156 0.633 $8 _1^{+} $ 

$ \rightarrow $ 

$6 _1^{+} $ 

0.1612 44.4 33.9 6.3(24) [17] / 19(3) [18] 116 152 $10 _1^{+} $ 

$ \rightarrow $ 

$8 _1^{+} $ 

− 597 510 − − − ${\rm{J}} _i^{\pi} $ 

$ \rightarrow $ 

${\rm{J}} _f^{\pi} $ 

$ \delta E_{\mathrm{expt}} $ a

$ B(M1)_{\mathrm{SM}} $ 

$ B(M1)_{\mathrm{NPA}} $ 

$ [T_{1/2}]_{\mathrm{expt}} $ 

$ [T_{1/2}]_{\mathrm{SM}} $ 

$ [T_{1/2}]_{\mathrm{NPA}} $ 

ħ MeV $ \mu_N^2 $ 

$ \mu_N^2 $ 

ns ns ns $10 _1^{-} $ 

$ \rightarrow $ 9

$ _1^{-} $ 

0.205 $ 5.64 \times 10^{-6} $ 

$ 1.65 \times 10^{-5} $ 

65(5) [17] 811 277 a Utilized for calculating the theoretical half-life. Table 3.
$ B(E2) $ and$ B(M1) $ values calculated by the shell model (SM) and nucleon-pair approximation (NPA), as well as the theoretical half-lives ($ [T_{1/2}]_{\mathrm{SM}} $ ,$ [T_{1/2}]_{\mathrm{NPA}} $ ) and experimental half-lives ($ [T_{1/2}]_{\mathrm{expt}} $ ).Regarding the calculation of other even-parity states, the 1500.7-keV state deexcited by the 925.6 keV transition is in good agreement with the
$ 4_2^{+} $ state calculated by the shell model, with a difference of within$ \approx $ 200 keV as shown in Table 2. The difference between this state and calculated$ 2_2^{+} $ state is relatively large. Therefore, the assignment of the spin-parity of the 1500.7 keV state to$ 4^{+} $ , as mentioned in Sec. II, is supported. The top two single-particle configurations for this state are π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^3_{5/2} $ $ p^3_{3/2}) $ and π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^2_{5/2}p^4_{3/2}) $ . The calculated$ 6_2^{+} $ and$ 6_3^{+} $ states are in excellent overlap, within 200 keV, with the corresponding experimental states (with energies of 1817.5 and 2024.0 keV, respectively). The top two configurations of the$ 6_2^{+} $ state are π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^3_{5/2} $ $ p^3_{3/2}) $ and π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^4_{5/2} $ $ p^2_{3/2}) $ . For the$ 6_3^{+} $ state, the configurations are π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^4_{5/2} $ $ p^2_{3/2}) $ and π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^2_{5/2}p^4_{3/2}) $ . For the 2206.3 keV level, deexcited by the 282.6 keV transition, the energies of$ 7_1^{+} $ and$ 9_1^{+} $ states, calculated by the shell model are within a reasonable range of the experimental energy. Therefore, the spin of this level cannot be confirmed by calculation. The 2174.7 and 2332.0-keV states with spin-parity$ 8^{+} $ proposed in this study are accurately predicted by the calculation, with the theoretical values differing from the experimental values within about 150 keV. The dominant configurations of these two states are π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^2_{5/2} $ $ p^4_{3/2}) $ and π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^4_{5/2}p^2_{3/2}) $ . The calculated energy of the$ 10^{+} $ state differs from its experimental value by approximately 250 keV. The dominant configurations of this state are π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^4_{5/2} $ $ p^2_{3/2}) $ and π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^2_{5/2}p^4_{3/2}) $ . Unfortunately, as mentioned earlier, the calculated$ 12^{+} $ state has a large discrepancy with the experimental value.Now, let us shift our focus to the results of the odd-parity states obtained from the shell model. The calculated energies of
$ 9_1^{-} $ and$ 10_1^{-} $ states are in good agreement with the experimental data, differing by less than 100 keV. Additionally, as shown in Table 3, the magnetic dipole reduced transition probability$ B(M1) $ for the$ 10_1^{-} $ $ \rightarrow $ $ 9_1^{-} $ transition, calculated in the shell model, is exceedingly small. This results in a long half-life for the$ 10_1^{-} $ isomer. The configurations with significantly high proportions of the$ 9_1^{-} $ state are π$ (h^4_{9/2})\otimes $ ν$ (f^3_{5/2}p^4_{3/2}i^{13}_{13/2}) $ and π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^5_{5/2} $ $ p^2_{3/2} $ $ i^{13}_{13/2}) $ , while the configurations with the highest proportions of the$ 10_1^{-} $ state are π$ (h^3_{9/2}i^1_{13/2}) $ $ \otimes $ ν$ (f^2_{5/2}p^4_{3/2}) $ and π$ (h^3_{9/2}i^1_{13/2}) $ $ \otimes $ ν$ (f^4_{5/2}p^2_{3/2}) $ . The configurations obtained by calculation reveal that a neutron excitation in the$ i_{13/2} $ orbit forms a hole state for$ 9_1^{-} $ state, whereas a proton excitation on the$ i_{13/2} $ orbit forms a particle state for$ 10_1^{-} $ state. A systematic comparison of neighboring nuclei reveals that the energy level structure of$ 9_1^{-} $ and$ 10_1^{-} $ states in$ ^{206} {\rm{Rn}}$ is very similar to that in$ ^{208} {\rm{Rn}}$ [6], with both exhibiting an$ M2 $ transition from$ 10_1^{-} $ state to$ 8_1^{+} $ state. Additionally, the shell-model calculations of$ ^{208} {\rm{Rn}}$ in Ref. [6] show that the configurations of$ 9_1^{-} $ and$ 10_1^{-} $ states are similar to those calculated in this study for$ ^{206} {\rm{Rn}}$ . This type of a structure is also observed in other neighboring nuclei. As observed from Fig. 5, the energy levels of the$ 9_1^{-} $ and$ 10_1^{-} $ states in$ ^{204,206,208} {\rm{Rn}}$ gradually increase with the increase in the neutron number. Furthermore,$ 9_1^{-} $ states in$ ^{202,204,206} {\rm{Po}}$ also increase gradually with the increase in the neutron number, and they are very close to the excitation energies of$ 9_1^{-} $ states in Rn isotopes. The newly observed$ 10^{-} $ state at 2961.7 keV in this experiment aligns well with the corresponding theoretical value from shell-model calculations, with a difference of approximately 100 keV. The configurations with significantly higher components in the calculations are π$ (h^4_{9/2})\otimes $ ν$ (f^3_{5/2}p^4_{3/2} $ $ i^{13}_{13/2}) $ and π$ (h^4_{9/2}) $ $ \otimes $ ν$ (f^4_{5/2} $ $ p^3_{3/2} $ $ i^{13}_{13/2}) $ .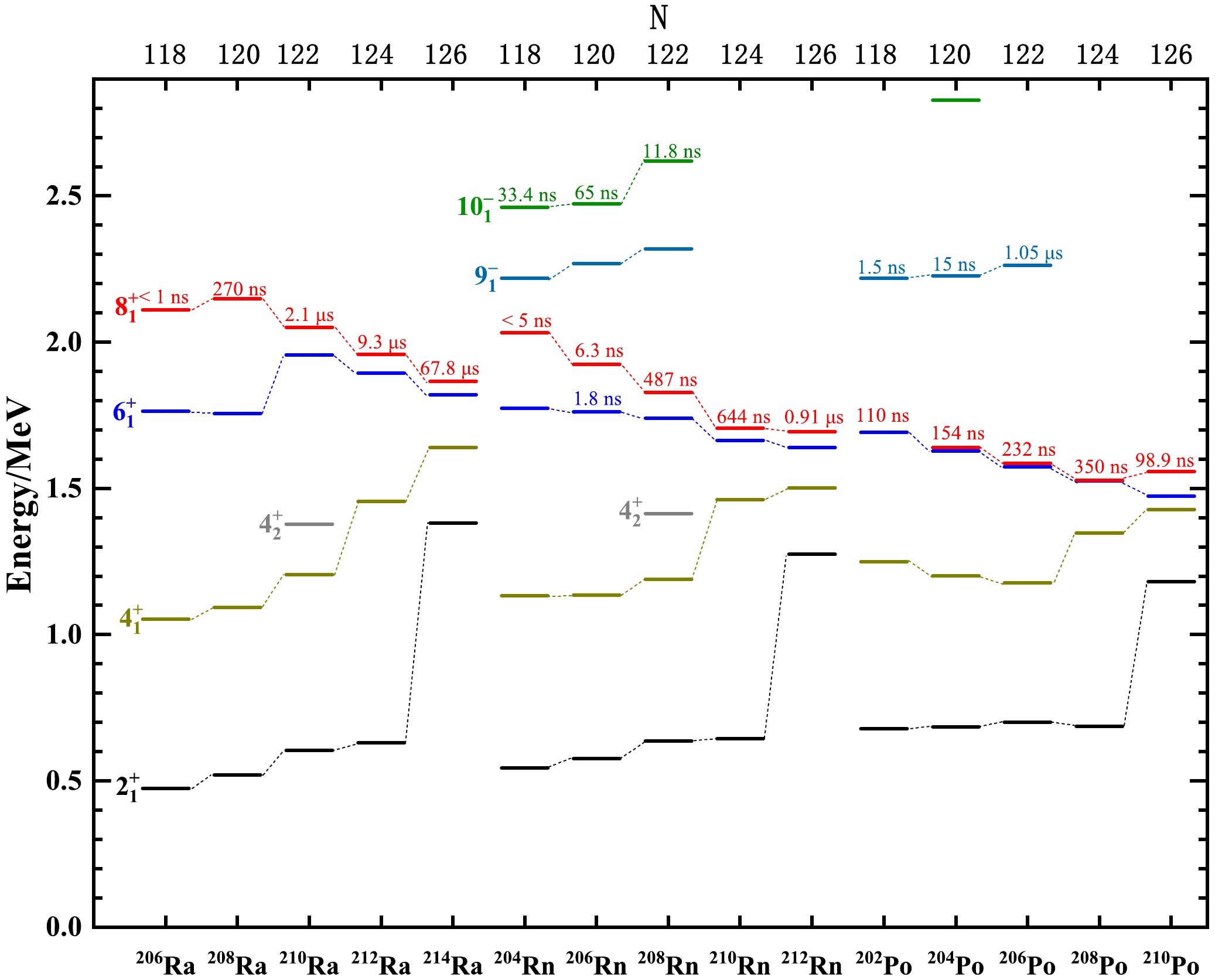
Figure 5. (color online) Systematics of selected energy levels and half-lives of
$ 8^{+} $ states in even-even$ _{88} $ Ra,$ _{86} {\rm{Rn}}$ , and$ _{84} {\rm{Po}}$ isotopes with$ N = 118 - 126 $ . The experimental data are sourced from NNDC [47]. -
In the previous section, we showed that the level energies calculated by the shell model are in good agreement with the experimental data. We also presented several important single-particle configurations in the state wave functions. Unfortunately, these configurations do not significantly enhance our understanding of the nuclear structure of these states. In this section, we will discuss the results of our NPA calculation, highlighting the coexistence of collectivity and seniority isomerism, and the interchange of neutron- versus proton-pair breaking in low-lying states of
$ ^{206} {\rm{Rn}}$ .As shown in Fig. 4, the level energies calculated by the NPA are reasonably close to those calculated by the shell model and experimental data. The dominant configurations in the yrast state wave functions are as follows:
$ |0_1^+\rangle:0.89|0\rangle $ $ |2_1^+\rangle:0.73|D_\nu\rangle,\; 0.51|D_\pi\rangle $ $ |4_1^+\rangle:0.71|G_\nu\rangle,\; -0.27|G_\pi\rangle $ $ |6_1^+\rangle:0.84|I_\pi\rangle $ $ |8_1^+\rangle:0.84|K_\pi\rangle $ $ |10_1^+\rangle:0.73|D_\nu K_\pi\rangle,\; 0.44|D_\pi K_\pi\rangle $ $ |9_1^-\rangle:0.80|L_\nu\rangle $ $ |10_1^-\rangle:0.48|M_\pi\rangle $ Here, we use
$ |0\rangle $ to denote the S-pair condensate, characterized by generalized seniority zero. For simplicity, we refer to generalized seniority as simply “seniority” in subsequent discussions. We use$ |D_\nu\rangle $ to denote the state in which one neutron S pair is broken to form a neutron D pair, while other S pairs remain unbroken, corresponding to seniority two. We use$ |D_\nu K_\pi\rangle $ to denote the state in which one neutron S pair and one proton S pair are broken to form a neutron D pair and proton K pair, respectively, which corresponds to seniority four. Other notations used in this context can be understood in a similar manner. We observe that$ 0_1^+ $ state of$ ^{206} {\rm{Rn}}$ has a 79% component of a seniority-zero state. Furthermore,$ 2_1^+ $ and$ 4_1^+ $ states exhibit$ \sim $ 50% components of a seniority-two state with a broken neutron pair, alongside small yet nonnegotiable components of a seniority-two state with a broken proton pair. This configuration mixing is due to residual proton-neutron interactions. Consequently, the spectral structure of$ 0_1^+ $ ,$ 2_1^+ $ , and$ 4_1^+ $ states follows the behavior of collective vibrational motion, as discussed further in Sec. IV. It is worth noting that the scenario of configuration mixing between the seniority-two state with a broken neutron pair and that with a broken proton pair has also been discussed for$ ^{204,206} {\rm{Po}}$ in Ref. [1] based on the empirical two-state mixing calculation. Remarkably,$ 6_1^+ $ and$ 8_1^+ $ states in$ ^{206} {\rm{Rn}}$ are primarily characterized by a seniority-two state with a broken proton pair, exhibiting a subtle configuration mixing effect. This phenomenon explains the reason for the close values of level energies of$ 6_1^+ $ and$ 8_1^+ $ states, a typical feature of seniority two.Another intriguing aspect is that although both
$ 6_1^+ $ and$ 8_1^+ $ states are isomers, the reasons for their isomerism differ. While the long half-life of the$ 8_1^+ $ state can be explained by the typical seniority-two feature, our NPA calculation indicates that the long half-life of$ 6_1^+ $ state arises because it is dominated by a seniority-two state with a broken proton pair. However,$ 4_1^+ $ state has its main component with a broken neutron pair. This difference in structure results in a very small$ B(E2) $ between them, consequently leading to the long half-life of$ 6_1^+ $ state.Above the seniority-two states, the NPA calculation shows that
$ 10_1^+ $ state is primarily composed of seniority-four states, comprising a$ \sim $ 50% component with a broken neutron pair and broken proton pair, along with a smaller but nonnegotiable component with two broken proton pairs. As listed in Table 3, the shell model and NPA calculations of the$ B(E2) $ for the transition from$ 10_1^+ $ to$ 8_1^+ $ state are comparable to those for the transition from the$ 2_1^+ $ to$ 0_1^+ $ state, representing typical$ B(E2) $ transitions between states with seniority differences equal to 2.As shown in Fig. 4, the NPA reasonably reproduces
$ 9_1^- $ and$ 10_1^- $ states. The$ 9_1^- $ state is predominantly characterized by a seniority-two state, in which the two unpaired neutrons contribute to$ I^{\pi} = 9^- $ . This result suggests that the angular momentum of the$ 9_1^- $ state primarily originates from neutron-pair breaking, aligning with the conclusions drawn from the shell model calculation. The calculated composition of$ 10_1^- $ state reveals a strong configuration mixing, with only 23% of the components comprising a seniority-two state, in which the two unpaired protons contribute to$ I^{\pi} = 10^- $ , a significant contribution of angular momentum from proton-pair breaking. This is consistent with the shell-model calculated results. Combining the calculations of the shell model provides a good explanation for the formation of the isomeric$ 10_1^- $ state. Furthermore, NPA calculations successfully reproduce the half-life of the$ 10_1^- $ isomer, albeit slightly higher than the experimental value. -
In this section, we investigate the systematics of low-lying energy levels in the even-even Po-Rn-Ra isotopes with
$ N = $ 118−126. The evolution of$ 2_1^{+} $ and$ 4_1^{+} $ energy levels in even-even nuclei reflects to a certain extent the changes in collectivity, with lower energy levels potentially indicating an enhancement of collectivity. As shown in Fig. 5,$ 2_1^{+} $ energy levels in the Po-Rn-Ra isotopes show a gradual increase with the increase in neutron number, with a sudden enhancement at$ N = $ 126. The rate of increase for the$ 2_1^{+} $ energy levels decreases as the proton number decreases. In the case of Po isotopes, the increase in the$ 2_1^{+} $ energy levels is less pronounced, and a minor drop is observed at$ N = $ 124. For the$ 4_1^{+} $ energy levels, the isotopes of Rn show a gradual increase with an increasing neutron number, with this trend being more pronounced in the Ra isotopes. The evolution of the$ 2_1^{+} $ and$ 4_1^{+} $ energy levels indicates that as neutrons depart from the$ N = 126 $ closed shell, the collectivity of low-lying states, particularly in the Rn and Ra isotopes, may gradually emerge and enhance. Similarly, for a fixed neutron number N in the range of 118−124, as the proton number increases and deviates from the$ Z = 82 $ closed shell, the$ 2_1^{+} $ energy levels decrease, potentially indicating an emergence and strengthening of collectivity. It is noteworthy that in Rn and Ra nuclei, with$ N = $ 122, two$ 4^{+} $ states have been observed [6, 11]. Although the higher energy$ 4_2^{+} $ state approximates a seniority-two state with proton pair breaking, the lower energy$ 4_1^{+} $ state does not represent a pure seniority-two state.Figure 6 presents the energy ratio
$ R_{4/2} $ $ \equiv $ $ E(4_1^{+})/E(2_1^{+}) $ for Po, Rn, and Ra nuclei as a function of neutron number. This ratio serves as a useful tool for approximately evaluating the collectivity of even-even nuclei. For instance, a seniority structure yields an$ R_{4/2} $ value of approximately 1.4, vibrational nuclei are typically associated with a value of 2, and the ratio tends to asymptotically approach 3.33 for rotational nuclei. As shown in Fig. 6, the value for$ R_{4/2} $ is 1.2 for the semimagic nuclei with$ N = 126 $ . In the range of$ N = $ 112−122,$ R_{4/2} $ values for Po-Rn-Ra isotopes gradually increase as the neutron number deviates from 126, again indicating a gradual enhancement of collectivity. The average$ R_{4/2} $ value for Rn and Ra isotopes is approximately 2, suggesting a vibrational nature of collectivity. Notably,$ R_{4/2} $ exhibits unexpectedly larger values at$ N = $ 124. This ambiguity can arise from the possibility that$ 4^{+} $ state is a seniority-two state, while$ 2^{+} $ state retains its collective nature. Further experimental and theoretical investigations are warranted to substantiate this possibility.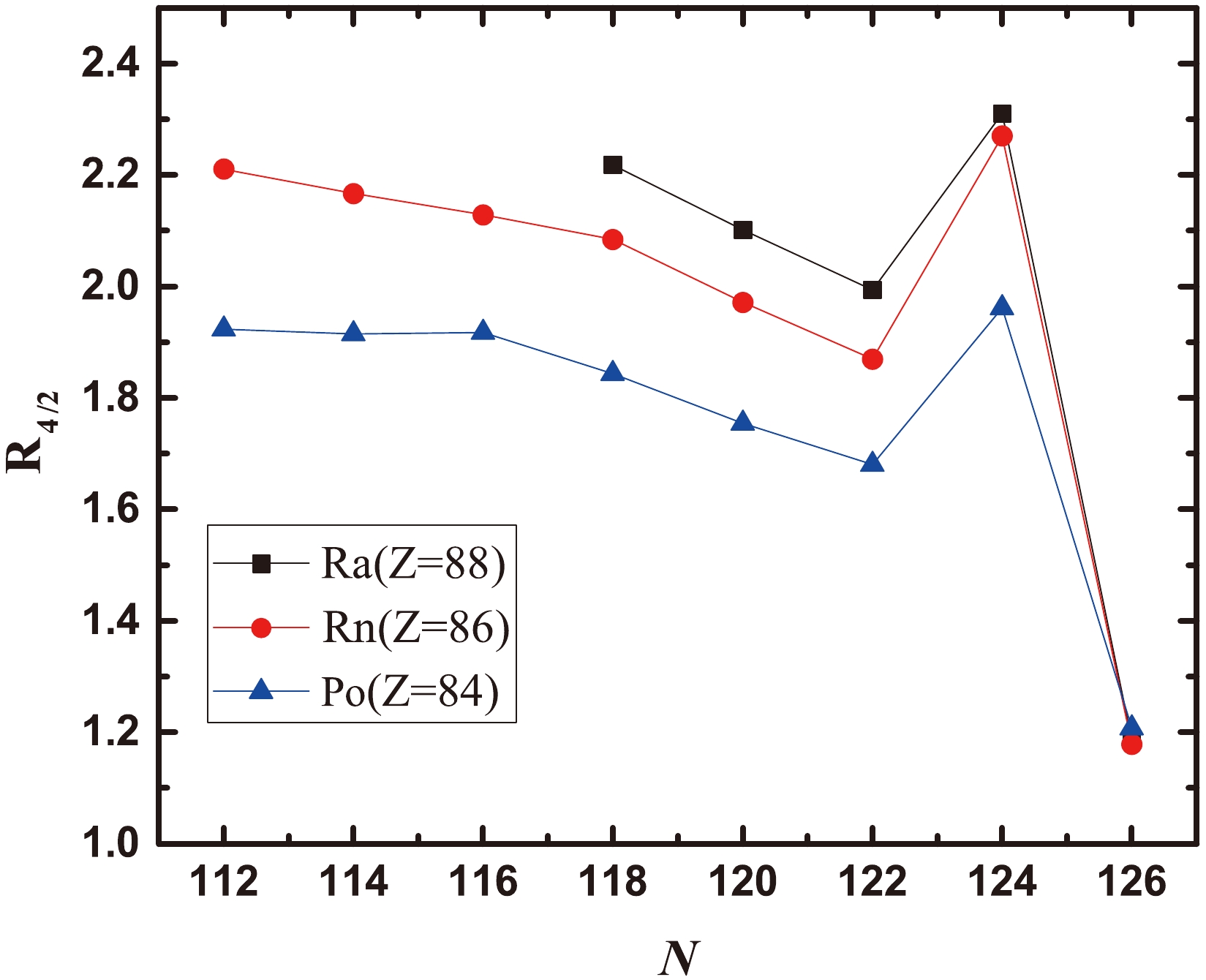
Figure 6. (color online) Evolution of
$ R_{4/2} $ values, where$ R_{4/2} $ $ \equiv $ $ E(4_1^{+})/E(2_1^{+}) $ , for Po, Rn, and Ra nuclei as a function of the neutron number.As depicted in Fig. 5, with the exception of
$ ^{206} $ Ra and$ ^{210} {\rm{Po}}$ , the evolution of$ 6_1^{+} $ and$ 8_1^{+} $ energy levels for Po-Rn-Ra isotopes is similar, exhibiting a gradual decrease as the neutron number increases. When the neutron number is constant, these levels also gradually decrease with decreasing proton numbers. Additionally, the half-lives of the$ 8_1^{+} $ states in Po-Rn-Ra isotopes generally decrease as the neutron number decreases. The$ B(E2) $ values for the$ 8_1^{+} $ $ \rightarrow $ $ 6_1^{+} $ transition in Ra isotopes also gradually decrease with decreasing neutron number, with$ ^{206} $ Ra exhibiting relatively larger$ B(E2) $ values [9]. Combining the theoretical calculations from Sec. III, it can be inferred that for Po-Rn-Ra isotopes with neutron numbers between 118 and 126, the$ 6_1^{+} $ and$ 8_1^{+} $ states can still be approximated as seniority-two states. However, as the neutron number decreases, the collectivity increases, which in turn weakens the seniority-two characteristics. For Ra isotopes with$ N \le 118 $ ,$ 6_1^{+} $ and$ 8_1^{+} $ states may not be adequately described simply by seniority-two states any more. Further theoretical calculations and experimental lifetime measurements are required to better understand the evolution from seniority to collectivity in the Po-Rn-Ra isotopes. -
The level scheme of
$ ^{206} {\rm{Rn}}$ has been revised and enriched via the reaction$ ^{197} {\rm{Au}}$ ($ ^{14} {\rm{N}}$ , 5n) at a 78-MeV beam energy. The spin-parities of several known and newly identified levels in$ ^{206} {\rm{Rn}}$ have been proposed based on DCO ratios and systematic analysis. The full configuration shell-model and NPA calculations were performed to interpret the observed excited states in$ ^{206} {\rm{Rn}}$ . Notably, the shell-model and NPA calculations reproduced$ 6^{+} $ ,$ 8^{+} $ , and$ 10^{-} $ isomers in$ ^{206} {\rm{Rn}}$ . The calculated results indicate that$ 9^{-} $ state primarily arises from a neutron$ i_{13/2} $ orbital excitation forming a hole state, while the$ 10^{-} $ state primarily originates from a proton$ i_{13/2} $ orbital excitation forming a particle state. Furthermore,$ 2_1^{+} $ and$ 4_1^{+} $ states appear to exhibit vibrational motion. This behavior is attributed to the configuration mixing of neutron- and proton-pair breaking, which is a result of residual proton-neutron interactions, according to shell model and NPA calculations. Additionally,$ 2_1^{+} $ and$ 4_1^{+} $ states cannot simply be approximated as pure seniority-two states. Our calculations indicate that the primary contributors to the angular momentum in$ 6_1^{+} $ and$ 8_1^{+} $ states are protons. These states can be approximately represented by a seniority-two state with proton-pair breaking. Furthermore, we investigated the systematics of low-lying energy levels in the Ra-Rn-Po isotopes. We showed that for these isotopes, the collective motion gradually emerges and intensifies in the$ 2^{+} $ and$ 4^{+} $ states as the nuclei deviate from the closed shells at$ N = 126 $ and Z = 82. Meanwhile, the$ 6^{+} $ and$ 8^{+} $ states may continue to exhibit characteristics of seniority-two states. -
We are grateful to the crew of the HI-13 tandem accelerator at the China Institute of Atomic Energy for their help in steady operation of the accelerator and for preparing the target.
Investigating the level structure of 206Rn: evolution from seniority regime to collective dynamics
- Received Date: 2024-06-14
- Available Online: 2024-11-15
Abstract: Excited states of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: