-
Following the discovery of the Higgs boson in 2012 [1, 2], the precision study of its properties has rapidly become one of the centerpieces of the physics program at the LHC. The expansion of this program beyond the LHC has become one of the key motivators for proposed future accelerators, including lepton colliders such as CEPC [3, 4], FCC-ee [5], ILC [6, 7], and CLIC [8, 9] that would operate in part as Higgs factories.
The potential gains of a precision Higgs program pursued at both the LHC and future colliders are innumerable. Confirmation of the Standard Model predictions for Higgs properties would mark a triumphant validation of the theory and illuminate phenomena never before seen in Nature. The observation of deviations from the Standard Model predictions, on the other hand, would point the way directly to additional physics beyond the Standard Model. Such deviations could take the form of changes in the Higgs couplings to itself or other Standard Model states, or they could appear as exotic decay modes not predicted by the Standard Model. The latter possibility has been extensively explored for prompt exotic decay modes in the context of both the LHC (see e.g. [10, 11]) and future Higgs factories [12].
However, an equally compelling possibility is for new physics to manifest itself in exotic decays of the Higgs boson to long-lived particles (LLPs). Such signals were first considered in the context of Hidden Valleys [13-15] and subsequently found to arise in a variety of motivated scenarios for physics beyond the Standard Model, including solutions to the electroweak hierarchy problem [16] and models of baryogenesis [17]; for an excellent recent overview, see [18]. The search for exotic Higgs decays into LLPs necessarily involves strategies outside the scope of typical analyses. The non-standard nature of these signatures raises the compelling possibility of discovering new physics that has been heretofore concealed primarily by the novelty of its appearance.
There is a rich and rapidly growing program of LLP searches at the LHC. A variety of existing searches by the ATLAS, CMS, and LHCb collaborations (e.g. [19-21]; for a recent review see [22]) constrain Higgs decays into LLPs at roughly the percent level across a range of LLP lifetimes. Significant improvements in sensitivity are possible in future LHC runs with potential advances in timing [23], triggers [24-26], and analysis strategies [27, 28]. Most notable among these is the possible implementation of a track trigger [24, 25], which would significantly lower the trigger threshold for Higgs decays into LLPs and potentially allow sensitivity to branching ratios of the order of
$ 10^{-6} $ in zero-background scenarios.While studies of prompt exotic Higgs decays at future colliders [12] have demonstrated the potential for significantly improved reach over the LHC, comparatively little has been said about the prospects for constraining exotic Higgs decays to long-lived particles at the same facilities①. In this work we take a first step towards filling this gap by studying the sensitivity of
$ e^+ e^- $ Higgs factories to hadronically-decaying new particles produced in exotic Higgs decays with decay lengths ranging from microns to meters. For the sake of definiteness we restrict our attention to circular Higgs factories operating at or near the peak rate for the Higgsstrahlung process$ e^+e^- \to hZ $ , namely CEPC and FCC-ee, while also sketching the corresponding sensitivity for the$ \sqrt{s} = 250 $ GeV stage of ILC. While essentially all elements of general-purpose detectors may be brought to bear in the search for long-lived particles, the distribution of decay lengths for a given average lifetime makes it advantageous to exploit detector elements close to the primary interaction point. We thus focus on signatures that can be identified in the tracker. In order to provide a faithful forecast accounting for realistic acceptance and background discrimination, we employ a realistic (at least at the level of theory forecasting) approach to the reconstruction and isolation of secondary vertices.A key question is the extent to which future Higgs factories can improve on the LHC sensitivity to Higgs decays to LLPs, insofar as the number of Higgs bosons produced at the LHC will outstrip that at the proposed Higgs factories by more than two orders of magnitude. Higgs decays to LLPs are sufficiently exotic that appropriate trigger and analysis strategies at the LHC should compensate for the higher background rate and messier detector environment. As we will see, there are two natural avenues for improved sensitivity at future lepton colliders: improved vertex resolution potentially increases sensitivity to LLPs with relatively short lifetimes, while lower backgrounds and a cleaner detector environment improves sensitivity to Higgs decays into lighter LLPs whose decay products are collimated.
The manuscript is organized as follows: In Section 2, we present a simplified signal model for Higgs decays into pairs of long-lived particles, which in turn travel a macroscopic distance before decaying to quark pairs. We further detail the components of our simulation pipeline and lay out an analysis strategy aimed at eliminating the majority of the Standard Model backgrounds. In Section 3, we translate this analysis strategy into the sensitivity of future lepton colliders to long-lived particles produced in Higgs decays as a function of the exotic Higgs branching ratio and the mass and decay length of the LLP. While these forecasts are generally applicable to any model giving rise to the signal topology, we additionally interpret the forecasts in terms of the parameter space of several motivated models in Section 4. We summarize our conclusions and highlight avenues for future development in Section 5.
-
Exotic decays of the Higgs to long-lived particles encompass a wide variety of intermediate and final states. The decay of the Higgs itself into LLPs can proceed through a variety of different topologies. Perhaps the most commonly-studied scenario is the decay of the Higgs into a pair of LLPs,
$ h \rightarrow XX $ , though decays involving additional visible or invisible particles (such as$ h \rightarrow X + {\rm invisible} $ , or$ h \rightarrow XX + {\rm invisible} $ ) are also possible. The long-lived particles in turn may have a variety of decay modes back to the Standard Model, including$ X \rightarrow \gamma \gamma, jj, \ell \bar \ell, $ or$ jj \ell, $ including various flavor combinations. These decay modes may also occur in the company of additional invisible states. Moreover, a given long-lived particle may possess a range of competing decay modes, as is the case for LLPs whose decays back to the Standard Model are induced by mixing with the Higgs.Our aim here is to be representative, rather than comprehensive, as each production and decay mode for a long-lived particle is likely to require a dedicated search strategy. For the purposes of this study, we adopt a simplified signal model in which the Higgs decays into a pair of long-lived scalar particles
$ X $ of mass$ m_X $ , which each decay in turn to pairs of quarks at an average "proper decay length"$ c \tau $ ①. Both the mass$ m_X $ and proper decay length$ c \tau $ are treated as free parameters, though they may be related in models that give rise to this topology. For the sake of definiteness, for$ m_X > 10 $ GeV , we take a branching ratio of$ 0.8 $ to$ b \bar b $ and equal branching ratios of$ 0.05 $ to each of$ u \bar u, d \bar d, s \bar s, c \bar c $ , though the precise flavor composition is not instrumental for our analysis. For$ m_X \leqslant 10 $ GeV , we take equal branching ratios into each of the lighter quarks. We further restrict our attention to Higgs factories operating near the peak of the$ e^+e^- \to hZ $ cross section, for which the dominant production process will be$ e^+e^- \to hZ $ followed by$ h \rightarrow XX $ . The associated$ Z $ boson provides an additional invaluable handle for background discrimination. Here, we develop the conservative approach of focusing on leptonic decays of the$ Z $ , though added sensitivity may be obtained by incorporating hadronic decays.Given the signal, there are a variety of possible analysis strategies sensitive to Higgs decays to long-lived particles, exploiting various parts of a general-purpose detector. Tracker-based searches are optimal for decay lengths below one meter, with sensitivity to shorter LLP decay lengths all the way down to the tracker resolution. Timing information, using timing layers between the tracker and electromagnetic calorimeter, offers optimal coverage for slightly longer decay lengths, while searches for isolated energy deposition in the electromagnetic calorimeter, hadronic calorimeter, and muon chambers provide sensitivity to decay lengths of the order of meters to tens of meters. In principle, instrumenting the exterior of a general-purpose detector with large volumes of scintillators may lend additional sensitivity to even longer lifetimes. In this work we will focus on tracker-based searches at future lepton colliders, as these may be simulated relatively faithfully, and ultimately are among the searches likely to achieve zero background while retaining high signal efficiency.
We define our signal model in FeynRules [32] and generate the signal
$ e^+e^- \to hZ \rightarrow XX + \ell \bar \ell $ at$ \sqrt{s} = 240 $ GeV using MadGraph 5 [33]. Where appropriate, we will also discuss prospects for Higgs factories operating at$ \sqrt{s} = 250 $ GeV (potentially with polarized beams), such as ILC, by rescaling rates with the appropriate leading-order cross section ratios. In order to correctly simulate displaced secondary vertices, the decay of the LLP$ X $ and all unstable Standard Model particles is then performed in Pythia 8 [34].In addition to the signal, we consider some of the leading backgrounds to our signal process and develop selection cuts aimed at achieving a zero-background signal region. The most significant irreducible backgrounds from the Standard Model processes include
$ e^+e^- \to hZ $ , with$ Z \rightarrow \ell \bar \ell $ and$ h \rightarrow b \bar b $ , as well as$ e^+ e^- \rightarrow ZZ \rightarrow \ell \bar \ell + b \bar b $ . Unsurprisingly, there are a variety of other Standard Model backgrounds, but they are typically well-controlled by imposing basic Higgsstrahlung cuts, and we do not simulate them with high statistics. In addition to the irreducible backgrounds from hard collisions, there are possible backgrounds from particles originating away from the interaction point, including cosmic rays, beam halo, and cavern radiation; algorithmic backgrounds originating from effects such as vertex merging or track crossing; and detector noise. Such backgrounds are well beyond the scope of the current study, and will require dedicated investigation with full simulation of the proposed detectors.Correctly emulating the detector response to LLPs using publicly-available fast simulation tools is notoriously challenging. In particular, we have found that the default clustering algorithms in the detector simulator Delphes [35] tend to cluster calorimeter hits from different secondary vertices into the same jets, significantly complicating the realistic reconstruction of secondary vertices. As such, we develop an analysis strategy using only ingredients from the Pythia output, although we further run events through Delphes and utilize ROOT [36] for analysis.
We implement two distinct tracker-based analyses with complementary signal parameter space coverage, which we denote as the 'large mass' and 'long lifetime' pipelines. We shall eventually see that the former will be effective for
$ m_X \gtrsim 10 $ GeV and proper decay lengths$ c\tau \gtrsim 1 \mu $ m, while the latter is able to push down in$ m_X $ by a factor of a few, but is only fully effective for$ c\tau\gtrsim 1 $ cm. Full cut tables for the irreducible backgrounds and a variety of representative signal parameter points appear in Tables 1 and 2.cut/selection ZZ background hZ background dilepton invariant mass 0.97 0.98 recoil mass 0.006 0.94 displaced cluster ( $\geqslant $ resolution)

0.004 0.94 invariant charged mass (6 GeV) 0 0.00005 invariant 'dijet' mass 0 0.00005 pointer track 0 0.00001 $m_X, c \tau$ 

${7.5, }10^{-4}$ 

${7.5, }10^{-2}$ 

${7.5, }10^0$ 

${10, }10^{-4}$ 

${10, }10^{-2}$ 

${10, }10^0$ 

$M_{\ell\ell}$ 

0.97 0.97 0.97 0.97 0.98 0.97 $M_{\rm{recoil}}$ 

0.93 0.93 0.93 0.93 0.94 0.93 $|\vec{d}_{\rm{cluster}}|$ 

0.93 0.93 0.41 0.93 0.94 0.50 $M_{\rm{charged}}$ 

0.27 0.28 0.08 0.55 0.55 0.21 $M_{\rm{cluster}}$ 

0.27 0.28 0.08 0.55 0.55 0.21 pointer 0.25 0.28 0.08 0.50 0.55 0.21 $m_X, c \tau$ 

${25, }10^{-4}$ 

${25, }10^{-2}$ 

${25, }10^0$ 

${50, }10^{-4}$ 

${50, }10^{-2}$ 

${50, }10^0$ 

$M_{\ell\ell}$ 

0.97 0.97 0.98 0.97 0.98 0.97 $M_{\rm{recoil}}$ 

0.92 0.92 0.93 0.92 0.92 0.93 $|\vec{d}_{\rm{cluster}}|$ 

0.92 0.92 0.80 0.92 0.92 0.93 $M_{\rm{charged}}$ 

0.76 0.77 0.57 0.82 0.85 0.81 $M_{\rm{cluster}}$ 

0.76 0.77 0.57 0.76 0.80 0.76 pointer 0.73 0.76 0.57 0.75 0.77 0.76 Table 1. Cut flow of the 'large mass' analysis for CEPC with entries of acceptance × efficiency. The top set of rows gives the cut flow on 500k
$Z(b \bar b)Z(\ell \bar \ell)$ events and 100k$h(b \bar b)Z(\ell \bar \ell)$ background events, which are used to confirm our analysis in the no-background regime. The next sets of rows give cut flows on 5k signal events at representative parameter points, where the different columns are labeled by$m_X$ /GeV,$c\tau/$ m. The full row labels are given in the top set of rows and the labels below are abbreviations for the same cuts or selections.cut/selection ZZ background hZ background dilepton invariant mass 0.97 0.98 recoil mass 0.006 0.94 displaced cluster ( $\geqslant 3$ cm)

0.004 0.62 charged invariant mass (2 GeV) 0 0.002 'dijet' invariant mass 0 0.002 pointer track 0 0.001 isolation 0 0.00005 $m_X, c \tau$ 

${2.5, }10^{-4}$ 

${2.5, }10^{-2}$ 

${2.5, }10^0$ 

${7.5, }10^{-4}$ 

${7.5, }10^{-2}$ 

${7.5, }10^0$ 

$M_{\ell\ell}$ 

0.97 0.97 0.98 0.97 0.97 0.97 $M_{\rm{recoil}}$ 

0.93 0.93 0.93 0.93 0.93 0.93 $|\vec{d}_{\rm{cluster}}|$ 

0.21 0.89 0.15 0.41 0.89 0.41 $M_{\rm{charged}}$ 

0 0.40 0.05 0 0.74 0.34 $M_{\rm{cluster}}$ 

0 0.40 0.05 0 0.74 0.34 pointer 0 0.40 0.05 0 0.74 0.34 isolation 0 0.33 0.045 0 0.51 0.33 $m_X, c \tau$ 

${15, }10^{-4}$ 

${15, }10^{-2}$ 

${15, }10^0$ 

${50, }10^{-4}$ 

${50, }10^{-2}$ 

${50, }10^0$ 

$M_{\ell\ell}$ 

0.97 0.98 0.97 0.97 0.98 0.97 $M_{\rm{recoil}}$ 

0.93 0.93 0.93 0.92 0.92 0.93 $|\vec{d}_{\rm{cluster}}|$ 

0.59 0.87 0.65 0.64 0.69 0.92 $M_{\rm{charged}}$ 

0.001 0.71 0.63 0 0.10 0.91 $M_{\rm{cluster}}$ 

0.001 0.71 0.63 0 0.09 0.90 pointer 0.001 0.65 0.60 0 0.08 0.84 isolation 0.0002 0.42 0.58 0 0.05 0.77 Table 2. Cut flow of the 'long lifetime' analysis for CEPC with entries of acceptance
$\times$ efficiency. The top set of rows gives the cut flow on 500k$Z(b \bar b)Z(\ell \bar \ell)$ events and 100k$h(b \bar b)Z(\ell \bar \ell)$ background events, which are used to confirm our analysis in the no-background regime. The next sets of rows give cut flows on 5k signal events at representative parameter points, where the different columns are labeled by$m_X$ /GeV,$c\tau$ /m. The full row labels are given in the top set of rows and the labels below are abbreviations for the same cuts or selections.As a first step in either analysis, we select Higgsstrahlung events by requiring that our events have an opposite sign electron (muon) pair in the invariant mass range
$ 70 \leqslant M_{ee} \leqslant 110 $ GeV ($ 81 \leqslant M_{\mu\mu} \leqslant 101 $ GeV) , and with the recoil mass$ M_{\rm{recoil}}^2 \equiv \big( (\sqrt{s}, \vec{0})^\mu - p^\mu_{\ell\ell}\big)^2 $ in the range$ 120 \leqslant M_{\rm{recoil}} \leqslant 150 $ GeV, with$ p^\mu_{\ell\ell} $ the momentum of the lepton pair. This allows to limit our background considerations to the irreducible backgrounds mentioned above and cuts down severely on the$ e^+ e^- \rightarrow ZZ $ background, as seen in Tables 1 and 2.We next identify candidate secondary vertices using a depth-first 'clustering' algorithm, which roughly emulates that performed in the CMS search [37]. We perform this clustering using all particles in the event, because at later points in the analysis we need this truth-level assignment of neutral particles to clusters, but we expect that this (admittedly unrealistic) inclusion does not significantly modify the performance of this algorithm. Beginning with a single particle as the 'seed' particle for our algorithm, we look through all other particles in the event and create a 'cluster' of particles consisting of the seed particle and any other whose origin is within
$\ell_{\rm{cluster}} = $ $ 7 \ {\mu} $ m (the projected tracker resolution of CEPC [4]) of the seed particle. We then add to that cluster any particle whose origin is within$ \ell_{\rm{cluster}} $ of any origin of a particle in the cluster, and do this step iteratively until no further particles are added to the cluster. We then choose a new seed particle, which has not yet been assigned to a cluster, and begin this clustering process again. We repeat this process until all particles in the event have been assigned to clusters. We assign to each cluster a location$ \vec{d}_{\rm{cluster}} $ , which is the average of the origins of all charged particles in the cluster. To ensure that our events contain displaced vertices, we impose a minimum bound on the displacement from the interaction point$ |\vec{d}_{\rm{cluster}}| > d_{\min} $ , and clusters satisfying this requirement constitute candidate secondary vertices. For our 'large mass' analysis, we set$ d_{\min} $ to be the impact parameter resolution ($ \simeq 5 \ \mu $ m for both CEPC and FCC-ee [4]), and so retain the sensitivity to very short$ X $ lifetimes. For our 'long lifetime' analysis, we set$ d_{\min} = 3 $ cm, which removes the vast majority of clusters coming from$ B $ hadron decays in the background events, as seen in Table 2. An upper bound$ |\vec{d}_{\rm{cluster}}| <$ $ r_{\rm{tracker}} $ is imposed by the outer radius of the tracker, where$ r_{\rm{tracker}} = 1.81 $ m for CEPC and$ r_{\rm{tracker}} = 2.14 $ m for FCC-ee are proposed.At this point, an experimental analysis might sensibly examine dijets containing candidate secondary vertices and impose an upper bound on the dijet invariant mass to remove backgrounds coming from the Standard Model
$ H $ or$ Z $ decays. As discussed above, we are limited to Pythia objects, but to mock up the (small) penalty to signal of such a selection we implement a selection on the total invariant mass of the clusters$ M_{\rm{cluster}}^2 \equiv (\sum_{i \in \rm{ cluster}} p_i^\mu)^2 $ . Since this is truth-level information, to turn it into an analog for the dijet invariant mass, we apply a Gaussian smearing with a standard deviation of 10 GeV to account for the dijet resolution. We then select only candidate secondary vertices with$ M_{\rm{cluster}} < m_h/2 $ . This has no effect on background in our simulation pipeline as the background candidate secondary vertices are the result of hadronic decays, so the invariant masses of these clusters are not analogs for dijet invariant masses. As emphasized above, the imposition of this cut is strictly to account for possible selections that might appear in a more realistic experimental analysis.While the total invariant mass of the clusters is not an experimental observable, the invariant mass of charged particles in the clusters
$ M_{\rm{charged}} = (\sum_{i \rm{ charged}} p_i^\mu)^2 $ is experimentally accessible. For our 'large mass' analysis, we select candidate secondary vertices with$ M_{\rm{charged}}> 6 $ GeV, which gets rid of nearly all clusters from hadronic decays, as seen in Table 1. For the 'long lifetime' analysis, while the increased displacement requirement removes$ b $ hadrons it still allows$ c, s $ hadrons, and so we select$ M_{\rm{charged}}> 2 $ GeV to address this, which Table 2 shows is again very effective.Next, we select the cluster closest to the beamline which passes the above selection requirements as our secondary vertex for the event. Choosing the closest one preferentially selects
$ X $ decay clusters over hadronic decay clusters in the jets to which the$ X $ decays, though this can be fooled by a non-zero fraction of 'back-flowing' quarks in$ X $ decays (quarks with momenta pointing toward the beamline).To remove displaced vertices coming from the decays of charged
$ b $ hadrons, we implement a 'pointer track' cut in both analyses as follows. For the cluster selected as the secondary vertex, we consider a sphere of radius$ r = 0.5 $ mm around the position$ \vec{d}_{\rm{cluster}} $ . We look for any charged particle whose origin is outside this sphere and whose momentum (at the point at which it was created) points into it, and veto the event if there are any such particles. The main effect of this cut is to remove clusters which were produced from the decay of a charged hadron. The sphere size has been chosen to maximize this effect, though this allows a small effect on the signal due to geometric coincidence. Since this cut is only on charged particles, roughly ~30% of background clusters are unaffected. For this cut, we ignore the effect of the magnetic field in the tracker, which should not highly impact the trajectories on short scales.For the 'long lifetime' analysis, we further implement an 'isolation' cut to remove neutral hadronic background decays. Given the cluster selected as the secondary vertex, we consider the plane perpendicular to the sum of momenta of charged particles in the cluster which passes through
$ \vec{d}_{\rm{cluster}} $ . We project the paths of prompt charged particles (vertex within$ 3 \ {\text{μ}} $ m of the primary vertex, the planned CEPC vertex resolution [4]) onto this plane (again ignoring the magnetic field), and veto the event if any come within$ R = 10 $ cm of the position of the secondary vertex. This radius was chosen to maximally reduce background, and does have a deleterious effect on short decay lengths$ \lesssim 10 $ mm, as can be seen in Table 2. This cut is not perfectly effective at rejecting background due to the non-negligible presence of jets whose prompt components have neutral fraction 1. -
To confirm that our analysis pipelines lead to the zero-background regime, we run both the 'long lifetime' and the 'large mass' analyses on 500k
$ e^+ e^- \rightarrow Z(b \bar b)Z(\ell \bar \ell) $ events and 100k$ e^+ e^- \rightarrow h(b \bar b) Z(\ell \bar \ell) $ background events. For both pipelines, we find that zero$ e^+ e^- \rightarrow Z(b \bar b)Z(\ell \bar \ell) $ events remain, while for$ e^+ e^- \rightarrow h(b \bar b) Z(\ell \bar \ell) $ , we find efficiencies of$ 5\times 10^{-5} $ and$ 1\times 10^{-5} $ , respectively. We then run each analysis on 5k signal events to get acceptance$ \times $ efficiencies for each$ (m_X, c\tau) $ point, for a selection of points with$ m_X$ from 2.5 GeV to 50 GeV, and$ c\tau $ from$ 1 \ \mu $ m to 50 m. In Table 2 , we give a cut table for both backgrounds and some representative signal parameter points for the 'long lifetime' analysis, and in Table 1 we do the same for the 'large mass' analysis.In the zero-background regime, Poisson statistics rules out model points which predict 3 or more signal events to 95% confidence (or better) if no signal is detected. We may then find a projected 95% upper limit on the branching ratio as
$ {\rm{Br}}(h\rightarrow XX)^{95} = \frac{N_{\rm sig}}{{\cal{L}}\times \sigma(e^+ e^- \rightarrow hZ) \times {\rm{Br}}(Z\rightarrow \ell \ell) \times A \times \varepsilon}, $

(1) with
$ N_{\rm sig} = 3 $ and$ A\times \varepsilon $ the result of our simulations. For both CEPC and FCC-ee, the most recent integrated luminosity projections [4, 38] give${\cal{L}}\times \sigma(e^+ e^- \rightarrow hZ) = $ $ 1.1 \times 10^6 $ Higgs bosons produced.In Fig. 1 , we show the projected 95% upper limits on
$ {\rm{Br}}(h\rightarrow XX) $ as a function of$ X $ mass and proper decay length. While we plot separate lines for CEPC and FCC-ee, we only use one set of signal events generated at$ \sqrt{s} = 240 $ GeV, and only account for the difference in tracker radii, so these overlap entirely for smaller lifetimes. Approximate limits for ILC can be obtained by multiplying the above branching ratio limits by a factor of$ \sim 1.8 $ (i.e. weakening the limit), to account for the leading order differences in center-of-mass energy, polarization and integrated luminosity at the$ \sqrt{s} = 250 $ GeV ILC run, assuming comparable acceptance and efficiency. ILC limits weaken slightly further for large decay lengths, as its proposed tracker radius is$ 1.25 $ m. Of course, adding the higher-energy ILC runs should significantly improve the sensitivity, given the analyses suitable for$ WW $ fusion production relevant at these energies.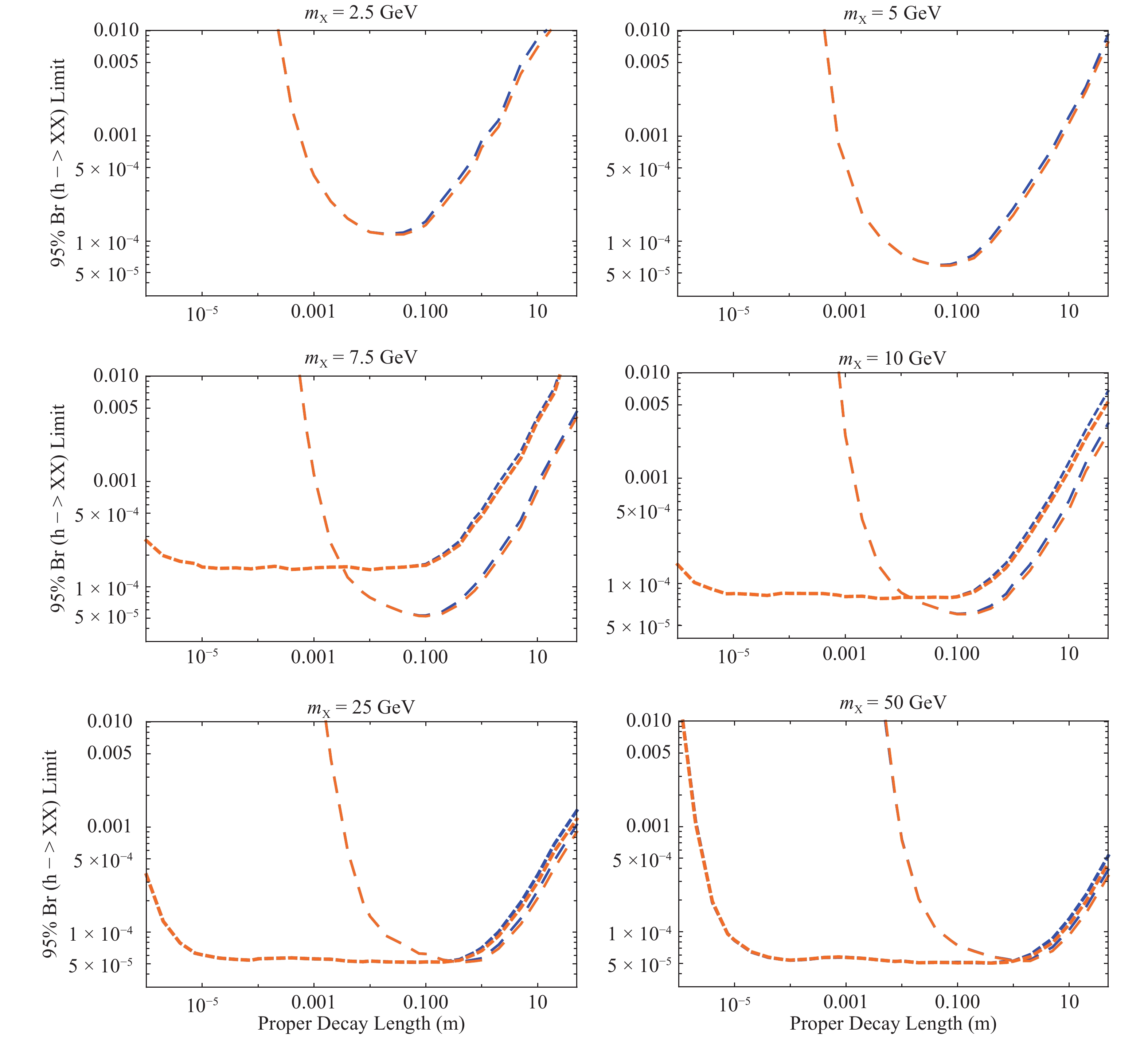
Figure 1. (color online) Projected 95%
$h \rightarrow XX$ branching ratio limits as a function of proper decay length for a variety of$X$ masses. Blue lines are for CEPC and orange lines are for FCC-ee, and where only one is visible they overlap. The larger dashes are the 'long lifetime' analysis and the smaller dashes are the 'large mass' analysis.For small masses, we are only able to use the 'long lifetime' analysis, which requires large displacement from the beamline to cut out the SM
$ b $ hadron background. As a result, we only retain good sensitivity to$ X $ decay lengths comparable with the tracker size, though the fact that we only require one displaced vertex (out of two$ X $ s per signal event) significantly broadens our sensitivity range. This fact also helps to retain the efficiency at low masses, as we are able to get down to a projected branching ratio limit of$ 1\times 10^{-4} $ for$ m_X = 2.5 $ GeV, despite our$ 2 $ GeV cut on charged invariant mass of the decay cluster. For larger masses, this cut has less effect, which allows to push down to even lower branching ratios$ \sim 5 \times 10^{-5} $ .The 'large mass' analysis begins to work well for masses not far above the
$ 6 $ GeV charged invariant mass cut, and provides sensitivity to far shorter decay lengths, reaching all the way down to and below the impact parameter resolution. For$ m_X = 10 $ GeV, where we are aided by the boost factor, we project a limit of$ 1\times 10^{-4} $ for a proper decay length of$ 1 $ micron. The sensitivity to extremely small decay lengths drops for larger masses, and for$ m_X = 50 $ GeV we cross below the$ 10^{-4} $ threshold at$ 7.5 \ {\text{μ}} $ m. For$ X $ masses high enough that the charged invariant mass cut does not remove a large amount of signal events, this analysis projects a branching ratio limit of$ \sim 5 \times 10^{-5} $ across roughly the entire range of decay lengths corresponding to the geometric volume of the detector. There is a slight dip in sensitivity for$ c\tau \sim 1 $ mm, where the pair of dijets from the two$ X $ decays are most likely to overlap and trigger the cut on 'pointer' tracks.The notable region of the parameter space in which our analyses does not provide good sensitivity is the low mass (
$ m_X \lesssim 6 $ GeV) and short proper decay length ($ c\tau \lesssim 1 $ cm) regime. The difficulty is that, from the perspective of the tracker,$ X $ looks more and more like a neutral SM hadron. An analysis making use of the impact parameter distribution of particles in clusters may help here [37], but we leave this to future work. Taking advantage of calorimeter data to distinguish between clusters in single jets versus dijets is also likely to provide good sensitivity, but we again leave this to future exploration.Broadly speaking, our results suggest a peak sensitivity of
$ {\rm Br}(h \rightarrow XX) \sim 5 \times 10^{-5} $ , weakening to$ \sim 10^{-4} $ for lower-mass LLPs. Significant additional improvement could be expected with the inclusion of hadronic$ Z $ decays, but this requires further study to ensure the control of corresponding Standard Model backgrounds. These limits are competitive with the LHC forecasts based on conventional Higgs triggers [27, 28], noting that the latter forecasts assume zero background. However, the lepton collider limits are potentially superseded by an efficient CMS track trigger [24, 25] for higher-mass LLPs, again assuming that zero background is achievable with high signal efficiency across a range of lifetimes. In this respect, the primary strength of the Higgs factories in searching for exotic Higgs decays to LLPs is the potential to push down to shorter decay lengths and lighter LLPs. In particular, the relatively clean and low-background environment of lepton colliders should enable efficient LLP searches even when LLP decay products become collimated, which remains a weakness of the corresponding LHC searches. -
While the bounds presented in the previous section apply to any scenario in which the Higgs decays into pairs of long-lived particles, which in turn decay (at least in part) into pairs of quarks, it is also useful to interpret these bounds in the context of specific models that relate the Higgs branching ratio to LLPs (and the LLP lifetime) to underlying parameters. This illustrates the potential for LLP searches at future lepton colliders to constrain motivated scenarios for physics beyond the Standard Model and allows to explore the potential complementarity between LLP searches and precision Higgs coupling measurements. To this end, we consider the implications of the LLP limits presented here in the context of both the original Higgs portal Hidden Valley model and a variety of models of neutral naturalness.
-
As a general proxy model for Higgs decays into LLPs, we first consider the archetypal Higgs portal Hidden Valley [14]. This entails the extension of the Standard Model by an additional real singlet scalar
$ \phi $ , which couples to the Standard Model through the Higgs portal [39-41] via$ \begin{split} {\cal{L}} \supset & \frac{1}{2} (\partial_\mu \phi)^2 - \frac{1}{2} M^2 \phi^2 - A |H|^2 \phi - \frac{1}{2} \kappa |H|^2 \phi^2 \\ &-\frac{1}{3!} \mu \phi^3 - \frac{1}{4!} \lambda_\phi \phi^4 - \frac{1}{2} \lambda_H |H|^4. \end{split} $

(2) If
$ \phi $ respects a$ \mathbb{Z}_2 $ symmetry under which$ \phi \rightarrow - \phi $ , this additionally sets$ \mu = A = 0 $ , such that the singlet scalar only couples to the Standard Model via the quartic interaction$ |H|^2 \phi^2 $ . After electroweak symmetry breaking, in unitary gauge$ H = \left(0, \displaystyle\frac{1}{\sqrt{2}} (h+v) \right) $ , the CP-even scalars$ h $ and$ \phi $ do not mix. Nonetheless, the quartic interaction provides a significant portal for the production of$ \phi $ , as$ \phi $ may be pair produced via the decay$ h \rightarrow \phi \phi $ for$ m_\phi < m_h / 2 $ . Of course,$ \phi $ is stable if the$ \mathbb{Z}_2 $ symmetry is exact, rendering it a potential (albeit highly constrained) dark matter candidate [42-44].This model gives rise to long-lived particle signatures [14] if
$ \mathbb{Z}_2 $ is broken by a small amount, such that$ A \neq 0 $ but e.g.$ A^2/M^2 \ll \kappa $ . The relative smallness of$ A $ is technically natural, as the$ \mathbb{Z}_2 $ symmetry is restored when$ A \rightarrow 0 $ . This then leads to mass mixing between the CP even scalars. As long as$ A $ is small compared to$ M $ and$ v $ , the mass eigenstates consist of an SM-like Higgs$ h_{\rm SM} $ and a mostly-singlet scalar$ s $ , related to the gauge eigenstates by$ \begin{split} h_{\rm SM} = h \cos \theta + \phi \sin \theta \end{split} $

(3) $ s = - h \sin \theta + \phi \cos \theta, $

(4) where
$ \theta \ll 1 $ is the mixing angle. There are now two parametrically distinct processes: pair production of the scalar$ s $ via Higgs decays, governed by the size of the$ \mathbb{Z}_2 $ -preserving coupling$ \kappa $ , and decay of the$ s $ scalar back to the Standard Model, governed by the size of the$ \mathbb{Z}_2 $ -breaking coupling$ A $ . In the limit of small mixing, the former process is of the order$ \Gamma(h \rightarrow ss) \approx \frac{\kappa^2 v^2}{32 \pi m_h} \sqrt{1 - 4 \frac{m_s^2}{m_h^2}}, $

(5) where we are neglecting subleading corrections proportional to
$ \lambda_H \sin^2 \theta $ . The latter process proceeds into whichever Standard Model states$ Y $ are kinematically available, with partial widths$ \Gamma(s \rightarrow YY) = \sin^2 \theta \times \Gamma (h_{\rm SM}[m_s] \rightarrow YY), $

(6) where
$ h_{\rm SM}[m_s] $ denotes a Standard Model-like Higgs of mass$ m_s $ . This naturally leads to a scenario in which$ s $ scalars may be copiously produced via Higgs decays, but travel macroscopic distances before decaying back to the Standard Model particles.This scenario may be constrained not only by direct searches for Higgs decays to LLPs (with scalar
$ s $ playing the role of LLP), but also by precision Higgs coupling measurements. Higgs coupling deviations in this scenario arise from two parametrically distinct effects: tree-level deviations proportional to$ \theta^2 $ due to Higgs-singlet mixing, and one-loop deviations proportional to$ \kappa $ due to$ s $ loops. Both effects result in a universal modification of Higgs couplings, which is best constrained at lepton colliders via the precision measurement of the$ e^+e^- \to hZ $ cross section [45, 46]. The net deviation in the$ e^+e^- \to hZ $ cross section due to these effects in the limit of small mixing is$ \frac{\delta \sigma_{hZ}}{\sigma_{hZ}^{\rm SM}} \approx - \theta^2 - {\rm Re} \left. \frac{{\rm d} {\cal{M}}_{hh}}{{\rm d} p^2} \right|_{p^2 = m_h^2}, $

(7) where the radiative correction [46]
$ \begin{split} \left. \frac{{\rm d} {\cal{M}}_{hh}}{{\rm d} p^2} \right|_{p^2 = m_h^2} =& - \frac{1}{16 \pi^2} \frac{\kappa^2 v^2}{2 m_h^2} \\& \times \left( 1 + \frac{4 m_s^2}{m_h^2} \sqrt{\frac{m_h^2}{m_h^2- 4 m_s^2}} \tanh^{-1} \left[ \sqrt{\frac{m_h^2}{m_h^2 - 4 m_s^2}} \right] \right) \end{split} $

(8) is approximated at
$ \theta = 0 $ . Either effect can dominate, depending on the relative size of$ A/M $ and$ \kappa $ .Constraints from a direct search for Higgs decays to LLPs and precision Higgs measurements as a function of the underlying parameters
$ \theta $ and$ \kappa $ are shown in Fig. 2 for the illustrative benchmarks$ m_s = 2.5, 10 $ , and 50 GeV. Unsurprisingly, in the regime where$ s $ is long-lived, the bounds from precision Higgs coupling measurements are modest and direct searches provide the leading sensitivity.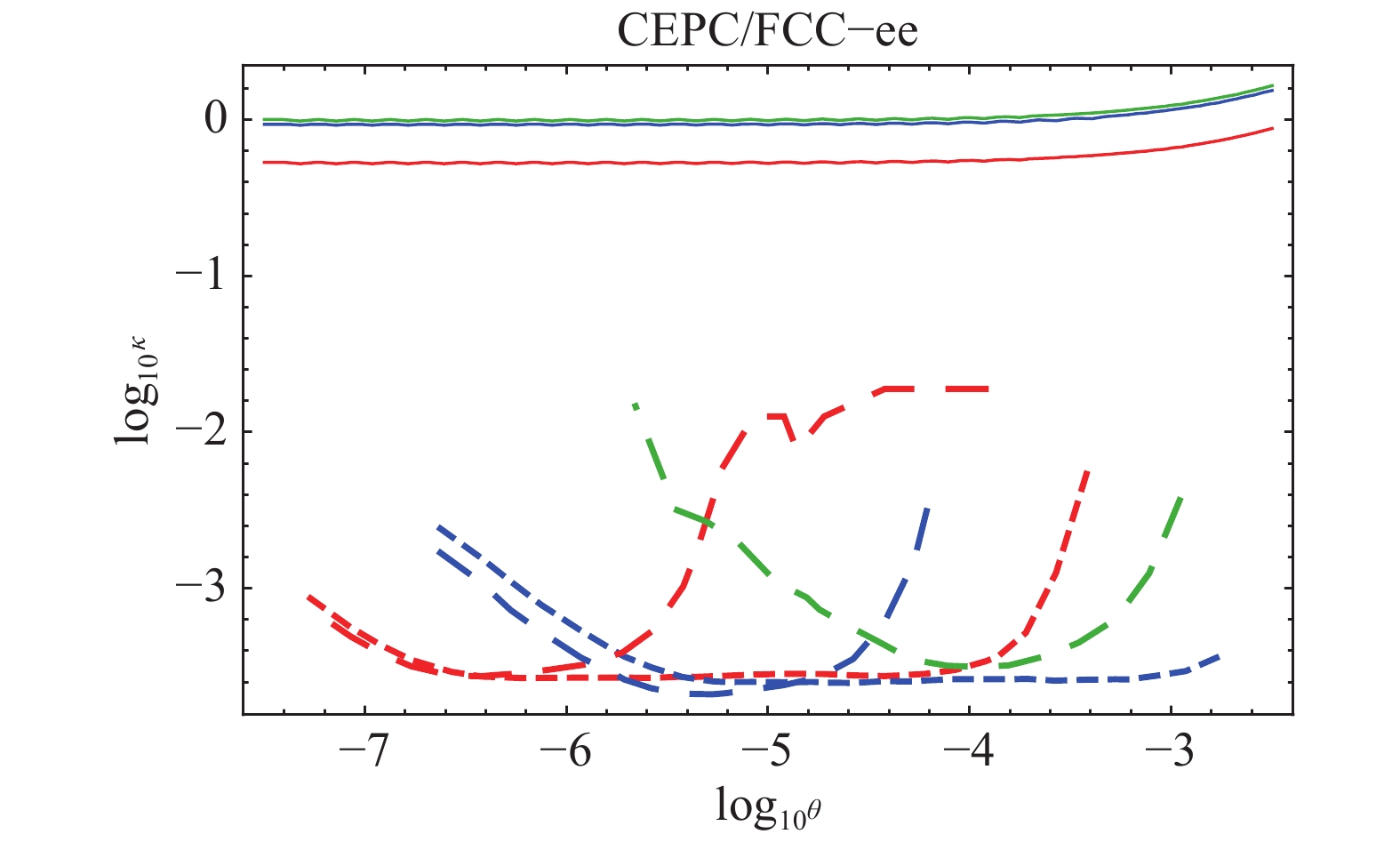
Figure 2. (color online) Projected 95% limits on the Higgs portal Hidden Valley model in the
$\kappa, \theta$ plane for three choices of$m_s$ ; green lines correspond to$m_s = 2.5$ GeV, blue to$m_s = 10$ GeV, and red to$m_s = 50$ GeV. The solid lines are the projected lower limits from precision Higgs measurements, taking the CEPC projections [4] for definiteness. The dashed lines are projected limits from this work, which are essentially identical for CEPC and FCC-ee. Long dashes are from the 'long lifetime' analysis and short dashes from the 'large mass' analysis. -
Higgs decays to LLPs are also motivated by naturalness considerations, arising frequently in models of neutral naturalness that address the hierarchy problem with SM-neutral degrees of freedom [47, 48]. In these models, partially or entirely SM-neutral partner particles that couple to the Higgs boson are charged under an additional QCD-like sector. Confinement in the additional QCD-like sector leads to a variety of bound states that couple to the Higgs and may be pair-produced in exotic Higgs decays with predictive branching ratios. The bound states with the same quantum numbers as the physical Higgs scalar typically decay back to the Standard Model by mixing with the Higgs. These decays occur on length scales ranging from microns to kilometers, making them a motivated target for LLP searches at colliders [16, 28].
For simplicity, here we will restrict our focus to scenarios with the sharpest predictions for the Higgs branching ratio to LLPs. In these cases, LLPs in question are typically glueballs of the additional QCD-like sector, of which
$ J^{PC} = 0^{++} $ is typically the lightest. The coupling of the SM-like Higgs to these LLPs is predominantly due to top partner loops, for which the scales and couplings are directly related to the naturalness of the parameter space. In the Fraternal Twin Higgs [16], the entirely SM-neutral fermionic partners of the top quark induce Higgs couplings to twin gluons, which then form glueballs; the$ 0^{++} $ states are the lightest in the twin QCD spectrum only if the other twin quarks are sufficiently heavy. In addition, there are tree-level deviations in Higgs couplings due to the pseudo-goldstone nature of the SM-like Higgs. In Folded SUSY [49], the scalar top partners carry electroweak quantum numbers, leading to radiative corrections of the standard Higgs decays, as well as to the existence of exotic decay modes. Loops of the scalar top partners again induce Higgs couplings to twin gluons, and without light folded quarks the$ 0^{++} $ glueball is generically the lightest state in the folded QCD spectrum. While there are no tree-level Higgs coupling deviations in this case, the electroweak quantum numbers of the scalar top partners induce significant corrections to the branching ratio$ h \rightarrow \gamma \gamma $ . Finally, in the Hyperbolic Higgs [50] (see also [51]), the scalar top partners are entirely SM-neutral, and induce couplings to$ 0^{++} $ glueballs that are generically the lightest states in the hyperbolic QCD spectrum. As with the Fraternal Twin Higgs, however, there are also tree-level Higgs coupling deviations due to mass mixing among CP-even neutral scalars.In each of these scenarios, the branching ratio of the SM-like Higgs can be parametrized as follows:
$ \begin{split} {\rm Br}(h \rightarrow 0^{++} 0^{++}) \approx \left( 2 v^2 \frac{\alpha_s^\prime(m_h)}{\alpha_s(m_h)} \left[ \frac{y^2}{M^2} \right] \right)^2 \\ \times {\rm Br}(h \rightarrow gg)_{\rm SM} \times \sqrt{1 - \frac{4 m_0^2}{m_h^2}} \end{split} $

(9) Here,
$ \alpha_s^\prime $ denotes the coupling of the additional QCD-like sector (whether twin, folded, or hyperbolic), which is necessarily of the same order as the SM QCD coupling$ \alpha_s $ , and$ m_0 $ is the mass of the glueball, which is determined in terms of the QCD-like confinement scale. Adopting the schematic notation of [28], the parameter$ \left[ \displaystyle\frac{y^2}{M^2} \right] $ encodes the model-dependence of the Higgs coupling to pairs of gluons in the QCD-like sector, with$ \left[ \displaystyle\frac{y^2}{M^2} \right] \approx \left \{ \begin{array}{ll} - \displaystyle\frac{1}{2v^2} \frac{v^2}{f^2} & {\rm Fraternal\; Twin\; Higgs} \\ \displaystyle\frac{1}{4v^2} \displaystyle\frac{m_t^2}{m_{\tilde t}^2} & {\rm Folded\; SUSY} \\ \displaystyle\frac{1}{4 v^2} \frac{v}{v_{\cal{H}}} \sin \theta & {\rm Hyperbolic\; Higgs} \end{array} \right. $

(10) For the Fraternal Twin Higgs,
$ f $ denotes the overall twin symmetry-breaking scale$ f^2 = v^2 + v^{\prime 2} $ in terms of the SM weak scale$ v $ and the fraternal weak scale$ v^\prime $ . For Folded SUSY,$ m_{\tilde t} $ denotes the mass of the scalar top partners, neglecting possible mixing effects. For the Hyperbolic Higgs,$ v_{\cal{H}} $ is the hyperbolic scale and$ \tan \theta \approx \frac{v}{v_{\cal{H}}} $ encodes tree-level mixing effects. In each case, the scales appearing in the effective coupling are related to the fine-tuning of the model, drawing a direct connection between the Higgs exotic branching ratio and the naturalness of the weak scale.In each case, the
$ 0^{++} $ glueballs of the additional QCD-like sector decay back to the Standard Model by mixing with the SM-like Higgs, with a partial width to pairs of SM particles$ Y $ given by$ \begin{split} \Gamma(0^{++} \rightarrow YY) =& \left( \frac{1}{12 \pi^2} \left[ \frac{y^2}{M^2} \right] \frac{v}{m_h^2 - m_0^2} \right)^2 \left(4 \pi \alpha_s^B F_{0^{++}}^S \right)^2 \\ &\times \Gamma(h_{SM}[m_0] \rightarrow YY), \end{split} $

(11) where
$ 4 \pi \alpha_s^B F_{0^{++}}^S \approx 2.3 m_0^3 $ and, as before,$ h_{\rm SM}[m_0] $ denotes a Standard Model-like Higgs of mass$ m_0 $ .Constraints on each model from direct search for Higgs decays to LLPs and precision Higgs measurements are shown in Fig. 3 as a function of the LLP mass
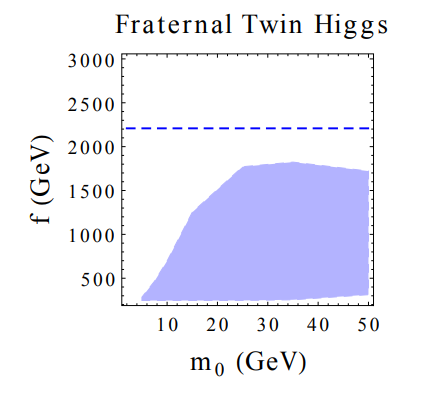
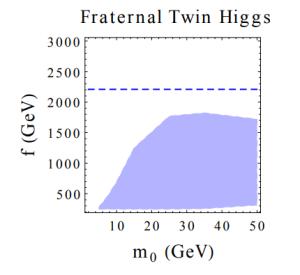
$ m_0 $ and the relevant scale ($ f, v_{\cal{H}} $ , and$ m_{\tilde t} $ , respectively). For precision Higgs measurements, we use the CEPC projections from [4]. In the Fraternal Twin Higgs and Hyperbolic Higgs, the dominant indirect constraint is from$ \sigma_{Zh} $ , while for Folded SUSY it is from$ {\rm Br}(h \rightarrow \gamma \gamma) $ . For both the Fraternal Twin Higgs and the Hyperbolic Higgs, tree-level Higgs coupling deviations make precision Higgs measurements the strongest test of the model. However, the sensitivity of LLP searches provides valuable complementarity in the event that Higgs coupling measurements yield a discrepancy from the Standard Model predictions. In particular, the size of an observed Higgs coupling deviation would single out the relevant overall mass scale ($ f $ or$ v_{\cal{H}} $ ), providing a firm target for LLP searches that would then validate or falsify these models as an explanation of the deviation. Note also that in the Fraternal Twin Higgs there may be additional contributions to the Higgs branching ratio into LLPs coming from the production of twin bottom quarks, which could lead to sensitivity in LLP search comparable to that of Higgs couplings. In the case of Folded SUSY, the absence of tree-level Higgs coupling deviations and the relatively weaker constraints on$ {\rm Br}(h \rightarrow \gamma \gamma) $ make LLP search the leading test of this model at Higgs factories.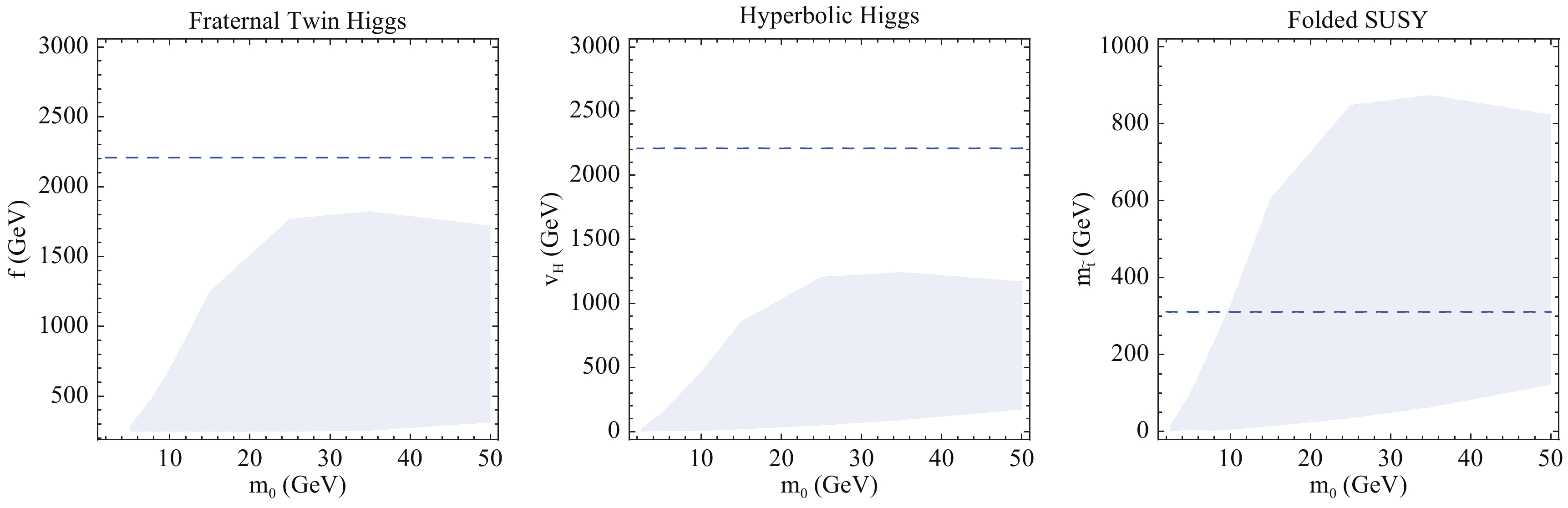
Figure 3. (color online) Projected 95% limits on the underlying scale as a function of the LLP mass
$m_0$ in three models of neutral naturalness: the Fraternal Twin Higgs ($f$ ), the Hyperbolic Higgs ($v_{\cal{H}}$ ), and Folded SUSY ($m_{\tilde t}$ ). The blue dashed line denotes the limit coming from precision Higgs coupling measurements, taking for definiteness the CEPC projections from [4]. For the Fraternal Twin Higgs and Hyperbolic Higgs, the dominant indirect constraint is from$\sigma_{Zh}$ , while for Folded SUSY it is from${\rm Br}(h \rightarrow \gamma \gamma)$ . The shaded region denotes the projected limits from direct LLP searches obtained in this work. -
The exploration of exotic Higgs decays is an integral part of the physics motivation for future lepton colliders. New states produced in these exotic Higgs decays may themselves decay in a variety of length scales, necessitating a range of search strategies. While considerable attention has been devoted to the reach of future lepton colliders for promptly-decaying states produced in exotic Higgs decays, the reach for long-lived particles is relatively unexplored.
In this paper we have made a first attempt to study the reach of proposed circular Higgs factories such as CEPC and FCC-ee (as well as approximate statements for the
$ \sqrt{s} = 250 $ GeV run of ILC) for long-lived particles produced in exotic Higgs decays, focusing on the pair production of LLPs and their subsequent decay to pairs of quarks. We have developed a realistic tracker-based search strategy motivated by the existing LHC searches that entails the reconstruction of displaced secondary vertices. Rather than relying on existing public fast simulation tools, which do not necessarily give a sensible parametrization of signal and background efficiencies for long-lived particle searches, we have implemented a realistic approach to clustering and isolation. This allows to characterize some of the leading irreducible Standard Model backgrounds in our search, and to determine reasonable analysis cuts necessary for a zero-background analysis. We obtain forecasts for the potential reach of CEPC and FCC-ee for the Higgs branching ratio to long-lived particles with a range of lifetimes. The projected reach is competitive with the LHC forecasts and potentially superior for lower LLP masses and shorter lifetimes. In addition to branching ratio limits, which may be freely interpreted in a variety of model frameworks, we interpret our results in the parameter space of a Higgs portal Hidden Valley and various incarnations of neutral naturalness, demonstrating the complementarity between direct searches for LLPs and precision Higgs coupling measurements.There are a variety of directions for future work. While we have attempted to investigate some of the leading irreducible backgrounds and impose realistic cuts, we have not attempted to estimate possible backgrounds coming from cosmic rays; algorithmic, detector, or beam effects; or other contributions. Our tracker-based analysis was focused on Higgs decays to pairs of hadronically-decaying LLPs, but a comprehensive picture of exotic Higgs decays would also suggest the investigation of Higgs decays to various LLP combinations, as well as the consideration of additional LLP decay modes. Moreover, tracker-based searches for displaced vertices are but one of many possible avenues for discovering long-lived particles. Analogous searches based on timing, or on isolated energy deposition in outer layers of the detector (including either the electromagnetic or hadronic calorimeter, the muon chambers, or potentially instrumented volumes outside of the main detector), would be valuable for building a complete picture of LLP sensitivity across a range of lifetimes.
More broadly, it is an ideal time to study the potential sensitivity of future Higgs factories to long-lived particles, as the results are likely to inform the design of detectors for these proposed colliders. This is a necessary step in motivating the physics case of future Higgs factories, and ensuring that they enjoy optimal coverage of possible physics beyond the Standard Model.
We thank Nick Amin, James Beacham, Stefania Gori, Simon Knapen, Eric Kuflik, Zhen Liu, Bennett Marsh, Simone Pagan Griso, Diego Redigolo, and Sicheng Wang for useful conversations.
Long live the Higgs factory: Higgs decays to long-lived particles at future lepton colliders
- Received Date: 2019-02-14
- Available Online: 2019-05-01
Abstract: We initiate the study of exotic Higgs decays to long-lived particles (LLPs) at proposed future lepton colliders, focusing on scenarios with displaced hadronic final states. Our analysis entails a realistic tracker-based search strategy involving the reconstruction of displaced secondary vertices and the imposition of selection cuts appropriate for eliminating the largest irreducible backgrounds. The projected sensitivity is broadly competitive with that of the LHC and potentially superior at lower LLP masses. In addition to forecasting branching ratio limits, which may be freely interpreted in a variety of model frameworks, we interpret our results in the parameter space of a Higgs portal Hidden Valley and various incarnations of neutral naturalness, illustrating the complementarity between direct searches for LLPs and precision Higgs coupling measurements at future lepton colliders.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: