-
Antimagnetic rotation (AMR) [1, 2], which is predicted by Frauendorf in analogy to antiferromagnetism in condensed matter physics, is an interesting exotic phenomenon observed in some nearly spherical or weakly deformed nuclei. In the AMR bands, the higher angular momentum and energy are obtained by the “two-shears-like” mechanism, i.e., by simultaneous alignment of the angular momentum vector of the two valence proton (neutron) holes towards the valence neutron (proton) particle. The AMR bands have regular sequences of energy levels differing in spin by
$ 2\hbar $ , which is the same as for normal rotation. However, due to the weakly deformed or nearly spherical core, they are connected by weak E2 transitions. Moreover, the B(E2) values in the AMR bands decrease with increasing spin.AMR has been investigated both experimentally and theoretically since it was proposed [2]. Up to now, evidence of AMR has been observed experimentally mainly in Cd (Z = 48) and Pd (Z = 46) isotopes including 105Cd [3], 106Cd [4], 107Cd [5], 108Cd [6, 7], 110Cd [8], 101Pd [9-11], and 104Pd [12]. Recently, possible AMR bands have also been reported in Eu (Z = 63) isotopes, including 143Eu [13] and 142Eu [14]. The existence of AMR still needs further investigation in 109Cd [15], 100Pd [16], 144Dy [17] and 112In [18] with lifetime measurements. AMR has been investigated theoretically mainly by the semi-classical particle rotor model [19], and the tilted axis cranking (TAC) model [20-22]. In particular, many investigations have been performed within the framework of microscopic-macroscopic model [4, 6, 16], pairing plus quadrupole model [2, 5], and the covariant density functional theory (CDFT) [23-26] based on the TAC model (for reviews please see Refs. [27, 28]).
In Ref. [12], the ground state band (GSB) of 104Pd after backbending is assigned as AMR. Using the semi-classical particle rotor model, its configuration was assumed to be
$ \pi g_{9/2}^{-2} \otimes \nu[h_{11/2}^2,(g_{7/2},d_{5/2})^2] $ [12]. However, this band was assigned a different configuration,$ \pi g_{9/2}^{-4} \otimes \nu[h_{11/2}^2, $ $ (g_{7/2},d_{5/2})^6]$ , in a recent investigation using TAC-CDFT [26] with the point coupling effective interaction PC-PK1 [29]. Note that these two configurations are both written with respect to the 100Sn core. It can be seen that these two configuration assignments have different number of proton$ g_{9/2} $ holes, which are very important to the formation of AMR. Therefore, it is necessary to clarify the AMR configuration in 104Pd. In this work, the particle-number-conserving (PNC) method [30, 31] , based on the cranked shell model (CSM), is used to investigate AMR in 104Pd. Note that PNC-CSM has already provided successful descriptions for the AMR bands in 105,106Cd [32] and 101Pd [33], and has shown the important role of pairing correlations for the moment of inertia (MOI) and the “two-shears-like” mechanism.Unlike the traditional Bardeen-Cooper-Schrieffer or Hartree-Fock-Bogoliubov approaches, the pairing interaction in the PNC method is diagonalized directly in a sufficiently large Fock-space [34]. Therefore, it is a shell-model like approach, so that the particle-number is conserved at all stages and the Pauli blocking effects are treated exactly. The PNC scheme has also been transplanted in relativistic and non-relativistic mean field models [35-38], and the total-Routhian-surface method [39].
This paper is organized as follows. The theoretical framework of PNC-CSM is presented in Section 2. The results and discussion of the AMR band in 104Pd are given in Section 3. Finally, a summary of the work is given in Section 4.
-
For an axially deformed nucleus, the cranked shell model Hamiltonian reads
${H_{{\rm{CSM}}}} = {H_0} + {H_{\rm{P}}} = {H_{{\rm{Nil}}}} - \omega {J_x} + {H_{\rm{P}}},$

(1) where
$ H_{\rm Nil} $ is the Nilsson Hamiltonian [40],$ -\omega J_x $ is the Coriolis interaction, and$ H_{\rm P} $ is the monopole pairing interaction with effective pairing strength G.$ H_{\rm P} $ reads${H_{\rm{P}}} = - G\sum\limits_{\xi \eta } {a_\xi ^\dagger } a_{\bar \xi }^\dagger {a_{\bar \eta }}{a_\eta },$

(2) where
$ \bar{\xi} $ ($ \bar{\eta} $ ) denotes the time-reversal state of$ \xi $ ($ \eta $ ).When treating the pairing correlations, a cranked many-particle configuration (CMPC) truncation is adopted, which ensures that the PNC calculations are both workable and sufficiently accurate [34, 41]. For the investigations of heavy nuclei, a dimension of 1000 for both protons and neutrons is adequate. By diagonalizing
$ H_\mathrm{CSM} $ in a sufficiently large CMPC space, sufficiently accurate solutions for low-lying excited eigenstates of$ H_\mathrm{CSM} $ can be obtained, which can be written as$|\Psi \rangle = \sum\limits_i {{C_i}} \left| i \right\rangle ,\;\;({C_i}\;{\rm{is}}\;{\rm{real}}),$

(3) where
$ | i \rangle $ is CMPC (the eigenstate of$ H_0 $ ) and$ C_i $ is the corresponding expandsion coefficient. The expectation value of any one-body operator (e.g., angular momentum$ J_x $ and quadrupole moment$ Q_{20} $ )$ {\mathcal {O}} = {\sum_{k = 1}^N} {\cal{O}}(k) $ can be written as$\left\langle {\Psi |{\cal O}|\Psi } \right\rangle = \sum\limits_i {C_i^2} \left\langle {i|{\cal O}|i} \right\rangle + 2\sum\limits_{i < j} {{C_i}} {C_j}\left\langle {i|{\cal O}|j} \right\rangle .$

(4) Since
$ \mathcal {O} $ is a one-body operator, the matrix element$ \langle i | \mathcal {O} | j \rangle $ between two CMPCs$ |i\rangle $ and$ |j\rangle $ is nonzero only when these CMPCs differ by one particle occupation [31]. After certain permutations of creation operators, these two CMPCs can be written as$|i\rangle = {( - 1)^{{M_{i\mu }}}}|\mu \cdots \rangle ,\;\;\;|j\rangle = {( - 1)^{{M_{j\nu }}}}|\nu \cdots \rangle ,$

(5) where
$ \mu $ and$ \nu $ are two single-particle states, and$ (-1)^{M_{i\mu}} = \pm1 $ ,$ (-1)^{M_{j\nu}} = \pm1 $ according to whether the number of permutations is even or odd. Therefore, the expectation value of the one-body operator$ \mathcal {O} $ can be separated into the diagonal$ \sum_{\mu} {\mathcal{O}}(\mu) $ and the off-diagonal$ 2\sum_{\mu <\nu} \mathcal{O}(\mu\nu) $ parts$\left\langle {\Psi |{\cal O}|\Psi } \right\rangle = \left( {\sum\limits_\mu {\cal O} (\mu ) + 2\sum\limits_{\mu < \nu } {{\cal O}(\mu \nu )} } \right),$

(6) ${\cal O}(\mu ) = \langle \mu |{\cal O}|\mu \rangle {n_\mu },$

(7) ${\cal O}(\mu \nu ) = \langle \mu |{\cal O}|\nu \rangle {\sum\limits_{i < j} {( - 1)} ^{{M_{i\mu }} + {M_{j\nu }}}}{C_i}{C_j},$

(8) where
$ n_{\mu} = \sum_{i}|C_{i}|^{2}P_{i\mu} $ is the occupation probability of the single-particle state$ |\mu\rangle $ and$ P_{i\mu} = 0 $ (1) if$ |\mu\rangle $ is empty (occupied) in$ |i\rangle $ .The kinematic MOI
$ J^{(1)} $ and dynamic MOI$ J^{(2)} $ are given by${J^{(1)}} = \frac{1}{\omega }\left\langle {\Psi |{J_x}|\Psi } \right\rangle ,\;\;{J^{(2)}} = \frac{{\rm{d}}}{{{\rm{d}}\omega }}\left\langle {\Psi |{J_x}|\Psi } \right\rangle .$

(9) The reduced B(E2) transition probability can be obtained from the semi-classical approximation as
$B(E2) = \frac{3}{8}{\left\langle {\Psi |Q_{20}^{\rm{p}}|\Psi } \right\rangle ^2},$

(10) where
$ Q_{20}^{\rm p} $ is the proton quadrupole moment given as${Q_{20}} = \sqrt {\frac{5}{{16\pi }}} (3{z^2} - {r^2}) = {r^2}{Y_{20}}.$

(11) -
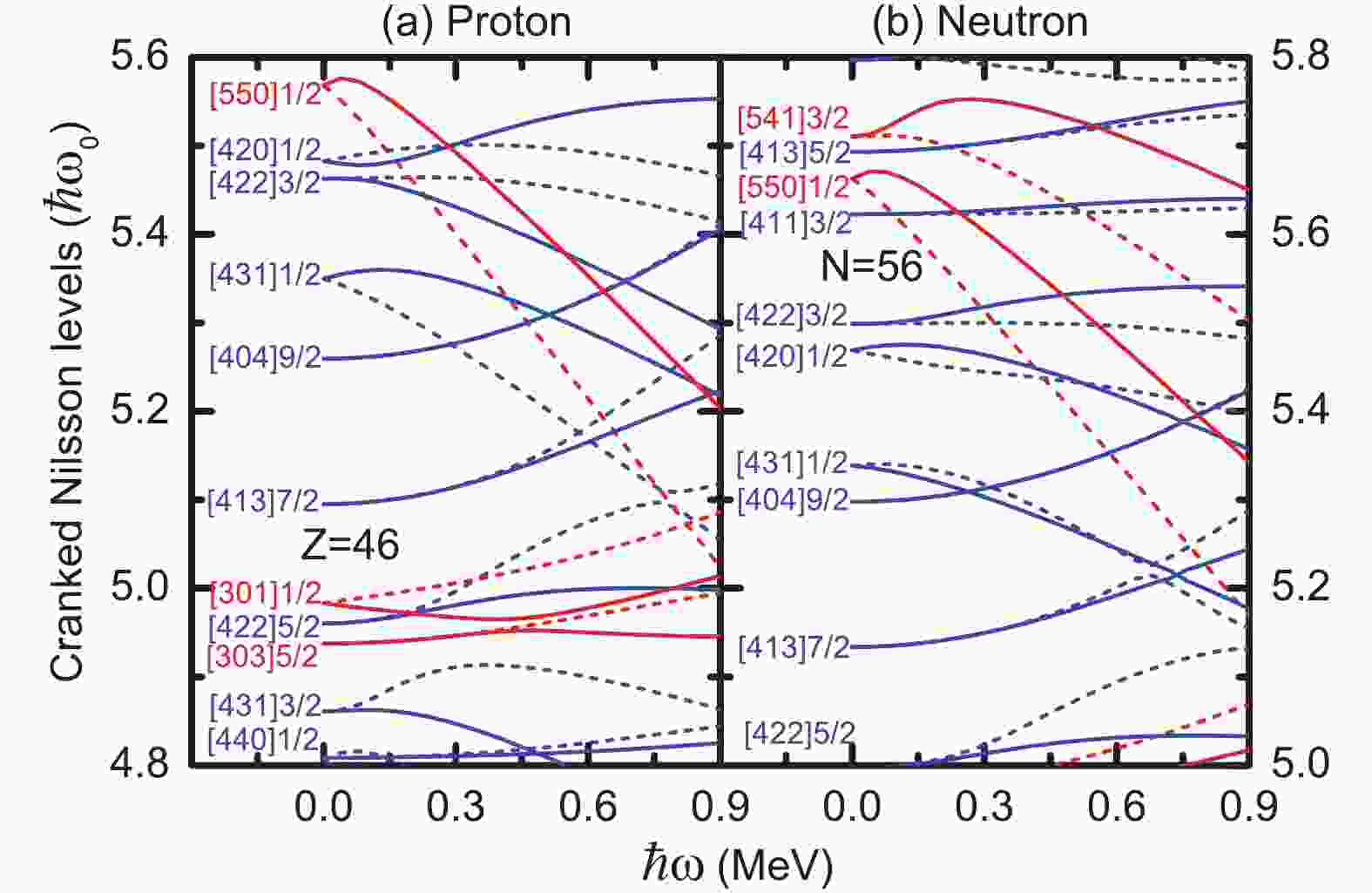
In the present work, the Nilsson parameters (
$ \kappa $ and$ \mu $ ) for 104Pd are taken from Ref. [42]. The deformation parameter$ \varepsilon_2 = 0.18 $ is the experimental value [12]. The valence single-particle space is constructed from N = 0 to N = 5 major shells both for protons and neutrons. Note that N = 0 to N = 3 major shells are closed shells (N = Z = 40) and are fully occupied, so that their contribution to the total angular momentum alignment is zero both for protons and neutrons. However, they are important for calculating the B(E2) values. As N = 0 to N = 3 major shells are included, there is no effective charge involved when calculating the B(E2) values. The effective monopole pairing strengths are determined by the experimental odd-even binding energy differences and MOIs. They are connected with the dimension of the truncated CMPC space, and are about 0.9$ \hbar\omega_0 $ for protons and 0.8$ \hbar\omega_0 $ for neutrons, respectively. In the present calculations, the dimension of the CMPC space is chosen as 1000 both for protons and neutrons, in which CMPCs with weights larger than 0.1% in the many-body wave-function (c.f., Eq. 3) are all included. The effective pairing strengths adopted in this work are$ G_{\rm p} $ = 0.5 MeV for protons and$ G_{\rm n} $ = 0.8 MeV for neutrons.The cranked Nilsson levels near the Fermi surface of 104Pd are shown in Fig. 1 for (a) protons and (b) neutrons. Due to deformation effects, the traditional magic shell gaps with proton number Z = 50 and neutron number N = 50 disappear. It should be noted that since the quadrupole deformation adopted in our calculations for 104Pd (
$ \varepsilon_2 = 0.18 $ ) is much larger than for 105Cd ($ \varepsilon_2 = 0.12 $ ), 106Cd ($ \varepsilon_2 = 0.14 $ ), and 101Pd ($ \varepsilon_2 = 0.125 $ ) in our previous works [32, 33], their single-particle structures close to the Fermi surface are quite different. It can be seen from Fig. 1 (a) that for GSB of 104Pd, there are four$ g_{9/2} $ proton holes ($ \pi 9/2^+[404] $ and$ \pi 7/2^+[413] $ ). For rotational frequency$ \hbar\omega = 0 $ MeV, they should be partly occupied due to the pairing correlations, and their occupation probabilities change with increasing rotational frequency. It can also be seen from Fig. 1 (b) that the neutron$ h_{11/2} $ orbital$ \nu 1/2^-[550] $ should be almost empty at rotational frequency$ \hbar\omega = 0 $ MeV, and with increasing rotational frequency the single-particle energy of this orbital quickly decreases. Unlike the AMR band in 101Pd [9-11], the$ \nu 1/2^-[550] $ orbital is not blocked in GSB of 104Pd, so that the neutron level crossing occurs with increasing rotational frequency. The data show that the possible AMR band in 104Pd is the yrast band after backbending [12]. Using the semi-classical particle rotor model, its configuration was assumed to be$ \pi g_{9/2}^{-2} \otimes \nu[h_{11/2}^2, $ $(g_{7/2},d_{5/2})^2] $ [12]. However, this band was assigned a different configuration,$ \pi g_{9/2}^{-4} \otimes \nu[h_{11/2}^2,(g_{7/2},d_{5/2})^6] $ , in a recent investigation using TAC-CDFT [26]. Therefore, to clarify its configuration, adiabatic calculations of GSB of 104Pd are performed in our investigation so that the configuration for this AMR band can be obtained automatically after neutron level crossings.
Figure 1. (color online) Proton (a) and neutron (b) cranked Nilsson levels near the Fermi surface of 104Pd. The positive and negative parity levels are denoted by blue and red lines, respectively. The signature
$\alpha = \pm1/2$ levels are denoted by solid and dotted lines, respectively.Figure 2 shows the experimental [12] and calculated kinematic MOIs
$ J^{(1)} $ with and without pairing correlations for GSB of 104Pd. MOIs and the corresponding rotational frequencies are extracted by using the relations
Figure 2. (color online) Experimental [12] and calculated kinematic MOIs
$J^{(1)}$ with and without pairing correlations for GSB of 104Pd.$\begin{split} \frac{{{J^{(1)}}(I)}}{{{\hbar ^2}}} =& \frac{{2I + 1}}{{{E_\gamma }(I + 1 \to I - 1)}},\\ \hbar \omega (I) =& \frac{{{E_\gamma }(I + 1 \to I - 1)}}{{{I_x}(I + 1) - {I_x}(I - 1)}}, \end{split}$

(12) where
$ I_{x}(I) = \sqrt{(I+1/2)^{2}-K^{2}} $ . The pairing correlations are crucial for reproducing the experimental data in the whole rotational frequency region. One can see from Fig. 2 that without pairing correlations MOIs of 104Pd are overestimated to a large extent, and that the calculated backbending frequency is much smaller than the experimental data ($ \hbar\omega \sim 0.4 $ MeV). When the pairing correlations are taken into account, the data can be reproduced very well. Note that the present calculations fail to reproduce the sharp backbending that appears in the experimental MOIs due to the defect of the cranking model. In order to obtain the backbending effect exactly, one has to go beyond the cranking model [43, 44]. Due to the fact that MOIs of GSB of 104Pd are reproduced very well by our PNC-CSM calculations, the predicted configuration of the AMR band should be reliable. The configuration obtained by our calculations is compared below with previous works [12, 26].Typical AMR has weak E2 transitions and large
$ J^{(2)}/B(E2) $ ratios, which reflect the nearly spherical or weakly deformed core. Moreover, due to the “two-shears-like” mechanism, the B(E2) values decrease with increasing spin. Figure 3 (a) shows the experimental [12] and calculated B(E2) values with and without pairing correlations for GSB of 104Pd. Previous works have shown that pairing correlations are important to reproduce the B(E2) values only when the proton level crossing occurs, and the reduced B(E2) values strongly depend on the deformation rather than on the superfluidity [32, 33]. It can be seen from Fig. 3 that the decrease of the B(E2) values with increasing rotational frequency can be obtained no matter whether the pairing correlations are taken into account or not. However, the calculated results are more consistent with the data after including the pairing correlations. Note that the experimental B(E2) values drop very quickly with increasing rotational frequency when$ \hbar\omega>0.6 $ MeV , and the present calculations with fixed deformation fail to reproduce this fact. Therefore, the “two-shears-like” mechanism alone is not enough to provide the decrease of B(E2) values. The PNC-CSM calculations when the deformation$ \varepsilon_2 $ changes from 0.18 to zero are also shown in Fig. 3 (a) by the blue dash-dotted line. The inset shows the deformation parameter$ \varepsilon_2 $ adopted in this calculation, which is obtained by fitting the experimental B(E2) values with increasing rotational frequency. It can be seen that in the lower rotational frequency region, the deformation is almost unchanged. When the rotational frequency increases, the deformation gradually decreases. When the rotational frequency$ \hbar\omega>0.65 $ MeV, the deformation shows a sharp reduction and decreases to zero rapidly at$ \hbar\omega \sim 0.75 $ MeV. Due to the fact that with the experimental deformation parameter$ \varepsilon_2 = 0.18 $ the B(E2) values can be reproduced quite well at the beginning of this AMR band, the involution of the deformation with rotational frequency should be reasonable. Therefore, the present calculations also imply a fast reduction of the deformation of GSB of 104Pd with increasing rotational frequency. Note that the TAC-CDFT calculations in Ref. [26], which treat the deformation self-consistently, can not reproduce such fast decrease of the B(E2) values neither. This may need further investigation. Figure 3 (b) shows the comparison of experimental and calculated$ J^{(2)}/B(E2) $ ratios. Because the B(E2) values in the higher spin region are not reproduced well by the PNC-CSM calculations with fixed deformation, only the first two data points of$ J^{(2)}/B(E2) $ can be reproduced reasonably well. It can also be seen that if the effects that change the deformation are taken into account, the$ J^{(2)}/B(E2) $ values can be well reproduced, which is shown by the blue dash-dotted line in Fig. 3 (b). In addition, the sharp peak at$ \hbar\omega \sim 0.45 $ MeV in$ J^{(2)}/B(E2) $ is due to backbending.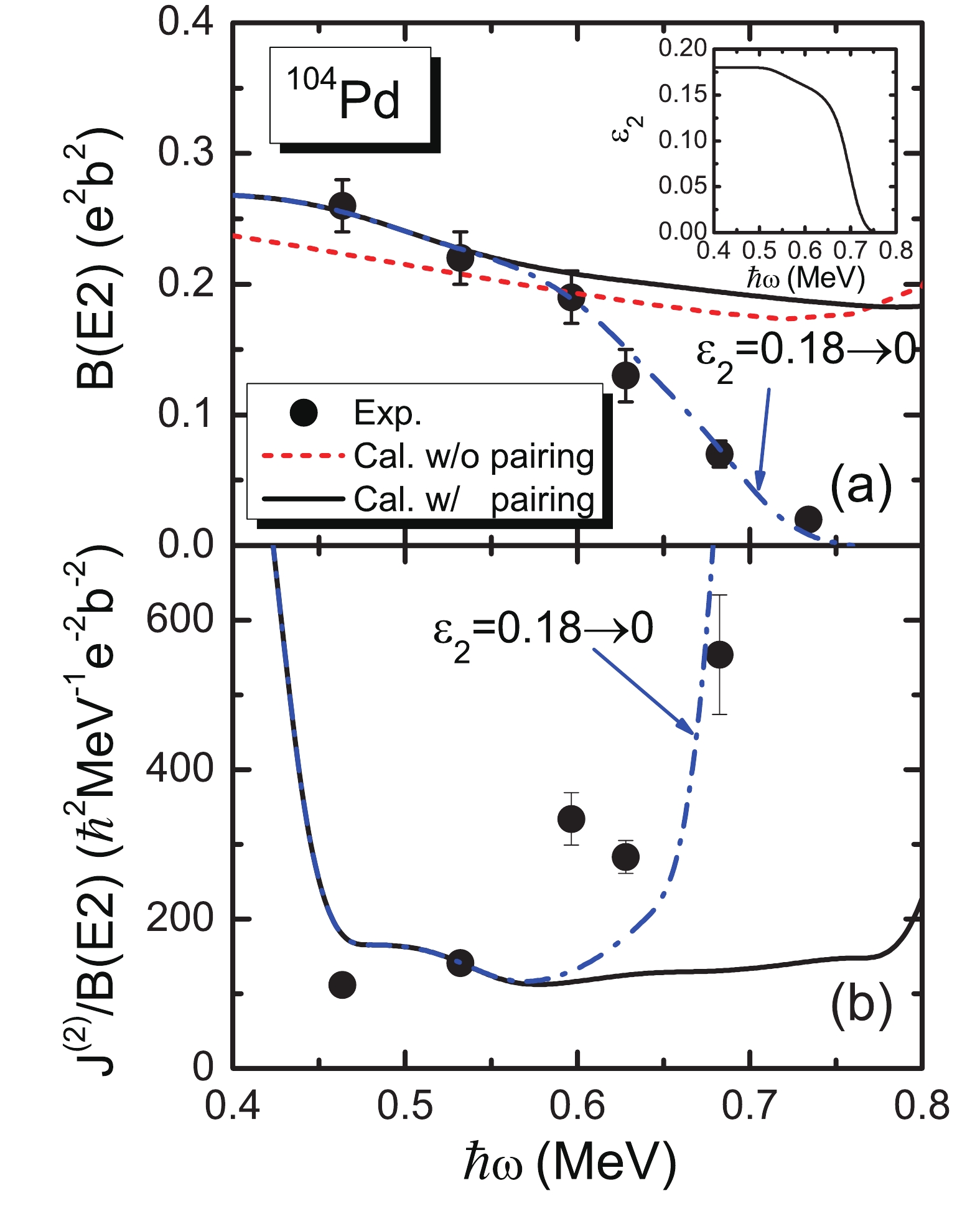
Figure 3. (color online) (a) Experimental [12] and calculated B(E2) values with and without pairing correlations for GSB of 104Pd. (b) Comparison of the experimental and calculated
$J^{(2)}/B(E2)$ ratios. The blue dash-dotted line shows the calculated results when the deformation$\varepsilon_2$ changes from 0.18 to zero, and the inset shows the deformation parameter$\varepsilon_2$ adopted in this calculation.Figure 4 shows the neutron and proton occupation probability
$ n_\mu $ of each orbital$ \mu $ (including both$ \alpha = \pm1/2 $ ) near the Fermi surface of GSB of 104Pd. It can be easily seen from Fig. 4 (a) that for rotational frequency$ \hbar\omega \sim 0.4 $ MeV, the occupation probability for the neutron$ h_{11/2} $ orbital$ \nu1/2^-[550] $ increases suddenly from about 0.4 to 2.0, while the occupation probabilities for some$ (g_{7/2},d_{5/2}) $ orbitals ($ \nu 3/2^+[411] $ ,$ \nu 5/2^+[413] $ , etc.) decrease. This indicates that backbending may mainly be caused by the alignment of one pair of$ h_{11/2} $ neutrons. Therefore, AMR in which the increase of angular momentum is caused by the contribution of a proton can happen in 104Pd only after neutron level crossing. It can also be seen from Fig. 4 (b) that for a similar rotational frequency the occupation probability for the proton$ g_{9/2} $ orbital$ \pi 7/2^+[413] $ drops from about 0.6 to about 0.1, while the occupation probabilities for other proton$ g_{9/2} $ orbitals, e.g.,$ \pi 5/2^+[422] $ and$ \pi 3/2^+[431] $ , increase gradually. Occupation rearrangements in the proton$ g_{9/2} $ orbitals may also contribute to backbending, which is similar to 101Pd [33]. The present calculations show that after backbending, due to the existence of pairing correlations, the proton configuration of the AMR band is that of four partly empty proton$ g_{9/2} $ holes. As for the neutron configuration, it is that of two aligned$ h_{11/2} $ particles and about six particles in the$ (g_{7/2},d_{5/2}) $ orbitals. Note that the proton holes and neutron particles are taken with respect to the 100Sn (N = 50 and Z = 50) core. When the pairing correlations are ignored, this configuration is consistent with that adopted in Ref. [26] using TAC-CDFT. In addition, one can see from Fig. 4 (b) that for rotational frequency$ \hbar\omega \sim 0.8 $ MeV, the occupation of$ \pi 1/2^+[431] $ increases from nearly zero to about 0.6, and the occupation of$ \pi 5/2^+[422] $ drops from 1.9 to 1.3. This is caused by the level crossing between these two orbitals due to the fast drop of$ \pi 1/2^+[431] $ with increasing rotational frequency, which can be easily seen from the cranked Nilsson levels in Fig. 1 (a). This indicates that the AMR band observed in 104Pd will be terminated around this rotational frequency and a four quasiparticle band will appear, which is similar to that observed in 143Eu [13].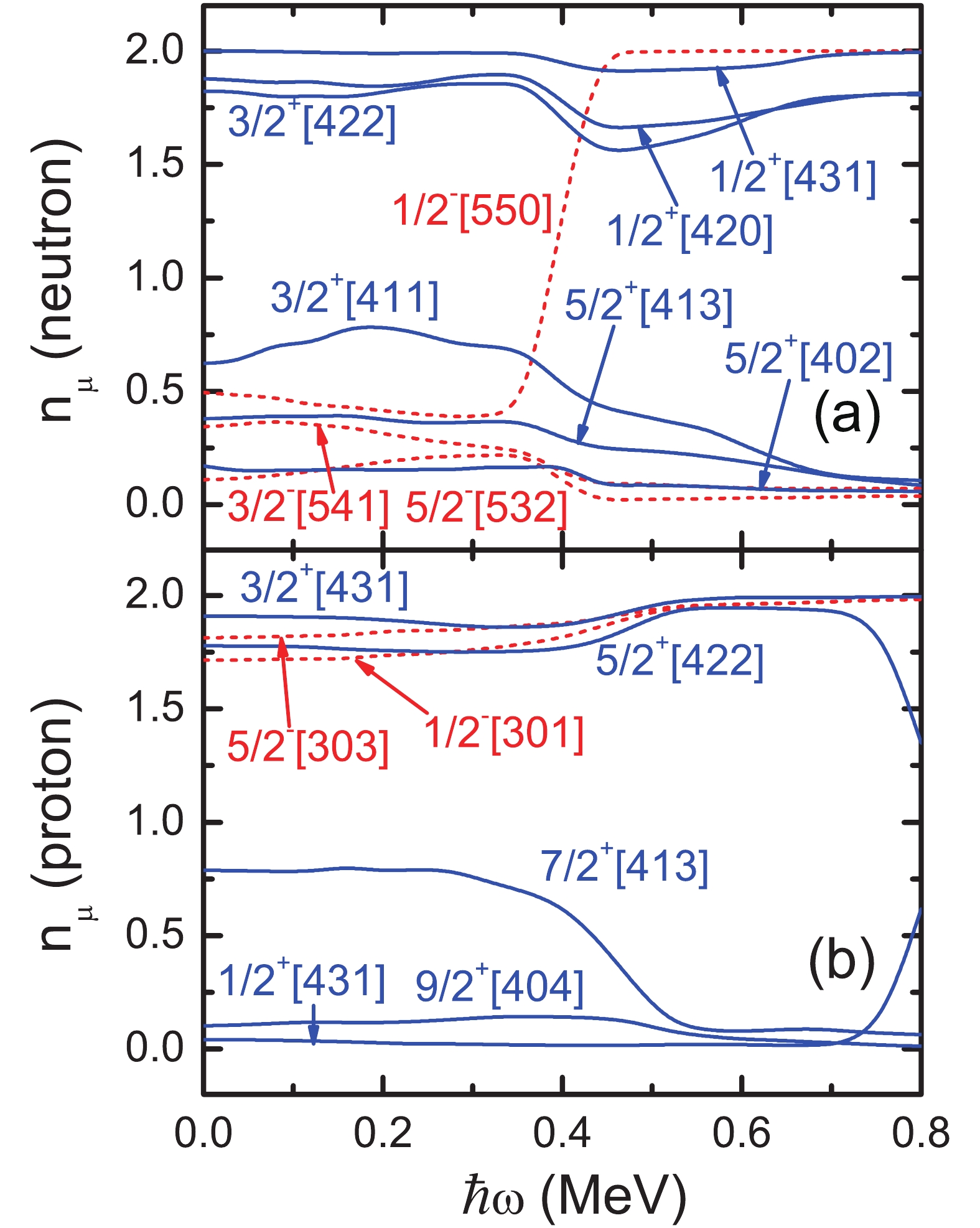
Figure 4. (color online) Neutron (a) and proton (b) occupation probability
$n_\mu$ of each orbital$\mu$ (including both$\alpha = \pm1/2$ ) close to the Fermi surface of GSB of 104Pd. The positive and negative parity levels are denoted by blue solid and red dashed lines. The Nilsson levels which are fully occupied ($n_{\mu}\sim0$ ) and fully empty ($n_{\mu}\sim2$ ) are not shown.Figure 5 shows the experimental and calculated angular momentum alignment
$ \langle J_x\rangle $ for GSB of 104Pd. It can be seen from Fig. 5 that there is a sharp increase of the neutron angular momentum alignment from rotational frequency$ \hbar\omega \sim 0.35 $ MeV to about 0.45 MeV, which indicates again that backbending mainly comes from the contribution of neutrons. From$ \hbar\omega \sim 0.40 $ MeV to about 0.55 MeV, the contribution from protons to$ \langle J_x\rangle $ also gradually increases. This increase comes from the rearrangement of proton occupation in the$ g_{9/2} $ orbitals, which is similar to that in 101Pd [33]. It can also be seen that before the rearrangement of proton occupations in the$ g_{9/2} $ orbitals is completed between$ \hbar\omega \sim 0.45 $ MeV to about 0.55 MeV, the contribution of protons to$ \langle J_x\rangle $ is larger than of neutrons. This indicates that the contribution from AMR to the increase of$ \langle J_x\rangle $ is larger than from normal rotation. For$ \hbar\omega > 0.55 $ MeV, the increase of the neutron angular momentum alignment is faster than of protons. This indicates that the contribution from AMR to the increase of$ \langle J_x\rangle $ is smaller than from normal rotation. Therefore, AMR in 104Pd separates into two stages.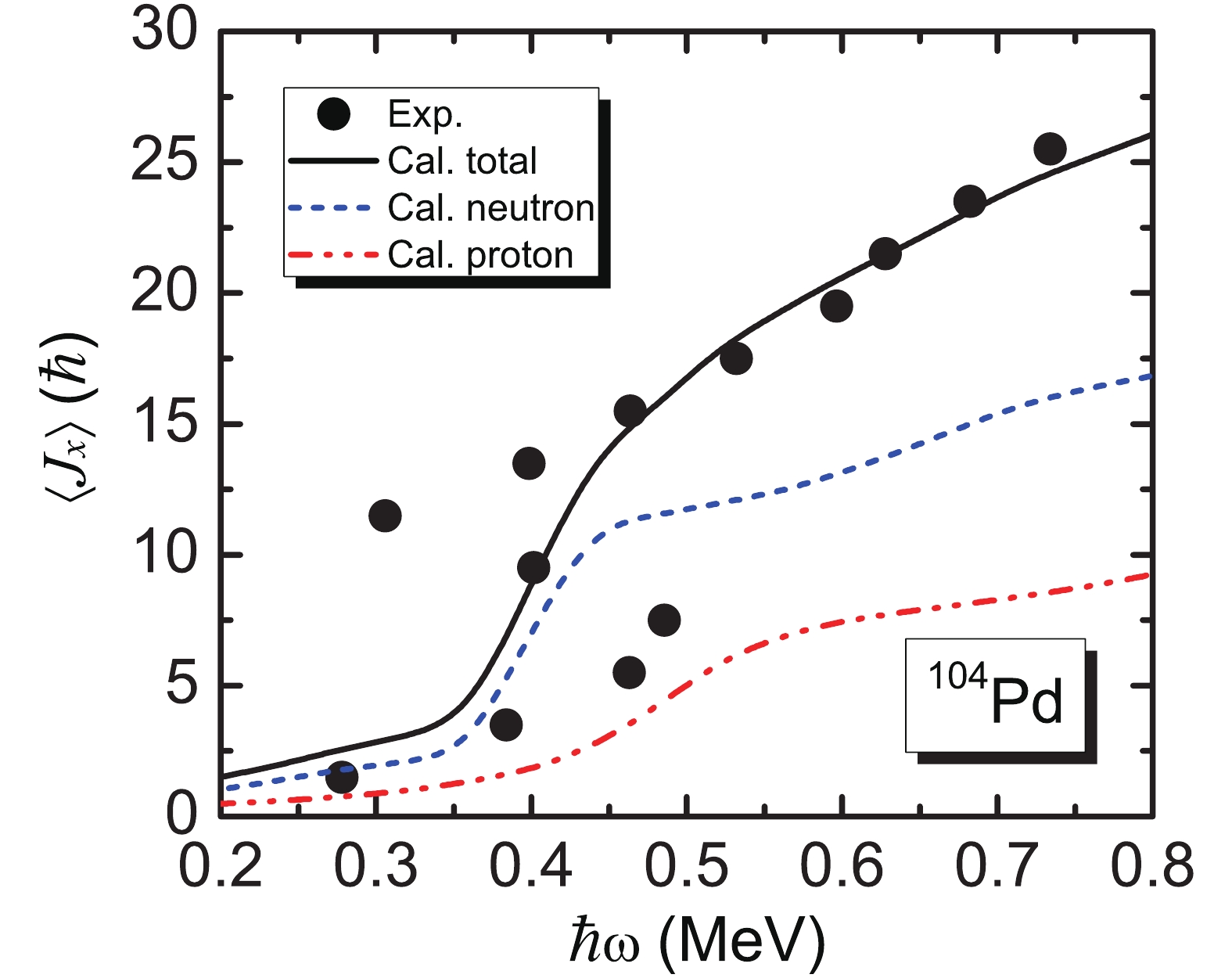
Figure 5. (color online) Experimental and calculated angular momentum alignment
$\langle J_x\rangle$ for GSB of 104Pd.To see the neutron and proton alignment process more clearly, the contributions of neutron and proton N = 4 and 5 major shells to the angular momentum alignment
$ \langle J_x\rangle $ for GSB of 104Pd are shown in Fig. 6. The contributions of diagonal$ \sum_{\mu} j_x(\mu) $ and off-diagonal parts$ \sum_{\mu<\nu} j_x(\mu\nu) $ in Eq. (6) from the neutron N = 5 and proton N = 4 major shell are denoted by dashed lines. It can be seen that backbending around$ \hbar\omega\sim $ 0.4 MeV mainly comes from the neutron N = 5 major shell, especially from the diagonal part. Furthermore, if one looks into the details, the neutron diagonal part$ j_x\left(\nu 1/2^-[550]\right) $ is mainly responsible for backbending. In addition, the neutron N = 4 major shell provides a gradual increase of the angular momentum alignment after the neutron level crossing. This originates from the contribution of the neutron$ (g_{7/2},d_{5/2}) $ orbitals close to the Fermi surface. Fig. 6 (b) shows that the proton N = 4 major shell also contributes to a gradual increase of the angular momentum alignment around the backbending frequency$ \hbar\omega\sim $ 0.4 MeV, and that the off-diagonal part contributes considerably. Furthermore, the proton off-diagonal parts$j_x(\pi 5/2^+ $ $ [422] \pi 7/2^+[413]) $ , and$ j_x\left(\pi 7/2^+[413] \pi 9/2^+[404]\right) $ are mainly responsible for this gradual increase in proton angular momentum alignment. It can also be seen that in the higher rotational frequency region$ \hbar\omega > 0.55 $ MeV, the increase of the angular momentum alignment from the proton N = 4 major shell is slower than from the neutron N = 4 major shell. This again tell us that the increase of the angular momentum alignment from AMR is smaller than that provided by the neutron$ (g_{7/2},d_{5/2}) $ orbitals in the higher rotational frequency region.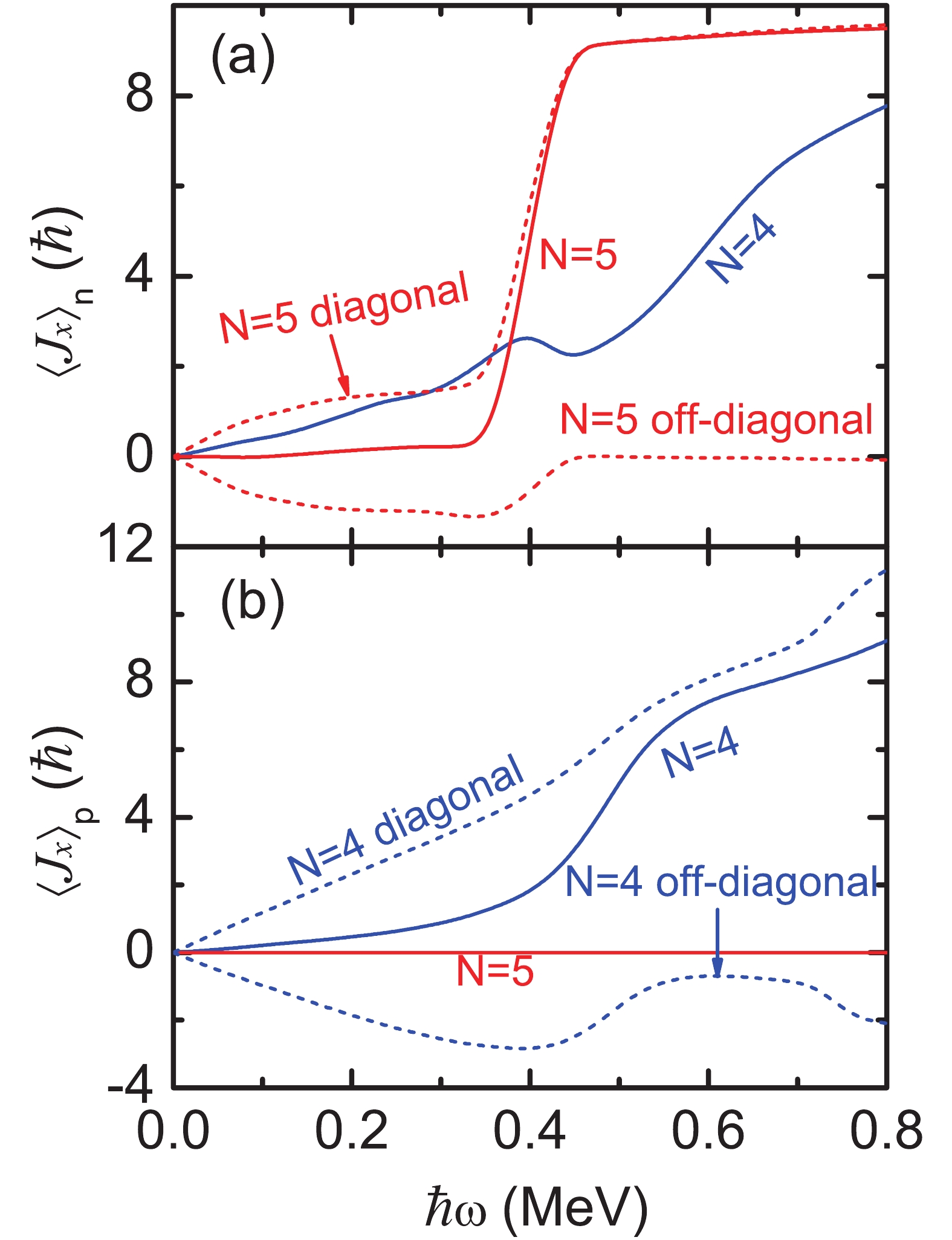
Figure 6. (color online) Contributions of (a) neutron and (b) proton N = 4 and 5 major shells to the angular momentum alignment
$\langle J_x\rangle$ for GSB of 104Pd. Contributions of diagonal$\sum_{\mu} j_x(\mu)$ and off-diagonal parts$\sum_{\mu<\nu} j_x(\mu\nu)$ (c.f., Eq. 6) from the neutron N = 5 and proton N = 4 major shells are denoted by dashed lines.Figure 7 shows the angular momentum vectors of the four proton
$ g_{9/2} $ holes ($ j_\pi $ ) and neutrons ($ J_\nu $ ) for GSB of 104Pd for rotational frequencies from 0.45 to 0.75 MeV. Each$ j_\pi $ includes the contribution from two proton$ g_{9/2} $ holes. Note that due to the pairing correlations, the contribution from the off-diagonal part$ \sum_{\mu<\nu} j_x(\mu\nu) $ of protons is not zero (c.f., Fig. 6), especially in the lower rotational frequency region ($ \hbar\omega $ = 0.45 to 0.60 MeV). Therefore, it is difficult to separate the contribution of each proton$ g_{9/2} $ hole to the angular momentum alignment to get the “umbrella”-like AMR mode as in Ref. [26]. However, for rotational frequency$ \hbar\omega>0.60 $ MeV, the four proton$ g_{9/2} $ holes are almost empty and the contribution from the off-diagonal part to$ J_x $ becomes small. Therefore, we can approximately separate the angular momenta of these four$ g_{9/2} $ holes by neglecting the contribution from the off-diagonal part to$ J_x $ , which has been shown as an inset in Fig. 7. According to Ref. [45],$ J_z $ is calculated approximately by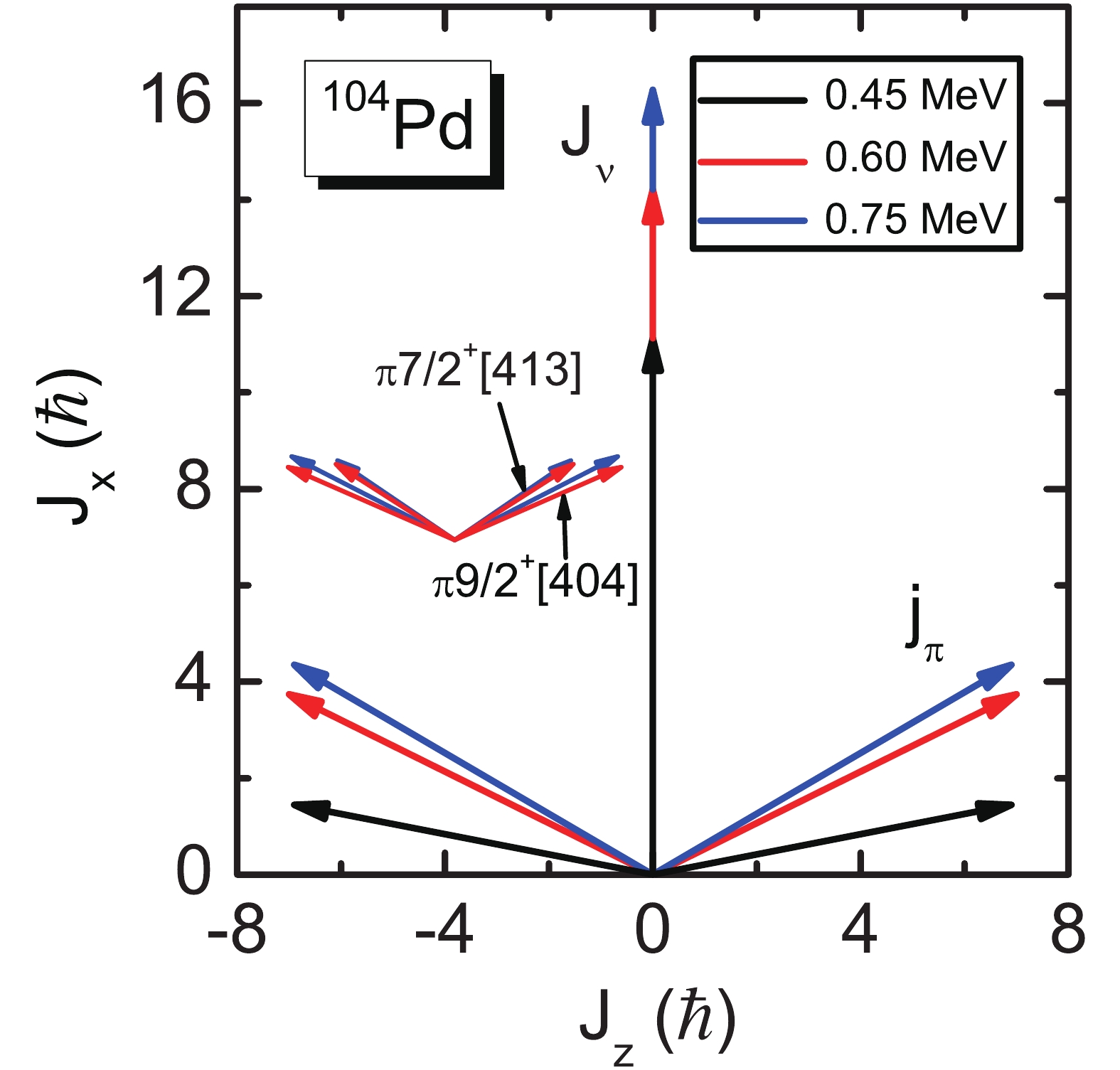
Figure 7. (color online) Angular momentum vectors of the four proton
$g_{9/2}$ holes ($j_\pi$ ) and neutrons ($J_\nu$ ) for GSB of 104Pd. Each$j_\pi$ includes the contribution from two proton$g_{9/2}$ holes. The inset shows the angular momentum vectors of the four proton$g_{9/2}$ holes ($\pi9/2^+[404]$ and$\pi7/2^+[413]$ ) separately by neglecting the off-diagonal part in Eq. (6).${J_z} = \sqrt {\langle \Psi |J_z^2|\Psi \rangle } $

(13) in the PNC-CSM formalism. By comparing the principal axis cranking with the particle rotor model, this method has already been demonstrated to be a good approximation. One can see from Fig. 7 that for
$ \hbar\omega = 0.45 $ MeV, the proton vectors$ j_\pi $ are pointing in opposite directions and are nearly perpendicular to the neutron vector$ J_\nu $ . As the rotational frequency increases, the two proton$ j_\pi $ vectors gradually close toward the neutron$ J_\nu $ vector, while the direction of the total angular momentum stays unchanged. Therefore, a higher angular momentum is generated due to the “two-shears-like” mechanism. For the rotational frequency$ \hbar\omega = 0.45 $ to 0.75 MeV, the neutron angular momentum alignment increases smoothly. This is due to the alignment of neutrons in the$ g_{7/2} $ and$ d_{5/2} $ orbitals, which is consistent with the TAC-CDFT calculations in Ref. [26]. The two proton blades close rapidly with rotational frequency for$ \hbar\omega = 0.45 $ to 0.60 MeV, and the magnitude of the two$ j_\pi $ vectors is no longer constant. This is similar to 101Pd [33], which originates from the occupation rearrangement in the proton$ g_{9/2} $ orbitals. It should be noted that since the pairing correlations are neglected in the TAC-CDFT calculations for 104Pd in Ref. [26], the four proton$ g_{9/2} $ holes are totally empty, and there is no proton occupation rearrangement process with increasing rotational frequency. Therefore, the proton blades with nearly constant magnitudes close steadily as the rotational frequency increases, which is quite different from the angular momenta picture in our PNC-CSM calculations. As the rotational frequency increases from 0.60 to 0.75 MeV, the closing of the two proton blades becomes slow and steady, which is similar to the typical AMR in 105,106Cd [32]. Therefore, two stages of AMR in 104Pd are clearly seen. It can also be seen from the inset of Fig. 7 that, as their magnitude is constant, the angular momentum vectors of the four proton$ g_{9/2} $ holes ($ \pi9/2^+[404] $ and$ \pi7/2^+[413] $ ) close simultaneously with increasing rotational frequency. In addition, the two$ \pi9/2^+[404] $ blades close faster than the$ \pi7/2^+[413] $ blades, which indicates that the two$ \pi9/2^+[404] $ holes contribute more angular momentum in the typical AMR mode. -
In summary, the particle-number-conserving method based on the cranked shell model was used to investigate the AMR band in 104Pd. The experimental MOIs are reproduced quite well. In order to reproduce the B(E2) values, a corresponding deformation change with increasing rotational frequency is necessary. The
$ J^{(2)}/B(E2) $ ratio has also been discussed. The occupation probability of each orbital close to the Fermi surface and the contribution of each major shell to the total angular momentum alignment as function of rotational frequency were analyzed. The backbending mechanism of the ground state band in 104Pd is clearly understood, and the configuration of AMR after backbending was clarified. The present calculations suggest that the configuration of the AMR band in 104Pd should be$ \pi g_{9/2}^{-4} \otimes \nu[h_{11/2}^2,(g_{7/2},d_{5/2})^6] $ when the pairing correlations are neglected, which is consistent with the TAC-CDFT calculations with PC-PK1. Furthermore, the crossing of a four quasiparticle state with this AMR band is also predicted. Finally, the “two-shears-like” mechanism for AMR was investigated by examining the shears angle, and two stages of AMR in 104Pd are clearly seen.
Theoretical investigation of the antimagnetic rotation in 104Pd
- Received Date: 2019-01-19
- Available Online: 2019-05-01
Abstract: The particle-number-conserving method based on the cranked shell model is used to investigate the antimagnetic rotation band in 104Pd. The experimental moments of inertia and reduced B(E2) transition probabilities are reproduced well. The J(2)/B(E2) ratios are also discussed. The occupation probability of each orbital close to the Fermi surface and the contribution of each major shell to the total angular momentum alignment as function of rotational frequency are analyzed. The backbending mechanism of the ground state band in 104Pd is understood clearly and the configuration of the antimagnetic rotation after backbending is clarified. In addition, the crossing of a four quasiparticle state with this antimagnetic rotation band is also predicted. By examining the closing of the angular momenta of four proton holes towards the neutron angular momentum, the " two-shears-like” mechanism for this antimagnetic rotation is investigated and two stages of antimagnetic rotation in 104Pd are clearly seen.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: