-
The discovery of
$^{59,60}{\rm{Ca}}$ and it's neighbouring isotopes, which are supposedly the most neutron-rich nuclei of different elements known today, opened the door to the possibility of the existence of more neutron-rich isotopes [1]. The$ ^{70} {\rm{Ca}}$ nucleus has inspired a lot of interest, as it could represent a double magic nucleus that could be weakly bound [1]. The decay modes of$ ^{61, 68} {\rm{Ca}}$ have been studied with machine learning [2]. Research in the area of extreme isotopes could provide extensive information on the nuclear structure, e.g., shell evolution, life-time, exotic particle emission, and cluster formation, etc. The RIKEN-BigRIPS two-stage in-flight separator, with its high precise identification ability, has played an important role in providing the neutron-rich 70Zn beam [3]. With the third generation of radioactive ion beam (RIB) facilities, the area of drip line nuclei is highly competitive due to the significant asymmetry of projectile nuclei in reality. Typically, experiments with 70Zn (neutron-rich) and$ ^{78} {\rm{Kr}}$ (neutron-deficient) have been performed, and important phenomena have been discovered on the RIKEN-BigRIPS.The planned Beijing Isotope-Separation-On Line Neutron-Rich Beam Facility (BISOL), which is a third generation RIB facility combining the advantages of the second generation of Isotope-Separation-On Line (ISOL) and projectile fragmentation (PF) facilities, is able to produce high density neutron-rich beams generated by fissile fragments from the China Advanced Research Reactor (CARR) from about 20 A MeV to 150 A MeV. In physics, for a projectile fragmentation reaction, more neutron-rich projectiles enhance the production of neutron-rich isotopes because of the isospin effect [4]. Fissile fragments, such as 80Zn, can serve as projectiles on BISOL, which makes it a highly competitive facility among the third generation RIB facilities around the world, in particular for intermediate energy heavy-ion reactions. Hence, it is of interest to estimate if the very neutron-rich nuclei, such as 70Ca, could be discovered by BISOL. The theoretical prediction for isotopes near the drip-line is required for experimental design.
Considering theoretical predictions for fragment production in PF reactions, the successful models include different types (provided in a recent review [5]), which specify general methods to predict the cross-sections of fragments. For the production of extreme isotopes near drip lines, FRACS [6] and FRACS-C [7] have been shown to successfully predict neutron-rich and neutron-deficient isotopes. In neutron-rich and neutron-deficient isotopes, even in the extreme cases, an exponential dependence on their average binding energy was observed [8–10]. Based on the measured cross-sections for
$ ^{59, 60} {\rm{Ca}}$ in the 345 A MeV$ ^{70} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reaction [1], we estimate the cross-section for$ ^{66, 70} {\rm{Ca}}$ combining the FRACS parametrization and the empirical formula between the isotopic cross-section and the average binding energy. Considering that the advantage energy range for the radioactive nuclear beam of the neutron-rich isotope is below 100 A MeV, three incident energies, i.e., 345, 80, and 60 A MeV for two reactions$ ^{70, 80} {\rm{Zn}}+^{9} {\rm{Be}}$ are investigated in this article. -
The FRACS parametrization [6] can predict cross-sections for fragments that survive in projectile fragmentation reactions above 140 A MeV. The FRACS parametrization originates from the EPAX3 parametrization [11], however, it overcomes the shortages of the latter's independence on the incident energy. For an isotope with mass number and charge number (A, Z), the cross-section is described as,
$ \sigma(A,Z) = Y(A)Y(Z_{\rm prob}-Z)\Delta_{\rm OES}(A,Z), $

(1) where
$ Y(A) $ is the mass yield that depends on the included incident energy dependencies terms. The isobaric distribution$ Y(Z_{\rm prob}-Z) $ , borrowed from the EPAX3 parametrization [11] shows that the form of the Gaussian distribution.$ \Delta_{\rm OES}(A,Z) $ is introduced in FRACS to deal with the odd-even staggering phenomenon in the cross-section distribution.An empirical correlation between the isotopic cross section and average binding energy was established by Tsang et al. [8,12], observing that the neutron-rich copper isotopes obey the formula suggested within the canonical ensemble theory. Further studies show that the neutron-deficient isotopes likewise obey this formula [9,10,13]. The suggested empirical formula is,
$ \sigma = C{\rm{exp}}\left[ {\left( {\left\langle {B'} \right\rangle - 8} \right)/\tau } \right], $

(2) where
$ C $ and$ \tau $ are free parameters.$\left\langle {B'} \right\rangle = (B - {\varepsilon _p})/A $ denotes the average binding energy per nucleon of the fragment, where$ \varepsilon_{p} $ is the pairing energy dealing with the odd-even staggering phenomenon in the isotopic cross-section distribution. The form of the pairing energy$ \varepsilon_{p} $ is as follows,$ \varepsilon_{p} = 0.5[(-1)^N + (-1)^Z]\varepsilon_{0}\cdot A^{-3/4}, $

(3) where
$ \varepsilon_{0} = $ 30 MeV was chosen according to Ref. [8]. If the value of$ C $ and$ \tau $ are known, the cross-section for an isotope can be predicted using its binding energy.In this study, both methods are used to predict the isotopic cross-section. A general procedure as described in the following section is maintained to predict the cross-sections for fragments. We first predict the isotopic cross-section using FRACS. Subsequently, from the fragments with measured binding energy reported in AME16 [14], we determine the values of
$ C $ and$ \tau $ for each isotopic chain. These are, in the following process, used to predict the cross-sections with the help of the binding energy calculated by the spherical relativistic continuum Hartree-Bogoliubov (RCHB) theory with the relativistic density functional PC-PK1 [15]. -
First, the isotopic cross-sections for fragments produced in the 345 A MeV
$ ^{70} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reaction are predicted by the FRACS parametrization, which are plotted in Fig. 1 and denoted by full symbols. The predicted results include the isotopes from$ Z = 15 - 30 $ . Compared to the measured cross-sections (half-full symbols) for$ ^{59} {\rm{Ca}}$ [($ 8.0\pm3.0 $ )$ \times10^{-13} $ mb] and$ ^{60} {\rm{Ca}}$ [($ 2.1\pm1.5 $ )$ \times10^{-13} $ mb], the FRACS predictions ($ 8.5\times10^{-13} $ mb and$ 3.5\times10^{-14} $ mb, respectively) are in good agreement.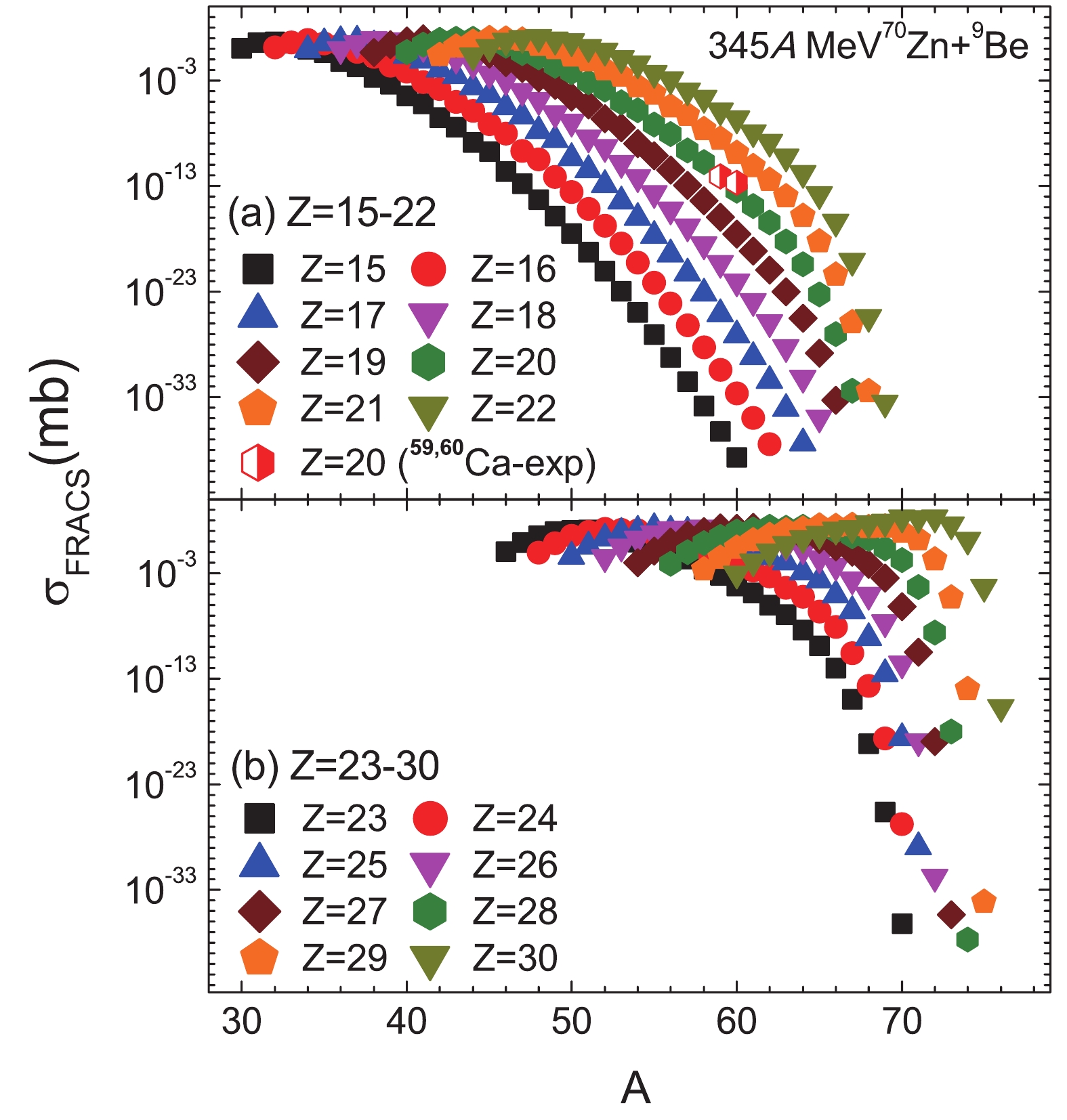
Figure 1. (color online) Predicted isotopic cross-section distributions for
$Z = 15 - 30$ fragments in the 345 A MeV 70Zn+9Be reaction by FRACS parametrization (full symbols). The measured cross-sections for$^{59}{\rm{Ca}}$ and$^{60}{\rm{Ca}}$ in the same reaction in Ref. [1] are denoted by the half-full symbols.From previous investigations, we can assume that the predicted results by FRACS are reliable for the isotopes with known experimental binding energies [6,10,13]. Hence, they can be used to verify whether the correlation in Eq. (2) is maintained in the isotopes near the neutron-drip line. In Fig. 2, the correlation between the isotopic cross section and the average binding energy is plotted in three panels, i.e., for the
$ Z = 15-19 $ [in panel (a)],$ Z = 20-25 $ [in panel (b)], and$ Z = 25-29 $ [in panel (c)], respectively. For the isotopes predicted by the FRACS parametrization, the binding energies are taken from AME16 [14] (denoted by full symbols). The exponential dependence of isotopic cross-section on$\left\langle {B'} \right\rangle $ is maintained, as seen from the figure. The values for$ C $ and$ \tau $ in Eq. (2) are obtained by fitting the correlation from the predictions obtained by the FRACS parametrization. The results show that the slopes of the distribution change slightly with$ Z $ , especially for$ Z \leqslant 19 $ isotopes, while this dependence becomes significantly smaller when$ Z \geqslant 25 $ . This phenomenon is discussed later. The cross-sections for the more neutron-rich isotopes are predicted by Eq. (2) with the fixed values of$ C $ and$ \tau $ for each isotopic chain by adopting the binding energy predicted by the RCHB (open symbols) method.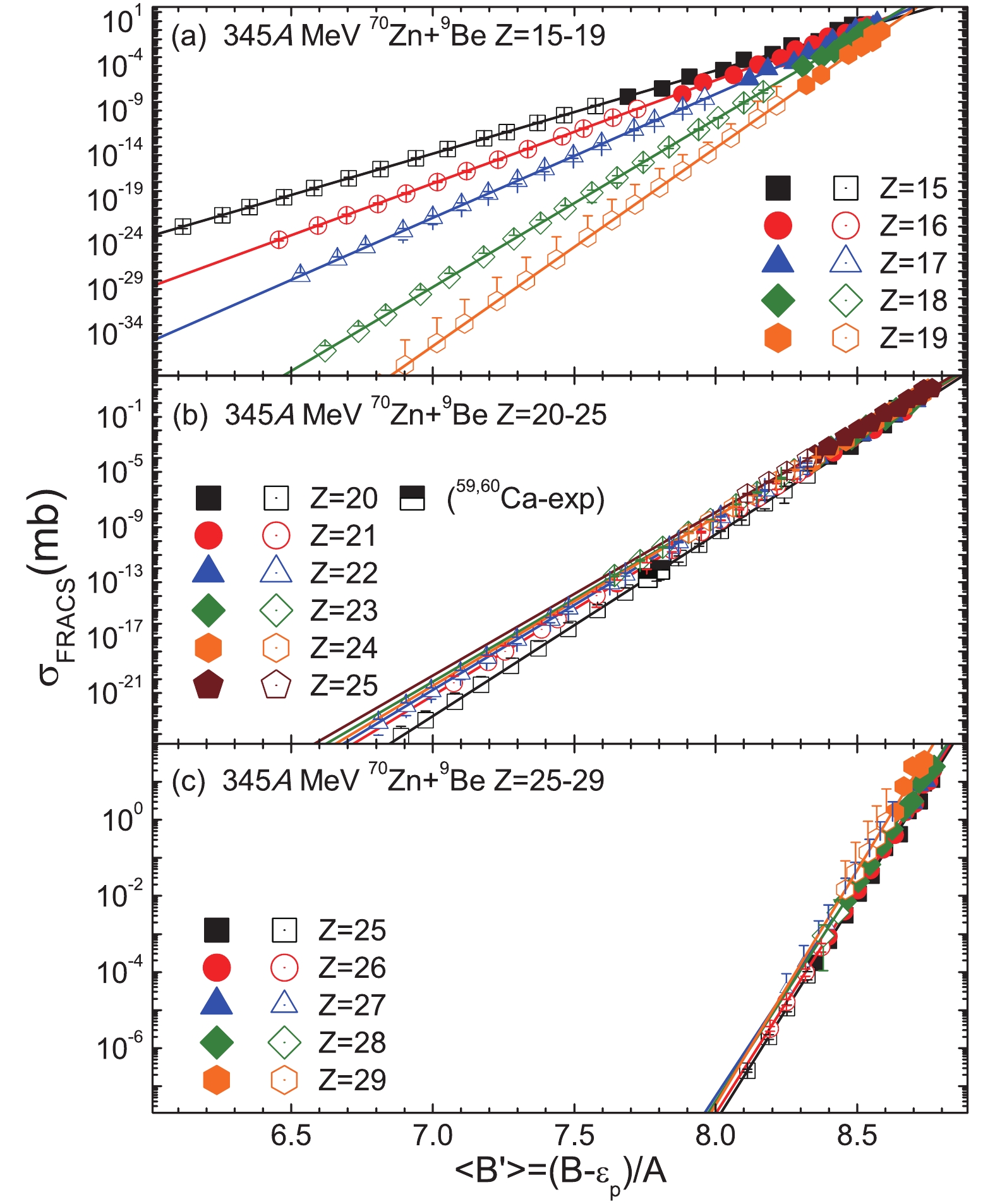
Figure 2. (color online) Exponential correlation between
$ \sigma $ and$\left\langle {B'} \right\rangle $ for neutron-rich$ Z = 15 - 29 $ isotopes produced in the 345 A MeV$ ^{70} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reaction. Lines are determined by fitting full symbols on the basis of Eq. (2). Full symbols denote the$ \sigma $ predicted by FRACS and the$\left\langle {B'} \right\rangle $ with the experimental binding energy taken from AME2016 [14]. The open symbols denote the predicted$ \sigma $ by Eq. (2) adopting the binding energy by a RCHB theory. Half-full symbols denote the predicted$\left\langle {B'} \right\rangle $ for$ ^{59, 60} {\rm{Ca}}$ using the measured cross-sections by Tarasov [1].The planned Beijing ISOL (BISOL) facility is aimed to provide more neutron-rich projectiles, such as 80Zn, which will extend the projectile system to one that is extremely neutron-rich. The ability provide the chance to found more neutron-rich isotopes, e.g.,
$ ^{70} {\rm{Ca}}$ (which is supposedly a double magic number nucleus). It is of great interest to determine the cross-section for extreme isotopes in the experiments that could be performed on BISOL. The isotopic cross-sections for fragments in the 80 A MeV and 60 A MeV$ ^{80} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reactions are predicted using the same methods as those in the 345 A MeV$ ^{70} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reactions described above. The isotopic cross-section distribution for the fragments predicted by the FRACS parametrization is plotted in Fig. 3. The correlation between the isotopic cross-section and$\left\langle {B'} \right\rangle $ is plotted in Figs. 4 and 5 for 80 A MeV and 60 A MeV 80Zn + 9Be reactions, respectively. Similar results as in the 345 A MeV$ ^{70} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reactions can be found, except that the slopes for the isotopic distributions are always changing.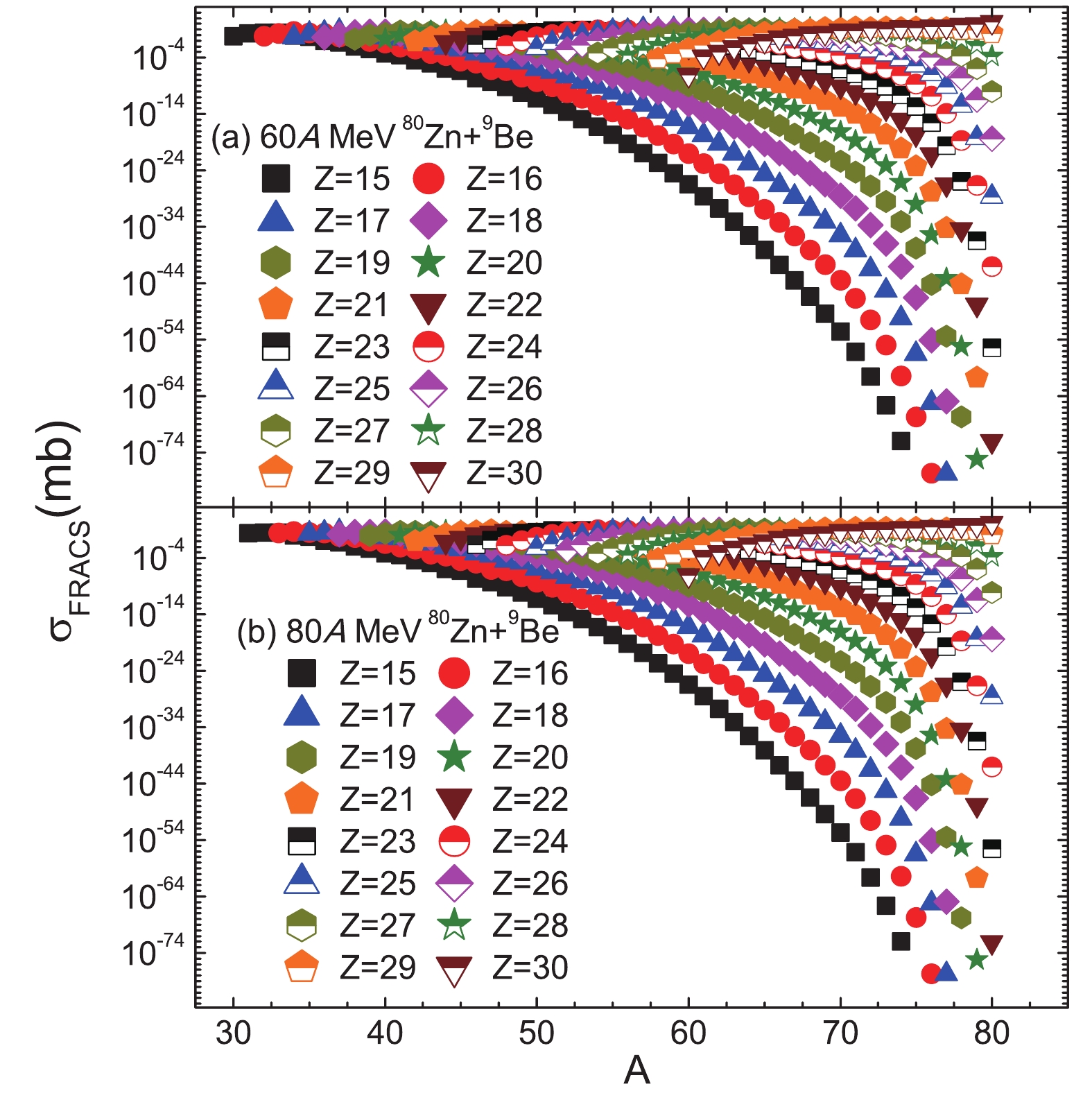
Figure 3. (color online) Predicted cross-section for neutron-rich
$ Z = 15 - 30 $ isotopes produced in the 60 and 80 A MeV$ ^{80} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reactions by the FRACS parametrization.
Figure 4. (color online) As Fig. 2, but for the predicted 60 A MeV
$ ^{80} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reaction.
Figure 5. (color online) As Fig. 2 but for the predicted 80 A MeV
$ ^{80} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reaction.The
$ C $ and$ \tau $ values can be compared for different isotopes, as well as for reactions at different incident energies, since the slope of the isotopic distribution varies with the charge number. Since two different projectiles (70,80Zn) were investigated, we likewise determine the$ C $ and$ \tau $ for the isotopic cross-section distributions for the 345 A MeV$ ^{80} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reaction (however, we do not show the results in this article), and compare the values of$ C $ and$ \tau $ in Fig. 6. For the$ ^{80} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reaction, the incident energy of the reactions show less influence on$ C $ and$ \tau $ , especially for the 60 A MeV and 80 A MeV reactions, while the difference between the 60 (80) A MeV reactions and 345 A MeV reactions becomes relatively large when Z > 25. This can be explained, since the FRACS parametrization has been verified to be effective above 140 A MeV [6], whereas below 140 A MeV, the incident energy dependence of fragment production should be further improved with the help of experimental results. It also can be concluded that$ C $ (and$ \tau $ ) significantly depends on the asymmetry of the projectile nucleus, since there are large gaps between the values for the$ ^{70} {\rm{Zn}}$ and$ ^{80} {\rm{Zn}}$ reactions.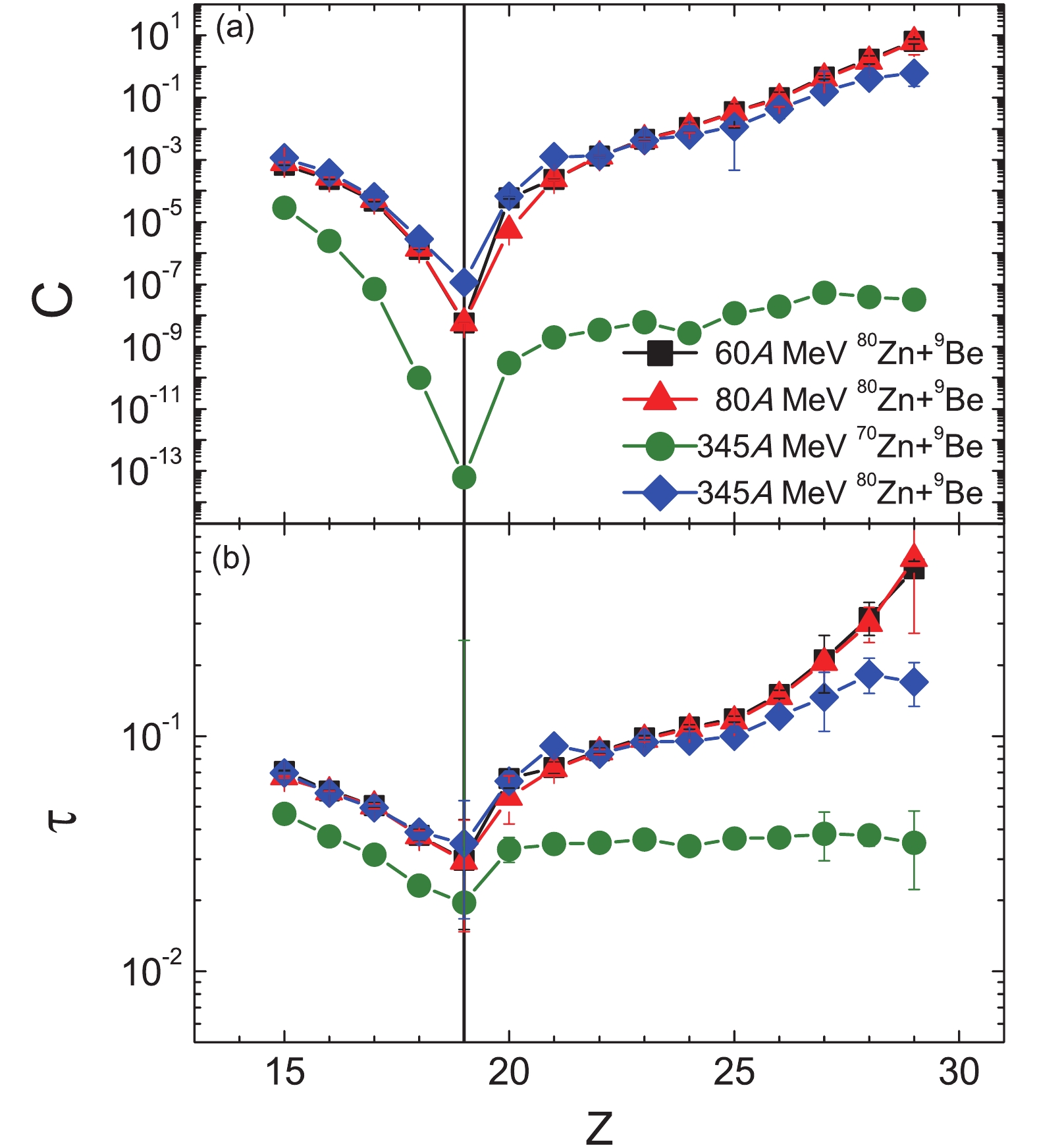
Figure 6. (color online) The determined values of
$ C $ [in panel (a)] and$ \tau $ [in panel (b)] for the isotopic cross-section distributions in the 345 A MeV$ ^{70} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reaction, and in the 60, 80, 345A MeV$ ^{80} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reactions.The values of
$ C $ and$ \tau $ clearly depend on the mass of the projectile nucleus, as well as the charge number$ Z $ of fragments. The reason has been discussed in Ref. [10] by comparing Eq. (2) to the canonical ensemble theory within grand canonical limitations. The trend of the dependence of$ C $ and$ \tau $ on$ Z $ changes around Z = 20. For$ Z < $ 20, the values of$ C $ and$ \tau $ decrease when$ Z $ increases, which has also been observed in the neutron-deficient isotopes of smaller$ Z $ [10]. For$ Z \geqslant $ 20, the values of$ C $ and$ \tau $ increase with$ Z $ for the$ ^{80} {\rm{Zn}}$ reactions, while the value of$ C $ slightly increases with$ Z $ , and$ \tau $ is relatively consistent for the 345 A MeV reactions. The magic number Z = 20, which indicates the shell closure for charge, plays an important role for$ C $ and$ \tau $ .Next, we discuss the cross sections for the neutron-rich calcium isotopes. In Fig. 7 and Table 1 shows the predicted isotopic cross-section distributions in the 60, 80, and 345 A MeV
$ ^{70, 80} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reactions by the FRACS and Eq. (2). Both the FRACS parametrization and Eq. (2) can efficiently predict the measured$ ^{59, 60} {\rm{Ca}}$ in the 345 A MeV$ ^{70} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reaction. Meanwhile, when the fragment becomes more neutron-rich, the results predicted by the FRACS parametrization drop much faster than those by Eq. (2), exhibiting a significant difference. This could be attributed to the FRACS parameterizations, where the parameters are fixed by existing experimental data with a limited neutron-richness of the fragment. When the fragment reaches the drip-line, the parameters become invalid. For the reactions of incident energy below 100 A MeV, the energy-dependent parameters in FRACS are not specially adjusted, and the prediction becomes worse [6] (A delicate improvement has been made for neutron-deficient isotopes below 140 A MeV in our recent work [7]). In Eq. (2), with both$ C $ and$ \tau $ fixed, the isotopic distribution obeys the same trend. In the 60 A MeV and 80 A MeV$ ^{80} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reactions, the cross-sections for$ ^{66} {\rm{Ca}}$ are predicted to be$2 \times 10^{-10} $ mb and$1 \times 10 ^{-12} $ mb, respectively; while for$ ^{70} {\rm{Ca}}$ the results are$7 \times 10^{-13} $ mb and$1 \times 10^{-15} $ mb, respectively. The predictions for$ ^{66, 70} {\rm{Ca}}$ in the 345 A MeV$ ^{80} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reaction are similar to those of the 60 A MeV reaction, since the values for$ C $ and$ \tau $ are likewise similar.$ ^{66} {\rm{Ca}}$ and$ ^{70} $ Ca are likely to be discovered with the delicate design of a reaction system and incident energy.$ ^{66} {\rm{Ca}}$ has the cross-section three magnitudes larger than 70Ca. With the very neutron-rich$ ^{80} {\rm{Zn}}$ projectile, the production of$ ^{59, 60, 70} {\rm{Ca}}$ will be significantly ($ 10^{6} $ ) enhanced compared to the$ ^{70} {\rm{Zn}}$ projectile.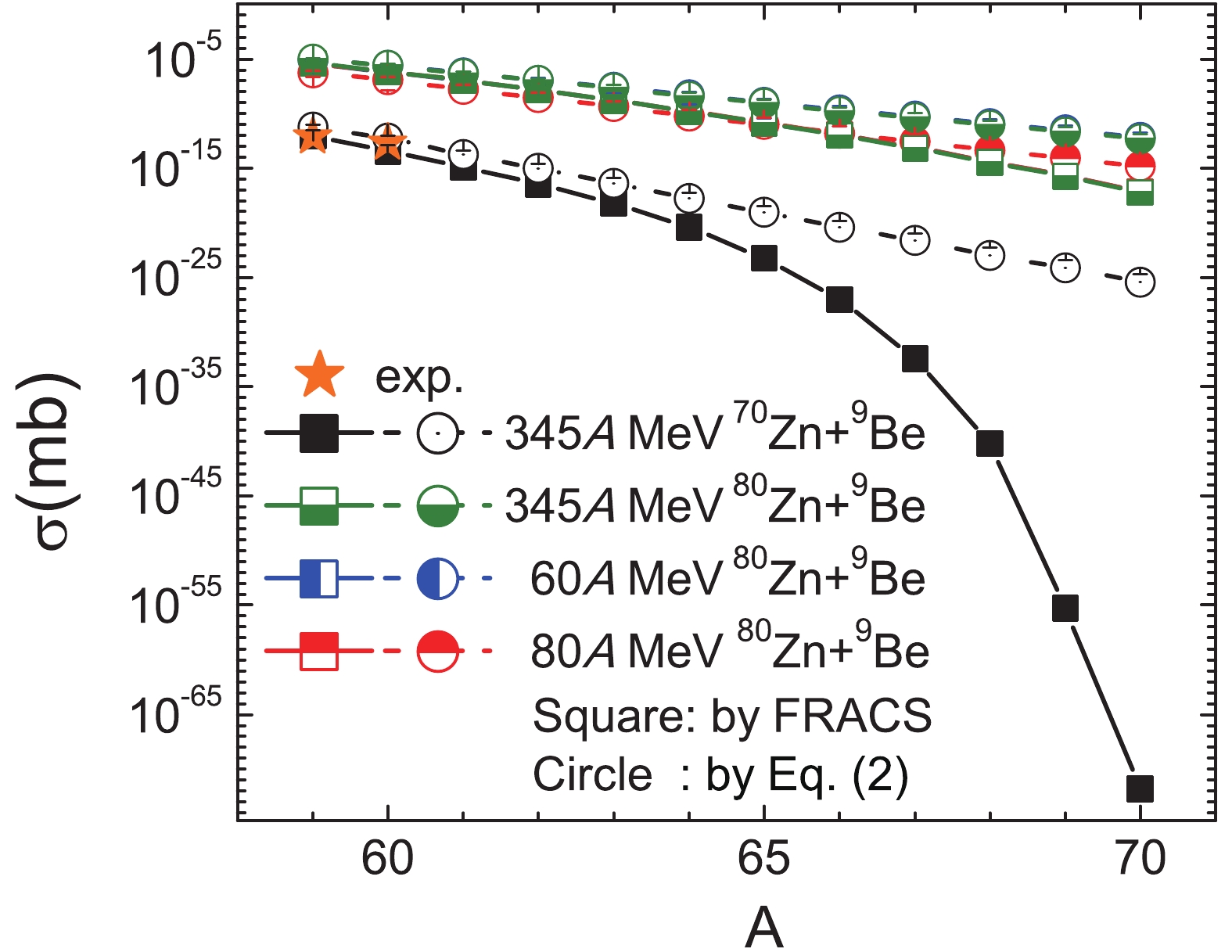
Figure 7. (color online) Predicted cross-sections for the neutron-rich
$ Z = 20 $ isotopes in the 345A MeV$ ^{70} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reaction, and the 60, 80, and 345 A MeV$ ^{80} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reactions by FRACS, Eq. (2), which are denoted by squares and circles, respectively. Measured cross-sections for$ ^{59, 60} {\rm{Ca}}$ in the 345 A MeV$ ^{70} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reaction are plotted as stars. The cross-sections for calcium isotopes overlap for$ ^{80} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reactions at different incident energies.E Proj. By 59Ca 60Ca 66Ca 70Ca 345 70Zn FRACS $ 9\times10^{-13} $ 

$ 4\times10^{-14} $ 

$ 9\times10^{-28} $ 

$ 1\times10^{-72} $ 

Eq.(2) $ 6\times10^{-12} $ 

$ 5\times10^{-13} $ 

$ 4\times10^{-21} $ 

$ 4\times10^{-26} $ 

80 80Zn FRACS $ 4\times10^{-6} $ 

$ 7\times10^{-7} $ 

$ 1\times10^{-12} $ 

$ 7\times10^{-18} $ 

Eq.(2) $ 5\times10^{-7} $ 

$ 1\times10^{-7} $ 

$ 1\times10^{-12} $ 

$ 1\times10^{-15} $ 

60 80Zn FRACS $ 3\times10^{-6} $ 

$ 6\times10^{-7} $ 

$ 1\times10^{-12} $ 

$ 7\times10^{-18} $ 

Eq.(2) $ 8\times10^{-6} $ 

$ 3\times10^{-6} $ 

$ 2\times10^{-10} $ 

$ 7\times10^{-13} $ 

Table 1. Predicted cross-sections for
$ ^{59, 60, 66, 70} {\rm{Ca}}$ by FRACS parametrization and Eq. (2). E has the unit of$ A $ MeV, and the cross-sections are in units of mb. -
In this study, the isotopic cross-sections were studied by the combination of FRACS parametrization and the empirical formula between the isotopic cross-section and average binding energy. The results show that both the FRACS parametrization and Eq. (2) efficiently predict the cross sections for 59, 60Ca, which are measured in the 345 A MeV
$ ^{70} {\rm{Zn}}+ ^{9} {\rm{Be}}$ reaction. Although FRACS and Eq. (2) are similar for calcium isotopes of$ A<64 $ , the difference between the two methods becomes very large for$ A>64 $ . Meanwhile, at lower incident energies (< 100 A MeV), the predictions by FRACS and Eq. (2) are similar. Further studies show that if the$ ^{80} {\rm{Zn}}$ projectile nucleus is selected and the incident energy of the reaction to 60 A MeV is lowered, the cross-sections for$ ^{59, 60, 66, 70} {\rm{Ca}}$ could be highly enhanced, and the drip-line nuclei$ ^{66, 70} {\rm{Ca}}$ could potentially be discovered. Considering the predicted results, the planned BISOL facility will provide a lot of opportunities in the area of research of extreme isotopes at the neutron-drip line.
Cross-section prediction for isotopes near neutron drip line in 70, 80Zn projectile fragmentation reactions
- Received Date: 2019-02-16
- Accepted Date: 2019-04-15
- Available Online: 2019-07-01
Abstract: The cross sections for 59, 60Ca, recently measured in the 345 A MeV





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: