-
At radioactive ion beam (RIB) facilities, the reactions induced by beryllium isotopes have been one of the most interesting research topics. In particular, the RIB provides the opportunity to study properties of exotic nuclei, such as
$ ^{11} {\rm Be}$ [1, 2]. In these reactions, the beryllium isotopes are usually employed as projectiles, which may comprise the stable weakly bound nucleus$ ^{9} {\rm Be}$ , tightly bound nucleus$ ^{10} {\rm Be}$ , radioactive non-halo nucleus$ ^{7} {\rm Be}$ , neutron halo nucleus$ ^{11} {\rm Be}$ , etc.To study the reactions involving beryllium isotopes, we often adopt the phenomenological optical model potential (OMP) to describe elastic scattering. The potential assumes a dependence by a number of adjustable parameters for the real and imaginary part, which characterize the shape of the nuclear density distribution and change with the projectile energy and target mass number [3]. In particular in the global phenomenological OMP, the prediction of basic observables is efficient for some energies and nuclides ranges [4].
To date, we have determined a new set of global phenomenological OMP parameters for the stable weakly bound nucleus
$ ^{9} {\rm Be}$ by simultaneously fitting the existing experimental data of the elastic scattering angular distributions and total reaction cross-sections [5]. The results can efficiently reproduce those data. For the$ ^{7,10,11,12} {\rm Be}$ isotopes, the elastic scattering experimental data is scarce. Especially for$ ^{12} {\rm Be}$ , no experimental data exists on elastic scattering angular distributions. Therefore, the global phenomenological OMPs for these beryllium isotopes cannot obtained by adjusting the corresponding experimental data. The weakly bound nucleus$ ^{7} {\rm Be}$ is an odd-A nucleus and has a negative parity spin,$ J^{\pi} $ = 3/2–, which are the same characteristics exhibited by the stable weakly bound nucleus$ ^{9} {\rm Be}$ . As mentioned in Ref. [6], one neutron added to$ ^{9} {\rm Be}$ makes the$ ^{10} {\rm Be}$ nucleus more tightly bound and achieve a breakup threshold of 6.8 MeV for n+$ ^{9} {\rm Be}$ configurations. Thus, it may be reasonableto apply the$ ^{9} {\rm Be}$ global OMP to describe the$ ^{10} {\rm Be}$ elastic scattering. Hence, we use the obtained$ ^{9} {\rm Be}$ global OMP to predict the elastic scattering observables of$ ^{7,10,11,12} {\rm Be}$ projectiles, which offer an excellent opportunity to perform systematic studies on them.In the present work, the elastic scattering angular distributions and total reaction cross-sections of
$ ^{7,10,11,12} {\rm Be}$ are predicted using the$ ^{9} {\rm Be}$ global OMP for targets in the mass number range from 24 to 209. The predictions are compared with the available experimental data at different incident energies. Furthermore, predictions for some lighter targets out of the mass number range are obtained.Section 2 presents the method employed in this study. The data used in this study are analyzed, and the comparison of calculated results with experimental data is further displayed and discussed in detail. Finally, a brief summary is presented in Section 3.
-
The OMP is expressed as the sum of the real part potential
$ V_{R}(r,E) $ , the imaginary part potential of surface absorption$ W_{S}(r,E) $ and volume absorption$ W_{V}(r,E) $ , and a Coulomb potential$ V_{C}(r) $ :$ V(r,E) = V_{R}(r,E)+i[W_{S}(r,E)+W_{V}(r,E)]+V_{C}(r), $

(1) As outlined in Ref. [5], the form factor of real and imaginary potentials use the Woods-Saxon function
$ V_{R}(r,E) = -\frac{V_{R}(E)}{1+\exp[(r-R_{R})/a_{R}]}, $

(2) $ W_{S}(r,E) = -4W_{S}(E)\frac{\exp[(r-R_{S})/a_{S}]}{\{1+\exp[(r-R_{S})/a_{S}]\}^{2}}, $

(3) $ W_{V}(r,E) = -\frac{W_{V}(E)}{1+\exp[(r-R_{V})/a_{V}]}. $

(4) where,
$ V_{R}(E) $ ,$ W_{S}(E) $ , and$ W_{V}(E) $ are the energy-dependent potential depths, expressed as$ V_{R}(E) = V_{0}+V_{1}E+V_{2}E^{2}, $

(5) $ W_{S}(E) = \max\{0,W_{0}+W_{1}E\}, $

(6) $ W_{V}(E) = \max\{0,U_{0}+U_{1}E\}. $

(7) The Coulomb potential
$ V_{C} $ is$ V_{C}(r) = \left\{ \begin{aligned} &\frac{zZe^{2}}{2R_{C}}\left(3-\frac{r^{2}}{R^{2}_{C}}\right) &\quad r<R_{C}, \\ &\frac{zZe^{2}}{r} & \quad\quad r\geqslant R_{C}, \end{aligned} \right. $

(8) where z and Z are the charge number of the projectile and target, respectively.
The radius
$ R_{i} $ is defined as$ R_{i} = r_{i}A^{\frac{1}{3}}, \; \; \; \; \; \; i = R, S, V, C, $

(9) where A is target mass numbers.
$ r_{R} $ ,$ r_{S} $ ,$ r_{V} $ , and$ r_{C} $ are the radius parameters of the real part potential, the imaginary part potential of the surface and volume, and the Coulomb potential, respectively. The corresponding and respective diffuseness parameters are$ a_{R} $ ,$ a_{S} $ , and$ a_{V} $ . The radius parameter of the real potential is defined by$ r_{R} = r_{R_{0}}+r_{R_{1}}A^{\frac{1}{3}}. $

(10) Based on the experimental data of elastic scattering angular distributions and total reaction cross-sections, we have achieved a new set of
$ ^{9} {\rm Be}$ global OMP parameters [5] for the targets in the mass number range from 24 to 209, below 100 MeV. The parameters of global OMP are listed in Table 1.Parameter Value Unit $V_{0}$ 

268.0671 MeV $V_{1}$ 

−0.180 $V_{2}$ 

−0.0009 $W_{0}$ 

52.149 MeV $W_{1}$ 

−0.125 $U_{0}$ 

2.965 MeV $U_{1}$ 

0.286 $r_{R_{0}}$ 

1.200 fm $r_{R_{1}}$ 

0.0273 fm $r_{S}$ 

1.200 fm $r_{V}$ 

1.640 fm $r_{C}$ 

1.556 fm $a_{R}$ 

0.726 fm $a_{S}$ 

0.843 fm $a_{V}$ 

0.600 fm Table 1. Global phenomenological OMP parameters for 9Be.
We employ the obtained
$ ^{9} {\rm Be}$ global OMP to predict the elastic scattering observables for$ ^{7,10,11,12} {\rm Be}$ projectiles and compared this with the available experimental data. -
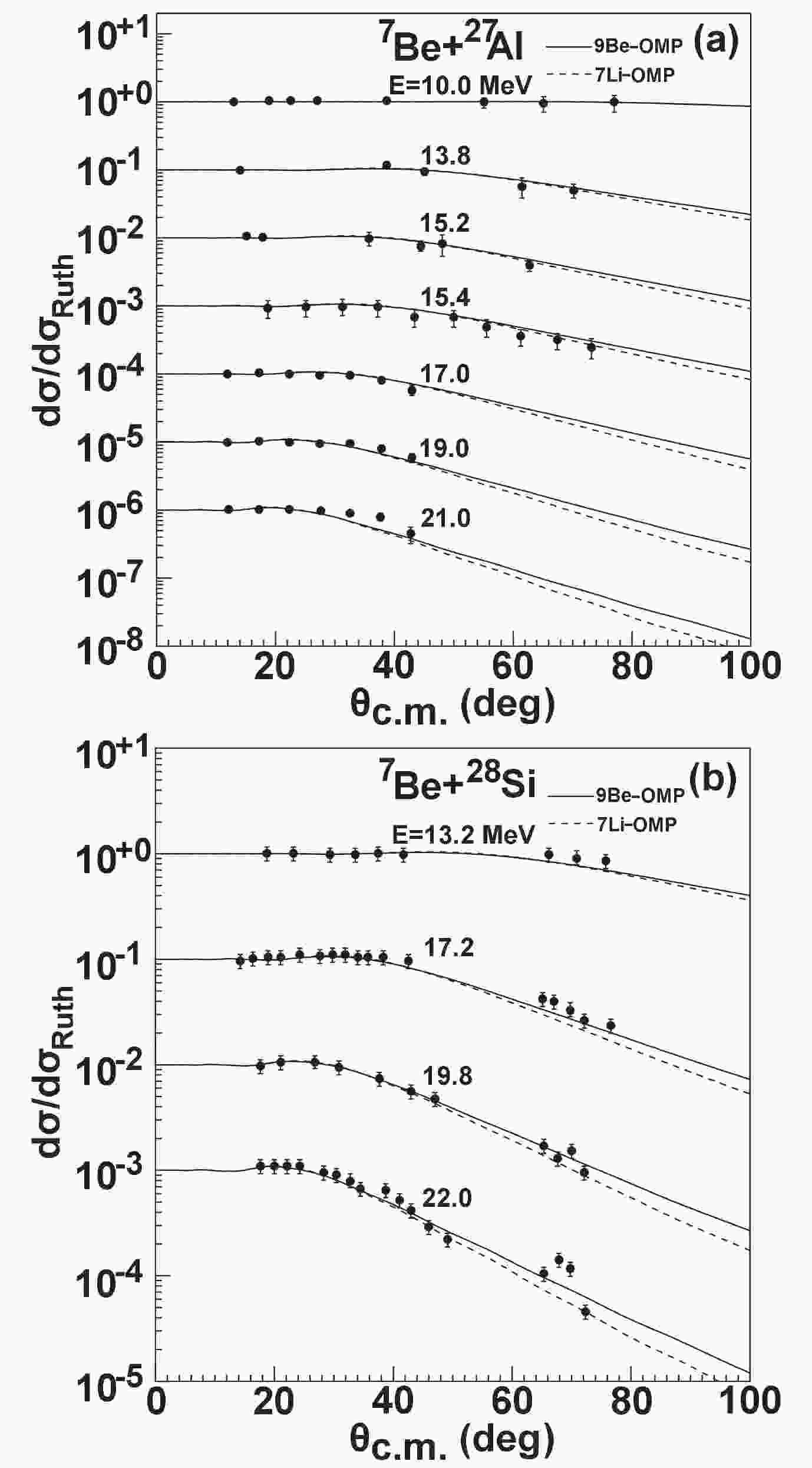
For the radioactive non-halo
$ ^{7} {\rm Be}$ projectile, the elastic scattering angular distributions are calculated using the$ ^{9} {\rm Be}$ global OMP. Figure 1 displays the comparison of theoretical results with the experimental data [7–9] for$ ^{7} {\rm Be}$ +$ ^{27} {\rm Al}$ and$ ^{7} {\rm Be}$ +$ ^{28} {\rm Si}$ systems. The incident energies of$ ^{7} {\rm Be}$ range from 10.0 MeV to 22.0 MeV. The theoretical results are highly consistent with these data. In contrast,$ ^{7} {\rm Li}$ is known as the mirror nucleus of$ ^{7} {\rm Be}$ , and the$ ^{7} {\rm Li}$ global OMP has been obtained by fitting existing experimental data of elastic scattering [10]. To further investigate the behavior of optical potentials for different projectiles, the elastic scattering angular distributions are also predicted using the$ ^{7} {\rm Li}$ global OMP. They are further compared with the corresponding experimental data and the predictions of$ ^{9} {\rm Be}$ global OMP. Most of the results agree and are consistent with the experimental data for these systems, and the results calculated using the$ ^{9} {\rm Be}$ global OMP fit the experimental data better than those of the$ ^{7} {\rm Li}$ global OMP for backward angles at individual incident energies.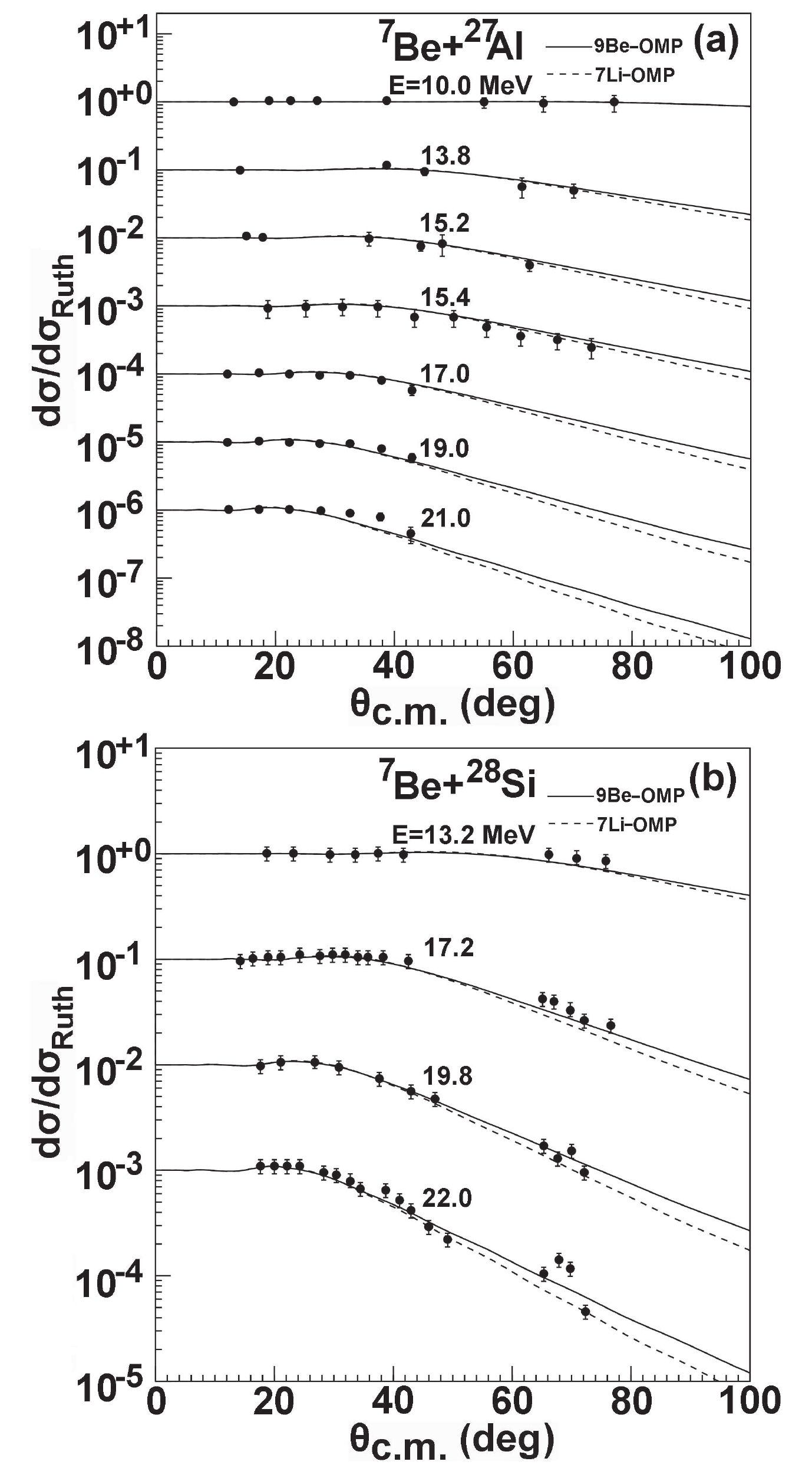
Figure 1. Comparisons of
$^{7}{\rm Be}$ elastic scattering angular distributions calculated using$^{9}{\rm Be}$ and$^{7}{\rm Li}$ global OMPs with corresponding experimental data for$^{27}{\rm Al}$ and$^{28}{\rm Si}$ .Figure 2 shows the comparison of elastic scattering angular distributions with the corresponding experimental data for
$ ^{51} {\rm V}$ ,$ ^{58} {\rm Ni}$ , and$ ^{208} {\rm Pb}$ targets [11–14]. The present calculations efficiently reproduce these experimental data, although the incident energies are above 100 MeV for the$ ^{7} {\rm Be}$ +$ ^{208} {\rm Pb}$ system. The results calculated using the$ ^{7} {\rm Li}$ global OMP are also shown. Compared with the predictions for the$ ^{7} {\rm Li}$ global OMP, the results predicted by the$ ^{9} {\rm Be}$ global OMP are in better agreement with the experimental data for$ ^{7} {\rm Li}$ +$ ^{208} {\rm Pb}$ . This may be because the influence of the Coulomb interaction is significant for different systems. Keeley et al. [15] calculated the elastic scattering angular distributions for$ ^{7} {\rm Li}$ ,$ ^{7} {\rm Be}$ +$ ^{208} {\rm Pb}$ systems by the continuum discretized coupled-channel (CDCC) method and noted that the behavior for$ ^{7} {\rm Be}$ +$ ^{208} {\rm Pb}$ was similar to that for$ ^{6} {\rm Li}$ +$ ^{208} {\rm Pb}$ [16] rather than to that for$ ^{7} {\rm Li}$ +$ ^{208} {\rm Pb}$ . In contrast, the constituents of these weakly bound projectiles strongly influence the cross-sections. The$ ^{7} {\rm Be}$ with a low breakup threshold behaves like$ ^{6} {\rm Li}$ and$ ^{9} {\rm Be}$ , rather than$ ^{7} {\rm Li}$ [7], which may contribute another reason why the global$ ^{9} {\rm Be}$ OMP is more suitable to describe the elastic scattering of$ ^{7} {\rm Be}$ . In the following figures, we only show the comparisons of the results predicted by the$ ^{9} {\rm Be}$ global OMP with the corresponding experimental data.
Figure 2. Same as Fig. 1, but for
$^{51}{\rm V}$ ,$^{58}{\rm Ni}$ , and$^{208}{\rm Pb}$ .The total reaction cross-sections of
$ ^{7} {\rm Be}$ are predicted for different targets. The comparisons with the available data for$ ^{27} {\rm Al}$ and$ ^{28} {\rm Si}$ are presented in Fig. 3. For$ ^{27} {\rm Al}$ , the data [8] are derived from the elastic scattering angular distributions at sub- and near-barrier energies. The calculations are in agreement with the data. Moreover, there is some experimental data [17] above 100 MeV, and a good agreement is likewise obtained in this region. For$ ^{28} {\rm Si}$ , some experimental data [18, 19] originate from the natural silicon target, and the theoretical results are in reasonable agreement. Meanwhile, these results are larger than other experimental data [20–22] obtained with$ ^{28} {\rm Si}$ .
Figure 3. Comparison of
$^{7}{\rm Be}$ total reaction cross-sections with experimental data for$^{27}{\rm Al}$ and$^{28}{\rm Si}$ .Figure 4 shows the calculations of total reaction cross-sections for
$ ^{58} {\rm Ni}$ and$ ^{208} {\rm Pb}$ . The results are compared with the available data [11, 14] which are derived from the measured elastic scattering angular distributions, and exhibit complete consistency.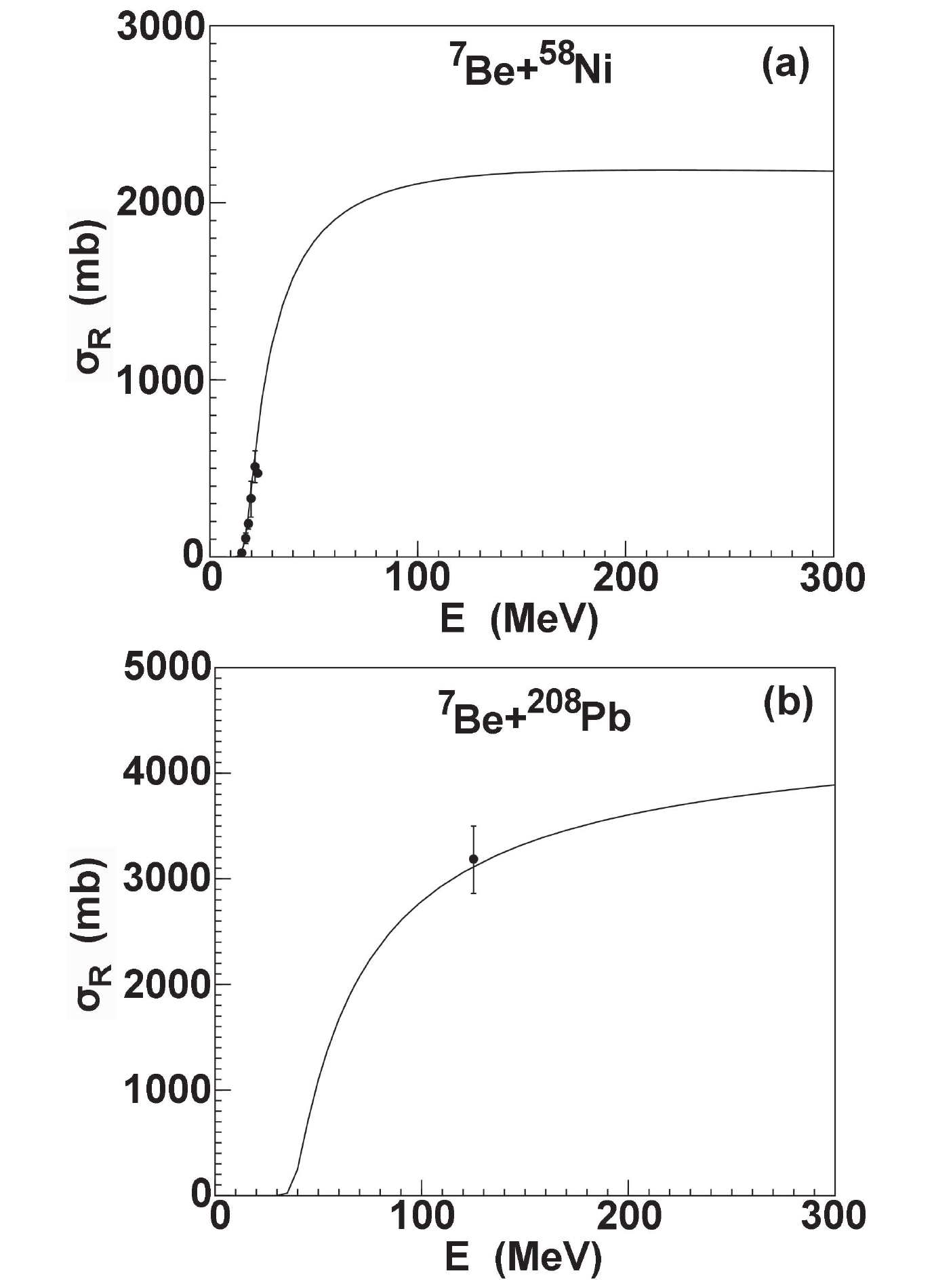
Figure 4. Same as Fig. 3, but for
$^{58}{\rm Ni}$ and$^{208}{\rm Pb}$ .The elastic scattering observables for
$ ^{7} {\rm Be}$ on some lighter targets are further predicted. Figure 5 presents the comparison of elastic scattering angular distributions with the experimental data [23–26] for$ ^{9} {\rm Be}$ ,$ ^{10} {\rm B}$ ,$ ^{12} {\rm C}$ and$ ^{14} {\rm N}$ at 18.8, 23.7, and 85.0 MeV. Reasonable agreements between them are obtained for$ ^{12} {\rm C}$ and$ ^{14} {\rm N}$ . There are some deviations at the extreme values for$ ^{9} {\rm Be}$ and$ ^{10} {\rm B}$ , where the theoretical results are smaller than the measured value. For these reactions of$ ^{7} {\rm Be}$ on these lighter targets, the influence of the other reaction channel on elastic scattering is important and must be considered in the calculations. To improve the results, the coupled-channel calculations will be considered in the future work.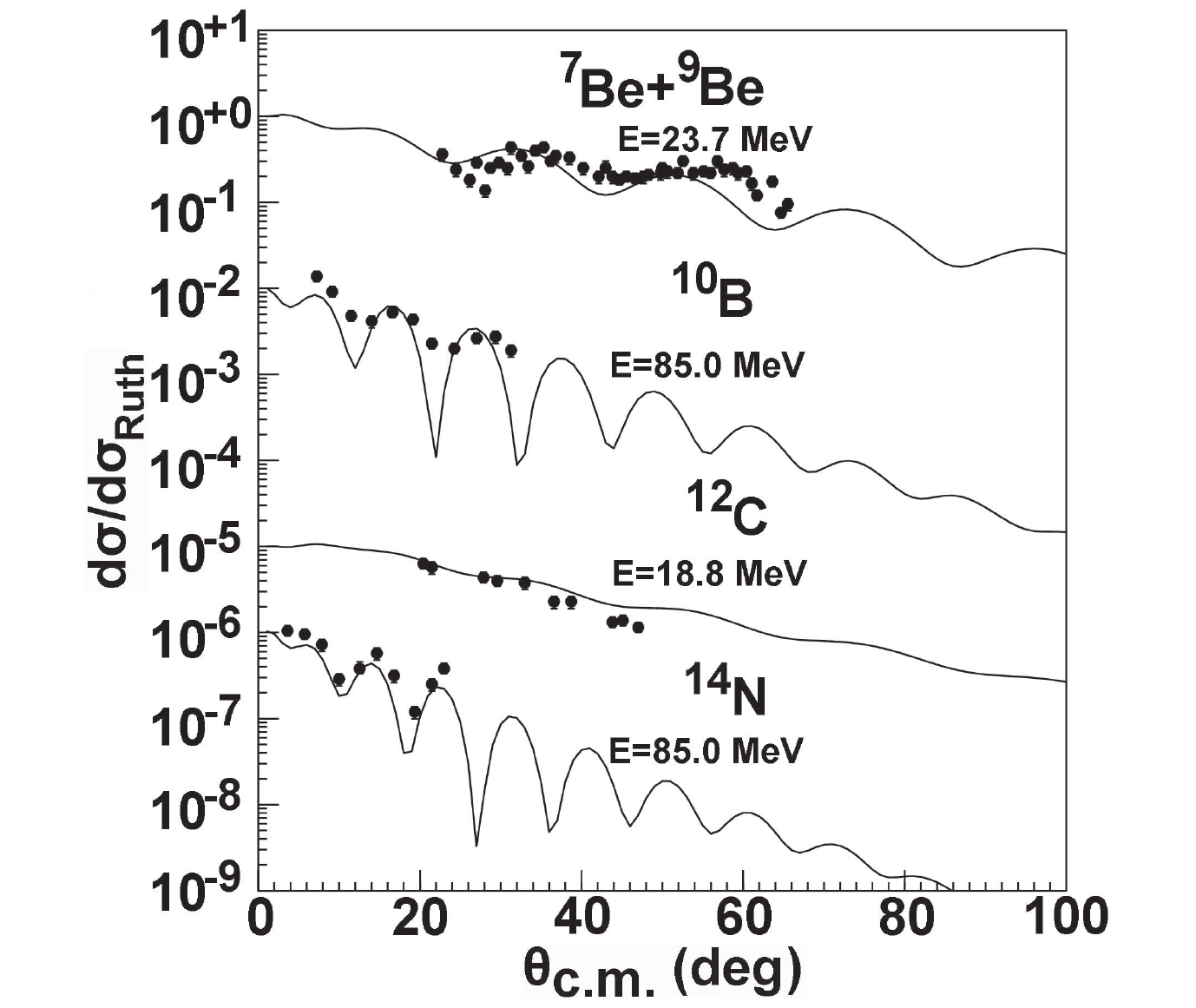
Figure 5. Same as Fig. 1, but for
$^{9}{\rm Be}$ ,$^{10}{\rm B}$ ,$^{12}{\rm C}$ , and$^{14}{\rm N}$ .For the total reaction cross-sections of
$ ^{7} {\rm Be}$ on light targets, only the experimental data [17] for$ ^{12} {\rm C}$ at incident energies of 224.0 and 350.7 MeV is available. The data at 18.8 MeV is obtained by analyzing the experimental data of elastic angular distributions [25, 26] using the coupled-channel method. The calculations of total reaction cross-sections are further compared with these data. A satisfactory agreement between these is obtained, as shown in Fig. 6.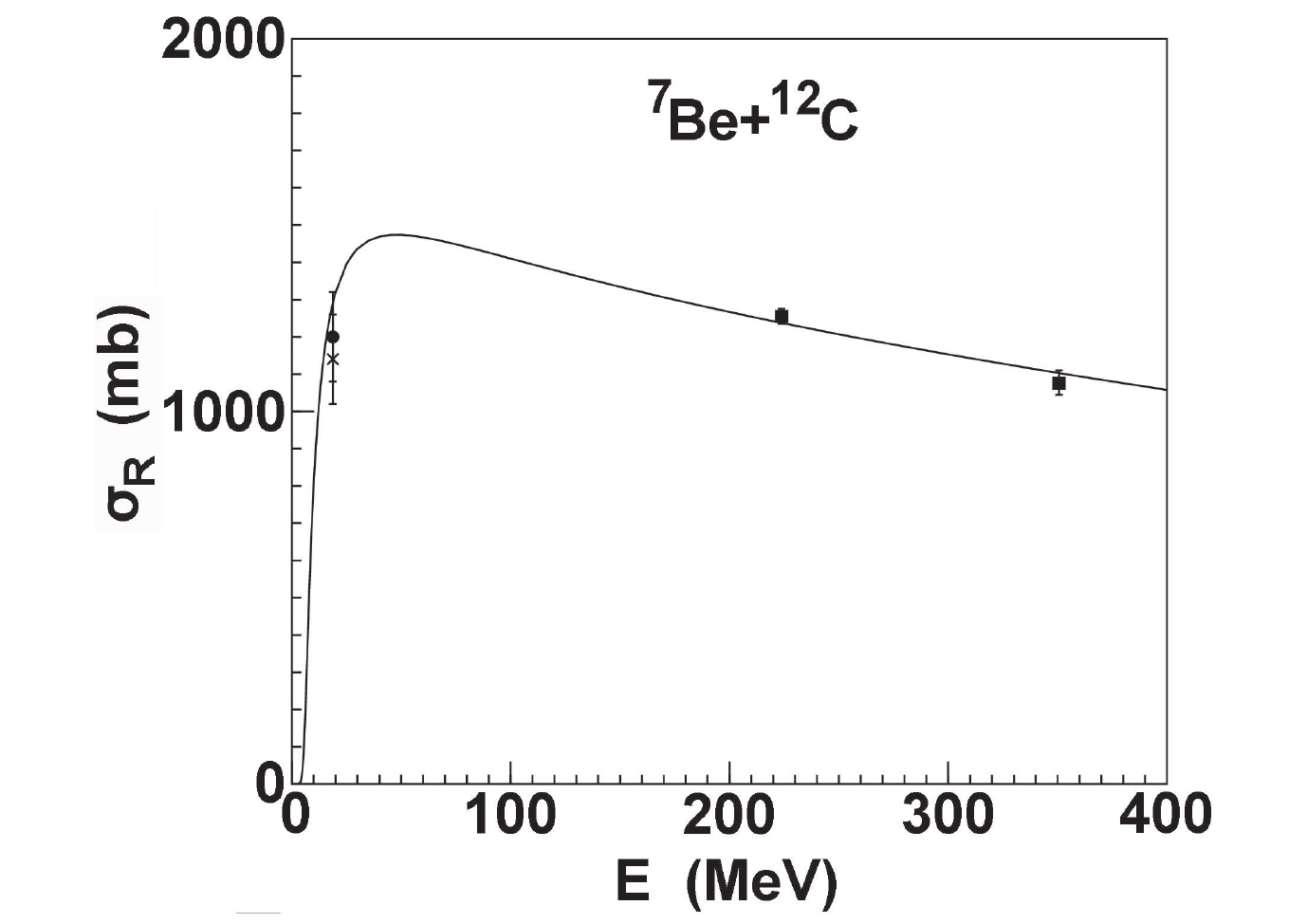
Figure 6. Same as Fig. 3, but for
$^{12}{\rm C}$ .For a tightly bound projectile
$ ^{10} {\rm Be}$ , the elastic angular distributions of$ ^{12} {\rm C}$ and$ ^{64} {\rm Zn}$ targets were measured [25, 27] at incident energies of 23.2 MeV and 29.4 MeV, respectively. In addition, the angular distribution for$ ^{208} {\rm Pb}$ at incident energies from 38.4 MeV to 43.9 MeV was also measured [28]. Calculations are compared with the existing experimental data, and a satisfactory agreement between them is obtained. The results are shown in Fig. 7.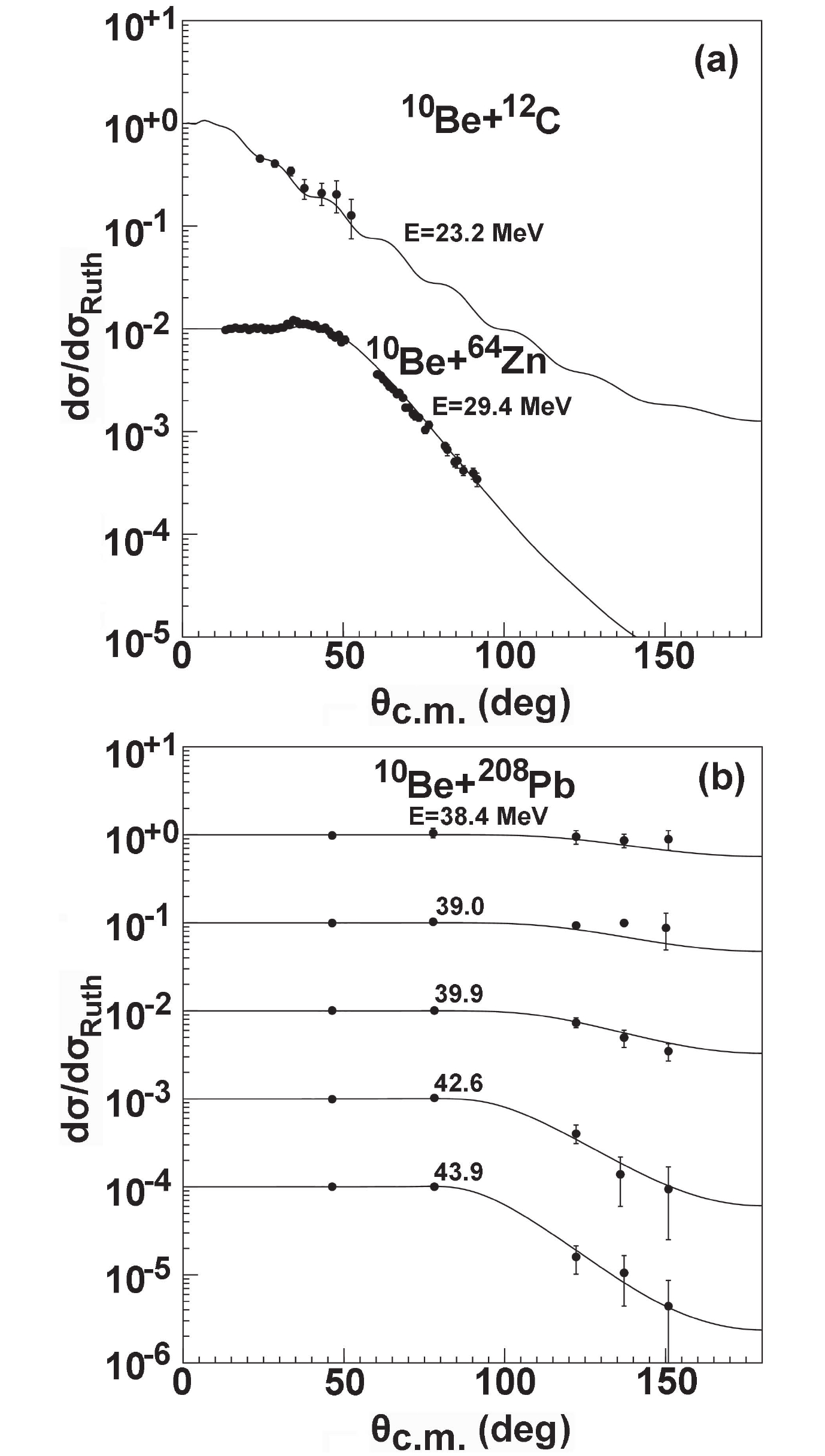
Figure 7. Comparison of
$^{10}{\rm Be}$ elastic scattering angular distributions with experimental data for$^{12}{\rm C}$ ,$^{64}{\rm Zn}$ , and$^{208}{\rm Pb}$ .For the total reaction cross-sections of
$ ^{10} {\rm Be}$ , only the experimental data [18, 29, 30] above 100 MeV is available for$ ^{28} {\rm Si}$ , natural Cu, and Pb targets. The predictions are further compared with the corresponding experimental data. They are found to be in agreement with the experimental data at 340.0 MeV and 480.0 MeV, while they were slightly larger at 310.0 MeV for$ ^{28} {\rm Si}$ . Hence, reasonable agreements were achieved for$ ^{63,65} {\rm Cu}$ and$ ^{208} {\rm Pb}$ . The results are shown in Fig. 8.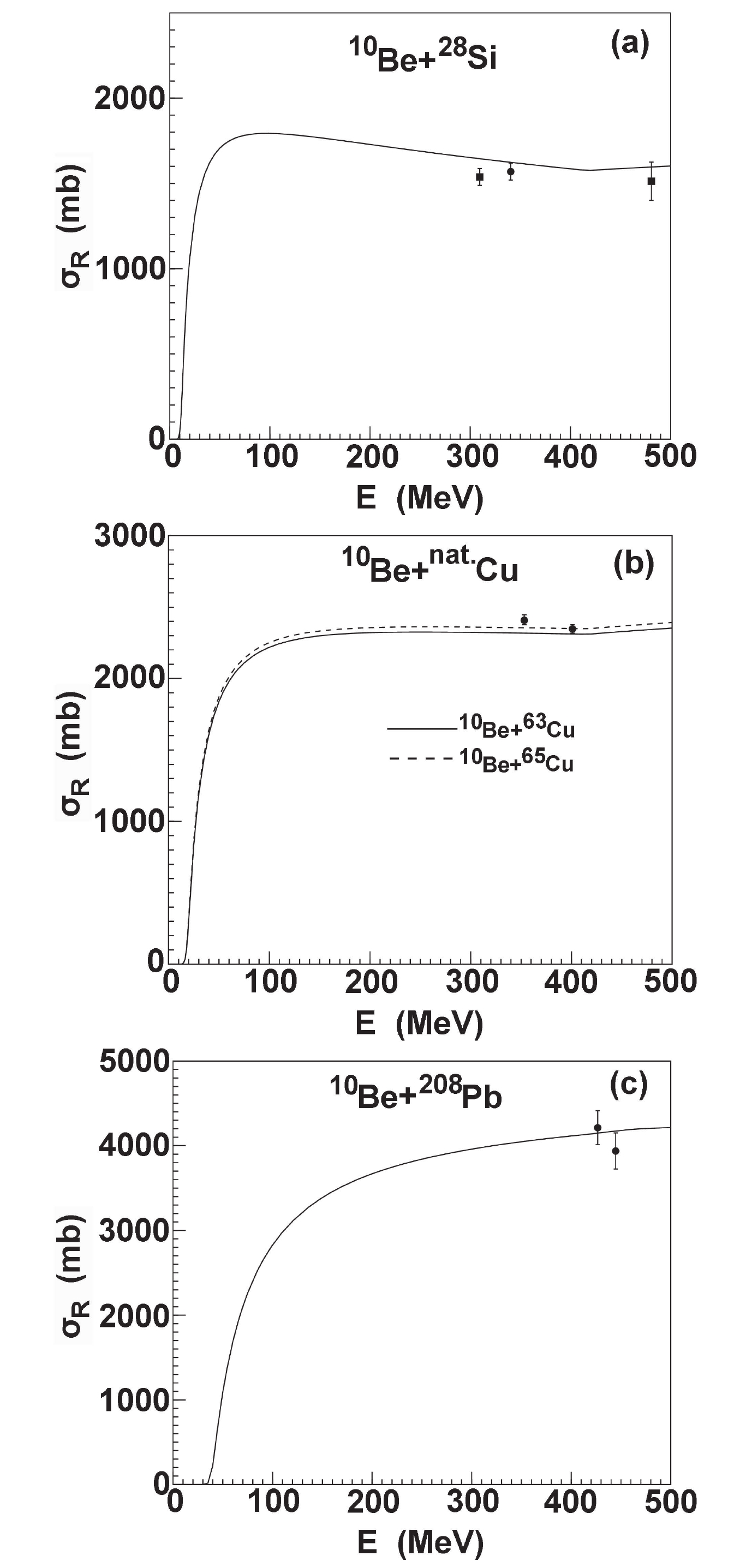
Figure 8. Comparison of
$^{10}{\rm Be}$ elastic scattering angular distributions with corresponding experimental data for$^{28}{\rm Si}$ ,$^{63,65}{\rm Cu}$ , and$^{208}{\rm Pb}$ .From the above comparison, the
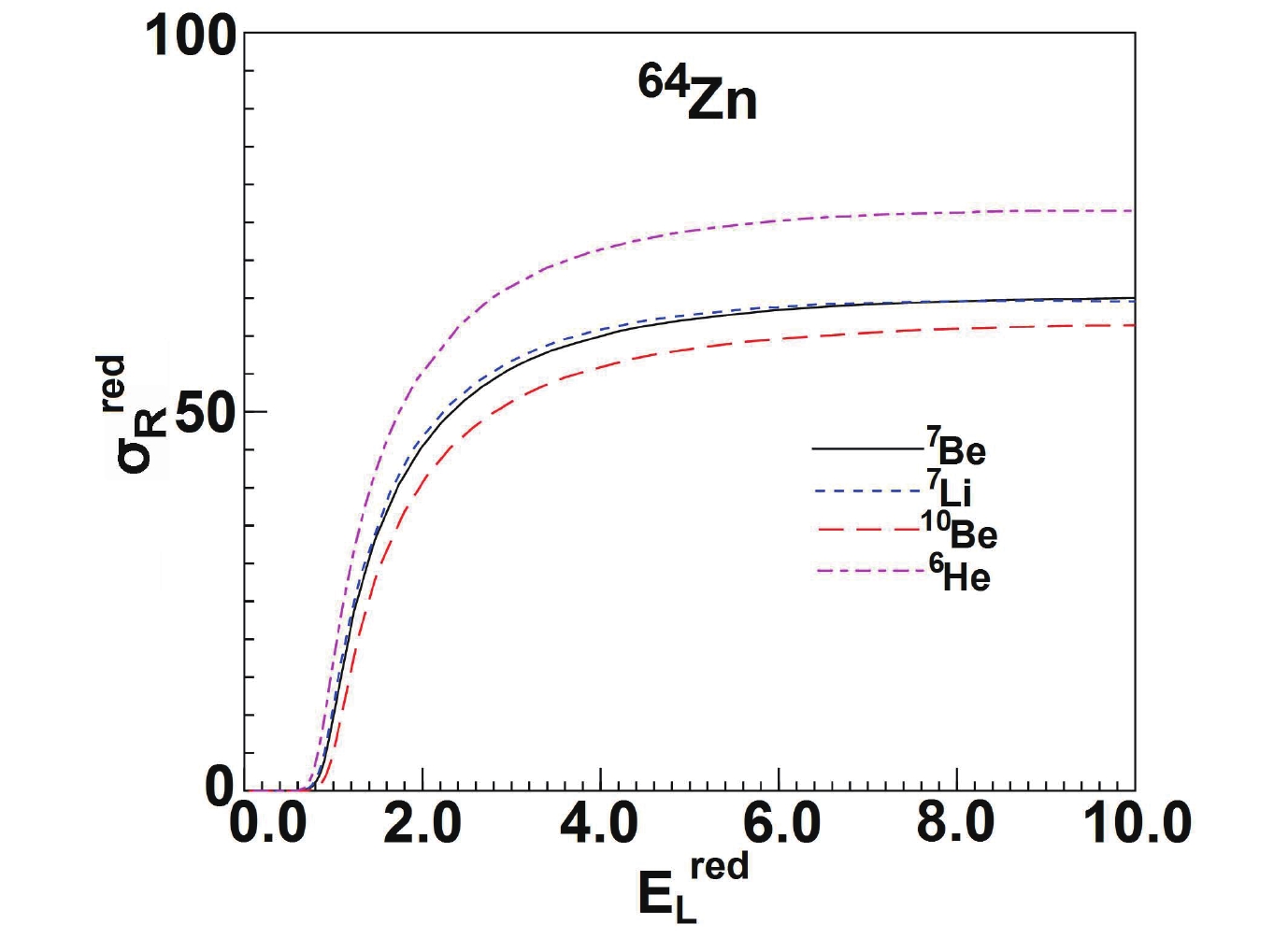
$ ^{9} {\rm Be}$ global phenomenological OMP gives a good description of$ ^{7,10} {\rm Be}$ elastic scattering. To further analyze the characteristics of$ ^{7,10} {\rm Be}$ , we compare the total reaction cross-sections calculated for different systems, including weakly bound nuclei$ ^{7} {\rm Be}$ and$ ^{7} {\rm Li}$ [10], and tightly bound nucleus$ ^{10} {\rm Be}$ , as well as a halo nucleus$ ^{6} {\rm He}$ [31]. The global OMPs of different projectiles obtained by the same method are employed to ensure consistency in the calculation. Moreover, as suggested by Aguilera et al. [11], the total reaction cross-section and the energy are divided by the factors$ (A_{p}^{1/3}+A_{T}^{1/3})^{2} $ and$Z_{p}Z_{T}/ $ $ (A_{p}^{1/3}+A_{T}^{1/3}) $ , respectively, where$ Z_{p}(Z_{T}) $ and$ A_{p}(A_{T}) $ are the charge and mass numbers of the projectile (target). The total reaction cross-sections are calculated for$ ^{7,10} {\rm Be}$ ,$ ^{7} {\rm Li}$ , and$ ^{6} {\rm He}$ projectiles on a medium mass target$ ^{64} {\rm Zn}$ , where the Coulomb breakup predominates over the nuclear breakup. The results are shown in Fig. 9. The total reaction cross-section of the weakly bound nucleus$ ^{7} {\rm Be}$ is similar to that of$ ^{7} {\rm Li}$ , which is larger compared to that involving the tightly bound nucleus$ ^{10} {\rm Be}$ . The total reaction cross-sections for halo nuclei$ ^{6} {\rm He}$ are largest among the presented systems. The effect of the weak binding energy seems to be switching on additional channels that would enhance the total reaction cross-sections [26]. The Coulomb polarization favors neutrons in the halo, residing in the region between the core and the target, which subsequently enhances the reaction probabilities [11]. -
The elastic scattering observables for
$ ^{11,12} {\rm Be}$ isotopes are likewise predicted using the global OMP. To date, the experimental data of elastic scattering angular distributions are scarce, and most of the total reaction cross-sections are measured above 200 MeV. For the$ ^{11} {\rm Be}$ projectile, the elastic scattering angular distributions are only measured for$ ^{64} {\rm Zn}$ and$ ^{120} {\rm Sn}$ at incident energies of 29.8 MeV and 32.0 MeV [27, 32]. The comparison of the predictions with the data is displayed in Fig. 10, exhibiting reasonable agreement between them.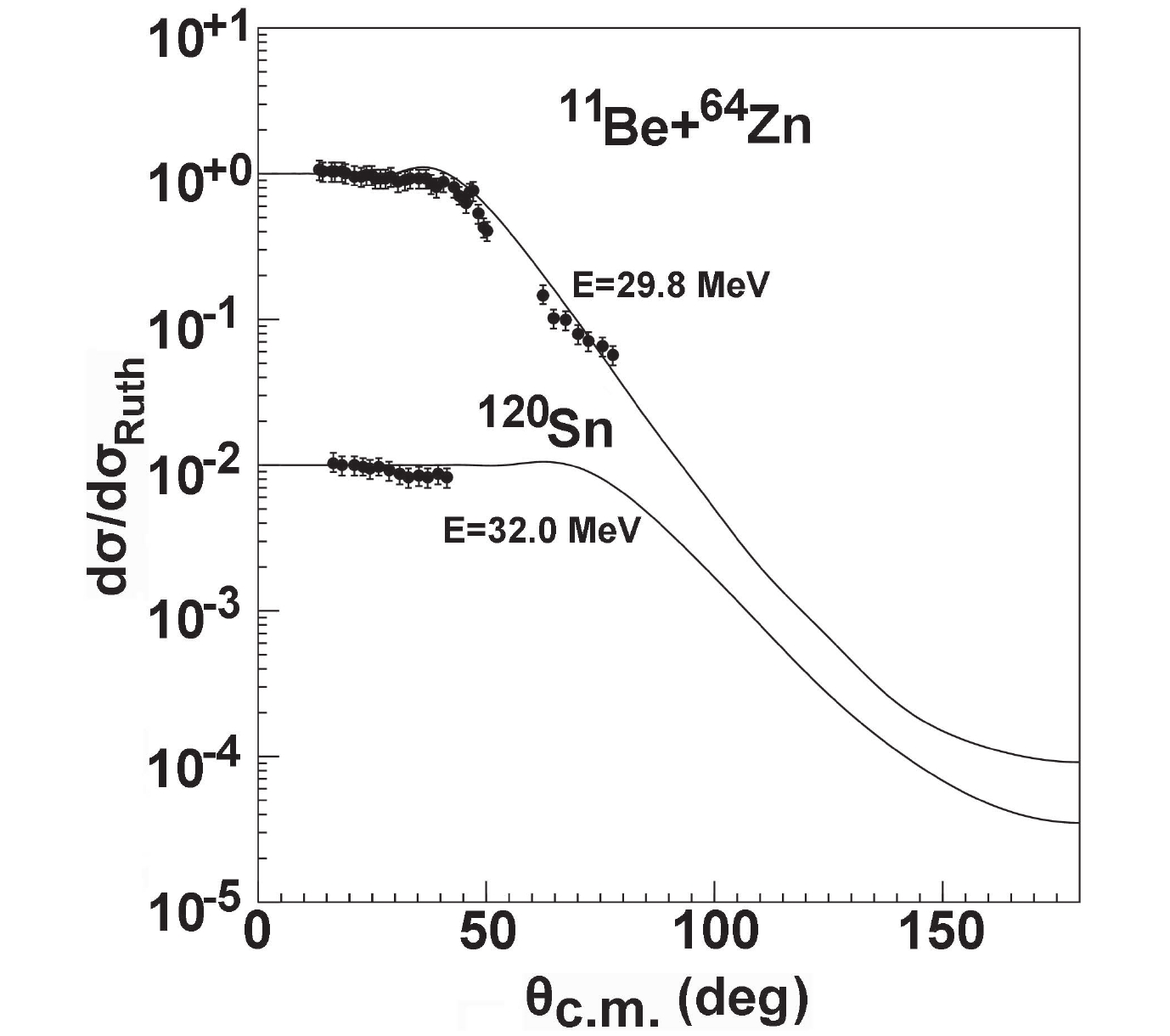
Figure 10. Comparison of
$^{11}{\rm Be}$ elastic scattering angular distributions with corresponding experimental data for$^{64}{\rm Zn}$ and$^{120}{\rm Sn}$ .For the total reaction cross-sections of
$ ^{11} {\rm Be}$ , only the experimental data [18, 22, 30] from$ ^{28} {\rm Si}$ and natural Cu targets is available. The calculations are compared with the existing experimental data, as shown in Fig. 11. For$ ^{28} {\rm Si}$ , the total reaction cross-sections are measured by different experiments at the incident energy of 330 MeV [18, 22]. The result is in reasonable agreement with the data within the error range. For the Cu target, we calculate the total reaction cross-sections of$ ^{63,65} {\rm Cu}$ and compare with the experimental data from natural Cu. The calculations provide smaller values than the experimental data. Moreover, we find that the experimental data of total reaction cross-sections for the$ ^{11} {\rm Be}$ projectile have a strong enhancement compared with those of$ ^{12} {\rm Be}$ and$ ^{10} {\rm Be}$ projectiles from the same experiment [30]. Nucleus$ ^{11} {\rm Be}$ has a well-known halo structure and a very small binding energy (0.504 MeV). The discrepancy may be that the neutron-halo structure leads to the anomalously large reaction cross-sections, which may be resolved by considering the contribution of transfer and breakup processes [1].
Figure 11. Comparison of
$^{11}{\rm Be}$ total reaction cross sections with corresponding experimental data for$^{28}{\rm Si}$ and$^{63,65}{\rm Cu}$ .In the case of the clustering nucleus
$ ^{12} {\rm Be}$ , there is no experimental data of elastic scattering angular distributions and the experimental data of total reaction cross sections are also above 300 MeV. The total reaction cross-sections for$ ^{28} {\rm Si}$ and$ ^{63,65} {\rm Cu}$ are calculated and compared with the corresponding experimental data [18, 22, 30, 33]. Reasonable agreement is obtained between them, although there is a slightly discrepancy at a certain energy point. These results are shown in Fig. 12.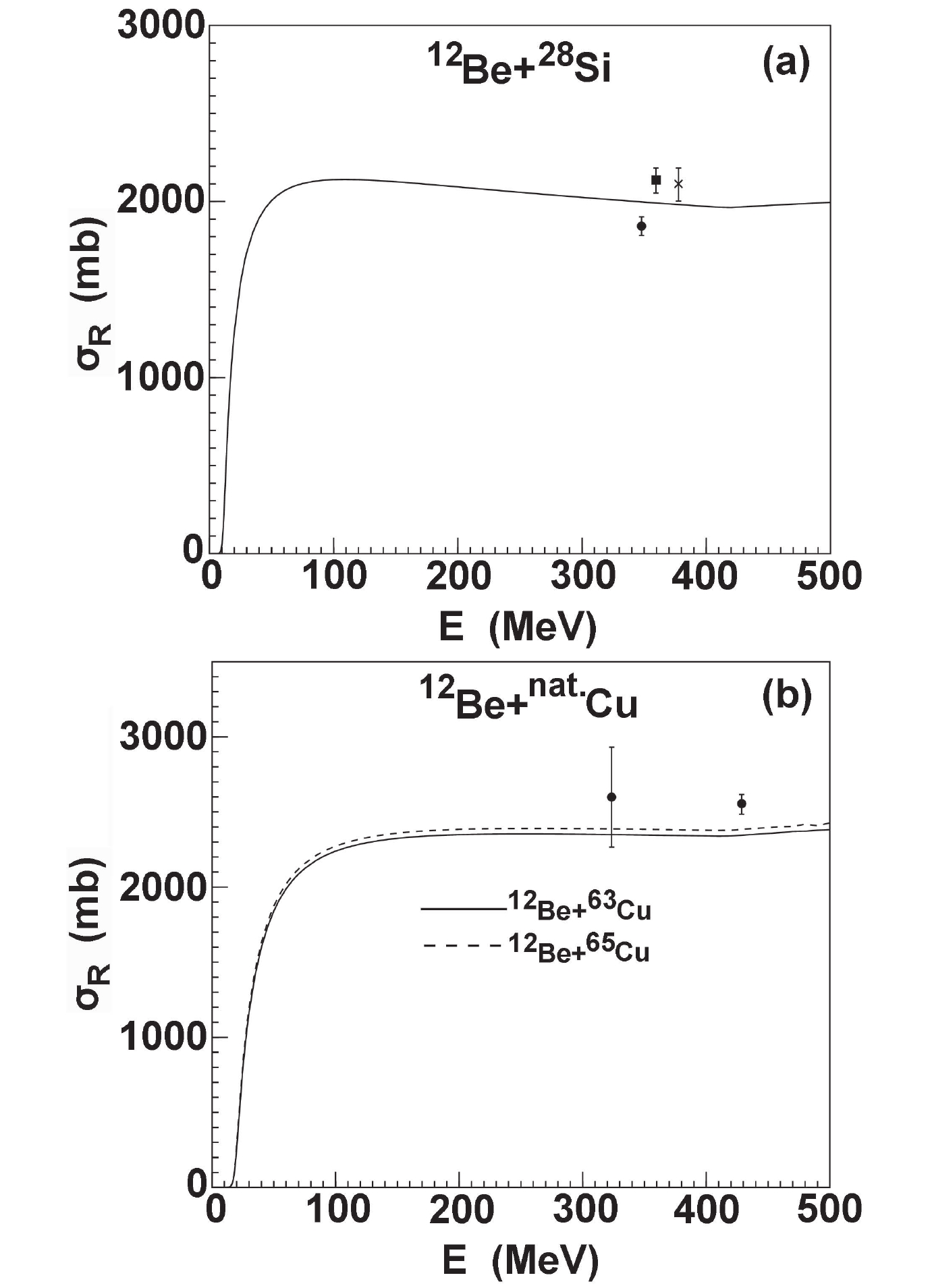
Figure 12. Comparison of the
$^{12}{\rm Be}$ total reaction cross-sections with corresponding experimental data for$^{28}{\rm Si}$ and$^{63,65}{\rm Cu}$ .Since the experimental data of elastic scattering observables are scarce for the neutron-rich nucleus
$ ^{11} {\rm Be}$ and clustering nucleus$ ^{12} {\rm Be}$ , tentative calculation are made for these elastic scattering observables and compared with the existing experimental data. The reliability, namely the$ ^{9} {\rm Be}$ global MOP applied to describe the elastic scattering of$ ^{11,12} {\rm Be}$ projectiles, needs to be further verified by new experimental data in the future. -
We employ the
$ ^{9} {\rm Be}$ global OMP to predict the elastic scattering angular distributions and total reactions cross-sections for$ ^{7,10,11,12} {\rm Be}$ isotopes. The comparison between the calculations and experimental data is made, and the corresponding analysis is performed. A satisfactory agreement is presented between these for$ ^{7,10} {\rm Be}$ . For$ ^{11,12} {\rm Be}$ isotopes, there is little or no experimental data of elastic scattering angular distributions, and most of total reactions cross-sections are at incident energies above 300 MeV. In this study, we perform a tentative calculation for these isotopes. We find some discrepancies between the calculations and experimental data for$ ^{11} {\rm Be}$ , which may be ascribed to the behavior of neutron-halo structure of$ ^{11} {\rm Be}$ . With the increasing amount of experimental data on elastic scattering, the reaction mechanisms of the halo nucleus$ ^{11} {\rm Be}$ and clustering nucleus$ ^{12} {\rm Be}$ will be the subject of systematic studies in the future. The calculations performed demonstrate that the global OMP is useful in future systematic studies for nuclear model calculations and experimental analysis involving$ ^{7,10,11,12} {\rm Be}$ projectiles.
Applicability of 9Be global optical potential to reactions of 7,10,11,12Be
- Received Date: 2019-04-29
- Available Online: 2019-09-01
Abstract: Elastic scattering angular distributions and total reaction cross-sections of 7,10,11,12Be projectiles are predicted by the systematic 9Be global phenomenological optical model potential for target mass numbers ranging from 24 to 209. These predictions provide a detailed analysis by their comparison with the available experimental data. Furthermore, these elastic scattering observables are also predicted for some targets out of the mass number range. The results are in reasonable agreement with the existing experimental data, and they are presented in this study.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: