-
The anomalous magnetic moment of the muon,
$ a_\mu = (g-2)_\mu/2 $ , is one of the most important precision observables to test the standard model (SM) and provide a complementary, non-collider constraint of beyond the standard model (BSM) physics. Currently, the discrepancy between the experimental measurement and the SM prediction is$ \sim 3.5 \sigma $ [1-8], where:$\Delta {a_\mu } = a_\mu ^{{\rm{Exp}}} - a_\mu ^{{\rm{SM}}} = 2.87(80) \times {10^{ - 9}}.$

(1) This opens a window of opportunity for quantum corrections driven by BSM particles [9-13]. In a model independent scenario, a detailed study [10] showed the contribution to
$ a_\mu $ for BSM particles of masses of a few 100 GeV. A complete two-loop contribution to$ a_\mu $ in the two-Higgs-doublet model (2HDM) is performed in [14, 15] to explain the anomaly,$ \Delta a_\mu $ , which constrains the parameter space of the model. These studies connect$ \Delta a_\mu $ with the collider studies at the Large Hadron Collider (LHC) and Fermilab experiments.In this study, we draw on our previous work, in which we studied the effects of a new scalar, H, heavier than the SM Higgs, in relation to Run 1 results from the LHC [16, 17]. From an effective Lagrangian approach, the best fit mass of H was determined as
$ m_H = 272^{+12}_{-9} $ GeV, where these past studies drew on (but were not limited to) the production of multiple leptons (in association with b-quarks), as had been studied in the search for SM Higgs. These studies were associated with the top quark. As a result of our earlier studies, the introduction of a scalar mediator, S, was necessary, such that our effective vertices were constructed using HSh, HSS, and Hhh interactions. Furthermore, the S could decay (in a Higgs-like manner) to SM particles [16].We made a number of predictions at high energy proton-proton collisions, related to the production of multiple leptons in [16, 17]. Assuming that the singlet scalar behaves like a SM Higgs-like boson, the data can be described with
$ m_H\approx 270 $ GeV and$ m_S\approx 150 $ GeV. These discrepancies have become statistically compelling with the available Run 2 data [18], where the mass points and parameters were fixed from our earlier studies, and as such were not altered in our model to better explain the data. The final states were selected as per the predictions in [16, 17], which predate the Run 2 data. These include the anomalous production of opposite-sign, same-sign, and three leptons in the presence and absence of b-quarks.The discrepancies that arise in final states and regions of the phase space, where different processes dominate the SM description, do not point to a likely mis-modeling of a specific SM process. Rather, the anomalies and their kinematic characteristics are reasonably well described by a simple ansatz, where
$ H\rightarrow Sh $ is produced via gluon-gluon fusion and in association with top quarks in high-energy proton-proton collisions. It is therefore appropriate to understand the possible connection of the above-mentioned spectroscopy with the$ \Delta a_\mu $ anomaly via loop corrections.The above-mentioned H and S can be embedded into a 2HDM scenario with an additional scalar, where S is a singlet under the SM gauge groups [16, 19, 20]. This was done explicitly in [19], where a study of this embedding's 2HDM+S parameter space was made that can accommodate the discrepancies between the SM and the data reported in [21]. Here, we investigate whether the 2HDM+S model with the parameter space identified in [21] can account for the
$ \Delta a_\mu $ anomaly or whether new degrees of freedom are necessary.While the multi-lepton anomalies reported in [18, 21] seem to be fairly well described with the simple ansatz mentioned above, in [18] a more complex picture was indicated in the data than provided by this 2HDM+S model. The specific processes that indicated this greater complexity were in the dilepton system, including the invariant mass, transverse mass, and the missing transverse energy. These tended to be wider than what is predicted by the
$ S\rightarrow W^+W^-\rightarrow \ell^+\ell^- \; (\ell = e,\mu) $ decay chain. New leptonic degrees of freedom could significantly alter the decays of S, thus modifying the differential distribution predicted by the model [21]. In this light, we explore what one can learn from the$ \Delta a_\mu $ anomaly with regard to these potential new degrees of freedom.In this short article, we connect
$ \Delta a_\mu $ with the constrained parameter space of the 2HDM+S at the LHC. We briefly explain the model considered for this study in Section 2, along with the constraints on the parameter space from previous studies. The one- and two-loop formulae are discussed in Section 3, and the results of the study are presented in Section 4. The implications of this study to other processes are discussed in Section 5. Finally, a summary and conclusion of this study is presented in Section 6. -
As mentioned in Section 1, we consider the 2HDM+S model as a possible explanation for
$ \Delta a_\mu $ . Following [19, 20, 22] this model is, in summary, based on the well-known 2HDM with the addition of a real singlet scalar S. The potential is given by the following:$\begin{split}& V({\Phi _1},{\Phi _2},{\Phi _S})= m_{11}^2{\left| {{\Phi _1}} \right|^2} + m_{22}^2{\left| {{\Phi _2}} \right|^2} - m_{12}^2\left( {\Phi _1^\dagger {\Phi _2} + {\rm{h}}.{\rm{c}}.} \right)\\& + \frac{{{\lambda _1}}}{2}{\left( {\Phi _1^\dagger {\Phi _1}} \right)^2} + \frac{{{\lambda _2}}}{2}{\left( {\Phi _2^\dagger {\Phi _2}} \right)^2} + {\lambda _3}\left( {\Phi _1^\dagger {\Phi _1}} \right)\left( {\Phi _2^\dagger {\Phi _2}} \right)\\ & + {\lambda _4}\left( {\Phi _1^\dagger {\Phi _2}} \right)\left( {\Phi _2^\dagger {\Phi _1}} \right) + \frac{{{\lambda _5}}}{2}\left[ {{{\left( {\Phi _1^\dagger {\Phi _2}} \right)}^2} + {\rm{h}}.{\rm{c}}.} \right]\\ & + \frac{1}{2}m_S^2\Phi _S^2 + \frac{{{\lambda _6}}}{8}\Phi _S^4 + \frac{{{\lambda _7}}}{2}\left( {\Phi _1^\dagger {\Phi _1}} \right)\Phi _S^2 + \frac{{{\lambda _8}}}{2}\left( {\Phi _2^\dagger {\Phi _2}} \right)\Phi _S^2,\\[-15pt] \end{split}$

(2) where the fields
$ \Phi_1 $ and$ \Phi_2 $ are the$ SU(2)_L $ Higgs doublets, while$ \Phi_S $ is the singlet scalar field. The first three lines correspond to the terms in the real 2HDM potential. The final four terms relate to the singlet S field. Models that have more than one Higgs doublet can have tree-level flavor changing neutral currents (FCNCs). To avoid these tree-level currents, the usual approach is to couple all quarks with the same charge to a single double.Because of the addition of a singlet scalar, this model has three physical CP-even scalars h, S, and H, with one CP-odd scalar A and charged scalar
$ H^\pm $ . Other parameters of this model are the mixing angles$ \alpha_1, \alpha_2, \alpha_3 $ , and$ \tan\beta $ , vacuum expectation values (vev)$ v, v_S $ , and the masses$ m_h, m_S, m_H, m_A, m_{H\pm} $ . As discussed in Section 1, the masses of a large number of these parameters are fixed a priori from previous studies [16, 19, 20], where the as yet constrained mass$ m_A $ , and to a lesser extent$ m_S $ , will be addressed in this study.The relevant Yukawa couplings between the SM fermions and 2HDM+S scalar mass eigenstates are given as follows:
$\begin{split}& - {\cal L}_Y^{{\rm{2HDM + S}}}\\ =& \sum\limits_{f = u,d,\ell } {\frac{{{m_f}}}{v}} [y_f^hh\bar ff + y_f^HH\bar ff + y_f^SS\bar ff - iy_f^AA\bar f{\gamma _5}f]\\ &+ [\sqrt 2 {V_{ud}}{H^ + }\bar u\left( {\frac{{{m_u}}}{v}y_u^A{P_L} + \frac{{{m_d}}}{v}y_d^A{P_R}} \right)\\ &+ \sqrt 2 \frac{{{m_\ell }}}{v}y_\ell ^A{H^ + }\bar \nu {P_R}\ell + {\rm{h}}.{\rm{c}}.]. \end{split}$

(3) For details on the couplings and other information, we refer the readers to [19, 20]. Furthermore, for our studies, we only consider type-II and lepton-specific (type-X) models within the parameter space considered in [19].
Because these types of models are highly constrained by many studies, we also considered a scenario by adding BSM leptons, which are singly charged. Specifically, we consider light leptons with a mass of
$ {\cal O}(10^2) $ GeV, which are not directly produced at colliders. This indicates that these leptons are to be treated as mediators, and would contribute via loop corrections to the$ \Delta a_\mu $ anomaly. For the sake of simplicity, and without any loss of generality, we consider singly charged SM singlet vector-like leptonic fermions with chiral components, which transform as follows [10]:${\cal L} \supset - y_{{f^\prime }}^S\overline {{l_R}} {\Phi _S}f_L^\prime - \sum\limits_{i = 1}^2 {y_{{f^\prime }}^i} \overline {{L_l}} {\Phi _i}f_R^\prime + {\rm{h}}.{\rm{c}}.,$

(4) where
$ l_{R} $ and$ L_l $ are the SM singlet and doublet leptons, and$ f^{\prime}_{L/R} $ are the BSM singly charged vector-like leptons with left and right chirality. Hence, under SM gauge transformations, different chiral components transform in the same way. The interaction Lagrangian, Eq. (4), can be easily cast in terms of the scalar mass eigenstates, as in Eq. (3). By adding these interactions to the 2HDM+S, we expanded our model to what we label as a 2HDM+S+f model. However, these fermions are also constrained by collider searches in terms of masses and model-dependent couplings, which we further explain in Section 5.The overall coupling should be constrained as
$ y_{f, f^\prime}^i\leqslant \sqrt{4\pi} $ , though it should be noted that all the couplings that appear in the interactions are functions of the mixing angles$ \alpha_i $ and$ \beta $ used to diagonalize the mass matrix appropriately in the model. Without loss of generality, we can assume$ -\pi/2 \leqslant \alpha_i \leqslant \pi/2 $ , scanning over$ \beta $ values in the coming sections, along with the mass of the new vector-like fermion, f. -
The 2HDM contributions to the
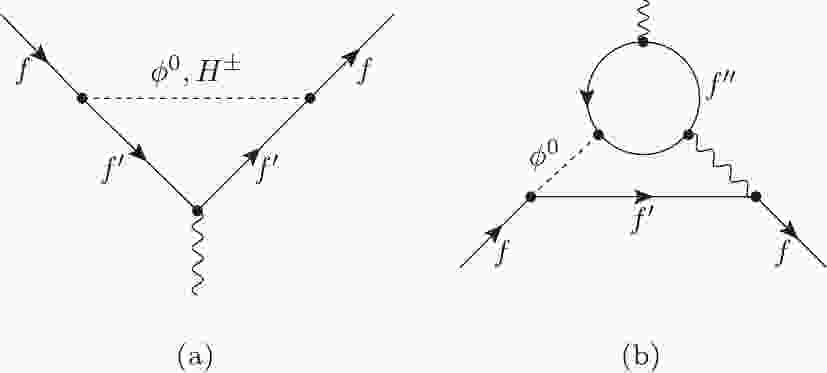
$ \Delta a_\mu $ have been calculated and are known up to the two-loop level [14, 15], where these calculations also apply for the 2HDM+S with appropriate coupling arrangements. The one- and two-loop diagrams contributing to$ \Delta a_\mu $ are shown in Fig. 1. The type-II and type-X (lepton specific) 2HDMs are suitable to explain the discrepancy with positive contributions to the$ \Delta a_\mu $ . In these models, the lepton couplings to the new bosons are enlarged, while the top Yukawa coupling are kept favorably small.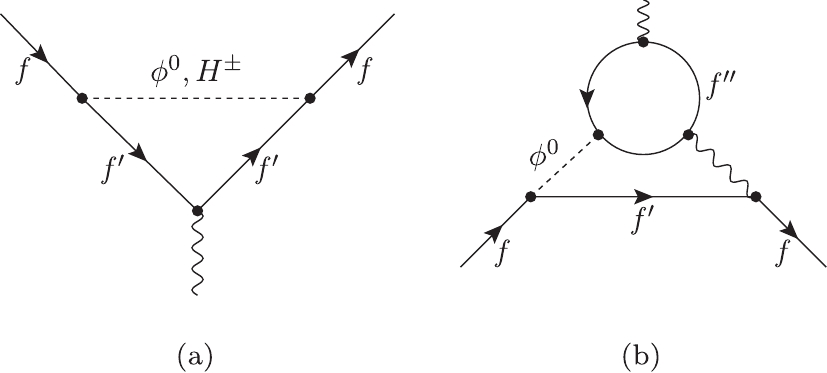
Figure 1. Representative (a) one-loop and (b) two-loop diagrams contributing to
$\Delta a_\mu$ . For 2HDMs,$\phi^0 = h, H, A$ while in the case of the 2HDM+S,$\phi^0$ also obtains a contribution from S. In a 2HDM or 2HDM+S scenario, the fermions f and$f^\prime$ can be considered as SM leptons, however$f^{\prime\prime}$ could be quarks and leptons. The dominant contributions come from$ f^{\prime\prime} = t, b, \tau$ . For 2HDM+S+f model,$f^\prime$ could be taken as BSM charged fermions with neutral scalars.The one loop contribution from neutral and charged scalars is given by the expression:
$\Delta {a_\mu }(1\;{\rm{loop}}) = \frac{{{G_F}m_\mu ^2}}{{4{\pi ^2}\sqrt 2 }}\:\sum\limits_j {{{(y_\mu ^j)}^2}} \:r_\mu ^j\:{f_j}(r_\mu ^j),$

(5) where
$ j = \{h, S, H, A, H^\pm \} $ ,$ r^j_\mu = m^2_\mu / M^2_j $ , and${f_{h,S,H}}(r) = \int_0^1 {\rm d} x\frac{{{x^2}(2 - x)}}{{1 - x + r{x^2}}},$

(6) ${f_A}(r) = \int_0^1 {\rm d} x\frac{{ - {x^3}}}{{1 - x + r{x^2}}},$

(7) ${f_{{H^\pm }}}(r) = \int_0^1 {\rm d} x\frac{{ - x(1 - x)}}{{1 - (1 - x)r}}.$

(8) The two loop contribution from neutral scalars is given by the expression:
$\Delta {a_\mu }(2\;{\rm{loop}}) = \frac{{{G_F}m_\mu ^2}}{{4{\pi ^2}\sqrt 2 }}\:\frac{{{\alpha _{em}}}}{\pi }\:\sum\limits_{i,f} {N_f^c} Q_f^2y_\mu ^iy_f^i\:r_f^i\:{g_i}(r_f^i),$

(9) where
$ i = \{h, S, H, A\} $ ,$ f = \{t, b, \tau\} $ ,$ r^i_f = m^2_f / M^2_i $ , and$ m_f $ ,$ Q_f $ , and$ N^c_f $ are the mass, charge, and number of color degrees of freedom of the fermion in the loop. The functions$ g_i(r) $ are:${g_i}(r) = \int_0^1 {\rm d} x\frac{{{{\cal N}_i}(x)}}{{x(1 - x) - r}}\ln \frac{{x(1 - x)}}{r},$

(10) where
$ {\cal N}_{h,S,H} (x) = 2x(1-x)-1 $ and$ {\cal N}_A (x) = 1 $ .In this study, we go one step further and use the 2HDM+S+f model discussed in Section 2, where the addition of BSM fermions yields a one-loop contribution to
$ \Delta a_\mu $ , as given by [10]:$\Delta a_\mu ^{{f^\prime }}({\rm{1}}\;{\rm{loop}}) = \frac{1}{{16{\pi ^2}}}\:\sum\limits_i {{{(y_{{f^\prime }}^i)}^2}} \:r_\mu ^i\:{F_i}(r_{{f^\prime }}^i),$

(11) where
$ i = \{h, S, H, A\} $ ,$ r^i_{f^\prime} = m^2_{f^\prime} / M^2_i $ , and$ r^i_\mu = m^2_\mu / M^2_i $ . The function$ F_i $ is defined as:${F_i}(r) = \frac{{{r^3} - 6{r^2} + 3r + 6r\ln (r) + 2}}{{6{{(1 - r)}^4}}}.$

(12) We now employ these formulae, inputting the numerical values of parameters from previous studies [16, 19, 20], to generate the
$ \Delta a_\mu $ , scanning across the parameters$ m_f $ ,$ m_A $ , and the mixing angles in the following section. -
For numerical calculations, we considered the masses of the scalars to be
$ m_h = 125 $ GeV,$ m_S $ = 140 – 150 GeV,$ m_H $ = 250 – 270 GeV, and$ m_A = m_{H^\pm} $ = 400 – 600 GeV and$ 0.5\leq \tan\beta \leq 1.0 $ . In a few cases, we have also scanned over light masses of A and discussed this where appropriate. The parameter space chosen here and in [20] is consistent with the following:a) theoretical constraints, such as vacuum stability from the global boundedness and minimum of the potential, as well as tree-level perturbative unitarity, etc.
b) experimental constraints from
$ B\to X_s \gamma $ [23–26] and from$ R_b $ [23, 27].c) compatibility with S, T, and U, i.e., the oblique parameters.
As a first test, we start with 2HDMs, where the positive one-loop contributions stem from the terms involving h and H, whereas the terms with A and
$ H^{\pm} $ yield negative contributions. Conversely, h and H provide the negative two-loop contributions, whereas A provides a positive contribution. In the region of large$ \tan\beta $ and small$ m_A $ , the 2HDM two-loop contributions become larger than the one-loop contributions, allowing for an explanation of the discrepancy. The required parameter space of the type-II and type-X 2HDMs is shown in Fig. 2. For a complete analysis of the 2HDM contributions, see [15].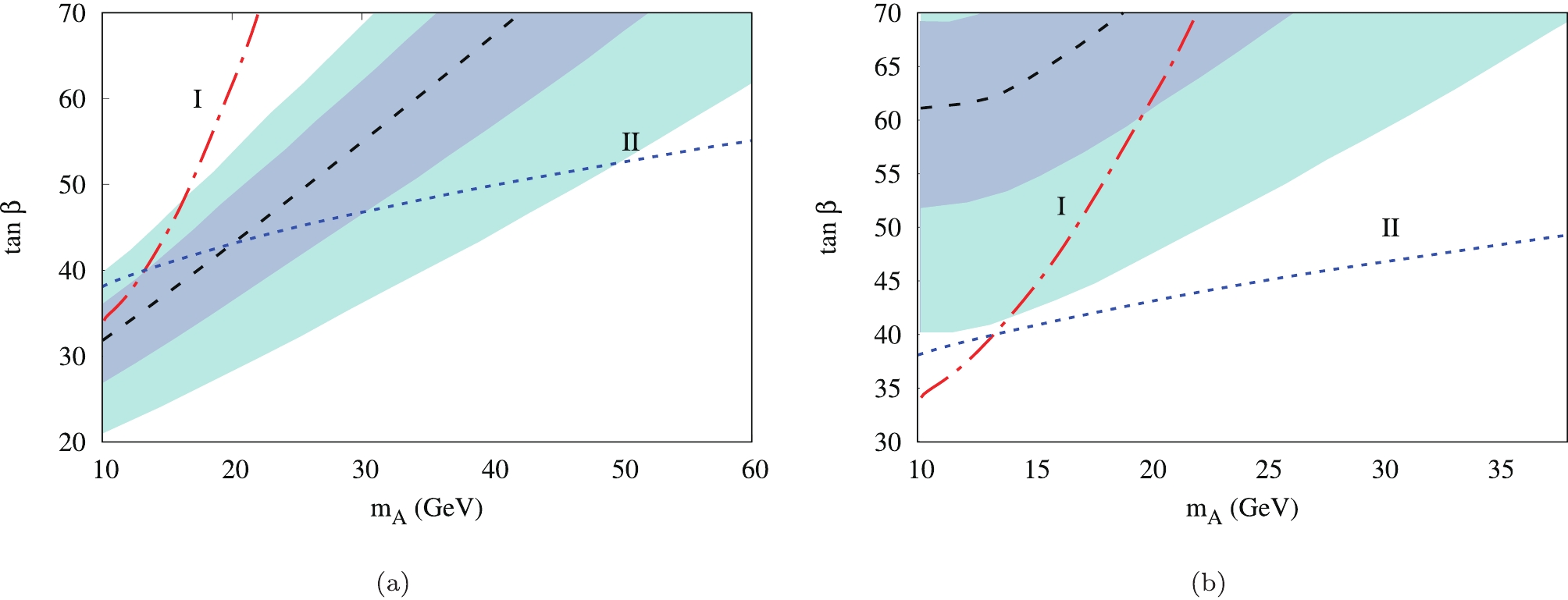
Figure 2. (color online) Values of
$ \tan\beta $ and$ m_A $ required to explain the$ \Delta a_\mu $ in (a) type-II and (b) type-X 2HDM. One and two sigma regions are shown in dark blue and light blue, respectively. This parameter space can be further constrained by experimental data. Regions I and II (above dashed red and blue lines respectively) are excluded by direct search at LEP and$ \tau $ decay ($ \tau \to \mu \nu_\mu \nu_\tau $ ), respectively, at 95% C.L. [28].Although the addition of S is necessary for the explanation of multi-lepton anomalies, it does not have a significant effect on the parameter space of the 2HDM required to account for
$ \Delta a_\mu $ , since the contributions from the CP-even scalars are suppressed with respect to that of the CP-odd scalar. This can be seen in a comparison of the plots in Fig. 2 and those in Fig. 3. In contrast to the existing constraints on the 2HDM+S, Fig. 3 shows that it requires a high value of$ \tan\beta $ and a relatively small mass of A. We also showed the constraints on the parameter space in the$ m_A $ -$ \tan\beta $ plane excluded by the direct searches at the LEP and the measurement of$ \tau \to \mu \nu_\mu \nu_\tau $ at 95% C.L. In all cases considered here,$ \tau $ -decays provide the most stringent constraints for both models and types. To calculate the leptonic$ \tau $ decay, we consider the leading one-loop diagrams and use the formula given in [28].
Figure 3. (color online) Values of
$ \tan\beta $ and$ m_A $ required to explain$ \Delta a_\mu $ in (a) type-II and (b) type-X 2HDM+S. One and two sigma regions are shown in dark blue and light blue, respectively. Note the similarity to the parameter space required by the 2HDM without S in Fig. 2. Regions I and II (above dashed red and blue lines respectively) are excluded by direct search at LEP and$ \tau $ decay ($ \tau \to \mu \nu_\mu \nu_\tau $ ), respectively, at 95% C.L [28].Following the model used in [19], where
$ m_A = 600 $ GeV and$ \tan\beta < 1 $ , the full two-loop contribution from 2HDM+S is shown in Fig. 4. From the plots in Fig. 4, it is clear that the existing constraints on$ \tan\beta $ and the particle masses in the 2HDM+S make the model not suitable to account for$ \Delta a_\mu $ .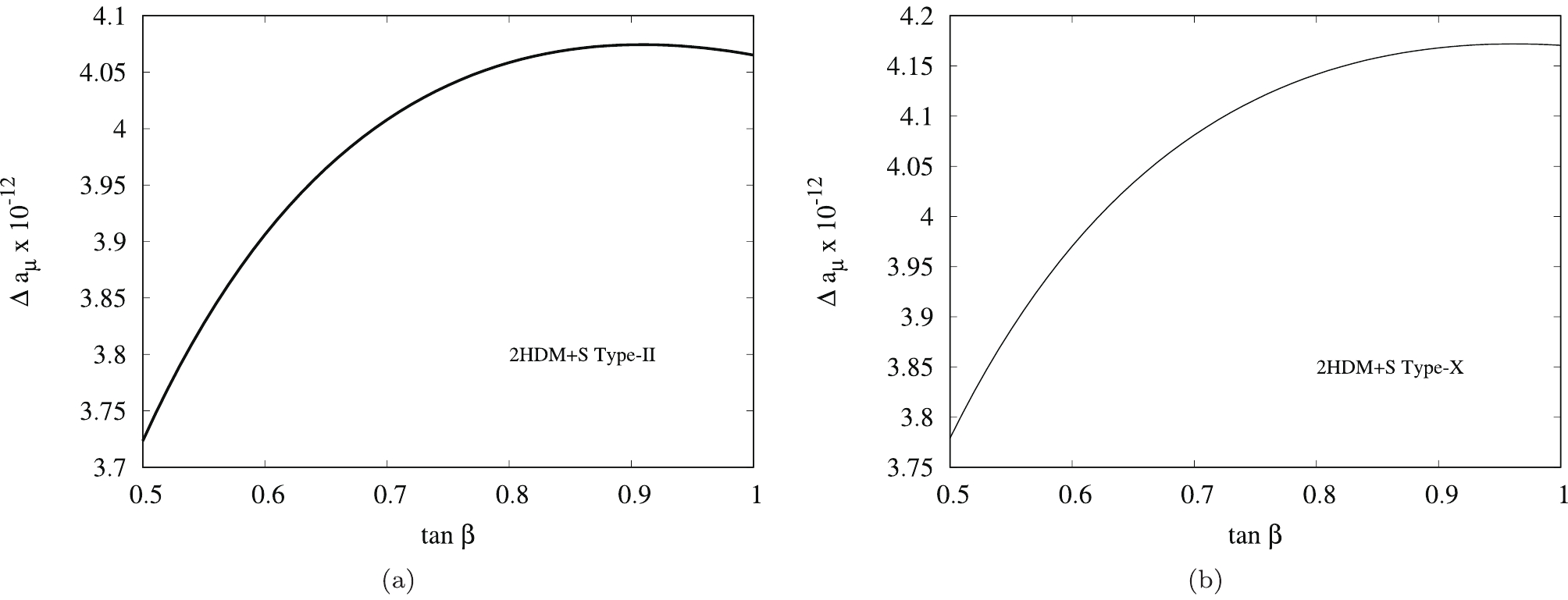
Figure 4. One- and two-loop contributions from 2HDM+S to
$ \Delta a_\mu $ using Eq. (5) and Eq. (9) in (a) type-II and (b) type-X 2HDM+S. Here$ m_A = 600 $ GeV is assumed.Addition of BSM fermions: Introducing additional fermionic degrees of freedom that interact with the 2HDM+S particles allows the one-loop contributions to become larger than the two-loop contributions. Fermions in the mass range 100 GeV to 1000 GeV enlarge the one-loop contributions sufficiently to account for
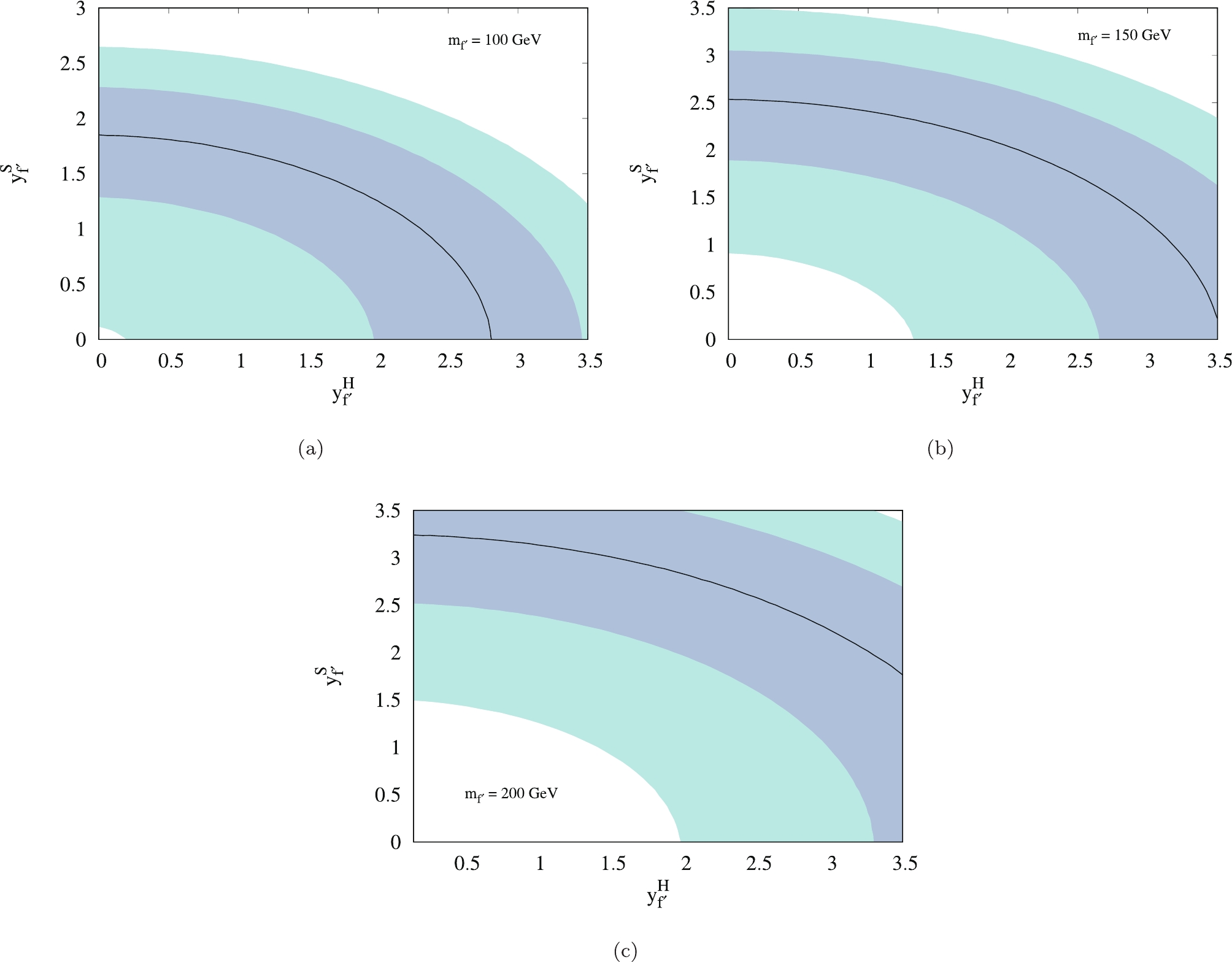
$ \Delta a_\mu $ . The one-loop diagram with the new fermions is explained in Fig. 1. In Fig. 5, we depict the contribution to the$ \Delta a_\mu $ using Eq. (11) for different choices of couplings. Because the contributions from the 2HDM+S without the BSM fermions and the two-loop diagrams containing the SM fermions are much smaller, only the one-loop contribution is considered here. In Fig. 6, we depict some of the couplings required by different fermion masses.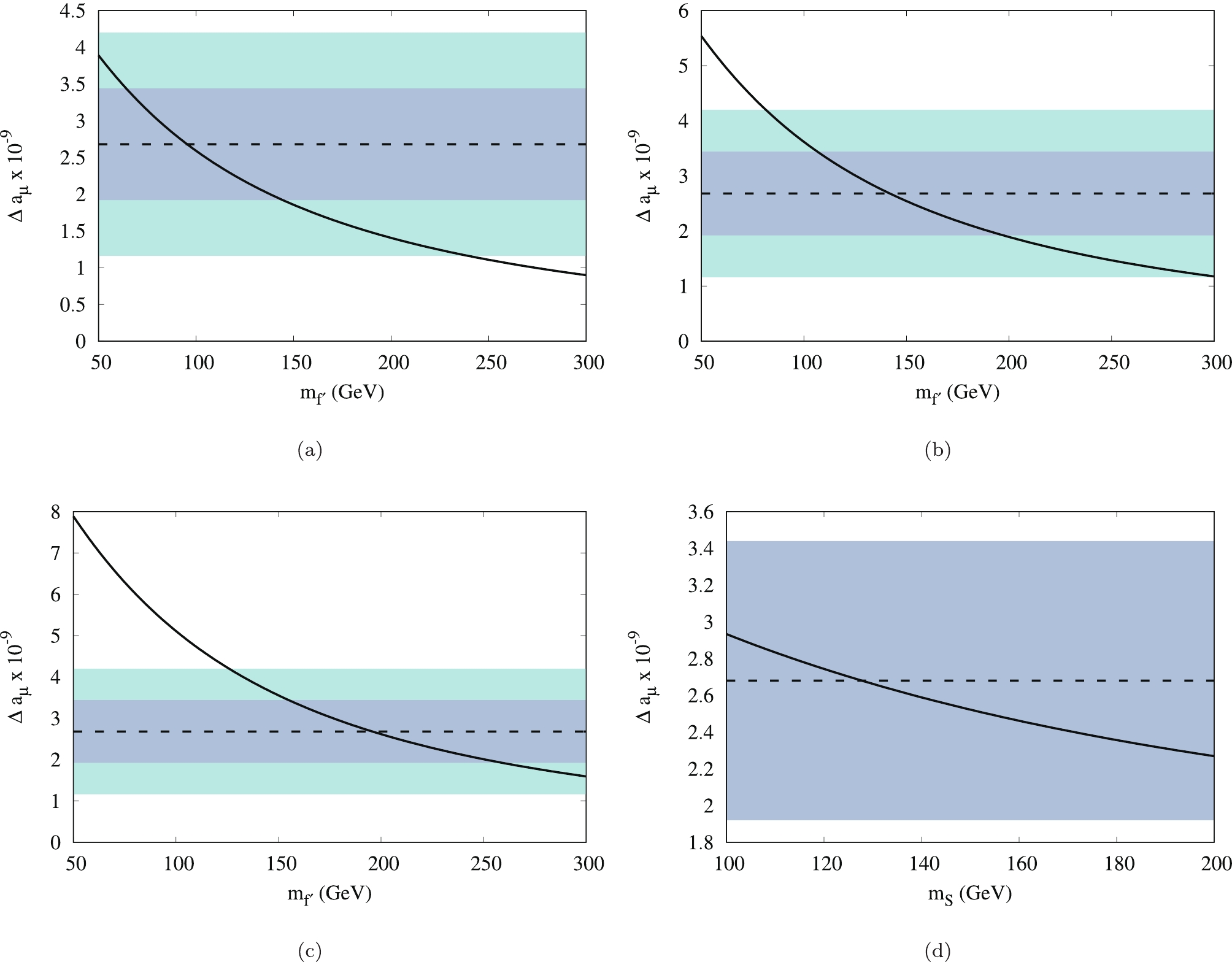
Figure 5. (color online) Contributions to
$ \Delta a_\mu $ from one-loop diagram in Fig. 1 by (a), (b), (c) varying fermion masses and (d) varying mass of S. Dashed line indicates the discrepancy, as given in Eq. (1), and one and two sigma regions are shown with dark blue and light blue, respectively. The fermion couplings are fixed at (a)$ y^h_{f^\prime} = 1 $ ,$ y^A_{f^\prime} = 3.5 $ ,$ y^S_{f^\prime} = y^H_{f^\prime} = 1.5 $ , (b)$ y^h_{f^\prime} = 1 $ ,$ y^A_{f^\prime} = 3.5 $ ,$ y^S_{f^\prime} = y^H_{f^\prime} = 2 $ , (c)$ y^h_{f^\prime} = 1 $ ,$ y^A_{f^\prime} = 3.5 $ ,$ y^S_{f^\prime} = y^H_{f^\prime} = 2.5 $ , (d)$ y^h_{f^\prime} = 1 $ ,$ y^A_{f^\prime} = 3.5 $ ,$ y^S_{f^\prime} = y^H_{f^\prime} = 1.5 $ , and$ m_{f^\prime} = 100 $ GeV. -
Thus far, we constrained the parameter space of 2HDM+S and 2HDM+S+f models by calculating the contributions to
$ \Delta a_\mu $ . However, there are other sources from which these model parameters can also be constrained. We discuss some of them in this section.Low energy bounds: The observed data of
$ B_s \to \mu^+ \mu^- $ highly constrains the parameter space of 2HDMs, and hence they also constrain the extended models considered here. The branching fraction of$ B_s \to \ell \ell $ has an enhancement of$ \tan^4 \beta $ in type II 2HDMs, arising from the mediation of the extra Higgses possible in the box and penguin type diagrams, as both charged leptons and down-type quarks have a coupling related to$ \tan\beta $ for the extra bosons. However, the same couplings in a type X 2HDM are enhanced by$ \tan\beta $ for leptons and$ \cot\beta $ for quarks, which implies no such$ \tan^4 \beta $ relationship in the$ B_s \to \ell \ell $ branching fraction in the type X case. In fact, for type X, the leading contribution is largely$ \tan\beta $ independent for large$ \tan\beta $ . A caveat to this (when comparing type X to type II 2HDM) is related to the contributions from A, the light CP-odd Higgs. A can provide large contributions to the branching fraction of$ B_s \to \mu^+ \mu^- $ , needed to explain the$ (g-2)_\mu $ anomaly. From the$ B_s \to \mu^+ \mu^- $ formula in [29], constraints on the parameter space are obtained in [28]. A similar observation is allowed for the models and parameters considered in this work.Furthermore, recent results from the CMS collaboration have presented the branching fraction as Br
$ (B_s \to \mu^+\mu^-) = [ 2.9^{+0.7}_{-0.6} ({\rm exp}) \pm 0.2 ({\rm frag})]\times10^{-9} $ , where the first uncertainty combines the experimental statistical and systematic contributions, and the second is due to the uncertainty in the ratio of the$ B_s^0 $ and the$ B^+ $ fragmentation functions [30]. This is in aggreement with our analysis.Muon mass corrections: Because of the addition of singly charged SM singlet vector-like leptonic fermions given in Eq. (4), the mixing between muon and vector-like singlet leptonic fermion
$ f^{\prime} $ can provide corrections to the muon mass. The quantum corrections from the vector-like leptons to the SM lepton masses are avoided by minimal flavor protections [10]. Here, the Yukawa coupling between the muon and the corresponding vector-like lepton$ f^{\prime} $ will contribute to the muon mass proportional to the Yukawa coupling, suppressed by the usual loop factor of$ {\cal O}(1/(4\pi) )$ . Perturbativity and the accepted mass correction impose constraints on the relevant Yukawa couplings in the muon sector. In this work, our choice of the couplings$ |y_{f^\prime}^i| $ are limited by these requirements, as shown in Fig. 5.Collider searches and limits: The results provided by the ATLAS collaboration at center of mass energies of
$ \sqrt{s} = 13 $ TeV have excluded singly charged ($ L^\pm $ ) and neutral ($ N^0 $ ) heavy leptons with masses below 560 GeV at 95% C.L., where the search was carried out in a simplified type-III seesaw model, assuming branching fractions to all lepton flavors to be equal [31]. This translates to the limits on the$ W^\pm L^\pm N^0 $ coupling. Several type-III seesaw heavy lepton searches were also performed in the past by the ATLAS in Run 1 at$ \sqrt{s} = 8 $ TeV [32], which excluded the heavy leptons with masses below 335 GeV. In Run 1, this search was complemented by another ATLAS search for heavy leptons using the three-lepton final state [33], excluding heavy lepton masses below 470 GeV. A Run 2 search by the CMS experiment at$ \sqrt{s} = 13 $ TeV [34] was performed on multi-lepton final states using at least three leptons, excluding the type-III seesaw heavy leptons with masses in the range up to 840 GeV.A similar analysis can be performed on the parameter space of the model considered here, through a process
$ p p \to H \to f^\prime f^\prime $ , where$ f^\prime \to Z \mu^\pm $ or$ f^\prime \to W^\pm \nu $ with final states as (semi-) leptonic and/or hadronic signatures with missing energy. In this work,$ m_S < 2 m_{f^\prime} $ , though similar search strategies can be followed with A. Here, we can derive similar limits, and we must note from earlier studies [16, 35] that the resonance production of S is suppressed. One should also consider$ m_H \gtrsim 2 m_{f^\prime} $ , which limits$ m_{f^\prime} \approx 150 $ GeV (for on-shell decay) according to the parameter choices considered here. Following the limits derived from [31], the couplings$ H{f^\prime}{f^\prime} $ and/or$ A{f^\prime}{f^\prime} $ should be in the range of$ \sim [0.4,1.0] $ to observe such final states. These analyses further strengthen the parameter space to explain$ \Delta a_\mu $ . We discussed a search strategy roughly, which can be taken as future work for full analyses. -
A number of predictions were made in [16, 17] pertaining to the anomalous production of multiple leptons at high energy proton-proton collisions. These could be connected with a heavy boson, with a mass around the electroweak scale decaying predominantly into a SM Higgs boson and a singlet scalar. Discrepancies in multi-lepton final states were reported with Run 1 data in [17, 21], and they have now become statistically compelling with the available Run 2 data [18]. These include the production of opposite-sign, same-sign, and three leptons with and without b-quarks. Discrepancies arising in final states and parts of the phase-space, where different SM processes can dominate, points to the unlikeliness of a mis-modeling of one particular SM process and led to a good description of the anomalies and their kinematic characteristics by a simple ansatz. This ansatz states that a H with mass of
$ m_H\approx 270 $ GeV, produced in association with top quarks via gluon fusion, can decay via$ H\to Sh $ , where$ m_S\approx 150 $ GeV. The H can be embedded into 2HDM, whilst the S can be an additional singlet (a 2HDM+S) [16, 19, 20]. The 2HDM+S model, which accommodates all these features of the data [19], is used here as a baseline.The long-standing discrepancy in the muon anomalous magnetic moment is explored in this study in connection with the suggested scalar boson spectroscopy and in the context of a constrained 2HDM+S model. The two-loop contribution from the 2HDM+S has been calculated, and it has been shown that this contribution is too small to account for the
$ \Delta a_\mu $ discrepancy. Furthermore, the values of$ \tan\beta $ and$ m_A $ required to explain the discrepancy within two sigma have been determined for the 2HDM+S. In both type- II and type-X 2HDM+S, a light pseudo-scalar is required, along with a high value of$ \tan\beta $ . This choice of parameters in the 2HDM+S model is not compliant with the features of the LHC data described here. To be able to explain the$ \Delta a_\mu $ discrepancy with the 2HDM+S model as constrained in [19], additional BSM fermionic degrees of freedom may be required. Given the size and the errors associated with the$ \Delta a_\mu $ anomaly, new leptons would need to be as heavy as$ {\cal O}(100) $ GeV. The impact of these new degrees of freedom on the model considered here and, in particular, on the decays of bosons, is beyond the scope of this study and will be addressed in subsequent work, although a brief discussion on the search strategies with other constraints is provided in Section 5.The authors are grateful for the support from the South African Department of Science and Innovation through the SA-CERN program and the National Research Foundation for various forms of support.
Connecting muon anomalous magnetic moment and multi-lepton anomalies at LHC
- Received Date: 2019-11-25
- Accepted Date: 2020-02-07
- Available Online: 2020-06-01
Abstract: In a previous paper by several of the authors a number of predictions were made in a study pertaining to the anomalous production of multiple leptons at the Large Hadron Collider (LHC). Discrepancies in multi-lepton final states have become statistically compelling with the available Run 2 data. These could be connected with a heavy boson, H, which predominantly decays into a standard model Higgs boson, h, and a singlet scalar, S, where






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: