-
There is compelling evidence from astrophysical and cosmological observations for the existence of Dark Matter. Despite this evidence, the nature of Dark Matter has not been made clear until now. Asymmetric Dark Matter is one of the alternatives that is contrary to the common assumption that the Majorana particle neutralino could be the candidate for Dark Matter. Neutralino is the most popular candidate of Weakly Interacting Massive Particles (WIMPs) appeared in supersymmetric theory. The idea for asymmetric Dark Matter arises from the possible link between the baryon number density and the Dark Matter energy density [1-12]. The average density of baryons with
$ \Omega_b = 0.046 $ is comparable to that of Dark Matter. It is well known that ordinary matter in the universe is almost completely made from baryons, with anti-baryons contributing only a small fraction. The connection between baryons and Dark Matter leads to the assumption that Dark Matter particles can be asymmetric, where particles and anti-particles are not identical, and that there are more Dark Matter particles than anti-particles (or vice versa).Refs. [13, 14] discussed the relic abundance of asymmetric Dark Matter in the standard cosmological scenario, which assumes that the asymmetric Dark Matter particles and anti-particles were in thermal equilibrium at the end of the radiation dominated era and were decoupled when they become nonrelativistic. In this scenario, it is usually assumed that anti-particles are completely annihilated away from their particles, and that there are particles in the end. They showed that the final abundances of asymmetric Dark Matter particles and anti-particles are determined not only by the annihilation cross section but also by the asymmetry factor, which is the deviation of co-moving densities of the particle and anti-particle, stated later in this paper.
In this work, we investigate asymmetric Dark Matter, which is coupled to the sufficiently light force mediators and the interaction between Dark Matter particles and anti-particles appearing as long-range interactions. In this case, the wavefunction of asymmetric Dark Matter particles and antiparticles is distorted by the long-range interaction, that is, the Sommerfeld effect [15]. The Sommerfeld effect enhances the late-time Dark Matter annihilation signals [16, 17], and the Sommerfeld enhancement is determined by the coupling of Dark Matter to the light force mediator. Asymmetric Dark Matter needs stronger couplings than symmetric Dark Matter of the same mass. Thus, the implications of the Sommerfeld enhancement for the phenomenology of asymmetric Dark Matter may be quite important compared with the symmetric Dark Matter case.
The effect of the Sommerfeld enhancement on the relic density for symmetric Dark Matter has been investigated in [18-24]. In Refs. [25-28], the authors discussed asymmetric thermal Dark Matter with the Sommerfeld enhancement, including the effect of the bound state. In this paper, we explore the relic density of asymmetric Dark Matter particles and anti-particles when the annihilation cross sections of asymmetric Dark Matter particles and anti-particles are enhanced by the Sommerfeld effect. Here, we only consider the Sommerfeld effect and neglect the effect of bound state formation on the relic density of asymmetric Dark Matter. We find that the particle abundance is not modified significantly when the annihilation rate is boosted by the Sommerfeld enhancement. However, for Dark Matter anti-particle, the decrease in abundance is more sizable than that for the case without including the effect of the Sommerfeld enhancement.
Although asymmetric Dark Matter particles and anti-particles dropped out of chemical equilibrium, they were still in kinetic equilibrium for a while through the scattering of relativistic standard model particles in the thermal plasma. When the annihilating asymmetric Dark Matter particles and anti-particles were both in chemical and kinetic equilibrium, their temperatures tracked the background radiation temperature T, i.e.,
$ T_{\chi,\bar\chi} = T $ . At some point, the rate of scattering fell below the expansion rate of the universe, and the asymmetric Dark Matter particles and anti-particles dropped out of kinetic equilibrium. After kinetic decoupling, the temperatures of asymmetric Dark Matter particles and anti-particles are related by$ T_{\chi,\bar\chi} = T^2/T_k $ with the background radiation temperature T, where$ T_k $ is the kinetic decoupling temperature [29, 30]. The thermal average of the cross section, which is appears in the Boltzmann equation, is different before and after kinetic decoupling due to the change in temperature dependence. This impacts the relic densities of asymmetric Dark Matter particles and anti-particles. Without the Sommerfeld enhancement, kinetic decoupling has no effect on the relic abundance of asymmetric Dark Matter for s-wave annihilation, since there is no temperature dependency in this case. However, there is a very small impact for the case of p-wave annihilation. In contrast, the effect is more significant for both the Sommerfeld enhanced s-wave and p-wave annihilations. The relic abundance of asymmetric Dark Matter continuously decreases until the Sommerfeld enhancement ceases to have an impact on the relic abundance.The effect of kinetic decoupling on the relic density of Dark Matter for the Sommerfeld enhancement was investigated in Refs. [21, 31-33]. Ref. [34] discussed the case that includes the effect of resonance for
$ m_{\phi} \neq 0 $ . The impact of early kinetic decoupling on the relic density was also investigated in Ref. [35]. In this work, we extend this discussion to asymmetric Dark Matter. We explore the effects of kinetic decoupling on the relic abundance of asymmetric Dark Matter particles and anti-particles in detail when the annihilation cross section of asymmetric Dark Matter is changed by the Sommerfeld enhancement. Here, we discuss the case where the mediator between asymmetric Dark Matter is massless, that is,$ m_{\phi} = 0 $ . We find that the relic abundances of asymmetric Dark Matter particles and anti-particles decrease after kinetic decoupling. This decrease is almost invisible for asymmetric Dark Matter particles; in contrast, the decrease is sizable for asymmetric Dark Matter anti-particles. The magnitude of the decrease depends on the asymmetry factor$ \eta $ , coupling strength$ \alpha $ , and the kinetic decoupling temperature$ T_k $ .The paper is arranged as follows. In Section II, we discuss the thermal average of the Sommerfeld enhanced annihilation cross section for asymmetric Dark Matter. In Section III, we study the numerical solution of asymmetric Dark Matter abundance, including the effect of the Sommerfeld enhancement. The analytic result for the relic density of asymmetric Dark matter is presented in Section IV. In Section V, we investigate the effects of kinetic decoupling on the relic abundance of asymmetric Dark Matter particles and anti-particles. In Section VI, the constraints on the parameter space are obtained using the observational data of Dark Matter. In the last section, we summarize our results.
-
For a massless light force carrier
$ m_{\phi} $ (in the limit$ m_{\phi} \rightarrow 0 $ ), the Sommerfeld factor for s-wave annihilation is$ S_s = \frac{2 \pi\alpha/v}{1-{\rm e}^{-2\pi\alpha/v}}, $

(1) and for p-wave annihilation,
$ S_p = \left[1 + \left(\frac{\alpha}{v}\right)^2\right]\frac{2 \pi\alpha/v}{1-{\rm e}^{-2\pi\alpha/v}}, $

(2) where v is the relative velocity of two annihilating asymmetric Dark Matter particles and anti-particles, and
$ \alpha $ is the coupling strength [36]. Here we only consider the annihilation of particle$ \chi $ and anti-particle$ \bar\chi $ . When the asymmetric Dark Matter particles and anti-particles decouple from the thermal background, they are non-relativistic. Without the Sommerfeld enhancement, the annihilation cross section for asymmetric Dark Matter particles and anti-particles can be expanded with respect to the relative velocity v as$ \langle \sigma v \rangle = a + b\, \langle v^2 \rangle + {\cal{O}}( \langle v^4 \rangle )\, , $

(3) where a is the s-wave contribution to
$ \sigma v $ when the p-wave is suppressed, and b describes the p-wave contribution to$ \sigma v $ . After including the Sommerfeld enhancement on the thermal average of annihilation cross section, we have$ {\langle \sigma v \rangle}_S = a\,\langle S_s\rangle + b\, \langle v^2 S_p \rangle+ {\cal{O}}( v^4 )\, . $

(4) Here we use
$ B_s $ and$ B_p $ to denote the Sommerfeld boost factor as$\begin{split} B_s =& \langle S_s\rangle = \frac{x^{3/2}}{2 \sqrt{\pi}}\,\int^{\infty}_0 {\rm d}v\; v^2 \; {\rm e}^{-\frac{x}{4} v^2}\, \frac{2 \pi \alpha/v}{1- {\rm e}^{- 2 \pi \alpha/v}}\, , \end{split}$

(5) and
$ \begin{split} B_p =& \langle v^2\, S_p\rangle = \frac{x^{3/2}}{2 \sqrt{\pi}}\,\int^{\infty}_0 {\rm d}v\; v^4 \; {\rm e}^{-\frac{x}{4} v^2}\,\\&\times \left[ 1 + (\frac{\alpha}{v})^2 \right] \frac{2 \pi \alpha/v}{1- {\rm e}^{- 2 \pi \alpha/v}}\, , \end{split}$

(6) where
$ x = m/T $ , with m being the mass of asymmetric Dark Matter. Next, we obtain the analytic result for the thermal average of the Sommerfeld enhanced annihilation cross section multiplied by the relative velocity in an approximate way [24]. For the case of$ \pi \alpha /v \ll 1 $ , we expand the factor$ (2 \pi \alpha/v)/(1- {\rm e}^{- 2 \pi \alpha/v}) $ in Eqs. (5) and (6) in the Taylor series up to the second order, as follows:$ \frac{2 \pi \alpha/v}{1- {\rm e}^{- 2 \pi \alpha/v}} = 1 + \frac{\pi \alpha}{v} + \frac{1}{3} \left(\frac{\pi \alpha}{v}\right)^2. $

(7) Plugging the Taylor series into Eq. (4), we obtain
$\begin{aligned}[b]{\langle \sigma v \rangle}_{S,{\rm{Taylor}}} =& a \left( 1 + \alpha \sqrt{\pi x} + \frac{1}{6}\pi^2 \alpha^2 \, x \right) \\& + b \left[\alpha^2 \left( 1 + \alpha \sqrt{\pi x} + \frac{1}{6}\pi^2 \alpha^2 \, x \right)\right. \\&\left.+ \frac{6}{x}\; \left( 1 + \frac{2}{3} \alpha \sqrt{\pi x} + \frac{1}{18}\pi^2 \alpha^2 x \right) \right]. \end{aligned} $

(8) When
$ \alpha = 0 $ , the standard annihilation cross section is recovered. For the opposite limit,$ \pi \alpha/v \gg 1 $ ,${\rm e}^{- 2 \pi \alpha/v}$ in the denominator of Eqs. (5) and (6) is negligible; then, the cross section is enhanced by$ 1/v $ , and we have$ \langle \sigma v \rangle_{s,{1/v}} = 2 \alpha \sqrt{\pi x}, $

(9) $ \langle \sigma v \rangle_{p,{1/v}} = 8\alpha \sqrt{\pi/x} + 2\alpha^3\sqrt{\pi x}\,. $

(10) Using Eq. (8) and applying the Pade method, we can find the well fitting rational functions that connect the two limiting cases and can reproduce the exact numerical results for the thermal average of the annihilation cross section multiplied by the relative velocity, that is,
$ {\langle \sigma v \rangle}_{S,{\rm{approx}}} = a\, B_{s, {\rm{approx}}} + b\, B_{p, {\rm{approx}}}, $

(11) where
$ B_{s, {\rm{approx}}} = \frac{ 1 + 7/4\; \alpha \sqrt{\pi x} + 3/2\; \alpha^2 \pi x + (3/2 - \pi/3 )\; (\alpha^2 \pi x)^{3/2} } { 1 + 3/4\; \alpha \sqrt{\pi x} + (3/4 - \pi/6)\; \alpha^2 \pi x }, $

(12) and
$ \begin{split} &B_{p, {\rm{approx}}} = \\& \alpha^2 \, \frac{ 1 + 7/4\; \alpha \sqrt{\pi x} + 3/2\; \alpha^2 \pi x + (3/2 - \pi/3 )\; (\alpha^2 \pi x)^{3/2} } { 1 + 3/4\; \alpha \sqrt{\pi x} + (3/4 - \pi/6)\; \alpha^2 \pi x } \\ & + \frac{6}{x}\, \frac{ 1+ 4/3\; \alpha \sqrt{\pi x} + (\pi + 4)/9\; \alpha^2 \pi x + 4/51\; \pi\; (\alpha^2 \pi x)^{3/2} } {1+ 2/3\; \alpha \sqrt{\pi x} + \alpha^2 \pi^2 x/18 }\, . \end{split} $

(13) We note that the choice is not unique. The approximation reproduces the exact results with an accuracy of less than 0.5%.
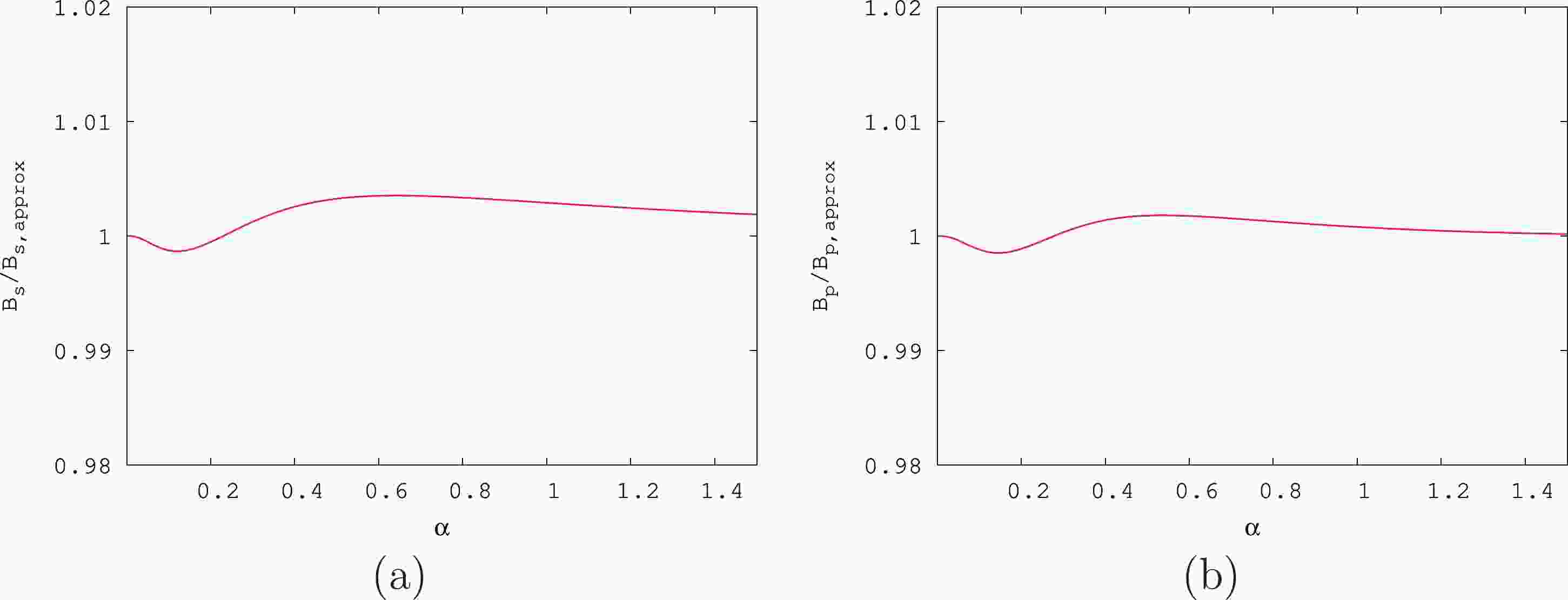
Figure 1 shows the ratio of the exact values of thermally averaged Sommerfeld boost factors,
$ B_s $ and$ B_p $ , and the approximations,$ B_{s, {\rm{approx}}} $ and$ B_{p, {\rm{approx}}} $ , as a function of$ \alpha $ for the typical inverse-scaled WIMP decoupling temperature$ m/T = 22 $ in$ (a) $ and$ (b) $ . We find that our approximation reproduces the exact results with an accuracy of less than 0.5% in both$ (a) $ and$ (b) $ . -
After including the Sommerfeld enhanced annihilation cross section in the Boltzmann equation, which describes the evolution of number densities of asymmetric Dark Matter particles and anti-particles, we have
$ \frac{{\rm d} n_{\chi,\bar\chi}}{{\rm d}t} + 3 H n_{\chi,\bar\chi} = - {\langle \sigma v\rangle}_S (n_{\chi} n_{\bar\chi} - n_{\chi,{\rm{eq}}} n_{\bar\chi,{\rm{eq}}})\,, $

(14) where
$ \chi $ is for particles and$ \bar\chi $ is for anti-particles. The expansion rate in the radiation dominated era is$ H = \pi T^2/M_{\rm{Pl}} \, \sqrt{g_*/90} $ , where$ M_{\rm{Pl}} = 2.4 \times 10^{18} $ GeV is the reduced Planck mass, with$ g_* $ being the effective number of relativistic degrees of freedom. The equilibrium number densities are$ n_{\chi,{\rm{eq}}} = g_\chi {\big[m T/(2 \pi) \big]}^{3/2}{\rm{e}}^{(-m+\mu_\chi)/T} $ and$ n_{\bar\chi,{\rm{eq}}} = g_\chi \,{\big[m T/(2 \pi) \big]}^{3/2} {\rm{e}}^{(-m - \mu_{\chi})/T} $ . Here the chemical potentials$ \mu_{\bar\chi} = - \mu_{\chi} $ in equilibrium, where$ g_{\chi} $ is the number of intrinsic degrees of freedom of the particle.The Boltzmann equation in terms of the ratio of the number densities of particles and anti-particles to entropy density
$ Y_{\chi,\bar\chi} = n_{\chi,\bar\chi}/s $ and x is$ \frac{{\rm d} Y_{\chi,\bar\chi}}{{\rm d}x} = - \frac{{\lambda \langle \sigma v \rangle}_S}{x^2}\, (Y_{\chi}\; Y_{\bar\chi} - Y_{\chi, {\rm{eq}}}\; Y_{\bar\chi, {\rm{eq}}} )\,, $

(15) where
$ s = 2 \pi^2 g_{*s}/45\, T^3 $ , with$ g_{*s} $ being the effective number of entropic degrees of freedom. Here we used the entropy conservation,$ \lambda = 1.32\,m M_{\rm{Pl}}\, \sqrt{g_*}\, $ , with$ g_*\simeq g_{*s} $ and${\rm d}g_{*s}/{\rm d}x\simeq 0$ . The subtraction of the Boltzmann equations for$ \chi $ and$ \bar\chi $ results in$ \frac{{\rm d} Y_{\chi}}{{\rm d} x} - \frac{{\rm d} Y_{\bar\chi}}{{\rm d} x} = 0. $

(16) This means that
$ Y_{\chi} - Y_{\bar\chi} = \eta\,, $

(17) where
$ \eta $ is a constant, and the difference of the co-moving densities of the particles and anti-particles is conserved. Inserting this into the Boltzmann equation (15) yields$ \frac{{\rm d} Y_{\chi}}{{\rm d}x} = - \frac{{\lambda \langle \sigma v \rangle}_S}{x^2}\; (Y_{\chi}^2 - \eta Y_{\chi} - Y^2_{\rm{eq}})\,, $

(18) $ \frac{{\rm d} Y_{\bar\chi}}{{\rm d}x} = - \frac{{\lambda \langle \sigma v \rangle}_S}{x^2}\; (Y_{\bar\chi}^2 + \eta Y_{\bar\chi} - Y^2_{\rm{eq}})\,, $

(19) where
$ Y^2_{\rm{eq}} = Y_{\chi,{\rm{eq}}} Y_{\bar\chi,{\rm{eq}}} = (0.145g_{\chi}/g_*)^2\,x^3{\rm e}^{-2x} $ . We note that$ Y^2_{\rm{eq}} $ does not depend on the chemical potential$ \mu_{\chi} $ .In the standard picture of particle evolution scenarios, it is assumed that the asymmetric Dark Matter particles and anti-particles are in thermal equilibrium with the standard model plasma in the early universe. They decouple from equilibrium whenever the interaction rate
$ \Gamma $ drops below the expansion rate H. At this point, the temperature is less than the mass of asymmetric Dark Matter particles, that is,$ T < m $ for$ m > |\mu_{\chi}| $ [13, 14, 37]. This is the freeze out temperature at which the number densities of asymmetric Dark Matter particles and anti-particles in co-moving space almost become constant.Figure 2 shows the evolution of abundances of Dark Matter particles and anti-particles when the annihilation cross section is enhanced by the Sommerfeld effect. It is plotted using the numerical solutions of equations (18), (19). In panel
$ (a) $ , the thick (red) lines are for relic abundances$ Y_{\chi} $ and$ Y_{\bar\chi} $ for asymmetric Dark Matter particles and anti-particles without the Sommerfeld effect. The dashed (blue) lines are for the case of the Sommerfeld factor$ \alpha = 0.1 $ , and dotted (black) lines are for the case of the Sommerfeld factor$ \alpha = 0.2 $ . The double dotted (red) line is for the equilibrium value of anti-particle abundance. It is shown that deviations between the particle abundances of the cases with and without the Sommerfeld enhancement are very small when$ \alpha = 0.1 $ and$ \alpha = 0.2 $ . We found that the particle abundance is not affected appreciably compared to the anti-particle abundance. The impact of the Sommerfeld enhancement on relic abundance of anti-particles is more significant when the Sommerfeld factor$ \alpha $ is larger. Similar results are obtained for the case of p-wave annihilation in plot$ (b) $ . The asymmetric Dark Matter decouples later due to the boosted annihilation rate compared to the case without the Sommerfeld enhancement, and hence, the relic abundances for particles and anti-particles are decreased in principle. For$ \alpha = 0.1 $ and$ \alpha = 0.2 $ in Fig. 2, if the decreases in anti-particle abundances are of a few orders less than that of$ \eta $ , the particle abundance remains the same order as that of$ \eta $ due to the relation$ Y_{\chi} - Y_{\bar\chi} = \eta $ , because the anti-particle abundance is too small to alter the particle abundance in Eq. (16). This is the reason why the particle abundance is not changed sizably compared to the anti-particle abundance. For the smaller value of$ \eta $ , as in Fig. 3, the decrease in asymmetric Dark Matter particle abundance is obvious. -
We follow the method used in [13, 14] to find the analytic solution. We first write the Boltzmann equation (19) in terms of
$ \Delta_{\bar\chi} = Y_{\bar\chi} - Y_{\bar\chi,{\rm{eq}}} $ as$ \frac{{\rm d} \Delta_{\bar\chi}}{{\rm d}x} = - \frac{{\rm d} Y_{\bar\chi,{\rm{eq}}}}{{\rm d}x} - \frac{{\lambda \langle \sigma v \rangle}_S}{x^2}\; \left[\Delta_{\bar\chi}(\Delta_{\bar\chi} + 2 Y_{\bar\chi,{\rm{eq}}}) + \eta \Delta_{\bar\chi} \right]\, . $

(20) For high temperature,
$ Y_{\bar\chi} \sim Y_{\bar\chi,{\rm{eq}}} $ ; therefore, we ignore$ \Delta^2_{\bar\chi} $ and${\rm d}\Delta_{\bar\chi}/{\rm d}x$ ; then,$ \Delta_{\bar\chi} \simeq \frac{2 x^2 Y^2_{\rm{eq}}} {\lambda {\langle \sigma v \rangle}_S\,(\eta^2 + 4 Y^2_{\rm{eq}})}\,, $

(21) where
$ Y_{\bar\chi,{\rm{eq}}} = - \eta/2 + \sqrt{\eta^2/4 + Y^2_{\rm eq}} $ , which is obtained by sol-ving the Boltzmann equation (19) in the equilibrium state. Eq. (21) is used to fix the freeze out temperature$ \bar{x}_F $ for$ \bar{\chi} $ .At a late time, when the temperature is low, i.e.,
$ x > \bar{x}_F $ , the equilibrium value of relic abundance$ Y_{\bar\chi,{\rm{eq}}} $ is negligible. Thus, after dropping the term that is related to$ Y_{\bar\chi,{\rm{eq}}} $ in Eq. (20), we have$ \frac{{\rm d} \Delta_{\bar\chi}}{{\rm d}x} = - \frac{\lambda {\langle \sigma v \rangle}_S}{x^2 } \left( \Delta_{\bar\chi}^2 + \eta \Delta_{\bar\chi} \right)\,, $

(22) where we assume that
$ \Delta_{\bar\chi}(\bar{x}_F)\gg \Delta_{\bar\chi}(x_{\infty}) $ and integrate Eq. (22) from$ \bar{x}_F $ to$ \infty $ , so that$ Y_{\bar\chi}(x_\infty) = \eta\,\left\{ \, {\rm{exp}} \left[\, 1.32\, \eta \, m M_{\rm{Pl}}\, \sqrt{g_*} \, \int^{\infty}_{\bar{x}_F} \frac{{\langle \sigma v \rangle}_S}{ x^2}{\rm d}x\,\right] -1\, \right\}^{-1} \,, $

(23) where
$ \begin{split} \int^{\infty}_{\bar{x}_F} \frac{{\langle \sigma v \rangle}_S}{ x^2} {\rm d}x =& (a + \alpha^2\,b) \left[ \frac{1}{\bar{x}_F} + 2 \alpha \sqrt{\frac{\pi}{\bar{x}_F}} + \frac{\pi^2 \alpha^2}{6}\; {\rm{ln}} \left( 1 + \frac{9 \alpha \sqrt{\pi \bar{x}_F} + 12 } {(9 - 2 \pi )\pi \alpha^2 \bar{x}_F }\right) \right. + \pi \alpha^2\; \frac{36 - 11 \pi}{\sqrt{3(117 - 32\pi)}} \\& \left. \times \left( \frac{\pi}{2} - {\rm{tan}}^{-1}\; \frac{ 2(9 - 2\pi) \alpha \sqrt{\pi \bar{x}_F} +9} {\sqrt{3(117 - 32 \pi)}} \right) \right] + b\left[ \frac{3}{\bar{x}_F^2} + \frac{8 \sqrt{\pi} \alpha}{3\bar{x}_F^{3/2}} + \frac{\pi^2 \alpha^2 }{3 \bar{x}_F} + \frac{8 \pi^{5/2} \alpha^3 } {153 \sqrt{\bar{x}_F}} + \frac{(16 + 13\pi) \pi^3 \alpha^4}{459 \sqrt{ \pi/2 -1}} \right. \\& \times \left( \frac{\pi}{2} - {\rm{tan}}^{-1}\frac{6 + \pi^{3/2} \alpha \sqrt{\bar{x}_F}}{ 3\sqrt{2(\pi -2)}} \right) - \left. \frac{(16 + 17\pi) \pi^3 \alpha^4 }{918}\; {\rm{ln}} \left( 1 + \frac{12}{\pi \alpha \sqrt{\pi \bar{x}_F}} + \frac{18}{\pi^2 \alpha^2 \bar{x}_F} \right) \right]\, . \end{split} $

(24) The relic abundance for the
$ \chi $ particle is obtained by using Eq. (17) as follows:$ Y_{\chi}(x_\infty) = \eta\, \left\{\, 1 - \exp \left[\, - 1.32\, \eta\, m M_{\rm{Pl}}\, \sqrt{g_*} \, \int^{\infty}_{x_F} \frac{{\langle \sigma v \rangle}_S}{ x^2}{\rm d}x \, \right]\, \right\}^{-1}\,, $

(25) where
$ x_F $ is the freeze out temperature for$ \chi $ . Eqs. (23) and (25) are only consistent with constraint (17) if$ x_F = \bar{x}_F $ . The total final Dark Matter relic density is$ \Omega_{\rm{DM}} h^2 = 2.76 \times 10^8\, \left[ Y_{\chi}(x_\infty) + Y_{\bar\chi}(x_\infty) \right]\,m, $

(26) where we use
$ \Omega_{\chi} = \rho_{\chi}/\rho_c $ with$ \rho_{\chi} = n_{\chi} m = s_0 Y_{\chi} $ and$ \rho_c = 3 H^2_0 M^2_{\rm{Pl}} $ . Here,$ s_0 \simeq 2900 $ cm$ ^{-3} $ is the present entropy density, and$ H_0 $ is the Hubble constant. We use the equality,$ \xi Y_{\bar\chi,{\rm{eq}}}( \bar{x}_F) = \Delta_{\bar\chi}(\bar{x}_F) $ , to fix the freezing out temperature; here,$ \xi $ is a constant, and usually, we take$ \xi = \sqrt{2} -1 $ [37]. We find that the analytic result matches with the numerical result within an accuracy of 10%. -
The effect of the Sommerfeld enhancement on the relic density of asymmetric Dark Matter was analyzed in the previous section. It was assumed that the temperatures of annihilating asymmetric Dark Matter particles and anti-particles track the background radiation temperature T when the annihilating asymmetric Dark Matter particles and anti-particles remain in chemical and kinetic equilibrium with the radiation background. During the radiation dominated era, the temperature of radiation scales as
$ T \propto 1/R $ , with R being the scale factor of the universe. Asymmetric Dark Matter particles and anti-particles are still in kinetic equilibrium after dropping out of chemical equilibrium. At some point$ T_k $ , asymmetric Dark Matter particles and anti-particles decouple from kinetic equilibrium, and the temperature of asymmetric Dark Matter scales as$ T_{\chi,\bar\chi} \propto 1/R^2 $ [29, 30, 38, 39]. The determination of the precise value of the kinetic decoupling temperature$ T_k $ depends on the models. In the supersymmetric models discussed in [30],$ T_k \approx (10^{-3} - 10^{-1}) T_F $ . In this work, we take$ T_k/T_F $ as a free parameter for generality, with the constraint$ T_k < T_F $ . Then, the relation between the temperatures of asymmetric Dark Matter$ T_{\chi,\bar\chi} $ and the radiation temperature T is [29, 30]$ T_{\chi,\bar\chi} = \frac{T^2}{T_k}. $

(27) This change will affect the thermal average of the annihilation cross section between the asymmetric Dark Matter particles and anti-particles. For the case of s-wave annihilation, the cross section is independent of
$ T_{\chi,\bar\chi} $ ; therefore, kinetic decoupling has no effect on the relic density of asymmetric Dark Matter in this case. For p-wave annihilation or Sommerfeld enhanced s- and p-wave annihilations, since there are temperature dependencies of the annihilation cross section, the relic density is affected by kinetic decoupling. After kinetic decoupling, the thermal average of the p-wave annihilation cross section becomes$ {\langle \sigma v\rangle}_p = 6b\, x_k/x^2 $ . The Boltzmann equations of asymmetric Dark Matter anti-particle for p-wave annihilation before and after kinetic decoupling are$ \frac{{\rm d} Y_{\bar\chi}}{{\rm d}x} = - 1.32\,m M_{\rm{Pl}}\, \sqrt{g_*} (6b\, x^{-3})\, (Y_{\bar\chi}^2 + \eta Y_{\bar\chi} - Y^2_{\rm{eq}})\,, $

(28) $ \frac{{\rm d} Y_{\bar\chi}}{{\rm d}x} = - 1.32\,m M_{\rm{Pl}}\, \sqrt{g_*} (6b\, x_k x^{-4})\, (Y_{\bar\chi}^2 + \eta Y_{\bar\chi} - Y^2_{\rm{eq}})\,. $

(29) The effect of kinetic decoupling on the final relic density of asymmetric Dark Matter for p-wave annihilation is estimated by integrating the Boltzmann equation (28) from
$ \bar{x}_F $ to$ x_k $ and Eq. (29) from$ x_k $ to$ \infty $ . When there is kinetic decoupling, we obtain the relic abundance for asymmetric Dark Matter anti-particles for p-wave annihilation as$ \begin{split} Y_{\bar\chi}(x_{\infty}) =& \eta\,\left\{ \, {\rm{exp}} \left[\, 1.32\, \eta \, m M_{\rm{Pl}}\, \sqrt{g_*} \, \left( \int^{x_k}_{\bar{x}_F} \frac{6b }{ x^3}\,{\rm d}x \right.\right.\right.\\&\left.\left.\left.+ \int^{\infty}_{x_k} \frac{6bx_k}{ x^4}\,{\rm d}x \right) \right] -1\, \right\}^{-1} \,. \end{split}$

(30) In Fig. 4, we plot the relic abundance of asymmetric Dark Matter particles
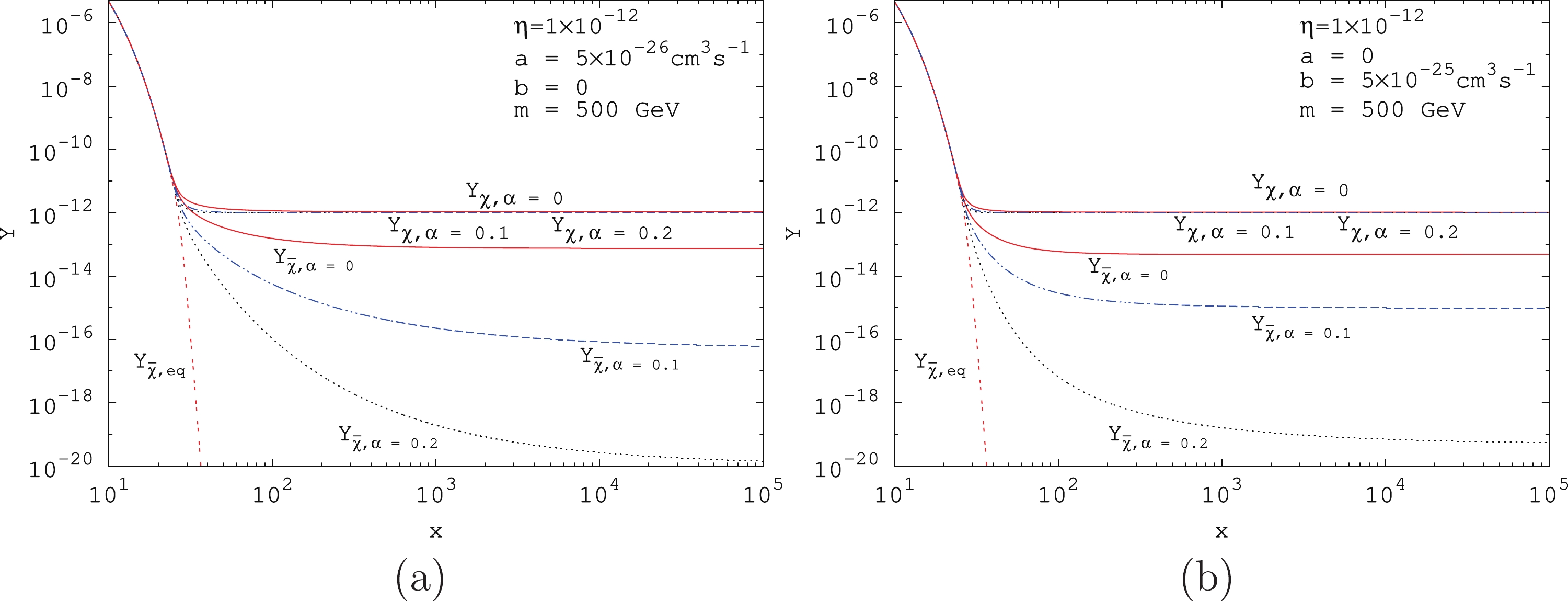
$ Y_{\chi} $ and anti-particles$ Y_{\bar\chi} $ as a function of the inverse-scaled temperature x for the p-wave annihilation cross section when the kinetic decoupling temperature is$ x_k = 5 x_F $ . Here,$ \alpha = 0 $ ,$ a = 0 $ ,$ b = 5 \times 10^{-25} $ $ {\rm{cm}}^3 \,{\rm{s}}^{-1} $ ,$ \eta = 1 \times 10^{-12} $ , and$ m = 500 $ GeV. The effects of kinetic decoupling on the asymmetric Dark Matter particle abundance$ Y_{\chi} $ and anti-particle abundance$ Y_{\bar\chi} $ are negligible when the kinetic decoupling temperature is$ x_k = 5 x_F $ . The Dark Matter particle abundance is almost not changed after kinetic decoupling. The difference between the anti-particle abundance before and after kinetic decoupling is changed by a factor of 1. Because we are discussing the case where kinetic decoupling occurs after the asymmetric Dark Matter particles and anti-particles decoupled from chemical equilibrium, we again assume that the kinetic decoupling occurs at a point that is five times the inverse-scaled chemical decoupling temperature; therefore, the effect is negligible in this case. This may have significant effects if the kinetic decoupling occurs earlier. In this case, one must solve the coupled Boltzmann equations, which for simplicity, we did not consider in our work [35].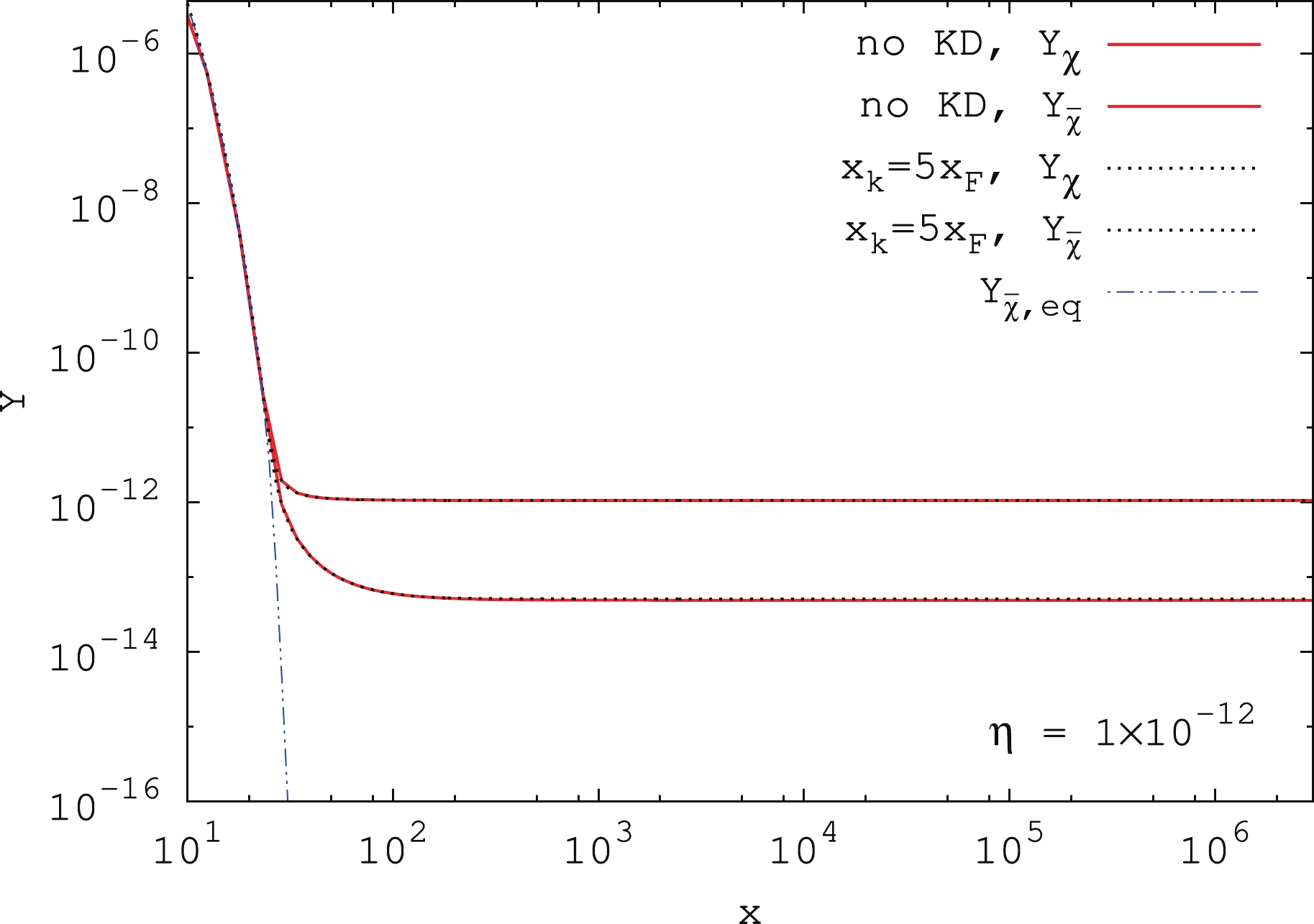
Figure 4. (color online) The effect of kinetic decoupling on the evolution of Y for particles and anti-particles as a function of x for the p-wave annihilation cross section. Here,
$ g_{\chi} = 2 $ ,$ g_* = 90 $ ,$ m = 500 $ GeV,$ x_F = 25 $ ,$ a = 0 $ , and$ b = 5 \times 10^{-25} $ $ {\rm{cm}}^3 \,{\rm{s}}^{-1} $ .The effect of kinetic decoupling is more noticeable for the case of Sommerfeld enhanced s-wave and p-wave annihilations. With the kinetic decoupling, the Sommerfeld enhanced annihilation cross sections become
$ \begin{split} {\langle \sigma v \rangle}_{S_k} \simeq & \frac{x^3}{2 \sqrt{\pi x^3_k}}\,\int^{\infty}_0 {\rm d}v\,{\rm e}^{-\frac{x^2}{4x_k} v^2} \Bigg\{ a\,v^2 \, \frac{2 \pi \alpha/v}{1- {\rm e}^{- 2 \pi \alpha/v}}\\& + b\,v^4 \, \left[ 1 + \left(\frac{\alpha}{v}\right)^2 \right] \frac{2 \pi \alpha/v}{1- {\rm e}^{- 2 \pi \alpha/v}}\Bigg\}\, . \end{split} $

(31) Next, the Boltzmann equation (19) of asymmetric Dark Matter anti-particles for Sommerfeld enhanced s- and p-wave annihilation cross sections is
$ \frac{{\rm d} Y_{\bar\chi}}{{\rm d}x} = - { 1.32\,m M_{\rm{Pl}}\, \sqrt{g_*} \langle \sigma v \rangle}_{S_k}\,x^{-2}\, (Y_{\bar\chi}^2 + \eta Y_{\bar\chi} - Y^2_{\rm{eq}})\,. $

(32) Figure 5 shows the evolution of
$ Y_{\chi} $ and$ Y_{\bar\chi} $ as a function of x for the s-wave annihilation cross section for$ \alpha = 0.1 $ in panels (a) and (c) and$ \alpha = 0.2 $ in panels (b) and (d). Here, the asymmetry factor$ \eta = 1 \times 10^{-12} $ in panels (a) and (b), and$ \eta = 5 \times 10^{-13} $ in (c) and (d);$ m = 500 $ GeV,$ a = 5 \times 10^{-26} $ $ {\rm{cm}}^3 \,{\rm{s}}^{-1} $ , and$ b = 0 $ . We plot the figure using the numerical solution of Eq. (19) from the range of$ \bar{x}_F $ to$ x_k $ and that of Eq. (32) from$ x_k $ to a large value of x; here, we use$ x = 3 \times 10^6 $ . We found that asymmetric Dark Matter particle abundance for different kinetic decoupling temperatures are almost same for the case wherein there is no kinetic decoupling. In contrast, after kinetic decoupling, the relic abundances for anti-particles are decreased continuously until the annihilation becomes inefficient. If we replace x with$ x_{\chi} = x^2/x_k $ in the analytic result of the s-wave Sommerfeld factor in Eq. (12), the Sommerfeld factor$ \propto x $ for sufficiently large x. After the integration of Eq. (32), for large x, the anti-particle abundance for s-wave annihilation cross section scales as$ Y_{\bar\chi} \propto \eta/x^c $ , where$ c \propto 1.32 \eta\, m\, M_{\rm{Pl}}\,\sqrt{g_*}\,\alpha\,a $ , which is constant. It matches with the numerical result. However, this decrease will eventually be stopped by one of the following three effects [34]. Firstly, the Sommerfeld enhancement is saturated at low velocity; it works for the massive mediator case. The second effect is the onset of matter domination. The last effect is the onset of structure formation, which finally eliminates the Sommerfeld effect. We use$ x_{\rm{cut}} $ to express the point at which the Sommerfeld effect is eliminated. In plot$ (a) $ , the relic abundance becomes constant at approximately$ x_{\rm{cut}} = 1.5 \times 10^5 $ for$ x_k = 5x_F $ ,$ 2.2 \times 10^5 $ for$ x_k = 10x_F $ , and$ 6.9 \times 10^5 $ for$ x_k = 100x_F $ . We obtained these points from the numerical data. The asymmetric Dark Matter annihilation rate is insignificant from those points, and$ Y_{\bar\chi} $ becomes stable. The inverse-scaled temperature at which the annihilations become inefficient is important for the correct determination of the relic density of asymmetric Dark Matter. The decrease in abundance of Dark Matter anti-particles is larger when the decoupling temperature is closer to the chemical freezing out point$ x_F $ . The reduction is also more sizable for larger$ \alpha $ . For the smaller asymmetry factor$ \eta = 5 \times 10^{-13} $ , the decrease in Dark Matter anti-particle abundance is less than that for the case of$ \eta = 1 \times 10^{-12} $ , which is shown in panels$ (c) $ and$ (d) $ .
Figure 5. (color online) The effects of kinetic decoupling on the evolution of Y for asymmetric Dark Matter particles and anti-particles as a function of x for Sommerfeld enhanced s-wave annihilation cross section for different asymmetry factors and coupling strengths. Here,
$ g_{\chi} = 2 $ ,$ g_* = 90 $ ,$ m = 500 $ GeV, and$ x_F = 25 $ .The cases of
$ \alpha = 0.1 $ and$ \alpha = 0.2 $ for Sommerfeld enhanced p-wave annihilation cross section are plotted in Fig. 6 for kinetic decoupling temperatures$x_k = 5 x_F , $ $ 10x_F, 100x_F $ . Here,$ \eta = 1 \times 10^{-12} $ ,$ m = 500 $ GeV,$ a = 0 $ , and$ b = 5 \times 10^{-25} $ $ {\rm{cm}}^3 \,{\rm{s}}^{-1} $ . Similar analysis with the s-wave annihilation can be performed for the case of p-wave annihilation. The abundance for asymmetric Dark Matter particles are nearly not changed for different kinetic decoupling temperatures. For asymmetric Dark Matter anti-particles, the decrease in abundance is very small for$ \alpha = 0.1 $ compared with the case of$ \alpha = 0.2 $ . In contrast, the decrease is larger for smaller inverse-scaled kinetic decoupling temperature$ x_k = 5x_F $ for the case when$ \alpha = 0.2 $ . In panel$ (b) $ , annihilations become insignificant at the point$ x_{\rm{cut}} = 4.1 \times 10^5 $ for$ x_k = 5x_F $ ,$ 2.6\times 10^5 $ for$ x_k = 10x_F $ , and$ 6.9\times 10^5 $ for$ x_k = 100x_F $ .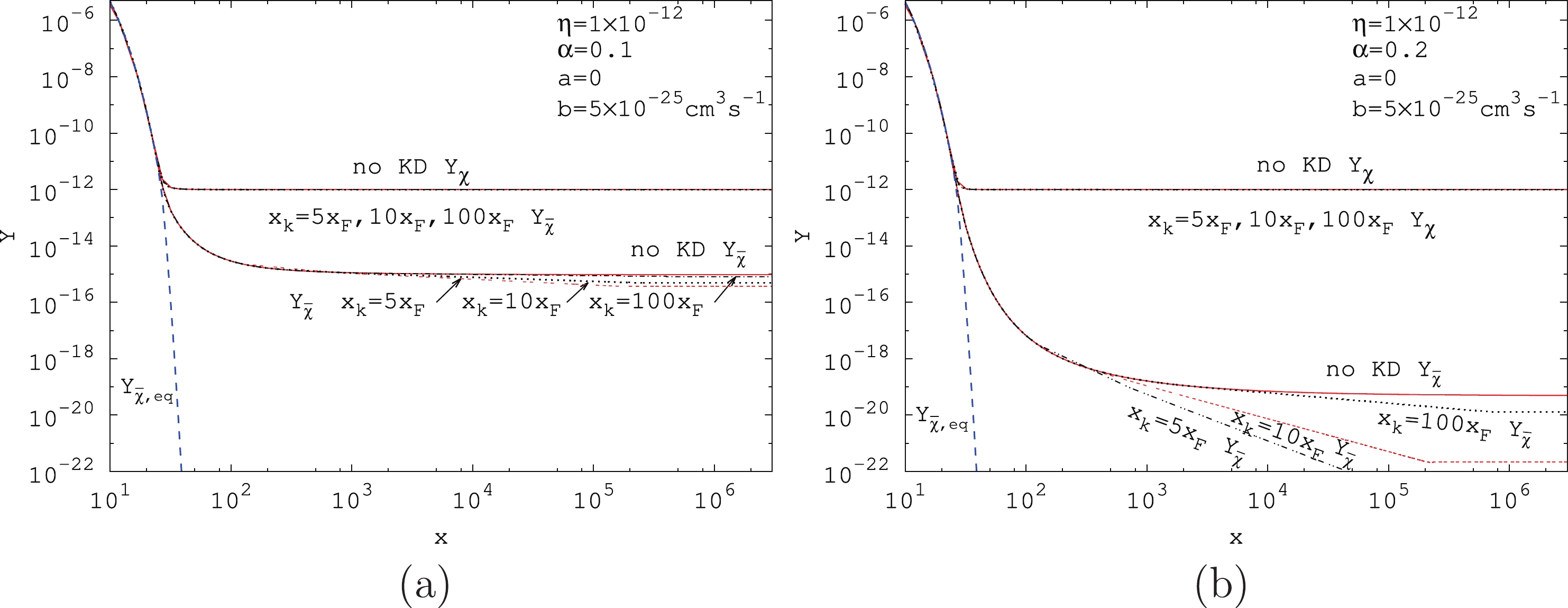
Figure 6. (color online) The effects of kinetic decoupling on the evolution of Y for the particles and anti-particles as a function of x for Sommerfeld enhanced p-wave annihilation cross section. Here,
$ g_{\chi} = 2 $ ,$ g_* = 90 $ ,$ m = 500 $ GeV, and$ x_F = 25 $ .The final relic abundance for asymmetric Dark Matter anti-particles for the Sommerfeld enhanced s- and p-wave annihilations is obtained by integrating the Boltzmann equation (19) from
$ \bar{x}_F $ to$ x_k $ and Eq. (32) from$ x_k $ to$ x_{\rm{cut}} $ . Then,$ \begin{split} Y_{\bar\chi}(x_{\rm{cut}}) =& \eta\,\left\{ \, {\rm{exp}} \left[\, 1.32\, \eta \, m M_{\rm{Pl}}\, \sqrt{g_*} \, \left( \int^{x_k}_{\bar{x}_F} \frac{{\langle \sigma v \rangle}_S}{ x^2}\,{\rm d}x \right.\right.\right.\\&\left.\left.\left.+ \int^{x_{\rm{cut}}}_{x_k} \frac{{\langle \sigma v \rangle}_{S_k}}{ x^2}\,{\rm d}x \right) \right] -1\, \right\}^{-1} \,.\end{split} $

(33) -
The Dark Matter relic density provided by the Planck data [40] is
$ \Omega_{\rm{DM}} h^2 = 0.1199 \pm 0.0022\, . $

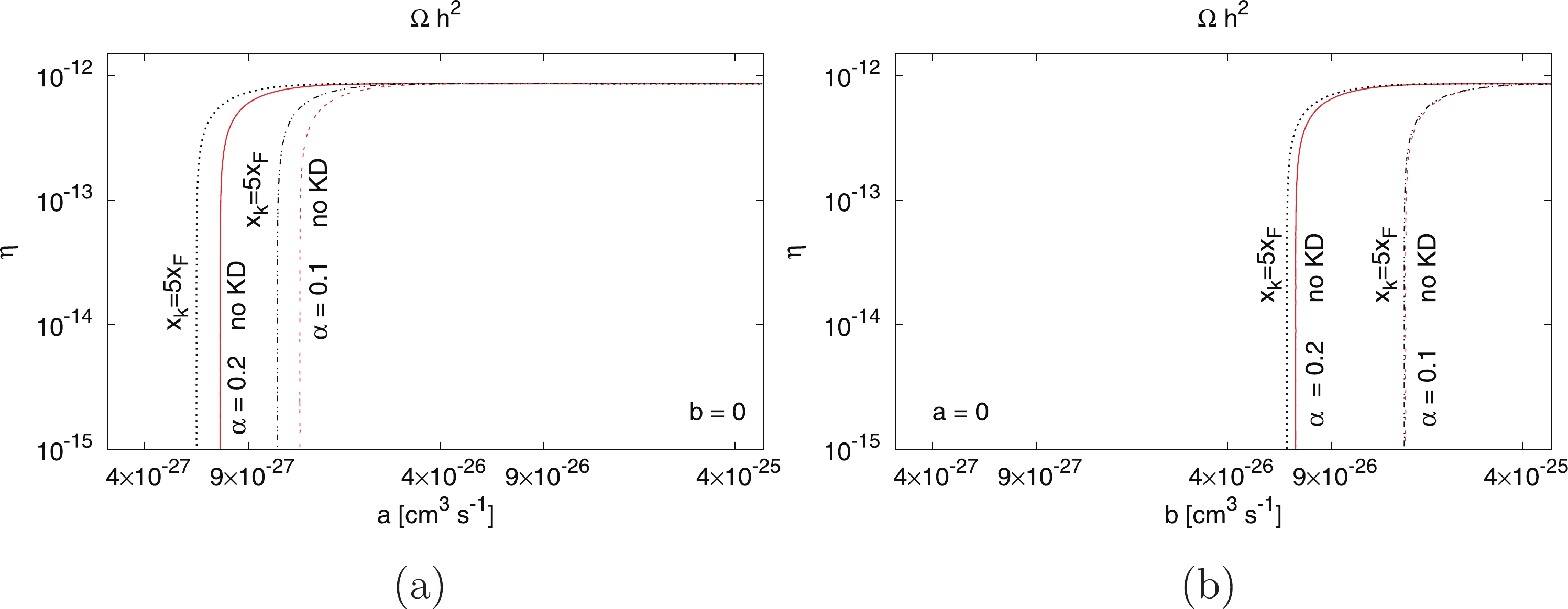
(34) Figure 7 shows the contour plots of s- (panel
$ (a) $ ) and p-wave (panel$ (b) $ ) annihilation cross sections and asymmetry factor$ \eta $ when$ \Omega_{\rm{DM}} h^2 = 0.1199 $ . The loosely dashed (red) line is for the case of the Sommerfeld enhancement without kinetic decoupling, and the dashed dotted (black) line is for the case of kinetic decoupling when$ \alpha = 0.1 $ , where the inverse-scaled kinetic decoupling temperature is$ x_k = 5x_F $ . The thick (red) line is for the case when there is no kinetic decoupling, and the dotted (black) line is for inverse-scaled kinetic decoupling temperature$ x_k = 5x_F $ when$ \alpha = 0.2 $ . We found that the required annihilation cross section with kinetic decoupling is smaller than that in the case without kinetic decoupling, i.e., when$ \alpha = 0.2 $ and$ \eta = 1.0\times 10^{-15} $ in panel (a), the required cross section is$ a = 5.99 \times 10^{-27} $ $ {\rm{cm}}^3 \,{\rm{s}}^{-1} $ for the case of kinetic decoupling and$ a = 7.20 \times 10^{-27} $ $ {\rm{cm}}^3 \,{\rm{s}}^{-1} $ for the case of no kinetic decoupling. The reason for this is that the relic density is decreased continuously after kinetic decoupling until the annihilation becomes inefficient. As a result, there is less relic density for the case with kinetic decoupling compared with the case without kinetic decoupling. In order to satisfy the observed range of Dark Matter relic density, when there is kinetic decoupling, the annihilation cross section should be smaller than that for the case without kinetic decoupling. In contrast, the required annihilation cross section for$ \alpha = 0.2 $ is two times smaller than that for the case of$ \alpha = 0.1 $ . We can see from Fig. 5 that the decrease in asymmetric Dark Matter anti-particle abundance is larger for larger coupling strength$ \alpha $ . A similar analysis was performed for the case of the p-wave annihilation cross section in panel (b) of Fig. 7. That is, for$ \alpha = 0.2 $ and$ \eta = 1.0 \times 10^{-15} $ , the required cross section is$ b = 6.35 \times 10^{-26} $ $ {\rm{cm}}^3 \,{\rm{s}}^{-1} $ for the case of kinetic decoupling and$ b = 6.80 \times 10^{-26} $ $ {\rm{cm}}^3 \,{\rm{s}}^{-1} $ for the case of no kinetic decoupling. The difference in the required cross section between the kinetic decoupling and no kinetic decoupling is very small for$ \alpha = 0.1 $ for p-wave annihilation. We can determine the reason for this from panels (a) and (b) of Fig. 6. After kinetic decoupling, asymmetric Dark matter particle abundance is almost same for$ \alpha = 0.1 $ and$ \alpha = 0.2 $ . The decrease in anti-particle abundance for$ \alpha = 0.1 $ is very small in panel (a) compared with the case of$ \alpha = 0.2 $ in panel (b). -
We investigated the relic density of asymmetric Dark Matter, which is coupled to the light force mediator. When the mediator is light enough, the interaction between the asymmetric Dark Matter particles and anti-particles emerges as long-range interaction, which distorts the wavefunction of two incoming asymmetric Dark Matter particles and anti-particles. It is indeed the Sommerfeld effect that enhances the annihilation rate of asymmetric Dark Matter at low velocity. The relic density of asymmetric Dark Matter is explored when the annihilation cross section is boosted by the Sommerfeld effect. First, we found the thermal average of the Sommerfeld enhanced annihilation cross section. Next, we derived the analytic formulae for relic abundance of asymmetric Dark Matter particles and anti-particles. We found that the abundance for asymmetric Dark Matter particles is not affected too much. In contrast, the decrease in the relic abundance of asymmetric Dark Matter anti-particles is more obvious than that for particles, due to the Sommerfeld enhancement. The size of the decrease depends on the Sommerfeld factor
$ \alpha $ . For larger$ \alpha $ , there is a sizable decrease in the relic abundance.Next, we discussed the effects of kinetic decoupling on the relic abundance of asymmetric Dark Matter particles and anti-particles when the annihilation cross section of asymmetric Dark Matter is changed by the Sommerfeld effect. After chemical decoupling, the asymmetric Dark Matter particles and anti-particles continue to stay in kinetic equilibrium. When the scattering rate falls below the expansion rate of the universe, asymmetric Dark Matter particles and anti-particles decouple from kinetic equilibrium. The temperatures of asymmetric Dark Matter are different before and after kinetic decoupling. This leaves its imprint on the relic density of asymmetric Dark Matter particles and anti-particles. There is no effect on the s-wave annihilation, while the impact is almost negligible for p-wave annihilation when there is no Sommerfeld enhancement. In contrast, when the annihilation cross section is increased by the Sommerfeld enhancement, there are significant effects on the relic density of asymmetric Dark Matter both for s- and p-wave annihilation cross sections.
In our work, we assumed that kinetic decoupling occurred after chemical decoupling. The kinetic decoupling point is at least five times the inverse-scaled freezing out temperature. We found that the decrease is negligible for the abundance of asymmetric Dark Matter particles. The asymmetric Dark Matter anti-particle abundance is continuously decreased after the kinetic decoupling until the annihilations become insignificant. The magnitude of decrease depends on the size of the kinetic decoupling temperature, the coupling strength
$ \alpha $ , and the asymmetry factor$ \eta $ . The decrease is larger when the kinetic decoupling temperature is closer to the freezing out point. The reduction of anti-particle abundance is more sizable for larger$ \alpha $ and also for a larger asymmetry factor$ \eta $ .Finally, we used Planck data and found the constraints on annihilation cross section and the asymmetry factor for the cases with and without kinetic decoupling. Our results show that the required cross section for Dark Matter should be smaller than that for the case of without kinetic decoupling in order to fall in the observation range of Dark Matter relic density. This is because there is less relic density of asymmetric Dark Matter due to kinetic decoupling. This result is important for determining the relic abundance of asymmetric Dark Matter when the Sommerfeld effect plays a role at low velocity. Sommerfeld effects imply that the indirect detection of signals from the annihilations of asymmetric Dark Matter anti-particles is significant. This provides us the possibility of probing asymmetric Dark Matter with observations of the Cosmic Microwave Background (CMB), the Milky way, and Dwarf galaxies.
Relic density of asymmetric Dark Matter with Sommerfeld enhancement
- Received Date: 2020-06-04
- Available Online: 2021-01-15
Abstract: We investigate the evolution of abundance of the asymmetric thermal Dark Matter when its annihilation rate at chemical decoupling is boosted by the Sommerfeld enhancement. Next, we discuss the effect of kinetic decoupling on the relic abundance of asymmetric Dark Matter when the interaction rate depends on velocity. Usually, the relic density of asymmetric Dark Matter is analyzed in the frame of chemical decoupling. Indeed, after decoupling from chemical equilibrium, asymmetric Dark Matter particles and anti-particles are still in kinetic equilibrium for a while. This has no effect for the case of s-wave annihilation since there is no temperature dependence in this case. However, kinetic decoupling has impacts for the case of p-wave annihilation and Sommerfeld enhanced s- and p-wave annihilations. We investigate in detail the extent to which kinetic decoupling affects the relic abundance of asymmetric Dark Matter particles and anti-particles. We find the constraints on the cross section and asymmetry factor using observational data of the relic density of Dark Matter.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: