-
The study of halo nuclei that are far from the valley of β-stability and close to the nucleon drip-line has become one of the main topics in modern nuclear structure physics. This halo phenomenon for exotic nuclei has created much interest and hundreds of papers since its discovery in the mid-1980s. The halo of a nucleus arises from the very weak binding of the last one or two valence nucleons (protons or neutrons) to the core containing all other nucleons that are tightly bound; this weak binding energy leads to the creation of a neutron/proton tail. These halo nuclei have small separation energy as a result of the presence of a halo neutron/proton tail, extended nucleon density distributions, or quite large root mean square (rms) radii, and the emitted nucleons have narrow momentum distributions [1-3]. It has been proven that there are two types of halo nuclei: neutron and proton halos, which depend on the type of nucleon arrangements of the halo structure. Nuclei that have a one proton halo include 8B and 26P; those that have a one neutron halo are 11Be and 19C. Nuclei that have a two proton halo are exhibited by 17Ne and 27S [4-6], and those that have a two neutron halo include 6He, 11Li, 17B, 19B, and 22C [7-11]. These halo nuclei consist of three body systems (an inert core nucleus plus two valence neutrons or two valence protons).
Exotic 11Li nuclei have attracted much theoretical and experimental interest as a typical case. Their first production was described by Postanzer et al. in 1966 [12], and some special properties such as their large matter radii were discovered by Tanihata et al. [1, 13]. The 11Li nucleus has numerous interesting properties. i) It consists of a core of three protons and six neutrons as well as a halo of two loosely bound neutrons; 11Li belongs to the three-body system (9Li+n+n), which is called a Borromean system [14, 15]. ii) The small separation energy (S2n) of the two-neutron halo is only S2n= 300 KeV [1], and in new research, it is found to be S2n= 378±5 KeV [15, 16]. This small separation energy leads to an increase in the matter radius of 11Li compared with other Li isotopes and forms a low-density halo, where nuclear radii increase with the mass number A of a nucleus as A1/3. Further, it has been found that the matter radius of a 11Li nucleus significantly deviates from the A1/3 law, whereas other Li isotopes follow this law exactly [16]. iii) The rms radius is quite large compared to that of 9Li (2.32±0.02) fm [13], which was found to be (3.12±0.16) fm [1, 13], and the latest measurements propose that it might be as large as (3.55±0.10) fm [2], where the size of the 11Li nucleus is approximately equal to the size of 41Ca and as large as 208Pb [16, 17], This means that two halo neutrons are mostly placed far from the 9Li core. iv) It cannot be used as a target because it has a very short half-life time of 8.2 ms [18] for β- decay. All these properties make the 11Li nucleus an interesting halo nucleus that can be used as a projectile on several targets for studying the structure.
In the last several decades, numerous studies have generated widespread interest in the interaction cross section of the 11Li nucleus as a projectile with several different targets [19-27]. The quasi-elastic scattering of 11Li on 12C was measured by Kolata et al. [20] at 60 MeV/n, and on 28Si at 29 MeV/n by Lewitowicz et al. [21]. They used the coupled-channels (CC) method to reproduce the data, where the energy resolution did not allow for the separation of the true elastic scattering from inelastic scattering. A recent experiment for 11Li scattering on 12C was performed by Peterson et al. [22] at 50 MeV/n. They successfully separated the elastic and inelastic reaction channels in the critical forward-angle region. All the previous experimental studies [20-22] of quasielastic scattering of the neutron-halo nucleus of 11Li with low-Z targets have reported and confirmed the strong refractive effect of this scattering process as first predicted by Satchler et al. [23]. This refractive effect has very long-range absorption due to 11Li breakup, which increases the reaction cross section and is required for reproducing the experimental data. Mermaz [24] showed that it is necessary to use a surface potential that peaked very far outside the nucleus in order to reproduce the forward interference minimum core. The necessity of adding this long tail, which was introduced by Mermaz to the real part of the optical model potential to fit 11Li scattering on 12C and 28Si, has been verified via S-matrix inversion techniques by Cooper and Mackintosh [25]. Several studies [19, 26, 27] treated the refractive long tail using the dynamic polarization potential (DPP) generated by the strong coupling of the breakup channels with the elastic one for 11Li scattering. Khalili [27] proposed a theoretical interpretation of the data using Faddeev three-body wave functions within a four-body Glauber model; however, the results were not sensitive to details of the 11Li wave function. The problem was that the required tail was much greater than that predicted by simple double folding (DF) model calculations, and the DPP corresponding to these models is repulsive in nature, rather than attractive.
Recently, the São Paulo potential (SPP) [28-31] has been used to successfully describe the elastic scattering and peripheral reaction channels for a large number of heavy-ion systems in a very wide energy region, as well as to describe the total reaction. In addition, it has been used for analyzing the elastic scattering of stable, weakly bound, and exotic nuclei on a variety of targets [32]. Khoa et al. [33] have generated the rearrangement term (RT) of the nucleon optical potential (OP) to modify the density and energy dependence of the CDM3Yn interactions, which succeeded in reproducing the Airy oscillation.
In this respect, we reanalyze the elastic scattering of 11Li within a two-body model (core+halo) on 28Si at 29 MeV/n and on 12C at 50 and 60 MeV/n in an attempt to obtain an interpretation for the strong refractive effect within the 11Li projectile structure. Our model is based on a semimicroscopic approach. The real part is calculated microscopically by folding several versions of M3Y effective nucleon-nucleon (NN) interaction (DDM3Y and CDM3Y6) in addition to the SPP. Three different densities for the 11Li nucleus in conjunction with one density for 12C and 28Si targets are used. The imaginary part is calculated in the phenomenological Wood-Saxon (WS) form. Moreover, the effect of the RT in cross section calculations is investigated. The present paper is organized as follows. A theoretical formalism is presented in Sec. II, while Sec. III shows the results of analysis and discussion. Finally, concluding remarks are summarized in Sec. IV.
-
The optical nucleus-nucleus potential used in the present work is given by
$ U\left(R\right)={U}_{\rm C}\left(R\right)+{N}_{R}{V}_{\rm DF}\left(R\right)+{\rm i}{W}_{v}\left(R\right), $

(1) where
$ {U}_{\rm C}\left(R\right) $ is the Coulomb potential,$ {V}_{\rm DF}\left(R\right) $ is the DF real potential, and Wv(R) is the imaginary potential in WS form. The real DF potential is calculated as$ {{\rm{V}}_{{\rm{DF}}}}\left( R \right) =\iint {\rho _{{P}}}\left( {\overrightarrow {{r_1}} } \right){\rho _{{T}}}\left( {\overrightarrow {{r_2}} } \right){v_{NN}}\left( S \right){\rm{d}}\overrightarrow {{r_1}} {\rm{d}}\overrightarrow {{r_2}}, $

(2) where
$ {\rho }_{P}\left({r}_{1}\right) $ ,$ {\rho }_{T}\left({r}_{2}\right) $ are the nuclear matter (NM) densities of the projectile and the target, respectively, while$ {v}_{NN}\left(S\right) $ is the effective NN interaction between two nucleons,$ S=\overrightarrow{R}- $ $\overrightarrow{{r}_{1}}+\overrightarrow{{r}_{2}}. $ $\begin{aligned}[b] {U_{\rm C}}\left( R \right) =& \frac{{{Z_1}{Z_2}{e^2}}}{{2{R_{\rm C}}}}\left( {3 - \frac{{{R^2}}}{{{R_{\rm C}}}}} \right)\;\;\;\;{\rm{for}}\;\;\;\;R \leqslant {R_{\rm C}},\\{\rm{or}}&\;\;\;\;\;\;\frac{{{Z_1}{Z_2}{e^2}}}{{{R_{\rm C}}}}\;\;\;\;{\rm{for}}\;\;\;\;R \geqslant {R_{\rm C}} \end{aligned}$

(3) and the phenomenological imaginary WS potential is defined as
$ W\left(R\right)=\frac{{W}_{0}}{1+{\rm exp}\left[\dfrac{R-{R}_{i}}{{a}_{i}}\right]}, $

(4) where W0, Ri, and ai are the depth, radius, and diffuseness of the potential, respectively;
$ {R}_{i}={r}_{i}\left({A}_{P}^{\frac{1}{3}}+{A}_{T}^{\frac{1}{3}}\right), $ where i refers to V, W; and AP andAT are the projectile and target mass numbers, respectively. -
For the projectile nucleus, three different density distributions are used, all of which consider that the structure of the 11Li nucleus consists of 9Li as the core and two halo neutrons. The first one is the cluster-orbital shell model approximation (COSMA), which can be expressed as [34]
$\begin{aligned}[b] \rho \left(r\right)=&{N}_{CX}\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(-{r}^{2}/{a}^{2}\right)}{{\pi }^{\frac{3}{2}}{a}^{3}}+{N}_{VX}\frac{2\mathrm{e}\mathrm{x}\mathrm{p}\left(-{r}^{2}/{a}^{2}\right)}{3{\pi }^{\frac{3}{2}}{b}^{5}}\\&\times\left[A{r}^{2}+\frac{B}{{b}^{2}}{\left({r}^{2}-\frac{3}{2}{b}^{2}\right)}^{2}\right], \;\; X=Z,N \end{aligned}$

(5) where Z and N refer to the atomic number (protons) and number of neutrons, respectively, and NCX and NVX are fixed numbers, where NCX refers to the number of protons and neutrons in the core nucleus, while NVX refers to the number of neutrons in the halo term; A= 0.81, B = 0.19,
$ {N}_{CZ} $ = 3,$ {N}_{CN} $ = 6,$ {N}_{VZ} $ = 0,$ {N}_{VN} $ = 2,$ a $ = 1.89 fm, and$ b $ = 3.68 fm [34].The second density distribution is taken in the semi-phenomenological density (SPD) form, where the total matter density distribution can be taken as
$ \rho \left(r\right)={\rho }_{n}\left(r\right)+{\rho }_{p}\left(r\right) $

(6) and
$ {\rho }_{n}\left(r\right)={\rho }_{\rm core}\left(r\right)+{\rho }_{\rm tail}\left(r\right). $

(7) Since
$ {\rho }_{\rm core}\left(r\right) $ is the density of the neutrons in the core nucleus, while$ {\rho }_{\rm tail}\left(r\right) $ represents the 2n-halo neutron density distribution, the core part of both neutron and proton density distributions can be written as follows [35, 36],$\begin{aligned}[b] {\rho }_{i}\left(r\right)=&\frac{{\rho }_{i}^{0}}{1+{\left[\left(\frac{{1+\left(\dfrac{r}{R}\right)}^{2}}{2}\right)\right]}^{{\alpha }_{i}}\left[\mathrm{e}\mathrm{x}\mathrm{p}\left(\dfrac{\left(r-R\right)}{{a}_{i}}\right)+\mathrm{e}\mathrm{x}\mathrm{p}\left(\dfrac{-\left(r+R\right)}{{a}_{i}}\right)\right]},\\ i=&p,n \end{aligned}$

(8) where p stands for protons, and n for neutrons. The central densities
$ {\rho }_{p}^{0} $ and$ {\rho }_{n}^{0} $ are determined from the normalization conditions:$ 4\pi \int {\rho }_{n}\left(r\right){r}^{2}{\rm d}r=N , $

(9) $ 4\pi \int {\rho }_{p}\left(r\right){r}^{2}{\rm d}r=Z , $

(10) where N (Z) is the total number of neutrons (protons) in the nucleus, and the other parameters (
$ {\alpha }_{i},{a}_{i}) $ can be determined in detail using Refs. [35, 36]. The tail/halo part can be written as [35]$ {\rho }_{\rm tail}\left(r\right)={N}_{0}\left(\frac{{r}^{2}}{{\left({r}^{2}+{R}^{2}\right)}^{2}}\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{-r}{{a}_{t}}\right), $

(11) where N0 is determined from the normalization
$ 4\pi \int {\rho }_{\rm tail}\left(r\right){r}^{2}{\rm d}r=2, $

(12) where 2 refers to the number of halo neutrons. Finally, the third density distribution form is that deduced using the simpler non-relativistic Hartree-Fock (HF) model [37].
For 12C and 28Si target nuclei, only the two-parameter Fermi model (FM) is used [38]
$ {\rho }_{T}^{^{12}{\rm C}\left(^{28}{\rm Si}\right)}=\frac{0.207\left(0.175\right)}{1+\mathrm{e}\mathrm{x}\mathrm{p}\left[\left(\dfrac{r-2.1545\left(3.15\right)}{0.425\left(0.475\right)}\right)\right]}, $

(13) where the rms radii, which are extracted from this density, are 2.298 and 3.012 fm for 12C and 28Si, respectively.
-
Based on the M3Y interaction, which is designed to reproduce the G-matrix elements for Paris and Reid [39, 40] effective NN interactions, two versions of the M3Y effective NN interaction are used. These versions depend on two different forms of the density and energy-dependence (DDM3Y and CDM3Y6). In addition to the SPP, the CDM3Y6 interaction, which was recently modified by the RT [33], is also used. The first method is the DDM3Y effective interaction, defined as [38]
$ \upsilon \left(E, \rho ,S\right)=g\left(E, S\right)F\left(E, \rho \right), $

(14) where
$ F\left(E, \rho \right)=C\left(E\right)\left[1+\alpha \left(E\right)\mathrm{e}\mathrm{x}\mathrm{p}(-\beta \left(E\right)\rho )\right], $

(15) $ C,\, \alpha $ , and$ \beta $ are the energy dependent parameters, and$ \rho ={(\rho }_{P}+{\rho }_{T}) $ . The factor$ g\left(E, S\right) $ is represents the original zero range M3Y-Reid NN interaction [38], which can be written in the form$ g\left(E, S\right)={\upsilon }_{D}\left(R\right)+{{\hat J}}\left(E\right)\delta \left(S\right), $

(16) where E is the laboratory energy per projectile nucleon,
$ \overrightarrow{s} $ is the inter-nucleon separation,$ \delta \left(s\right) $ is the delta function,$ {{\hat J}}\left(E\right) $ represents the effects of the knock-on exchange between interacting nucleons, and$ {\upsilon }_{D}\left(r\right) $ represents the direct parts. The term$ {{\hat J}}\left(E\right) $ is taken as [38]${{\hat J}}\left( E \right) = - 276\left[ {1 - 0.005\left( {E/A} \right)} \right]\;{\rm{MeV}}.{\rm{f}}{{\rm{m}}^3},$

(17) with the direct part in the M3Y-Paris as
${\upsilon _D}\left( R \right) = \left[ {11062\frac{{{\rm{exp}}( - 4R)}}{{4R}} - 2538\frac{{{\rm{exp}}( - 2.5R)}}{{2.5R}}} \right]\;{\rm{MeV.}}$

(18) The next NN effective interaction used is the other density dependent version (CDM3Y6) for the direct and exchange terms, where the full CDM3Y6 interaction form is defined as [41]
$ {\upsilon }_{D\left(Ex\right)}\left(\rho ,R\right)=g\left(E\right)F\left(\rho \right){\upsilon }_{D\left(Ex\right)}\left(R\right), $

(19) where the direct part
$ {\upsilon }_{D}\left(r\right) $ is that in Eq. (18), and the knock-on exchange parts in the infinite-range exchange are taken as$\begin{aligned}[b] {\upsilon }_{Ex}\left(R\right)=&\left[-1524\frac{\mathrm{e}\mathrm{x}\mathrm{p}(-4R)}{4R}-518.8\frac{\mathrm{e}\mathrm{x}\mathrm{p}(-2.5R)}{2.5R}\right.\\&\left.-7.847\frac{\mathrm{e}\mathrm{x}\mathrm{p}(-0.7072R)}{0.7072R}\right]\;{\rm{MeV}},\end{aligned} $

(20) with the function
$ F\left(\rho \right) $ written as [41, 42],$ F\left(\rho \right)=0.2658\left[1+3.8033\mathrm{e}\mathrm{x}\mathrm{p}\left(-1.41\rho \right)-4.0 \rho \right], $

(21) and
$ g\left(E\right) $ is the energy dependent factor, given by [41]$g\left( E \right) = \left[ {1 - 0.003\left( {E/A} \right)} \right].$

(22) For reproducing the saturation properties of symmetric NM in the standard HF calculation, and to have a reliable density dependent interaction for use at different energies (the high-momentum part of the HF single-nucleon potential), the modified CDM3Y6 interaction (CDM3Y6-RT) with the RT contribution has been carried out. The density dependence of ΔF
$( \rho ) $ obtained from the exact expression of the RT given as [33]$ \varDelta F\left(\rho \right)=1.5\left[\mathrm{e}\mathrm{x}\mathrm{p}\left(-0.833 \rho \right)-1\right]. $

(23) In contrast, we use the SPP, where the radial and energy dependence is written as follows [43]:
$ V\left(R,E\right)={V}_{F}\left(R\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-4{\beta }^{2}\right), $

(24) where β= v/c, v is the local relative velocity between the two nuclei, and VF (R) is a folding potential, such as the expression in Eq. (2) where
$ {\upsilon }_{nn}(S=\overrightarrow{R}-\overrightarrow{{r}_{1}}-\overrightarrow{{r}_{2}}) $ is a physical NN interaction given by$ {\upsilon }_{nn}\left(S\right)= {V}_{0}\delta \left(S\right) $ using$ {V}_{0}=-456\; {\rm MeV}\;{\rm fm}^{3} $ , and the usage of the delta function corresponds to the zero range approach. Systemizations of the nuclear densities were achieved in Ref. [44], providing a good explanation of matter and charge distribution. In this work, for the target 12C, we assume that$ {a}_{m}=0.53 $ fm and$ {a}_{c}=0.56 $ fm for the matter and charge diffuseness, respectively. The matter and charge distribution radii are given by$ {R}_{M}=1.3{A}^{1/3}-0.84 $ and$ {R}_{C}=1.76{Z}^{1/3}-0.96 $ , respectively. The matter density of the projectile nucleus is used as tabulated in numerical form. -
The analysis of 11Li+12C, 28Si elastic scattering is carried out by using the OPs generated from Eq. (1). The DF real parts of the OPs are evaluated using several versions of the M3Y density- and energy dependent effective interactions such as DDM3Y (14), CDM3Y6 (19), and CDM3Yn-RT (23), in addition to the SPP. The imaginary potential is calculated using Eq. (4) as a phenomenological WS form with three parameters. The obtained potentials are then fed into the HIOPTM-94 [45] computer code to calculate the elastic scattering differential cross sections. For obtaining the best fit, searches on the potential parameters are performed using the HIOPTM-94 code to achieve the minimum
$ {\chi }^{2} $ value, defined as [46, 47]${\chi ^2} = \frac{1}{N}\sum\nolimits_{K = 1}^N {{{\left[ {\frac{{{\sigma _{\rm th}}\left( {{\theta _K}} \right) - {\sigma _{\rm ex}}\left( {{\theta _K}} \right)}}{{\Delta {\sigma _{\rm ex}}\left( {{\theta _k}} \right)}}} \right]}^2}}, $

(25) $ {\sigma }_{\rm th}\left({\sigma }_{\rm ex}\right) $ is the theoretical (experimental) cross section at an angle$ {\theta }_{K} $ in the c.m. system,$ {\Delta \sigma }_{\rm ex} $ is the experimental error, and N is the number of the data points. For the experimental errors of all measured data, an average value of 10% is used. For semi-microscopic analysis, searches are carried out on four parameters (the real renormalization factor (NR) in conjunction with the three WS imaginary potential parameters W0, Ri and ai). In contrast, for the phenomenological WS approach, searches are performed on six free parameters (three WS real potential parameters, Vv, Rv, and av, and three imaginary potential parts, W0, Ri, and ai). -
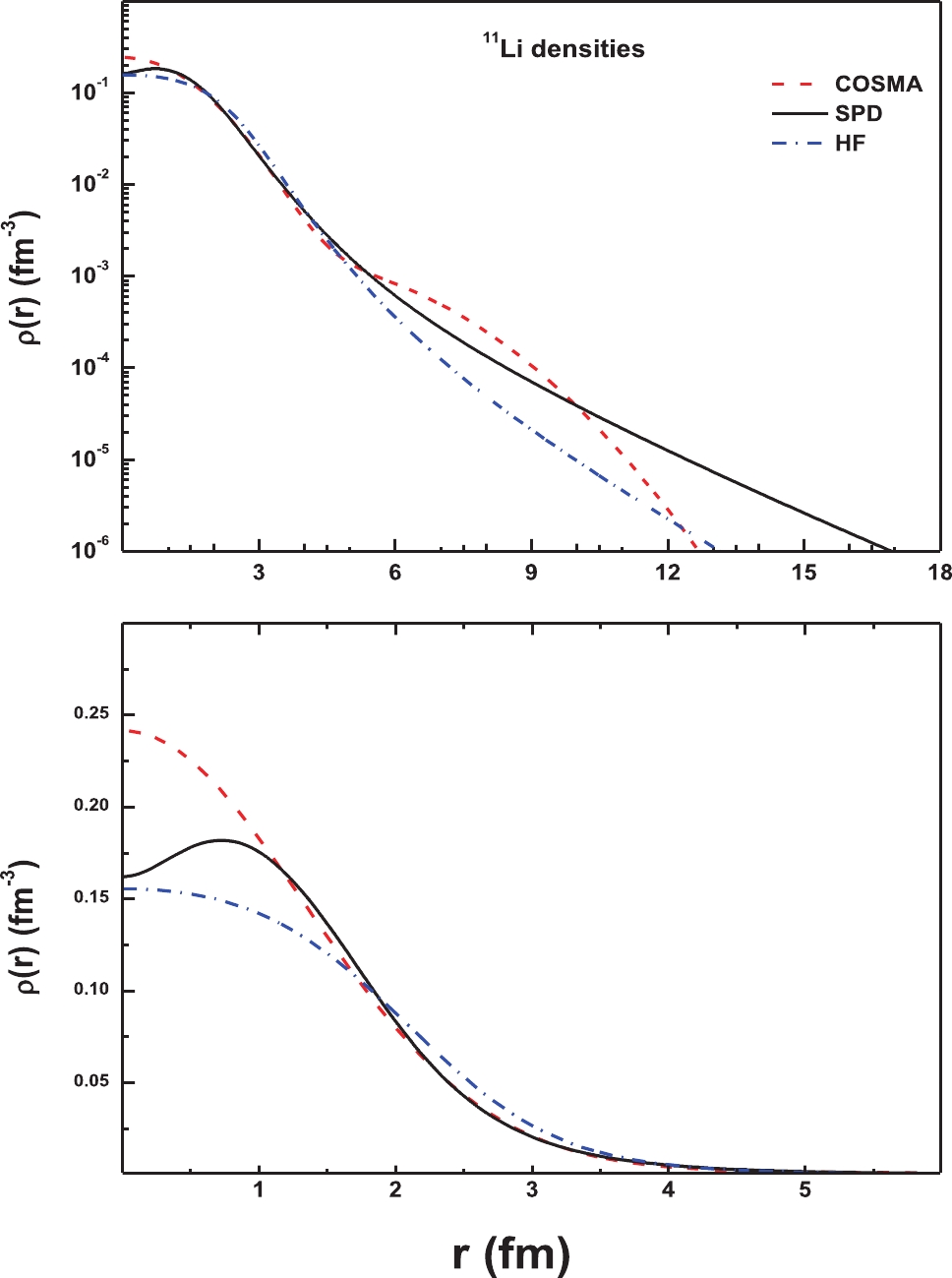
The radial shapes of the considered different types of density distributions of 11Li are shown in Fig. 1, in linear and logarithmic scale. The corresponding calculated rms radii of protons, neutrons, and matter for all used density distributions of the 11Li nucleus are listed in Table 1, as compared with previous works and experimental data. The present results agree with the previous calculations that predict a long tail halo for the 11Li nucleus, in comparison with the experimental data, as summarized in Table 1. Further, our calculations agree well with the previous rms values; however, there is a slight difference compared with the experimental data. Moreover, previous studies have extracted these quantities [24, 48-51], which agree with the present calculations, but it is noticed that, in the important study of Mermaz [24], the value
$ {\langle {R}_{m}\rangle }^{\frac{1}{2}}=3.74 $ was extracted, which is greater than the experimental and other theoretical calculations.Table 1. Calculated rms proton (Rp), neutron (Rn), and mass (Rrms) radii in fermis for the three NM densities of the 11Li nucleus.
The results of the considered density distributions are illustrated in Fig. 1. It can be seen that COSMA density has a larger value than those of the SPD and HF at small distances (r ≤ 1 fm), while the latter density has the smallest value. At large distances (r ≥ 10 fm), we can see that all the used densities have a long tail due to the structure of 11Li as a core with two valence neutrons. The SPD density has the longest tail, so it gives a successful description for the largest radius of 11Li. In contrast, investigation of the halo densities for the 11Li nucleus and the considered NN effective interaction effects is performed through the calculation of the DF potential of Eq. (2). The real parts of the OPs are calculated with the DDM3Y, CDM3Y6, and CDM3Y6-RT effective NN interactions in addition to the SPP folded with the considered three densities, COSMA, SPD, and HF, at energies of 50 and 60 MeV/n, for 11Li scattered by 12C, and at 29 MeV/n, for the 11Li+ 28Si system. The physical observations related to the resulted potentials for 12C at an energy of 60 MeV/n are presented in Table 2 and Fig. 2, as one case.
E/(MeV/n) density -J/(MeV fm3) Rrms/fm CDM3Y6 CDM3Y6-RT SPP DDM3Y CDM3Y6 CDM3Y6-RT SPP DDM3Y 11Li + 12C 50 COSMA 301.12 271.42 271.0 252.74 4.692 4.88 4.40 4.789 SPD 300.84 271.28 275.5 251.99 4.691 4.86 4.45 4.772 HF 302.57 274.86 271.4 254.37 4.272 4.41 4.03 4.358 60 COSMA 281.71 256.50 254.5 235.63 4.694 4.89 4.39 4.799 SPD 281.50 262.70 257.1 234.99 4.693 4.87 4.33 4.772 HF 283.31 259.91 253.2 237.43 4.278 4.42 3.90 4.360 11Li + 28Si 29 COSMA 358.79 311.71 314.7 297.64 5.128 5.31 4.79 5.20 SPD 358.07 311.30 309.4 296.43 5.127 5.29 4.65 5.18 HF 359.04 314.73 314.1 297.49 4.737 4.87 4.45 4.81 Table 2. The calculated volume integrals and rms radii of the folded potentials for 11Li+12C, 28Si systems at 50 and 60 MeV/n for 12C and 29 MeV/n for 28Si, using the four NN effective interactions with the three densities without NR.
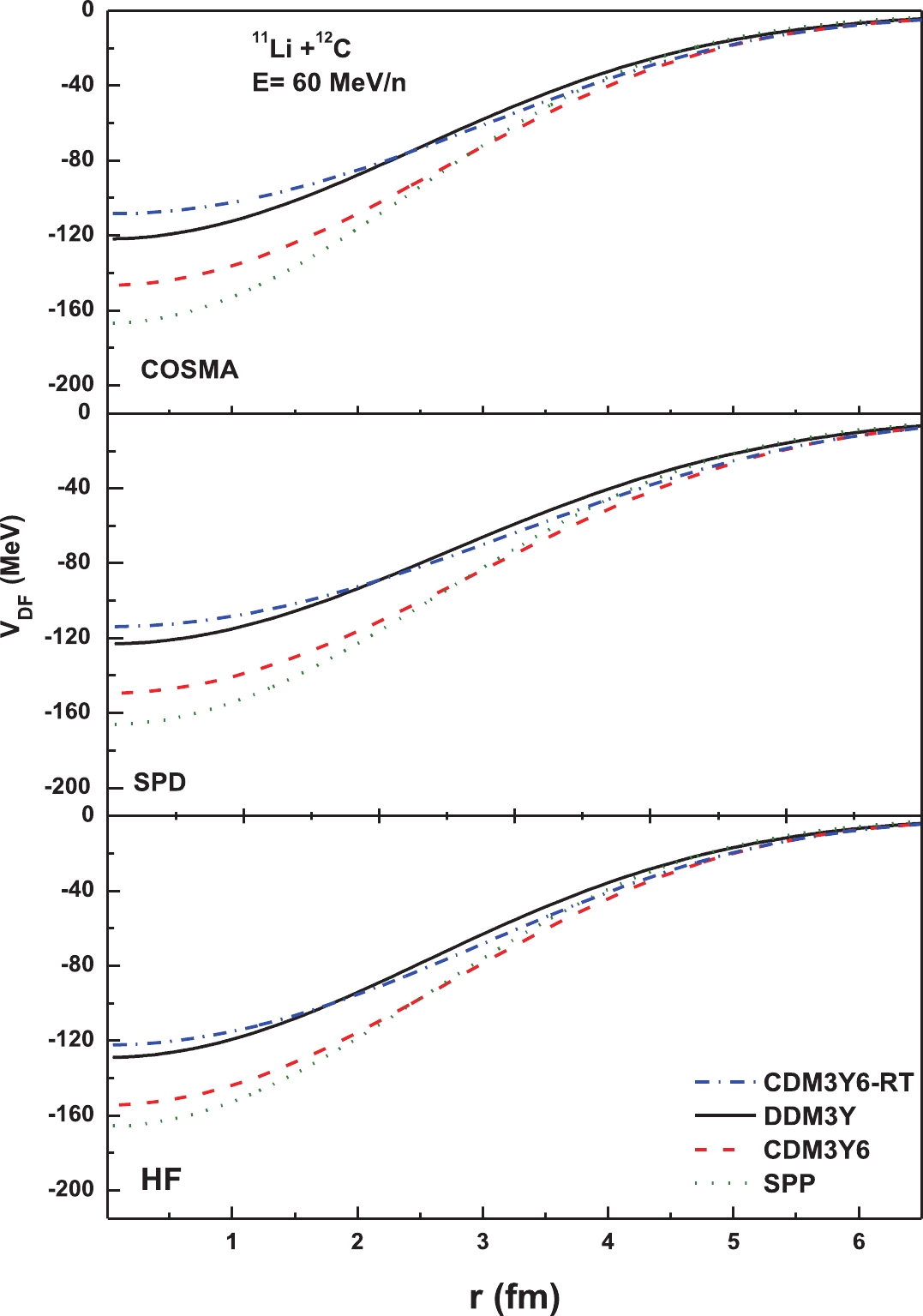
Figure 2. (color online) The real DF for 11Li+12C at 60 MeV/n using the three densities with DDM3Y, CDM3Y6, and CDM3Y6-RT effective NN interactions and the SPP with NR=1.0 with a linear scale.
The folded potentials in the present work are calculated as a sum of two parts for projectile (11Li) density, and halo (neutrons) density plus core density is folded with target density and NN effective interaction. The effects of different densities of 11Li structure and the considered effective interaction on our potential model represent our focused study point.
Generally, as we have seen from Fig. 2 and Table 2, the folded potentials using the considered densities and effective interaction have approximately the same depths and behavior for the density-dependent effective NN interaction with a slight difference. From Table 2, we notice that the long potential rms is to be achieved with COSMA and SPD densities, CDM3Y6-RT, and DDM3Y effective interactions, while the smallest potential tail is to be achieved with HF density, SPP, and CDM3Y6 effective interactions. In addition, the energy dependence for the real potential volume integral of the 12C target is observed, where it decreases with increasing energy. Fig. 2 confirms these results, where the SPP gives the largest depth compared to those using the DDM3Y and CDM3Y6, while CDM3Y6-RT gives the smallest value among all; this arises in the interior region at r (r
$ < $ 2 fm). The folded potentials of the other (50 MeV/n) energies and those for the 28Si target at 29 MeV/n have the same behavior as those at 60 MeV/n, but with different depths, where the depths of the potentials increase with decreasing energy. The obtained potential agrees well with the systematic suggested potential models based on the break up potential of Yabana [52], the DP potential of Khalili [27], and the folded potentials of Khoa [26]. However, the extracted real folded potentials have a shorter tail in facing the successful Mermaz potential [24]. -
Many attempts have been made to generate appropriate OPs for analyzing the angular distribution cross section of 11Li projectile reactions. The result drawn from all previous theoretical studies [19, 23-27] is that the nearside/farside interference minimum is missing or greatly attenuated in the elastic scattering of 11Li with low-Z targets at intermediate energies. The presence of a sharp minimum at 40 in the calculated angular distributions was due to the contamination by 9Li ions resulting from projectile breakup [22]. The successful theoretical work that explained this discrepancy at forward angles was proposed by Mermaz [24] using phenomenological potential with coupling for low excited inelastic channels and many adjusted free parameters.
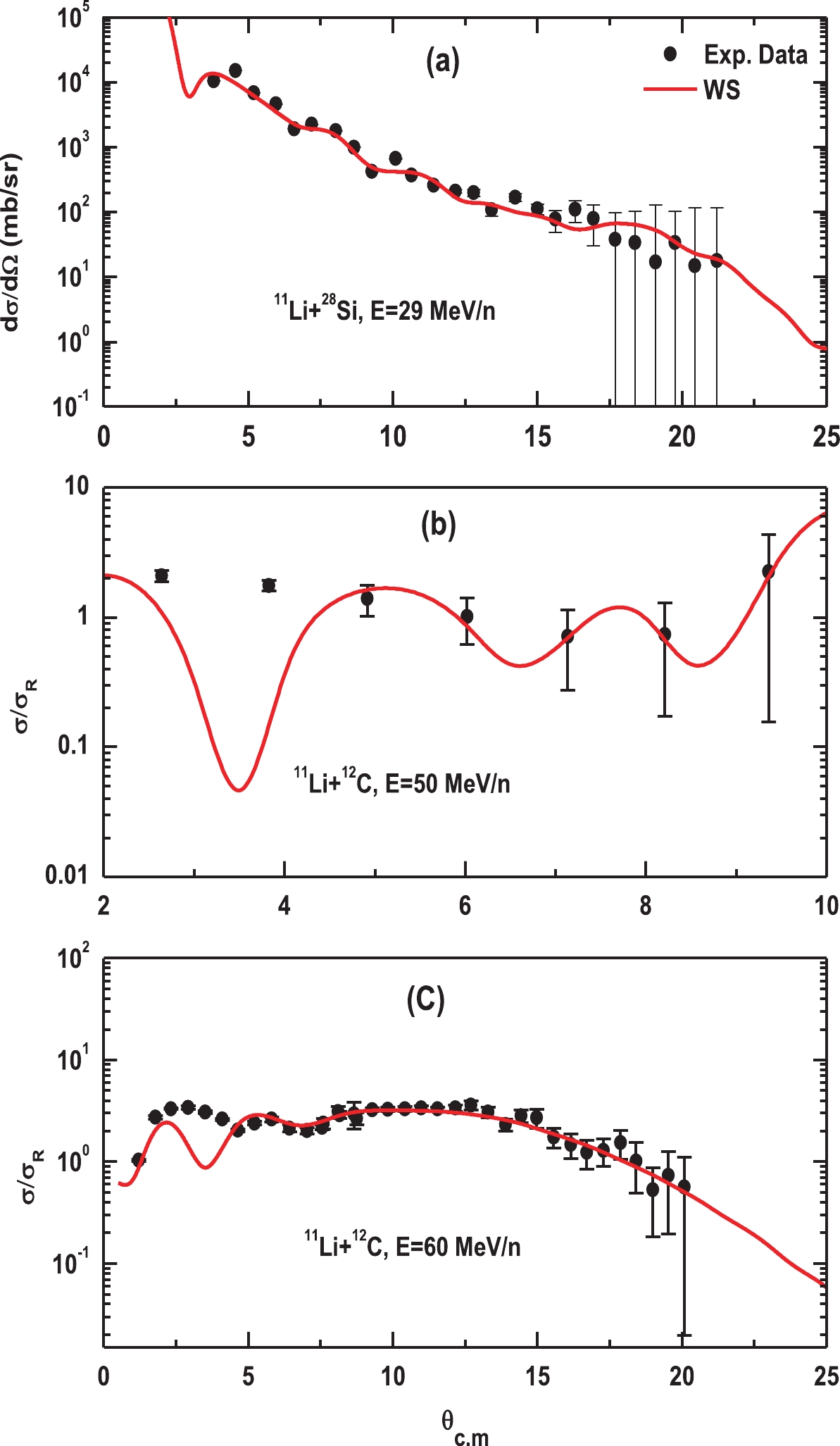
The same type of analysis as previously used has been presented, that is, the one with WS potential. To improve the agreement with the considered experimental data, we employ the widely used phenomenological WS potential with six parameters. More parameters in such a famous model means more flexibility in order to obtain the best fit that can be used later as a guide. The elastic scattering for the 11Li nucleus from 12C at the two energies, 50 and 60 MeV/n, and that from 28Si at 29 MeV/n have been analyzed in the framework of the conventional optical model by using the standard WS form, as in Eq. (4). Moreover, a semi-microscopic optical DF folding potential has been generated to study the sensitivity of NN interaction, as well as the form of the halo density distributions of 11Li on reaction differential cross sections. The obtained results are listed in Tables 3 to 5 and shown in Figs. 3 to 6.
E/(MeV/n) V/MeV rv/fm av/fm W/MeV ri/fm ai/fm -J/(MeV fm3) $ {\chi }^{2} $ 

$ {\sigma }_{R} $ 

JR JI 11Li + 12C 50 116.4 0.83 0.81 2.83 2.19 0.057 286.03 86.68 13.0 2009 60 295.92 0.21 1.35 20.72 0.92 1.20 233.33 86.12 5.2 1400 11Li + 28Si 29.0 261.91 0.41 1.78 7.029 2.29 0.362 201.57 33.05 2.96 1495 Table 3. Best fit OP parameters of the WS model.
E/(MeV/n) density potential NR -J/(MeV fm3) W/MeV ri/fm ai/fm $ {\chi }^{2} $ 

$ {\sigma }_{R} $ 

JR JI 29 COSMA CDM3Y6-RT 0.64 198.76 45.12 14.69 2.188 0.767 4.53 1460 DDM3Y 0.82 242.49 52.12 15.65 2.235 0.709 4.53 1528 CDM3Y6 0.69 247.20 50.45 15.40 2.227 0.728 4.60 1518 SPP 0.899 282.99 46.04 14.79 2.198 0.772 5.00 1485 SPD CDM3Y6-RT 0.62 193.58 45.23 15.73 2.174 0.795 5.31 1457 DDM3Y 0.81 238.51 51.81 15.61 2.234 0.718 5.01 1527 CDM3Y6 0.68 243.41 50.53 15.60 2.220 0.740 5.34 1516 SPP 0.896 277.11 46.15 14.82 2.198 0.770 5.85 1483 HF CDM3Y6-RT 0.58 181.83 45.95 16.60 2.128 0.849 6.37 1442 DDM3Y 0.77 229.06 52.00 16.11 2.218 0.736 5.62 1517 CDM3Y6 0.64 233.83 50.95 16.16 2.204 0.750 6.22 1504 SPP 0.87 273.86 51.08 17.76 2.148 0.803 7.17 1481 Table 5. The best fit parameters for the elastic scattering data for the 11Li+28Si system at an energy of 29 MeV/n using NN interaction (DDM3Y, CDM3Y6, CDM3Y6-RT, and SPP) with the considered three densities (COSMA, SPD, and HF).
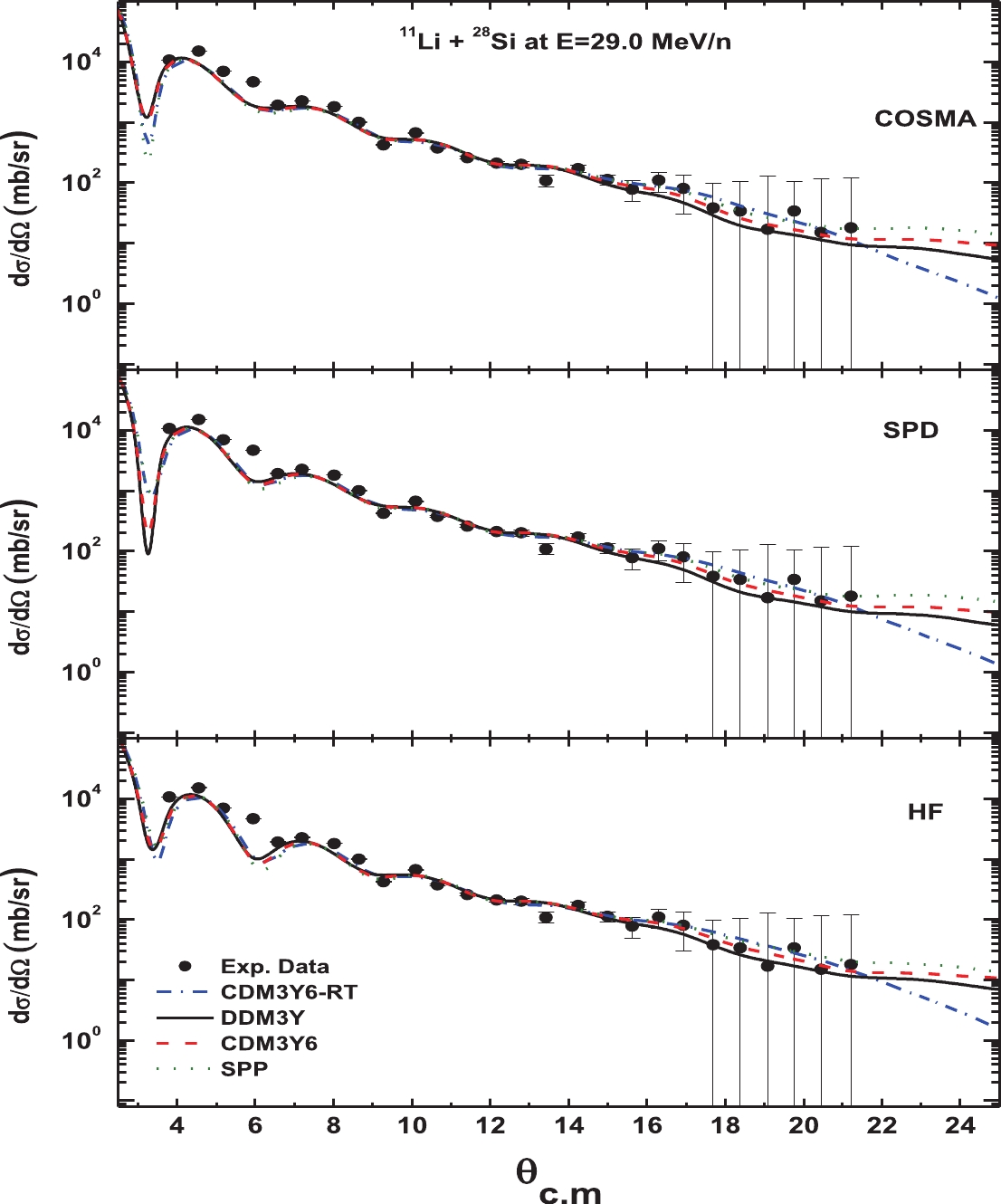
The results of angular distributions obtained using the WS optical model are compared with experimental data in Fig. 3, and their potential parameters are listed in Table 3. As shown in Fig. 3(a), the best fit with experimental data has been achieved for the 28Si target without an anomaly at near or far angles. The results are more successful than those of previous studies that used a combination of elastic and inelastic parts to achieve a reasonable result [21]. In contrast, a reasonable fit with data has been obtained for the 12C target at the two energies, 50 and 60 MeV/n, as shown in Fig. 3(b, c), but with a sharp minimum between
$(2.5)^\circ $ and$ 4^\circ$ .The results displayed in Tables 4 and 5 as well as Figs. 4 to 6 have been obtained using the semi-microscopic potentials. Firstly, it is noticed that the NR coefficients are close to one, i.e., 1.0±0.01 for energies 50 and 60 MeV/n for the 12C target and 0.8±0.01 for the 28Si target, providing a satisfactory agreement with experimental data. These results are more successful than those achieved in previous studies that used the CC model [21], quasielastic potential [26], Glauber of four body model [27], the breakup effect [51], and the JLM potential [53].
E/(MeV/n) density potential NR -J/(MeV fm3) W/MeV ri/fm ai/fm $ {\chi }^{2} $ 

$ {\sigma }_{R} $ 

JR JI 50 COSMA CDM3Y6-RT 1.18 320.27 104.23 4.529 1.889 1.122 11.17 2300 DDM3Y 1.15 289.27 105.71 4.926 1.840 1.124 14.60 2273 CDM3Y6 0.92 278.36 95.06 4.393 1.852 1.092 12.96 2146 SPP 0.86 233.51 80.11 4.727 1.675 1.169 14.72 1872 SPD CDM3Y6-RT 1.16 314.55 105.07 4.217 1.959 1.041 13.97 2324 DDM3Y 1.13 283.91 110.30 4.724 1.905 1.086 17.36 2356 CDM3Y6 0.91 274.07 99.950 4.219 1.925 1.031 15.68 2229 SPP 0.93 257.02 100.27 4.818 1.799 1.225 16.45 2236 HF CDM3Y6-RT 1.06 291.83 103.05 3.900 2.019 0.918 14.57 2290 DDM3Y 1.06 270.07 111.37 4.382 1.977 1.012 17.85 2389 CDM3Y6 0.87 261.79 101.15 3.946 1.994 0.946 16.20 2258 SPP 0.85 229.75 94.16 4.150 1.867 1.188 18.21 2190 60 COSMA CDM3Y6-RT 1.18 303.45 136.83 50.00 0.674 1.371 6.21 1737 DDM3Y 1.20 283.39 124.32 49.57 0.650 1.342 6.03 1625 CDM3Y6 0.94 264.15 116.92 44.16 0.725 1.214 5.82 1484 SPP 0.85 215.98 92.40 39.03 0.750 1.032 6.61 1187 SPD CDM3Y6-RT 1.12 293.94 140.90 60.06 0.569 1.459 7.19 1811 DDM3Y 1.18 276.33 126.92 53.02 0.607 1.400 6.76 1678 CDM3Y6 0.92 258.60 120.01 47.52 0.684 1.269 6.50 1536 SPP 0.85 213.14 95.12 39.81 0.742 1.066 6.74 1228 HF CDM3Y6-RT 1.05 272.94 137.63 50.00 0.676 1.373 7.73 1741 DDM3Y 1.07 254.89 131.36 84.24 0.384 1.490 7.33 1720 CDM3Y6 0.84 238.26 124.09 67.91 0.517 1.355 7.11 1572 SPP 0.80 204.70 101.33 50.90 0.628 1.182 7.24 1313 Table 4. The best fit parameters obtained for elastic scattering data for the 11Li+12C system at energies of 50 and 60 MeV/n using NN interaction (DDM3Y, CDM3Y6, CDM3Y6-RT, and SPP) with the considered three densities (COSMA, SPD, and HF).
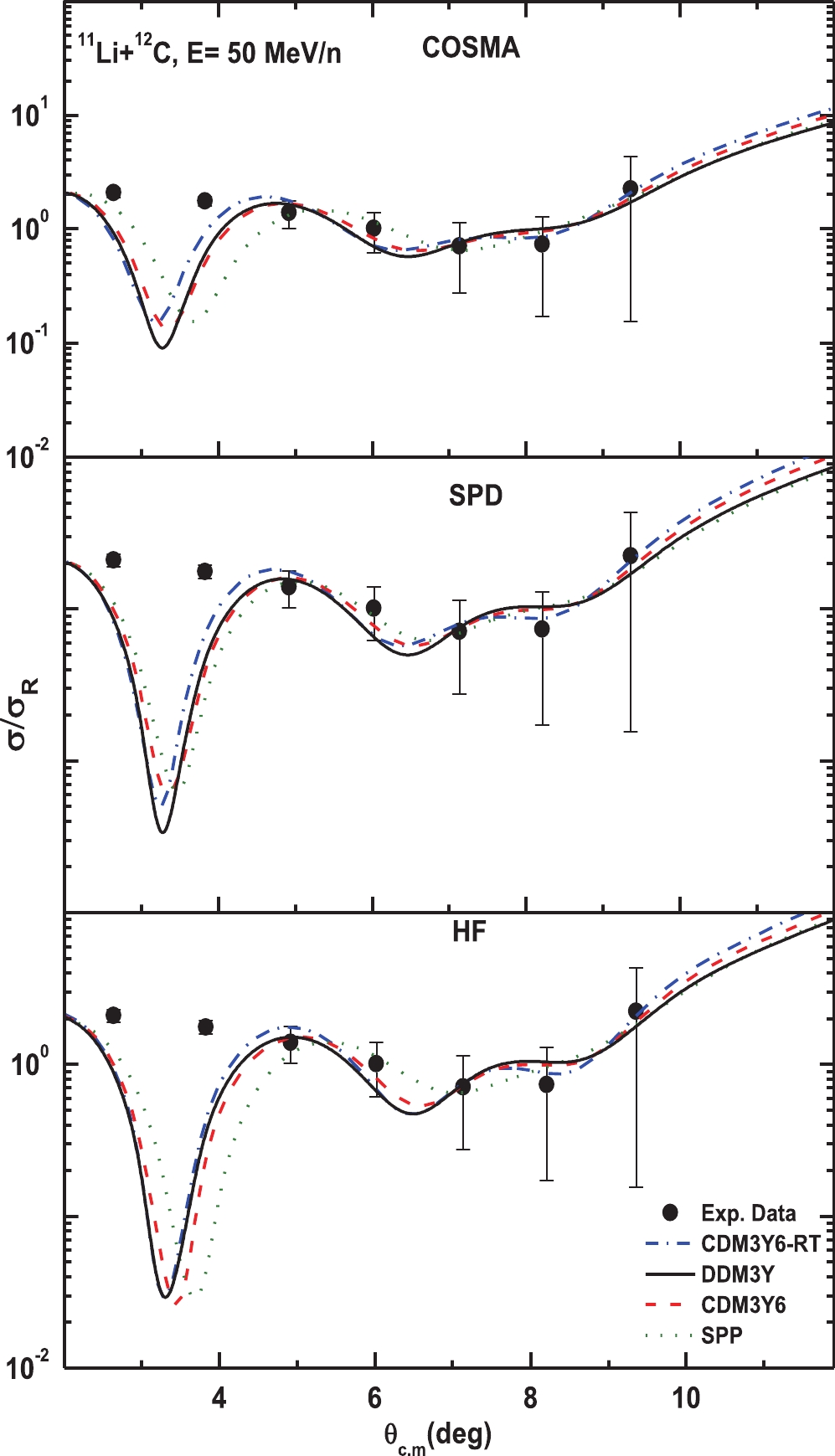
Figure 4. (color online) The best fit angular distributions of elastic scattering of 11Li from 12C at 50 MeV/n calculated with the semi-microscopic real DF potentials, CDM3Y6-RT (dashed-dotted line), DDM3Y (sold line), CDM3Y6 (dashed line), and SPP (dotted line). The symbol is a representation of the experimental data from Ref. [22]. Upper panel for COSMA density, middle panel for SPD density, and bottom panel for HF density.
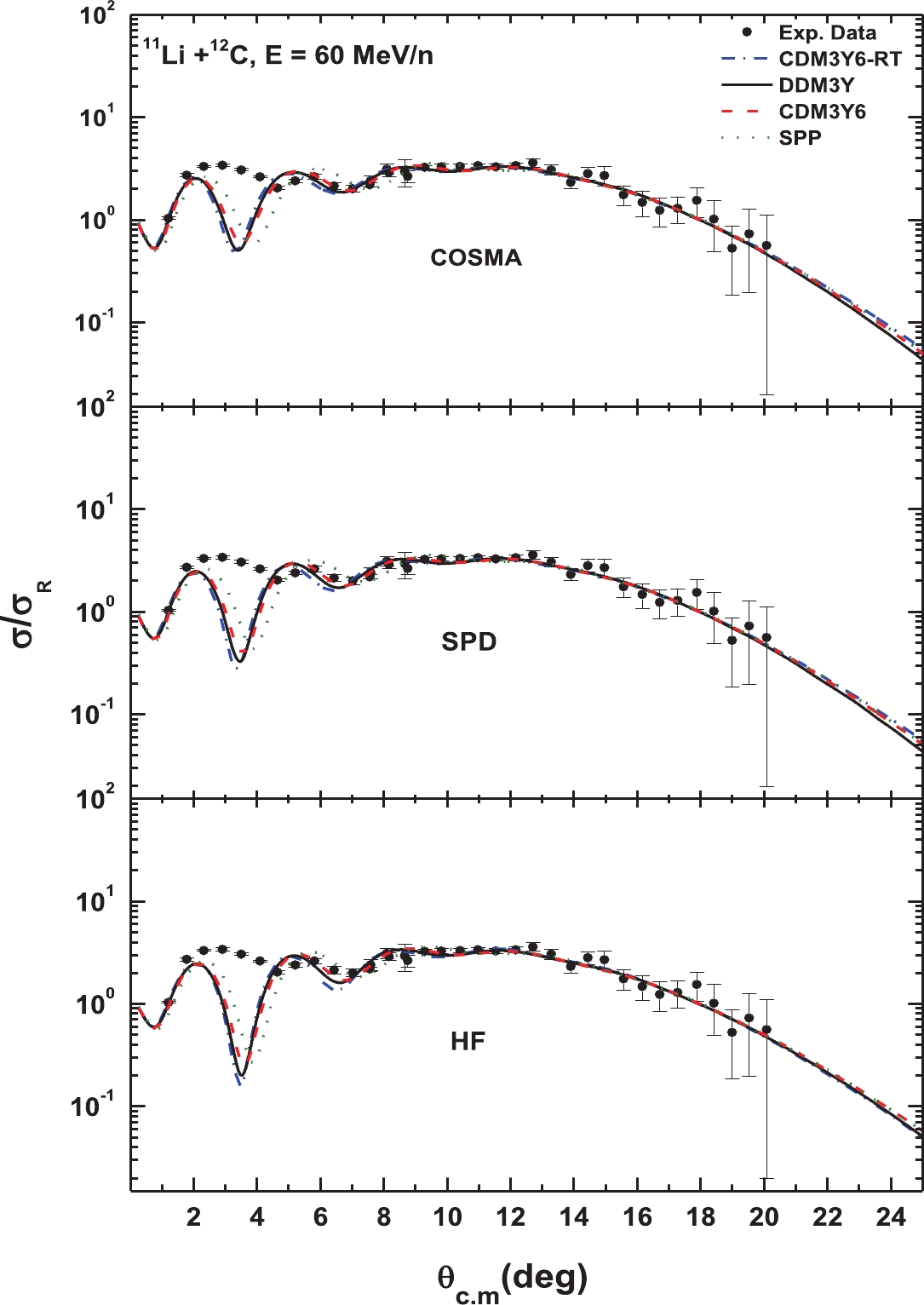
Generally, the results corresponding to Figs. 4 to 6 show that the considered effective interactions and densities predict the best agreement with the experimental results. It is clear that the three angular distributions resulting from DDM3Y, DDM3Y6, and DDM3Y6-RT are very similar to each other; however, a small shift in the forward angle between (2.5)0 and 40 for SPP is noticed.
Figure 4 shows the results in comparison with the measured experimental data for the 12C target at an energy of 50 MeV/n, where the agreement with the data is reasonable and is of higher quality than that obtained from the quasielastic calculation of Peterson et al. [22]. Likewise, Fig. 5 shows the good agreement of the predictions of our calculations with the experimental data for the 12C target at an energy of 60 MeV/n, in comparison with those from previous attempts by many authors [26, 27, 52, 53]. Meanwhile, the same results for the 28Si target at an energy of 29 MeV/n, which agree more with the experimental data than the results of [21, 48, 53, 54], have been obtained, as shown in Fig. 6. Despite the success achieved in the data analysis for practical data, anomalies at small angles still exist. In this angular range, the optical model amplitude is insensitive to the potential used due to a breakdown of the optical model in the explanation of the small-angle cross section for the halo nucleus, which could be attributed to the extreme peripheral nature of these reactions at intermediate energies due to the surface transparent potential.
-
In order to understand the formation of a halo around the core of radioactive nuclei, which is very difficult, it is useful to study the reaction cross section (RCS) in addition to differential cross sections of the exotic nucleus 11Li from targets. The RCS
$ {\sigma }_{R} $ represents an important constraint on the OP calculation. The average total RCSs$ {\sigma }_{R} $ for the present calculations are listed in Table 6. The behavior of the reaction mechanism is extrapolated for a range of low and high energies (30, 75 and 85 MeV/n). These results are listed together with the previous values [19, 21, 23, 26, 48, 52], in conjunction with the experimental values of Refs. [55-57], and are illustrated in Fig. 7. Unfortunately,$ {\sigma }_{R} $ was not measured at 50 MeV/n.Table 6. The calculated mean value and the previous calculations comparable to the experimental results of the reaction cross section
$ {\sigma }_{R} $ (mb) for 11Li+12C, 28Si systems at 50 and 60 MeV/n for 12C and 29 MeV/n for 28Si.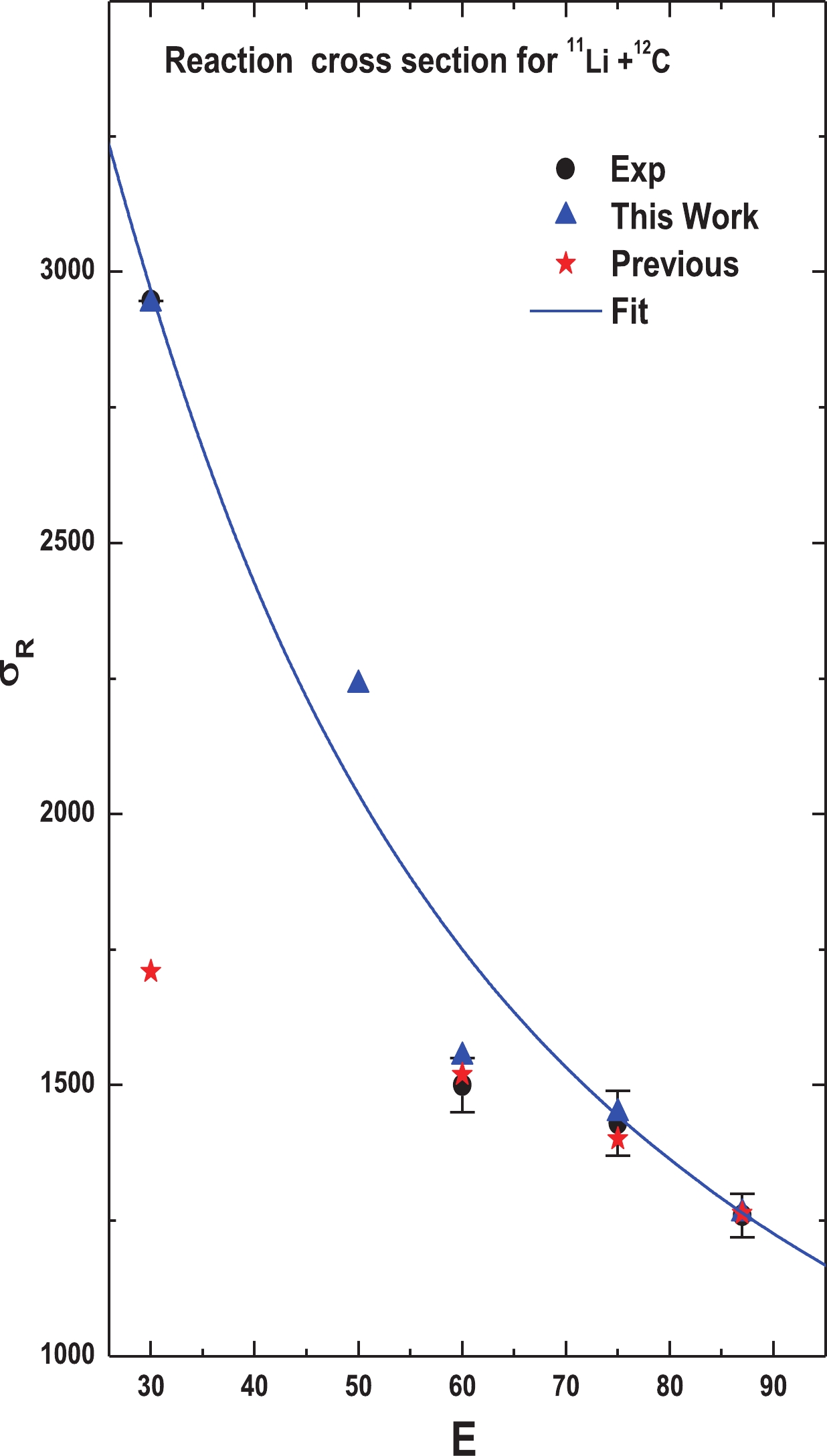
Figure 7. (color online) Energy dependence of the reaction cross section in the optical limit of the DF model using the present model for 11L+12C. The triangles denote the mean obtained results with considered potentials, the star shapes denote the previous calculations, and the circles denote the experimental data taken from Refs. [48, 55-57].
As seen in Table 6, the present calculated
$ {\sigma }_{R} $ generally agrees with the previous theoretical calculations, and on average, our results in Fig. 7 are closer to the experimental cross sections measured or those estimated from the systematics at relevant bombarding energies for the 12C target. The calculated energy dependence of the total cross sections is well approximated by the expression$ {\sigma }_{R}^{\rm cal.}\left(E\right)=1.3 \pi {\left({A}_{p}^{\frac{1}{3}}+{A}_{T}^{\frac{1}{3}}\right)}^{2}\left(\frac{1459.4}{E}-\frac{11621.4}{{E}^{2}} \right), $

(i26) where
$ E $ represents the value of energy per nucleon. It is obvious from Fig. 7 and the results listed in Table 6 that the behavior of the generated results reflects the success of our potentials in reproducing the exotic nuclei reactions. For the 28Si target, while the present results of$ {\sigma }_{R} $ agree with previous theoretical calculations, they are lesser than the results of the experimental data. The reason for this discrepancy could be the effect of the coupling of the low-lying exited states of 28Si to the elastic channels, which must be included or separated from the elastic events by those inelastic states. In addition, the value$ {\mathrm{\sigma }}_{{R}}=2947\pm 386\;\mathrm{m}\mathrm{b} $ corresponds to an energy of 25.5 MeV/n. -
Explaining the discrepancy between the experimental and calculated differential cross sections at forward angles for the interaction of 11Li with low-Z targets at intermediate energies can be divided into two stages. First, the studies could not predict this anomaly as a highly refractive nature for a quasi-elastic scattering process. Second, successful results were generated by Meermaz [24] and confirmed by the recent experimental study of Peterson et. al. [22], in which the elastic and inelastic reaction channels were cleanly separated in the forward angle. They verified that the 9Li contamination data are responsible for the displayed interference minima. The purpose of the present paper is to provide a new attempt to describe the elastic scattering of 11Li from 12C and 28Si through DF.
In the context of the DF optical model potential and as an extension of our studies [58-60], the elastic scattering of 11Li+12C and 11Li+28Si has been reanalyzed. The nucleus-nucleus interaction potential has been constructed microscopically from folding the density-dependent effective NN interactions DDM3Y, CDM3Y6, and SPP over the NM distributions of the interacting nuclei. The resulting potentials are used as the real part of the OP, while the imaginary component is treated phenomenologically through the WS form to calculate the angular distributions of the elastic scattering differential cross sections. Successful predictions were obtained by using our potentials generated for different energies within the measured angular ranges. The results indicate that using a unified energy dependent real potential is adequate to successfully fit the data in the considered energy range. Looking at the chi-square values mentioned in the above tables, we found that, with different versions for the NM density of the lithium nucleus, the smallest values at energies 50 and 60 MeV were obtained using CDM3Y6-RT and CDM3Y6, respectively.
Due to the repulsive contribution of the RT to the real folding potential, especially at a small internuclear distance, this contribution has been shown to be vital in the application of the folding model to the study of elastic 11Li+12C and 11Li+28Si scattering in order to obtain the realistic shape and strength of the real potentials. The prediction capability of the folding model for 11Li+12C and 11Li+28Si is good. For this type of foldingpotential, systematic folding model studies of the elastic and inelastic nucleus-nucleus scattering over a wide range of energies are encouraged.
In contrast, the total reaction cross sections for the considered reactions together with extended energies are investigated. It is observed that the RCS increases linearly with rising energy at lower energies. It is also noted that both the observed data and those theoretically obtained from previous elastic scattering studies are in good agreement with the values generated by the current elastic scattering calculations.
Finally, we can argue that the simple calculated semi-microscopic potential of the DF model is considered as an advanced result and is more accurate compared with those from the previous complicated studies. The present results encourage us to modify the present potential calculation approach for full microscopic analysis to explain the discrepancy of the interaction of 11Li with low-Z targets at intermediate energies and to extend the analysis to other halo reactions.
Analysis of strong refractive effect within 11Li projectile structure
- Received Date: 2020-08-03
- Available Online: 2021-02-15
Abstract: In the context of the double folding optical model, the strong refractive effect for elastic scattering of 11Li + 12C and 11Li + 28Si systems at incident energies of 29, 50, and 60 MeV/n is studied. Real folded potentials are generated based on a variety of nucleon-nucleon interactions with the suggested density distributions for the halo structure of 11Li nuclei. The rearrangement term (RT) of the extended realistic density dependent CDM3Y6 effective interaction is considered. The imaginary potential was taken in the traditional standard Woods-Saxon form. Satisfactory results for the calculated potentials are obtained, with a slight effect of the RT in CDM3Y6 potential. Successful reproduction with a normalization factor close to one for the observed angular distributions of the elastic scattering differential cross section has been achieved using the derived potentials. The obtained reaction cross-section is studied as a guide by extrapolating our calculations and previous results.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: