-
Several cosmological and astrophysical observations at cosmic and galactic scales point towards the existence of dark matter in the Universe. The dark matter constitutes roughly 23% of the energy density of the Universe and roughly 75% of all the matter existing in the Universe. The Planck Collaboration [1] has measured the dark matter (DM) density to great precision and has given the relic density value
$\Omega_{\rm DM} h^2 = 0.1198 \pm 0.0012$ . The nature of DM, however, so far remains undetermined. Features of DM interactions can be determined from direct and indirect detection experiments. Direct detection experiments like DAMA/LIBRA [2, 3], CoGeNT [4], CRESST [5], CDMS [6], XENON100 [7, 8], LUX [9] and PandaX-II [10] are designed to measure the recoil momentum of a scattered atom or nucleon by DM in the chemically inert medium of the detector. These experiments involving spin-independent (SI) and spin-dependent scattering cross-sections in the non-relativistic (NR) regime have reached a sensitivity level where$\sigma_{\rm SI} > 8 \times 10^{-47}$ cm$ ^2 $ for DM mass$ \sim 30 $ GeV. Collider reaches in the present [11-13] and proposed [14-16] colliders aim at identifying the signature of DM particle production involving mono or di-jet events accompanied by missing energy. So far no experimental observation has made any confirmed detection and as a result a huge DM parameter space has been excluded. Indirect experiments such as FermiLAT [17-19], HESS [20] and AMS-02 [21, 22] are looking for evidence of excess cosmic rays produced in DM annihilation to Standard Model (SM) particles such as photons, leptons,$ b\ \bar{b} $ and gauge boson pairs, and so on.In the last several years, experiments like PAMELA [23, 24] have reported an excess in the positron flux without any significant excess in the proton to antiproton flux. These peaks in the
$ e^+ \, e^- $ channel have also been observed in the ATIC [25] and PPB-BETS [26] balloon experiments at around 1 TeV and 500 GeV respectively. Recently, the Dark Matter Particle Explorer (DAMPE) experiment [27] has also observed a sharp peak around$ \sim $ 1.4 TeV, favouring a lepto-philic DM annihilation cross-section of the order of$ 10^{-26} $ cm$ ^3 $ /s. The excess in$ e^+ \, e^- $ can either be due to astrophysical events like high energy emissions from pulsars, or result from DM pair annihilation, preferentially to the$ e^+\, e^- $ channel, in our galactic neighborhood. Since the aforementioned experiments have not observed any significant excess in the anti-proton channel, the DM candidates, if any, appears to be lepton friendly, lepto-philic, and have suppressed interactions with quarks at the tree level.Most of the effort in understanding the DM phenomenon has revolved around the hypothesis that DM is a weakly interacting massive particle (WIMP) with mass lying between several GeV to a few TeV. WIMPs provide the simplest production mechanism for the DM relic density from the early Universe. Various UV-complete new physics extensions of the SM have been proposed essentially to solve the gauge hierarchy problem in the top-down approach, which includes theories like extra dimensions [28], supersymmetry [29-31], little Higgs [32, 33], extended two-Higgs-doublet models (2HDM) with singlets as a portal of DM interactions [34] and so on. These models naturally provide DM candidates or WIMPs whose mass scales are close to that of electroweak physics. However, the direct detection experiments have shrunk the parameter space of the simplified and popular models where the WIMPs are made to interact with the visible world via neutral scalars or gauge bosons.
The model-independent DM-SM particle interactions have also been studied in an effective field theory (EFT) approach where the DM-SM interaction mediator is believed to be much heavier than the lighter mass scale of DM and SM interactions. The EFT approach provides a simple, flexible approach to investigate various aspects of DM phenomenology. The EFT approach treats the interaction between DM and SM particles as a contact interaction described by non-renormalizable operators. In the context of DM phenomenology, each operator describes different processes, such as DM annihilation, scattering and DM production in collider searches, with each process at its own energy scale, which is required to be smaller than the cut-off scale
$ \Lambda_{\rm{eff}} \gg $ the typical energy E. The nature of these interactions is encapsulated in a set of coefficients corresponding to a limited number of Lorentz and gauge-invariant dimension-5 and dimension-6 effective operators constructed with the light degrees of freedom. The constrained parameter space from various experimental data then essentially maps the viable UV-complete theoretical models. The generic effective Lagrangian for scalar, pseudo-scalar, vector and axial vector interactions of SM particles with dark matter candidates of spin$0,\ {1}/{2}, 1$ and${3}/{2}$ have been studied in the literature [35-40].Sensitivity analyses for DM-quark effective interactions at the LHC have been performed [12, 13, 41-44] in a model-independent way for the dominant (a) mono-jet +
${\not\!\! E}_{\rm{T}}$ , (b) mono-b jet +${\not\!\! E}_{\rm{T}}$ and (c) mono-t jet +${\not\!\! E}_{\rm{T}}$ processes. Similarly, analyses of DM-gauge boson effective couplings at the LHC have been done in Refs. [45-47]. Sensitivity analyses of the coefficients for the lepto-philic operators have also been performed through the$e^+e^-\to \gamma\ +\ {\not\!\! E}_{\rm{T}}$ [48-50] and$e^+e^-\to Z^0 + {\not\!\! E}_{\rm{T}}$ [16, 51] channels.In the context of deep inelastic lepton-hadron scattering, Gross and Wilczek [52] analyzed the twist-2 operators appearing in the operator-product expansion of two weak currents along with the renormalization group equations of their coefficients for asymptotically free gauge theories. A similar analysis was done in Ref. [53] for the effective DM-nucleon scattering induced by twist-2 quark operators in the supersymmetric framework where DM is identified with the lightest supersymmetric particle - the neutralino. In Refs. [54-56], the one-loop effect in DM-nucleon scattering induced by twist-2 quark and gluonic operators for scalar, vector and fermionic DM particles was calculated.
Although there exist many studies of dimension-5 and dimension-6 lepto-philic operators, only a few of them are invariant under SM gauge symmetry. As discussed above, the contributions of the cosmologicallyconstrained effective operators are not only sensitive at DM direct and indirect detection experiments but are also important in direct searches at high energy colliders. In fact, operators which do not meet the SM gauge symmetry requirement will not be able to maintain perturbative unitarity [57] due to their bad high energy behaviour at collider-accessible energies comparable to the electroweak scale
$ \sim 246 $ GeV. Thus the remaining dimension-5 and dimension-6 operators based on SM gauge symmetry and on the principle of perturbative unitarity may not contribute to the$ 2 \to 2 $ scattering processes relevant for direct detection experiments and should not be considered in production channels at high energy colliders. It is in this context that the study of additional SM gauge-invariant operators of dimension greater than six is important and needs to be undertaken [58, 59].In this paper we consider a DM current that couples primarily to the SM leptons through the
$ SU(2)_L \times U(1)_Y $ gauge-invariant effective operators. To ensure the invariance of SM gauge symmetry at all energy scales, we restrict our dark matter candidates to be self-conjugate: a Majorana fermion, a real spin 0 or a real spin 1 SM gauge singlet. In Section II, we formulate the effective interaction Lagrangian for fermionic, scalar and vector DM with SM leptons via twist-2 dimension-8 operators. In Section III, the coefficients of the effective Lagrangian are constrained from the observed relic density and a consistency check is performed from indirect and direct experiments. The constraints from LEP and the sensitivity analysis of the coefficients of the effective operators at the proposed ILC are discussed in Section IV. We summarise our results in section V. -
Following earlier authors [60-62], the interaction between dark matter particles (
$ \chi^0,\ \phi^0\ \&\ V^0 $ ) and SM leptons is assumed to be mediated by a heavy mediator which can be a scalar, vector or a fermion. The effective contact interaction between the dark matter particles and leptons is obtained by evaluating the Wilson coefficients appropriate for the contact interaction terms up to dimension 8. The mediator mass is assumed to be greater than all the other masses in the model and sets the cut-off scale$ \Lambda_{\rm{eff}} $ . We then obtain the following effective operators for self-conjugate spin-$ \frac{1}{2} $ , spin-$ 0 $ and spin-$ 1 $ dark matter particles interacting with the leptons:$ {\cal L}_{\rm{eff.\, Int.}}^{\rm{spin \,1/2 \,DM}} = \frac{{\alpha^{\chi^0}_{S}}}{\Lambda_{\rm {eff}}^4} {\cal{O}}_{S}^{1/2}+\frac{{\alpha^{\chi^0}_{T_1}}}{\Lambda_{\rm {eff}}^4} {\cal{O}}_{T_1}^{1/2} + \frac{{\alpha^{\chi^0}_{AV}}}{\Lambda_{\rm {eff}}^2} {\cal{O}}_{AV}^{1/2}, $

(1) $ {\cal L}_{\rm{eff.\, Int.}}^{\rm{spin \,0 \,DM} } = \frac{{\alpha^{\phi^0}_{S}}}{\Lambda_{\rm {eff}}^4} {\cal{O}}_{S}^{0}+ \frac{{\alpha^{\phi^0}_{T_2}}}{\Lambda_{\rm {eff}}^4} {\cal{O}}_{T_2}^{0}, $

(2) $ {\cal L}_{\rm{eff.\, Int.}}^{\rm{spin \,1 \,DM} } = \frac{{\alpha^{V^0}_{S}}}{\Lambda_{\rm {eff}}^4} {\cal{O}}_{S}^{1} + \frac{{\alpha^{V^0}_{T_2}}}{\Lambda_{\rm {eff}}^4} {\cal{O}}_{T_2}^{1} + \frac{{\alpha^{V^0}_{AV}}}{\Lambda_{\rm {eff}}^2} {\cal{O}}_{AV}^{1} , $

(3) with
$ {\cal{O}}^{1/2}_S\equiv m_{\chi^0}\ \left(\bar{\chi^0}\,\chi^0\; \right) \,\, m_l\,\, \left(\overline{l}\,l\right), $

(4) $ {\cal{O}}^{1/2}_{T_1}\equiv \bar{\chi^0}\,i\,\partial^\mu \,\gamma^\nu\, \chi^0 \,\,\,{\cal{O}}^l_{\mu\nu} \ +\ {\rm{h.c.}} , $

(5) $ {\cal{O}}^{1/2}_{\rm{AV}}\equiv\bar{\chi^0}\,\gamma_\mu\,\gamma_5\,\chi^0 \,\,\, \left(\overline{l}\,\gamma^\mu\,\gamma_5\,l\right), $

(6) $ {\cal{O}}^{0}_S\equiv m_{\phi^0}^2 \ {\phi^0}^2 \,\, m_l\,\, \left(\overline{l}\,l\right) , $

(7) $ {\cal{O}}^{0}_{T_2}\equiv \,\,\phi^0\,\, i\, \partial^\mu \,\,i\,\partial^\nu\,\, \phi^0\,\, {\cal{O}}^{l}_{\mu\nu}\ +\ {\rm{h.c.}}, $

(8) $ {\cal{O}}^{1}_S\equiv m_{V^0}^2\ {V^0}^\mu \, {V^0}_\mu \,\, m_l\,\, \left(\overline{l}\,l\right), $

(9) $ {\cal{O}}^{1}_{T_2}\equiv \ {V^0}^\rho\,\, i\, \partial^\mu \,\,i\,\partial^\nu\,\, {V^0}_\rho\,\, {\cal{O}}^{l}_{\mu\nu} \ +\ {\rm{h.c.}}, $

(10) $ {\cal{O}}^{1}_{\rm{AV}}\equiv i \ \epsilon_{\mu\nu\rho\sigma}\,\, {V^0}^\mu\ i\ \partial^\nu \ {V^0}^\rho\,\,\, \left(\overline{l}\,\gamma^\sigma \, \gamma_5\,l \right). $

(11) The effective operators given above can be seen to be
$ SU(2)_L \otimes U(1)_Y $ gauge-invariant by noting that the leptonic bilinear terms written in terms of left- and right-handed gauge eigenstates$ l_L $ and$ e_R $ can be combined to give the above operators. The term proportional to the lepton mass$ m_l $ is obtained by integrating out the Higgs in the EFT formalism. However, this term is only valid up to the weak scale.The twist-2 operators
$ {\cal{O}}^{l}_{\mu\nu} $ for charged leptons are defined as:$ \begin{aligned}[b] {\cal{O}}^{l}_{\mu\nu}\equiv&\frac{\rm i}{2}\ \overline{l_L}\ \left( {D}_\mu^L\gamma_\nu^{} +{{D}_\nu^{L}}\gamma_\mu^{}-\frac{1}{2}g_{\mu\nu}^{} {{\not\!\! D}^L}\right)\ l_L\ \\ &+\ \frac{\rm i}{2}\ \overline{e_R}\ \left( {D}_\mu^R\gamma_\nu^{} +{{D}_\nu^{R}}\gamma_\mu^{}-\frac{1}{2}g_{\mu\nu}^{} {{\not\!\! D}^R}\right)\ e_R , \end{aligned} $

(12) where
$ {D_\mu}^L $ and$ {D_\mu}^R $ are the covariant derivatives given by:$ \begin{aligned}[b] & D_\mu^L\equiv {\rm i}\ \partial_\mu\ -\ \dfrac{1}{2}g\ \overrightarrow{\tau}\cdot \overrightarrow{W}_\mu\ +\ \dfrac{1}{2}g^\prime\ B_\mu ,\\ &D_\mu^R\equiv {\rm i}\ \partial_\mu\ +\ g^\prime\ B_\mu. \end{aligned} $

(13) The Lorentz structure of the operators determines the nature of dominant DM pair annihilation cross-sections. It turns out that the scalar and axial-vector operator contributions for fermionic and vector DM respectively are p-wave suppressed.
-
In the early Universe the DM particles were in thermal equilibrium with the plasma through the creation and annihilation of DM particles. The relic density contribution of the DM particles is obtained by numerically solving the Boltzmann equation [63] to give:
$ \begin{aligned}[b] \Omega_{\rm{DM}} { h}^2 =& \frac{\pi\,\sqrt{{g_{\rm{eff}}}(x_F)}}{\sqrt{90}}\frac{x_F\,T_0^3\ g}{M_{Pl}\,\rho_c\,\langle\sigma^{ann} \left\vert \vec{v}\right\vert\rangle\, { g_{\rm{eff}}}(x_F)}\\ \\ \approx &0.12 \, \frac{x_F}{28} \, \frac{\sqrt{ g_{\rm{eff}}(x_F)}}{10}\, \frac{2\times10^{-26} cm^3/s}{\langle\sigma^{ann}\left\vert \vec v\right\vert\rangle} , \end{aligned} $

(14) and
$ x_F $ at freeze-out is given by:$ x_F = \log \left[a\,\left(a+2\right)\, \sqrt{\frac{45}{8}}\,\frac{ g \,M_{Pl}\, m_{\rm{DM}}\,\langle\sigma^{ann}\left\vert \vec v\right\vert\rangle}{2\,\pi^3\, \sqrt{x_F\, g_{\rm{eff}}(x_F)}} \right], $

(15) where a is a parameter of the order of one.
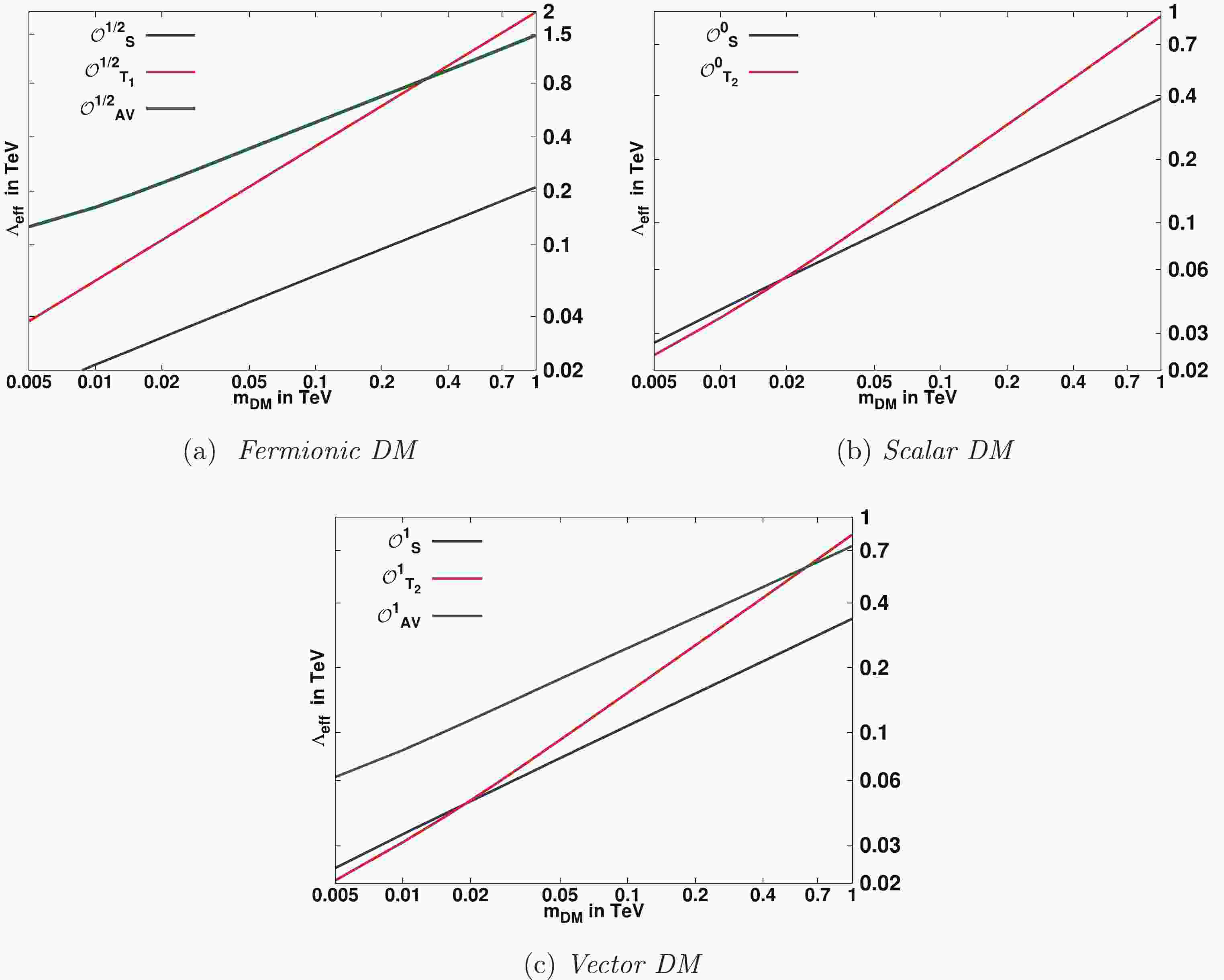
$ g_{\rm{eff}} $ is the effective number of degrees of freedom and is taken to be$ 92 $ near the freeze-out temperature, and$ g = 2,\ 1\ {\rm{and}}\ 3 $ for fermionic, scalar and vector DM particles respectively.The relevant annihilation cross-sections are given in Appendix A. We have computed the relic density numerically using MadDM [64] and MadGraph [65], generating the input model file using the Lagrangian given in Eqs. (1)-(11). Figure 1 shows the contour graphs in the effective cut-off
$ \Lambda_{\rm{eff}} $ and DM mass plane for the fermionic, scalar and vector DM particles. For arbitrary values of the coupling$ \alpha $ , the effective cut-off$ \Lambda_{\rm{eff}} $ is obtained by noting that$ \Lambda_{\rm{eff}} $ for scalar and twist-2 tensor operators scales as$ \alpha^{1/4} $ whereas for AV operators$ \Lambda_{\rm{eff}} $ scales as$ \alpha^{1/2} $ . We have shown the graphs by taking one operator at a time and taking the coupling$ \alpha's = 1 $ . We have made sure that perturbative unitarity of the EFT is maintained for the entire parameter space scanned in Fig. 1. The points lying on the solid lines satisfy the observed relic density$\Omega_{\rm DM} h^2 = 0.1198$ . The region below the corresponding solid line is the cosmologically allowed parameter region of the respective operator. We find from Fig. 1(a) that the scalar operator for the fermionic DM is sensitive to the low DM mass.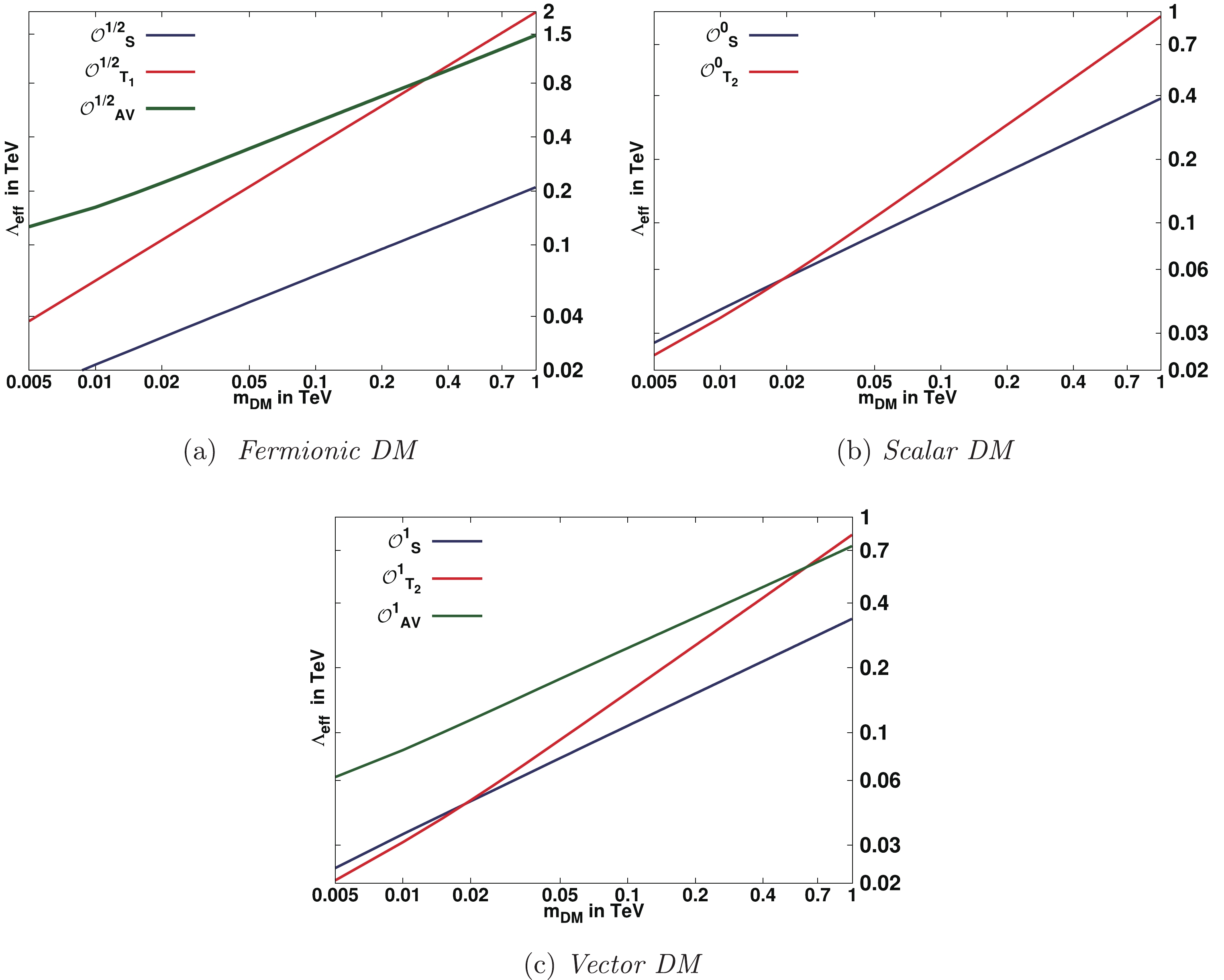
Figure 1. (color online) Relic density contours satisfying
$ \Omega_{\rm{DM}}h^2 $ =$ 0.1198 \pm 0.0012 $ in the DM mass -$ \Lambda_{\rm{eff}} $ plane. All contours are drawn assuming universal lepton flavor couplings of effective DM-lepton interactions. The region below the corresponding solid line is the cosmologically allowed parameter region of the respective operator. -
DM annihilation in the dense regions of the Universe would generate a high flux of energetic SM particles. The Fermi Large Area Telescope (LAT) [17-19] has produced the strongest limit on DM annihilation cross-sections for singular annihilation final states to
$ b\ \bar{b},\ \tau\ \bar{\tau} $ , etc. In the case of DM particles annihilating into multiple channels, the bounds on cross-sections have been analysed in Ref. [66]. In our case we display the bounds from Fermi-LAT in Fig. 2, assuming the DM particles considered in this article to couple only to$ \tau $ -leptons i.e.$ \tau $ -philic DM.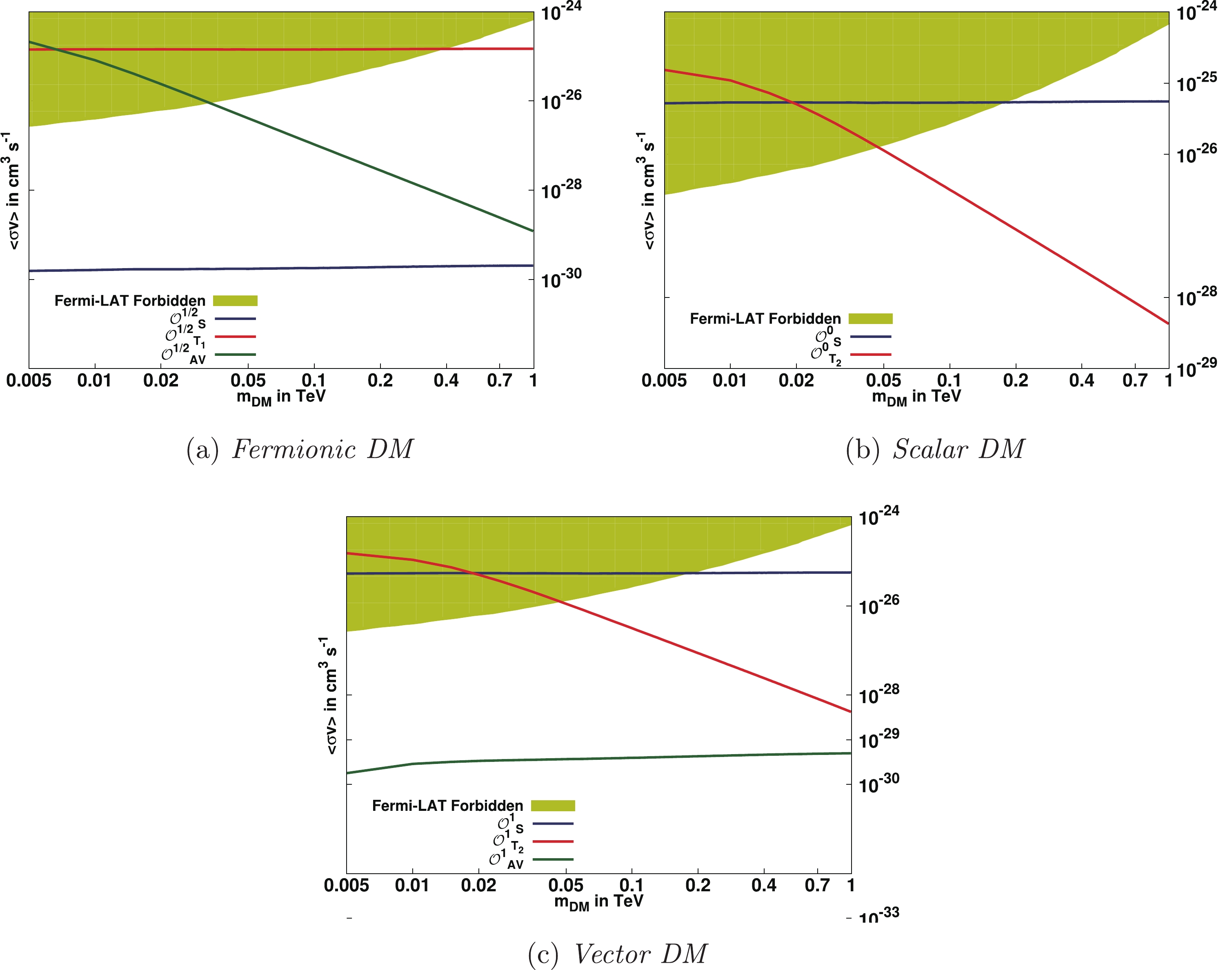
Figure 2. (color online) DM annihilation cross-section to
$ \tau^+ \tau^- $ . Solid lines in all figures show the variation of DM annihilation cross-section with DM mass where all other parameters are taken from the observed relic density. The median of the DM annihilation cross-section, derived from a combined analysis of the nominal target sample for the$ \tau^+ \tau^- $ channel assuming 100% branching fraction, restricts the allowed shaded region from above. v is taken to be$ \sim 10^{-3}\ c $ .In Fig. 2 we show the prediction for dark matter annihilation cross-section into
$ \tau^+ \tau^- $ for the set of parameters which satisfy the relic density constraints for the$ \tau $ -philic DM particles. These cross-sections are compared with the upper bounds on the allowed annihilation cross-sections in the$ \tau^+ \tau^- $ channel obtained from the Fermi-LAT data [17-19]. The Fermi-LAT data puts a lower limit on the DM particle mass even though allowed by the relic-density observations. Likewise Fermi-LAT puts severe constraints on the twist-2$ {\cal{O}}_{T_1}^{1/2} $ operator (Fig. 2(a)) for fermionic DM and the$ {\cal{O}}_{S}^0 $ operator (Fig. 2(b)) for scalar DM. There is a minimum dark matter particle mass allowed by Fermi-LAT observations. -
Direct detection experiments [2-10] look for the scattering of a nucleon or atom by DM particles. These experiments are designed to measure the recoil momentum of the nucleons or atoms of the detector material. This scattering can be broadly classified as (a) DM-nucleon, (b) DM-atom and (c) DM-electron scattering. Since lepto-philic DM does not have direct interaction with quarks or gluons at the tree level, the DM-nucleon interaction can only be induced at the loop levels.
It has been shown [67] and has been independently verified by us that the event rate for direct detection of DM-atom scattering is suppressed by a factor of
$ \sim 10^{-7} $ with respect to the DM-electron elastic scattering, which is in turn is suppressed by a factor of$ \sim 10^{-10} $ with respect to the loop-induced DM-nucleon scattering. In this article we restrict ourselves to the scattering of DM particles with free electrons.$ \begin{aligned}[b]\sigma_{S}^{\chi^0\, e^-} = & \frac{{\alpha^{\chi^0}_{S}}^2}{\pi}\ \frac{m_{\chi^0}^2}{\Lambda_{\rm{eff}}^8}\ m_e^4\ \\ \simeq &\ {\alpha^{\chi^0}_{S}}^2\ \left(\frac{m_{\chi^0}}{200\ {\rm{GeV}}}\right)^2\ \left( \frac{1 \ {\rm{TeV}}}{\Lambda_{\rm{eff}}} \right)^8\ 3.09 \times 10^{-61}\ {\rm{cm}}^2 ,\end{aligned} $

(16) $ \begin{aligned}[b]\sigma_{T_1}^{\chi^0\, e^-} = &36\ \frac{{\alpha^{\chi^0}_{T_1}}^2}{\pi}\ \frac{m_{\chi^0}^2}{\Lambda_{\rm{eff}}^8}\ m_e^4\ \\ \simeq&\ {\alpha^{\chi^0}_{T_1}}^2\ \left(\frac{m_{\chi^0}}{200\ {\rm{GeV}}}\right)^2\ \left( \frac{1 {\rm{TeV}}}{\Lambda_{\rm{eff}}} \right)^8\ 1.11 \times 10^{-59}\ {\rm{cm}}^2 , \end{aligned}$

(17) $ \begin{aligned}[b] \sigma_{AV}^{\chi^0\, e^-} = & 3\ \frac{{\alpha^{\chi^0}_{AV}}^2}{\pi}\ \frac{m_e^2}{\Lambda_{\rm{eff}}^4}\ \\ \simeq&\ {\alpha^{\chi^0}_{AV}}^2\ \left( \frac{1 {\rm{TeV}}}{\Lambda_{\rm{eff}}} \right)^4\ 9.27 \times 10^{-47}\ {\rm{cm}}^2 , \end{aligned}$

(18) $ \begin{aligned}[b] \sigma_{S}^{\phi^0 \,e^-} = & \frac{{\alpha^{\phi^0}_{S}}^2}{\pi}\ \frac{m_{\phi^0}^2}{\Lambda_{\rm{eff}}^8}\ m_e^4\ \\ \simeq &\ {\alpha^{\phi^0}_{S}}^2\ \left(\frac{m_{\phi^0}}{200\ {\rm{GeV}}}\right)^2\ \left( \frac{1 {\rm{TeV}}}{\Lambda_{\rm{eff}}} \right)^8\ 3.09 \times 10^{-61}\ {\rm{cm}}^2 ,\end{aligned} $

(19) $ \begin{aligned}[b] \sigma_{T_2}^{\phi^0 \,e^-} =& \frac{9}{16}\ \frac{{\alpha^{\phi^0}_{T_2}}^2}{\pi}\ \frac{m_{\phi^0}^4}{\Lambda_{\rm{eff}}^8}\ m_e^2\ \\ \simeq&\ {\alpha^{\phi^0}_{T_2}}^2\ \left(\frac{m_{\phi^0}}{200\ {\rm{GeV}}}\right)^4\ \left( \frac{1 {\rm{TeV}}}{\Lambda_{\rm{eff}}} \right)^8\ 2.78 \times 10^{-50}\ {\rm{cm}}^2 , \end{aligned} $

(20) $ \begin{aligned}[b]\sigma_{S}^{V^0\, e^-} =& \frac{{\alpha^{V^0}_{S}}^2}{\pi}\ \frac{m_{V^0}^2}{\Lambda_{\rm{eff}}^8}\ m_e^4\ \\ \simeq&\ {\alpha^{V^0}_{S}}^2\ \left(\frac{m_{V^0}}{200\ {\rm{GeV}}}\right)^2\ \left( \frac{1 {\rm{TeV}}}{\Lambda_{\rm{eff}}} \right)^8\ 3.09 \times 10^{-61}\ {\rm{cm}}^2 , \end{aligned} $

(21) $ \begin{aligned}[b] \sigma_{T_2}^{V^0\, e^-} = &\frac{9}{16}\ \frac{{\alpha^{V^0}_{T_2}}^2}{\pi}\ \frac{m_{V^0}^4}{\Lambda_{\rm{eff}}^8}\ m_e^2\ \\ \simeq&\ {\alpha^{V^0}_{T_2}}^2\ \left(\frac{m_{V^0}}{200\ {\rm{GeV}}}\right)^4\ \left( \frac{1 {\rm{TeV}}}{\Lambda_{\rm{eff}}} \right)^8\ 2.78 \times 10^{-50}\ {\rm{cm}}^2 , \end{aligned} $

(22) $ \begin{aligned}[b] \sigma_{AV}^{V^0\, e^-} = &\frac{1}{144}\ \frac{{\alpha^{V^0}_{AV}}^2}{\pi}\ \frac{1}{\Lambda_{\rm{eff}}^4}\ \frac{m_e^4}{m_{V^0}^2}\ v^4\ \\ \simeq&\ {\alpha^{V^0}_{AV}}^2\! \left(\frac{200\ {\rm{GeV}}}{m_{V^0}}\right)^2\left( \frac{1 {\rm{TeV}}}{\Lambda_{\rm{eff}}} \right)^4 v^4\ 1.34 \times 10^{-60}\ {\rm{cm}}^2 ,\end{aligned} $

(23) We find that the electron-DM scattering cross-sections are dominated by the effective interactions mediated by the
$ AV $ operator$ {\cal{O}}_{AV}^{1/2} $ for fermionic DM and by the twist-2 operators$ {\cal{O}}_{T_2}^{0} $ and$ {\cal{O}}_{T_2}^{1} $ for scalar and vector DM respectively. In Fig. 3, we plot the DM-free electron scattering cross-section as a function of DM mass only for the dominant operators as discussed above. The other operator contributions are negligible in comparison. The cross-sections for a given DM mass are computed with the corresponding value of$ \Lambda_{\rm{eff}} $ satisfying the observed relic density for these operators. These results are then compared with the null results of DAMA/LIBRA [2, 3] at 90% confidence level for DM-electron scattering and XENON100 [7, 8] at 90% confidence level for inelastic DM-atom scattering.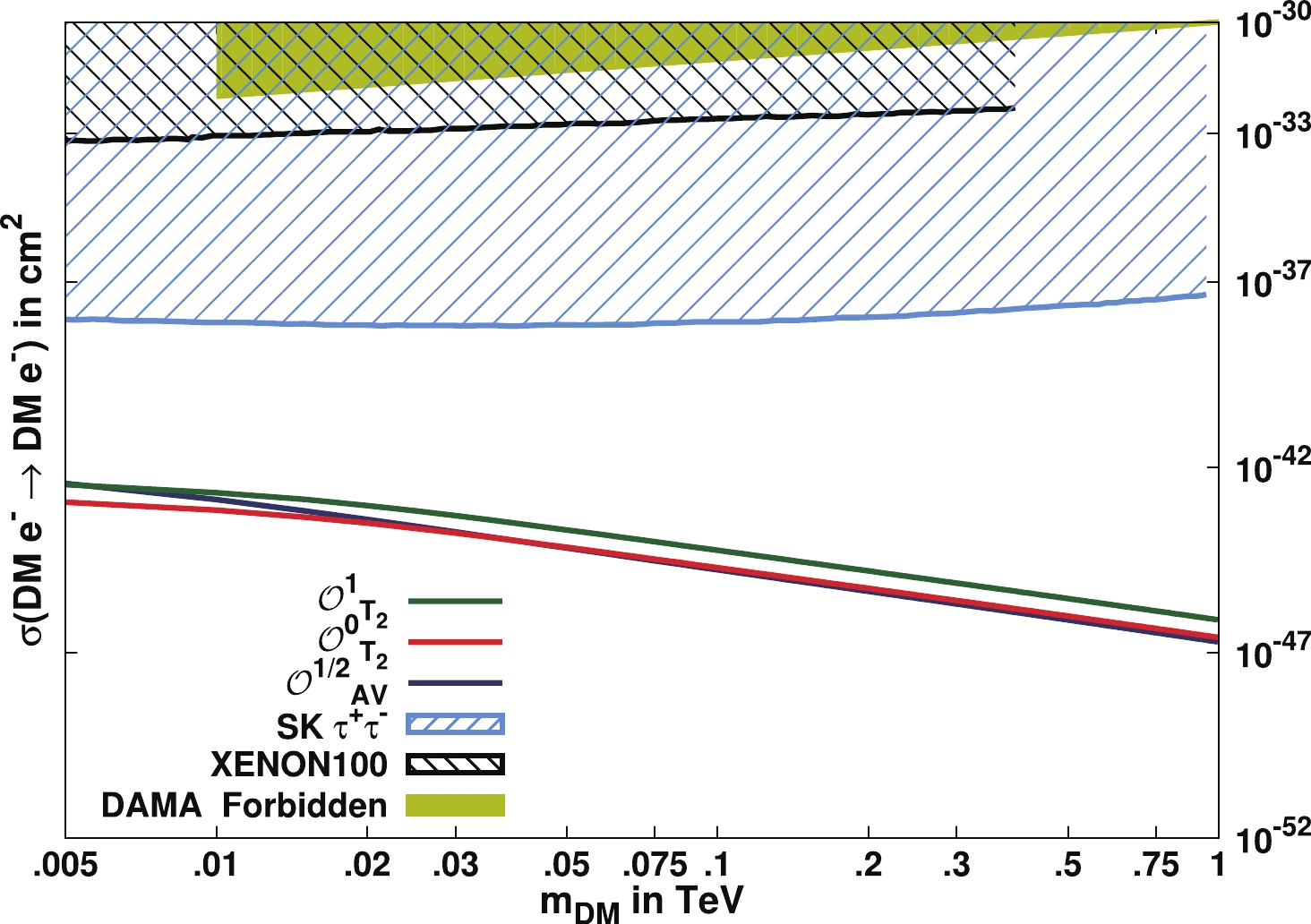
Figure 3. (color online) DM-free electron elastic scattering cross-section as a function of DM mass. The solid lines are drawn for the dominant operators
$ {\cal{O}}_{AV}^{1/2},\ {\cal{O}}_{T_2}^{0} $ and$ {\cal{O}}_{T_2}^{1} $ for fermionic, scalar and vector DM particles respectively. The exclusion plots from DAMA at 90% C.L. for the case of DM-electron scattering are also shown [67]. Bounds at 90% C.L. are shown for XENON100 from inelastic DM-atom scattering [68]. The dashed curves show the 90% C.L. constraint from the Super-Kamiokande limit on neutrinos from the Sun, by assuming annihilation into$ \tau^+\tau^- $ [67]. -
Existing results and observations from LEP data can be used for putting constraints on the effective operators. The cross-section for the process
$ e^+e^-\to \gamma^\star + \, {\rm{DM \ pair}} $ is compared with the combined analysis from the DELPHI and L3 collaborations for$ e^+e^-\to \gamma^\star + Z \to q_{i}\bar q_{i} + \nu_{l_j}\bar\nu_{l_j} $ at$ \sqrt{s} $ =$ 196.9 $ GeV and an integrated luminosity of 679.4 pb$ ^{-1} $ , where$ q_i\equiv u,\,d,\,s $ and$ \nu_{l_j}\equiv \nu_e,\,\nu_{\mu},\nu_\tau $ . The Feynman diagrams contributing to the production of$ \gamma / \gamma^\star $ with missing energy induced by lepto-philic operators at a lepton$ e^-\,e^+ $ collider are shown in Fig. 4. The measured cross-section from the combined analysis for the said process is found to be$ 0.055 $ pb, with the measured statistical error$ \delta\sigma_{\rm{stat}} $ , systematic error$ \delta\sigma_{\rm{syst}} $ and total error$ \delta\sigma_{\rm{tot}} $ of$ 0.031 $ pb,$ 0.008 $ pb and$ 0.032 $ pb respectively [69]. Hence, the contribution due to an additional channel containing the final-state DM pairs and resulting in the missing energy along with two quark jets can be constrained from the observed$ \delta\sigma_{\rm{tot}} $ . In Fig. 5, we have plotted the 95% C.L. solid line contours satisfying$ \delta\sigma_{\rm{tot}} $ $ \approx $ $ 0.032 $ pb, corresponding to the operators in the DM mass-$ \Lambda_{\rm{eff}} $ plane. The region under the solid lines corresponding to the operator as shown is disallowed by the combined LEP analysis. The phenomenologically interesting DM mass range$ \leqslant 50 $ GeV is completely disfavored by the LEP experiments, except for the operator$ {\cal{O}}_{AV}^{1/2} $ .
Figure 4. Feynman diagrams contributing to the production of
$ \gamma / \gamma^\star $ with missing energy induced by lepto-philic operators (5)-(11) at a lepton$ e^-\,e^+ $ collider.
Figure 5. (color online) Solid lines depict the contours in the plane defined by DM mass and the kinematic reach of for
$ e^+e^-\to {\rm{DM\, pairs}} + \gamma^\star \to \,\,\not\!\!\!E_T + q_{i}\bar q_{i} $ at$ \sqrt{s} $ = 196.9 GeV and an integrated luminosity of 679.4 pb$ ^{-1} $ , satisfying the constraint$ \delta\sigma_{\rm{tot}} $ =0.032 pb obtained from combined analysis of DELPHI and L3 [69]. The regions below the solid lines are forbidden by LEP observation. The regions below the dashed lines corresponding to respective operators satisfy the relic density constraint$ \Omega_{\rm{DM}}h^2 \le $ $ 0.1198 \pm 0.0012 $ . -
In this subsection we study the DM pair production processes accompanied by an on-shell photon at the proposed International Linear Collider (ILC) for the DM mass range
$ \sim $ 50 - 500 GeV: (a)$ e^+\,e^-\,\rightarrow \,\chi^0\,\bar{\chi^0}\,\gamma $ , (b)$ e^+\,e^-\,\rightarrow \,\phi^0\,\phi^0\,\gamma $ , and (c)$e^+\,e^-\,\rightarrow $ $ V^0\,V^0\,\gamma $ as shown in Figs 8-10. The dominant SM background for the$ e^+e^-\to \not \!\! E_T + \gamma $ signature comes from the$ Z\gamma $ production process:$ e^+\,e^-\,\rightarrow\,Z+\gamma \to \sum \nu_i\,\bar{\nu}_i + \gamma $ .The analyses for the background and the signal processes corresponding to the accelerator parameters as conceived in the Technical Design Report for ILC [70, 71], given in Table 1, were performed by simulating SM backgrounds and DM signatures using Madgraph [65], MadAnalysis 5 [72] and the model file generated by FeynRules [73]. We impose the following cuts to reduce the backgrounds for the DM pair production in association with a mono-photon:
ILC-250 ILC-500 ILC-1000 $\sqrt{s} \left(\rm in \;GeV\right )$ 

250 500 1000 $L_{\rm int} \left(\rm in \;fb^{-1}\right )$ 

250 500 1000 $\sigma_{\rm BG}\rm \;(pb)$ 

1.07 1.48 2.07 $ \bullet $ Transverse momentum of photon$ p_{T_{\gamma}} \geqslant $ 10 GeV,$ \bullet $ Pseudo-rapidity of photon is restricted to$ \left\vert\eta_\gamma\right\vert\leqslant $ 2.5,$ \bullet $ disallowed recoil photon energy against on-shell Z${2\,E_\gamma}/{\sqrt{s}} \not\!\epsilon \left[0.8,0.9\right]$ ,$ \left[0.95,0.98\right] $ and$ \left[0.98,0.99\right] $ for$ \sqrt{s} $ = 250 GeV, 500 GeV and 1 TeV respectively.The shape profiles corresponding to the mono-photon with missing energy processes can be studied in terms of the kinematic observables
$ p_{T_{\gamma}} $ and$ \eta_\gamma $ , as they are found to be the most sensitive. We generate the normalized one-dimensional distributions for the SM background processes and signals induced by the relevant operators. To study the dependence on DM mass, we plot the normalized differential cross-sections in Figs. 6 and 7 for three representative values of DM mass,$ 75,\ 225 $ and$ 325 $ GeV, at center of mass energy$ \sqrt{s} = 1 $ TeV and an integrated luminosity 1${\rm ab}^{-1}$ .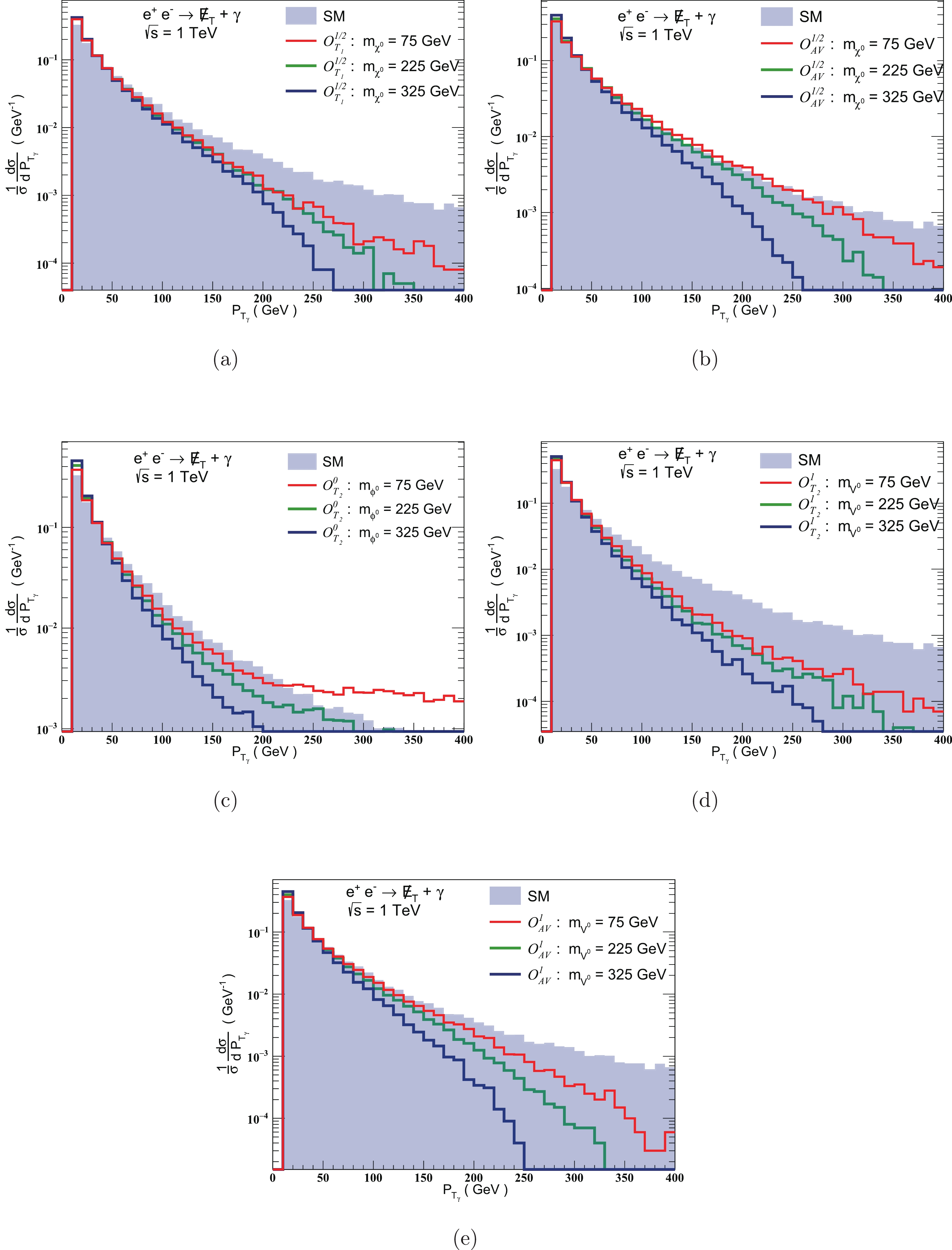
Figure 6. (color online) Normalized 1-dimensonal differential cross-sections with respect to
$ p_{T_\gamma} $ corresponding to the SM processes, and those induced by lepto-philic operators at three representative values of DM mass: 75, 225 and 325 GeV.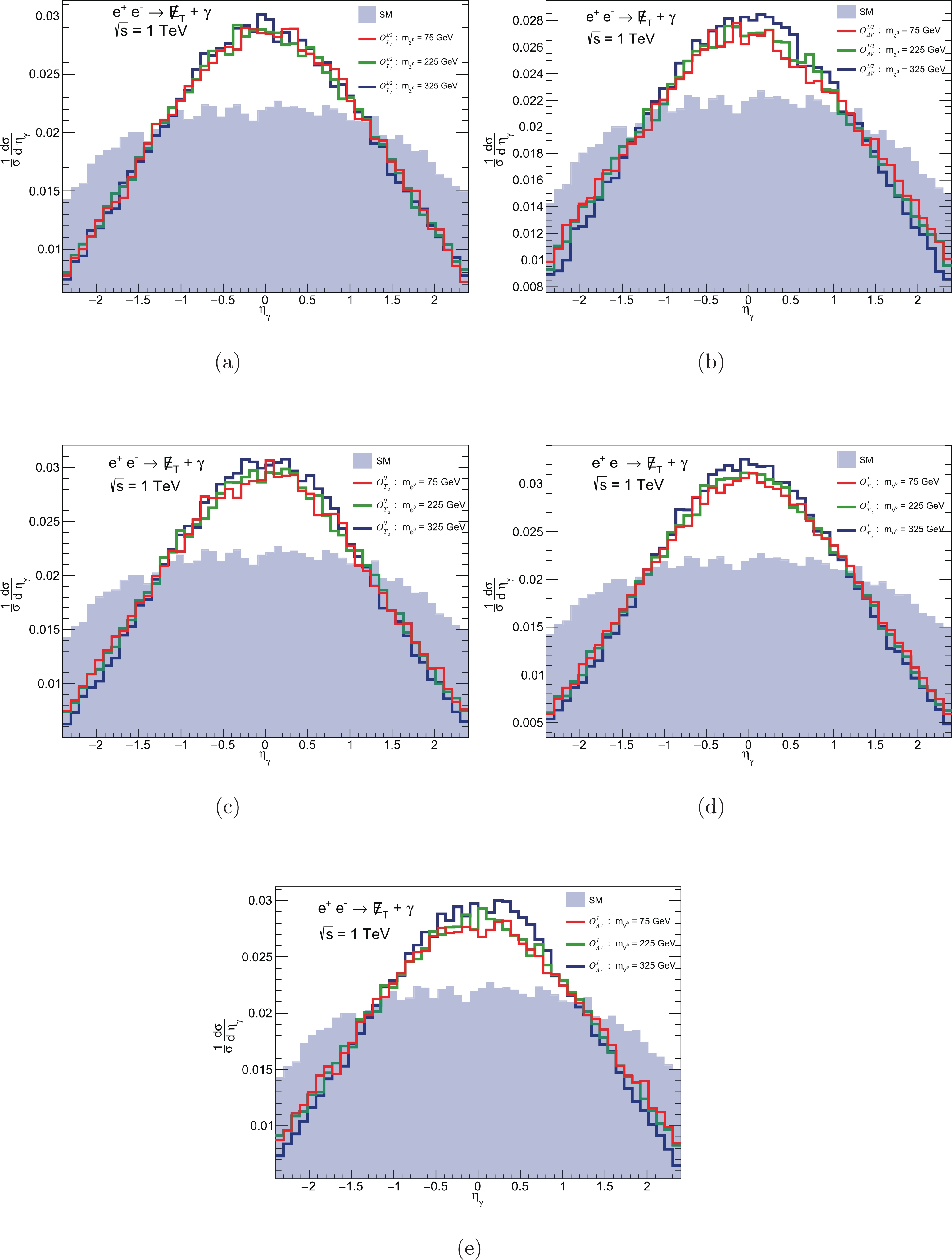
Figure 7. (color online) Normalized 1-dimensonal differential cross-sections with respect to
$ \eta_{\gamma} $ corresponding to the SM processes, and those induced by lepto-philic operators at the three representative values of DM mass: 75, 225 and 325 GeV.The sensitivity of
$ \Lambda_{\rm{eff}} $ with respect to DM mass is enhanced by computing the$ {\cal{X}}^2 $ with the double differential distributions of kinematic observables$ p_{T_\gamma} $ and$ \eta_\gamma $ corresponding to the background and signal processes for: (i) 50 GeV$ \leqslant m_{\rm{DM}} \leqslant $ 125 GeV at$ \sqrt{s} $ = 250 GeV and an integrated luminosity of 250 fb$ ^{-1} $ ; (ii) 100 GeV$ \leqslant m_{\rm{DM}} \leqslant $ 250 GeV at$ \sqrt{s} $ = 500 GeV and an integrated luminosity of 500 fb$ ^{-1} $ ; and (iii) 100 GeV$ \leqslant m_{\rm{DM}} \leqslant $ 500 GeV at$ \sqrt{s} $ = 1 TeV and an integrated luminosity of 1 ab$ ^{-1} $ . The$ {\cal{X}}^2 $ is defined as$ \begin{aligned}[b] {\cal{X}}^2\equiv&{\cal{X}}^2 \left(m_{\rm{DM}},\, \frac{\alpha_i}{\Lambda_{\rm {eff}}^n} \right) \\ =& \sum\limits_{j = 1}^{n_1}\sum\limits_{i = 1}^{n_2} \left [ \dfrac{\dfrac{\Delta N_{ij}^{\rm NP}}{\left(\Delta p_{T_\gamma}\right)_i\, \left(\Delta \eta_\gamma\right)_j}}{\sqrt{ \dfrac{\Delta N_{ij}^{\rm SM+NP}} {\left(\Delta p_{T_\gamma}\right)_i\, \left(\Delta \eta_\gamma\right)_j} +\delta_{\rm{sys}}^2\left\{ \dfrac{\Delta N_{ij}^{\rm SM+NP}}{\left(\Delta p_{T_\gamma}\right)_i\, \left(\Delta \eta_\gamma\right)_j}\right\}^2} }\right ]^2 , \end{aligned}$

(24) where
$\Delta N_{ij}^{\rm NP}$ and$\Delta N_{ij}^{\rm SM+NP}$ are the number of New Physics and total differential events respectively in the two-dimensional$ \left[\left(\Delta p_{T_\gamma}\right)_i-\left(\Delta \eta_\gamma\right)_j\right]^{\rm{th}} $ grid. Here$ \delta_{\rm{sys}} $ represents the total systematic error in the measurement.Adopting a conservative value of 1% for the systematic error and using the collider parameters given in Table 1, we simulate the two-dimension differential distributions to calculate the
$ {\cal{X}}^2 $ . In Figs. 8-10, we have plotted the$ 3\sigma $ contours at 99.73% C.L in the$m_{\rm DM}-\Lambda_{\rm{eff}}$ plane corresponding to$ \sqrt{s} = 250 $ GeV, 500 GeV and 1 TeV respectively for the effective operators satisfying perturbative unitarity.
Figure 8. (color online) Solid lines depict
$ 3\sigma $ with 99.73 % C.L. contours in the$ m_{DM}-\Lambda_{\rm{eff}} $ plane from the$ {\cal{X}}^2 $ analyses of the$e^+e^-\to {\not\!\! E}_T +\gamma$ signature at the proposed ILC designed for$ \sqrt{s} $ = 250 GeV with an integrated luminosity 250 fb$ ^{-1} $ . The regions below the solid lines corresponding to the respective contour are accessible for discovery with$ \geqslant $ 99.73% C.L. The regions below the dashed lines corresponding to respective operators satisfy the relic density constraint$ \Omega_{\rm{DM}}h^2 \leqslant $ $ 0.1198 \pm 0.0012 $ .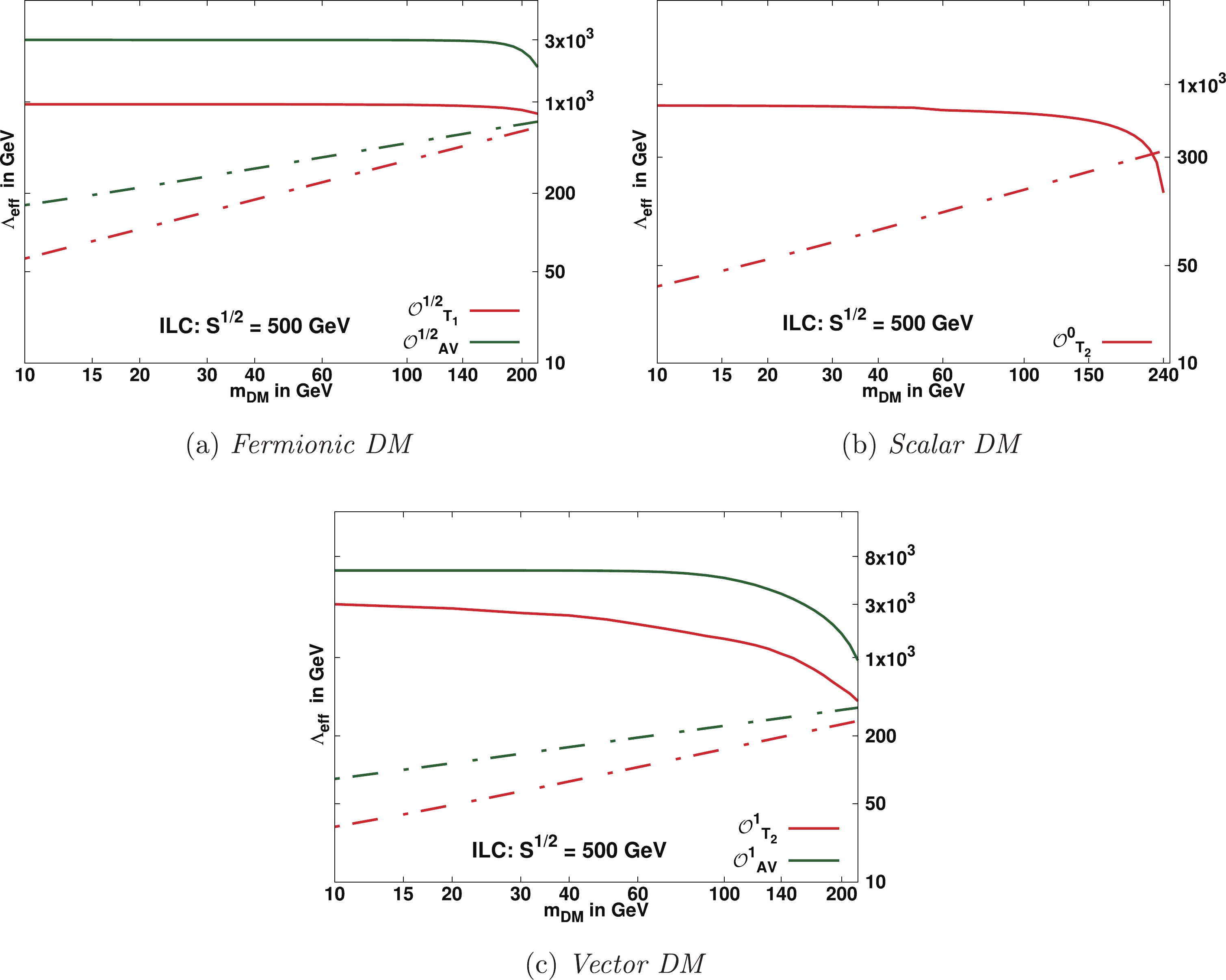
Figure 9. (color online) Solid lines depict
$ 3\sigma $ with 99.73 % C.L. contours in the$m_{\rm DM}-\Lambda_{\rm{eff}}$ plane from the$ {\cal{X}}^2 $ analyses of the$e^+e^-\to {\not\!\! E}_T +\gamma$ signature at the proposed ILC designed for$ \sqrt{s} $ = 500 GeV with an integrated luminosity 500 fb$ ^{-1} $ . The regions below the solid lines corresponding to the respective contour are accessible for discovery with$ \geqslant $ 99.73% C.L. The regions below the dashed lines corresponding to respective operators satisfy the relic density constraint$ \Omega_{\rm{DM}}h^2 \leqslant $ $ 0.1198 \pm 0.0012 $ .
Figure 10. (color online) Solid lines depict
$ 3\sigma $ with 99.73 % C.L. contours in the$m_{\rm DM}-\Lambda_{\rm{eff}}$ plane from the$ {\cal{X}}^2 $ analyses of the$e^+e^-\to {\not\!\! E}_T +\gamma$ signature at the proposed ILC designed for$ \sqrt{s} $ = 1 TeV with an integrated luminosity 1 ab$ ^{-1} $ . The regions below the solid lines corresponding to the respective contour are accessible for discovery with$ \geqslant $ 99.73% C.L. The regions below the dashed lines corresponding to respective operators satisfy the relic density constraint$ \Omega_{\rm{DM}}h^2 \leqslant $ $ 0.1198 \pm 0.0012 $ .The sensitivity of mono-photon searches can be improved by considering the polarised initial beams [74, 75]. For illustration, we consider +80 % polarised
$ e^- $ and -30 % polarised$ e^+ $ initial beams. In Table 2, we show the$ 3 \sigma $ reach of the cut-off$ \Lambda_{\rm{eff}} $ from$ {\cal{X}}^2 $ analysis for two representative values of DM mass,$ 75 $ and$ 225 $ GeV, at the proposed ILC for$ \sqrt{s} = 500 $ GeV with an integrated luminosity$500\ \rm fb^{-1}$ for unpolarised and polarised initial beams, and find improvement in the$ \Lambda_{\rm{eff}} $ sensitivity for the polarised beams.Unpolarised Polarised $\sqrt{s}$ in GeV

500 500 $ L$ in fb

$^{-1}$ 

500 500 $\left(P_{e^-},\, P_{e^+}\right)$ 

(0, 0) (0.8, −0.3) $m_{DM}$ in GeV

$75$ 

$225$ 

$75$ 

$225$ 

${\cal{O}}^{1/2}_{T_1} $ 

$956.1$ 

$766.4$ 

$1135.7$ 

$948.0$ 

${\cal{O}}^{1/2}_{\rm{AV}}$ 

$2994.4$ 

$1629.4$ 

$2998.6$ 

$2345.5$ 

${\cal{O}}^{0}_{T_2}$ 

$461.8$ 

$319.1$ 

$767.8$ 

$373.2$ 

${\cal{O}}^{1}_{T_2}$ 

$1751.4$ 

$361.8$ 

$1651.2$ 

$444.3$ 

${\cal{O}}^{1}_{\rm{AV}}$ 

$5718.0$ 

$777.3$ 

$5976.2$ 

$1129.8$ 

Table 2. Estimation of
$3 \sigma$ reach of the cut-off$\Lambda_{\rm{eff}}$ in GeV from${\cal{X}}^2$ analysis for two representative values of DM mass,$75$ and$225$ GeV, at proposed ILC for$\sqrt{s}=500$ GeV with an integrated luminosity$500\ \rm fb^{-1}$ , for unpolarised and polarised initial beams. -
In this article we have studied DM phenomenology in an effective field theory framework. We have considered SM gauge-invariant contact interactions between dark matter particles and leptons up to dimension 8. To ensure the invariance of SM gauge symmetry at all energy scales, we have restricted ourselves to self-conjugate DM particles, namely a Majorana fermion, a real scalar or a real vector. We have estimated their contribution to the relic density and obtained constraints on the parameters of the theory from the observed relic density
$\Omega_{\rm DM} h^2 = 0.1198 \pm 0.0012$ . Indirect detection data from FermiLAT puts a lower limit on the allowed DM mass. The data also puts severe constraints on the twist-2$ {\cal{O}}^{1/2}_{T_1} $ operator for the fermionic DM and scalar$ {\cal{O}}^0_S $ operator for scalar DM.Analysis of the existing LEP data disallows the phenomenologically interesting DM mass range
$ \leqslant 50 $ GeV, except for the${\cal{O}}^{1/2}_{\rm AV}$ operator. We then performed$ {\cal{X}}^2 $ -analysis for the pair production of DM particles at the proposed ILC for DM mass range$ \sim 50-500 $ GeV, for the relevant operators discussed in Table 1 We find that in the$m_{\rm DM}-\Lambda_{\rm{eff}}$ region allowed by the relic density and indirect detection data, higher sensitivity can be obtained from the dominant mono-photon signal at the proposed ILC, particularly for twist-2 operators. -
For low mass DM, our attention was drawn by the referee to the fact that in addition to on-shell Z production at LEP, the future FCC-ee and CEPC will be sources of large numbers of Zs, producing Tera Zs. This may result in competitive constraints [76, 77] on the twist-2 operators with covariant derivatives compared to the ISR and FSR processes considered from the ILC.
-
We thank Sukanta Dutta for discussions and his initial participation in this work. HB thanks Mihoko Nojiri and Mamta Dahiya for suggestions. HB acknowledges the CSIR-JRF fellowship and support from CSIR grant 03(1340)/ 15/ EMR-II.
-
Annihilation cross-sections for the operators given in Eqs. (4) - (11) are given respectively as:
$\tag{A1} \sigma_{S}^{\rm{ann}} \left\vert \vec v\right\vert \left(\chi^0\,\bar{\chi^0}\to l^+l^-\right) \!=\! \frac{1}{8\pi} \frac{{\alpha^{\chi^0}_S}^2}{\Lambda_{\rm{eff}}^8}\, m^4_{\chi^0}m_l^2\left[ 1- \frac{m_l^2}{m_{\chi^0}^2} \right]^{3/2} \left\vert \vec v\right\vert^2 , $

$ \tag{A2} \begin{aligned}[b] \sigma_{T_1}^{\rm{ann}} \left\vert \vec v\right\vert \left(\chi^0\,\bar{\chi^0}\!\to\! l^+l^-\right) \!=& \frac{1}{2 \pi} \frac{{\alpha^{\chi^0}_{T_1}}^2}{\Lambda_{\rm{eff}}^8}m^6_{\chi^0}\sqrt{1-\frac{m_l^2}{m_{\chi^0}^2} } \\ &\times\left[2\!+\!\frac{m_l^2}{m_{\chi^0}^2}\!+\!\left( \frac{7}{6}\!-\!\frac{11}{16} \frac{m_l^2}{m_{\chi^0}^2}\right.\right.\!\!\!\!\!\!\!\\ &\left.\left.-\frac{65}{48}\, \frac{m_l^4}{m_{\chi^0}^4} \right) \left\vert \vec v\right\vert^2 \right], \end{aligned} $

$ \sigma_{AV}^{\rm{ann}} \left\vert \vec v\right\vert \left(\chi^0\,\bar{\chi^0}\to l^+l^-\right) = \frac{1}{2 \pi }\ \frac{{\alpha^{\chi^0}_{\rm AV}}^2}{\Lambda_{\rm{eff}}^4}\ m^2_l\ \sqrt{1-\frac{m_l^2}{m_{\chi^0}^2} } \left[1+ \left( \frac{1}{3}\frac{m_{\chi^0}^2}{m_l^2} -\frac{5}{6}-\frac{7}{6}\frac{m_l^2}{m_{\chi^0}^2}\right)\ \left\vert \vec v\right\vert^2 \right], \tag{A3} $

$\sigma_{S}^{\rm{ann}} \left\vert \vec v\right\vert \left(\phi^0\,{\phi^0}\to l^+l^-\right) = \frac{1}{4 \pi}\ \frac{{\alpha^{\phi^0}_S}^2}{\Lambda_{\rm{eff}}^8}\, \, m^4_{\phi^0}\ m_l^2 \sqrt{1-\frac{m_l^2}{m_{\phi^0}^2} } \left[ 1- \frac{m_l^2}{m_{\phi^0}^2} + \left( -\frac{3}{2}+ \frac{15}{4} \frac{m_l^2}{m_{\phi^0}^2} \right)\ \left\vert \vec v\right\vert^2 \right],\tag{A4} $

$ \sigma_{T_2}^{\rm{ann}} \left\vert \vec v\right\vert \left(\phi^0\,{\phi^0}\to l^+l^-\right) = \frac{1}{4 \pi }\ \frac{{\alpha^{\phi^0}_{T_2}}^2}{\Lambda_{\rm{eff}}^8}\, \, m^6_{\phi^0}\ \sqrt{1-\frac{m_l^2}{m_{\phi^0}^2}} \times \left[ \frac{m_l^2}{m_{\phi^0}^2} - \frac{m_l^4}{m_{\phi^0}^4} + \left(\frac{5}{12} \frac{m_l^2}{m^2_{\phi^0}}- \frac{13}{24}\frac{m_l^4}{m^4_{\phi^0}} \right) \ \left\vert \vec v\right\vert^2 \right], \tag{A5} $

$ \sigma_{S}^{\rm{ann}} \left\vert \vec v\right\vert \left(V^0\,{V^0}\to l^+l^-\right) = \frac{1}{12\pi}\ \frac{{\alpha^{V^0}_S}^2}{\Lambda_{\rm{eff}}^8}\, \, m^4_{V^0}\ m_l^2\ \sqrt{1-\frac{m_l^2}{m_{V^0}^2}} \times \left[ 1- \frac{m_l^2}{m_{V^0}^2} + \left( \frac{1}{2} + \frac{7}{4} \frac{m_l^2}{m_{V^0}^2} \right) \ \left\vert \vec v\right\vert^2 \right], \tag{A6} $

$ \sigma_{T_2}^{\rm{ann}} \left\vert \vec v\right\vert \left(V^0\,{V^0}\to l^+l^-\right) = \frac{1}{12\ \pi }\ \frac{{\alpha^{V^0}_{T_2}}^2}{\Lambda_{\rm{eff}}^8}\, \, m^6_{V^0}\ \sqrt{1-\frac{m_l^2}{m_{V^0}^2}} \times \left[ \frac{m_l^2}{m_{V^0}^2} - \frac{m_l^4}{m_{V^0}^4} + \left(\frac{3}{4} \frac{m_l^2}{m^2_{V^0}}- \frac{7}{8} \frac{m_l^4}{m^4_{V^0}} \right) \ \left\vert \vec v\right\vert^2 \right], \tag{A7} $

$ \sigma_{\rm AV}^{\rm{ann}} \left\vert \vec v\right\vert \left(V^0\,{V^0}\to l^+l^-\right) = \frac{1}{54 \pi}\ \frac{{\alpha^{V^0}_{AV}}^2}{\Lambda_{\rm{eff}}^4}\, \, m^2_{V^0}\ \sqrt{1-\frac{m_l^2}{m_{V^0}^2}} \left[ 4- 7\frac{m_l^2}{m_{V^0}^2} \right] \ \left\vert \vec v\right\vert^2 .\tag{A8} $

Effective field theory approach to lepto-philic self-conjugate dark matter
- Received Date: 2020-09-01
- Available Online: 2021-02-15
Abstract: We study self-conjugate dark matter (DM) particles interacting primarily with Standard Model (SM) leptons in an effective field theoretical framework. We consider SM gauge-invariant effective contact interactions between Majorana fermion, real scalar and real vector DM with leptons by evaluating the Wilson coefficients appropriate for interaction terms up to dimension 8, and obtain constraints on the parameters of the theory from the observed relic density, indirect detection observations and from the DM-electron scattering cross-sections in direct detection experiments. Low energy LEP data has been used to study sensitivity in the pair production of low mass (






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: