New observable for measuring the CP property of top-Higgs interaction

In the standard model (SM) of particle physics, the Higgs boson is a CP-even scalar boson with $J^{PC} = 0^{++}$. Any deviation from this prediction is clear evidence of new physics (NP) beyond the SM. Therefore, measuring the CP nature of the Higgs boson is a hot topic at the Large Hadron Collider (LHC) [1-4]. The interaction between the top quark and Higgs boson has recently been verified in the $t\bar{t}H$ channel [5, 6], and the next target is to measure the CP property of the $Ht\bar{t}$ interaction in the $t\bar{t}H$ channel [7, 8]. The effective Lagrangian of the $Ht\bar{t}$ interaction can be parameterized as

where $\alpha$ denotes the CP-phase angle. Many observables and methods have been proposed in the literature [9-21], and most of them require the complete reconstruction of the kinematics of both the top quark and the antitop quark, which is very challenging. In this work, we propose a novel observable that requires reconstruction of only the top quark.

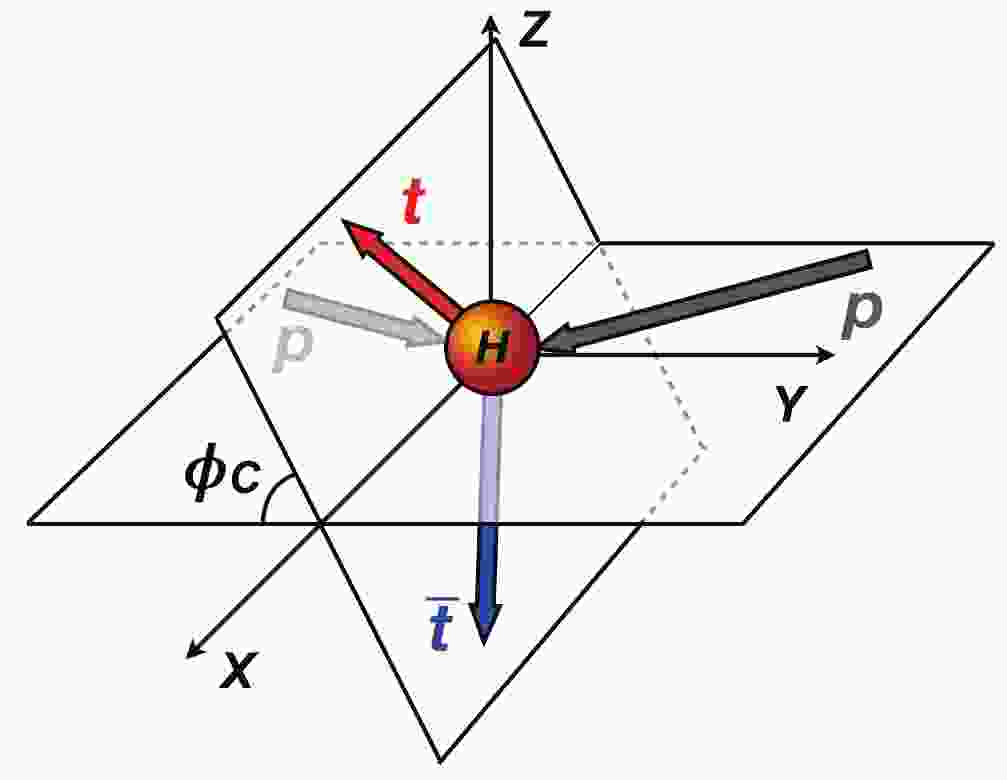
The observable is a dihedral angle ($\phi_C$) between the plane spanned by the incoming protons and the plane spanned by the $t\bar t$ pair in the rest frame of the Higgs boson, as depicted in Fig. 1. The head-on collision, $pp\to t\bar{t}H$, in the laboratory frame can be viewed approximately as a non-head-on “$2\to 2$” scattering in the rest frame of the Higgs boson, i.e., the two colliding protons produce two moving top quarks and one Higgs boson at rest. In such a picture, the non-zero 3-momenta of the incoming parton pair is equal to that of the top quark pair in the final state, while the Higgs boson merely carries away a rest energy.

Figure 1.  (color online) Dihedral angle $\phi_C$ between the plane of incoming protons and the plane of the $t\bar{t}$ pair in the rest frame of the Higgs boson.

The normalized 3-momenta of the protons, top quark, and antitop quark in the Higgs rest frame are denoted as ${{n}}_{p_1},{{n}}_{p_2},{{n}}_{t}$, and ${{n}}_{\bar t}$, respectively; then, the cosine of the dihedral angle is

Without loss of generality, we choose the $XY$-plane as the plane of the incoming protons and the positive X-axis along the direction of the total 3-momenta of the incoming protons. The Z-axis is chosen such that $\vec{p}_z^{\; t}>0$. As the two protons are identical, it is meaningless to distinguish between $\phi_C$ and $\pi-\phi_C$; therefore, we restrict the range of $\cos\phi_C$ to $[0,1]$. Figure 2(a) displays the normalized $\phi_C$ distributions at the 14 TeV LHC for four benchmark CP phase angles, $\alpha$, i.e., $\alpha = 0$ (CP-even), $\pi/4$, $\pi/3$, and $\pi/2$ (CP-odd). Note that the possibility of the Higgs boson being a purely CP-odd scalar fades away when various Higgs boson production channels are considered [22-26]. The simulation is performed using MadGraph5 [27] with the CT14llo parton distribution function (PDF) [28]. While the CP-odd Higgs-top interaction exhibits a peak in the small $\phi_C$ region, the CP-even coupling has a flat distribution. The difference can be used to measure phase angle $\alpha$.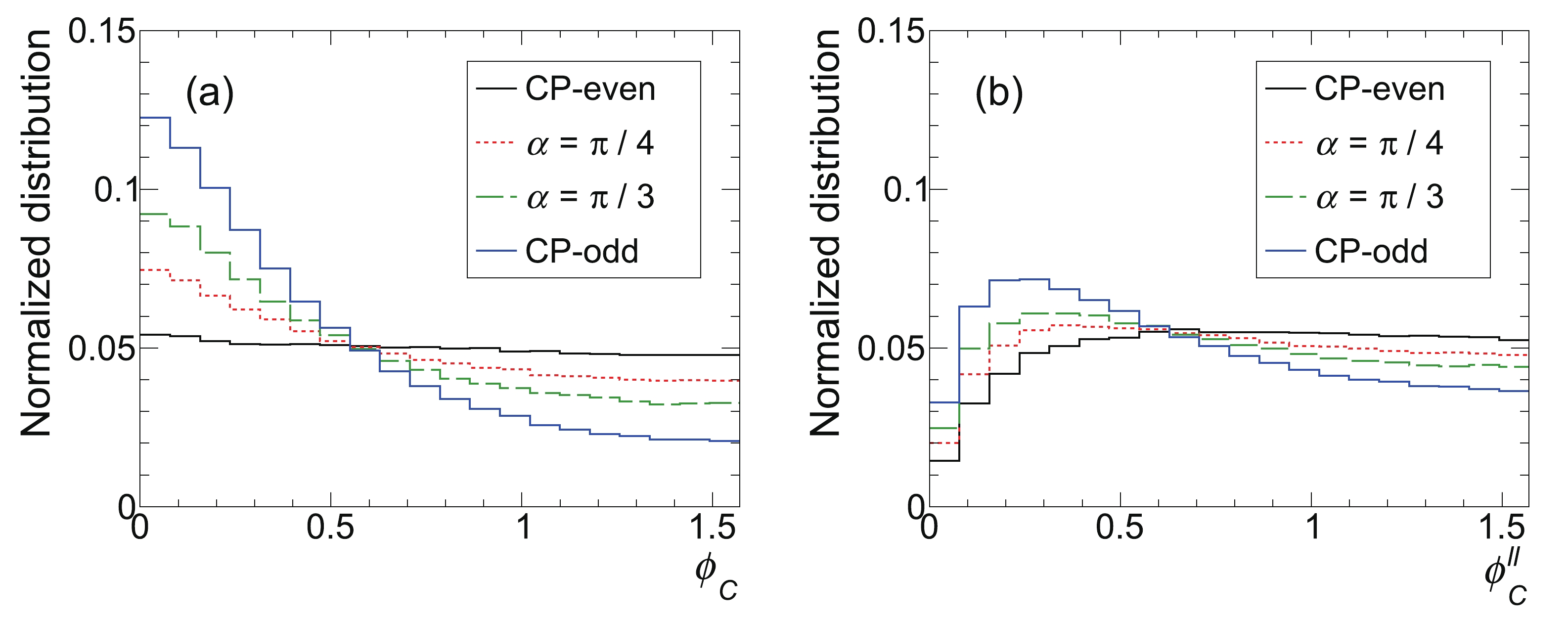

Figure 2.  (color online) Normalized distributions of $\phi_C$ (a) and $\phi_C^{\ell\ell}$ (b) for various CP phase angles: $\alpha=0$ (CP-even), $\pi/4$, $\pi/3$, and $\pi/2$ (CP-odd).

To suppress the SM background, the dileptonic decay mode of $t\bar t$ in the final state is often used. Unfortunately, reconstruction of the (anti) top quark kinematics is challenging in this case. Because the charged lepton from the (anti) top quark decay is maximally correlated with the spin of the (anti) top quark [29-33], we define the dihedral angle between the plane of two charged leptons and the plane of incoming protons as follows:

Figure 2(b) displays the $\phi_C^{\ell\ell}$ distributions for the four CP phases. The $\phi_C^{\ell\ell}$ distribution is distorted in the small angle region but can still be used to discriminate the CP properties of the $Ht\bar{t}$ interaction.

The $\alpha$-dependence of the $t\bar{t}H$ production cross section at the leading order (LO) at the 14 TeV LHC can be parameterized as

We perform a fast collider simulation at the parton level to demonstrate the potential of the dihedral angles, $\phi_C$ and $\phi_C^{\ell\ell}$, in the measurement of the CP phase of the $Ht\bar{t}$ interaction. Because the dihedral angles are defined in the rest frame of the Higgs boson, it is important to reconstruct the full kinematics of the Higgs boson. Hence, we focus on the $H\to b\bar b$ and $H\to \gamma\gamma$ decay modes of the Higgs boson. Furthermore, we only consider the dominant SM backgrounds. Our cut-based parton-level analysis demonstrates that the dihedral angle distributions are acceptable for measuring the CP phase $\alpha$, such that it can be used to expedite the BDT method.

We generate the signal and background events at the LO using MadGraph5 [27] with the CT14llo PDF [28]. The $t\bar tH$ production rate is rescaled such that the total cross section for the CP-even Higgs case is the NLO cross section, which includes both QCD and EW corrections [34]. To mimic the detector effects, we introduce the Gaussian smearing effects in the transverse momentum ($p_{\rm T}$) of charged leptons, jets, and photons as follows:

The b-tagging efficiency is chosen as 80%, whereas the rate of a charm-jet faking a b-jet is chosen as 10%, and the fake-rate of a light-jet is 1%.

In this channel, to retain more signal events, we require the semileptonic decay mode of the $t\bar t$ in the final state, i.e., $t\bar{t}\to b\bar{b}jj\ell^\pm\nu$. The event topology of the signal events consists of one isolated charged lepton ($e^\pm$ or $\mu^\pm$), two b-tagged jets, two photons arising from the Higgs boson decay, two non-b-tagged jets, and large missing transverse energy from the invisible neutrino. The dominant SM background is from the channel of $pp\to t\bar t\gamma\gamma$, whereas the other backgrounds, e.g., $pp\to VV jj \gamma\gamma$, are sub-dominant.

We impose a set of pre-selection cuts as follows:

where $\Delta R_{ik}$ is the angular distance between objects i and k and is defined as

and $m_H$ denotes the mass of the Higgs boson, which is chosen to be $m_H = 125\; {\rm{GeV}}$ throughout this work. Assuming that the $j\to \gamma$ fake-rate is $10^{-5}$, we find that the cross sections of the background processes of $t\bar t\gamma j$, $t\bar t jj$, and $VVjj\gamma\gamma$ are approximately $10^{-4}\; {{\rm{fb}}}$ after the pre-selection cuts and can be ignored in our analysis.

It is straightforward to reconstruct the kinematics of the Higgs boson from the two energetic photons. Furthermore, we demand three cuts, based on the property of the top quark decays, as follows:

to suppress the backgrounds. The likelihood fitting method is used to pick up the correct combinations of those jets from the W-boson decay and the top quark decay. We fit the invariant mass distributions of the $(b\ell)$, $(\ell\nu)$, $(b\ell\nu)$, $(jj)$, and $(bjj)$ systems using the likelihood functions as follows:

where parameter m is in GeV. Minimizing the following logarithm of the likelihood function (LL)

with the Z-direction component of neutrino $p_z^\nu$ as a variable, we determine which b-jet is from the leptonic decaying (anti-)top quark and simultaneously solve $p_z^\nu$. The cross sections of the signal and dominant SM background after the pre-selection cuts and reconstruction are shown in Table 1. The number of signal events after event reconstruction is small because of the small branching ratio, ${\rm{Br}}(H\to \gamma\gamma)$.

	$\alpha=0$	$\alpha=\pi/2$	$t\bar t\gamma\gamma$
after pre-selection cuts	$0.0345$	$0.0140$	$0.0056$
after reconstruction	$0.0189$	$0.0074$	$0.0029$

Table 1.  Cross section (in the unit of fb) of the signal process ($\alpha=0$ and $\alpha=\pi/2$) and major background process $t\bar{t}\gamma\gamma$ in the semileptonic mode of the top quark pair.

Once the full kinematics of the top quark and the Higgs boson are reconstructed, we calculate the $\phi_C$ angle, defined in Eq. (2). The normalized $\phi_C$ distribution is plotted in Fig. 3. The difference between the CP-even and CP-odd Higgs bosons still remains after event reconstruction.

Figure 3.  (color online) Normalized $\phi_C$ distribution in the $pp\to t\bar tH\to \gamma\gamma\ell^\pm \bar bbjj+ {\not E}_{\rm{T}}$ channel after event reconstruction.

To suppress the SM background, we consider the dileptonic decaying mode of $t\bar t$, i.e., $t\bar{t}\to b\bar{b}\ell^+\ell^-\nu\bar{\nu}$. The dominant SM background is $pp\to t\bar tb\bar b$. The event topology of the signal contains two opposite-sign charged leptons ($e^\pm$ or $\mu^\pm$), four b-tagged jets, and large missing transverse momentum. To select the signal event, we impose a set of pre-selection cuts as follows:

When the two charged leptons are of the same flavor, e.g., $e^+e^-$ or $\mu^+\mu^-$, we require that they not be close to the Z pole, i.e.,

to suppress the $Z+{\rm{jets}}$ background. In addition, we require $m_{\mu^+\mu^-}>20$ GeV to suppress the background from heavy flavor hadron decay.

When the two b-jets are from the Higgs boson decay, their invariant mass must peak near $m_h$; therefore, we require at least one pair of b-jets satisfying the following invariant mass cut:

The other two b-jets and two charged leptons are from the top quark decay. The invariant mass of the b-jet and the charged lepton, if they originate from the same top quark decay, is less than 140 GeV because of the spin correlation effect.

For event reconstruction, it is crucial to determine which two b-jets are from the Higgs boson decay, which is accomplished using the likelihood fitting method in our analysis. The likelihood function of the invariant mass of the $b\bar b$ pair from the Higgs boson decay is

after imposing all the cuts. Parameter m is again in GeV. The $b\ell^\pm$ distributions are used to decrease contamination from the b-jets from the top quark decay. We require that any pair of b-jets and the charged leptons must satisfy the following condition,

and then fit the invariant mass distributions of the $b\ell^\pm$ pair with the likelihood function, $L_{b\ell}$, given in Eq. (9). By minimizing the discriminator,

we identify the two b-jets from the Higgs boson decay. In addition, a cut of $D<0$ is imposed to optimize the signal-to-background ratio.

Table 2 shows the cross section of the signal ($\alpha = 0$ and $\alpha = \pi/2$) and the dominant SM backgrounds after the pre-selection cut and the event reconstruction. The rates of other backgrounds, e.g., $W^+W^-+4j$, $W^+W^-+1b3j$, $W^+W^-+2b2j$, and $W^+W^-+3b1j$, are smaller than $10^{-5}\; {\rm{fb}}$ after the pre-selection cuts and can be ignored in our analysis.

	$\alpha=0$	$\alpha=\pi/2$	$t\bar tb\bar b$	$t\bar tbj$	$t\bar tjj$	$WW4b$
pre-selection	0.601	0.295	1.261	0.0215	0.0460	0.0007
reconstruction	0.558	0.273	0.945	0.0160	0.0343	0.0005

Table 2.  Cross section (in the unit of fb) of the signal and background processes, where j denotes the light-flavor jet from $g,\;u,\;d,\;s,\;c$.

After identifying the two b-jets from the Higgs boson decay, the other two b-jets are treated as from the top quark decays. Because of the two invisible neutrinos in the final state, it is difficult to reconstruct the top quark and antitop quark. We consider the $\phi_C^{\ell\ell}$ defined in Eq. (3) and plot the normalized distributions in Fig. 4. The CP-even Higgs boson (red) and the SM background (black) have nearly the same distribution. Conversely, the CP-odd Higgs boson (black curve) exhibits a distinct distribution.

Figure 4.  (color online) Normalized $\phi_C^{\ell\ell}$ distribution in the $pp\to t\bar tH \to 4b+\ell^+\ell^-+{\not\!\! E_{\rm{T}}}$ channel.

A purely CP-odd scalar is severely limited by the global fitting of the single Higgs boson production, the $t\bar{t}H$ production, and the $t\bar{t}t\bar{t}$ production [23, 25, 26]. It is still important to probe the CP phase directly from a single scattering process. Equipped with the $\phi_C$ and $\phi_C^{\ell\ell}$ distributions for both the CP-even and the CP-odd Higgs bosons, we are ready to discuss how well the CP-odd Higgs boson can be distinguished from the CP-even one. In our study, we divide the $\phi_C$ and $\phi_C^{\ell\ell}$ distributions into 10 bins and use the binned likelihood function, which is defined as follows:

where $N_{\rm{bin}} = 10$, $\mu$ is the strength of the signal, $b_i$ and $n_i$ are the number of the background and observed event in the ith bin, respectively, and $s_i(\alpha)$ is the number of the signal event in the ith bin for CP phase $\alpha$.

The recent measurement of the $t\bar{t}H$ production shows that the signal event number is inconsistent with the SM prediction [6, 35]. Thus, we rescale $\mu$ for all the $\alpha$ to match the signal strength of the SM value. The logarithm of the likelihood function ratio is defined as

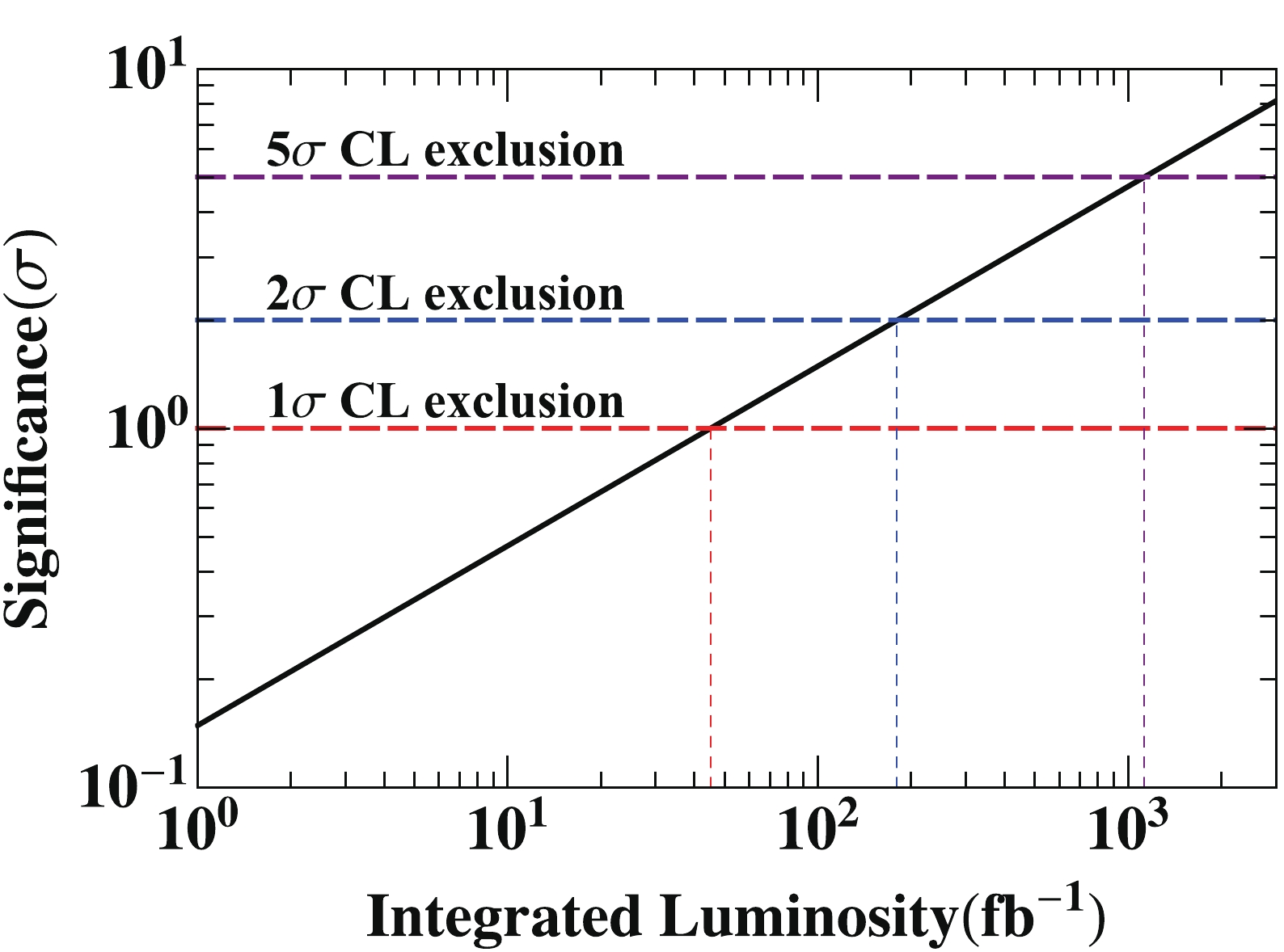
where $\hat\mu_k\; (k = 0,1)$ is determined by minimizing $-2\log L(\hat\mu_k,\alpha_k)$. Setting $n_i = \hat\mu_0s(\alpha_0)_i+b_i$, hypothesis 1 is excluded versus hypothesis 0 with $\sqrt{-2\log\lambda(\alpha_1|\alpha_0)}\sigma$ confidence level (CL). Using this relation, we combine the diphoton and the $b\bar b$ channels to obtain the statistical significance of distinguishing between a CP-odd Higgs boson and a CP-even Higgs boson. Figure 5 displays the exclusion significance as a function of the integrated luminosity at the 14 TeV LHC. It shows that, if the Higgs boson is a pure CP-even scalar, to exclude the pure CP-odd hypothesis at a 95% CL, an integrated luminosity of $\sim 180\; {\rm{fb}}^{-1}$ is needed.

Figure 5.  (color online) Statistical significance of discriminating the CP-odd Higgs boson from the CP-even Higgs boson as a function of the integrated luminosity at the 14 TeV LHC.

Now, we discuss how well CP-phase angle $\alpha$ can be measured from the $\phi_C$ and $\phi_C^{\ell\ell}$ distributions. In general, the $\phi_C$ and $\phi_C^{\ell\ell}$ distributions of the signal channel can be written as

Note that the A and C terms correspond to the CP-even and CP-odd contributions, respectively, and the B term is zero for the $t\bar{t}H$ production. After dividing the $\phi_C$ and $\phi_C^{\ell\ell}$ distributions into 10 bins, we read out the CP-even ($\alpha = 0$) and the CP-odd ($\alpha = \pi/2$) contributions in each bin, defined as $s_i(0)$ and $s_i(\pi/2)$, respectively. Therefore, the distribution of the signal event is given by

The $t\bar{t}H$ production has been confirmed recently by both the ATLAS and the CMS collaborations, assuming a purely CP-even Higgs boson [6, 35]. The current data of the signal strength, $\mu = 1.18^{+0.30}_{-0.27}$ [35], are consistent with the SM theory, although a large experimental uncertainty exists. To explore the potential of measuring angle $\alpha$ in future experiments, we rescale the signal strength, $\mu$, of input angle $\alpha$ to be the same as the SM theoretical prediction.

We vary the signal strength, $\mu$, for each input $\alpha$ to minimize the logarithm of the likelihood function ratio (the signal strength that minimizes the $-2\log L(\mu,\alpha)$ is denoted as $\hat\mu$ here), defined as

to obtain the projected sensitivity of the $\alpha$ measurement. The following condition,

yields the $1\sigma$ confidence interval of the measured $\alpha$ angle for a given input $\alpha_0$. As shown in Eq. (17), the signal rate depends on $\sin^2\alpha$ rather than directly on $\alpha$; therefore, we first obtain the sensitivity of a future LHC experiment on $\sin^2\alpha$. Figure 6(a) displays the projected experimental measurement of $\sin^2\alpha_{\rm{out}}$ versus theoretical input $\sin^2\alpha_{\rm{in}}$ at the 14 TeV LHC with integrated luminosities of $300\; {{\rm{fb}}}^{-1}$ (green) and $3000\; {{\rm{fb}}}^{-1}$ (yellow), respectively. The uncertainty of the $\sin^2\alpha$ measurement is large in the region where $\alpha\sim 0$ and is reduced in the region where $\alpha \sim \pi/2$. Increasing the integrated luminosity significantly reduces the uncertainties; see the yellow band. Figure 6(b) shows the correlation between $\alpha_{\rm{out}}$ and $\alpha_{\rm{in}}$. Because of the small production rate, it is still very challenging to obtain precise information concerning CP-phase $\alpha$ at the high-luminosity LHC.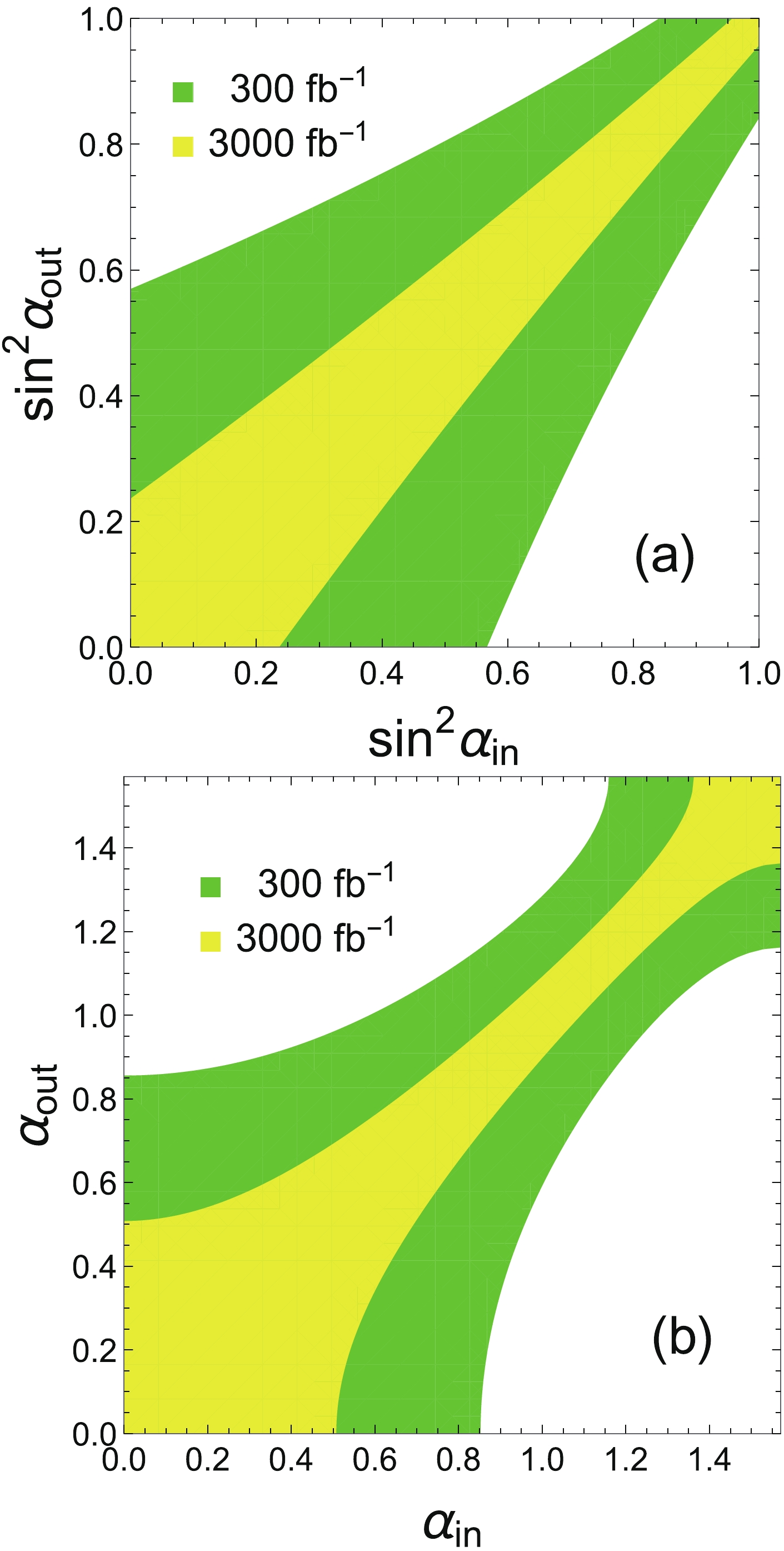

Figure 6.  (color online) Projected accuracy of the $\alpha$ measurement versus the input value at the LHC with integrated luminosities of $300~{\rm{fb}}^{-1}$ (green) and $3000~{\rm{fb}}^{-1}$ (yellow), respectively.

The behavior of the contours can be qualitatively understood as follows. From the definition of the likelihood ratio given in Eq. (16), it is easy to show that

where $n_i = \hat\mu_0s_i(\alpha_0)+b_i$. We require that the number of the signal event be the same as that in the SM case to respect the current data. As a result, this yields

Note that the above condition is valid only after summing over all the bins. Using a rough approximation of each bin,

we expand the logarithm of the likelihood ratio function to the second order and obtain

By definition, $\hat\mu_0 = 1$ when $\alpha_0 = 0$, which yields

Through simple algebra, one can show that

which explains the linear behavior of the contour in Fig. 6(a).

We proposed a novel observable $\phi_C$ for measuring the CP property of the top quark Yukawa coupling in $t\bar t H$ production. The observable $\phi_C$ is the dihedral angle between the plane of the incoming protons and the plane of the top quark pair in the rest frame of the Higgs boson. We carry out a fast simulation of the $t\bar{t}H$ production with two decay modes of the Higgs boson, $H\to b\bar{b}$ and $H\to \gamma\gamma$, and the SM background process of $t\bar{t}\gamma\gamma$. The CP-even $Ht\bar{t}$ coupling and the SM background process of $t\bar{t}\gamma\gamma$ have a similar shape in the $\phi_C$ distribution before and after the kinematic cuts. Conversely, the CP-odd coupling exhibits different $\phi_C$ distributions, such that it serves well in searching for the CP-odd coupling. At the 14 TeV LHC, with an integrated luminosity of $\sim 180\; \rm{fb}^{-1}$, one can distinguish between the CP-odd coupling and the CP-even hypothesis at the 95% confidence level.