-
Following the Higgs discovery at the LHC [1-3], substantial attention has been focused on precision testing of the Higgs boson properties. Thus far, the measurements of its couplings with fermions and gauge bosons indicate an SM interpretation; however, given that only several of these have been probed [4], there remains room for new physics. In particular, regarding the Higgs-fermion couplings, the LHC has directly or indirectly measured only the coupling with the top, bottom, and tau pairs, all of which appear to fit the SM predictions. That is, these couplings lie on a straight line as function of the fermion mass [5]. However, the precision level achieved to date allows for other possibilities; for example, it may be that each fermion type acquires its mass from its own "private" Higgs [6-8], in which case the corresponding Higgs-fermion couplings would lie on different lines. An extension of the Higgs sector not only can predict modifications of the SM couplings, but could also include new types of interactions, such as FCNC Higgs fermion couplings, as well as a rich spectrum of heavier neutral and charged Higgs particles.
In particular, multi-doublet Higgs models are a straightforward extension of the SM, in which the total vacuum expectation value (VEV) is given by
$ v^{2} = v_{1}^{2}+ v_{2}^{2}+\cdots +v_{n}^{2} = (246\:\; {\rm{GeV}})^{2} $ , and$ v_{i} = \langle 0 \lvert H^0_{i} \lvert 0\rangle $ is the VEV of the neutral component of each Higgs doublet$ H_i $ ($ i = 1,2,\cdots,n $ ) [9]. In this case, there are deviations from the SM predictions for Higgs couplings$ hWW $ and$ hZZ $ , with$ h = h_{1}^{0} $ being the SM-like Higgs boson; that is, the lightest neutral$ {\rm{CP}}- $ even Higgs within the scalar spectrum. Such models offer also the possibility of having flavor-changing neutral Higgs couplings, which have been studied in the past, including the case in which fermion hierarchy is reproduced through the FN mechanism [10, 11]. Within the most general version of the 2HDM, both Higgs doublets couple to all fermion types. In this case, the diagonalization of the full mass matrix does not imply that each Yukawa matrix is diagonalized with the same rotations; therefore, flavor-changing neutral currents (FCNCs) can appear at the tree level. Within this general model, the observed fermion masses and mixing angles must be reproduced, while the FCNC level must simultaneously satisfy current experimental bounds [12]. One possible means of achieving this is the assumption that the Yukawa matrices have a certain texture form; that is, with zeros in different elements, and in particular, it is known that the four-zero texture is consistent with data from flavor physics.Furthermore, supersymmetry (SUSY) has been studied extensively as a possibility to solve, or at least to ameliorate, the hierarchy problem [13]. The minimal SUSY model (MSSM) includes two Higgs doublets and its structure is such that each doublet couples to only one fermion type, and thus, FCNCs are not allowed in the model. The next multi-doublet SUSY Higgs model must include four Higgs doublets, where each doublet is denoted as
$ H_i (i = 1,2,3,4) $ [14, 15]; in this case, more possibilities for flavor physics exist [16, 17]. This type of model may also be motivated, for instance, by considerations from$ LR $ symmetry or unification [18]. The phenomenology of this model has been studied recently in Refs. [19-21], and depends on a large number of free-parameters.In this study, we consider a four-Higgs doublet SUSY model with a more restricted parameter space, which is achieved by considering a version of the model of the "private type." This model is defined by requiring that one doublet gives masses to each fermion type, namely,
$ H_{1}\equiv H_{u_1} $ gives masses to up-type quarks,$ H_{2}\equiv H_d $ gives masses to down-type quarks, and$ H_{3}\equiv H_l $ gives masses to charged leptons. Thus, we remain with an extra Higgs doublet ($ H_4 $ ); however, this doublet should have the same hypercharge as$ H_{u_1} $ in order for the anomalies to be canceled. Therefore, it should only couple to up-type quarks, and we refer to this doublet as$ H_4\equiv H_{u_2} $ . Thus, in this "private" SUSY Higgs model, we can only have FCNCs in the up-type quarks, which would predict that the decays$ t\rightarrow ch $ and$ H^0_i\rightarrow t \overline{c} $ occur at a certain level, where$ h = H^0_1 $ and$ H^0_i $ are part of the Higgs spectrum.The goal of this study is to construct this private SUSY Higgs model, and to derive the interactions of the Higgs boson with gauge bosons and fermions. Moreover, we aim to identify regions of the parameter space that are consistent with high-energy data on the Higgs couplings, as derived from the LHC. As FCNCs only occur in the up-type quark sector in our model, the constraints from low-energy flavor physics would need to be considered; however, these are rather mild. In fact, the LHC data on Higgs couplings to gauge bosons and fermions (including FCNC top decay
$ t\rightarrow ch $ ) provide stronger constraints [22]. Thus, these constraints are used to evaluate the FCNC decay of the next heavier Higgs boson$ H\rightarrow t \bar{c} $ .The remainder of this paper is organized as follows. In Section II, we review the model construction, including the Higgs potential (for this, we closely follow Ref. [19]), and then, we perform the minimization of the Higgs potential (V) and derive the scalar mass matrices; we also present an approximate diagonalization of the
$ 4\times4 $ matrix, including the leading radiative corrections to the Higgs mass originating from the top-stop system, using the effective potential technique. Furthermore, we discuss the Yukawa Lagrangian, assuming a four-texture Yukawa matrix, and derive the interactions of the Higgs bosons with the fermions and gauge boson. Section III presents the analysis of Higgs couplings and the constraints obtained from the LHC. Section IV outlines our study of FCNC decay for the lightest Higgs boson$ t\rightarrow ch $ , as well as the FCNC decay of the next heavier neutral Higgs boson$ H_2 \rightarrow t \bar{c} $ , including a signal-versus-background study to determine the detectability of the signals at the LHC. Finally, our conclusions are presented in Section V. -
The minimal supersymmetric extension of the standard model (MSSM) includes two Higgs doublets, and it can be extended by enlarging its Higgs content. In particular, we are interested in studying a supersymmetric version of the four Higgs doublet model (SS-4HDM) [19]. The gauge symmetry is the same as in the SM; thus, the model includes the usual MSSM gauge bosons and gauginos. Similarly, the model includes the same MSSM particle content for quarks, leptons, and their superpartners (squarks and sleptons). Thus, the fermion-sfermion interactions will be almost the same as in the MSSM, and the possible modifications arising from a modified Yukawa sector will be neglected in a consistent manner, as explained in the following.
-
The starting point when studying the Higgs and Yukawa sectors in a supersymmetric model is to describe the corresponding superpotential. This model includes four Higgs chiral superfields, each of which includes both the scalar and fermion components, namely the Higgses and Higgsinos. Owing to the anomaly cancellation, two of these,
$ \hat{H}_{u1}, \hat{H}_{u2} $ , should have a weak hypercharge$ Y = -1 $ , whereas the other two,$ \hat{H}_{d} $ and$ \hat{H}_l $ must have$ Y = +1 $ . The general superpotential includes the usual MSSM Yukawa term ($ W_{\rm Yuk} $ ) and the μ-terms, which now take the following form:$ W = W_{\rm Yuk} + \sum\limits_i [ \mu_ {i1} \hat{H}_{ui} \cdot \hat{H}_{d} + \mu_ {i2} \hat{H}_{ui} \cdot \hat{H}_{l}]. $

(1) Thereafter, the rules of supersymmetry can be followed to derive the scalar Higgs potential. That is, the corresponding F-terms are derived from the superpotential, following which the D-terms are added. Finally, the allowed SUSY soft-breaking terms need to be included.
In turn, the form of the Yukawa superpotential (
$ W_{\rm Yuk} $ ) is dependent on whether or not one accepts a certain level of FCNCs in the model, which should come with a suppression mechanism to satisfy the current FCNC bounds. However, as we are interested in the class of models in which the masses of the leptons and up- and down-quarks originate from their private Higgs doublets, the possibilities are quite limited. Furthermore, given the assignment of hypercharges, the model is quite constrained. That is, if the masses of the down-quarks and leptons originate from two of the Higgs doublets, namely$ \hat{H}_{d} $ and$ \hat{H}_l $ , respectively, the only remaining possibility is to have FCNCs in the up-quark sector, because the remaining Higgs superfields$ \hat{H}_{u1}, \hat{H}_{u2} $ are those that can couple with up-type quarks (and up-type squarks). Thus, the Yukawa superpotential of our model takes the form:$ \begin{aligned}[b] W_{\rm Yuk} =& [ \hat{Q} Y_{u1} \hat{H}_{u1} \hat{U} + \hat{Q} Y_{u2} \hat{H}_{u2} \hat{U}] \\& + \hat{Q} Y_ {d} \hat{H}_d \hat{D} + \hat{L} Y_l \hat{H}_{l} \hat{E}. \end{aligned}$

(2) There are many possibilities for motivating the private Higgs assignments; for example, one can use a set of discrete symmetries. Thus, the mass matrix for the up-type quarks will receive contributions from two Yukawa matrices, which will induce FCNC-Higgs couplings for up-type quarks①. These assignments can be obtained in various manners, such as incorporating a set of discrete symmetries (
$ k_u, k_d, k_l $ ) with parities, as indicated in Table 1.$ H_u,\bar{u} $ 

$ H_d,\bar{d} $ 

$ H_l,\bar{l} $ 

Q L $ k_u $ 

$ - $ 

+ + + + $ k_d $ 

+ $ - $ 

+ + + $ k_l $ 

$ - $ 

+ $ - $ 

+ + Table 1. Discrete symmetries for our SUSY 4HDM.
The power of these discrete symmetries is such that it permits the classification of different types of multi-Higgs models. For example, when considering a two-Higgs doublet model (2HDM), one can discuss types I, II, or III; in this model, both doublets
$ H_u $ ,$ H_d $ have the same quantum numbers, so in principle, both could couple to all fermion types, and type III would be mandatory. However, owing to the selection of appropriate discrete symmetries, one can build a model in which only one Higgs doublet couples to each fermion type (2HDM of type II) or only one doublet performs the task of generating all fermion masses (as in the 2HDM type I). Similarly, we can use the discrete symmetries of Table 1 to define our "SUSY private Higgs model," which only allows FCNCs in the up sector, and not for the down type quarks and leptons. Other discrete symmetries could be used to forbid FCNCs completely, but having a fourth Higgs doublet with the correct quantum numbers makes it more natural to explore possible FCNCs in the up type quarks.The discrete symmetries may cause some of the μ-terms to vanish. Furthermore, these discrete symmetries may be imposed on the soft-breaking terms. Thus, the question arises as to whether the resulting Higgs spectrum is viable, namely one can have a light SM-like Higgs boson with
$ m_h = 125 $ GeV, accompanied with heavier neutral and charged Higgs bosons that are sufficiently heavy to satisfy the current bounds from the LHC on extra Higgs particles. This is demonstrated in the following section, after discussing the minimization of the Higgs potential and Higgs mass matrices. -
In this section, we discuss the general Higgs potential for the supersymmetric model with four Higgs doublets, following the notation of Ref. [19]. After discussing the minimization conditions, the general form of the Higgs mass matrices is derived.
The Higgs doublets are the scalar components of the Higgs chiral multiplets, and are written as follows:
$ \begin{aligned}[b]& {H_{ui}} = \left( {\begin{array}{*{20}{c}} {H_{ui}^ + }\\ {H_{ui}^0} \end{array}} \right)(i = 1,2),\\&{H_d} = \left( {\begin{array}{*{20}{c}} {H_d^0}\\ {H_d^ - } \end{array}} \right),\\&{H_l} = \left( {\begin{array}{*{20}{c}} {H_l^0}\\ {H_l^ - } \end{array}} \right), \end{aligned}$

(3) where
$ H^0_k $ is given by$ H^0_k = \frac{1}{\sqrt{2}}(v_k+\eta_k+i\chi_k)\;\;\;\;{\rm{and}}\;\;\;\;(k = u_1,d,l,u_2). $

(4) As in the MSSM,
$ H_{ui} $ should have a hypercharge that is equal to −1, whereas it is +1 for$ H_{d,l} $ . The Higgs doublets with a hypercharge of +1 give mass to the down-type quarks sector$ (H_d) $ and charged leptons$ (H_l) $ .As demonstrated in [19, 20], the scalar potential of the Higgs fields takes the following form:
$ \begin{aligned}[b] V =& \sum\limits_{i = 1}^2\bigg((|\mu_{i1}|^2+|\mu_{i2}|^2+\tilde{m}_{ui}^2)(|H_{ui}^0|^2+|H_{ui}^+|^2)+(|\mu_{1i}|^2+|\mu_{2i}|^2+\tilde{m}_{di}^2)(|H_{di}^0|^2+|H_{di}^+|^2)\bigg)\\ &+ \bigg((\mu_{11}^*\mu_{21}+\mu_{12}^*\mu_{22})(H_{u1}^{0*}H_{u2}^{0}+H_{u1}^{+*}H_{u2}^{+})+(\mu_{11}^{*}\mu_{12}+\mu_{21}^{*}\mu_{22})(H_{d1}^{0*}H_{d2}^{0}+H_{d1}^{-*}H_{d2}^{-})+c.c\bigg)\\ &+\Bigg(\sum\limits_{i = 1}^{2}\sum\limits_{j = 1}^{2}b^2_{ij}(H_{ui}^{+}H_{dj}^{-}-H_{ui}^{0}H_{dj}^{0})+c.c.\Bigg)+\frac{g^2+g'^2}{8}\Bigg(\sum\limits_{i = 1}^{2}(|H_{ui}^{0}|^2+|H_{ui}^{+}|^2-|H_{di}^{0}|^2+|H_{di}^{-}|^2)\Bigg)^2\\ &+\frac{g^2}{2}\bigg(\sum\limits_{i = 1}^{2}|(H_{ui}^{+*}H_{ui}^{0}+H_{di}^{0*}H_{di}^{-})|^2-\sum\limits_{i = 1}^{2}\sum\limits_{j = 1}^{2}(|H_{ui}^{0}|^2-|H_{di}^{0}|^2)(|H_{uj}^{+}|^2-|H_{dj}^{-}|^2)\bigg), \end{aligned} $

(5) where
$ H_{d_2} = H_l $ . In general, the parameters$ \mu_{ij} $ ,$ \tilde{m}_{ui,di} $ , and$ b_{ij} $ can be complex, but for the sake of simplicity in this paper, we take them to be real parameters. The VEVs are parametrized in terms of the total SM VEV (v), and the angles$ \alpha,\;\beta $ and$ \omega $ , as follows:$ v_{1} = \frac{\sqrt{2}M_Z}{\sqrt{(g^2+g'^2)(1+\tan^2\omega)}}\cos\beta, $

(6) $ v_{4} = \frac{\sqrt{2}M_Z}{\sqrt{(g^2+g'^2)(1+\tan^2\omega)}}\tan\omega\sin\alpha, $

(7) $ v_d = \frac{\sqrt{2}M_Z}{\sqrt{(g^2+g'^2)(1+\tan^2\omega)}}\sin\beta, $

(8) $ v_l = \frac{\sqrt{2}M_Z}{\sqrt{(g^2+g'^2)(1+\tan^2\omega)}}\tan\omega\cos\alpha. $

(9) The minimization conditions
$ \dfrac{\partial V}{\partial H_{ui}^0} = 0 $ and$ \dfrac{\partial V}{\partial H_{di}^0} = 0 $ evaluated in the VEVs take the following form:$ \Delta_{u_1}+\left(\mu _{11} \mu _{21}+\mu _{12} \mu _{22}\right)c^{-1}_\beta s_\alpha t_\omega - b^2_{12}c^{-1}_\beta c_\alpha t_\omega- b^2_{11} t _\beta+\frac{1}{4}{{Mz}}^2\left(c_{2 \beta}c^2_\omega -c_ {2 \alpha}s ^2_\omega\right) = 0, $

(10) $ \Delta_d+\left(\mu _{11} \mu _{12}+\mu _{21} \mu _{22}\right)s^{-1}_\beta c_\alpha t_\omega-b^2_{21}s^{-1}_\beta s_\alpha t_\omega- b^2_{11}t^{-1}_\beta+\frac{1}{4}{{Mz}}^2 \left( c_{2 \alpha} s ^2_\omega -c_{2\beta}c ^2_\omega\right) = 0, $

(11) $ \Delta_l - b^2_{21}s_\beta t^{-1}_\omega s^{-1}_\alpha+ \left(\mu _{11} \mu _{21}+\mu _{12} \mu _{22}\right)c_\beta t^{-1}_\omega s^{-1}_\alpha-b^2_{22}t^{-1}_ \omega s^{-1}_\alpha c_\alpha+\frac{1}{4}{{Mz}}^2 s_\omega\left[c_{2\beta} c_\omega-c_{2\alpha} s_\omega\right] = 0, $

(12) $ \Delta_{u_2} - b^2_{12}c_\beta c^{-1}_\alpha t^{-1}_\omega-(\mu_{11}\mu_{12}+\mu_{21}\mu_{22})s_\beta c^{-1}_\alpha t^{-1}_\omega-t_\alpha t^{-1}_\omega b^2_{22}+\frac{1}{4}{{Mz}}^2\left[c_{2\alpha}s^2_\omega-c_{2\beta}c^2_\omega\right] = 0, $

(13) where
$ \Delta_{u1} = \mu_{11}^2+\mu_{12}^2+\tilde{m}_{u1}^2 $ ,$ \Delta_{d} = \mu_{11}^2+\mu_{21}^2+\tilde{m}_{d}^2 $ ,$ \Delta_{u2} = \mu_{21}^2+ \mu_{22}^2+\tilde{m}_{u2}^2 $ , and$ \Delta_{l} = \mu_{12}^2+\mu_{22}^2+\tilde{m}_{l}^2 $ . In this case, we have renamed$ \tilde{m}_{d2} = \tilde{m}_{l} $ . This will be used next in the construction of the Higgs mass matrices. -
We consider the CP-invariant case and focus on the neutral CP-even Higgs fields, which are obtained from the real parts of the neutral components. In the basis (
$ H_{u1}^0,H_{d1}^0, H_{l}^0, H_{u2}^0, $ ), the mass matrix can be expressed as follows:$ {{\cal{M}}^2} = \left( {\begin{array}{*{20}{c}} {m_{{u_1}{u_1}}^2}&{m_{{u_1}d}^2}&{m_{{u_1}l}^2}&{m_{{u_1}{u_2}}^2}\\ {m_{d{u_1}}^2}&{m_{dd}^2}&{m_{dl}^2}&{m_{{u_2}d}^2}\\ {m_{l{u_1}}^2}&{m_{ld}^2}&{m_{ll}^2}&{m_{{u_2}l}^2}\\ {m_{{u_2}{u_1}}^2}&{m_{{u_2}d}^2}&{m_{{u_2}l}^2}&{m_{{u_2}{u_2}}^2} \end{array}} \right), $

(14) where each element of the matrix (Eq. (14)) takes the following form:
$ m^2_{u_1u_1} = \frac{1}{2}\Delta_{u1}+\frac{1}{8}m_Z^2\left((2 \cos2\beta+1)\cos ^2\omega-\cos2\alpha\sin ^2\omega \right), $

(15) $ m^2_{u_1 d} = -\frac{1}{2} b^2_{11}-\frac{1}{2}m_Z^2\sin 2\beta \cos ^2\omega, $

(16) $ m^2_{u_1l} = \frac{1}{2}\left(\mu_{11} \mu _{21}+\mu _{12}\mu _{22}\right)+\frac{1}{2}m_Z^2\cos\beta\sin\alpha \sin 2\omega, $

(17) $ m^2_{dd} = \frac{1}{2}\Delta_d+\frac{1}{8}m_Z^2 \left((1-2 \cos2 \beta) \cos ^2\omega+\cos 2 \alpha \sin ^2\omega\right), $

(18) $ m^2_{dl} = -\frac{1}{2}b^2_{21}-\frac{1}{2} m_Z^2\sin\alpha\sin\beta\sin 2\omega, $

(19) $ m^2_{ll} = \frac{1}{2}\Delta_l+ \frac{1}{8}m_Z^2\left((1-2 \cos 2\alpha) \sin ^2\omega+\cos 2\beta\cos ^2\omega\right), $

(20) $ m_{u_2u_2}^2 = \frac{1}{2}\Delta_{u_2}+\frac{1}{8}m_Z^2\left((2\cos{2\alpha}+1)\sin^2\omega-\cos{2\beta} \cos^2\omega\right), $

(21) $ m_{u_2u_1}^2 = -\frac{1}{2}b^2_{12}-\frac{1}{2}m_Z^2\cos\alpha\cos\beta\sin 2\omega, $

(22) $ m_{u_2 d}^2 = \frac{1}{2}(\mu_{11}\mu_{12}+\mu_{21}\mu_{22})+\frac{1}{2}m_Z^2\cos\alpha\sin\beta\sin 2\omega, $

(23) $ m_{u_2 l}^2 = -\frac{1}{2}b^2_{22}-\frac{1}{2}m_Z^2\sin 2\alpha \sin^2\omega. $

(24) As the CP-even Higgs mass matrix is symmetric, we only need to provide the 10 independent components.
-
We assume that the
$ i4 $ ($ i = 1,2,3 $ ) entries of the mass matrix are small compared to the remaining entries; that is,$ {\cal{M}}^2\approx \left( {\begin{array}{*{20}{c}} {m_{{u_1}{u_1}}^2}&{m_{{u_1}d}^2}&{m_{{u_1}l}^2}&{{\epsilon_1}}\\ {m_{d{u_1}}^2}&{m_{dd}^2}&{m_{dl}^2}&{{\epsilon_2}}\\ {m_{l{u_1}}^2}&{m_{ld}^2}&{m_{ll}^2}&{{\epsilon_3}}\\ {{\epsilon_1}}&{{\epsilon_2}}&{{\epsilon_3}}&{m_{{u_2}{u_2}}^2} \end{array}} \right).$

(25) Thus, we can perform approximate diagonalization; that is, the matrix
$ O(\delta_i) $ is defined as follows:$ \left( {\begin{array}{*{20}{c}} {{h_1}}\\ {{h_2}}\\ {{h_3}}\\ {{h_4}} \end{array}} \right) = O({\delta _i})\left( {\begin{array}{*{20}{c}} {{\eta _1}}\\ {{\eta _d}}\\ {{\eta _l}}\\ {{\eta _2}} \end{array}} \right),$

(26) and
$ {\cal{M}}^2 = {O^T}({\delta _i})\left( {\begin{array}{*{20}{c}} {m_{{h_1}}^2}&0&0&0\\ 0&{m_{{h_2}}^2}&0&0\\ 0&0&{m_{{h_3}}^2}&0\\ 0&0&0&{m_{{h_4}}^2} \end{array}} \right)O({\delta _i}). $

(27) The
$ O(\delta_i) $ matrix will have the following form (with$ i = 1,2,3 $ ) [23]$ {O^T}({\delta _i}) \!=\! \left(\!\! {\begin{array}{*{20}{c}} \!\!{{c_{{\delta _1}}}{c_{{\delta _2}}}}\!\!&\!\!{ - {c_{{\delta _3}}}{s_{{\delta _1}}} - {c_{{\delta _1}}}{s_{{\delta _2}}}{s_{{\delta _3}}}}\!\!&\!\!{{s_{{\delta _1}}}{s_{{\delta _3}}} - {c_{{\delta _1}}}{c_{{\delta _3}}}{s_{{\delta _2}}}}\!\!&\!\!0\!\!\\ \!\!{{c_{{\delta _2}}}{s_{{\delta _1}}}}\!\!&\!\!{{c_{{\delta _1}}}{c_{{\delta _3}}} - {s_{{\delta _1}}}{s_{{\delta _2}}}{s_{{\delta _3}}}}\!\!&\!\!{ - {c_{{\delta _3}}}{s_{{\delta _1}}}{s_{{\delta _2}}} - {c_{{\delta _1}}}{s_{{\delta _3}}}}\!\!&\!\!0\!\!\\ \!\!{{s_{{\delta _2}}}}\!\!&\!\!{{c_{{\delta _2}}}{s_{{\delta _3}}}}\!\!&\!\!{{c_{{\delta _2}}}{c_{{\delta _3}}}}\!\!&\!\!0\!\!\\ 0\!\!&\!\!0\!\!&\!\!0\!\!&\!\!1 \end{array}} \!\!\right). $

(28) Subsequently, we obtain the following expressions for the
$ \eta_i $ fields, which are written in terms of the mass eigenstates$ H_i $ ($ i = 1,4 $ ):$ \eta_1 = c_{\delta _1}c_{\delta _2}h_1 -(c_{\delta _3 }s_{\delta _1}+c_{\delta _1}s_{\delta _2}s_{\delta _3} )h_2+ (s_{\delta _1}s_{\delta _3}-c_{\delta _1}c_{\delta _3} s_{\delta _2} )h_3, $

(29) $ \eta_d = c_{\delta _2}s_{\delta _1}h_1 +(c_{\delta _1}c_{\delta _3}-s_{\delta _1}s_{\delta _2}s_{\delta _3})h_2 -(c_{\delta _3}s_{\delta _1}s_{\delta _2}+c_{\delta _1}s_{\delta _3})h_3, $

(30) $ \eta_l = s_{\delta _2}h_1 +c_{\delta _2}s_{\delta _3}h_2 +c_{\delta _2}c_{\delta _3}h_3, $

(31) $ \eta_4 = h_4. $

(32) These expressions are used in the following to derive the Higgs interactions with fermions and gauge bosons.
-
At this point, we should verify that the resulting Higgs spectrum is viable, namely that we have a light SM-like Higgs boson with
$ m_h = 125 $ GeV, accompanied with heavier neutral and charged Higgs bosons, which are in agreement with the current LHC bounds on the Higgs particles. To explore the model parameters and symmetries, we consider the case in which the discrete symmetries for the Yukawa sector also apply for the supersymmetric$ \mu $ -terms, namely$ \mu_{ij} = 0 $ . In this case, it is relevant to include the leading SUSY radiative corrections to the Higgs mass, which are dominated by the stop-top loops. These radiative corrections are dependent on the stop-top interactions, for which we neglect the flavor-violating interactions, as we know that the current bounds on the FCNC processes causes them to be small, which is a consistent approximation. Following the effective potential technique to include the leading radiative stop-top corrections, we obtain the following expression for the mass of the lightest Higgs boson ($ h ( = H_1) $ ):$\begin{aligned}[b] m^2_{h}=& \frac{m_Z^2}{8} F(\alpha, \beta, \delta_i, \omega) - s_{\delta_1} c_ {\delta_1} c^2_{\delta_2} b^2_{11} - s_{\delta_1} s_{\delta_2} c_{\delta_2} b^2_{21} \\ &+\frac{1}{2} \tilde{m}_{u_1}^2 c^2_{\delta_1} c^2_{\delta_2}+\frac{1}{2} \tilde{m}_d^2 s^2_{\delta_1} c^2_{\delta_2}+\frac{1}{2} \tilde{m}_l^2 s^2_{\delta_2}\\& +\frac{3G_F}{\sqrt{2}\pi^2}\frac{m_t^4}{r_{1u}}\log\frac{m^2_{\rm stop}}{m^2_t}, \end{aligned}$

(33) where
$ r_{1u} = v^2_1/v^2 $ and$ \begin{aligned}[b] F (\alpha, \beta, \delta_i, \omega) = & \left[ \right. c^2_{\delta_1} c ^2_{\delta_2} \left( (2 c_{ 2 \beta} +1) c^2_{\omega} - c_{ 2 \alpha} s^2_\omega \right) \\&+ s ^2_{\delta_1} c ^2_{\delta_2} \left( c_{ 2 \alpha} s ^2_\omega +(1-2 c_{ 2 \beta} ) c ^2_\omega\right) \\& +s ^2_{\delta_2} \left( (1-2 c_{ 2 \alpha} ) s ^2_\omega +c_{ 2 \beta} c^2_\omega \right) \\ &+c_ \beta c_{\delta_1} \left( s_{\alpha} s_{ 2 \delta_2} s_{ 2 \omega} - 4 s_ {\beta} s_{\delta_1} c ^2_{\delta_2}c ^2_\omega \right) \\& -4 s_\alpha s_\beta s_{\delta_1} s_{\delta_2} c_{\delta_2} s_\omega c_\omega \left.\right]. \end{aligned}$

(34) Similar formulae can be derived for the mases of the heavier CP-even Higgs bosons.
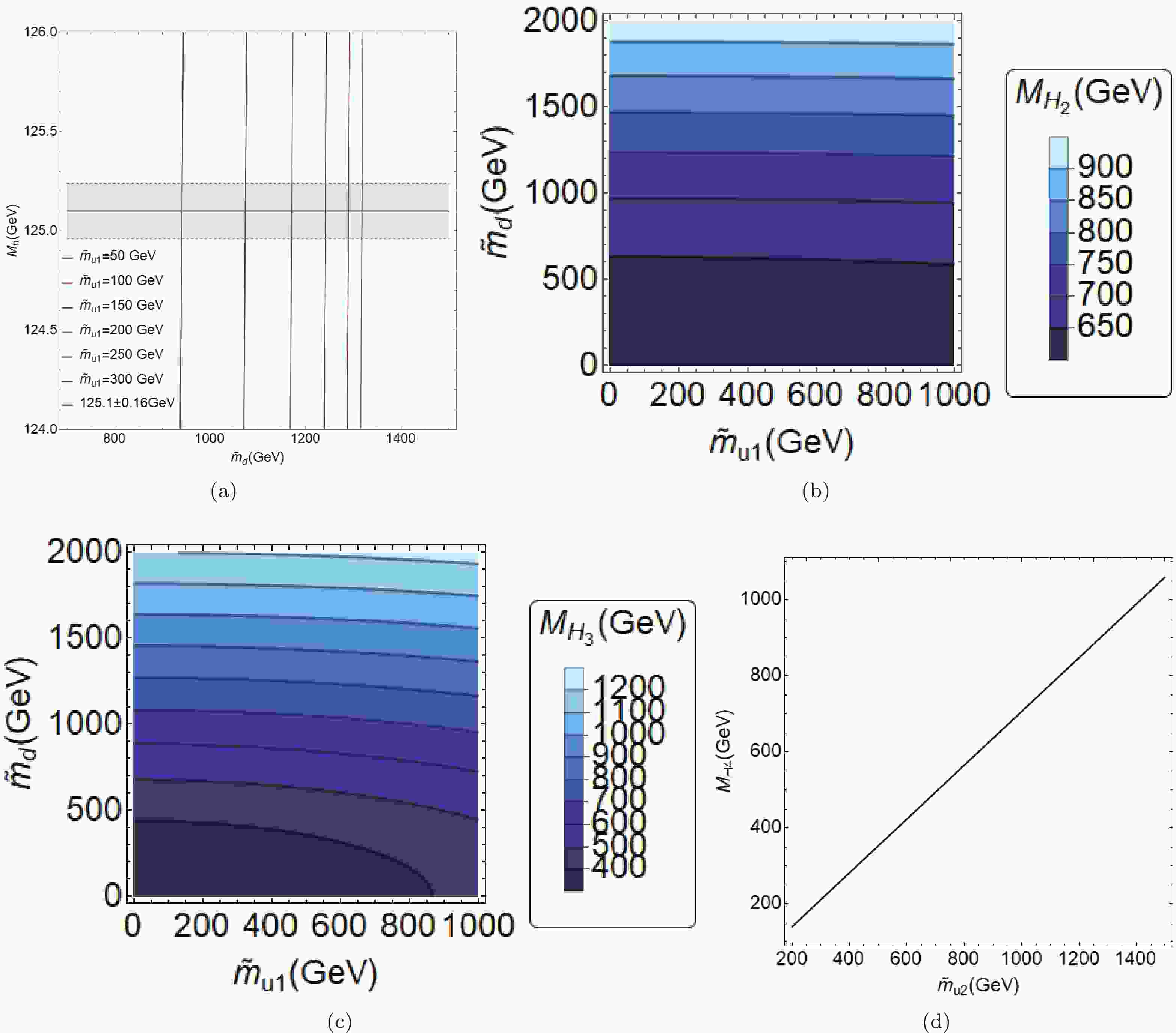
Then, in Fig. 1(a) we show
$ m_h $ as a function of$ \tilde{m}_{d} $ for the stop mass$ m_{\rm stop} = 1 $ TeV, where the different lines correspond to the soft Higgs mass parameter$ \tilde{m}_{u1} = $ 300, 400, 500, 600, 700 GeV, and for the fixed value$ \tilde{m}_l = 500 $ GeV, whereas the b-terms are fixed as$ b_{11} = 550 $ GeV and$ b_{21} = 50\;{\rm{GeV}} $ . The relevant angles are selected as follows:$ \alpha = 0.01, \, \beta = 0.45, \, \omega = 0.37, \, \delta_1 = 0.31, \, \delta_2 = 0,37, \delta_3 = 2.1 $ .② We can observe that the experimental value$ m_{h} \simeq 125 $ GeV (solid horizontal line) crosses all of the lines indicated in Fig. 1(a).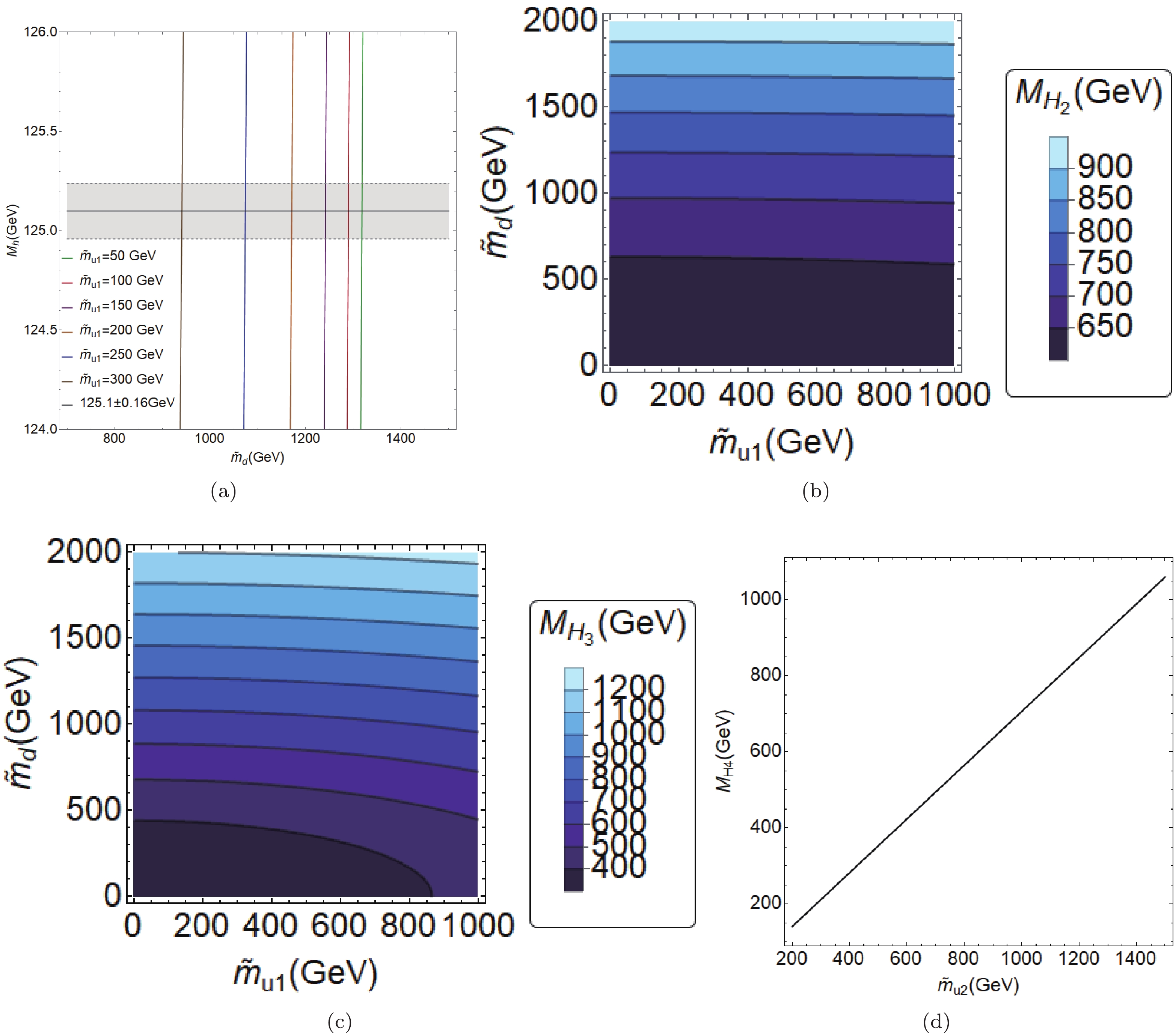
Figure 1. (color online) (a) Values of
$ m_{h} $ as function of$ \tilde{m}_{u1} $ , (b) contour regions of$ m_{H_2} $ in plane$ \tilde{m}_{u1}- \tilde{m}_{d} $ , (c) contour regions of$ m_{H_3} $ in plane$ \tilde{m}_{u1}- \tilde{m}_{d} $ , and (d) values of$ m_{H_4} $ as function of$ \tilde{m}_{u2} $ .Thereafter, in Figs. 1(b)-(c), we present the contour regions for the mass of the heavier scalars
$ m_{H_i} $ ($ i = 1,2 $ ) in the plane$ \tilde{m}_{u1}vs\tilde{m}_{d} $ , assuming again that$ m_{\rm stop} = 1\;{\rm{TeV}} $ . Our selection for the remaining parameters is the same as that for$ m_h $ (in Fig. 1(a)), which is also assumed to evaluate$ m_{H_4} $ , but in this case, the mass formula includes one extra free parameter:$ \tilde{m}_{u2} $ , and we opt to plot$ m_{H_4} $ precisely as a function of$ \tilde{m}_{u2} $ (Fig. 1(d)). These parameters define our benchmark point, which not only produces the value$ m_h \simeq 125 $ GeV, but also achieves masses for the heavy Higgs bosons ($ H_2,\; H_3,\; H_4 $ ), which are larger than approximately$ O(0.5) $ TeV. In fact, we can observe from Figs. 1(b), (c), and (d) that the masses of the heavier Higgs bosons can fall within the range of 400 GeV to 1 TeV, which could be an interesting target for the HL-LHC. -
As discussed in the motivations, in our model, we assign one Higgs doublet to each fermion type; that is, each fermion type has its "private Higgs." Thus, the down quarks and charged leptons only couple with a single Higgs, whereas the up quark sector may have couplings with two Higgs doublets simultaneously:
$ H_{u1} $ and$ H_{u2} $ . -
The Yukawa Lagrangian for this model can be derived from the corresponding superpotential after eliminating the auxiliary fields (F-terms), and it can eventually be written as follows
$ \begin{aligned}[b]{\cal{L}} =& \bar{u}_{i{\rm L}}u_{j{\rm R}}(Y^u_1)_{ij}H^0_{u1}+\bar{u}_{i{\rm L}}u_{j{\rm R}}(Y^u_4)_{ij}H^0_{u2}\\&+\bar{d}_{i{\rm L}}d_{j{\rm R}}(Y^d)_{ij}H^0_d+\bar{l}_{i{\rm L}}l_{j{\rm R}}(Y^l)_{ij}H^0_l+{\rm h.c.} \end{aligned} $

(35) Unlike the up sector, which interacts with two Higgs doublets simultaneously, the down type quarks and charged leptons only interact with a single one, implying that the corresponding mass matrices are given by
$ M_f = Y ^f \frac{v_f}{\sqrt{2}}, $

(36) where
$ f = d, l $ .After rotating to the mass eigenstate basis, both the charged leptons and down type quark Yukawa matrices become diagonal:
$ \bar{Y}^f = \frac{\sqrt{2}}{v_f}\bar{M}_f. $

(37) On the other hand, both Higgs doublets
$ H_{u1} $ and$ H_{u2} $ couple with up-type fermions through the Yukawa matrices$ Y^u_1 $ and$ Y^u_4 $ . Following spontaneous symmetry breaking, these matrices are combined to produce a fermion mass matrix with a certain structure. The corresponding mass matrix receives contributions from both VEVs$ v_1 $ and$ v_4 $ ; that is:$ M_u = \frac{1}{\sqrt{2}}\left(v_1 Y^u_1+v_4 Y^u_4\right). $

(38) To obtain the physical fermion masses, we need to diagonalize the mass matrix, which is achieved through a bi-unitary transformation
$ {\cal{V}}_{\rm L,R} $ ; that is,$ \bar{M}_u = {\cal{V}}_{\rm L} M_u{\cal{V}}^\dagger_{\rm R} = {\cal{V}}_{\rm L} \frac{1}{\sqrt{2}}\left(v_1 Y^u_1+v_4 Y^u_4\right) {\cal{V}}^\dagger_{\rm R}, $

(39) where the form of the matrix
$ {\cal{V}}_{\rm L,R} $ depends on the texture type of$ M_u $ ; closed expressions have been obtained for the four- and six-texture Hermitian and non-Hermitian cases. Although$ {\cal{V}}_{\rm L,R} $ diagonalizes the matrix$ M_u $ , it does not necessarily diagonalize each of the Yukawa matrices that constitute$ M_u $ ; thus, a neutral flavor that violates the Higgs-fermion interactions will be induced in principle. -
In the use of textures within the context of the 2HDM, a specific form with six zeroes was first considered [24], and it was found that the textures implied a pattern for the Higgs-fermion couplings of the form
$ \dfrac{\sqrt{m_im_j}}{v} $ , which is known asthe Cheng-Sher ansatz. Such a vertex satisfies limits on the FCNC mediated by the Higgs bosons, with masses that are lighter than$ {\cal{O}} $ (TeV). The case with four-zero textures was presented in [25, 26], and its implications were studied in [27-30]. Other variations of the Yukawa matrices were discussed in [31-33].For completeness, we include the form of the four-zero texture matrix, namely
$ {M_u} = \left( {\begin{array}{*{20}{c}} 0&D&0\\ {D*}&C&B\\ 0&{B*}&A \end{array}} \right). $

(40) We assume that the Yukawa matrices in the up-sector (
$ Y^u_{1}, Y^u_{4} $ ) have this four-texture structure, but rather than focusing on a specific model, we consider the general features of this case. We invoke this mass texture to control the FCNC Higgs interactions, but the phenomenology will be analyzed in terms of the Yukawa matrix elements in the mass-basis.The Lagrangian for the up-quarks sector is
$ {\cal{L}}_u = \bar{u}_{i{\rm L}}u_{j{\rm R}}(Y^u_1)_{ij}H^0_{u1}+\bar{u}_{i{\rm L}}u_{j{\rm R}}(Y^u_4)_{ij}H^0_{u2}+{\rm h.c.} $

(41) After substituting
$ H^0_{u1} $ and$ H^0_{u2} $ , the Lagrangian becomes:$ \begin{aligned}[b] {\cal{L}}_u =& \bar{u}_{i{\rm L}}u_{j{\rm R}}(Y^u_1)_{ij}\frac{1}{\sqrt{2}}(v_1+\eta_1+{\rm i}\chi_1)\\&+\bar{u}_{i{\rm L}}u_{j{\rm R}}(Y^u_4)_{ij}\frac{1}{\sqrt{2}}(v_4+\eta_4+{\rm i}\chi_4)+{\rm h.c.}, \end{aligned}$

(42) and by maintaining only the real part and factorizing, one obtains
$ \begin{aligned}[b] {\cal{L}}_u =& \bar{u}_{\rm L}\left[\frac{1}{\sqrt{2}}(v_1Y^u_1+v_4Y^u_4)\right]u_{\rm R}\\&+\bar{u}_{\rm L}\left[\frac{1}{\sqrt{2}}(\eta_1Y^u_1+\eta_4Y^u_4)\right]u_{\rm R}+{\rm h.c.},\\ =& \bar{u}_{\rm L}M_u u_{\rm R}+\bar{u}_{\rm L}\left[\frac{1}{\sqrt{2}}(\eta_1Y^u_1+\eta_4Y^u_4)\right]u_{\rm R}+{\rm h.c.} \end{aligned}$

(43) Subsequently, the rotated mass matrix can be expressed as follows:
$ \begin{aligned}[b] \bar{M_u} =& V_{\rm L} M_u V_{\rm R}^\dagger = \frac{v_1}{\sqrt{2}}V_{\rm L}Y^u_1V^\dagger_{\rm R}\\&+\frac{v_2}{\sqrt{2}}V_{\rm L}Y^u_4V^\dagger_{\rm R} \\=& \frac{v_1}{\sqrt{2}}\tilde{Y}^u_1+\frac{v_2}{\sqrt{2}}\tilde{Y}^u_4, \end{aligned}$

(44) where
$ V_{\rm L,R} $ denote the diagonalizing matrices in the up-quark sector and$ \tilde{Y}^u_{1,4} $ are the rotated Yukawa matrices in the mass-basis. Then, in the mass basis, the Yukawa lagrangian becomes:$ {\cal{L}}_u = \bar{u}_{\rm L}\bar{M}_u u_{\rm R}+\bar{u}_{\rm L}\left[\frac{1}{\sqrt{2}}(\eta_1\tilde{Y}^u_1+\eta_4\tilde{Y}^u_4)\right]u_{\rm R}+{\rm h.c.} $

(45) Thereafter, one of the Yukawa matrices can be expresed in terms of the other one and the diagonal mass matrix, as follows:
$ \tilde{Y}^u_1 = \frac{\sqrt{2}}{v_1}\bar{M}_u-\frac{v_4}{v_1}\tilde{Y}^u_4, $

(46) and it can be observed that
$ \bar{M}_u $ is diagonal whereas$ \tilde{Y}^u_i $ are not, with$ i = 1,4 $ .When rewriting the Lagrangian in terms of
$ \tilde{Y}^u_{4} $ , one obtains:$ \begin{aligned}[b] {\cal{L}}_u =& \bar{u}_{\rm L}\bar{M}_u u_{\rm R}+\frac{1}{\sqrt{2}}\bar{u}_{\rm L}\left[\left(\frac{\sqrt{2}}{v_1}\bar{M}_u-\frac{v_4}{v_1}\tilde{Y}^u_4\right)\eta_1\right.\\&+\tilde{Y}^u_4\eta_4\Bigg]u_{\rm R}+{\rm h.c.} \end{aligned}$

(47) From the last equation, it can be observed that it is now only necessary to provide information regarding the
$ \tilde{Y}^u_4 $ matrix. Subsequently, we simply need to express the neutral fields$ \eta_{1,2} $ in terms of the Higgs mass eigenstates to derive the Higgs-fermion couplings in the up sector.Thus, by using Eq. (26), we obtain the Higgs couplings in the up-type quark sector (with
$ c^{-1}_\omega = 1/\cos \omega $ ),$ g_{h_1u_iu_j} = \frac{c_\omega c_{\delta _1}c_{\delta _2}}{vc_\beta}\left[\sqrt{2}(\bar{M}_u)_{ij}-vt_\omega s_\alpha c^{-1}_\omega (\tilde{Y}^u_4)_{ij}\right], $

(48) $ \begin{aligned}[b] g_{h_2u_iu_j} =& -\frac{c_\omega(c_{\delta _3 }s_{\delta _1}+c_{\delta _1}s_{\delta _2}s_{\delta _3} )}{vc_\beta}\\&\times\left[\sqrt{2}(\bar{M}_u)_{ij}-vt_\omega s_\alpha c^{-1}_\omega (\tilde{Y}^u_4)_{ij}\right], \end{aligned}$

(49) $\begin{aligned}[b] g_{h_3u_iu_j} =& \frac{c_\omega(s_{\delta _1}s_{\delta _3}-c_{\delta _1}c_{\delta _3} s_{\delta _2} )}{vc_\beta}\\&\times\left[\sqrt{2}(\bar{M}_u)_{ij}-vt_\omega s_\alpha c^{-1}_\omega (\tilde{Y}^u_4)_{ij}\right], \end{aligned} $

(50) $ g_{h_4u_iu_j} = (\tilde{Y}^u_4)_{ij}, $

(51) whereas for the down sector, we obtain:
$ g_{h_1dd} = \frac{\bar{M}_d}{vs_\beta}c_\omega c_{\delta _2}s_{\delta _1}, $

(52) $ g_{h_2dd} = \frac{\bar{M}_d}{vs_\beta}c_\omega(c_{\delta _1}c_{\delta _3}-s_{\delta _1}s_{\delta _2}s_{\delta _3}), $

(53) $ g_{h_3dd} = -\frac{\bar{M}_d}{vs_\beta}c_\omega(c_{\delta _3}s_{\delta _1}s_{\delta _2}+c_{\delta _1}s_{\delta _3}), $

(54) and finally, for the lepton sector, we obtain:
$ g_{h_1ll} = \frac{\bar{M}_l}{vt_\omega c_\alpha}c_\omega s_{\delta _2}, $

(55) $ g_{h_2ll} = \frac{\bar{M}_l}{vt_\omega c_\alpha} c_\omega c_{\delta _2}s_{\delta _3}, $

(56) $ g_{h_3ll} = \frac{\bar{M}_l}{vt_\omega c_\alpha} c_\omega c_{\delta _2}c_{\delta _3}. $

(57) Moreover, we can derive the
$ h_iVV $ couplings by expanding the covariant derivatives of the Higgs doublets. The couplings$ h_iWW $ are expressed as follows:$ g_{h_1WW} = 2\frac{m^2_W}{v}c_\omega[c_\beta c_{\delta _1}c_{\delta _2}+ s_\beta c_{\delta _2}s_{\delta _1}+ t_\omega s_\alpha s_{\delta _2}], $

(58) $\begin{aligned}[b] g_{h_2WW} =& 2\frac{m^2_W}{v}c_\omega[-c_\beta(c_{\delta _3}s_{\delta _1}+c_{\delta _1}s_{\delta _2}s_{\delta _3})\\&+ s_\beta (c_{\delta _1}c_{\delta _3}-s_{\delta _1}s_{\delta _2}s_{\delta _3})+ t_\omega s_\alpha c_{\delta _2}s_{\delta _3}], \end{aligned}$

(59) $ \begin{aligned}[b] g_{h_3WW} =& 2\frac{m^2_W}{v}c_\omega[c_\beta(s_{\delta _1}s_{\delta _3}-c_{\delta _1}c_{\delta _3}s_ {\delta _2}) \\& -s_\beta(c_{\delta _3} s_{\delta _1}s_{\delta _2}+c_{\delta _1}s_{\delta _3}) + t_\omega s_\alpha c_{\delta _2}c_{\delta _3}], \end{aligned}$

(60) $ g_{h_4WW} = 2\frac{m^2_W}{v}c_\omega t_\omega c_\alpha. $

(61) Similar results are obtained for the vertices
$ h_iZZ $ .Having determined all of the relevant Higgs couplings, we are ready to work on the Higgs phenomenology. However, prior to this, we find it interesting to comment on the MSSM limit of our model. In fact, this was discussed in Ref. [34], which works in the so-called Higgs-basis, where only two doublets develop VEVs. The authors of this reference discussed in detail the issue of the decoupling limit, and although they confirmed that the model was reduced to the SM, in the limit in which all mass-parameters are very large; that is, with no non-decoupling effects from the extra degrees of freedom, they also identified several "quasi-decoupling" effects, which prevented the model from being reduced to the MSSM in that limit. This is owing to the mixing with the extra Higgs doublets, unless the extra b-terms are set to zero, such that no mixing is allowed. However, when using our parameterization for the VEVs, we can observe that in the limits
$ \alpha \to 0 $ and$ \omega \to 0 $ , the leptons are massless, whereas the fourth Higgs doublet does not develop a VEV. Furthermore, by taking$ \delta_2, \delta_3 \to 0 $ , we notice that the third and fourth neutral CP-even Higgs bosons ($ H_3, H_4 $ ) do not mix with the two lightest MSSM-like Higgs bosons$ H_1 ( = h) $ and$ H_2 $ . Thus, this limit resembles the MSSM Higgs sector, but with massless leptons. -
Having analyzed the Yukawa and Higgs sectors, we can focus on the constraints of the 4HDM parameters involved in our study. For this purpose, we need to specify possible values for the following parameters:
● The mixing angles
$ \delta_i $ ($ i = 1,\,2,\,3 $ ) that appear in the rotation mass matrix; Eq. (28).● Angles that parameterize the VEVs:
$ \alpha,\,\beta,\,\omega $ ; Eq. (6).● Heavy scalar masses: mainly
$ m_{H_2} $ .● Yukawa matrix elements
$ \left(\tilde{Y}_4^u\right)_{tt}\equiv Y_{tt} $ and$ \left(\tilde{Y}_4^u\right)_{tc}\equiv Y_{tc} $ .Moreover, we need to specify the soft SUSY-breaking terms, but these are essentially fixed by requiring the light Higgs boson mass of 125 GeV and the remaining neutral CP-even Higgs masses to be larger than approximately 0.5 TeV.
To provide a realistic scenario, we use the most up-to-date experimental measurements reported by the ATLAS and CMS collaborations [35, 36]; namely, the signal strengths
$ {\cal{R}}_{X} $ , which are defined as follows:$ {\cal{R}}_{X} = \frac{\sigma(pp\to h)\cdot BR(h\to X)}{\sigma(pp\to h^{{\rm{SM}}})\cdot BR(h^{{\rm{SM}}}\to X)}, $

(62) where
$ \sigma(pp\to H_i) $ is the production cross-section of$ H_i $ , with$ H_i = h,\,h^{{\rm{SM}}} $ ; here, h is the SM-like Higgs boson originating from an extension of the SM and$ h^{{\rm{SM}}} $ is the SM Higgs boson and$ BR(H_i\to X) $ is the branching ratio of$ H_i $ decaying into$ X = b\bar{b},\;\tau^-\tau^+,\;\mu^-\mu^+,\;WW^*,\;ZZ^*,\;\gamma\gamma $ . From the Higgs-fermion couplings (Eq. (48)), we observe that the term outside the brackets must be close to the unity, while the second term inside the brackets must be close to zero to result in small derivations from the SM couplings. This is ensured by assuming that$ c_{\omega}\sim c_{\beta}\sim c_{\delta_i}\sim 1 $ and$ s_{\alpha}\ll 1 $ .Figure 2 presents the plane
$ c_{\delta_1}-c_{\delta_2} $ , in which the filled areas represent the regions allowed by$ {\cal{R}}_{b} $ (green),$ {\cal{R}}_{\tau} $ (pink),$ {\cal{R}}_{W} $ (yellow),$ {\cal{R}}_{Z} $ (blue), and$ {\cal{R}}_{\gamma} $ (orange). In turn, the intersection of all allowed regions is represented by the red area. The graph was generated using the$ {\texttt{SpaceMath}} $ package [37]. In Table 2 we present the values for the additional parameters that are used to find that plane.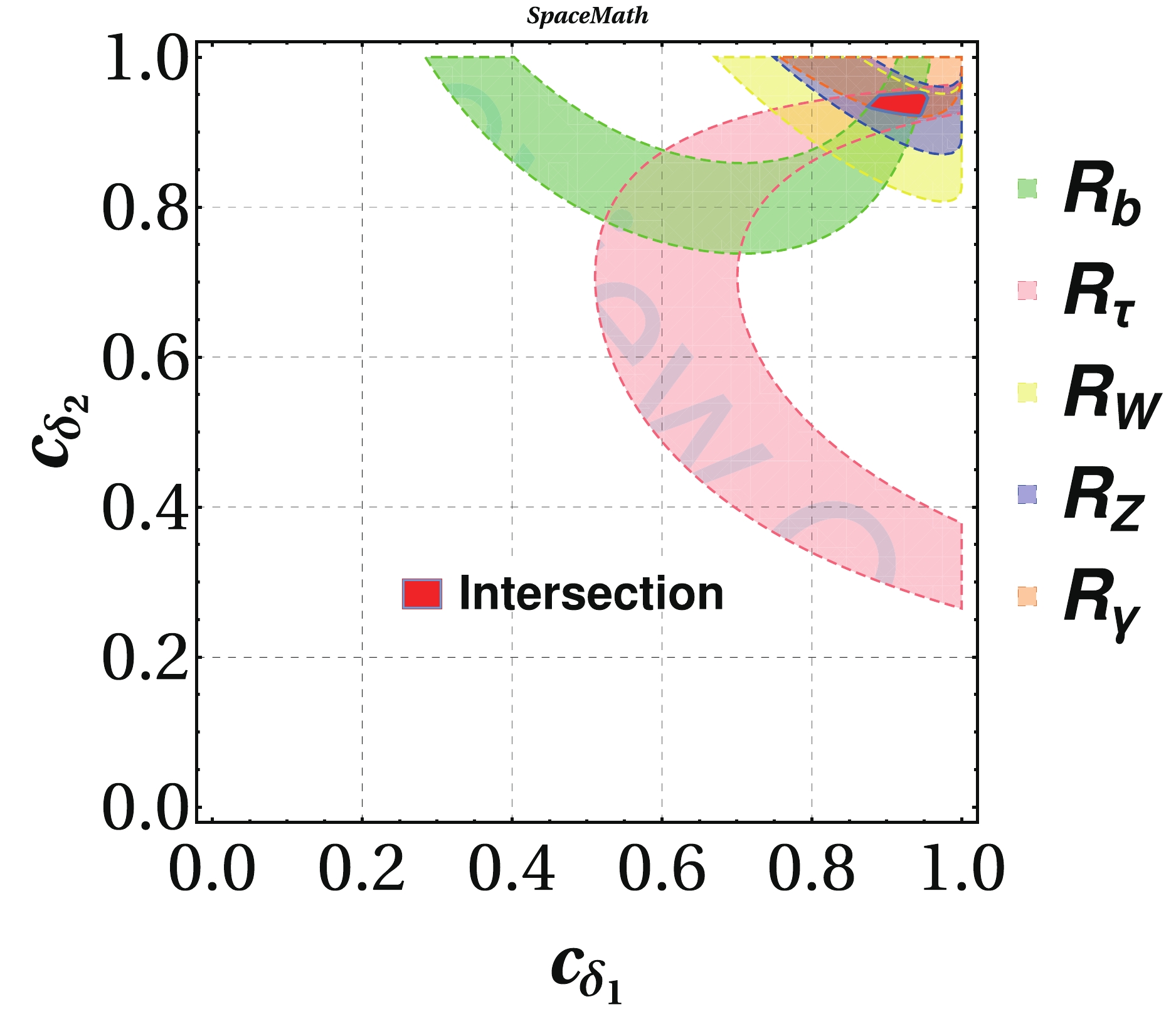
Figure 2. (color online) Allowed region in plane
$ c_{\delta_1}-c_{\delta_2} $ from our analysis of the ratios$ {\cal{R}}_{b} $ (green),$ {\cal{R}}_{\tau} $ (pink),$ {\cal{R}}_{W} $ (yellow),$ {\cal{R}}_{Z} $ (blue), and$ {\cal{R}}_{\gamma} $ (orange) in plane$ c_{\delta_1}-c_{\delta_2} $ . The red area represents the intersection of all individual allowed regions.Parameter Value $c_{\omega}$ 

$0.93$ 

$s_{\alpha}$ 

$0.01$ 

$c_{\beta}$ 

$0.9$ 

$(\tilde{Y}^u_4)_{tt}$ 

$0.1$ 

Table 2. Values for additional parameters used to evaluate
${\cal{R}}_{x\bar{x}}$ .Furthermore, we are required to determine the values of the matrix elements
$ Y_{tc} $ (in the following, we denote$ Y_{tc} = (\tilde{Y}^u_4)_{tc} $ ), because it is a fundamental parameter in our analysis, as we are interested in possible evidence of the flavor-changing decays$ H_2\to tc $ and$ t\to ch $ , the couplings of which are proportional to$ Y_{tc} $ . To constrain this, we first consider the high-energy constraints originating from the LHC bounds on the rare top decay$ t \to ch $ , following which we compare this with the low-energy constraints, particularly$ D-\bar{D} $ mixing.For the high-energy constraints, we use the direct upper limit on
$ BR(t\to ch)<1.1\times 10^{-3} $ [38]; with this value, we obtain a bound on$ Y_{tc} $ of order 1, depending on the values of$ c_{\beta} $ . Nevertheless, the authors of Ref. [39] obtained an estimation by extrapoling the number of events for the signal and backgrounds from 36.1 to 3000 fb$ ^{-1} $ , assuming that the experimental details and analysis remained unchanged. This resulting upper limit is given by$ BR(t\to ch)<7.69\times 10^{-5} $ .Figure 3 depicts the allowed regions in the plane
$ c_{\beta}-Y_{tc} $ , where the shaded areas represent the allowed regions obtained from the direct upper limit reported in Ref. [38] on$ BR(t\to ch) $ (blue area) and by the extrapolation analysis (red area). We note that, by considering$ c_{\beta} = 0.9 $ (see Table 2),$ Y_{tc} $ can reach a value of up to approximately 0.4, after taking into account the extrapolation analysis.
Figure 3. (color online) Plane
$ c_{\beta}-Y_{tc} $ . The filled areas represent the allowed regions from the direct upper limit reported by the ATLAS collaboration on$ BR(t\to ch) $ (blue region) and by extrapolation (red region).Regarding the low-energy constraints, Ref. [40] presented a detailed analysis of the FCNC arising from the 2HDM by incorporating the Cheng-Sher anzast, where the couplings of the Higgs bosons (
$ H_a $ ) with fermions$ f_i f_j H_a $ were of the form$ \chi^a_{ij}(m_i m_j)^{1/2}/v $ . It was found that the limits on the coefficients$ \chi^a_{ij} $ lay in the range$ 0.1-0.5 $ , which already required some moderate fine-tuning. However, such analysis does not apply completely to our model, as in our case, there are extra suppression factors originating from the mixing angles. In particular, the low-energy-constraints on the parameter$ Y_{tc} $ , resulting from the one-loop contribution to the$ D-\bar{D} $ mixing with neutral Higgs exchange, were considered recently in Refs. [41, 42], with further comments in Ref. [43]. It was found that the bound on the product$ |\rho_{tc} \rho_{tu}| \leqslant 0.02 $ , with$ \rho_{tc} \simeq g_{H_2tc} $ , modulo a certain mixing-angle factor. Within our model, we find that the coupling$ H_2 tc $ is approximately$ g_{H_2tc} \simeq 10^{-4} $ for$ Y_{tc} \simeq 0.1 $ , which satisfies this constraint.Regarding the tree-level neutral Higgs contribution to
$ D-\bar{D} $ mixing, which is sensitive to$ Y_{uc} $ , we have obtained an estimate of this effect for the parameters (mixing angles) that are favored by the Higgs LHC data. We worked along the lines of the analysis presented in Ref. [44], which was conducted for 2HDM-III and claims that no significant bound on$ Y_{uc} $ is obtained for that model. We find that the contributions from the lightest neutral Higgs bosons within our model (h and$ H_2 $ , with$ m_{H_2} = 400 $ GeV) are below the experimental uncertainties, even for$ Y_{uc} = 1.5 $ .Thus, our model parameters satisfy all low-energy constraints, and in fact, the strongest constraints will result from the LHC studies. Table 2 summarizes the benchmark point for the parameters of our model to be used in the subsequent calculations. Furthermore, we set
$ c_{\delta_1} = c_{\delta_2} = 0.95 $ , unless stated otherwise. -
Top quark rare decays have been studied for several years as a means of searching for new physics [45-47], including various theoretical calculations for
$ BR(t\to ch) $ . As discussed previously, our model allows for FCNC couplings in the up sector; therefore, we can obtain a prediction for both the FCNC top quark and$ H_i $ decays. On the other hand, Refs. [22, 48, 49] provided several estimates for the branching ratios for$ t\rightarrow ch $ that could be proved at the different phases of the LHC. For example, it was claimed that the top decay processes provide the best channel for discovering top FCNC interactions, whereas it is surpassed by single top production only in certain cases, when up and charm quark interactions are involved. In some of the examples discussed in Ref. [22], the maximum rates are predicted to be observable with a 3$ \sigma $ statistical significance or greater for one LHC year, with a luminosity of 6000 fb$ ^{-1} $ .In the following subsection, we present a detailed study of the detection of the decay
$ t\to ch $ at the forthcoming high-luminosity phase of the LHC (HL-LHC), following which we present an analysis to determine the viability of the LHC for detecting the decay$ H_2\to tc $ at the HL-LHC. -
The branching ratio for the decay
$ t\to c h $ at the tree level can be to computed through the following expression:$ {BR}(t\rightarrow c h) = \frac{\Gamma(t\rightarrow ch)}{\Gamma_{\rm tot}}, $

(63) where the total top width is given by
$ \Gamma_{\rm tot} = \Gamma(t\to Wb)+ \Gamma(t\to ch) $ GeV and the width for the FCNC top decay is$\begin{aligned}[b] \Gamma(t\rightarrow ch) =& \frac{m_t}{16\pi}g_{htc}^2\left[(1+r_{tc})^2-r_{ht}^2\right] \\&\times\sqrt{1-(r_{ht}+r_{tc})^2}\sqrt{1-(r_{ht}-r_{tc})^2}, \end{aligned} $

(64) where
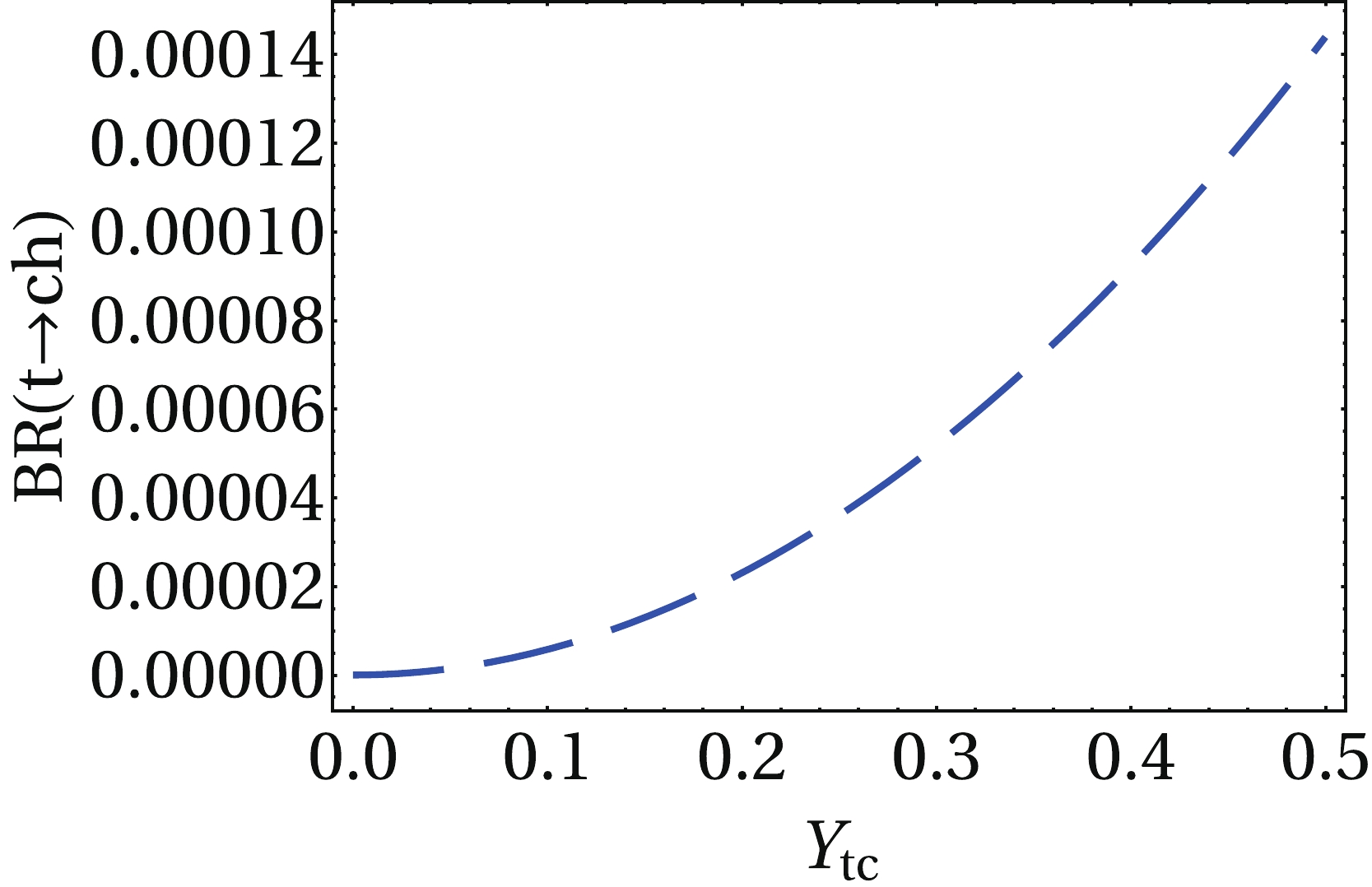
$ g_{htc} $ is obtained by Eq. (48),$ r_{ht} = m_{h}/m_{t} $ ,$ r_{tc} = m_{c}/m_{t} $ , and$ v = 246 $ GeV.In Fig. 4, we display
$ BR(t\to ch) $ as a function of$ Y_{tc} $ , where we use values for the additional parameters as indicated in Table 2. We observe that the top FCNC branching ratio can reach values of the order$ 10^{-4} $ , which is very promising and motivates us to undertake a study of the detectability of the signal at the future stages of the LHC.The analysis is carried out for the LHC and its next stage; that is, the HL-LHC [50]. We first discuss both the signal and main SM backgrounds for the decay channels of the Higgs boson to be considered. We adopt the strategy carried out by the ATLAS and CMS collaborations [51, 52].
● Signal
We consider top pair production, and subsequently, one top is decayed via the FCNC mode, whereas the other one is decayed through the SM mode. Thus, the signature is
$ pp\to t\bar{t}\to hc+Wb\to Xc+\ell\nu_{\ell}b $ , and we consider the Higgs decays$ X = \gamma\gamma $ or a$ b\bar{b} $ pair. Thus, we identify the final state by the modes$ \gamma\gamma bj\ell\nu_{\ell} $ or$ b\bar{b}bj\ell\nu_{\ell} $ .● Background
1. In the case of the diphoton-channel, we study the backgrounds resulting from:
–
$ pp\to t\bar{t}h $ ,–
$ pp\to hjjW^{\pm} $ ,–
$ pp\to t\bar{t}\gamma\gamma $ ,–
$ pp\to \gamma\gamma jj W^{\pm} $ .2. For the mode
$ bb-channel $ , we include the background from:–
$ pp\to t\bar{t}\to b\ell^+\nu\bar{b}\bar{c}s+X $ or$ pp\to t\bar{t}\to bc\bar{s}\bar{b}\ell^-\bar{\nu}+X $ with a c-jet that is mis-identified as a b-jet,–
$ pp\to t\bar{t}\to b\ell\nu\bar{b}u\bar{d} $ ,–
$ pp\to b\bar{b}b\bar{b}\ell\nu $ , and–
$ pp\to b\bar{b}c\bar{c}\ell\nu $ .However, regarding our computation scheme, we first implement the Feynman rules of the model via
$ {\texttt{LanHEP}} $ routines for$ {\texttt{MadGraph5}} $ [53] and$ {\texttt{CalcHEP}} $ [54]. In this manner, the signal and background events are generated by$ {\texttt{MAdGraph5}} $ interfaced with$ {\texttt{Pythia6}} $ [55] and$ {\texttt{Delphes3}} $ [56] for the detector analysis. We generate$ 10^5 $ events for both the signal and background using the CT10 parton distribution functions [57].We now turn to evaluate the number of signal events produced as a function of
$ c_{\beta} $ and$ Y_{tc} $ . In Fig. 5, we present the signal events for the (a) diphoton-channel and (b)$ bb-channel $ in the plane$ c_{\beta} $ -$ Y_{tc} $ for the HL-LHC, with an integrated luminosity of$ 3 $ ab$ ^{-1} $ . We observe that the number of signal events produced at the HL-LHC will be of the order 250 (60000) for the diphoton-channel ($bb-channel$ ), assuming$ Y_{tc}\sim 0.4 $ and$ c_{\beta}\sim 1 $ . For the LHC, the number of signal events is approximately$ 0.1 $ (one tenth) of the events expected for the HL-LHC.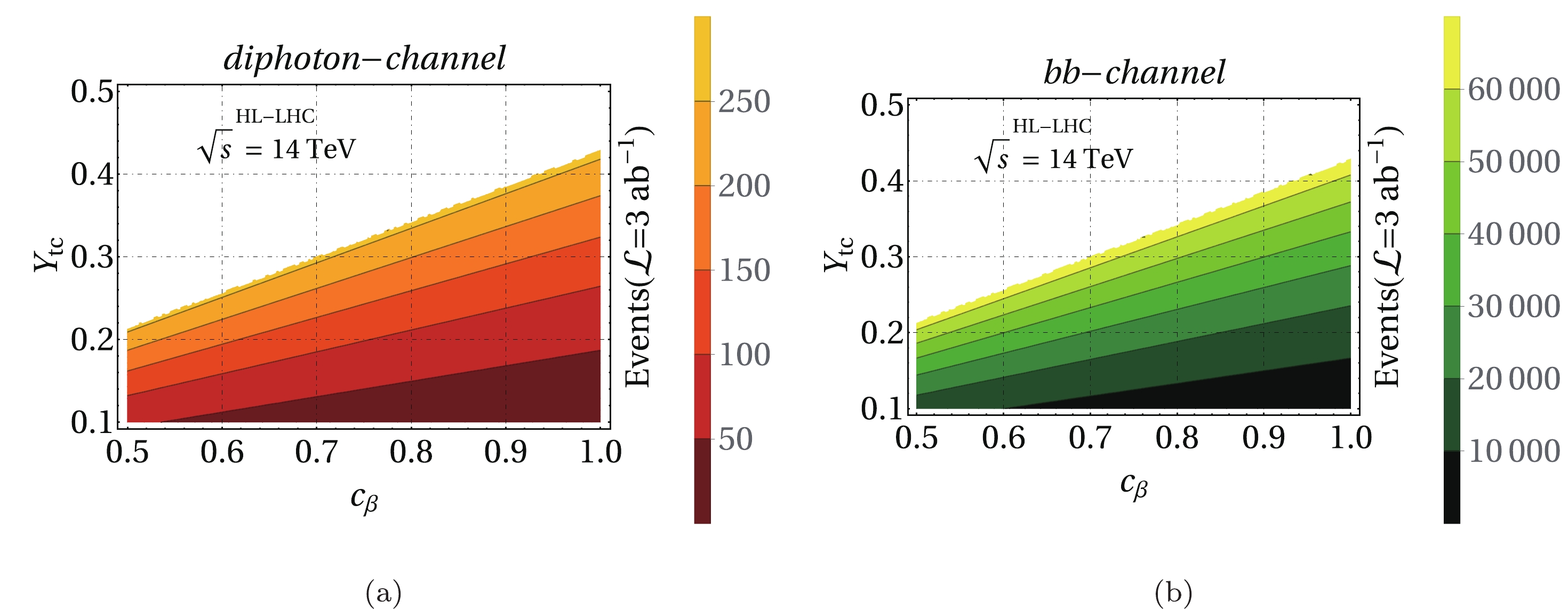
Figure 5. (color online) Number of signal events as function of
$ c_{\beta} $ and$ Y_{tc} $ for (a) diphoton-channel and (b)$ bb-channel $ . In both cases, we use the optimal integrated luminosity searched by the HL-LHC. We use the parameters presented in Table 2.The ATLAS and CMS collaborations [51, 52] searched for the decay
$ t\to ch $ in both the diphoton-channel and bb-channel; nevertheless, no significant deviation from the SM prediction was observed. We follow these strategies, using the same kinematic cuts, for our analysis. These cuts are:● diphoton-channel
1. We require exactly one
$ b- $ jet and two photons.2. We identify the charged leptons and photons emerging from the signal imposing
$ p_T^{\gamma,\,\ell}>25 $ GeV.3. The main variable for searching the Higgs boson decay into the diphoton system is the invariant mass
$ M_{\gamma\gamma} $ , which is selected to lie between$ 120\leqslant M_{\gamma\gamma}\leqslant 130 $ GeV.4. Owing to the Higgs boson decays into the diphoton system, it is required that the invariant mass associated with the top quark falls between
$ 160\leqslant M_{\gamma\gamma j}\leqslant 190 $ GeV.5. The separations between the photons resulting from Higgs boson decay must be
$ 1.8<\Delta R_{\gamma,\,\gamma}<5.0 $ .6. The separation between the diphoton system and jet is
$ \Delta R_{\gamma\gamma,\,j}<1.8 $ .7. Owing to the non-detected neutrino in the final state, we demand a missing transverse energy
$ {\not\!\! E}_T>30 $ GeV.8. The tagging and mistagging efficiencies selected are as follows:
–
$ \epsilon_b = 70 $ %,–
$ \epsilon_c = 14 $ %, and–
$ \epsilon_j = 1 $ %.● bb-channel
1. We require exactly four jets: three of them are tagged as
$ b- $ jets with$ p_T^{j,\,b}>30 $ GeV and$ |\eta^j<2.5| $ .2. Exactly one isolated lepton with
$ p_T^{\ell}>20 $ GeV and$ |\eta^{\ell}| < 2.5. $ 3. To obtain a neutrino that emerges in the final state, the missing transverse energy
$ {\not\!\! E}_T>30 $ GeV is required.4. To reconstruct the top quark mass associated with the FCNC, it is required that
$ |M_{b_1b_2j}-m_t|\leqslant 26 $ GeV.5. Regarding the reconstruction of the Higgs boson mass, it is imposed that
$ |M_{b_1b_2}-m_h|\leqslant 0.15\;m_h $ .6. It is required that
$ \Delta R $ between each jet and charged lepton be$ \sqrt{\Delta\phi^2+\Delta\eta^2}>0.4 $ .7. The tagging and mistagging efficiencies selected are as follows:
–
$ \epsilon_b = 70 $ %,–
$ \epsilon_c = 14 $ %, and–
$ \epsilon_j = 1 $ %.Subsequently, we evaluate the signal significance
$ {\cal{S}} = N_{\rm S}/\sqrt{N_{\rm S}+N_{\rm B}} $ , where$ N_{\rm S} $ is the number of signal events and$ N_{\rm B} $ is the number of background events, once the kinematic cuts have been applied. Figure 6 presents the corresponding signal significance that can be achieved at the HL-LHC, as a function of$ c_{\delta_1} $ and$ Y_{tc} $ .
Figure 6. (color online) Signal significance as function of
$ c_{\delta_1} $ and$ Y_{tc} $ : (a) bb-channel and (b) diphoton-channel. We set$ c_{\delta_2} = 0.95 $ and the parameters indicated in Table 2. The regions constrained by the LHC Higgs data, as derived in the previous section, are also shown.We can appreciate that for both channels, the values of the significance are of the order 1 for
$ c_{\delta_1} $ within the range allowed by$ {\cal{R}}_X $ and$ Y_{tc}\sim {\cal{O}}(0.4) $ . -
First, we evaluate the relevant decay modes of
$ H_2 $ into final states with two particles; the corresponding branching ratios are presented in Fig. 7, with (a) the modes at the tree level and (b) the modes at the one-loop level.
Figure 7. (color online) Branching ratio of decays
$ H_2\to XX $ : (a) tree level modes and (b) one-loop level modes. We use the values of the parameters indicated in Table 2.We observe that the FCNC mode
$ H_2 \to tc $ reaches values of the order$ 10^{-4} $ for a mass$ m_{H_2} \sim 2 m_t $ . Above this mass, this branching ratio reaches values of the order$ 10^{-6}-10^{-5} $ . The dominant decay modes for$ m_{H_2}\leqslant 2m_t $ are into$ bb $ and$ VV $ ($ V = \,W,\,Z $ ) pairs, for which the branching ratios are of the orders$ 0.9 $ and$ 10^{-2} $ , respectively. Once the$ tt $ channel is open, it becomes the dominant decay mode, with a branching ratio of the order$ 1 $ . Regarding the one-loop level decays, the mode$ H_2\to gg $ has the largest branching ratio, reaching values of the order$ 10^{-2} $ ($ 10^{-3} $ ) for$ m_{H_2}\leqslant 2m_t $ ($ m_{H_2}>2m_t $ ). The decay$ H_2\to\gamma\gamma $ has a branching ratio of the order$ 3 \times 10^{-4}-5\times 10^{-6} $ in the interval$ 2m_t-1000 $ GeV. Finally, we find that$ BR(H_2\to Z\gamma) $ can reach values as high as$ 7\times 10^{-5} $ .For the production of the heavy Higgs boson, we focus on the gluon fusion mechanism, which is the dominant production mechanism for the SM case. The corresponding cross-section is displayed in Fig. 8(a), whereas the number of signal events, considering the optimal integrated luminosity (
$ {\cal{L}} = 3 $ ab$ ^{-1} $ ) to be achieved at the HL-LHC, is depicted in Fig. 8(b).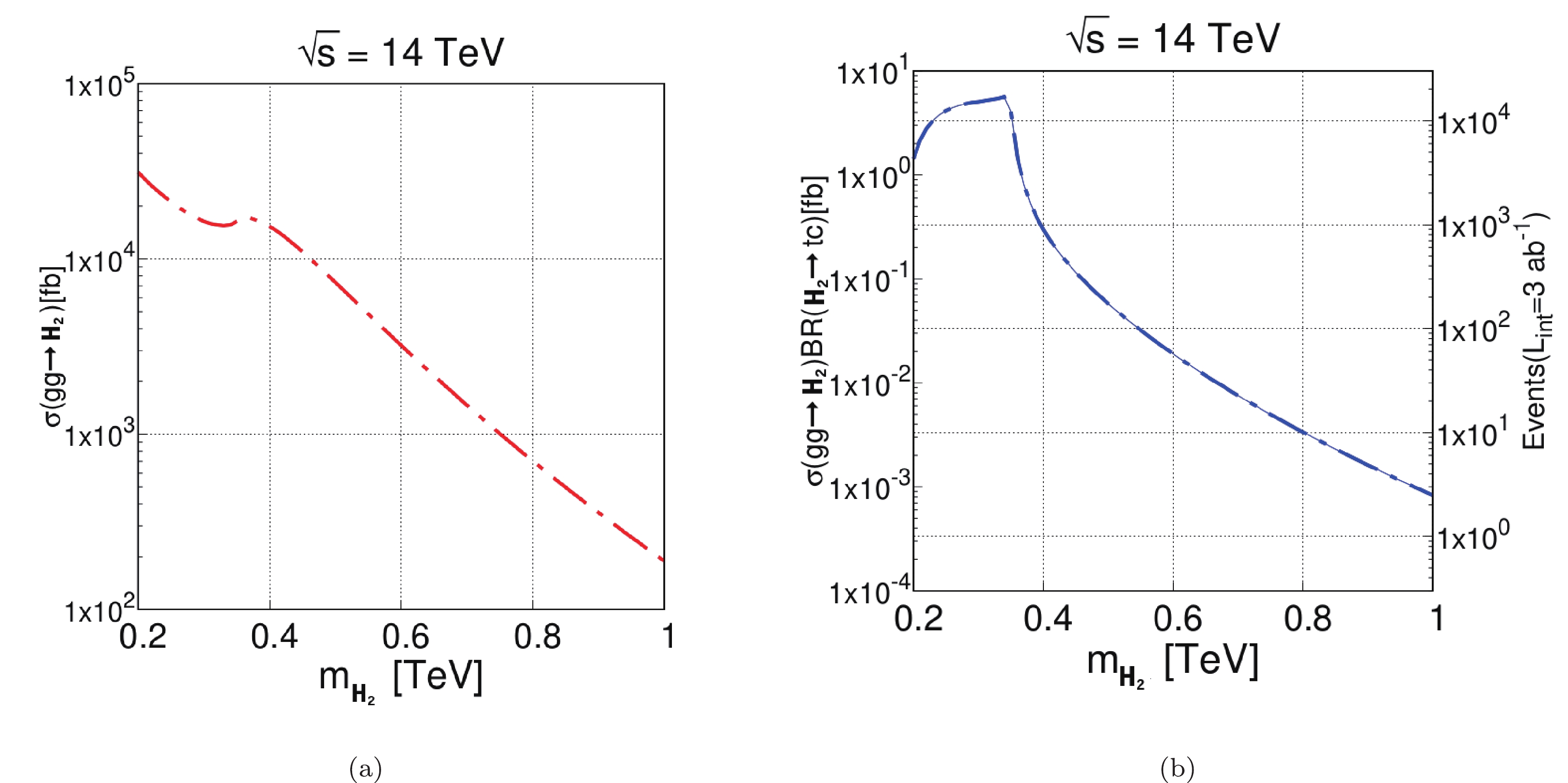
Figure 8. (color online) (a)
$ H_2 $ cross-section as function of$ m_{H_2} $ through gluon fusion mechanism and (b) number of signal events at center-of-mass energy equal to 14 TeV and integrated luminosity of 3 ab$ ^{-1} $ . We use the values of the parameters shown in Table 2.As in the previous section, we first define both the signal and the main SM background processes, as follows:
● Signal:
The signature searched is
$ gg\to h_2\to tc\to b\ell\nu_{\ell}c $ , where$ \ell = e,\,\mu $ .● Background:
The dominant SM background processes to the final state
$ bj\ell\nu_{\ell} $ originates from:1.
$ Wjj+Wb\bar{b}; $ 2. s and t channel single top
$ tb+tj; $ 3. Another important background is the
$ t\bar{t} $ production, where one of the two leptons is missed for both top quarks decaying semileptonically, or two of the four jets are missed when only one of the top quarks decays semileptonically.The kinematic cuts imposed are as follows:
● The main kinematic cut to isolate the signal is the transverse mass
$ M_{\rm T} $ , which is defined as:$ M_{\rm T}^{\ell} = \sqrt{2|\vec{P}_{\rm T}^{\ell}||\vec{E}_{\rm T}^{\rm{miss}}|(1-\cos\Delta\phi_{\vec{P}_{\rm T}^{\ell}-\vec{E}_{\rm T}^{\rm{miss}}})}. $

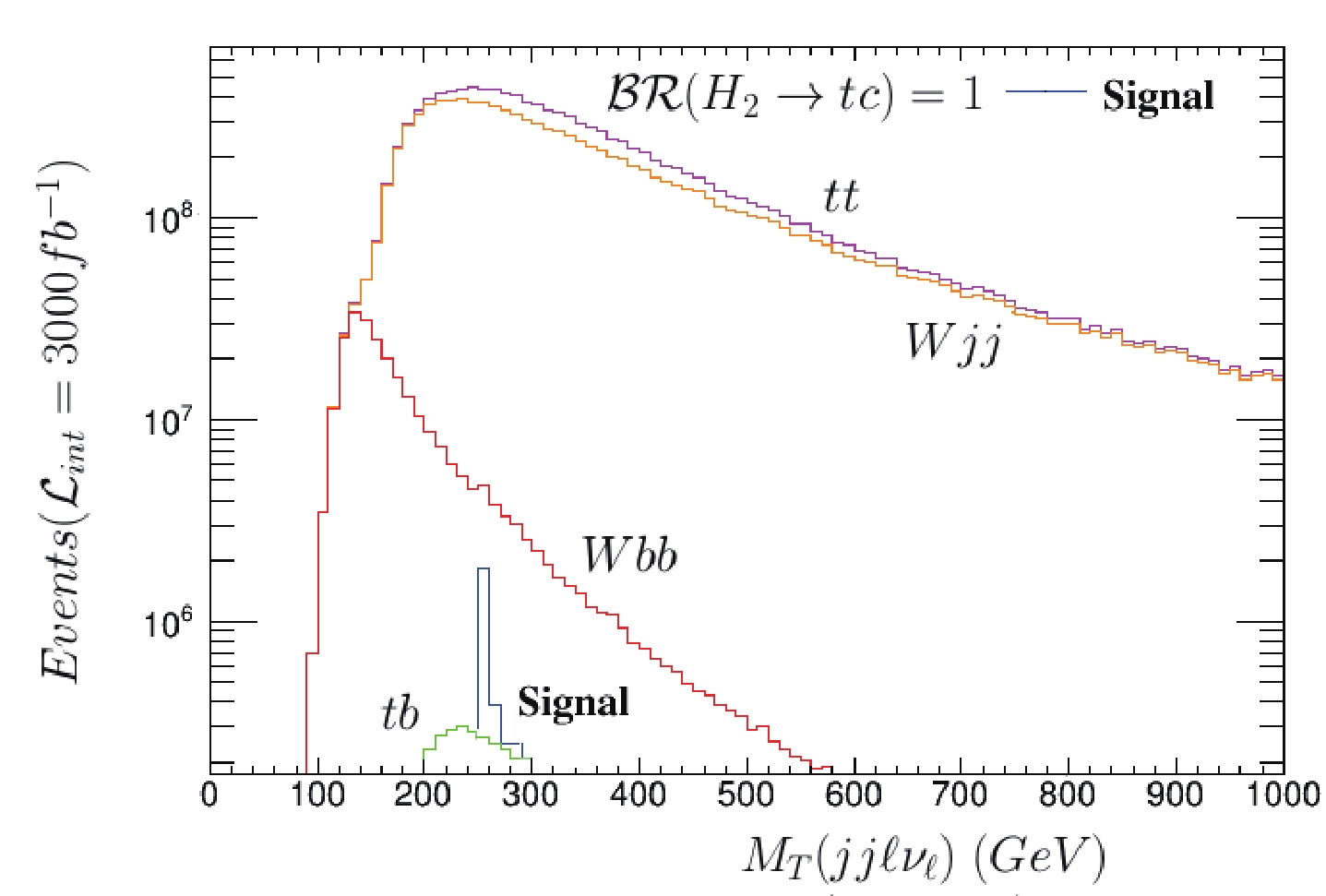
(65) Figure 9 presents the transverse mass distribution of the signal and backgrounds, without cuts, where we assume that
$ BR(H_2\to tc) = 1 $ to highlight the signal. Thereafter, we impose the cut to highlight the signal. Subsequently, we impose the cut:$ m_{H_2}-15<M_{\rm T}^{\ell}<m_{H_2}+15 $ (GeV).● We require two jets with
$ |\eta^j|<2.5 $ and$ p_{\rm T}^j>30 $ GeV, one of which is tagged as a b-jet.● We require one isolated lepton (
$ e\;{\rm{or}}\;\mu $ ) with$ |\eta^{\ell}|<2.5 $ and$ p_T^{\ell}>20 $ GeV.● We also consider a cut for the missing transverse energy
$ {\not \!\!E}_T>40 $ GeV owing to undetected neutrinos.After applying the above kinematic cuts (and also considering tagging and mistagging efficiencies as in the previous section) to the signal and main background processes, we can compute the signal significance, which is defined as
$ N_{\rm S}/\sqrt{N_{\rm S}+N_{\rm B}} $ , where$ N_{\rm S} $ ($ N_{\rm B} $ ) is the number of signal (background) events once the kinematic cuts have been applied.Meanwhile, in Fig. 10, we present the contours of the signal significance as a function of the Higgs boson mass
$ M_{H_2} $ , and display (in colors) the integrated luminosity.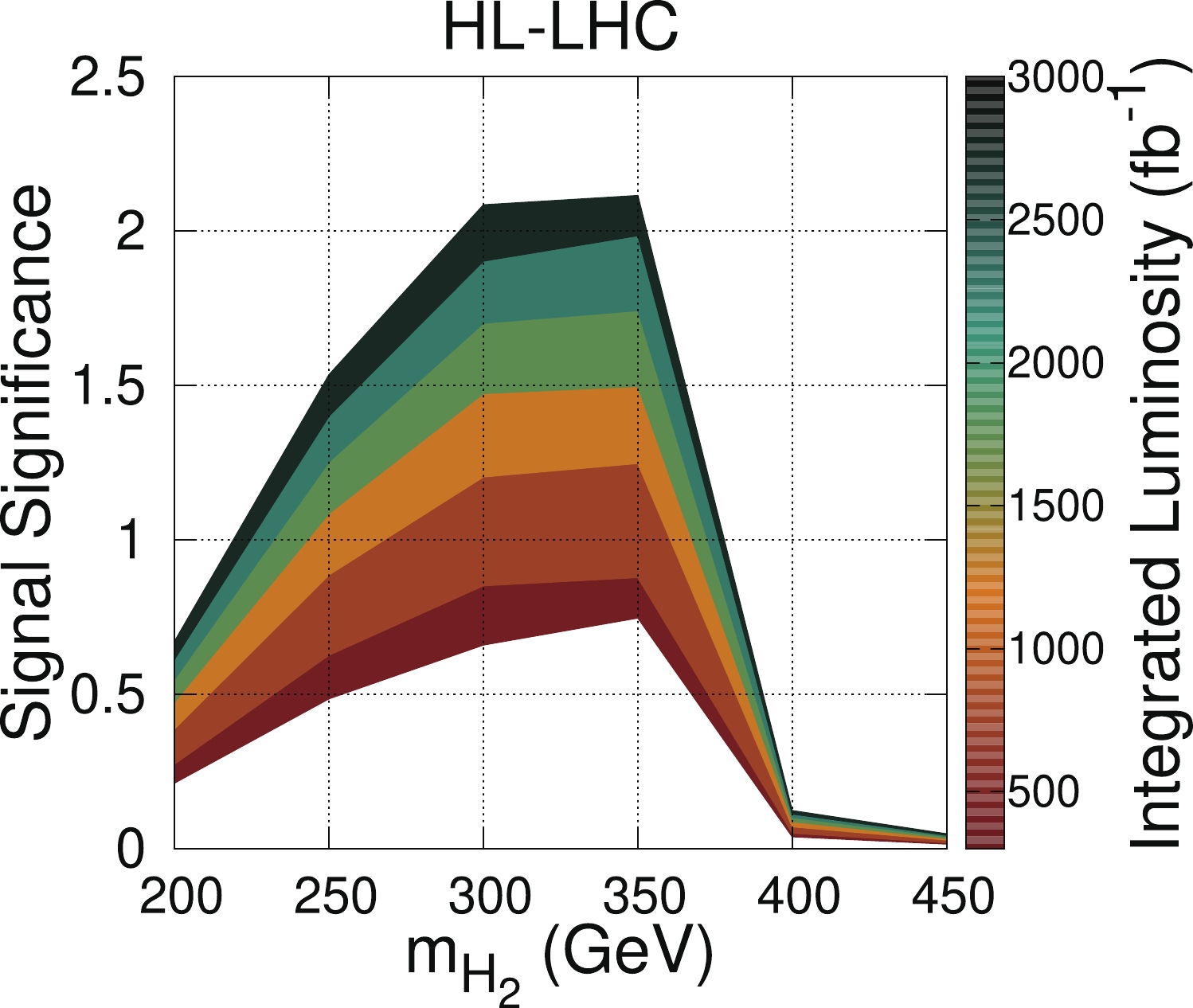
Figure 10. (color online) Signal significance as function of integrated luminosity and
$ m_{H_2} $ , using parameters shown in Table 2.From Fig. 10 that the largest significance can be achieved with the largest luminosity for a certain range of Higgs masses. For example, it will be possible to achieve a significance of 2.1
$ \sigma $ for a luminosity of the order 3000 fb$ ^{-1} $ for$ m_{H_2}\sim 2m_t $ , whereas in the final stage of the LHC (with an integrated luminosity of 300 fb$ ^{-1} $ ), the signal significance will only be approximately 0.75$ \sigma $ . -
We have presented a "private" SUSY Higgs model that includes four Higgs doublets, in which each fermion type (up, down, and charged leptons) obtains its mass from a different Higgs doublet
$ H_f $ , with$ f = u1, d, e $ , involving three of the four Higgs doublets of the model. According to the anomaly cancellation constraint, the remaining doublet$ H_{2u} $ could couple at most with up-type quarks, and thus, in principle, this model could allow for the presence of FCNCs in the up-quark sector. We studied the Yukawa Lagrangian and the Higgs potential of the model to identify the Higgs mass eigenstates and their interactions. Thereafter, we identified the Yukawa couplings for the lighter scalars$ H_1 ( = h) $ and$ H_2 $ . Using the LHC results on the signal strengths, we derived constraints on the parameter space of our "private Higgs" model, including those obtained by the LHC on the FCNC decay$ t \rightarrow ch $ . In general, the constraints on the FCNC parameters ($ \chi_{ij} $ ) of the two-Higgs models of type-III, which are expected to be of$ O(1) $ , are now becoming close to$ O(0.1) $ , which signals the need for some fine-tuning for the consistency of such models.For the allowed region of the parameter space, we calculated the branching ratio for the decay
$ t \rightarrow ch $ , which reaches values of the order$ BR (t \rightarrow ch) \approx {\cal{O}}(10^{-4} - 10^{-5} ) $ . We subsequently studied the prospects to improve the detection of this mode in the future HL-LHC phase, focusing on the channels$ t \to c h(\to \gamma\gamma) $ and$ t \to c h(\to b\bar{b}) $ , with a set of kinematic cuts inspired by the current searches of CMS and ATLAS. As a result we found that it is possible to cover such a level of branching ratios with significances of slightly below$ 1\sigma $ for the channel$ t \to c h(\to b\bar{b}) $ with$ Y_{tc} \simeq 0.3 $ , whereas the significance for the mode$ t \to c h(\to \gamma\gamma) $ is slightly above$ 1\sigma $ for$ Y_{tc} \simeq 0.3 $ . Clearly, further work is required to find better means of improving the sensitivity of the HL-LHC to the top quark decay$ t \to ch $ through these Higgs decay modes.We also studied the FCNC decay of the next-to-lightest neutral CP-even Higgs boson,
$ H_2 \rightarrow tc $ , which can also reach$ BR(H_2 \rightarrow tc) \approx {\cal{O}}(10^{-4} - 10^{-5} ) $ . The detectability of the signal at the HL-LHC was also studied, with a set of standard cuts imposed for both the signal and backgrounds, and it was found that it could be possible to achieve a significance of 2.1$ \sigma $ in the mass range$ \simeq 300-350 $ GeV, with an integrated luminosity of 3000 fb$ ^{-1} $ . Our results are relevant because they can be viewed as additional motivation for the LHC experiments to improve the search for the FCNC top decays, and to explore the heavy Higgs spectrum through the FCNC decay modes. -
We would like to acknowledge the support of CONACYT and SNI. M. A. Pérez de León is supported by a CONACYT graduate student fellowship. CIFFU is supported by VIEP-BUAP as a special project. B.L. is grateful for the support of UNAH.
A private SUSY 4HDM with FCNC in the up-sector
- Received Date: 2020-08-13
- Available Online: 2021-02-15
Abstract: We present a SUSY model with four Higgs doublets of the "private type," in which all fermion types (up, down, and charged leptons) obtain their masses from a different Higgs doublet





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: