Abstract
HTML
Reference
Related
PDF
-
The
B0→J/ψK+K− decay was first observed by the LHCb experiment with a branching fraction of(2.51±0.35±0.19)×10−6 [1]. It proceeds primarily through the Cabibbo-suppressedˉb→ˉccˉd transition. TheK+K− pair can come either directly from theB0 decay via ansˉs pair created in the vacuum, or from the decay of intermediate states that contain bothdˉd andsˉs components, such as thea0(980) resonance①. There is a potential contribution from theϕ meson as an intermediate state. The decayB0→J/ψϕ is suppressed by the Okubo-Zweig-Iizuka (OZI) rule that forbids disconnected quark diagrams [2-4]. The size of this contribution and the exact mechanism to produce theϕ meson in this process are of particular theoretical interest [5-7]. Under the assumption that the dominant contribution is via a smalldˉd component in theϕ wave-function, arising fromω−ϕ mixing (Fig. 1(a)), the branching fraction of theB0→J/ψϕ decay is predicted to be of the order of10−7 [5]. Contributions toB0→J/ψϕ decays from the OZI-suppressed tri-gluon fusion (Fig. 1(b)), photoproduction and final-state rescattering are estimated to be at least one order of magnitude lower [7]. Experimental studies of the decayB0→J/ψϕ could provide important information about the dynamics of OZI-suppressed decays.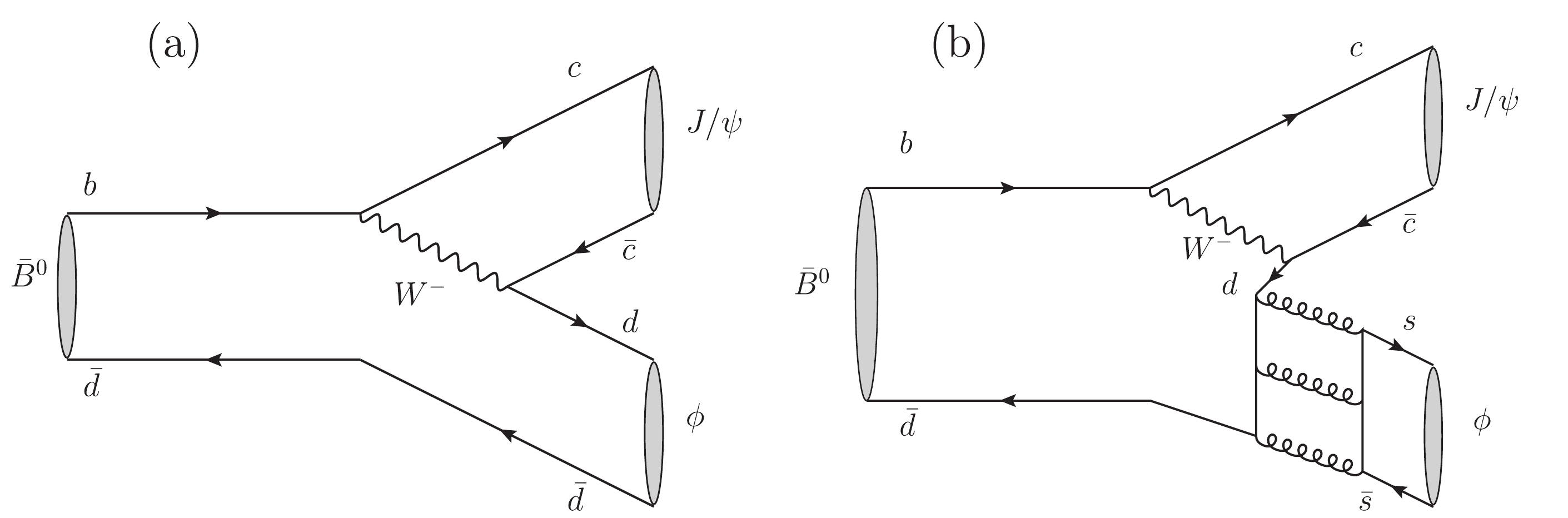
Figure 1. Feynman diagrams for the decay
B0→J/ψϕ via (a)ω−ϕ mixing and (b) tri-gluon fusion.No significant signal of
B0→J/ψϕ decay has been observed in previous searches by several experiments. Upper limits on the branching fraction of the decay have been set by BaBar [8], Belle [9] and LHCb [1]. The LHCb limit was obtained using a data sample corresponding to an integrated luminosity of 1fb−1 ofpp collision data, collected at a centre-of-mass energy of 7TeV . This paper presents an update on the search forB0→J/ψϕ decays using a data sample corresponding to an integrated luminosity of 9fb−1 , including 3fb−1 collected at 7 and 8TeV , denoted as Run 1, and 6fb−1 collected at 13TeV , denoted as Run 2.The LHCb measurement in Ref. [1] is obtained from an amplitude analysis of
B0→J/ψK+K− decays over a widem(K+K−) range from theK+K− mass threshold to 2200MeV/c2 . This paper focuses on theϕ(1020) region, with theK+K+ mass in the range 1000–1050MeV/c2 , and on studies of theJ/ψK+K− andK+K− mass distributions, to distinguish theB0→J/ψϕ signal from the non-resonant decayB0→J/ψK+K− and background contaminations. The abundant decayB0s→J/ψϕ is used as the normalisation channel. The choice of mass fits over a full amplitude analysis is motivated by several considerations. The sharpϕ mass peak provides a clear signal characteristic and the lineshape can be very well determined using the copiousB0s→J/ψϕ decays. On the other hand, interference of the S-wave (eithera0(980)/f0 (980) or non-resonant) and P-wave amplitudes vanishes in them(K+K−) spectrum, up to negligible angular acceptance effects, after integrating over the angular variables. Furthermore, significant correlations observed betweenm(J/ψK+K−) ,m(K+K−) and angular variables make it challenging to describe the mass-dependent angular distributions of both signal and background, which are required for an amplitude analysis. Finally, the power of the amplitude analysis in discriminating the signal from the non-ϕ contribution and background is reduced by the large number of parameters that need to be determined in the fit. In addition, a good understanding of the contamination fromB0s→J/ψK+K− decays in theB0 mass-region is essential in the search forB0→J/ψϕ . -
The LHCb detector [10, 11] is a single-arm forward spectrometer covering the pseudorapidity range
2<η<5 , designed for the study of particles containing b or c quarks. The detector includes a high-precision tracking system consisting of a silicon-strip vertex detector surrounding thepp interaction region, a large-area silicon-strip detector located upstream of a dipole magnet with a bending power of about4Tm , and three stations of silicon-strip detectors and straw drift tubes placed downstream of the magnet. The tracking system provides a measurement of the momentum, p, of charged particles with a relative uncertainty that varies from 0.5% at low momentum to 1.0% at 200GeV/c . The minimum distance of a track to a primary vertex (PV), the impact parameter (IP), is measured with a resolution of(15+29/pT)μm , wherepT is the component of the momentum transverse to the beam, inGeV/c . Different types of charged hadrons are distinguished using information from two ring-imaging Cherenkov detectors. Photons, electrons and hadrons are identified by a calorimeter system consisting of scintillating-pad and preshower detectors, an electromagnetic and a hadronic calorimeter. Muons are identified by a system composed of alternating layers of iron and multiwire proportional chambers.Samples of simulated decays are used to optimise the signal candidate selection and derive the efficiency of selection. In the simulation,
pp collisions are generated using PYTHIA [12, 13] with a specific LHCb configuration [14]. Decays of unstable particles are described by EVTGEN [15], in which final-state radiation is generated using PHOTOS [16]. The interaction of the generated particles with the detector, and its response, are implemented using the GEANT4 toolkit [17, 18] as described in Ref. [19]. -
The online event selection is performed by a trigger, which consists of a hardware stage, based on information from the calorimeter and muon systems, followed by a software stage, which applies a full event reconstruction. An inclusive approach for the hardware trigger is used to maximise the available data sample, as described in Ref. [20]. Since the centre-of-mass energies and trigger thresholds are different for the Run 1 and Run 2 data-taking, the offline selection is performed separately for the two periods, following the procedure described below. The resulting data samples for the two periods are treated separately in the subsequent analysis procedure.
The offline selection comprises two stages. First, a loose selection is used to reconstruct both
B0→J/ψϕ andB0s→J/ψϕ candidates in the same way, given their similar kinematics. Two oppositely charged muon candidates withpT>500MeV/c are combined to form aJ/ψ candidate. The muon pair is required to have a common vertex and an invariant mass,m(μ+μ−) , in the range 3020–3170MeV/c2 . A pair of oppositely charged kaon candidates identified by the Cherenkov detectors is combined to form aϕ candidate. TheK+K− pair is required to have an invariant mass,m(K+K−) , in the range 1000–1050MeV/c2 . TheJ/ψ andϕ candidates are combined to form aB0(s) candidate, which is required to have good vertex quality and invariant mass,m(J/ψK+K−) , in the range 5200–5550MeV/c2 . The resultingB0(s) candidate is assigned to the PV with which it has the smallestχ2IP , whereχ2IP is defined as the difference in the vertex-fitχ2 of a given PV reconstructed with and without the particle being considered. The invariant mass of theB0(s) candidate is calculated from a kinematic fit for which the momentum vector of theB0(s) candidates is aligned with the vector connecting the PV to theB0(s) decay vertex andm(μ+μ−) is constrained to the knownJ/ψ meson mass [21]. In order to suppress the background due to the random combination of a promptJ/ψ meson and a pair of charged kaons, the decay time of theB0(s) candidate is required to be greater than 0.3ps .In a second selection stage, a boosted decision tree (BDT) classifier [22, 23] is used to further suppress combinatorial background. The BDT classifier is trained using simulated
B0s→J/ψϕ decays representing the signal, and candidates withm(J/ψK+K−) in the range 5480–5550MeV/c2 as background. Candidates in both samples are required to have passed the trigger and the loose selection described above. Using a multivariate technique [24], theB0s→J/ψϕ simulation sample is corrected to match the observed distributions in background-subtracted data, including that of thepT and pseudorapidity of theB0s , theχ2IP of theB0s decay vertex, theχ2 of the decay chain of theB0s candidate [25], the particle identification variables, the track-fitχ2 of the muon and kaon candidates, and the numbers of tracks measured simultaneously in both the vertex detector and tracking stations.The input variables of the BDT classifier are the minimum track–fit
χ2 of the muons and the kaons, thepT of theB0(s) candidate and theK+K− combination, theχ2 of theB0(s) decay vertex, particle identification probabilities for muons and kaons, the minimumχ2IP of the muons and kaons, theχ2 of theJ/ψ decay vertex, theχ2IP of theB0(s) candidate, and theχ2 of theB0(s) decay chain fit. The optimal requirement on the BDT response for theB0(s) candidates is obtained by maximising the quantityε/√N , whereε is the signal efficiency determined in simulation and N is the number of candidates found in the±15MeV/c2 region around the knownB0 mass [21].In addition to combinatorial background, the data also contain fake candidates from
Λ0b→J/ψpK− (B0→J/ψK+π− ) decays, where the proton (pion) is misidentified as a kaon. To suppress these background sources, aB0(s) candidate is rejected if its invariant mass, computed with one kaon interpreted as a proton (pion), lies within±15MeV/c2 of the knownΛ0b (B0 ) mass [21] and if the kaon candidate also satisfies proton (pion) identification requirements.A previous study of
B0s→J/ψϕ decays found that the yield of the background fromB0→J/ψK+π− decays is only 0.1% of theB0s→J/ψϕ signal yield [20]. Furthermore, only 1.2% of these decays, corresponding to about one candidate (three candidates) in the Run 1 (Run 2) data sample, fall in theB0 mass region 5265–5295MeV/c2 , according to simulation. Thus this background is neglected. The fraction of events containing more than one candidate is 0.11% in Run 1 data and 0.70% in Run 2 data and these events are removed from the total data sample. The acceptance, trigger, reconstruction and selection efficiencies of the signal and normalization channels are determined using simulation, which is corrected for the efficiency differences with respect to the data. The ratio of the total efficiencies ofB0→J/ψϕ andB0s→J/ψϕ is estimated to be0.99±0.03±0.03 for Run 1 and0.99±0.01±0.02 for Run 2, where the first uncertainties are statistical and the second ones are associated with corrections to the simulation. The polarisation amplitudes are assumed to be the same inB0→J/ψϕ andB0s→J/ψϕ decays. The systematic uncertainty associated with this assumption is found to be small and is neglected. -
There is a significant correlation between
m(J/ψK+K−) andm(K+K−) inB0(s)→J/ψK+K− decays, as illustrated in Fig. 2. Hence, the search forB0→J/ψϕ decays is carried out by performing sequential fits to the distributions ofm(J/ψK+K−) andm(K+K−) . A fit to them(J/ψK+K−) distribution is used to estimate the yields of the background components in the±15MeV/c2 regions around theB0s andB0 nominal masses. A subsequent simultaneous fit to them(K+K−) distributions of candidates falling in the twoJ/ψK+K− mass windows, with the background yields fixed to their values from the first step, is performed to estimate the yield ofB0→J/ψϕ decays.
Figure 2. (color online) Distributions of the invariant mass
m(K+K−) in differentm(J/ψK+K−) intervals with boundaries at 5220, 5265, 5295, 5330, 5400 and 5550MeV/c2 . They are obtained using simulatedB0s→J/ψϕ decays and normalised to unity.The probability density function (PDF) for the
m(J/ψK+K−) distribution of both theB0→J/ψK+K− andB0s→J/ψK+K− decays is modelled by the sum of a Hypatia [26] and a Gaussian function sharing the same mean. The fraction, the width ratio between the Hypatia and Gaussian functions and the Hypatia tail parameters are determined from simulation. Them(J/ψK+K−) shape of theΛ0b→J/ψpK− background is described by a template obtained from simulation, while the combinatorial background is described by an exponential function with the slope left to vary. The PDFs ofB0→J/ψK+K− andB0s→J/ψK+K− decays share the same shape parameters, and the difference between theB0s andB0 masses is constrained to the known mass difference of87.23±0.16 MeV/c2 [21].An unbinned maximum-likelihood fit is performed in the
m(J/ψK+K−) range 5220–5480MeV/c2 for Run 1 and Run 2 data samples separately. The yield ofΛ0b→J/ψpK− is estimated from a fit to theJ/ψpK− mass distribution with one kaon interpreted as a proton. This yield is then constrained to the resulting estimate of399±26 (1914±47 ) in theJ/ψK+K− mass fit for the Run 1 (Run 2). Them(J/ψK+K−) distributions, superimposed by the fit results, are shown in Fig. 3. Table 1 lists the obtained yields of theB0→J/ψK+K− andB0s→J/ψK+K− decays, theΛ0b background and the combinatorial background in the full range as well as in the±15 MeV/c2 regions around the knownB0s andB0 masses.
Figure 3. (color online) The distributions of
m(J/ψK+K−) , superimposed by the fit results, for (left) Run 1 and (right) Run 2 data samples. The top row shows the fullB0s signals in logarithmic scale while the bottom row is presented in a reduced vertical range to make the B0 peaks visible. The violet (red) solid lines represent theB0(s)→J/ψK+K− decays, the orange dotted lines show theΛ0b background and the green dotted lines show the combinatorial background.Data Category Full B0s region
B0 region
Run 1 B0s→J/ψK+K− 
55498 ± 238 51859 ± 220 35 ± 6 B0→J/ψK+K− 
127 ± 19 0 119 ± 18 Λ0b→J/ψpK− 
407 ± 26 55 ± 8 61 ± 8 Combinatorial background 758 ± 55 85 ± 11 94 ± 11 Run 2 B0s→J/ψK+K− 
249670 ± 504 233663 ± 472 153 ± 12 B0→J/ψK+K− 
637 ± 39 0 596 ± 38 Λ0b→J/ψpK− 
1943 ± 47 261 ± 16 290 ± 17 Combinatorial background 2677 ± 109 303 ± 20 331 ± 21 Table 1. Measured yields of all contributions from the fit to
J/ψK+K− mass distribution, showing the results for the full mass range and for theB0s andB0 regions.Assuming the efficiency is independent of
m(K+K−) , theϕ meson lineshape fromB0→J/ψϕ (B0s→J/ψϕ ) decays in theB0 (B0s ) region is given bySϕ(m)≡PBPRF2R(PR,P0,d)(PRm′)2LR|Aϕ(m′;m0,Γ0)|2⊗G(m−m′;0,σ),
(1) where
Aϕ is a relativistic Breit-Wigner amplitude function [27] defined asAϕ(m;m0,Γ0)=1m20−m2−im0Γ(m),Γ(m)=Γ0(PRP0)2LR+1m0mF2R(PR,P0,d).
(2) The parameter m (
m′ ) denotes the reconstructed (true)K+K− invariant mass,m0 andΓ0 are the mass and decay width of theϕ(1020) meson,PB is theJ/ψ momentum in theB0s (B0 ) rest frame,PR (P0 ) is the momentum of the kaons in theK+K− (ϕ(1020) ) rest frame,LR is the orbital angular momentum between theK+ andK− ,FR is the Blatt-Weisskopf function, and d is the size of the decaying particle, which is set to be 1.5(GeV/c)−1∼ 0.3 fm [28]. The amplitude squared is folded with a Gaussian resolution function G. ForLR=1 ,FR has the formFR(PR,P0,d)=√1+(P0d)21+(PRd)2,
(3) and depends on the momentum of the decay products
PR [27].As is shown in Fig. 2, due to the correlation between the reconstructed masses of
K+K− andJ/ψK+K− , the shape of them(K+K−) distribution strongly depends on the chosenm(J/ψK+K−) range. The top two plots in Fig. 3 show them(J/ψK+K−) distributions for Run 1 and Run 2 separately, where a smallB0 signal can be seen on the tail of a largeB0s signal. Therefore, it is necessary to estimate the lineshape of theK+K− mass spectrum fromB0s→J/ψϕ decays in theB0 region. Them(K+K−) distribution of theB0s→J/ψϕ tail leaking into theB0 mass window can be effectively described by Eq. (1) with modified values ofm0 andΓ0 , which are extracted from an unbinned maximum-likelihood fit to theB0s→J/ψϕ simulation sample.The non-
ϕ K+K− contributions toB0→J/ψK+K− (B0s→J/ψK+K− ) decays include that froma0 (980) [1] (f0 (980) [29]) and nonresonantK+K− in an S-wave configuration. The PDF for this contribution is given bySnon(m)≡PBPRFB2(PBmB)2|AR(m)×eiδ+ANR|2,
(4) where m is the
K+K− invariant mass,mB is the knownB0(s) mass [21],FB is the Blatt-Weisskopf barrier factor of theB0(s) meson,AR andANR represent the resonant (a0 (980) orf0 (980)) and nonresonant amplitudes, andδ is a relative phase between them. The nonresonant amplitudeANR is modelled as a constant function. The lineshape of thea0 (980) (f0 (980)) resonance can be described by a Flatté function [30] considering the coupled channelsηπ0 (ππ ) andKK . The Flatté functions are given byAa0(m)=1m2R−m2−i(g2ηπρηπ+g2KKρKK)
(5) for the
a0 (980) resonance andAf0(m)=1m2R−m2−imR(gππρππ+gKKρKK)
(6) for the
f0 (980) resonance. The parametermR denotes the pole mass of the resonance for both cases. The constantsgηπ (gππ ) andgKK are the coupling strengths ofa0 (980) (f0 (980)) to theηπ0 (ππ ) andKK final states, respectively. Theρ factors are given by the Lorentz-invariant phase space:ρππ=23√1−4m2π±m2+13√1−4m2π0m2,
(7) ρKK=12√1−4m2K±m2+12√1−4m2K0m2,
(8) ρηπ=√(1−(mη−mπ0)2m2)(1−(mη+mπ0)2m2).
(9) The parameters for the
a0 (980) lineshape aremR=0.999±0.002GeV/c2 ,gηπ=0.324±0.015GeV/c2 , andg2KK/g2ηπ=1.03±0.14 , determined by the Crystal Barrel experiment [31]; the parameters for thef0 (980) lineshape aremR=0.9399±0.0063GeV/c2 ,gππ=0.199±0.030GeV/c2 , andgKK/gππ=3.0±0.3 , according to the previous analysis ofB0s→J/ψπ+π− decays [32].For the
Λ0b→J/ψpK− background, no dependency of them(K+K−) shape onm(J/ψK+K−) is observed in simulation. Therefore, a common PDF is used to describe them(K+K−) distributions in both theB0s andB0 regions. The PDF is modelled by a third-order Chebyshev polynomial function, obtained from the unbinned maximum-likelihood fit to the simulation shown in Fig. 4.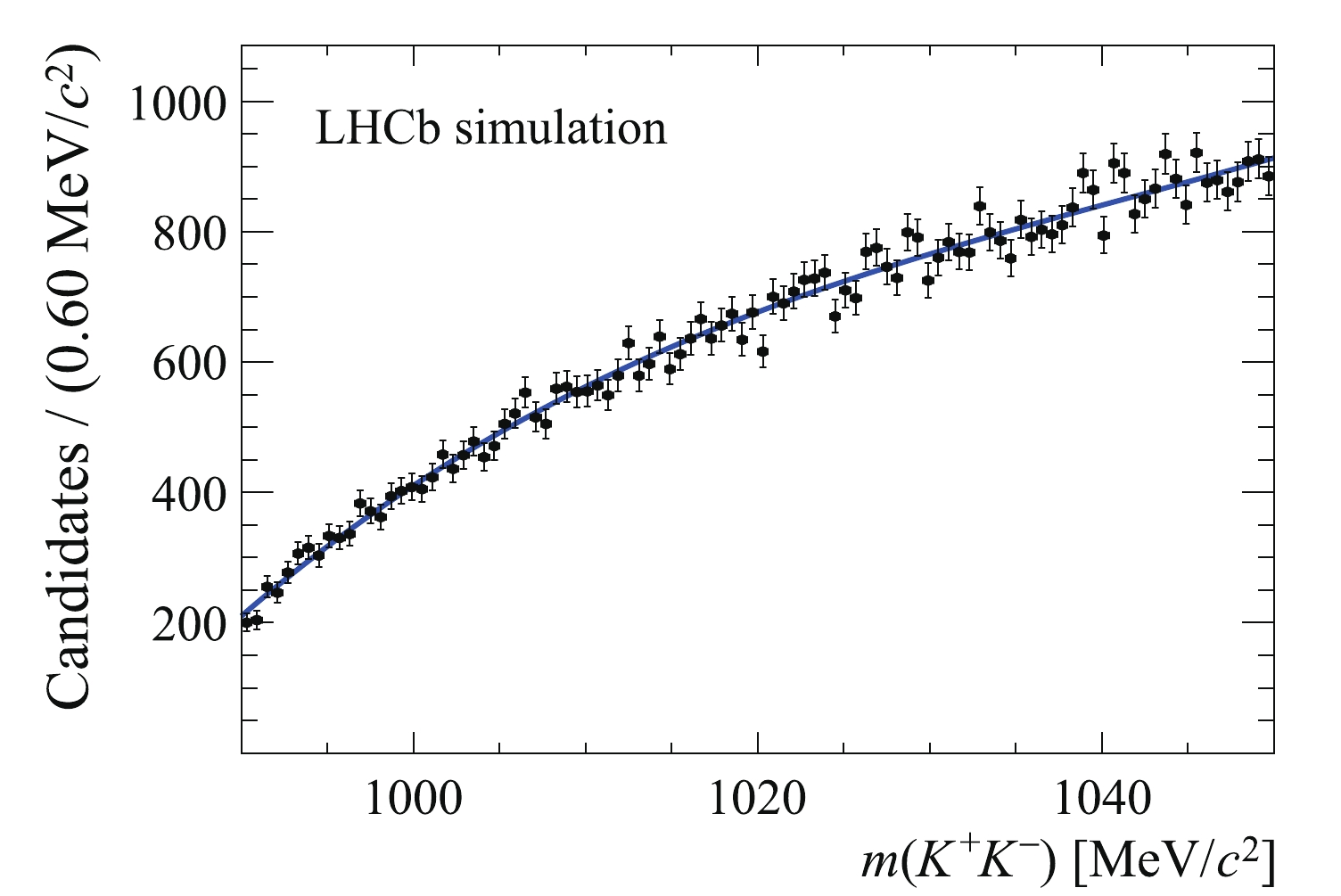
Figure 4. Distribution of
m(K+K−) in aΛ0b→J/ψpK− simulation sample superimposed with a fit to a polynomial function.In order to study the
m(K+K−) shape of the combinatorial background in theB0 region, a BDT requirement that strongly favours background is applied to form a background-dominated sample. SimulatedΛ0b→J/ψpK− andB0s→J/ψϕ events are then injected into this sample with negative weights to subtract these contributions. The resultingm(K+K−) distribution is shown in Fig. 5, which comprises aϕ resonance contribution and randomK+K− combinations, where the shape of the former is described by Eq. (1) and the latter by a second-order Chebyshev polynomial function. To validate the underlying assumptions of this procedure, them(K+K−) shape has been checked to be compatible in differentJ/ψK+K− mass regions and with different BDT requirements.
Figure 5. (color online)
m(K+K−) distributions of the enhanced combinatorial background in the (left) Run 1 and (right) Run 2 data samples. TheB0s→J/ψϕ andΛ0b→J/ψpK− backgrounds are subtracted by injecting simulated events with negative weights.A simultaneous unbinned maximum-likelihood fit to the four
m(K+K−) distributions in bothB0s andB0 regions of Run 1 and Run 2 data samples is performed. Theϕ resonance inB0(s)→J/ψϕ decays is modelled by Eq. (1). The non-ϕ K+K− contribution toB0(s)→J/ψK+K− decays is described by Eq. (4). The tail ofB0s→J/ψϕ decays in theB0 region is described by the extracted shape from simulation. TheΛ0b background and the combinatorial background are described by the shapes shown in Figs. 4 and 5, respectively. Allm(K+K−) shapes are common to theB0 andB0s regions, except that of theB0s tail, which is only needed for theB0 region. The mass and decay width ofϕ(1020) meson are constrained to their PDG values [21] while the width of them(K+K−) resolution function is allowed to vary in the fit. The pole mass off0 (980) (a0 (980)) and the coupling factors, includinggππ ,gKK/gππ ,g2ηπ andg2KK/g2ηπ , are fixed to their central values in the reference fit. The amplitudeANR is allowed to vary freely, while the relative phaseδ between thef0 (980) (a0 (980)) and nonresonance amplitudes is constrained to−255±35 (−60±26 ) degrees, which was determined in the amplitude analysis ofB0s→J/ψK+K− (B0→J/ψK+K− ) decays [1, 29]. The yields of theΛ0b background, theB0s→J/ψϕ tail leaking into theB0 region and the combinatorial background are fixed to the corresponding values in Table 1, while the yields of non-ϕ K+K− forB0s andB0 decays as well as the yield ofB0s→J/ψϕ decays take different values for Run 1 and Run 2 data samples and are left to vary in the fit.The branching fraction
B(B0→J/ψϕ) , the parameter of interest to be determined by the fit, is common for Run 1 and Run 2. The yield ofB0→J/ψϕ decays is internally expressed according toNB0→J/ψϕ=NB0s→J/ψϕ×B(B0→J/ψϕ)B(B0s→J/ψϕ)×εB0εB0s×1fs/fd,
(10) where the branching fraction
B(B0s→J/ψϕ) has been measured by the LHCb collaboration [29],εB0/εB0s is the efficiency ratio given in Sec. III,fs/fd is the ratio of the production fractions ofB0s andB0 mesons inpp collisions, which has been measured at 7TeV to be0.256±0.020 in the LHCb detector acceptance [33]. The effect of increasing collision energy onfs/fd is found to be negligible for 8TeV and a scaling factor of1.068±0.046 is needed for 13TeV [34]. The parametersB(B0s→J/ψϕ) ,εB0/εB0s andfs/fd are fixed to their central values in the baseline fit and their uncertainties are propagated toB(B0→J/ψϕ) in the evaluation of systematic uncertainties.The
m(K+K−) distributions in theB0s andB0 regions are shown in Fig. 6 for both Run 1 and Run 2 data samples. The branching fractionB(B0→J/ψϕ) is found to be(6.8±3.0(stat.))×10−8 . The significance of the decayB0→J/ψϕ , over the background-only hypothesis, is estimated to be 2.3 standard deviations using Wilks' theorem [35].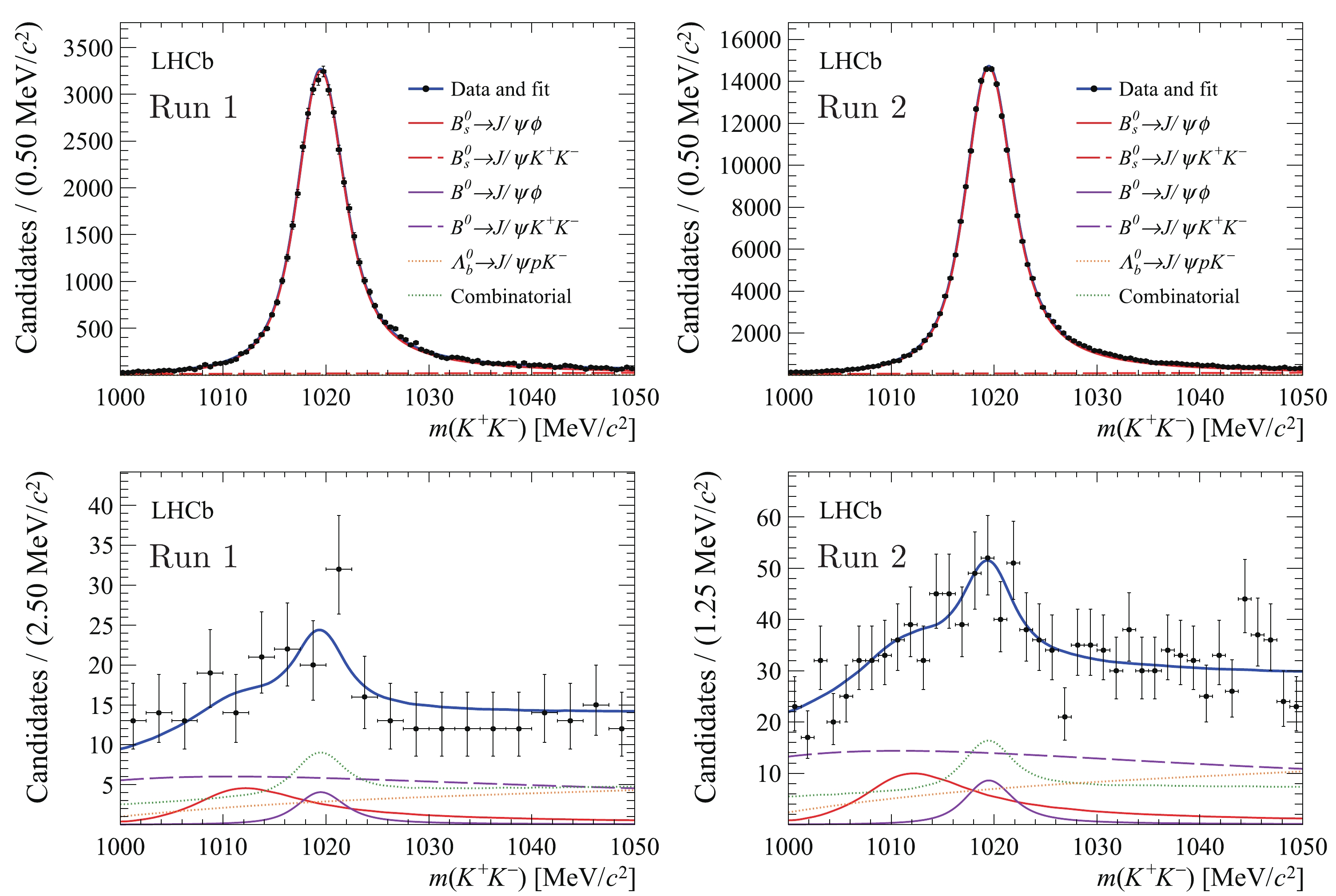
Figure 6. (color online) Distributions in the (top)
B0s and (bottom)B0 m(K+K−) regions, superimposed by the fit results. The left and right columns show the results for the Run 1 and Run 2 data samples, respectively. The violet (red) solid lines areB0(s)→J/ψϕ decays, violet (red) dashed lines are non-ϕ B0(s)→J/ψK+K− signal, green dotted lines are the combinatorial background component, and the orange dotted lines are theΛ0b background component.To validate the sequential fit procedure, a large number of pseudosamples were generated according to the fit models for the
m(J/ψK+K−) andm(K+K−) distributions. The model parameters were taken from the result of the baseline fit to the data. The fit procedure described above was applied to each pseudosample. The distributions of the obtained estimate ofB(B0→J/ψϕ) and the corresponding pulls are found to be consistent with the reference result, which indicates that the procedure has negligible bias and its uncertainty estimate is reliable. A similar check has been performed using pseudosamples generated with an alternative model for theB0→J/ψK+K− decays, which is based on the amplitude model developed for theB0s→J/ψK+K− analysis [20] and includes contributions from P-waveB0→J/ψϕ decays, S-waveB0→J/ψK+K− decays and their interference. In this case, the robustness of the fit method has also been confirmed. -
Two categories of systematic uncertainties are considered: multiplicative uncertainties, which are associated with the normalisation factors; and additive uncertainties, which affect the determination of the yields of the
B0→J/ψϕ andB0s→J/ψϕ modes.The multiplicative uncertainties include those propagated from the estimates of
B(B0s→J/ψϕ) ,fs/fd andεB0s/εB0 . Using thefs/fd measurement at 7TeV [29, 33],B(B0s→J/ψϕ) was measured to be(10.50±0.13(stat.)±0.64(syst.)±0.82(fs/fd))×10−4 . The third uncertainty is completely anti-correlated with the uncertainty onfs/fd , since the estimate ofB(B0s→J/ψϕ) is inversely proportional to the value used forfs/fd . Taking this correlation into account yieldsB(B0s→J/ψϕ)×fs/fd=(2.69±0.17)×10−4 for 7TeV . The luminosity-weighted average of the scaling factor forfs/fd for 13TeV has a relative uncertainty of 3.4%. For the efficiency ratioεB0s/εB0 , its luminosity-weighted average has a relative uncertainty of 1.8%. Summing these three contributions in quadrature gives a total relative uncertainty of 7.3% onB(B0→J/ψϕ) .The additive uncertainties are due to imperfect modeling of the
m(J/ψK+K−) andm(K+K−) shapes of the signal and background components. To evaluate the systematic effect associated with them(J/ψK+K−) model of the combinatorial background, the fit procedure is repeated by replacing the exponential function for the combinatorial background with a second-order polynomial function. A large number of simulated pseudosamples were generated according to the obtained alternative model. Each pseudosample was fitted twice, using the baseline and alternative combinatorial shape, respectively. The average difference ofB(B0→J/ψϕ) is0.03×10−8 , which is taken as a systematic uncertainty.In the
m(K+K−) fit, the yields ofΛ0b→J/ψpK− decay, combinatorial backgrounds under theB0 andB0s peaks, and that of theB0s tail leaking into theB0 region are fixed to the values in Table 1. Varying these yields separately leads to a change ofB(B0→J/ψϕ) by0.05×10−8 forΛ0b→J/ψpK− ,0.61×10−8 for the combinatorial background and0.24×10−8 for theB0s tail in theB0 region, and these are assigned as systematic uncertainties onB(B0→J/ψϕ) .The constant d in Eq. (3) is varied between 1.0 and 3.0
(GeV/c)−1 . The maximum change ofB(B0→J/ψϕ) is evaluated to be0.01×10−8 , which is taken as a systematic uncertainty.The
m(K+K−) shape of theB0s tail under theB0 peak is extracted using aB0s→J/ψϕ simulation sample. The statistical uncertainty due to the limited size of this sample is estimated using the bootstrapping technique [36]. A large number of new data sets of the same size as the original simulation sample were formed by randomly cloning events from the original sample, allowing one event to be cloned more than once. The spread in the results ofB(B0→J/ψϕ) obtained by using these pseudosamples in the analysis procedure is then adopted as a systematic uncertainty, which is evaluated to be0.29×10−8 .In the reference model, the
m(K+K−) shape of theΛ0b→J/ψpK− background is determined from simulation, under the assumption that this shape is insensitive to them(J/ψK+K−) region. A sideband sample enriched withΛ0b→J/ψpK− contributions is selected by requiring one kaon to have a large probability to be a proton. An alternativem(K+K−) shape is extracted from this sample after subtracting the random combinations, and used in them(K+K−) fit. The resulting change ofB(B0→J/ψϕ) is0.28×10−8 , which is assigned as a systematic uncertainty.The
m(K+K−) shape of the combinatorial background is represented by that of theJ/ψK+K− combinations with a BDT selection that strongly favours the background over the signal, under the assumption that this shape is insensitive to the BDT requirement. Repeating them(K+K−) fit by using the combinatorial background shape obtained with two non-overlapping sub-intervals of BDT response, the result forB(B0→J/ψϕ) is found to be stable, with a maximum variation of0.16×10−8 , which is regarded as a systematic uncertainty.In Eqs. (7)–(9), the coupling factors
gηπ ,g2KK/g2ηπ ,gππ andgKK/gππ , are fixed to their mean values from Ref. [31, 32]. The fit is repeated by varying each factor by its experimental uncertainty and the maximum variation of the branching fraction is considered for each parameter. The sum of the variations in quadrature is0.06×10−8 , which is assigned as a systematic uncertainty.The systematic uncertainties are summarised in Table 2. The total systematic uncertainty is the sum in quadrature of all these contributions.
Multiplicative uncertainties Value (%) B(B0s→J/ψϕ) 
6.2 Scaling factor for fs/fd 
3.4 εB0/εB0s 
1.8 Total 7.3 Additive uncertainties Value (10−8) m(J/ψK+K−) model of combinatorial background
0.03 Fixed yields of Λ0b in
m(K+K−) fit
0.05 Fixed yields of combinatorial background in m(K+K−) fit
0.61 Fixed yields of B0s contribution in
m(K+K−) fit
0.24 Constant d 0.01 m(K+K−) shape of
B0s contribution
0.29 m(K+K−) shape of
Λ0b 
0.28 m(K+K−) shape of combinatorial background
0.16 m(K+K−) shape of non-
ϕ 
0.06 Total 0.80 Table 2. Systematic uncertainties on
B(B0→J/ψϕ) for multiplicative and additive sources.A profile likelihood method is used to compute the upper limit of
B(B0→J/ψϕ) [37, 38]. The profile likelihood ratio as a function ofB≡B(B0→J/ψϕ) is defined asλ0(B)≡L(B,ˆˆν)L(ˆB,ˆν),
(11) where
ν represents the set of fit parameters other thanB ,ˆB andˆν are the maximum likelihood estimators, andˆˆν is the profiled value of the parameterν that maximises L for the specifiedB . Systematic uncertainties are incorporated by smearing the profile likelihood ratio function with a Gaussian function which has a zero mean and a width equal to the total systematic uncertainty:λ(B)=∫+∞−∞λ0(B′)×G(B−B′,0,σsys(B′))dB′.
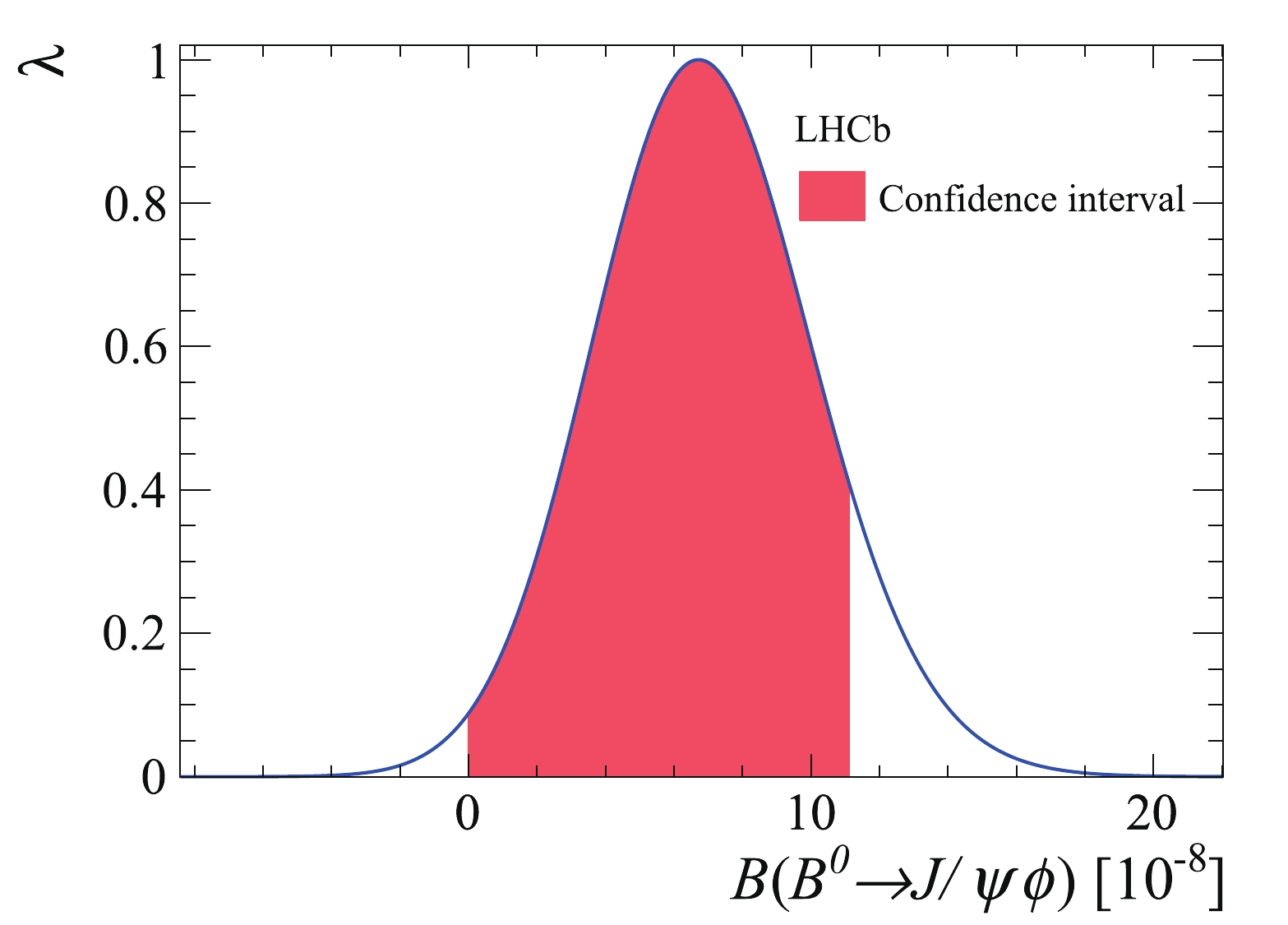
(12) The smeared profile likelihood ratio curve is shown in Fig. 7. The 90% confidence interval starting at
B=0 is shown as the red area, which covers 90% of the integral of theλ(B) function in the physical region. The obtained upper limit onB(B0→J/ψϕ) at 90% CL is1.1×10−7 .
Figure 7. (color online) Smeared profile likelihood ratio curve shown as the blue solid line, and the 90% confidence interval indicated by the red area.
-
A search for the rare decay
B0→J/ψϕ has been performed using the full Run 1 and Run 2 data samples ofpp collisions collected with the LHCb experiment, corresponding to an integrated luminosity of 9fb−1 . A br-anching fraction ofB(B0→J/ψϕ)=(6.8±3.0±0.9)×10−8 is measured, which indicates no statistically significant excess of the decayB0→J/ψϕ above the background-only hypothesis. The upper limit on its branching fraction at 90% CL is determined to be1.1×10−7 , which is compatible with theoretical expectations and improved compared with the previous limit of1.9×10−7 obtained by the LHCb experiment using Run 1 data, with a corresponding integrated luminosity of 1fb−1 . -
We express our gratitude to our colleagues in the CERN accelerator departments for the excellent performance of the LHC. We thank the technical and administrative staff at the LHCb institutes. We acknowledge support from CERN and from the national agencies: CAPES, CNPq, FAPERJ and FINEP (Brazil); MOST and NSFC (China); CNRS/IN2P3 (France); BMBF, DFG and MPG (Germany); INFN (Italy); NWO (Netherlands); MNiSW and NCN (Poland); MEN/IFA (Romania); MSHE (Russia); MICINN (Spain); SNSF and SER (Switzerland); NASU (Ukraine); STFC (United Kingdom); DOE NP and NSF (USA). We acknowledge the computing resources that are provided by CERN, IN2P3 (France), KIT and DESY (Germany), INFN (Italy), SURF (Netherlands), PIC (Spain), GridPP (United Kingdom), RRCKI and Yandex LLC (Russia), CSCS (Switzerland), IFINHH (Romania), CBPF (Brazil), PL-GRID (Poland) and OSC (USA). We are indebted to the communities behind the multiple open-source software packages on which we depend.
Search for the rare decay B0 → J/ψϕ
- Received Date: 2020-11-16
- Available Online: 2021-04-15
Abstract: A search for the rare decay
DownLoad: