-
Dark matter (DM) is always a fascinating topic, given that there is much evidence in astrophysical observations [1-3]. Weakly interacting massive particle (WIMP) is an influential candidate for cold dark matter, which is generated by the freeze-out production mechanism [4, 5]. However, recent results of direct detection of dark matter established strong constraints to WIMP at the electroweak scale. Studying the correlation between the nature of WIMP DM and its scattering with nucleon and checking the status of possible WIMP dark matter under current direct detection constraints are urgent tasks.
Supersymmetry (SUSY) is an attractive concept that builds an internal symmetry between fermions and bosons and ensures the unification of three gauge interactions. The
$ \mu $ -problem in the Minimal Supersymmetric extension to the Standard Model (MSSM), which is the simplest implementation of SUSY, can be solved by introducing a complex singlet superfield$ \hat{S} $ called the Next-to Minimal Supersymmetric Standard Model (NMSSM). The NMSSM has attracted a lot of attention especially after the Higgs discovery [6-31]. The NMSSM with non-universal Higgs masses (NUHM) [32-37] that relaxes the Higgs sector at GUT scale is known as a semi-constrained NMSSM (scNMSSM). It can satisfy current constraints including Higgs data, LHC searches for sparticles, DM relic density, direct searches for dark matter, and muon g-2 [38].In previous studies of ours on the NMSSM-NUHM [38], we developed a novel efficient method to scan the parameter space of NMSSM-NUHM that consists of Heuristically Search (HS) and Generative Adversarial Network (GAN). We found that NMSSM-NUHM can satisfy all the constraints, including DM relic density, and that the new method is efficient. Then, we studied light DM and Higgs invisible decay in the NMSSM-NUHM [39], and found four funnel-annihilation mechanisms for the lightest supersymmetric particle (LSP)
$ \tilde{\chi}^0_1 $ , namely$ h_2 $ -, Z-,$ h_1 $ -, and$ a_1 $ -funnels. In the NMSSM-NUHM, the light DM can only be singlino-higgsino like, while in the conventional NMSSM, without assumptions of parameter unifications at GUT scale, the light DM can also be bino-like, but more free parameters are needed [40, 41].In this study, we comprehensively analyzed the direct detection of light dark matter in the NMSSM-NUHM, including spin-dependent (SD) and spin-independent (SI) scattering with nucleons. The main difference between SD and SI scattering is that for SI scattering, the cross section depends on each nucleon inside a nucleus equally, and hence, it is proportional to the square of the nucleon number; however, for SD scattering, the cross section depends on the total spin of nucleons such that the contributions of additional nucleons are suppressed by Clebsch-Gordan coefficients, and hence, the SD cross section does not increase with the nucleon number [42, 43]. The correlation between the SI and SD direct detections of dark matter was studied in Ref. [44]. The SD direct detection of dark matter in MSSM, which was studied in Refs. [45-50], is determined by the higgsino component in the dark matter. The singlino-higgsino dark matter in the NMSSM was studied in Refs. [51-65], and there is another singlet component that is not contained in MSSM. Thus, in this study, we specially focused on the correlation between the SD cross section and the so-called 'higgsino asymmetry' in the NMSSM-NUHM. We also studied the SI cross section for comparison.
The rest of this paper is organized as follows. In Sec. II, we briefly introduce the model NMSSM-NUHM, especially its electroweakino sector, and perform some analytic calculations of DM-nucleon scattering. In Sec. III, we present and discuss our numerical results. Finally, we present our conclusions in Sec. IV.
-
The NMSSM extends the MSSM with a singlet superfield
$ \hat{S} $ , in addition to the up- and down-doublet ones$ \hat{H}_{u,d} $ . The superpotential with$ {\mathbb{Z}}_3 $ symmetry is expressed as follows:$ W_{\rm{NMSSM}} = W_{\rm{MSSM}}^{\not{\mu}} + \lambda \hat{S} \hat{H}_u \cdot \hat{H}_d + \frac{\kappa}{3} \hat{S}^3 \, , $

(1) where
$ W_{\rm{MSSM}}^{\not{\mu}} $ is the superpotential of MSSM without the$ \mu $ -term, and$ \lambda $ and$ \kappa $ are dimensionless coupling constants. After electroweak symmetry breaking, the scalar fields$ H_{u,d} $ and S take their vacuum expectation values (VEVs)$ v_{u,d} $ and$ v_s $ , with parameters$ \tan\beta\equiv v_u/v_d $ and$ \mu_{\rm{eff}}\equiv \lambda v_s $ . Then, the gauge eigenstates mix to form 3 CP-even ($ h_{1,2,3} $ ) and 2 CP-odd mass-eigenstate Higgs ($ a_{1,2} $ ).The soft breaking term in NMSSM is expressed as follows:
$ \begin{aligned}[b] -{\cal{L}}_{\rm{NMSSM}}^{\rm{soft}} = &- {\cal{L}}_{\rm{MSSM}}^{{\rm{soft}},{\not{\mu}}} + {M}_S^2 |S|^2 \\ &+ \lambda A_\lambda S H_u \cdot H_d + \frac{\kappa}{3} A_\kappa S^3 + {\rm h.c.} \,, \end{aligned} $

(2) where
$ {M}_S^2 $ is the soft mass of the singlet field S, and$ A_{\lambda,\kappa} $ are the trilinear couplings with mass dimension.In the NMSSM-NUHM, the soft masses in the Higgs sector
$ M^2_{H_{u},H_{d}} $ and$ M^2_S $ are assumed to be non-uniform, and they can transform to parameters$ \lambda,\; \kappa,\; \mu_{\rm{eff}} $ . Then, the model can be determined by the following nine parameters:$ \lambda,\,\, \kappa,\,\, \tan\beta,\,\, \mu_{\rm{eff}},\,\, A_\lambda,\,\, A_\kappa,\,\, A_0,\,\, M_{1/2}, \,\,M_0 \, , $

(3) where
$ M_0 $ and$ M_{1/2} $ are the uniformed sfermion and gaugino masses, and$ A_0 $ is the uniformed trilinear coupling in the sfermion sector.The neutralino sector:
The five super partners bino
$ \tilde{B} $ , wino$ \tilde{W}^{0} $ , higgsinos$ \tilde{H}_{u,d} $ , and singlino$ \tilde{S} $ have the same quantum numbers. Thus, they can mix to five mass-eigenstate neutralinos. In the base$ \psi_i = (\tilde{B}, \tilde{W}^{0}, \tilde{H}_{d}, \tilde{H}_{u}, \tilde{S}) $ (with$ i = 1,2,3,4,5 $ ), the neutralino mass matrix is given by [66]$ M_{\tilde{\chi}^{0}} = \left( {\begin{array}{*{20}{c}} M_{1} & 0 & -\cos \beta \sin \theta_{\rm{W}} m_Z & \sin \beta \sin \theta_{\rm{W}} m_Z & 0 \\ 0 & M_{2} & \cos \beta \cos \theta_{\rm{W}} m_Z & -\sin \beta \cos \theta_{\rm{W}} m_Z & 0 \\ -\cos \beta \sin \theta_{\rm{W}} m_Z & \cos \beta \cos \theta_{\rm{W}} m_Z & 0 & -\mu_{\rm{eff}} & -\lambda v_{d} \\ \sin \beta \sin \theta_{\rm{W}} m_Z & -\sin \beta \cos \theta_{\rm{W}} m_Z & -\mu_{\rm{eff}} & 0 & -\lambda v_{u} \\ 0 & 0 & -\lambda v_{d} & -\lambda v_{u} & 2\kappa v_s \\ \end{array}} \right) \,, $

(4) where
$ \theta_W $ is the electroweak mixing angle.After diagonalization, the mass-eigenstate neutralinos can be obtained in mass order:
$ \tilde{\chi}^0_i = N_{ij} \psi_j \,, $

(5) where
$ N_{ij} $ means the$ \psi_j $ component in$ \tilde{\chi}^0_i $ , and$ \psi_j = (\tilde{B}, \tilde{W}^{0}, \tilde{H}_{d}, \tilde{H}_{u}, \tilde{S}) $ .In previous studies of ours on NMSSM-NUHM, we found that bino and wino are constrained to be very heavy because of the high mass bounds of gluino. Therefore, they can be decoupled from the light sector, unlike that in the scenario of non-universal gaugino masses [67]. Then, the following approximations for
$ N_{ij} $ can be found [58, 68]:$ \begin{aligned}[b] & N_{i3}:N_{i4}:N_{i5} \\ = & \left[ \frac{m_{\tilde{\chi}^0_{ i}}}{\mu_{\rm{eff}}} \sin \beta - \cos \beta\right] : \left[ \frac{m_{\tilde{\chi}^0_{ i}}}{\mu_{\rm{eff}}} \cos \beta - \sin \beta\right] : \frac{\mu_{\rm{eff}} - m_{\tilde{\chi}^0_{ i}}}{\lambda v}. \end{aligned} $

(6) When we neglect the bino and wino components in the LSP
$ \tilde{\chi}^0_1 $ , the singlino and higgsino components of LSP might have the relation$ N_{13}^2+N_{14}^2+N_{15}^2 \approx 1 \, . $

(7) Given that
$ \tan \beta \gg 1 $ , we have$ \sin \beta \approx 1 $ and$ \cos \beta \approx 0 $ . Then, for components in the LSP, we can write$ N_{13}:N_{14}:N_{15} = \frac{m_{\tilde{\chi}^0_{ 1}}}{\mu_{\rm{eff}}} : - 1 : \frac{\mu_{\rm{eff}} - m_{\tilde{\chi}^0_{ 1}}}{\lambda v} \, . $

(8) Given that
$ \tilde{B}, \;\tilde{W}^{0},\; \tilde{S} $ have no interaction with the Z boson, the coupling between Z and$ \tilde{\chi}^0_{1} $ is expressed as$ \begin{aligned}[b] C_{Z \tilde{\chi}_1^{0} \tilde{\chi}_1^{0} } = &-\frac{\rm i}{2} (g_1 \sin\theta_W \!+\! g_2 \cos\theta_W)(N^2_{1 3} \!-\! N^2_{1 4} )\gamma_{\mu} P_{\rm L} \\ &+ \frac{\rm i}{2} (g_1 \sin\theta_W \!+\! g_2 \cos\theta_W)(N^2_{1 3}\!-\! N^2_{1 4})\gamma_{\mu} P_{\rm R} \,, \end{aligned} $

(9) which means the coupling is proportional to the so-called 'higgsino asymmetry'
$ |N^2_{1 3}- N^2_{1 4}| $ [43, 69].For WIMP dark matter, such as the LSP
$ \tilde{\chi}^0_1 $ in the NMSSM, the principle of direct detections exploits its scattering with nucleons. The$ \tilde{\chi}^0_1 $ -nucleon scattering cross section can be described by an effective four-fermion operator$ g_{N N \tilde{\chi}_{1}^{0} \tilde{\chi}_{1}^{0}} $ , similar to that in Fermi's theory.For SI scattering, the dominated contribution is from the channels of Higgs boson exchanging, given that the squarks are heavy. In the NMSSM, the SI cross section is approximated to be [3, 70]
$ \sigma_{\rm{SI}} \approx \frac{4 m_{\chi^{0}}^{2} m_N^{2}}{\pi\left(m_{\chi^{0}}+m_N\right)^{2}}\left[Z f_{p}+(A-Z) f_{n}\right]^{2} \,, $

(10) where Z and A are the nucleon and proton numbers in the nucleus, respectively. And
$ f_{p,n} $ denote the couplings of DM with protons and neutrons, respectively, expressed as [3, 70]$ \frac{f_{p, n}}{m_{p, n}} = \sum\limits_{q = u, d, s} f_{T_{q}}^{(p, n)} \frac{a_{q}}{m_{q}}+\frac{2}{27} f_{T G}^{(p, n)} \sum\limits_{q = c, b, t} \frac{a_{q}}{m_{q}} \,, $

(11) where
$ a_{q} $ are the couplings between DM and quarks, and$ f_{T_{q}}^{(p, n)} $ and$ f_{T G}^{(p, n)} $ are the mass fractions in the proton and neutron contributed by light quarks$ q = u,\,d,\,s $ and heavy quarks, respectively. Given that in the NMSSM-NUHM the squarks are heavy, Higgs exchanging dominates in the SI DM-nucleon scattering. The DM-quark couplings$ a_{q} $ are expressed as [51]$ a_q = \sum\limits_{i = 1}^{3} \frac{C_{h_i \tilde{\chi}_{1}^{0}\tilde{\chi}_{1}^{0}} C_{h_i q q} }{m_{h_{i}}^{2}} \,, $

(12) where
$ C_{h_i \tilde{\chi}_{1}^{0}\tilde{\chi}_{1}^{0}} $ is the coupling of$ h_i $ with DM given by$ \begin{aligned}[b] C_{h_i \tilde{\chi}_{1}^{0}\tilde{\chi}_{1}^{0}} = &\sqrt{2} \lambda ( -S_{i1}N_{15} N_{14} + S_{i2}N_{15} N_{13} + S_{i3}N_{13}N_{14}) \\ &- \sqrt{2} \kappa S_{i3} N_{15}^2 \, . \end{aligned} $

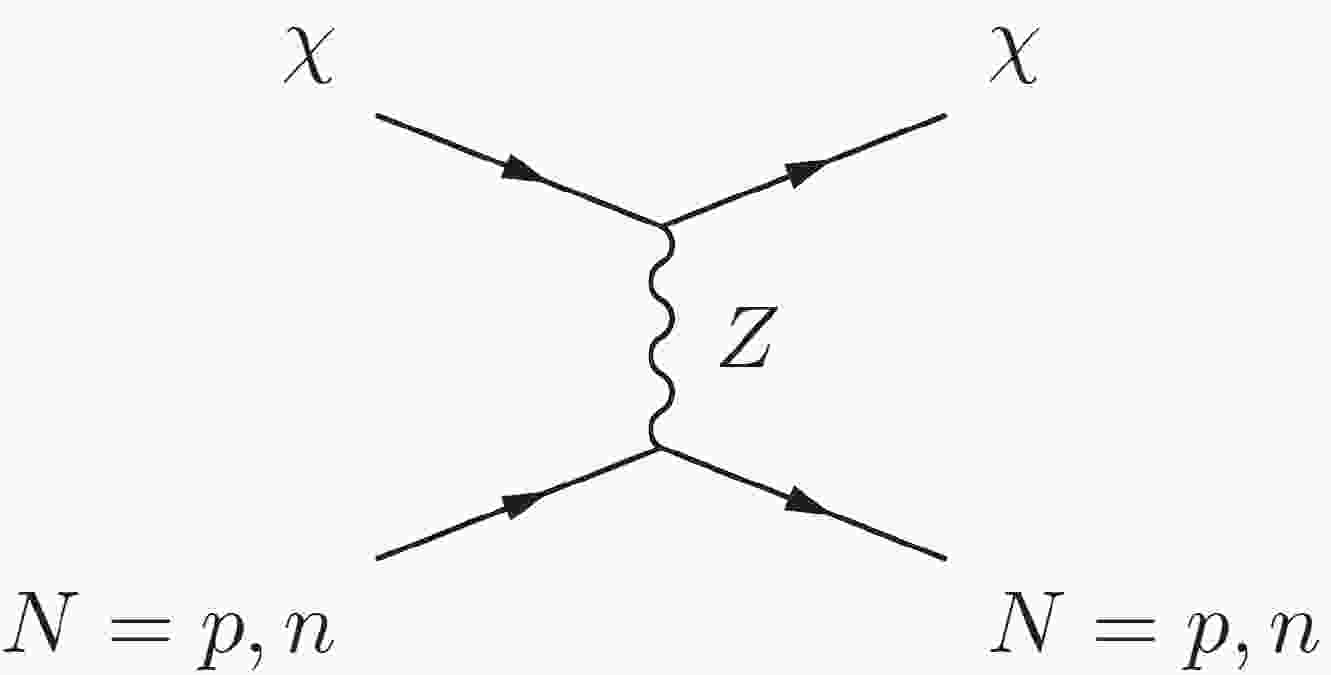
(13) Concerning SD scattering, the dominated contribution is from the channel of Z boson exchanging, as shown in Fig. 1. There is also a Higgs portal, but it is suppressed by a factor of
$ m_N/v\ll1 $ and can be neglected in comparison with that of Z boson.
Figure 1. Scattering of dark matter and nucleons, mediated by Z boson, where
$ \chi$ indicates dark matter and N indicates nucleons, including protons p and neutrons n.For DM
$ \tilde{\chi}_{1}^{0} $ in the NMSSM-NUHM, the SD cross section is expressed as [42]$ \sigma_{\rm{SD}}\left(\tilde{\chi}_{1}^{0} N \rightarrow \tilde{\chi}_{1}^{0} N\right) \approx \frac{4 g_{N N \tilde{\chi}_{1} \tilde{\chi}_{1}^{0}}^{2} }{\pi} \frac{m_{N}^{2}}{\Lambda^{4}}. $

(14) In combination with Eq. (9) and assuming that the SM coupings are constant, the correlation between the SD cross section and the higgsino asymmetry can be obtained:
$ \sigma_{\rm{SD}}\left(\tilde{\chi}_{1}^{0} N \rightarrow \tilde{\chi}_{1}^{0} N\right) \propto |N^2_{1 3}- N^2_{1 4}|^2 \,. $

(15) The SD cross section is proportional to the square of higgsino asymmetry. This relation is also supported in the NMSSM, given that only the coupling
$ C_{Z \tilde{\chi}_1^{0} \tilde{\chi}_1^{0} } $ determines this relation, and the SD cross section is proportional to the coupling$ C_{Z \tilde{\chi}_1^{0} \tilde{\chi}_1^{0} } $ .To obtain the DM relic density, we need to solve the number density from Boltzmann equation:
$ \frac{{\rm d}n_{\chi}}{{\rm d}t} + 3 H n_{\chi} = - \langle \sigma v \rangle \left( (n_{\chi})^2 - (n_{\chi}^{\rm{eq}})^2 \right) \,, $

(16) where H is the Hubble rate,
$ n_{\chi} $ and$ n_{\chi}^{\rm{eq}} $ denote the number density of DM and its value in thermal equilibrium, respectively, and$ \langle \sigma v \rangle $ is the average total cross section timing velocity of dark matter annihilation. Although there is no closed-form analytic solution to the Boltzmann equation, there is a relatively simple analytic approximation [3]. The relic density can be expressed as [71]$ \Omega_\chi h^2 \equiv m_\chi n_0 \frac{h^2}{\rho_{\rm c}} = 0.752 \left(\frac{m_{\chi}/T_{\rm{f}}}{10}\right)\sqrt{\frac{g_*}{100}} \frac{10^{-10} \; {{\rm{GeV}}}^{-2}}{\langle v \sigma \rangle} \,, $

(17) where
$ T_{\rm{f}} $ is the freezing-out temperature of DM,$ n_0 $ is its current number density,$ g_* $ is the total effective degree of freedom, and$ \rho_{\rm c}\! = \!3H_0^2/(8\pi G_N) $ is the critical density of our universe. The DM relic density is inversely proportional to its average annihilation cross section timing velocity.The detailed calculation of dark matter observables in the NMSSM is performed with
$ {\textsf{micrOMEGAs 5.0}}$ [72-75], including DM relic density, direct detection, and annihilation processes. -
In this study, we comprehensively analyzed the direct-detection constraints to light dark matter
$ \tilde{\chi}^0_{1} $ , whose mass is lighter than half of the SM-like Higgs$ m_{h_2} $ . Given that the higgsino asymmetry correlates with the SD detection of dark matter, we extended the region of$ \mu_{\rm{eff}} $ to 100-1000 GeV and updated our scan result in Ref. [38]. In this scan, we used$ {\textsf{NMSSMTools-5.5.2}}$ [76-78] to generate the particle spectrum by imposing the corresponding constraints there, employed$ {\textsf{HiggsBounds-5.8.0}}$ [79-83] to constrain the extra Higgs bosons, and used$ {\textsf{SModelS-v1.2.4}}$ [84-91] to constrain the sparticle sectors. Thus, eventually, the surviving samples shown hereafter will satisfy the constraints, including Higgs data, muon g-2, B physics, and sparticle searches. Specifically, details about dark matter constraints are listed next:● The upper bound of DM relic density is
$ \Omega h^2 \leqslant 0.131 $ [92-94];● The SI DM-nucleon cross section is constrained by XENON1T [95], which is rescaled by
$ \Omega/\Omega_0 $ with$ \Omega_0 h^2 = 0.1187 $ ;● The SD DM-proton cross section is constrained by LUX [96], XENON1T [97], and PICO-60 [98], which is also rescaled by
$ \Omega/\Omega_0 $ .●
$ \langle \sigma v \rangle $ is constrained by the indirect search from excess$ \gamma $ -ray emission of dwarf galaxies by the Fermi-LAT Collaboration [99].Similar to the results described in Ref. [38], the mass regions of most particles in this scenario are listed in Table 1. Next, we focus on the light DM
$ \tilde{\chi}^0_{1} $ in the NMSSM-NUHM: its scattering cross sections with nucleons and their correlations with higgsino asymmetry.mass/parameter minimum maximum $M_{1/2} / {{\rm{GeV}}}$ 

1045 1564 $M_{\tilde{g}} / {{\rm{GeV}}}$ 

2296 3328 $M_{\tilde{q}_{1,2}} / {{\rm{GeV}}}$ 

2000 3021 $M_2 \; (M_{\rm{SUSY}}) /{{\rm{GeV}}}$ 

825 1238 $M_1 \; (M_{\rm{SUSY}})/{{\rm{GeV}}}$ 

451 683 $\mu_{\rm{eff}}/ {{\rm{GeV}}}$ 

118 335 $| 2 \kappa \cdot \mu_{\rm{eff}} / \lambda | / {{\rm{GeV}}}$ 

0.3 62 $m_{\tilde{\chi}^0_1} / {{\rm{GeV}}}$ 

0.4 63 $m_{\tilde{\chi}^0_2} / {{\rm{GeV}}}$ 

123 331 $m_{\tilde{\chi}^0_3} / {{\rm{GeV}}}$ 

133 348 $m_{\tilde{\chi}^\pm_1} / {{\rm{GeV}}}$ 

120 337 $m_{\tilde{\chi}^0_4} / {{\rm{GeV}}}$ 

449 675 $m_{\tilde{\chi}^0_5}, \; m_{\tilde{\chi}^\pm_2}/ {{\rm{GeV}}}$ 

852 1271 $m_{\tilde{{\rm{\tau }}}_1}/{{\rm{GeV}}}$ 

93 608 $m_{\tilde{\nu}_{\rm{\tau }}} / {{\rm{GeV}}}$ 

62 644 $m_{\tilde{\mu}_1}/ {{\rm{GeV}}}$ 

382 830 $m_{\tilde{\nu}_\mu}/ {{\rm{GeV}}}$ 

375 826 $m_{\tilde{t}_1}/ {{\rm{GeV}}}$ 

700 2164 $m_{h_1} / {{\rm{GeV}}}$ 

2.5 111 $m_{a_1} / {{\rm{GeV}}}$ 

0.1 191 Table 1. Regions of some particle masses and related parameters.
In Fig. 2, the surviving samples are projected in the
$ \kappa $ versus$ \lambda $ planes, with colors indicating$ \mu_{\rm{eff}} $ , DM mass$ m_{\tilde{\chi}^0_1} $ , and the singlino component$ |N_{15}|^2 $ , respectively. The dashed lines indicate$ \kappa/\lambda = 125/400\approx0.31 $ , which means that, for the inner samples, the singlino-like neutralino is lighter than half of SM-like Higgs mass, given that the minimum of$ \mu_{\rm{eff}} $ is approximately$ 100 \; {{\rm{GeV}}} $ . The following observations can be made from this figure: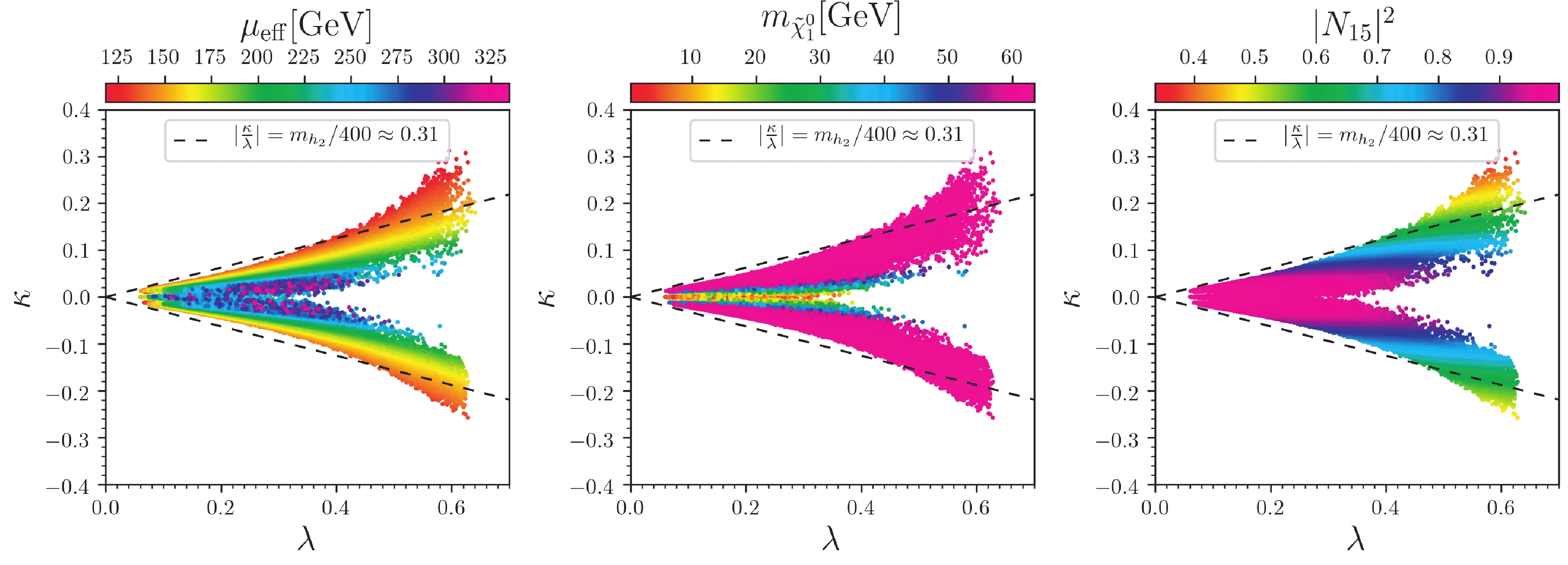
Figure 2. (color online) Surviving samples in the
$\kappa$ versus$\lambda$ planes. From left to right, colors indicate$\mu_{\rm{eff}}$ , DM mass$m_{\tilde{\chi}^0_1}$ , and the singlino component in the DM$|N_{15}|^2$ , respectively. The dashed lines indicate$|\kappa/\lambda| = 125/400\approx0.31$ . In all these planes, samples with larger$\mu_{\rm{eff}}$ are projected on top of smaller ones.● The maximum of
$ \mu_{\rm{eff}} $ is approximately$ 335 \; {{\rm{GeV}}} $ . In combination with Table 1, we can see that this also approximates the maximum of$ \tilde{\chi}^0_{2,3} $ and$ \tilde{\chi}^\pm_1 $ , given that they are mainly higgsino-dominated.● For samples with large
$ \mu_{\rm{eff}} $ ,$ \tilde{\chi}^0_1 $ are highly singlino-dominated with mass$ m_{\tilde{\chi}^0_1}\approx 2|\kappa\mu_{\rm{eff}}/\lambda| $ , given that they have very small$ |\kappa/\lambda| $ .● Most of the surviving samples are between the two dashed lines, which means these samples are singlino-dominated.
In Fig. 3, we show the surviving samples in the
$ \kappa $ versus$ \lambda $ planes, with colors indicating the DM relic density$ \Omega h^2 $ , SD DM-neutron cross section$ \sigma_{\rm{SD}} $ , and the higgsino asymmetry$ |N_{13}^2-N_{14}^2| $ , respectively. We checked that the SD DM-proton cross section is almost the same as the SD DM-neutron cross section. Six benchmark points are listed in Table 2. The following observations can be made from this figure: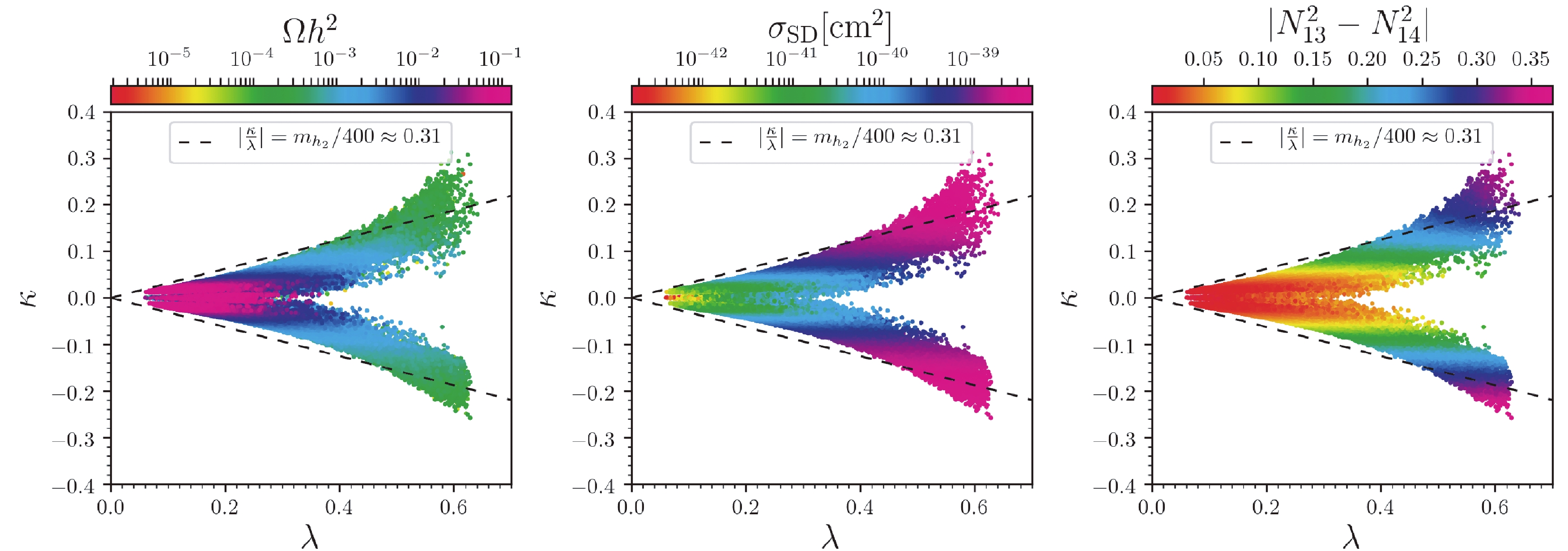
Figure 3. (color online) Surviving samples in the
$\kappa$ versus$\lambda$ planes. From left to right, the colors indicate the DM relic density$\Omega h^2$ , spin-dependent DM-neutron cross section$\sigma_{\rm{SD}}$ , and the Higgsino asymmetry$| N_{13}^2-N_{14}^2|$ , respectively. The dashed line is the same as those in Fig. 2. In all these planes, samples with larger DM relic density$\Omega h^2$ are projected on top of smaller ones.P1 P2 P3 P4 P5 P6 $\lambda$ 

$9.04\times 10^{-2}$ 

$2.81\times 10^{-1}$ 

$2.68\times 10^{-1}$ 

$2.59\times 10^{-1}$ 

$5.95\times 10^{-1}$ 

$6.28\times 10^{-1}$ 

$\kappa $ 

− $1.45\times 10^{-2}$ 

− $6.27\times 10^{-3}$ 

− $2.33\times 10^{-3}$ 

− $1.36\times 10^{-2}$ 

$3.12\times 10^{-1}$ 

− $2.58\times 10^{-1}$ 

$\mu_{\rm{eff} } /{\rm{GeV} }$ 

140 285 195 335 118 134 $m_{\tilde{\chi}^0_1 } /{\rm{GeV} }$ 

46 12 3 34 61 62 $|N_{13}|^2$ 

1.4% 2.7% 5.1% 1.8% 49% 45% $|N_{14}|^2$ 

0.1% 0.01% 0.0008% 0.04% 16% 8% $|N_{15}|^2$ 

98.4% 97.2% 94.8% 98.2% 34% 47% $|N_{13}^2-N_{14}^2|$ 

1.3% 2.7% 5.1% 1.7% 33% 37% $\Omega h^2$ 

0.1114 0.1290 0.1220 $1.37\times 10^{-3}$ 

$2.52\times 10^{-4}$ 

$1.84\times 10^{-4}$ 

$\sigma_{\rm{SI} } /{\rm{cm} }^2$ 

$1.49\times 10^{-49}$ 

$1.17\times 10^{-47}$ 

$5.62\times 10^{-49}$ 

$2.78\times 10^{-46}$ 

$2.13\times 10^{-44}$ 

$1.22\times 10^{-44}$ 

$\sigma_{\rm{SD} } /{\rm{cm} }^2$ 

$5.45\times 10^{-42}$ 

$2.11\times 10^{-41}$ 

$4.92\times 10^{-41}$ 

$9.23\times 10^{-42}$ 

$3.39\times 10^{-39}$ 

$4.34\times 10^{-39}$ 

Table 2. Related information for the six benchmark points in the NMSSM-NUHM, where
$|N_{13}|^2$ ,$|N_{14}|^2$ , and$|N_{15}|^2$ respectively are the up-type higgsino, down-type higgsino, and singlino components in the DM$\tilde{\chi}^0_1$ .● The samples with enough DM relic density are highly singlino-dominated, with smaller
$ \kappa $ and$ \lambda $ , smaller SD DM-neutron cross section$ \sigma_{\rm{SD}} $ , and smaller higgsino asymmetry.● From the middle and right planes in Fig. 3, we can conclude that the SD DM-neutron cross section
$ \sigma_{\rm{SD}} $ is proportional to the higgsino asymmetry. We also checked that the SI DM-nucleon cross section$ \sigma_{\rm{SI}} $ have no such correlation.● For samples with enough DM relic density, given that
$ \tilde{\chi}^0_1 $ present tiny higgsino components, the asymmetry between higgsino components,$ |N_{13}^2-N_{14}^2| $ , cannot be large, thus the SD DM-neutron cross section$ \sigma_{\rm{SD}} $ is also very small.In Fig. 4, we show the correlation between the SD DM-neutron cross section
$ \sigma_{\rm{SD}} $ and higgsino asymmetry$ |N_{13}^2-N_{14}^2| $ in detail. The following observations can be made from this figure: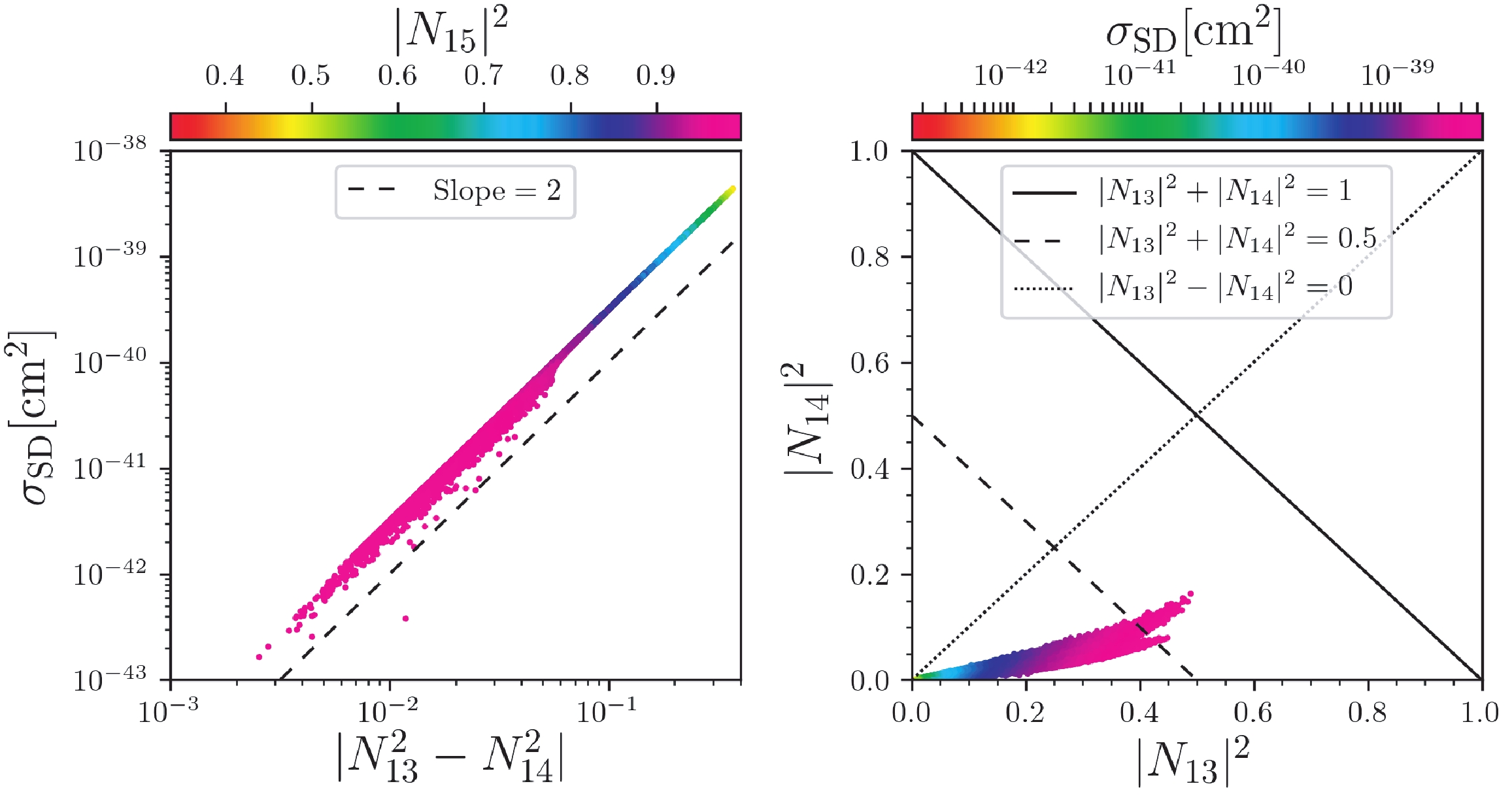
Figure 4. (color online) Surviving samples in the planes of spin-dependent DM-neutron cross section
$\sigma_{\rm{SD}}$ versus the higgsino asymmetry$|N_{13}^2-N_{14}^2|$ (left), and higgsino components in the DM$|N_{13}|^2$ versus$|N_{14}|^2$ , with colors indicating the singlino component in the LSP$|N_{15}|^2$ and spin-dependent DM-neutron cross section$\sigma_{\rm{SD}}$ , respectively. In the left panel, the slope of the black dashed line is 2. In the right panel, the black solid, dashed, and dotted lines indicate$|N_{13}|^2+|N_{14}|^2 = 1$ ,$|N_{13}|^2+|N_{14}|^2 = 0.5$ , and$|N_{13}|^2 = |N_{14}|^2$ , respectively.● In the left log-log panel, the slope of the black dashed line is 2. Given that the surviving samples distribute parallel to the line, the correlation between the SD DM-neutron cross section and the higgsino asymmetry is
$ \sigma_{\rm{SD}} \propto |N^2_{1 3}- N^2_{1 4}|^2 \, . $

(18) ● From the left panel, we can also conclude that the higgsino asymmetry is anti-correlated with the singlino component in
$ |N_{15}|^2 $ . In combination with Figs. 2 and 3, we can also conclude that the SD cross section is anti-correlated with the relic density. Thus, the samples can escape the constraints of SD direct-detection even if the higgsino asymmetry is large.● From the right panel, we can see that for most samples
$ |N_{13}|^2 \ll |N_{14}|^2\lesssim 0.5 $ .● Given that
$ 118\lesssim\mu_{\rm{eff}}\lesssim335 \; {{\rm{GeV}}} $ and$ m_{\tilde{\chi}^0_1}\lesssim 63 \; {{\rm{GeV}}} $ according to Table 1, the component ratio in the LSP$ \tilde{\chi}^0_1 $ can be approximated according to Eq. (8) as$ N_{13}:N_{14} \approx \frac{m_{\tilde{\chi}^0_{ 1}}}{\mu_{\rm{eff}}} : - 1 \, , $

(19) and hence, the higgsino asymmetry cannot be too small unless the higgsino components are small. However, when the higgsino components are large, the singlino component is small and the relic density is not sufficient.
In Fig. 5, we show the DM direct-detection constraints. The SI DM-nucleon cross section
$ \sigma_{\rm{SI}} $ and SD DM-neutron cross section$ \sigma_{\rm{SD}} $ are both rescaled by a ratio$ \Omega/\Omega_0 $ with$ \Omega_0 h^2 = 0.1187 $ . For the sake of comparison with the SD cross section, we also studied the SI cross section in detail. In our scenario,$ h_1 $ is highly singlet-dominated, and the components of up- and down-type doublet can be related by$ S_{1u}/S_{1d} \sim \tan\beta \gg 1 $ [29]. Thus, we checked that the Yukawa couplings of$ h_1 $ and up- and down-type quarks divided by corresponding quark mass are roughly equal and sizable compared with the corresponding SM-like values, that is,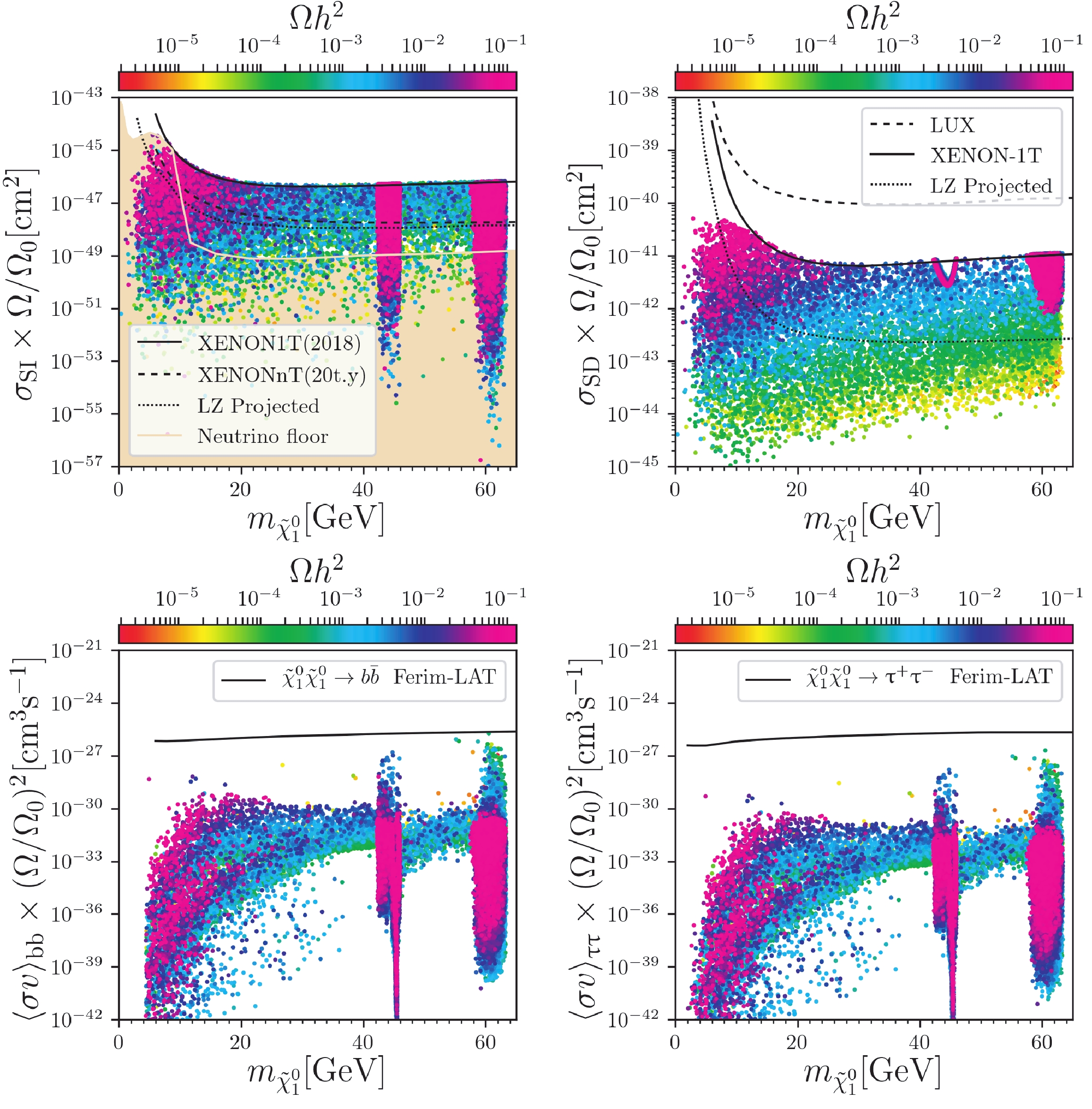
Figure 5. (color online) Upper panels: Surviving samples in the planes of rescaled spin-independent
$\sigma_{\rm{SI}} \times \Omega/\Omega_0$ (left) and spin-dependent cross section$\sigma_{\rm{SD}} \times \Omega/\Omega_0$ (right) versus DM mass$m_{\tilde{\chi}^0_1}$ , respectively, with colors indicating DM relic density$\Omega h^2$ . In the left panel, the black solid, dashed, and dotted curves indicate the spin-independent detection limit by XENON1T (2018) [95], and future experiments of XENONnT and LUX-ZEPLIN (LZ), respectively. The neutrino floor [100] is indicated by the orange shaded region. In the right panel, the dashed, solid, and dotted curves indicate the spin-dependent detection limit by LUX [96], XENON1T (2018) [97], and future LZ projections [101], respectively. Samples with larger DM relic density$\Omega h^2$ are projected on top of smaller ones. Lower panels: Surviving samples in the the planes of rescaled average DM annihilation cross section times velocity$\langle \sigma v \rangle$ in$\tilde{\chi}_1^{0} \tilde{\chi}_1^{0} \to b \bar{b}$ (left) and$\tilde{\chi}_1^{0} \tilde{\chi}_1^{0} \to {\rm{\tau }}^+ {\rm{\tau }}^-$ (right) channels versus the DM mass$m_{\tilde{\chi}^0_1}$ , respectively, with colors indicating DM relic density$\Omega h^2$ . The solid curves indicate the 95% C.L. upper limits on$\langle \sigma v \rangle$ from searching for excess$\gamma$ -ray emission from dwarf galaxies by the Fermi-LAT Collaboration [99].$ \frac{C_{h_1u_iu_i}}{m_{u_i}} \sim \frac{C_{h_1d_id_i}}{m_{d_i}} \sim \frac{1}{\sqrt{2}v}\approx \frac{C_{h_2qq}}{m_q} \,. $

(20) For Higgs coupling with DM, we checked that
$ C_{h_1 \tilde{\chi}_{1}^{0}\tilde{\chi}_{1}^{0}} \approx -C_{h_2 \tilde{\chi}_{1}^{0}\tilde{\chi}_{1}^{0}} \,. $

(21) We also checked that the SI cross section can be roughly proportional to
$ \sigma_{\rm{SI}} \propto \left[ \frac{C_{h_1 \tilde{\chi}_{1}^{0}\tilde{\chi}_{1}^{0}}}{m_{h_{1}}^{2}} \frac{ C_{h_1 dd}}{m_d} + \frac{C_{h_2 \tilde{\chi}_{1}^{0}\tilde{\chi}_{1}^{0}}}{m_{h_{2}}^{2}} \frac{1}{\sqrt{2}v} \right]^2 \,. $

(22) That is, SI scattering occurs mainly through
$ h_1 $ and$ h_2 $ exchange, which usually cancel each other. Moreover, the former can be as large as the latter for some samples, leaving the SI cross section smaller by a few orders of magnitude than that of one individual channel. The following observations can be made from Fig. 5:● The constraints from the SI DM-nucleon cross section are stronger than those from the SD DM-nucleon cross section. The reason is that the SI DM-nucleon cross section
$ \sigma_{\rm{SI}} $ is enhanced by the square of the nucleon number in the nucleus, and the SD DM-nucleon cross section$ \sigma_{\rm{SD}} $ does not have such enhancement.● The SD cross section of the surviving samples is much larger than the SI cross section. This is because the LSP
$ \tilde{\chi}^0_{ 1} $ in NMSSM-NUHM is a Majorana fermion. The SD scattering can have a Z boson exchange channel, while SI scattering takes place mainly through Higgs bosons exchange. Note from the upper left and right panels that the SD cross section$ \sigma_{\rm{SD}} $ is larger than the SI cross section$ \sigma_{\rm{SI}} $ by approximately 3-6 orders of magnitude.● From Fig. 2 and Fig. 3, we can conclude that for samples with large SD DM-nucleon cross section, the LSP
$ \tilde{\chi}^0_{ 1} $ is higgsino-dominated and has large higgsino asymmetry. From the upper right panel of Fig. 5, we can conclude that the higgsino-dominated LSP with sufficient DM relic density is excluded by SD cross sections; only when these sections present very small DM relic density, approximately$ 10^{-3}-10^{-5} $ , they can escape the direct-detection constraints.● From the upper right panel, we can conclude that surviving samples in the
$ h_2 $ - and Z-funnel annihilation channels with right relic density can be covered by future LZ 7-ton in spin-dependent detections. In combination with the results in Ref. [39], we conclude that the other samples are in$ a_1 $ - or$ h_1 $ -funnel annihilation channels.● In the lower panels, we show rescaled average DM annihilation cross section timing velocity
$ \langle \sigma v \rangle $ in the$ \tilde{\chi}_1^{0} \tilde{\chi}_1^{0} \to b \bar{b} $ and$ \tilde{\chi}_1^{0} \tilde{\chi}_1^{0} \to {\rm{\tau }}^+ {\rm{\tau }}^- $ channels. Note that the DM indirect detection constraints from the Fermi-LAT Collaboration [99] do not set strong constraints to our scenario. Moreover, we checked that with very small higgsino asymmetry, the main annihilating channels are$ b\bar{b} $ and$ {\rm{\tau }}^+ {\rm{\tau }}^- $ mediated by$ h_{1,2} $ or$ a_1 $ , and with$ m_{\phi}-2m_{\tilde{\chi}_{1}^{0}}\gg \Gamma_{\phi} $ , the average cross section timing velocity$ \langle \sigma v \rangle_{f\bar{f}} $ can be roughly proportional to$ \left( \frac{C_{\phi \tilde{\chi}_{1}^{0}\tilde{\chi}_{1}^{0}} C_{\phi f\bar{f}} }{4m_{\tilde{\chi}_{1}^{0}}^2 - m_{\phi}^{2}} \right)^2 $

(23) with
$ \phi = h_1,h_2,a_1 $ ,$ f\bar{f} = b\bar{b},{\rm{\tau }}^+ {\rm{\tau }}^- $ , and for average value,$ v\ll c $ ; with sizable higgsino asymmetry annihilation rate to$ Z\gamma $ through loops [102, 103], it can also be sizable.In a previous study of ours [39], we also studied the invisible Higgs decay to light dark matter in detail. We found that the four funnel annihilation scenarios can all survive the constraints of invisible Higgs decay and cannot be distinguished well by the corresponding future measurements at HL-LHC and even CEPC. The signals of light dark matter at colliders can also involve missing energy plus mono-X (X = jets,
$ W^\pm $ , Z, Higgs) [104-108]. Given that missing-energy signatures can be reinterpreted as any neutral particle interacting weakly with detectors or decaying outside detectors, the collider searches for DM in mono-X channels may not provide the most efficient probes for DM detection, and we left these in our future works. Combining with the above results and discussions, we find that SD direct detection of dark matter by LZ projected one is most effective to distinguish these four funnel annihilation scenarios.The prediction on muon g-2 is shown in Fig. 6, from which we can see that the main contributions are from chargino-sneutrino loops. The light chargino is higgsino-dominated, with mass
$ m_{\tilde{\chi}_1^{\pm}} \approx \mu_{\rm{eff}} $ . The heavy chargino is wino-dominated, with mass$ m_{\tilde{\chi}_2^{\pm}}\approx M_2 $ . Given that the lower mass bound of gluino is$ 2 \; {\rm{TeV}} $ , and gauginos unify at the GUT scale, the wino-dominated chargino cannot be light. Thus, the parameter$ \mu_{\rm{eff}} $ is constrained to be smaller than$ 335 \; {{\rm{GeV}}} $ by the current muon g-2 result. The upcoming muon g-2 result at Fermilab, with probably smaller error [109], may set a stronger constraint to our scenario, especially to the parameter$ \mu_{\rm{eff}} $ .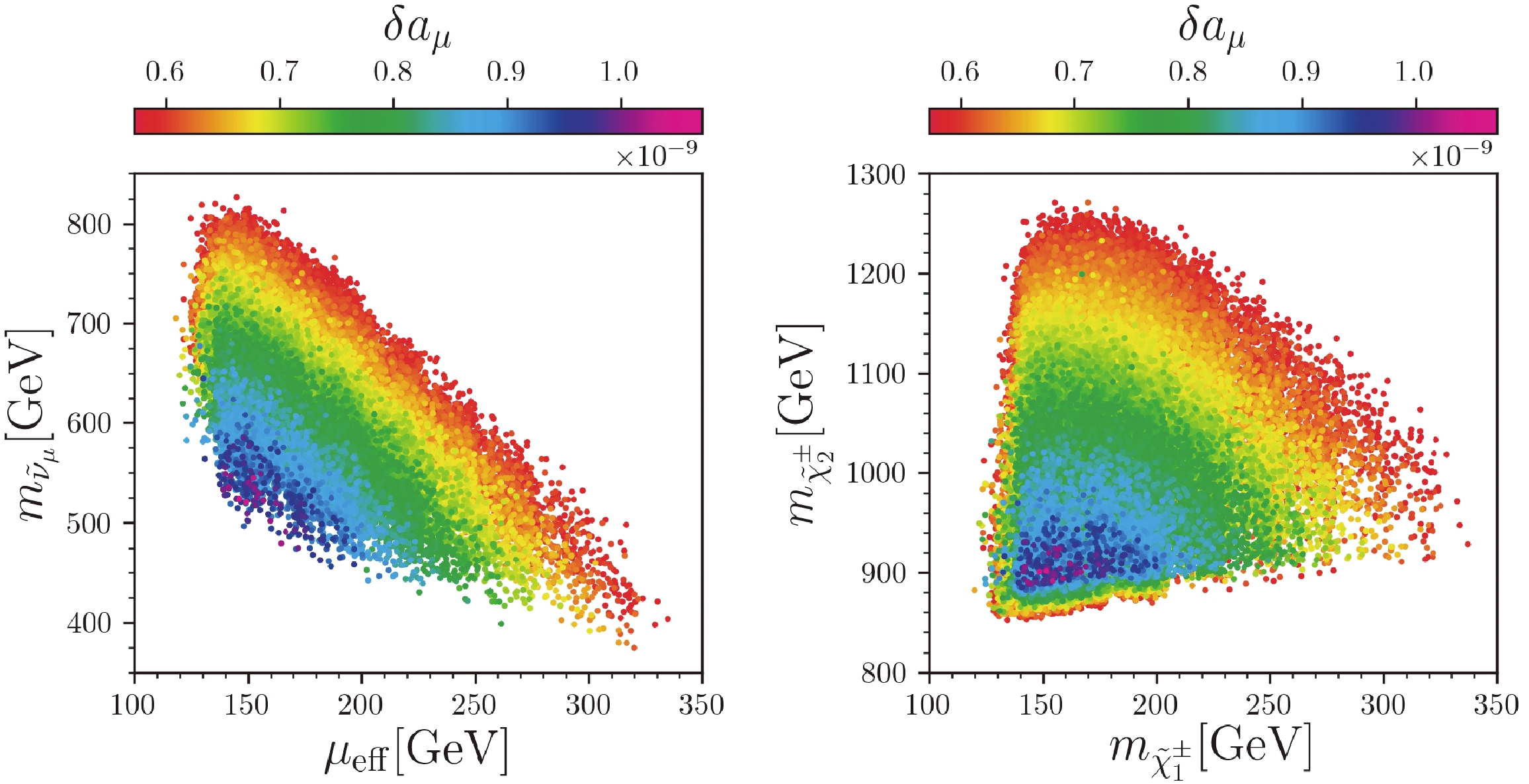
Figure 6. (color online) Surviving samples in the planes of muon-sneutrino mass
$m_{\tilde{\nu}_\mu}$ versus$\mu_{\rm{eff}}$ (left), and heavy-chargino mass$m_{\tilde{\chi}_2^{\pm}}$ versus light-chargino mass$m_{\tilde{\chi}_1^{\pm}}$ (right), respectively, with colors indicating calculated muon g-2 values$\delta a_{\mu}$ . Samples with larger$\delta a_{\mu}$ are projected on top of smaller ones. -
In this study, we analyzed the direct-detection constraints of light dark matter in the NMSSM with non-universal Higgs masses (NMSSM-NUHM). In particular, we focused on the correlation between higgsino asymmetry and spin-dependent cross section. We first updated the scan result in a previous study of ours [38] with broader
$ \mu_{\rm{eff}} $ regions. We considered the related theoretical and experimental constraints, including Higgs data, muon g-2, B physics, sparticle searches at the LHC, and DM relic density. We also paid special attention to direct detections of light DM.In the NMSSM-NUHM scenario considered in this study, the bino and wino are decoupled from the sector of light neutralinos, and the lightest neutralino
$ \tilde{\chi}^0_1 $ , given that the dark matter is lighter than half of the SM-like Higgs, is mixed by singlino and higgsinos. We studied properties of the dark matter$ \tilde{\chi}^0_1 $ , especially its constraints from direct detection. We drew the following conclusions:● The spin-dependent cross section is also proportional to the square of higgsino asymmetry in dark matter
$ \tilde{\chi}^0_1 $ in the NMSSM-NUHM.● The higgsino-mass parameter
$ \mu_{\rm{eff}} $ is smaller than approximately$ 335 \; {{\rm{GeV}}} $ in the NMSSM-NUHM due to the current muon g-2 constraint, but our scenario with light dark matter can still be alive under current constraints, including the direct detection of dark matter in the spin-dependent channel.● For higgsino-dominated LSP, the higgsino asymmetry is sizable, and to escape the spin-dependent detection, the relic density is as small as
$ 10^{-3}\sim10^{-5} $ .● For singlino-dominated LSP, the higgsino components and higgsino asymmetry are small. Thus, it can easily escape the spin-dependent detection with sufficient relic density.
● Light dark matter in the
$ h_2 $ - and Z-funnel annihilation channels with sufficient relic density can be covered by future LZ 7-ton in spin-dependent detections.● The spin-independent cross section is dominated by
$ h_1 $ - and$ h_2 $ -exchanging channels, which can even cancel each other in some samples, leaving a spin-independent cross section smaller by a few orders of magnitude than that of one individual channel.
Higgsino asymmetry and direct-detection constraints of light dark matter in the NMSSM with non-universal Higgs masses
- Received Date: 2020-11-27
- Available Online: 2021-04-15
Abstract: In this study, we analyze the direct-detection constraints of light dark matter in the next-to minimal supersymmetric standard model (NMSSM) with non-universal Higgs masses (NUHM); we specially focus on the correlation between higgsino asymmetry and spin-dependent (SD) cross section. We draw the following conclusions. (i) The SD cross section is proportional to the square of higgsino asymmetry in dark matter






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: