-
In general, chemical environments and physical conditions, such as pressure and electric field, do not control the half-life of a radioactive nucleus. However, electronic structures can be modified under these conditions; therefore, properties of atomic structure, such as the distribution of electron density, are varied in species. In 1947, Segrè [1] and Daudel [2] first suggested that the nuclear decay rate is dependent on the density of the electron near the nucleus in electron capture (EC) and internal conversion (IC) processes.
The EC decay is directly determined by converting a proton into a neutron as defined by the two-body reaction:
$ p + e^- \rightarrow n +\nu_e, $

(1) where p,
$ e^- $ , n, and$ \nu_e $ represent the proton, electron, neutron, and electron neutrino, respectively. The probability of realizing EC decay depends on the distribution of the electron density near the nucleus.Assuming nuclear wavefunctions are unaffected by chemical or physical conditions, the change in the EC decay rate,
$ {\rm d}\lambda_{\rm EC} $ , can be represented as [3, 4]$ {\rm d}\lambda_{\rm EC} = \left(\frac{\rho_e}{\rho_{e_{\rm ref}}}-1\right)\lambda_{\rm ref}, $

(2) where
$ \rho_e $ represents electron density at the nucleus. In addition,$ \rho_{e_{\rm ref}} $ and$ \lambda_{\rm ref} $ represent the electron density and decay rate of the reference nucleus, respectively. Eq. (2) shows that the variation in the EC decay rate is proportional to the change in the electron density at the nucleus.The
$ ^7\mathrm{Be} $ nucleus decays to the$ ^7\mathrm{Li} $ nucleus via the EC reaction. Because the electron configuration of the Be atom is$ 1{{{s}}}^2 \:2{s}^2 $ , the$ ^7\mathrm{Be} $ is a suitable nucleus to study variations in the nuclear decay rate. The contribution of the 2s valence electrons to the total electron density at the$ ^7\mathrm{Be} $ nucleus is relatively significant (3.2%), implying that the external environment could induce a measurable change of half-life of the$ ^7\mathrm{Be} $ nucleus.The study of decay rate of the
$ ^7\mathrm{Be} $ nucleus is significant to scientists in nuclear physics and astrophysics fields. The interest in the study on the$ ^7\mathrm{Be} $ decay rate change in different environment arises because the decay rate of$ ^7\mathrm{Be} $ at the solar core plays an important role in calculating the$ ^{8}\mathrm{B} $ solar neutrino flux. The failure of density functional calculations to elucidate the observed increase in$ ^7\mathrm{Be} $ decay rate under compression indicates a possible increase in the uncertainties surrounding the calculated$ ^7\mathrm{Be} $ decay rate at the solar core and the corresponding$ ^{8}\mathrm{B} $ solar neutrino flux [5].A few experimental and theoretical investigations have been conducted to study the change in the decay rate of the
$ ^7\mathrm{Be} $ nucleus. Johlige et al. [6] measured changes in the$ ^7\mathrm{Be} $ half-life (53.3 days) up to 0.2% among various$ ^7\mathrm{Be} $ compounds. However, the change in the$ ^7\mathrm{Be} $ half-life was observed at approximately 1.5% in the BeO structure relative to that of$ ^7\mathrm{Be} $ in the Be metal [7]. Furthermore, the change in the half-life of the$ ^7\mathrm{Be} $ implanted in Li [8], Al [9, 10], Cu [9, 11], Ta [8], Pt [10], and Au [12-14] was measured. Furthermore, the decay rate of$ ^7\mathrm{Be} $ was investigated in large molecules, such as$ \mathrm{C}_{36} $ [15],$ \mathrm{C}_{60} $ [16-21],$ \mathrm{C}_{70} $ fullerenes [22], and carbon nanotube [23]. Recently, the dependency of the$ ^7\mathrm{Be} $ decay rate on its position in$ \mathrm{C}_{36}$ and$ \mathrm{C}_{60} $ fullerenes was investigated [24]. In addition, the confinement effect on the$ ^7\mathrm{Be} $ half-life in host environments has also been investigated [25].Furthermore, the decay rate of
$ ^7\mathrm{Be} $ can be altered with an increase in pressure. In 1973, it was determined that the decay rate of$ ^7\mathrm{Be} $ can decrease less than 1% when pressure is increased to approximately 270 kbar [26]. In addition, the half-life of the$ ^7\mathrm{Be} $ nucleus in the compressed$ \mathrm{Be}(\mathrm{OH})_2 $ gel increased approximately 1% at 400 kbar [27]. Furthermore, Tossell [4] predicted that the change in the decay rate of$ ^7\mathrm{Be} $ is approximately 1.33% at a pressure of 68 GPa in the$ \mathrm{Be}(\mathrm{OH})_4 $ structure. In another research, Bibikov et al. [28] studied the influence of pressure on the$ ^7\mathrm{Be} $ decay rate in BeO and$ \mathrm{Be}(\mathrm{OH})_2 $ structures.Moreover, temperature dependence on the nuclear half-life is investigated by cooling samples to a temperature of
$ T = 12\: \mathrm{K} $ . For example, the half-life of the$ ^{210}\mathrm{Po} $ nucleus was determined to be shorter in the Cu sample [29]. For the$ \beta^+ $ -decay, the experimental observations indicate a shorter half-life for$ ^{22}\mathrm{Na} $ nucleus [30], whereas for the$ \beta^- $ -decay, a longer half-life was determined for$ ^{198}\mathrm{Au} $ in Pd and Au structures [31]. In addition, the half-life of the$ ^7\mathrm{Be} $ nucleus increases in Po and In samples by the cooling species [32]. However, precision measurements of the$ ^{197}\mathrm{Ru} $ [33],$ ^{7}\mathrm{Be} $ [11], and$ ^{198}\mathrm{Au} $ [11] half-lives indicate that temperature dependence is absent in a metallic environment. From the theoretical perspective, Eliezer et al. [34] calculated the alpha tunneling effect by including the electron screening and obtained no significant effect by cooling the metal to low temperatures.Furthermore, the influence of ultra-strong magnetic fields on the EC decay rate has been investigated, where decay rates of
$ ^{55}\mathrm{Co} $ and$ ^{56}\mathrm{Ni} $ could be substantially increased in the ultra-strong magnetic fields [35]. In this study, we investigate the effects of electric fields on the change in the$ ^7\mathrm{Be} $ decay rate. Accordingly, the electronic properties of Be and BeO are studied within the density functional theory (DFT) calculations while an electric field is applied. -
First-principle calculations based on DFT or Hartree-Fock (HF) can be adopted to obtain electron density at the nucleus. All calculations were performed using the Amsterdam Density Functional (ADF) package [36], which employs Slater-type orbitals (STOs) to represent molecular and atomic orbitals.
ADF can apply the electric field in a single-point calculation or geometry optimization. The package allows the structure to rotate relative to the field vector within geometry optimization. In computations, a homogeneous external electric field can be included in the Fock operator,
$ F(\rho) $ . The Fock operator is an effective one-electron energy operator, which is given by$ F_i(\rho) = h_i (\rho)+\sum\limits_{j}^{N_{\rm elec}} (J_i(\rho)-K_i(\rho)), $

(3) where the one-electron operator,
$ h_i (\rho) $ , describes the kinetic energy of an electron, as well as the attraction to all the nuclei. In addition, the Coulomb ($ J_i(\rho) $ ) and exchange ($ K_i(\rho) $ ) operators describe the repulsion of all other electrons [37]. The change in the binding energy triggered by applying an electric field,$ {\rm d}B $ , can be reformulated as$ {\rm d}B = \int {\rm d}r \{ (\rho_{f}(r) - \rho_{i}(r))\int_{\rho_{i}}^{\rho_{f}} {\rm d}\rho F[\rho(r)] \}, $

(4) where
$ \rho_{i} $ and$ \rho_{f} $ represent the charge in the density of the system in initial and final states, respectively.The accuracy of the DFT method depends on the approximation of the exchange-correlation functional; therefore, meta generalized gradient approximation (meta-GGA) was adopted by including the Minnesota 2006 local functional (M06-L). To obtain accurate results, all‐electron quadruple zeta plus four polarization (QZ4P) basis sets were applied for all atoms.
For these calculations, homogeneous electric fields were applied perpendicularly to periodic surface slabs. In addition, the strength of the electric field was increased by 0.01 a.u. in each step.
The electron density at the nucleus can be predicted upon the geometry optimization. Because we investigated electronic properties in the Be atom, we did not consider relativistic effects in the calculations. Furthermore, the nuclear model adopted is a point nucleus. The finite nuclei and relativistic effects are suitable for systems containing heavy nuclei [36].
The package provides the electron density at the nuclei for a unit cell in the structure. Owing to the existence of the dipole moment, the obtained results were different for atoms in a unit cell. Therefore, a simple average was applied for each result.
-
Initially, the effect of the electric field on system energy was estimated. The correction of the binding energy,
$ \Delta B $ , owing to the Stark effect can be expessed as [38]$ \Delta B = - \mu_{\rm ind} E, $

(5) where
$ \mu_{\rm ind} $ and E represent the induced dipole moment and applied electric field, respectively. In our sign convention, the induced dipole moment of the system ($ \mu_{\rm ind} $ ) was considered negative.Figure 1 illustrates the influence of the electric field on the change in the binding energy of Be and BeO structures. This figure shows that the correction of the binding energy in the BeO structure is more than that of the Be metal in a similar electric field.
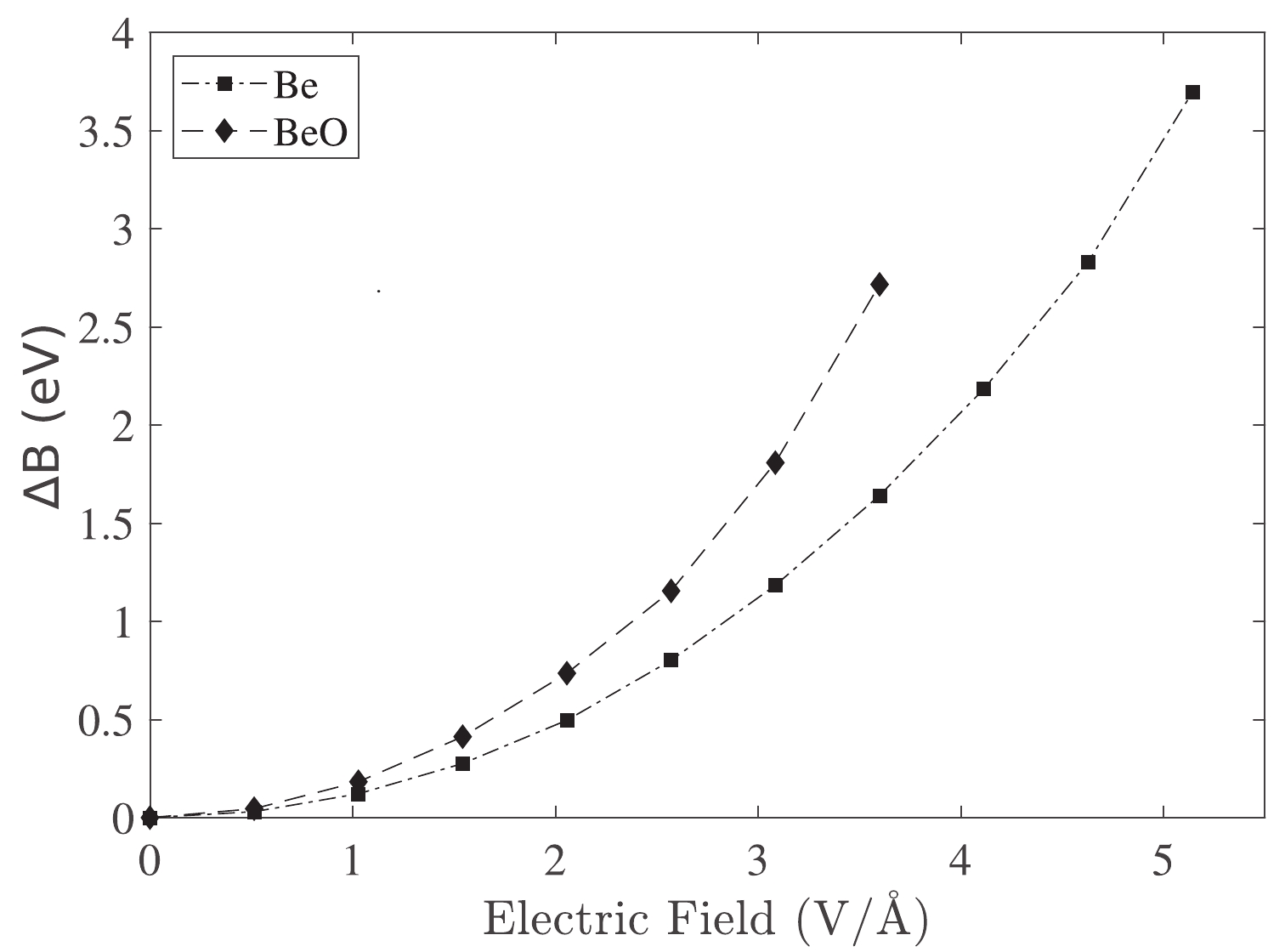
Figure 1. Correction of the binding energy owing to the electric field application in the Be and BeO samples.
When an electric field is applied, electrons move toward an atom. Therefore, an electric dipole moment is induced in systems that can increase with the increment of the electric field strength (Fig. 1).
-
The Be metal has a hexagonal close-packed (hcp) structure with the P
$ 6_3 $ /mmc space group at ambient temperature and pressure. For these conditions, the ratio of lattice parameters is c/a = 1.57 with a = 2.28 Å.Computational results relative to the electron density at the
$ ^7\mathrm{Be} $ nucleus are plotted in Fig. 2. In this figure, the electron density at the$ ^7\mathrm{Be} $ nucleus initially decreases to a minimum value at the electric field strength of approximately 3 V/Å, and then it increases.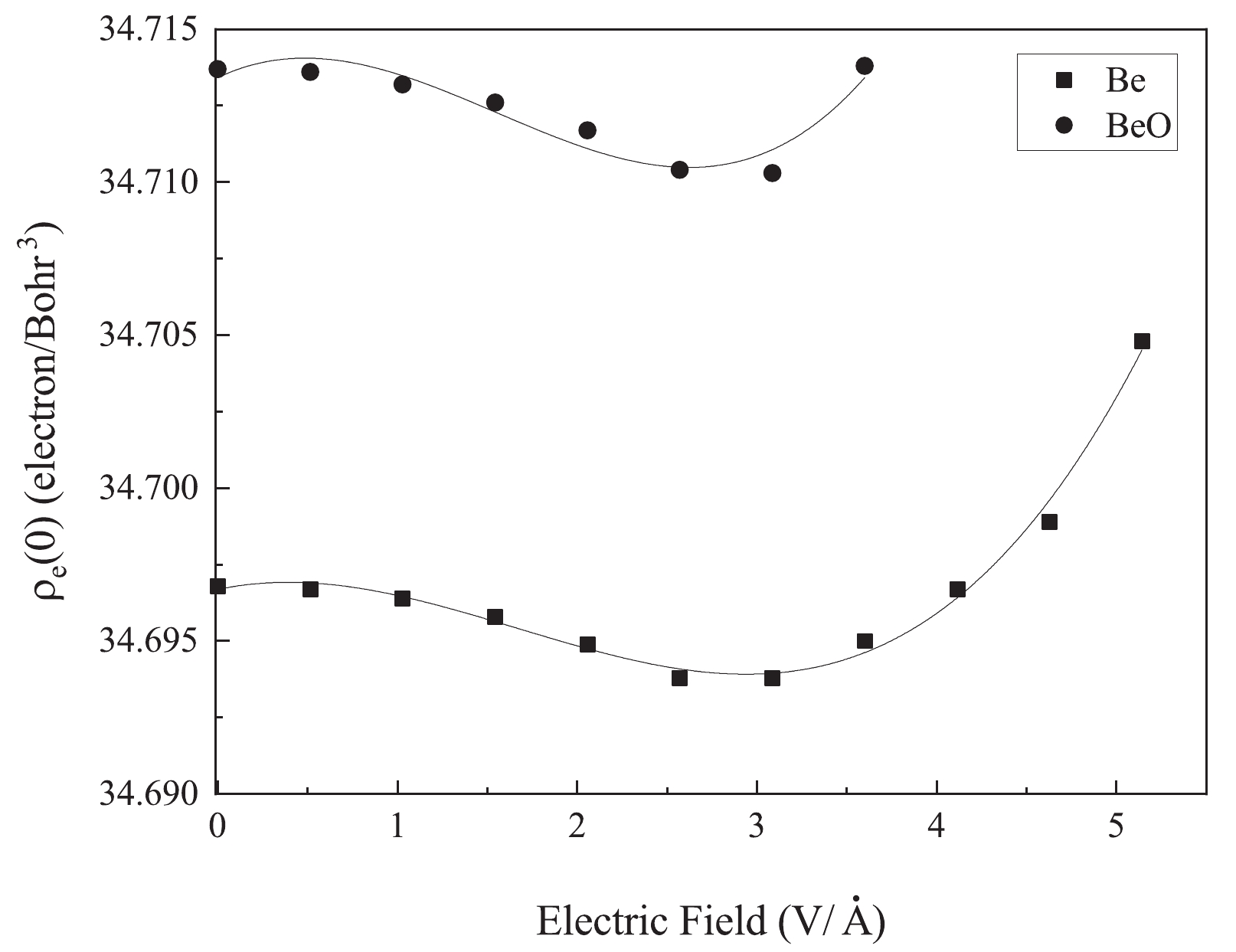
Figure 2. Changes in the electron density based on the increase in the electric field along the z-axis of Be and BeO structures.
Based on these results, we have obtained the following cubic fit for the variation in the electron density at the nucleus,
$ \rho_e (0)$ , with the applied electric field:$ \begin{aligned}[b]\rho_e (0) =& 34.697+1.26 \times 10^{-3} E-1.81 \times 10^{-3} E^2\\&+3.6 \times 10^{-4} E^3, \end{aligned}$

(6) where
$ \rho_e (0) $ is given in electron/$ \mathrm{Bohr}^3 $ and the electric field, E, in V/Å.Subsequently, this function results in the following dependence for the EC decay rate:
$ \frac{{\rm d} \lambda_{\rm EC}}{\lambda_{\rm EC}} = 3.63\times10^{-5} E-5.22\times10^{-5} E^2+1.04 \times10^{-5}E^3, $

(7) where E is in V/Å. The obtained results indicate that the decay rate of the
$ ^7\mathrm{Be} $ nucleus in the Be structure is altered up to 0.02% with a 5.14 V/Å (0.1 a.u.) electric field strength compared to that of$ ^7\mathrm{Be} $ in a zero electric field strength. -
The beryllium oxide (BeO) is crystallized in the hcp wurtzite (WZ) structure with the P
$ 6_3 $ /mmc space group at ambient conditions. The ratio of lattice parameters, c/a, is 1.62 with a = 2.7 Å. Figure 2 illustrates changes in the electron density at the$ ^7\mathrm{Be} $ nucleus of the BeO structure, where the average value decreases until 3.08 V/Å, and then increases.Accordingly, we obtained the cubic fit on the
$ \rho_e (0) $ relative to electric field values:$\begin{aligned}[b] \rho_e (0) =&34.714+2.94 \times 10^{-3} E-3.22 \times 10^{-3} E^2\\&+6.89 \times 10^{-4}E^3,\end{aligned}$

(8) where
$ \rho_e (0) $ is given in electron/$ \mathrm{Bohr}^3 $ and E in V/Å.In the following equation, the relative change in the EC decay rate is obtained by
$ \frac{{\rm d} \lambda_{\rm EC}}{\lambda_{\rm EC}} = 8.47 \times 10^{-5} E-9.28 \times 10^{-5} E^2 +1.98 \times 10^{-5}E^3, $

(9) where E is given in V/Å.
Because the BeO sample is an insulator, the change in the electron density of the BeO structure is less than that of the Be metal. Moreover, an oxygen atom (an atom with a high electronegativity value) bonds with the Be atom in this structure. Therefore, the electric field has a lower effect on electron density at the
$ ^7\mathrm{Be} $ nucleus in the BeO structure relative to that of the Be metal. -
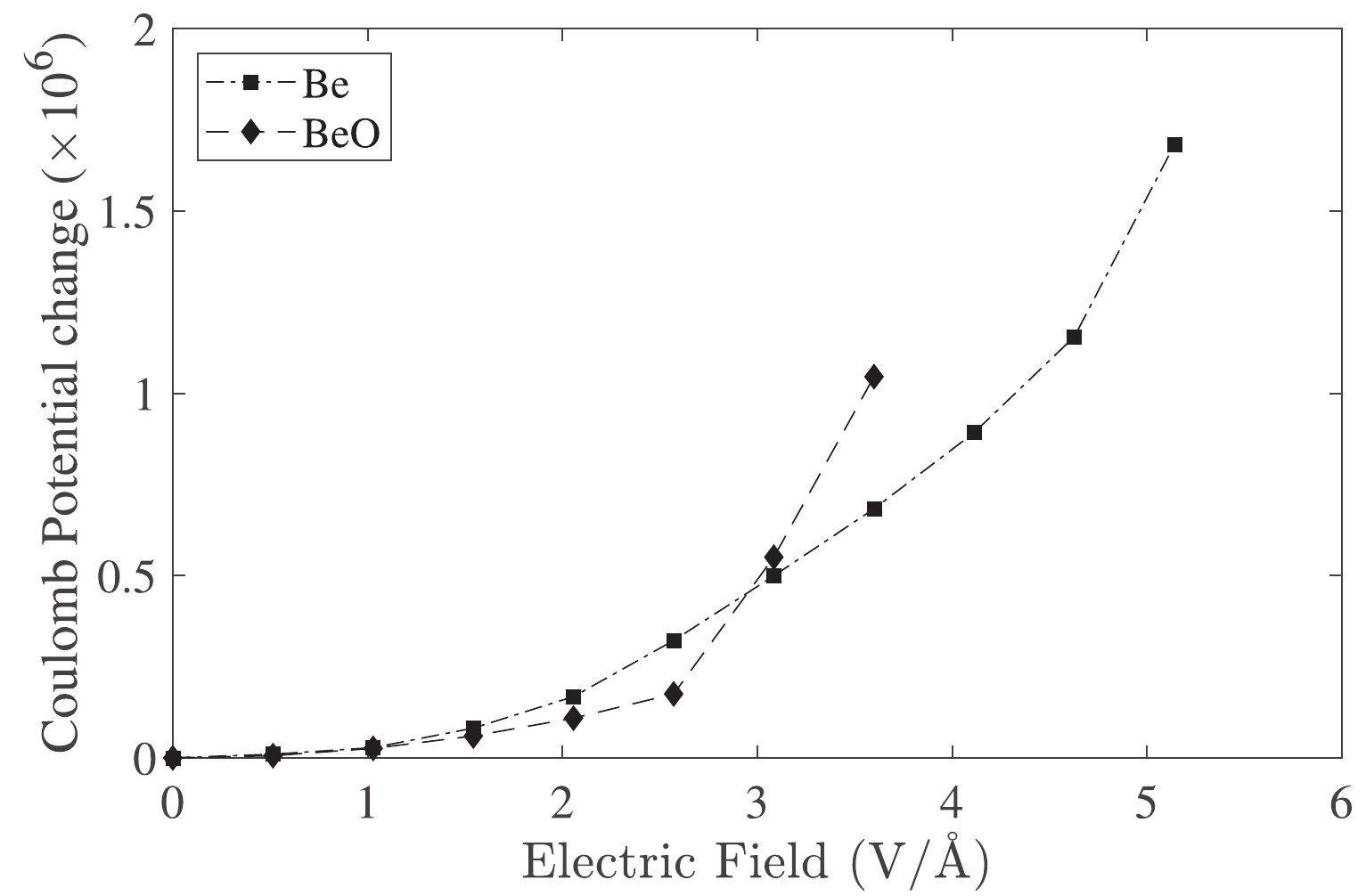
Qualitatively, changes in the electron density at the nucleus can be determined at low electric fields with a change in coulomb potential. Figure 3 presents the changes in the Coulomb potential at the
$ ^7\mathrm{Be} $ nucleus of Be and BeO samples.Changes in the Coulomb potential correspond to the correction of the binding energy (Fig. 1). However, changes in the Coulomb potential are considerably altered to approximately 3.08 V/Å (0.06 a.u.) in the BeO structure.
-
The applied electric field creates electric dipoles by shifting the
$ ^7\mathrm{Be} $ nuclei, as well as the corresponding 2s electrons, in the opposite directions. Consequently, the 2s electron density at the nucleus initially starts decreasing with the increase in the electric field. Therefore, the total electron density at the nucleus decreases, and the half-life of the$ ^7\mathrm{Be} $ nucleus increases. The 2s electrons also screen the 1s orbital electrons; thus, the screening effect of the 2s electrons decreases as the applied electric field increases. Hence, the 1s electron density at the nucleus increases as the applied electric field increases, and the decay rate of the$ ^7\mathrm{Be} $ nucleus also increases.Owing to these two opposing effects, the total electron density (sum of 1s and 2s electron densities) at the nucleus initially decreases as the applied electric field increases, and then, the total electron density at the nucleus increases with the increase in the applied electric field as the screening effect of the 2s electrons starts playing the dominant role.
Our results indicate that the changes in the
$ ^7\mathrm{Be} $ decay rate are consistent with electron screening effects. The electron density at the$ ^7\mathrm{Be} $ nucleus initially decreased with the increase in the electric field strength. At approximately 4.11 V/Å (0.08 a.u.), the electron density at the nucleus is equal to that of the result at the zero electric fields; hence, both effects cancel each other. Furthermore, the effect of screening electrons significantly increased at high electric fields, such that they can substantially contribute to the capture process; therefore, the electron density at the nucleus increases at strong electric fields (Fig. 2). -
In addition to chemical environments and confinement effects [24, 25], our computations indicate that the half-life of the
$ ^7\mathrm{Be} $ nucleus can be altered by applying an electric field. It was determined that the half-life was altered approximately 0.02% in the Be metal at 5.14 V/Å electric field strength, whereas it was not signifcantly altered in the BeO sample.The energy of screening electrons depends on the strength of the applied electric field. It was determined that the obtained results within the DFT calculations are consistent with the electron screening effects in decay rate variations.
Effects of electric fields on 7Be half-life
- Received Date: 2021-12-30
- Available Online: 2021-07-15
Abstract: First-principle calculations based on the density functional theory (DFT) method are adopted to investigate the influence of a strong electric field on the 7Be half-life. Accordingly, electronic structures of Be and BeO are examined in the presence of a homogeneous electric field. The electron density at the nucleus is estimated upon the geometry optimization. Our computations for the Be metal indicate a 0.02% increase in the decay rate of the 7Be nucleus, corresponding to a 0.02% decrease in the 7Be half-life, both at 5.14 V/Å (0.1 a.u.). Furthermore, it is determined that the decay rate of 7Be is not considerably altered up to 3.6 V/Å in the BeO structure. Our results show that the screening energy of the electron can be dependent on the applied electric field strength. Furthermore, we predict variations in the Coulomb potential at the 7Be nucleus due to electric field application.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: