-
Tunneling is a quantum mechanical phenomenon, in which a wave function can penetrate a potential barrier [1]. A classical particle will rebound from the barrier at the position
$ x_0 $ where$ E = V(x_0) $ , i.e., the total energy of the particle E is equal to the potential$ V(x) $ . The region beyond$ x_0 $ where$ E<V(x) $ is then called the "classically forbidden" (CF) region. However, a wave function can penetrate to this CF region, depending on the height and the width of the barrier. This effect plays an important role in different fields, such as in alpha radioactivity, nuclear fusion, quantum computing, and scanning tunneling microscopy.A nucleus is a complex quantum many-body system that is self-bound by neutrons and protons. Quantum tunneling allows neutrons and protons to penetrate to the CF region, which could contribute to the density distribution in the exterior region. In particular, tunneling can be easier for neutrons or protons that are weakly bound. In the past few decades, due to an extensive exploration toward the nuclear drip line, people found many exotic phenomena in weakly bound neutron/proton-rich nuclei. The neutron halo is one of these exotic phenomena, in which the weakly bound valence neutrons can move far away from the nuclear center, which leads to an abnormal increase in the root-mean-square (rms) radius compared with a stable nucleus [2]. There have been many investigations on the mechanism of the halo phenomenon. Those weakly bound states with a small angular momentum l became the focus of these discussions, as its wave functions are easier to extend far outside the low centrifugal barrier [3, 4]. Moreover, the pairing correlation could scatter neutrons above the Fermi energy into the continuum in a weakly bound nucleus. The wave functions of continuum states also have a large contribution to the density distribution in the exterior region [5, 6]. Therefore, it is interesting to investigate how many weakly bound and continuum neutrons could penetrate to the CF region, and what the relation is between this number and the halo phenomenon.
The first investigation on the relation between the number of neutrons/protons in the CF region and the halo phenomenon was performed by Im and Meng [7, 8], using the Skyrme Hartree-Fock (HF) theory. They found a fast increase in the neutron number in the CF region in neutron-rich Ca isotopes, which is quite similar to the increase in neutron rms radius in a halo nucleus. Therefore, they claimed that the number of particles in the CF region can give information on the appearance of a halo or skin. In
$ ^{68} {\rm{Ca}}$ , they counted more than$ 6 $ neutrons in the CF region. Recently, Zhang et al. [9] examined this problem in neutron-rich Mg isotopes using the deformed relativistic Hartree-Bogoliubov theory, which included pairing and deformation effects that were neglected in the work of Im and Meng [7, 8]. They found a notable increase in the neutron number in the CF region for the predicted halo nuclei$ ^{42} {\rm{Mg}}$ and$ ^{44} {\rm{Mg}}$ , due to contributions from the continuum states by considering both the pairing and deformation effects. However, this increase only due to the pairing effect is much smaller in these two nuclei.Comparing the abovementioned two works, it is interesting to find that they used different definitions of the CF region. Namely, one could define the starting position of the CF region
$ r_{\rm{CF}} $ with$ \varepsilon_i = U(r_{\rm{CF}}) $ , where$ \varepsilon_i $ is the single-particle energy and$ U(r) $ is the corresponding single-particle potential. In Im and Meng’s work, they included the centrifugal barrier in$ U(r) $ , while Zhang et al. did not, as they investigated a deformed nuclei, in which the angular momentum is no longer a good quantum number. In this work, we will first take the neutron-rich nucleus$ ^{68} {\rm{Ca}}$ as an example to show the obvious difference in the neutron numbers in the CF region calculated with these two definitions within the same Skyrme HF model, especially for bound states. Furthermore, for the weakly bound and continuum states, we will examine the contributions to the neutron number in the CF region by including the pairing effect in the Skyrme Hartree-Fock-Bogoliubov (HFB) method. In particular, their wave functions will be carefully calculated using the Green’s function method. It has been demonstrated that the Green’s function method can properly describe asymptotic wave functions for weakly bound and continuum states and thus provide a good description for the extended density distribution of neutron-rich nuclei [10]. This method can also nicely describe the resonant energy and width in the continuum, especially taking into account the contribution from the resonant width to the energy density functional self-consistently [10-12]. Recently, the canonical states in the HFB model, corresponding to single-particle states in the HF model but including the pairing effects, were obtained via the diagonalization of the density matrix constructed by the Green’s function method [13, 14]. These canonical states can be used to investigate the neutron numbers in the CF region in neutron-rich nuclei. -
In the Skyrme HF model, the single-particle wave function
$ \varphi_{i}( {{r}} \sigma) $ satisfies the Schrödinger equation,$ \hat{h}\varphi_{i} = \varepsilon_{i}\varphi_{i} $ , where the single-particle Hamiltonian$ \hat{h} = \hat{T}+{U}_q+\hat{U}_{\rm{s.o.}} $ includes the kinetic term$ \hat{T} = $ $ - {\bf{\nabla}}\cdot \dfrac{\hbar^2}{2m^*_q( {{r}})} {\bf{\nabla}} $ , the mean-field potential$ {U}_q $ and the spin-orbit term$ \hat{U}_{\rm{s.o.}} = {{W}}_q( {{r}})\cdot (-{\rm i})( {\bf{\nabla}}\times {{\sigma}}) $ . The explicit expressions of the effective mass$ m^*_q( {{r}}) $ , the mean-field potential$ U_q( {{r}}) $ , the spin-orbit form factor$ {{W}}_q( {{r}}) $ for neutrons ($ q = n $ ) and protons ($ q = p $ ) as a function of the densities can easily be found in literature, such as in [7, 15].With the assumption of a spherical symmetry for the nucleus, the single-particle wave function for nucleons can be written as
$ \varphi_{i}( {{r}}\sigma) = \dfrac{R_{i}(r)}{r}Y_{ljm}(\hat{ {{r}}}\sigma), \; i = (nljm) $ , where$ R_{i}(r) $ is the radial wave function, and$ Y_{ljm}(\hat{ {{r}}}\sigma) $ are the spinor spherical harmonics. As a result, the radial Schrödinger equation can be obtained as follows:$ \begin{aligned}[b]& - \frac{\hbar^2}{2m^*_q}\frac{{\rm d}^2R_i(r)}{{\rm d}r^2} - \frac{\rm d}{{\rm d}r}\left(\frac{\hbar^2}{2m^*_q}\right)\frac{{\rm d}R_i(r)}{{\rm d}r} \\&+ \left\{ \frac{\hbar^2}{2m^*_q} \frac{l(l+1)}{r^2} + \frac{1}{r} \frac{\rm d}{{\rm d}r}\left(\frac{\hbar^2}{2m^*_q}\right) \right. \\ & \left. +U_q(r)+ \left[j(j+1)-l(l+1)-\frac{3}{4} \right] \frac{1}{r}W_q(r) \right\} R_i(r) \\=& \varepsilon_{i}R_i(r), \end{aligned} $

(1) where
$ \varepsilon_i $ is the energy of the single-particle state. The number of particles in the CF region for the single-particle state i can be calculated as [7]$ N_{\rm{CF}} = \int^{\infty}_{r_{\rm{CF}}} v^2_i (2j+1) R^2_i(r){\rm d}r, $

(2) where the occupation probability
$ v^2_i $ is determined by the filling approximation in the HF model. As mentioned before, the starting point of the CF region$ r_{\rm{CF}} $ is defined as the position at which the single-particle energy is equal to its single-particle potential, i.e.,$ \varepsilon_i = U_i(r_{\rm{CF}}) $ . In Ref. [7], the single-particle potential was determined from the Schrödinger Eq. (1)$\begin{aligned} U_i(r) =& \frac{\hbar^2}{2m^*_q}\frac{l(l+1)}{r^2}+\frac{1}{r}\frac{\rm d}{{\rm d}r}\left( \frac{\hbar^2}{2m^*_q}\right)+U_q\\&+ \left[ j(j+1)-l(l+1)-\frac{3}{4}\right] \frac{1}{r} W_q(r). \end{aligned}$

(3) However, one should note that the centrifugal term
$ \dfrac{\hbar^2}{2m^*_q}\dfrac{l(l+1)}{r^2} $ and the surface term$ \dfrac{1}{r}\dfrac{\rm d}{{\rm d}r}\left( \dfrac{\hbar^2}{2m^*_q}\right) $ actually come from the kinetic term$ \hat{T} $ . Here, the pure potential energy should be$ V_i(r) = U_q+ \left[ j(j+1)-l(l+1)-\frac{3}{4}\right] \frac{1}{r} W_q(r), $

(4) which only includes the mean-field and spin-orbit potentials. In contrast, Ref. [9] worked in the deformed relativistic Hartree-Bogoliubov theory, whereby they just used the mean-field potential
$ \varepsilon_i = U_q(r_{\rm{CF}}) $ to define the boundary of the CF region. In the following section, we will use the neutron-rich nucleus$ ^{68} {\rm{Ca}}$ as an example for calculating the number of neutrons in the CF region using the Skyrme HF model with SkM* [16], and show the results given by the different definitions of the boundary of the CF region. -
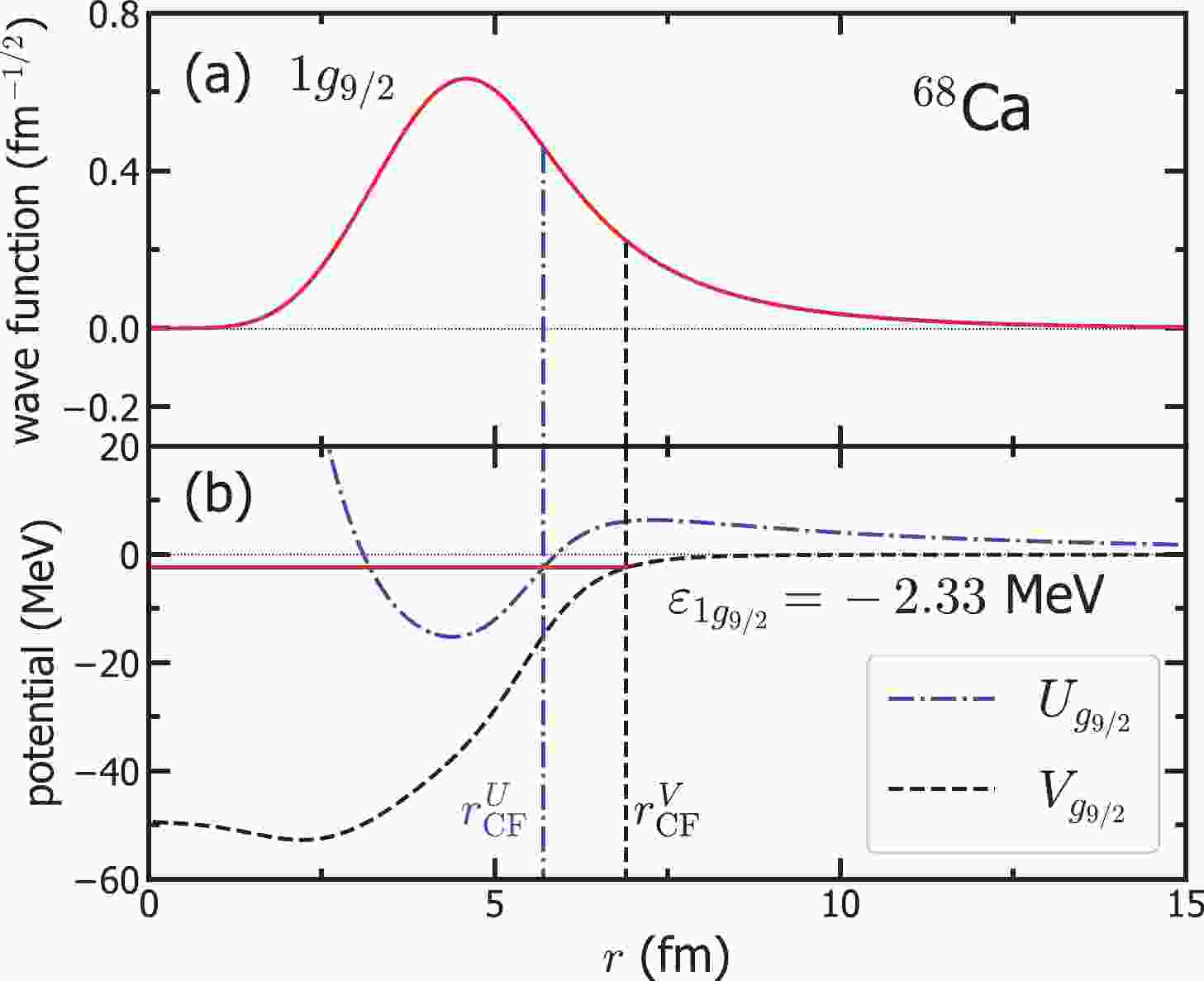
Figure 1 (a) shows the single-particle wave function
$ R_{1g_{9/2}}(r) $ for the state$ 1g_{9/2} $ in$ ^{68} {\rm{Ca}}$ . It has the energy$ \varepsilon_{1g_{9/2}} = -2.33 $ MeV, which is the Fermi energy of this nucleus with an occupation probability of$ v^2_i = 0.8 $ . In Fig. 1 (b), we present the single-particle potential$ U_{g_{9/2}} $ defined by Eq. (3) and$ V_{g_{9/2}} $ defined by Eq. (4). Obviously, one can see that the potential$ U_{g_{9/2}} $ diverges near the origin and has a$ 6 $ -MeV-high barrier at$ r\approx 7 $ fm due to the centrifugal term for this state. The definition$ \varepsilon_{1g_{9/2}} = U_{g_{9/2}}(r_{\rm{CF}}^U) $ shows the boundary of the CF region at$ r_{\rm{CF}}^U = 5.7 $ fm. One may notice that there is another point at$ r\approx 3 $ fm with$ \varepsilon_{1g_{9/2}} = U_{g_{9/2}} $ . Therefore, the region$ 0<r\lesssim 3 $ fm with$ \varepsilon_{1g_{9/2}}<U_{g_{9/2}} $ is also "forbidden" by the huge centrifugal term for a classical particle. However, according to Ref. [7], only neutrons in the region$ r>5.7 $ fm are counted as being in the CF region, and the result is$ N_{\rm{CF}}^U\approx 1.43 $ .
Figure 1. (color online) (a) Single-particle wave function
$ R_{1g_{9/2}}(r) $ (solid curve), (b) energy level$ \varepsilon_{1g_{9/2}} $ (solid line) and the potentials for the state$ 1g_{9/2} $ in$ ^{68} {\rm{Ca}}$ calculated by the Skyrme HF model with SkM*. The dash-dotted and dashed curves in panel (b) denote the potentials$ U_{g_{9/2}} $ and$ V_{g_{9/2}} $ defined by Eq. (3) and Eq. (4), respectively. The corresponding vertical lines denote the boundary of the CF region$ r_{\rm{CF}}^U $ and$ r_{\rm{CF}}^V $ defined by the single-particle potentials$ U_{g_{9/2}} $ and$ V_{g_{9/2}} $ , respectively.In contrast, the potential
$ V_{g_{9/2}} $ does not have such an obvious barrier. The main contribution comes from the mean-field potential$ U_q $ , while the spin-orbit potential$ U_{\rm{s.o.}} $ is almost negligible. If we define the boundary of the CF region by$ \varepsilon_{1g_{9/2}} = V_{g_{9/2}}(r_{\rm{CF}}^V) $ , one could get a further starting point at$ r_{\rm{CF}}^V = 6.9 $ fm. Using the same single-particle wave function$ R_{1g_{9/2}}(r) $ as shown in Fig. 1(a), the calculated neutron number in the CF region is$ N_{\rm{CF}}^V\approx 0.32 $ , much smaller than$ N_{\rm{CF}}^U\approx 1.43 $ as defined by the full single-particle potential$ U_{g_{9/2}} $ .For other bound single-particle states in
$ ^{68} {\rm{Ca}}$ , the energy and the occupation probability, the neutron numbers in the CF region$ N_{\rm{CF}}^{U} $ and$ N_{\rm{CF}}^{V} $ calculated by using different boundaries$ r_{\rm{CF}}^U $ and$ r_{\rm{CF}}^V $ defined by the single-particle potentials$ U_i $ and$ V_i $ are listed in Table 1. It is easily explained that for the$ s_{1/2} $ states, the two results$ N_{\rm{CF}}^{U} $ and$ N_{\rm{CF}}^{V} $ are identical, as there is no centrifugal barrier. As the angular momentum l increases, the difference between the two results becomes more obvious. The growth of the centrifugal barrier draws the boundary of the CF region$ r_{\rm{CF}}^U $ closer to the origin than$ r_{\rm{CF}}^V $ and thus results in a larger neutron number$ N_{\rm{CF}}^{U} $ . By summing all the contributions from$ N_{\rm{CF}}^{U} $ of the occupied single-particle states, the total number of neutrons in the CF region is$ N^{\rm{tot}}_{\rm{CF}}\approx 6.5 $ , which is consistent with the result shown in Ref. [7] but almost twice that of$ N^{\rm{tot}}_{\rm{CF}}\approx 3.6 $ determined by summing$ N_{\rm{CF}}^{V} $ . Therefore, the boundary of the CF region defined by different single-particle potentials will lead to quite different neutron numbers in the CF region. It is worth mentioning that Ref. [9] used the mean-field potential$ U_q $ to define the boundary of the CF region, which is rather close to the present single-particle potential$ V_i = U_q+U_{{\rm{s.o.}}} $ . Indeed, when we consider a neutron-rich or neutron halo nucleus, the centrifugal barrier is quite essential in determining whether the neutron’s wave function can extend far outside or not. When counting the number of neutrons in the CF region, one should better clarify the definition of the CF region and whether the centrifugal barrier is included or not.state HF HFB $ \varepsilon_i $ 

$ v^2_i $ 

$ N^U_{\rm{CF}} $ 

$ N^V_{\rm{CF}} $ 

$ \varepsilon_i $ 

$ v^2_i $ 

$ N^{\rm{box}}_{\rm{CF}} $ 

$ N^{\rm{GF}}_{\rm{CF}} $ 

$ 1s_{1/2} $ 

−40.489 1 0.2307 0.2307 −40.334 0.9999 0.2267 0.2266 $ 2s_{1/2} $ 

−17.477 1 0.2076 0.2076 −17.370 0.9982 0.2035 0.2034 $ 3s_{1/2} $ 

−0.011 0 0 0 0.655 0.0686 0.1372 0.1384 $ 1p_{1/2} $ 

−28.961 1 0.2555 0.2024 −28.557 0.9996 0.1907 0.1907 $ 2p_{1/2} $ 

−5.900 1 0.3450 0.3110 −5.750 0.9727 0.2928 0.2929 $ 1p_{3/2} $ 

−31.134 1 0.4389 0.3429 −30.930 0.9997 0.3401 0.3401 $ 2p_{3/2} $ 

−7.952 1 0.6106 0.5429 −7.823 0.9868 0.5438 0.5438 $ 1d_{3/2} $ 

−16.778 1 0.4848 0.2623 −16.382 0.9981 0.2490 0.2490 $ 2d_{3/2} $ 

1.245 0 0 0 2.755 0.0283 0.1131 0.1138 $ 1d_{5/2} $ 

−21.437 1 0.6194 0.3704 −21.225 0.9988 0.3889 0.3888 $ 2d_{5/2} $ 

−0.024 0 0 0 0.279 0.1266 0.7593 0.7614 $ 1f_{5/2} $ 

−4.635 1 0.8749 0.3540 −4.376 0.9432 0.3324 0.3326 $ 1f_{7/2} $ 

−11.778 1 0.9994 0.4934 −11.547 0.9938 0.4941 0.4941 $ 1g_{7/2} $ 

3.373 0 0 0 6.575 0.0131 0.1052 0.1054 $ 1g_{9/2} $ 

−2.333 0.8 1.4271 0.3243 −2.075 0.6992 0.2255 0.2255 $ N^{\rm{con}}_{\rm{CF}} $ 

0 0 1.5826 1.6007 $ N^{\rm{tot}}_{\rm{CF}} $ 

6.4939 3.6419 5.0699 5.0884 Table 1. Single-particle energies
$ \varepsilon_i $ (MeV) for neutrons in$ ^{68} {\rm{Ca}}$ , their occupation probabilities$ v^2_i $ , and contribution to the number of neutrons in the CF region as calculated by the HF model with SkM*, HFB model with SkM* and DDDI pairing force. In the HF calculation, the value$ N_{\rm{CF}}^{U(V)} $ denotes the number of neutrons in the CF region defined by potential$ U(V)_{i} $ , respectively. In the HFB model, the results$ N^{\rm{box}}_{\rm{CF}} $ and$ N^{\rm{GF}}_{\rm{CF}} $ are calculated by the canonical single-particle states obtained by the box-discretized and Green’s function methods, respectively. The last two lines$ N^{\rm{tot}}_{\rm{CF}} $ and$ N^{\rm{con}}_{\rm{CF}} $ are the total number of neutrons in the CF region and those contributed from the positive-energy canonical states.In the following discussions, we will use the single-particle potential
$ V_i $ to define the boundary of the CF region and explore the influence of the pairing correlation on the neutron number in the CF region using the HFB model with the same SkM* functional as for$ ^{68} {\rm{Ca}}$ . We use the density-dependent delta interaction (DDDI) for the pairing field,$ \Delta(r) = \frac{1}{2}V_0 \left[1-\eta \left( \frac{\rho_q( r)}{\rho_0} \right)^{\alpha}\right]\tilde{\rho}_q(r), \; \; \; q = n\; \; {\rm{or}}\; \; p, $

(5) where
$ \rho_q(r) $ and$ \tilde{\rho}_q(r) $ are the local particle and pair densities, respectively. The parameters$ V_0 = -458.4 $ MeV fm$ ^{-3} $ ,$ \eta = 0.73 $ ,$ \alpha = 0.61 $ , and the energy cut-off$ 60 $ MeV are adjusted according to the experimental gaps of the Ca isotopes [17, 18].First, one should notice that in the HFB model, the "single-particle state" corresponding to the HF single-particle state is actually the "canonical state", which is obtained by diagonalizing the density matrix and includes the effect of the pairing correlation on the single-particle state [19-21]. The eigenvalues of this diagonalization are the occupation probabilities
$ v^2_i $ of the canonical states, and the eigenvectors lead to the canonical wave functions. The energy$ \varepsilon_i $ is the expectation value of the single-particle Hamiltonian$ \hat{h} $ on the canonical wave function. The density matrix can be constructed from the quasiparticle wave functions obtained by either discretization under the box boundary condition [20, 21] ("box-discretized method" for short in the following), or expanded on the Woods-Saxon basis [9, 22, 23]. The density matrix can be also calculated directly from the contour integration of the Green’s function on the complex energy plane [13, 14]. In this way, the asymptotic wave function can be properly described for the continuum states, and the bad asymptotic behavior under the box boundary condition can be avoided.Taking the canonical state
$ 2d_{5/2} $ as an example, its wave function obtained by the box-discretized method and the Green’s function method are shown in Fig. 2 (a). One can see that the wave functions obtained by the two methods are almost the same but different in the asymptotic region, as shown in the inset. The energy of this state and its single-particle potential$ V_{d_{5/2}} $ are shown in Fig. 2 (b). The energy$ \varepsilon_{2d_{5/2}} = 0.28 $ MeV is rather close to and above the continuum threshold. According to the explanation in Ref. [9], although the energy is higher than its single-particle potential$ V_{d_{5/2}} $ , this state cannot be occupied by a classical particle; otherwise, this particle will be scattered out from the potential. Therefore, all particles in this state should contribute to the number of particles in the CF region, i.e., the boundary of the CF region in Eq. (2) starts from the origin$ r_{\rm{CF}} = 0 $ . Using the different canonical wave functions obtained by the box-discretized and Green’s function methods shown in panel (a), one can determine the neutron numbers in the CF region as$ N^{\rm{box}}_{\rm{CF}} = 0.7593 $ and$ N^{\rm{GF}}_{\rm{CF}} = 0.7614 $ , respectively. Indeed, the result given by the Green’s function method is slightly larger as its wave function decays slowly in the asymptotic region; however, actually, the difference between the two results is negligibly small.
Figure 2. (color online) (a) Canonical single-particle wave function, (b) energy level
$ \varepsilon_{2d_{5/2}} $ (solid line) and the potential$ V_{d_{5/2}} $ (dashed curve) for the state$ 2d_{5/2} $ in$ ^{68} {\rm{Ca}}$ calculated by the HFB model with SkM* and DDDI pairing force. The dash-dotted and solid curves denote the canonical single-particle wave functions obtained by the box-discretized (box) and Green’s function (GF) methods, respectively, in panel (a).For other canonical states, the energies
$ \varepsilon_i $ and the corresponding occupation probabilities$ v^2_i $ obtained by the HFB model with the box-discretized method are listed in Table 1. These results obtained by the Green’s function method are almost the same and thus not listed here. Using the boundary of the CF region defined by the single-particle potential$ V_i $ but different canonical wave functions obtained by the two methods, the calculated neutron numbers in the CF region$ N^{\rm{box}}_{\rm{CF}} $ and$ N^{\rm{GF}}_{\rm{CF}} $ are listed.Compared with the single-particle energies
$ \varepsilon_i $ given by the HF model, all canonical energies given by the HFB model are slightly raised up due to the pairing correlation. As a result, using the almost unchanged single-particle potential$ V_i $ for the bound single-particle states, the neutron numbers$ N_{\rm{CF}} $ calculated by the HFB model are a bit smaller than those by the HF model. More interestingly, the states$ 3s_{1/2} $ and$ 2d_{5/2} $ are rather weakly bound and not-occupied states in the HF model, while they have positive energies in the HFB model and can be occupied due to the pairing correlation. Moreover, states$ 2d_{3/2} $ and$ 1g_{7/2} $ also have positive energies in both the HF and HFB models. These positive-energy canonical states can be occupied and contribute to the particle number in the CF region only due to the pairing correlation. Their total contributions are summed up as$ N^{\rm{con}}_{\rm{CF}}\approx 1.6 $ . As a result, the total neutron number in the CF region given by the HFB model is$ N^{\rm{tot}}_{\rm{CF}}\approx 5.1 $ , which is approximately 40% higher than the result of the HF model,$ N^{\rm{tot}}_{\rm{CF}}\approx 3.6 $ , due to the pairing correlation. Comparing the neutron numbers$ N^{\rm{box}}_{\rm{CF}} $ and$ N^{\rm{GF}}_{\rm{CF}} $ calculated by the box-discretized and Green’s function methods, there are some visible but small differences for the canonical states with positive energies. Therefore, the asymptotic wave functions given by the box-discretized and Green’s function methods do not result in any obvious differences in the neutron number in the CF region. -
Neutrons in the neutron-rich nucleus
$ ^{68} {\rm{Ca}}$ tunneling into the CF region were investigated using the Skyrme HF and HFB models. First, the definition of the CF region was discussed by using different single-particle potentials within the HF model for the bound states. It was found that the centrifugal term will push the single-particle potential up for states$ l>0 $ , and thus, the starting point of the CF region was drawn closer to the origin. This resulted in a much larger neutron number in the CF region. Therefore, to count the number of neutrons in the CF region, one should better clarify the definition of the CF region insofar as to whether the centrifugal barrier is included or not. Then, we discussed the effect of the pairing correlation on the neutron number in the CF region by comparing the results of the HF and HFB models. Some unoccupied weakly bound and continuum HF single-particle states were raised up to partially-occupied canonical states with positive energies due to pairing. The neutrons in these states were also counted in the CF region. Therefore, the pairing correlation can obviously result in a larger neutron number in the CF region. Finally, we discussed the influence of the different asymptotic wave functions of these positive-energy canonical states given by the box-discretized and Green’s function methods on the neutron number in the CF region. However, this influence turned out to be not obvious. As our next step, we will systematically investigate the neutron numbers in the CF region of other isotopes using different Skyrme functionals to further verify the abovementioned conclusions. -
The author Y. Z. would like to thank K. Y. Zhang, X. Y. Qu, and J. N. Hu for helpful discussions during this work.
Neutrons in the classically forbidden region in neutron-rich nucleus 68Ca
- Received Date: 2021-02-03
- Available Online: 2021-07-15
Abstract: Neutrons tunneling to the classically forbidden (CF) region in the neutron-rich nucleus





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: