-
Recently, the BESIII collaboration observed an excess over known contributions of the conventional charmed mesons near the
$ D_s^- D^{*0} $ and$ D^{*-}_s D^0 $ mass thresholds in the$ K^{+} $ recoil-mass spectrum with the significance of 5.3$ \sigma $ in the processes of$ e^+e^-\to $ $ K^+ (D_s^- D^{*0} + D^{*-}_s D^0) $ [1]. This is the first candidate of the charged hidden-charm tetraquark state with strangeness. The Breit-Wigner mass and width of the new structure,$ Z_{cs}(3985) $ , were determined to be$ 3985.2^{+2.1}_{-2.0}\pm1.7\;\rm{MeV} $ and$ 13.8^{+8.1}_{-5.2}\pm4.9\;\rm{MeV} $ , respectively. According to the production mode, it is clear to draw the conclusion that$ Z_{cs}(3985) $ must be a cousin of the well-known$ Z_c(3885/3900) $ with strangeness.$ Z_c(3885) $ was observed in the process$ e^{+}e^{-} \to (D\bar{D}^{*})^-\pi^+ $ [2], which means that$ Z_c(3885) $ and$ Z_{cs}(3985) $ are governed by a similar production mechanism and have a similar quark structure$ c\bar{c}q\bar{u} $ with$ q = d $ or s. The discovery of$ Z_{cs}(3985) $ may provide some unique hints to uncover the secrets of the charged exotic$ Z_c $ structures.The existence of an exotic
$ Z_{cs} $ state with a mass, which lies near the$ D_s^- D^{*0} $ and$ D^{*-}_s D^0 $ thresholds$ 3975.2$ and$ 3977.0\;\rm{MeV} $ respectively, has been predicted in several theoretical models, including the diquark-antidiquark type tetraquark model [3, 4], the$ D_s\bar{D}^* $ molecule model [5, 6], the hadro-quarkonium model [4, 7], and the initial-single-chiral-particle-emission mechanism [8]. Similar to$ Z_c $ states, the decay rate of$ Z_{cs} $ to open-charm final states is expected to be larger than the decay rate to charmonium final states.After the discovery of
$ Z_{cs}(3985) $ , several possible explanations for its nature were proposed, such as the tetraquark state [9, 10],$ D^* \bar{D}_s-D \bar{D}_s^* $ hadronic molecular state, dynamically generated resonance with coupled-channel effects [9, 11-16], and re-scattering effects [17, 18]. We study its nature with the photo-production [19].In Ref. [20], we investigate the spin-parity
$ J^P = 1^+ $ hidden-charm tetraquark states without strangeness in the framework of the QCD sum rules, and examine the dependence of the masses and pole residues on the energy scales$ \mu $ of the spectral densities at the quark-gluon level, at length, for the first time. Our reliable calculations support identifying$ X(3872) $ and$ Z_c(3900) $ as the diquark-antidiquark type tetraquark states having hidden-charm with the quantum numbers$ J^{PC} = 1^{++} $ and$ 1^{+-} $ , respectively. In Ref. [21], we take the diquark and antidiquark operators in the color antitriplet and color triplet, respectively, as the fundamental building blocks to construct the scalar, axialvector, and tensor four-quark local currents to investigate the mass spectrum of the ground state tetraquark states with hidden-charm but without strangeness in the framework of the QCD sum rules comprehensively, and revisit the possible identifications of the existing tetraquark candidates with hidden-charm, such as$ X(3860) $ ,$ X(3872) $ ,$ X(3915) $ ,$ X(3940) $ ,$ X(4160) $ ,$ Z_c(3900) $ ,$ Z_c(4020) $ ,$ Z_c(4050) $ ,$ Z_c(4055) $ ,$ Z_c(4100) $ ,$ Z_c(4200) $ ,$ Z_c(4250) $ ,$ Z_c(4430) $ , and$ Z_c(4600) $ .In Refs. [20, 21], we choose the local axialvector four-quark currents
$ \eta^N_\mu(x) $ and$ \eta^P_\mu(x) $ ,$ \begin{aligned}[b] \eta^N_{\mu}(x) =&\dfrac{\varepsilon^{ijk}\varepsilon^{imn}}{\sqrt{2}}\Big\{u^{T}_j(x)C\gamma_5 c_k(x) \bar{d}_m(x)\gamma_\mu C \bar{c}^{T}_n(x)\\ &-u^{T}_j(x)C\gamma_\mu c_k(x)\bar{d}_m(x)\gamma_5 C \bar{c}^{T}_n(x) \Big\} \, , \\ \eta^P_{\mu}(x) =&\dfrac{\varepsilon^{ijk}\varepsilon^{imn}}{\sqrt{2}}\Big\{u^{T}_j(x)C\gamma_5 c_k(x) \bar{d}_m(x)\gamma_\mu C \bar{c}^{T}_n(x)\\ &+u^{T}_j(x)C\gamma_\mu c_k(x)\bar{d}_m(x)\gamma_5 C \bar{c}^{T}_n(x) \Big\} \, , \end{aligned} $

(1) to investigate the lowest tetraquark states with the quantum numbers
$ J^{PC} = 1^{+-} $ and$ 1^{++} $ , respectively, where i, j, k, m, and n are color indices. The four-quark current$ \eta^N_\mu(x) $ has the quantum numbers$ J^{PC} = 1^{+-} $ and potentially couples to$ Z_c^+(3900) $ . In fact,$ Z_c^\pm(3900) $ have non-zero electric charge, do not have definite charge conjugation, and are not eigenstates of the charge conjugation. Only the electric neutral state$ Z_c^0(3900) $ has definite charge conjugation. If$ Z_{cs}^-(3985) $ is truly a tetraquark state, irrespective of whether it is the diquark-antidiquark type or meson-meson type tetraquark state, its valence quarks are$ c\bar{c}s\bar{u} $ , and it has no definite electric conjugation. Indeed, to be more precise, we suppose that it has definite conjugation, just like its cousins$ c\bar{c}q\bar{q} $ and$ c\bar{c}s\bar{s} $ . In the present work, we tentatively identify the$ Z_{cs}^-(3985) $ as the diquark-antidiquark type axialvector tetraquark state with the four valence quarks$ c\bar{c}s\bar{u} $ and examine its mass in the framework of the QCD sum rules at length. Then ,we take into account the light flavor$ SU(3) $ mass-breaking effect to explore the mass spectrum of the diquark-antidiquark type tetraquark states with hidden-charm and with strangeness according to our previous studies.The article is arranged as follows: in Sec. II, we obtain the QCD sum rules for the masses and pole residues of the
$ J^P = 1^+ $ tetraquark states with hidden-charm and strangeness; in Sec. III, we obtain numerical results and present the discussion; and Sec. IV presents our conclusion. -
If we choose the favorable diquark configurations, the scalar (S) and axialvector (A) diquark states in the color antitriplet, as the fundamental building blocks to construct the diquark-antidiquark type tetraquark states, we obtain two nonets with the symbolic structures,
$ \begin{aligned}[b] I = 1 :\; & [uc]_S[\bar{d}\bar{c}]_A-[uc]_A[\bar{d}\bar{c}]_S\, , \,[dc]_S[\bar{u}\bar{c}]_A-[dc]_A[\bar{u}\bar{c}]_S\, ,\, \\ &\;\dfrac{[uc]_S[\bar{u}\bar{c}]_A-[uc]_A[\bar{u}\bar{c}]_S-[dc]_S[\bar{d}\bar{c}]_A+[dc]_A[\bar{d}\bar{c}]_S}{\sqrt{2}}\, ; \\ I = 0 : \; &\dfrac{[uc]_S[\bar{u}\bar{c}]_A-[uc]_A[\bar{u}\bar{c}]_S+[dc]_S[\bar{d}\bar{c}]_A-[dc]_A[\bar{d}\bar{c}]_S}{\sqrt{2}}\, ,\\ &\;[sc]_S[\bar{s}\bar{c}]_A-[sc]_A[\bar{s}\bar{c}]_S\, ; \\ I = \dfrac{1}{2} :\; & [qc]_S[\bar{s}\bar{c}]_A-[qc]_A[\bar{s}\bar{c}]_S\, , \,[sc]_S[\bar{q}\bar{c}]_A-[sc]_A[\bar{q}\bar{c}]_S\, , \end{aligned} $

(2) and
$ \begin{aligned}[b] I = 1 : \;& [uc]_S[\bar{d}\bar{c}]_A+[uc]_A[\bar{d}\bar{c}]_S\, , \,[dc]_S[\bar{u}\bar{c}]_A+[dc]_A[\bar{u}\bar{c}]_S\, ,\, \\ \;&\dfrac{[uc]_S[\bar{u}\bar{c}]_A+[uc]_A[\bar{u}\bar{c}]_S-[dc]_S[\bar{d}\bar{c}]_A-[dc]_A[\bar{d}\bar{c}]_S}{\sqrt{2}} \, ; \\ I = 0 : \;& \dfrac{[uc]_S[\bar{u}\bar{c}]_A+[uc]_A[\bar{u}\bar{c}]_S+[dc]_S[\bar{d}\bar{c}]_A+[dc]_A[\bar{d}\bar{c}]_S}{\sqrt{2}}\, ,\\ \;&[sc]_S[\bar{s}\bar{c}]_A+[sc]_A[\bar{s}\bar{c}]_S\, ; \\ I = \dfrac{1}{2} : \;&[qc]_S[\bar{s}\bar{c}]_A+[qc]_A[\bar{s}\bar{c}]_S\, , \,[sc]_S[\bar{q}\bar{c}]_A+[sc]_A[\bar{q}\bar{c}]_S\, , \end{aligned} $

(3) where the
$ I = 1 $ ,$ 0 $ ,$ \dfrac{1}{2} $ are the isospins of the hidden-charm tetraquark states,$ q = u $ , d.In the first nonet, only the charge-neutral tetraquark states
$\dfrac{1}{\sqrt{2}}\Big([uc]_S[\bar{u}\bar{c}]_A\!-\![uc]_A[\bar{u}\bar{c}]_S\!-\![dc]_S[\bar{d}\bar{c}]_A\!+\! [dc]_A[\bar{d}\bar{c}]_S \Big)$ ,$\dfrac{1}{\sqrt{2}}\Big([uc]_S[\bar{u}\bar{c}]_A-[uc]_A[\bar{u}\bar{c}]_S+[dc]_S[\bar{d}\bar{c}]_A-[dc]_A[\bar{d}\bar{c}]_S\Big)$ and$ [sc]_S[\bar{s}\bar{c}]_A-[sc]_A[\bar{s}\bar{c}]_S $ are eigenstates of the charge conjugation operators, and have the definite charge conjugation$ C = - $ .In the second nonet, only the charge-neutral tetraquark states
$ \dfrac{1}{\sqrt{2}}\Big([uc]_S[\bar{u}\bar{c}]_A\!+\![uc]_A[\bar{u}\bar{c}]_S\!-\![dc]_S[\bar{d}\bar{c}]_A\!-\! [dc]_A [\bar{d}\bar{c}]_S\Big) $ ,$\dfrac{1}{\sqrt{2}}\Big([uc]_S[\bar{u}\bar{c}]_A+[uc]_A[\bar{u}\bar{c}]_S+[dc]_S[\bar{d}\bar{c}]_A+[dc]_A[\bar{d}\bar{c}]_S \Big)$ and$ [sc]_S[\bar{s}\bar{c}]_A+[sc]_A[\bar{s}\bar{c}]_S $ are eigenstates of the charge conjugation operators, and have the definite charge conjugation$ C = + $ .Thereafter, we assume that the first and second nonets have negative and positive charge conjugations, respectively, such as to distinguish the two nonets, and we must bear in mind that the charge conjugation is not a good quantum number.
Routinely, we write down the two-point vacuum Green's functions
$ \Pi_{\mu\nu}(p) $ ,$ \begin{array}{l} \Pi_{\mu\nu}(p) = {\rm i}\int {\rm d}^4x {\rm e}^{{\rm i}p \cdot x} \langle0|T\left\{J_\mu(x)J^{\dagger}_\nu(0)\right\}|0\rangle \, , \end{array} $

(4) where the interpolating currents
$ J_\mu(x) = J^N_\mu(x) $ and$ J^P_\mu(x) $ ,$ \begin{aligned}[b] J^N_{\mu}(x) =& \dfrac{\varepsilon^{ijk}\varepsilon^{imn}}{\sqrt{2}}\Big\{u^{T}_j(x)C\gamma_5 c_k(x) \bar{s}_m(x)\gamma_\mu C \bar{c}^{T}_n(x)\\ &-u^{T}_j(x)C\gamma_\mu c_k(x)\bar{s}_m(x)\gamma_5 C \bar{c}^{T}_n(x) \Big\} \, , \\ J^P_{\mu}(x) = &\frac{\varepsilon^{ijk}\varepsilon^{imn}}{\sqrt{2}}\Big\{u^{T}_j(x)C\gamma_5 c_k(x) \bar{s}_m(x)\gamma_\mu C \bar{c}^{T}_n(x)\\ &+u^{T}_j(x)C\gamma_\mu c_k(x)\bar{s}_m(x)\gamma_5 C \bar{c}^{T}_n(x) \Big\} \, , \end{aligned} $

(5) the superscripts N and P stand for the negative and positive charge conjugations, respectively, as i, j, k, m, and n are color indices. We suppose that the interpolating four-quark currents
$ J^N_\mu(x) $ and$ J_\mu^P(x) $ have the negative and positive charge conjugations, respectively, in the sense of the limit$ J_\mu(x)|_{s \to u} $ or$ J_\mu(x)|_{u \to s} $ , which must be understood in the same way as in the two tetraquark nonets in Eqs. (2), (3). In Refs. [20, 21], we choose the four-quark currents$ \eta^N_\mu(x) $ and$ \eta^P_\mu(x) $ to explore the axialvector tetraquark states$ uc\bar{d}\bar{c} $ , and observe that the$ uc\bar{d}\bar{c} $ states with the quantum numbers$ J^{PC} = 1^{+-} $ and$ 1^{++} $ have almost degenerate masses. The currents$ J^N_\mu(x) $ and$ J^P_\mu(x) $ are the$ SU(3) $ partners of the currents$ \eta^N_\mu(x) $ and$ \eta^P_\mu(x) $ , respectively, with the simple relation$ d \leftrightarrow s $ . Now, we also expect that the four-quark currents$ J^N_\mu(x) $ and$ J_\mu^P(x) $ couple potentially to the$ J^{PC} = 1^{+-} $ and$ 1^{++} $ tetraquark states with almost the same masses.At the hadron side, we insert a complete set of intermediate tetraquark states with hidden-charm, strangeness and other quantum numbers, such as the spin, parity, charge conjugation, as the four-quark current operators
$ J_\mu(x) $ , into the Green's functions$ \Pi_{\mu\nu}(p) $ to obtain the hadron spectral representation [22-24], and separate the lowest tetraquark states$ Z_{N/P} $ with hidden-charm and with strangeness (or the lowest pole terms), and obtain the results:$ \begin{aligned}[b] \Pi_{\mu\nu}(p) = & \dfrac{\lambda_Z^2}{M^2_Z-p^2}\left(-g_{\mu\nu}+\frac{p_{\mu}p_{\nu}}{p^2} \right) +\cdots \, ,\\ = &\Pi(p^2)\left(-g_{\mu\nu}+\frac{p_{\mu}p_{\nu}}{p^2} \right) +\cdots\, , \end{aligned} $

(6) where the pole residues
$ \lambda_Z $ (in other works, the decay constants) are defined by$ \langle 0|J_\mu(0)|Z_{N/P}(p)\rangle = \lambda_Z\varepsilon_\mu $ , the$ \varepsilon_\mu $ are the polarization vectors of the axialvector tetraquark states$ Z_{N/P} $ . In contrast, there are two-particle scattering state contributions from the two-meson pairs$ K J/\psi $ ,$ \eta_c K^* $ ,$ D_s \bar{D}^* $ ,$ D^* \bar{D}_s $ ,$ \cdots $ , as the quantum field theory does allow non-vanishing couplings between the four-quark currents and two-particle scattering states in case that they share the same quantum numbers. In Ref. [25], we investigate the$ Z_c(3900) $ as an axialvector tetraquark state with the quantum numbers$ J^{PC} = 1^{+-} $ in the framework of the QCD sum rules at length by considering the two-particle scattering state contributions and nonlocal effects between the two colored constituents (diquark and antidiquark) in the four-quark current operator, and obtain the conclusion that the contribution of the$ Z_c(3900) $ as a pole term plays a non-substitutable role, we can saturate the QCD sum rules at the hadron side no matter with or without the two-meson scattering state contributions. The net effects of the two-particle scattering states of the intermediate meson pairs can be effectively taken into account by adding an energy-dependent finite width to the pole term. In the present case, the energy-dependent Breit-Wigner width$ 13.8^{+8.1}_{-5.2}\pm4.9\;\rm{MeV} $ of the$ Z_{cs}(3985) $ is really small enough so as to be neglected safely.On the QCD side, we carry out the operator product expansion up to the vacuum condensates of dimension 10 in a consistent manner, as in our previous studies [20, 21], in the deep Euclidean region
$ P^2 = $ $ -p^2\to\infty $ or$ \gg \Lambda^2_{\rm QCD} $ , which corresponds to the small spatial distance and time interval$ \vec{x}\sim t\sim \dfrac{1}{\sqrt{P^2}} $ . We take into account or calculate the vacuum condensates$ \langle\bar{q}q\rangle $ ,$ \langle\bar{s}s\rangle $ ,$ \langle\bar{q}g_{s}\sigma Gq\rangle $ ,$ \langle\bar{s}g_{s}\sigma Gs\rangle $ ,$ \left\langle\dfrac{\alpha_{s}GG}{\pi}\right\rangle $ ,$ \langle\bar{q}q\rangle\langle\bar{s}s\rangle $ ,$ \langle\bar{q}q\rangle $ $ \left\langle\dfrac{\alpha_{s}GG}{\pi}\right\rangle $ ,$ \langle\bar{s}s\rangle \left\langle\dfrac{\alpha_{s}GG}{\pi}\right\rangle $ ,$ \langle\bar{q}q\rangle \langle\bar{s}g_{s}\sigma Gs\rangle $ ,$ \langle\bar{s}s\rangle \langle\bar{q}g_{s}\sigma Gq\rangle $ ,$ \langle\bar{q}q\rangle $ $ \langle\bar{s}s\rangle \left\langle\dfrac{\alpha_{s}GG}{\pi}\right\rangle $ , and$ \langle\bar{q}g_{s}\sigma Gq\rangle\langle\bar{s}g_{s}\sigma Gs\rangle $ , which are the vacuum expectation values of the quark-gluon operators of the orders$ \mathcal{O}(\alpha_s^k) $ with the restriction$ k\leqslant 1 $ as$ \alpha_s = \dfrac{g_s^2}{4\pi} $ . The vacuum condensates$ \langle g_s^3f_{abc}G^aG^bG^c\rangle $ ,$ \left\langle\dfrac{\alpha_sGG}{\pi}\right\rangle^2 $ ,$ \left\langle\dfrac{\alpha_sGG}{\pi}\right\rangle $ $ \langle \bar{q}g_s\sigma G q\rangle $ , and$ \langle \bar{q}q\rangle\langle g_s^3f_{abc}G^aG^bG^c\rangle $ are of the dimensions$ 6 $ ,$ 8 $ ,$ 9 $ , and$ 9 $ , respectively, and are vacuum expectation values of the quark-gluon operators of the orders$ \mathcal{O}(\alpha_s^{\frac{3}{2}}) $ ,$ \mathcal{O}(\alpha_s^{2}) $ ,$ \mathcal{O}(\alpha_s^{\frac{3}{2}}) $ , and$ \mathcal{O}(\alpha_s^{\frac{3}{2}}) $ , respectively. These are neglected in the present study, as in our previous ones [21, 26-31], as direct calculations confirm that those contributions are indeed miniscule [32]. In the calculations, we assumed vacuum saturation for the sake of factorizing the higher dimensional vacuum condensates into the lowest ones to reduce the number of fundamental parameters, which works very well in the large color numbers limit.Once we obtain the analytical expressions of the correlation (or Green's) functions
$ \Pi(p^2) $ at the degrees of freedom of the quarks and gluons, we resort to dispersion relation to obtain spectral densities at the quark level in a straightforward manner, and match the two sides of the correlation (Green's) functions$ \Pi(p^2) $ (i.e., the hadron side and QCD side), accomplish the quark-hadron duality (in other words, the current-hadron duality) below the thresholds$ s_0 $ of the continuum states or higher resonances, complete the Borel transform in regard to the variable or parameter$ P^2 = -p^2 $ and acquire the QCD sum rules:$ \lambda_{Z}^2\exp\left( -\frac{M_{Z}^2}{T^2}\right) = \int_{4m_c^2}^{s_0}{\rm d}s \,\rho_{\rm QCD}(s)\,\exp\left( -\frac{s}{T^2}\right)\, , $

(7) where the explicit expressions of the spectral densities
$ \rho_{\rm QCD}(s) $ at the quark level are neglected for simplicity.We differentiate both sides of the above equation with regard to the parameter
$ \dfrac{1}{T^2} $ , then eliminate the pole residues$ \lambda_{Z} $ by introducing a fraction, and reach the QCD sum rules for the masses of the hidden-charm axialvector tetraquark states with strangeness,$ M^2_{Z} = \dfrac{-\displaystyle\int_{4m_c^2}^{s_0}{\rm d}s \dfrac{\rm d}{{\rm d}(1/T^2)}\, \rho_{\rm QCD}(s)\,\exp\left( -\dfrac{s}{T^2}\right)}{\displaystyle\int_{4m_c^2}^{s_0}{\rm d}s \, \rho_{\rm QCD}(s)\,\exp\left( -\dfrac{s}{T^2}\right)}\, . $

(8) -
We adopt the standard or conventional values of all vacuum condensates
$ \langle\bar{q}q \rangle = -(0.24\pm 0.01\; \rm{GeV})^3 $ ,$\langle\bar{q}g_s\sigma G q \rangle\! =\! m_0^2\langle \bar{q}q \rangle$ ,$\langle\bar{s}s \rangle \!=\! (0.8\pm0.1)\langle\bar{q}q \rangle$ ,$\langle\bar{s}g_s\sigma G s \rangle \!=\! $ $ m_0^2\langle \bar{s}s \rangle$ ,$m_0^2 = (0.8 \!\pm\! 0.1)\;\rm{GeV}^2$ ,$\left\langle \dfrac{\alpha_s GG}{\pi}\right\rangle \!= \!0.012\!\pm \! 0.004\,\rm{GeV}^4$ at the typical energy scale$ \mu = 1\; \rm{GeV} $ [22-24, 33-35], and prefer the$ \overline{MS} $ masses of the charm and strange quarks,$ m_{c}(m_c) = (1.275\pm0.025)\;\rm{GeV} $ and$ m_s(\mu = 2\;\rm{GeV}) = (0.095\pm $ $ 0.005)\;\rm{GeV} $ , from the Particle Data Group [36], just like in our previous studies [20, 21]. Furthermore, we take into account the energy-scale dependence of all the input parameters at the quark level, such as the quark condensates$ \langle\bar{q}q \rangle $ ,$ \langle\bar{s}s \rangle $ , the mixed quark condensates$ \langle\bar{q}g_s\sigma G q \rangle $ ,$ \langle\bar{s}g_s\sigma G s \rangle $ , and the$ \overline{MS} $ masses$ m_c(\mu) $ ,$ m_s(\mu) $ in the light of renormalization group equation [37],$ \begin{aligned}[b] &\langle\bar{q}q \rangle(\mu) = \langle\bar{q}q\rangle({\rm 1 GeV})\left[\frac{\alpha_{s}({\rm 1 GeV})}{\alpha_{s}(\mu)}\right]^{\frac{12}{33-2n_f}}\, , \\ &\langle\bar{s}s \rangle(\mu) = \langle\bar{s}s \rangle({\rm 1 GeV})\left[\frac{\alpha_{s}({\rm 1 GeV})}{\alpha_{s}(\mu)}\right]^{\frac{12}{33-2n_f}}\, , \\ &\langle\bar{q}g_s \sigma Gq \rangle(\mu) = \langle\bar{q}g_s \sigma Gq \rangle({\rm 1 GeV})\left[\frac{\alpha_{s}({\rm 1 GeV})}{\alpha_{s}(\mu)}\right]^{\frac{2}{33-2n_f}}\, ,\\ &\langle\bar{s}g_s \sigma Gs \rangle(\mu) = \langle\bar{s}g_s \sigma Gs \rangle({\rm 1 GeV})\left[\frac{\alpha_{s}({\rm 1 GeV})}{\alpha_{s}(\mu)}\right]^{\frac{2}{33-2n_f}}\, ,\\ &m_c(\mu) = m_c(m_c)\left[\frac{\alpha_{s}(\mu)}{\alpha_{s}(m_c)}\right]^{\frac{12}{33-2n_f}} \, ,\\ &m_s(\mu) = m_s({\rm 2GeV} )\left[\frac{\alpha_{s}(\mu)}{\alpha_{s}({\rm 2GeV})}\right]^{\frac{12}{33-2n_f}}\, ,\\ &\alpha_s(\mu) = \frac{1}{b_0t}\left[1-\frac{b_1}{b_0^2}\frac{\log t}{t} +\frac{b_1^2(\log^2{t}-\log{t}-1)+b_0b_2}{b_0^4t^2}\right]\, , \end{aligned} $

(9) where
$t = \log \dfrac{\mu^2}{\Lambda^2} ,\;\ b_0 = \dfrac{33-2n_f}{12\pi} ,\;\ b_1 = \dfrac{153-19n_f}{24\pi^2}$ ,$b_2 = $ $\dfrac{2857\!\!-\!\!\dfrac{5033}{9}n_f\!\!+\!\!\dfrac{325}{27}n_f^2}{128\pi^3}$ ,$\Lambda \!\!=\! \!213$ ,$ 296 $ and$ 339\;\rm{MeV} $ for the quark flavor numbers$ n_f = 5 $ ,$ 4 $ , and$ 3 $ , respectively [36]. In the present study, we investigate the hidden-charm tetraquark states$ c\bar{c}u\bar{s} $ with strangeness. It is thus better to adopt the quark flavor numbers$ n_f = 4 $ and then evolve all the input parameters at the quark level to a typical energy scale$ \mu $ , which satisfies the restriction of the energy scale formula$ \mu = \sqrt{M_{Z}-(2{\mathbb{M}}_c)^2} $ with the updated effective charm quark mass$ {\mathbb{M}}_c = 1.82\;\rm{GeV} $ [21, 26-31]. If we take$ Z_{cs}(3985) $ as the ground state tetraquark candidate for the$ Z_{N/P} $ with hidden-charm, with strangeness, and with$ J^P = 1^+ $ , the best energy scales (or our preferred energy scales) of the spectral densities at the quark level are$ \mu = 1.6\;\rm{GeV} $ .Now, let us take a short digression to discuss the energy scale dependence of the QCD sum rules. In preforming the operator product expansion, we can choose any energy scale if the perturbative calculations are feasible at this special energy scale, and the physical quantities extracted from the QCD sum rules must be independent on selections of the energy scales. In this sense, the correlation functions
$ \Pi(p^2) $ are independent on the energy scales,$ \dfrac{\rm d}{{\rm d} \mu}\Pi(p^2) = 0 $ .In contrast, the two-quark (three-quark, four-quark,
$ \cdots $ ) currents$ J(x) $ are operators, and they are renormalized at special energy scales, thus they are defined at special energy scales and are energy scale dependent quantities,$ \begin{array}{l} J(x,\mu) = L^{\gamma_{J}} J(x,\mu_0)\, , \end{array} $

(10) where
$ L = \dfrac{\alpha_s(\mu_0)}{\alpha_s(\mu)} $ , and the$ \gamma_J $ are the anomalous dimensions of the currents$ J(x) $ . We usually neglect renormalization of the hadron states, and set the anomalous dimensions of the pole residues (or decay constants) to be the anomalous dimensions of the current operators,$ \begin{aligned}[b] \langle 0|J(0,\mu)|H(p)\rangle = \;&\lambda_H(\mu)\, , \\ = \;& L^{\gamma_{J}}\langle 0| J(0,\mu_0)|H(p)\rangle\\ = \; &L^{\gamma_{J}} \lambda_H(\mu_0)\, . \end{aligned} $

(11) In fact, even in the QCD sum rules for the conventional D meson, where the radiative corrections of the perturbative terms have been calculated up to the order
$ \mathcal{O}(\alpha_s^2) $ and the radiative corrections of the quark condensate have been calculated up to the order$ \mathcal{O}(\alpha_s^1) $ [38-41], the relation for the decay constant$ f_D(\mu) = L^{\frac{12}{25}}f_D(\mu_0) $ cannot take account of the energy scale dependence of the QCD sum rules in a consistent manner.On the one hand, the non-local operators
$ J(x)J(0) $ have their own anomalous dimensions$ \gamma_{JJ} $ ,$ \gamma_{JJ}\neq 2\gamma_J $ , just like re-normalization of the quark fields$ q(x) $ alone is not sufficient for the conventional current operators$ J(x) = $ $ \bar{q}(x)\Gamma q(x) $ , where the$ \Gamma $ stand for some Dirac$ \gamma $ -matrixes. On the other hand, we usually neglect the radiative corrections due to cumbersome calculations and factorize the higher dimensional vacuum condensates to the lower dimension vacuum condensates in performing the operator product expansion, the energy scale dependence of the QCD sum rules is modified. Furthermore, we introduce the continuum threshold parameters$ s_0 $ to exclude the contaminations of the higher resonances and continuum states, the correlation between the thresholds and continuum thresholds is not clear.The energy scale dependence cannot be absorbed into the pole residues alone, and we cannot obtain energy scale independent QCD sum rules for the masses, selections of the energy scales of the QCD spectral densities influence the masses extracted from the QCD sum rules. We can rewrite the energy scale formula in another form,
$ \begin{array}{l} M^2_{X/Y/Z} = \mu^2+C\, , \end{array} $

(12) where the constants
$ C = 4{\mathbb{M}}_c^2 $ , and then explain the energy scale formula in another way. We conjecture that the predicted tetraquark masses and pertinent energy scales of the QCD spectral densities have a Regge-trajectory-like relation, as in Eq. (12), where C is a free parameter and fitted by the QCD sum rules. Direct calculations have shown that C has universal values and works well for all the tetraquark (molecular) states.The standard values of the quark and mixed condensates determined in the original works still survive [22, 23, 33-35], while the value of the gluon condensate was occassionally updated in literature; however, the standard value determined in the original studies [22, 23] is still feasible [35]. The gluon condensate is the vacuum expectation value of the gluon operator of the order
$ \mathcal{O}(\alpha_s^1) $ , and plays a minor important role in the present work, the standard and updated values do not make a significant difference. The most important parameter is the c-quark mass$ m_c(m_c) $ . In 2006, R. D. Matheus et al. investigated$ X(3872) $ as the diquark-antidiquark type tetraquark state with QCD sum rules by carrying out the operator product expansion up to the vacuum condensates of dimension 8 [42]. Thereafter, the QCD sum rules became a powerful theoretical approach in studying the exotic X, Y, and Z states. In Ref. [42], the$ \overline{MS} $ mass$ m_c(m_c) = 1.23 \pm 0.05 \; \rm {GeV} $ was chosen, and thereafter, the value was adopted without or with slightly modified uncertainty [43]. Only in the recent years, new values$ m_c(m_c) = 1266 \pm 6\;\rm{MeV} $ [44] and$ 1.275\pm0.025\;\rm{GeV} $ [9] and$ 1.275^{+0.025}_{-0.035}\;\rm{GeV} $ [16] were chosen. The values of the$ \overline{MS} $ mass of the c-quark listed in The Review of Particle Physics in 2012, 2014, 2016, 2018, and 2020 were$ 1.275\pm $ $ 0.025 $ ,$ 1.275\!\!\pm\!\! 0.025$ ,$ 1.27\!\! \pm\!\! 0.03 $ ,$ 1.275^{+0.025}_{-0.035} $ , and$ 1.27 \pm 0.02 $ GeV, respectively. We fitted the constants C with the value$ 1.275\pm0.025\;\rm{GeV} $ from The Review of Particle Physics (2012) [26, 27], and adopted the value ever since.The energy gaps between ground states (or 1S) and first radial excited states (or 2S) of the hidden-charm tetraquark states without strangeness or with hidden-strangeness are approximately
$ 0.6\;\rm{GeV} $ [21, 29, 45-49]. We tentatively adopt the continuum threshold parameters as$ \sqrt{s_0} = M_{Z}+0.55\pm $ $ 0.10\;\rm{GeV} = 4.55\pm10\;\rm{GeV} $ , and vary the Borel parameters$ T^2 $ to satisfy the two requirements that the pole contributions dominate the QCD sum rules at the hadron side and the operator product expansions converge rather quickly at the QCD side via trial and error. In doing so, we must bear in mind that if our numerical results do no support identifying$ Z_{cs}(3985) $ as the axialvector tetraquark state, we must refit the best continuum threshold parameters and best energy scales of the spectral densities at the quark level to obtain the real ground state tetraquark masses.Finally, we acquire the Borel windows (or working Borel parameters) and pole contributions in the two QCD sum rules for the currents
$ J_\mu^N(x) $ and$ J^P_\mu(x) $ , and show them plainly in Table 1. The contributions of the lowest pole terms are about 42-62%, while the central values exceed 50%, such that we can say confidently that the contributions of the pole terms dominate the QCD sum rules at the hadron side, and one of the fundamental criteria is satisfied well. In Fig. 1, we plot the absolute values of the contributions of the vacuum condensates with the centroids of the values of all input parameters under the condition that the total contributions are normalized to be one. From the figure, we clearly see that the largest contributions come from quark condensates$ \langle\bar{q}q\rangle $ and$ \langle\bar{s}s\rangle $ , the vacuum condensates of the dimensions$ 7 $ ,$ 8 $ , and$ 10 $ play a small role, the operator product expansion converges efficiently. Now, we can confidently acquire the conclusion that it is reliable and reasonable to extract the tetraquark masses in Borel windows.$ J^{PC} $ 

$T^2/\rm{GeV}^2$ 

$\sqrt{s_0}/\rm{GeV}$ 

$\mu/\rm{GeV}$ 

pole $M/\rm{GeV}$ 

$\lambda/\rm{GeV}^5$ 

$ 1^{+-} $ 

$ 3.0-3.4 $ 

$ 4.55\pm0.10 $ 

1.6 (42-63)% $ 3.99\pm0.09 $ 

$ (2.85\pm0.45)\times10^{-2} $ 

$ 1^{++} $ 

$ 3.0-3.4 $ 

$ 4.55\pm0.10 $ 

1.6 (41-62)% $ 3.99\pm0.09 $ 

$ (2.85\pm0.45)\times10^{-2} $ 

Table 1. Borel windows, continuum threshold parameters, ideal energy scales, pole contributions, masses and pole residues for the axialvector tetraquark states with strangeness.
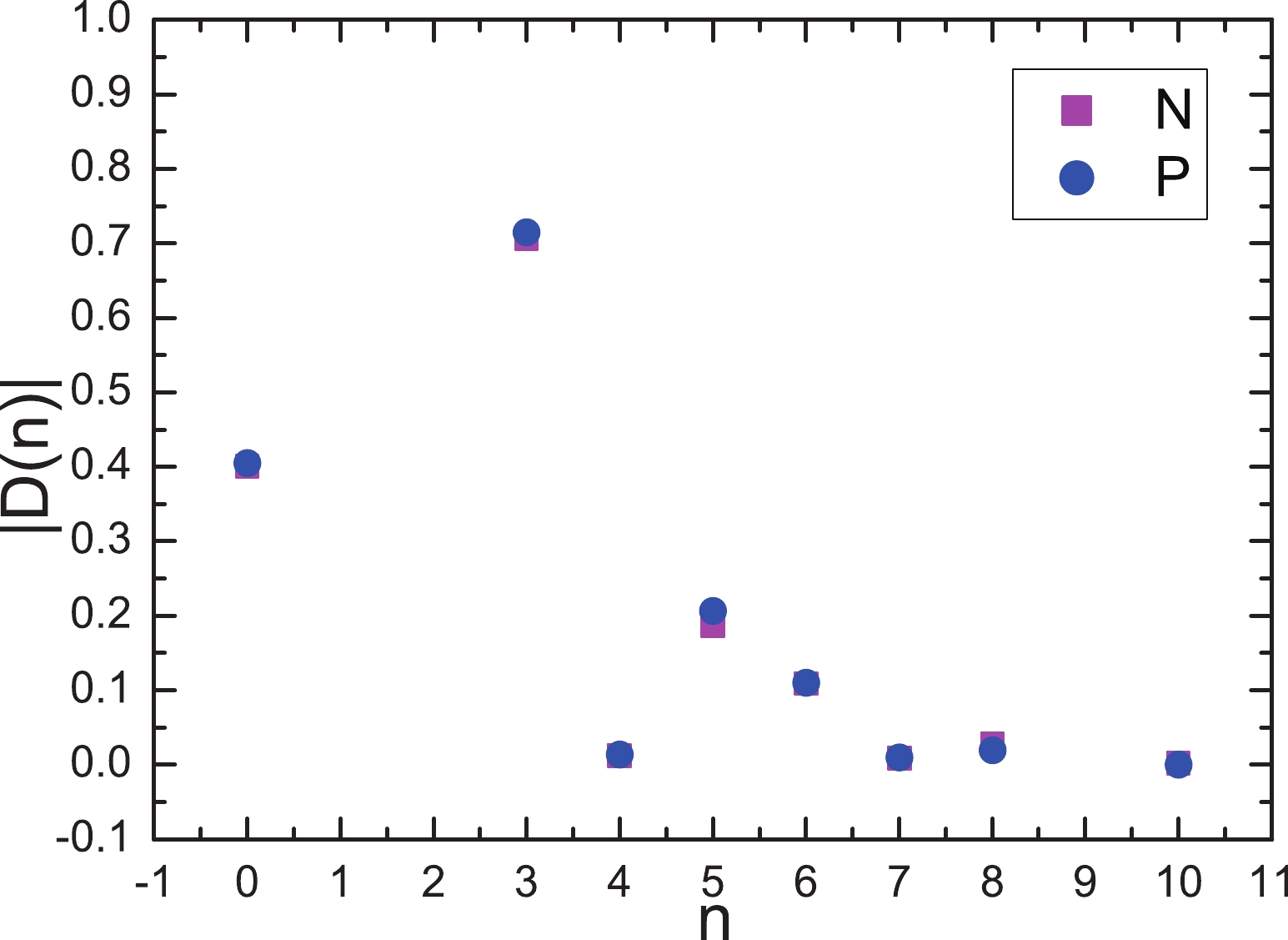
Figure 1. (color online) Absolute values of contributions of vacuum condensates in condition of central values of input parameters, where the N and P stand for the negative and positive charge conjugation, respectively.
We take into account all uncertainties of the input parameters to accomplish the error analysis, and acquire the values of the masses and pole residues of the axialvector tetraquark states with hidden-charm and with the strangeness
$ S = 1 $ , which are presented explicitly in Table 1 and Fig. 2. From Table 1, we see clearly that the energy scale$ \mu = 1.6\;\rm{GeV} $ is consistent with the mass$ 3.99\;\rm{GeV} $ inferred from the energy scale formula$ \mu = \sqrt{M_{Z}-(2{\mathbb{M}}_c)^2} $ or the relation between the tetraquark masses and the energy scales of the QCD spectral densities$ M_Z^2 = \mu^2+4\mathbb{M}_c^2 $ . In Fig. 2, we plot the predicted tetraquark masses with respect to variations of the Borel parameters at significantly larger regions than the Borel windows; furthermore, we show the experimental value of the mass of the$ Z_{cs}(3985) $ from the BESIII collaboration for the sake of comparison [1]. From the figure, we see clearly that very flat platforms appear in the Borel windows. In the Borel windows, the mass of the$ Z_{cs}(3985) $ overlaps with the central values of the masses of the tetraquark states with strangeness and sharing the quantum numbers$ J^{PC} = 1^{+\pm} $ . From Table 1, we see plainly that the axialvector tetraquark states with the negative and positive charge conjugation have degenerated masses. In fact, the central values of the masses of the axialvector tetraquark states with the negative and positive charge conjugation are$ 3.98669 $ GeV and$ 3.99303 $ GeV, respectively, and the axialvector tetraquark states with$ J^{PC} = 1^{++} $ have slightly larger masses than the corresponding states with$ J^{PC} = 1^{+-} $ [21]. In all the calculations, including the present work, we observe that if we choose the same values of the input parameters, such as the quark masses, vacuum condensates, continuum threshold parameters, and Borel parameters, the predicted masses of the$ J^{PC} = 1^{++} $ tetraquark states are slightly larger than that of the$ J^{PC} = 1^{+-} $ tetraquark states. However, we must bear in mind that the miniscule mass difference cannot be quantified considering the uncertainties of the QCD sum rules.
Figure 2. (color online) Masses of axialvector tetraquark states with variations of Borel parameter
$ T^2 $ , where N and P stand for the negative and positive charge conjugation, respectively. Regions between the two vertical lines are the Borel windows, the Expt stands for the experimental value of the mass of$ Z_{cs}(3985). $ In Fig. 3, we plot the predicted masses of the
$ J^{PC} = $ $ 1^{+-} $ and$ 1^{++} $ tetraquark states with variations of the energy scales of the QCD spectral densities in the condition of central values of the input parameters. The predicted masses decrease monotonously with the increase of the energy scales. If we set$ {\mathbb{M}}_c = 1.82\;\rm{GeV} $ [21, 26-31], we can obtain the dash-dotted line$ M_{Z} \!=\! \sqrt{\mu^2+4\times(1.82\;\rm{GeV})^2} $ , which intersects with the lines of the masses of the$ J^{PC} = 1^{+-} $ and$ 1^{++} $ tetraquark states at the energy scales about$ \mu = 1.6\;\rm{GeV} $ . In this manner, we choose the energy scales of the QCD spectral densities in a consistent manner. As a byproduct, we can see clearly, if we choose the same input parameters, the predicted masses of the$ J^{PC} = 1^{++} $ tetraquark states are slightly larger than that of the$ J^{PC} = 1^{+-} $ tetraquark states.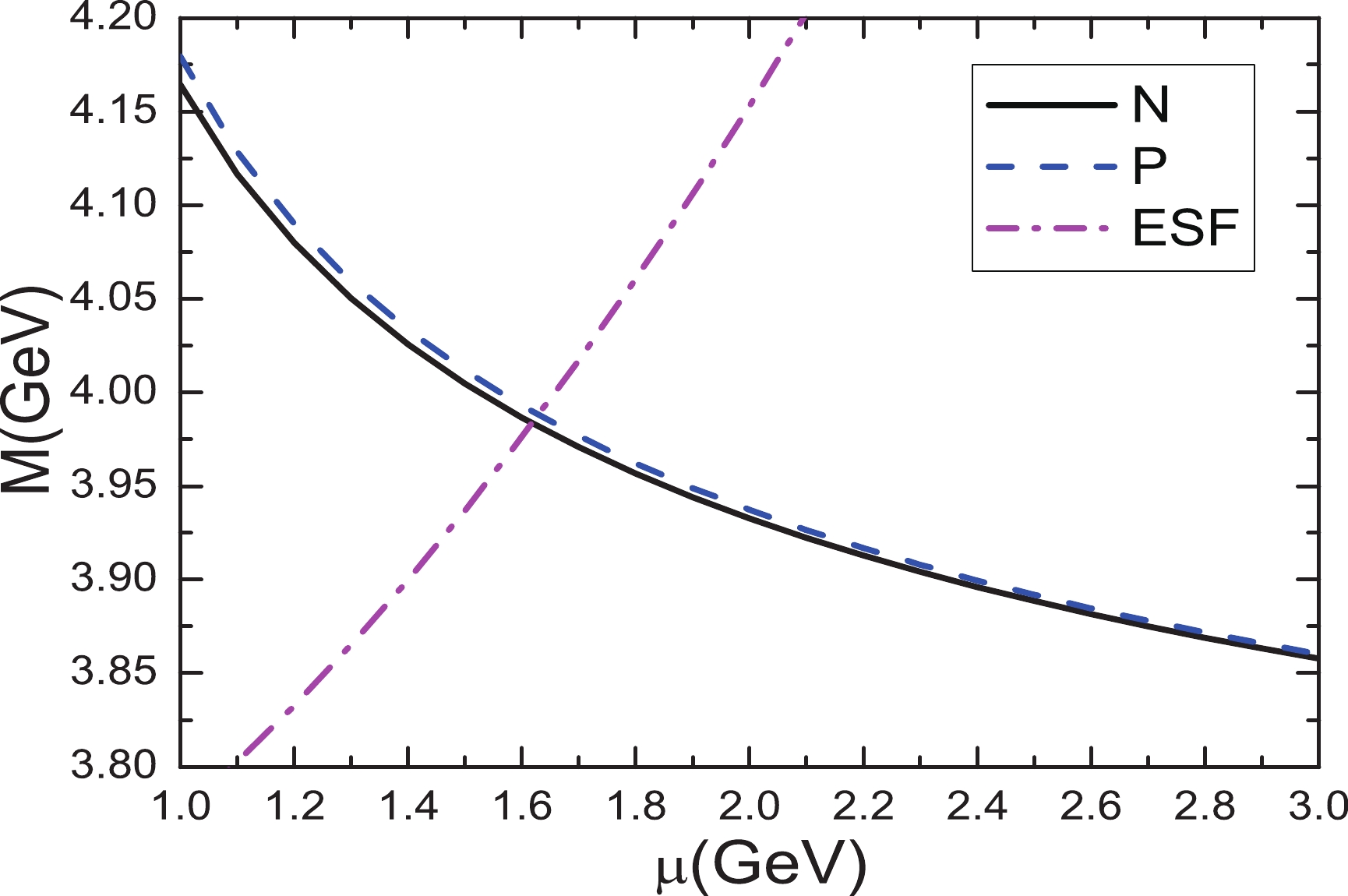
Figure 3. (color online) Masses of axialvector tetraquark states with variations of energy scales
$ \mu $ in condition of central values of input parameters, where N and P stand for the negative and positive charge conjugation, respectively, and ESF denotes the formula$ M = $ $ \sqrt{\mu^2+4\times (1.82\;\rm{GeV})^2}. $ When we contract the quark fields in the correlation functions
$ \Pi_{\mu\nu}(p) $ with the Wick theorem, we obtain the formula,$ \begin{aligned}[b] \Pi_{\mu\nu}(p) =& -\dfrac{{\rm i}\varepsilon^{ijk}\varepsilon^{imn}\varepsilon^{i^{\prime}j^{\prime}k^{\prime}}\varepsilon^{i^{\prime}m^{\prime}n^{\prime}}}{2}\int {\rm d}^4x {\rm e}^{{\rm i}p \cdot x} \\ &\times \Bigr\{{\rm Tr}\left[ \gamma_5C^{kk^{\prime}}(x)\gamma_5 CU^{jj^{\prime}T}(x)C\right] \\ &\times {\rm Tr}\left[ \gamma_\nu C^{n^{\prime}n}(-x)\gamma_\mu C S^{m^{\prime}mT}(-x)C\right] \\ &+{\rm Tr}\left[ \gamma_\mu C^{kk^{\prime}}(x)\gamma_\nu CU^{jj^{\prime}T}(x)C\right] \\ &\times{\rm Tr}\left[ \gamma_5 C^{n^{\prime}n}(-x)\gamma_5 C S^{m^{\prime}mT}(-x)C\right] \\ &\mp{\rm Tr}\left[ \gamma_\mu C^{kk^{\prime}}(x)\gamma_5 CU^{jj^{\prime}T}(x)C\right] \\ &\times {\rm Tr}\left[ \gamma_\nu C^{n^{\prime}n}(-x)\gamma_5 C S^{m^{\prime}mT}(-x)C\right] \\ &\mp{\rm Tr}\left[ \gamma_5 C^{kk^{\prime}}(x)\gamma_\nu CU^{jj^{\prime}T}(x)C\right] \\ &\times {\rm Tr}\left[ \gamma_5 C^{n^{\prime}n}(-x)\gamma_\mu C S^{m^{\prime}mT}(-x)C\right] \Bigr\} \, , \end{aligned} $

(13) where
$ \mp $ corresponds to the positive and negative charge conjugations of the currents, respectively, the$ U_{ij}(x) $ ,$ S_{ij}(x) $ , and$ C_{ij}(x) $ are the full u, s, and c quark propagators, respectively. By carrying out the operator product expansion, we observe that the dominant contributions come from the first two terms in the bracket, and the contributions come from the last two terms in the bracket play a miniscule role. Hence, we obtain the almost degenerated tetraquark masses.From Table 1, we see clearly that the predicted tetraquark masses
$ M_Z = 3.99\pm0.09\;\rm{GeV} $ are in excellent agreement with the experimental value$ 3985.2^{+2.1}_{-2.0}\pm1.7\;\rm{MeV} $ from the BESIII collaboration [1], and support identifying$ Z_{cs}(3985) $ to be the tetraquark state with hidden-charm, with strangeness and with$ J^{PC} = 1^{+-} $ . We prefer the quantum numbers$ J^{PC} = 1^{+-} $ to the quantum numbers$ J^{PC} = 1^{++} $ , as$ Z_{cs}(3985) $ was observed in the$ D_s^- D^{*0} $ and$ D^{*-}_s D^0 $ mass spectrum [1], just like the$ Z_c(3900) $ , which was observed in the$ D\bar{D}^{*} $ mass spectrum [2]. However, the assignment$ J^{PC} = 1^{++} $ cannot be excluded, as the charge conjugation is not a good quantum number.In Ref. [21], we introduce the four-vector
$ t^\mu = (1,\vec{0}) $ to project the axialvector and vector components of the tensor diquark operators, and take the color-antitriplet diquark operators$ \varepsilon^{ijk}q^{T}_j C\gamma_5 q^{\prime}_k $ (S),$ \varepsilon^{ijk}q^{T}_j C q^{\prime}_k $ (P),$ \varepsilon^{ijk}q^{T}_j C\gamma_\mu q^{\prime}_k $ (A),$ \varepsilon^{ijk}q^{T}_j C\sigma^v_{\mu\nu} q^{\prime}_k $ ($ \widetilde{A} $ ),$ \varepsilon^{ijk}q^{T}_j C\gamma_\mu\gamma_5 q^{\prime}_k $ (V), and$ \varepsilon^{ijk}q^{T}_j C\sigma^t_{\mu\nu} q^{\prime}_k $ ($ \widetilde{V} $ ) as the fundamental building blocks to construct the four-quark currents to investigate the mass-spectrum of the tetraquark states with hidden-charm but without strangeness in a comprehensive way, where the S, P,$ A/\widetilde{A} $ and$ V/\widetilde{V} $ stand for the scalar, pseudoscalar, axialvector, and vector diquark operators, respectively,$ \sigma^t_{\mu\nu} = \dfrac{i}{2}\Big[\gamma^t_\mu, \gamma^t_\nu \Big] $ ,$ \sigma^v_{\mu\nu} = \dfrac{i}{2}\Big[\gamma^v_\mu, \gamma^t_\nu \Big] $ ,$ \gamma^v_\mu = \gamma \cdot t t_\mu $ ,$ \gamma^t_\mu = \gamma_\mu-\gamma \cdot t t_\mu $ . In Table 2, we plainly show the mass-spectrum of the hid den-charm tetraquark states$ c\bar{c}u\bar{d} $ obtained via the QCD sum rules in Ref. [21] with possible assignments.$ Z_c $ (

$ X_c $ )

$ J^{PC} $ 

$M_Z /\rm{GeV}$ 

Assignments $ Z_c^\prime $ (

$ X_c^\prime $ )

$ [uc]_{S}[\overline{dc}]_{S} $ 

$ 0^{++} $ 

$ 3.88\pm0.09 $ 

? $ X(3860) $ 

$ [uc]_{A}[\overline{dc}]_{A} $ 

$ 0^{++} $ 

$ 3.95\pm0.09 $ 

? $ X(3915) $ 

$ [uc]_{\tilde{A}}[\overline{dc}]_{\tilde{A}} $ 

$ 0^{++} $ 

$ 3.98\pm0.08 $ 

$ [uc]_{V}[\overline{dc}]_{V} $ 

$ 0^{++} $ 

$ 4.65\pm0.09 $ 

$ [uc]_{\tilde{V}}[\overline{dc}]_{\tilde{V}} $ 

$ 0^{++} $ 

$ 5.35\pm0.09 $ 

$ [uc]_{P}[\overline{dc}]_{P} $ 

$ 0^{++} $ 

$ 5.49\pm0.09 $ 

$ [uc]_S[\overline{dc}]_{A}-[uc]_{A}[\overline{dc}]_S $ 

$ 1^{+-} $ 

$ 3.90\pm0.08 $ 

? $ Z_c(3900) $ 

? $ Z_c(4430) $ 

$ [uc]_{A}[\overline{dc}]_{A} $ 

$ 1^{+-} $ 

$ 4.02\pm0.09 $ 

? $ Z_c(4020/4055) $ 

? $ Z_c(4600) $ 

$ [uc]_S[\overline{dc}]_{\widetilde{A}}-[uc]_{\widetilde{A}}[\overline{dc}]_S $ 

$ 1^{+-} $ 

$ 4.01\pm0.09 $ 

? $ Z_c(4020/4055) $ 

? $ Z_c(4600) $ 

$ [uc]_{\widetilde{A}}[\overline{dc}]_{A}-[uc]_{A}[\overline{dc}]_{\widetilde{A}} $ 

$ 1^{+-} $ 

$ 4.02\pm0.09 $ 

? $ Z_c(4020/4055) $ 

? $ Z_c(4600) $ 

$ [uc]_{\widetilde{V}}[\overline{dc}]_{V}+[uc]_{V}[\overline{dc}]_{\widetilde{V}} $ 

$ 1^{+-} $ 

$ 4.66\pm0.10 $ 

? $ Z_c(4600) $ 

$ [uc]_{V}[\overline{dc}]_{V} $ 

$ 1^{+-} $ 

$ 5.46\pm0.09 $ 

$ [uc]_P[\overline{dc}]_{V}+[uc]_{V}[\overline{dc}]_P $ 

$ 1^{+-} $ 

$ 5.45\pm0.09 $ 

$ [uc]_S[\overline{dc}]_{A}+[uc]_{A}[\overline{dc}]_S $ 

$ 1^{++} $ 

$ 3.91\pm0.08 $ 

? $ X(3872) $ 

$ [uc]_S[\overline{dc}]_{\widetilde{A}}+[uc]_{\widetilde{A}}[\overline{dc}]_S $ 

$ 1^{++} $ 

$ 4.02\pm0.09 $ 

? $ Z_c(4050) $ 

$ [uc]_{\widetilde{V}}[\overline{dc}]_{V}-[uc]_{V}[\overline{dc}]_{\widetilde{V}} $ 

$ 1^{++} $ 

$ 4.08\pm0.09 $ 

? $ Z_c(4050) $ 

$ [uc]_{\widetilde{A}}[\overline{dc}]_{A}+[uc]_{A}[\overline{dc}]_{\widetilde{A}} $ 

$ 1^{++} $ 

$ 5.19\pm0.09 $ 

$ [uc]_P[\overline{dc}]_{V}-[uc]_{V}[\overline{dc}]_P $ 

$ 1^{++} $ 

$ 5.46\pm0.09 $ 

$ [uc]_{A}[\overline{dc}]_{A} $ 

$ 2^{++} $ 

$ 4.08\pm0.09 $ 

? $ Z_c(4050) $ 

$ [uc]_{V}[\overline{dc}]_{V} $ 

$ 2^{++} $ 

$ 5.40\pm0.09 $ 

Table 2. Possible assignments of ground state hidden-charm tetraquark states, where the isospin limit is implied [21].
If we assign
$ Z_{cs}(3985) $ to be the cousin of$ Z_c(3900) $ with strangeness, the mass gap or the light flavor$ SU(3) $ mass-breaking effect$ M_{Z_{cs}(3985)}-M_{Z_c(3900)} = $ $ 94\;\rm{MeV} $ , then we take the light flavor$ SU(3) $ mass-breaking effect$ m_s = 0.09\;\rm{GeV} $ , and estimate the mass spectrum of the tetraquark states with hidden-charm and with strangeness based on our previous work [21], which are shown explicitly in Table 3. We should bear in mind that the charge conjugation is not a very good quantum number in the present case. We cannot exclude that the$ Z_{cs}(3985) $ can be identified as the axialvector hidden-charm tetraquark state with the quantum numbers$ J^{PC} = 1^{++} $ .$ Z_c $ (

$ X_c $ )

$ J^{PC} $ 

$M_Z /\rm{GeV}$ 

Assignments $ [uc]_{S}[\overline{sc}]_{S} $ 

$ 0^{++} $ 

$ 3.97\pm0.09 $ 

$ [uc]_{A}[\overline{sc}]_{A} $ 

$ 0^{++} $ 

$ 4.04\pm0.09 $ 

$ [uc]_{\tilde{A}}[\overline{sc}]_{\tilde{A}} $ 

$ 0^{++} $ 

$ 4.07\pm0.08 $ 

$ [uc]_{V}[\overline{sc}]_{V} $ 

$ 0^{++} $ 

$ 4.74\pm0.09 $ 

$ [uc]_{\tilde{V}}[\overline{sc}]_{\tilde{V}} $ 

$ 0^{++} $ 

$ 5.44\pm0.09 $ 

$ [uc]_{P}[\overline{sc}]_{P} $ 

$ 0^{++} $ 

$ 5.58\pm0.09 $ 

$ [uc]_S[\overline{sc}]_{A}-[uc]_{A}[\overline{sc}]_S $ 

$ 1^{+-} $ 

$ 3.99\pm0.09 $ 

? $ Z_{cs}(3985) $ 

$ [uc]_{A}[\overline{sc}]_{A} $ 

$ 1^{+-} $ 

$ 4.11\pm0.09 $ 

$ [uc]_S[\overline{sc}]_{\widetilde{A}}-[uc]_{\widetilde{A}}[\overline{sc}]_S $ 

$ 1^{+-} $ 

$ 4.10\pm0.09 $ 

$ [uc]_{\widetilde{A}}[\overline{sc}]_{A}-[uc]_{A}[\overline{sc}]_{\widetilde{A}} $ 

$ 1^{+-} $ 

$ 4.11\pm0.09 $ 

$ [uc]_{\widetilde{V}}[\overline{sc}]_{V}+[uc]_{V}[\overline{sc}]_{\widetilde{V}} $ 

$ 1^{+-} $ 

$ 4.75\pm0.10 $ 

$ [uc]_{V}[\overline{sc}]_{V} $ 

$ 1^{+-} $ 

$ 5.55\pm0.09 $ 

$ [uc]_P[\overline{sc}]_{V}+[uc]_{V}[\overline{sc}]_P $ 

$ 1^{+-} $ 

$ 5.54\pm0.09 $ 

$ [uc]_S[\overline{sc}]_{A}+[uc]_{A}[\overline{sc}]_S $ 

$ 1^{++} $ 

$ 3.99\pm0.09 $ 

? $ Z_{cs}(3985) $ 

$ [uc]_S[\overline{sc}]_{\widetilde{A}}+[uc]_{\widetilde{A}}[\overline{sc}]_S $ 

$ 1^{++} $ 

$ 4.11\pm0.09 $ 

$ [uc]_{\widetilde{V}}[\overline{sc}]_{V}-[uc]_{V}[\overline{sc}]_{\widetilde{V}} $ 

$ 1^{++} $ 

$ 4.17\pm0.09 $ 

$ [uc]_{\widetilde{A}}[\overline{sc}]_{A}+[uc]_{A}[\overline{sc}]_{\widetilde{A}} $ 

$ 1^{++} $ 

$ 5.28\pm0.09 $ 

$ [uc]_P[\overline{sc}]_{V}-[uc]_{V}[\overline{sc}]_P $ 

$ 1^{++} $ 

$ 5.55\pm0.09 $ 

$ [uc]_{A}[\overline{dc}]_{A} $ 

$ 2^{++} $ 

$ 4.17\pm0.09 $ 

$ [uc]_{V}[\overline{dc}]_{V} $ 

$ 2^{++} $ 

$ 5.49\pm0.09 $ 

Table 3. Possible assignments of ground state hidden-charm tetraquark states with strangeness.
-
In present study, we choose the scalar and axialvector diquark operators (in color antitriplet) and antidiquark (in color triplet) operators as the fundamental building blocks to construct the four-quark currents and investigate the diquark-antidiquark type axialvector tetraquark states
$ c\bar{c}u\bar{s} $ with the QCD sum rules in the condition that we accomplish the operator product expansion up to the vacuum condensates of dimension$ 10 $ , consistently based on our reasonable analysis and successful experience; then, we apply the energy scale formula$ \mu = \sqrt{M_{Z}-(2{\mathbb{M}}_c)^2} $ using the effective charmed quark mass$ {\mathbb{M}}_c = 1.82\;\rm{GeV} $ to fix the best energy scales of the spectral densities at the quark level. The predicted tetraquark mass$ M_Z = 3.99\pm0.09\;\rm{GeV} $ is in excellent agreement with the experimental value$ 3985.2^{+2.1}_{-2.0}\pm1.7\;\rm{MeV} $ from the BESIII collaboration and supports identifying$ Z_{cs}(3985) $ as the cousin of$ Z_c(3900) $ with the quantum numbers$ J^{PC} = 1^{+-} $ . Furthermore, we obtain the mass of the corresponding tetraquark state$ c\bar{c}u\bar{s} $ with quantum numbers$ J^{PC} = 1^{++} $ , which can be compared to the international high energy experimental data in the future. We take into account the light flavor$ SU(3) $ mass-breaking effect at approximately$ 90\;\rm{MeV} $ and make crude estimations of the mass spectrum of the diquark-antidiquark type tetraquark states with hidden-charm and strangeness.Note added:
After the manuscript was submitted to https://arxiv.org/, the LHCb collaboration reported two new exotic states with the valence quarks
$ c\bar{c}u\bar{s} $ in the$ J/\psi K^+ $ mass spectrum in the decays$ B^+ \to J/\psi \phi K^+ $ [50]. The most significant state,$ Z_{cs}(4000) $ , has a mass of$ 4003 \pm 6 {}^{+4}_{-14}\;\rm{MeV} $ , a width of$ 131 \pm 15 \pm 26\;\rm{MeV} $ , and spin-parity$ J^P = 1^+ $ , while the broader state,$ Z_{cs}(4220) $ , has a mass of$ 4216 \pm 24{}^{ +43}_{-30}\;\rm{MeV} $ , a width of$ 233 \pm 52 {}^{+97}_{-73}\;\rm{MeV} $ , and spin-parity$ J^P = 1^+ $ or$ 1^- $ , with a$ 2\sigma $ difference in favor of the first hypothesis [50]. As there exist two tetraquark nonets (see Eqs. (2)-(3)) and there may exist mixings between the two tetraquark nonets, there is sufficient room to accommodate$ Z_{cs}(3985) $ and$ Z_{cs}(4000) $ as the diquark-antidiquark type axialvector tetraquark states with strangeness.
Analysis of Zcs(3985) as the axialvector tetraquark state
- Received Date: 2021-02-19
- Available Online: 2021-07-15
Abstract: In this study, we choose the scalar and axialvector diquark operators in the color antitriplet as the fundamental building blocks to construct four-quark currents and investigate the diquark-antidiquark type axialvector tetraquark states






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: