-
The standard model (SM) of elementary particle physics has been proposed for more than fifty years [1-3], and it is verified as a very effective description of this field [4]. The electro-weak symmetry breaking (EWSB) [5-8] mechanism predicts the existence of a physical Higgs boson, which is observed at the Large Hadron Collider (LHC) in 2012 [9, 10]. Although the SM is significantly strong, there are still a few unelucidated problems in particle physics. The typical problems are Higgs mass naturalness, gauge coupling unification, fermion mass hierarchy, electro-weak vacuum stability, dark matter, matter anti-matter asymmetry, etc. Many new physics beyond the SM (BSM) are aimed at solving or partially solving these problems. In some of these BSM models, vector-like quarks (VLQs) [11, 12] are introduced to circumvent the quantum anomaly.
For the up-type VLQ, the T quark can interact with the SM particles via the
$ TbW,\;TtZ $ , and Tth interactions. Constraints on these couplings are crucial, because they can help us elucidate the nature of the EWSB. For the strong interaction mediated pair production of VLQs, we can solely constrain the partial decay branching ratios of the T quark. To bound these couplings, the single production of VLQ needs to be considered. Unfortunately, it is difficult to directly detect the flavor changing neutral (FCN) interactions$ TtZ,Tth $ , owing to the suppression of the single T production from the$ tZ,\;th $ fusion. Here, we will focus on the FCN Yukawa (FCNY) interaction Tth. After the Higgs boson detection, we can obtain more information on new physics from the Higgs precision measurements [13-16]. The FCNY interaction can emerge in loop induced processes, for example,$ h\rightarrow\gamma Z $ and$ gg\rightarrow hh $ . In our previous work [17], we demonstrated the possibility of constraining the FCNY coupling via the$ h\rightarrow\gamma Z $ decay mode indirectly. The double Higgs production is also an appealing channel for elucidating the FCNY interaction, which is free of electro-weak gauge interactions. The constraints from$ h\rightarrow\gamma Z $ and$ gg\rightarrow hh $ are independent of exotic decay modes and total width of the T quark.In this paper, we first discuss the framework of the developed FCN couplings in Sec. II. Sec. III is devoted to the theoretical and experimental constraints on the simplified model. In Sec. IV, we compute the new physics contributions to the parton level cross section of
$ gg\rightarrow hh $ . Then we perform the numerical constraints on the FCNY interactions in Sec. V. Finally, we provide the summary and conclusions in Sec. VI. -
The SM gauge group is
$ SU_{\rm C}(3)\otimes SU_{\rm L}(2)\otimes U_{\rm Y}(1) $ , under which the singlet up-type VLQs have the representation (3, 0, 2/3). Let us start with the minimal extension of SM by adding a pair of singlet$ T_{\rm L},T_{\rm R} $ [11, 12], which is named as the VLQT model. Note that the mass mixing term$ \bar{T}_{\rm L}t_{\rm R} $ can be discarded with field redefinition [18, 19]. Then, the Lagrangian can be written as [12]$ \begin{aligned}[b] {\cal{L}} =& {\cal{L}}_{\rm SM}+{\cal{L}}_T^{\rm Yukawa}+{\cal{L}}_T^{\rm gauge},\\ {\cal{L}}_T^{\rm Yukawa} =& -\Gamma_T^i\bar{Q}_{\rm L}^i\widetilde{\Phi}T_R-M_T\bar{T}_{\rm L}T_R+{\rm{h.c.}},\\{\cal{L}}_T^{\rm gauge} =& \bar{T}_{\rm L}{\rm i}{\not \!\!D}T_{\rm L}+\bar{T}_{\rm R}{\rm i}{\not\!\! D}T_{\rm R}, \end{aligned} $

(1) where
$ \widetilde{\Phi} = {\rm i}\sigma_2\Phi^{\ast} $ , and the covariant derivative is defined as$ D_{\mu} = \partial_{\mu}-{\rm i}g^{\prime}Y_TB_{\mu} $ .$ Y_T $ and$ Q_T $ are the$ U_{\rm Y}(1) $ and electric charge of the T quark, respectively. The Higgs doublet is parametrized as$\Phi^T = \left[\phi^+,\; \dfrac{v+h+{\rm i}\chi}{\sqrt{2}}\right]$ . It is reasonable to ignore the mixings between heavy particles and the first two generations because of mass hierarchy and the bounds from flavor physics [20-22]. Here, for simplicity, we only consider the mixings between the third generation and heavy quarks.To diagonalize the t and T quark mass terms, we can perform the transformations
$\begin{aligned}[b]& \left[ {\begin{array}{*{20}{c}} {{t_{\rm L}}}\\ {{T_{\rm L}}} \end{array}} \right] \to \left[ {\begin{array}{*{20}{c}} {\cos {\theta _{\rm L}}}&{\sin {\theta _{\rm L}}}\\ { - \sin {\theta _{\rm L}}}&{\cos {\theta _{\rm L}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{t_{\rm L}}}\\ {{T_{\rm L}}} \end{array}} \right],\\ & \left[ {\begin{array}{*{20}{c}} {{t_{\rm R}}}\\ {{T_{\rm R}}} \end{array}} \right] \to \left[ {\begin{array}{*{20}{c}} {\cos {\theta _{\rm R}}}&{\sin {\theta _{\rm R}}}\\ { - \sin {\theta _{\rm R}}}&{\cos {\theta _{\rm R}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{t_{\rm R}}}\\ {{T_{\rm R}}} \end{array}} \right].\end{aligned} $

(2) In fact, we obtain the relationship
$ m_T\tan\theta_{\rm R} = m_t\tan\theta_{\rm L} $ . Subsequently, we will consider$ s_{\rm L},\;c_{\rm L},\;s_{\rm R},\;c_{\rm R} $ as short forms for$ \sin\theta_{\rm L},\;\cos\theta_{\rm L},\;\sin\theta_{\rm R},\;\cos\theta_{\rm R} $ , respectively. Then, we can obtain the mass eigenstate Yukawa interactions:$\begin{aligned}[b] {\cal{L}}_{\rm Yukawa}\supset&-m_t\bar{t}t-m_T\bar{T}T-\frac{m_t}{v}c_{\rm L}^2h\bar{t}t-\frac{m_T}{v}s_{\rm L}^2h\bar{T}T\\&-\frac{m_T}{v}s_{\rm L}c_{\rm L}h(\bar{t}_{\rm L}T_{\rm R}+\bar{T}_{\rm R}t_{\rm L})-\frac{m_t}{v}s_{\rm L}c_{\rm L}h(\bar{T}_{\rm L}t_{\rm R}+\bar{t}_{\rm R}T_{\rm L}), \end{aligned}$

(3) and gauge interactions
$ \begin{aligned}[b] {\cal{L}}_{\rm gauge}\supset &\frac{g}{c_W}Z_{\mu}\left[\left(\frac{1}{2}c_{\rm L}^2-\frac{2}{3}s_W^2\right)\bar{t}_{\rm L}\gamma^{\mu}t_{\rm L}+\left(\frac{1}{2}s_{\rm L}^2-\frac{2}{3}s_W^2\right)\bar{T}_{\rm L}\gamma^{\mu}T_{\rm L}+\frac{1}{2}s_{\rm L}c_{\rm L}(\bar{t}_{\rm L}\gamma^{\mu}T_{\rm L}+\bar{T}_{\rm L}\gamma^{\mu}t_{\rm L})\right.\\& \left.-\frac{2}{3}s_W^2\bar{t}_{\rm R}\gamma^{\mu}t_{\rm R}-\frac{2}{3}s_W^2\bar{T}_{\rm R}\gamma^{\mu}T_{\rm R}\right]+\frac{gc_{\rm L}}{\sqrt{2}}(W_{\mu}^+\bar{t}_{\rm L}\gamma^{\mu}b_{\rm L}+W_{\mu}^-\bar{b}_{\rm L}\gamma^{\mu}t_{\rm L})+\frac{gs_{\rm L}}{\sqrt{2}}(W_{\mu}^+\bar{T}_{\rm L}\gamma^{\mu}b_{\rm L}+W_{\mu}^-\bar{b}_{\rm L}\gamma^{\mu}T_{\rm L}). \end{aligned} $ 
(4) Here, we have two independent extra parameters
$ m_T $ and$ \theta_{\rm L} $ . For more details, please refer to our previous work [17]. -
In addition to the singlet VLQs, the scalar sector can be enlarged in the non-minimally extended models. For example, we can also introduce a real gauge singlet scalar [23, 24], Higgs doublet [25], and even both the singlet-doublet scalars simultaneously [25, 26]. In these models, the T quark can possess other decay channels [27, 28]. Here, we will adopt a general framework [29]. Accordingly, the simplified related mass eigenstate interactions can be expressed as [17]
$ \begin{aligned}[b] {\cal{L}}\supset&-m_t\bar{t}t-m_T\bar{T}T-eA_{\mu}\sum_{f = t,T}Q_f\bar{f}\gamma^{\mu}f+eZ_{\mu}\Big[\bar{t}\gamma^{\mu}(g_{\rm L}^t\omega_-+g_{\rm R}^t\omega_+)t+\bar{T}\gamma^{\mu}(g_{\rm L}^T\omega_-+g_{\rm R}^T\omega_+)T\\& +\bar{t}\gamma^{\mu}(g_{\rm L}^{tT}\omega_-+g_{\rm R}^{tT}\omega_+)T+\bar{T}\gamma^{\mu}(g_{\rm L}^{tT}\omega_-+g_{\rm R}^{tT}\omega_+)t\Big]-\frac{m_t}{v}h\bar{t}(\kappa_t+{\rm i}\gamma^5\widetilde{\kappa}_t)t+h\bar{T}(y_T+{\rm i}\gamma^5\widetilde{y}_T)T\\& +h\bar{t}(y_{\rm L}^{tT}\omega_-+y_{\rm R}^{tT}\omega_+)T+h\bar{T}((y_{\rm L}^{tT})^{*}\omega_++(y_R^{tT})^{*}\omega_-)t+\frac{gc_{\rm L}}{\sqrt{2}}(W_{\mu}^+\bar{t}_{\rm L}\gamma^{\mu}b_{\rm L}+W_{\mu}^-\bar{b}_{\rm L}\gamma^{\mu}t_{\rm L})\\& +\frac{gs_{\rm L}}{\sqrt{2}}(W_{\mu}^+\bar{T}_{\rm L}\gamma^{\mu}b_{\rm L}+W_{\mu}^-\bar{b}_{\rm L}\gamma^{\mu}T_{\rm L})-\lambda_{hhh}h^3, \end{aligned} $ 
(5) where
$ \omega_{\pm} $ are the chirality projection operators$ (1\pm\gamma^5)/2 $ and the gauge couplings are presented as$ \begin{aligned}[b] g_{\rm L}^t =& \frac{1}{s_Wc_W}\left(\frac{1}{2}c_{\rm L}^2-\frac{2}{3}s_W^2\right),\;\;\; g_{\rm L}^T = \frac{1}{s_Wc_W}\left(\frac{1}{2}s_L^2-\frac{2}{3}s_W^2\right),\; \\g_{\rm L}^{tT} =& \frac{s_{\rm L}c_{\rm L}}{2s_Wc_W}, \; \; \; g_{\rm R}^t = -\frac{2s_W}{3c_W},\;\;\; g_{\rm R}^T = -\frac{2s_W}{3c_W},\;\;\; g_{\rm R}^{tT} = 0. \end{aligned} $

(6) The triple Higgs coupling
$ \lambda_{hhh} $ can deviate from the SM value$ \lambda_{hhh}^{\rm SM} = \dfrac{m_h^2}{2v} $ in many new physics models [30-39]. Here,$ m_T,\;\theta_ L,\;\kappa_t,\;\widetilde{\kappa}_t,\;y_T,\;\widetilde{y}_T $ are all real parameters, while$ y_{\rm L}^{tT},\;y_{\rm R}^{tT} $ can be complex. Henceforth, we will turn off the parameters$ \widetilde{\kappa}_t $ and$ \widetilde{y}_T $ for simplicity.Next, we will demonstrate how to constrain the FCNY couplings via the
$ gg\rightarrow hh $ channel. Although the FCNY couplings$ y_{\rm L,R}^{tT} $ are not free parameters in the above VLQT model, they can be free in more complex models. If we can extend the SM by the singlet$ T_{\rm L},\;T_{\rm R} $ and many new scalars, there can be enough degrees of freedom. Therefore, we can consider them as free parameters in realizing a general analysis. -
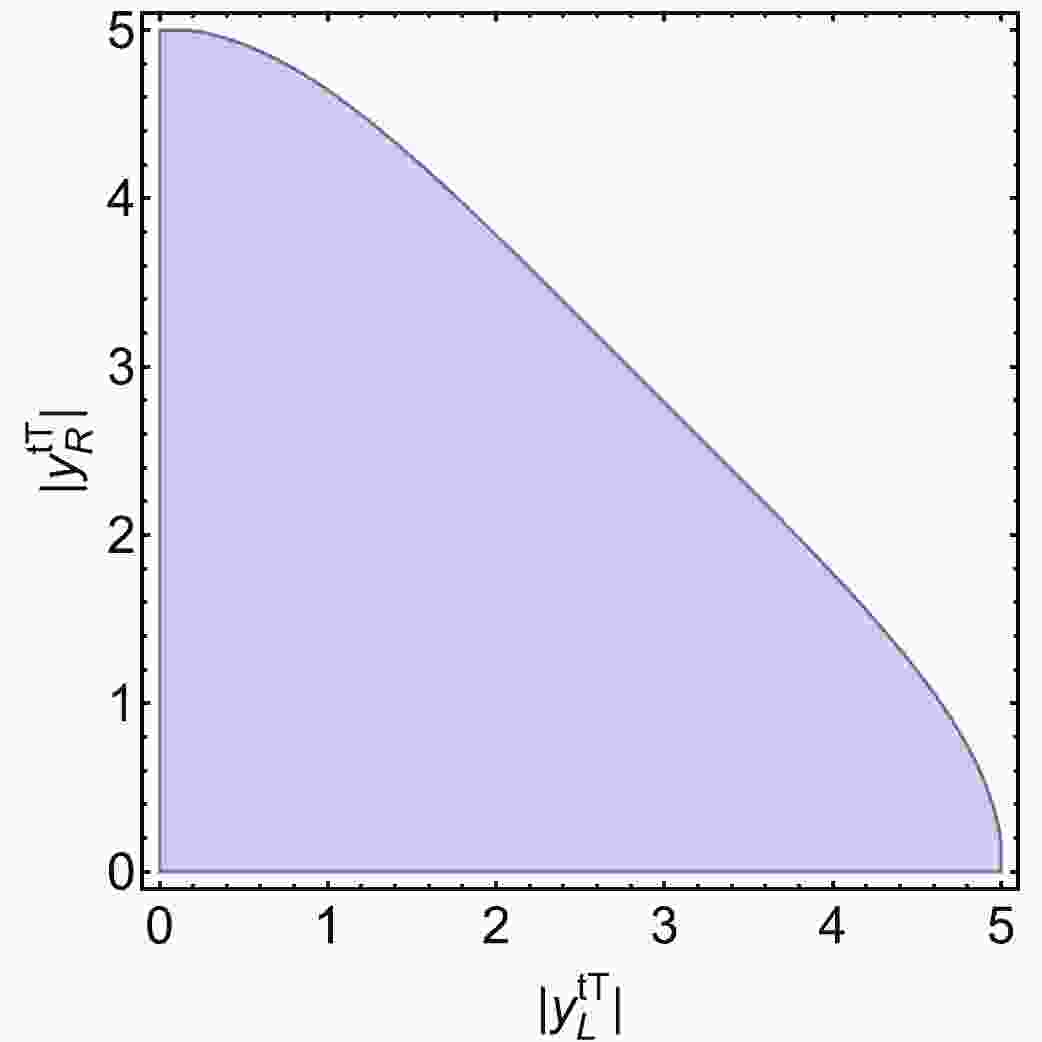
In this section, we will review the theoretical and experimental constraints on the simplified model. Specific details can be obtained from our previous study [17]. The S-wave unitarity will lead to the bound [17]
$ \sqrt{(|y_{\rm L}^{tT}|^2+|y_{\rm R}^{tT}|^2)^2+12|y_{\rm L}^{tT}|^2|y_{\rm R}^{tT}|^2}+|y_{\rm L}^{tT}|^2+|y_{\rm R}^{tT}|^2\leqslant 16\pi. $

(7) In Fig. 1, we present the unitarity allowed region in the plane of
$ |y_{\rm L}^{tT}|-|y_{\rm R}^{tT}| $ . Higgs signal strength and top quark physics provide relatively loose constraints. Direct search can bound the VLQ mass as light as 400 GeV without specific assumptions [28]. The strongest constraints on$ m_T $ and$ s_{\rm L} $ originate from the electro-weak precision measurements. Here, we consider the S and T parameters [22, 40-43]. In Fig. 2, we present the allowed parameter space regions from the global fits at$ 1\sigma $ and$ 2\sigma $ confidence levels (CLs). In this study, the input parameters are selected as$ m_Z = $ $ 91.1876\; {\rm{GeV}} $ ,$ m_W = 80.387\; {\rm{GeV}} $ ,$ m_h = 125.09\; {\rm{GeV}} $ ,$ m_t = 172.74\; {\rm{GeV}} $ ,$G_F =1.1664\times $ $ 10^{-5}\; {\rm{GeV}}^{-2}$ , and$c_W = $ $ m_W/m_Z$ [4].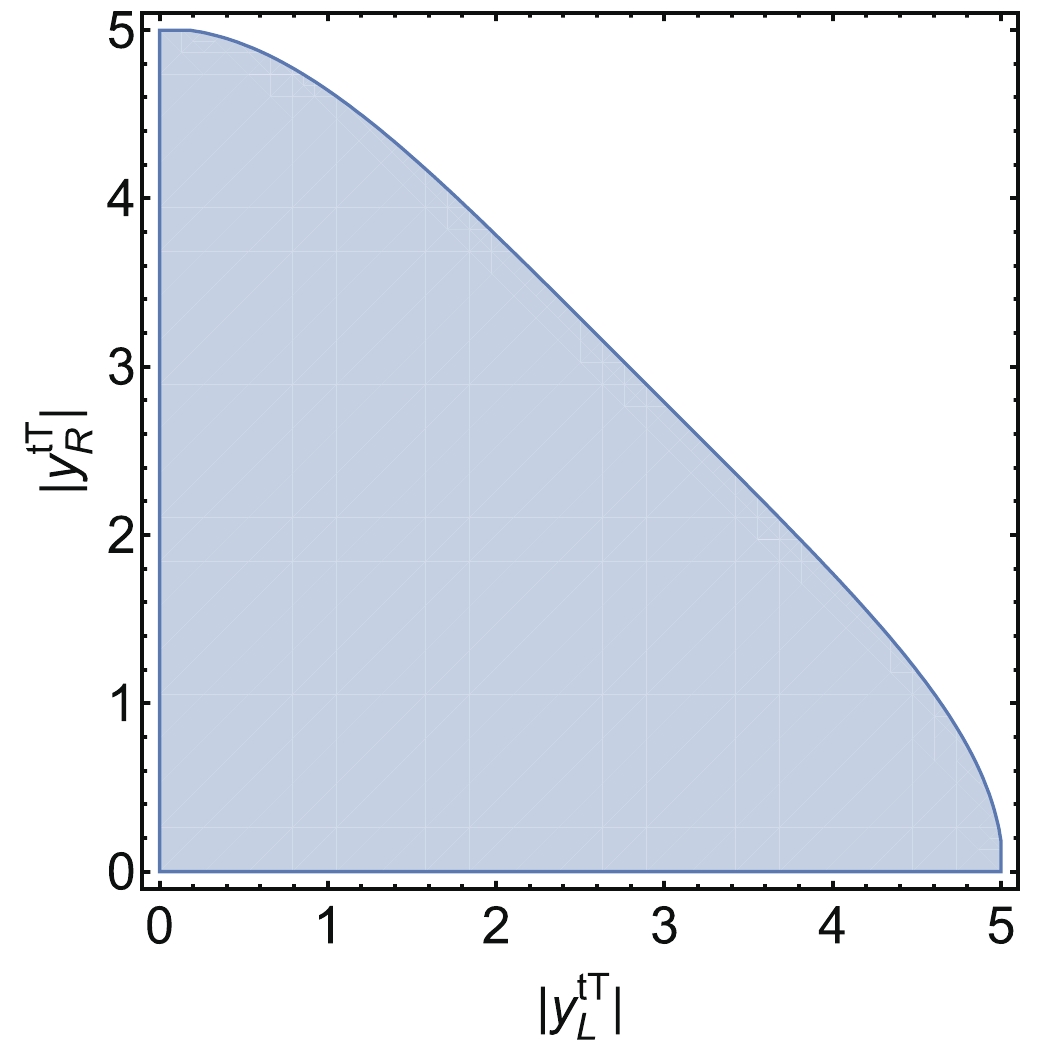
Figure 1. (color online) Parameter region allowed by the perturbative unitarity. Figure from Ref. [17].
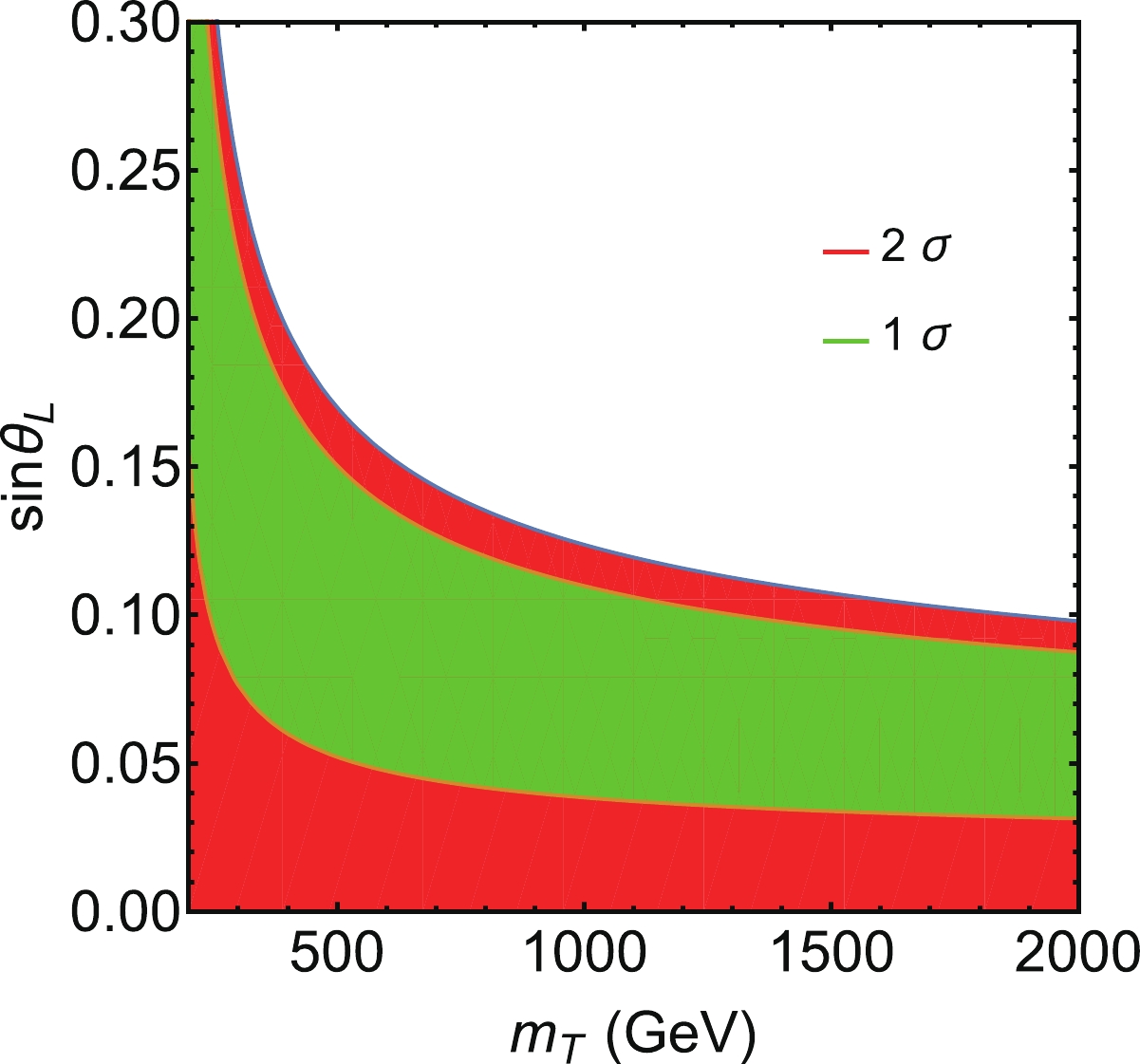
Figure 2. (color online) Constraints on
$m_T,\;s_{\rm L}$ from the S and T parameters. Here, the green and red colors depcit the allowed regions at$1\sigma$ and$2\sigma$ CLs, respectively. Figure from Ref. [17].Next, we consider the constraints from the top quark electric dipole moment (EDM). If CP violation exists in the FCNY interactions, it will contribute to the EDM type interaction
$ -\dfrac{\rm i}{2}d_t^{\rm EDM}\bar{t}\sigma^{\mu\nu}\gamma^5tF_{\mu\nu} $ . The$ d_t^{\rm EDM} $ is calculated as$ d_t^{\rm EDM} = \frac{eQ_Tm_T[y_{\rm R}^{tT}(y_{\rm L}^{tT})^*-y_{\rm L}^{tT}(y_{\rm R}^{tT})^*]}{16\pi^2{\rm i}}C_1, $

(8) with
$ C_1 $ defined as$\begin{aligned}[b] C_1 =& \frac{1}{4m_t^2}[B_0(m_t^2,m_T^2,m_h^2)-B_0(0,m_T^2,m_T^2)\\&+(m_T^2-m_t^2-m_h^2)C_0(m_t^2,0,m_t^2,m_h^2,m_T^2,m_T^2)].\end{aligned} $

As can be observed from the identity
$ [y_{\rm R}^{tT}(y_{\rm L}^{tT})^*- $ $ y_{\rm L}^{tT}(y_{\rm R}^{tT})^*] = $ $ 2{\rm i}({\rm{Re}}y_{\rm L}^{tT}{\rm{Im}}y_{\rm R}^{tT}-{\rm{Re}}y_{\rm R}^{tT}{\rm{Im}}y_{\rm L}^{tT}) $ ,$ d_t^{\rm EDM} $ will vanish if we turn off both the imaginary parts of$ y_{\rm L,R}^{tT} $ . The top quark EDM can be bounded as$ |d_t^{\rm EDM}|<5\times10^{-20}e\cdot $ cm at 90% CL [44-46] with the ACME results [47]. In fact, we can rescale the limit to be$ |d_t^{\rm EDM}|<6.3\times10^{-21}e\cdot $ cm or$ |m_td_t^{\rm EDM}/e|<5.5\times10^{-5} $ with the improved data [17, 48]. If we consider$ m_T = 400\; {\rm{GeV}} $ , the top EDM sets the upper limit of$|y_{\rm R}^{tT}(y_{\rm L}^{tT})^*-y_{\rm L}^{tT}(y_{\rm R}^{tT})^*|$ to be 0.12 at 90% CL. If we take$ m_T = 800\; {\rm{GeV}} $ , the corresponding upper limit of$ |y_{\rm R}^{tT}(y_{\rm L}^{tT})^*-y_{\rm L}^{tT}(y_{\rm R}^{tT})^*| $ is 0.24 at 90% CL. The looseness of the constraints increases with$ m_T $ . -
The double Higgs production is a trending topic in the field of Higgs physics. The di-Higgs production cross section has been calculated in SM for several years [49, 50]. The new physics effects have also garnered considerable attention in this community [51-55]. A few studies on di-Higgs production are based on the SM effective field theory (EFT) [56-61] and non-linearly realized EFT [62-65]. There are also several studies considered in specific models, such as the Higgs singlet model [66-68], two Higgs doublet model [69-72], VLQ models [73-75], composite Higgs models [76, 77], minimal supersymmetric standard model (MSSM) [78-80], next-to-MSSM [81, 82], and many other new physics models.
For VLQ models, there are additional fermion contributions: the pure new quark loops and loops with both SM and new quarks. In Figs. 3 and 4, we present the Feynman diagrams from the pure quark loops and mixed quark loops, respectively①. The latter will be induced by FCNY interactions. The FCNY contributions are less considered in most studies, as they are smaller than the same flavor terms. However, this channel can be sensitive to large FCNY couplings.
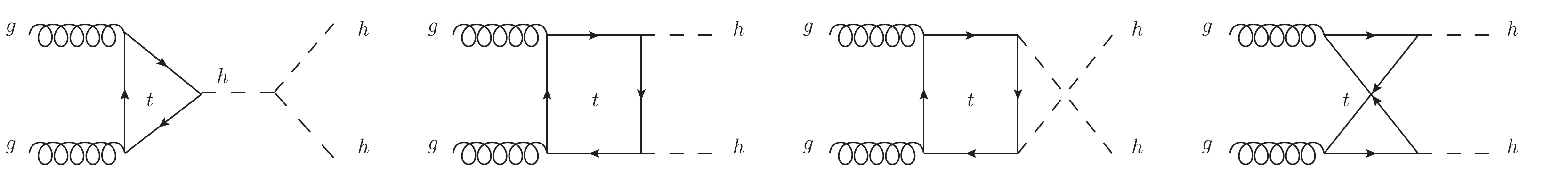
Figure 3. Typical Feynman diagrams contributing to the
$g(k_1,\mu)g(k_2,\nu)\rightarrow h(p_1)h(p_2)$ production with pure top (and T) quarks running in the loops, where the counter-clockwise diagrams should be included.
Figure 4. Typical Feynman diagrams contributing to the
$g(k_1,\mu)g(k_2,\nu)\rightarrow h(p_1)h(p_2)$ production with both top and T quarks running in the loops, where the counter-clockwise diagrams should be included.Starting from the Lagrangian in Eq. (5), the amplitude of
$ gg\rightarrow hh $ can be parametrized as$ {\rm i}{\cal{M}}(\hat{s}) = -{\rm i}\frac{g_s^2\hat{s}}{16\pi^2v^2}\epsilon_{\mu}^{a,r_1}(k_1)\epsilon_{\nu}^{a,r_2}(k_2)(A^{\mu\nu}f_A+B^{\mu\nu}f_B+C^{\mu\nu}f_C), $

(9) where a and
$ r_{1,2} $ represent the color and spin indices, respectively, and the tensor structures$ A^{\mu\nu},\; B^{\mu\nu},\; C^{\mu\nu} $ are given by$ \begin{aligned}[b] A^{\mu\nu}\equiv & g^{\mu\nu}-\frac{k_2^{\mu}k_1^{\nu}}{k_1\cdot k_2},\qquad\qquad C^{\mu\nu}\equiv \frac{k_{1\rho}k_{2\sigma}\epsilon^{\mu\nu\rho\sigma}}{k_1\cdot k_2},\\ B^{\mu\nu}\equiv& g^{\mu\nu}+\frac{m_h^2k_2^{\mu}k_1^{\nu}}{p_T^2(k_1\cdot k_2)}-\frac{2(k_1\cdot p_1)k_2^{\mu}p_1^{\nu}}{p_T^2(k_1\cdot k_2)}-\frac{2(k_2\cdot p_1)p_1^{\mu}k_1^{\nu}}{p_T^2(k_1\cdot k_2)}\\&+\frac{2p_1^{\mu}p_1^{\nu}}{p_T^2}\quad(p_T^2\equiv\frac{\hat{t}\hat{u}-m_h^4}{\hat{s}}). \end{aligned} $

(10) These structures possess the orthonormal relationships
$ A^{\mu\nu}A_{\mu\nu} = B^{\mu\nu}B_{\mu\nu} = $ $ C^{\mu\nu}C_{\mu\nu} = 2 $ and$ A^{\mu\nu}B_{\mu\nu} = A^{\mu\nu}C_{\mu\nu} = B^{\mu\nu}C_{\mu\nu} = 0 $ . The coefficients$ f_{A,B,C} $ receive contributions from the t and T quark loops and can be written as$ f_{A,B,C}\equiv f_{A,B,C}^t+ f_{A,B,C}^T+f_{A,B,C}^{tT} $ . Here$ f_{A,B,C}^{t(T)} $ represents the contributions from pure$ t(T) $ quark loops, while$ f_{A,B,C}^{tT} $ indicate the contributions from mixed t and T quark loops. When we set$ \kappa_t^2 = 1 $ and turn off the couplings$ y_{\rm L,R}^{tT} $ , they move straight to the SM result. After a few lengthy calculations, we can obtain their explicit expressions.The pure top quark contribution to
$ f_A $ is given by②$ f_A^t = \kappa_tf_A^{t,\triangle}+\kappa_t^2f_A^{t,\Box1} $ . Here,$ f_A^{t,\triangle} $ and$ f_A^{t,\Box1} $ are defined as$ \begin{aligned}[b] f_A^{t,\triangle} =& \frac{6m_h^2m_t^2}{\hat{s}(\hat{s}-m_h^2)}\Big[2+(4m_t^2-\hat{s})C_0^t(\hat{s})\Big],\\ f_A^{t,\Box1} =& \frac{2m_t^2}{\hat{s}}\Bigg\{4m_t^2C_0^t(\hat{s})+\frac{2(m_h^2-4m_t^2)}{\hat{s}}\Big[(\hat{t}-m_h^2)C_0^t(\hat{t})\\&+(\hat{u}-m_h^2)C_0^t(\hat{u})\Big] +m_t^2(8m_t^2-\hat{s}-2m_h^2)\\&\times\Big[D_0^t(\hat{t},\hat{s})+D_0^t(\hat{u},\hat{s})+D_0^t(\hat{t},\hat{u})\Big]\\&+2+\frac{\hat{t}\hat{u}-m_h^4}{\hat{s}}(4m_t^2-m_h^2)D_0^t(\hat{t},\hat{u})\Bigg\}. \end{aligned} $

(11) The pure T quark contribution to
$ f_A $ is given by$ f_A^T = \left(-\dfrac{vy_T}{m_T}\right)f_A^{T,\triangle}+\left(\dfrac{vy_T}{m_T}\right)^2f_A^{T,\Box1} $ . Here,$ f_A^{T,\triangle} $ and$ f_A^{T,\Box1} $ are defined as$ \begin{aligned}[b]f_A^{T,\triangle} =& \frac{6m_h^2m_T^2}{\hat{s}(\hat{s}-m_h^2)}\Big[2+(4m_T^2-\hat{s})C_0^T(\hat{s})\Big],\\ f_A^{T,\Box1} =& \frac{2m_T^2}{\hat{s}}\Bigg\{4m_T^2C_0^T(\hat{s})+\frac{2(m_h^2-4m_T^2)}{\hat{s}}\Big[(\hat{t}-m_h^2)C_0^T(\hat{t})\\&+(\hat{u}-m_h^2)C_0^T(\hat{u})\Big] +m_T^2(8m_T^2-\hat{s}-2m_h^2)\\&\times\Big[D_0^T(\hat{t},\hat{s})+D_0^T(\hat{u},\hat{s})+D_0^T(\hat{t},\hat{u})\Big]\\&+2+\frac{\hat{t}\hat{u}-m_h^4}{\hat{s}}(4m_T^2-m_h^2)D_0^T(\hat{t},\hat{u})\Bigg\}. \end{aligned} $

(12) The top and T quark mixed contributions to
$ f_A $ is given by$f_A^{tT} \!=\! (|y_{\rm L}^{tT}|^2+|y_{\rm R}^{tT}|^2)f_A^{tT,\Box1}\!+\![y_{\rm L}^{tT}(y_{\rm R}^{tT})^*\!+\!y_{\rm R}^{tT}(y_{\rm L}^{tT})^*]f_A^{tT,\Box2}$ . Here,$ f_A^{tT,\Box1} $ and$ f_A^{tT,\Box2} $ are defined as:$ \begin{aligned}[b]f_A^{tT,\Box1} =& \frac{2v^2}{\hat{s}}\Bigg\{2m_t^2C_0^t(\hat{s})+2m_T^2C_0^T(\hat{s})+\frac{m_h^2-m_t^2-m_T^2}{\hat{s}}\Big[(\hat{t}-m_h^2)(C_0^{tT}(\hat{t})+C_0^{Tt}(\hat{t}))+(\hat{u}-m_h^2)(C_0^{tT}(\hat{u})+C_0^{Tt}(\hat{u}))\Big]\\ &+(m_t^2+m_T^2-m_h^2)\Big[m_t^2(D_0^{tT}(\hat{t},\hat{s})+D_0^{tT}(\hat{u},\hat{s})+D_0^{tT}(\hat{t},\hat{u}))+m_T^2(D_0^{Tt}(\hat{t},\hat{s})+D_0^{Tt}(\hat{u},\hat{s})+D_0^{Tt}(\hat{t},\hat{u}))\Big]\\ &+2+\frac{\hat{t}\hat{u}-m_h^4}{\hat{s}}(m_t^2+m_T^2-m_h^2)D_0^{tT}(\hat{t},\hat{u})\Bigg\},\\ f_A^{tT,\Box2} =& \frac{m_tm_Tv^2}{\hat{s}^2}\Bigg\{4(m_h^2-\hat{t})\Big[C_0^{tT}(\hat{t})+C_0^{Tt}(\hat{t}))\Big]+4(m_h^2-\hat{u})\Big[C_0^{tT}(\hat{u})+C_0^{Tt}(\hat{u})\Big]\\ &+\hat{s}(4m_t^2-\hat{s})\Big[D_0^{tT}(\hat{t},\hat{s})+D_0^{tT}(\hat{u},\hat{s})+D_0^{tT}(\hat{t},\hat{u})\Big]+\hat{s}(4m_T^2-\hat{s})\Big[D_0^{Tt}(\hat{t},\hat{s})+D_0^{Tt}(\hat{u},\hat{s})+D_0^{Tt}(\hat{t},\hat{u})\Big]\\ &+4(\hat{t}\hat{u}-m_h^4)D_0^{tT}(\hat{t},\hat{u})\Bigg\}. \end{aligned} $ 
(13) The pure top quark contribution to
$ f_B $ is given by$ f_B^t = \kappa_t^2f_B^{t,\Box1} $ . Here,$ f_B^{t,\Box1} $ is defined as$ \begin{aligned}[b] f_B^{t,\Box1} =& \frac{m_t^2}{\hat{s}}\Bigg\{-2\hat{s}C_0^t(\hat{s})+2(m_h^2-\hat{t})C_0^t(\hat{t})+2(m_h^2-\hat{u})C_0^t(\hat{u})-2(8m_t^2+\hat{s}-2m_h^2)C_0^t(m_h^2)\\& +2m_t^2(8m_t^2+\hat{s}-2m_h^2)\Big[D_0^t(\hat{t},\hat{s})+D_0^t(\hat{u},\hat{s})+D_0^t(\hat{t},\hat{u})\Big]\\ &+\frac{1}{\hat{t}\hat{u}-m_h^4}\Big[\hat{s}\hat{t}(8m_t^2\hat{t}-\hat{t}^2-m_h^4)D_0^t(\hat{t},\hat{s})+\hat{s}\hat{u}(8m_t^2\hat{u}-\hat{u}^2-m_h^4)D_0^t(\hat{u},\hat{s})\\ & +(8m_t^2+\hat{s}-2m_h^2)\Big(\hat{s}(\hat{s}-2m_h^2)C_0^t(\hat{s})+\hat{s}(\hat{s}-4m_h^2)C_0^t(m_h^2)+2\hat{t}(m_h^2-\hat{t})C_0^t(\hat{t})+2\hat{u}(m_h^2-\hat{u})C_0^t(\hat{u})\Big)\Big]\Bigg\}. \end{aligned} $

(14) The pure T quark contribution to
$ f_B $ is given by$ f_B^T = \left (\dfrac{vy_T}{m_T}\right )^2f_B^{T,\Box1} $ . Here,$ f_B^{T,\Box1} $ is defined as$ \begin{aligned}[b] f_B^{T,\Box1} =& \frac{m_T^2}{\hat{s}}\Bigg\{-2\hat{s}C_0^T(\hat{s})+2(m_h^2-\hat{t})C_0^T(\hat{t})+2(m_h^2-\hat{u})C_0^T(\hat{u})-2(8m_T^2+\hat{s}-2m_h^2)C_0^T(m_h^2)\\ & +2m_T^2(8m_T^2+\hat{s}-2m_h^2)\Big[D_0^T(\hat{t},\hat{s})+D_0^T(\hat{u},\hat{s})+D_0^T(\hat{t},\hat{u})\Big]\\ & +\frac{1}{\hat{t}\hat{u}-m_h^4}\Big[\hat{s}\hat{t}(8m_T^2\hat{t}-\hat{t}^2-m_h^4)D_0^T(\hat{t},\hat{s})+\hat{s}\hat{u}(8m_T^2\hat{u}-\hat{u}^2-m_h^4)D_0^T(\hat{u},\hat{s})\\ & +(8m_T^2+\hat{s}-2m_h^2)\Big(\hat{s}(\hat{s}-2m_h^2)C_0^T(\hat{s})+\hat{s}(\hat{s}-4m_h^2)C_0^T(m_h^2)+2\hat{t}(m_h^2-\hat{t})C_0^T(\hat{t})+2\hat{u}(m_h^2-\hat{u})C_0^T(\hat{u})\Big)\Big]\Bigg\}. \end{aligned} $

(15) The top and T quark mixed contributions to
$ f_B $ is given by$f_B^{tT} = (|y_{\rm L}^{tT}|^2+|y_{\rm R}^{tT}|^2)f_B^{tT,\Box1}+\Big[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*+y_{\rm R}^{tT}(y_{\rm L}^{tT})^*\Big]f_B^{tT,\Box2}$ . Here,$ f_B^{tT,\Box1} $ is defined as:$ \begin{aligned}[b] f_B^{tT,\Box1} =& \frac{2v^2}{\hat{s}}\Bigg\{-\frac{\hat{s}}{2}\Big[C_0^t(\hat{s})+C_0^T(\hat{s})\Big]-\frac{1}{2}(\hat{s}-2m_h^2+2m_t^2+2m_T^2)\Big[C_0^{tT}(m_h^2)+C_0^{Tt}(m_h^2)\Big]+\frac{m_h^2-\hat{t}}{2}\Big[C_0^{tT}(t)+C_0^{Tt}(t)\Big]\\ &+\frac{m_h^2-\hat{u}}{2}\Big[C_0^{tT}(u)+C_0^{Tt}(u)\Big]+\frac{1}{2}(m_t^2-m_T^2)(\hat{s}+m_t^2+m_T^2-m_h^2)\Big[D_0^{tT}(\hat{t},\hat{s})+D_0^{tT}(\hat{u},\hat{s})-D_0^{Tt}(\hat{t},\hat{s})-D_0^{Tt}(\hat{u},\hat{s})\Big]\\ & +\frac{(m_t^2+m_T^2)}{4}(\hat{s}-2m_h^2+2m_t^2+2m_T^2)\Big[D_0^{tT}(\hat{t},\hat{s})+D_0^{tT}(\hat{u},\hat{s})+D_0^{tT}(\hat{t},\hat{u})+D_0^{Tt}(\hat{t},\hat{s})+D_0^{Tt}(\hat{u},\hat{s})+D_0^{Tt}(\hat{t},\hat{u})\Big]\\ & +\frac{1}{4(\hat{t}\hat{u}-m_h^4)}\Big[\hat{s}(\hat{s}-2m_h^2)(\hat{s}-2m_h^2+2m_t^2+2m_T^2)\Big(C_0^t(\hat{s})+C_0^T(\hat{s})\Big)\\& +2\hat{s}(m_T^2-m_t^2)(\hat{s}-2m_h^2+2m_T^2+2m_t^2)\Big(C_0^t(\hat{s})-C_0^T(\hat{s})\Big)+\hat{s}(\hat{s}-4m_h^2)(\hat{s}-2m_h^2+2m_t^2+2m_T^2)\Big(C_0^{tT}(m_h^2)+C_0^{Tt}(m_h^2)\Big)\\ & +2\hat{t}(m_h^2-\hat{t})(\hat{s}-2m_h^2+2m_t^2+2m_T^2)\Big(C_0^{tT}(\hat{t})+C_0^{Tt}(\hat{t})\Big)+2\hat{u}(m_h^2-\hat{u})(\hat{s}-2m_h^2+2m_t^2+2m_T^2)\Big(C_0^{tT}(\hat{u})+C_0^{Tt}(\hat{u})\Big)\\ & +\hat{s}(m_t^2-m_T^2)^2(\hat{s}-2m_h^2+2m_t^2+2m_T^2)\Big(D_0^{tT}(\hat{t},\hat{s})+D_0^{tT}(\hat{u},\hat{s})+D_0^{tT}(\hat{t},\hat{u})+D_0^{Tt}(\hat{t},\hat{s})+D_0^{Tt}(\hat{u},\hat{s})+D_0^{Tt}(\hat{t},\hat{u})\Big)\\ & +2\hat{s}\hat{t}(m_t^2-m_T^2)(\hat{s}-2m_h^2+2m_t^2+2m_T^2)\Big(D_0^{tT}(\hat{t},\hat{s})-D_0^{Tt}(\hat{t},\hat{s})\Big)\\ & +2\hat{s}\hat{u}(m_t^2-m_T^2)(\hat{s}-2m_h^2+2m_t^2+2m_T^2)\Big(D_0^{tT}(\hat{u},\hat{s})-D_0^{Tt}(\hat{u},\hat{s})\Big)\\ & -\hat{s}\hat{t}\Big(\hat{t}^2+m_h^4-2\hat{t}(m_t^2+m_T^2)\Big)\Big(D_0^{tT}(\hat{t},\hat{s})+D_0^{tT}(\hat{u},\hat{s})\Big)-\hat{s}\hat{u}\Big(\hat{u}^2+m_h^4-2\hat{u}(m_t^2+m_T^2)\Big)\Big(D_0^{Tt}(\hat{t},\hat{s})+D_0^{Tt}(\hat{u},\hat{s})\Big)\Big]\Bigg\}, \end{aligned} $

(16) and
$ f_B^{tT,\Box2} $ is defined as$ \begin{aligned}[b] f_B^{tT,\Box2} =& \frac{2m_tm_Tv^2}{\hat{s}}\Bigg\{-2\Big[C_0^{tT}(m_h^2)+C_0^{Tt}(m_h^2)\Big]+2m_t^2\Big[D_0^{tT}(\hat{t},\hat{s})+D_0^{tT}(\hat{u},\hat{s})+D_0^{tT}(\hat{t},\hat{u})\Big]\\ & +2m_T^2\Big[D_0^{Tt}(\hat{t},\hat{s})+D_0^{Tt}(\hat{u},\hat{s})+D_0^{Tt}(\hat{t},\hat{u})\Big]+\frac{1}{\hat{t}\hat{u}-m_h^4}\Big[\hat{s}(\hat{s}-2m_h^2)\Big(C_0^t(\hat{s})+C_0^T(\hat{s})\Big)-2\hat{s}(m_t^2-m_T^2)\Big(C_0^t(\hat{s})-C_0^T(\hat{s})\Big)\\ & +\hat{s}(\hat{s}-4m_h^2)\Big(C_0^{tT}(m_h^2)+C_0^{Tt}(m_h^2)\Big)+ 2\hat{t}(m_h^2-\hat{t})\Big(C_0^{tT}(\hat{t})+C_0^{Tt}(\hat{t})\Big)+2\hat{u}(m_h^2-\hat{u})\Big(C_0^{tT}(\hat{u})+C_0^{Tt}(\hat{u})\Big)\\ & +\hat{s}\Big(\hat{t}^2+(m_t^2-m_T^2)^2\Big)\Big(D_0^{tT}(\hat{t},\hat{s})+D_0^{Tt}(\hat{t},\hat{s})\Big)+\hat{s}\Big(\hat{u}^2+(m_t^2-m_T^2)^2\Big)\Big(D_0^{tT}(\hat{u},\hat{s})+D_0^{Tt}(\hat{u},\hat{s})\Big)\\ & +2\hat{s}\hat{t}(m_t^2-m_T^2)\Big(D_0^{tT}(\hat{t},\hat{s})-D_0^{Tt}(\hat{t},\hat{s})\Big)+2\hat{s}\hat{u}(m_t^2-m_T^2)\Big(D_0^{tT}(\hat{u},\hat{s})-D_0^{Tt}(\hat{u},\hat{s})\Big)+2\hat{s}(m_t^2-m_T^2)^2D_0^{tT}(\hat{t},\hat{u})\Big]\Bigg\}. \end{aligned} $

(17) The pure top quark contribution to
$ f_C $ is proportional to$ \widetilde{\kappa}_t $ ; hence, we set$ f_C^t $ to be zero. Similarly, the pure T quark contribution to$ f_C $ is also turned off. The top and T quark mixed contributions to$ f_C $ is given by$ f_C^{tT} = -{\rm i}\Big[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*- y_{\rm R}^{tT}(y_{\rm L}^{tT})^*\Big]f_C^{tT,\Box} $ . Here,$ f_C^{tT,\Box} $ is defined as$\begin{aligned}[b] f_C^{tT,\Box} =& m_tm_Tv^2\Big[D_0^{tT}(\hat{t},\hat{s})+D_0^{tT}(\hat{u},\hat{s})+D_0^{tT}(\hat{t},\hat{u})\\&+D_0^{Tt}(\hat{t},\hat{s})+D_0^{Tt}(\hat{u},\hat{s})+D_0^{Tt}(\hat{t},\hat{u})\Big].\end{aligned} $

(18) -
In the limit
$ \dfrac{m_h^2,\hat{s},\hat{t},\hat{u}}{m_{t}^2}\ll1 $ , the coefficients of pure top quark loops$ f_A^t,\; f_B^t $ can be expanded as$ \begin{aligned}[b] f_A^{t,\triangle} =& \frac{2m_h^2}{\hat{s}-m_h^2}\left[1+\frac{7\hat{s}}{120m_t^2}+{\cal{O}}\left(\frac{1}{m_t^4}\right)\right],\\f_A^{t,\Box1} =& -\frac{2}{3}\left[1+\frac{7m_h^2}{20m_t^2}+{\cal{O}}\left(\frac{1}{m_t^4}\right)\right],\\ f_B^{t,\Box1} = &\frac{11(m_h^4-\hat{t}\hat{u})}{90m_t^2\hat{s}}+{\cal{O}}\left(\frac{1}{m_t^4}\right). \end{aligned} $

(19) Regarding the coefficients of pure T quark loops, they are just the ones with
$ m_t $ replaced by$ m_T $ .For the case of t and T quark mixed loops, there are more complications. In the limit
$ \dfrac{m_h^2,\hat{s},\hat{t},\hat{u}}{m_{t,T}^2}\ll1 $ , the coefficients$ f_A^{tT},\; f_B^{tT},\; f_C^{tT} $ can be expanded as$ \begin{aligned}[b] f_A^{tT,\Box1} =& {\cal{O}}\left(\frac{1}{m_{t,T}^4}\right),\;\;\;\;\; f_A^{tT,\Box2} = -\frac{2v^2}{3m_tm_T}+{\cal{O}}\left(\frac{1}{m_{t,T}^4}\right),\\ f_C^{tT,\Box} =& \frac{v^2}{m_tm_T}+{\cal{O}}\left(\frac{1}{m_{t,T}^4}\right),\\ f_B^{tT,\Box1} =& \frac{v^2(\hat{t}^2-\hat{u}^2)}{m_T^2(\hat{t}\hat{u}-m_h^4)}\cdot\frac{(1+r_{tT}^2)(1+2r_{tT}^2\log r_{tT}^2-r_{tT}^4)}{2r_{tT}^2(1-r_{tT}^2)^2}\\ &+{\cal{O}}\left(\frac{1}{m_{t,T}^4}\right), \end{aligned} $

$ \begin{aligned}[b] f_B^{tT,\Box2} = {\cal{O}}\left(\frac{1}{m_{t,T}^4}\right). \end{aligned} $

(20) In the above,
$ r_{tT} $ is defined as$ r_{tT}\equiv\dfrac{m_t}{m_T} $ . -
When averaging the initial spin and color degrees of freedom, we can obtain the partonic cross section of
$ gg\rightarrow hh $ at the leading order (LO) as follows:$ \begin{aligned}[b] \hat{\sigma}_{\rm LO}(gg\rightarrow hh;\hat{s}) =& \frac{\alpha_S^2G_F^2\sqrt{\hat{s}(\hat{s}-4m_h^2)}}{128(4\pi)^3}\int_{-1}^1{\rm d}\cos\theta\; (|f_A|^2+|f_B|^2+|f_C|^2)\\ =& \frac{\alpha_S^2G_F^2}{64(4\pi)^3}\int_{\hat{t}_{\rm min}}^{\hat{t}_{\rm max}}{\rm d}\hat{t}\; (|f_A|^2+|f_B|^2+|f_C|^2)\Bigg(\hat{t}_{\rm min} = -\frac{1}{4}\Big(\sqrt{\hat{s}}+\sqrt{\hat{s}-4m_h^2}\Big)^2,\;\;\;\; \hat{t}_{\rm max} = -\frac{1}{4}\Big(\sqrt{\hat{s}}-\sqrt{\hat{s}-4m_h^2}\Big)^2\Bigg), \end{aligned} $ 
(21) where
$ f_A,f_B,f_C $ are calculated as$ \begin{aligned}[b] f_A =& f_A^t+f_A^T+f_A^{tT} = \kappa_tf_A^{t,\triangle}+\kappa_t^2f_A^{t,\Box1}+\left(-\frac{vy_T}{m_T}\right)f_A^{T,\triangle}+\left(\frac{vy_T}{m_T}\right)^2f_A^{T,\Box1}+(|y_{\rm L}^{tT}|^2+|y_{\rm R}^{tT}|^2)f_A^{tT,\Box1}+\Big[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*+y_{\rm R}^{tT}(y_{\rm L}^{tT})^*\Big]f_A^{tT,\Box2},\\ f_B =& f_B^t+f_B^T+f_B^{tT} = \kappa_t^2f_B^{t,\Box1}+\left(\frac{vy_T}{m_T}\right)^2f_B^{T,\Box1}+(|y_{\rm L}^{tT}|^2+|y_{\rm R}^{tT}|^2)f_B^{tT,\Box1}+\Big[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*+y_{\rm R}^{tT}(y_{\rm L}^{tT})^*\Big]f_B^{tT,\Box2},\\ f_C =& f_C^t+f_C^T+f_C^{tT} = -{\rm i}\Big[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*-y_{\rm R}^{tT}(y_{\rm L}^{tT})^*\Big]f_C^{tT,\Box}. \end{aligned} $

(22) Note that there is a
$ \dfrac{1}{2} $ factor in the partonic cross section because of the identical final states. In general, the anomalous triple Higgs coupling$ \lambda_{hhh} $ will also alter the di-Higgs production cross section. Its effects can be captured with$ f_A^{f,\triangle},f_C^{f,\triangle}(f = t,T) $ multiplied by the factor$ 1+\delta_{hhh}\equiv\lambda_{hhh}/\lambda_{hhh}^{SM} $ .After folding the partonic cross section with the gluon luminosity, we can get the hadron level cross section
$\begin{aligned}[b] \sigma_{\rm LO}(pp\rightarrow hh) =& \int_\frac{4m_h^2}{s}^1{\rm d}\tau\int_\tau^1\frac{{\rm d}x}{x}f(x,\mu_F^2)\\&\times f\left(\frac{\tau}{x},\mu_F^2\right)\hat{\sigma}_{\rm LO}(gg\rightarrow hh;\hat{s} = \tau s), \end{aligned}$

(23) where f represents the gluon parton distribution function (PDF) and
$ \mu_F $ is the factorization scale. -
Similar to the VLQT model, for simplicity, we consider
$ \kappa_t = c_{\rm L}^2, y_T = -\dfrac{m_T}{v}s_{\rm L}^2 $ , but let$ {\rm{Re}}(y_{\rm L}^{tT}),{\rm{Re}}(y_{\rm R}^{tT}), $ $ {\rm{Im}}(y_{\rm L}^{tT}),{\rm{Im}}(y_{\rm R}^{tT}) $ to be free. Then we can select several benchmark scenarios and estimate the constraints on the magnitude and sign of the FCNY couplings. Now, we need to normalize the cross section to the SM ones numerically for fixed$ m_T $ and$ s_{\rm L} $ , which is defined as$ \mu_{hh}\equiv\frac{\sigma_{\rm LO}(pp\rightarrow hh)}{\sigma_{\rm LO}^{\rm SM}(pp\rightarrow hh)}. $

(24) Up to LO level,
$ \mu_{hh} $ can be parametrized as$ \begin{aligned}[b] \mu_{hh} =& 1+A_1+A_0^{hhh}\delta_{hhh}+A_1^{hhh}\delta_{hhh}^2+(A_2+A_2^{hhh}\delta_{hhh})(|y_{\rm L}^{tT}|^2+|y_{\rm R}^{tT}|^2)\\ &+(A_3+A_3^{hhh}\delta_{hhh})[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*+y_{\rm R}^{tT}(y_{\rm L}^{tT})^*]+A_4(|y_{\rm L}^{tT}|^2+|y_{\rm R}^{tT}|^2)^2+A_5[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*+y_{\rm R}^{tT}(y_{\rm L}^{tT})^*]^2\\ &+A_6(|y_{\rm L}^{tT}|^2+|y_{\rm R}^{tT}|^2)[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*+y_{\rm R}^{tT}(y_{\rm L}^{tT})^*]-A_7[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*-y_{\rm R}^{tT}(y_{\rm L}^{tT})^*]^2, \end{aligned} $ 
(25) From the observation of Eqs. (21) and (22), we can infer that
$ A_1,\; A_2,\; A_3 $ ,$ A_0^{hhh},\; A_1^{hhh},\; A_2^{hhh},\; A_3^{hhh} $ depend on the choices of both$ m_T $ and$ s_{\rm L} $ , whereas$ A_4,\; A_5,\; A_6,\; A_7 $ solely depend on$ m_T $ . Moreover,$ A_1^{hhh} $ ,$ A_4,\; A_5,\; A_7 $ are always non-negative, and$ A_1 $ vanishes as$ s_{\rm L} $ tends to zero.Although
$ \sigma^{\rm SM}(pp\rightarrow hh) $ has been calculated with high precision [86-94], we will not consider this complex calculation here. Here, we only keep the LO results because a large part of the QCD corrections can be cancelled in the ratio [57, 65, 95, 96]. To obtain the numerical results of cross sections, we write a model file using FeynRules [97, 98], FeynArts [99], and NLOCT [100]. Then, this file is linked to MadGraph [101]. Before the numerical calculations, we use the following default settings:$ \bullet $ Proton contains b and$ \bar{b} $ , that is, we adopt the 5 flavor scheme.$ \bullet $ We adopt the PDF choice "MSTW2008lo68cl" (LHAPDF ID 21000 [102]).$ \bullet $ The default "$ dynamical_{\_}scale_{\_}choice $ " is set to be 3 (see [103]).$ \bullet $ The input parameters are selected as$ m_h = 125.09\; {\rm{GeV}}, \; G_F = 1.1664\times 10^{-5}\; {\rm{GeV}}^{-2} $ ,$ m_t = 172.74\; $ $ {\rm{GeV}} $ , and$ \alpha_s(m_Z) = $ $ 0.1184 $ ; hence,$ v = 246.221\; {\rm{GeV}} $ .Currently, the Higgs pair production is bounded to be
$ |\mu_{hh}|\leqslant 6.9 $ at 95% confidence level (CL) [104, 105]. At the high luminosity LHC (HL-LHC), di-Higgs production measurement is accessible. The expected signal strength is$ \mu_{hh} = 1.00_{-0.39}^{+0.41} $ with$ 1\sigma $ uncertainty [106]. We set the benchmark points as$ m_T = 400\; {\rm{GeV}},\; s_{\rm L} = 0.2 $ and$ m_T = 800\; {\rm{GeV}},\; s_{\rm L} = 0.1 $ , and the following discussions are based on the two benchmark points. Now, we should determine the specific values of$ A_1,\; A_2,\; A_3,\; A_4,\; A_5,\; A_6,\; A_7 $ and$ A_0^{hhh},\; A_1^{hhh},\; A_2^{hhh},\; A_3^{hhh} $ . First, we have$ \sigma_{\rm LO}^{\rm SM}(pp\rightarrow hh) = $ 24.7 fb. When setting different values of$ \delta_{hhh},\; y_{\rm L}^{tT},\; y_{\rm R}^{tT} $ , we can obtain different normalized cross sections (see Tables 1 and 2). Then, the numerical values of$ A_1,...,A_7 $ and$ A_0^{hhh},\; A_1^{hhh},\; A_2^{hhh},\; A_3^{hhh} $ can be solved from the first seven and last four equations seperately. Their results are presented in Table 3.$\delta_{hhh}$ 

$(~y_{\rm L}^{tT},~y_{\rm R}^{tT})$ 

expressions of $\mu_{hh}$ 

numerical values of $\mu_{hh}$ 

0 $(0,~0)$ 

$1+A_1$ 

0.8081 $(0,~1)$ 

$1+A_1+A_2+A_4$ 

1.254 $(0,~\dfrac{1}{2})$ 

$1+A_1+\dfrac{1}{4}A_2+\dfrac{1}{16}A_4$ 

0.9057 $(1,~1)$ 

$1+A_1+2A_2+2A_3+4A_4+4A_5+4A_6$ 

10.92 $(1,~-1)$ 

$1+A_1+2A_2-2A_3+4A_4+4A_5-4A_6$ 

1.695 $(1,~i)$ 

$1+A_1+2A_2+4A_4+4A_7$ 

14.13 $(\dfrac{1}{2},~\dfrac{1}{2})$ 

$1+A_1+\dfrac{1}{2}A_2+\dfrac{1}{2}A_3+\dfrac{1}{4}A_4+\dfrac{1}{4}A_5+\dfrac{1}{4}A_6$ 

2.206 1 $(0,~0)$ 

$1+A_1+A_0^{hhh}+A_1^{hhh}$ 

0.3877 $(0,~1)$ 

$1+A_1+A_0^{hhh}+A_1^{hhh}+A_2+A_2^{hhh}+A_4$ 

0.6996 $(1,~1)$ 

$ \begin{array}{l}1+A_1+A_0^{hhh}+A_1^{hhh}+2(A_2+A_2^{hhh})+2(A_3+A_3^{hhh})\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;+4A_4+4A_5+4A_6 \end{array}$ 

8.235 -1 $(0,~0)$ 

$1+A_1-A_0^{hhh}+A_1^{hhh}$ 

1.779 Table 1. Normalized cross sections for different
$\delta_{hhh},~y_{\rm L}^{tT},~y_{\rm R}^{tT}$ values with$m_T=$ 400 GeV and$s_{\rm L}=0.2$ at$\sqrt{s}$ =14 TeV.$\delta_{hhh}$ 

$(~y_{\rm L}^{tT},~y_{\rm R}^{tT})$ 

expressions of $\mu_{hh}$ 

numerical values of $\mu_{hh}$ 

0 $(0,~0)$ 

$1+A_1$ 

0.9506 $(0,~1)$ 

$1+A_1+A_2+A_4$ 

1.098 $(0,~\dfrac{1}{2})$ 

$1+A_1+\dfrac{1}{4}A_2+\dfrac{1}{16}A_4$ 

0.9838 $(1,~1)$ 

$1+A_1+2A_2+2A_3+4A_4+4A_5+4A_6$ 

5.255 $(1,~-1)$ 

$1+A_1+2A_2-2A_3+4A_4+4A_5-4A_6$ 

0.3376 $(1,~i)$ 

$1+A_1+2A_2+4A_4+4A_7$ 

5.247 $(\dfrac{1}{2},~\dfrac{1}{2})$ 

$1+A_1+\dfrac{1}{2}A_2+\dfrac{1}{2}A_3+\dfrac{1}{4}A_4+\dfrac{1}{4}A_5+\dfrac{1}{4}A_6$ 

1.675 1 $(0,~0)$ 

$1+A_1+A_0^{hhh}+A_1^{hhh}$ 

0.4502 $(0,~1)$ 

$1+A_1+A_0^{hhh}+A_1^{hhh}+A_2+A_2^{hhh}+A_4$ 

0.5526 $(1,~1)$ 

$\begin{array}{l}1+A_1+A_0^{hhh}+A_1^{hhh}+2(A_2+A_2^{hhh})+2(A_3+A_3^{hhh})\\ \;\;\;\;\;\;\;\;\;\;\;\;+4A_4+4A_5+4A_6\end{array}$ 

3.519 -1 $(0,~0)$ 

$1+A_1-A_0^{hhh}+A_1^{hhh}$ 

2.013 Table 2. Normalized cross sections for different
$\delta_{hhh},~y_{\rm L}^{tT},~y_{\rm R}^{tT}$ values with$m_T=$ 800 GeV and$s_{\rm L}=0.1$ at$\sqrt{s}$ =14 TeV.$\sqrt{s}$ /TeV

( $m_T$ /GeV,

$s_{\rm L}$ )

$A_1$ 

$A_2$ 

$A_3$ 

$A_4$ 

$A_5$ 

$A_6$ 

$A_7$ 

14 (400, 0.2) $-0.1919$ 

0.3717 1.672 0.07449 1.114 0.3166 3.071 (800, 0.1) $-0.04939$ 

0.1279 1.087 0.01943 0.378 0.0711 0.9907 $\sqrt{s}$ /TeV

( $m_T$ /GeV,

$s_{\rm L}$ )

$A_0^{hhh}$ 

$A_1^{hhh}$ 

$A_2^{hhh}$ 

$A_3^{hhh}$ 

14 (400, 0.2) $-0.6958$ 

0.2754 $-0.1343$ 

$-0.9956$ 

(800, 0.1) $-0.7814$ 

0.281 $-0.04494$ 

$-0.5731$ 

-
For the case of
$ m_T = $ 400 GeV and$ s_{\rm L} = 0.2 $ , the numerical results of$ \mu_{hh} $ are evaluated as$ \begin{aligned}[b] \mu_{hh} =& 1-0.1919-0.6958\; \delta_{hhh}+0.2754\; \delta_{hhh}^2+(0.3717-0.1343\; \delta_{hhh})(|y_{\rm L}^{tT}|^2+|y_{\rm R}^{tT}|^2)\\& +(1.672-0.9956\; \delta_{hhh})[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*+y_{\rm R}^{tT}(y_{\rm L}^{tT})^*]+0.07449(|y_{\rm L}^{tT}|^2+|y_{\rm R}^{tT}|^2)^2+1.114[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*+y_{\rm R}^{tT}(y_{\rm L}^{tT})^*]^2\\& +0.3166(|y_{\rm L}^{tT}|^2+|y_{\rm R}^{tT}|^2)[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*+y_{\rm R}^{tT}(y_{\rm L}^{tT})^*]-3.071[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*-y_{\rm R}^{tT}(y_{\rm L}^{tT})^*]^2. \end{aligned} $ 
(26) In this case, the present di-Higgs production experiments provide the constraints
$ \delta_{hhh}\in(-3.61, 6.13) $ and$ {\rm{Re}}y_{\rm L}^{tT},{\rm{Im}}y_{\rm L}^{tT},{\rm{Re}}y_{\rm R}^{tT},{\rm{Im}}y_{\rm R}^{tT}\in(-2.62, 2.62) $ at 95% CL by setting one parameter at a time. In Table 4, we provide the expected constraints on the parameters$ \delta_{hhh},{\rm{Re}}y_{\rm L}^{tT},{\rm{Im}}y_{\rm L}^{tT}, $ $ {\rm{Re}}y_{\rm R}^{tT},{\rm{Im}}y_{\rm R}^{tT} $ at HL-LHC. It can be observed that both the current and expected constraints at HL-LHC are stronger than the unitarity bound, because the highest power in di-Higgs production cross section is proportional to$ (y_{\rm L,R}^{tT})^4 $ .method CL $\delta_{hhh}$ 

${\rm{Re}}y_{\rm L}^{tT}$ 

${\rm{Im}}y_{\rm L}^{tT}$ 

${\rm{Re}}y_{\rm R}^{tT}$ 

${\rm{Im}}y_{\rm R}^{tT}$ 

individual $1~\sigma$ 

(−0.681, 0.327) $\cup$ (2.20, 3.21)

(−1.13, 1.13) (−1.13, 1.13) (−1.13, 1.13) (−1.13, 1.13) $2~\sigma$ 

(−1.03, 3.56) (−1.40, 1.40) (−1.40, 1.40) (−1.40, 1.40) (−1.40, 1.40) marginalized $1~\sigma$ 

(−3.76, 3.99) (−1.91, 1.91) (−1.91, 1.91) (−1.91, 1.91) (−1.91, 1.91) $2~\sigma$ 

(−4.48, 4.66) (−2.09, 2.09) (−2.09, 2.09) (−2.09, 2.09) (−2.09, 2.09) Table 4. Expected
$1\sigma$ and$2\sigma$ bounds at HL-LHC for the parameters$\delta_{hhh},{\rm{Re}}y_{\rm L}^{tT},{\rm{Im}}y_{\rm L}^{tT},{\rm{Re}}y_{\rm R}^{tT},{\rm{Im}}y_{\rm R}^{tT}$ under the benchmark point$m_T=$ 400 GeV and$s_{\rm L}=0.2$ . Here, we adopt two different methods: (1) turn on one parameter at a time (individual method) and (2) turn on all five parameters (marginalized method).As mentioned above, there are four interesting parameters
$ {\rm{Re}}(y_{\rm L}^{tT}),{\rm{Re}}(y_R^{tT}),{\rm{Im}}(y_{\rm L}^{tT}),{\rm{Im}}(y_{\rm R}^{tT}) $ . Accordingly, we can plot the reached two-dimensional parameter space by setting two of them to be zeros or imposing two conditions. Here, we select six scenarios: ①$ y_{\rm L,R}^{tT} $ are both real (similar to both imaginary number case); ②$ y_{\rm R}^{tT} $ is real and$ y_{\rm L}^{tT} $ is imaginary (similar to the real$ y_{\rm L}^{tT} $ and imaginary$ y_{\rm R}^{tT} $ case); ③$ y_{\rm R}^{tT} = 0 $ (similar to the$ y_{\rm L}^{tT} = 0 $ case); ④$ y_{\rm L}^{tT} = y_{\rm R}^{tT} $ ; ⑤$ y_{\rm L}^{tT} = -y_{\rm R}^{tT} $ ; ⑥$ y_{\rm L}^{tT} = (y_{\rm R}^{tT})^* $ .In Figs. 5 and 6, we present the plots with
$ \delta_{hhh} = 0 $ and$ \delta_{hhh} = 0.5 $ , respectively. From these plots, we observe that$ {\rm{Re}}(y_{\rm L,R}^{tT}) $ and$ {\rm{Im}}(y_{\rm L,R}^{tT}) $ are constrained to be in the range$ (-2,\; 2) $ approximately at$ 2\; \sigma $ CL. In some of these scenarios, the$ 2\; \sigma $ interval can be as tight as$ (-0.4,\; 0.4) $ . The reach regions of$ 1\; \sigma $ and$ 2\; \sigma $ are quite different. The value of$ \delta_{hhh} $ has significant effects on the extraction of$ y_{\rm L,R}^{tT} $ . For the first (upper left) plot, the first and third quadrants are more constrained. This can be understood from Eq. (22), because there is constructive interference between the positive$ [y_{\rm L}^{tT}(y_{\rm R}^{tT})^*+y_{\rm R}^{tT}(y_{\rm L}^{tT})^*] $ term and other box diagram induced terms. However, it is a destructive interference if$ [y_{\rm L}^{tT}(y_{\rm R}^{tT})^*+y_{\rm R}^{tT}(y_{\rm L}^{tT})^*] $ is negative. The last five plots are symmetric, relative to the horizontal and vertical axes. For the second (upper central) and sixth (lower right) plots, they receive contributions from the$ [y_{\rm L}^{tT}(y_{\rm R}^{tT})^*-y_{\rm R}^{tT}(y_{\rm L}^{tT})^*] $ term. Because$ |f_C|^2 $ in Eq. (21) is always positive, the constraints are stronger. For the fourth (lower left) plot, positive$ [y_{\rm L}^{tT}(y_{\rm R}^{tT})^*+y_{\rm R}^{tT}(y_{\rm L}^{tT})^*] $ induces the constructive interference; therefore, the bounds are also stronger. For the third (upper right) plot, both$ [y_{\rm L}^{tT}(y_{\rm R}^{tT})^*+y_{\rm R}^{tT}(y_{\rm L}^{tT})^*] $ and$ [y_{\rm L}^{tT}(y_{\rm R}^{tT})^*-y_{\rm R}^{tT}(y_{\rm L}^{tT})^*] $ vanish; hence, it is less constrained than other plots. In addition, there can be more cancellations between the triangle and box diagrams for larger$ \delta_{hhh} $ . Therefore, the constraints are usually looser than the zero$ \delta_{hhh} $ ones.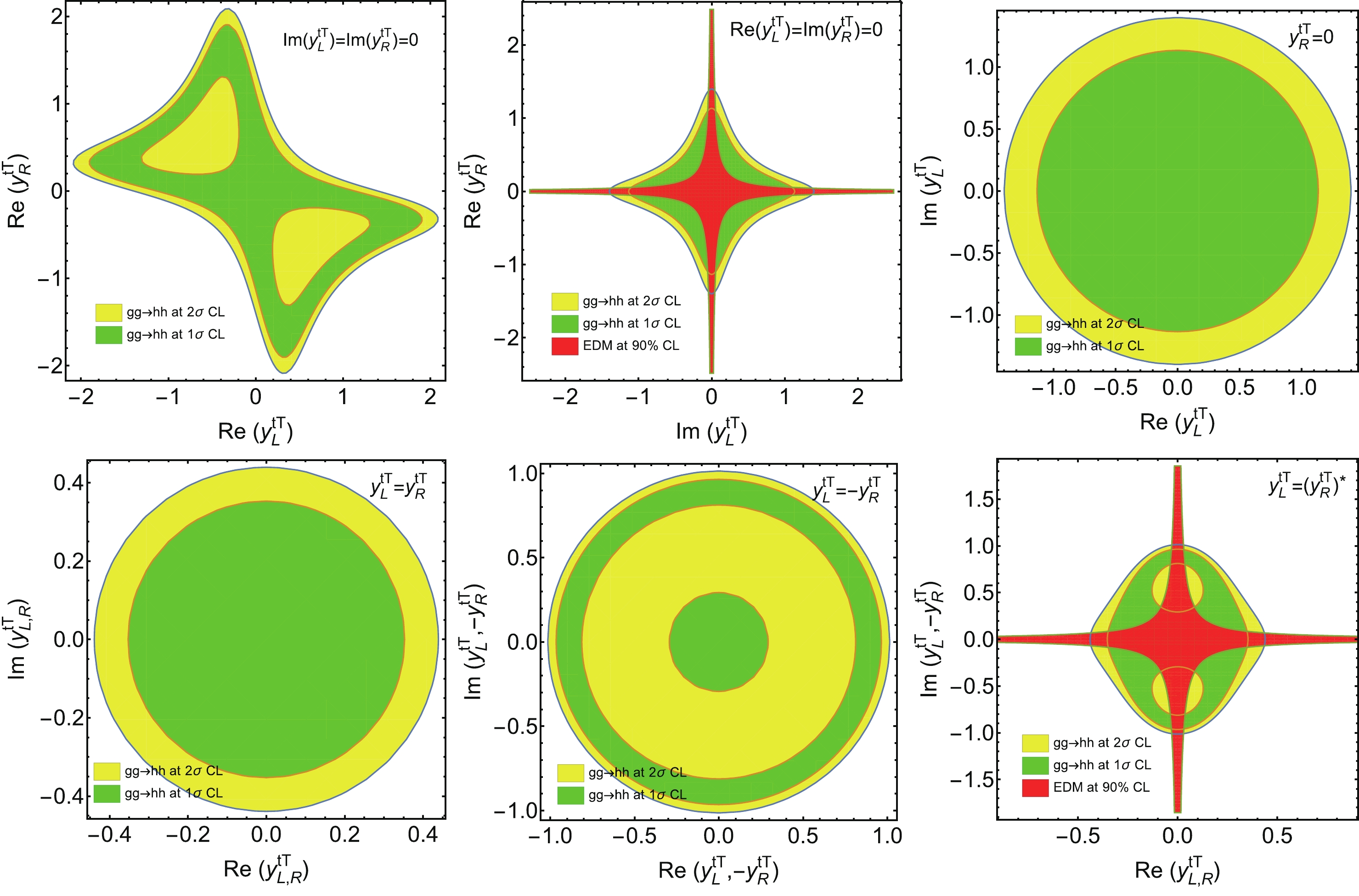
Figure 5. (color online) Reach regions of
$y_{\rm L}^{tT},y_{\rm R}^{tT}$ at HL-LHC with$\delta_{hhh}=0$ for the case of$m_T$ = 400 GeV and$s_{\rm L}=0.2$ . In the above plots, we take${\rm{Im}}(y_{\rm L}^{tT})={\rm{Im}}(y_{\rm R}^{tT})=0$ (upper left),${\rm{Re}}(y_{\rm L}^{tT})={\rm{Im}}(y_{\rm R}^{tT})=0$ (upper central),$y_{\rm R}^{tT}=0$ (upper right),$y_{\rm L}^{tT}=y_{\rm R}^{tT}$ (lower left),$y_{\rm L}^{tT}=-y_{\rm R}^{tT}$ (lower central), and$y_{\rm L}^{tT}=(y_{\rm R}^{tT})^*$ (lower right). We also consider the top quark EDM constraint for the scenarios${\rm{Re}}(y_{\rm L}^{tT})={\rm{Im}}(y_{\rm R}^{tT})=0$ (upper central) and$y_{\rm L}^{tT}=(y_{\rm R}^{tT})^*$ (lower right), where the reach regions of$y_{\rm L}^{tT},y_{\rm R}^{tT}$ are depicted in red at 90% CL.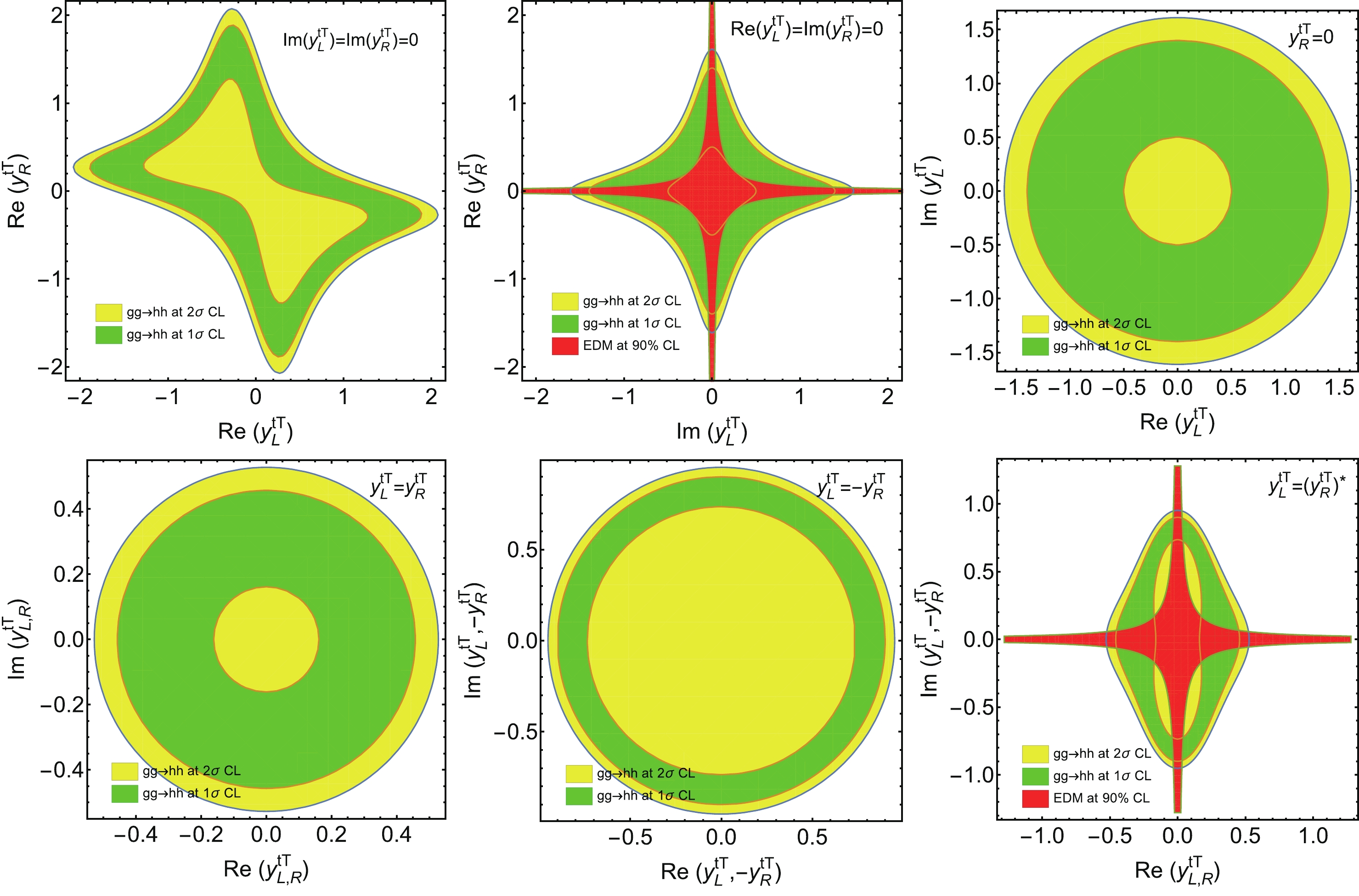
Figure 6. (color online) Reach regions of
$y_{\rm L}^{tT},y_{\rm R}^{tT}$ at HL-LHC with$\delta_{hhh}=0.5$ for the case of$m_T$ = 400 GeV and$s_{\rm L}=0.2$ . In the above plots, we take${\rm{Im}}(y_{\rm L}^{tT})={\rm{Im}}(y_{\rm R}^{tT})=0$ (upper left),${\rm{Re}}(y_{\rm L}^{tT})={\rm{Im}}(y_{\rm R}^{tT})=0$ (upper central),$y_{\rm R}^{tT}=0$ (upper right),$y_{\rm L}^{tT}=y_{\rm R}^{tT}$ (lower left),$y_{\rm L}^{tT}=-y_{\rm R}^{tT}$ (lower central), and$y_{\rm L}^{tT}=(y_{\rm R}^{tT})^*$ (lower right). We also consider the top quark EDM constraint for the scenarios${\rm{Re}}(y_{\rm L}^{tT})={\rm{Im}}(y_{\rm R}^{tT})=0$ (upper central) and$y_{\rm L}^{tT}=(y_{\rm R}^{tT})^*$ (lower right), where the reach regions of$y_{\rm L}^{tT},y_{\rm R}^{tT}$ are shown in red at 90% CL.In fact, we infer that the di-Higgs production at HL-LHC can give stronger constraints than those from perturbative unitarity and
$ h\rightarrow\gamma Z $ decay [17]. When we consider the top quark EDM bound, the two scenarios$ {\rm{Re}}(y_{\rm L}^{tT}) = {\rm{Im}}(y_{\rm R}^{tT}) = 0 $ and$ y_{\rm L}^{tT} = (y_{\rm R}^{tT})^* $ can also be constrained. For the other scenarios$ y_{\rm R}^{tT} = 0,y_{\rm L}^{tT} = \pm y_{\rm R}^{tT}, $ $ {\rm{Im}}y_{\rm L}^{tT} = {\rm{Im}}y_{\rm R}^{tT} = 0 $ , they are insensitive to the top quark EDM, because we have the relationship$ d_t^{\rm EDM}\sim y_{\rm R}^{tT}(y_{\rm L}^{tT})^*- $ $ y_{\rm L}^{tT}(y_{\rm R}^{tT})^* = 2{\rm i}({\rm{Re}}y_{\rm L}^{tT}{\rm{Im}}y_{\rm R}^{tT}-{\rm{Re}}y_{\rm R}^{tT}{\rm{Im}}y_{\rm L}^{tT}) $ . For the scenarios$ {\rm{Re}}(y_{\rm L}^{tT}) = {\rm{Im}}(y_{\rm R}^{tT}) = 0 $ and$ y_{\rm L}^{tT} = (y_{\rm R}^{tT})^* $ , we compare the bounds from di-Higgs production and top quark EDM for$ \delta_{hhh} = 0 $ (Fig. 5) and$ \delta_{hhh} = 0.5 $ (Fig. 6), respectively. From these plots, we can observe that the off-axis regions can be strongly bounded by the top EDM, whereas it will lose the constraining power in the near axis regions. -
For the case of
$ m_T = $ 800 GeV and$ s_{\rm L} = 0.1 $ , the numerical results of$ \mu_{hh} $ are evaluated as:$ \begin{aligned}[b] \mu_{hh} =& 1-0.04939-0.7814\; \delta_{hhh}+0.281\; \delta_{hhh}^2+(0.1279-0.04494\; \delta_{hhh})(|y_{\rm L}^{tT}|^2+|y_{\rm R}^{tT}|^2)\\& +(1.087-0.5731\; \delta_{hhh})\Big[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*+y_{\rm R}^{tT}(y_{\rm L}^{tT})^*\Big]+0.01943(|y_{\rm L}^{tT}|^2+|y_{\rm R}^{tT}|^2)^2+0.378\Big[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*+y_{\rm R}^{tT}(y_{\rm L}^{tT})^*\Big]^2\\& +0.0711(|y_{\rm L}^{tT}|^2+|y_{\rm R}^{tT}|^2)\Big[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*+y_{\rm R}^{tT}(y_{\rm L}^{tT})^*\Big]-0.9907\Big[y_{\rm L}^{tT}(y_{\rm R}^{tT})^*-y_{\rm R}^{tT}(y_{\rm L}^{tT})^*\Big]^2. \end{aligned} $ 
(27) In this case, the present di-Higgs production experiments give the constraints
$ \delta_{hhh}\in(-3.42, 6.20) $ and$ {\rm{Re}}y_{\rm L}^{tT}, $ $ \;{\rm{Im}}y_{\rm L}^{tT},\;{\rm{Re}}y_{\rm R}^{tT},\;{\rm{Im}}y_{\rm R}^{tT}\in(-3.81, 3.81) $ at 95% CL by setting one parameter at a time. In Table 5, we provide the expected constraints on the parameters$ \delta_{hhh},\;{\rm{Re}}y_{\rm L}^{tT}, $ $ \; {\rm{Im}}y_{\rm L}^{tT},\; {\rm{Re}}y_{\rm R}^{tT}, {\rm{Im}}y_{\rm R}^{tT} $ at HL-LHC.method CL $\delta_{hhh}$ 

${\rm{Re}}y_{\rm L}^{tT}$ 

${\rm{Im}}y_{\rm L}^{tT}$ 

${\rm{Re}}y_{\rm R}^{tT}$ 

${\rm{Im}}y_{\rm R}^{tT}$ 

individual $1~\sigma$ 

(−0.499, 0.541) $\cup$ (2.24, 3.28)

(−1.61, 1.61) (−1.61, 1.61) (−1.61, 1.61) (−1.61, 1.61) $2~\sigma$ 

(−0.852, 3.63) (−2.04, 2.04) (−2.04, 2.04) (−2.04, 2.04) (−2.04, 2.04) marginalized $1~\sigma$ 

(−4.12, 3.89) (−2.82, 2.82) (−2.82, 2.82) (−2.82, 2.82) (−2.82, 2.82) $2~\sigma$ 

(−4.80, 4.51) (−3.05, 3.05) (−3.05, 3.05) (−3.05, 3.05) (−3.05, 3.05) Table 5. Expected
$1\sigma$ and$2\sigma$ bounds at HL-LHC for the parameters$\delta_{hhh},{\rm{Re}}y_{\rm L}^{tT},{\rm{Im}}y_{\rm L}^{tT},{\rm{Re}}y_{\rm R}^{tT},{\rm{Im}}y_{\rm R}^{tT}$ under the benchmark point$m_T=$ 800 GeV and$s_{\rm L}=0.1$ . Here, we adopt two different methods: (1) turn on one parameter at a time (individual method) and (2) turn on all five parameters (marginalized method).We will also plot the reached two-dimensional parameter space by setting two of them to be zeros or imposing two conditions. In Figs. 7 and 8, similar plots are presented for the six scenarios with
$ \delta_{hhh} = 0 $ and$ \delta_{hhh} = 0.5 $ , respectively. From these plots, we infer that$ {\rm{Re}}(y_{\rm L,R}^{tT}) $ and$ {\rm{Im}}(y_{\rm L,R}^{tT}) $ are constrained to be in the range$ (-3,\; 3) $ approximately at$ 2\; \sigma $ CL. In some of these scenarios, the$ 2\; \sigma $ interval can be as tight as$ (-0.5,\; 0.5) $ . The reach regions are similar to those in the$ m_T = $ 400 GeV and$ s_{\rm L} = 0.2 $ case. Di-Higgs production at HL-LHC will give stronger constraints than those from$ h\rightarrow\gamma Z $ decay under these scenarios [17]. For the scenarios$ {\rm{Re}}(y_{\rm L}^{tT}) = {\rm{Im}}(y_{\rm R}^{tT}) = 0 $ and$ y_{\rm L}^{tT} = (y_{\rm R}^{tT})^* $ , we also compare the bounds from di-Higgs production and top quark EDM for$ \delta_{hhh} = 0 $ (Fig. 7) and$ \delta_{hhh} = 0.5 $ (Fig. 8), respectively. When$ m_T $ becomes larger,$ y_{\rm L,R}^{tT} $ are constrained more loosely. When$ s_{\rm L} $ becomes very small, the pure top quark contributions are SM-like, and the pure T quark contributions are highly suppressed. Therefore, the main deviation of$ \mu_{hh} $ is from the FCNY interactions.
Figure 7. (color online) Reach regions of
$y_{\rm L}^{tT},\;y_{\rm R}^{tT}$ at HL-LHC with$\delta_{hhh}=0$ for the case of$m_T$ = 800 GeV and$s_{\rm L}=0.1$ . In the above plots, we take${\rm{Im}}(y_{\rm L}^{tT})={\rm{Im}}(y_{\rm R}^{tT})=0$ (upper left),${\rm{Re}}(y_{\rm L}^{tT})={\rm{Im}}(y_{\rm R}^{tT})=0$ (upper central),$y_{\rm R}^{tT}=0$ (upper right),$y_{\rm L}^{tT}=y_{\rm R}^{tT}$ (lower left),$y_{\rm L}^{tT}=-y_{\rm R}^{tT}$ (lower central), and$y_{\rm L}^{tT}=(y_{\rm R}^{tT})^*$ (lower right). We also consider the top quark EDM constraint for the scenarios${\rm{Re}}(y_{\rm L}^{tT})={\rm{Im}}(y_{\rm R}^{tT})=0$ (upper central) and$y_{\rm L}^{tT}=(y_{\rm R}^{tT})^*$ (lower right), where the reach regions of$y_{\rm L}^{tT},\;y_{\rm R}^{tT}$ are depicted in red at 90% CL.
Figure 8. (color online) Reach regions of
$y_{\rm L}^{tT},\;y_{\rm R}^{tT}$ at HL-LHC with$\delta_{hhh}=0.5$ for the case of$m_T$ = 800 GeV and$s_{\rm L}=0.1$ . In the above plots, we take${\rm{Im}}(y_{\rm L}^{tT})={\rm{Im}}(y_{\rm R}^{tT})=0$ (upper left),${\rm{Re}}(y_{\rm L}^{tT})={\rm{Im}}(y_{\rm R}^{tT})=0$ (upper central),$y_{\rm R}^{tT}=0$ (upper right),$y_{\rm L}^{tT}=y_{\rm R}^{tT}$ (lower left),$y_{\rm L}^{tT}=-y_{\rm R}^{tT}$ (lower central), and$y_{\rm L}^{tT}=(y_{\rm R}^{tT})^*$ (lower right). We also consider the top quark EDM constraint for the scenarios${\rm{Re}}(y_{\rm L}^{tT})={\rm{Im}}(y_{\rm R}^{tT})=0$ (upper central) and$y_{\rm L}^{tT}=(y_{\rm R}^{tT})^*$ (lower right), where the reach regions of$y_{\rm L}^{tT},\;y_{\rm R}^{tT}$ are depicted in red at 90% CL.By the way, the FCNY coupling may be probed via other processes too. For example, we can probe the FCNY coupling Tth via the direct production processes
$ pp\rightarrow T\bar{t}h,T\bar{t},ThW,Thj $ . However, they are limited by low event rate, and the detailed analyses in these channels are beyond the scope of this work. -
We have assumed
$ T_{\rm L,R} $ to be singlets throughout this work, although they can be components of the doublet or triplet VLQs. There are two doublet and two triplet VLQs containing the T quark:$ (X,T)_{\rm L,R},\;(T,B)_{\rm L,R},\;(X,T,B)_{\rm L,R},\; $ $ (T,B,Y)_{\rm L,R} $ . Here$ X,B,Y $ carry$ \dfrac{4}{3},-\dfrac{1}{3},-\dfrac{4}{3} $ electric charges, respectively. For the doublet$ (X,T)_{\rm L,R} $ , the Higgs particle solely interacts with the$ T_{\rm L,R} $ . For the doublet$ (T,B)_{\rm L,R} $ and triplets$ (X,T,B)_{\rm L,R},\;(T,B,Y)_{\rm L,R} $ , the B quark can mix with the SM bottom quark. Thus, the Higgs particle will interact with both the T and B quarks. Let us denote left (right) up-type and down-type quark mixing angles as$ \theta_{\rm L}^t $ ($ \theta_R^t $ ) and$ \theta_{\rm L}^b $ ($ \theta_{\rm R}^b $ ), respectively. They can be related with each other [12].● For the triplet
$ (X,T,B)_{\rm L,R} $ , we obtain the relationships$ \tan\theta_R^t = \dfrac{m_t}{m_T}\tan\theta_{\rm L}^t $ and$ \tan\theta_{\rm R}^b = \dfrac{m_b}{m_B}\tan\theta_{\rm L}^b $ .$ \theta_{\rm L}^t $ and$ \theta_{\rm L}^b $ can be related via the identity$ \sin2\theta_{\rm L}^b = \sqrt{2}\dfrac{m_T^2-m_t^2}{m_B^2-m_b^2} \sin2\theta_{\rm L}^t $ . Thus, there is only one independent mixing angle$ \theta_{\rm L}^t $ .● For the triplet
$ (T,B,Y)_{\rm L,R} $ , we have the relationships$ \tan\theta_{\rm R}^t = \dfrac{m_t}{m_T}\tan\theta_{\rm L}^t $ and$ \tan\theta_{\rm R}^b = \dfrac{m_b}{m_B}\tan\theta_{\rm L}^b $ .$ \theta_{\rm L}^t $ and$ \theta_{\rm L}^b $ can be related via the identity$ \sin2\theta_{\rm L}^b = $ $ \dfrac{1}{\sqrt{2}}\dfrac{m_T^2-m_t^2}{m_B^2-m_b^2}\sin2\theta_{\rm L}^t $ . Therefore, there is only one independent mixing angle$ \theta_{\rm L}^t $ .● For the doublet
$ (X,T)_{\rm L,R} $ , we have the relationship$ \tan\theta_{\rm L}^t = \dfrac{m_t}{m_T}\tan\theta_{\rm R}^t $ . Thus, there is only one independent mixing angle$ \theta_R^t $ .● For the doublet
$ (T,B)_{\rm L,R} $ , we have the relationships$ \tan\theta_{\rm L}^t = \dfrac{m_t}{m_T}\tan\theta_{\rm R}^t $ and$\tan\theta_{\rm L}^b = \dfrac{m_b}{m_B}\tan\theta_{\rm R}^b$ . Hence, there are two independent mixing angles$ \theta_{\rm R}^t $ and$ \theta_{\rm R}^b $ .For the doublet
$ (X,T)_{\rm L,R} $ , the constraints on FCNY couplings from di-Higgs production are similar to those in the singlet$ T_{\rm L,R} $ case. Compared to the singlet$ T_{\rm L,R} $ , there are extra$ BBh,Bbh $ -type Yukawa interactions for the doublet$ (T,B)_{\rm L,R} $ and triplets$ (X,T,B)_{\rm L,R},(T,B,Y)_{\rm L,R} $ . Therefore, the constraints on FCNY interactions are expected to be looser. -
Top partners are well motivated in many new physics models, and FCNY interactions can appear between top quark and the new heavy quark. To elucidate the nature of the flavor structure and EWSB, it is important to probe the FCNY interactions. However, it is challenging to directly constrain the Tth coupling at both current and future experiments.
In this study, we introduced a simplified model and summarized the main constraints from theoretical and experimental perspectives first. Then we calculated the amplitude of di-Higgs production. After selecting
$ m_T = 400\; {\rm{GeV}},\;s_{\rm L} = 0.2 $ and$ m_T = 800\; {\rm{GeV}},s_{\rm L} = 0.1 $ as benchmark points, we evaluated the numerical cross sections. It is inferred that the present constraints from di-Higgs production have already surpassed the unitarity bound, owing to the$ (y_{\rm L,R}^{tT})^4 $ behavior in di-Higgs production cross section. The constraints from di-Higgs production at HL-LHC are also stronger than the$ h\rightarrow\gamma Z $ decay. For the case of$ m_T = 400\; {\rm{GeV}} $ and$ s_{\rm L} = 0.2 $ ,$ {\rm{Re}}y_{\rm L,R}^{tT} $ and$ {\rm{Im}}y_{\rm L,R}^{tT} $ are expected to be bounded in the range$ (-2, 2) $ and even$ (-0.4, 0.4) $ in some scenarios at HL-LHC with$ 2\sigma $ CL approximately. For the case of$ m_T = 800\; {\rm{GeV}} $ and$ s_{\rm L} = 0.1 $ ,$ {\rm{Re}}y_{\rm L,R}^{tT} $ and$ {\rm{Im}}y_{\rm L,R}^{tT} $ are expected to be bounded in the range$ (-3, 3) $ , and even$ (-0.5, 0.5) $ in some scenarios at HL-LHC with$ 2\sigma $ CL approximately. The value of$ \delta_{hhh} $ can have significant effects on the constraints of$ y_{\rm L,R}^{tT} $ . In simple terms, larger$ \delta_{hhh} $ values trigger looser constraints on$ y_{\rm L,R}^{tT} $ , as there can be more cancellations between the triangle and box diagrams. Finally, we determined that the top quark EDM can provide stronger bounds of$ y_{\rm L,R}^{tT} $ in the off-axis regions for some scenarios. -
We would like to thank Gang Li, Zhao Li, Ying-nan Mao, and Hao Zhang for their helpful discussions. We also thank Olivier Mattelaer for MadGraph program discussions via the launchpad platform.
-
The definitions of
$ C_0 $ and$ D_0 $ functions related to pure top quark loops are given as$\tag{A1} \begin{aligned}[b] C_0^t(\hat{s})\equiv& C_0(0,0,\hat{s},m_t^2,m_t^2,m_t^2),\\ C_0^t(m_h^2)\equiv& C_0(m_h^2,m_h^2,\hat{s},m_t^2,m_t^2,m_t^2),\\ C_0^t(\hat{t})\equiv& C_0(0,m_h^2,\hat{t},m_t^2,m_t^2,m_t^2),\\ C_0^t(\hat{u})\equiv& C_0(0,m_h^2,\hat{u},m_t^2,m_t^2,m_t^2),\\ D_0^t(\hat{t},\hat{s})\equiv& D_0(m_h^2,0,0,m_h^2,\hat{t},\hat{s},m_t^2,m_t^2,m_t^2,m_t^2),\\ D_0^t(\hat{u},\hat{s})\equiv& D_0(m_h^2,0,0,m_h^2,\hat{u},\hat{s},m_t^2,m_t^2,m_t^2,m_t^2),\\ D_0^t(\hat{t},\hat{u})\equiv& D_0(m_h^2,0,m_h^2,0,\hat{t},\hat{u},m_t^2,m_t^2,m_t^2,m_t^2). \end{aligned} $

The definitions of
$ C_0 $ and$ D_0 $ functions related to pure T quark loops are given as$ \tag{A2} \begin{aligned}[b] C_0^T(\hat{s})\equiv& C_0(0,0,\hat{s},m_T^2,m_T^2,m_T^2),\\ C_0^T(m_h^2)\equiv& C_0(m_h^2,m_h^2,\hat{s},m_T^2,m_T^2,m_T^2),\\ C_0^T(\hat{t})\equiv& C_0(0,m_h^2,\hat{t},m_T^2,m_T^2,m_T^2),\\ C_0^T(\hat{u})\equiv& C_0(0,m_h^2,\hat{u},m_T^2,m_T^2,m_T^2),\\ D_0^T(\hat{t},\hat{s})\equiv& D_0(m_h^2,0,0,m_h^2,\hat{t},\hat{s},m_T^2,m_T^2,m_T^2,m_T^2),\\ D_0^T(\hat{u},\hat{s})\equiv& D_0(m_h^2,0,0,m_h^2,\hat{u},\hat{s},m_T^2,m_T^2,m_T^2,m_T^2),\\ D_0^T(\hat{t},\hat{u})\equiv& D_0(m_h^2,0,m_h^2,0,\hat{t},\hat{u},m_T^2,m_T^2,m_T^2,m_T^2). \end{aligned} $

The definitions of
$ C_0 $ and$ D_0 $ functions related to mixed t and T quark loops are given as$ \tag{A3} \begin{aligned}[b] C_0^{tT}(m_h^2)\equiv& C_0(m_h^2,m_h^2,\hat{s},m_t^2,m_T^2,m_t^2),\\ C_0^{tT}(\hat{t})\equiv& C_0(0,m_h^2,\hat{t},m_t^2,m_t^2,m_T^2),\\ C_0^{tT}(\hat{u})\equiv& C_0(0,m_h^2,\hat{u},m_t^2,m_t^2,m_T^2),\\ D_0^{tT}(\hat{t},\hat{s})\equiv& D_0(m_h^2,0,0,m_h^2,\hat{t},\hat{s},m_T^2,m_t^2,m_t^2,m_t^2),\\ D_0^{tT}(\hat{u},\hat{s})\equiv& D_0(m_h^2,0,0,m_h^2,\hat{u},\hat{s},m_T^2,m_t^2,m_t^2,m_t^2),\\ D_0^{tT}(\hat{t},\hat{u})\equiv& D_0(m_h^2,0,m_h^2,0,\hat{t},\hat{u},m_t^2,m_T^2,m_T^2,m_t^2), \end{aligned} $

and
$ \tag{A4} \begin{aligned}[b] C_0^{Tt}(m_h^2)\equiv& C_0(m_h^2,m_h^2,\hat{s},m_T^2,m_t^2,m_T^2),\\ C_0^{Tt}(\hat{t})\equiv& C_0(0,m_h^2,\hat{t},m_T^2,m_T^2,m_t^2),\\ C_0^{Tt}(\hat{u})\equiv& C_0(0,m_h^2,\hat{u},m_T^2,m_T^2,m_t^2),\\ D_0^{Tt}(\hat{t},\hat{s})\equiv& D_0(m_h^2,0,0,m_h^2,\hat{t},\hat{s},m_t^2,m_T^2,m_T^2,m_T^2),\\ D_0^{Tt}(\hat{u},\hat{s})\equiv& D_0(m_h^2,0,0,m_h^2,\hat{u},\hat{s},m_t^2,m_T^2,m_T^2,m_T^2),\\ D_0^{Tt}(\hat{t},\hat{u})\equiv& D_0(m_h^2,0,m_h^2,0,\hat{t},\hat{u},m_T^2,m_t^2,m_t^2,m_T^2). \end{aligned} $

(A4) In fact, we have the relationship
$ D_0^{tT}(\hat{t},\hat{u}) = $ $ D_0^{Tt}(\hat{t},\hat{u}) $ . -
$ C_0 $ function is defined as$ \tag{A5} \begin{aligned}[b]& C_0(k_1^2,k_{12}^2,k_2^2,m_0^2,m_1^2,m_2^2)\\ \equiv& \frac{(2\pi\mu)^{4-D}}{{\rm i}\pi^2}\int {\rm d}^Dq\frac{1}{(q^2-m_0^2)[(q+k_1)^2-m_1^2][(q+k_2)^2-m_2^2]}\\ =& -\int_0^1\!\!\int_0^1\!\!\int_0^1{\rm d}x{\rm d}y{\rm d}z\frac{\delta(x+y+z-1)}{xm_0^2+ym_1^2+zm_2^2-xyk_1^2-xzk_2^2-yzk_{12}^2}, \end{aligned} $

(A5) where
$ k_{12}\equiv k_1-k_2 $ and D is the dimension of space time. When the three internal masses are all equal, the$ C_0 $ function can be expanded as [86]$ \tag{A6} \begin{aligned}[b]& C_0(k_1^2,k_{12}^2,k_2^2,m_t^2,m_t^2,m_t^2)\\ =& -\int_0^1\int_0^1\int_0^1{\rm d}x{\rm d}y{\rm d}z\frac{\delta(x+y+z-1)}{m_t^2-xyk_1^2-xzk_2^2-yzk_{12}^2}\\ =& -\frac{1}{2m_t^2}-\frac{k_1^2+k_2^2+k_{12}^2}{24m_t^4}-\frac{k_1^4+k_2^4+k_{12}^4+k_1^2k_2^2+k_1^2k_{12}^2+k_2^2k_{12}^2}{180m_t^6}\\&+{\cal{O}}\left(\frac{k^6}{m_t^8}\right). \end{aligned} $

(A6) In particular, we obtain the following results:
$ \tag{A7} \begin{aligned}[b] C_0^t(\hat{s})\approx&-\frac{1}{2m_t^2}\left(1+\frac{\hat{s}}{12m_t^2}+\frac{\hat{s}^2}{90m_t^4}\right),\\ C_0^t(m_h^2)\approx&-\frac{1}{2m_t^2}\left(1+\frac{2m_h^2+\hat{s}}{12m_t^2}+\frac{3m_h^4+2m_h^2\hat{s}+\hat{s}^2}{90m_t^4}\right),\\ C_0^t(\hat{t})\approx&-\frac{1}{2m_t^2}\left(1+\frac{m_h^2+\hat{t}}{12m_t^2}+\frac{m_h^4+m_h^2\hat{t}+\hat{t}^2}{90m_t^4}\right). \end{aligned} $

(A7) The expansion of
$ C_0^t(\hat{u}) $ functions can be obtained when replacing the$ \hat{t} $ in$ C_0^t(\hat{t}) $ with$ \hat{u} $ . The expansion of$ C_0^T $ functions can be obtained when replacing the$ m_t $ in$ C_0^t $ with$ m_T $ .When the first two internal masses are equal, the
$ C_0 $ function can be expanded as:$ \tag{A8} \begin{aligned}[b] C_0(k_1^2,k_{12}^2,k_2^2,m_t^2,m_t^2,m_T^2) =& -\int_0^1\int_0^1\int_0^1{\rm d}x{\rm d}y{\rm d}z\frac{\delta(x+y+z-1)}{(x+y)m_t^2+zm_T^2-xyk_1^2-xzk_2^2-yzk_{12}^2}\\ =& -\int_0^1\int_0^1\int_0^1{\rm d}x{\rm d}y{\rm d}z\frac{\delta(x+y+z-1)}{(x+y)m_t^2+zm_T^2}\left[1+\frac{xyk_1^2+xzk_2^2+yzk_{12}^2}{(x+y)m_t^2+zm_T^2}+\frac{(xyk_1^2+xzk_2^2+yzk_{12}^2)^2}{((x+y)m_t^2+zm_T^2)^2}\right]+{\cal{O}}\left(\frac{k^6}{m_{t,T}^8}\right)\\ \approx& \frac{1+\log r_{tT}^2-r_{tT}^2}{m_T^2(1-r_{tT}^2)^2}-\frac{2+6r_{tT}^2\log r_{tT}^2+3r_{tT}^2-6r_{tT}^4+r_{tT}^6}{12m_T^4r_{tT}^2(1-r_{tT}^2)^4}k_1^2\\&+\frac{5+2(1+2r_{tT}^2)\log r_{tT}^2-4r_{tT}^2-r_{tT}^4}{4m_T^4(1-r_{tT}^2)^4}(k_2^2+k_{12}^2)\\ & -\frac{3-30r_{tT}^2-20r_{tT}^4(1+3\log r_{tT}^2)+60r_{tT}^6-15r_{tT}^8+2r_{tT}^{10}}{180m_T^6r_{tT}^4(1-r_{tT}^2)^6}k_1^4\\ & +\frac{10+9r_{tT}^2+3(1+6r_{tT}^2+3r_{tT}^4)\log r_{tT}^2-18r_{tT}^4-r_{tT}^6}{9m_T^6(1-r_{tT}^2)^6}(k_{12}^4+k_2^2k_{12}^2+k_2^4)\\ & -\frac{3+44r_{tT}^2+12r_{tT}^2(2+3r_{tT}^2)\log r_{tT}^2-36r_{tT}^4-12r_{tT}^6+r_{tT}^8}{36m_T^6r_{tT}^2(1-r_{tT}^2)^6}k_1^2(k_2^2+k_{12}^2). \end{aligned} $ 
(A8) When the first and third internal masses are equal, the
$ C_0 $ function can be correlated with the first two mass equal cases via the following relationships:$ \tag{A9} \begin{aligned}[b]& C_0(k_1^2,k_{12}^2,k_2^2,m_t^2,m_T^2,m_t^2) = C_0(k_2^2,k_{12}^2,k_1^2,m_t^2,m_t^2,m_T^2),\\& C_0(k_1^2,k_{12}^2,k_2^2,m_T^2,m_t^2,m_T^2) = C_0(k_2^2,k_{12}^2,k_1^2,m_T^2,m_T^2,m_t^2). \end{aligned} $

In particular, we obtain the following results:
$ \tag{A10} \begin{aligned}[b] C_0^{tT}(\hat{t})\approx&\frac{1}{m_T^2}\cdot\frac{1+\log r_{tT}^2-r_{tT}^2}{(1-r_{tT}^2)^2}+\frac{m_h^2+\hat{t}}{m_T^4}\cdot\frac{5+2(1+2r_{tT}^2)\log r_{tT}^2-4r_{tT}^2-r_{tT}^4}{4(1-r_{tT}^2)^4}\\& +\frac{m_h^4+m_h^2\hat{t}+\hat{t}^2}{m_T^6}\cdot\frac{10+3(1+6r_{tT}^2+3r_{tT}^4)\log r_{tT}^2+9r_{tT}^2-18r_{tT}^4-r_{tT}^6}{9(1-r_{tT}^2)^6},\\ C_0^{tT}(m_h^2)\approx&\frac{1}{m_T^2}\cdot\frac{1+\log r_{tT}^2-r_{tT}^2}{(1-r_{tT}^2)^2}-\frac{\hat{s}}{m_T^4}\cdot\frac{2+6r_{tT}^2\log r_{tT}^2+3r_{tT}^2-6r_{tT}^4+r_{tT}^6}{12r_{tT}^2(1-r_{tT}^2)^4}\\ & +\frac{m_h^2}{m_T^4}\cdot\frac{5+2(1+2r_{tT}^2)\log r_{tT}^2-4r_{tT}^2-r_{tT}^4}{2(1-r_{tT}^2)^4}+\frac{m_h^4}{m_T^6}\cdot\frac{10+3(1+6r_{tT}^2+3r_{tT}^4)\log r_{tT}^2+9r_{tT}^2-18r_{tT}^4-r_{tT}^6}{3(1-r_{tT}^2)^6}\\& -\frac{m_h^2\hat{s}}{m_T^6}\cdot\frac{3+12r_{tT}^2(2+3r_{tT}^2)\log r_{tT}^2+44r_{tT}^2-36r_{tT}^4-12r_{tT}^6+r_{tT}^8}{18r_{tT}^2(1-r_{tT}^2)^6}\\& -\frac{\hat{s}^2}{m_T^6}\cdot\frac{3-30r_{tT}^2-60r_{tT}^4\log r_{tT}^2-20r_{tT}^4+60r_{tT}^6-15r_{tT}^8+2r_{tT}^{10}}{180r_{tT}^4(1-r_{tT}^2)^6}. \end{aligned} $

(A10) Maintaining the terms up to
$ {\cal{O}}\left(\dfrac{1}{m_T^4}\right) $ , and considering the$ \log r_{tT}^2 $ enhanced terms, they can be simplified as$ \tag{A11} \begin{aligned}[b] C_0^{tT}(\hat{t})\approx&\frac{1}{m_T^2}\big[1+\log r_{tT}^2+r_{tT}^2(1+2\log r_{tT}^2)+\frac{m_h^2+\hat{t}}{4m_T^2}(5+2\log r_{tT}^2)\big],\\ C_0^{tT}(m_h^2)\approx&\frac{1}{m_T^2}\big[1+\log r_{tT}^2+r_{tT}^2(1+2\log r_{tT}^2)-\frac{\hat{s}}{12m_T^2}\left(\frac{2}{r_{tT}^2}+11+6\log r_{tT}^2\right)+\frac{m_h^2}{2m_T^2}(5+2\log r_{tT}^2)\big]. \end{aligned} $

(A11) Similarly, we can obtain the following results
$ \tag{A12} \begin{aligned}[b] C_0^{Tt}(\hat{t})\approx&-\frac{1}{m_T^2}\cdot\frac{1+r_{tT}^2\log r_{tT}^2-r_{tT}^2}{(1-r_{tT}^2)^2}-\frac{m_h^2+\hat{t}}{m_T^4}\cdot\frac{1+2r_{tT}^2(2+r_{tT}^2)\log r_{tT}^2+4r_{tT}^2-5r_{tT}^4}{4(1-r_{tT}^2)^4}\\& -\frac{m_h^4+m_h^2\hat{t}+\hat{t}^2}{m_T^6}\cdot\frac{1+3r_{tT}^2(3+6r_{tT}^2+r_{tT}^4)\log r_{tT}^2+18r_{tT}^2-9r_{tT}^4-10r_{tT}^6}{9(1-r_{tT}^2)^6},\\ C_0^{Tt}(m_h^2)\approx&-\frac{1}{m_T^2}\cdot\frac{1+r_{tT}^2\log r_{tT}^2-r_{tT}^2}{(1-r_{tT}^2)^2}-\frac{\hat{s}}{m_T^4}\cdot\frac{1-6r_{tT}^2-6r_{tT}^4\log r_{tT}^2+3r_{tT}^4+2r_{tT}^6}{12(1-r_{tT}^2)^4}\\ & -\frac{m_h^2}{2m_T^4}\cdot\frac{1+2r_{tT}^2(2+r_{tT}^2)\log r_{tT}^2+4r_{tT}^2-5r_{tT}^4}{(1-r_{tT}^2)^4}-\frac{m_h^4}{m_T^6}\cdot\frac{1+3r_{tT}^2(3+6r_{tT}^2+r_{tT}^4)\log r_{tT}^2+18r_{tT}^2-9r_{tT}^4-10r_{tT}^6}{3(1-r_{tT}^2)^6}\\& -\frac{m_h^2\hat{s}}{m_T^6}\cdot\frac{1-12r_{tT}^2-12r_{tT}^4(3+2r_{tT}^2)\log r_{tT}^2-36r_{tT}^4+44r_{tT}^6+3r_{tT}^8}{18(1-r_{tT}^2)^6}\\& -\frac{\hat{s}^2}{m_T^6}\cdot\frac{2-15r_{tT}^2+60r_{tT}^4+60r_{tT}^6\log r_{tT}^2-20r_{tT}^6-30r_{tT}^8+3r_{tT}^{10}}{180(1-r_{tT}^2)^6}. \end{aligned} $

(A12) Keeping the terms up to
$ {\cal{O}}\left(\dfrac{1}{m_T^4}\right) $ , and considering the$ \log r_{tT}^2 $ -enhanced terms, they can be simplified as$ \tag{A13} \begin{aligned}[b] C_0^{Tt}(\hat{t})\approx-\frac{1}{m_T^2}\left[1+r_{tT}^2(1+\log r_{tT}^2)+\frac{m_h^2+\hat{t}}{4m_T^2}\right],\quad\quad C_0^{Tt}(m_h^2)\approx-\frac{1}{m_T^2}\left[1+r_{tT}^2(1+\log r_{tT}^2)+\frac{\hat{s}}{12m_T^2}+\frac{m_h^2}{2m_T^2}\right]. \end{aligned} $

(A13) -
$ D_0 $ function is defined as$ \tag{A14} \begin{aligned}[b]& D_0(k_1^2,k_{12}^2,k_{23}^2,k_3^2,k_2^2,k_{13}^2,m_0^2,m_1^2,m_2^2,m_3^2) \\\equiv& \frac{(2\pi\mu)^{4-D}}{i\pi^2}\int {\rm d}^Dq\frac{1}{(q^2-m_0^2)[(q+k_1)^2-m_1^2][(q+k_2)^2-m_2^2][(q+k_3)^2-m_3^2]}\\ =& \int_0^1\int_0^1\int_0^1\int_0^1{\rm d}x{\rm d}y{\rm d}z{\rm d}w\frac{\delta(x+y+z+w-1)}{[xm_0^2+ym_1^2+zm_2^2+wm_3^2-xyk_1^2-xzk_2^2-xwk_3^2-yzk_{12}^2-ywk_{13}^2-zwk_{23}^2]^2}, \end{aligned} $

(A14) where
$ k_{12}\equiv k_1-k_2 $ ,$ k_{23}\equiv k_2-k_3 $ , and$ k_{13}\equiv k_1-k_3 $ . When the four internal masses are all equal, the$ D_0 $ function can be expanded as [86]$ \tag{A15} \begin{aligned}[b] D_0(k_1^2,k_{12}^2,k_{23}^2,k_3^2,k_2^2,k_{13}^2,m_t^2,m_t^2,m_t^2,m_t^2) =& \int_0^1\int_0^1\int_0^1\int_0^1{\rm d}x{\rm d}y{\rm d}z{\rm d}w\frac{\delta(x+y+z+w-1)}{[m_t^2-xyk_1^2-xzk_2^2-xwk_3^2-yzk_{12}^2-ywk_{13}^2-zwk_{23}^2]^2}\\ =& \frac{1}{6m_t^4}\Bigg[1+\frac{k_1^2+k_{12}^2+k_{23}^2+k_3^2+k_2^2+k_{13}^2}{10m_t^2}+\frac{1}{140m_t^4}\Big(2(k_1^4+k_2^4+k_3^4+k_1^2k_2^2+k_1^2k_3^2+k_2^2k_3^2)\\ & +2(k_{12}^4+k_{13}^4+k_{23}^4+k_{12}^2k_{13}^2+k_{12}^2k_{23}^2+k_{13}^2k_{23}^2)+2k_1^2(k_{12}^2+k_{13}^2)+2k_2^2(k_{12}^2+k_{23}^2)\\ &+2k_3^2(k_{13}^2+k_{23}^2) +(k_1^2k_{23}^2+k_2^2k_{13}^2+k_3^2k_{12}^2)\Big)+{\cal{O}}\left(\frac{k^6}{m_t^6}\right)\Bigg]. \end{aligned} $

(A15) In particular, we obtain the following results:
$\tag{A16} \begin{aligned}[b] D_0^t(\hat{t},\hat{s})\approx&\frac{1}{6m_t^4}\left[1+\frac{2m_h^2+\hat{s}+\hat{t}}{10m_t^2}+\frac{6m_h^4+4m_h^2(\hat{s}+\hat{t})+2\hat{s}^2+2\hat{t}^2+\hat{s}\hat{t}}{140m_t^4}\right],\\ D_0^t(\hat{t},\hat{u})\approx&\frac{1}{6m_t^4}\left[1+\frac{2m_h^2+\hat{t}+\hat{u}}{10m_t^2}+\frac{5m_h^4+4m_h^2(\hat{t}+\hat{u})+2\hat{t}^2+2\hat{u}^2+\hat{t}\hat{u}}{140m_t^4}\right]. \end{aligned} $

(A16) The expansion of
$ D_0^t(\hat{u},\hat{s}) $ can be obtained when replacing the$ \hat{t} $ in$ D_0^t(\hat{t},\hat{s}) $ with$ \hat{u} $ . The expansion of$ D_0^T $ functions can be obtained when replacing the$ m_t $ in$ D_0^t $ with$ m_T $ .When three internal masses are equal, the
$ D_0 $ function can be expanded as$ \tag{A17} \begin{aligned}[b]& D_0(k_1^2,k_{12}^2,k_{23}^2,k_3^2,k_2^2,k_{13}^2,m_T^2,m_t^2,m_t^2,m_t^2)\\ =& \int_0^1\int_0^1\int_0^1\int_0^1{\rm d}x{\rm d}y{\rm d}z{\rm d}w\frac{\delta(x+y+z+w-1)}{[xm_T^2+(y+z+w)m_t^2-xyk_1^2-xzk_2^2-xwk_3^2-yzk_{12}^2-ywk_{13}^2-zwk_{23}^2]^2}\\ =& \int_0^1\!\int_0^1\!\int_0^1\!\int_0^1\!{\rm d}x{\rm d}y{\rm d}z{\rm d}w\frac{\delta(x+y+z+w-1)}{[xm_T^2+(y+z+w)m_t^2]^2}\left[1\!+\!\frac{2(xyk_1^2+xzk_2^2+xwk_3^2+yzk_{12}^2+ywk_{13}^2+zwk_{23}^2)}{xm_T^2+(y+z+w)m_t^2}\right]\!+\!{\cal{O}}\left(\frac{k^4}{m_{t,T}^8}\right)\\ \approx& \frac{1}{m_T^4}\cdot\frac{1+2r_{tT}^2\log r_{tT}^2-r_{tT}^4}{2r_{tT}^2(1-r_{tT}^2)^3}+\frac{(k_1^2+k_2^2+k_3^2)}{m_T^6}\cdot\frac{1+6r_{tT}^2(1+r_{tT}^2)\log r_{tT}^2+9r_{tT}^2-9r_{tT}^4-r_{tT}^6}{6r_{tT}^2(1-r_{tT}^2)^5}\\ &+\frac{(k_{12}^2+k_{23}^2+k_{13}^2)}{m_T^6}\cdot\frac{1-8r_{tT}^2-12r_{tT}^4\log r_{tT}^2+8r_{tT}^6-r_{tT}^8}{24r_{tT}^4(1-r_{tT}^2)^5}. \end{aligned} $

(A17) We only expand this equation up to
$ {\cal{O}}\left(\dfrac{k^2}{m_{t,T}^6}\right) $ , because the general results will be relatively lengthy. For the integral$ D_0^{tT}(\hat{t},\hat{s}) $ , we obtain the expression up to$ {\cal{O}}\left(\dfrac{k^4}{m_{t,T}^8}\right) $ $\tag{A18} \begin{aligned}[b] D_0^{tT}(\hat{t},\hat{s}) = & \int_0^1\int_0^1\int_0^1\int_0^1{\rm d}x{\rm d}y{\rm d}z{\rm d}w\frac{\delta(x+y+z+w-1)}{[xm_T^2+(y+z+w)m_t^2-x(y+w)m_h^2-xzt-yws]^2}\\ =& \int_0^1\int_0^1\int_0^1\int_0^1{\rm d}x{\rm d}y{\rm d}z{\rm d}w\frac{\delta(x+y+z+w-1)}{[xm_T^2+(y+z+w)m_t^2]^2}\cdot \left(1+\frac{2[x(y+w)m_h^2+xzt+yws]}{xm_T^2+(y+z+w)m_t^2}+\frac{3[x(y+w)m_h^2+xzt+yws]^2}{[xm_T^2+(y+z+w)m_t^2]^2}\right)\\&+{\cal{O}}\left(\frac{1}{m_{t,T}^{10}}\right) \approx \frac{1}{m_T^4}\cdot\frac{1+2r_{tT}^2\log r_{tT}^2-r_{tT}^4}{2r_{tT}^2(1-r_{tT}^2)^3}+\frac{(2m_h^2+\hat{t})}{m_T^6}\cdot\frac{1+6r_{tT}^2(1+r_{tT}^2)\log r_{tT}^2+9r_{tT}^2-9r_{tT}^4-r_{tT}^6}{6r_{tT}^2(1-r_{tT}^2)^5}\\& +\frac{\hat{s}}{m_T^6}\cdot\frac{1-8r_{tT}^2-12r_{tT}^4\log r_{tT}^2+8r_{tT}^6-r_{tT}^8}{24r_{tT}^4(1-r_{tT}^2)^5} +\frac{\hat{s}^2}{m_T^8}\cdot\frac{1-9r_{tT}^2+45r_{tT}^4-45r_{tT}^8+9r_{tT}^{10}-r_{tT}^{12}+60r_{tT}^6\log r_{tT}^2}{180r_{tT}^6(1-r_{tT}^2)^7}\\& +\frac{\hat{s}(\hat{t}+4m_h^2)}{m_T^8}\cdot\frac{1-15r_{tT}^2-80r_{tT}^4+80r_{tT}^6+15r_{tT}^8-r_{tT}^{10}-60r_{tT}^4(1+r_{tT}^2)\log r_{tT}^2}{120r_{tT}^4(1-r_{tT}^2)^7}\\ & +\frac{\hat{t}^2+2m_h^2\hat{t}+3m_h^4}{m_T^8}\cdot\frac{1+28r_{tT}^2-28r_{tT}^6-r_{tT}^8+12r_{tT}^2(1+3r_{tT}^2+r_{tT}^4)\log r_{tT}^2}{12r_{tT}^2(1-r_{tT}^2)^7}. \end{aligned} $

(A18) Keeping the terms up to
$ {\cal{O}}\left(\dfrac{1}{m_T^6}\right) $ , and considering the$ \log r_{tT}^2 $ enhanced terms, they can be simplified as$\tag{A19} \begin{aligned}[b] D_0^{tT}(\hat{t},\hat{s})\approx&\frac{1}{2m_T^4}\left[\frac{1}{r_{tT}^2}+3+2\log r_{tT}^2+r_{tT}^2(5+6\log r_{tT}^2)\right]+\frac{(2m_h^2+\hat{t})}{6m_T^6}\left(\frac{1}{r_{tT}^2}+6\log r_{tT}^2+14\right)\\ & +\frac{\hat{s}}{24m_T^6}\left(\frac{1}{r_{tT}^4}-\frac{3}{r_{tT}^2}-12\log r_{tT}^2-25\right). \end{aligned} $

(A19) Similarly, we can obtain the following results:
$ \tag{A20} \begin{aligned}[b] D_0^{Tt}(\hat{t},\hat{s})\approx&\frac{1}{m_T^4}\cdot\frac{1+2r_{tT}^2\log r_{tT}^2-r_{tT}^4}{2(1-r_{tT}^2)^3}+\frac{(2m_h^2+\hat{t})}{m_T^6}\cdot \frac{1+9r_{tT}^2+6r_{tT}^2(1+r_{tT}^2)\log r_{tT}^2-9r_{tT}^4-r_{tT}^6}{6(1-r_{tT}^2)^5}\\& +\frac{\hat{s}}{m_T^6}\cdot\frac{1-8r_{tT}^2-12r_{tT}^4\log r_{tT}^2+8r_{tT}^6-r_{tT}^8}{24(1-r_{tT}^2)^5} +\frac{\hat{s}^2}{m_T^8}\cdot\frac{1-9r_{tT}^2+45r_{tT}^4-45r_{tT}^8+9r_{tT}^{10}-r_{tT}^{12}+60r_{tT}^6\log r_{tT}^2}{180(1-r_{tT}^2)^7}\\& +\frac{\hat{s}(\hat{t}+4m_h^2)}{m_T^8}\cdot\frac{1-15r_{tT}^2-80r_{tT}^4+80r_{tT}^6+15r_{tT}^8-r_{tT}^{10}-60r_{tT}^4(1+r_{tT}^2)\log r_{tT}^2}{120(1-r_{tT}^2)^7}\\ & +\frac{\hat{t}^2+2m_h^2\hat{t}+3m_h^4}{m_T^8}\cdot\frac{1+28r_{tT}^2-28r_{tT}^6-r_{tT}^8+12r_{tT}^2(1+3r_{tT}^2+r_{tT}^4)\log r_{tT}^2}{12(1-r_{tT}^2)^7}. \end{aligned} $

(A20) Keeping the terms up to
$ {\cal{O}}\left(\dfrac{1}{m_T^6}\right) $ , and considering the$ \log r_{tT}^2 $ -enhanced terms, they can be simplified as:$\tag{A21} D_0^{Tt}(\hat{t},\hat{s})\approx\frac{1}{2m_T^4}(1+3r_{tT}^2+2r_{tT}^2\log r_{tT}^2)+\frac{2m_h^2+\hat{t}}{6m_T^6}+\frac{\hat{s}}{24m_T^6}. $

(A21) When two internal masses are equal individually, we obtain the following relationships:
$ \tag{A22} \begin{aligned}[b] D_0(k_1^2,k_{12}^2,k_{23}^2,k_3^2,k_2^2,k_{13}^2,m_t^2,m_T^2,m_T^2,m_t^2) =& D_0(k_1^2,k_3^2,k_{23}^2,k_{12}^2,k_{13}^2,k_2^2,m_T^2,m_t^2,m_t^2,m_T^2)\\ =& D_0(k_{23}^2,k_3^2,k_1^2,k_{12}^2,k_2^2,k_{13}^2,m_T^2,m_t^2,m_t^2,m_T^2). \end{aligned} $

(A22) $ D_0 $ function can be expanded as:$ \tag{A23} \begin{aligned}[b] &D_0(k_1^2,k_{12}^2,k_{23}^2,k_3^2,k_2^2,k_{13}^2,m_t^2,m_T^2,m_T^2,m_t^2)\\ =& \int_0^1\int_0^1\int_0^1\int_0^1{\rm d}x{\rm d}y{\rm d}z{\rm d}w\frac{\delta(x+y+z+w-1)}{[(y+z)m_T^2+(x+w)m_t^2-xyk_1^2-xzk_2^2-xwk_3^2-yzk_{12}^2-ywk_{13}^2-zwk_{23}^2]^2}\\ =& \int_0^1\!\int_0^1\!\int_0^1\!\int_0^1\!{\rm d}x{\rm d}y{\rm d}z{\rm d}w\frac{\delta(x+y+z+w-1)}{[(y+z)m_T^2+(x+w)m_t^2]^2}\left[1\!+\!\frac{2(xyk_1^2+xzk_2^2+xwk_3^2+yzk_{12}^2+ywk_{13}^2+zwk_{23}^2)}{(y+z)m_T^2+(x+w)m_t^2}\right]\!+\!{\cal{O}}\left(\frac{k^4}{m_{t,T}^8}\right)\\ \approx& -\frac{1}{m_T^4}\cdot\frac{2+(1+r_{tT}^2)\log r_{tT}^2-2r_{tT}^2}{(1-r_{tT}^2)^3}-\frac{k_1^2+k_2^2+k_{13}^2+k_{23}^2}{m_T^6}\cdot\frac{3+(1+4r_{tT}^2+r_{tT}^4)\log r_{tT}^2-3r_{tT}^4}{2(1-r_{tT}^2)^5}\\& +\frac{k_3^2}{m_T^6}\cdot\frac{1+6r_{tT}^2(1+r_{tT}^2)\log r_{tT}^2+9r_{tT}^2-9r_{tT}^4-r_{tT}^6}{6r_{tT}^2(1-r_{tT}^2)^5}+\frac{k_{12}^2}{m_T^6}\cdot\frac{1+6r_{tT}^2(1+r_{tT}^2)\log r_{tT}^2+9r_{tT}^2-9r_{tT}^4-r_{tT}^6}{6(1-r_{tT}^2)^5}. \end{aligned} $

(A23) We only expand it up to
$ {\cal{O}}\left(\dfrac{k^2}{m_{t,T}^6}\right) $ , because the general results will be relatively lengthy. For the integral$ D_0^{tT}(\hat{t},\hat{u}) $ , we obtain the expression up to$ {\cal{O}}\left(\dfrac{k^4}{m_{t,T}^8}\right) $ $ \tag{A24} \begin{aligned}[b] D_0^{tT}(\hat{t},\hat{u}) =& \int_0^1\int_0^1\int_0^1\int_0^1{\rm d}x{\rm d}y{\rm d}z{\rm d}w\frac{\delta(x+y+z+w-1)}{[(x+w)m_t^2+(y+z)m_T^2-(xy+zw)m_h^2-xzt-ywu]^2}\\ =& \int_0^1\int_0^1\int_0^1\int_0^1{\rm d}x{\rm d}y{\rm d}z{\rm d}w\frac{\delta(x+y+z+w-1)}{[(x+w)m_t^2+(y+z)m_T^2]^2}\cdot\\ & \left(1+\frac{2[(xy+zw)m_h^2+xzt+ywu]}{(x+w)m_t^2+(y+z)m_T^2}+\frac{3[(xy+zw)m_h^2+xzt+ywu]^2}{[(x+w)m_t^2+(y+z)m_T^2]^2}\right)+{\cal{O}}\left(\frac{1}{m_{t,T}^{10}}\right)\\ \approx& -\frac{1}{m_T^4}\cdot\frac{2+(1+r_{tT}^2)\log r_{tT}^2-2r_{tT}^2}{(1-r_{tT}^2)^3}-\frac{2m_h^2+\hat{t}+\hat{u}}{m_T^6}\cdot\frac{3+(1+4r_{tT}^2+r_{tT}^4)\log r_{tT}^2-3r_{tT}^4}{2(1-r_{tT}^2)^5}\\& - \frac{5m_h^4+4m_h^2(\hat{t}+\hat{u})+2\hat{t}^2+\hat{t}\hat{u}+2\hat{u}^2}{m_T^8}\cdot\frac{11+27r_{tT}^2-27r_{tT}^4-11r_{tT}^6+3(1+9r_{tT}^2+9r_{tT}^4+r_{tT}^6)\log r_{tT}^2}{18(1-r_{tT}^2)^7}. \end{aligned} $

(A24) Keeping the terms up to
$ {\cal{O}}\left(\dfrac{1}{m_T^4}\right) $ , and considering the$ \log r_{tT}^2 $ enhanced terms, they can be simplified as$\tag{A25}\begin{aligned}[b] D_0^{tT}(\hat{t},\hat{u})\approx-\frac{1}{m_T^4}\Big[2+\log r_{tT}^2+4r_{tT}^2(1+\log r_{tT}^2)\Big]-\frac{4m_h^2-\hat{s}}{2m_T^6}(3+\log r_{tT}^2).\end{aligned} $

(A25) In the above calculations, the t and T quark mixed
$ C_0 $ and$ D_0 $ integrals will agree with the pure top quark integrals in the limit of$ m_t=m_T $ (or$ r_{tT}\rightarrow1 $ ). In addition, these expansion results have been numerically verified by LoopTools [107].
Di-Higgs production as a probe of flavor changing neutral Yukawa couplings
- Received Date: 2021-03-26
- Available Online: 2021-07-15
Abstract: Top partners are well motivated in many new physics models. Usually, vector like quarks,






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF































 DownLoad:
DownLoad: