Abstract
HTML
Reference
Related
PDF
-
The allowed regions for the neutrino oscillation parameters, including neutrino mass squared differences, leptonic mixing angles, and the Dirac CP violating phase, taken from Ref. [1], are shown in Table 1. This confirms that the Standard Model (SM) must be extended to explain these experimental data.
Parameters NormalHierarchy(NH) 
Invertedhierarchy(IH) 
bfp±1σ 
bfp±1σ 
sin2θ12 
0.318±0.016 
0.318±0.016 
sin2θ23 
0.574±0.014 
0.578+0.010−0.017 
sin2θ1310−2 
2.200+0.069−0.062 
2.225+0.064−0.070 
δCP/π 
1.08+0.13−0.12 
1.58+0.15−0.16 
Δm22110−5eV2 
7.50+0.22−0.20 
7.50+0.22−0.20 
|Δm231|10−3eV2 
2.55+0.02−0.03 
2.45+0.02−0.03 
Table 1. Neutrino oscillation parameters taken from Ref. [1].
Among various extensions of the SM, the
B−L gauge model [2-21] is a promising candidate because it can explain various phenomena, such as the neutrino mass [14], leptogenesis [7, 21], dark matter [9-13, 16], the muon anomalous magnetic moment [14], gravitational wave radiation [8], and inflation [20]. However, by itself, this model cannot give a natural explanation for fermion mixing. Non-Abelian discrete symmetries have shown many outstanding advantages in explaining the observed patterns of fermion masses and mixing, and have been widely used in literature.An observed lepton mixing scenario can be successfully described using the cobimaximal mixing pattern (a pattern that predicts
θ13≠0,θ23=π4 andδCP=−π2 ), which has recently gained wider attention [22-29]. In order to explain the cobimaximal neutrino mixing pattern, alternative discrete symmetries have been used [22-29] with more than oneSU(2)L Higgs doublet. However, the cobimaximal neutrino mixing pattern has not previously been considered in models withQ4 symmetry. There are substantial differences between previous studies and this study regarding the explanation of the cobimaximal neutrino mixing pattern [22-29], namely, the cobimaximal lepton mixing form obtained withA4 symmetry and threeSU(2)L Higgs doublets in the lepton sector with a general neutrino mass matrix [23], in one loop with the symmetryZ2×A4×Z2×U(1)D and twoSU(2)L Higgs doublets [24], with the symmetryS3×Z2 and twoSU(2)L doublets [25], with the symmetryS3×Z2 and fourSU(2)L doublets [26], with the symmetryU(1)X×U(1)L×U(1)D×Δ(27)× Z2×Z3 and threeSU(2)L doublets [27], with the symmetryU(1)X×Δ(27)×Z4×RL and fourSU(2)L doublets [28], and with the symmetryΔ(27)×Z2×Z10 and twoSU(2)L doublets [29]. In this study, we suggest a non-renormalizable gaugeB−L model based on the flavor symmetryQ4×Z4×Z2 in which the first family of the left-handed lepton (ψ1L ) is put in12 while the two others (ψ2,3L ) are put in2 ofQ4 . For the right-handed leptons, the first family (l1R ) is put in14 while the two others (l2,3R ) are put in2 ofQ4 . For the right-handed neutrinos, the first family (ν1R ) is put in11 while the two others (ν2,3R ) are put in2 ofQ4 . As a result, the neutrino mass hierarchies, the tiny neutrino masses, and the cobimaximal lepton mixing pattern are generated at tree-level.Q4 is the smallest group of the binary dihedral groupQN withN=4 , whose five irreducible representations are denoted as1k(k=1,2,3,4) and2 , which are presented in Refs. [30-33]. We will consider the two-dimensional representation2 ofQ4 to be pseudo-real [30-33], i.e.,2∗(a∗1,a∗2)=2(a∗2,−a∗1) , and its basic tensor product rule is2(a1,a2)⊗2(b1,b2)=11(a1b2−a2b1)⊕12(a1b1−a2b2)⊕13(a1b1+a2b2)⊕14(a1b2+a2b1).
This paper is organized as follows. In Section II, we present the particle content as well as the lepton sector of the model. Section III deals with the numerical analysis, and Section IV contains our conclusions.
-
In this study, the
B−L model [14, 17] is supplemented byQ4×Z4×Z2 symmetry; the total symmetry of our model isΓ≡SU(3)C×SU(2)L×U(1)Y×U(1)B−L× Q4×Z4×Z2 . Moreover, threeSU(2)L singlet scalars (χ,ρ,η ) withB−L=0 and oneSU(2)L singlet scalar (φ ) withB−L=2 are added to theB−L model particle content to describe the observed lepton mixing. The particle content of the model is summarized in Table 2.Fields ψ1L 
ψαL 
l1R 
lαR 
ν1R 
ναR 
H χ 
ρ 
η 
ϕ 
φ 
SU(3)C 
1 
1 
1 
1 
1 
1 
1 
1 
1 
1 
1 
1 
SU(2)L 
2 
2 
1 
1 
1 
1 
2 
1 
1 
1 
1 
1 
U(1)Y 
−12 
−12 
−1 
−1 
0 
0 
12 
0 
0 
0 
0 
0 
U(1)B−L 
−1 
−1 
−1 
−1 
−1 
−1 
0 
0 
0 
0 
2 
2 
Q4 
12 
2 
14 
2 
11 
2 
11 
13 
14 
2 
11 
12 
Z4 
1 
1 
−i 
−i 
i i i 1 
1 
1 
−1 
−1 
Z2 
+ 
+ 
− 
− 
+ 
+ 
− 
+ 
− 
− 
+ 
+ 
Table 2. Particle and scalar content of the model (
α=2,3 ).The scalar potential minimum condition, as shown in Appendix A, yields the vacuum expectation value (VEV) of scalars.
⟨H⟩=(0vH)T,⟨χ⟩=vχ,⟨ρ⟩=vρ,⟨η⟩=(⟨η1⟩,⟨η2⟩),⟨η1⟩=⟨η2⟩=vη,⟨ϕ⟩=vϕ,⟨φ⟩=(⟨φ1⟩,⟨φ2⟩),⟨φ1⟩=⟨φ2⟩=vφ.
(1) From the particle content given in Table 2 and the tensor products of
Q4 , the charged lepton masses can arise from the couplings ofˉψ(1,α)Ll(1,α)R to scalars, whereˉψ1Ll1R transform to(1,2,−12,0,13,−i,−) ,ˉψ1LlαR∼ˉψαLl1R ∼(1,2,−12,0,2,−i,−) , andˉψαLlαR∼(1,2,−12, 0,11⊕12 ⊕13 ⊕14,−i,−) . Thus, to generate masses for the charged leptons, we require oneSU(2)L doublet H and oneSU(2)L singletχ placed in11 and13 underQ4 , respectively. The Yukawa interactions in the charged lepton sector are−LclepY=xcl1Λ(ˉψ1Ll1R)13(Hχ)13+xcl2(ˉψαLlαR)11H+xcl3Λ(ˉψαLlαR)13(Hχ)13+H.c.
(2) It is noted that
(¯ψ1Ll1R)H is forbidden by theZ4 symmetry;(¯ψ1Ll1R)Hρ and(¯ψ1Ll1R)Hη are forbidden by theQ4 symmetry;(¯ψ1Ll1R)Hϕ and(¯ψ1Ll1R)Hφ are forbidden by two symmetries,Q4 andB−L ;(¯ψ1LlαR)H and(¯ψ1LlαR)Hχ are forbidden by theQ4 symmetry;(¯ψ1LlαR)Hρ is forbidden by theQ4 andZ2 symmetries;(¯ψ1LlαR)Hη is forbidden by theZ2 symmety;(¯ψ1LlαR)Hϕ and(¯ψ1LlαR)Hφ are forbidden by three symmetries,Q4,Z4 , andB−L ;(¯ψαLlαR)Hρ and(¯ψαLlαR)Hη are forbidden by two symmetries,Q4 andZ2 ; and(¯ψαLlαR)Hϕ and(¯ψαLlαR)Hφ are forbidden by three symmetries,Q4,Z4 , andB−L . In the charged-lepton sector, the invariant Yukawa interactions are shown in Eq. (2). With the help of Eq. (1), the Lagrangian mass term of the charged leptons can be written in the form−Lmassl=(ˉl1L,ˉl2L,ˉl3L)Ml(l1R,l2R,l3R)T+H.c,
(3) where
Ml=(al000bl−cl0clbl),
(4) with
al=xcl1ΛvHvχ,bl=xcl2vH,cl=xcl3ΛvHvχ.
(5) Let us first define a Hermitian matrix
ml , given byml=M+LML=(αl000βliγl0−iγlβl),
(6) where
αl=a20l,βl=b20l+c20l,γl=2b0lc0lsinφl,
(7) and
φl=φb−φc,a0l=|al|,b0l=|bl|,c0l=|cl| , andφb= arg(bl),φc=arg(cl) .The matrix
ml can be diagonalized byuL,R , satisfyingu+LmluR=diag(m2e,m2μ,m2τ) , whereuL=uR=1√2(√2000ii0−11),
(8) m2e=αl,m2μ,τ=βl∓γl.
(9) Comparing the obtained result in Eq. (9) with the experimental values of the charged lepton masses at the weak scale taken from Ref. [34],
me=0.51099MeV,mμ= 105.65837MeV,mτ=1776.86MeV , we getαl=0.261MeV,βl=1.58×106MeV,γl=1.57×106MeV.
(10) Regarding the neutrino sector, the Dirac mass terms are generated from the couplings of
ˉψiLνjR(i,j=1,2,3) to scalars, whereˉψ1Lν1R∼(1,2,12,0,12,i,+) ,ˉψ1LναR∼ˉψαLν1R ∼(1,2,12,0,2,i,+) , andˉψαLναR∼(1,2,12,0,11⊕ 12⊕13⊕14, i,+) . The Majorana neutrino masses are generated from the couplings ofˉνciRνjR(i,j=1,2,3) to scalars, whereˉνc1Rν1R∼(1,1,0,−2,11,−1,+) ,ˉνc1RναR∼ˉνcαRν1R∼(1,1,0,−2, 2,−1,+) , andˉνcαRναR∼(1,1,0,−2,11⊕12⊕13⊕ 14,−1,+) . The Yukawa interactions in the neutrino sector are−LνY=x1νΛ(ˉψ1LναR+ˉψαLν1R)2(˜Hη)2+x2νΛ(ˉψαLναR)13(˜Hρ)13+y1ν2(ˉνc1Rν1R)ϕ+y2ν2(ˉνcαRναR)12φ+H.c.
(11) In the neutrino sector,
(¯ψ1Lν1R)˜H and(¯ψ1Lν1R)˜Hχ are forbidden by two symmetries,Q4 andZ2 ;(¯ψ1Lν1R)˜Hρ and(¯ψ1Lν1R)˜Hη are forbidden by theQ4 symmetry;(¯ψ1Lν1R)˜Hϕ is forbidden by four symmetries,Q4,Z4,Z2,B−L ;(¯ψ1Lν1R)˜Hφ is forbidden by three symmetriesZ4,Z2 , andB−L .(¯ψ1LναR)˜H and(¯ψ1LναR)˜Hχ are forbidden by two symmetries,Q4 andZ2 ;(¯ψ1LναR)˜Hρ is forbidden by theQ4 symmetry;(¯ψ1LναR)˜Hϕ and(¯ψ1LναR)˜Hφ are forbidden by four symmetries,Q4,Z4,Z2 , andB−L .(¯ψαLναR)˜H and(¯ψαLναR)˜Hχ are forbidden by theZ2 symmetry;(¯ψαLναR)˜Hη is forbidden by theQ4 symmetry;(¯ψαLναR)˜Hϕ and(¯ψαLναR)˜Hφ are forbidden by three symmetries,Z4,Z2 , andB−L . Furthermore,(¯νc1Rν1R)H is forbidden by four symmetries,Y,B−L,Z4 , andZ2 ;(¯νc1Rν1R)χ is forbidden by three symmetries,B−L,Q4 , andZ4 ;(¯νc1Rν1R)ρ and(¯νc1Rν1R)η are forbidden by four symmetries,B−L,Q4,Z4 , andZ2 ; and(¯νc1Rν1R)φ is forbidden by theQ4 symmetry.(¯νc1RναR)H is forbidden by five symmetries,Y,B−L,Q4,Z4 , andZ2 ;(¯νc1RναR)χ is forbidden by three symmetries,B−L,Q4 , andZ4 ;(¯νc1RναR)ρ and(¯νc1RναR)η are forbidden by four symmetries,B−L,Q4,Z4 , andZ2 ; and(¯νc1RναR)φ and(¯νc1RναR)ϕ are forbidden by theQ4 symmetry.(¯νcαRναR)H is forbidden by four symmetries,Y,B−L,Z4 , andZ2 ;(¯νcαRναR)χ is forbidden by two symmetries,B−L andZ4 ;(¯νcαRναR)ρ is forbidden by three symmetries,B−L,Z4 , andZ2 ; and(¯νcαRναR)η is forbidden by four symmetries,B−L,Q4,Z4 , andZ2 . All other terms of the form(¯νc1Rν1R)Φ,(¯νc1RναR)Φ , and(¯νcαRναR)Φ , whereΦ are the combinations of scalar fields such asHχ,Hρ,Hη,Hϕ,Hφ;χρ,χη,χϕ,χφ , are forbidden by one or some of the model's symmetries. In addition,(¯νcαRναR)11ϕ=(¯νc2Rν3R−¯νc3Rν2R)11ϕ=0 . For the neutrino sector, the invariant Yukawa interactions are shown in Eq. (11).With the VEVs given in Eq. (1), we obtain the Dirac and Majorana neutrino mass matrices using the following:
MD=(0−aDaDaD0bDaDbD0),MR=(aR000bR000−bR),
(12) where
aD=x1νΛvHvη,bD=x2νΛvHvρ,aR=y1νvϕ,bR=y2νvφ.
(13) The effective neutrino mass matrix is obtained through the type-I seesaw mechanism as follows:
Meff=−MDM−1RMTD=(0aDbDbR−aDbDbRaDbDbRb2DbR−a2DaRa2DaR−aDbDbRa2DaR−a2DaR−b2DbR).
(14) The mass matrix
Meff in Eq. (14) has three eigenvalues:m1=0,m2,3=−α∓β,
(15) with
α=a2DaR,β=√a4Db2R+a2Rb2D(2a2D+b2D)aRbR.
(16) The corresponding mixing matrix is
K=(κ√κ2+2κ1√κ21+τ21+1κ2√κ22+τ22+1−1√κ2+2τ1√κ21+τ21+1τ2√κ22+τ22+1−1√κ2+21√κ21+τ21+11√κ22+τ22+1),
(17) where
κ,κ1,2 , andτ1,2 are given byκ=bDaD,κ1,2=2aDaRbDaRb2D+a2DbR±√Ω,τ1,2=±√Ω−aR(a2D+b2D)a2D(aR−bR),Ω=a4Db2R+a2Rb2D(2a2D+b2D),
(18) which satisfy the following relations:
1+κ1κ2+τ1τ2=0,1−κκ1+τ1=0,1−κκ2+τ2=0.
(19) Whether the neutrino mass spectrum has a normal or inverted hierarchy depends on the sign of
Δm231 [34]. For NH,0=m1≪m2∼m3 . For IH,0=m3≪m1∼m2 . The neutrino mass matrixMeff in Eq. (14) is diagonalized asuTνMeffuν={(0000−α−β000−α+β),uν=(κ√κ2+2κ1√κ21+τ21+1κ2√κ22+τ22+1−1√κ2+2τ1√κ21+τ21+1τ2√κ22+τ22+1−1√κ2+21√κ21+τ21+11√κ22+τ22+1)forNH,(−α−β000−α+β0000),uν=(κ1√κ21+τ21+1κ2√κ22+τ22+1κ√κ2+2τ1√κ21+τ21+1τ2√κ22+τ22+1−1√κ2+21√κ21+τ21+11√κ22+τ22+1−1√κ2+2)forIH, (20) where
α,β ,κ,κ1,2 , andτ1,2 are given in Eqs. (16) and (19). The corresponding leptonic mixing matrix is defined as follows:ULep=u†Luν={(κ√κ2+2κ1√κ21+τ21+1κ2√κ22+τ22+1i+1√2√κ2+2−1+iτ1√2√κ21+τ21+1−1+iτ2√2√κ22+τ22+1i−1√2√κ2+21−iτ1√2√κ21+τ21+11−iτ2√2√κ22+τ22+1)forNH,(κ1√κ21+τ21+1κ2√κ22+τ22+1κ√κ2+2−1+iτ1√2√κ21+τ21+1−1+iτ2√2√κ22+τ22+1i+1√2√κ2+21−iτ1√2√κ21+τ21+11−iτ2√2√κ22+τ22+1i−1√2√κ2+2)forIH.
(21) In the three neutrino oscillation picture [34-37], the leptonic Jarlskog invariant
JCP , which determines the magnitude of CP violation in neutrino oscillations and the lepton mixing angles, is obtained as follows:JCP=Im(U23U∗13U12U∗22)=s12c12s13c213s23c23sinδ,
(22) s213=|U13|2,t212=|U12U11|2,t223=|U23U23|2,
(23) where
tij=sijcij,sij=sinθij,cij=cosθij(ij=12,23) withθ12 ,θ23 , andθ13 are the solar angle, atmospheric angle, and reactor angle, respectively.Combining Eqs. (21), (22), and (23) yields
κ22(τ22−1)2(κ22+τ22+1)(2κ22+(τ2+1)2)=s12c12s13c213s23c23sinδ,
(24) s213=κ22κ22+τ22+1,t212=κ22(τ2−1)2(τ2+1)2(κ22+τ22+1),t223=1.
(25) Solving the system of equations in (24)-(25), with the help of Eq. (19), we obtain a solution
θ23=π4,sinδ=−1(δ=−π2),
(26) κ={−√2c13√s213+t212forNH,√2t13forIH,κ1={−√2c13t12√s213+t212s13t12(s13+t12)+s13−t12forNH,√2c13s13−t12forIH,κ2={√2t13√t212+s213t12+s13forNH,√2c13t12(s13t12+1)32forIH,
(27) τ1={−2c213t12s13t12(s13+t12)+s13−t12−1forNH,s13+t12s13−t12forIH,τ2={2s13s13+t12−1forNH,1−2s13t12+1forIH,JCP=−12s12c12s13c213forbothNHandIH.
(28) Equation (20) implies that
α,β , and neutrino masses can be expressed in terms of two squared mass differencesΔm221 andΔm232 ,α={−12(√Δm231+√Δm221)forNH,√Δm231−√Δm221−Δm2312forIH,
(29) β={12(√Δm231−√Δm221)forNH,Δm2212(√Δm221−Δm231−√Δm231)forIH.
(30) {m1=0,m2=√Δm221,m3=√Δm231forNH,m1=√−Δm231,m2=√Δm221−Δm231,m3=0forIH. (31) ∑νmν≡3∑i=1mi={√Δm221+√Δm231forNH,√−Δm231+√Δm221−Δm231forIH.
(32) The effective neutrino masses governing the beta decay (
mβ ) and neutrinoless double beta decay (⟨mee⟩ ) [38-42] have the formsmβ=(3∑i=1|Uei|2m2i)12={√Δm221s212c213+Δm231s213forNH,c13√(Δm221−Δm231)s212−Δm231c212forIH,
(33) ⟨mee⟩=|3∑i=1U2eimi|={√Δm221s212c213+√Δm231s213forNH,c213(√−Δm231c212+√Δm221−Δm231s212)forIH.
(34) Equations (27)-(34) show that
κ,κ1,2,τ1,2 , andJCP depend on two experimental parametersθ12 andθ13 ;α,β ,m2,3 (NH),m1,2 (IH), and∑νmν depend on two squared mass differencesΔm221 andΔm231 ; andmβ,⟨mee⟩ depend on four parametersθ12,θ13,Δm221 , andΔm231 in whichθ12,θ13,Δm221 , andΔm231 have been measured with relatively high precision [1]. The sign ofΔm231 is now undetermined and allows for two possible types of neutrino mass spectra. -
Expression (27) implies that
κ,κ1,2 , andτ1,2 depend on two experimental parameterss12 ands13 , which are plotted in Figs. 1 and 2, respectively, within a1σ range of the best-fit values taken from Ref. [1]; these ares12∈(0.550,0.578) ands13∈(0.146,0.151) for NH ands13∈(0.147,0.151) for IH. Figures 1 and 2 show the ranges ofκ,κ1,2 , andτ1,2 :
Figure 1. (color online)
κ andκ1,2 as functions ofs12 ands13 withs12∈(0.550,0.578) ands13∈(0.146,0.151) for NH (left panel) ands13∈(0.147,0.151) for IH (right panel).
Figure 2. (color online)
τ1,2 as functions ofs12 ands13 withs12∈(0.550,0.578) ands13∈(0.146,0.151) for NH (left panel) ands13∈(0.147,0.151) for IH (right panel).κ∈{(1.94,2.06)forNH,(0.210,0.216)forIH,κ1∈{(1.44,1.52)forNH,(−2.75,−2.50)forIH,
κ2∈{(0.176,0.181)forNH,(0.84,0.89)forIH,τ1∈{(1.93,2.01)forNH,(−1.59,−1.53)forIH,τ2∈{(−0.655,−0.630)forNH,(−0.822,−0.808)forIH.
(35) Expression (28) implies that
JCP depends on two parameterss12 ands13 , which is plotted in Fig. 3 withs12∈(0.550,0.578) ands13∈(0.146,0.151) for NH ands13∈(0.147,0.151) for IH. This shows that our model predicts a Jarlskog invariant range ofJCP∈(−3.46, −3.30)10−2 for NH andJCP∈(−3.48,−3.30)10−2 for IH.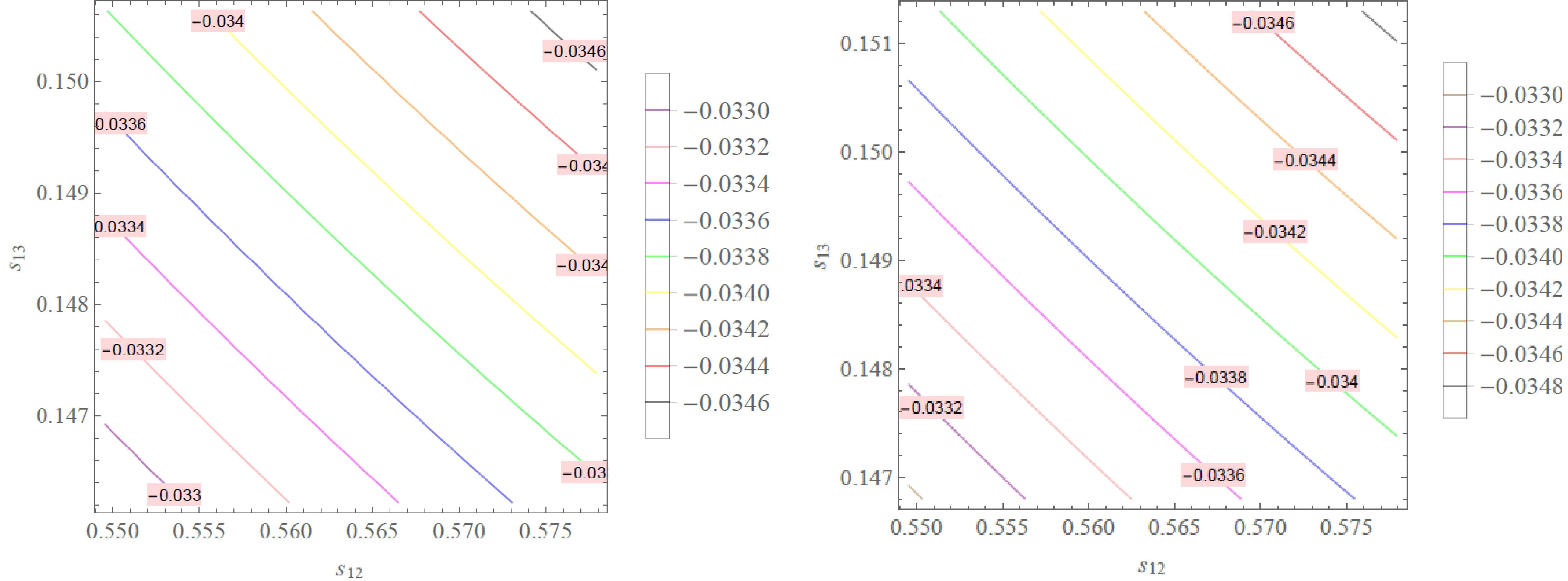
Figure 3. (color online)
JCP as a function ofs12 ands13 withs12∈(0.550,0.578) ands13∈(0.146,0.151) for NH (left panel) ands13∈(0.147,0.151) for IH (right panel).Expressions (30)-(32) show that
α,β , and neutrino massesm2,3 (NH),m1,2 (IH) as well as the sum of neutrino masses∑νmν depend onΔm221 andΔm231 , which are plotted in Figs. 4, 5, and 6, respectively, within a1σ range of the best-fit values taken from Ref. [1]. These areΔm221∈(7.30,7.72)×10−5eV2 andΔm231∈(2.52,2.57) ×10−3eV2 for NH andΔm231∈(−2.47,−2.42)×10−3eV2 for IH. Figure 4 shows that the ranges ofα andβ are as follows:
Figure 4. (color online)
α andβ as functions ofΔm221 andΔm231 withΔm221∈(7.30,7.72)×10−5eV2 andΔm231∈(2.52,2.57)×10−3eV2 for NH (left panel) andΔm231∈(−2.47,−2.42)×10−3eV2 for IH (right panel).
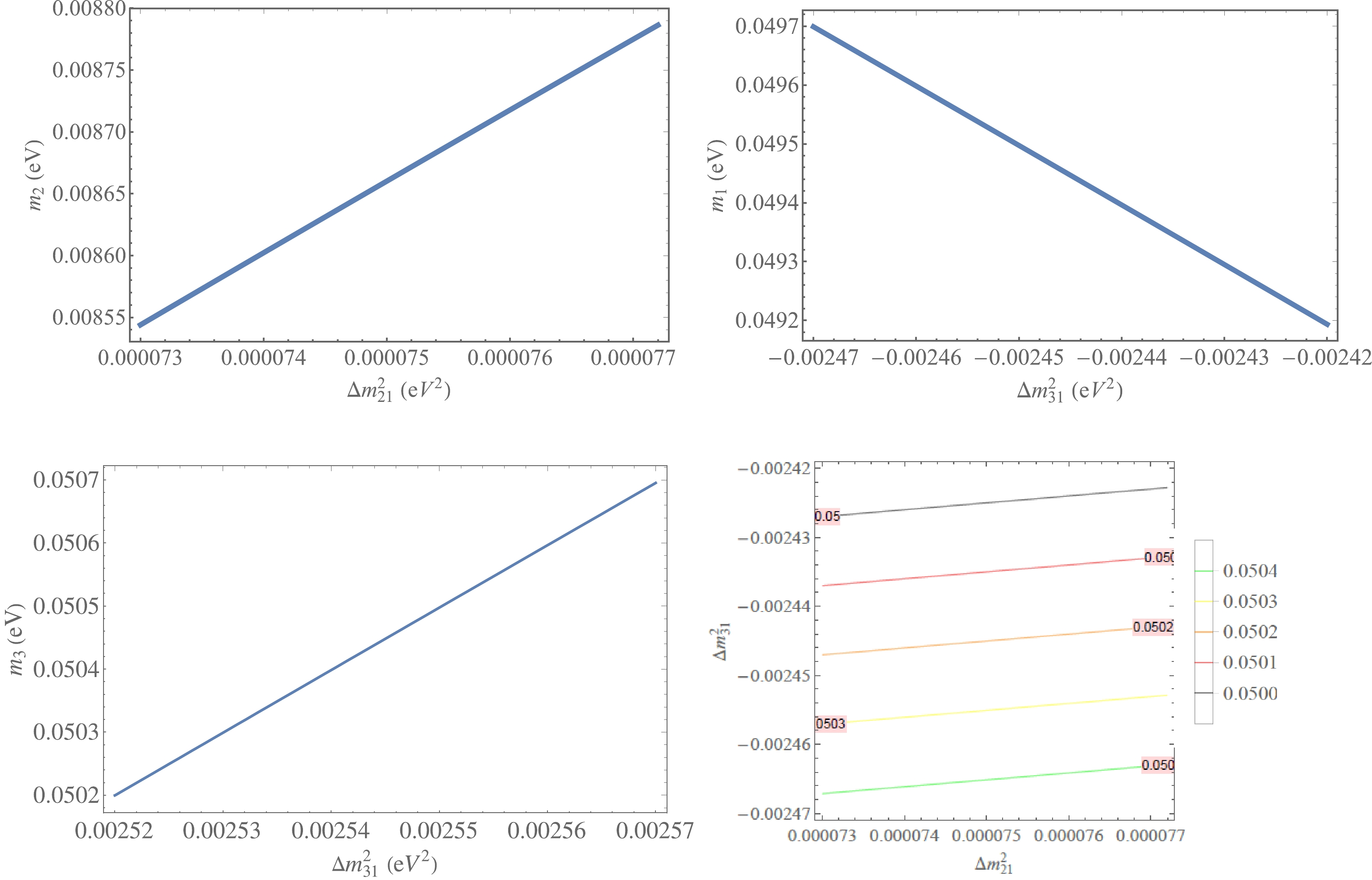
Figure 5. (color online)
m2(m3) as a function ofΔm221(Δm231) for NH (left panel) andm1 as a function ofΔm231 andm2 as a function ofΔm221 andΔm231 for IH (right panel) withΔm221∈(7.30,7.72)×10−5eV2 andΔm231∈(2.52,2.57)×10−3eV2 for NH andΔm231∈(−2.47,−2.42)×10−3eV2 for IH.
Figure 6. (color online)
∑νmν as a function ofΔm221 andΔm231 withΔm221∈(7.30,7.72)×10−5eV2 andΔm231∈(2.52,2.57)×10−3eV2 for NH (left panel) andΔm231∈(−2.47,−2.42)×10−3eV2 for IH (right panel).α∈{(−2.97,−2.94)×10−2eVforNH,(−5.00,−4.96)×10−2eVforIH,
(36) β∈{(2.075,2.105)×10−2eVforNH,(3.65,3.88)×10−4eVforIH.
(37) Figure 5 shows that our model predicts the range of neutrino masses.
{m2∈(8.55,8.80)×10−3eV,m3∈(5.02,5.07)×10−2eVforNH,m1∈(4.92,4.97)×10−2eV,m2∈(5.00,5.04)×10−2eVforIH.
(38) Figure 6 shows that our model predicts the range of the sum of neutrino masses.
∑νmν∈{(5.88,5.94)×10−2eVforNH,(9.92×10−2,10−1)eVforIH.
(39) By taking the best-fit values of neutrino mass squared splittings for NH [1], as given in Table 1,
Δm221= 7.50×10−5eV2,Δm231=2.55×10−3eV2 , we obtainα={−2.96×10−2eVforNH,−4.99×10−2eVforIH,β={2.09×10−2eVforNH,3.76×10−4eVforIH.
(40) These produce the following neutrino masses:
{m1=0,m2=8.66×10−3eV,m3=5.05×10−2eVforNH,m1=4.95×10−2eV,m2=5.02×10−2eV,m3=0forIH.
(41) The sum of the neutrino masses has the explicit values
∑m3i=1={5.92×10−2eVforNH,9.97×10−2eVforIH.
(42) At present, there are various bounds on
∑mi ; for instance, for NH, the upper limit on the sum of the neutrino masses is∑mi<0.13eV at a2σ range [1], the strongest bound from cosmology [43] is∑mν<0.078eV , the upper bound taken from [44] is∑mν<0.12÷0.69eV , and the constraint in Ref. [45] is∑mν<0.118eV . For IH, the tightest2σ upper limit is∑mi<0.15eV [1], and the upper limit taken from [46] is∑mν<1.1eV . Therefore, the prediction of our model in Eq. (39) is in good agreement.Expressions (33) and (34) imply that
mβ and⟨mee⟩ depend on four experimental parametersΔm221,Δm231,s12 , ands13 . At the best-fit points of the two neutrino mass-squared differences, two neutrino effective masses⟨mee⟩ andmβ depend on two parameterss12 ands13 , which is plotted in Fig. 7 withs12∈(0.550,0.578) ands13∈(0.146,0.151) for NH ands13∈ (0.147, 0.151) for IH. This shows that our model predicts the range of the effective neutrino mass parameters as follows: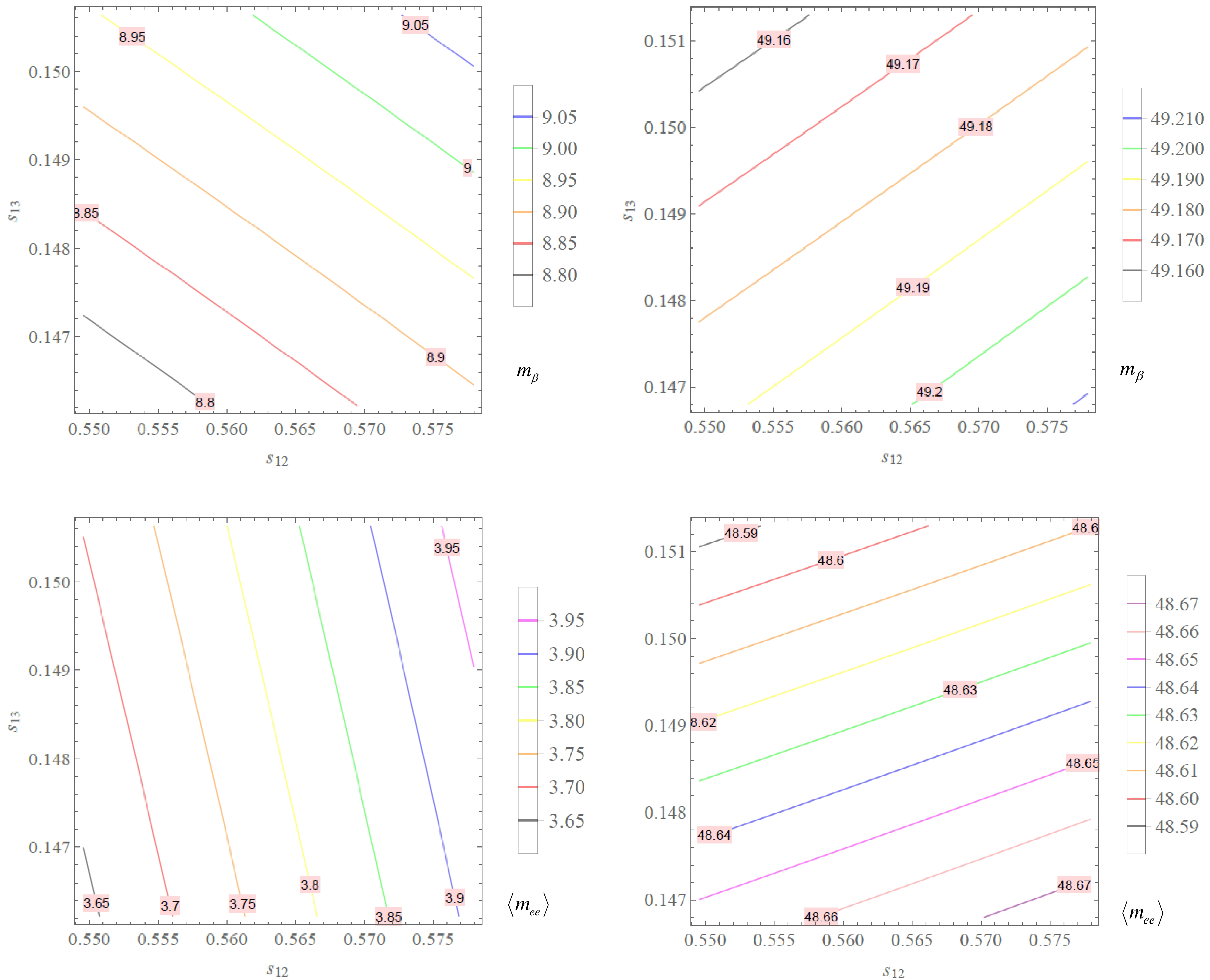
Figure 7. (color online)
mβ and⟨mee⟩ (in meV) as functions ofs12 ands13 withs12∈(0.550,0.578) ands13∈(0.146,0.151) for NH (left panel) ands13∈(0.147,0.151) for IH (right panel).mβ(meV)∈{(8.80,9.05)forNH,(49.16,49.21)forIH,
(43) ⟨mee⟩(meV)∈{(3.65,3.95)forNH,(48.59,48.67)forIH.
(44) At the best-fit points of
s12 ands13 taken from [1], as given in Table 1, we obtainκ={2.00forNH,0.213forIH,κ1={1.48forNH,−2.62forIH,κ2={0.178forNH,0.867forIH,τ1={1.97forNH,−1.56forIH,τ2={−0.643forNH,−0.815forIH,
(45) JCP={−3.38×10−2forNH,−3.40×10−2forIH,
(46) mβ={8.91meVforNH,49.20meVforIH,
⟨mee⟩={3.80meVforNH,48.60meVforIH.
(47) The corresponding mixing matrices are
ULep={(0.8170.5580.1480.289+0.289i−0.266−0.523i−0.588+0.378i−0.289+0.289i0.266−0.523i0.588+0.378i)forNH,(−0.8170.5580.149−0.220+0.344i−0.445+0.371i0.494+0.494i0.220+0.344i0.445+0.371i−0.494+0.494i)forIH, (48) which are unitary and in good agreement with the entry constraint of the lepton mixing matrix in Ref. [47].
Global data analyses [44, 47] show that
δCP is close to−π2 , and the best fit value ofδCP in [47, 48] is close to−π2 for both NH and IH. ForδCP andθ23 , as shown in Eq. (26), our model predictsδCP=−π2 andθ23=π4 , respectively, which are consistent with the cobimaximal mixing pattern and within the3σ range of the best-fit values taken from Ref. [1]. The resulting effective neutrino mass parameters in Eq. (47) are below the upper bound arising from present0νββ decay experiments; however, they are highly consistent with the future large and ultra-low background liquid scintillator detectors, which have been discussed in Ref. [49]. ThemeV limit of the effective neutrino mass can be reached by planning future experiments [43, 50-56]. -
We have constructed a non-renormalizable gauge
B−L model based onQ4×Z4×Z2 symmetry that leads to the successful cobimaximal lepton mixing scheme. Small active neutrino masses and both neutrino mass hierarchies are produced via the type-I seesaw mechanism at the tree-level. The model is predictive; hence, it reproduces the cobimaximal lepton mixing scheme, and the reactor neutrino mixing angleθ13 and the solar neutrino mixing angleθ12 can obtain best-fit values from recent experimental data. Our model also predicts the effective neutrino mass parameters ofmβ∈(8.80,9.05)meV and⟨mee⟩∈(3.65,3.95)meV for normal ordering (NO) andmβ∈(49.16,49.21)meV and⟨mee⟩∈(48.59,48.67)meV for inverted ordering (IO), which are highly consistent with recent experimental constraints. -
The total scalar potential invariant under all of the model's symmetries is given by①
Vtotal=V(H)+V(χ)+V(ρ)+V(η)+V(ϕ)+V(φ)+V(H,χ)+V(H,ρ)+V(H,η)+V(H,ϕ)+V(H,φ)+V(χ,ρ)+V(χ,η)+V(χ,ϕ)+V(χ,φ)+V(ρ,η)+V(ρ,ϕ)+V(ρ,φ)+V(η,ϕ)+V(η,φ)+V(ϕ,φ)+Vmultiple, where②
V(H)=μ2H(H†H)11+λH(H†H)11(H†H)11,
V(χ)=μ2χχ2+λχ1χ4+λχ2(χ∗χ)12(χ∗χ)12,V(ρ)=V(χ→ρ),
V(η)=μ2η(η∗η)11+λη1(ηη)13(ηη)13+λη2(ηη)14(ηη)14+λη3(η∗η)11(η∗η)11+λη4(η∗η)12(η∗η)12,
V(ϕ)=μ2ϕ(ϕ∗ϕ)11+λϕ(ϕ∗ϕ)11(ϕ∗ϕ)11,V(φ)=V(ϕ→φ),V(H,χ)=λHχ1(H†H)11(χ2)11+λHχ2(H†χ)13(χH)13,V(H,ρ)=λHρ1(H†H)11(ρ2)11+λHρ2(H†ρ)14(ρH)14,
V(H,η)=λHη1(H†H)11(η∗η)11+λHη2(H†η)2(η∗H)2,V(H,ϕ)=λHϕ1(H†H)11(ϕ∗ϕ)11+λHϕ2(H†ϕ)11(ϕ∗H)11,V(H,φ)=λHφ1(H†H)11(φ∗φ)11+λHφ2(H†φ)12(φ∗H)12,
V(χ,ρ)=λχρ1χ2ρ2+λχρ2(χρ)12(ρχ)12+λχρ3(χ∗χ)12(ρ∗ρ)12+λχρ4(χ∗ρ)11(ρ∗χ)11,
V(χ,η)=λχη1χ2(η∗η)11+λχη2(χ∗χ)12(η∗η)12+λχη3(χη∗)2(ηχ)2+λχη4(χ∗η)2(η∗χ)2,
V(χ,ϕ)=λχϕ1χ2(ϕ∗ϕ)11+λχϕ2(χϕ)13(ϕ∗χ)13,V(χ,φ)=λχφ1χ2(φ∗φ)11+λχφ2(χφ)14(φ∗χ)14,
V(ρ,η)=λρη1ρ2(η∗η)11+λρη2(ρ∗ρ)12(η∗η)12+λρη3(ρη∗)2(ηρ)2+λρη4(ρ∗η)2(η∗ρ)2,
V(ρ,ϕ)=λρϕ1ρ2(ϕ∗ϕ)11+λρϕ2(ρϕ)14(ϕ∗ρ)14,V(ρ,φ)=λρφ1ρ2(φ∗φ)11+λρφ2(ρφ)13(φ∗ρ)13,
V(η,ϕ)=ληϕ1(η∗η)11(ϕ∗ϕ)11+ληϕ2(η∗ϕ)2(ϕ∗η)2,V(η,φ)=V(η,ϕ→φ),
V(ϕ,φ)=λϕφ1(ϕ∗ϕ)11(φ∗φ)11+λϕφ2(ϕ∗φ)12(φ∗ϕ)12,Vmultiple=0.
All the other terms with three or more different scalars are forbidden by one or some of the model's symmetries. For cubic couplings, ten couplings of H and two different scalars in the set of
{χ,ρ,η,ϕ,φ} are prevented by theU(1)Y symmetry; four couplingsχρη,χϕφ,ρϕ∗φ andηϕ∗φ are forbidden by theQ4 symmetry; and six couplingsχρϕ,χρφ,χηϕ,χηφ,ρηϕ andρηφ are prevented by theU(1)B−L symmetry. For quartic couplings, ten couplings of H and three different scalars in the set of{χ,ρ,η,ϕ,φ} are prevented by theU(1)Y symmetry; four couplingsχρηϕ,χρηφ,χηϕφ , andρηϕφ are forbidden by theQ4 symmetry; and the couplingχρϕ∗φ is prevented by theZ2 symmetry. For quintic couplings, five couplings of H and four different scalars in the set of{χ,ρ,η,ϕ,φ} are prevented by theU(1)Y symmetry; the couplingχρηϕ∗φ is forbidden by theQ4 symmetry; andH+Hϕ∗φχ andH+Hϕ∗φρ are prevented by theQ4 symmetry.To show that the scalar fields with the VEV alignments in Eq. (1) are natural solutions of the minimum condition of
Vscalar in Eqs. (A1)-(A13), we putv∗H=vH,v∗χ=vχ,v∗ρ=vρ,vη1=vη2=vη,v∗η=vη,v∗ϕ=vϕ andv∗φ=vφ , which leads to∂Vscalar∂v∗j=Vscalar∂vj,∂2Vscalar∂v∗2j= Vscalar∂v2j(vj=vH,vχ,vρ,vη,vϕ,vφ) , and the minimization condition ofVscalar reduces to∂Vscalar∂vj=0,∂2Vscalar∂v2j>0.
For simplicity, we use the following notations:
λχ=λχ1+λχ2,λρ=λρ1+λρ2,λη=4∑k=1ληk,λHχ=λHχ1+λHχ2,λχρ=4∑k=1λχρk,λHρ=λHρ1+λHρ2,λHη=λHη2−λHη1,λHϕ=λHϕ1+λHϕ2,λHφ=λHφ1+λHφ2,λχη=λχη1+λχη2+λχη3−λχη4,λχϕ=λχϕ1+λχϕ2,λχφ=λχφ1+λχφ2,λρη=λρη1+λρη2+λρη3−λρη4,λρϕ=λρϕ1+λρϕ2,λρφ=λρφ1+λρφ2,ληφ=ληφ1+ληφ2,ληϕ=ληϕ1+ληϕ2,λϕφ=λϕφ1+λϕφ2. Thus, the minimization conditions in Eq. (A14) reduce to
μ2H+2λHφv2φ+λHχv2χ+2λHηv2η+2λHv2H+λHϕv2ϕ+λHρv2ρ=0,
μ2χ+λχφv2φ+2λχv2χ−2λχηv2η+λHχv2H+λχϕv2ϕ+λχρv2ρ=0,
μ2ρ+λρφv2φ+λχρv2χ−2λρηv2η+λHρv2H+λρϕv2ϕ+2λρv2ρ=0,
2μ2η+2(ληφv2φ+λχηv2χ−4ληv2η−λHηv2H+ληϕv2ϕ)+2λρηv2ρ=0,
μ2ϕ+λϕφv2φ+λχϕv2χ−2ληϕv2η+λHϕv2H+2λϕv2ϕ+λρϕv2ρ=0,
μ2φ+2λφv2φ+λχφv2χ−2ληφv2η+2λHφv2H+λϕφv2ϕ+λρφv2ρ=0,
μ2H+2λHφv2φ+λHχv2χ+2λHηv2η+6λHv2H+λHϕv2ϕ+λHρv2ρ>0,
μ2χ+λχφv2φ+6λχv2χ−2λχηv2η+λHχv2H+λχϕv2ϕ+λχρv2ρ>0,
μ2ρ+λρφv2φ+λχρv2χ−2λρηv2η+λHρv2H+λρϕv2ϕ+6λρv2ρ>0,
−2μ2η−2(ληφv2φ+λχηv2χ−12ληv2η−λHηv2H+ληϕv2ϕ)−2λρηv2ρ>0,
μ2ϕ+λϕφv2φ+λχϕv2χ−2ληϕv2η+λHϕv2H+6λϕv2ϕ+λρϕv2ρ>0,
μ2φ+6λφv2φ+λχφv2χ−2ληφv2η+2λHφv2H+λϕφv2ϕ+λρφv2ρ>0.
The system of Eqs. (A16)–(A21) always have the following solutions:
λH=−(λHχv2χ+2λHηv2η+λHϕv2ϕ+λHρv2ρ+2λHφv2φ+μ2H)/(2v2H),
λχ=−(μ2χ+λχφv2φ−2λχηv2η+λHχv2H+λχϕv2ϕ+λχρv2ρ)/(2v2χ),
λρ=−(μ2ρ+λρφv2φ+λχρv2χ−2λρηv2η+λHρv2H+λρϕv2ϕ)/(2v2ρ),
λη=(μ2η+ληφv2φ+λχηv2χ−λHηv2H+ληϕv2ϕ+λρηv2ρ)/(4v2η),
λϕ=−(μ2ϕ+λϕφv2φ+λχϕv2χ−2ληϕv2η+λHϕv2H+λρϕv2ρ)/(2v2ϕ),
λφ=−(μ2φ+λχφv2χ−2ληφv2η+2λHφv2H+λϕφv2ϕ+λρφv2ρ)/(2v2φ).
Next, with
λH,λχ,λρ,λη,λϕ , andλφ in Eqs. (A28)–(A33), there exist possible regions of the model's parameters such that the inequalities (A22)–(A27) are always satisfied by the solution, as shown in Eq. (1). For instance, with the benchmark pointvH≃vχ≃vρ≃vη≃1011eV,vφ≃vϕ=1012eV,
μ2H≃μ2χ≃μ2ρ≃μ2η≃μ2ϕ≃μ2φ=−1016eV2,
λχη=λρη=ληϕ=ληφ=−λρφ=−λHχ=−λHη=−λHρ=−λHϕ=−λHφ=−λρϕ=−λχϕ=−λχρ=−λχφ=λ0,
the expressions in (A22)–(A27) are always satisfied in the case of
λ0∈(10−4,10−2) , which is shown in Fig. A1. Therefore, the VEVs in Eq. (1) are natural solutions of the potential minimum condition.
A non-renormalizable B-L model with Q4 × Z4 × Z2 flavor symmetry for cobimaximal neutrino mixing
- Received Date: 2021-08-13
- Available Online: 2021-12-15
Abstract: We construct a non-renormalizable gauge
DownLoad: