-
Two-proton (
$ 2p $ ) radioactivity was firstly predicted by Zel'dovich in 1960s, followed by the description of this process given by Goldansky [1-4]. Subsequently, a great deal of effort on experiments and/or theories have been devoted to exploring the probable$ 2p $ radioactivity phenomena, which opens a new window for study of the decay modes and ground-state masses of exotic nuclei near or beyond the proton drip line [5-19]. Moreover, the study of$ 2p $ radioactivity can extract abundant nuclear structure information, such as the sequences of particle energies, the wave function of the two emitted protons, the deformation effect and so on [20-22]. However, because of the limitations of experimental techniques, it was extremely difficult to observe the$ 2p $ radioactivity phenomenon from a nuclear ground state in the early experiments. With the development of experimental facilities and detection technologies, not true$ 2p $ radioactivity ($ Q_{2p} > 0 $ and$ Q_p > 0 $ , where$ Q_p $ and$ Q_{2p} $ are the released energy of proton radioactivity and two-proton radioactivity, respectively) were observed from a very short-lived nuclear ground state, such as 6Be [23], 12O [24] and 16Ne [25]. In 2002, true$ 2p $ radioactivity ($ Q_{2p} > 0 $ and$ Q_p < 0 $ ) [26] was discovered from ground state of 45Fe at GSI [27] and GANIL [28]. Thereafter, a series of other true$ 2p $ radioactivity phenomena were also detected, such as 54Zn [29, 30], 19Mg [31] and so on [32–34].From the theoretical point of view, several approaches have been proposed to analyze
$ 2p $ radioactivity during the recent decades [6, 7, 35-41], which can be roughly divided into two categories. The first considers the two emitted protons from the parent nucleus being strongly correlated and forming a 2He-like cluster. This category includes the effective liquid drop model (ELDM) [42], Gamow-like model [14], generalized liquid drop model (GLDM) [43], etc. The second category refers to the two-proton emission process being an isotropic emission with no angular correlation, which treats the parent nucleus as composed of two protons and a remnant core. This is usually called three-body radioactivity [6, 8, 44-54]. Furthermore, empirical formulas were also proposed to investigate$ 2p $ radioactivity, such as the four-parameter and two-parameter empirical formulas which were proposed by Sreeja et al. [15] and Liu et al. [55], respectively. Within these approaches and empirical formulas, the experimental$ 2p $ radioactivity half-lives are reproduced with different accuracies.The proximity potential based on the proximity force theorem was firstly put forward by Blocki et al. [56] and widely applied to nuclear physics [57-66], such as heavy-ion fusion reaction [67], heavy-ion elastic scattering [68], fusion barriers [69], etc. For its simple and accurate formalism with the advantage of adjustable parameters, using the proximity potential to replace the nuclear potential, Santhosh et al. proposed the Coulomb and proximity potential model (CPPM) [70] to deal with cluster radioactivity in 2002. CPPM [70] was extended to study α decay [61, 71-75], proton radioactivity [16, 76], α decay fine structure [77, 78], heavy ion fusion and ternary fission [62, 63, 79, 80] and predict the α decay chains of superheavy nuclei [81, 82]. Considering that the
$ 2p $ radioactivity process shares the same theory as α decay and proton radioactivity, i.e., all are barrier penetration processes, it is desirable to ask whether or not the CPPM can be extended to study$ 2p $ radioactivity. To this end, we extend the CPPM to systematically study the$ 2p $ radioactivity half-lives of proton-rich nuclei with 12 < Z < 36.This article is organized as follows. In the next section, the theoretical framework of the Coulomb and proximity potential model is presented. Results and discussion are shown in Sec. III. Finally, a summary is given in Sec. IV
-
The
$ 2p $ radioactivity half-life is generally calculated by$ T_{1/2} = \frac{\ln 2}{\lambda}, $

(1) where λ is the decay constant, which can be expressed as
$ {\lambda} = S_{2p} \nu P. $

(2) Here ν is the assault frequency related to the harmonic oscillation frequency presented in the Nilsson potential [83]. It can be expressed as
$ h\nu = \hbar\omega\simeq\frac{41}{A^{1/3}}, $

(3) where h,
$ \hbar $ , ω, and A are the Planck constant, reduced Plank constant, angular frequency, and mass number of the parent nucleus, respectively.$ S_{2p} = G^2[A/(A-2)]^{2n}\chi^2 $ represents the preformation probability of the two emitted protons in the parent nucleus, which is obtained by the cluster overlap approximation with$ G^2 = (2n)!/ $ $ [2^{2n}(n!)^2] $ [84, 85]. Here$ n\,\approx(3Z)^{1/3} $ –1 is the average principal proton oscillator quantum number [86] and$ \chi^2 $ is set as 0.0143 according to Ref. [43].P is the penetration probability, which can be calculated by the semi-classical Wentzel–Kramers–Brillouin (WKB) approximation and expressed as
$ P = {\rm exp}\left[-2\int_{r_{\rm in}}^{r_{\rm out}} K(r)\,{\rm d}r\right], $

(4) where
$ K(r) = \sqrt{\frac{2 \mu}{\hbar^2}|{V(r)-Q_{2p}}|} $ is the wave number of the two emitted protons.$ \mu = \dfrac{m_{2p}m_d}{m_{2p}+m_d} \approx 938.3 \times 2 \times A_d/ $ $ A \;{\rm{MeV/c}}^2 $ denotes the reduced mass with$ m_{2p} $ and$ m_d $ being the masses of the two emitted protons and the daughter nucleus, respectively [14]. r is the mass center distance between the two emitted protons and the daughter nucleus.$r_{\rm in}$ and$r_{\rm out}$ are classical inner and outer turning points of potential barrier which satisfied the conditions$V(r_{\rm in}) = V(r_{\rm out}) = Q_{2p}$ .$ V(r) $ is the whole interaction potential between the two emitted protons and the daughter nucleus, including the nuclear potential$ V_{N}(r) $ , Coulomb potential$V_{\rm C}(r)$ and centrifugal potential$ V_{l}(r) $ . It can be expressed as$ V(r) = V_{N}(r)+V_{\rm C}(r)+V_{l}(r). $

(5) In the CPPM [70], the nuclear potential was replaced by the proximity potential, which was firstly put forward by Blocki et al. as a simple formalism in 1977 [56]. In this work, we choose the proximity potential formalism 1981 (Prox. 81) [87] to obtain the nuclear potential between the two emitted protons and the daughter nucleus. In this proximity potential, the nuclear potential
$ V_N(r) $ can be expressed as$ V_N(r) = 4 \pi \gamma b \bar {R}\Phi(\xi), $

(6) where
$ \gamma = \gamma_0\left[1-k_s1.7826\left(\dfrac{N-Z}{A}\right)^2\right] $ is the surface energy coefficient, with surface energy constant$ \gamma_0 = 0.9517 $ MeV/fm2 and the surface asymmetry constant$ k_s $ = 1.7826. Here N, Z and A are the neutron number, proton number and mass number of the parent nucleus, respectively. b is the diffuseness of the nuclear surface, taken as unity, and R is the mean curvature radius which can be written as$ \bar{R} = \frac{C_1C_2}{C_1+C_2}. $

(7) Here
$ C_1 $ and$ C_2 $ denote the matter radii of daughter nucleus and two emitted protons, respectively. They have the following form$ C_i = R_i\left[1-\left(\frac{b}{R_i}\right)^2\right]\quad(i = 1,2), $

(8) where
$ R_1 $ and$ R_2 $ are the radii of daughter nucleus and two emitted protons, respectively. The nuclear radii [88] can be parameterized as$ R_i = 1.28A_i^{1/3}-0.76+ -0.8A_i^{-1/3} $ $ (i = 1,2) $ . For the universal function$ \Phi(\xi) $ , it is expressed as$ {\Phi(\xi) = \left\{\begin{array}{ll} -1.7817+0.9270\xi+0.143\xi^2-0.09\xi^3 &\xi<0,\\ -1.7817+0.9270\xi+0.01696\xi^2-0.05148\xi^3 &0\le\xi\le1.9475,\\ -4.41e^{-\xi/0.7176} &\xi>1.9475\\ \end{array}\right.} $ 
(9) where
$ \xi = \dfrac{r-C_1-C_2}{b} $ represents the distance between the near surface of the daughter nucleus and two emitted protons.The Coulomb potential
$V_{\rm C}(r)$ is hypothesized as the potential of a uniformly charged sphere with sharp radius R. It is expressed as${V_{\rm C}}(r) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{Z_1}{Z_2}{e^2}}}{{2R}}\left[3 - \left(\dfrac{r}{R}\right)\right],}&{r < R,}\\ {\dfrac{{{Z_1}{Z_2}{e^2}}}{r},}&{r > R,} \end{array}} \right.$

(10) where
$ R = R_1+R_2 $ is the separation radius.$ Z_1 $ and$ Z_2 $ are the proton number of the daughter nucleus and the two emitted protons, respectively.For the centrifugal potential
$ V_l(r) $ , because$l(l+1)\to $ $ \left(l+\dfrac{1}{2}\right)^2$ is a necessary correction for one-dimensional problems [89], we choose the Langer modified form. This can be written as$ V_l(r) = \frac{\hbar^2(l+\frac{1}{2})^2}{2\mu r^2}, $

(11) where l is the obrital angular momentum taken away by the two emitted protons. The minimum orbital angular momentum
$l_{\min}$ can be obtained by the parity and angular momentum conservation laws. -
In order to describe the interaction potential between any two nuclei in the separation degree of freedom, based on the proximity force theorem, Blocki et al. proposed the proximity potential for the first time in 1977 [56]. Since, various nuclear proximity potentials have been widely applied to study nuclear physics [90-94]. In 2002, using the proximity potential to replace the nuclear potential, Santhosh et al. proposed the Coulomb and proximity potential model (CPPM) to study cluster radioactivity. Later on, the CPPM was more broadly used to investigate α decay and proton radioactivity [16, 76, 81, 82]. For
$ 2p $ radioactivity, it may share the same theory, i.e., barrier penetration process, as α decay, proton radioactivity and cluster radioactivity. In this work, we extend the CPPM to systematically study the$ 2p $ radioactivity half-lives of the nuclei with 12 <Z < 36.First, we performed calculations on the
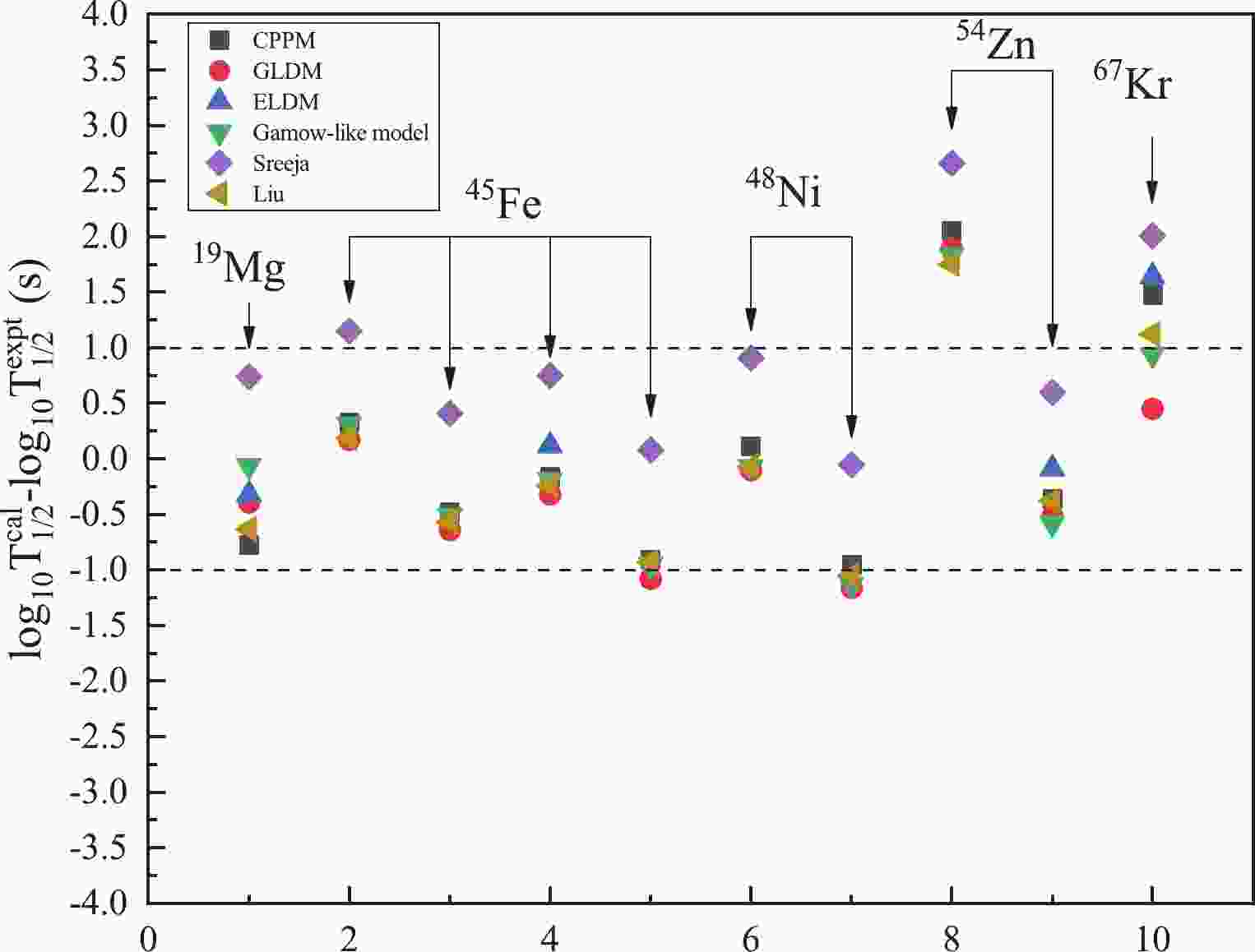
$ 2p $ radioactivity half-lives of the true$ 2p $ radioactive nuclei of 19Mg, 45Fe, 48Ni, 54Zn and 67Kr, amounting to 10 experimental datasets within the CPPM. All the detailed calculated results are presented in Table 1. For comparison, the experimental$ 2p $ radioactivity half-lives and the calculated values obtained from the effective liquid drop model (ELDM) [42], generalized liquid drop model (GLDM) [43], and Gamow-like model [14] are also listed in Table 1. In this table, the first four columns represent the radioactive parent nucleus, the$ 2p $ radioactivity released energy$ Q_{2p} $ , the angular momentum l taken away by the two emitted protons and the logarithmic form of experimental$ 2p $ radioactivity half-life (denoted as$ \log T_{1/2}^{\rm{expt}} $ ), respectively. The last six columns represent the logarithmic form of calculated$ 2p $ radioactivity half-life (denoted as$ \log_{10}T^{\rm{calc}}_{1/2} $ ) calculated by different theoretical models and empirical formulas, namely CPPM, GLDM [43], ELDM [42], Gamow-like model [14], Sreeja formula [15] and Liu formula [55], respectively. From this table, we can clearly see that our calculated results using CPPM have the same magnitude as the ones obtained using the above-mentioned theoretical models and empirical formulas. In order to further demonstrate the degree of agreement, we plot the differences ($ \log_{10}T^{\rm{calc}}_{1/2} - \log_{10}T^{\rm{exp}}_{1/2}$ ) between the experimental values and the values calculated by different theoretical models and empirical formulas in Fig. 1. From this figure, it is clearly seen that the deviations for$ 2p $ radioactive nuclei are almost entirely in the range$ -1 \to +1 $ except for 54Zn ($ Q_{2p} $ = 1.28 MeV) and 67Kr. For the case of 54Zn ($ Q_{2p} $ = 1.28 MeV), it is not difficult to find that the calculated results within all of theoretical approaches mentioned above have a evident deviation from the experimental value, meanwhile the calculated results are very close to the experimental value for$ Q_{2p} $ = 1.48 MeV. Due to the significant deviations between the experimental half-lives and the values obtained by theoretical approaches mentioned above, we suspect the experimental data may not be accurate enough, either the released energies or the half-lives. As well as errors in detecting the experimental values, the discrepancy may be caused by deformation of daughter and parent nucleus, which plays a momentous role in the$ 2p $ radioactivity half-life, as pointed out by Goigoux et al. [34]. In addition, the three-body asymptotic behavior and configuration mixing are noted as key factors for$ 2p $ radioactivity [34, 95, 96]. Therefore, it is crucial to improve CPPM by taking the factors mentioned above into account to make more reliable predictions in future work.Nuclei Q2p /MeV l $\log _{10}^{\rm{cal}}{{T}_{1/2}}({\rm{s}})$ 

EXPT CPPM GLDM [43] ELDM [42] Gamow-like [14] Sreeja [15] Liu [55] 19Mg 0.75 [31] 0 −11.40 [31] −12.17 −11.79 −11.72 −11.46 −10.66 −12.03 45Fe 1.10 [27] 0 −2.40 [27] −2.07 −2.23 − −2.09 −1.25 −2.21 1.14 [28] 0 −2.07 [28] −2.55 −2.71 − −2.58 −1.66 −2.64 1.15 [97] 0 −2.55 [97] −2.71 −2.87 −2.43 −2.74 −1.80 −2.79 1.21 [36] 0 −2.42 [36] −3.33 −3.50 − −3.37 −2.34 −3.35 48Ni 1.29 [98] 0 −2.52 [98] −2.41 −2.62 − −2.59 −1.61 −2.59 1.35 [97] 0 −2.08 [97] −3.03 −3.24 − −3.21 −2.13 −3.13 54Zn 1.28 [30] 0 −2.76 [30] −0.71 −0.87 − −0.93 −0.10 −1.01 1.48 [29] 0 −2.43 [29] −2.79 −2.95 −2.52 −3.01 −1.83 −2.81 67Kr 1.69 [34] 0 −1.70 [34] −0.22 −1.25 −0.06 −0.76 0.31 −0.58 Table 1. Comparison between experimental 2p radioactivity half-lives and calculated values using CPPM, GLDM, ELDM, Gamow-like model, and two empirical formulas. The experimental 2p radioactivity half-lives and released energy
$Q_{2p}$ are taken from the corresponding references.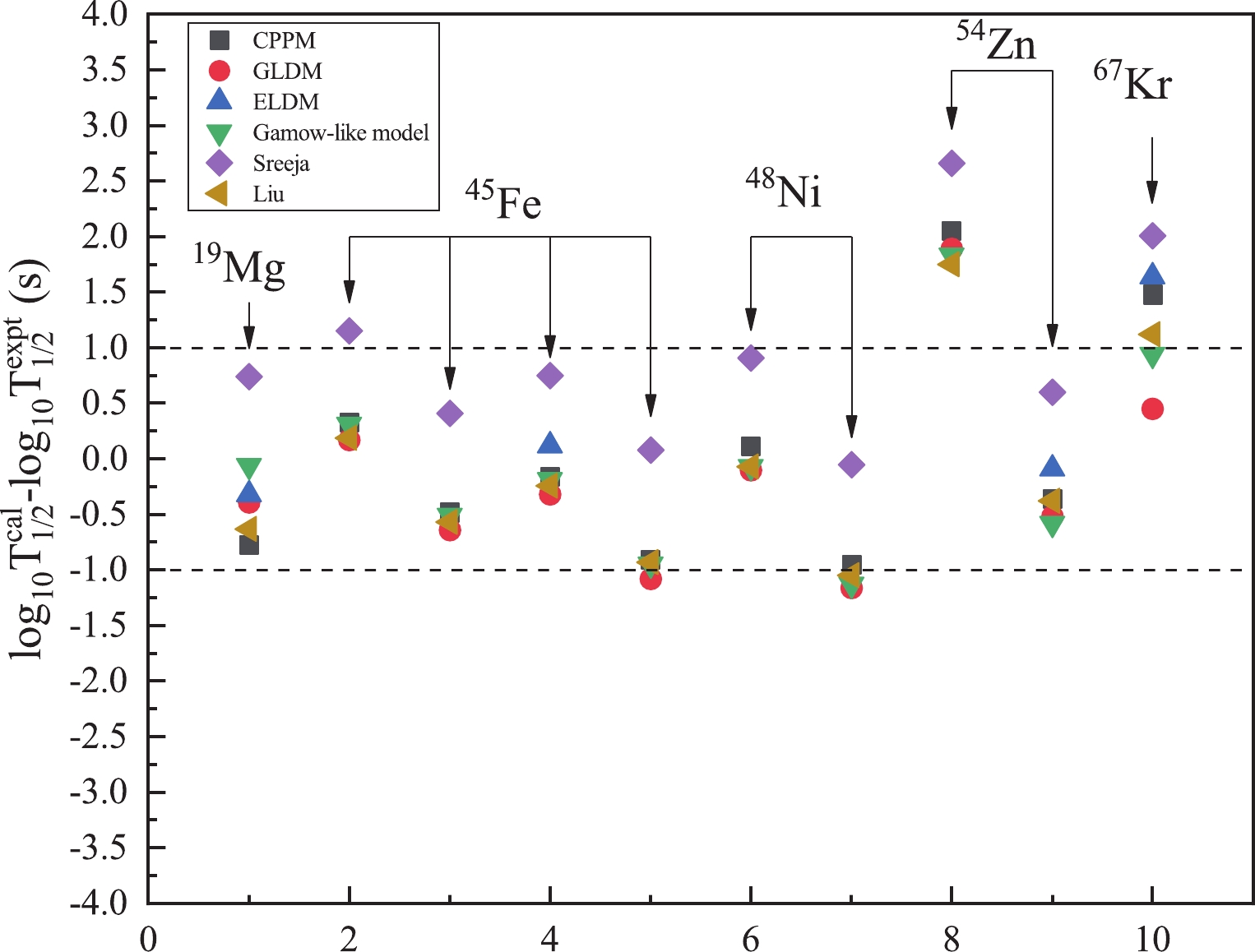
Figure 1. (color online) Deviations between the experimental data and the calculated 2p radioactivity half-lives obtained by GLDM, ELDM, Gamow-like model, Sreeja formula and Liu formula.
Given the good agreement between the calculated results from CPPM and the experimental data, we use this model to predict the half-lives of possible
$ 2p $ radioactive candidates with$ Q_{2p}> 0$ and$ Q_p< 0$ , extracted from the 2016 Atomic Mass Evaluation (AME) mass table [99-101]. The predicted results are listed in Table 2. In this table, the first three columns represent the radioactive parent nuclei,$ Q_p $ and$ Q_{2p} $ , respectively. The predicted results obtained by the CPPM, GLDM, ELDM, Gamow-like model, Sreeja formula and Liu formula are listed in the 4th to 9th column, respectively. From this table, we can clearly see the newly predicted results are quite different from those obtained using GLDM, ELDM, Gamow-like model, Sreeja formula and Liu formula when the values of the$ Q_{2p} $ are below 1 MeV. This may be caused by penetration probability P. From Eq. (4), we can clearly see that P has a strong sensitivity to$r_{\rm in}$ and$r_{\rm out}$ , which are obtained by the conditions$V(r_{\rm in}) = $ $ V(r_{\rm out}) = Q_{2p}$ . To illustrate the consistency of the predicted results using different models with CPPM, we plot the logarithmic predicted half-lives of possible candidates in Fig. 2. From this figure, it is clearly seen that the predicted results are in good agreement with the ones obtained by GLDM, ELDM and the Gamow-like model except for 55Zn and 64Se. It may need future experiments to check this phenomenon.Nuclei Qp /MeV Q2p /MeV $\log _{10}^{\rm{pre} }{ {T}_{1/2} }/\rm{s}$ 

CPPM GLDM [43] ELDM [42] Gamow-like model [14] Sreeja [15] Liu [55] $_{14}^{22}{\rm{Si}}$ 

−0.94 1.28 −13.73 −13.30 −13.32 −13.25 −12.30 −13.74 $^{34}_{20}{\rm{Ca}}$ 

−0.48 1.47 −10.33 −10.71 −9.91 −10.10 −8.65 −9.93 $^{39}_{22}{\rm{Ti}}$ 

−0.84 0.76 −1.24 −1.34 −0.81 −0.91 −0.28 −1.19 $^{42}_{24}{\rm{Cr}}$ 

−0.88 1.00 −2.74 −2.88 −2.43 −2.65 −1.78 −2.76 $^{49}_{24}{\rm{Ni}}$ 

−0.59 0.49 10.23 14.46 14.64 14.54 12.78 12.43 $^{55}_{30}{\rm{Zn}}$ 

−0.45 0.48 11.87 17.94 − − − − $^{60}_{32}{\rm{Ge}}$ 

−0.62 3.63 11.47 13.55 14.62 14.24 12.40 12.04 $^{64}_{34}{\rm{Se}}$ 

−0.49 0.46 15.04 24.44 − − − − Table 2. Comparison between the experimental 2p radioactivity half-lives and calculated values using CPPM, GLDM, ELDM, Gamow-like model, and two empirical formulas. The experimental 2p radioactivity half-lives and released energy
$Q_{2p}$ are taken from the corresponding references. -
In this work, we extend the Coulomb and proximity potential (CPPM) to systematically investigate the half-lives of two-proton (
$ 2p $ ) radioactive nuclei including 19Mg, 45Fe, 48Ni, 54Zn and 67Kr. In calculations, the proximity potential is chosen as proximity potential formalism 1981 (Prox. 81). The preformation probability ($ S_{2p} $ ) of the two protons in the parent nucleus is taken into consideration. The calculated results from the CPPM are in good agreement with the experimental data, other theoretical models and empirical formulas. In addition, we predict the half-lives of possible$ 2p $ radioactive candidates. This may provide a theoretical reference for future experiments. -
We would like to thank Jun-Gang Deng, Xiao Pan, Hai-Feng Gui for valuable discussions and suggestions for this work.
Two-proton radioactivity within Coulomb and proximity potential model
- Received Date: 2021-10-05
- Available Online: 2022-04-15
Abstract: Considering the preformation probability of the two emitted protons in the parent nucleus, we extend the Coulomb and proximity potential model (CPPM) to systematically study two-proton (2p) radioactivity half-lives of the nuclei close to proton drip line. The proximity potential chosen is Prox. 81 proposed by Blocki et al. in 1981. Furthermore, we apply this model to predict the half-lives of possible 2p radioactive candidates whose 2p radioactivity is energetically allowed or observed but not yet quantified in the evaluated nuclear properties table NUBASE2016. The predicted results are in good agreement with those from other theoretical models and empirical formulas, namely the effective liquid drop model (ELDM), generalized liquid drop model (GLDM), Gamow-like model, Sreeja formula and Liu formula.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: