-
Kaonic nuclei, bound states of a negatively-charged kaon
$ K^- $ and a normal nucleus, can provide valuable information concerning the kaon-nucleon interactions at low energies. Since Kishimoto suggested that kaonic nuclei can be produced by the$ (K^-,p) $ and$ (K^-,n) $ reactions [1], and Akaishi and Yamazaki discussed the possibility of$ K^- $ nuclei in few-body systems [2],$ K^- $ nuclei have become one of the important problems that attracts attention from both experimental and theoretical sides in the study of strangeness physics.While electromagnetically-bound kaonic atoms have been studied experimentally and theoretically for a long time [3–6], in the past fifteen years the properties of strongly-bound (light)
$ K^- $ nuclei have been explored actively in several experiments [7, 8]. For example, in 2005 the FINUDA collaboration succeeded to detect a kaon bound state$ K^-pp $ through its two-body decay into a Λ hyperon and a proton and determined the corresponding binding energy and decay width [9]. In 2010, a deeply-bound and compact$ K^-pp $ state formed in the$ pp \rightarrow K^+ + K^-pp $ reaction was found by analyzing the data of the DISTO experiment on the exclusive$ pp\rightarrow p\Lambda K^+ $ reaction [10]. Its mass and width were also obtained. Recently, the bound state$ K^-pp $ was detected by the E15 and E27 collaborations at J-PARC. The E15 collaboration found a bound state$ K^-pp $ with a binding energy of$ 42 \pm 3^{+3}_{-4}\, $ MeV [11, 12]. The E27 collaboration observed a deeply-bound state$ K^-pp $ produced by the reaction$ \pi^+ + n + p \rightarrow K^-pp +K^+ \rightarrow \Sigma^0 + p + K^+ $ [13]. Note that the main focus of the current experiments is on the simplest kaonic nucleus$ K^-pp $ ; thus, searching for heavier kaonic nuclei in the future is necessary, which can open new opportunities for theoretical studies. Recently, E15 [14] and AMADEUS [15] published new results on kaon absorption in 12C.On the theoretical side, various models were used to study the properties of strongly-bound
$ K^- $ nuclei. For example, the antisymmetrized molecular dynamics model [16], the effective chiral Lagrangian for the kaon-baryon interaction combined with a nonrelativistic baryon-baryon interaction model [17], the 0s-orbital model [18], the chiral SU(3) model [19–22], the self-consistent meson-baryon coupled-channels interaction models [23–38], the non-relativistic Faddeev and Faddeev-Yakubovsky calculations [39, 40], the relativistic mean field (RMF) models [41–46], the Skyrme-Hartree-Fock (SHF) model [47–49], and the phenomenological density-dependent optical potential model of fitting the$ K^- $ atomic data [4, 50–52].However, there is still much controversy on the
$ K^- $ -nucleus bound states and the depth of the kaon nuclear optical potential. Recent experiments explored the possible existence of a deeply-bound$ K^-pp $ state [11, 12] to obtain experimental constraints on this problem, but the issue is still quantitatively unsolved [53]. Theoretical calculations yield widely varying results for the$ K^- $ optical potential. For example, in the optical potential model [4, 50–52] it was found to be strongly attractive, with a depth of$ 150-200{\;\rm{MeV}} $ in the nuclear interior, whereas several chiral models predicted a lower range of$ 85- $ $ 120{\;\rm{MeV}} $ [22, 41, 54]. In the RMF model [42], the static properties of$ K^- $ nuclei from$ ^{12}_{K^-} $ C to$ ^{44}_{K^-} $ Ti were studied with similar potential depths of$ 85-100{\;\rm{MeV}} $ . However, a recent experimental analysis of$ ^{12}_{K^-} $ C favored even lower values of about 80 MeV [14, 15]. Within the SHF model [47–49], the mean fields, density distributions, and potential energy surfaces of several$ K^- $ nuclei ($ ^{\ 8}_{K^-} {\rm{Be}}$ ,$ ^{16}_{K^-} {\rm{O}}$ ,$ ^{20}_{K^-} {\rm{Ne}}$ ,$ ^{36}_{K^-} {\rm{Ar}}$ ,$ ^{40}_{K^-} {\rm{Ca}}$ , and$ ^{208}_{K^-} {\rm{Pb}}$ ) were studied for various effective$ K^-N $ interaction strengths and an instability of the solutions for a too strong$ K^-N $ interaction was found, which determined a maximum value of kaon binding in this approach.Kaonic nuclei can feature a dense nuclear core at supra-normal density due to the shrinkage effect, and therefore it is theoretically feasible to obtain constraints on the nuclear equation of state (EOS) both in the low-density and high-density regions by analyzing structural properties of kaonic nuclei that encompass the information of a large density range. The determination of the nuclear EOS with a certain accuracy is crucial for the understanding of the phenomena related to relativistic heavy-ion collisions and astrophysical objects, such as neutron stars, gravitational waves, etc. [55–59]. More-over, the properties of exotic nuclei, such as their halo structure, have played a special role in constraining the nuclear forces, which are usually restrained to the neighborhood of the drip lines. The effects of kaons on the drip lines may provide a novel mechanism for the formation of exotic structure [57].
Note that the pioneering works discussed above focussed mainly on the ground-state properties of stable nuclei. However, a general understanding of strange nuclear systems requires the evaluation of the global strange nuclear chart, with strangeness as the third dimension. This motivated us to investigate the ground-state properties of nuclei far away from the β-stability line to understand the limits of the strong force to hold together the nucleons in a bound system. There are many studies concerning the drip lines in normal nuclear systems, but fewer works regarding strangeness. Only for Λ hypernuclei the neutron drip lines have been investigated, e.g., in Refs. [60–62]. We hope the predictions of such a study could be of importance in the future, although nowadays the relative experimental technologies are still out of reach for the kaonic nuclear region far away from the β-stability line.
Therefore, based on our previous work that reveals limits of the
$ K^-N $ interaction strength, the present work aims to extend the investigation of the effects of an additional$ K^- $ on the ground-state properties from stable to unstable nuclei within the SHF approach. We consider the isotopes of the typical nuclei Be, O, and Ne as examples. While most of the Be and Ne isotopes are deformed, the deformations of O isotopes are small. Many of the isotopes have short lifetimes, such that any experimental investigation appears unrealistic. However, others are long-lived, and experimental studies in the (remote) future are not excluded. In any case we consider this work as a conceptual study, pointing out qualitative phenomena that might be explored quantitatively by more refined theoretical approaches and experimental techniques in the future.The paper is organized as follows. Sec. II introduces the extended SHF approach as well as the Skyrme-type
$ K^-N $ force. Sec. III presents the energies of the highest-occupied single-particle levels, one-nucleon separation energies, binding energies, and quadrupole deformations of$ K^- $ nuclei and their corresponding core nuclei in Be, O, and Ne isotopes together with the available experimental data. Finally, Sec. IV summarizes the work. -
The purpose of the present work is to qualitatively discuss the effect of an additional
$ K^- $ meson on the ground-state properties of nuclei in the SHF approach combined with a simple density-dependent Skyrme-type$ K^-N $ interaction. In this approach the total energy of the nucleus is expressed as [47, 49, 63–69]$ E = \int {\rm d}^3{\boldsymbol{r}}\, {\varepsilon}({\boldsymbol{r}}) \:,\quad {\varepsilon} = {\varepsilon}_{NN} + {\varepsilon}_{KN} + {\varepsilon}_{\rm C} \:, $

(1) where
$ {\varepsilon}_{NN} $ denotes the energy density of the nucleon-nucleon part,$ {\varepsilon}_{KN} $ is the energy density due to the kaon-nucleon strong interaction, and$ {\varepsilon}_{\rm C} $ is the Coulomb contribution of protons and kaons.For each single-particle (s.p.) state
$ \phi_q^i $ $ (q=n,p,K) $ , the minimization of the total energy E in Eq. (2) implies the SHF Schrödinger equation$ \left[ -\nabla \cdot \frac{1}{2m^*_q({\boldsymbol{r}})} \nabla + V_q({\boldsymbol{r}}) - {i}{\boldsymbol{W}}_q({\boldsymbol{r}}) \cdot (\nabla\times{\boldsymbol{\sigma}}) \right] \phi_q^i({\boldsymbol{r}}) = e_q^i \phi_q^i({\boldsymbol{r}}) \:, $

(2) with the mean fields
${V_K} = \frac{{\partial {\varepsilon _{KN}}}}{{\partial {\rho _K}}} - {V_{\rm C}} , $

(3) ${V_q} = V_q^{{\rm{SHF}}} + V_q^{(K)}\,, $

(4) $ V_q^{(K)} = \frac{{\partial {\varepsilon _{KN}}}}{{\partial {\rho _q}}},\;(q = n,p) , $

(5) where
$ V_{\rm C} $ denotes the Coulomb field,$ V^{\rm{SHF}}_q $ the standard nucleonic Skyrme mean field,$ {\boldsymbol{W}}_q $ the nucleonic spin-orbit mean field, and$ V_q^{(K)} $ the change of the nucleonic mean fields by the$ K^-N $ interaction.For the nucleonic part, we use the standard Skyrme force SLy4 [70]. For the kaonic energy-density contribution, a simple linear energy density functional is assumed as in Ref. [49],
$ {\varepsilon}_{KN} = -a_0 \rho_K [(1+x_0)\rho_p + (1-x_0)\rho_n] \:, $

(6) where
$ a_0 $ and$ x_0 $ are the$ K^-N $ interaction strength parameters. Under this assumption, the mean fields in Eqs. (3) and (4) are [49]$V_K = -a_0 [(1+x_0)\rho_p + (1-x_0)\rho_n] - V_{\rm C} \:, $

(7) $V_{p,n}^{(K)} = -a_0(1 \pm x_0)\rho_K . $

(8) In the following calculations, we use a (p,n)-symmetric
$ K^-N $ interaction, i.e.,$ x_0=0 $ and$ a_0=500{\;{\rm{MeV}}\,{\rm{fm}}^{3}} $ , which were justified as reasonable values in Ref. [49], to which we refer for more information. This choice yields a mean field$ V_K\approx130{\;\rm{MeV}} $ for the$ ^{12}_{K^-}{\rm{C}} $ nucleus. In that reference we also studied the extreme case of$ x_0=1 $ , neglecting the$ K^-n $ interaction completely, which required smaller values of$ a_0 $ to cause similar effects as$ x_0=0 $ . We delay the decision on more realistic values of$ a_0 $ and$ x_0 $ (and eventual further nonlinear interaction parameters) to the future when experimental results will hopefully allow a more realistic analysis.The pairing interaction of the nucleonic part employs a density-dependent δ pairing force [71],
$ V_q({\boldsymbol{r}}_1,{\boldsymbol{r}}_2) = -V_0 \left[1-\frac{\rho_N(({\boldsymbol{r}}_1+{\boldsymbol{r}}_2)/2)}{0.16 \; {\,{\rm{fm}}^{-3}}}\right] \delta({\boldsymbol{r}}_1-{\boldsymbol{r}}_2), \: $

(9) with a pairing strength
$ V_0=410{\;{\rm{MeV}}\,{\rm{fm}}^{3}} $ for both neutrons and protons [72–76]. A smooth energy cutoff is included in the BCS calculation [76]. In the case of a nucleus with an odd number of nucleons, the orbit occupied by the last odd nucleon is blocked, as described in Ref. [77]. Dobaczewski et al. [78] stated that the SHF+BCS method was not well suited to describe nuclei close to the neutron-drip line due to the neutron gas effect. However, Anguiano et al. [79] studied the importance of this effect in the description of nuclei with large neutron excess within the BCS approach and concluded that from the quantitative point of view, the neutron gas problem was irrelevant and SHF+BCS calculations were reliable in all regions of the nuclear chart. In the present work, we thus use this approach in a pragmatic way.We assume axially-symmetric mean fields and the properties of axially-deformed nuclei are studied in cylindrical coordinates. The coupled SHF+BCS equations for nucleons and kaon are solved self-consistently by iteration within a coordinate-space representation, imposing the quadrupole deformation parameter
$ \beta_2 = \sqrt{\frac{\pi}{5}} \frac{\langle 2z^2-r^2 \rangle}{\langle z^2+r^2 \rangle} $

(10) as additional constraint. The physical value of
$ \beta_2 $ is taken as the one minimizing the total energy [64, 67, 68, 80]. Specifically, the r-space box sizes for nucleons and antikaons are the same and depend on the mass of the nucleus and the range of input deformation. The results are converged and confirmed to be independent of the box and step sizes.At this point, we also comment on the imaginary part of the
$ K^-N $ interaction (optical potential), due to the decay channels$ KN \rightarrow \pi Y $ and$ KNN \rightarrow YN $ ($ Y=\Lambda,\Sigma $ ) [32, 35, 36]. This is a difficult and intensely studied theoretical problem, also due to the presence of the$ \Lambda(1405) $ resonance [81] as a possible intermediate state,$ KN \rightarrow $ $ \Lambda(1405) \rightarrow \pi\Sigma $ [18, 34]. In this work, we neglect the imaginary part in attendance of reliable data. It has been found that the effect of a moderate$ {\rm{Im}}\,V_K\lesssim 20 $ MeV (neglecting the kaon multinucleon absorption) on the real part is negligible, whereas too large widths might make kaon bound states unobservable [35, 36]. We consider this feature an open problem that can only be solved by future confrontation with accurate data.However, we estimated the qualitative effect in our formalism in Ref. [49] by solving the SHF Schrödinger Eq. (2) incorporating a complex kaon potential
$ V_K({\boldsymbol{r}}) = V_R({\boldsymbol{r}}) + {i}V_I({\boldsymbol{r}}) $ . The imaginary part modified the kaon wave function, single-particle energy, density distribution, and the kaon removal energy$ B_K $ . In Ref. [49], we found that the change in$ B_K $ is small, even up to a large magnitude of the imaginary part. Furthermore, a given value of$ B_K $ could always be restored by adjusting the value of the interaction parameter$ a_0 $ in this model. This demonstrated that the imaginary part of the kaon mean field did not play a key role in the SHF model, at least regarding its effect on the real part and the kaon removal energy. The treatment of real and imaginary parts can be fairly well separated. Equivalent results have been found in the RMF model [42]. Of course, more experimental information is required for a final quantitative determination of this feature. -
To study in detail the effects of an additional
$ K^- $ meson on the ground-state properties of nuclei (comprising unstable nuclei), we examine the one-nucleon separation energies$S_n \equiv E[^AZ] - E[^{A-1}Z] , $

(11) $S_p \equiv E[^AZ] - E[^{A-1}(Z-1)] , $

(12) which provide the location of unstable nuclei, and we compare the results obtained for normal and kaonic nuclei. In addition, we focus on the highest-occupied (valence) nucleon s.p. levels (the last level with occupation probability
$ v^2>0.5 $ ), which become weakly bound for unstable nuclei. If the s.p. energy of the highest-occupied nucleon levels is still negative in the minimum of the total energy, the nucleus is supposed to exist [60]. -
In Fig. 1, the energies of the highest-occupied nucleon s.p. levels
$ -e_q $ (a), the one-nucleon separation energies$ S_q $ (b), the binding energies E (c), and the quadrupole deformations$ \beta_2 $ (d) of Be isotopes and their corresponding$ K^- $ nuclei are presented in comparison with the available experimental results from Ref. [82]. As indicated by the theoretical$ e_q $ and$ S_q $ values, the nuclei with$ N=2 – 8 $ neutrons and their corresponding$ K^- $ nuclei exist. However, 13,17,19Be ($ N=9,13,15 $ ) are unbound systems due to pair breaking. Experimentally, the nuclei from 6Be ($ N=2 $ ) to 16Be ($ N=12 $ ) have been observed [82], but the experimental values of$ S_n $ for 13Be ($ N=9 $ ) and$ S_p $ for 7B ($ N=2 $ ) are negative. Therefore, the proton and neutron drip lines locate at 6Be ($ N=2 $ ) and 12Be ($ N=8 $ ), respectively. Note that the SHF mean-field approach makes rather good predictions for the binding and separation energies even for the lightest isotopes 6,7Be.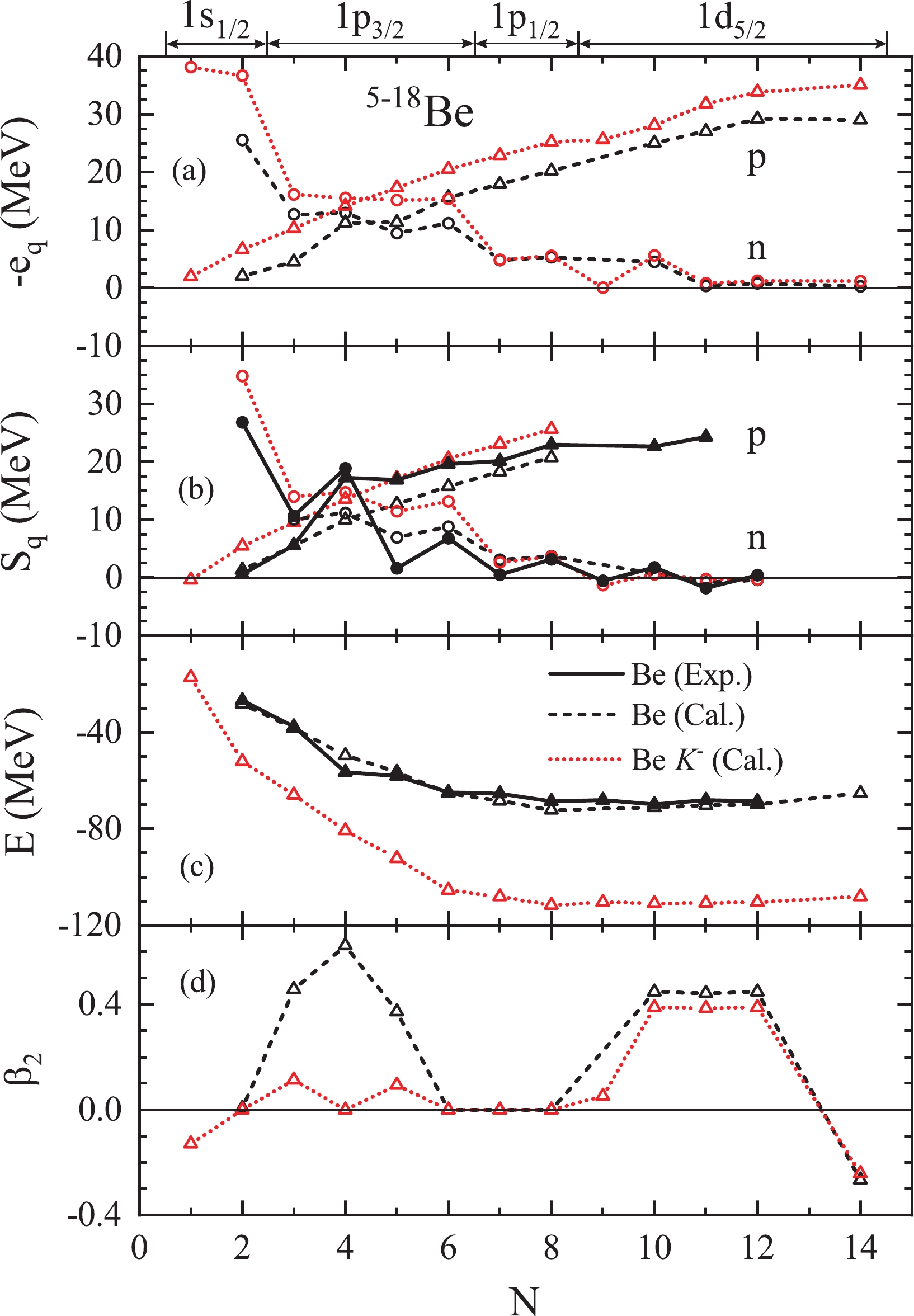
Figure 1. (color online) (a) Energies of the highest-occupied nucleon s.p. levels
$ -e_q $ ($ q=n,p $ ) (the neutron level is indicated on the top; the proton level is$ 1p_{3/2} $ ), (b) one-nucleon separation energies$ S_q $ , (c) binding energies E, (d) quadrupole deformations$ \beta_2 $ of Be isotopes (dashed black lines) and their corresponding$ K^- $ nuclei (dotted red lines), obtained with$ a_0=500{\;{\rm{MeV}}\,{\rm{fm}}^{3}} $ and$ x_0=0 $ in Eqs. (6), (7). The experimental$ S_q $ and E values of normal nuclei obtained from Ref. [82] are also included for comparison (solid black lines). The spherical shells on the top are the approximate quantum numbers in case of deformation.The additional
$ K^- $ meson clearly shifts down the energies of the highest-occupied nucleon s.p. levels$ e_q $ (most notable for those in strongly-bound inner orbits) and thus increases the total binding energies. The shift of the proton levels is larger than that of the neutron levels, even for weakly-bound states, which is due to the additional$ K^-p $ Coulomb attraction. The decrease in quadrupole deformations, as shown in Fig. 1 (d), is due to the attractive$ K^-N $ interaction [49]. With an additional$ K^- $ meson,$ ^{17}_{K^-} {\rm{Be}}$ ($ N=13 $ ) and$ ^{19}_{K^-} {\rm{Be}}$ ($ N=15 $ ) remain unbound, while$ ^{13}_{K^-} {\rm{Be}}$ ($ N=9 $ ) becomes marginally bound, but its$ S_n $ is still negative. Moreover, due to the major impact on the proton levels, a bound nucleus$ ^{\ \ 5}_{K^-} {\rm{Be}}$ ($ N=1 $ ) is found, but its one-proton separation energy$ S_p $ remains negative. An extension effect of the additional$ K^- $ meson on Be isotopes is thus found, which can be attributed to the strong$ K^-p $ attraction including the Coulomb interaction. A similar phenomenon was also found by additional Λ hyperons due to the attractive$ \Lambda N $ interaction in [60].Fig. 2 shows the preceding results for 11-28O (
$ N=3-20 $ ) as well as the corresponding$ K^- $ nuclei. In this case all isotopes are nearly spherical as illustrated in panel (d). The theoretical results of the total energies are in good agreement with the experimental values. All isotopes from 12O ($ N=4 $ ) to 28O ($ N=20 $ ) exist with negative$ e_n $ and$ e_p $ . The separation energies$ S_n $ and$ S_p $ of all nuclei with$ N=5-16 $ are positive, whereas$ S_n $ becomes negative at$ N=17 $ theoretically and experimentally [82], and thus the neutron drip line locates at 24O ($ N=16 $ ). The theoretical proton drip line is reached at$ N=4 $ with 13F ($ Z=9,\;N=4 $ ) being unbound, whereas experimentally it lies at$ N=5 $ , where the experimental one-proton separation energy$ S_p $ of 14F ($ Z=9,\;N=5 $ ) is negative. 11O ($ N=3 $ ) does not exist theoretically and experimentally.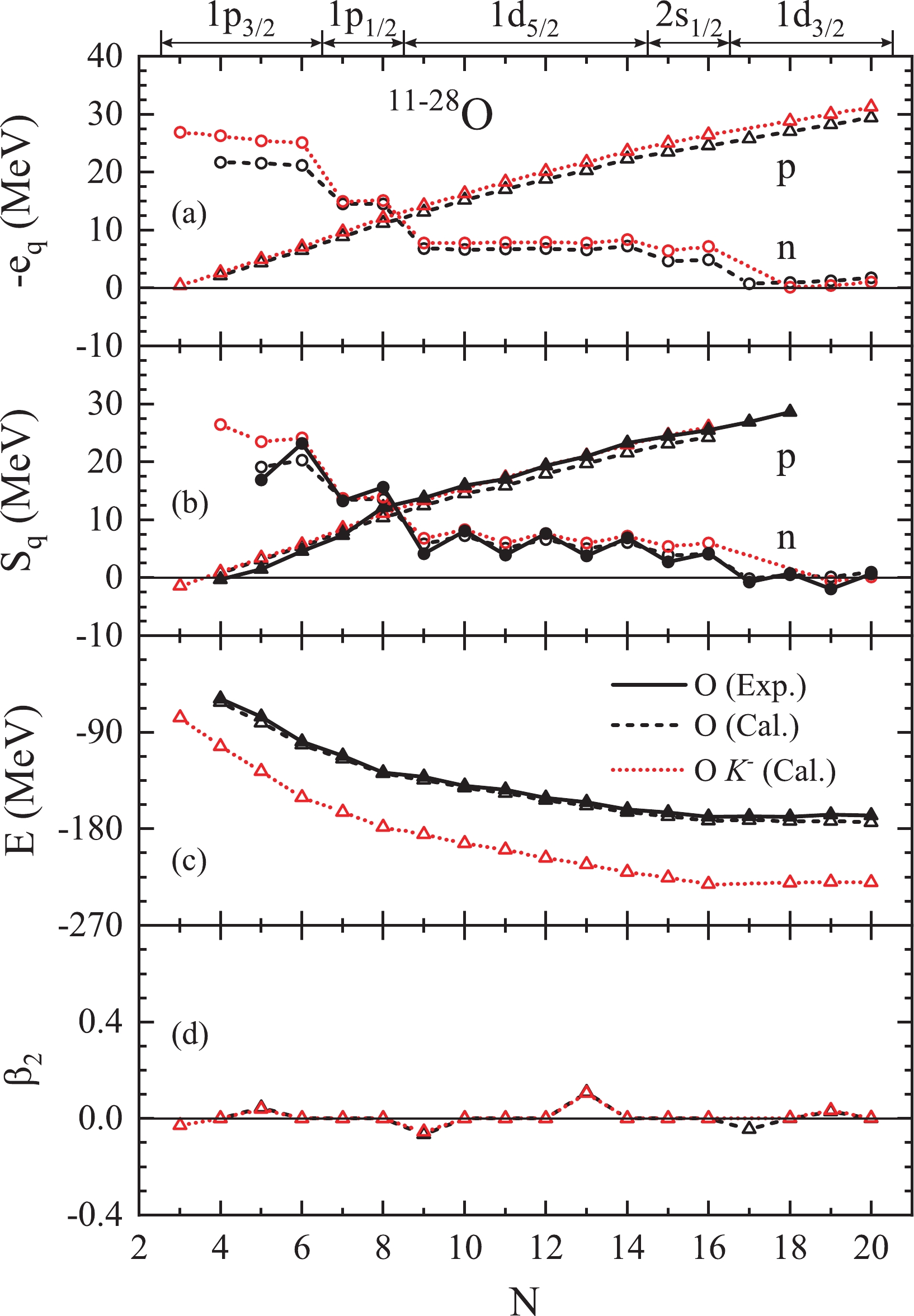
Figure 2. (color online) Same as Fig. 1, but for O isotopes.
In contrast to the results of Be isotopes in Fig. 1, the additional
$ K^- $ meson increases slightly the energies of the highest-occupied neutron s.p. levels of$ ^{11-24}_{\hskip1em K^-} {\rm{O}}$ ($ N= $ $ 3 - 16 $ ), but decreases those of$ ^{25-28}_{\hskip1em K^-} {\rm{O}}$ (valence neutron levels$ 1d_{3/2} $ ). Therefore,$ ^{25}_{K^-} {\rm{O}}$ becomes unbound and the neutron removal energies of$ ^{27-28}_{\hskip1em K^-} {\rm{O}}$ are reduced. Thus, a reducing effect of the$ K^- $ on neutron-rich O isotopes is found. This is an interesting result and is analyzed in detail in the following. However, a bound$ ^{11}_{K^-} {\rm{O}}$ and increasing one-proton separation energies of$ ^{12-24}_{\hskip1em K^-} {\rm{O}}$ are found. Thus, an extension effect of the$ K^- $ meson on the proton-rich O isotopes is evident.The same phenomenon occurs for Ne isotopes, as observed in Fig. 3. All isotopes 16-34Ne (
$ N=6-24 $ ) exist, as experimentally [82]. 35,36Ne are unbound systems. For 17-30Ne ($ N=7 - 20 $ ),$ S_n $ and$ S_p $ are positive both experimentally and theoretically, while$ S_n $ of 31Ne ($ N=21 $ ) is negative theoretically but marginally positive experimentally. Thus, the neutron drip line locates at 30Ne ($ N=20 $ ) theoretically and at 32Ne ($ N=22 $ ) experimentally. The proton drip line is not reached for nuclei with$ N>6 $ experimentally and theoretically. A weakly bound 16Ne ($ Z=10,\;N=6 $ ) and an unbound 15F ($ Z=9,\;N=6 $ ) are found on the theoretical side, while the experimental$ S_p $ of 16Ne is slightly negative [82].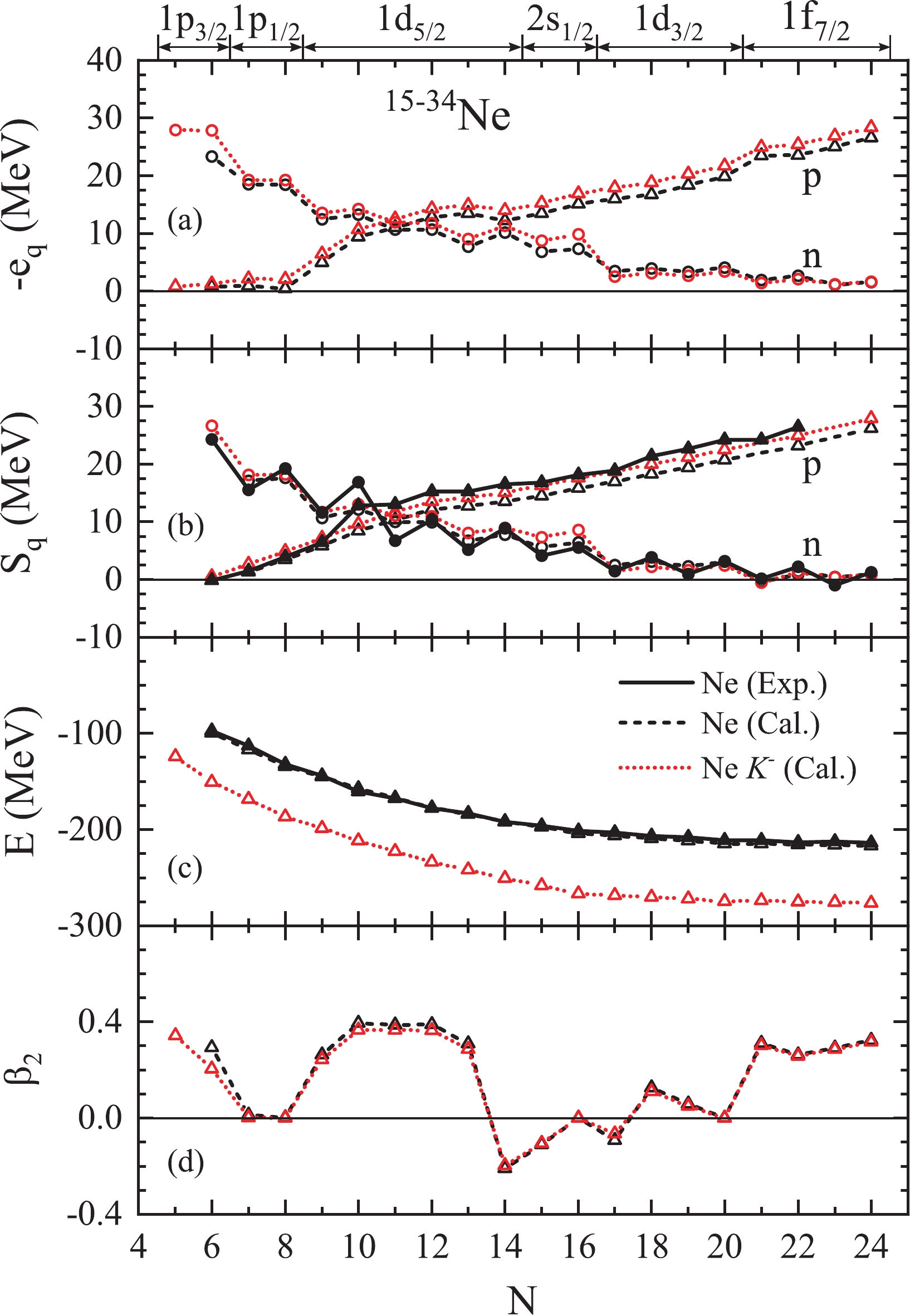
Figure 3. (color online) Same as Fig. 1, but for Ne isotopes.
However,
$ ^{16}_{K^-} {\rm{Ne}}$ with positive$ S_p $ and$ ^{15}_{K^-} \;{\rm{F}}$ with negative$ S_p $ are bound nuclei and thus the additional$ K^- $ meson firmly establishes the proton drip line at$ ^{16}_{K^-} {\rm{Ne}}$ for$ N=6 $ nuclei, and in fact also$ ^{15}_{K^-} {\rm{Ne}}$ becomes bound. All kaonic nuclei$ ^{15-34}_{\hskip1em K^-} {\rm{Ne}}$ ($ N=5 - 24 $ ) exist. Thus, the additional$ K^- $ meson does not affect the existence of neutron-rich Ne isotopes, although the energies of the highest-occupied neutron s.p. level ($ 1d_{3/2} $ ,$ 1f_{7/2} $ ) of$ ^{27-32}_{\hskip1em K^-} {\rm{Ne}}$ ($ N=17-22 $ ) decrease due to the additional$ K^- $ meson. This is like the case of O isotopes as displayed in Fig. 2. In addition, in these larger nuclei, the deformation changes due to the kaon are much smaller than those of Be isotopes in Fig. 1(d). -
As mentioned in Sec. II, the results of
$ K^- $ nuclei shown in the previous figures are obtained with the$ K^-N $ interaction strength$ a_0=500{\;{\rm{MeV}}\,{\rm{fm}}^{3}} $ . Because of the uncertainty of this value, we explore the energies of the highest-occupied neutron s.p. levels of$ ^{27-32}_{\hskip1em K^-} {\rm{Ne}}$ ($ N= $ $ 17 - 22 $ ) with$ K^-N $ interaction strengths$ a_0= 100, $ $ 200,\; \ldots,\; 600{\;{\rm{MeV}}\,{\rm{fm}}^{3}} $ in Fig. 4. It is interesting to note that the$ K^- $ meson does not always increase the energies of the highest-occupied neutron s.p. levels as increasing the$ K^-N $ interaction strength. For the weakly bound$ 1f_{7/2} $ levels, a weak$ K^-N $ interaction ($ a_0=100 $ and$ 200{\;{\rm{MeV}}\,{\rm{fm}}^{3}} $ ) causes a slight increase of binding, whereas repulsion only set in for$ a_0 \gtrsim 300 $ $ {{\rm{MeV}}\,{\rm{fm}}^{3}} $ . The reason will be analyzed later.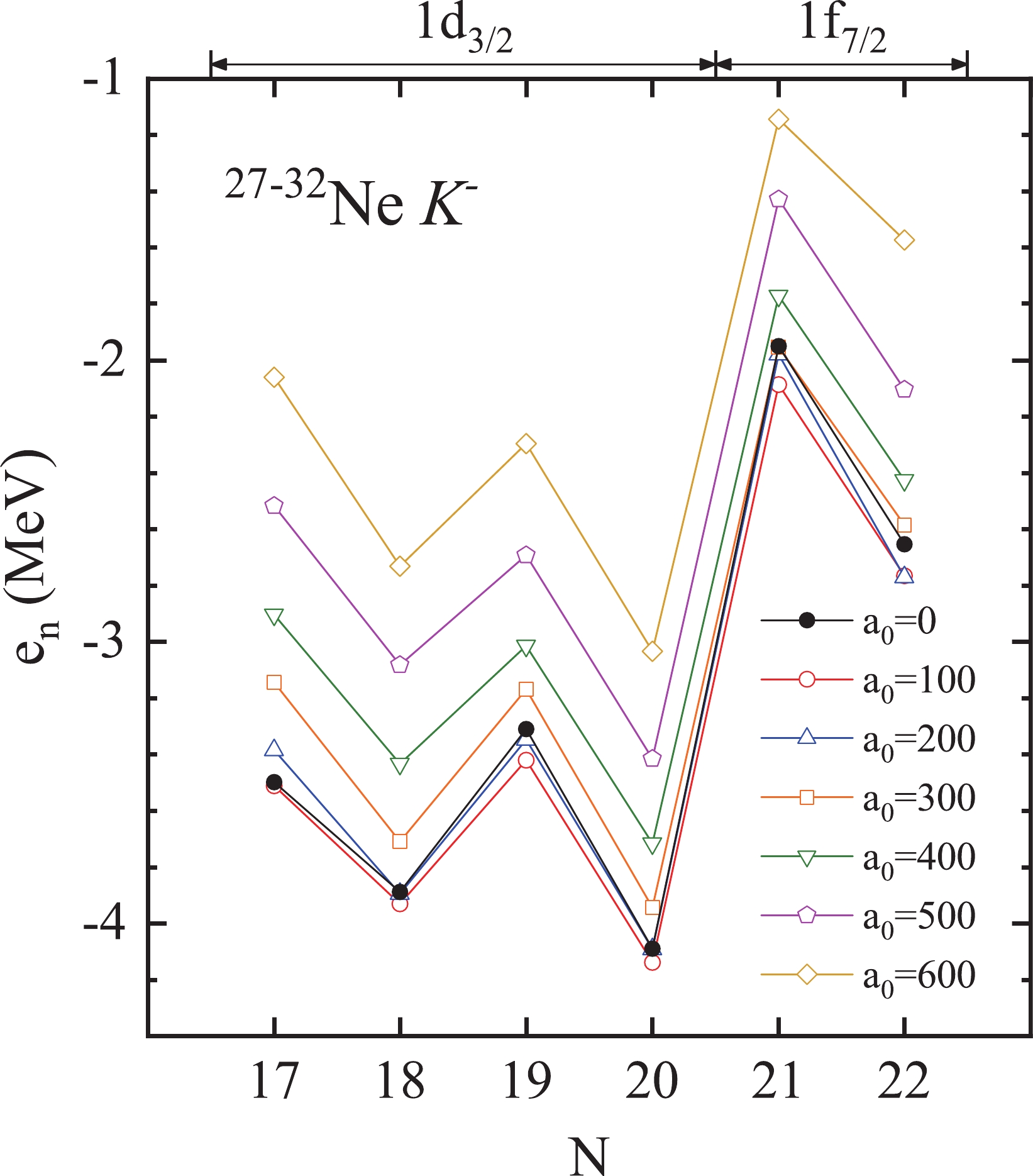
Figure 4. (color online) Energies of the highest-occupied neutron s.p. levels of
$ ^{27-32}_{\hskip1em K^-} {\rm{Ne}}$ and their corresponding normal nuclei$ (a_0=0) $ obtained with different$ K^-N $ interaction strengths$ a_0 $ (in units of$ {\;{\rm{MeV}}\,{\rm{fm}}^{3}} $ ).To illustrate the above features, we show in Fig. 5 the effect of an additional
$ K^- $ meson on the neutron s.p. levels of the spherical drip-line nuclei 12Be, 28O, and 30Ne with three different$ K^-N $ interaction strengths$ a_0=100,\; 300,\; 500{\;{\rm{MeV}}\;{\rm{fm}}^{3}} $ . The spin-orbit splitting of the orbitals$ 1p_{1/2,\; 3/2} $ and$ 1d_{3/2,\; 5/2} $ in$ K^- $ nuclei is larger than that in the corresponding normal nuclei. This effect reduces the binding of the$ 1d_{3/2} $ valence levels in$ ^{28}_{K^-} {\rm{O}}$ and$ ^{30}_{K^-} {\rm{Ne}}$ . Here we also note that the level inversion between orbitals$ 2s_{1/2} $ and$ 1d_{5/2} $ in light kaonic nuclei obtained by the RMF model in Ref. [58] is not found in our SHF calculations.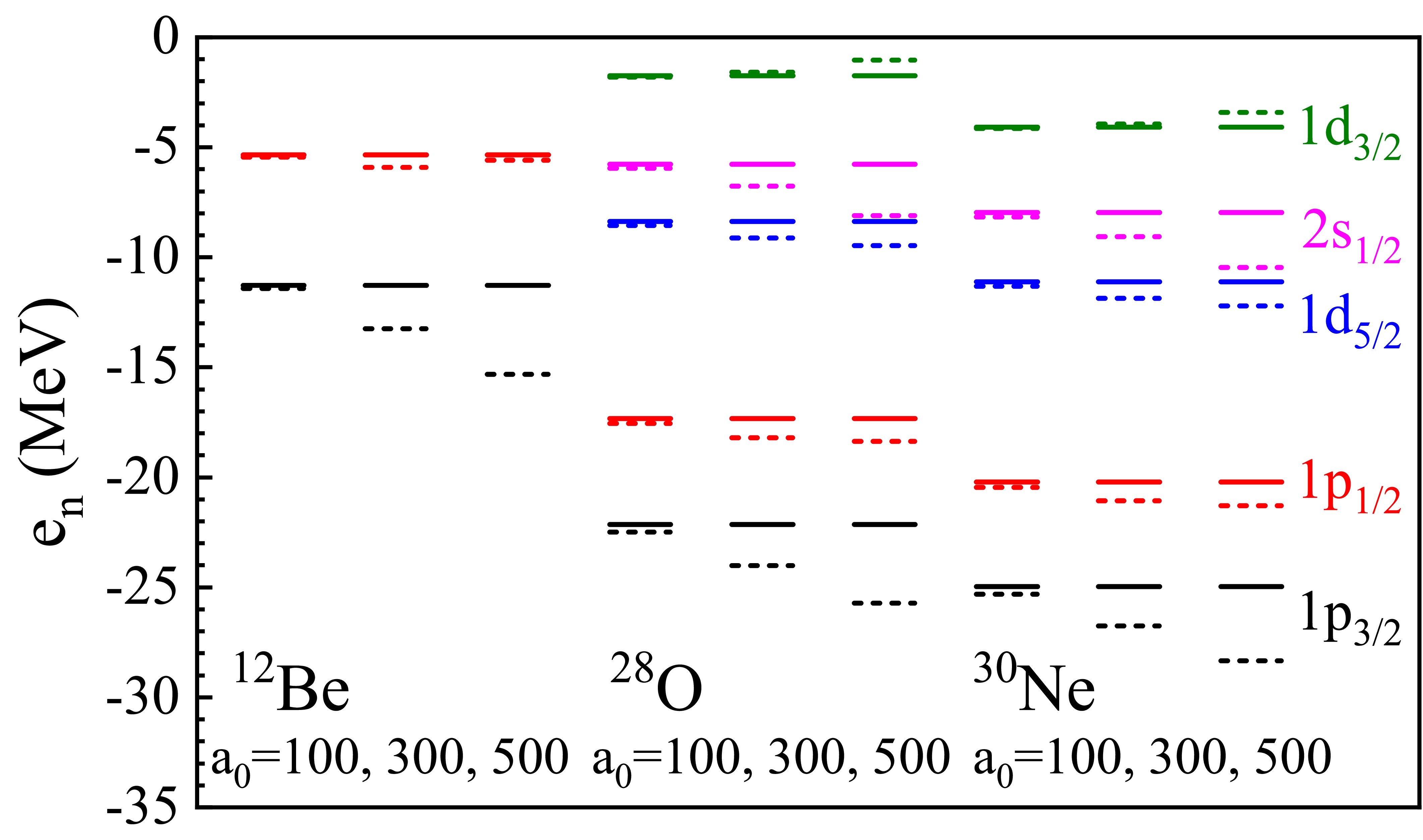
Figure 5. (color online) Partial neutron s.p. levels of spherical nuclei 12Be, 28O, 30Ne (solid bars), and their corresponding
$ K^- $ nuclei (dashed bars) with$ a_0=100 , \;300, \; 500{\;{\rm{MeV}}\;{\rm{fm}}^{3}} $ .To understand the shift of the neutron s.p. levels by the addition of a kaon, we analyze the Schrödinger Eq. (2). Note that both the central potential
$ V_n $ and the spin-orbit potential$ W_n $ are modified when including a kaon [47, 49]. We note that the spin-orbit potential of nucleons in the SHF approach with SLy4 force is [63, 70]$ W_q = \frac{W_0}{2}(\nabla\rho+\nabla\rho_q) \:, $

(13) with
$ q=n $ or p. Qualitatively, the strong$ K^-N $ attraction shrinks the nucleus. Similar effects have been discussed in the case of Λ hyperons [80, 83–85] or antiprotons [86, 87] bound in nuclei. This leads to a deepening of the mean fields in the core region of the nucleus, but a weakening in the peripheral part that is essential for weakly-bound valence neutrons. Moreover, there is always a delicate competition between$ V_n $ and$ W_n $ for some levels. To visualize these effects, we compare in Fig. 6 the potentials$ V_n(r) $ and$ W_n(r) $ of the drip-line nuclei 12Be, 30Ne, and their corresponding$ K^- $ nuclei, together with the partial densities$ \rho_i = 4\pi r^2 v_i^2 |\phi_i(r)|^2 $ of the various occupied neutron s.p. levels. Note that indeed the attractive$ K^-N $ interaction contracts the density distributions and thus enhances self-consistently the mean fields in the core region.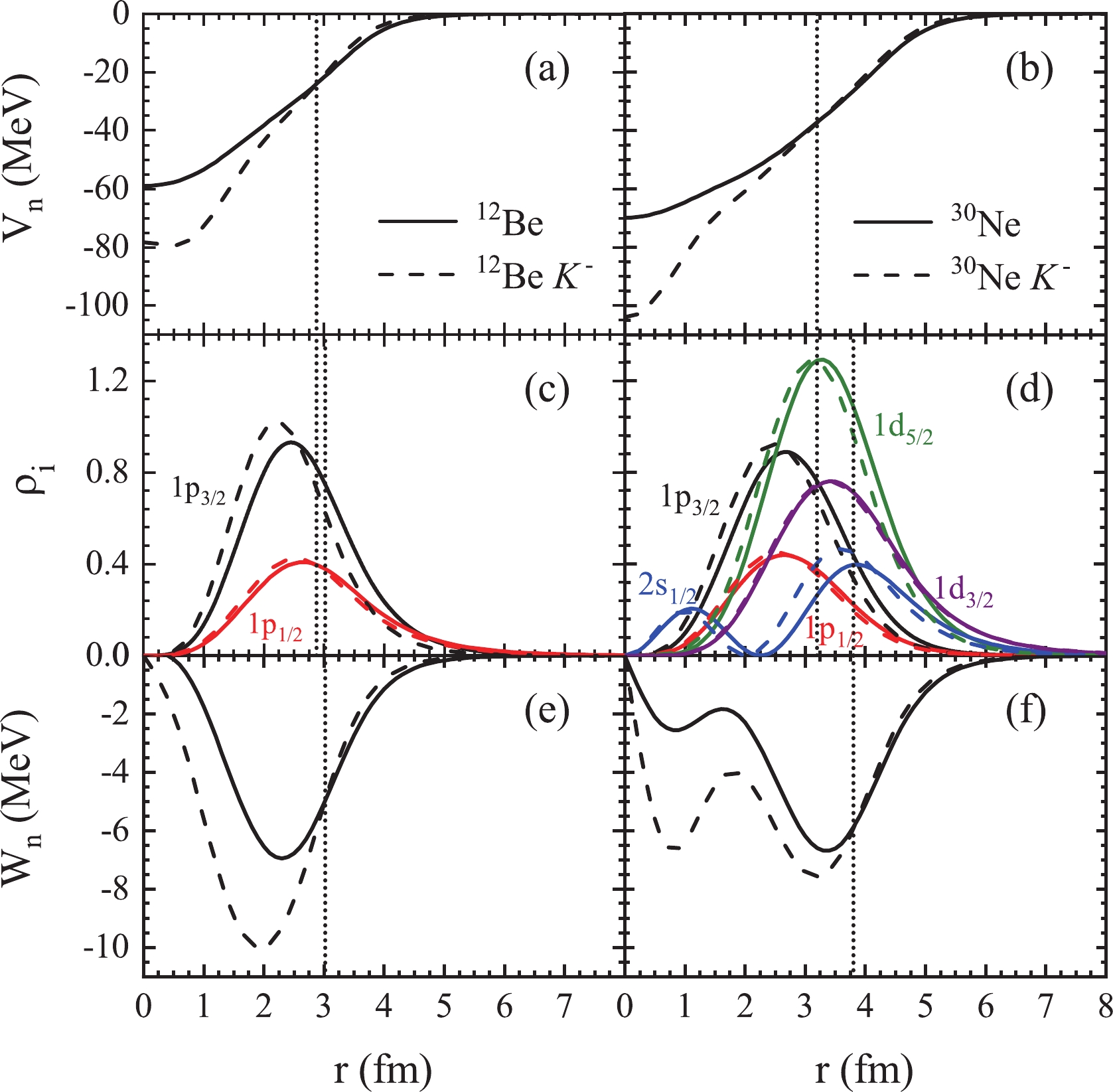
Figure 6. (color online) Mean fields
$ V_n(r) $ and spin-orbit potentials$ W_n(r) $ , and the partial densities$ \rho_i(r)= 4\pi r^2 v_i^2 |\phi_i(r)|^2 $ normalized to the actual occupation numbers of all occupied neutron s.p. levels in the normal nuclei 12Be and 30Ne and their corresponding$ K^- $ nuclei with$ a_0=500{\;{\rm{MeV}}\,{\rm{fm}}^{3}} $ . The vertical dotted lines label the crossings between the$ V_n(r) $ and$ W_n(r) $ of normal and$ K^- $ nuclei.Note that
$ V_n(r) $ and$ W_n(r) $ of$ ^{12}_{K^-} {\rm{Be}}$ and$ ^{30}_{K^-} {\rm{Ne}}$ are deeper than those of their normal nuclei for$ r\lesssim 2.9\; {\rm{fm}}$ ,$ r\lesssim 3.0\; {\rm{fm}}$ , and$ r\lesssim 3.2\; {\rm{fm}}$ ,$ r\lesssim 3.8\; {\rm{fm}}$ , respectively (dotted vertical lines). The strongly-bound neutron levels$ 1p_{1/2,3/2} $ ,$ 1d_{5/2} $ , and$ 2s_{1/2} $ of 30Ne are concentrated well within the core region$ r\lesssim3\; {\rm{fm}}$ , which indicates their gain of energy and the larger splitting of$ 1p_{1/2} $ and$ 1p_{3/2} $ in$ K^- $ nuclei, see Fig. 5. Similar phenomena are found in 12Be. On the contrary, a large amount of the$ 1d_{3/2,5/2} - $ state neutrons locate in the range of$ 3.2-3.8\; {\rm{fm}}$ , where the central potentials are smaller and the spin-orbit potentials are larger in$ K^- $ nuclei than in the normal nuclei. Therefore, the splitting of$ 1d_{5/2} $ and$ 1d_{3/2} $ is still enhanced in$ K^- $ nuclei. However, the most peripheral$ 1d_{3/2} $ neutrons are embedded in weaker both central and spin-orbit mean fields at$ r\gtrsim3.8\; {\rm{fm}}$ , which accounts for the upward shift of that level.These considerations explain the possible reduction of the neutron drip line by an added kaon. One might wonder whether a similar effect is possible for the proton dripline of heavier nuclei in spite of the additional
$ K^-p $ Coulomb attraction in this case, which causes an extension of the proton dripline in light nuclei, as observed before for$ ^{\ 5}_{K^-} {\rm{Be}}$ and$ ^{11}_{K^-} {\rm{O}}$ . This is addressed in Fig. 7 for the 36Ca nucleus, comparing calculations with and without Coulomb interaction, and note that even with Coulomb interaction the additional$ K^- $ meson still decreases the energy of the highest-occupied proton s.p. levels$ 1d_{3/2} $ . Thus, both an extension or reduction of the proton drip line are in principle possible, depending on the balance between the core shrinking effect and the Coulomb attraction. The quantitative realization of these effects depends in our current model on the values of the interaction parameters$ a_0 $ and$ x_0 $ , which can hopefully be fixed better with the aid of future experimental data.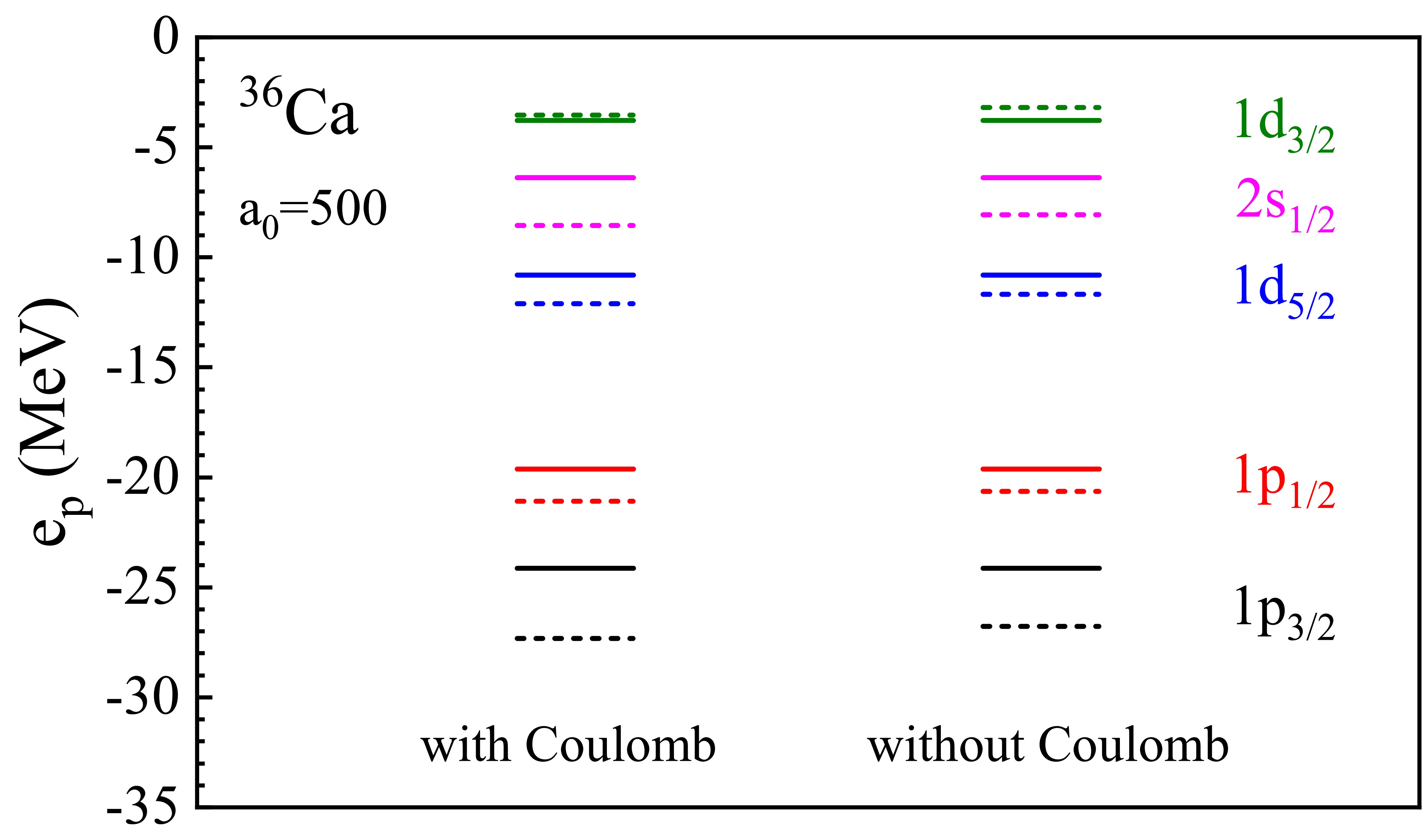
Figure 7. (color online) Partial proton s.p. levels of the spherical nucleus 36Ca (solid bars) and corresponding
$ K^- $ nucleus (dashed bars) with or without$ K^-p $ Coulomb interaction with$ a_0=500{\;{\rm{MeV}}\,{\rm{fm}}^{3}} $ .In conclusion, the
$ K^- $ meson increases the total binding energies for all nuclei, whereas it shows obvious impact on their deformation only for the lighter nuclei without shell closure. Moreover, the effect of an additional$ K^- $ meson on the nuclei near the neutron drip line depends on the highest-occupied neutron s.p. level. If this level is an orbit without spin-orbit splitting (e.g.,$ 2s_{1/2} $ ) or the lower orbit with splitting (e.g.,$ 1p_{3/2} $ and$ 1d_{5/2} $ ), the additional$ K^- $ may allow new unstable isotopes or only make the isotopes more stable, and thus extend or not shift the neutron drip line. If instead, this level is an upper orbit with splitting (e.g.,$ 1d_{3/2} $ ), the additional$ K^- $ can make some weakly bound nuclei unbound and reduce the neutron drip line, such as for O isotopes. The same mechanism is found for the proton dripline because of the small$ K^-p $ Coulomb interaction. This effect is caused by the shrinking of the nucleon wave functions due to a particularly strong attractive$ K^-N $ interaction. A similar role of an additional$ K^- $ in influencing s.p. levels was pointed out in the RMF approach [58]. -
We explore the effects of an additional
$ K^- $ meson on the ground-state properties of Be, O, and Ne isotopes using a SHF approach with a simple$ K^-N $ Skyrme-type force and the nuclear SLy4 force including a pairing contribution. The single-particle levels, binding energies, and quadrupole deformations are obtained by solving the SHF equations self-consistently. Owing to the attractive$ K^-N $ interaction, the additional 1s-state$ K^- $ meson shrinks the nucleon density distribution and increases its gradient. This increases the binding of strongly-bound inner single-particle orbits; however, this might decrease that of peripheral valence orbits, also by an enhanced spin-orbit splitting in the kaonic nuclei. Since the highest-occupied nucleon single-particle levels and one-nucleon separation energies determine the position of the unstable nuclei and driplines, corresponding effects are observed and analyzed in this paper.We note at this point that the treatment of kaonic nuclei in the static SHF approach can only be approximated, as their lifetime is short and an improved dynamical approach would be required for a more realistic description, including at least the imaginary parts of kaon wave function and mean field. In Ref. [49], we demonstrated already that the imaginary part influences only very weakly the
$ K^- $ removal energy.For a more quantitative evaluation, experimental data on medium-size kaonic nuclei are required. Recently the J-PARC E05 collaboration measured the inclusive missing-mass spectrum of the
$ ^{12}{\rm{C}}(K^-,p) $ reaction and extracted both real and imaginary parts of the potential depth [14]. Thus, in the future, our model could be improved by devising a more realistic kaon-nucleon Skyrme force and specifying the imaginary part of the kaon optical potential, aided by this current and future experimental data concerning$ K^- $ nuclei. Furthermore, the mean-field approximation employed here might be inadequate for light nuclei and weakly bound states, and a beyond-mean-field treatment [85, 88, 89] might be required for a more realistic modeling.
Effects of a kaonic meson on the ground-state properties of nuclei
- Received Date: 2021-12-20
- Available Online: 2022-06-15
Abstract: The effects of an additional





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: