-
The majority of the Universe's visible mass exists in the form of hadronic matter, and the underlying theory of hadrons is quantum chromodynamics (QCD). How the hadron acquires its mass is a fundamental and profound question [1–7], which is closely related to the confinement and hadron structure. The color confinement and nonperturbative structure of the hadrons are the peculiar challenging questions that garner considerable interest. Studying the meson structure provides a novel and excellent direction to understand the QCD predictions, because a meson is a simple object made of a quark and an anti-quark in the quark model.
There are two mass generating mechanisms for the hadron: Higgs Boson (HB) mechanism for the current quark mass and the Emergent Hadron Mass (EHM) mechanism for the complex interactions of quarks and gluons [8, 9]. Dynamical chiral symmetry breaking is a feature of the QCD theory [10–12]. Based on the mass function of gluon from QCD's Schwinger function, the gluon acquires a mass scale of
$ m_0\sim 0.43 $ GeV, at zero momentum [13–15]. In the infrared region, the quark also becomes heavy due to the radiations and absorptions of the gluons with the effective mass. A vivid metaphor is that the quark dresses up with gluons and turns into the constituent quark. For the proton mass decomposition, the chiral-limit mass from dynamical symmetry breaking is dominant; however, for the kaon mass decomposition, the interference between HB and EHM plays a dominant role with no chiral-limit mass. Kaon is the Nambu-Goldstone boson mode of QCD, thus the kaon is massless if the chiral symmetry is non-explicitly broken. In the real world, the masses of the dressed quarks in kaon are largely canceled by the attraction potential based on the wave function calculation of two-body bound state [4, 5, 8, 16].Together with the emergence of the kaon mass, Dyson-Schwinger equations (DSE) predict a broadening quark distribution function for the light quarks at the hadronic scale (a quite low scale
$ Q_0^2 $ where only the valence components of a hadron are resolved by a probe) [6, 17–21]. Compared to the up valence quark distribution, the strange valence quark distribution is narrower, owing to the heavier mass from the HB mechanism. Measuring the kaon structure will provide a critical test on this significant HB modulation of the EHM strange quark distribution [6, 21]. To completely understand the EHM phenomenon, we should simultaneously answer why the proton mass is heavy while the pion and kaon masses are light. Investigating the kaon structure provides a clear way to see the interplay between HB and EHM, owing to the large coupling of strange quark to Higgs boson. Moreover, the kaon structure measurement will test the fruitful calculations from the nonperturbative approaches such as the continuum phenomenology of DSE [6, 18, 21–24] and lattice QCD (LQCD) [25–29].In the experiment, the proton structure function has been measured precisely with the help of high energy lepton beams or colliders worldwide. However, the experimental data on the kaon structure function are extremely scarce. There are only eight data points related to the quark distribution inside kaon, which were accessed via the kaon-induced Drell-Yan process of the NA3 experiment at CERN more than fourty years ago [30]. Therefore, an increasing number of experimental projects are proposed to achieve better understanding of the kaon structure and EHM mechanism in the pseudoscalar meson sector. On the AMBER facility at CERN, the implementation of the kaon beam will provide an extraction of the parton distribution functions (PDFs) of real kaon from the Drell-Yan reaction [31]. With the upgrade, the precision of the data at AMBER will be better than that of NA3 data. At the JLab of 12 GeV upgrade, the Λ tagged deep inelastic scattering (DIS) process will be exploited to study the structure of the virtual kaon [32, 33]. This approach is similar to the leading neutron tagged DIS performed at HERA decades ago [34, 35], for the determination of the pion structure function. To acquire the kaon structure over a wide range of
$ Q^2 $ and$ x_{\rm K} $ , a high center-of-mass (c.m.) energy of the scattering is required. Thus, the electron-ion collider in US (EIC-US) [36–38] and in China (EicC) [7, 39, 40] will provide the good opportunities for realization of this goal.As there is almost no experimental data on kaon structure, there is also no global analysis on the kaon PDFs to date. Nevertheless, in our previous work [41, 42], we have determined the kaon PDFs from a model-dependent analysis of the eight data points of NA3 experiment [30], based on the dynamical parton distribution model. According to the JAM analysis of pion PDFs [43], the addition of the leading neutron tagged DIS data of H1 [34] and ZEUS [35] significantly reduce the uncertainties of sea quark and gluon distributions. Similarly, the leading Λ tagged DIS data in the future will help in fixing the sea quark and gluon distributions of the kaon.
Now there are ongoing discussions on building a polarized electron-ion collider in China, by adding an electron beam to the high-intensity heavy ion accelerator facility [7, 39, 40]. The optimal c.m. energy of the collision at EicC will be around 17 GeV [40]. This would provide an excellent opportunity to probe the kaon structure in the range of
$0.02\lesssim x_{\rm K} \lesssim 1$ , i.e., from the sea quark region to the valence quark region. Judged by the c.m. energy, EicC optimally bridges the measurement at JLab-12 GeV [32, 33] and the measurement at EIC-US [36–38], which will play an essential role in the full mapping of the kaon structure. The AMBER facility at CERN [31] will run at a similar c.m. energy to EicC; however, the measurement is on the Drell-Yan reaction, which differs from the tagged DIS process. Hence, the direct comparison between the AMBER and EicC data at the similar scale will cross check each other and provide us a more definitive conclusion of the kaon structure in the sea quark and valence quark region. In this work, we suggest a kaon structure experiment at EicC via the leading Λ baryon tagged DIS process. The feasibility and impact of the experiment will be demonstrated based on a simulation. This work is similar to our previous simulation study of the pion structure at EicC [44].The remainder of this paper is organized as follows. The underdiscussed EicC is briefly introduced in Sec. II. The model for the leading Λ baryon tagged DIS is described in Sec. III. The input kaon PDFs for the simulation are presented in Sec. IV. The invariant kinematic and finalstate kinematic distributions of the Monte-Carlo simulation are presented in Sec. V. The error projections of the proposed kaon structure function measurement are presented in Sec. VI. The background processes and detector capabilities are discussed in Sec. VII. Finally, some discussions and a concise summary are provided in Sec. VIII.
-
The proposed polarized electron-ion collider in China is a future high-energy nuclear physics project that attempts to achieve the precise measurements of the nucleon structure in the sea quark region, exotic hadron states, nuclear matter effect, etc. EicC will cover the variable c.m. energies from 15 to 20 GeV, with the luminosity above
$ 10^{33} $ cm$ ^{-2} $ s$ ^{-1} $ [40]. In this work, we assume EicC runs with the electron beam energy of 3.5 GeV and the proton beam energy of 20 GeV. The luminosity of EicC will be around 100 times of the previous HERA collider in Germany [34, 35]. Therefore EicC will provide more precision data on the sea quark structures of the hadrons. The EIC in US will focus on the gluon-dominant region. In the future, significantly more details will be unveiled by the new facilities in the high precision era.For the conceptual design of EicC, the central detector and end-cap detector systems will be constructed inside and around the solenoid magnet with the cutting-edge technologies [40]. The forward detector complex of high performance would also be implemented in both beam directions, such as the Roman pot inside the beam pipe, the off-momentum detectors around the beam line, and the zero-degree calorimeter (ZDC). Hence, the EicC facility would provide us a good opportunity to tag the high energy Λ baryon of high pseudorapidity, measure the leading Λ tagged DIS. In addition, reconstruction the
$ \Lambda $ from the decay proton and$ \pi^{-} $ encounters numerous difficulties due to the deflections of the charged particles by the complicated magnets around the beam pipe and the challenges of particle identifications of high energy electron, pion, kaon, and proton. It is more feasible to reconstruct the Λ baryon by measuring its neutral decays (neutron and$ \pi^0 $ ) with ZDC. Identifications of neutron and$ \pi^0 $ could be realized by differentiating the hadronic and electromagnetic showers. -
To probe the kaon structure in the high-energy
$ e-p $ collision, we exploit the abundant "kaon cloud" from proton dissociation due to the large coupling$g_{\rm N\Lambda K}$ . This type of electron-"meson cloud" scattering dominates in the t channel with one meson exchange, called the Sullivan process [45], which is shown in Fig. 1. To ensure that the electron beam hits the "kaon cloud," we need to tag the leading Λ of high energy and small transverse momentum. The Λ baryon acts as the spectator carrying a large fraction of the incoming proton's momentum and going far-forward. To measure the kaon structure, we also need to ensure that the virtual kaon is broken up by the high energy probe. In literature, the internal structure of the quasi-real kaon in the process resembles the internal structure of the real kaon, provided the momentum transfer is not large ($ \lesssim 0.9 $ GeV$ ^2 $ ) [46].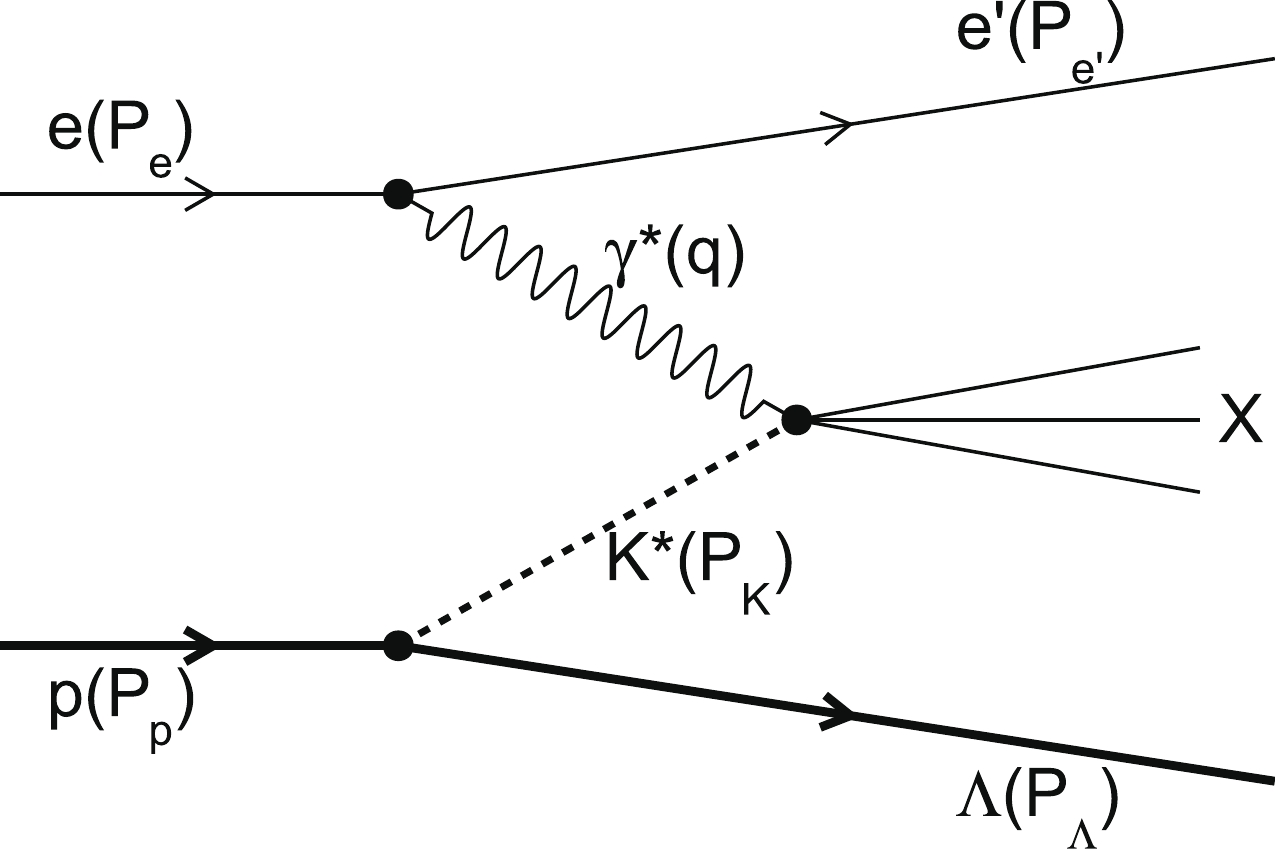
Figure 1. The Sullivan process [45] for deep inelastic scattering with the production of a leading Λ baryon. The leading Λ carries a significant amount of the momentum of the beam proton.
The invariant kinematical variables describing the leading Λ tagged DIS are: the momentum square
$ Q^2 $ of the photon probe, Bjorken variable$x_{\rm B}$ , inelasticity y of the scattering, longitudinal momentum fraction$ x_{\rm L} $ carried by the Λ baryon, and square of the momentum transfer t from the proton to the virtual kaon. According to the momenta of the particles labeled in Fig. 1, these kinematical variables are defined as,$ \begin{aligned}[b] Q^2 \equiv &-q^2,\quad x_{\rm B} \equiv \frac{Q^{2}}{2P_{\rm p} \cdot q},\quad y \equiv \frac{P_{\rm p} \cdot q}{P_{\rm p} \cdot P_{\rm e}},\\ x_{\rm L} \equiv & \frac{P_{\rm \Lambda}\cdot q}{P_{\rm p}\cdot q},\quad t \equiv (P_{\rm p} - P_{\rm \Lambda})^2 = p_{\rm K}^2. \end{aligned} $

(1) In the definition,
$ x_{\rm L} $ denotes the longitudinal momentum fraction (energy fraction approximately) of the final Λ baryon to the incoming proton. In the DIS experiment, the leading Λ tagged process dominates in the large-$x_{\rm L}$ region ($ \gtrsim 0.5 $ ), hence a proper cut on the$x_{\rm L}$ variable efficiently selects the events that are sensitive to the kaon structure. In addition, t denotes the momentum square of the virtual kaon, which is an important variable for the extrapolation of the real kaon structure.To estimate the statistical error of the measurement, we need to know the number of events of the interests. Therefore, we first need to know the cross section of the reaction. With the azimuthal angle integrated, the four-fold differential cross section of the leading Λ tagged DIS is expressed as [34, 35, 47],
$ \begin{aligned}[b] \frac{{\rm d}^4\sigma({ep\rightarrow e\Lambda X})}{{\rm d}x_{\rm B}{\rm d}Q^2{\rm d}x_{\rm L}{\rm d}t} =& \frac{4\pi\alpha^2}{x_{\rm B}Q^4}\left(1-y+\frac{y^2}{2}\right)F_2^{\rm L\Lambda(4)}(Q^2, x_{\rm B}, x_{\rm L}, t)\\ =& \frac{4\pi\alpha^2}{x_{\rm B}Q^4}\left(1-y+\frac{y^2}{2}\right)\\&\times F_2^{\rm K}\left(\frac{x_{\rm B}}{1-x_{\rm L}} ,Q^2\right)f_{\rm K^+/p}(x_{\rm L},t).\\[-15pt] \end{aligned} $

(2) From this equation, it can be found that we can extract the four-fold leading-Λ structure function
$ F^{\rm L\Lambda(4)}_2 $ . In the kaon pole model, the leading-Λ structure function can be factorized into the product of the kaon structure function$ F_2^{\rm K} $ and kaon flux around the proton$ f_{\rm K^+/p} $ . In an effective theory of the kaon pole, the kaon flux is given by [34, 35, 47],$ \begin{aligned}[b] f_{\rm K^+/p}(x_{\rm L},t)= & \frac{1}{2\pi}\frac{g^2_{\rm N\Lambda K}}{4\pi}(1-x_{\rm L})\\& \times \frac{-t}{(m_{\rm K}^2-t)^2} {\rm exp}\left(-R^2_{\rm \Lambda K}\frac{t-m_{\rm K}^2}{1-x_{\rm L}}\right), \end{aligned} $

(3) in which the coupling is
$ g_{\rm N\Lambda K}^2/4\pi = 14.7 $ , and$ R_{\rm \Lambda K} = 1 $ GeV$ ^{-1} $ is a form-factor parameter representing the radius of the proton's$\Lambda-\rm K$ Fock state. With these formulae presented above, we can compute the cross section of the leading Λ baryon tagged DIS process. -
To estimate the cross section and build an event generator for the process, the last input is the PDFs of kaon. Because there is almost no experimental data on the kaon structure, no global analysis exists on the kaon PDFs to date. Therefore in this work, we adopt the kaon PDFs provided by a model-dependent analysis of the NA3 data only [41]. This analysis is based on the dynamical parton distribution model with only valence quark distributions at
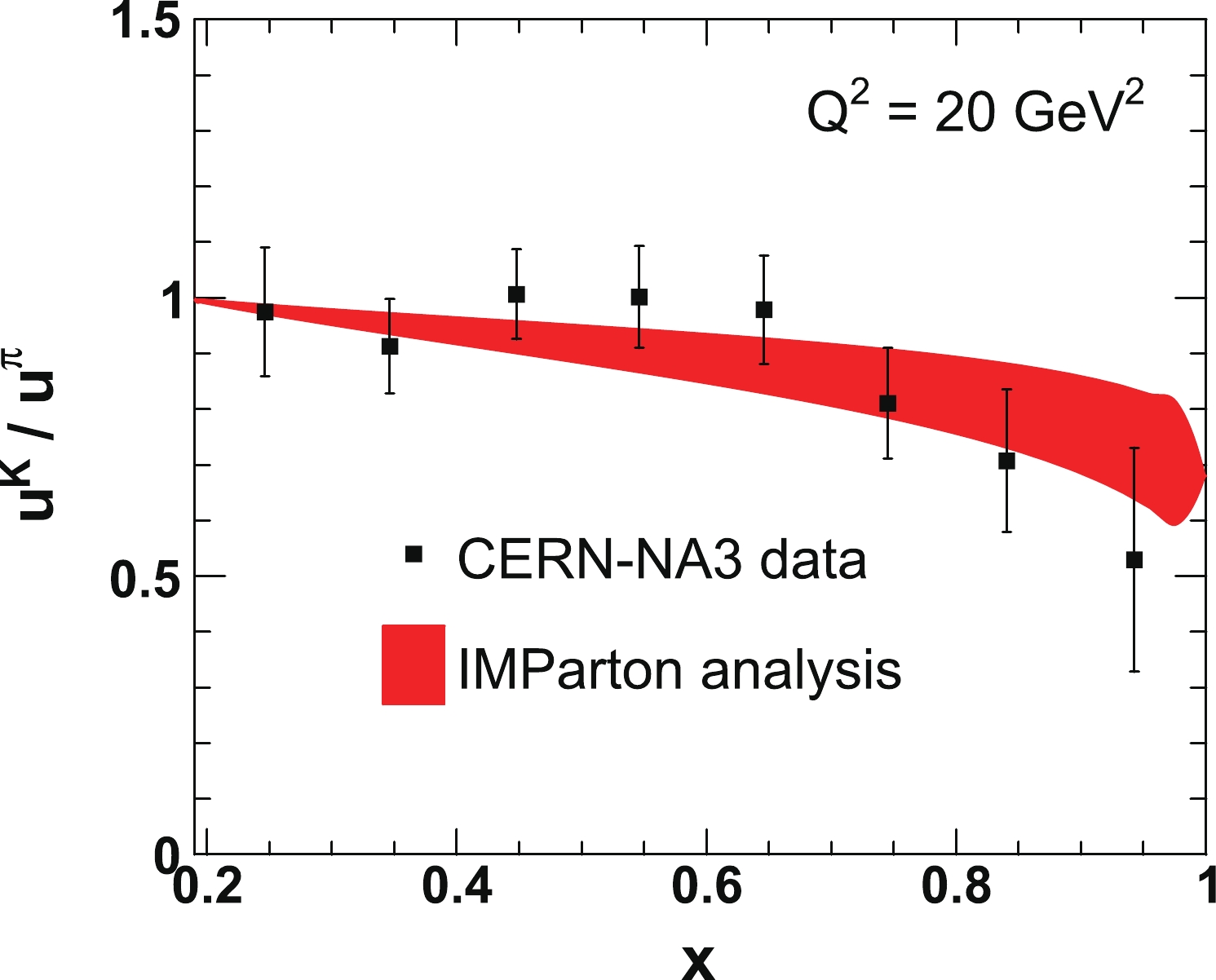
$ Q_0^2 $ , where the sea quark and gluon distributions are completely produced from the QCD fluctuations. Fig. 2 presents the ratios of the kaon$ \bar{u} $ distribution to the pion$ \bar{u} $ distribution, compared with the NA3 data. The experimental data indicate that the kaon up quark distribution is lower than the pion up quark distribution in the valence region. We observe that the used kaon PDFs in this work are consistent with the only experimental data obtained decades ago [30].Using the cross-section model described in the previous section and kaon PDFs, we calculate the differential cross section of leading Λ tagged DIS as a function of
$ x_{\rm L} $ , which is displayed in Fig. 3. The model prediction for the differential cross section of the leading neutron tagged DIS process is also presented in this figure. It can be observed that the cross section of the leading Λ tagged process is substantially smaller than that of the leading neutron tagged process. The other finding is that the cross section of the leading Λ tagged DIS dominates in a relatively lower$ x_{\rm L} $ region. This is because the "kaon cloud" (with a heavier mass than the "pion cloud") also carries a considerable amount of the momentum of the beam proton. Hence, in the analysis, we should adopt a lower cut on$ x_{\rm L} $ to select the events of interests.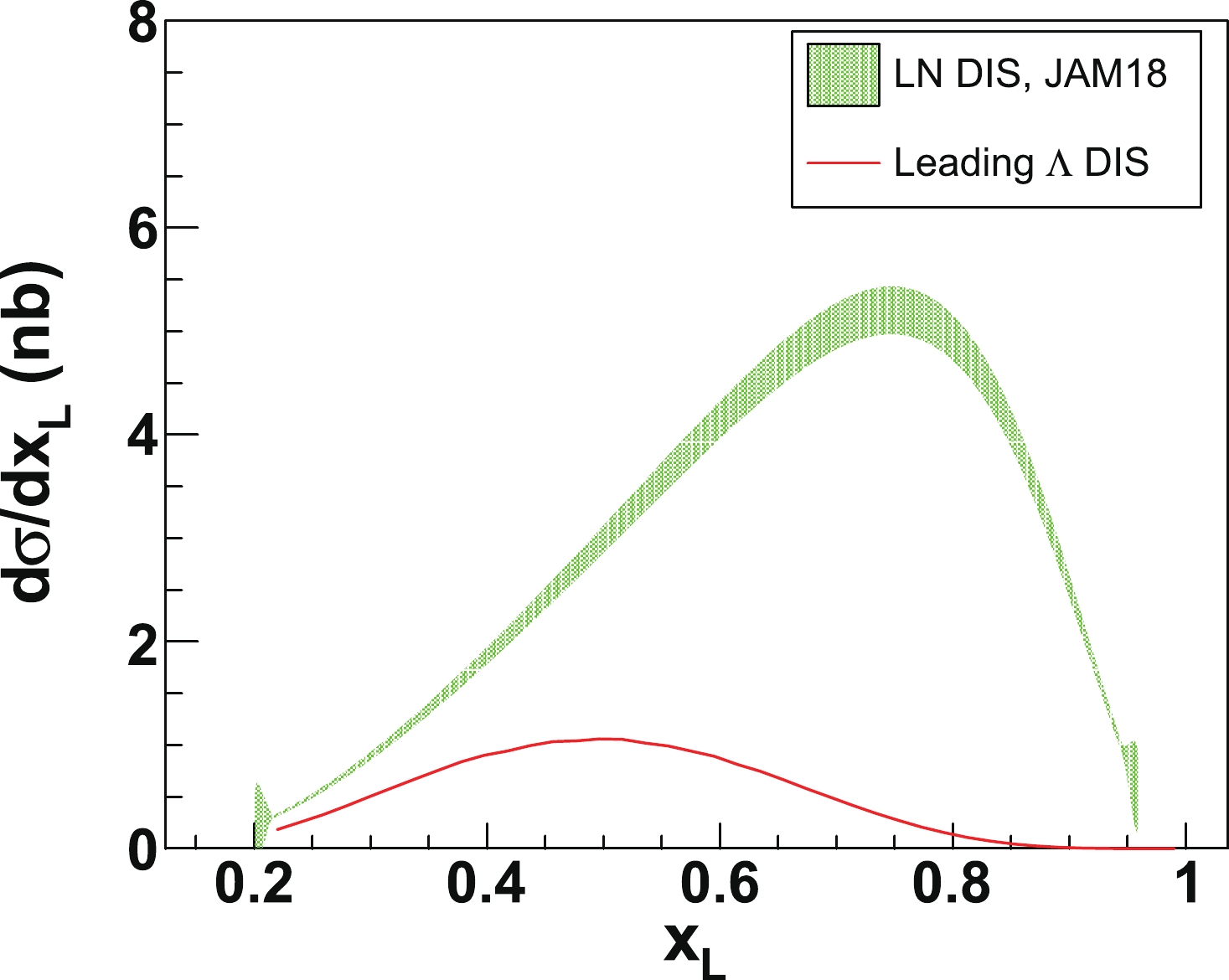
Figure 3. (color online) The one-fold differential cross section as a function of the longitudinal momentum fraction
$ x_{\rm L} $ of the far-forward Λ. The cross section of leading Λ tagged DIS is based on the model described in this work. The cross section of leading neutron tagged DIS is taken from the reference [44] for comparison, which is based on the JAM pion PDFs [43]. -
Following the theoretical framework discussed in Sections III and IV, we develop an event generator program for the leading Λ tagged DIS process. In the simulation, the electron and proton beam energies are taken to be 3.5 GeV and 20 GeV, respectively. The z direction of the coordinate is chosen to be the momentum of the incoming proton beam. To efficiently generate the events in the kinematic region of interests, we set the following ranges of kinematics in the Monte-Carlo simulation:
$ x_{\rm B,min}<x_{\rm B}<1 $ ,$ 1\; {\rm GeV}^2 < Q^2 < 50\; {\rm GeV}^2 $ ,$ 0.01\; {\rm GeV}^2 < $ $ -t < 1\; {\rm GeV}^2 $ , and$ 0.5 < x_{\rm L} < 1 $ .Figure 4 presents the cross-section weighted invariant kinematical distributions of the leading Λ tagged DIS events simulated, which are projected in two-dimensional spaces. The events are mainly distributed in the region of low
$ Q^2 $ , small$ x_{\rm B} $ , small$ x_{\rm K} $ , and small y. Figure 5 presents the energy and pseudorapidity distributions of the final-states: electron, Λ, and neutral decays of Λ (neutron and$ \pi^0 $ ). It can be observed that all the scattered electrons can be collected with the central detectors at EicC, while the leading Λ of high energy and large rapidity can only be detected with the forward detectors. The decay neutron of Λ mainly distributes around the pseudorapidity of 5. The decay$ \pi^0 $ of Λ primarily distributes around the pseudorapidity of 3.5. There is a small portion of$ \pi^0 $ that moves toward the end-cap detector system.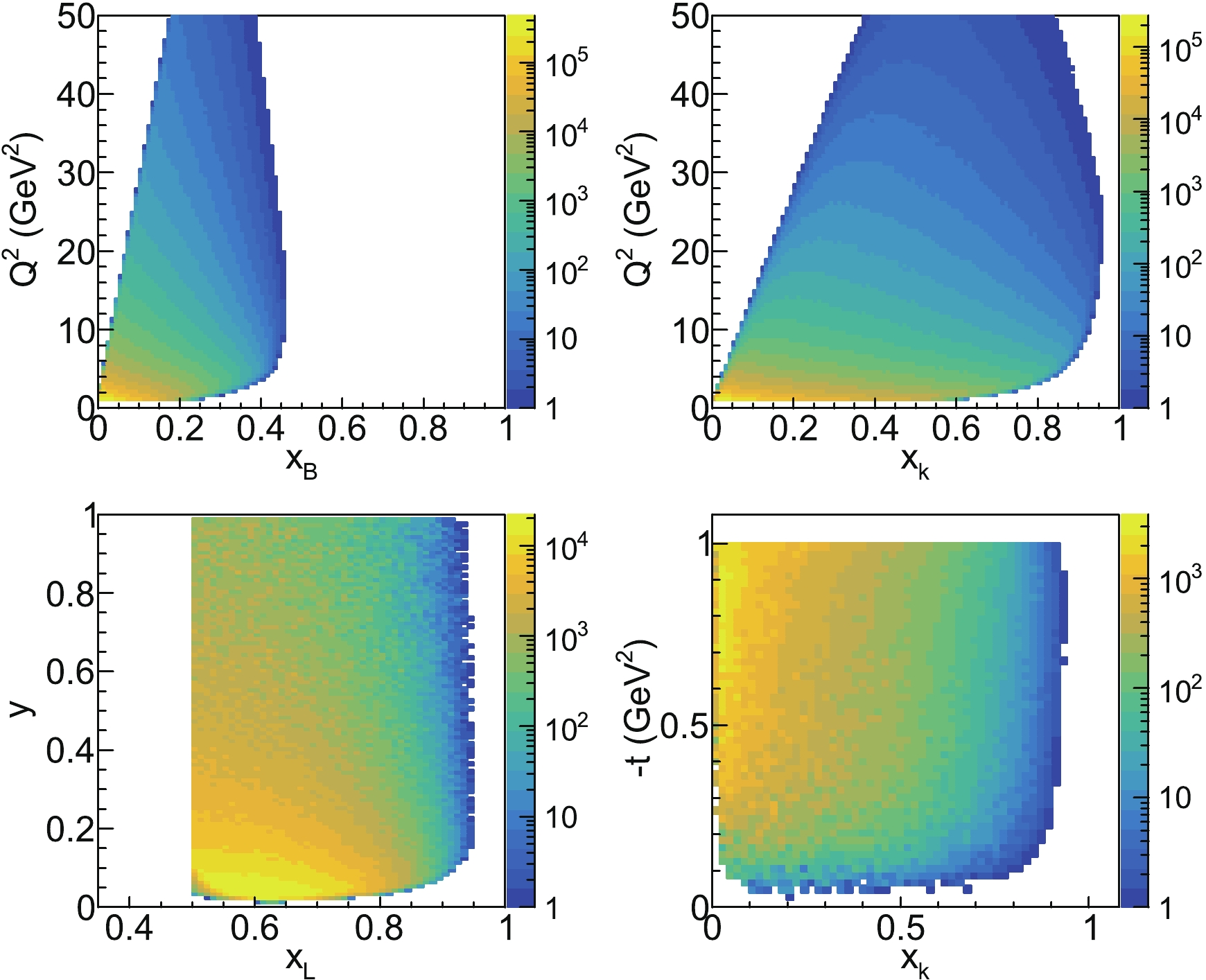
Figure 4. (color online) The distributions of the invariant kinematical variables
$ Q^2 $ ,$ x_{\rm B} $ ,$ x_{\rm K} $ ,$ x_{\rm L} $ , y, and$ -t $ , for the simulation data of leading Λ baryon tagged DIS at EicC.
Figure 5. (color online) The Monte-Carlo simulated energy and pseudorapidity distributions of the measured final-state particles: electron and Λ. The distributions of the decays (neutron and
$ \pi^0 $ ) of Λ are also shown.To comprehensively investigate the forward Λ decay, we also present the distributions of the two photons from the
$ \pi^0 $ decay. Figure 6 presents the energy and θ angle distributions of Λ, n,$ \pi^0 $ , and γ. It can be observed that most of the neutrons from Λ decay move to ZDC. However, some photons of low energy from the$ \pi^0 $ decay move toward the central and end-cap detectors, and some photons of high energy from$ \pi^0 $ decay move to ZDC. To discard the background noise of the detector, we set the low-energy threshold to be 200 MeV for the high energy photon detection. According to the conceptual design of EicC, we choose the θ angle cut to be$ \theta_{\gamma}<3^\circ $ or$ 6^\circ <\theta_{\gamma}<174^\circ $ .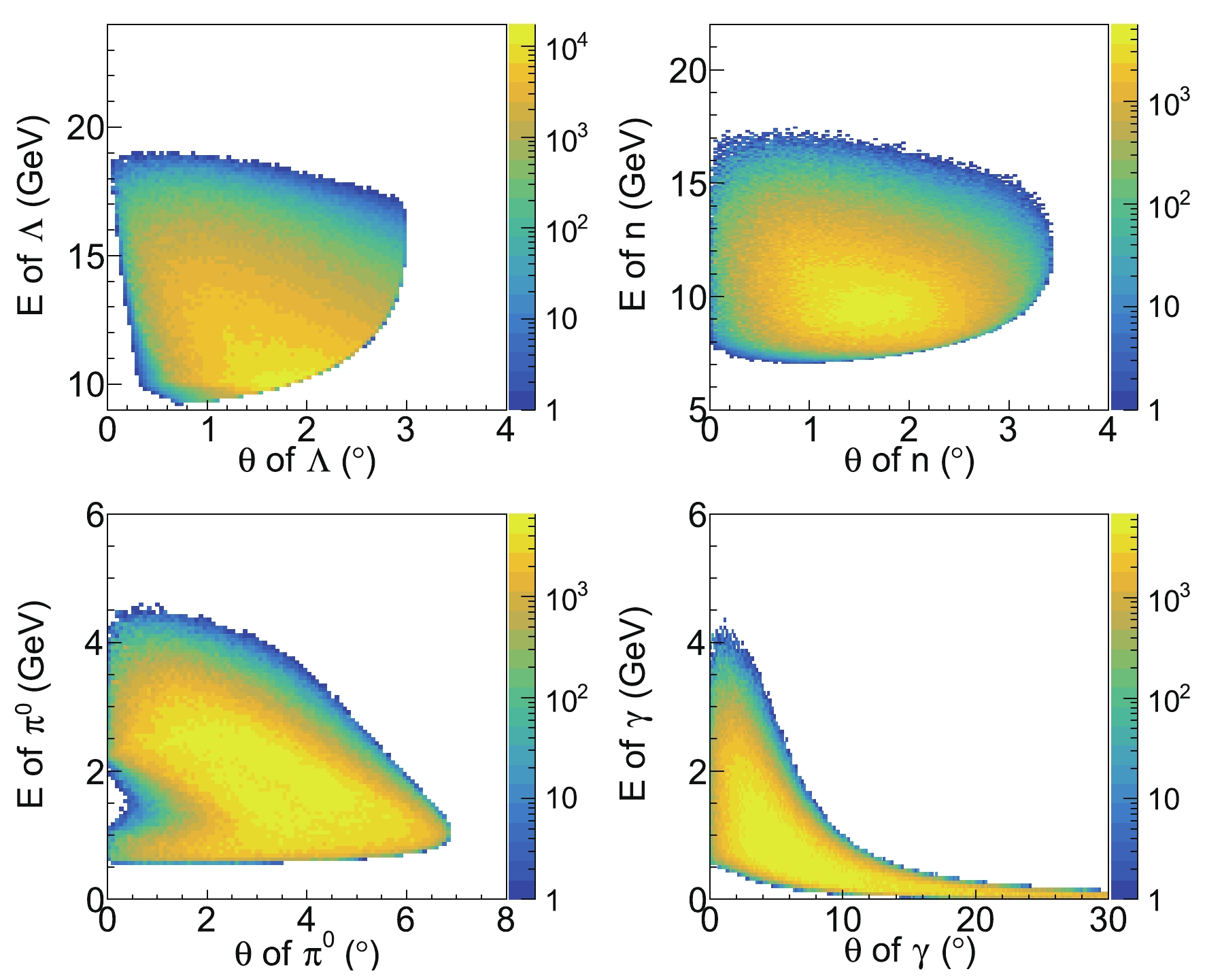
Figure 6. (color online) The energy and θ angle distributions of high momentum far-forward Λ baryon and its decay chains, for the simulation data of leading Λ baryon tagged DIS at EicC.
The decay vertexes of the leading Λ's from the Sullivan process are presented in Fig. 7, which can provide some guidance for the future analysis of the vertex reconstruction. The decay vertexes spread in a broad range of space. Most of the decay vertexes are close to the beam line with a small transverse distance. In addition, most of the decay vertexes are within 200 cm from the production vertex. We could choose a proper cut to select the leading Λ tagged DIS events.
-
To compute the statistical error of the kaon structure function, we simply need to compute the statistical error of the cross section, because these two experimental observables are directly related. The statistical uncertainty of the cross section measurement depends on the number of events collected during the experiment. To estimate the number of events of an experiment, we need to know the cross section of the reaction (provided by the model described in above sections), the integrated luminosity of the experiment, and the event selection criteria of the reaction. For a year operation of good quality beams, EicC could accumulate approximately 50 fb
$ ^{-1} $ integrated luminosity of$ e-p $ collisions. Hence, we take the integrated luminosity of 50 fb$ ^{-1} $ for the simulation. To ensure that the collected events are mainly from electron-"kaon cloud" collisions, we take the following event selection criteria:$ x_{\rm L}>0.55 $ ,$ P_{\rm T}^{\rm \Lambda}<0.5 $ GeV,$M_{X} > 1$ GeV, and$ W>2 $ GeV.$ x_{\rm L}>0.55 $ and$ P_{\rm T}^{\rm \Lambda}<0.5 $ GeV ensure that the events are from the Sullivan process of the t channel, while$ W > 2 $ GeV is the conventional DIS criterium. Figure 8 presents the energy and pseudorapidity distributions of the Λ and its decays, after the event selection criteria, geometrical acceptance of the detectors, and low energy threshold of the calorimeters. The zero-degree calorimeter is suggested to cover the angle from 0 to 3 degrees around the beam, to collect more neutrons and photons.
Figure 8. (color online) The energy and θ angle distributions of high momentum far-forward Λ baryon and its decay chains, with the geometric cut and energy threshold of electromagnetic calorimeters applied, for the simulation data of leading Λ baryon tagged DIS at EicC.
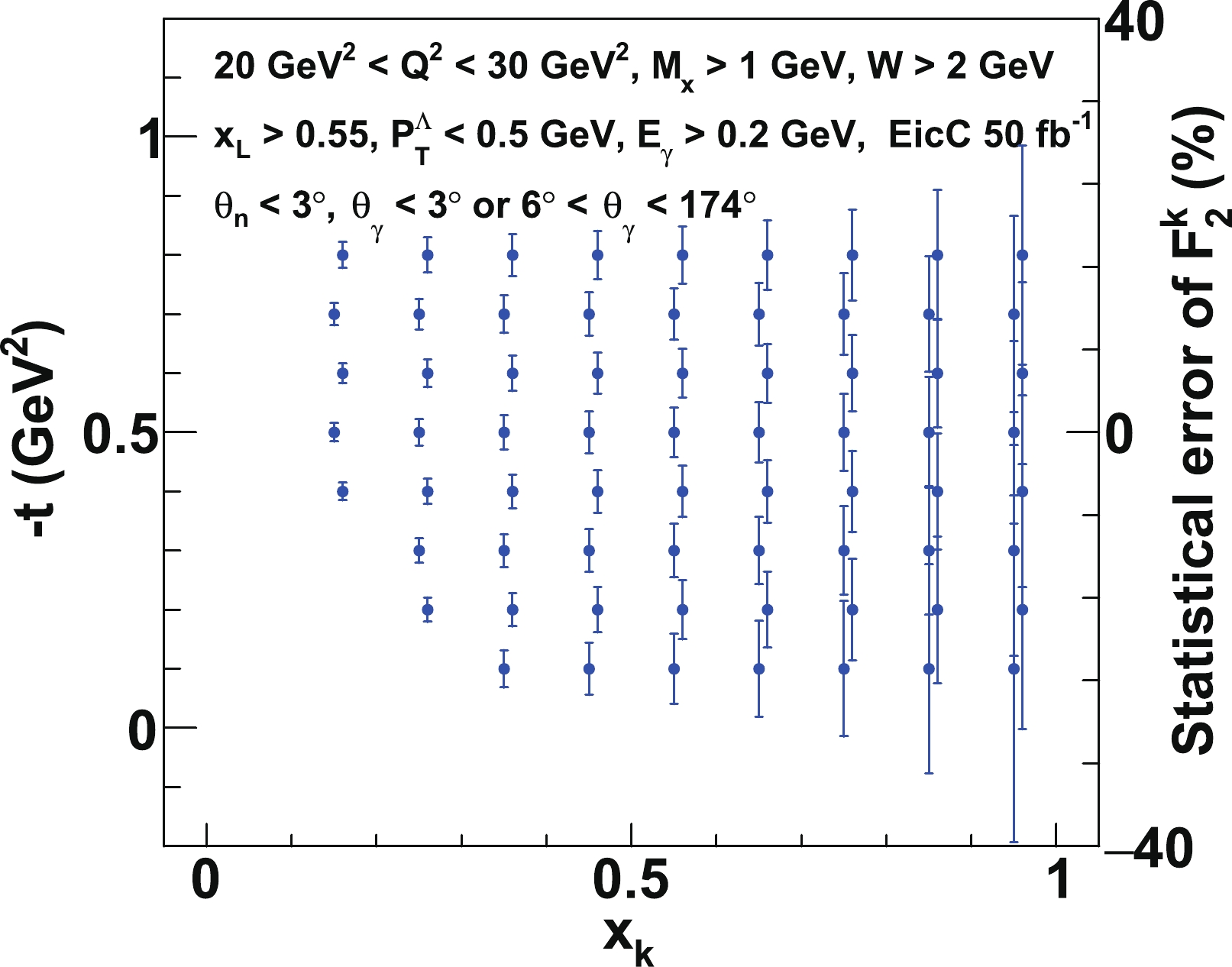
To obtain the cross section at each kinematical point, we need to count the number of events in different kinematical bins. The typical kinematical binning is presented in Fig. 9, for the events in the
$ Q^2 $ range of$ (3,5) $ GeV$ ^2 $ . We focus on the events at relatively small$ |t| $ ($ <0.85 $ GeV$ ^2 $ ), a condition suggested by DSE calculation to ensure that the extrapolation to the real kaon structure is valid and effective [46]. With the event selection criteria discussed in the above paragraph, we calculate the number of events in each bin, using the following formula,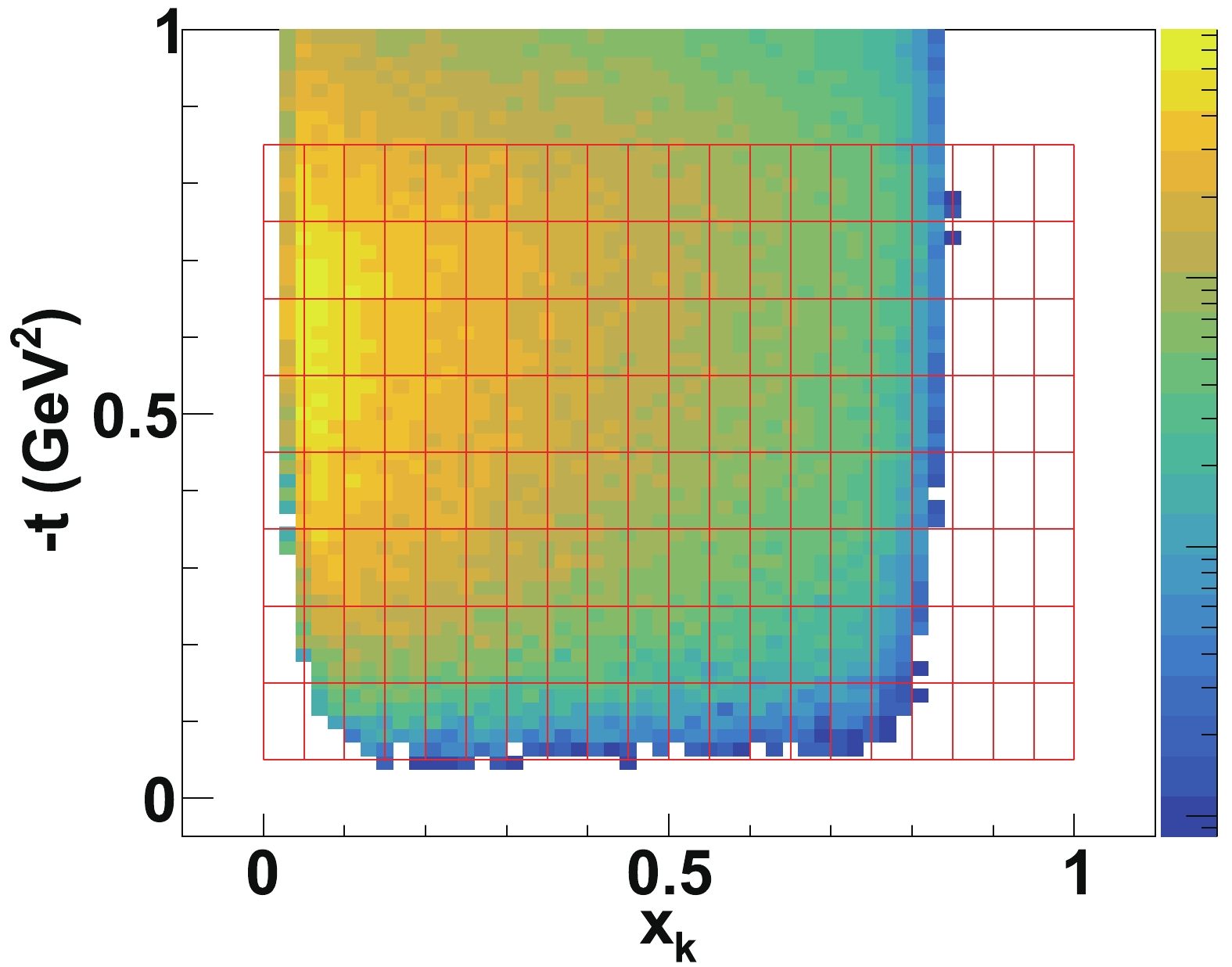
Figure 9. (color online) The binning scheme in
$ -t $ versus$ x_{\rm K} $ plane for the Monte-Carlo data in$ Q^2 $ range of$ (3,5) $ GeV$ ^2 $ .$ \begin{align} N_{i} = L \overline{\sigma}_{i} B_r \epsilon \Delta x_{\rm K} \Delta Q^2 \Delta x_{\rm L} \Delta t (1-x_{\rm L}), \end{align} $

(4) where L is the integrated luminosity of the suggested experiment,
$\overline{\sigma}_{i}$ is the averaged differential cross section in kinematical bin i,$ B_r $ is the branching ratio of Λ decaying into the neutron and two photons,$ \epsilon $ is the detector efficiency for collecting all the final states of the reaction, i.e.,$ \epsilon = \epsilon_n * \epsilon_{\gamma_1} * \epsilon_{\gamma_2} $ , the factor$(1-x_{\rm L})$ is the Jacobian coefficient for the transform from$ x_{\rm B} $ space to$ x_{\rm K} $ space, and together, the other factors express the size of the kinematical bin. For the detectors of common performance, we assume$ \epsilon_{\gamma} = $ 90% for detecting and identifying the photons from$ \pi^0 $ decay, and$ \epsilon_n = $ 50% for detecting and identifying the far-forward neutrons. Finally, the relative statistical error of the kaon structure function$ \delta(F_2^{\rm K}) / F_2^{\rm K} $ in each kinematical bin is estimated to be$1/\sqrt{N_{i}}$ .By counting the simulated events in each kinematical bin, we calculate the statistical uncertainty of the kaon structure function for the proposed experiment at EicC. Fig. 10 presents the relative statistical error of
$ F_2^{\rm K} $ in the kinematical bin of$ 3\; {\rm GeV^2}<Q^2<5\; {\rm GeV^2} $ . It can be observed in the plot that the statistical uncertainty increases with an increase in$ x_{\rm K} $ . For the data at$ x_{\rm K}<0.3 $ , the projected statistical uncertainty is smaller than 1%. With the$ x_{\rm K} $ increasing up to approximately 0.85, the statistical uncertainty is approximately 5%. In the future, these precise data will provide an excellent test of the predictions of lattice QCD and DSE. At higher$ Q^2 $ values up to 50 GeV$ ^2 $ , the statistical uncertainty projections are also projected and illustrated in Fig. 11 ($ Q^2\sim 25 $ GeV$ ^2 $ ) and Fig. 12 ($ Q^2\sim 40 $ GeV$ ^2 $ ). With wider kinematical bins and fewer data points, the estimated statistical precision of$ F_2^{\rm K} $ measurement remains optimal. For the data points in the region of$ x_{\rm K}<0.6 $ , the relative statistical uncertainties are less than 5%. In addition, for the data points in the region of$ x_{\rm K}<0.8 $ , the relative statistical uncertainties are less than 10%. These experimental data over a wide range of$ Q^2 $ will provide an interesting opportunity to test the QCD evolution equations in the kaon sector, as well as extract the gluon distribution in the kaon via the scaling violation.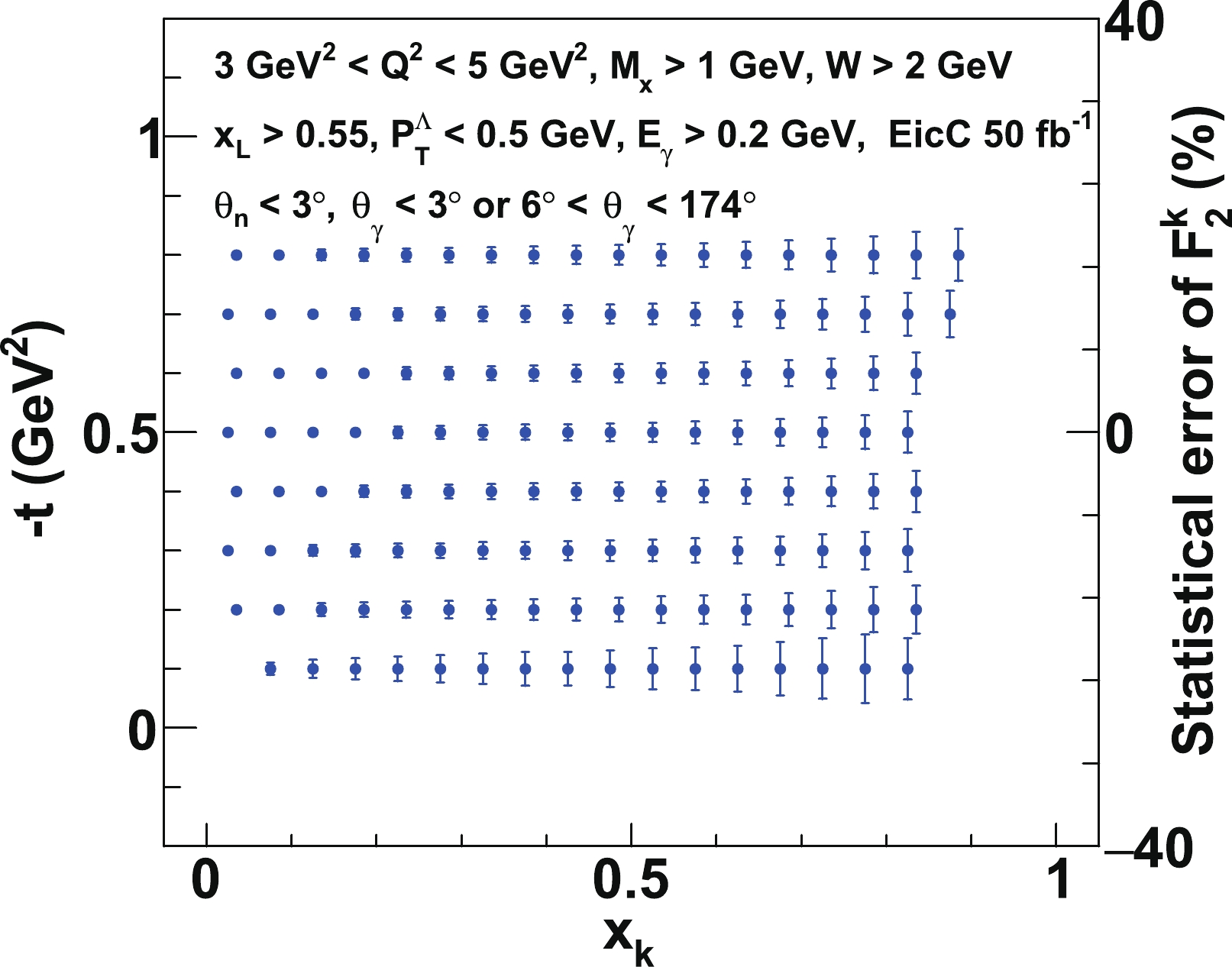
Figure 10. (color online) The statistical error projections of the kaon structure function at
$ Q^2 \sim 4 $ GeV$ ^2 $ . We calculate the statistical error at each bin center. The right axis is a scale indicating the size of the statistical error. -
In addition to the Sullivan process shown in Fig. 1, the conventional DIS also produces Λ baryons. The Λ baryon that originates from the parton hadronization process is the background of the Sullivan process of interests. To estimate the strength of the background from the conventional DIS process, we performed a simulation of e-p collisions with a pythia6.4 event generator [48]. Figure 13 presents the
$x_{\rm L}$ -distributions of the Sullivan and conventional DIS processes. Both event distributions correspond to the integrated luminosity of 50 fb$ ^{-1} $ . It can be observed that the Λ baryons generated from the Sullivan process are primarily distributed in the large-$x_{\rm L}$ region and the Λ baryons generated from parton fragmentations of normal DIS are mainly distributed in the small-$x_{\rm L}$ region. For current technology, the energy resolution of a hadronic calorimeter can reach 35%/$ \sqrt{E/{\rm GeV}} $ . Assuming such an energy resolution, the reconstructed$x_{\rm L}$ -distributions of high energy Λ's ($ >5 $ GeV) are also presented in Fig. 13. It is clearly observed that with such energy resolution and the$x_{\rm L}$ cut ($x_{\rm L} > 0.55$ ), we can distinguish the Sullivan events from the background, with high purity.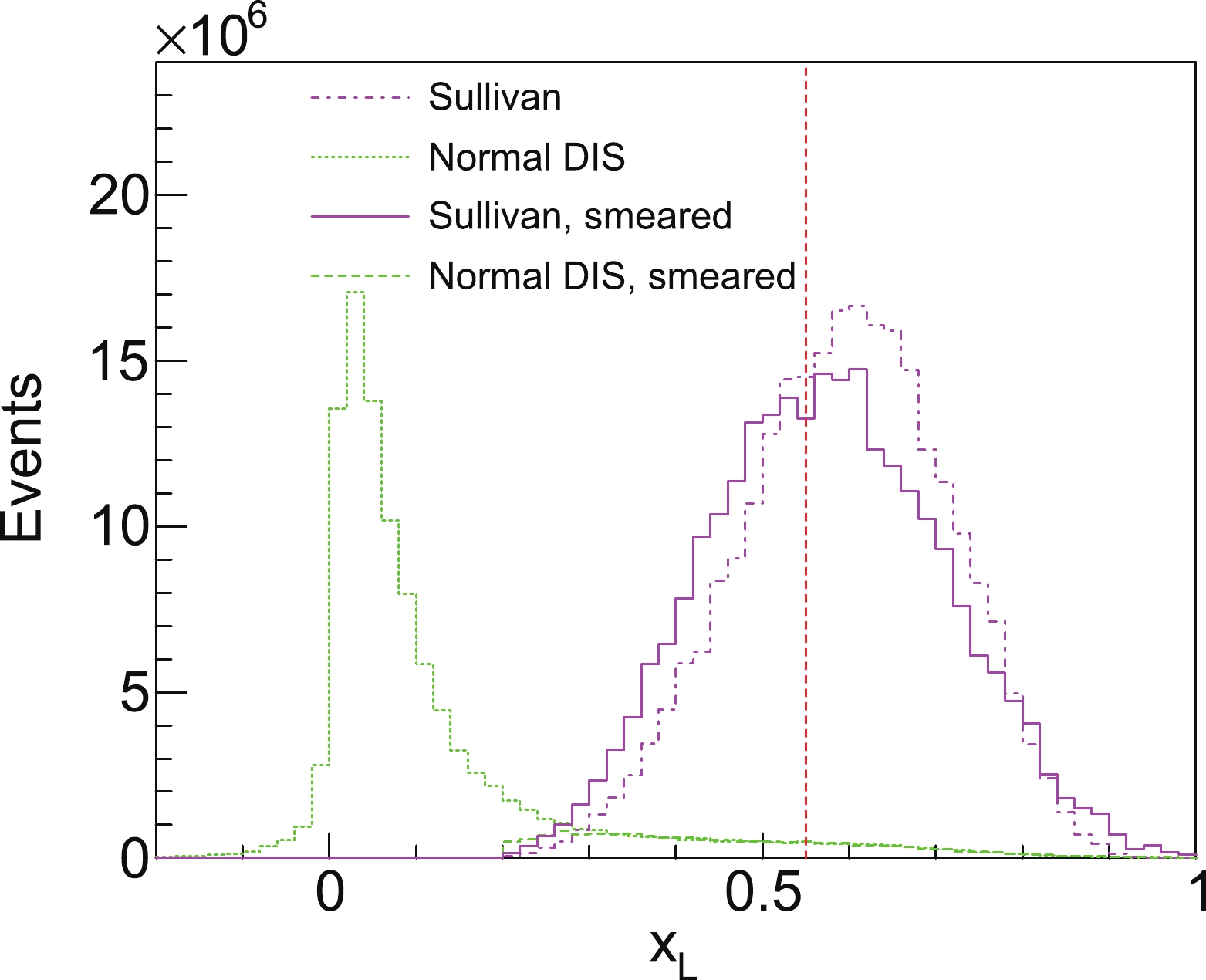
Figure 13. (color online) The distributions of the longitudinal momentum fraction of the final Λ baryon (see Eq. (1) for the definition), under the integrated luminosity of 50 fb
$ ^{-1} $ . The dashed-dotted histogram shows the$x_{\rm L}$ distribution from Sullivan process. The solid histogram shows the$x_{\rm L}$ distribution from Sullivan process with the detector resolution considered. The dotted histogram shows the$x_{\rm L}$ distribution from normal DIS. The dashed histogram shows the$x_{\rm L}$ distribution from normal DIS with the detector resolution considered ($ E_{\Lambda}>5 $ GeV).The other issue is whether the ZDC can identify a Λ baryon and its decay
$ \pi^0 $ from the measured invariant mass distributions. In this study, we propose the reconstruction of the Λ baryon from its neutral decays (n and$ \pi^0 $ ), using the ZDC only. To measure$ \pi^0 $ , we suggest an installation of an electromagnetic calorimeter in front of the hadronic calorimeter. For the energy resolution of the electromagnetic calorimeter, we assume it to be 3%/$ \sqrt{E/{\rm GeV}} $ , which is between the typical resolutions of the homogeneous calorimeter and the sampling calorimeter. We assume the ZDC placed at 50 m from the interaction point. The spatial resolution of the electromagnetic calorimeter is conservatively assumed to be 2 cm, while the spatial resolution of hadronic calorimeter is conservatively assumed to be 5 cm. The assumed angular resolution can then reach 1 mrad for the hadronic calorimeter. For the forward neutron detector at the HERA collider, the spatial resolution achieved a few millimeters at a proton beam energy of 820 GeV [49].With the above assumptions for the ZDC, the invariant mass distribution of the two photons from the
$ \pi^0 $ decay of the Sullivan process is presented in Fig. 14. The background distribution is simulated with the pythia6.4 event generator [48], which is given by the processes that are not from the$ \pi^0 $ decay. The background distribution is also illustrated in Fig. 14. It can be observed that in the region around the pion mass, the invariant mass distribution of$ \pi^0 $ decay is significantly higher than the background distribution. The distribution from the η decay is evidently separated from the distribution of the$ \pi^0 $ decay. Finally, the invariant mass distribution of one neutron and one$ \pi^0 $ from Λ decay is illustrated in Fig. 15. We deduce that the invariant mass of Λ decays is mainly distributed in the region lower than 1.2 GeV. The background distribution that is not from Λ decay is significantly lower than the Λ distribution in such a lower mass range. Therefore, the ZDC can effectively identify the Λ baryon from the reconstructed invariant mass distribution. The background events are under control around the Λ mass region via the coincidence measurement of the neutron and$ \pi^0 $ . The background events increase quickly when the invariant mass increases to 1.5 GeV, owing to the contributions of nucleon resonances. The assumed performance of ZDC is sufficient to separate the Λ baryon from the nucleon resonances in the high mass region. Therefore, it is feasible to perform an experiment at EicC to extract the kaon structure function via the measurement of the leading Λ tagged DIS process.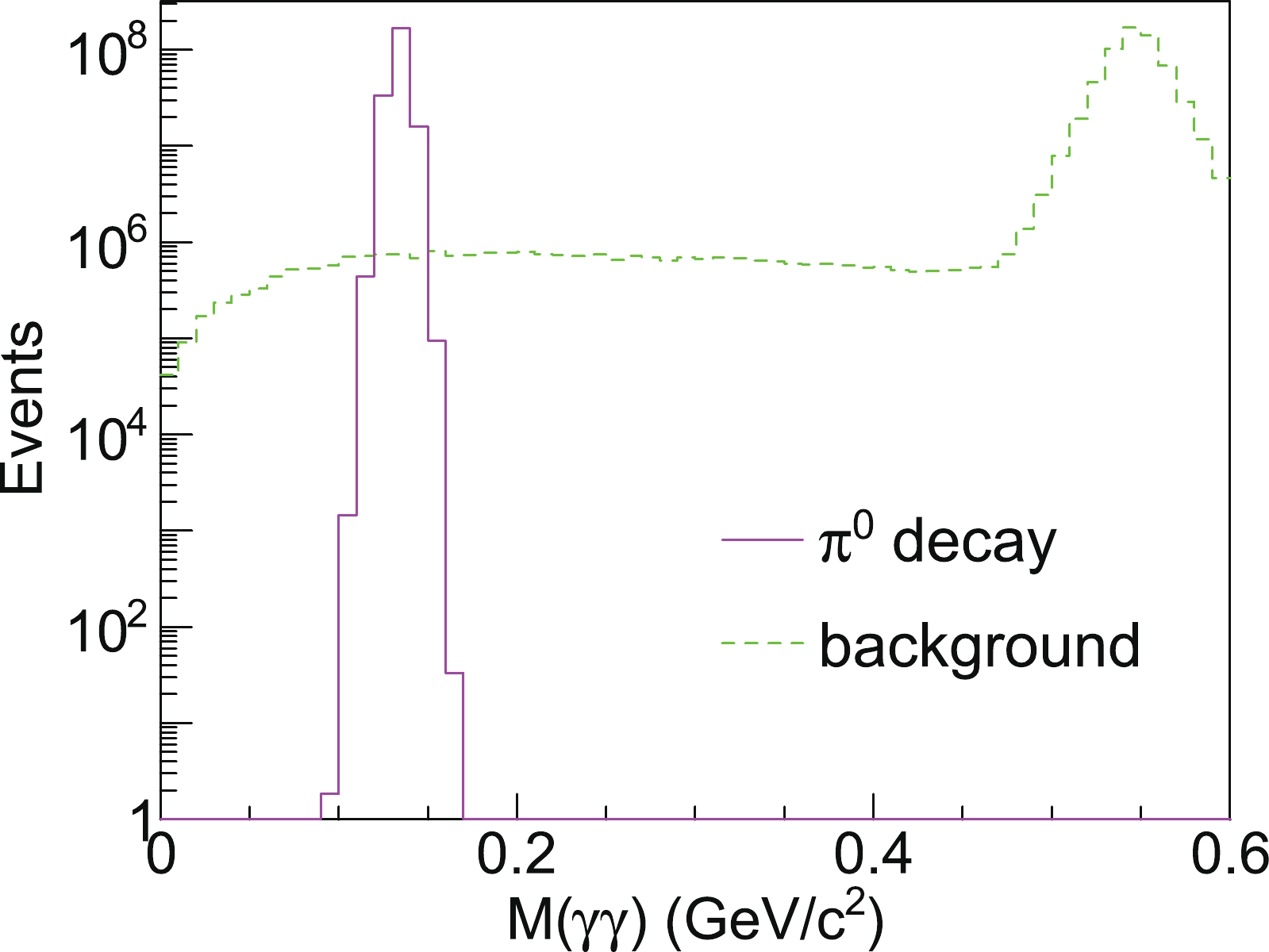
Figure 14. (color online) The invariant mass distributions of two photons from
$ \Lambda\rightarrow n\pi^0\rightarrow n\gamma\gamma $ (solid histogram) and other processes as the background (dashed histogram), under the integrated luminosity of 50 fb$ ^{-1} $ . The simple smearing from the detector angular and energy resolutions are considered for the histograms. The peak from η decay is away from the pion mass, which is clearly seen in the background distribution. The energy of the photon is required to be greater than 100 MeV.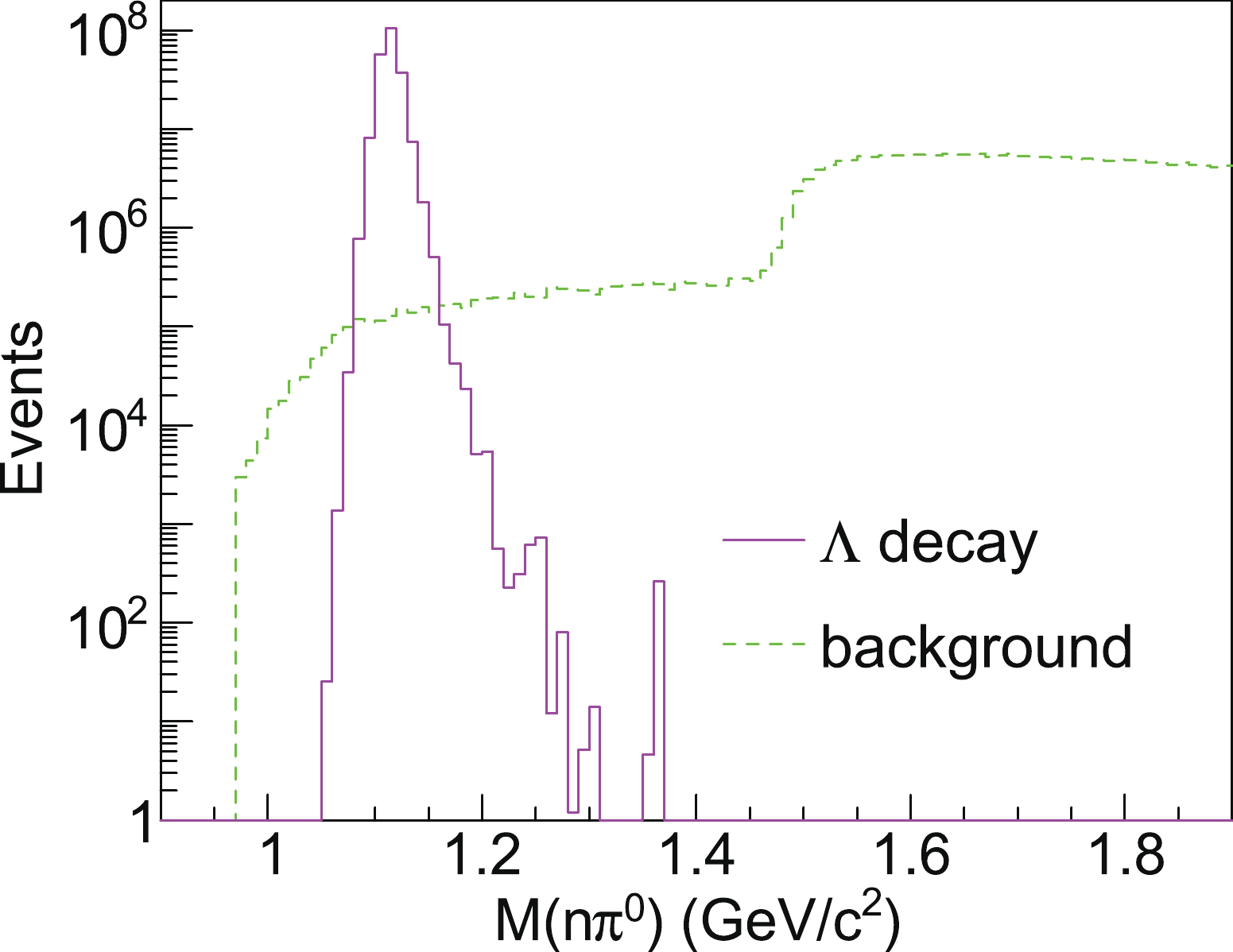
Figure 15. (color online) The invariant mass distributions of one neutron and one
$ \pi^0 $ from$ \Lambda\rightarrow n\pi^0 $ (solid histogram) and other processes as the background (dashed histogram), under the integrated luminosity of 50 fb$ ^{-1} $ . The simple smearing from the detector angular and energy resolutions are considered for the histograms. The nucleon resonances result in the fast growth of the background in the region above 1.5 GeV, which is clearly shown in the figure. -
The leading Λ tagged DIS experiment at EicC was simulated to study the kaon structure function. The charged decays (p and
$ \pi^- $ ) from Λ of high energy were deflected by the beam magnets and are difficult to be separated from the beam protons. Moreover, particle identifications of the high-energy charged particles around the beam pipe and beam magnets were significantly challenging. It is more feasible to measure the neutral decays (n and$ \pi^0 $ ) of Λ with ZDC, because the neutral particles are not deflected by the beam magnets. From our simulation, the high energy neutrons were collected with ZDC, while the photons from$ \pi^0 $ decay were collected with both ZDC and end-cap electromagnetic calorimeter in the interaction region of EicC. Hopefully, the forward proton and$ \pi^{-} $ from the decay of forward Λ can also be identified and measured, such that we can acquire more leading Λ tagged DIS events.We suggest the ZDC at EicC covers the θ angle from 0 to 3 degrees, to collect as many as possible forward neutrons. In the future, the angular (position) and energy resolutions of ZDC should be studied in detail. Nevertheless, we conducted a feasibility study with the simulations, assuming the conservative angular and energy resolutions of the ZDC. It is crucial to obtain a small angular resolution for two reasons. First, the small angular resolution of ZDC is important in measuring the t-dependence of the cross section, to achieve an optimal extrapolation to the real kaon structure. Second, we need a small angular resolution to separate the clusters of the energy depositions of the multiple neutral particles. For the shashlik calorimeter, the position resolution can be smaller than 1 cm, which is quite promising. The particle identification ability of ZDC is also important for the success of the experiment. The ZDC is suggested to comprise an electromagnetic calorimeter in the front and a hadronic calorimeter at the back. The longitudinal profiles of the electromagnetic and hadronic showers are different. It is a mature technique to differentiate the photons from the neutrons with the information from the electromagnetic and hadronic calorimeters.
We performed our simulations considering only the ZDC of the forward detector complex. From our simulation, we deduce that the kaon structure experiment at EicC is feasible with the high-performance ZDC. With the assumed performance of ZDC, the
$ \pi^0 $ and Λ can be well identified from the reconstructed invariant mass distributions. Based on the pythia simulations, the background of the Sullivan process can almost be ignored in the large-$x_{\rm L}$ region ($ >0.55 $ ). Based on the detection resolution, the background presented in the invariant mass distribution of two photons is significantly lower than the peak from the$ \pi^0 $ decay. The background presented in the invariant mass distribution of the neutron and$ \pi^0 $ is also substantially lower than the peak from Λ decay. However, we should note that the single and multiple photon productions are usually magnitudes more than that predicted with the typical event generator, such as pythia. The single$ \pi^{0} $ and single neutron productions are often underestimated in pythia. These high background rates would place stricter requirements on the ZDC performance. The high-rate neutral background and capacities (resolutions and efficiencies) of ZDC would introduce significant systematic uncertainties for the proposed measurement in this study. These issues require more future studies.We made the projections on the statistical errors of the kaon structure function based on a cross section model of the Λ tagged DIS, with an assumed integrated luminosity of 50 fb
$ ^{-1} $ and the acceptances of the conceptual EicC detectors. At the c.m. energy of the collision at approximately 17 GeV, EicC covers a broad kinematical range of$ 0.05\lesssim x_{\rm K} \lesssim 0.9 $ , with the resolution scale$ Q^2 $ up to 50 GeV$ ^2 $ . In the small-$ x_{\rm K} $ and low-$ Q^2 $ ($ <10 $ GeV$ ^2 $ ) regions, the statistical uncertainty is smaller than 1%. At high$ x_{\rm K}\sim 0.85 $ and a low$ Q^2\sim 4 $ GeV$ ^2 $ , the statistical uncertainty is simply around 5%. At a high$ Q^2 $ and with fewer kinematical bins, the statistical uncertainties are less than 5% for the data points in the region of$ x_{\rm K}<0.6 $ . The assumptions for the ZDC at the current stage are made for the ideal case. The angular coverage of ZDC may be reduced owing to the limited space in the forward region. Therefore the statistical uncertainty may increase for the actual experiment in the future. Nevertheless, we could reduce the statistical uncertainty by running the experiment with longer time. In addition, the statistical uncertainty, systematic uncertainties from the abundant background, and ZDC detector should be considered in the future. Owing to the challenges of fabricating the suggested high-performance and high-acceptance ZDC, the systematic uncertainty from ZDC would be at the same magnitude of the statistical uncertainty or even larger.The high luminosity experiments at EicC would elucidate the difference between the pion and kaon PDFs in the valence and sea quark regions. The gluon distribution of the kaon can also be extracted with the scaling violation described by QCD evolution equations, owing to the wide
$ Q^2 $ coverage of EicC. The future leading Λ tagged DIS experiment will provide several details on the interplay between EHM and HB mechanisms, by determining the strange valence quark distribution in the kaon, which has a significantly larger coupling to the Higgs boson than the up or down quark. In summary, a future EicC experiment on the kaon structure will have the potential for elucidating the nature of quasi Nambu-Goldstone particles in QCD, answering the question on why the kaon mass is small (compared to hyperon), and testing nonperturbative predictions such as LQCD and DSE calculations. -
We thank Prof. Craig D. Roberts for suggestions and discussions. We thank Prof. Yutie Liang for help on the background simulation with pythia6.4.
Tackling the kaon structure function at EicC
- Received Date: 2021-09-22
- Available Online: 2022-06-15
Abstract: Measuring the kaon structure beyond proton and pion structures is a prominent topic in hadron physics, as it is one way to understand the nature of the Nambu-Goldstone boson of QCD and observe the interplay between the EHM and HB mechanisms for hadron mass generation. In this study, we present a simulation of the leading Λ baryon tagged deep inelastic scattering experiment at EicC (Electron-ion collider in China), which is engaged to unveil the internal structure of kaon via the Sullivan process. According to our simulation results, the suggested experiment will cover the kinematical domain of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF























 DownLoad:
DownLoad: