-
Black hole (BH) physics is currently a hot field in physics and astronomy. Its primary object of study is understanding the quantum effects near the event horizon of a BH. These problems involve quantization of gravity and are therefore very complex [1]. With the emergence of observational evidence for BHs, these problems have become more prominent in recent years [2, 3]. Of course, scientists are very interested in how to test the related theoretical models from a practical perspective. So far, the most direct way to detect a BH is to make measurements with the BH Event Horizon Telescope (EHT) [3]. The EHT is based on very long baseline interferometry (VLBI) to measure the BH shadow. It has focused on the supermassive BH at the center of the Milky Way and the M87 supermassive BH. On April 10, 2019, it released observations of the M87 supermassive BH, which was found to have a mass of
$ 6.5\times 10^{9}M_{\odot} $ . Since this event, much research has been conducted with respect to general relativity using the M87 data [3–10].The basic picture of the BH shadow is that when a photon passes near the BH to the Earth, the strong gravitational field of the BH causes the background photon to only pass through space-time beyond a specific region of the BH. The BH shadow is then observed, and its shape and size depend on the parameters of the central BH; therefore, scientists can infer the presence of a BH by measuring its shadow and use that as a basis for studying the strong gravitational field [11–19].
The shadow of a Schwarzschild BH was first calculated by Synge [20]. Since then, the problem of the BH shadow has not received much attention. In the last few years, using analytic methods to calculate the BH shadow has become a hot topic [20–40]. The accretion process of a BH can affect the image of the BH, so it is necessary to study this process using analytical methods and numerical simulation [41–47]. Xu et al., 2018, calculated the effect of the distribution of the dark matter (DM) halo at the center of the Milky Way on the BH shadow [48–50]. They found that if the resolution of the EHT is further improved, it will be possible to detect the DM effect near the Sgr A* BH and distinguish the state properties of ambient matter near the BH.
We now discuss the interesting question of whether it is possible to use future EHT measurements to study the quantum effect near a BH. We discuss this problem in the classical case by looking for modified forms of space-time of ageometric BH under quantum effects and then calculating the possible observational effects of these modified BH metrics [51–56]. Kazakov et al. began this research in 1994 by studying the quantum modification of the Schwarzschild BH [51]. Based on this approach, scientists then calculated the potential function satisfied by the quantum field in the space-time background of the Schwarzschild BH [52]. In reference [53], Calmet et al. calculated the quantum modification of the Schwarzschild BH in general relativity based on the effective field theory method. Good et al. proposed a Schwarzschild BH solution for the BH evaporation model, in which the BH information is not lost [57]. Recently, Berry et al. obtained the universal form of the quantum deformed BH metric based on previous work [58]. Xu et al. extended the BH metric to the case of a rotating BH [59]. Based on these results, we will calculate the shadow of a rotating quantum-deformed BH, thus proposing the possibility of using the EHT to test a quantum deformed BH.
The basic structure of this article is as follows. In Sec. II, we introduce spherically symmetric and axisymmetric quantum deformed BHs. In Sec. III, the geodesic equations of light rays are derived analytically, and the general analytical solutions are obtained. In Sec. IV, we calculate the change in the quantum deformation parameters with respect to the shape of the BH shadow. In Sec. V, we calculate the change in the quantum deformation parameters with respect to the energy emission rate. Finally, we summarize the entire article.
-
The quantum deformed BH introduced here is primarily related to the theory of two-dimensional dilaton gravity [51, 58, 60]. In this theory of gravity, the action S is
$ \begin{equation} S=-\dfrac{1}{8}\int {\rm d}^{2}z\sqrt{-g}\left[r^{2}R^{(2)}-2(\nabla r)^{2}+\dfrac{2}{\kappa}U(r)\right], \end{equation} $

(1) where g is a metric determinant,
$ R^{(2)} $ is a two-dimensional Ricci scalar, κ is a dimensionless constant, and$ U(r) $ is the dilaton potential energy. By variational calculation of the action (Eq. (1)), the corresponding field equation can be obtained. Then, by solving the field equation, we can obtain the space-time metric$ \begin{equation} {\rm d}s^{2}=-f(r){\rm d}t^{2}+\dfrac{1}{f(r)}{\rm d}r^{2}+r^{2}\left({\rm d}\theta^{2}+\sin^{2}\theta {\rm d}\phi^{2}\right), \end{equation} $

(2) where the mathematical relation between the metric coefficient function
$ f(r) $ and the dilaton potential energy is$ \begin{equation} f(r)=\dfrac{1}{r}\int^{r}U(\rho){\rm d}\rho-\dfrac{2M}{r}. \end{equation} $

(3) By selecting the form of the potential function
$ U(r) $ , the modified form of the spherically symmetric BH in two-dimensional dilaton gravity theory can be obtained. For example, for a special quantum modified BH, Kazakov and Solodukhin chose the potential function$ U(r) $ in the following form [51]:$ \begin{equation} U(r)=\dfrac{r}{\sqrt{r^{2}-m^{2}}}. \end{equation} $

(4) In Eqs. (2) and (4), M is the mass of the spherically symmetric BH, and its physical meaning is the total mass of the system when the radial distance is infinite; m is a quantum deformation parameter, which represents the modification of the spherically symmetric metric by quantum effects after considering the two-dimensional dilaton gravity theory.
According to the two-dimensional dilaton theory of gravity, as long as the potential function
$ U(r) $ satisfies the modified gravitational field, the equation can be used as a suitable choice. On this basis, Berry, Simpson, and Visser generalized the space-time metric to the following form [58]$ \begin{equation} f(r)=f_{n}(r)=\left(1-\dfrac{m^{2}}{r^{2}}\right)^{{n}/{2}}-\dfrac{2M}{r}, \end{equation} $

(5) where the quantum deformation parameter
$ m\geq 0 $ , and$ n=0, \;1, \;3, \;5... $ , where n is a parameter that characterizes the type of quantum-deformed black hole (the different values of n are described below). It is worth noting that when$ n=0 $ or$ m=0 $ , Eq. (5) reduces to the case of the Schwarzschild BH. In addition, for general parameter selection, the space-time metric is the modified BH space-time. For example, when$ n=1 $ , the space-time metric degrades to the case of Kazakov-Solodukhin [51], and the quantum modified BH exhibits a series of special properties that can be analytically calculated. When$ n=3 $ or$ 5 $ , the space-time metric changes to Christoffel-symbol-regular and Curvature-regular space-time. When$ n>5 $ , the space-time metric is the Curvature-regular space-time (more detailed descriptions are available in the literature [58]), and this space-time metric provides a basis for analyzing the influences of the quantum effect on the Schwarzschild BH. -
On the basis of a spherically symmetric quantum deformed BH (Eqs. (2) and (5)), Xu and Tang generalized it to the case of an axisymmetric BH using the Newman-Janis method based on complex transformation [59]. If the spherically symmetric metric satisfies
$ f(r)=g(r) $ (where$ g(r) $ is$ g_{rr}^{-1} $ ), regardless of the form of$ h(r) $ , Einstein gravitational field equations can be solved by solving partial differential equations. Through more complicated derivation, they found that the metric of the quantum deformed BH under rotational symmetry is$ \begin{aligned}[b] {\rm d}s^{2}=&-\left[1-\dfrac{r^{2}+2Mr-r^{2}\left(1-\dfrac{m^{2}}{r^{2}}\right)^{{n}/{2}}}{{\Sigma}^{2}}\right]{\rm d}t^{2}+\dfrac{\Sigma^{2}}{\Delta}{\rm d}r^{2}\\& -\dfrac{2a\sin^{2}\theta {\rm d}\phi {\rm d}t}{\Sigma^{2}}\left[r^{2}+2Mr-r^{2}\left(1-\dfrac{m^{2}}{r^{2}}\right)^{{n}/{2}}\right]\\ & +\Sigma^{2}{\rm d}\theta^{2}+\dfrac{\sin^{2}\theta}{\Sigma^{2}}\left[\left(r^{2}+a^{2}\right)^{2}-a^{2}\Delta\sin^{2}\theta \right]{\rm d}\phi^{2} , \end{aligned} $

(6) where the unknown functions in the metric are expressed as follows:
$ \begin{aligned}[b] & \Sigma^{2}=r^{2}+a^{2}\cos^{2}\theta, \\ & \Delta=r^{2}\left(1-\dfrac{m^{2}}{r^{2}}\right)^{\frac{n}{2}}-2Mr+a^{2}. \end{aligned} $

(7) As mentioned earlier, when the quantum deformation parameter
$ m=0 $ (or$ n=0 $ ), the axisymmetric quantum deformed BH (Eq. (6)) degenerates into the Kerr BH; when$ n=1 $ , Eq. (6) degrades into a rotational promotion of the case of Kazakov-Solodukhin, and the BH spin can be increased to an extreme situation. Other values of n and m correspond to various types of axisymmetric quantum deformed BHs [59].From this axisymmetric quantum deformed BH, it is possible to calculate the influences of the quantum effect on various BH related observations.
-
Based on the metric (Eq. (6)) of the axisymmetric BH, we calculate the geodesic motion of a test particle in space-time. Here, we will deal with it according to the Hamilton-Jacobi equation and Carter variable separation method [61]. In the general space-time background, the form of the Hamilton-Jacobi equation is as follows:
$ \begin{equation} \dfrac{\partial S}{\partial \eta}=-\dfrac{1}{2}g^{\mu\nu}\dfrac{\partial S}{\partial x^{\mu}}\dfrac{\partial S}{\partial x^{\nu}}. \end{equation} $

(8) where η is an affine parameter on a geodesic and S is the Jacobi action. In the Carter variable separation method, Jacobi action S can be written as
$ \begin{equation} S=\dfrac{1}{2}\bar{m}^{2}\eta-Et+L\phi+S_{r}(r)+S_{\theta}(\theta). \end{equation} $

(9) where
$ \bar{m} $ is the mass of the test particle, and E and L are the energy and angular momentum of the particle, respectively.$ S_{r}(r) $ is a radial unknown function, and$ S_{\theta}(\theta) $ is an angular unknown function. Substituting the Jacobi action equation (Eq. (9)) into the Hamilton-Jacobi equation (Eq. (8)), by simple derivation, we can obtain motion equations, namely the geodesic equations, satisfied by the test particle in the space-time of the quantum deformed BH. In BH physics, the geodesic equations can be expressed as [62]:$ \begin{equation} \Sigma^{2}\dfrac{{\rm d}t}{{\rm d}\eta}=\dfrac{r^{2}+a^{2}}{\Delta}\left[E \left(r^{2}+a^{2} \right)-aL \right]-a \left(aE\sin^{2}\theta-L \right), \end{equation} $

(10) $ \Sigma^{2}\dfrac{{\rm d}r}{{\rm d}\eta}=\sqrt{R}, $

(11) $ \Sigma^{2}\dfrac{{\rm d}\theta}{{\rm d}\eta}=\sqrt{{H}}, $

(12) $ \Sigma^{2}\dfrac{{\rm d}\phi}{{\rm d}\eta}=\dfrac{a}{\Delta}\left[E\left(r^{2}+a^{2}\right)-aL \right]-\left(aE-\dfrac{L}{\sin^{2}\theta}\right). $

(13) In the geodesic Eq. (10)
$ \sim $ Eq. (13), the basic expressions of the newly introduced functions R and$ {H} $ are$ \begin{equation} R=\left[E\left(r^{2}+a^{2}\right)-aL\right]^{2}-\Delta \left[m^{2}r^{2}+(aE-L)^{2}+K \right], \end{equation} $

(14) $ {H}=K-\left(\dfrac{L^{2}}{\sin^{2}\theta}-a^{2}E^{2}\right)\cos^{2}\theta. $

(15) In the above two equations, K is the Carter constant. Eqs. (10)
$ \sim $ (15) fully describe the motion of the test particle. In this study, we are interested in the geodesic motion of photons near the event horizon of a BH, and the test particle has a rest mass of$ 0 $ . Near the BH, the boundary of the photon sphere (because of the strong gravitational field of the BH, photons can move around the BH many times in the vicinity of the BH horizon, thus forming the BH photon sphere) and its shape are determined by the unstable orbit of the particle. Therefore, the boundary of the photon sphere (or photon shell) must be satisfied:$ R=0, $

(16) $ \dfrac{\partial R}{\partial r}=0. $

(17) For an observer at infinity on the equatorial plane of the BH space-time, the photon geodesic satisfying Eqs. (16) and (17) can be expressed by two parameters, which are defined as follows:
$ \xi=\dfrac{L}{E}, $

(18) $ \bar{\eta}=\dfrac{K}{E^{2}}. $

(19) Combining Eqs. (16)
$ \sim $ (19) and substituting the expression of R, the differential equations satisfied by parameters ξ and$ \bar{\eta} $ can be obtained$ \begin{equation} \left[\bar{\eta}+(\xi-a)^{2}\right]\left(r^{2}f(r)+a^{2}\right)-\left(r^{2}+a^{2}-a\xi\right)^{2}=0, \end{equation} $

(20) $ \begin{equation} \left[\bar{\eta}+(\xi-a)^{2}\right]\left(2rf(r)+r^{2}f^{'}(r)\right)-4r\left(r^{2}+a^{2}-a\xi\right)=0. \end{equation} $

(21) The solution of the above equations is
$ \begin{equation} \xi=\dfrac{\left(r^{2}+a^{2}\right)\left(rf^{'}(r)+2f(r)\right)-4\left(r^{2}f(r)+a^{2}\right)}{a \left(rf^{'}(r)+2f(r)\right)}, \end{equation} $

(22) $ \begin{equation} \bar{\eta}=\dfrac{r^{2}\left[8a^{2}f^{'}(r)-r\left(2f(r)-rf^{'}(r)\right)^{2}\right]}{a^{2}\left(rf^{'}(r)+2f(r)\right)^{2}}. \end{equation} $

(23) According to Eq. (5), the expression of
$ f^{'}(r)=f_{n}^{'}(r) $ is$ \begin{equation} f^{'}(r)=f_{n}^{'}(r)=\dfrac{2M}{r^{2}}+\dfrac{nm^{2}}{r^{3}}\left(1-\dfrac{m^{2}}{r^{2}} \right)^{({n-2})/{2}}. \end{equation} $

(24) Using Eq. (12) and making
$ H\geq 0 $ , the value range of the orbit radius$ (r_{c}) $ of the spherical photon orbit in the photon region can be obtained, and the result is$ \begin{equation} (4r\Delta-\Sigma^{2}\Delta^{'})^{2}\mid_{r=r_{c}}\;\leq 16a^{2}r^{2}\Delta \sin^{2}\theta\mid_{r=r_{c}}, \end{equation} $

(25) where
$ \Delta^{'}={{\rm d}\Delta}/{{\rm d}r} $ . Let$ r_{c-} $ and$ r_{c+} $ be the minimum and maximum of the photon sphere radius in the photon region, respectively. The spherical photon orbit radius satisfies$ r_{c-}\leq r_{c}\leq r_{c+} $ . If BH spin$ a=0 $ , the axisymmetric quantum deformed BH degenerates into a spherically symmetric quantum deformed BH, which means that the photon region degenerates into a photon sphere. Its radius satisfies the following equation:$ \begin{equation} 2r^{2}_{c}\left(1-\dfrac{m^{2}}{r^{2}_{c}}\right)^{{n}/{2}}-6Mr_{c}-nm^{2}\left(1-\dfrac{m^{2}}{r^{2}_{c}}\right)^{{n}/{2}-1}=0. \end{equation} $

(26) -
In the previous section, we calculated the geodesic equations of a photon and the shape of the photon sphere, but these quantities are not the physical quantities measured by an observer on Earth. Compared with a BH, an observer on Earth can be approximated as an observer at infinity; therefore, for observers on Earth, the celestial coordinate system can be introduced, whose components α and β are defined as follows:
$ \begin{equation} \alpha=\lim\limits_{r_{0}\to\infty}\left[-r_{0}^{2}\sin\theta_{0}\dfrac{{\rm d}\phi}{{\rm d}r} \right], \end{equation} $

(27) $ \begin{equation} \beta=\lim\limits_{r_{0}\to\infty}\left[r_{0}^{2}\dfrac{{\rm d}\theta}{{\rm d}r} \right]\Big|_{\theta=\theta_{0}}, \end{equation} $

(28) where
$ r_{0} $ is the distance between the observer and the BH, that is, the distance between the Earth and the BH;$ \theta_{0} $ is the angle between the observer's line of sight and the spin axis of the BH; and α and β are the projections of the BH shadow on the celestial coordinate system. Substituting the photon geodesic Eqs. (10)$ \sim $ (13) into Eqs. (27) and (28), we obtain the following relations:$ \begin{equation} \alpha=-\dfrac{\xi}{\sin\theta_{0}}\Big|_{\theta_{0}={\pi}/{2}}=-\xi, \end{equation} $

(29) $ \begin{equation} \beta=\pm\sqrt{\bar{\eta}+a^{2}\cos^{2}\theta_{0}-\xi^{2}\cot^{2}\theta_{0}}\big|_{\theta_{0}={\pi}/{2}}=\pm\sqrt{\bar{\eta}}. \end{equation} $

(30) Using Eqs. (22), (23), (29), and (30), we draw the shape of the BH shadow, as shown in Figs. 1 and 2, and the main results are as follows:

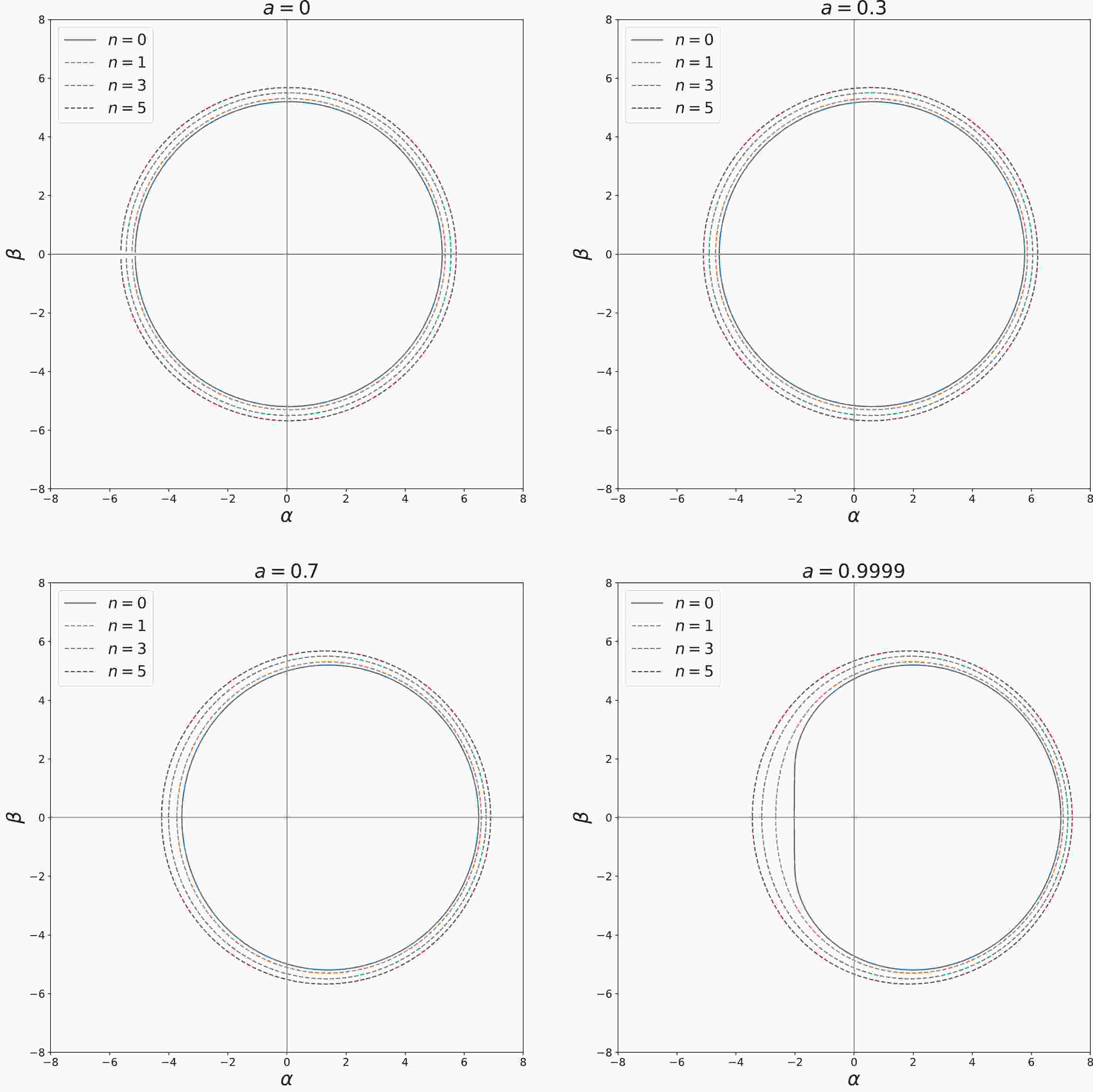
Figure 1. (color online) Shape of BH shadow for various types of quantum deformed BHs (
$ n=0, \;1,\; 3, \;5 $ ). Here, the quantum deformation parameter$ m=0.5 $ .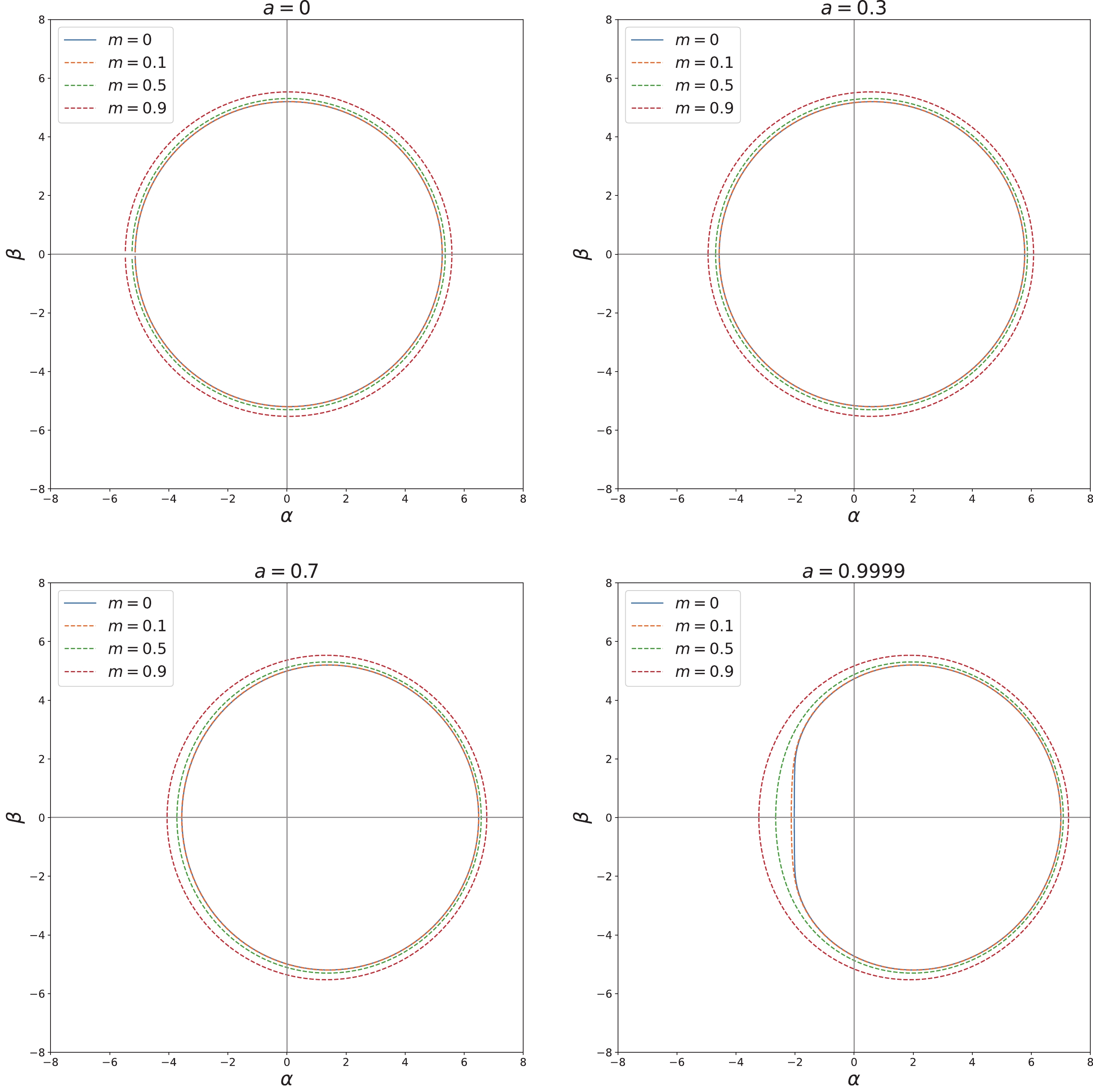
Figure 2. (color online) Shape of the Kerr-BH (
$ n=1 $ ) shadow with various spin ($ a=0,\; 0.3, \;0.7, \;0.9999 $ ) and quantum deformation parameters ($ m=0, \;0.1,\; 0.5, \;0.9 $ ).(1) According to the results of numerical calculation (Fig. 1), the BH shadows of various types of quantum deformed BH are different. When
$ n=0 $ , the BH metric Eq. (6) degenerates to the case of the Kerr BH, whose BH shadow is exactly the same as that of the Kerr BH. When$ n=1 $ ,$ 3 $ , or$ 5 $ , the scale of the shadow of the quantum deformed BH increases with an increase in n, which indicates that the Kerr BH ($ n=0 $ ) has the smallest shadow and the curvature-regular BH ($ n=5 $ ) has the largest shadow.(2) When the spin of the BH is
$ 0 $ , the BH shadow of the quantum deformed BH is a standard circle. As spin a grows, the shape of the BH shadow becomes more and more distorted; when$ a\rightarrow 1 $ , the distortion of the BH shadow shape reaches its maximum. These results are consistent with the case of the Kerr BH, except that the modification of the BH shadow by quantum effects is considered here.(3) The numerical results of the influence of the quantum deformation parameter m on the shape of shadow are shown in Fig. 2, indicating that when the quantum deformation parameter is not considered (
$ m=0 $ ), the results are completely consistent with that of the Kerr BH; with increasing quantum deformation parameter m, the scale of the shadow will also increase. When the type of BH is determined (e.g., n=1), an increase in the quantum deformation parameter m causes the BH shadow to be closer to a circle. Because the shadow region increases in quantum-deformed BHs, future EHT observations are more likely to constrain this model.The modification parameters m and n, reflecting quantum effects, have obvious effects on the shadow shape of the quantum deformed BH. Using these results, it will be possible to examine whether the shape changes of the BH shadows are caused by quantum effects and to study the details of quantum effects of a BH through future observations in the EHT (further improve resolution) project.
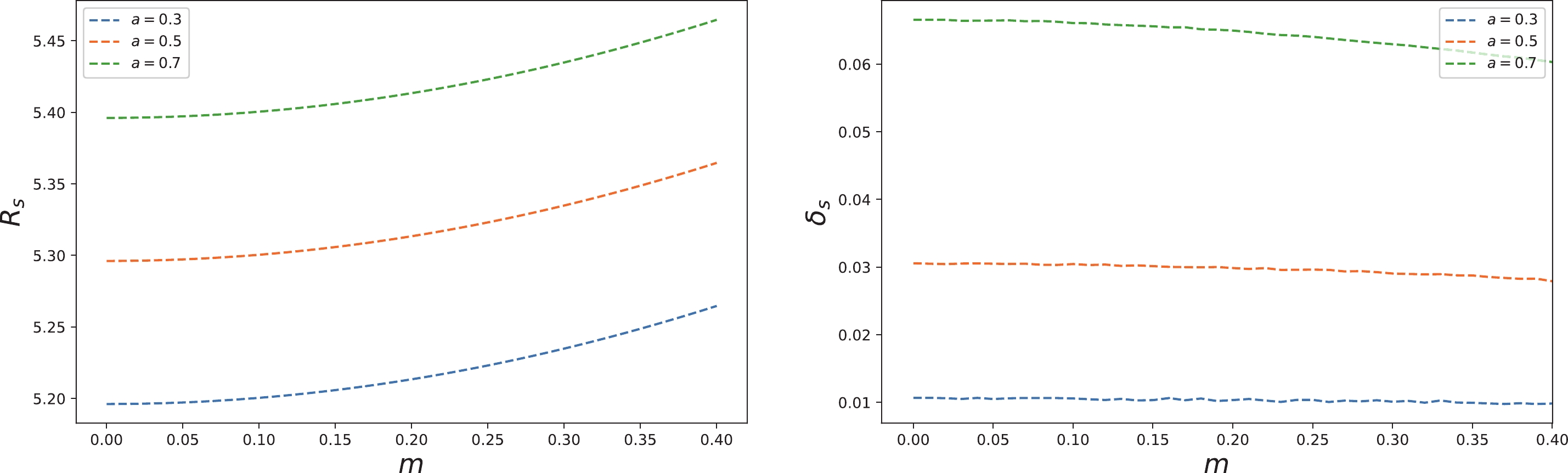
In the previous part, we only studied the BH shadow from the shape, although also quantitative, but the description of the BH shadow is not detailed enough. Here, we will use two observational parameters to describe the shape of the BH shadow, which are the BH shadow radius
$ R_{s} $ and distortion parameter$ \delta_{s} $ , respectively [48, 49, 63]. The shadow radius$ R_{s} $ can be defined as the radius of the circle determined by$ A(\alpha_{r}, 0) $ ,$ B(\alpha_{t}, \beta_{t}) $ , and$ D(\alpha_{b}, \beta_{b}) $ ; The distortion parameter$ \delta_{s} $ can be defined as the distortion degree of the BH shadow relative to a standard circle.$ R_{s} $ and$ \delta_{s} $ can basically describe the details of the scale and shape of the BH shadow (Fig. 3). According to the definition,$ R_{s} $ and$ \delta_{s} $ can be expressed as follows: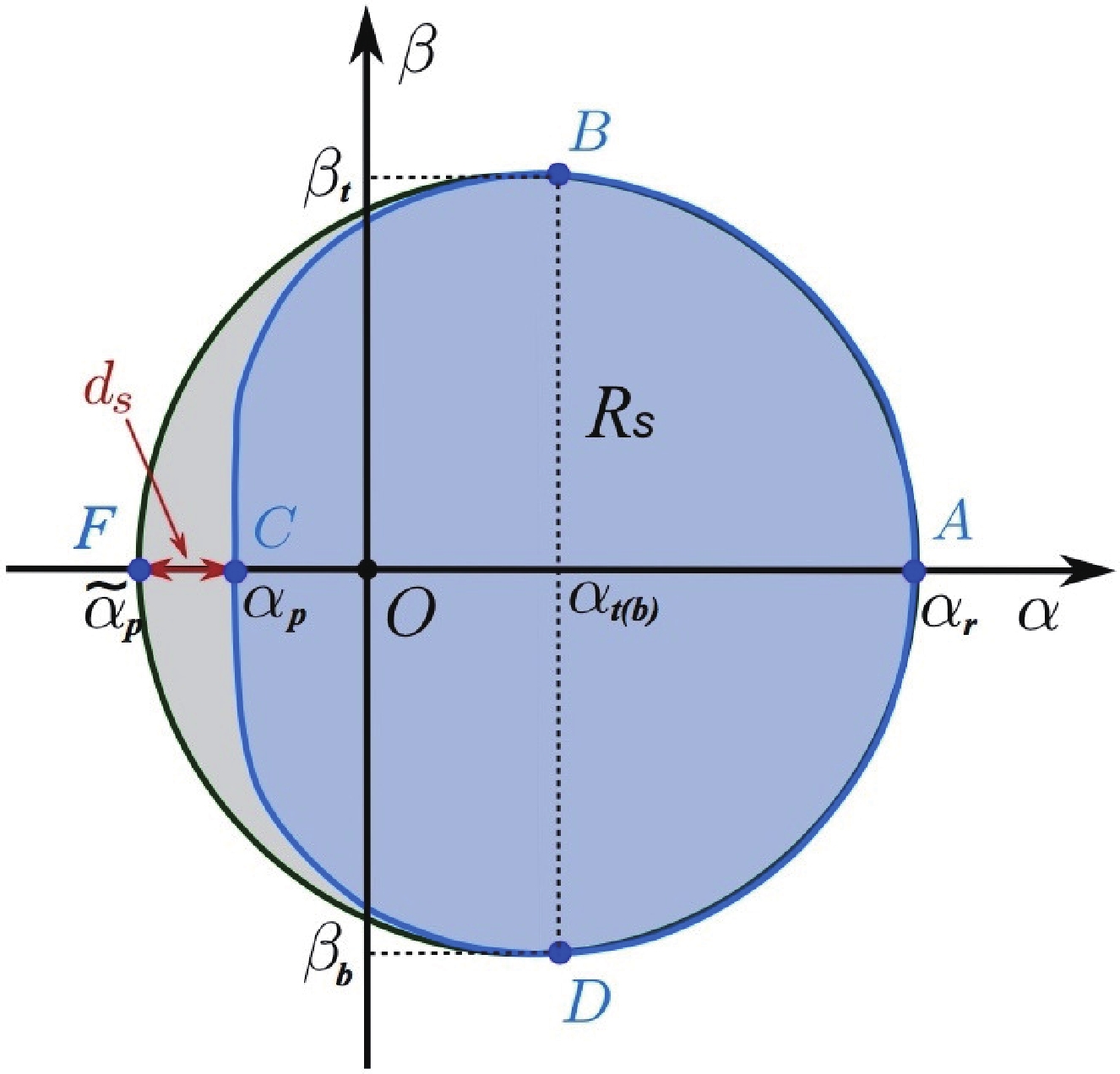
Figure 3. (color online) Reference circle and BH shadow diagram [49].
$ \begin{equation} R_{s}=\dfrac{\beta_{t}^{2}+(\alpha_{t}-\alpha_{r})^{2}}{2|\alpha_{r}-\alpha_{t}|}, \end{equation} $

(31) $ \begin{equation} \delta_{s}=\dfrac{d_{s}}{R_{s}}=\dfrac{|\alpha_{p}-\tilde{\alpha}_{p}|}{R_{s}}, \end{equation} $

(32) where
$ d_{s} $ is the distance between the points$ C(\alpha_{p}, 0) $ and$ F(\bar{\alpha}_{p}, 0) $ ,$ C(\alpha_{p}, 0) $ is the left intersection of the BH shadow and the α axis, and$ F(\bar{\alpha}_{p}, 0) $ is the left intersection of the reference circle and the α axis. Interestingly, the shape of the shadow of a BH with zero spin is a standard circle, without any distortion in shape.Figs. 4–6 show the changes in the BH shadow radius
$ R_{s} $ and the distortion parameter$ \delta_{s} $ with the model parameters. By analyzing the numerical results, we find the following: (1) with an increase in the BH type parameter n, that is, from the Schwarzchild BH case, to the metric-regular case, to the Christoffel-symbol-regular case, and then to the Curvature-regular case,$ R_{s} $ and$ \delta_{s} $ show monotone increasing and decreasing functions, respectively; (2) when$ n=1 $ , that is, considering the metric-regular case,$ R_{s} $ is an increasing function of the quantum deformation parameter m, and$ \delta_{s} $ is a decreasing function of m; (3) for an ordinary quantum deformed BH, i.e.,$ m\neq 0 $ , we find that$ R_{s} $ and$ \delta_{s} $ both increase with the spin of the BH.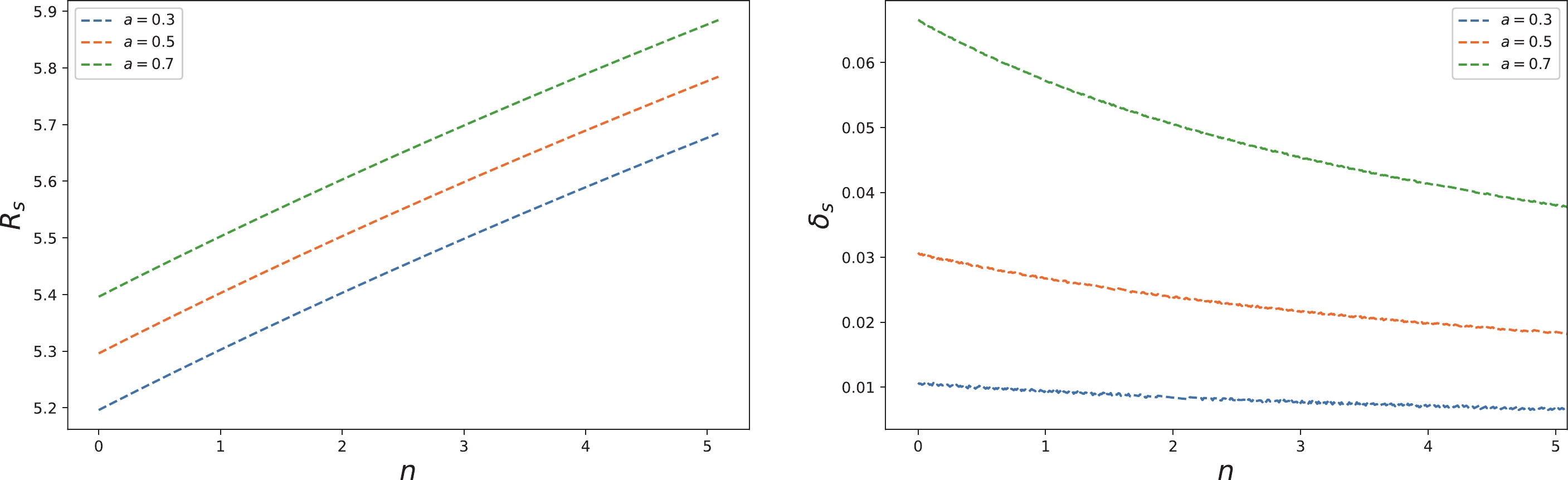
Figure 4. (color online) Radius
$ R_{s} $ (left) and distortion parameter$ \delta_{s} $ (right) of the BH shadow varying with the model parameter ① n under various BH spins ($ a=0.3,\; 0.5, \;0.7 $ ), where the quantum deformation parameter$ m=0.5 $ . -
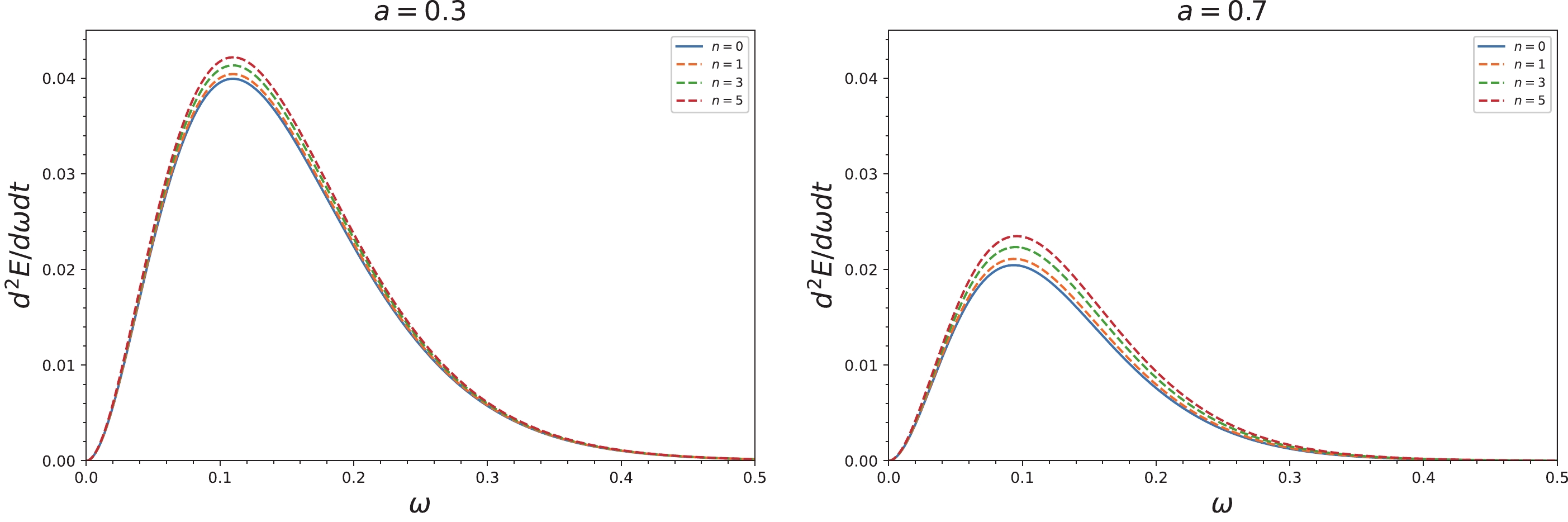
When the observer is at infinity, the size of the BH shadow is proportional to the high energy absorption cross section of the particle, which is similar to considering the BH shadow as a black body. Scientists have found that the high energy absorption cross section (
$ \sigma_{\rm{lim}} $ ) oscillates around a constant. For a spherically symmetric quantum deformed BH, the geometric cross sections of$ \sigma_{\rm{lim}} $ and the photon sphere are approximately equal, i.e.,$ \sigma_{\rm{lim}}\approx \pi R_{s}^{2} $ [64, 65], where$ R_{s} $ is the radius of the reference circle defined in the previous section. In our work, as shown in Figs. 1 and 2, except for the extreme and near-extreme Kerr BH, the shadow shapes of other BHs are close to a circle, so it is approximately reasonable to apply the results of the spherically symmetric BH to the axisymmetric BH. Therefore, the energy emission rate of a general axisymmetric quantum deformed BH is$ \begin{equation} \dfrac{{\rm d}^{2}E(\omega)}{{\rm d}\omega {\rm d}t}=\dfrac{2\pi^{2}\omega^{3}\sigma_{\rm{lim}}}{{\rm e}^{{\omega}/{T}}-1}. \end{equation} $

(33) Here, T is the Hawking temperature corresponding to the event horizon of the quantum deformed BH, and ω is the frequency of photon. According to the definition of BH temperature, its expression is as follows
$ \begin{equation} T=\lim\limits_{\theta \to 0, r \to r_+}\dfrac{1}{2\pi\sqrt{g_{rr}}}\dfrac{\partial \sqrt{g_{tt}}}{\partial r}. \end{equation} $

(34) The specific expressions of
$ g_{tt} $ and$ g_{rr} $ are shown in Eqs. (6) and (7). By substituting the metric coefficients into Eq. (34), we can obtain the general form of the Hawking temperature$ \begin{equation} T=\dfrac{2a^{2}r_+[f(r_+)-1]+r_+^{2}f^{'}(r_+)\left(r_+^{2}+a^{2}\right)}{4\pi^{2}\left(r_+^{2}+a^{2}\right)^{2}}. \end{equation} $

(35) Numerical calculation is performed for Eq. (33), as shown in Figs. 7 and 8. The main results are as follows: (1) the energy emission rate of various types of quantum deformed BH (
$ n=0, 1, 3, 5 $ ) decreases with an increase in n value; (2) the energy emission rate of the quantum deformed BH decreases with an increase in the quantum deformation parameter m, i.e., as the quantum effect becomes more significant, the energy emission rate decreases; (3) for a particular quantum deformed BH, when the spin is$ 0 $ , the energy emission rate is the largest, and the energy emission rate decreases with increasing spin. -
In this work, we study the properties of the shadow of a quantum deformed BH and discuss the possibility of using the EHT to test the quantum properties of the BH. An observer at infinity (an observer on Earth can be approximated as an observer at infinity) would see that the shadow of a spherically symmetric BH is a circle whose size is closely related to the parameters of the quantum deformed BH. For the quantum deformed Kerr BH, the shape of the BH shadow is distorted as the spin of the BH increases, and the details of the distortion are determined by the model parameters (including the BH type parameter n, quantum deformed parameter m, and BH spin a) of the quantum deformed BH. The main results are as follows: (1) when the BH type parameter
$ n=0 $ or quantum deformed parameter$ m=0 $ , the shape and properties of the BH shadow degenerate to the Kerr BH, that is, with an increase in the BH spin, the shape of the BH shadow gradually deviates from that of the reference circle; (2) for the same BH spin, the BH shadows corresponding to the Kerr BH (n=0), Kazakov-Solodukhin spacetime (n=1), Christoffel-symbol-regular spacetime (n=3), and the Curvature-regular spacetime (n=5) increase successively, and the shadow gets closer and closer to being circular, which also suggests that the Brzek-regular space-time is more likely to have observational constraints; (3) for the same type of quantum deformed BH (e.g., n=1) and BH spin, the shadow of the BH becomes larger and its shape gradually approaches that of the reference circle as the value of the quantum deformation parameter m increases; (4) with an increase in the quantum deformed BH type parameter (n), the change in the BH shadow behavior is similar to the increase related to the quantum deformed BH parameter m, which shows that the parameters n and m are similar to "degenerate phenomenon", and the existence of this phenomenon increases the difficulty of EHT testing of this model (we expect to analyze the "degenerate phenomenon"in future work).Based on these results, we believe that if the resolution of the EHT is further improved, it will be possible to distinguish the quantum effects of a BH in EHT measurements, thus providing a new way to test the quantum effects of a BH by observation. This paper contains the theoretical calculation of this idea.
-
We acknowledge the anonymous referee for a constructive report that has significantly improved this paper.
Testing the quantum effects near the event horizon with respect to the black hole shadow
- Received Date: 2022-01-03
- Available Online: 2022-08-15
Abstract: In recent years, the study of quantum effects near the event horizon of a black hole (BH) has attracted extensive attention. It has become one of the important methods to explore BH quantum properties using the related properties of a quantum deformed BH. In this work, we study the effect of a quantum deformed BH on the BH shadow in two-dimensional Dilaton gravity. In this model, quantum effects are reflected by the quantum correction parameter m. By calculation, we find that: (1) the shape of the shadow boundary of a rotating BH is determined by the BH spin a, the quantum correction parameter m, and the BH type parameter n; (2) when the spin






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: