-
In recent studies, a novel
$ 1/2^- $ negative parity nucleon state named as$ N^*(890) $ was suggested to exist in the$ S_{ 1 1} $ channel πN scattering amplitude [1–3]. The pole is found using the production representation [4–8] (see also Ref. [9] for a review). Later the existence of$ N^*(890) $ is also confirmed by a K–matrix analysis [10] and the$ N/D $ studies [11, 12]. Because the existence of$ N^*(890) $ does not seem to be well accepted yet in the physics community, further evidence needs to be gathered, which may be done by making a study in flavor$ S U(3) $ basis by associating$ N^*(890) $ with (sub-threshold) resonances investigated in other channels (which is the main purpose of this study).There have been many such studies in the literature, and these studies mainly concentrated on the strangeness,
$ s=-1 $ sector. For example, In Ref. [13], a unitarized$ S U(3) $ $ O(p^1) $ χPT amplitude is used to study meson–baryon scatterings in the$ s=-1 $ sector. An extension to the$ O(p^2) $ level is performed in Refs. [14, 15], and the twin pole structure around$ \Lambda^*(1405) $ (namely,$ \Lambda^*(1405) $ and$ \Lambda^*(1380) $ ) is found. At higher energies, a pole$ \Lambda^*(1670) $ is also found in Ref. [14]. The I=1 sector is also investigated in Ref. [14] and the$ \Sigma^*(1620) $ and$ \Sigma^*(1750) $ poles are found. Similar discussions are also made in Refs. [16–19]. In Ref. [16], no negative parity Σ resonances are found. In Ref. [18], two$ \Sigma^* $ poles located at$ 1401-40{\rm i} $ and$ 1488-114{\rm i} $ are found. The former mainly couples to$ \pi\Sigma, \bar KN $ while the latter mainly couples to$ \pi\Sigma $ and$ K\Xi $ . In Ref. [19], two narrow Σ poles at$ 1425-6.5{\rm i} $ and$ 1468-13{\rm i} $ are found with strong couplings to the$ \pi\Sigma $ channel. Furthermore, in Refs. [20, 21], it is suggested that introducing an explicit${1}/{2}^- $ $ \Sigma(1380) $ resonance field in the effective Lagrangian gives a better description of the experimental data$ \gamma p \to K^+\Sigma^{0*}(1385) $ ,$ \gamma n \to K^+\Sigma^{-*}(1385) $ and$ K^-p\to \Lambda\pi^+\pi^- $ . In Ref. [22], a Hamiltonian approach of the effective chiral Lagrangian is performed, and two Λ poles are found. A comparison with the lattice study is made, and it is concluded that the$ \Lambda(1405) $ pole is of molecule type when the quark masses are small.Discussions on the possible existence of low-lying
$ 1/2^- $ Ξ state can also be found in the literature. A Bethe–Salpeter (BS) equation approach is made in studying the$ s=-2 $ sector in Ref. [23]. The$ O(p^1) $ contact term extracted from a chiral meson baryon interaction Lagrangian is used as the BS kernel. Two$ 1/2^- $ Ξ poles are found:$ \Xi^*(1620) $ and$ \Xi^*(1670) $ , in addition to the twin pole structure near$ \Lambda^*(1405) $ . Finally, a review on related physics may also be found in Refs. [24, 25]. See also Ref. [26] for related discussions.In this study, we try to assimilate these results on low-lying
$ 1/2^- $ resonances in different sectors into a unified picture through$ S U(3) $ argument. We start by considering these (extra)$ 1/2^- $ resonances as dynamically generated, i.e., they do not appear as explicit degrees of freedom in the effective Lagrangian, which is to be unitarized and fit to the data. This picture is different from the strategy adopted in, for example, Refs. [20, 21]. We see that this picture gives a reasonable description of experimental data. Next, we also discuss the possibility that these low-lying resonances are explicit degrees of freedom written in the effective Lagrangian. We find, however, that these poles in the effective Lagrangian flee away in the complex plane and play little role in improving chi-squared. Hence, we conclude that that all of the$ 1/2^− $ octet baryons predicated here are dynamically generated and are of molecular type.The
$ S U(3) $ χPT Lagrangian describing the lowest-lying$ 1/2^+ $ baryon–meson interactions at$ O(p^2 $ ) level are$ \begin{aligned}[b] {\cal L}^{(1)} =& {\rm{Tr}}[\bar{B}{\rm i}\gamma^\mu[D_\mu,B]] -M_0\cdot {\rm{Tr}}[\bar{B}B] \\ & + D\cdot {\rm{Tr}}[\bar{B}\gamma^\mu\gamma^5\{u_\mu,B\}] + F\cdot {\rm{Tr}}[\bar{B}\gamma^\mu\gamma^5[u_\mu,B]]\ , \end{aligned} $

(1) $ \begin{aligned}[b] {\cal L}^{(2)} =& b_0\langle \bar{B}B\rangle\langle\chi_+\rangle + b_D\langle\bar{B}\{\chi_+,B\}\rangle + b_F\langle\bar{B}[\chi_+,B]\rangle\\ & +b_1\langle\bar{B}[u_\mu,[u^\mu,B]]\rangle+b_2\langle\bar{B}\{u_\mu,\{u^\mu,B\}\}\rangle\\ & +b_3\langle\bar{B}\{u_\mu,[u^\mu,B]\}\rangle+b_4\langle\bar{B}B\rangle\langle u_\mu u^\mu\rangle + \cdots \ . \end{aligned} $

(2) The notations and symbols are standard, following, for example Refs. [27, 28]. The relations between baryon masses and
$ S U(3) $ parameters are listed in the following:$ \begin{aligned}[b]& M_N = M_0 - 2(b_0+2b_F)m_\pi^2 - 4(b_0+b_D-b_F)m_K^2\ ,\\ & M_\Lambda = M_0 -2(b_0 -\frac{2}{3}b_D)m_\pi^2 - 4(b_0 +\frac{4}{3}b_D)m_K^2\ ,\\ & M_\Sigma = M_0 - 2(b_0 +2b_D)m_\pi^2 - 4b_0m_K^2\ ,\\ & M_\Xi = M_0 - 2(b_0-2b_F) m_\pi^2 -4(b_0+b_D+b_F)m_K^2\ , \end{aligned} $

(3) where
$ m_\pi^2 = 2B_0 m_u $ ,$ m_K^2 = B_0(m_u + m_s) $ , and$ m_\eta^2 = {2}/{3} B_0(m_u+2m_s) $ . Only three out of four relations given above are independent and can be used to fix three parameters on the$ r.h.s. $ , leaving only one ($ M_0 $ ) free.The Feynman diagrams describing meson baryon → meson baryon scatterings at
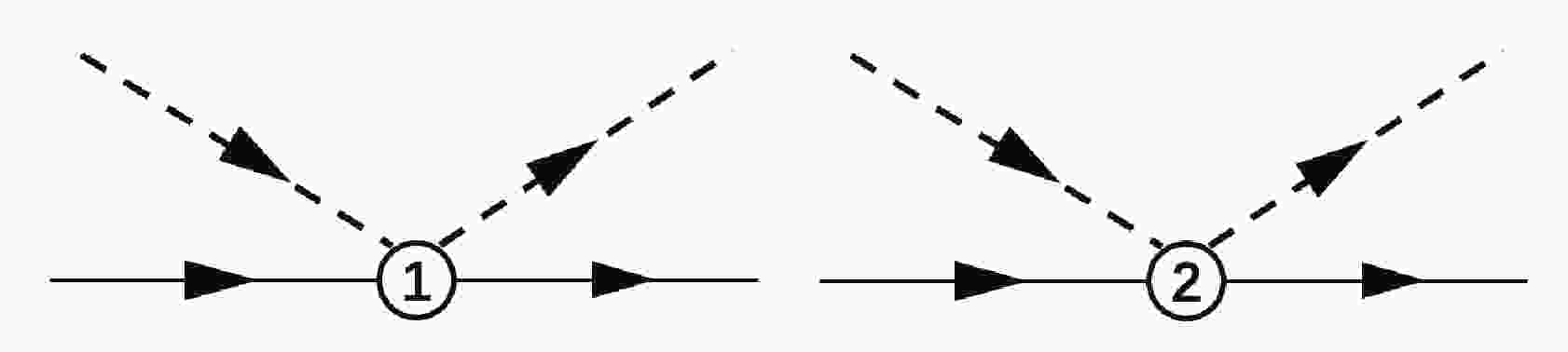
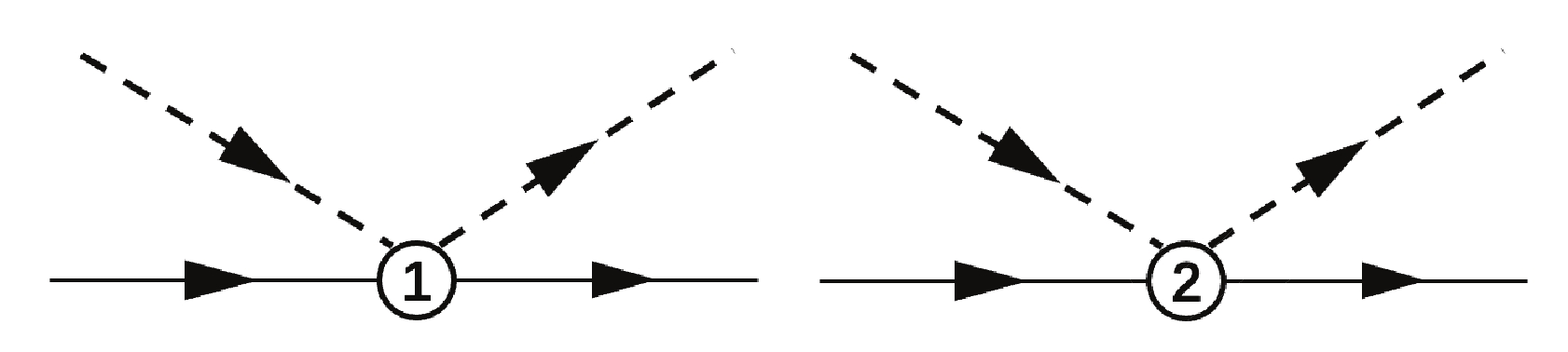
$ O(p^2) $ level, generated by the Lagrangian Eqs. (1) and (2) are depicted in Figs. 1 and 2. We use a simple K-matrix unitarization scheme to improve the$ O(p^2) $ perturbation amplitudes. A useful auxiliary function,$ {\boldsymbol{g}}(s)\equiv {\rm{diag}}\{g_i(s)\} $ , is introduced,$ g_i(s) = \int \frac{{\rm d}^4q}{(2\pi)^4} \frac{1}{(q^2-M_i^2+{\rm i}\epsilon)((P-q)^2-m_i^2+{\rm i}\epsilon)},\,\, (s = P^2) $

(4) where
$ M_i $ is the baryon mass and$ m_i $ is the meson mass in the i-th channel. The expression of$ g_i(s) $ in Eq. (4) is renormalized using standard dimensional regularization, which introduces an explicit renormalization scale (μ) dependence (see for example Ref. [29]). Notice that in our fit we choose different μ parameters in channels with different strangeness numbers. Though it is expected these μ parameters do not differ much, in practice we use the relation:$ {\boldsymbol{T}}^{-1} = {\boldsymbol{K}}^{-1} - {\boldsymbol{g}}(s), $

(5) where
$ {\boldsymbol{K}} $ is the tree level$ S_{ 1 1} $ channel scattering amplitude and$ {\boldsymbol{T}} $ the unitarized scattering T matrix.The processes under concern are
$ N\pi \to N\pi $ ,$ K^-p \to K^-p $ ,$ K^-p \to \overline{K}^0 n $ ,$ K^-p \to \pi^+\Sigma^- $ ,$ K^-p \to \pi^-\Sigma^+ $ ,$ K^-p \to \pi^0\Sigma^0 $ ,and$ K^-p \to \pi^0\Lambda $ . In the beginning, we start with a$ 2\times2 \; I=1/2 $ matrix amplitude fit for the$ \pi N $ and$ N\eta $ channels; a$ 3\times 3 \; I=1 $ matrix amplitude fit for$ \Lambda\pi $ ,$ \Sigma\pi $ , and$ N\bar K $ channels; and a$ 2\times2 \; I=0 $ matrix amplitude fit for$ \Sigma\pi $ and$ N\bar{K} $ channels, while neglecting higher thresholds. The fit parameters are listed in Table 1, and the fit curves are plotted in Figs. 3 and 4. In the fit, the s–wave approximation is used. It should be noted that the main contribution to the chi-squared comes from the fit to the$ S_{ 1 1} $ channel phase shift data, which contain very small error bars. (Here we follow a similar strategy to that of Ref. [1] and define an error assigned to every point as the sum in quadrature of a systematic plus a statistical error,$ {\rm err}(\delta) = \sqrt{e_s^2+e_r^2\delta^2} $ , where$ e_s(=0.1^\circ) $ is the systematic error and$ e_r(=2\%) $ the relative one) The fit quality, as seen in Fig. 3, is not very good. We ascribe the defect to the simple K-matrix fit being crude for the accurate$ \pi N $ data. (In Ref. [10] a good K matrix fit can be obtained by adding more background terms) What we only want to emphasize is the qualitative result, that is the$ N^*(890) $ co-exists with other resonances found in the literature.Paraneter $ \chi^2_{d.o.f} = 5.1 $ 

D 0.4 F 0.23 $f_0/\rm{MeV}$ 

103.8 $M_0/\rm{GeV}$ 

1.1 $b_0/\rm{GeV^{-1}}$ 

−0.044 $b_D/\rm{GeV^{-1}}$ 

0.026 $b_F/\rm{GeV^{-1}}$ 

−0.189 $b_1/\rm{GeV^{-1}}$ 

$ 0.647\pm 0.048 $ 

$b_2/\rm{GeV^{-1}}$ 

$ 0.672\pm 0.062 $ 

$b_3/\rm{GeV^{-1}}$ 

$ -0.121\pm 0.016 $ 

$b_4/\rm{GeV^{-1}}$ 

$ -0.701\pm 0.063 $ 

$\mu_{S=0}/\rm{GeV}$ 

$ 0.703\pm 0.053 $ 

$\mu_{S=-1}/\rm{GeV}$ 

$ 0.727\pm 0.008 $ 


Figure 3. (color online) The fit to the phase shift data in the region
$ \sqrt{s}= 1.08 - 1.16 $ GeV (data from Ref. [30]).
Figure 4. (color online) Fit to the experimental data in the
$ s = -1 $ sector. The data points represented by black diamonds, crimson squares, orange circles, green crosses, cyan down-triangles, and green up-triangles in the first four panels are taken from Refs. [31–36], respectively. The data in the fifth and sixth panels are from Ref. [37].The amplitudes poles on different sheets are searched for in this study. In the
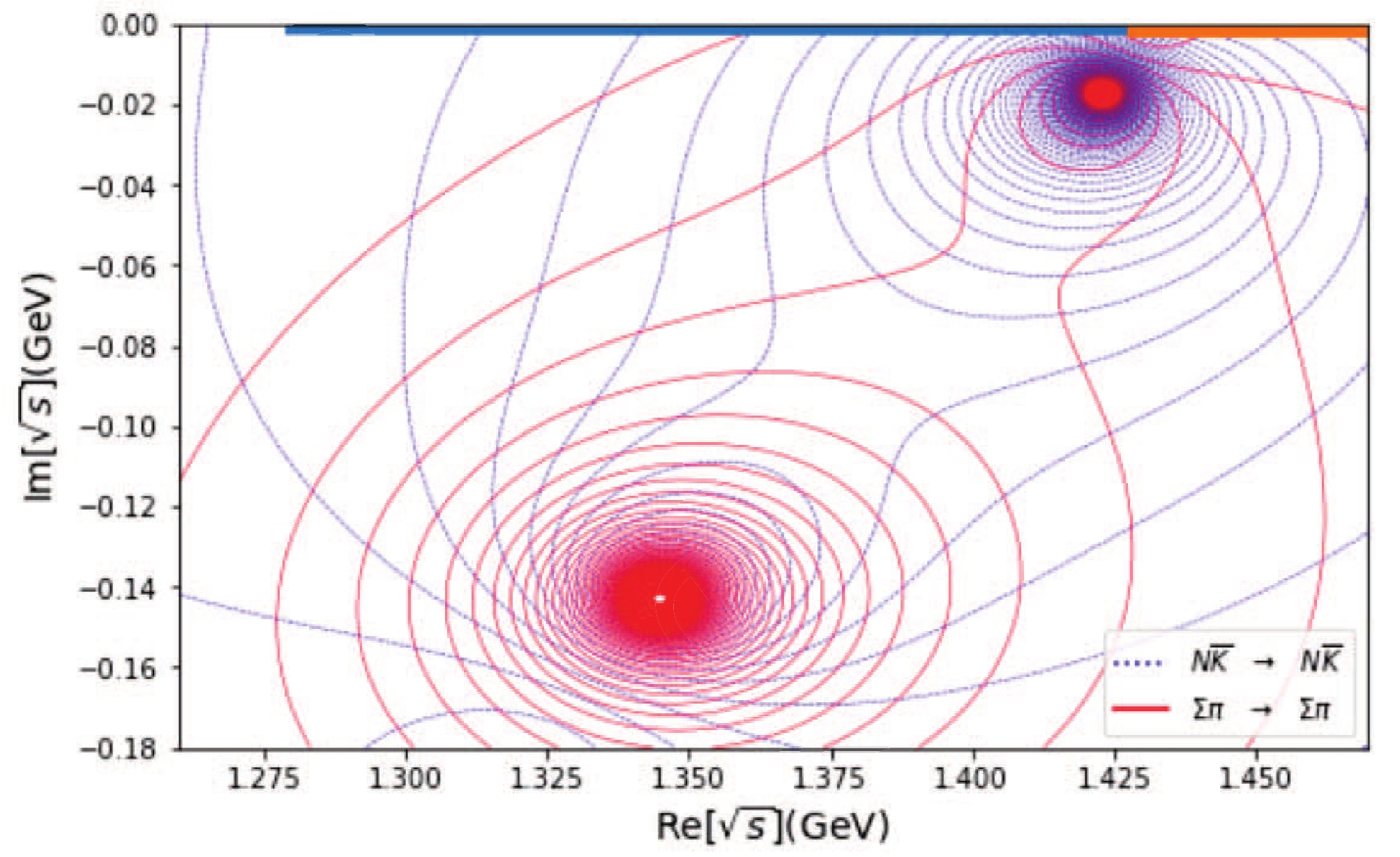
$ N\pi $ and$ N\eta $ channels, it is clearly seen from Fig. 5 the pole location of the wanted$ N^*(890) $ and$ N^*(1535) $ . The precise location of the two poles and their couplings are listed in Table 2. Notice that the$ \pi N $ data are used only in a small region of the pole at 1535 in Table 2 and is not actually stable. We just used one "satisfactory" solution. This is not a severe problem since our primary goal is proving the existence of the$ N^*(890) $ pole and its stability.③ Meanwhile, results in the$ s=-1,\; I=0 $ ($ N\bar{K} $ ,$ \Lambda\eta $ ) sector are listed in Fig. 6 and Table 3. It is worth emphasizing that in the present$ 2\times2 $ fit, there are only two poles, as shown in Table 3. This "twin pole" structure has been extensively discussed in literature, and our results may be considered as a further confirmation. Moreover, when one goes to the complete$ 4\times 4 $ fit by including$ \Lambda\eta $ and$ \Xi K $ channels, another$ 1/2^- $ Λ baryon resonance appears at$\sqrt{s}=1.81-{\rm i}0.04$ GeV, in qualitative agreement with the$ \Lambda(1670) $ pole found in Ref. [14].Pole location $ |g_{N\pi}| $ 

$ |g_{N\eta}| $ 

$ N^* $ (890)

$1.066- 0.280 {\rm i}$ 

0.617 0.436 $ N^* $ (1535)

$1.553- 0.056 {\rm i}$ 

0.645 1.031 Table 2. Pole locations and channel couplings in the
$ s = 0 $ , I =$ {1}/{2} $ sector. All numbers in the table (and hereafter) are in units of GeV.Pole location $ |g_{\Sigma \pi}| $ 

$ |g_{N\overline{K}}| $ 

$ \Lambda^* $ (1380)

$1.345- 0.143 {\rm i}$ 

1.032 0.702 $ \Lambda^* $ (1405)

$1.423- 0.017 {\rm i}$ 

0.453 0.966 Table 3. Pole locations and channel couplings in the
$ s = -1, \;I = 0 $ sector.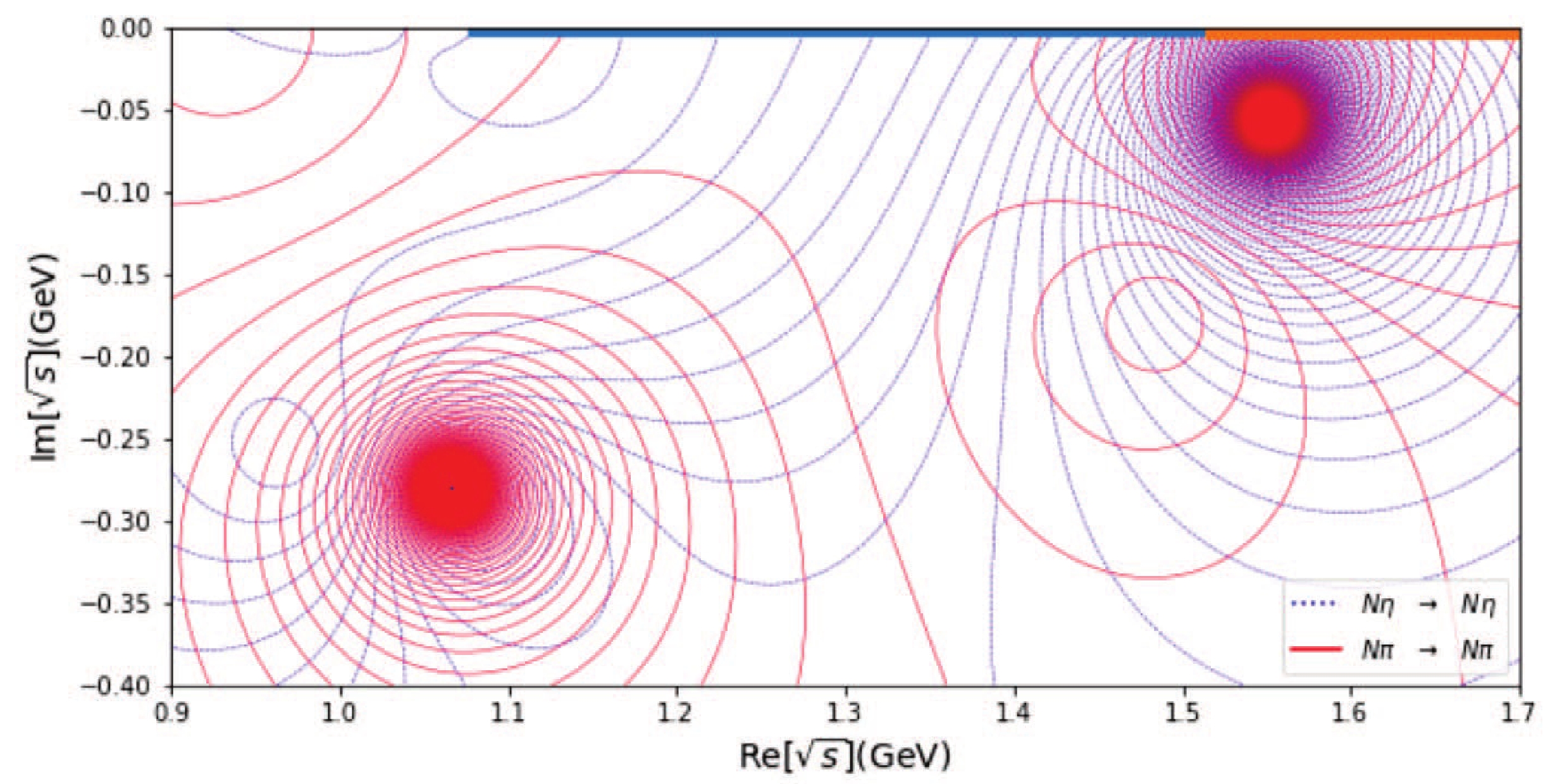
Figure 5. (color online) The
$ N^* $ (890) and$ N^* $ (1535) poles in sheet (−,+). The corresponding thresholds are marked with thick lines in the upper edge of the box.Another
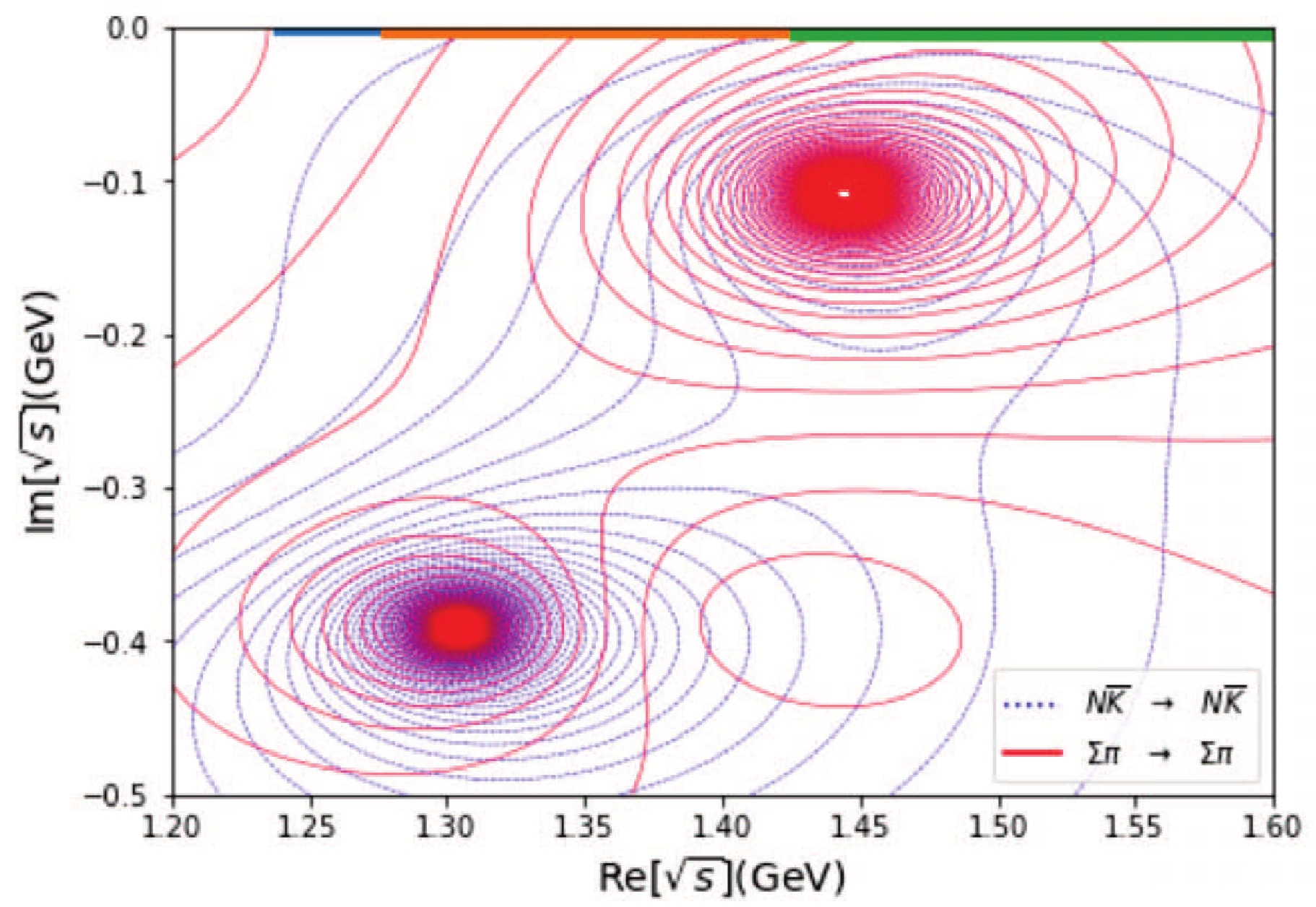
$ 3\times3 $ fit in the$ s=-1, \:I=1 $ sector ($ \Sigma\pi $ ,$ N\bar{K} $ ,$ \Lambda\eta $ ) is depicted in Fig. 7 and Table 4. It is remarkable to notice that the results listed in Table 4 are in agreement with the result of Refs. [18, 19].Pole Location $ |g_{\Sigma \pi}| $ 

$ |g_{N\overline{K}}| $ 

$ \Sigma^* $ (1380)

$ 1.305- 0.392 {\rm i} $ 

0.578 1.346 $ \Sigma^* $ (1650)

$ 1.444- 0.109 {\rm i} $ 

0.940 1.084 Table 4. Pole locations and channel couplings in the
$s = -1, \;I = 1$ sector.At last, we also listed in Fig. 8 and Table 5 the results in the
$ s=-2 $ sector. Here, we analyze a triple channel amplitude ($ \Xi\pi,\Lambda\bar{K},\Sigma\bar{K} $ ), in accordance with Ref. [38].④ Notice that in Table 5, one of the poles contains a too small width. But, we think this is not worrisome since the choice of the μ parameter is somewhat arbitrary. The most important fact is that there are two$ \Xi^* $ poles which coincides with the result of Ref. [23].Pole Location $ |g_{\Xi \pi}| $ 

$ |g_{\Lambda \overline{K}}| $ 

Pole1 $ 1.636-0.0001{\rm i} $ 

0.262 0.335 Pole2 $ 1.696-0.246{\rm i} $ 

1.087 1.208 Table 5. Pole locations and channel couplings in the in
$s= -2,\; I = {1}/{2}$ sector.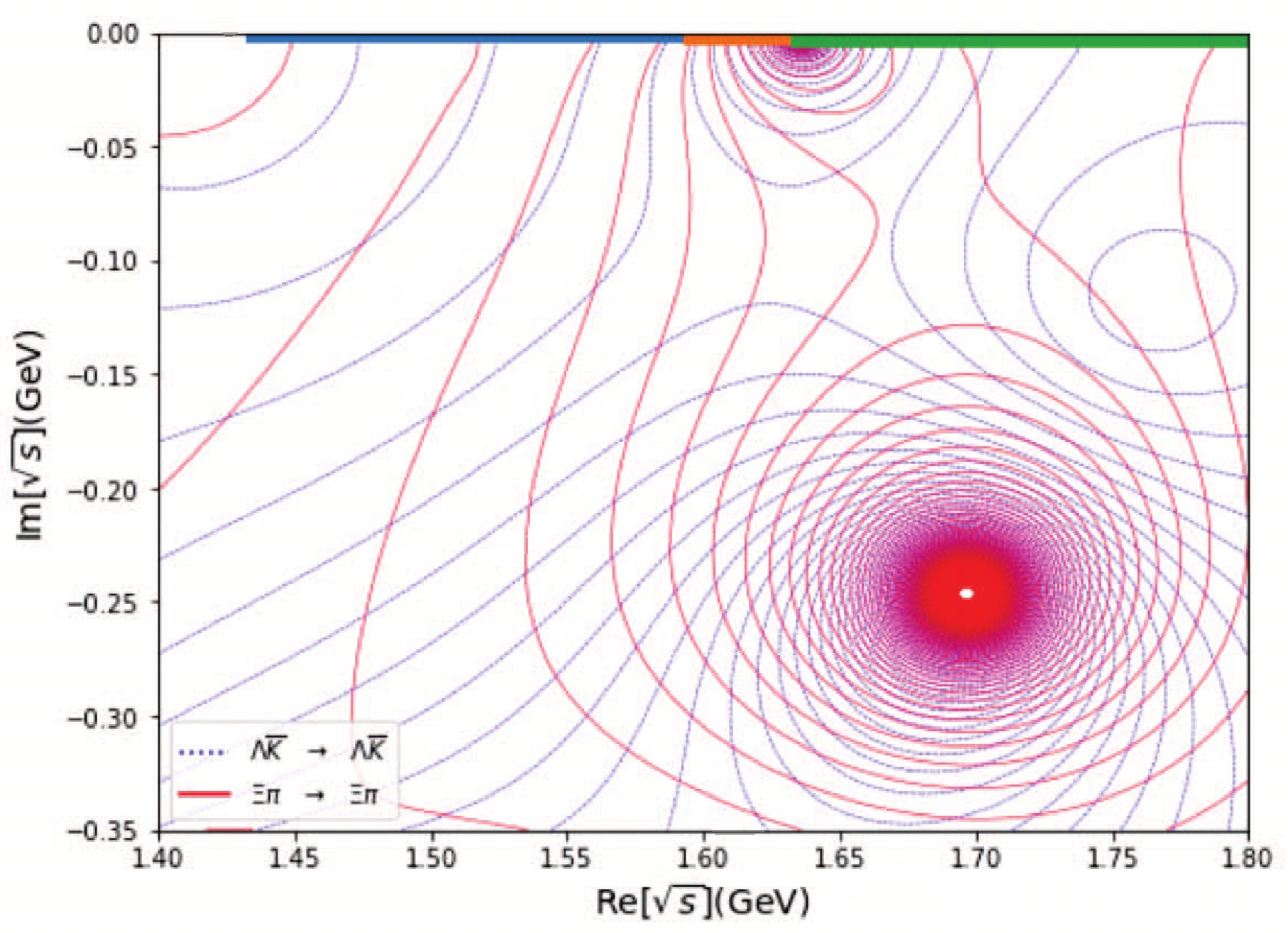
Figure 8. (color online) Pole locations and channel couplings in the
$s = -2,\; I=1/2$ sector, in sheet (−,+,+).It is seen from Fig. 4 that the last diagram (the fit to the
$ \sigma(K^-p\to\pi^0\Lambda) $ ) is not fit well. This can be improved in another fit solution at the cost that the fit to the$ S_{ 1 1} $ phase shift gets slightly worse, and that the$ N^*(1535) $ pole and one of the$ \Xi^* $ poles in Fig. 8 flee away. Nevertheless, the existence of the$ N^*(890) $ , as well as the "twin pole structure" of$ \Lambda^* $ and$ \Sigma^* $ , are not influenced. Finally, one may question that the$ N^*(890) $ pole location determined here is too high as compared with previous determinations. Given the crude fit to the$ \pi N $ data, the present study should be viewed as an exploratory study only. We think that is because a fit using a simple K-matrix model, as adopted here, is not quite suitable for the accurate$ \pi N $ data, hence influencing the pole determination. In Ref. [10], a good K-matrix fit can be obtained by adding more background terms, providing a rather low$ N^*(890) $ location. Here, we only want to emphasize the qualitative picture, that is the$ N^*(890) $ has the same chance of existing as other resonances found in the literature. Also, being slightly above or below the threshold, as we believe, is not the key issue. In both cases, the pole has a large width and only contributes a slow, but steady, rise of the phase shift (i.e., the physical role is very similar).Notice that all the
$ J^P=1/2^- $ baryons discussed above are generated from an effective Lagrangian without them. That is to say, these negative parity baryons are generated dynamically. In order to seriously address the question whether these states are of "elementary" nature or only hadronic molecules, one probably needs to make a study starting from an effective Lagrangian with built-in negative parity baryonic fields. For this purpose, we write:$ \begin{aligned}[b] {\cal L} =&\operatorname{Tr}\left[\bar{B} {\rm i} \gamma^{\mu}\left[D_{\mu}, B\right]\right]-M_{0} \cdot \operatorname{Tr}[\bar{B} B] \\&+ \operatorname{Tr}\left[\bar{B}_- {\rm i} \gamma^{\mu}\left[D_{\mu}, B_-\right]\right]-M^{*}_{0} \cdot \operatorname{Tr}[\bar{B}_- B_-] \\ &+D \operatorname{Tr}\left[\bar{B} \gamma^{\mu} \gamma^{5}\left\{u_{\mu}, B\right\}\right]+F \operatorname{Tr}\left[\bar{B} \gamma^{\mu} \gamma^{5}\left[u_{\mu}, B\right]\right]\\ &+D_- \operatorname{Tr}\left[\bar{B}_- \gamma^{\mu} \gamma^{5}\left\{u_{\mu}, B_-\right\}\right]+F_- \operatorname{Tr}\left[\bar{B}_- \gamma^{\mu} \gamma^{5}\left[u_{\mu}, B_-\right]\right]\\ & + D_{1}\left\{ \operatorname{Tr}\left[\bar{B}_- \gamma^{\mu} \left\{u_{\mu}, B\right\}\right]+ \operatorname{Tr}\left[\bar{B} \gamma^{\mu} \left\{u_{\mu}, B_-\right\}\right]\right\} \\ &+ F_{1}\left\{ \operatorname{Tr}\left[\bar{B}_- \gamma^{\mu} [u_{\mu}, B]\right]+ \operatorname{Tr}\left[\bar{B} \gamma^{\mu} [u_{\mu}, B_-]\right]\right\}\ , \end{aligned} $

(6) $ \begin{aligned}[b] {\cal L}^{1}_{\rm SB} =& b_{0}\langle\bar{B} B\rangle\langle\chi_+\rangle+b_{D}\langle\bar{B}\left\{\chi_+, B\right\}\rangle+b_{F}\langle\bar{B}\left[\chi_+, B\right]\rangle \\& + b^{'}_{0}\langle\bar{B}_- B_-\rangle\langle\chi_+\rangle+b^{'}_{D}\langle\bar{B}_-\left\{\chi_+, B_-\right\}\rangle\\&+b^{'}_{F}\langle\bar{B}_-\left[\chi_+, B_-\right]\rangle\ , \end{aligned} $

(7) $ \begin{aligned}[b] {\cal L}^{2}_{\rm SB} =& e (\langle\bar{B}\chi_-B_-\rangle - \langle\bar{B}_-\chi_- B\rangle)\\& +h (\langle\bar{B} B_-\chi_-\rangle - \langle\bar{B}_-B\chi_-\rangle)\ , \end{aligned} $

(8) where
$ B_- $ denotes a$ 1/2^- $ baryon octet and$ {\cal L}_{\rm tot.} ={\cal L} + {\cal L}^{1}_{SB} + {\cal L}^{2}_{SB} $ . In the fit, however, we find that including negative parity baryons explicitly in the effective Lagrangian does not improve the fit quality much. Furthermore, the locations of the newly introduced poles are very unstable and have little influence on the locations of the dynamical poles, as discussed in Figs. 5–8. Therefore, we think that it is not necessary to include extra "elementary" negative baryon fields, in disagreement with some claims found in the literature.At last, one needs to discuss the fate of those poles in the
$ S U(3) $ limit for the purpose of pinning down the property of the desired$ N^*(890) $ . To study this, it is realized that [39] the$ S U(3) $ symmetry only exists in the sheet with the same sign, i.e., in sheet$ (+,+,\cdots,+) $ or sheet$ (-,-,\cdots,-) $ , and all channels should be taken into consideration. Taking the$ N^*(890) $ for example, there were only two channels being considered (i.e.,$ N \pi $ ,$ N\eta $ ). Now, one has to go to four channels ($ N\pi $ ,$ N\eta $ ,$ \Lambda K $ ,$ \Sigma K $ ) in sheet$ (-,-,-,-) $ . In our strategy, we first take the$ S U(3) $ limit,$ m_K^2\to m_\pi^2 $ , and trace the trajectories starting from the sheet where the pole locates, i.e, sheet$ (-,+,+,+) $ . Then we multiply the channel phase space factors ,$ \rho_i $ ($ i=2,3,4 $ ), by a factor k, and let k change smoothly from$ +1 $ to$ -1 $ . In this way, one can trace the trajectory of the$ N^*(890) $ pole moving from the physical location to its destiny in the$ S U(3) $ limit, in sheet (−,−,−,−). We find that$ N^*(890) $ and$ N^*(1535) $ have different destinations, i.e., they belong to different octets. This is not surprising as it is known that in$ S U(3) $ limit there exist actually two octets, as$ 8\otimes 8=1\oplus8\oplus8\oplus10\oplus\bar{10} \oplus27 $ . We do not trace other pole trajectories any more, as they are model and are scheme dependent, and have been extensively discussed already in the literature.In this study, we have carefully investigated the possible correlations between the newly proposed
$ N^*(890) $ resonance and those having been discussed extensively in the literature, e.g.,$ \Lambda^*(1405) $ and$ \Lambda^*(1380) $ . Since they exist on the same footing, and the negative parity Λ baryons are well accepted [40], there is little doubt to the authors on the existence of the$ N^*(890) $ . The present work may also be further improved by going to$ S U(3) $ loop calculations to verify the conclusions made in this note.
HTML
-
We would like to thank Z. H. Guo for a careful reading of the manuscript and very helpful discussions.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: