Abstract
HTML
Reference
Related
PDF
-
In recent years, an increasing number of heavy baryons have been confirmed by the Belle, LHCb, and CDF collaborations, and the spectra of the charm and bottom baryon families have become increasingly abundant. For excited bottom baryons in particular, scientists have achieved significant progress in theoretical and experimental studies in recent years, such as for
Λb(5912) ,Λb(5920) [1, 2],Λb(6072) [3, 4],Ξb(6227) [5–7], andΞb(6100) [8]. In 2019, the LHCb collaboration reported the discovery of two bottom baryon states,Λb(6146)0 andΛb(6152)0 , by analyzing theΛ0bπ+π− invariant mass spectrum frompp collisions [9]. The measured masses and widths aremΛb(6146)0=6146.17±0.33±0.22±0.16 MeV,ΓΛb(6146)0=2.9±1.3±0.3 MeV,mΛb(6152)0=6152.51±0.26±0.22±0.16 MeV,ΓΛb(6152)0=2.1±2.1±0.8±0.3 MeV.
By studying their strong decays using quark model or
3P0 model, scholars interpreted these two states as aΛb(1D) doublet [6, 10–13]. Before this observation, different collaborations predicted the masses of this doublet using the quark model [14–17], whose results were not consistent with each other and with experiments, and they require further confirmation using different theoretical methods and models.Very recently, the LHCb collaboration reported the observation of two new excited
Ξb states in theΛbK−π+ mass spectrum [18]. The measured masses and widths weremΞb(6327)=6327.28+0.23−0.21(stat)±0.08(syst)±0.24(mΛb) MeV, ΓΞb(6327)<2.20 MeV, mΞb(6333)=6332.69+0.17−0.18(stat)±0.03(syst)±0.22(mΛb) MeV, ΓΞb(6327)<1.55 MeV.
By comparing with the quark-model predictions[6, 10], Chen et al. interpreted these two states as a
1D (Ξb ) doublet withJP=3/2+ and5/2+ .Many theoretical methods and models have been used over the past decades to investigate bottom baryons, including the quark model [12, 14–16, 19–41], heavy hadron chiral perturbation theory [42–47],
3P0 decay model [48–54], lattice quantum chromodynamics (QCD) [55–58], light cone QCD sum rules [59–66], and QCD sum rules [67–79]. For more discussions on bottom baryon states, please consult Refs. [17, 80–88] and the references therein. Through the efforts of theoretical and experimental physicists, some bottom baryon states have been observed and confirmed, such asΞb(5797) [89],Λb(5620) [89],Λb(5912) [89],Λb(5920) [89], andΛb(6072) [3, 4], whose quantum numbers were determined to be 1S(1/2+ ), 1S(1/2+ ), 1P(1/2− ), 1P(3/2− ), and 2S(1/2+ ), respectively. However, the inner structures of the newly observed baryon statesΞb(6327) ,Ξb(6333) ,Λ(6146) , andΛ(6152) require further confirmation theoretically. The other bottom baryon states, such as the radially excited D-waveΞb andΛb baryons, have not been observed.The QCD sum rule method has been proven to be the most effective non-perturbative method in studying the properties of mesons and baryons [70, 90–98], and it has been extended to studying multiquark states [99–106]. In our previous study, we systematically studied the D-wave charmed baryons
Λc(2860) ,Λc(2880) ,Ξc(3055) , andΞc(3080) [71], the P-waveΩc states,Ωc(3000) ,Ωc(3050) ,Ωc(3066) ,Ωc(3090) , andΩc(3119) [107, 108], and theΩb states,Ωb(6316) ,Ωb(6330) ,Ωb(6340) , andΩb(6350) [109] using the method of QCD sum rules. As a continuation of our previous research, we study the1D and2D states ofΞb andΛb baryons with orbital excitations (Lρ,Lλ)= (0,2 ), (2,0 ), and (1,1 ). The motivation of this study was to further confirm the structures ofΛb(6146) ,Λb(6152) ,Ξb(6327) , andΞb(6333) , decode their excitation modes, and predict the masses and pole residues of1D and2DΞb andΛb baryons.The remainder this paper is outlined as follows: in Sec. II, we first construct three types of interpolating currents for D-wave bottom baryons
Λb andΞb ; in Sec. III, we derive QCD sum rules for the masses and pole residues of these states with spin-parity3/2+ and5/2+ from two-point correlation function; in Sec. IV, we present the numerical results and discussions; and Sec. V presents our conclusions. -
In the heavy quark limit, one heavy quark within a heavy baryon system is decoupled from two light quarks. Under this scenario, the dynamics of a heavy baryon state can be separated into two parts: the
ρ -mode, which is for the degree of freedom between two light quarks, and theλ -mode, which denotes the degree between the center of mass of diquarks and the heavy quark. In this diquark-quark model, the orbital angular momentum between the two light quarks is denoted byLρ , and the angular momentum between the light diquarks and heavy quark is denoted byLλ . The D-wave (L=2 ) bottom baryon has three orbital excitation modes: (Lρ,Lλ)=( 2,0 ), (0,2 ), and (1,1 ). The color antitriplet diquarks with quantum numbers ofLρ=0 andsl=0 can be expressed asεijkqTjCγ5q′k , which has the spin-parity ofJPd=0+d . The spin-parity of relative P-wave and D-wave are denoted asJPρ/λ=LPρ/λ=1−ρ/λ and2+ρ/λ , respectively. IfJPb=(1/2)+b is the spin-parity of b-quark, we can obtain the final states of D-wave bottom baryons according to direct product of angular momentumJP=0+d⨂JPρ/λ⨂12+b .For the excitation mode (
Lρ,Lλ)= (1,0) , the P-wave diquark system withJP=1− can be constructed by applying a derivative between two light quarks:ϵijk[∂βqTi(x)Cγ5q′j(x)−qTi(x)Cγ5∂βq′j(x)].
(1) Based on this, we introduce an additional derivative between the two light quarks in Eq. (1) to obtain the excitation mode of (
Lρ,Lλ)= (2,0) ϵijk{[∂α∂βqTi(x)Cγ5q′j(x)−∂βqTi(x)Cγ5∂αq′j(x)]−[∂αqTi(x)Cγ5∂βq′j(x)−qTi(x)Cγ5∂α∂βq′j(x)]}.
(2) For the excitation mode (
Lρ,Lλ)= (0,2) , we must apply two derivatives between the diquark system and b-quark field. It should be noted that the b-quark in the bottom baryon is static in the heavy quark limit. Thus,↔∂μ is reduced to←∂μ when operating on the b-quark field, and the light diquark state withJP=2+ is expressed as∂α∂β[ϵijkqTi(x)Cγ5q′j(x)]=ϵijk[∂α∂βqTi(x)Cγ5q′j(x)+∂βqTi(x)Cγ5∂αq′j(x)]+∂αqTi(x)Cγ5∂βq′j(x)+qTi(x)Cγ5∂α∂βq′j(x)].
(3) For the (
Lρ,Lλ)= (1,1 ) state, we require an additional derivative between the P-wave diquark (Eq. (1)) and b-quark field:∂αϵijk[∂βqTi(x)Cγ5q′j(x)−qTi(x)Cγ5∂βq′j(x)]=ϵijk[∂α∂βqTi(x)Cγ5q′j(x)+∂βqTi(x)Cγ5∂αq′j(x)−∂αqTi(x)Cγ5∂βq′j(x)−qTi(x)Cγ5∂α∂βq′j(x)]Γαβμνck(x).
(4) Considering the symmetrization of the Lorentz indexes μ and ν, the light diquark state with (
Lρ,Lλ)= (1,1 ) can be expressed in a simpler form:ϵijk[∂α∂βqTi(x)Cγ5q′j(x)−qTi(x)Cγ5∂α∂βq′j(x)].
(5) Finally, we combine the above light diquark systems with the b-quark field to form
JP=3/2+ or5/2+ baryon states that have three excitation modes, (Lρ,Lλ)= (2,0 ), (0,2 ), and (1,1 ). For more details about the construction of the interpolating currents of baryons, please consult Refs. [71, 72, 97]. We can now classify these constructed interpolating currents as follows:(Lρ,Lλ)=(0,2) for J1μ/η1μ(x),J1μν/η1μν(x),(Lρ,Lλ)=(2,0) for J2μ/η2μ(x),J2μν/η2μν(x),(Lρ,Lλ)=(1,1) for J3μ/η3μ(x),J3μν/η3μν(x),
where
Jμ ,ημ are forΞb andΛb with quantum numbers1/2+ ;Jμν ,ημν denote3/2+Ξb andΛb baryons, respectively. The interpolating currents for different excitation modes (Lρ,Lλ)= (0,2 ), (2,0 ), and (1,1 ) are denoted asJn andηn withn=1 ,2 , and3 , respectively, which can be expressed asJ1μ(x)=ϵijk[∂α∂βqTi(x)Cγ5sj(x)+∂αqTi(x)Cγ5∂βsj(x)+∂βqTi(x)Cγ5∂αsj(x)+qTi(x)Cγ5∂α∂βsj(x)]Γαβμbk(x),J2μ(x)=ϵijk[∂α∂βqTi(x)Cγ5sj(x)−∂αqTi(x)Cγ5∂βsj(x)−∂βqTi(x)Cγ5∂αsj(x)+qTi(x)Cγ5∂α∂βsj(x)]Γαβμbk(x)J3μ(x)=ϵijk[∂α∂βqTi(x)Cγ5sj(x),−qTi(x)Cγ5∂α∂βsj(x)]Γαβμbk(x),
(6) η1μ(x)=ϵijk[∂α∂βqTi(x)Cγ5q′j(x)+∂αqTi(x)Cγ5∂βq′j(x)+∂βqTi(x)Cγ5∂αq′j(x)+qTi(x)Cγ5∂α∂βq′j(x)]Γαβμbk(x),η2μ(x)=ϵijk[∂α∂βqTi(x)Cγ5q′j(x)−∂αqTi(x)Cγ5∂βq′j(x)−∂βqTi(x)Cγ5∂αq′j(x)+qTi(x)Cγ5∂α∂βq′j(x)]Γαβμbk(x),η3μ(x)=ϵijk[∂α∂βqTi(x)Cγ5q′j(x)−qTi(x)Cγ5∂α∂βq′j(x)]Γαβμbk(x),
(7) J1μν(x)=ϵijk[∂α∂βqTi(x)Cγ5sj(x)+∂αqTi(x)Cγ5∂βsj(x)+∂βqTi(x)Cγ5∂αsj(x)+qTi(x)Cγ5∂α∂βsj(x)]Γαβμνbk(x),
J2μν(x)=ϵijk[∂α∂βqTi(x)Cγ5sj(x)−∂αqTi(x)Cγ5∂βsj(x)−∂βqTi(x)Cγ5∂αsj(x)+qTi(x)Cγ5∂α∂βsj(x)]Γαβμνbk(x)J3μν(x)=ϵijk[∂α∂βqTi(x)Cγ5sj(x),−qTi(x)Cγ5∂α∂βsj(x)]Γαβμνbk(x),
(8) η1μν(x)=ϵijk[∂α∂βqTi(x)Cγ5q′j(x)+∂αqTi(x)Cγ5∂βq′j(x)+∂βqTi(x)Cγ5∂αq′j(x)+qTi(x)Cγ5∂α∂βq′j(x)]Γαβμνbk(x)η2μν(x)=ϵijk[∂α∂βqTi(x)Cγ5q′j(x)−∂αqTi(x)Cγ5∂βq′j(x)−∂βqTi(x)Cγ5∂αq′j(x),+qTi(x)Cγ5∂α∂βq′j(x)]Γαβμνbk(x)η3μν(x)=ϵijk[∂α∂βqTi(x)Cγ5q′j(x),−qTi(x)Cγ5∂α∂βq′j(x)]Γαβμνbk(x),
(9) where
Γαβμ andΓαβμν are the projection operatiors, whose explicit forms are:Γαβμ=(gαμgβν+gανgβμ−12gαβgμν)γνγ5,
(10) Γαβμν=gαμgβν+gανgβμ−16gαβgμν−14gαμγβγν−14gανγβγμ−14gβμγαγν−14gβνγαγμ+124γαγμγβγν+124γαγνγβγμ+124γβγμγαγν+124γβγνγαγμ.
(11) Note that we can select either the partial derivative
∂μ or the covariant derivativeDμ to construct the interpolating currents. The current with the covariant derivative is gauge invariant but blurs the physical interpretation of↔Dμ being the angular momentum. The current with the partial derivative∂μ is not gauge invariant but manifests the physical interpretation of↔∂μ being the angular momentum. In the calculations with these two currents in QCD sum rules, the difference is that the current with the covariant derivativeDμ emits a gluon at a interaction vertex. This gluon field contributes to the gluon condensate terms. Our research indicates that the contributions of these condensate terms from the vertex result in negligible difference in the final results [98]. Thus, we neglect the contributions from the vertex in gluon condensate terms and use the current with the partial derivative∂μ as our interpolating currents. -
The first step of the analysis with QCD sum rules is to write down the following two-point correlation functions:
Πμν(p)=i∫d4xeip.x⟨0|T{Jμ/ημ(x)¯Jν/¯ην(0)}|0⟩,Πμναβ(p)=i∫d4xeip.x⟨0|T{Jμν/ημν(x)¯Jαβ/¯ηαβ(0)}|0⟩,
(12) where T is the time ordered product. The currents
Jμ/ημ(0) andJμν/ημν(0) in these correlations couple potentially to1D bottom statesB3/2± andB5/2± , respectively, and couple also to2D statesB′3/2± andB′5/2± with the quantum numbers3/2+ and5/2+ :⟨0|J/ημ(0)|B(′)+3/2(p)⟩=λ(′)+3/2U+μ(p,s),⟨0|J/ημν(0)|B(′)+5/2(p)⟩=λ(′)+5/2U+μν(p,s),
(13) ⟨0|J/ημ(0)|B(′)−32(p)⟩=λ(′)−3/2iγ5U−μ(p,s),⟨0|J/ημν(0)|B(′)−5/2(p)⟩=λ(′)−5/2iγ5U−μν(p,s).
(14) -
At the hadron level, a complete set of intermediate baryon states with the same quantum numbers as the current operators
Jμ/ημ(x) ,Jμν/ημν(x) ,iγ5Jμ/ημ(x) , andiγ5Jμν/ημν(x) are inserted into the correlation functionsΠμν(p) andΠμναβ(p) . After separating the pole terms of the lowest1D and2D states, we obtain the following results:Πμν(p)=(λ+23/2p̸+M+3/2M+23/2−p2+λ−23/2p̸−M−3/2M−23/2−p2+λ′+23/2p̸+M′+3/2M′+23/2−p2+λ′−23/2p̸−M′−3/2M′−23/2−p2)×(−gμν+γμγν3+2pμpν3p2−pμγν−pνγμ3√p2)+⋯=Π3/2(p2)(−gμν)+⋯
(15) Πμν(p)=(λ+25/2p̸+M+5/2M+25/2−p2+λ−25/2p̸−M−5/2M−25/2−p2
+λ′+25/2p̸+M′+5/2M′+25/2−p2+λ′−25/2p̸−M′−5/2M′−25/2−p2)×[˜gαμ˜gβν+˜gαν˜gβμ2−˜gαβ˜gμν5−110(γμγα+pαγμ−pμγα√p2−pμpαp2)˜gβν−110(γμγβ+pβγμ−pμγβ√p2−pμpβp2)˜gαμ]+⋯=Π5/2(p2)gαμgβν+gανgβμ2+⋯,
(16) where
˜gμν=gμν−(pμpν)/p2 ;M+j andM′+j denote the masses of the1D and2D states with positive parity and angular momentum j; andM−j andM′−j are for the states with negative parity. In these derivations, we use the following relations about the spinorsU±μ(p,s) andU±μν(p,s) :∑sUμ¯Uν=(p̸+M(′)±)(−gμν+γμγν3+2pμpν3p2−pμγν−pνγμ3√p2),
(17) ∑sUαβ¯Uμν=(p̸+M(′)±){˜gαμ˜gβν+˜gαν˜gβμ2−˜gαβ˜gμν5−110(γαγμ+pμγα−pαγμ√p2−pαpμp2)˜gβν−110(γβγμ+pμγβ−pβγμ√p2−pβpμp2)˜gαν−110(γαγν+pνγα−pαγν√p2−pαpνp2)˜gβμ−110(γβγν+pνγβ−pβγν√p2−pβpνp2)˜gαμ},
(18) where
p2=M±2 andp2=M(′)±2 on mass-shell for1D and2D states, respectively. From the imaginary part, we can obtain the spectral densities at the hadron side:ImΠj(s)π=p̸[λ+2jδ(s−M+2j)+λ−2jδ(s−M−2j)+λ′+2jδ(s−M′+2j)+λ′−2jδ(s−M′−2j)]+[M+jλ+2jδ(s−M+2j)−M−jλ−2jδ(s−M−2j)+M′+jλ′+2jδ(s−M′+2j)−M′−jλ′−2jδ(s−M′−2j)],=p̸ρ1j,H(s)+ρ0j,H(s).
(19) Subsequently, through a dispersion relation and Borel transformation, we obtain the QCD sum rules at the hadron side:
∫s0m2b[√sρ1j,H(s)+ρ0j,H(s)]exp(−sT2)ds=2λ+2jM+jexp(−M+2jT2)+2λ′+2jM′+jexp(−M′+2jT2),∫s0m2b[√sρ1j,H(s)−ρ0j,H(s)]exp(−sT2)ds=2λ−2jM−jexp(−M−2jT2)+2λ′−2jM′−jexp(−M′−2jT2),
(20) where j denotes the total angular momentum
3/2 or5/2 , and the subscript H denotes the hadron side. The parameters0 is the continuum thresholds, andT2 are the Borel parameters. From Eq. (20), we observe that the bottom states with positive parity and those with negative parity are successfully separated according to the combination ofρ1j,H(s) andρ0j,H(s) . -
At the QCD side, the correlation function is approximated at very large
P2=−p2 by contracting all quark fields using Wick's theorem. In our calculations, we use the full light quark propagatorsSijq(x) in the coordinate space and the full heavy quark propagatorSijQ(x) in the momentum spaces:Sijq(x)=ix̸2π2x4δij−mq4π2x2δij−⟨¯qq⟩12(1−imq4x̸)−x2192m20⟨¯qq⟩(1−imq6x̸)−taij[x̸σθη+σθηx̸]i32π2x2gsGaθη−18⟨¯qjσμνqi⟩σμν⋯,
(21) SijQ(x)=i(2π)4∫d4ke−ik.x{δijk̸−mQ−gsGcαβtcij4σαβ(k̸+mQ)+(k̸+mQ)σαβ(k2−m2Q)2−g2s(tatb)ijGaαβGbμν(fαβμν+fαμβν+fαμνβ)4(k2−m2Q)5⋯},
(22) where
fαβμν=(k̸+mQ)γα(k̸+mQ)γβ(k/+mQ)×γμ(k̸+mQ)γν(k̸+mQ),
(23) q=u,d,s ,ta=λa/2 , andλa is the Gell-Mann matrix. After completing the integrals both in the coordinate and momentum spaces, we obtain the QCD spectral density through the imaginary part of the correlation:ImΠj(s)π=p/ρ1j,QCD(s)+ρ0j,QCD(s).
(24) In calculations, we observe that the condensate contributions primarily result from
⟨¯qq⟩ ,⟨¯ss⟩ ,⟨(αsGG)/π⟩ ,⟨¯qgsσGq⟩ ,⟨¯sgsσGs⟩ ,⟨¯qgsσGq⟩2 , and⟨¯qgsσGq⟩ ⟨¯sgsσGs⟩ . The explicit form of the QCD spectral densitiesρ1j,QCD(s) andρ0j,QCD(s) are listed in the Appendix. Similar to the hadron side, we can obtain the sum rules at the QCD side. Subsequently, we apply the quark-hadron duality below the continuum thresholdss0 to obtain the QCD sum rules:2M+jλ+2jexp(−M+2jT2)+2M′+jλ′+2jexp(−M′+2jT2)=∫s0m2b[√sρ1j,QCD(s)+ρ0j,QCD(s)]exp(−sT2)ds.
(25) First, we select low continuum threshold parameters
s0 to include only the contributions of the1D state. Thereafter, we differentiate Eq. (25) with respect to1/T2 to obtain the masses of the1DΞb andΛb states withJp=3/2+ and5/2+ :M+2j=−dd(1/T2)∫s0m2b[√sρ1j,QCD(s)+ρ0j,QCD(s)]exp(−sT2)ds∫s0m2b[√sρ1j,QCD(s)+ρ0j,QCD(s)]exp(−sT2)ds.
(26) After the mass
M+j is obtained, it is treated as a input parameter to obtain the pole residues:λ+2j=∫s0m2b[√sρ1j,QCD(s)+ρ0j,QCD(s)]exp(−sT2)ds2M+exp(−M2+T2)ds.
(27) Now, we use the masses and pole residues of the
1D states as input parameters and postpone the continuum threshold parameterss0 to larger values to include the contributions of the2D states, and we obtain the QCD sum rules for the masses and pole residues of the2D states:M′+2j=−dd(1/T2){∫s′0m2b[√sρ1j,QCD(s)+ρ0j,QCD(s)]exp(−sT2)ds−2M+jλ+2jexp(−M+2jT2)} ∫s0m2b[√sρ1j,QCD(s)+ρ0j,QCD(s)]exp(−sT2)ds−2M+jλ+2jexp(−M+2jT2),
(28) λ′+2j=∫s′0m2b[√sρ1j,QCD(s)+ρ0j,QCD(s)]exp(−sT2)ds−2M+jλ+2jexp(−M+2jT2)2M′+jexp(−M′+2jT2)ds.
(29) -
The calculated results from QCD sum rules depend on input parameters such as the vacuum condensates, masses of quarks, continuum threshold
s0 , and Borel parametersT2 . For the values of the vacuum condensates used in this paper, we first obtain the standard values at the energy scaleμ=1 GeV [110, 111]:⟨¯qq⟩=−(0.24±0.01 GeV)3,⟨¯ss⟩=(0.8±0.1)⟨¯qq⟩,⟨¯qgsσGq⟩=m20⟨¯qq⟩,⟨¯sgsσGs⟩=m20⟨¯ss⟩,m20=(0.8±0.1) GeV2,⟨αsGGπ⟩=(0.33 GeV)4.
For the masses of quarks, we set
mu=md=0 owing to their small current quark masses, and the masses of the b-quark and s-quark are selected to bemb(mb) =(4.18±0.03 ) GeV andms (μ=2 GeV)=(0.095±0.005 ) GeV [89]. Subsequently, we consider the energy-scale dependence of the above input parameters from the re-normalization group equation:⟨¯qq⟩(μ)=⟨¯qq⟩(Q)[αs(Q)αs(μ)]4/9,⟨¯ss⟩(μ)=⟨¯ss⟩(Q)[αs(Q)αs(μ)]4/9,⟨¯qgsσGq⟩(μ)=⟨¯qgsσGq⟩(Q)[αs(Q)αs(μ)]2/27,⟨¯sgsσGs⟩(μ)=⟨¯sgsσGs⟩(Q)[αs(Q)αs(μ)]2/27,mb(μ)=mb(mb)[αs(μ)αs(mb)]12/23,ms(μ)=ms(2GeV)[αs(μ)αs(2GeV)]4/9,
αs(μ)=1b0t[1−b1b20logtt+b21(log2t−logt−1)+b0b2b40t2],
where
t=logμ2Λ2,b0=33−2nf12π,b1=153−19nf24π2,b2=2857−50339nf+32527n2f128π3
Λ=213 ,296 ,339 MeV for the flavorsnf=5 ,4 , and3 , respectively [89], and we evolve these parameters to the optimal energy scales μ to extract the masses of the bottom baryon states. To determine the optimal energy scales, we have developed an empirical formulaμ=√M2H−(nMQ)2 , whereMH is the mass of a hadron,MQ is the effective mass of a heavy quark, and n is the number of heavy quarks within a hadron. Since this formula was proposed to determine the optimal energy scales μ in the calculations of QCD sum rules [112–114], it has successfully been used to study the hidden-charm (hidden-bottom) tetraquark and molecular states [112– 114], hidden-charm pentaquark states [115], charmed and bottom states [116], etc. In this article, we set the effective mass of b-quark asMb=5.17 GeV, which was fitted in a study on the diquark-antidiquark type hidden-bottom tetraquark states [117].For selecting the working interval of the parameter
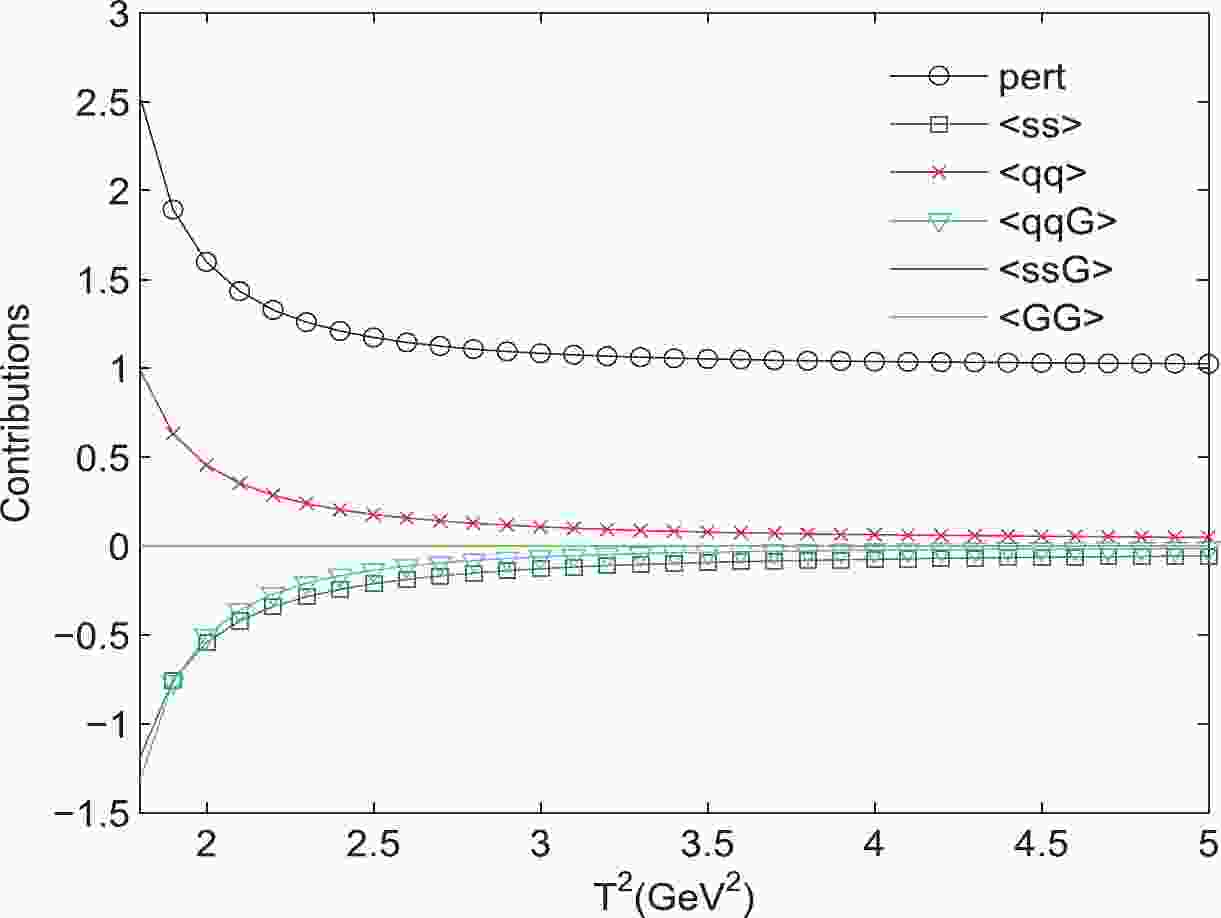
T2 and continuum threshold parameterss0 , some criteria should be satisfied, i.e., pole dominance, convergence of operator product expansion (OPE), and appearance of the Borel platforms, in addition to satisfying the energy scale formula. In other words, the pole contribution should be as large as possible (commonly larger than40 %) compared with the contributions of the high resonances and continuum states. Meanwhile, we should also determine a plateau (Borel platforms), which will ensure OPE convergence and the stability of the final results. The plateau is often called the Borel window. As an example, we can analyze the convergence of operator production expansion ofΞb (3/2+ ) with the excitation mode (Lρ,Lλ)= (0,2 ). The contributions of the vacuum condensates of dimension n can be expressed asD(n)=∫s0m2bρQCD,n(s)exp(−sT2)ds∫s0m2bρQCD(s)exp(−sT2)ds,
(30) where
D(n) represents the contribution of condensate term with dimension n. In Fig. 1, we show the dependence of these condensate terms on the Borel parametersT2 , from which we can observe good OPE convergence.
Figure 1. (color online) Contributions of different condensate terms for
Ξb (3/2+ ) of the excitation mode (Lρ,Lλ)= (0,2 ), with variations in the Borel parametersT2. After repeated adjustment and comparison, we finally determine the optimal energy scales μ, the Borel windows, the continuum threshold parameters
s0 , and the pole contributions, which are presented in Tables 1, 2. As an example, the results for1D states with different excitation modes are shown explicitly in Figs. 2–25. Note that we plot the masses and pole residues with variations in the Borel parameters at much larger intervals than the Borel windows shown in Tables 1, 2. Additionally, the uncertainties of the masses and pole residues are marked as the upper and lower bounds in these figures. From Tables 1, 2, we observe that the pole contributions are about40 , and the pole dominance criterion is satisfied. However, we can observe that flat platforms appear in Figs. 2–25, and the uncertainties originating from the Borel parametersT2 in the Borel window are small (≤3 %). In other words, all of the criteria of QCD sum rules are satisfied, and it is reliable to extract the final results about the D-wave bottom baryons. Considering all uncertainties of the input parameters, we obtain the masses and pole residues of1D and2D states ofΛb andΞb baryons, which are also presentd in Tables 1, 2.Ξb(Lρ,lλ) 
JP 
μ/GeV2 T2/GeV2 √s0/GeV 
M/GeV Refs. [15, 18]/GeV λ/(10−1 GeV5) pole Ξb (
2,0 )
5/2+ (
1D )
3.7 
3.8−4.2 
7.0±0.1 
6.43+0.10−0.10 
1.59+0.20−0.18 
49%−59% 
Ξb (
2,0 )
3/2+ (
1D )
3.5 
3.9−4.3 
7.0±0.1 
6.42+0.09−0.09 
4.64+0.60−0.59 
47%−57% 
Ξb (
0,2 )
5/2+ (
1D )
3.6 
4.3−4.7 
6.9±0.1 
6.36+0.11−0.12 
6.333 [18]
0.67+0.08−0.07 
41%−56% 
Ξb (
0,2 )
3/2+ (
1D )
3.6 
3.6−4.0 
6.9±0.1 
6.34+0.12−0.11 
6.327 [18]
2.98+0.38−0.32 
41%−61% 
Ξb (
1,1 )
5/2+ (
1D )
3.6 
4.2−4.6 
6.9±0.1 
6.41+0.09−0.11 
0.80+0.11−0.12 
42%−58% 
Ξb (
1,1 )
3/2+ (
1D )
3.7 
3.8−4.2 
7.0±0.1 
6.41+0.09−0.11 
2.82+0.30−0.32 
47%−57% 
Ξb (
2,0 )
5/2+ (
2D )
4.1 
3.9−4.3 
7.3±0.1 
6.77+0.12−0.11 
2.46+0.23−0.19 
65%−77% 
Ξb (
2,0 )
3/2+ (
2D )
4.2 
3.9−4.3 
7.3±0.1 
6.73+0.09−0.10 
7.13+0.55−0.60 
66%−76% 
Ξb (
0,2 )
5/2+ (
2D )
4.1 
4.3−4.7 
7.2±0.1 
6.69+0.13−0.11 
6.696 [15]
0.98+0.10−0.12 
60%−68% 
Ξb (
0,2 )
3/2+ (
2D )
4.1 
3.7−4.1 
7.2±0.1 
6.62+0.10−0.13 
6.690 [15]
4.29+0.42−0.38 
53%−75% 
Ξb (
1,1 )
5/2+ (
2D )
4.1 
4.2−4.6 
7.2±0.1 
6.72+0.11−0.13 
1.19+0.13−0.15 
57%−70% 
Ξb (
1,1 )
3/2+ (
2D )
4.1 
3.8−4.2 
7.3±0.1 
6.79+0.12−0.09 
3.53+0.35−0.40 
65%−78% 
Table 1. Optimal energy scales μ, Borel parameters
T2 , continuum threshold parameterss0 , pole contributions (pole) and masses, and pole residues for the D-wave bottom baryon statesΞb , where the results of Ref. [15] are the quark-model predictions.Λb 
(Lρ,lλ) 
JP 
μ/GeV 2 
T2 /GeV
2 
√s0 /GeV
M/GeV Ref. [9, 15]/GeV λ/( 10−1 GeV
5 )
pole Λb (
2,0 )
5/2+ (
1D )
3.2 
3.5−3.9 
6.8±0.1 
6.28+0.10−0.10 
0.96+0.10−0.13 
42%−58% 
Λb (
2,0 )
3/2+ (
1D )
3.2 
3.3−3.7 
6.7±0.1 
6.21+0.10−0.10 
2.23+0.35−0.33 
44%−56% 
Λb (
0,2 )
5/2+ (
1D )
3.2 
3.7−4.1 
6.7±0.1 
6.15+0.13−0.15 
6.153 [9]
0.37+0.05−0.04 
41%−56% 
Λb (
0,2 )
3/2+ (
1D )
3.2 
3.4−3.8 
6.6±0.1 
6.13+0.10−0.09 
6.146 [9]
1.45+0.21−0.22 
44%−59% 
Λb (
1,1 )
5/2+ (
1D )
3.2 
3.9−4.3 
6.8±0.1 
6.29+0.08−0.06 
0.54+0.08−0.09 
45%−60% 
Λb (
1,1 )
3/2+ (
1 D)
3.4 
3.5−3.9 
6.8±0.1 
6.30+0.08−0.07 
1.77+0.31−0.28 
42%−57% 
Λb (
2,0 )
5/2+ (
2D )
3.9 
3.7−4.1 
7.1±0.1 
6.57+0.12−0.11 
1.84+0.18−0.20 
59%−73% 
Λb (
2,0 )
3/2+ (
2D )
3.9 
3.6−4.0 
7.0±0.1 
6.50+0.11−0.11 
4.65+0.42−0.38 
56%−67% 
Λb (
0,2 )
5/2+ (
2D )
3.8 
3.9−4.3 
7.0±0.1 
6.53+0.14−0.14 
6.531 [15]
0.83+0.08−0.07 
61%−71% 
Λb (
0,2 )
3/2+ (
2 D)
3.8 
3.6−4.0 
6.9±0.1 
6.47+0.09−0.10 
6.526 [15]
3.00+0.31−0.30 
50%−65% 
Λb (
1,1 )
5/2+ (
2D )
3.9 
4.1−4.5 
7.1±0.1 
6.62+0.10−0.08 
1.05+0.12−0.13 
53%−66% 
Λb (
1,1 )
3/2+ (
2D )
3.9 
3.7−4.1 
7.1±0.1 
6.60+0.09−0.09 
2.96+0.42−0.39 
56%−72% 
Table 2. Optimal energy scales μ, Borel parameters
T2 , continuum threshold parameterss0 , pole contributions (pole) and masses, and pole residues for the D-wave bottom baryon statesΛb , where the results of Ref. [15] are the quark-model predictions.
Figure 2. (color online) Mass of the bottom baryon state
Ξb (0,2,5/2 ) with variations in the Borel parametersT2.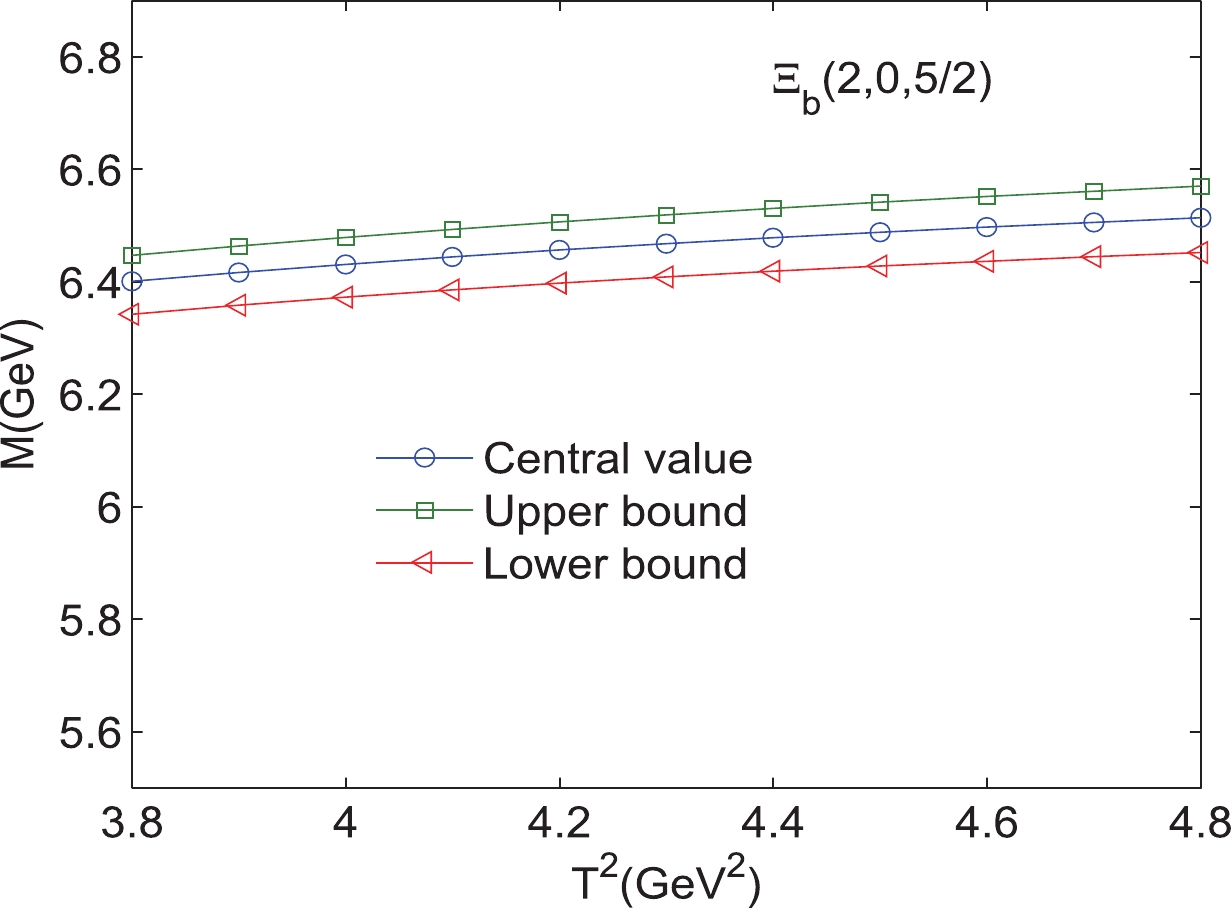 
Figure 3. (color online) Mass of the bottom baryon state
Ξb (2,0,5/2 ) with variations in the Borel parametersT2. 
Figure 4. (color online) Mass of the bottom baryon state
Ξb (0,2,3/2 ) with variations in the Borel parametersT2. 
Figure 5. (color online) Mass of the bottom baryon state
Ξb (2,0,3/2 ) with variations in the Borel parametersT2.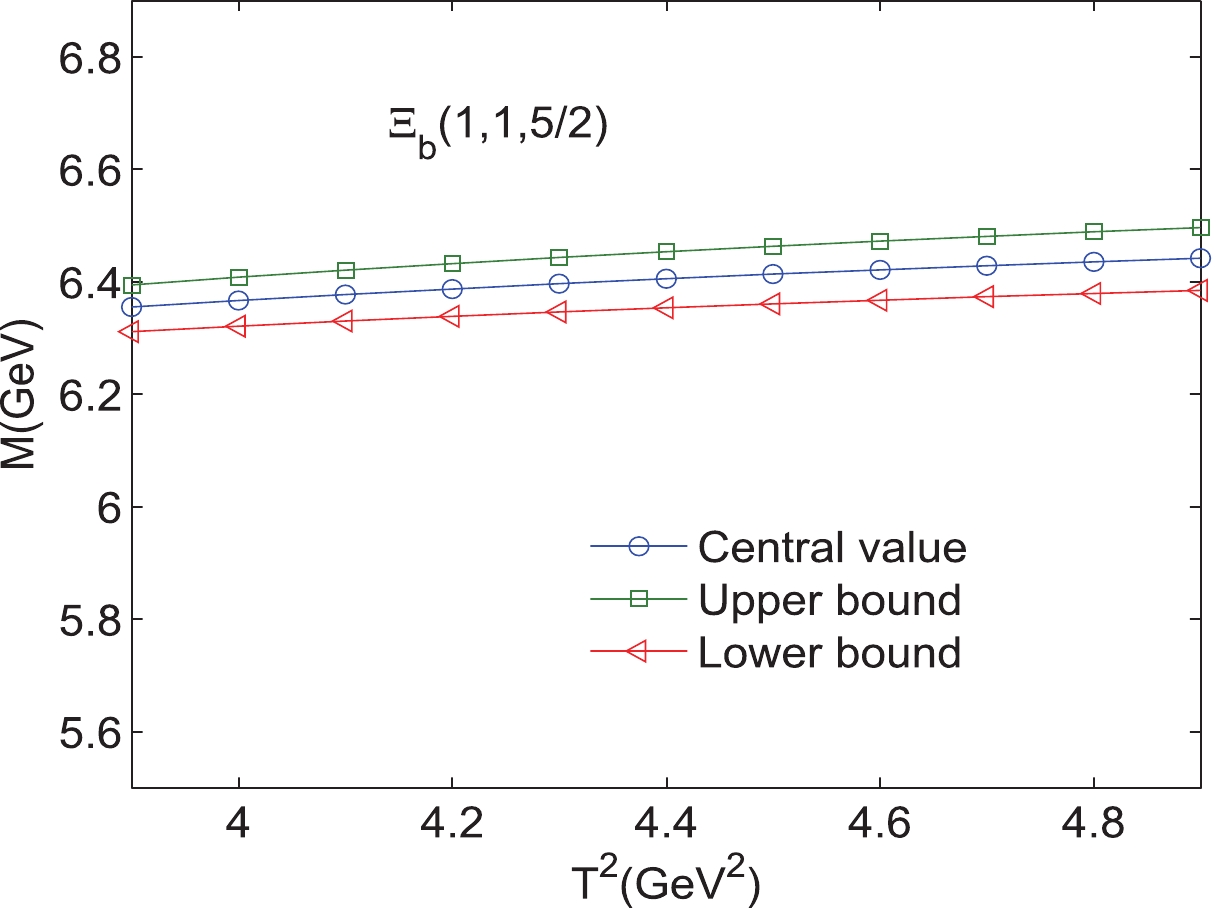 
Figure 6. (color online) Mass of the bottom baryon state
Ξb (1,1,5/2 ) with variations in the Borel parametersT2.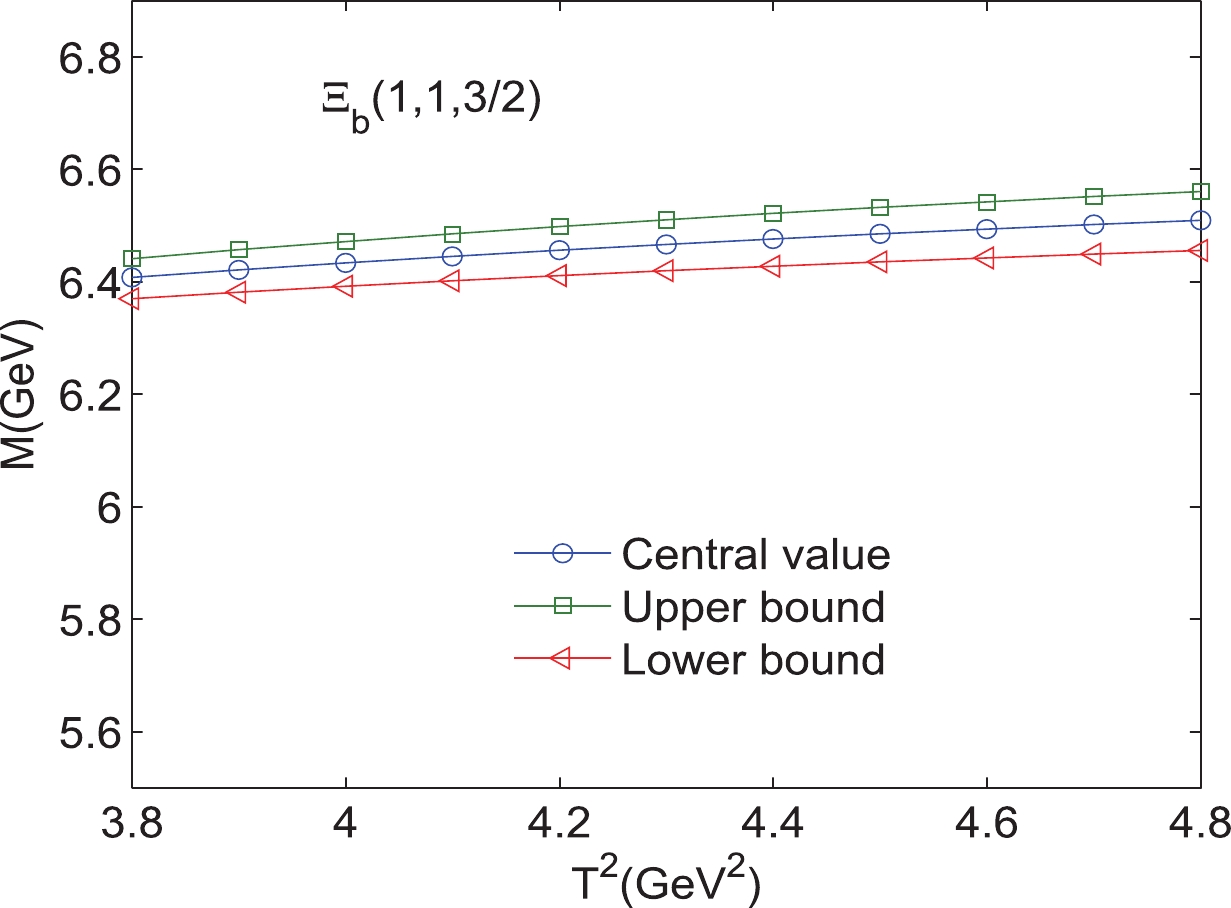 
Figure 7. (color online) Mass of the bottom baryon state
Ξb (1,1,3/2 ) with variations in the Borel parametersT2.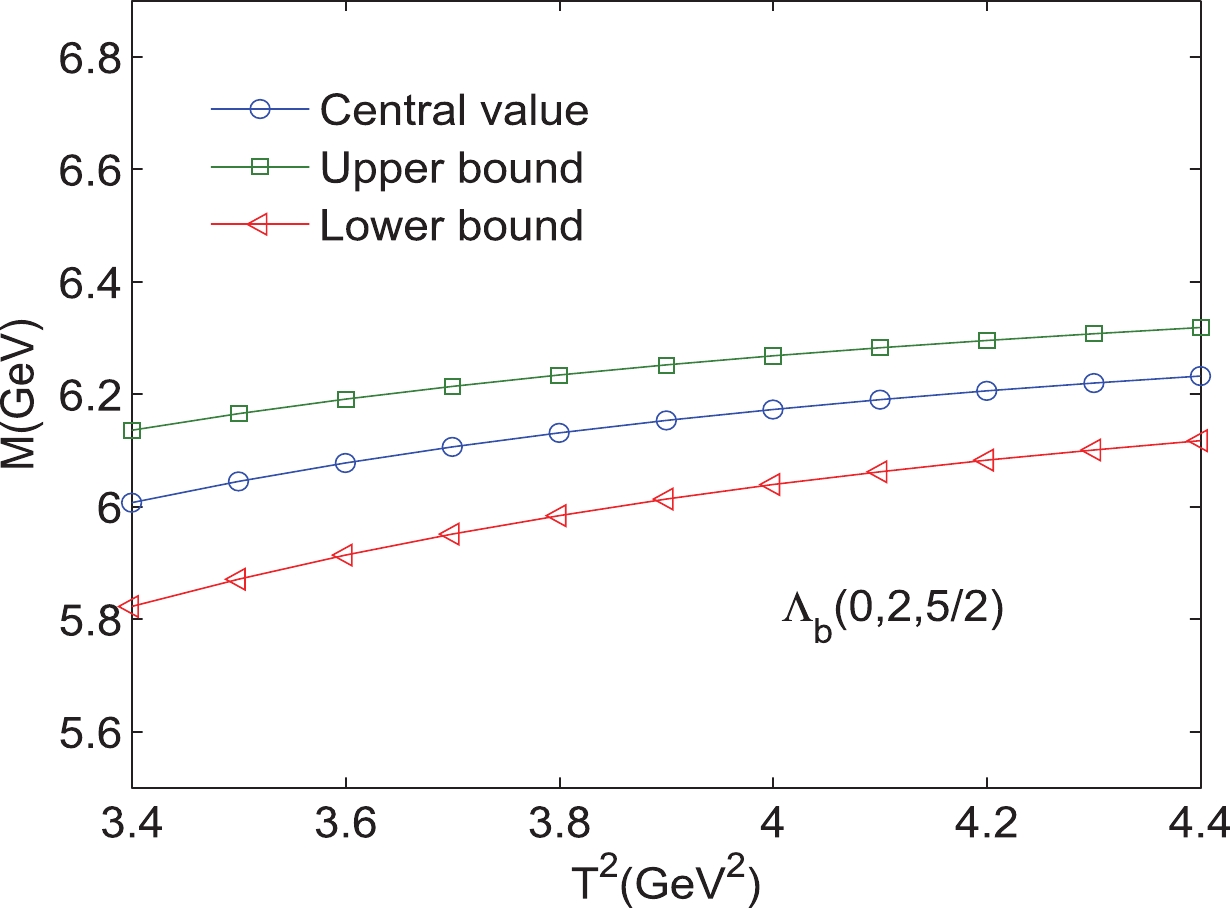 
Figure 8. (color online) Mass of the bottom baryon state
Λb (0,2,5/2 ) with variations in the Borel parametersT2.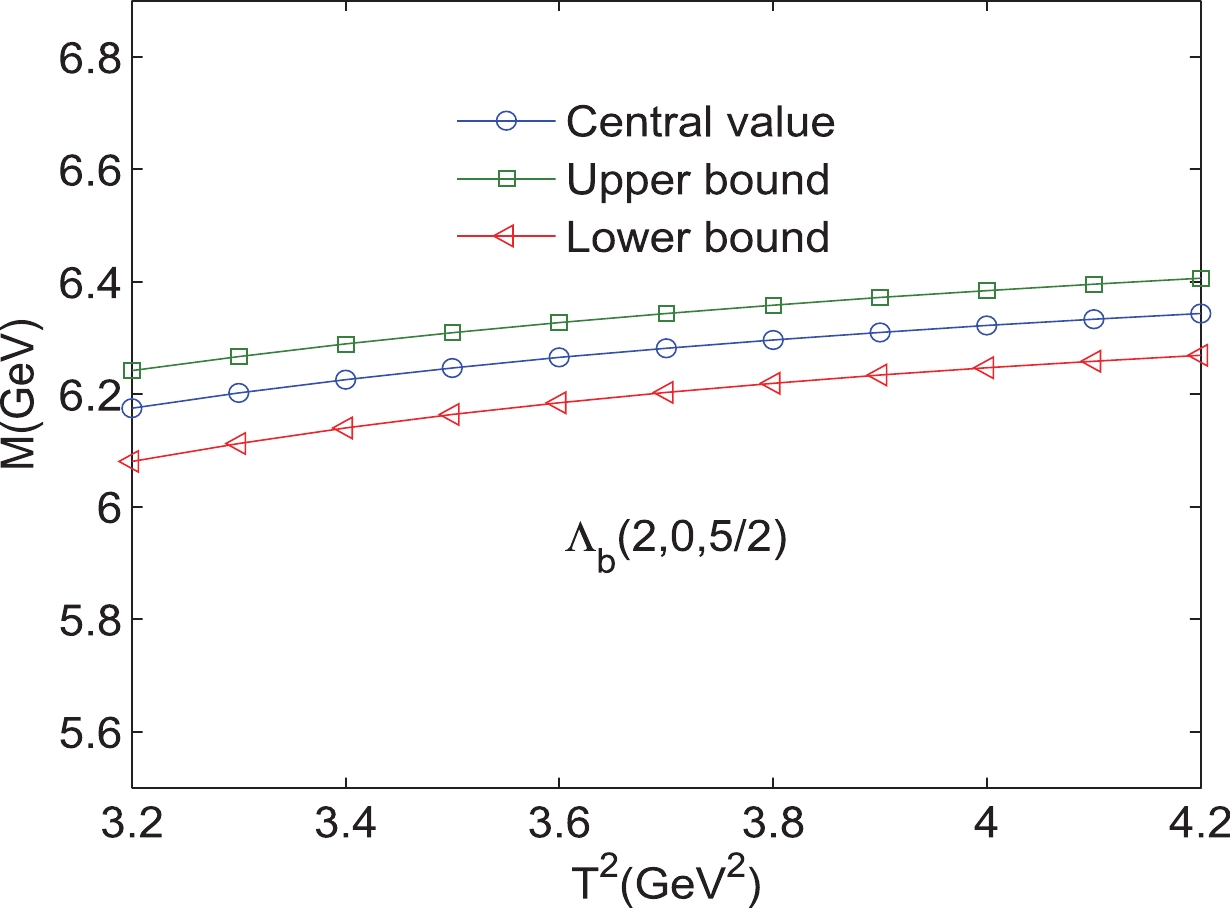 
Figure 9. (color online) Mass of the bottom baryon state
Λb (2,0,5/2 ) with variations in the Borel parametersT2. 
Figure 10. (color online) Mass of the bottom baryon state
Λb (0,2,3/2 ) with variations in the Borel parametersT2. 
Figure 11. (color online) Mass of the bottom baryon state
Λb (2,0,3/2 ) with variations in the Borel parametersT2. 
Figure 12. (color online) Mass of the bottom baryon state
Λb (1,1,5/2 ) with variations in the Borel parametersT2.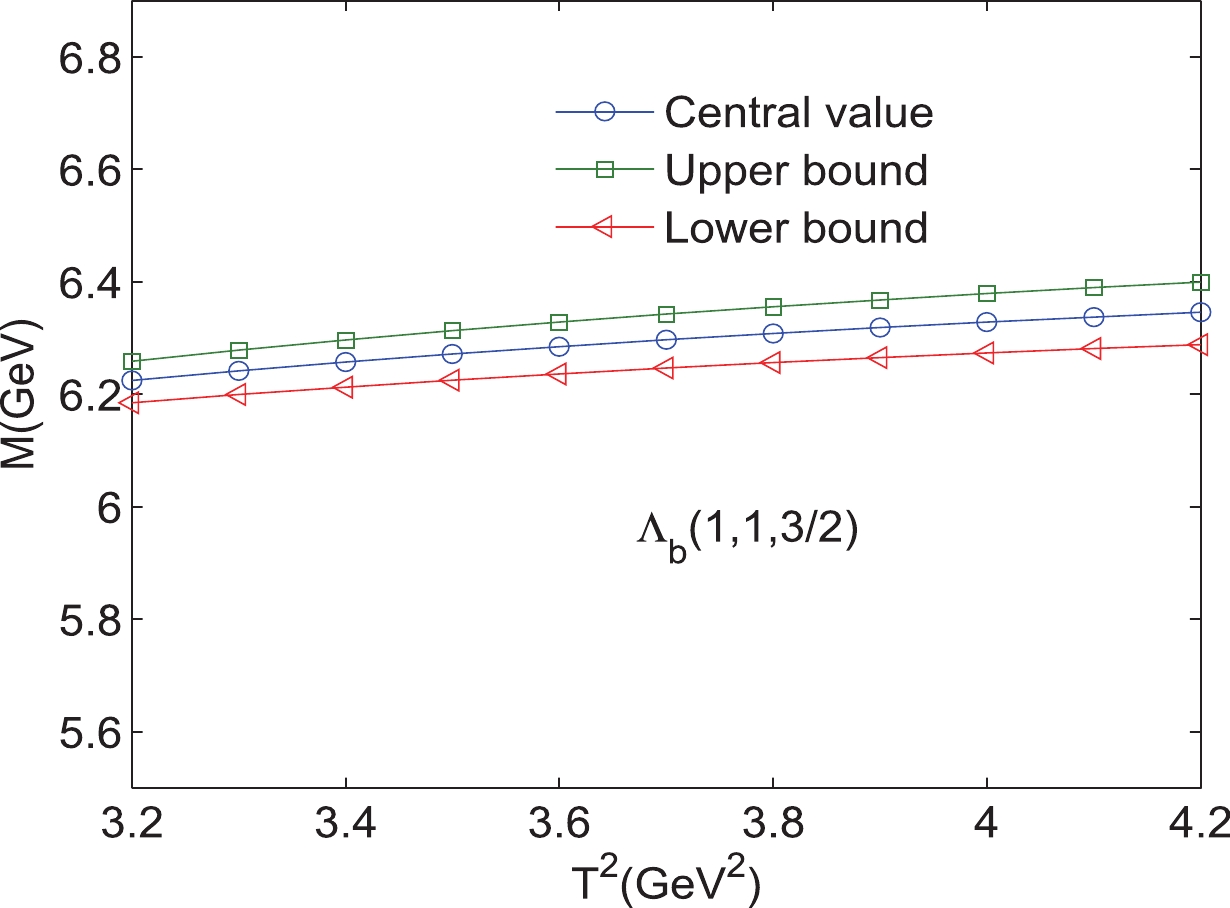 
Figure 13. (color online) Mass of the bottom baryon state
Λb (1,1,3/2 ) with variations in the Borel parametersT2. 
Figure 14. (color online) Pole residues of the bottom baryon state
Ξb (0,2,5/2 ) with variations in the Borel parametersT2. 
Figure 15. (color online) Pole residues of the bottom baryon state
Ξb (2,0,5/2 ) with variations in the Borel parametersT2. 
Figure 16. (color online) Pole residues of the bottom baryon state
Ξb (0,2,3/2 ) with variations in the Borel parametersT2.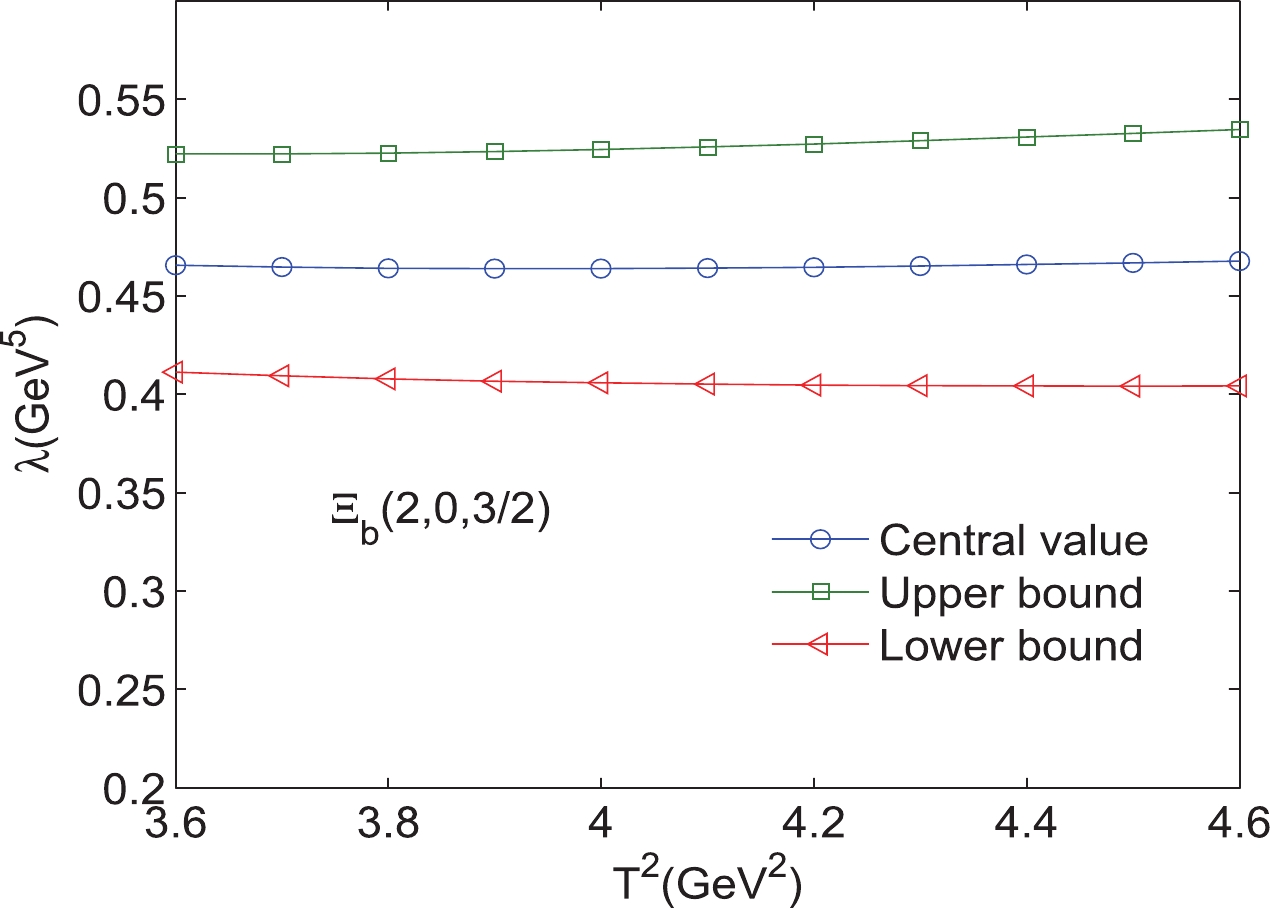 
Figure 17. (color online) Pole residues of the bottom baryon state
Ξb (2,0,3/2 ) with variations in the Borel parametersT2. 
Figure 18. (color online) Pole residues of the bottom baryon state
Ξb (1,1,5/2 ) with variations in the Borel parametersT2.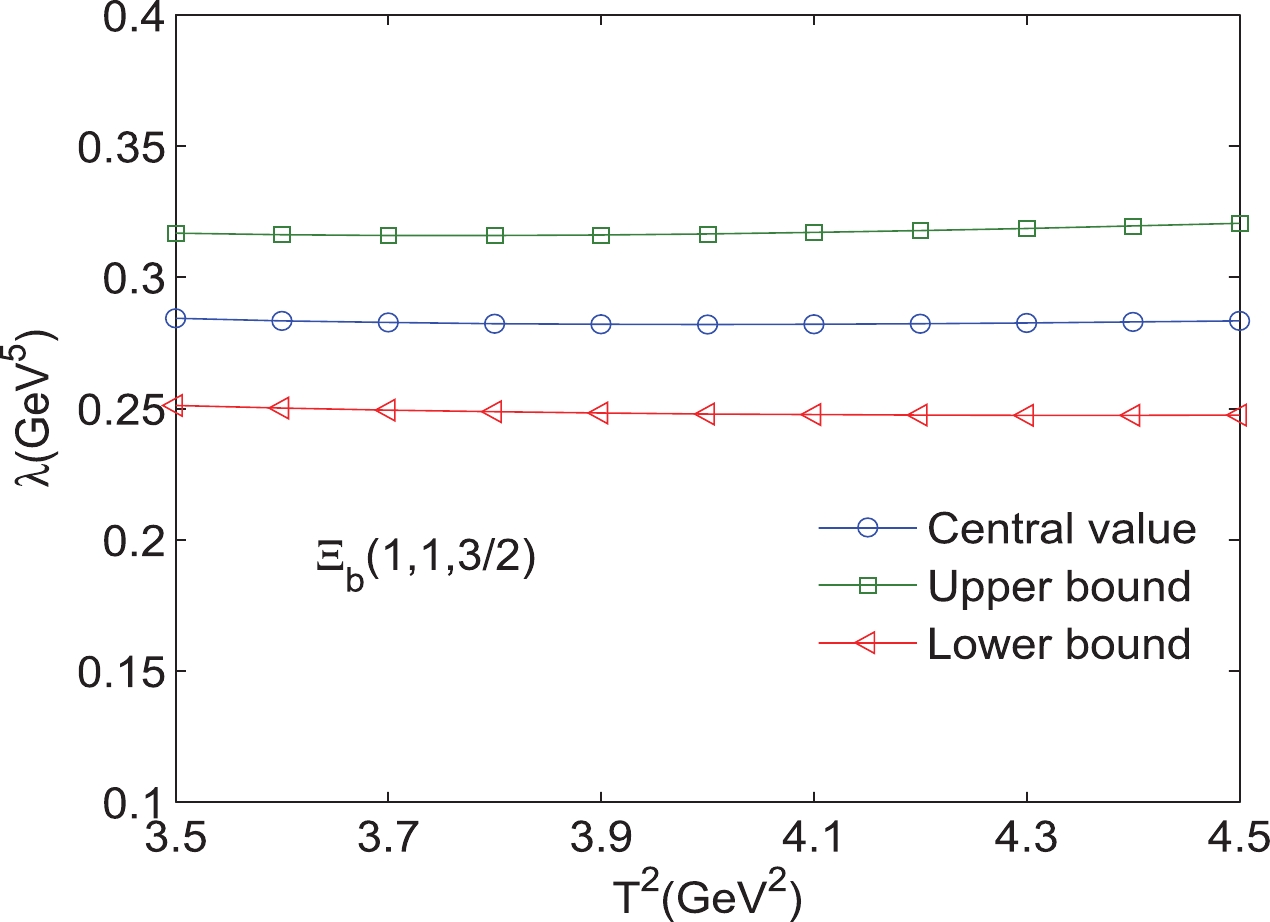 
Figure 19. (color online) Pole residues of the bottom baryon state
Ξb (1,1,3/2 ) with variations in the Borel parametersT2. 
Figure 20. (color online) Pole residues of the bottom baryon state
Λb (0,2,5/2 ) with variations in the Borel parametersT2.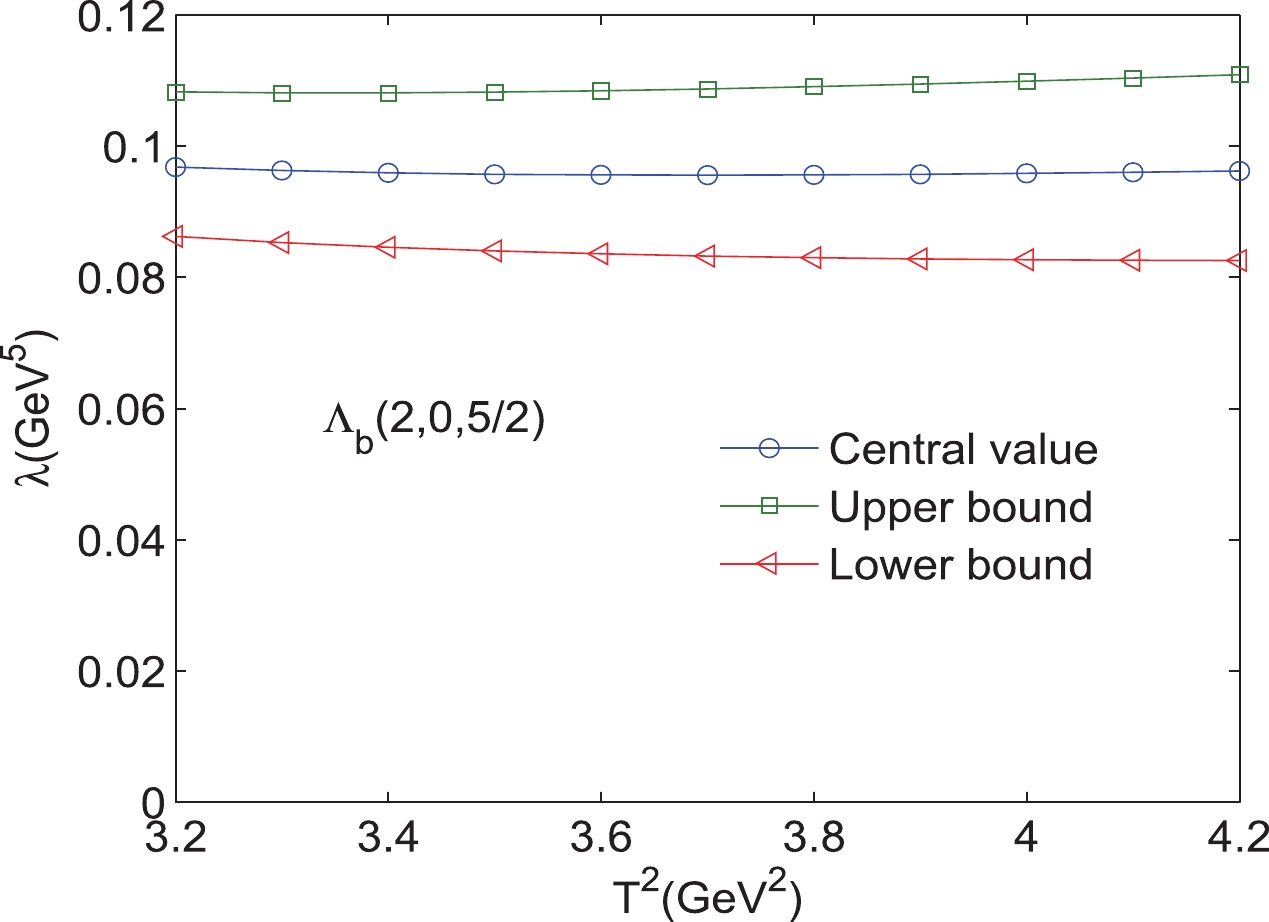 
Figure 21. (color online) Pole residues of the bottom baryon state
Λb (2,0,5/2 ) with variations in the Borel parametersT2.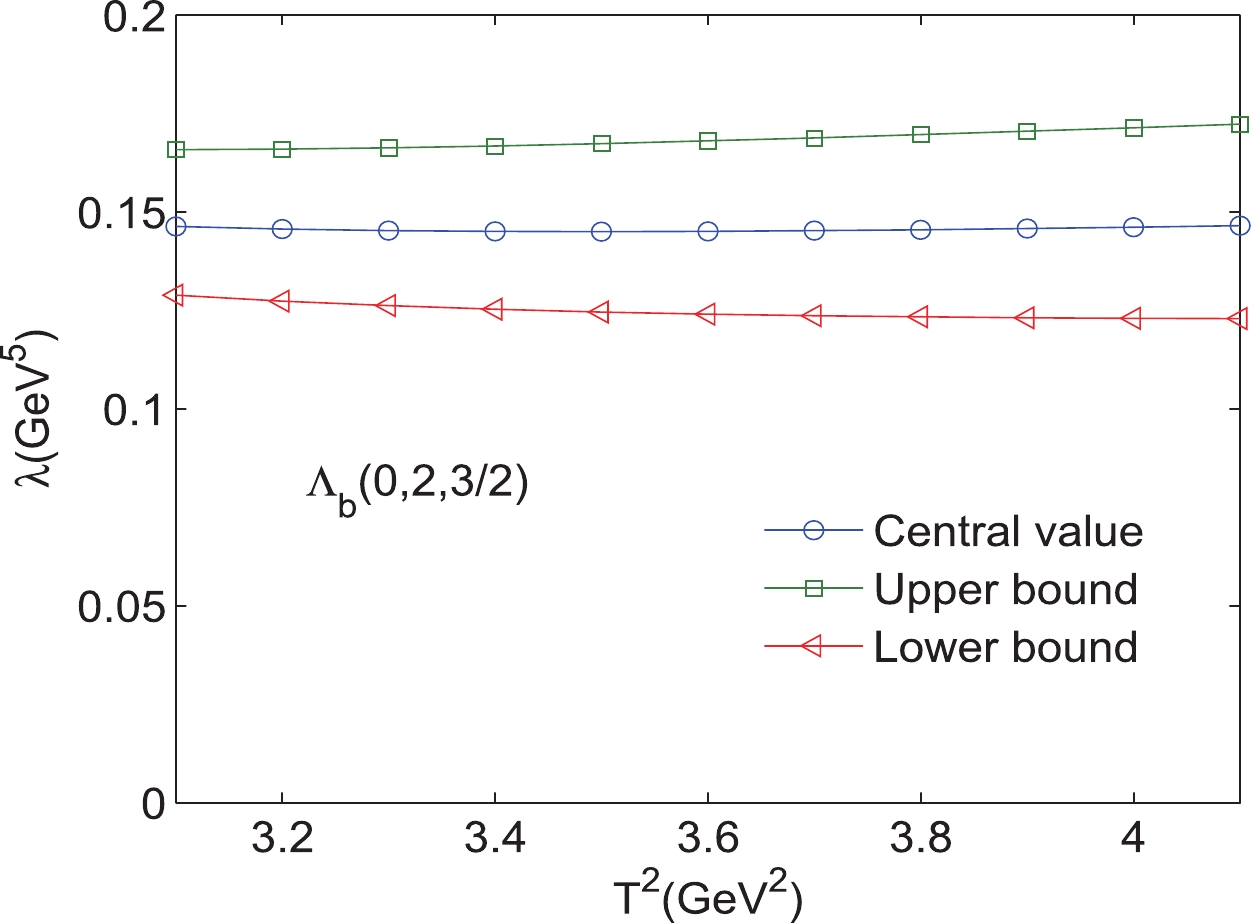 
Figure 22. (color online) Pole residues of the bottom baryon state
Λb (0,2,3/2 ) with variations in the Borel parametersT2.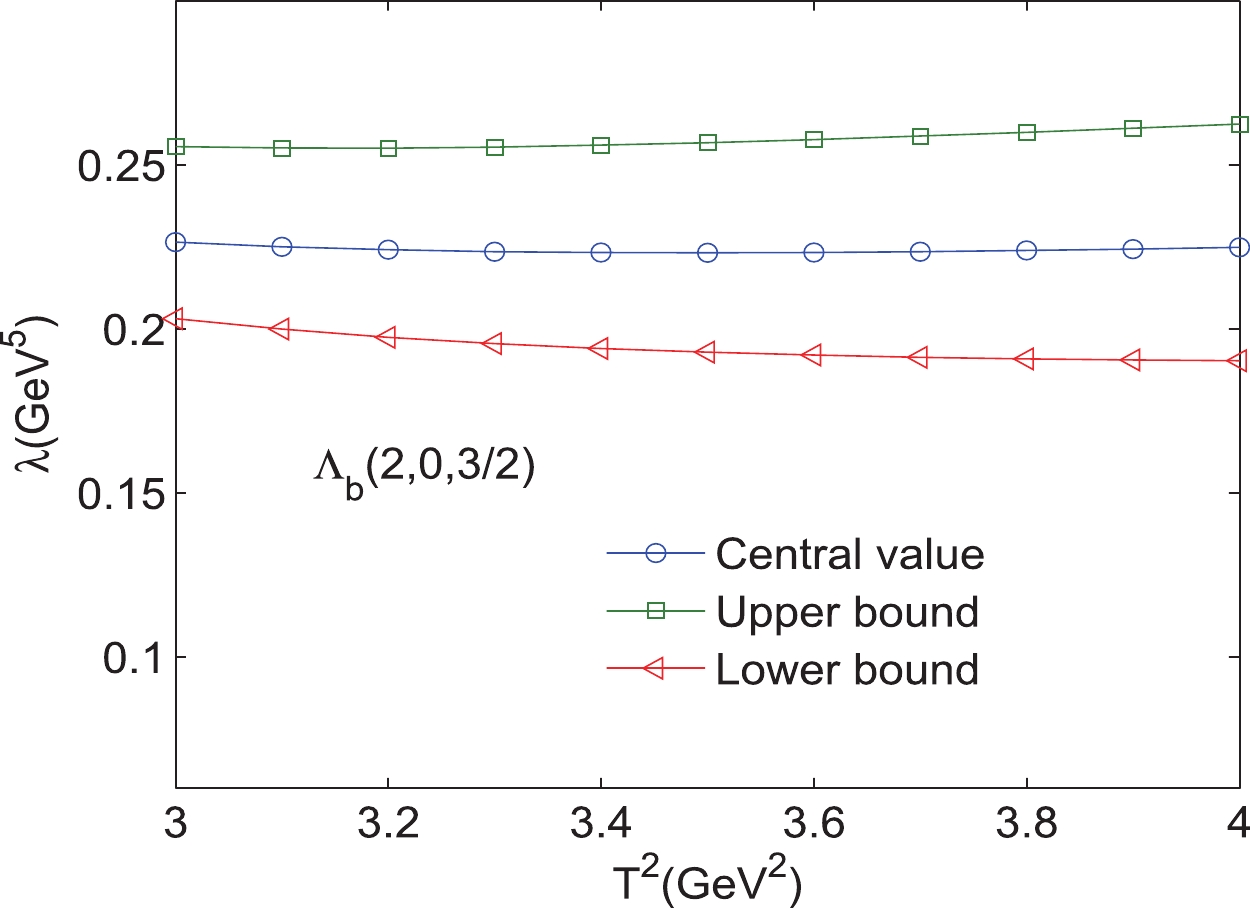 
Figure 23. (color online) Pole residues of the bottom baryon state
Λb (2,0,3/2 ) with variations in the Borel parametersT2.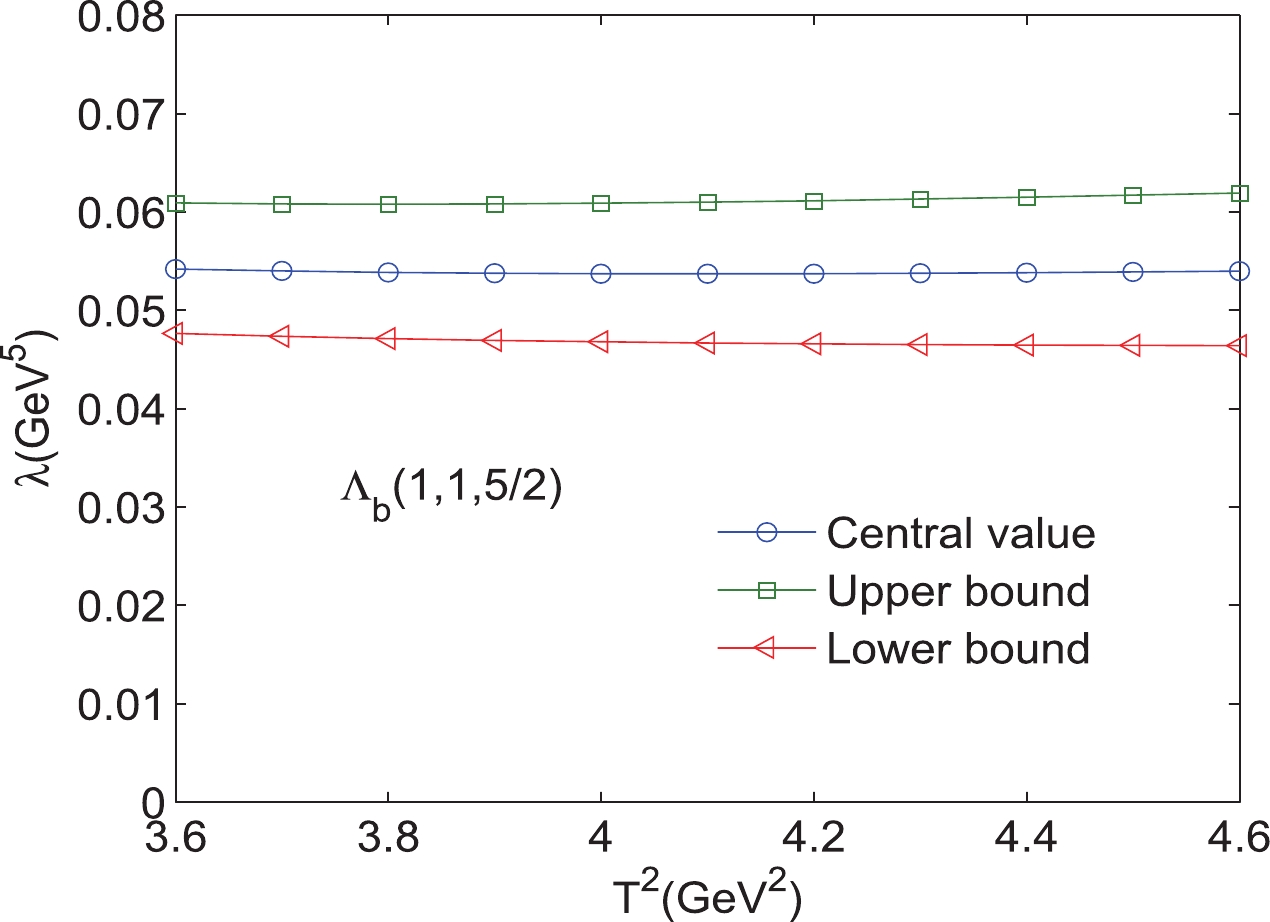 
Figure 24. (color online) Pole residues of the bottom baryon state
Λb (1,1,5/2 ) with variations in the Borel parametersT2. 
Figure 25. (color online) Pole residues of the bottom baryon state
Λb (1,1,3/2 ) with variations in the Borel parametersT2. The LHCb collaboration observed two structures with the masses of
mΛb(6146)0=6146.17±0.33±0.22±0.16 MeV andmΛb(6152)0=6152.51±0.26±0.22±0.16 MeV and suggested their possible interpretation as a doublet of theΛb(1D) state. The quark-model predictions from different collaborations for the masses of this doublet (3/2+ ,5/2+ ) were (6.145 ,6.165 GeV) [14], (6.190 ,6.196 GeV) [15], (6.181 ,6.183 GeV) [16] and (6.147 ,6.153 GeV) [17]. Our predictions for this doublet with the excitation mode (Lρ,Lλ– (0,2 ) arem3/2+Λb=6.13+0.10−0.09 GeV andm5/2+Λb=6.15+0.13−0.15 GeV, respectively. This result is consistent with experimental data [9] and quark-model predictions [14, 17], which supports assigningΛb(6146) andΛb(6152) as the1DΛb doublet with the quantum numbers (Lρ,Lλ)=( 0,2 ) andJp= 32+ ,5/2+ .To date, the 1S, 1P, and 1D
Λb baryons have been established, but as for theΞb sector, only the ground stateΞb(5797) has been confirmed [89]. In particular, for radially excitedΞb andΛb states, fewer experimental results have been reported [3]. In Ref. [15], the mass spectra ofΞb baryons were calculated in the heavy-quark-light-diquark picture in the framework of the QCD-motivated relativistic quark model. In Refs. [6, 10], the masses and strong decay properties of1DΞb baryons withJp= 3/2+ and5/2+ were studied using the quark and3P0 models. These calculations with the quark model were performed by considering bottom baryons as the excitation mode (Lρ,Lλ)= (0,2 ). Their predicted masses for the1DΞb doublet were (6366 MeV,6373 MeV) in Ref. [15] and (6327 MeV,6330 MeV) in Refs. [6, 10], respectively. Table 1 shows that the QCD sum rule predictions for the masses of this doublet with excitation mode (Lρ,Lλ)= (0,2 ) arem3/2+=6.34+0.12−0.11 GeV andm5/2+=6.36+0.11−0.12 GeV, which are consistent with experiments [18] and the predictions in Refs. [6, 10]. Thus, it is reasonable to describe theΞb(6327) andΞb(6333) baryons as the1D (Ξb ) doublet with the excited mode (Lρ,Lλ)= (0,2 ) and quantum numbersJp= 3/2+ and5/2+ . For the2DΛb andΞb doublets, their masses withλ− mode were predicted as (6526 MeV,6531 MeV) and (6690 MeV,6696 MeV) in Ref. [15], which is roughly compatible with our results (6.47+0.09−0.10 GeV,6.53+0.14−0.14 GeV) and (6.62+0.10−0.13 GeV,6.69+0.13−0.11 GeV). From Tables 1–2, we also observe that for either the1D or2D state, the prediction for the mass of the orbital excitation mode (Lρ,Lλ)= (0,2 ) is slightly lower than those of the other excitation modes. Except for the1DΞb states, the predicted mass for the excitation mode (Lρ,Lλ)= (1,1 ) is slightly higher than the others.Finally, we would like to note that in addition to masses, decay and production properties are useful for revealing the inner structure of heavy baryons. The predicted pole residues for the D-wave
Ξb andΛb baryons in this paper will be useful parameters in studying the strong decay properties in the future. With the operation of the LHCb, we expect these excitedΞb andΛb baryons to be observed in the near future. -
In summary, theoretical and experimental physicists have achieved significant progress in the field of single bottom baryons such as
Λb(6072) [3, 4],Λb(6146) [10–13],Λb(6152) [10–13],Ξb(6227) [5–7],Ξb(6100) [8],Ξb(6327) [10, 18], andΞb(6333) [10, 18]. Stimulated by the observations of these new bottom states, we systematically study the1D and2D Λb andΞb baryons using the method of QCD sum rules. According to the heavy quark effective theory, we categorize the D-wave bottom baryons into three types, which are denoted by their orbital excitation modes:(Lρ,Lλ)=(0,2) ,(2,0) , and(1,1) . According to these excitation modes, we construct three types of interpolating currents to study the1D and2D bottom baryons with spin-parityJp=3/2+ and5/2+ . In our calculations, we successfully separate the contributions of the positive and negative states, which causes the QCD sum rules to refrain from the contamination of the bottom baryon states with negative parity. We perform the OPE up to the vacuum condensates of dimension10 to warrant the reliability of the final results. Our predictions favor assigningΛb(6146) andΛb(6152) as a1DΛb doublet with quantum numbers of(Lρ,Lλ)=(0,2) andJP= (3/2+ ,5/2+ ), respectively. This conclusion is consistent with experiments and with those of other collaborations [9, 14, 17]. As for theΞb (1D ) states, we predict the masses of the excitation mode(Lρ,Lλ)=(0,2) asm3/2+=6.34+0.12−0.11 GeV andm5/2+=6.36+0.11−0.12 GeV. This result is compatible with the experimental data [18] as well as the quark-model predictions [6, 10]. Thus, these two states can be interpreted as theΞb (1D ) doublet with the quantum numbers(Lρ,Lλ)=(0,2) andJP= 3/2+ ,5/2+ , respectively. Finally, our results show that the prediction for the mass of the excitation mode(Lρ,Lλ)=(0,2) is the smallest in these three excitation modes, and the mass of(Lρ,Lλ)=(1,1) is the largest, except for the1DΞb state. The pole residues predicted in this paper are useful parameters in studying the strong decay properties of the1D and2DΞb andΛb states. -
ρ0,Ξb5/2,2,0(s)=∫1m2b/s{169120π4(132−494x+665x2−360x3+50x4−2x5+9x6)×(s−m2bx)4+ms(5⟨¯ss⟩−2⟨¯qq⟩)96π2×(x2−2x3+x4)×(s−m2bx)2−ms⟨¯qgsσGq⟩36π2×(4−7x+3x2)×(s−m2bx)+ms⟨¯sgsσGs⟩216π2×(31−58x+27x2)×(s−m2bx)+134560π2⟨αsGGπ⟩×(665+132/x2−494/x−360x+50x2−2x3+9x4)×(s−m2bx)2+16192π2⟨αsGGπ⟩×(46−72x+15x2+2x3+9x4)×(s−m2bx)2}dx+⟨¯qgsσGq⟩⟨¯sgsσGs⟩72δ(s−m2b),
ρ1,Ξb5/2,2,0(s)=∫1m2b/s{169120π4(128x−457x2+575x3−290x4+70x5−53x6+27x7)×(s−m2bx)4−ms(5⟨¯ss⟩−2⟨¯qq⟩)288π2×(x2−11x3+19x4−9x5)×(s−m2bx)2+ms⟨¯qgsσGq⟩72π2×(x−18x2+35x3−18x4)×(s−m2bx)−ms⟨¯sgsσGs⟩216π2×(4x−74x2+151x3−81x4)×(s−m2bx)+16192π2⟨αsGGπ⟩×(40x−57x2+21x3−31x4+27x5)×(s−m2bx)2−m2b51840π2⟨αsGGπ⟩×(575+128/x2−457/x−290x+70x2−53x3+27x4)×(s−m2bx)}dx+5⟨¯qgsσGq⟩⟨¯sgsσGs⟩432δ(s−m2b),
ρ0,Ξb5/2,0,2(s)=∫1m2b/s{−14608π4(2x−11x2+24x3−26x4+14x5−3x6)×(s−m2bx)4+ms(⟨¯ss⟩−2⟨¯qq⟩)96π2×(x2−2x3+x4)×(s−m2bx)2+m2b3456π2⟨αsGGπ⟩×(24+2/x2−11/x−26x+14x2−3x3)×(s−m2bx)+12304π2⟨αsGGπ⟩×(11−2/x−24x+26x2−14x3+3x4)×(s−m2bx)2+1768π2⟨αsGGπ⟩×(x2−2x3+x4)×(s−m2bx)2}dx+⟨¯qgsσGq⟩⟨¯sgsσGs⟩72δ(s−m2b),
ρ1,Ξb5/2,0,2(s)=∫1m2b/s{14608π4(x2+5x3−30x4+50x5−35x6+9x7)×(s−m2bx)4−ms(⟨¯ss⟩−2⟨¯qq⟩)288π2×(x2−11x3+19x4−9x5)×(s−m2bx)2−m2b3456π2⟨αsGGπ⟩×(5+1/x−30x+50x2−35x3+9x4)×(s−m2bx)−12304π2⟨αsGGπ⟩×(x2−11x3+19x4−9x5)×(s−m2bx)2}dx+5⟨¯qgsσGq⟩⟨¯sgsσGs⟩432δ(s−m2b),
ρ0,Ξb5/2,1,1(s)=∫1m2b/s{−113824π4(3−20x+47x2−48x3+17x4+4x5−3x6)×(s−m2bx)4+ms(3⟨¯ss⟩−2⟨¯qq⟩)96π2×(x2−2x3+x4)×(s−m2bx)2−ms⟨¯qgsσGq⟩48π2×(x−3x2+2x3)×(s−m2bx)+5ms⟨¯sgsσGs⟩432π2×(x−4x2+3x3)×(s−m2bx)−m2b10368π2⟨αsGGπ⟩×(48−3/x3+20/x2−47/x−17x−4x2+3x3)×(s−m2bx)−16192π2⟨αsGGπ⟩×(47+3/x2−20/x−48x+17x2+4x3−3x4)×(s−m2bx)2−14608π2⟨αsGGπ⟩×(1−12x+15x2+2x3−6x4)×(s−m2bx)2}dx,
ρ1,Ξb52,1,1(s)=∫1m2bs{113824π4(2x+6x2−35x3+40x4−22x6+9x7)×(s−m2bx)4−ms(3⟨¯ss⟩−2⟨¯qq⟩)288π2×(x2−11x3+19x4−9x5)×(s−m2bx)2+ms⟨¯qgsσGq⟩288π2×(x−22x2+57x3−36x4)×(s−m2bx)−ms⟨¯sgsσGs⟩432π2×(x−24x2+68x3−45x4)×(s−m2bx)+m2b10368π2⟨αsGGπ⟩×(35−2/x2−6/x−40x+22x3−9x4)×(s−m2bx)+14608π2⟨αsGGπ⟩×(x2+16x3−35x4+18x5)×(s−m2bx)2}rmdx
ρ0,Ξb3/2,2,0(s)=∫1m2b/s{13072π4(33−128x+182x2−108x3+17x4+4x5)×(s−m2bx)4+7ms⟨¯qgsσGq⟩24π2×(x−x2)×(s−m2bx)−6ms⟨¯sgsσGs⟩24π2×(x−x2)×(s−m2bx)+m2b2304π2⟨αsGGπ⟩×(108−33/x3+128/x2−182/x−17x−4x2)×(s−m2bx)+11536π2⟨αsGGπ⟩×(182+33/x2−128/x−108x+17x2+4x3)×(s−m2bx)2+1768π2⟨αsGGπ⟩×(31−54x+15x2+8x3)×(s−m2bx)2}dx+3⟨¯qgsσGq⟩⟨¯sgsσGs⟩32δ(s−m2b),
ρ1,Ξb3/2,2,0(s)=∫1m2b/s{53072π4(9x−32x2+38x3−12x4−7x5+4x6)×(s−m2bx)4+ms(25⟨¯ss⟩−10⟨¯qq⟩)16π2×(x2−2x3+x4)×(s−m2bx)2−ms⟨¯qgsσGq⟩4π2×(4−11x+7x2)×(s−m2bx)+ms⟨¯sgsσGs⟩24π2×(33−97x+64x2)×(s−m2bx)−5m2b2304π2⟨αsGGπ⟩×(38+9/x2−32/x−12x−7x2+4x3)×(s−m2bx)+1768π2⟨αsGGπ⟩×(35−36x−33x2+34x3)×(s−m2bx)2}dx+5⟨¯qgsσGq⟩⟨¯sgsσGs⟩96δ(s−m2b),
ρ0,Ξb3/2,0,2(s)=∫1m2b/s{11024π4(3−16x+34x2−36x3+19x4−4x5)×(s−m2bx)4+m2b768π2⟨αsGGπ⟩×(36−3/x3+16/x2−34/x−19x+4x2)×(s−m2bx)+1512π2⟨αsGGπ⟩×(4+3/x2−16/x−36x+19x2−4x3)×(s−m2bx)2}dx+3⟨¯qgsσGq⟩⟨¯sgsσGs⟩32δ(s−m2b),
ρ1,Ξb3/2,0,2(s)=∫1m2b/s{71024π4(1−10x2+20x3−15x4+4x5)×(s−m2bx)4+ms(5⟨¯ss⟩−10⟨¯qq⟩)16π2×(x2−2x3+x4)×(s−m2bx)2+7m7b768π2⟨αsGGπ⟩×(10−1/x2−20x+15x2−4x3)×(s−m2bx)+5128π2⟨αsGGπ⟩×(x2−2x3+x4)×(s−m2bx)2}dx+5⟨¯qgsσGq⟩⟨¯sgsσGs⟩96δ(s−m2b),
ρ0,Ξb3/2,1,1(s)=∫1m2b/s{−1768π4(3−13x+22x2−18x3+7x4−x5)×(s−m2bx)4−ms⟨¯sgsσGs⟩48π2×(x−x2)×(s−m2bx)−mm2bb576π2⟨αsGGπ⟩×(18−3/x3+13/x2−22/x−7x+x2)×(s−m2bx)−1384π2⟨αsGGπ⟩×(22+3/x2−13/x−18x+7x2−x3)×(s−m2bx)2−11024π2⟨αsGGπ⟩×(5−18x+21x2−8x3)×(s−m2bx)2}dx,
ρ1,Ξb3/2,1,1(s)=∫1m2b/s{1768π4(7−20x+10x2+20x3−25x4+8x5)×(s−m2bx)4+ms(15⟨¯ss⟩−10⟨¯qq⟩)16π2×(x2−2x3+x4)×(s−m2bx)2−5ms⟨¯qgsσGq⟩16π2×x(1−4x+3x2)×(s−m2bx)+ms⟨¯sgsσGs⟩48π2×x(11−49x+38x2)×(s−m2bx)−m2b576π2⟨αsGGπ⟩×(10+7/x2−20/x+20x−25x2+8x3)×(s−m2bx)+11024π2⟨αsGGπ⟩×x(15+14x−73x2+44x3)×(s−m2bx)2}dx,
ρ0,Λbj,lρ,lλ(s)=ρ0,Ξbj,lρ,lλ(s)|ms→0,⟨¯ss⟩→⟨¯qq⟩,⟨¯sgsσGs⟩→⟨¯qgqσGs⟩,ρ1,Λbj,lρ,lλ(s)=ρ1,Ξbj,lρ,lλ(s)|ms→0,⟨¯ss⟩→⟨¯qq⟩,⟨¯sgsσGs⟩→⟨¯qgqσGs⟩,
ρ0j,QCD=mbρ0,Ξb(Λb)j,lρ,lλ(s),ρ1j,QCD=ρ1,Ξb(Λb)j,lρ,lλ(s).
1D and 2D Ξb and Λb baryons
- Received Date: 2022-04-25
- Available Online: 2022-09-15
Abstract: Recently, scientists have achieved significant progress in experiments searching for excited
DownLoad: