-
The black hole is one of the most intriguing predictions of Einstein's general relativity. It is a particular spacetime region typically created by the gravitational collapse of a compact object in its late stage, when its mass exceeds the upper limit of neutron stars [1]. From both theoretical and experimental perspectives, the subject has gained much interest over the past few decades. As the culmination of continuous efforts, the recent advent of empirical detection of gravitational waves emanating from black holes has elicited further interest. In particular, the merger signals of a black hole binary captured by the LIGO and Virgo collaboration [2] furnished the first direct piece of evidence of black holes and subsequently inaugurated a novel era of gravitational-wave astronomy.
The quasinormal modes (QNMs) carry the characteristic sound of a black hole. In terms of dissipative oscillations, they bear the essential properties of the underlying spacetime metric [3]. The associated temporal profile constitutes the ringdown phase of the collapse, from which a black hole is formed. On the one hand, such signals are mathematically straightforward compared with those emanating from the merger process. On the other hand, the strength of the associated gravitational radiation is speculated to still fall within the scope of the ongoing space-borne gravitational wave detector programs, such as LISA and TianQin [4, 5]. In particular, studies have been performed to evaluate the detector signal-to-noise ratio regarding the feasibility of an eventual detection [6, 7].
Theoretically, QNMs can be investigated using black hole perturbation theory. Among the earliest endeavors, Regge and Wheeler created the framework of the metric perturbations in spherically symmetric black holes [8]. Subsequent developments by Zerill [9] and Moncrief [10] further refined a few pertinent aspects. For rotating black holes, Teukolsky first derived the linearized scalar and metric perturbation equations for the Kerr spacetime [11, 12]. Although the physical system is dissipative and therefore non-Hermitian, the mathematical procedure to obtain QNMs can be effectively considered an eigenvalue problem. Subsequently, the emergence of discrete complex frequencies is attributed to the ingoing and outgoing boundary conditions, respectively, applied at the horizon and outer spatial bound (often located at infinity). By using the continued fraction method proposed by Leaver [13, 14], we encounter the discrete complex frequencies reminiscent of the atomic spectrum of hydrogen in quantum mechanics. The eigenvalue nature of the problem is also transparently considered in terms of the matrix method [15–18], in which we explicitly solve a matrix secular equation for the quasinormal frequencies. In contrast, Leaver proposed the Green's function approach, which reformulates the general solution in terms of the spectrum decomposition [3, 19]. From this perspective, the main characteristics of the perturbation fields are attributed to the intrinsic singularities of the relevant Green's function. Specifically, the QNMs correspond to the poles of the Green's function, whereas the branch cuts essentially govern the late-time tails. In addition to the QNMs, the late-time tail is a topic of pertinent relevance. On the one hand, the time profile of QNMs decays exponentially; on the other hand, the late-time tail largely follows a power-law form. Therefore, the final stage of the temporal evolution of the perturbations is dominated primarily by the late-time tail. As mentioned earlier, mathematically, the origin of the late-time tail is attributed to the branch cut and cannot be obtained by summing the QNM poles. For instance, for massless scalar perturbations, the tail is due to a branch cut on the negative imaginary axis in the frequency domain, which stretches from the origin. Researchers have argued that the presence of the branch cut sensitively depends on the asymptotical structure of the potential [20]. Additionally, it is often interpreted in the literature as the backscattering of perturbed wave packets by the spacetime far away from the horizon [21–23]. Price was the first to observe an inverse power-law tail,
$ {t^{ - (2l + 3)}} $ or$ {t^{ - (2l + 2)}} $ , for massless scalar perturbations in the Schwarzschild black hole metric [24]. Extensive studies for different metrics further indicated that such an inverse power-law form is a rather general characteristic for massless perturbations in spherical spacetimes that are asymptotically flat [21, 25, 26]. Moreover, the temporal profile for massive perturbations might be qualitatively different from their massless counterparts. For insignificant mass, Hod and Piran discovered that the time-domain profile at the intermediate-late time in Reissner-Nordström spacetime has an oscillatory tail with a decay rate of$ {t^{ - (l + 3/2)}}\sin (\mu t) $ [27], where μ is the mass of the field. Moreover, Koyama and Tomimatsu analytically showed that the asymptotical late-time tail in the Schwarzschild spacetime is$ {t^{ - 5/6}}\sin (\mu t) $ [28, 29]. For some specific cases, the asymptotical form was recenetly reported to also be$ {t^{ - 1}}\sin (\mu t) $ [30] in the limit of vanishing scalar mass. In all the massive cases, the branch cut can be conveniently selected to be on the real axis in a finite interval determined by the scalar mass. It is also worth noting that such a decay rate does not depend on the angular momentum l. In addition to the power-law form, the exponential tails have also been observed in asymptotically de Sitter spacetimes for various types of fields [31–33]. Notably, the Dirac perturbations eventually decay to a non-zero constant [23, 34]. These distinctive characteristics have significantly enriched the physical content regarding the late-time waveforms. More recently, Cardoso et al. proposed [35] that the late-time ringdown may serve to probe the horizon and discriminate between different gravitational systems, inclusively, the exotic compact objects such as gravastar and wormhole. Based on this, black hole echoes [36], and particularly, their connections with the QNMs and late-time tail [37, 38] have also attracted much interest.The magnetic field is another indispensable assembly piece of the universe. Experimentally, employing the rotation measures, information on the magnetic field in the disk of galaxies can be extracted for a large number of pulsars [39]. In particular, strong magnetic fields, as high as
$ {\rm{1}}{{\rm{0}}^{\rm{4}}} \sim {\rm{1}}{{\rm{0}}^{\rm{8}}} $ G, have been observed in the vicinity of stellar-mass or supermassive black holes [40]. Therefore, relevant studies on black hole metrics, including their perturbations, have to be placed in the context of a realistic astrophysical environment. A stationary axisymmetric black hole solution with a uniform magnetic field placed along the symmetry axis was first derived by Wald [41]. The solution for the Kerr-Newman black hole was subsequently obtained by Ernst and Wild [42]. Among many important developments, the magnetic field was observed to have an essential role in the stability of the dynamic system. The latter encompass the superradiance instability [43] and black hole QNMs [44, 45]. In particular, the Zeeman effect was recently uncovered in the QNM spectrum of charged scalar perturbations in a magnetized Schwarzschild black hole [44]. Moreover, the instability of the metric can be triggered by tuning the effective scalar mass, which is modified by the interaction between the charge and magnetic field.As an alternative theory of general relativity, Rastall gravity was formulated based on the possible breaking of the conservation law of the stress energy-momentum tensor [46]. The theory aims at addressing several unsettled problems in general relativity regarding the largest scale when compared with cosmological observation. In the literature, various intriguing aspects of the theory have been explored, which include black hole physics [47–50] and cosmology [51–55]. Among others, the theory inherently results in a particle creation mechanism, which naturally supplies an alternative implementation for dark energy [56]. It is meaningful to further investigate the impact of the magnetic field in Rastall theory on spacetime stability.
This paper is motivated by the above considerations. We investigate the QNMs and late-time tails of charged massless scalar perturbations of a magnetized black hole solution derived from generalized Rastall gravity. First, we generalize the black hole solution in Rastall gravity into a more realistic context by including the magnetic field. We then analyze the effect of the magnetic field on the spacetime stability in the context of Rastall gravity by exploring the quasinormal oscillations. For this, the study of massless scalar perturbations is sufficient for the purpose. For stable spacetime configurations, we know that massless and massive scalar fields behave distinctively in the late-time evolution. Therefore, it would be rather interesting to investigate the implications for Rastall's theory with the presence of a magnetic field. In particular, we observe that the exponent of the power-law tail is modified. This can be attributed to the fact that the effective mass of the field is "dressed up" owing to the interaction between the magnetic field and charge.
The remainder of the paper is organized as follows. In the Sec. II, we present the metric of a magnetized black hole investigated in this study. The QNMs are explored in Sec. III by employing the Wentzel-Kramers-Brillouin (WKB) approximation, matrix method, and finite difference method. In Sec. IV, we analyze the late-time tail of the massless scalar perturbations and the effect of the magnetic field. Both the Green's function and the finite difference method are utilized. Further discussions and concluding remarks are provided in the final section.
-
According to Rastall's recipe [46], the breaking of the conservation law of the stress energy-momentum tensor is
$ \begin{array}{*{20}{l}} {T^v}_{\mu ;v} = \lambda {R_{,\mu }}\ , \end{array} $

(1) where λ is the Rastall coupling parameter, and R is the Ricci scalar. If
$ \lambda = 0 $ , the stress energy-momentum tensor is conserved and Rastall gravity falls back to general relativity. Moreover, the corresponding field equation can be expressed as$ {R_{\mu \nu }} + \left(\kappa \lambda-\frac12\right) {g_{\mu \nu }}R = \kappa {T_{\mu \nu }} , $

(2) where
$ {\kappa} $ is a constant related to the trace anomaly of the energy momentum tensor in Rastall gravity.In this paper, we consider a spherically symmetric black hole solution surrounded by a quintessence fluid and power-Maxwell field first derived in [57]. Specifically, the metric of a static, spherically symmetric four-dimensional spacetime is expressed as
$ \begin{array}{*{20}{l}} {\rm d}{s^2} = - f(r){\rm d}{t^2} + f{(r)^{ - 1}}{\rm d}{r^2} + {r^2}{\rm d}{\theta ^2} + {r^2}{\sin ^2}\theta {\rm d}{\phi ^2}. \end{array} $

(3) The action for the electromagnetic sector is of a nonlinear form, which can be expressed as [58]
$ \begin{array}{*{20}{l}} {\cal L}_{ F} = - {( - \xi {\cal F})^s}, \end{array} $

(4) where
$ {\cal F} = {F_{\mu \nu }}{F^{\mu v}}{\rm{ }} $ ,$ {F_{\mu \nu }} $ is the Faraday tensor, and s and ξ are constants.$ s = 1 $ corresponds to the case of a linear electromagnetic field. Owing to the presence of the electromagnetic field and quintessence fluid, the resulting energy momentum tensor has the form$ \begin{array}{*{20}{l}} T_v^\mu = E_v^\mu + T_v^{*\mu }, \end{array} $

(5) where the electromagnetic part,
$ E_v^\mu $ , is given by$ E_\mu ^v = - {( - \xi )^s}{({\cal F})^{s - 1}}\left( {2s{F_{\sigma \mu }}{F^{\sigma v}} - \frac{1}{2}\delta _\mu ^v{\cal F}} \right). $

(6) $ T_v^{*\mu } $ is the energy-momentum tensor of the quintessence field. If we assume a barotropic equation of state$ p = w\rho $ , it can be expressed as$ T_t^{*t} = T_r^{*r} = - \rho (r),\;\;T_\theta ^{*\theta } = T_\varphi ^{*\varphi } = \frac{1}{2}\rho (r)(3w + 1). $

(7) By substituting the energy momentum tensor into the field equation Eq. (2), we can show that the black hole metric is [57]
$ \begin{aligned}[b] f(r) =& 1 - \frac{{2M}}{r} + \frac{{{Q^2}{r^{\frac{2}{{1 - 2s}}}}{{( - 1 + 2s)}^{\frac{{3 - 2s}}{{1 - 2s}}}}}}{{(3 - 2s)s}} \\&+ \frac{{{C_a}{r^{\frac{{1 - 6\kappa \lambda + w (3 - 6\kappa \lambda )}}{{ - 1 + 3(1 + w)\kappa \lambda }}}} \times {{(1 - 3(1 + w)\kappa \lambda )}^2}}}{{3( - 1 + 4\kappa \lambda )(\kappa \lambda + w( - 1 + \kappa \lambda ))}} , \end{aligned} $

(8) where
$ {C_a} $ is a constant of integration, and M is related to the mass of the black hole.For this study, we will focus on the case of the linear electromagnetic field with
$ s=1 $ and the sole presence of a constant magnetic field, namely, the electric charge vanishes,$ Q=0 $ . When black hole is in the magnetic field, as a good approximation①, the vector potential of the electromagnetic field can be expressed as$ {A_\mu } = \frac{1}{2}B{r^2}{\sin ^2}\theta (0,0,0,1). $

(9) -
The temporal evolution of a massless charged scalar field is governed by the Klein-Gordon equation, as follows:
$ \begin{array}{*{20}{l}} {g^{\mu \nu }}\left( {{\nabla _\mu } - {\rm i} q{A_\mu }} \right)\left( {{\nabla _\nu } - {\rm i}q{A_\nu }} \right)\Phi = 0 . \end{array} $

(10) To simplify the above equation, we introduce some reasonable assumptions [45]. First, we obtain
$ {\nabla _\alpha }{A^\alpha } = 0 $ by selecting the Lorentz gauge. Additionally, we assume that$ {q^2}{B^2} \ll 1 $ by considering the scenario in which the coupling between the scalar and electromagnetic fields is sufficiently weak. Under these conditions, Eq. (10) can be rewritten as$ \frac{1}{{{r^2}}}\frac{\partial }{{\partial r}}\left( {{r^2}f\frac{{\partial \Phi }}{{\partial r}}} \right) - \left( {\frac{{{L^2}}}{{{r^2}}} - qB{L_z}} \right)\Phi - \frac{1}{f}\frac{{{\partial ^2}\Phi }}{{\partial {t^2}}} = 0 , $

(11) where
$ {{L^2} = - \left[ {\frac{1}{{\sin \theta }}\frac{\partial }{{\partial \theta }}\left( {\sin \theta \frac{\partial }{{\partial \theta }}} \right) + \frac{1}{{{{\sin }^2}\theta }}\frac{{{\partial ^2}}}{{\partial {\phi ^2}}}} \right]} $

(12) and
$ {{L_z} = - {\rm i} \frac{\partial }{{\partial \phi }}} . $

(13) Now, we may employ the method of separation of variables by expressing the wave function as
$ \Phi (t,r,\theta ,\phi ) = \frac{1}{{2\pi }}\int {\rm d} \omega {{\rm e}^{ -{\rm i}\omega t}}\sum\limits_l {\frac{{{R_{lm}}(r,\omega )}}{r}} {Y_{lm}}(\theta ,\phi ) , $

(14) where
$ {Y_{\ell m}}(\theta,\phi) $ are the spherical harmonics, and the radial part of the wave function$ {R_{\ell m}}(r,\omega) $ satisfies$ \left( {\frac{{{{\rm d}^2}}}{{{\rm d}{r_*}^2}} + {\omega ^2} - {V_{\rm eff}}(r)} \right){R_{lm}}(r,\omega ) = 0 , $

(15) where the effective potential is given by
$ {V_{\rm eff}}(r) = f(r)\left[ {\frac{{l(l + 1)}}{{{r^2}}} + \frac{{f'(r)}}{r} - mqB} \right], $

(16) and
$ {r_*} $ is the tortoise coordinate defined by${\rm d} {r_*} = \dfrac{{{\rm d}r}}{{f(r)}}$ . We note that${V_{\rm eff }} = - mqB$ as$ r \to \infty $ .In the following, we evaluate the QNMs using the sixth order WKB approximation [59–64] and matrix method [15–18]. Additionally, the temporal evolutions of the perturbation are investigated using the finite difference method [20, 65]. We also study the dependence of the resulting quasinormal frequencies on the spacetime configurations. Moreover, we use the Prony method [66, 67] to extract the complex frequencies and compare them to those obtained using the WKB approximation and matrix method. The matrix method discretizes the master equation and approximates it using a matrix equation that can eventually be solved by a nonlinear equation solver. Of course, the QNMs can also be investigated using other well-known approaches, such as the continued fraction method [13]. Specifically, the parameterization given by Eq. (17) is analytic; therefore, we expect that we can derive a three-term recurrence relation and apply the method. However, for this study, we focus on the three methods discussed above. Regarding the QNM frequencies, we are interested in the role of the magnetic field. In addition to the choice of
$ s=1 $ and$ Q=0 $ as discussed earlier, we consider a simplied form of the metric by assuming the following metric parameters:$ w = - \dfrac{{10}}{9} $ ,$ \kappa = 1 $ ,$ {C_a} = - 9 $ , and$ \lambda = - 16 $ . The resultant metric is expressed as$ \begin{array}{*{20}{l}} f = 1 - \dfrac{{2M}}{r} + \dfrac{3}{{10{r^3}}}. \end{array} $

(17) The resultant quasinormal frequencies are presented in Tables 1–2 and Figs. 1–4. From Tables 1–2, we first conclude that the results obtained using the three different approaches are in reasonable agreement. In particular, the results of the matrix method and sixth-order WKB approximation are mostly consistent. We observe that the term
${m_{\rm eff}} = - mqB$ functions as an effective "mass" of the initially massless scalar field. For positive effective mass${m_{\rm eff}}$ , as the effective mass increases, the real part of the quasinormal frequency increases, whereas the magnitude of the imaginary part decreases. This indicates that the period of the dissipative oscillations decreases, whereas the amplitude decreases slower in time. At vanishing magnetic quantum number$ m=0 $ , as expected, the quasinormal frequencies are independent of the strength of the magnetic field B.l m $ qB = 0 $ 

$ qB = 0.05 $ 

$ qB = 0.1 $ 

$ qB = 0.15 $ 

WKB Matrix method WKB Matrix method WKB Matrix method WKB Matrix method 1 1 0.298-0.096i 0.298-0.096i 0.277-0.108i 0.281-0.109i 0.256-0.120i 0.266-0.127i 0.236-0.130i 0.200-0.178i 0 0.298-0.096i 0.298-0.096i 0.298-0.096i 0.298-0.096i 0.298-0.096i 0.298-0.096i 0.298-0.096i 0.298-0.096i −1 0.298-0.096i 0.298-0.096i 0.320-0.083i 0.320-0.085i 0.342-0.069i 0.343-0.069i 0.363-0.052i 0.363-0.053i 2 2 0.492-0.095i 0.492-0.095i 0.462-0.105i 0.464-0.104i 0.433-0.115i 0.438-0.115i 0.404-0.124i 0.438-0.115i 1 0.492-0.095i 0.492-0.095i 0.477-0.100i 0.477-0.100i 0.462-0.105i 0.464-0.104i 0.448-0.111i 0.451-0.108i 0 0.492-0.095i 0.492-0.095i 0.492-0.095i 0.492-0.095i 0.492-0.095i 0.492-0.095i 0.492-0.095i 0.492-0.095i −1 0.492-0.095i 0.492-0.095i 0.508-0.090i 0.508-0.091i 0.523-0.085i 0.524-0.085i 0.539-0.080i 0.539-0.079i −2 0.492-0.095i 0.492-0.095i 0.523-0.085i 0.524-0.085i 0.555-0.074i 0.555-0.073i 0.587-0.062i 0.587-0.063i Table 1. QNMs of the massless charged scalar field in the magnetized black hole metric in Rastall gravity. The sixth order WKB approximation and matrix method have been employed for the calculations, by assuming the metric given by Eq. (17).
$ l $ 

$ m $ 

$ qB = 0 $ 

$ qB = 0.05 $ 

$ qB = 0.1 $ 

$ qB = 0.15 $ 

1 1 0.293-0.098i 0.272-0.113i 0.247-0.108i 0.229-0.206i 0 0.293-0.098i 0.293-0.098i 0.293-0.098i 0.293-0.098i −1 0.293-0.098i 0.316-0.084i 0.339-0.070i 0.370-0.051i 2 2 0.484-0.097i 0.453-0.108i 0.427-0.120i 0.377-0.114i 1 0.484-0.097i 0.468-0.102i 0.453-0.108i 0.438-0.113i 0 0.484-0.097i 0.484-0.097i 0.484-0.097i 0.484-0.097i −1 0.484-0.097i 0.500-0.091i 0.516-0.086i 0.532-0.080i −2 0.484-0.097i 0.516-0.086i 0.548-0.074i 0.581-0.061i Table 2. QNMs of the massless charged scalar field in the magnetized black hole metric in Rastall gravity obtained using the code of Prony's method developed in [66].
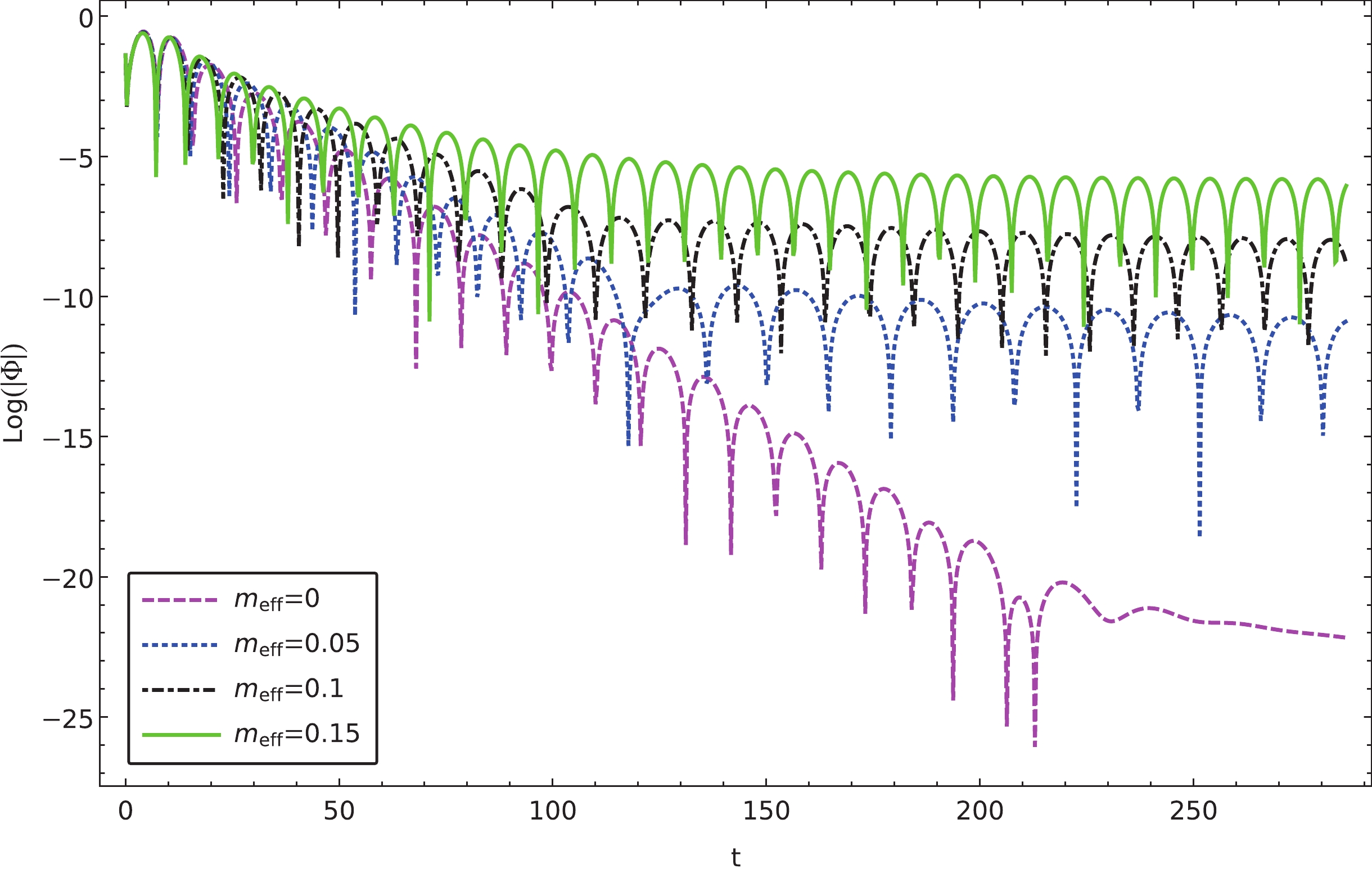
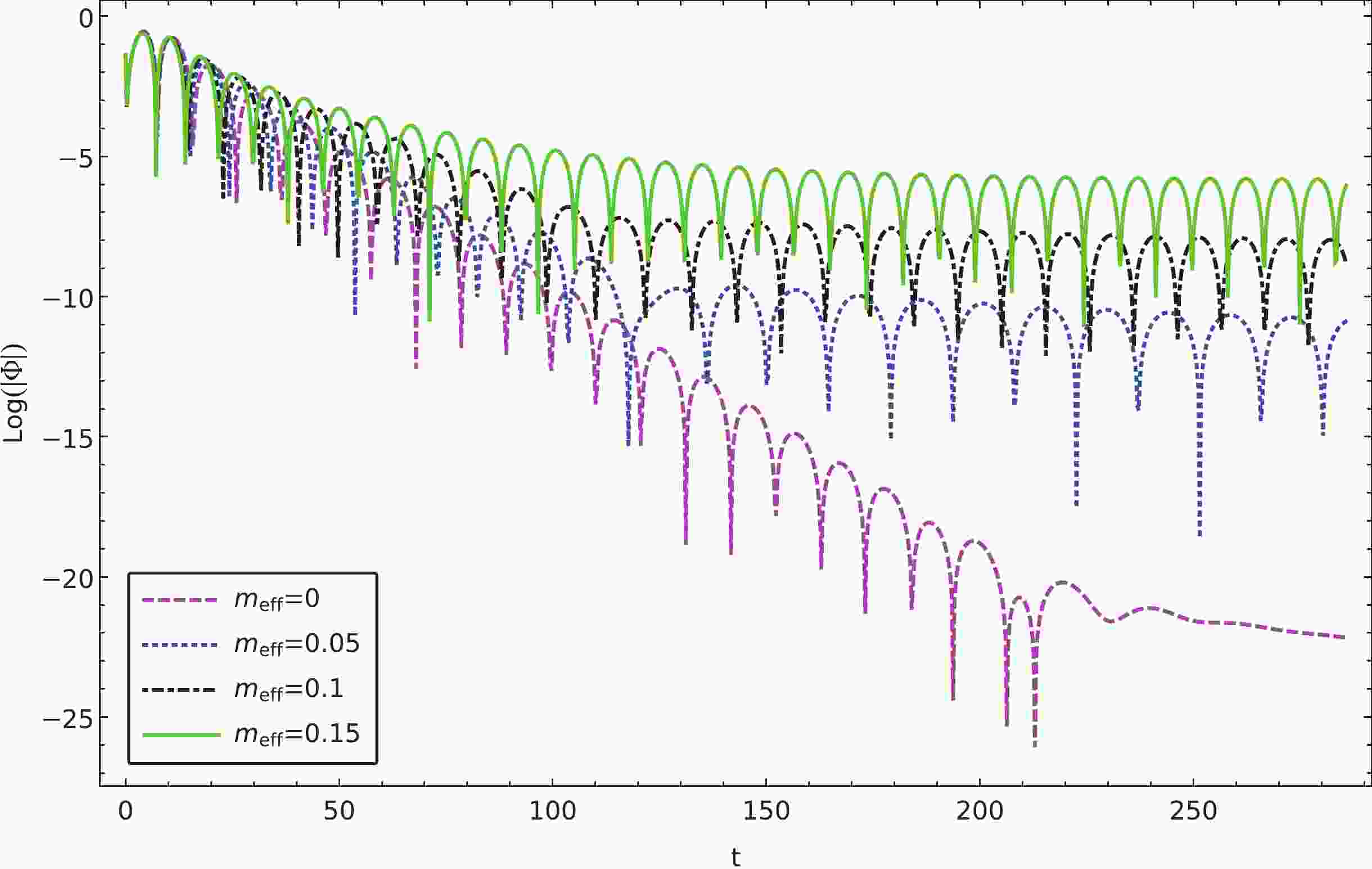
Figure 1. (color online) Calculated temporal evolutions of charged massless scalar perturbations for different values of the effective mass. The results are obtained using the finite difference method using the paramters
$ l=1 $ and$ M=1 $ .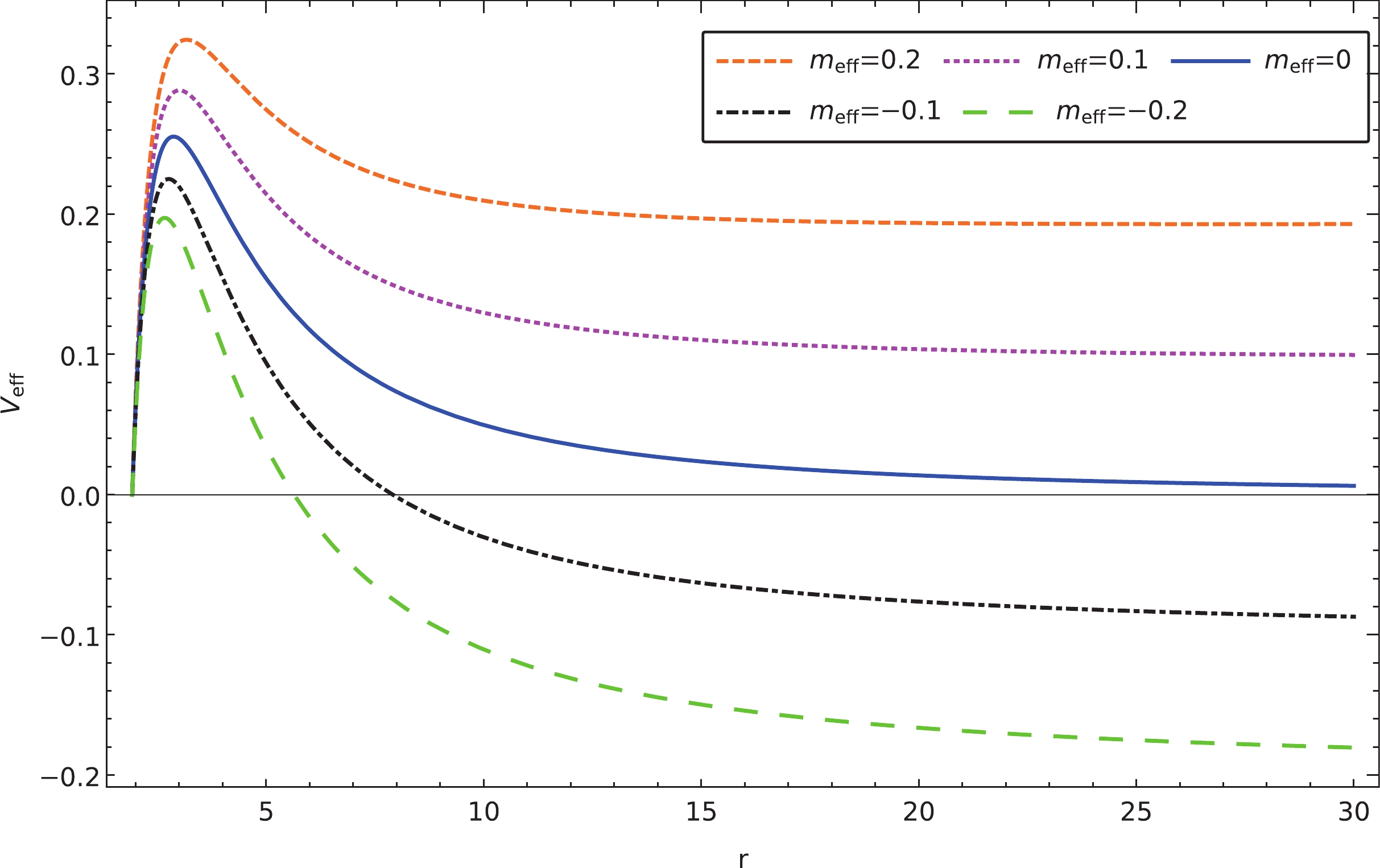
Figure 4. (color online) Effective potentials
${V_{\rm eff}}(r)$ for$ l = 2 $ and different effective mass.These results are also in agreement with the temporal evolution calculated using the finite difference method shown in Fig. 1. In particular, as also shown in Fig. 2, as the value of
${m_{\rm eff}}$ increases, the imaginary part eventually becomes insignificant as the envelope of the oscillations tends to lie horizontally. It is depicted explicitly in Fig. 3, where we calculate the quasinormal frequencies as functions of the effective mass using the matrix method. As the effective increase, the real part of the quasinormal frequency increases, and the imaginary part decreases to approach zero. Subsequently, the resulting temporal evolutions are featured by the so-called quasi-resonance [68, 69]. When we further increase the effective mass until it exceeds a critical value, the quasinormal oscillation will disappear entirely. The latter is demonstrated in Fig. 3 as the quasinormal spectrum approaches the real axis as the magnetic field increases. As discussed in the next section, such a configuration becomes favorable for investigating the properties of the late-time tail in a more transparent fashion.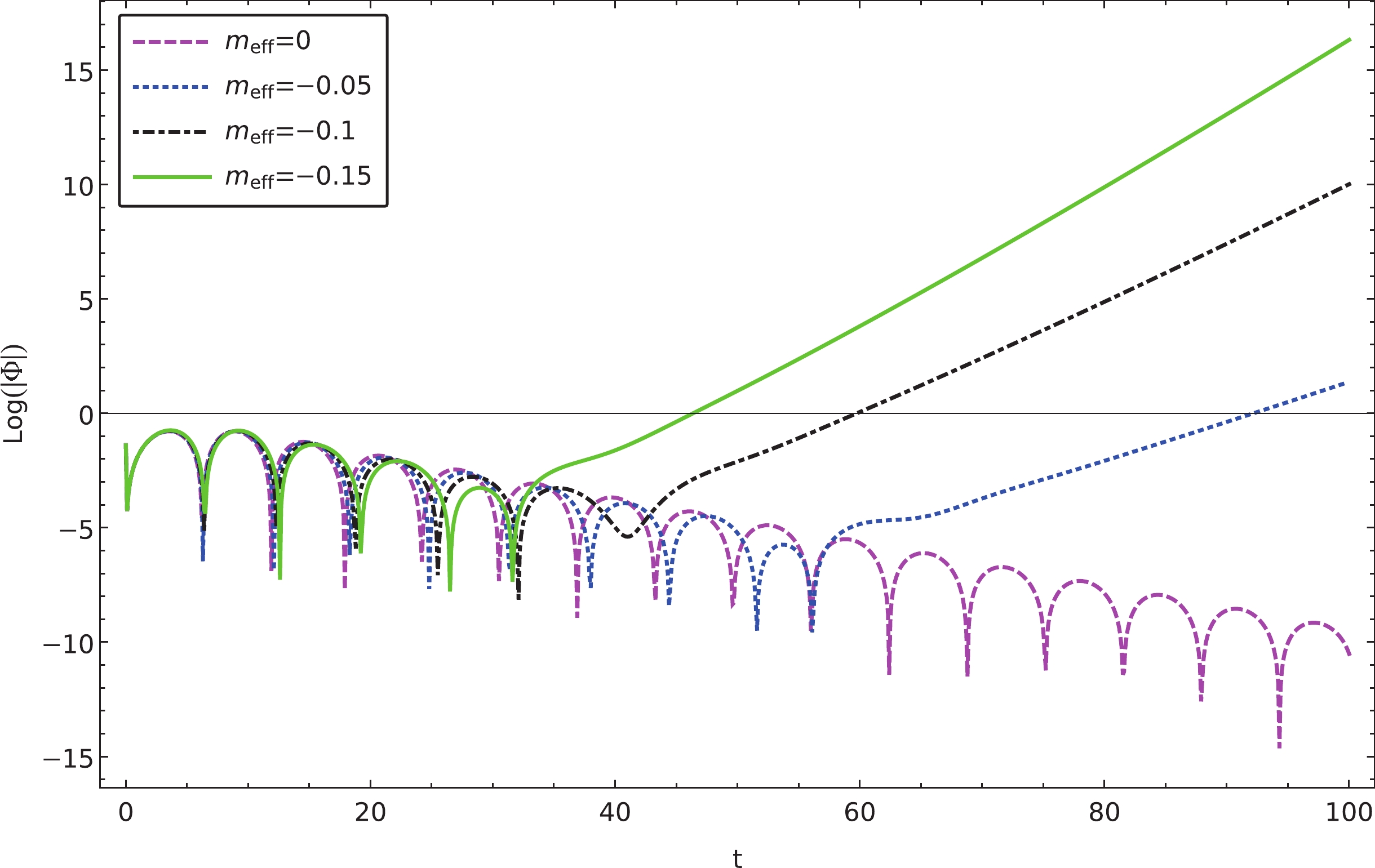
Figure 2. (color online) Calculated temporal evolutions of charged massless scalar perturbations, where instability is observed for a negative effective mass. The results are obtained using the finite difference method for the parameters
$ l=1 $ and$ M=1 $ .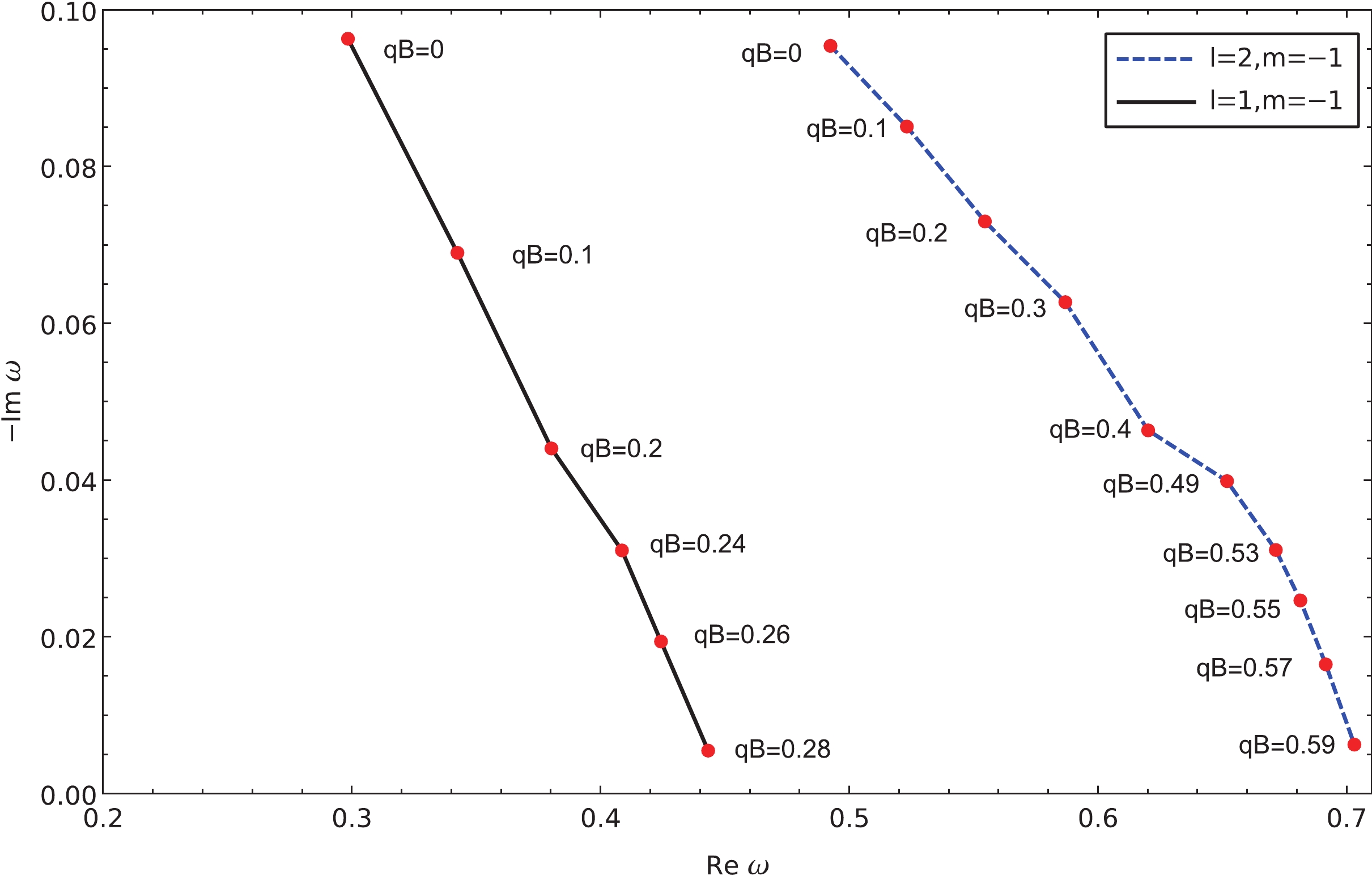
Figure 3. (color online) QNMs of different effective masses calculated using the matrix method for the massless charged scalar field with
$ l = 1,2 $ ,$ m = -1 $ , and$ n = 0 $ .For negative
${m_{\rm eff}} < 0$ , the WKB and matrix methods fail to produce meaningful results, and we resort to the finite difference method entirely. This is signaled by the fact that the corresponding effective potential has a region of negative values, which indicates possible instability. The form of the relevant effective potential, governed by Eq. (16), is shown in Fig. 4. Similar to Ref. [45], we observe that such a configuration indeed results in instability by exploring the temporal evolution of the initial perturbations. To further verify this instability, we use the finite difference method to determine the temporal evolution of the massless charged scalar perturbations. As demonstrated in Fig. 2, as we gradually decrease the value of the effective mass, the oscillation eventually becomes unstable. Moreover, note that there is a distinction between the quasinormal oscillation and the late-time tail in the limit when the magnetic field vanishes, which is elaborated in the next section. -
In this section, we explore the late-time tails of the charged massless scalar perturbations using the analytic method proposed in Ref. [19] and the numerical integration.
In terms of the Green's function, the wave function of the scalar field can be given by [70]
$ \begin{aligned}[b] \psi \left( {{r_*},t} \right) =& \int [ G\left( {{r_*},{r_*}^\prime ;t} \right){\psi _t}\left( {{r_*}^\prime ,0} \right) \\&+ {G_t}\left( {{r_*},{r_*}^\prime ;t} \right)\psi \left( {{r_*}^\prime ,0} \right) ] {\rm d} {r_*}^\prime , \end{aligned} $

(18) where the initial conditions are encoded in
$ {\psi \left({{r_*},0} \right)} $ and$ \psi_t\equiv {\partial _t}\psi ({r_*},0) $ , and the Green's function$ {G\left({{r_*},{r_*}^\prime;t} \right)} $ is defined by$ \left[ {\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{{{\partial ^2}}}{{\partial r_*^2}} + V} \right]G\left( {{r_*},{r_*}^\prime ;t} \right) = \delta (t)\delta \left( {{r_*} - {r_*}^\prime } \right), $

(19) When
$ \tilde G\left({{r_*},{r_*}^\prime;\omega } \right) $ is obtained, the evolution of an arbitrary initial perturbation can be obtained through the integration given by Eq. (18). Indeed, both the QNM and late-time tail can be understood in terms of the singularities and branch cuts of the Fourier transform of the Green's function.$ \tilde G\left( {{r_*},{r_*}^\prime ;\omega } \right) = \int_{{0^ - }}^{ + \infty } G \left( {{r_*},{r_*}^\prime ;t} \right){{\rm e}^{{\rm i}\omega t}}{\rm d}t, $

(20) whose inverse transform is given by
$ G\left( {{r_*},{r_*}^\prime ;t} \right) = - \frac{1}{{2\pi }}\int_{ - \infty + {\rm i}c}^{\infty + {\rm i}c} {\tilde G} \left( {{r_*},{r_*}^\prime ;\omega } \right){{\rm e}^{ -{\rm i}\omega t}}{\rm d}\omega , $

(21) where c is a positive constant. Therefore, the analysis of the properties of the Green's function becomes an essential task.
It is well-known that the Green's function
$ \tilde G\left({{r_*},{r_*}^\prime;\omega } \right) $ can be constructed using two independent solutions of the corresponding homogeneous equation$ \left( {\frac{{{{\rm d}^2}}}{{{\rm d}r_*^2}} + {\omega ^2} - V} \right){\tilde \psi _i} = 0 . $

(22) These two solutions,
$ {{{\tilde \psi }_1}\left({{r_*},\omega } \right)} $ and$ {{{\tilde \psi }_2}\left({{r_*},\omega } \right)} $ , satisfy the appropriate boundary condition at both spatial boundaries [71], namely,$ \begin{array}{*{20}{l}} \begin{array}{l} {{\tilde \psi }_1}\left( {{r_*},\omega } \right) \sim \left\{ {\begin{array}{*{20}{l}} {{{\rm e}^{ - {\rm i}\omega {r_*}}}}&{{r_*} \to - \infty }\\ {A(\omega ){{\rm e}^{{\rm i}\omega {r_*}}} + B(\omega ){{\rm e}^{ -{\rm i}\omega {r_* }}}}&{{r_*} \to + \infty } \end{array}} \right. , \end{array} \end{array} $

(23) $ \begin{array}{*{20}{l}} \begin{array}{l} {{\tilde \psi }_2}\left( {{r_*},\omega } \right) \sim \left\{ {\begin{array}{*{20}{l}} {C(\omega ){{\rm e}^{{\rm i}\omega {r_*}}} + D(\omega ){{\rm e}^{-{\rm i}\omega {r_*}}}}&{{r_*} \to - \infty }\\ {{{\rm e}^{ +{\rm i}\omega {r_*}}}}&{{r_*} \to + \infty } \end{array}} \right. . \end{array} \end{array} $

(24) We can easily show that the following form satisfies Eq. (19):
$ \tilde G\left( {{r_*},{r_*}^\prime ;\omega } \right) = - \dfrac{1}{{W(\omega )}}\left\{ {\begin{array}{*{20}{l}} {{{\tilde \psi }_1}\left( {{r_*}^\prime ,\omega } \right){{\tilde \psi }_2}\left( {{r_*},\omega } \right)},&{\quad {r_*}^\prime > {r_*}}\\ {{{\tilde \psi }_1}\left( {{r_*},\omega } \right){{\tilde \psi }_2}\left( {{r_*}^\prime ,\omega } \right)},&{\quad {r_*}^\prime < {r_*}}, \end{array}} \right. $

(25) where
$ \begin{array}{*{20}{l}} W(\omega) \equiv {\tilde \psi }_1\left( {{r_*} ,\omega } \right){\tilde \psi }_{2,r_*}\left( {{r_*} ,\omega }\right) - {\tilde \psi }_2\left( {{r_*} ,\omega } \right) {\tilde \psi }_{1,r_*}\left( {{r_*} ,\omega } \right) \end{array} $

(26) is the Wronskian of
$ {\tilde \psi }_1\left({{r_*},\omega } \right) $ and$ {\tilde \psi }_2\left({{r_*},\omega } \right) $ .Research shows [24] that the late-time tails of quasinormal oscillations can be attributed to the branch cut of the Green's function. For the massless scalar field, the branch cut lies on the negative part of the imaginary axis [21]. For the massive scalar field, Hod and Piran [27] were the first to indicate that the branch cut lies on the real axis between the two branch points governed by the mass. Using reasonable approximation, an appropriate estimation of the contribution from the branch cut subsequently yields the main characteristic of the late-time tail. From a physical perspective, because the low-frequency waveforms are more likely to be backscattered by the curvature at the asymptotic infinity, the late-time tail is primarily dominated by the low-frequency contributions [27]. Mathematically, this is because both types of late-time tails originate from the branch cut, which remains closer to the real axis than any QNM pole.
To proceed, we introduce
$ {R_{lm}}(r,\omega ) = {\left( {1 - \frac{{2M}}{r} + {r^{ - (2 + a)}}} \right)^{ - 1/2}}\tilde \psi . $

(27) By further referring to Refs. [27, 29, 72, 73], we assume that the initial perturbation and observer are both located away from the black hole. Subsequently, the master equation can be simplified by expanding Eq. (15) in
$ \dfrac{M}{r} $ ②. Specifically, we ignore the terms of order$ \dfrac{c}{{{r^{\alpha }}}} $ with$ \alpha > 2 $ and obtain$ \left[ {\frac{{{{\rm d}^2}}}{{{\rm d}{r^2}}} + {\omega ^2} + Bqm + \frac{{4M{\omega ^2} + Bqm2M}}{r} - \frac{{l\left( {l + 1} \right)}}{{{r^2}}}} \right]\tilde \psi = 0. $

(28) By further introducing
$ \begin{aligned}[b] \tilde \psi =& {z^{l + 1}}{{\rm e}^{ - \frac{z}{2}}}\Phi (z), \\ z=& 2\sqrt { - Bqm - {\omega ^2}} r \equiv 2\varpi r ,\\ \lambda =& \frac{{M( - Bqm)}}{\varpi } - 2M\varpi , \end{aligned} $

(29) we can express two relevant solutions for homogeneous equation Eq. (22) as follows
$ \begin{aligned}[b] {{\tilde \psi }_1} = A' {M_{\lambda ,(l + \frac{1}{2})}}(2\varpi r) ,\quad {{\tilde \psi }_2} = B'{W_{\lambda ,(l + \frac{1}{2})}}(2\varpi r) , \end{aligned} $

(30) where
$ A' = C' \varpi^{-\left(l+1\right)} $ and$ B', C' $ are some one-valued even functions of ϖ.$ M_{k, m} $ and$ W_{k, m} $ are the Whittaker functions, which can be expressed in terms of the solutions of Kummer's equation$ M(a,b,z) $ and$ U(a,b,z) $ , namely, the confluent hypergeometric functions [74],$ \begin{aligned}[b] {M_{\lambda ,(l + \frac{1}{2})}}(2\varpi r) =& {{\rm e}^{ - \varpi r}}{(2\varpi r)^{(l + \frac{1}{2}) + \frac{1}{2}}}M\left( {l + 1 - \lambda ,2l + 2,2\varpi r} \right) ,\\ {W_{\lambda ,(l + \frac{1}{2})}}(2\varpi r) =& {{\rm e}^{ - \varpi r}}{(2\varpi r)^{(l + \frac{1}{2}) + \frac{1}{2}}}U\left( {l + 1 - \lambda ,2l + 2,2\varpi r} \right) . \end{aligned} $

(31) Note that the specific choice of
$ C' $ guarantees the proper in-going wave boundary condition at the horizon. Moreover, as discussed later,$ {\tilde \psi }_1 $ satisfies Eq. (38) as it does not contain any discontinuity when crossing the branch cut [29, 72, 73]. In contrast,$ {\tilde \psi }_2 $ yields the outgoing wave at spatial infinity that has two branch points and, subsequently, a branch cut joining them. As initially proposed in [27], we may conveniently place the branching cut on the real axis of the ω-plane, as shown in Fig. 5. In this context, the late-time tail is primarily governed by the properties of$ {\tilde \psi }_2 $ . Note that it is mandatory to show that the branch cut is in the lower half of the complex plane. Moreover, for the result to be physically meaningful, the specific choice of the branch cut's location must also be irrelevant. A detailed account of this point was discussed recently in Ref. [30].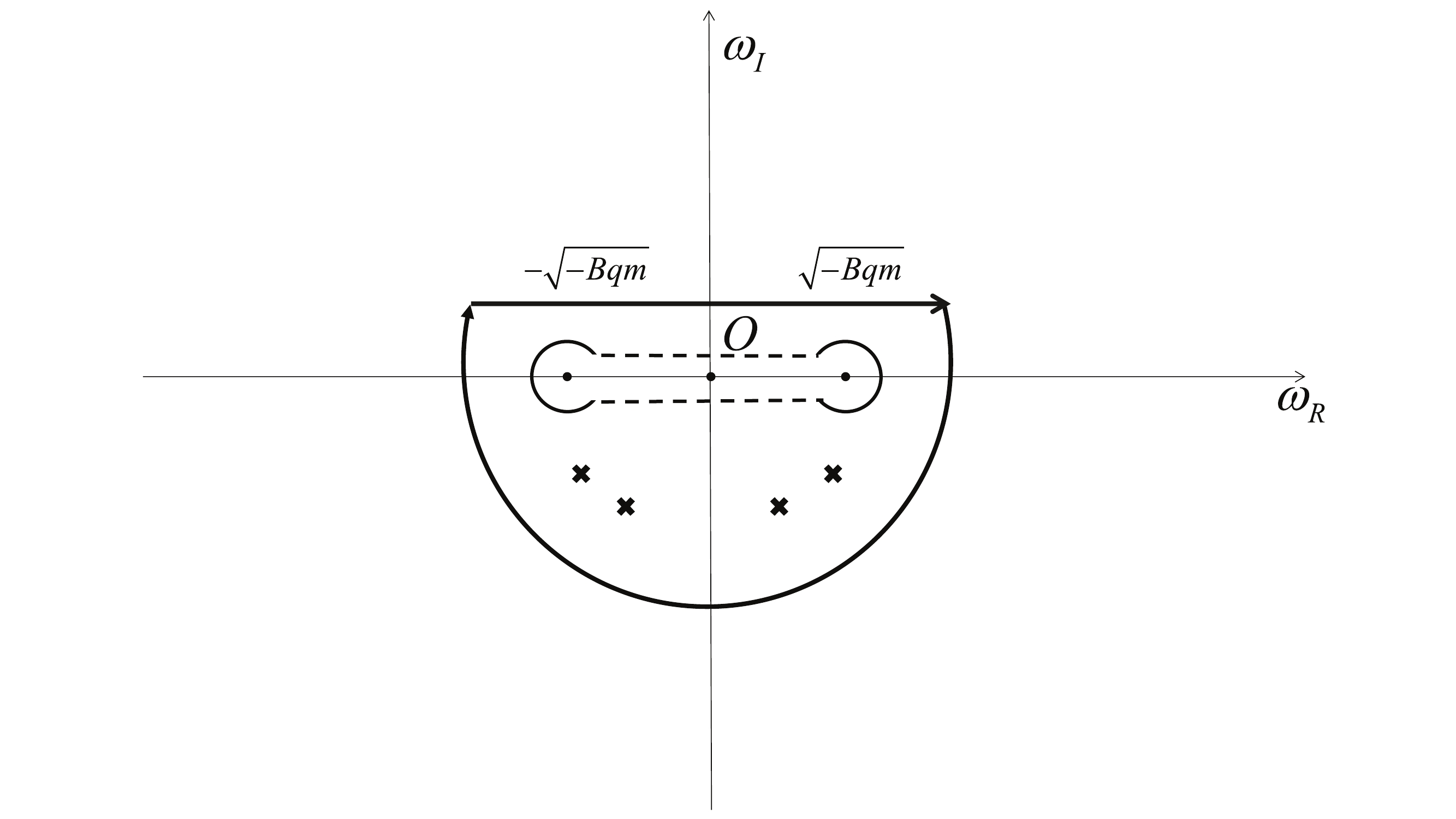
Figure 5. Relevant contour of the integration on the complex frequency plane of the Green's function. The inverse Fourier transform corresponds to the integral along the upper side of the real axis. It can be complemented by an integral along a large semicircle in the lower half of the complex plane, which is subsequently deformed to go around the quasinormal poles and brach cuts indicated in the plot.
By using the explicit forms of Eqs. (30)–(31), we can evaluate the contribution from the difference between the two sides of the branch cut. Therefore, the inverse Fourier transform Eq. (21) yields
$ {G^C}\left( {{r_*},r_*^\prime ;t} \right) = \frac{1}{{2\pi }}\int_{ - \sqrt { - Bqm} }^{\sqrt { - Bqm} } F (\varpi ){{\rm e}^{ -{\rm i}\omega t}}{\rm d}\omega , $

(32) where
$ F (\varpi )\equiv {\frac{{{{\tilde \psi }_1}\left( {r_*^\prime ,\varpi {{\rm e}^{{\rm i}\pi }}} \right){{\tilde \psi }_2}\left( {{r_*},\varpi {{\rm e}^{{\rm i}\pi }}} \right)}}{{W\left( {\varpi {{\rm e}^{{\rm i}\pi }}} \right)}} - \frac{{{{\tilde \psi }_1}\left( {r_*^\prime ,\varpi } \right){{\tilde \psi }_2}\left( {{r_*},\varpi } \right)}}{{W(\varpi )}}} . $

(33) Regarding the integrand in Eq. (32), we first calculate the Wronskian in the denominator using the following relations [74]
$ \begin{aligned}[b] {W_{\lambda ,l + \frac{1}{2}}}(2\varpi r) =& \frac{{\Gamma ( - 2l - 1)}}{{\Gamma ( - l - \lambda )}}{M_{\lambda ,l + \frac{1}{2}}}(2\varpi r) \\&+ \frac{{\Gamma (2l + 1)}}{{\Gamma (l + 1 - \lambda )}}{M_{\lambda , - \left( {l + \frac{1}{2}} \right)}}(2\varpi r) . \end{aligned} $

(34) and the non-vanishing Wronskian between the confluent hypergeometric functions
$ W\left\{ {{M_{\lambda ,l + \frac{1}{2}}}(2\varpi r),{M_{\lambda , - \left( {l + \frac{1}{2}} \right)}}(2\varpi r)} \right\} = - (2l + 1)(2\varpi ). $

(35) We observe that
$ W(\varpi ) = {A^\prime }{B^\prime }( - 2l - 1)(2\varpi )\frac{{\Gamma (2l + 1)}}{{\Gamma (l + 1 - \lambda )}}. $

(36) To account for the discontinuity of the integrand across the branch cut, we use
$ {M_{\pm\lambda ,l + \frac{1}{2}}}\left( {{{\rm e}^{{\rm i}\pi }}2\varpi r} \right) = {{\rm e}^{(l + 1){\rm i}\pi }}{M_{ \mp \lambda ,l + \frac{1}{2}}}(2\varpi r), $

(37) to evaluate
${\tilde \psi }_{1,2}\left({r_*,\varpi {{\rm e}^{{\rm i}\pi }}} \right)$ as follows:$ {\tilde \psi }_1\left( {r_* ,\varpi {{\rm e}^{{\rm i}\pi }}} \right) = {{\tilde \psi }_1}\left( {r_* ,\varpi } \right) , $

(38) $ \begin{aligned}[b] {\tilde \psi }_2\left( {{r_*},\varpi {{\rm e}^{{\rm i}\pi }}} \right) =& {B^\prime }\Bigg[{{\rm e}^{\left( {l + 1} \right){\rm i}\pi }}\frac{{\Gamma ( - 2l - 1)}}{{\Gamma \left( { - l + \lambda } \right)}}{M_{ \lambda ,l + \frac{1}{2}}}(2\varpi {r_*}) \\&+ {{\rm e}^{\left( { - l} \right){\rm i}\pi }}\frac{{\Gamma (2l + 1)}}{{\Gamma \left( {l + 1 + \lambda } \right)}}{M_{ \lambda , - (l + \frac{1}{2})}}(2\varpi {r_*})\Bigg] . \end{aligned} $

(39) In the above results, note that the subscripts λ of the Whittaker functions remain unchanged. Eq. (38) manifestly indicates that
$ {{\tilde \psi }_1} $ does not have any branch cut as it is also a generic physical requirement [21, 27, 29]. Additionally, the Wronskian yields$ W\left( {\varpi {{\rm e}^{{\rm i}\pi }}} \right) = A'{B^\prime }( - 2l - 1)(2\varpi )\frac{{\Gamma (2l + 1)}}{{\Gamma (l + 1 + \lambda )}}{{\rm e}^{( - l){\rm i}\pi }} $

(40) We note that in deriving the above result, we should always take note of Eqs. (38) and (39). Specifically, the discontinuity associated with the factor
$ \varpi^{-(l+1)} $ embeded in$ A' $ does not manifest itself, whereas the factor${\rm e}^{-l{\rm i}\pi}$ on the r.h.s. of Eq. (39) does.By consolidating all the pieces, i.e., Eqs. (38), (39), and (40), we observe that the integrand of Eq. (32) yields
$ F(\varpi ) = \frac{1}{{( - 2l - 1)(2\varpi ){A^\prime }^2}}{{\tilde \psi }_1}\left( {r_*^\prime ,\varpi } \right)\tilde F(\varpi ){{\tilde \psi }_1}\left( {{r_*},\varpi } \right) $

(41) where
$ \begin{aligned}[b] \tilde F(\varpi ) =& {\rm e}^{(2l+1){\rm i}\pi}\frac{\Gamma\left(-2l-1\right)\Gamma\left(l+1+\lambda\right)}{\Gamma\left(-l+\lambda\right)\Gamma\left(2l+1\right)} \\&-\frac{\Gamma\left(-2l-1\right)\Gamma\left(l+1-\lambda\right)}{\Gamma\left(-l-\lambda\right)\Gamma\left(2l+1\right)} . \end{aligned} $

(42) Here, owing to Eq. (38),
$ {\tilde \psi }_1\left({r_*}^\prime,\varpi \right) $ can be readily factorized out. The remaining term,$ {\tilde \psi }_2\left({r_*},\varpi \right) $ , can be simplified by removing irrelevant contributions that have the identical discontinuity of the Wronskian. As a result, a second$ {\tilde \psi }_1\left({r_*},\varpi \right) $ can be removed.For the intermediate-late time scale, which corresponds to the range
$ M \ll r \ll t \ll M/(- qBm{M^2}) $ , the frequency$ \varpi = O(\sqrt {\sqrt { - qBm} /t}) $ results in a major contribution to the integral, which implies$ \lambda \ll 1 $ owing to Eq. (29). In this case, the term proportional to$ \frac{1}{r} $ in Eq. (28), which describes the backscattering due to the curvature of asymptotic infinity, is insignificant [28, 29]. Subsequently, the inverse Fourier transform of the Green's function at the limit$ \lambda \ll 1 $ can be performed mostly analytically, which results in$ \begin{aligned}[b]\\[-3pt] {G^C}\left( {{r_*},r_*^\prime ;t} \right) = \frac{{\left( {1 - {{\rm e}^{(2l + 1){\rm i}\pi }}} \right)\Gamma ( - 2l - 1)\Gamma (l + 1)\Gamma \left( {l + \dfrac{3}{2}} \right){{( - qBm)}^{\frac{{2l + 1}}{4}}}{{\left( {r_*^\prime {r_*}} \right)}^{l + 1}}{t^{ - \frac{{2l + 3}}{2}}}}}{{\pi (4l + 2){2^{ - 3l - \frac{5}{2}}}\Gamma (2l + 1)\Gamma ( - l)}}\times \cos \left[ {\sqrt { - qBm} t - \pi \left( {\frac{{2l + 3}}{4}} \right)} \right]. \end{aligned} $ 
(43) In other words, we observe that at the intermediate-late time, the tail is dominated by the form
$ {t^{ - l - \frac{3}{2}}}\cos \left[ {\sqrt { - qBm} t - \pi \left(\frac{l}{2} + \frac{3}{4}\right)} \right] . $

It oscillates while decaying through a power-law form. In addition to the magnetic field, the intermediate-late time tail depends on the multipole number l and azimuthal number m. In particular, the presence of the magnetic field results in an effective mass that significantly modifies the properties of the tail. However, if we remove the magnetic field, the tail governed by taking the limit
$ B\to 0 $ in Eq. (43) does not simply fall back to its massless counterpart. Specifically, while the synodal oscillation is suppressed, the remaining power-law exponent becomes${\rm e}^{-l-\frac32}$ , which differs from the late-time tail${\rm e}^{-2l-3}$ observed for a massless scalar in the Schwarzschild background. Moreover, as discussed later, at the limit of the vanishing magnetic field, the power-law exponent of the late-time tail does not match that of its massless counterpart. We postpone further discussions of this intriguing characteristic to the end of this section.Now, we discuss the asymptotic behavior of the late-time tails. At a significant time scale
$ \sqrt { - qBm} t \gg 1/{(\sqrt { - qBm} M)^2} $ , the relevant terms in the master equation behave differently from the case of intermediate-late time tail. The backscattering from the spacetime curvature at asymptotic infinity can no longer be ignored for this scenario. Thus, because both the$ {\tilde \psi }_1 $ factors in Eq. (41) do not depend sensitively on the frequency ω, we only require to focus on the term Eq. (42). By applying the above approximation and using the asymptotical forms of Γ functions [74], we obtain$ \tilde F(\varpi ) \approx \frac{\Gamma\left(-2l-1\right)}{\Gamma\left(2l+1\right)}\lambda^{2l+1}\left[{\rm e}^{(2l+1){\rm i}\pi} - \frac{\eta_+ {\rm e}^{{\rm i}\pi \lambda} + \eta_- {\rm e}^{-{\rm i}\pi \lambda}}{\eta_- {\rm e}^{{\rm i}\pi \lambda} + \eta_+ {\rm e}^{-{\rm i}\pi \lambda}}\right] , $

(44) where
$ \begin{eqnarray} \eta_\pm = \mp {\rm e}^{\pm {\rm i}\pi l} . \end{eqnarray} $

(45) The resulting integral of the inverse Fourier transform is somewhat complicated, but its asymptotic properties are governed by the terms related to λ. At small frequencies, we obtain
$ \varpi\to 0 $ and$ \lambda\to \infty $ . Their product, which appears in the argument of the Bessel functions, yields$ \lambda \varpi = \left(\frac{{M( - Bqm)}}{\varpi } - 2M\varpi \right)\varpi = M( - Bqm) + O(\varpi^2), $

which is finite and varies gradually in the low-frequency region
$ \omega \to \sqrt{ - Bqm}_+ $ [72]. Both the terms$ \lambda^{2l+1} $ and${\rm e}^{\pm {\rm i}\pi \lambda}$ of Eq. (44) oscillate significantly as$ \lambda\to \infty $ , whereas the latter type is even more dramatic compared with the former. This indicates that the integral's main contribution results from these terms. In most cases, we may follow the arguments of Koyama and Tomimatsu [28] that the main contribution of the integral can be obtained by employing the method of steepest descent. The strategy of such a treatment involves isolating the part that oscillates significantly and then encountering the saddle point, where the oscillations evolve the slowest. The remaining part might be tedious in form but varies moderately. We rewrite the integrand as$ \tilde F(\varpi ){\rm e}^{-{\rm i}\omega t} \approx \frac{\Gamma\left(-2l-1\right)}{\Gamma\left(2l+1\right)}\lambda^{2l+1}{{\rm e}^{{\rm i}\phi }} {\rm e}^{{\rm i}(2\pi\lambda-\omega t)}, $

(46) where the phase can be defined by
$ {{\rm e}^{{\rm i}\phi }} = - \frac{\eta_+ + \eta_- {\rm e}^{-2{\rm i}\pi \lambda}}{\eta_+ + \eta_- {\rm e}^{2{\rm i}\pi \lambda} } . $

(47) As shown in [30], the variation in the phase ϕ precisely cancels that in the term
${\rm e}^{2{\rm i}\pi\lambda}$ . In this case, the integral cannot be evaluated using the method of steepest descent. Nonetheless, we may still evaluate the most dominant term of the integral and obtain$ \begin{eqnarray} {G^C}\left(r_*, {r'}_*; t\right)\sim t^{-1}\sin(\mu t +\varphi) , \end{eqnarray} $

(48) where the phase shift φ contains some minor dependence on t. The temporal dependence of Eq. (48) implies that late-time tail evaluated regarding the contribution from the saddle point is
$ \sim {t^{ - 1}} $ . Note that the obtained exponential does not depend on either the angular momentum number or the strength of the magnetic field.We present the numerical results in Figs. 6–9. To confirm the above analytical results, we perform the numerical calculations using numerical integration. The resultant temporal evolutions of the intermediate-late time are presented in Figs. 6–7. In Fig. 6, we show the temporal evolutions at the intermediate-late time for different effective masses. For a given l, through Eq. (43), the period of the oscillations increases as the effective mass decreases. Moreover, Fig. 7 shows that when the effective mass is fixed, the oscillating frequency largely remains unchanged for different values of l. Furthermore, the attenuation becomes more significant as l increases. In Fig. 7, the time profiles obtained numerically are also compared against the analytic ones shown in dashed curves given by Eq. (43). The extracted exponent from the envelope of the oscillation yields
$ {t^{ - \beta }} $ , where$ \beta = 2.5087 \pm 0.0020 $ and$ \beta = 3.5015 \pm 0.0020 $ with respect to$ l = 1 $ ,$ l = 2 $ . Therefore, the asymptotic form$ t^{ - (l + 3/2)} $ for the intermediate-late time agrees well with the numerical results for different l values.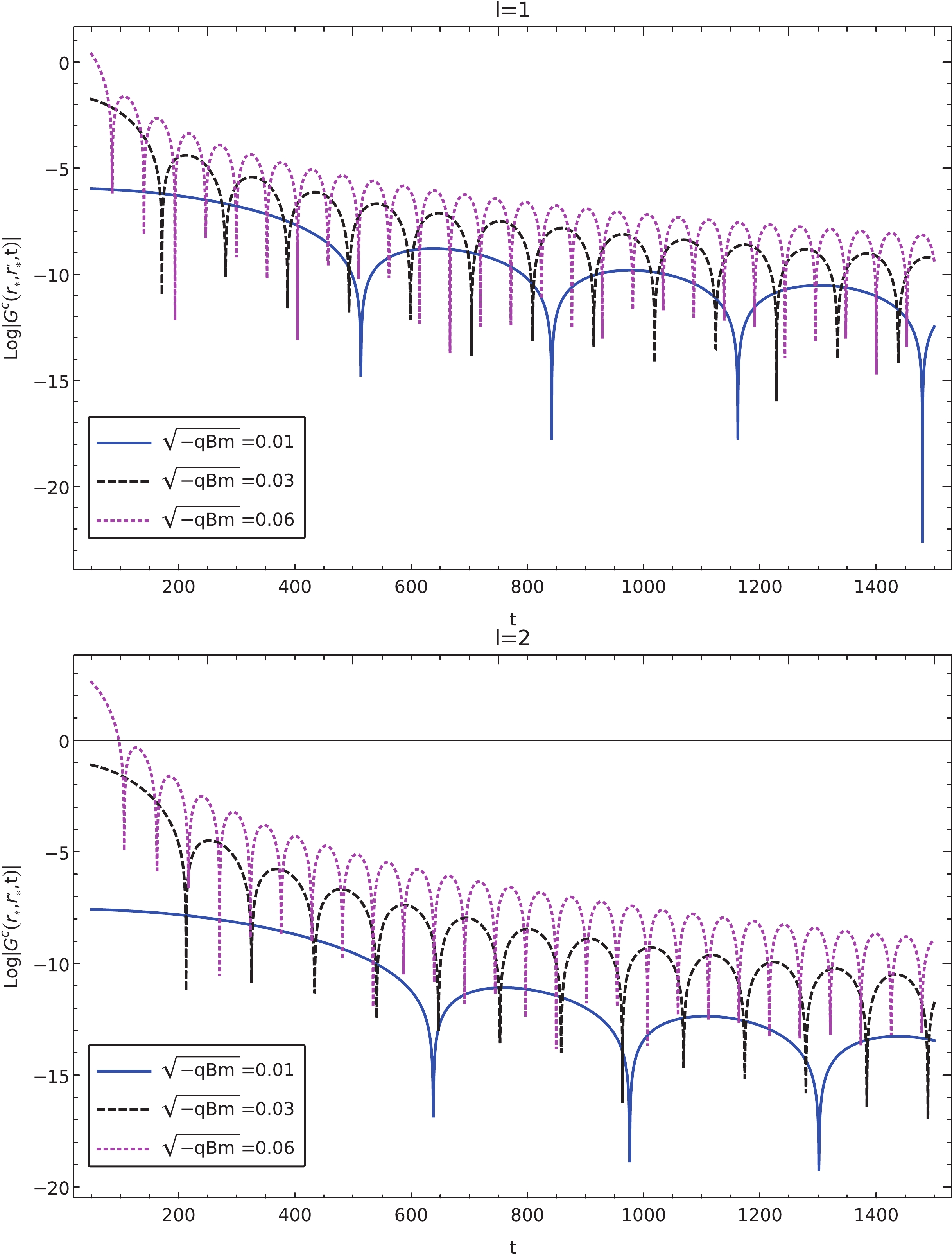
Figure 6. (color online) Calculated intermediate-late time tail in the Green's function of charged massless scalar perturbations in a magnetized black hole in Rastall gravity. The results are obtained using numerical integration for different effective masses with
$ l = 1, 2 $ .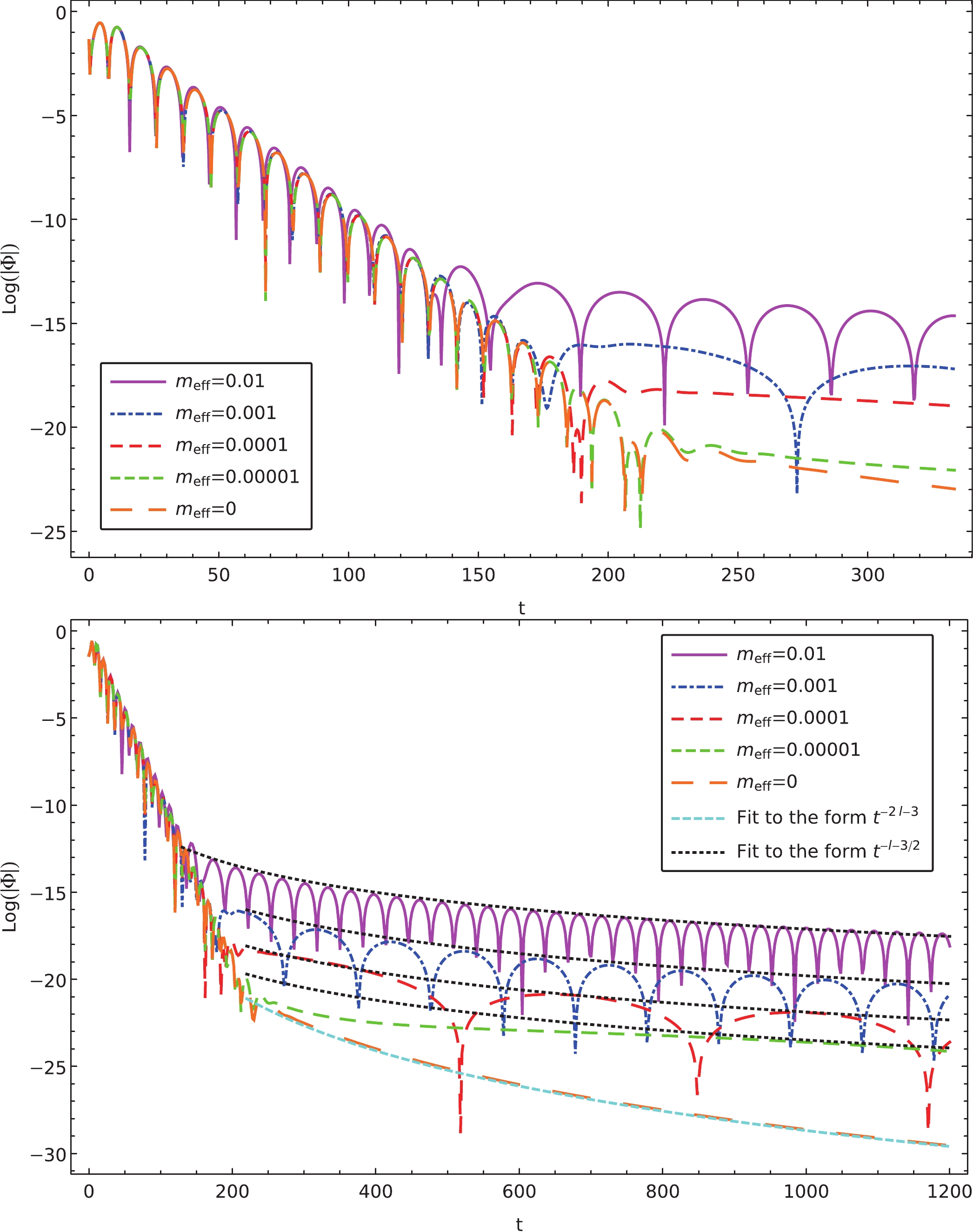
Figure 9. (color online) Calculated quasinormal oscillations and late-time tails of charged massless scalar perturbations in a magnetized black hole in Rastall gravity. The calculations aim to explore the asymptotic behavior of the QNMs and tails as the effective mass gradually vanishes. The results are obtained using the parameters
$ l = 1 $ and$ M=1 $ . Top: The quasinormal oscillations are shown to converge to the case of massless perturbations as the effective mass approaches zero. Bottom: The envelopes of the tails are compared with the analytic forms$ t^{ - l-3/2} $ and$ t^{ - 2l-3} $ , respectively. The results indicate that the tails' asymptotic behavior does not fall back to that of massless perturbations, as discussed in the text.
Figure 7. (color online) Calculated intermediate-late time tail in the Green's function of charged massless scalar perturbations in a magnetized black hole in Rastall gravity. The results are obtained using numerical integration for different effective masses with
$ l = 1, 2 $ . The envelopes of dissipative oscillations shown in dashed curves are compared with the analytic ones$ t^{ - (l + 3/2)} $ given in the text.The temporal evolutions of the late-time tails are presented in Fig. 8. The calculations are performed for different effective masses and angular momenta. Again, by comparing the two plots in Fig. 8, as the effective mass increases, we observe that the oscillation frequency also increases, but the attenuation rate remains the same. Moreover, as shown in the bottom plot of Fig. 8, neither the attenuation rate nor the oscillation period depends on the angular momentum l. We also show in dashed curves the nonlinear fitting to the envelope of the oscillations. The extracted exponents from the a power-law form
$ {t^{ - \beta }} $ for the two cases are$ \beta = 0.9978 \pm 0.0068 $ and$ \beta = 0.9762 \pm 0.0082 $ , respectively, which are reasonably consistent with the analytic result$ t^{-1} $ .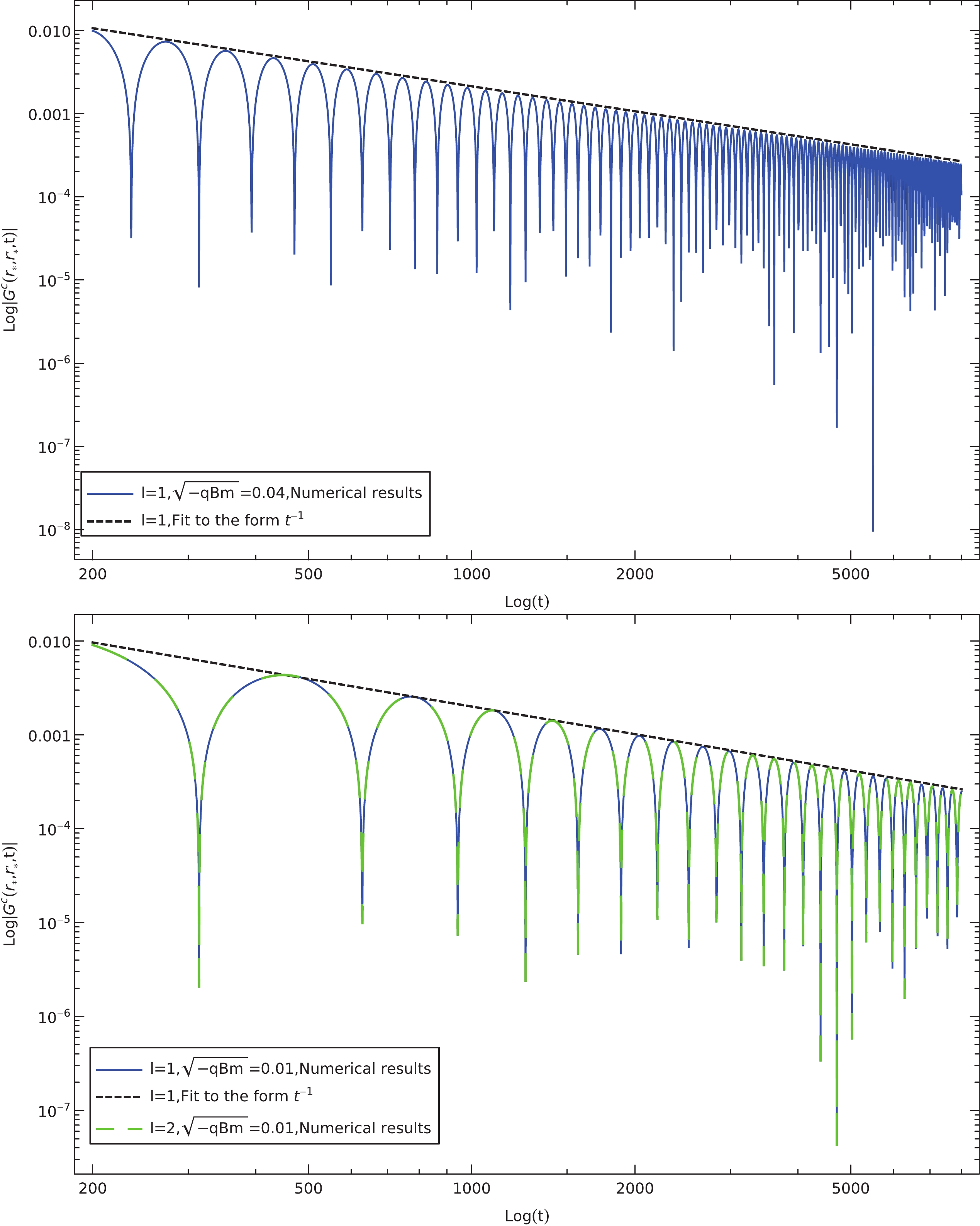
Figure 8. (color online) Calculated late-time tail in the Green's function of charged massless scalar perturbations in a magnetized black hole in Rastall gravity. The results are obtained using numerical integration for different effective masses with the parameters
$ l = 1, 2 $ and$ M=1 $ . The envelopes of dissipative oscillations shown in dashed curves are compared with the analytic ones$ t^{ - 1} $ given in the text.Finally, we elaborate on the specific role of the magnetic field in this study. A distinct characteristic of the present spacetime configuration is that the effective mass is generated by the magnetic field; therefore, the effect on the late-time tail is dynamic. In particular, we are allowed to consider a process in which one gradually tunes the magnetic field to approach the limit
$ B\to 0 $ . Based on the preceding discussions, although the quasinormal frequencies are observed to vary continuously, we conclude that the resultant tail would not converge to its massless counterpart. This phenomenon is manifestly shown in Fig. 9. The top plot of Fig. 9 shows that as the effective mass decreases, the dissipative oscillations converge to the case of massless perturbations. This is consistent with the numerical results obtained in Table 3, where the Prony method [66, 67] has again been employed to extract the complex frequencies from the time profiles. In contrast, as shown in the bottom plot of Fig. 9, the late-time tail of massless perturbations is distinct from the remaining ones. Specifically, the massless perturbation indicated by the orange curve does oscillate at a finite period, whereas the oscillation periods of massive perturbations are more significant (c.f., the green and dark red curves). Regarding the attenuation rate, all the curves of massive perturbations are essentially parallel, which differs from that of the massless one. Quantitatively, the values extracted from the numerical fitting deviate from one another, as indicated in the caption of the plot.${m_{\rm eff} }$ 

Prony WKB Matrix method 0 0.29861-0.09614i 0.29842-0.09636i 0.29845-0.09622i 0.00001 0.29861-0.09614i 0.29842-0.09636i 0.29845-0.09622i 0.0001 0.29865-0.09612i 0.29846-0.09634i 0.29849-0.09620i 0.001 0.29904-0.09590i 0.29885-0.09611i 0.29884-0.09600i 0.01 0.30288-0.09421i 0.30276-0.09384i 0.30246-0.09408i Table 3. QNMs for the metric Eq. (17) are calculated by gradually reducing the effective mass. The Prony method, sixth order WKB approximations, and matrix method are used for the calculations. The results are obtained for
$ M = 1, l = 1 $ .We now argue that the case of massless perturbation corresponds to a scenario in which the magnetic field does not exist in the first place. Such an interesting difference is somewhat reminiscent of the demagnetization process in ferromagnetic materials. Mathematically, this can be understood as follows. The convergence of the quasinormal frequencies can be understood as the analytic properties of the effective potential essentially remaining unchanged as the effective mass varies continuously. However, the origin of a massive field's late-time tail is associated with the presence of two branch points on the real axis and the absence of any branch point at infinity. As the effective mass approaches zero, the two branch points become degenerate, but a new branch cut will not appear, which extends to infinity. Moreover, a single branch point will be located at the origin in the case of a massless field. The branch cut on the negative imaginary axis connects the origin with the second branch point at infinity. As a result, the relevant structure on the frequency plane due to a massless field is intrinsically different from that of a massive perturbation, although the mass is insignificant. In other words, if we gradually remove the magnetic field from a magnetized black hole, the perturbation will evolve differently from the spacetime configuration in which the magnetic field in question does not ever exist. We note that the above picture is plausible only when the time scale of the demagnetization process is significantly smaller than the inverse of the typical distance between adjacent quasinormal frequencies. This is because the resulting effective potential is now a function of time. Therefore, the notion that QNMs correspond to the zeros of the Wronskian and subsequently the poles of the frequency domain Green's function [3] is only approximately valid when the process can be considered quasistatic. In literature, the master equation with a time-dependent potential is mostly treated numerically [75–77].
-
In this study, we investigate the QNMs and late-time tails of charged massless scalar perturbations in a magnetized black hole in Rastall gravity. We show that the magnetic field has a significant role in both aspects of the resultant properties of the scalar perturbation. Specifically, the massless scalar acquires an effective mass through the magnetic field, which significantly affects the temporal evolution of the initial perturbations. For the quasinormal oscillations, the complex frequencies are distorted and might become either quasinormally resonant or unstable for specific parameters. For the intermediate and late-time tails, power-law forms are obtained analytically and numerically, reminiscent of those of massive scalar perturbations. Moreover, owing to the dynamic nature of the effective mass generated by the magnetic field, we argue that it has an interesting characteristic. In particular, as we gradually reduce the external magnetic field, while the quasinormal frequencies converge to its massless counterpart, the behavior of the late-time tail deviates from the latter. From a mathematical perspective, this can be understood by analyzing the structure of branch points and cuts on the complex frequency plane of the relevant Green's function.
-
We wish to thank Rui-Hong Yue for enlightening discussions.
-
In this Appendix, we show that when the magnetic field is small, the metric given by Eqs. (3)–(9) is a valid approximation. For simplicity, we assume that the strength of the magnetic field is insignificant and does not consider the "backreaction" to the metric. First, we readily verify that Eq. (9) satisfies the Maxwell equation for linear electromagnetic field in Schwarzschild's solution of Einstein gravity. For the Schwarzschild solution Eq. (8) of generalized Rastall gravity, we must ascertain that the deviation for Eq. (9) as linear electromagnetic field (
$ s=1 $ ) is of higher-order, consistent with the approximation performed later. To show this, we rewrite the deviation from Eq. (17) as$ \tilde f = f + \delta f , \tag{A1} $

and solve the Maxwell equation for
$ \delta f $ .Evidently,
$ \delta f $ satisfies$ 2\delta f + 2r\delta f' = \frac{6}{5r^3} , \tag{A2}$

which implies the magnitude of the correction
$\delta f \sim O(r^{-3})$ , irrelevant to the effective potential in the master equation Eq. (28).
Quasinormal oscillations and late-time tail of massless scalar perturbations of a magnetized black hole in Rastall gravity
- Received Date: 2022-04-19
- Available Online: 2022-10-15
Abstract: In this study, we investigate the quasinormal mode and late-time tail of charged massless scalar perturbations of a black hole in generalized Rastall gravity. The black hole metric in question is spherically symmetric, accompanied by a power-Maxwell field surrounded by a quintessence fluid. We show that the massless scalar field, when dressed up with the magnetic field, acquires an effective mass, which significantly affects the properties of the resultant quasinormal oscillations and late-time tails. Specifically, the quasinormal frequencies become distorted and might even be unstable for particular spacetime configurations. Additionally, the exponent of the usual power-law tail is modified according to the modification in the structure of the branch cut of the retarded Green's function. In particular, as the effective mass is generated dynamically owing to the presence of the magnetic field, we may consider a process through which the field is gradually removed from the spacetime configuration. In this context, while the quasinormal oscillations converge to the case of massless perturbations, we argue that the properties of resultant late-time tails do not fall back to their massless counterpart. The relevant characteristics are investigated using numerical and analytic approaches.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: