-
Nuclei are examples of many particle open quantum systems, in which there is a complex aggregation of nucleons that interact with each other through exchange of mesons, giving rise to both bound and free states, which can be strongly coupled. Currently, it is of great interest to analyze the fusion reactions for a wide range of nuclei. Heavy ion fusion reactions at energies near the Coulomb barrier have been an important topic for nuclear physics in the last 20 years. Various types of fusion beams lead to different nuclear interests. For instance, the reaction with stable beams reveals a clear figure of nuclear structure and fusion unlike that of exotic beams, thereby opening new perspectives to investigate the impact of weak binding energies and large isospin in fusion reactions [1]. According to partial wave analysis, the total cross section is the sum of the scattering cross section and reaction cross section, which further includes different partial reaction cross sections. For low-energy collision reactions, the fusion channel is prime among all channels. Mathematically, it is difficult to extract the part from the total reaction cross section (
$ \sigma_{r} $ ) so that it can exactly account for fusion cross section ($ \sigma_{{\rm fus}} $ ). To produce a clear picture of fusion reactions and fusion dynamics, many calculation approaches have been proposed, such as the coupled channel (CC) [2] calculation. However, many of these theoretical approaches were unable to explain the observed spin distribution and average angular momenta related to fusion cross section. In the calculations hereby presented, we use the optical model potential (OMP) [ 3] with a U type pocket shape in the interior part of the effective potential that generates the resonance states due to standing waves in nuclear well. This method was successfully employed for light and bound systems, e.g.,$\rm ^6Li + ^{209}Bi$ [4] and$\rm ^{16}O + ^{58,62}Ni$ [5], in previous studies conducted by our co-authors. The potential consists of a real part and an imaginary part. The real part corresponds to scattering, whereas the imaginary part corresponds to the fusion cross section for compound nucleus formation. It is known that scattering is a surface phenomenon, while fusion is an interior activity. All the parameters are set hereby fitting the measured data of elastic scattering cross sections at various energies. With the same potential, we explain the fusion cross section of the$\rm ^{16}O + ^{92}Zr$ system. Hence, we aim to find an energy independent set of optical potential parameters; this is the main motivation of our study for this system. According to the concept of OMP, the expectation value of the imaginary part of the potential with the distorted wave function of the full potential in the elastic channel accounts for$ \sigma_{r} $ , which can easily be obtained by adding the absorption cross sections of different regions of the potential where the imaginary part is actively present. We introduce the same wave function as the one used to explain elastic scattering data to obtain the absorption cross section$ \sigma_{i}^{A} $ in infinitesimally small ith radial interval, represented as$ \delta r_{i} $ . Thus, the total absorption cross section can be written as$ \sigma_{A}=\sum_{i=1}^n \sigma_{A}^{i} $ , where n is the total number of intervals of the potential, and the range of potential$ R=\sum_{i=1}^{n}\delta r^{i} $ .Given that the fusion of nuclei is an interior phenomenon, it occurs in the interior part of the radial position of the electrostatic Coulomb barrier. The absorption in the region of
$ 0<r<R_{B} $ should account for the$ \sigma_{{\rm fus}}^{{\rm exp}} $ data. The exact value of the radius up to which the absorption cross section is accountable for the experimental fusion cross section$ \sigma_{{\rm fus}}^{{\rm exp}} $ is called fusion radius. In this study, we propose a method suitable for calculating the region wise absorption in the reaction process. In this process, we model the potential as a number of small rectangular parts. Using the exact wave functions and the boundary conditions in between the neighboring rectangular parts, we obtain the expression of the scattering matrix (S-matrix). Using the S-matrix value, we can obtain the absorption cross section in each $ i^{{\rm th}} $ radial interval. Calculating the absorption for all the rectangular parts using the above method throughout the potential, we can find the total reaction cross section$ \sigma_(r) $ by taking their sum. However, the sum over a limited region$ 0<r< R_{{\rm fus}} $ within the radial position$ R_{B} $ of the Coulomb barrier represents the value of fusion cross section$ \sigma_{{\rm fus}} $ . The variation of$ \sigma_{{\rm fus}} $ with bombarding center of mass energy${ E}_{{\rm c.m.}}$ is a smoothly varying curve without any structure information. Nevertheless, the barrier distribution function$D(E_{{\rm c.m.}})=\dfrac{{\rm d}^{2}(E_{{\rm c.m.}}\sigma_{{\rm fus}})}{{\rm d}E_{{\rm c.m.}}^{2}}$ shows peculiar oscillatory structure in its variation with the center of mass energy${ E}_{{\rm c.m.}}$ , thereby generating resonance states. The theoretical results of$\sigma_{{\rm fus}}$ and$D(E_{{\rm c.m.}})$ of our system, i.e.,$\rm ^{16}O+^{92}Zr$ , were compared with the corresponding experimental results [6]. Interestingly, we successfully explain the peak structure in Sec. III.C. The selected potential shows two significant characteristics: (i) a very deep real part with a small diffuseness, which is useful for explaining the effect of coupling, and (ii) a weak imaginary part, which indicates a less absorptive nature of the potential. This nature is useful for explaining the (experimentally unobserved) [7] shape resonance states. These resonances are the cause for the oscillatory structure in the variation of$D(E_{{\rm c.m.}})$ as a function of${E}_{{\rm c.m.}}$ . There is a special interest to study the fusion cross section for the collision of one nucleus with a given element along isotopic chains. In this study, we investigated the isotopic dependence of fusion probabilities for oxygen nuclei and$\rm ^{92}Zr$ . We also investigated the dependence of the fusion cross section by the addition or removal of neutrons from the projectile nucleus. These reactions provide knowledge regarding the possibilities of synthesis of new neutron rich nuclei. The isotopic study of fusion probability was conducted based on the N/Z ratio of the compound nuclei.Section II contains the theoretical formulation for the analytical expression of the S-matrix and region-wise absorption. Section III contains the analysis of experimental data of
$\dfrac{{\rm d}\sigma{(\theta)}}{{\rm d}\sigma_{R}(\theta)}$ ,$ \sigma_{{\rm fus}}(E_{{\rm c.m.}}) $ , and$ D(E_{{\rm c.m.}}) $ for the$\rm ^{16}O+^{92}Zr$ system. The results are summarized in Sec. IV. -
A smoothly varying potential U(r) can be considered as a chain of "n" number of rectangular potentials, each having an arbitrarily small width "w." Simulating the potential up to a maximum range
$r=R_{{\rm max}}$ , we have$R_{{\rm max}}=\Sigma_i^nw_i$ , where$ w_i=w $ is the width of the ith rectangle. Let us consider the jth region,$ \Sigma_{i=1}^{j-1}w_i<r\leq\Sigma_{i=1}^jw_i $ , in which the strength and width of the potential are denoted by$ U_j $ and$ w_j $ , respectively. The reduced Schrödinger equation in this region is$ \begin{equation} \frac{{\rm d}^2 \Phi (r)}{{\rm d}r^2}+\frac{2m}{\hbar^2}(E-U_j)\Phi (r)=0, \end{equation} $

(1) with solution
$ \begin{equation} \Phi_j (r)=a_j {\rm e}^{{\rm i}k_j r}+b_j{\rm e}^{-{\rm i}k_jr}, \end{equation} $

(2) where the wave number
$ k_j $ is defined as$k_j= $ $ \sqrt{\dfrac{2m}{\hbar^2}(E-U_j)}$ for the j-th segment of width$ w_j $ . Here, E indicates incident energy and m denotes the mass of the particle. Using the exact Coulomb wave function, i.e.,$ G_l $ and$ F_l $ , and their derivatives in the outer region$r\geq R_{{\rm max}}$ and the wave function$ \Phi_n(r) $ and its derivative in the left side of$r=R_{{\rm max}}$ , and matching them at$r=R_{{\rm max}}$ , we obtain the expression for the partial wave S-matrix:$ \eta_{\ell} $ as$ \begin{equation} \eta_{\ell}=2{\rm i}C_{\ell}+1, \end{equation} $

(3) $ \begin{equation} C_{\ell}=\frac{kF_{\ell}^{\prime}-F_{\ell} H}{H(G_{\ell}+{\rm i}F_{\ell}) -k(G_{\ell}^\prime+{\rm i}F_{\ell}^{\prime})}, \end{equation} $

(4) $ \begin{equation} H =\frac{\Phi_n^\prime}{\Phi_n}= {\rm i}k_n\;\frac{D^{(\ell)}\;{\rm e}^{{\rm i}k_nR_{max}}-{\rm e}^{-{\rm i}k_nR_{{\rm max}}}} {D^{(\ell)}\;{\rm e}^{{\rm i}k_nR_{{\rm max}}}+{\rm e}^{-{\rm i}k_nR_{{\rm max}}}}, \end{equation} $

(5) $ \begin{aligned}[b] D^{(\ell)}=&\frac{a_n}{b_n}=q_{n,n-1,n-2,\cdots 1}\\ =&\frac{q_{n,n-1}+q_{n-1,n-2,\cdots 1}{\rm e}^{2{\rm i}k_{n-1}w_{n-1}}} {1+q_{n,n-1}\times q_{n-1,n-2,\cdots 1}{\rm e}^{2{\rm i}k_{n-1}w_{n-1}}}, \end{aligned} $

(6) with
$ q_{21} $ = –1. We use the notation$ q_{ji}=-q_{ij}=\dfrac{k_j-k_i}{k_j+k_i} $ . Using the above expression (3) for$ \eta_{\ell} $ , we can explain the elastic scattering of the$ ^{16} $ O+$ ^{92} $ Zr system. For the total reaction cross section, the following formula can be used:$ \begin{equation} \sigma_{r}=\frac{\pi}{k^2}\sum\limits_{\ell}(2\ell+1)(1-|\eta_\ell|^2). \end{equation} $

(7) This is equal to the absorption cross section:
$ \begin{equation} \sigma_{{\rm abs}}=\frac{\pi}{k^2}\sum\limits_{\ell} (2\ell +1) \left(1-\frac{\mid a_n \mid ^2} {\mid b_n \mid ^2}\right) =\frac{\pi}{k^2}\sum\limits_{\ell}(2\ell +1)\left(\sum\limits_{j=1}^{n}I_j^{(\ell)}\right). \end{equation} $

(8) Taking the complex conjugate of the Schrödinger Eq. (1) and rearranging, we have
$ \begin{equation} 1-\frac{\mid a_n \mid ^2}{\mid b_n \mid ^2}=I_1+I_2+\cdots , \end{equation} $

(9) Simplifying the corresponding integral:
$ \begin{aligned}[b] I_j=&\left(-\frac{1}{k_n}\right)\frac{{\rm Im} U_j}{\mid b_n \mid^2}\Bigg[\frac{\mid b_j \mid^2}{2{\rm Im} k_j} {\rm e}^{-2{\rm Im} k_j\;w_{j-1}} ({\rm e}^{2{\rm Im} k_j\;w_j}-1)\\& -\frac{\mid b_j \mid^2}{2{\rm Im} k_j}{\rm e}^{2{\rm Im} k_j\;w_{j-1}} ({\rm e}^{-2{\rm Im} k_j\;w_j}-1)\\& +\frac{1}{{\rm Re} k_j}{\rm Im} \Big{(}a_jb_j^{\ast} {\rm e}^{2{\rm Im} k_j\;w_{j-1}}({\rm e}^{2i{\rm Re} k_j\;w_j}-1)\Big{)}\Bigg]. \end{aligned} $

(10) The symbol * indicates the complex conjugate of the respective quantity. The problem of higher partial wave can be treated as scattering by the effective potential
$ V_N(r)+V_{\rm C}(r)+V_{\ell}(r) $ , and one can adopt the MP approximation method described above for this effective potential. The contribution to the absorption or reaction cross section from any part within the range$ 0-R_{{\rm max}} $ can be obtained by considering the corresponding number of segments in the above summation. This is the unambiguous calculation of region-wise absorption in the collision process with no disturbance of potential and hence the wave function explains the angular distribution of elastic-scattering data. If one wishes to obtain the amount of absorption cross section in the region$ 0<r<R_{{\rm fus}} $ , where$ R_{{\rm fus}}<R_{{\rm max}} $ , the total number of segments to be considered in the summation (9) is$ n_{{\rm fus}}=\dfrac{R_{{\rm fus}}}{w} $ . The resulting cross section$ \begin{equation} \sigma_{{\rm fus}}= \frac{\pi}{k^2}\sum\limits_{\ell}(2\ell +1)\left(\sum\limits_{j=1}^{n_{{\rm fus}}}I_j^{(\ell)}\right) \end{equation} $

(11) corresponds to the fusion cross section in the framework of the direct reaction model (DRM) proposed by Udagawa et al. [8].
This multi-step (MP) approach is the simplest computation to the solution of the differential equation as compared to the well-accepted method explained in Refs. [9–21]. The advantage and significance of this method are reported in previous studies of ours, Refs. [3, 22]. However, note that the way of transparency to estimate the contribution of absorption in each part of the effective potential with this MP method is highly popular. This is why we use the MP method instead of the most successful Runge-Kutta method [23], which requires re-normalization of the wave function at different stages of the phase shift calculations [24]. To examine the feasibility and pertinence of this MP method, we studied both scattering and fusion phenomena of
$ ^{16} $ O+$ ^{92} $ Zr systems simultaneously and also applied the same to the isotopes of the projectile. Thus, the results calculated in this study can be useful for future experimental studies in heavy-ion collisions. -
The formulation developed in the above section is applied to the
$ ^{16} $ O+$ ^{92} $ Zr system to analyze the collision data and obtain a unified and consistent description and measurement of elastic scattering and fusion cross section. The value of$\sigma_{{\rm fus}}$ was calculated not only for the$ ^{16} $ O+$ ^{92} $ Zr reaction but also for$ ^{18, 20} $ O+$ ^{92} $ Zr reactions using the same potential. The formulation was also applied to study the peculiar peak structure in the variation of the barrier distribution function$D(E_{{\rm c.m.}})$ as a function of$E_{{\rm c.m.}}$ . According to optical model potential (OMP) analysis of scattering, the potential that describes the scattering of nuclei of mass number$ A_{1} $ and$ A_{2} $ and atomic number$ Z_{1} $ and$ Z_{2} $ is given by$V(r) = V_{N}f(r,R_{V}, a_{V})-{\rm i}W g(r,R_{W}, a_{W})+V_{\rm C}(r)$ in the entrance channel.The form factor used in this study is
$ f(r, R, a) = g(r, R, a)= \left[1+\exp{\dfrac{(r-R)}{a}}\right]^{-1} V_{N} $ , and W is the strength of the real and imaginary parts of the OMP. The radius parameters are expressed as$ r_{V}=\dfrac{R_{V}}{A_{1}^{1/3}+A_{2}^{1/3}} $ and$ r_{W}=\dfrac{R_{W}}{A_{1}^{1/3}+A_{2}^{1/3}} $ , where$ a_{V} $ and$ a_{W} $ represent diffuseness parameters. The Coulomb potential$V_{\rm C}(r)$ is given by$V_{\rm C}(r)=Z_{1}Z_{2}{\rm e}^{2}\left(3-\dfrac{r^{2}}{R_{\rm C}^{2}}\right)$ :$ r < < R_{\rm C} V_{\rm C}(r)=Z_{1}Z_{2}\dfrac{{\rm e}^{2}}{r} $ :$r > R_{\rm C}$ , where$R_{\rm C}=r_{\rm C}(A_{1}^{\frac{1}{3}}+A_{2}^{\frac{1}{3}})$ , and$r_{\rm C}$ represents the Coulomb radius parameter. The optical potential we adopted was in the form of the DRM [8], and the radius parameter was the same as that of Eq. (7b) reported in Ref. [8] and by Moore et al. [9]. Note that there are many optical potential parameter sets to explain scattering and fusion phenomena, but they are energy dependent. A few of them can be found in Refs. [6, 10–18]. Particularly, in page number 10 of Ref. [10], the authors clearly conclude that "the potential is essentially energy dependent," which further increases the importance of the present study, in which we found an energy independent parameter set. There are a total of seven parameters, namely$ V_N $ ,$ r_V $ ,$ a_V $ , W,$ r_W $ ,$ a_W $ , and$r_{\rm C}$ , in this OMP. -
Despite the existence of several parameters to describe the potential as well as angular distribution of elastic scattering, we selected the aforementioned seven parameters, which are energy independent. We also gave importance to the complex nature of the potential, with a deep real part [25, 26] featuring less diffuseness and a weak imaginary part.
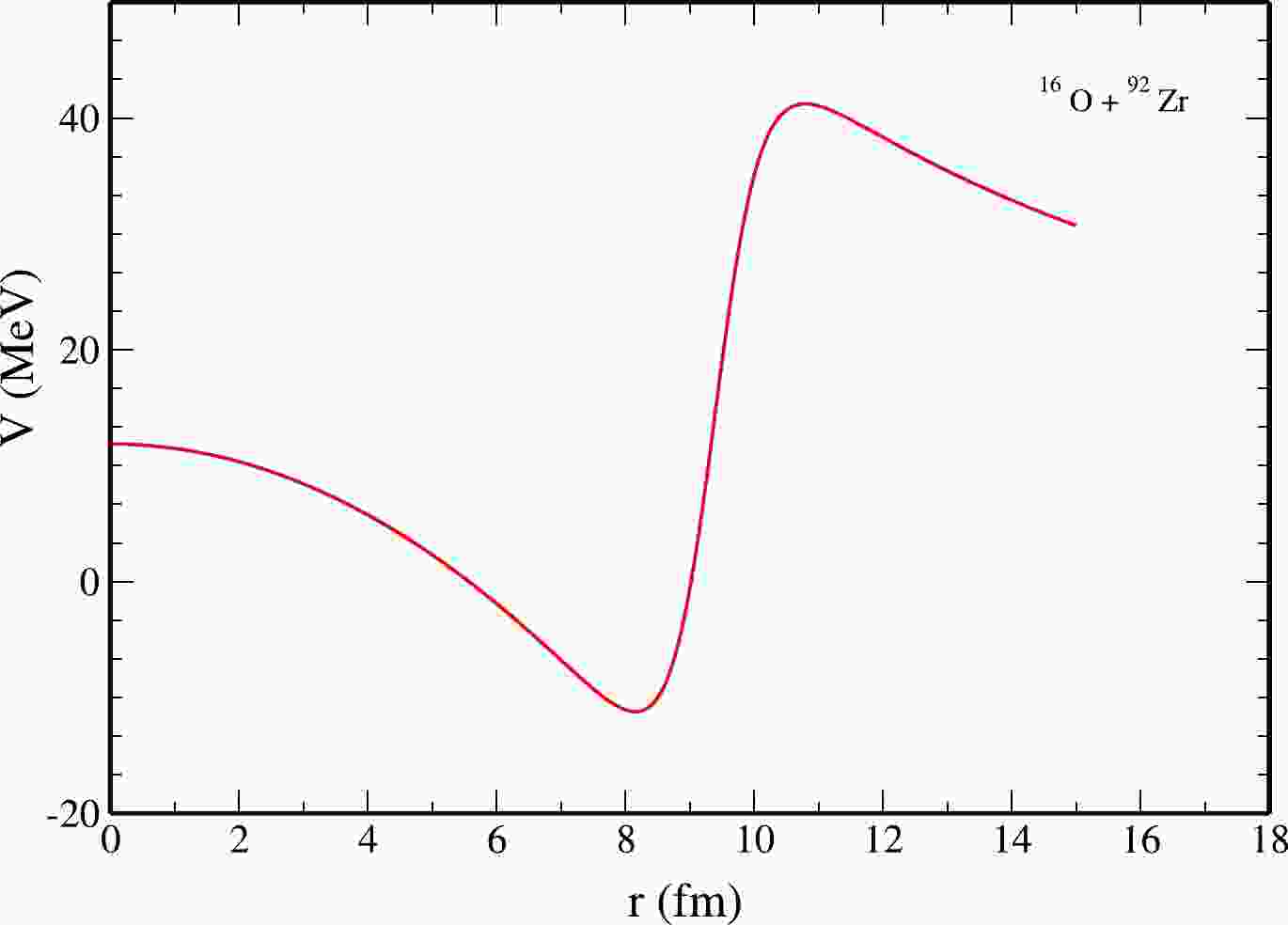
For the
$ ^{16} $ O+$ ^{92} $ Zr system, the real part is made deep with depth$V_{N}=-70.0\:\:\: {\rm MeV}$ and less diffused with the diffuseness parameter$a_{V}=0.367\:\:\: {\rm fm}$ ; moreover,$r_{V}= 1.337~ {\rm fm}$ , the Coulomb radius parameter$r_{\rm C}=1.2\:\:\: {\rm fm}$ , and the shallow imaginary potential of strength W = 4.0 MeV. Other parameters are$ r_{W}=1.35\:\:\: {\rm fm} $ and$ a_{W}=0.15\:\:\: {\rm fm} $ . The variation of the real part of the combined nuclear and the Coulomb potentials for the s-wave as a function of radial distance are shown in Fig. 1. Note that there can be several sets of parameters that explain elastic scattering and fusion cross section individually. All the seven parameters we found are energy independent, noting that the resonance should be manifested if and only if the imaginary part W is weak. Furthermore, such a weak absorption is sufficient if the real part is considered deep and less diffused. The value of the Coulomb radius parameter is taken as 1.2 fm, is a bit lower than the usual value$ r_{\rm C} $ = 1.25 fm. This does not affect the results of the elastic-scattering cross section in our calculations. When we explain the experimental data of fusion cross section at higher energy, we need to increase the$ r_{\rm C} $ value, which is equivalent to incorporate indirectly the energy dependence for the total potential. However, we focused on the unified description of elastic and fusion cross section calculation in$ ^{16} $ O+$ ^{92} $ Zr system. Note here that, for the analysis of both elastic and fusion cross sections, we used smaller values for diffuseness parameter$ a_V $ . The resulting sharply falling potential in the interior side of the Coulomb barrier depicted in Fig. 1 is found to be crucial in explaining the elastic-scattering cross sections in an energy-independent way. If the value of$ a_V $ in a given system is increased to fit the fusion cross-section$\sigma_{{\rm fus}}$ data, we have to further decrease the value of fusion radius parameter$R_{{\rm fus}}$ , which would force us to be energy dependent.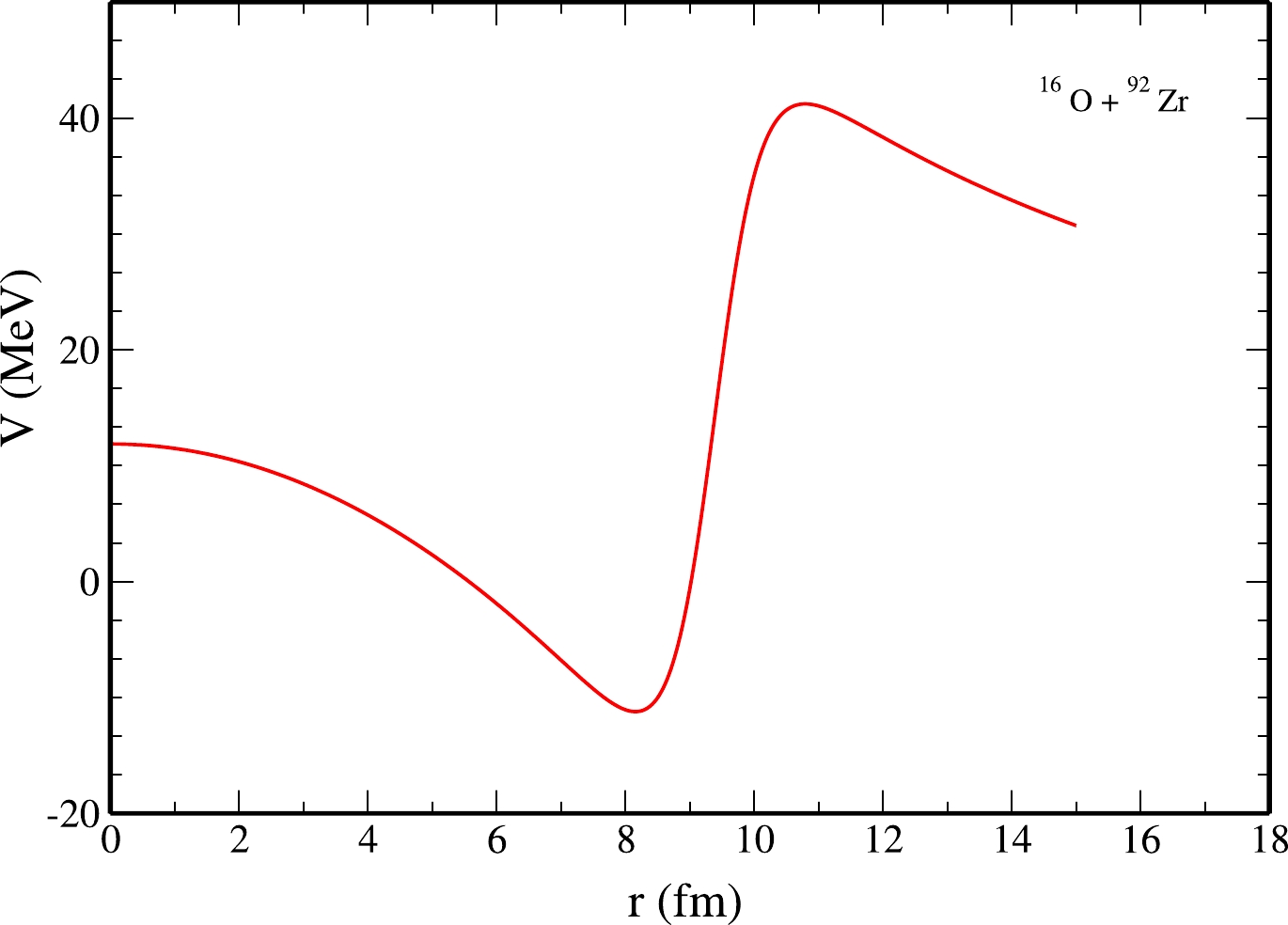
Figure 1. (color online) Plot of the real part of nuclear plus Coulomb potentials for partial wave l = 0 as a function of radial distance.
A sharp fall of the repulsive barrier in the interior side of position
$ R_{B}=10.80\:\:\: {\rm fm} $ and from a height of$ V_{B}=41.13\:\:\: {\rm MeV} $ is shown in Table 1. In the region of$ 0<r<R_{{\rm max}} $ , the effective potential is a combination of nuclear, Coulombic, and centrifugal terms, and it is taken as a combination of n rectangular parts each of width w; however, at$ r > R_{{\rm max}} $ , the potential is no longer a combination of all three potentials. On the contrary, it is only the result of combining the Coulombic potential along with the centrifugal term. Using the partial wave S-matrix$ \eta_\ell $ given by Eq. (3) in Sec. II, results of angular variation for differential scattering cross section at laboratory energies of 56, 48, 47, 46, and 45 MeV are obtained. The results are shown as solid curves in Fig. 2.System $V_{N}/{\rm MeV}$ 

$r_{V}/{\rm fm}$ 

$a_{V}/{\rm fm}$ 

W /MeV $r_{W}/{\rm fm}$ 

$a_{W}/{\rm fm}$ 

$r_{\rm C}/{\rm fm}$ 

$V_{B}/{\rm MeV}$ 

$R_{B}/{\rm fm}$ 

$R_{{\rm fus}}/{\rm fm}$ 

$\rm ^{16}O+^{92}Zr$ 

−70.0 1.337 0.367 4.0 1.35 0.15 1.2 41.13 10.80 8.4 $\rm ^{18}O+^{92}Zr$ 

−70.0 1.355 0.367 4.0 1.35 0.15 1.2 40.10 11.10 8.4 $\rm ^{20}O+^{92}Zr$ 

−70.0 1.373 0.367 4.0 1.35 0.15 1.2 39.17 11.37 8.4 Table 1. Optical model potential parameters used in the calculations.
$ V_{B} $ and$ R_{B} $ represent height and radial position of the Coulomb barrier, respectively.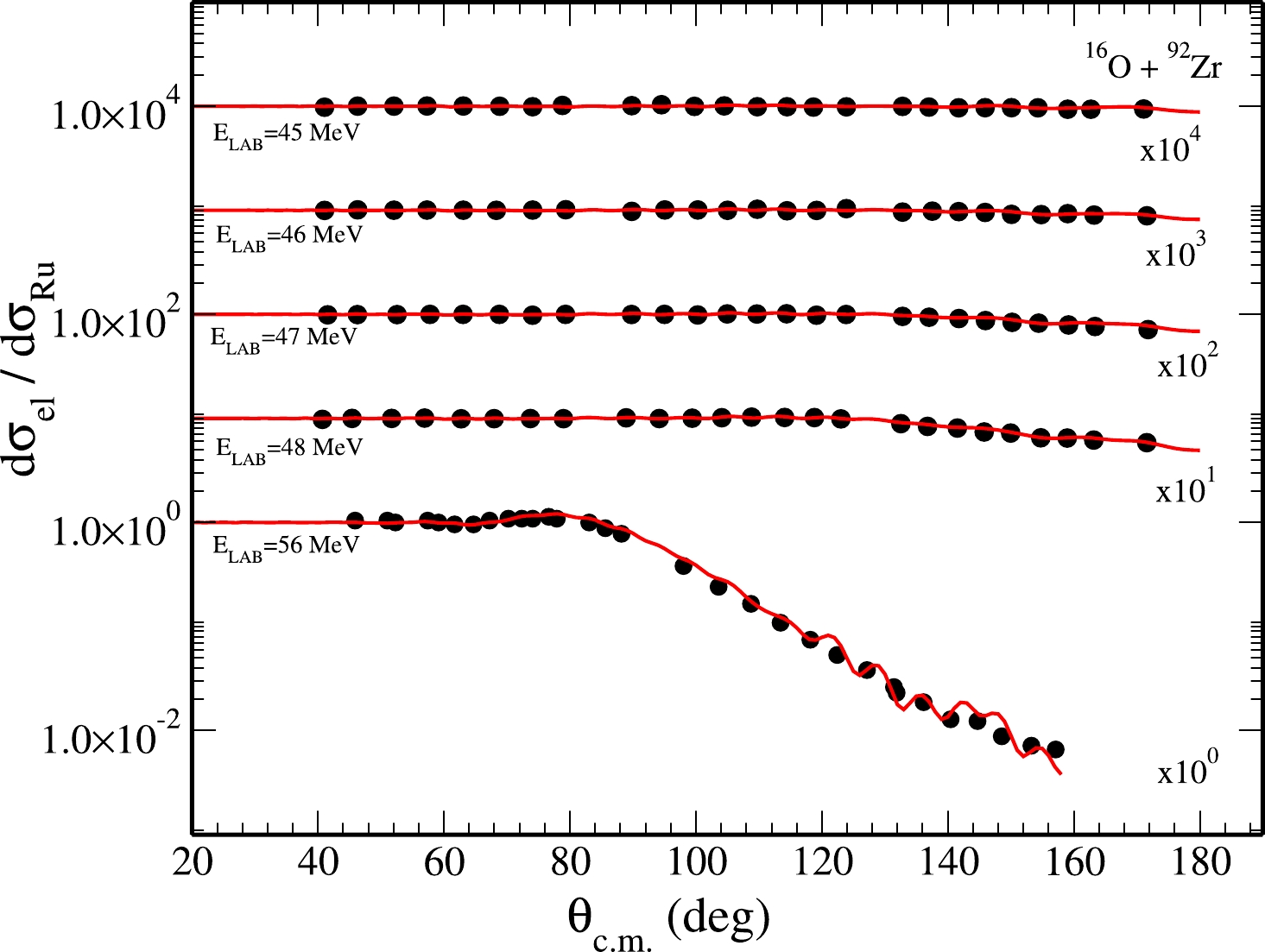
Figure 2. (color online) Angular distribution of elastic scattering cross section (ratio to Rutherford) of the
$\rm^{16}O+^{92}Zr$ system at different laboratory energies. The full drawn curves are theoretical results of present optical model calculation. The circles indicate the experimental cross sections extracted from Refs. [ 27, 28].The solid dots represent experimental data taken from Refs. [27, 28]. The theoretical calculations show a remarkable agreement with the experimental data. We used the same set of OMP parameters shown in Table 1. Given that the OMP parameters are energy independent, the same set of OMP parameters mentioned in Table 1 were used to explain the angular distribution of elastic scattering cross section for energy range between 45 to 56 MeV. The value of
$r_{\rm C}$ was set as 1.2 fm, which is slightly less than the usual$r_{\rm C}$ value. Still, the elastic scattering cross section remains unaffected in terms of the potential of weakly bound nuclei. -
As a result of studying scattering and fusion cross sections simultaneously in low energy collision process, we extracted the fusion cross section
$ \sigma_{{\rm fus}} $ from the total reaction cross section$ \sigma_{r} $ . Note that it is extremely difficult to extract the part from$ \sigma_{r} $ to exactly account for the measured results of$ \sigma_{{\rm fus}} $ at various incident energies over a wide range. To overcome this difficulty, we adopted the region wise absorption method mentioned in the DRM by Udagawa et al. [ 8]. Here, the radius$ R_{{\rm fus}} $ is less than$ R_{B} $ , and$ R_{B} $ is known as the radial position of the s-wave Coulomb barrier for a given nucleus-nucleus system. The value of$ \sigma_{{\rm fus}} $ is calculated using Eq. (11) and the aforementioned DRM principle. The results are shown in Figs. 3 and 5.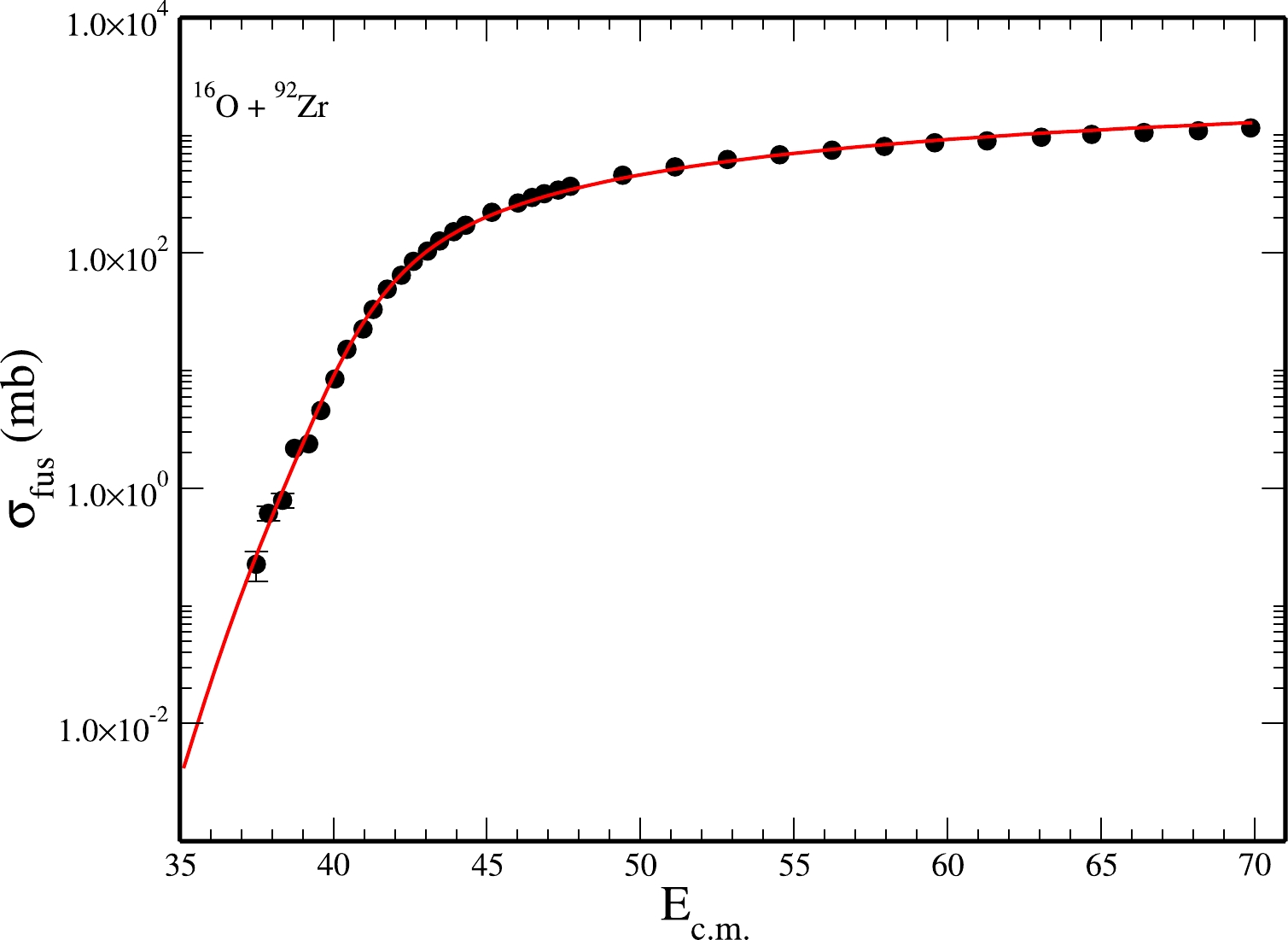
Figure 3. (color online) Variation of
$\sigma_{{\rm fus}}$ as a function of${E}_{{\rm c.m.}}$ for the$\rm ^{16}O+^{92}Zr$ system. The full drawn curves represent calculated results. The experimental data shown by solid dots are obtained from [6].
Figure 5. (color online) Variation of
$\sigma_{{\rm fus}}$ as a function of${E}_{{\rm c.m.}}$ for the$^{16, 18, 20}$ O+$^{92}$ Zr system. The full drawn curves represent calculated results. The experimental data shown by solid dots are obtained from Ref. [ 6].Using
$ R_{{\rm fus}}=8.4\;{\rm{fm}} $ , we obtain the results of$ \sigma_{{\rm fus}} $ for the$\rm ^{16}O+^{92}Zr$ system and compare it (solid curve) in Fig. 3 with the experimental data (solid dots) from Ref. [6]. The data show a very well agreement with the experimental measurements. The values of the parameters of the OMP are the same as those used to explain the elastic scattering data. The values of$ R_{{\rm fus}}=8.4\;{\rm{fm}} $ is less than the value of the Coulomb radius$R_{B}=10.80\:\:\: {\rm fm}$ because fusion is an interior phenomenon.Given that scattering is a surface phenomenon, similar values for different parameters of the Wood-Saxon potential are obtained. However, being an interior phenomena fusion cross-section, it will be different for different potential parameters. This is because the depth and slope in the interior of the effective potential as well as the value of
$ R_{{\rm fus}} $ is different for different sets of parameters, unlike the height$ V_{B} $ and radial position$ R_{B} $ of the Coulomb barrier. They have the same value, fixed for all sets of potential parameters. Thus, to describe these two phenomena simultaneously, we chose energy independent parameters. We also set a single potential to describe both elastic and fusion cross sections. This energy independent nature of$ R_{{\rm fus}} $ assists in calculating the barrier distribution function, which is the energy derivative of$ E_{{\rm c.m.}}\sigma_{{\rm fus}} $ .Fusion cross-section also depends upon the strength of the imaginary part W. A greater value of W results in a decrease in the amplitude of the wave function in the interior, which requires a larger value of
$ R_{{\rm fus}} $ to account for the experimental data of the fusion cross-section$ \sigma_{{\rm fus}} $ . However, with a comparatively small W,$ R_{{\rm fus}} $ is small when it comes to matching the$ \sigma_{{\rm fus}} $ data.Along with the imaginary strength, fusion cross-section also depends on the diffuseness parameter
$ a_{V} $ . With an increase in$ a_{V} $ ,$ R_{{\rm fus}} $ has to be decreased to obtain suitable data for$ \sigma_{{\rm fus}} $ . Thus, we set a smaller value for the diffuseness parameter$ a_{V} $ , as shown in Table 1 for the OMP, to analyze both elastic scattering and fusion cross sections. The sharply falling potential in the interior side of the Coulomb barrier shown in Fig. 1 is a key feature for describing the elastic scattering cross section in an energy independent way.The method of region wise absorption used in our calculations while extracting
$ \sigma_{{\rm fus}} $ is a unique method for explaining fusion reaction. However, to overcome the energy dependent nature of the imaginary part, we set a very strong real part of the nuclear potential so that the results of elastic scattering and fusion were not affected. The experimental results of$ \sigma_{{\rm fus}} $ [6] are shown as solid dots in Fig. 3, whereas our results are shown as a solid curve in the same figure. We set$ R_{{\rm fus}}=8.4\;{\rm{fm}} $ , which is less than$ R_{B}= $ 10.80 fm for a barrier height$V_{B}=41.13~ {\rm MeV}$ . To achieve this, we changed the value of$ r_{V} $ from 1.337 fm to 1.334 fm. In this study, we mainly focused on the unified description of an elastic-scattering cross section and fusion cross section$ \sigma_{{\rm fus}} $ as well as the results of$D(E_{{\rm c.m.}})= \dfrac{{\rm d}^{2}(E_{{\rm c.m.}} \sigma_{{\rm fus}})}{{\rm d}E_{{\rm c.m.}}^{2}}$ in the lower energy region covering near and sub barrier energies around the Coulomb barrier. Moreover, we chose energy independent parameters for our potential because a fusion reaction channel is prominent among all reaction channels in the lower energy region. Thus, for the simultaneous explanation of fusion and scattering by a unique potential, we needed an energy-independent potential along with the structure information in heavy ion collision processes. This potential helps us in explaining the oscillatory structure of the barrier distribution function$D(E_{{\rm c.m.}})= \dfrac{{\rm d}^{2}(E_{{\rm c.m.}} \sigma_{{\rm fus}})}{{\rm d}E_{{\rm c.m.}}^{2}}$ -
The variation of
$ \sigma_{{\rm fus}} $ as a function of${E}_{{\rm c.m.}}$ depicted in Fig. 3 does not exhibit any structure. The smooth curve of$ \sigma_{{\rm fus}} $ as a function of${E}_{{\rm c.m.}}$ is shown in Fig. 3; it cannot provide any idea about the experimental peculiarities that might have been taking place during fusion. To attain some insight, we studied$ \sigma_{{\rm fus}} $ in a different form: the barrier distribution function was set equal to$ D(E_{{\rm c.m.}})=\dfrac{{\rm d}^{2}(E_{{\rm c.m.}} \sigma_{{\rm fus}})}{{\rm d}E_{{\rm c.m.}}^{2}} $ .The variation of
$ D(E_{{\rm c.m.}}) $ as a function of${E}_{{\rm c.m.}}$ shows some oscillatory structure (see Fig. 4). To calculate$ D(E_{{\rm c.m.}}) $ , we used the following point difference formula: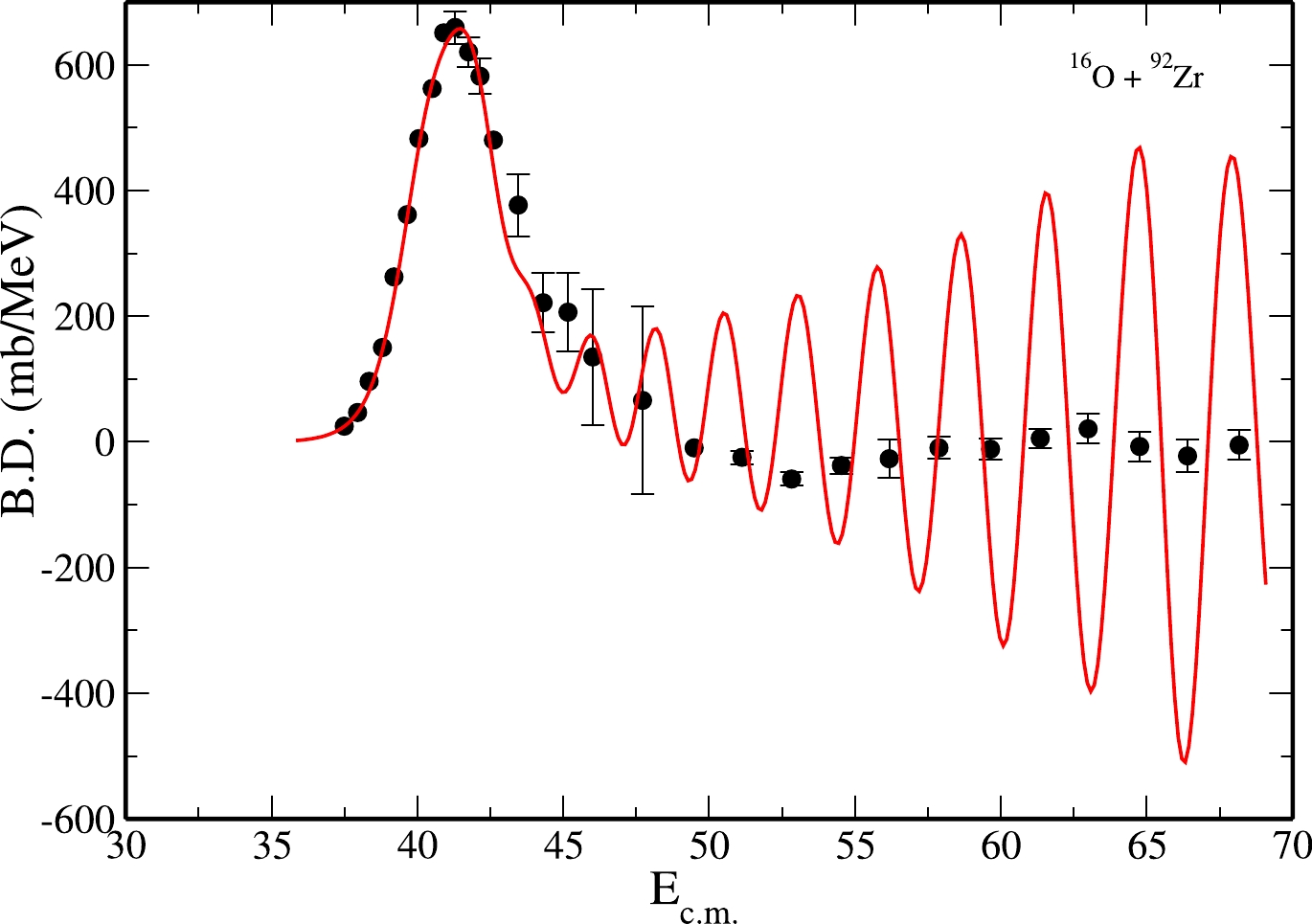
Figure 4. (color online) Variation of
$D(E_{{\rm c.m.}})=\frac{{\rm d}^{2}(E_{{\rm c.m.}}\sigma_{{\rm fus}})}{{\rm d}E_{{\rm c.m.}}^{2}}$ as a function of energy$E_{\rm c.m.}$ . The full curves represent our calculated results. The experimental data shown by solid dots were extracted from Ref. [ 6].$ \begin{align} D(E)=\frac{[(E-\Delta{E})\sigma_--2E\sigma +(E+\Delta{E})\sigma_+]}{(\Delta {E})^{2}}, \end{align} $

(12) where
$ \sigma_{-} $ , σ, and$ \sigma_{+} $ denote the fusion cross section$ \sigma_{{\rm fus}} $ at center of mass energies$ E-\Delta{E} $ , E, and$ E+\Delta{E} $ , respectively, with energy gap$ \Delta{E} $ . The experimental results for$ D(E_{{\rm c.m.}}) $ as a function of${E}_{{\rm c.m.}}.$ for the$ ^{16} $ O+$ ^{92} $ Zr system were extracted from Ref. [6]. They are shown as solid dots, whereas the theoretically calculated results are shown as solid curves in Fig. 4.The solid curve shows a main peak and some smaller oscillatory structures. The theoretical and experimental structures clearly match for our
$ ^{16} $ O+$ ^{92} $ Zr system. They show very good agreement, especially in the lower energy region. In the higher energy region, the plot of barrier distribution with incident energy shows some deeps of negative nature which are accounted for quite well.However, the oscillatory structure vanishes when the strength of the imaginary part W or the step size
$ \Delta{E} $ in Eq. (12) is increased. A larger value of Coulomb radius$r_{\rm C}$ also destroys the oscillatory structures of the barrier distribution function$ D(E_{{\rm c.m.}}) $ . The values of W and$r_{\rm C}$ were fixed according to the accurate explanation of measured results for$ \sigma_{{\rm fus}} $ and$ D(E_{{\rm c.m.}}) $ . The value of$ r_{c} $ was 1.2 fm and that of W was 4.0 MeV to match the measured data of$ D(E_{{\rm c.m.}}) $ well along with the$\sigma_{\rm fus}$ data shown in Fig. 3 and Fig. 4, respectively. The peak structures are related to the theory of such a physical phenomenon taking place in the process of fusion of two nuclei within the region where the imaginary part is actively present. The nature of potential is very important in explaining the oscillatory structures of$ D(E_{{\rm c.m.}}) $ . A potential having a deep pocket followed by a thick barrier gives rise to resonance states that remain experimentally unobserved [7]. Here, these resonances are observed as the peaks in reaction cross sections$ (\sigma_{r}) $ vs. incident energies${E}_{{\rm c.m.}}$ shown in Fig. 4. The shape of the pocket region is also controlled by the Coulomb radius parameter$r_{\rm C}$ . With a smaller value of$r_{\rm C}$ , we obtained a U-shaped pocket region that generated more oscillation in$ \sigma_{r} $ , leading to resonances. Each partial wave gives rise to a resonance structure. Thus, it is the cumulative effect of all these resonance structures that is primarily responsible for the oscillation in D(E$ _{{\rm c.m.}} $ ). The width of a resonance becomes large when the potential is more absorptive, which can be achieved by adding a larger imaginary part to the real part of the potential. The larger width of resonance leads to extinction of the corresponding resonance state in the collision process. However, the potential we choose to explain the fusion of$ ^{16} $ O+$ ^{92} $ Zr is characterized by a deep real part and weak imaginary strength capable of generating many resonances, which are clearly visible in the form of peaks in the variation of partial wave reaction cross section as a function of energy in different partial wave ($ \ell_s $ ) trajectories. Our calculations and Ref. [6] indicate that these oscillations play a critical role in fusion cross sections. From the above discussion, it may be speculated that the formation of a compound nucleus occurs through the fusion of two nuclei at low energy and is represented by shape resonances. -
So far, we have successfully explained various factors, such as the differential scattering cross section, fusion cross section, and barrier distribution as functions of center of mass energies (
${E}_{{\rm c.m.}}$ ) having the same potential and energy independent potential parameters. Next, we extend our study by analyzing the isotopic dependence of interacting potential and fusion cross section. We introduce two more isotopes such as$\rm ^{18, 20}O$ of oxygen. We consider the fusion reaction of these two isotopes of oxygen with$\rm ^{92}Zr$ to investigate the dependence of fusion probability on various factors. The isotopic study of fusion probability was conducted based on the$ N/Z $ ratio of the compound nuclei. We kept the same value for the$ R_{{\rm fus}} $ parameter to calculate$ \sigma_{{\rm fus}} $ for the$ ^{18, 20} $ O+$ ^{92} $ Zr systems as that used to calculate$ \sigma_{{\rm fus}} $ for the$ ^{16} $ O+$ ^{92} $ Zr reaction.Recently, Lin Gan Group [29] derived a linear relationship between Woods-Saxon parameters with the mass of projectile and target. We partially used the same relationship to study the isotopic effect in the sub barrier fusion cross section while keeping
$ R_{{\rm fus}} $ constant, as shown in Fig. 5. The results we obtained were successfully compared with the experimental results (represented as solid dots in the same figure) [ 6]. From these results, we found that, when the values of the radius parameter$ R_{V}=r_{V}{(A_{1}^{1/3}+A_{2}^{1/3})} $ for the respective$ ^{16, 18, 20} $ O+$ ^{92} $ Zr systems increase with the decrease in barrier height$ V_{B} $ , the fusion probability increases. Therefore, our study requires experimental verification, particularly in the sub-barrier region. -
We analytically solved the Schrödinger equation composed of an optical model potential to derive an expression for the scattering matrix (S-matrix), which further led us to calculate the region-wise absorption cross section to account for the reaction cross section. We applied this formulation to the
$\rm ^{16}O+^{92}Zr$ and$\rm ^{18, 20}O+^{92}Zr$ systems to study the isotopic dependence of fusion probability. Throughout the study, the parameters of the effective potential remained unchanged. The other experimental data that were analyzed consistently were (i) the angular variation of the differential scattering cross section at several energies around the Coulomb barrier, (ii) the fusion cross section$ \sigma_{{\rm fus}} $ as a function of the energy over a wide range covering the Coulomb barrier region, and (iii) the extracted result of the quantity$D(E_{{\rm c.m.}})=\dfrac{{\rm d}^{2}(E_{{\rm c.m.}}\sigma_{{\rm fus}})}{{\rm d}E^{2}_{{\rm c.m.}}}$ . Some important features we derived with the above analysis are as follows: (i) an energy independent complex nuclear potential in the Wood-Saxons form, with a large depth and small diffuseness in the real part and less absorption (weak strength) in the imaginary part, successfully explains elastic scattering data at several energies with great success; (ii) the calculation of the fusion cross section by the extraction of the parts of the reaction through the proposed region-wise absorption method is a natural process in the sense that we did not use any extra energy dependency in the process of extraction or arbitrarily partition the imaginary part; (iii) the peaks in the variation of the barrier distribution as a function of${E}_{{\rm c.m.}}$ in Fig. 4 are explained successfully by our calculated results of$ \sigma_{{\rm fus}} $ ; (iv) the oscillatory nature of the$ D(E_{{\rm c.m.}}) $ is simply represented as resonance states occurring during the collision of two nuclei, and these resonance states are allowed because of the less absorptive nature of the optical potential; and (v) with the addition/removal of neutrons, the fusion cross sections follow a linear dependence for all considered isotopic systems. Therefore, further research in the sub-barrier region is still needed.
Scattering and fusion reaction dynamics of O + Zr system around Coulomb barrier
- Received Date: 2022-07-12
- Available Online: 2022-12-15
Abstract: A partial wave scattering matrix for the total effective complex potential of nucleus nucleus collisions is proposed to easily analyze the angular variations of elastic scattering and fusion cross-sections simultaneously with a unique potential. The expectation value of the imaginary part of the potential calculated using the distorted waves from the full potential in the elastic channel accounts for





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: