-
In the expanding Universe, there are many ways of defining the distance between two objects. Among these, the luminosity distance and angular diameter distance are two widely used definitions. The former is defined by the fact that the brightness of a distant source viewed by an observer is inversely proportional to the distance squared, whereas the latter is defined by the fact that the angular size of an object viewed by an observer is inversely proportional to the distance. In the standard cosmological model, the luminosity distance (
$ D_L $ ) is related to the angular diameter distance ($ D_A $ ) by the distance duality relation (DDR), i.e.,$ D_L(z)=(1+z)^2D_A(z) $ [1], where z is the cosmic redshift. The DDR holds true as long as photons travel along null geodesics and the number of photons is conserved. The DDR is a fundamental and crucial relation in modern cosmology. Any violation of the DDR would imply the existence of new physics. Violation of the DDR could be caused by, e.g., the coupling of photons with non-standard particles [2], dust extinction [3], and the variation of fundamental constants [4]. Therefore, testing the validity of the DDR with different independent observations is of great importance.Owing to the difficulty in simultaneously measuring the luminosity distance and angular diameter distance of an object, the most common method of testing the DDR is comparing the two distances observed from different objects but at approximately the same redshift. Many studies have been devoted to testing the DDR with different observational data [5–13]. Type Ia supernovae (SNe Ia) are perfect standard candles and are widely used to measure the luminosity distance, while the angular diameter distance is usually obtained from various observations. For example, the angular diameter distance obtained from galaxy clusters can be combined with SNe Ia to test the DDR [5–7, 13]. Li et al. [9] tested the DDR using a combination of SNe Ia and ultra-compact radio sources. Liao et al. [8] proposed a model-independent method that applies strong gravitational lensing (SGL) systems and SNe Ia to test the DDR. However, owing to the redshift limitation of SNe Ia, SGL systems whose source redshift is larger than 1.4 cannot be used to test the DDR because no SNe can match these SGL systems at the same redshift. Hence, there were significantly fewer available data pairs than the total number of SGL systems. Lin et al. [10, 11] showed that the luminosity distance and angular diameter distance can be measured simultaneously from strongly lensed gravitational waves and hence can be used to test the DDR.
Recently, the newest and largest SNe Ia sample known as the Pantheon compilation was published, which consists of 1048 SNe Ia with the highest redshift of up to
$ z_{\rm max}\approx 2.3 $ [14]. Combining the Pantheon sample and 205 SGL systems, Zhou et al. [15] obtained 120 pairs of data points in the redshifts range from 0.11 to 2.16 and verified the DDR at a 1σ confidence level. Many methods have been proposed to extend the redshift range. Lin et al. [16] reconstructed the distance-redshift relation from the Pantheon sample with Gaussian processes (GP) and combined it with galaxy clusters + baryon acoustic oscillations to constrain the DDR. Their results verified the validity of the DDR. Ruan et al. [17] also confirmed the validity of the DDR in a redshift range up to$ z\sim2.33 $ based on SGL and the reconstruction of the HII galaxy Hubble diagram using GP. However, the reconstruction with GP is unreliable beyond the data region, and the uncertainty is large in the region where data points are sparse. Hence, not all SGL systems are available for DDR testing. To make use of the full SGL sample, Qin et al. [18] reconstructed the high-redshift quasar Hubble diagram using the B$ \acute{\rm e} $ zier parametric fit and combined it with 161 SGL systems to test the DDR up to the redshift$ z\sim3.6 $ . However, this method depends on the parametric form of the Hubble diagram. Several studies extended the luminosity distance to the redshift range of gamma-ray burst (GRBs) [19, 20]. By combining SNe Ia and high-redshift GRBs data ($ z\sim10 $ ) calibrated with the Amati relation, the DDR can be investigated up to a high redshift. In these studies, the Amati correlation used to calibrate GRBs was assumed to be universal over the entire redshift range. However, several studies indicated that the Amati relation possibly evolves with redshift [21–23].In this paper, we test the DDR by performing the deep learning method to reconstruct the luminosity distance. Deep learning is a type of machine learning based on artificial neural network research [24]. It is powerful in large-scale data processing and highly complex data fitting owing to the universal approximation theorem. Hence, deep learning can output a value infinitely approximating the target by training deep neural networks with observational data. Generally, a neural network is constructed with several layers; the first layer is the input layer for receiving the feature, several hidden layers are used for transforming the information from the previous layer, and the last layer is the output layer for exporting the target. In each layer, hundreds of nonlinear neurons process data information. The deep learning method has been widely employed in various fields, including cosmological research [12, 23, 25–28]. In this study, we test the DDR with the combined data of SNe Ia and SGL, while the luminosity distance is reconstructed from SNe Ia using deep learning. Compared with previous methods, such as GP and the B
$ \acute{\rm e} $ zier parametric fit, our method of reconstructing the data is neither cosmologically model-dependent nor relies on a specific parametric form. Additionally, deep learning can capture the internal relation in training data. In particular, deep learning can reconstruct the curve beyond the data range with a relatively small uncertainty. Thus, the full SGL sample can be used to test the DDR up to the highest redshift of SGL.The rest of this paper is organized as follows. In Sec. II, we introduce the method for testing the DDR with a combination of SGL and SNe Ia. In Sec. III, the observational data and deep learning method are introduced. In Sec. IV, the constraining results on the DDR are presented. Finally, the discussion and conclusion are given in Sec. V.
-
The most direct way to test the DDR is to compare the luminosity distance
$ D_L $ and angular diameter distance$ D_A $ at the same redshift. However, it is difficult to measure$ D_L $ and$ D_A $ simultaneously from a single object. Generally,$ D_L $ and$ D_A $ are obtained from different types of objects approximately at the same redshift. In our study, we determine$ D_L $ from SNe Ia and determine$ D_A $ from SGL systems. The details of the method are presented below.With an increasing number of galaxy-scale SGL systems being discovered in recent years, they are widely used to investigate gravity and cosmology. In the specific case in which the lens perfectly aligns with the source and observer, an Einstein ring appears. In the general case, only part of the ring appears, from which the radius of the Einstein ring can be deduced. The Einstein radius depends on not only the geometry of the lensing system but also the mass profile of the lens galaxy. To investigate the influence of the mass profile of the lens galaxy, we consider three types of lens models that are widely discussed in literature: the singular isothermal sphere (SIS) model, power-law (PL) model, and extended power-law (EPL) model.
In the SIS model, the mass density of the lens galaxy scales as
$ \rho\propto r^{-2} $ , and the Einstein radius takes the form [29]$ \begin{equation} \theta_{\rm E}=\frac{D_{A_{ls}}}{D_{A_s}}\frac{4\pi\sigma^2_{\rm{SIS}}}{{\rm c}^2}, \end{equation} $

(1) where c is the speed of light in vacuum,
$ \sigma_{\rm SIS} $ is the velocity dispersion of the lens galaxy,$ D_{A_s} $ and$ D_{A_{ls}} $ are the angular diameter distances between the observer and the source and between the lens and the source, respectively. From Eq. (1), we see that the Einstein radius depends on the distance ratio$ R_A\equiv D_{A_{ls}}/D_{A_s} $ , which can be obtained from the observables$ \theta_{\rm E} $ and$ \sigma_{\rm SIS} $ using$ \begin{equation} R_A=\frac{{\rm c}^2\theta_{\rm{E}}}{4\pi\sigma^2_{\rm{SIS}}}. \end{equation} $

(2) Note that it is not necessary for
$ \sigma_{\rm{SIS}} $ to be equal to the observed stellar velocity dispersion$ \sigma_0 $ [30]. Thus, we phenomenologically introduce the parameter f to account for the difference, i.e.,$ \sigma_{\rm{SIS}}=f\sigma_0 $ [31–33]. Here, f is a free parameter that is expected to be in the range$ 0.8<f^2<1.2 $ . The actual SGL data usually measure the velocity dispersion within the aperture radius$ \theta_{\rm ap} $ , which can be transformed to$ \sigma_0 $ according to the aperture correction formula [34]$ \begin{equation} \sigma_0=\sigma_{\rm ap}\left(\frac{\theta_{\rm{eff}}}{2\theta_{\rm{ap}}}\right)^{\eta}, \end{equation} $

(3) where
$ \sigma_{\rm ap} $ is the luminosity weighted average of the line-of-sight velocity dispersion inside the aperture radius,$ \theta_{\rm{eff}} $ is the effective angular radius, and η is the correction factor, which takes the value$ \eta=-0.066\pm0.035 $ [35, 36].$ \sigma_{\rm ap} $ propagates its uncertainty to$ \sigma_0 $ , and further to$ \sigma_{\rm SIS} $ . The uncertainty on the distance ratio$ R_A $ is propagated from that of$ \theta_{\rm E} $ and$ \sigma_{\rm SIS} $ . We take the fractional uncertainty on$ \theta_{\rm E} $ at the level of$5$ % [8].In the PL model, the mass density of the lensing galaxy follows the spherically symmetric PL distribution
$ \rho\propto r^{-\gamma} $ , where γ is the power-law index. In this model, the distance ratio can be written as [37]$ \begin{equation} R_A=\frac{{\rm c}^2\theta_{\rm{E}}}{4\pi\sigma^2_{\rm{ap}}}\left(\frac{\theta_{\rm ap}}{\theta_{\rm E}}\right)^{2-\gamma}f^{-1}(\gamma), \end{equation} $

(4) where
$ \begin{equation} f(\gamma)=-\frac{1}{\sqrt{\pi}}\frac{(5-2\gamma)(1-\gamma)}{3-\gamma}\frac{\Gamma(\gamma-1)}{\Gamma(\gamma-3/2)}\left[\frac{\Gamma(\gamma/2-1/2)}{\Gamma(\gamma/2)}\right]^2. \end{equation} $

(5) The PL model reduces to the SIS model when
$ \gamma=2 $ . Considering the possible redshift evolution of the mass density profile, we parameterize γ with the form$ \gamma(z_l)=\gamma_0+\gamma_1z_l $ , where$ \gamma_0 $ and$ \gamma_1 $ are two free parameters, and$ z_l $ is the redshift of the lens galaxy.In the EPL model, the luminosity density profile
$ \nu(r) $ is usually different from the total-mass density profile$ \rho(r) $ owing to the contribution of the dark matter halo. Therefore, we assume that the total mass density profile$ \rho(r) $ and the luminosity density of stars$ \nu(r) $ take the forms$ \begin{equation} \rho(r)=\rho_0\left(\frac{r}{r_0}\right)^{-\alpha}, \ \nu(r)=\nu_0\left(\frac{r}{r_0}\right)^{-\delta}, \end{equation} $

(6) respectively, where α and δ are the PL index parameters,
$ r_0 $ is the characteristic length scale, and$ \rho_0 $ and$ \nu_0 $ are two normalization constants. In this case, the distance ratio can be expressed as [38]$ \begin{equation} R_A=\frac{{\rm c}^2\theta_{\rm{E}}}{2\sigma_0^2\sqrt{\pi}}\frac{3-\delta}{(\xi-2\beta)(3-\xi)}\left(\frac{\theta_{\rm eff}}{\theta_{\rm E}}\right)^{2-\alpha}\left[\frac{\lambda(\xi)-\beta\lambda(\xi+2)}{\lambda(\alpha)\lambda(\delta)}\right], \end{equation} $

(7) where
$ \xi=\alpha+\delta-2 $ ,$ \lambda(x)=\Gamma(\frac{x-1}{2})/\Gamma(\frac{x}{2}) $ , and β is an anisotropy parameter characterizing the anisotropic distribution of the three-dimensional velocity dispersion, which is marginalized with the Gaussian prior$ \beta=0.18\pm0.13 $ [39]. We parameterize α with the form$ \alpha=\alpha_0+\alpha_1z_l $ to inspect the possible redshift-dependence of the lens mass profile and treat δ as a free parameter. When$ \alpha_0=\delta=2 $ and$ \alpha_1=\beta=0 $ , the EPL model reduces to the standard SIS model.In a flat Universe, the comoving distance is related to the angular diameter distance by
$ r_l=(1+z_l)D_{A_l} $ ,$ r_s=(1+z_s)D_{A_s} $ , and$ r_{ls}=(1+z_s)D_{A_{ls}} $ . Using the distance-sum rule$ r_{ls}=r_s-r_l $ [40], the distance ratio$ R_A $ can be expressed as$ \begin{equation} R_A=\frac{D_{A_{ls}}}{D_{A_s}}=1-\frac{(1+z_l)D_{A_l}}{(1+z_s)D_{A_s}}, \end{equation} $

(8) in which the ratio of
$ D_{A_l} $ and$ D_{A_s} $ can be converted to the ratio of$ D_{L_l} $ and$ D_{L_s} $ using the DDR.To test the possible violation of the DDR, we parameterize it with the form
$ \begin{equation} \frac{D_A(z)(1+z)^2}{D_L(z)}=1+\eta_0z, \end{equation} $

(9) where
$ \eta_0 $ is a parameter characterizing the deviation from the DDR. The standard DDR is the case in which$ \eta_0\equiv0 $ . Combining Eqs. (8) and (9), we obtain$ \begin{equation} R_A(z_l,z_s)=1-R_L P(\eta_0;z_l,z_s), \end{equation} $

(10) where
$ R_L\equiv D_{L_l}/D_{L_s} $ is the ratio of luminosity distance, and$ \begin{equation} P\equiv\frac{(1+z_s)(1+\eta_0z_l)}{(1+z_l)(1+\eta_0z_s)}. \end{equation} $

(11) The ratio of luminosity distance
$ R_L $ can be obtained from SNe Ia. At a certain redshift z, the distance modulus of SNe Ia is given by [14]$ \begin{equation} \mu=5\log_{10}\frac{D_L(z)}{ \rm{Mpc}}+25=m_B-M_B+\alpha x(z)-\beta c(z), \end{equation} $

(12) where
$ m_B $ is the apparent magnitude observed in the B-band,$ M_B $ is the absolute magnitude, x and c are the stretch and color parameters, respectively, and α and β are nuisance parameters. For the SNe Ia sample, we choose the largest and latest Pantheon dataset in the redshift range$ z\in[0.01,2.30] $ [14]. The Pantheon sample is well-calibrated by a new method known as BEAMS with Bias Corrections, and the effects of$ x(z) $ and$ c(z) $ have been corrected in the reported magnitude$ m_{B, \rm{corr}}=m_B+ \alpha x(z)-\beta c(z) $ . Thus, the nuisance parameters α and β are fixed at zero in Eq. (12), and$ m_B $ is replaced by the corrected magnitude$ m_{B, \rm corr} $ . For simplify, we use m to represent$ m_{B, \rm corr} $ hereafter. The distance ratio$ R_L $ can then be written as$ \begin{equation} R_L\equiv D_{L_l}/D_{L_s}=10^{\frac{m(z_l)-m(z_s)}{5}}, \end{equation} $

(13) where
$ m(z_l) $ and$ m(z_s) $ are the corrected apparent magnitudes of SNe Ia at redshifts$ z_l $ and$ z_s $ , respectively. As shown in the above equation, the absolute magnitude$ M_B $ exactly cancels out. The uncertainty on$ R_L $ propagates from the uncertainties on$ m(z_l) $ and$ m(z_s) $ using the standard error propagation formula.Combining SNe Ia and SGL, the parameter η can be constrained by maximizing the likelihood
$ \begin{equation} \mathcal{L}({\rm Data}|p,\eta_0)\propto\exp\left[-\frac{1}{2}\sum\limits_{i=1}^N\frac{\left(1-R_{L,i}P_i(\eta_0;z_l,z_s)-R_{A,i}\right)^2}{\sigma_{{\rm total},i}^2}\right], \end{equation} $

(14) where
$ \sigma_{\rm total}=\sqrt{\sigma_{R_A}^2+P^2\sigma_{R_L}^2} $ is the total uncertainty, and N is the total number of data points. There are two sets of parameters, that is, the parameter$ \eta_0 $ relating to the violation of the DDR, and the parameter p relating to the lens mass model ($ p=f $ in the SIS model,$ p=(\gamma_0,\gamma_1) $ in the PL model, and$ p=(\alpha_0,\alpha_1,\delta) $ in the EPL model). -
The SGL sample used in this study is compiled by Chen et al. [36], which contains 161 galaxy-scale SGL systems with both high resolution imaging and stellar dynamical data. All lens galaxies in the SGL sample are early-type galaxies and do not have significant substructures or close massive companions. Thus, the spherically symmetric approximation is valid when modelling the lens galaxy. The redshift of the lens ranges from 0.064 to 1.004, and that of the source ranges from 0.197 to 3.595. Hence, we can test the DDR up to
$ z\sim3.6 $ .In previous studies [5, 6, 8], SNe Ia located at the redshift
$ z_l $ and$ z_s $ in each SGL system were found by comparing the redshift difference$ \Delta z $ between the lens (source) and SNe Ia with the criterion$ \Delta z\leq0.005 $ . In this method, the SGL systems are under-utilized owing to the fact that there may be no SNe at the redshift$ z_l $ or$ z_s $ . To increase the available SGL sample, several studies employed the GP method to reconstruct the distance-redshift relation from SNe Ia [17, 39]. However, SGL systems whose source redshift is higher than the maximum redshift of SNe are still unusable because the GP method cannot precisely reconstruct the curve beyond the redshift range of observational data. To make use of all SGL systems and match the lens and source redshifts of the SGL sample with SNe Ia one-to-one, we apply a model-independent deep learning method to reconstruct the distance-redshift relation from SNe Ia, covering the entire redshift range of the SGL sample.Deep learning is a dramatic method for discovering intricate structures in a large and complex dataset by considering artificial neural networks (ANNs) as an underlying model, such as convolutional neural networks (CNNs), recurrent neural networks (RNNs), and Bayesian neural networks (BNNs). These neural networks are usually composed of multiple processing layers, in which each layer receives information from the previous layer and transforms it to the next layer, and are trained to be ideal networks to represent the data. Thereinto, RNNs are powerful in tackling sequential data and predicting the future after learning the representation of the data. Hence, we can feed RNNs with the Pantheon data to obtain the distance-redshift relation and train it to predict the distance at any redshift, even beyond the redshift range of the observational data. However, RNNs are incapable of estimating the uncertainty on the prediction. Thus, we must introduce BNNs into our network as a supplementary of RNNs to calculate the uncertainty on the prediction. In our recent paper [23], we constructed a network combining RNNs and BNNs to represent the relationship between the distance modulus μ and redshift z from the Pantheon data. In this study, instead of reconstructing the
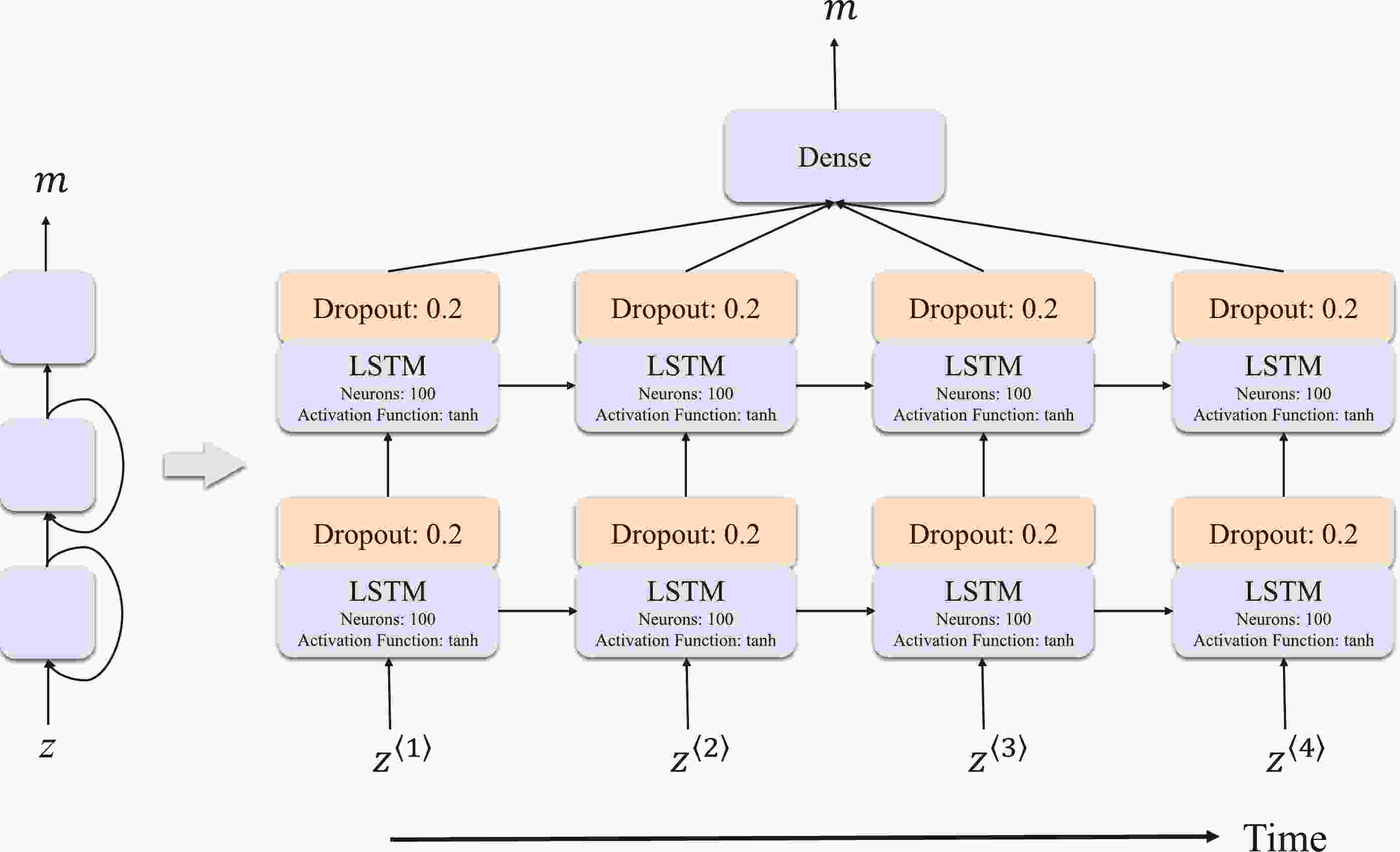
$ \mu(z) $ curve, we reconstruct the apparent magnitude curve$ m(z) $ from the Pantheon data because the latter depends on neither the absolute magnitude of SNe nor the Hubble constant. Considering a constant difference between the distance modulus μ and apparent magnitude m, we directly use our previous network to reconstruct m but without setting the absolute magnitude and Hubble constant. The construction of our network is briefly introduced as follows (see Tang et al. [23] for further details):The architecture of our network is shown in Fig. 1. The main structure of RNNs is composed of three layers: the input layer to receive the feature (the redshift z), one hidden layer to transform the information from the previous layer to the next layer, and the output layer to export the target (the apparent magnitude m). Information not only propagates forward from the first layer through the hidden layer to the last layer but also propagates backward. This can be observed more obviously from the unrolled RNN in the right panel of Fig. 1. At each time step t, the neurons of the RNN receive the input as well as the output from the previous time step
$ t-1 $ . The RNN unfolded in the time step can be regarded as a deep network in which the number of hidden layers is more than 1. It takes a long time to train RNNs when handling long sequential data. Moreover, it is difficult to store information in RNNs for a long time. To solve this problem, we set the time step as$ t=4 $ and employ the long short-term memory (LSTM) cell as the basic cell. The LSTM cells augment the RNN with an explicit memory so that the network is aware of what to store, throw away, and read. The input and hidden layers are constructed using LSTM cells with 100 neurons each. Feeding in the Pantheon data, the RNN is trained to represent the relationship between the magnitude m and redshift z by minimizing the loss function, which depicts the difference between predictions and observations. In our network, we choose the mean-squared-error (MSE) function as the loss function, and the Adam optimizer is adopted to find its minimum. Additionally, a non-linear activation function$ A_f $ is introduced to enhance the performance of the network. In our previous study [23], we showed that the tanh function [41] performs better than the other three activation functions (relu [42], elu [43], and selu [44]) in reconstructing the distance moduli$ \mu(z) $ . Considering that the apparent magnitude is connected to the distance modulus with a overall constant, we directly choose the tanh function as the activation function.
Figure 1. (color online) Architecture of an RNN with one hidden layer (left), unrolled through the time step
$ t=4 $ (right). The input and output are the redshift sequence and the corresponding apparent magnitudes, respectively. The number of neurons in each LSTM cell is 100. The activation function in each LSTM cell is tanh, and the dropout between two adjacent LSTM layers is set to 0.2.Regarding BNNs, it should be noted that a traditional BNN is too complex to design. According to Gal & Ghahramani [45–47], the dropout in a deep neural network can be seen as an approximate Bayesian inference in deep GP. The dropout contributes an additional loss to the training process besides the difference between predictions and observations. Minimizing the objective relating to the total loss in the network results in the same optimal parameters as when maximizing the objective log evidence lower bound in GP approximation [46]. In other words, a network with a dropout is mathematically equivalent to the Bayesian model. Hence, we apply the dropout technique to the RNN to realize a BNN. When the RNN is well trained, the network executed n times can determine the confidence region of the prediction, which is equivalent to the BNN. Furthermore, the dropout is a type of regularization technique that prevents the network from over-fitting caused by a large number of its internal hyperparameters. Considering the risks of over-fitting and under-fitting, we set the dropout employed between two adjacent LSTM layers to 0.2 in this study [48–50]. The hyper-parameters used in our network are presented in Fig. 1.
Now, we start the reconstruction of
$ m(z) $ . First, we normalize the apparent magnitude and sort the data points ($ z_i,m_i,\sigma_{m_i} $ ) in ascending redshift order, before re-arranging them into four sequences. In each sequence, the redshifts and the corresponding magnitudes are the input and output vectors, respectively. The inverse of the squared uncertainty ($ w_i=1/\sigma_{m_i}^2 $ ) is treated as the weight of data point in the network. Second, we train the network constructed as above 1000 times using TensorFlow① and save this well-trained network. Finally, we execute the trained network 1000 times to predict the magnitude m at any redshift in the range$ z\in[0, 4] $ . Fig. 2 shows the distribution of the magnitude at redshifts$ z=1 $ and$ z=2 $ in the 1000 runs of the network. We find that the distribution of magnitude can be well fitted with a Gaussian distribution. The mean value and standard deviation of the Gaussian distribution are regarded as the central value and$ 1\sigma $ uncertainty of the prediction, respectively.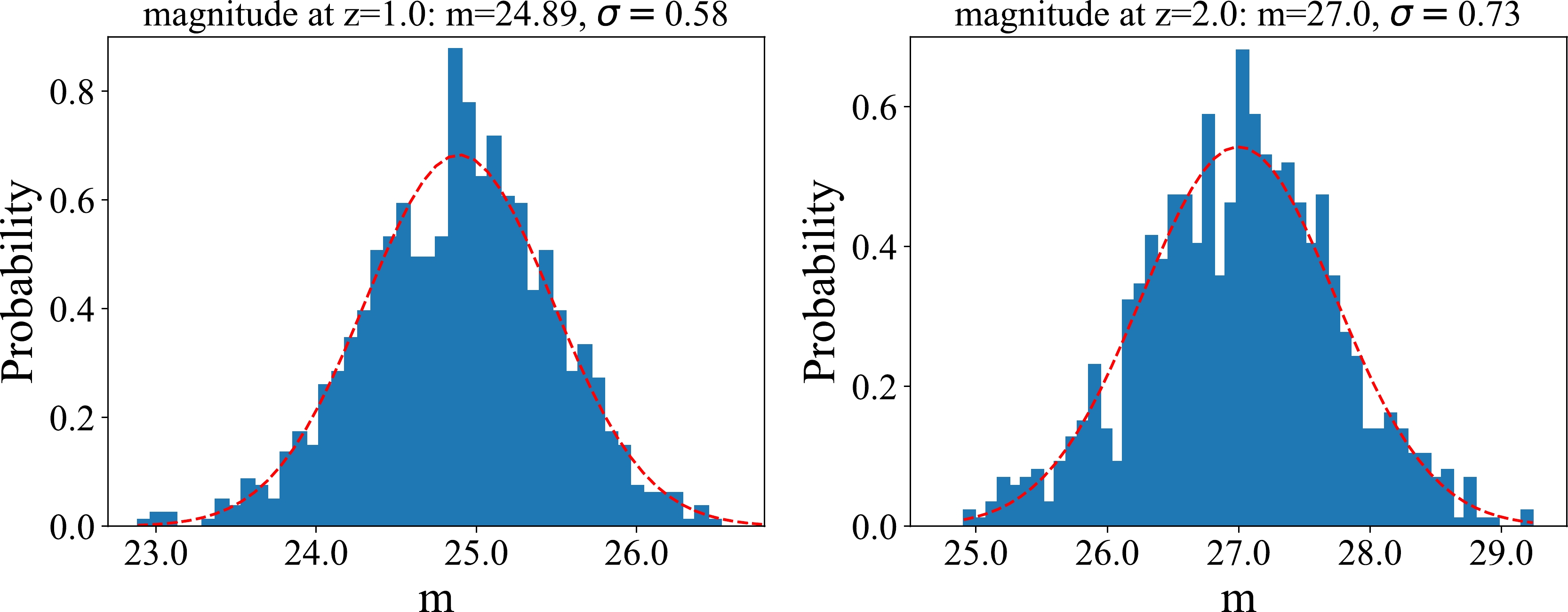
Figure 2. (color online) PDFs of magnitude at redshifts of 1.0 (left panel) and 2.0 (right panel), respectively. The red-dashed line is the best-fit Gaussian distribution.
Finally, we obtain the
$ m(z) $ relation in the redshift range$ 0<z<4 $ and plot it in Fig. 3. For comparison, we also plot the best-fit ΛCDM curve of the Pantheon sample. We find that the reconstructed curve is highly consistent with the ΛCDM curve, and most of the data points fall into the$ 1\sigma $ range of the reconstruction. Although the uncertainty on the reconstructed curve using the deep learning method is slightly larger than that using the GP method in the data region, the merit of deep learning is that it can reconstruct the curve with a relatively small uncertainty beyond the data region, thus allowing us to match SGL with SNe one-by-one, so that the full SGL sample can be used to test the DDR.
Figure 3. (color online) Reconstruction of corrected apparent magnitude-redshift relation
$ m(z) $ from the Pantheon dataset. The red dots with$ 1\sigma $ error bars are the Pantheon data points. The light-blue dots are the central values of the reconstruction. The dark and light blue regions are the 1σ and 2σ uncertainties, respectively. The black line is the best-fit ΛCDM curve.Note that the uncertainty on the reconstructed
$ m(z) $ relation is larger than the uncertainty on the data points, especially at a high redshift. This is because of the sparsity and scattering of data points at a high redshift. To check the reliability of the reconstruction, we constrain the matter density parameter$ \Omega_m $ of the flat ΛCDM model using a mock sample generated from the reconstruction, whose redshifts are same as the Pantheon sample, and the magnitudes and uncertainties are calculated from the reconstructed$ m(z) $ relation. Fixing the absolute magnitude$ M_B=-19.36 $ and Hubble constant$ H_0=70 $ km/s/Mpc, the matter density is constrained as$ \Omega_m=0.281\pm0.025 $ , which is highly consistent with that constrained from the Pantheon sample,$ \Omega_m = 0.278\pm0.008 $ . This proves that our reconstruction of the$ m(z) $ relation is reliable. -
With the reconstruction of the
$ m(z) $ relation, all SGL systems are available to test the DDR. To investigate how the inclusion of high-redshift SGL data affects the constraints on the DDR, we constrain the parameters with two samples. Sample I includes SGL data whose source redshift is below$ z_s<2.3 $ , which consists of 135 SGL systems, and Sample II includes all 161 SGL systems in the redshift range$ z_s<3.6 $ . We perform a Markov Chain Monte Carlo (MCMC) analysis to calculate the posterior probability density function (PDF) of parameter space using the publicly available python code$\textsf{emcee}$ [51]. Flat priors are used for all free parameters. The best-fit parameters in the SIS, PL, and EPL models are presented in Table 1. The corresponding 1σ and 2σ confidence contours and posterior PDFs for parameter space are plotted in Fig. 4.Sample SIS model PL model EPL model $ \eta_0 $ 

f $ \eta_0 $ 

$ \gamma_0 $ 

$ \gamma_1 $ 

$ \eta_0 $ 

$ \alpha_0 $ 

$ \alpha_1 $ 

δ $ z<2.3 $ 

$ -0.268^{+0.033}_{-0.029} $ 

$ 1.085^{+0.013}_{-0.013} $ 

$ 0.134^{+0.125}_{-0.100} $ 

$ 2.066^{+0.042}_{-0.044} $ 

$ -0.219^{+0.239}_{-0.205} $ 

$ -0.349^{+0.021}_{-0.020} $ 

$ 2.166^{+0.037}_{-0.044} $ 

$ -1.117^{+0.408}_{-0.358} $ 

$ 2.566^{+0.091}_{-0.066} $ 

$ z<3.6 $ 

$ -0.193^{+0.021}_{-0.019} $ 

$ 1.077^{+0.012}_{-0.011} $ 

$ -0.014^{+0.053}_{-0.045} $ 

$ 2.076^{+0.032}_{-0.032} $ 

$ -0.257^{+0.125}_{-0.116} $ 

$ -0.247^{+0.014}_{-0.013} $ 

$ 2.129^{+0.037}_{-0.037} $ 

$ -0.642^{+0.274}_{-0.346} $ 

$ 2.586^{+0.117}_{-0.100} $ 

Table 1. Best-fit parameters in three types of lens models.
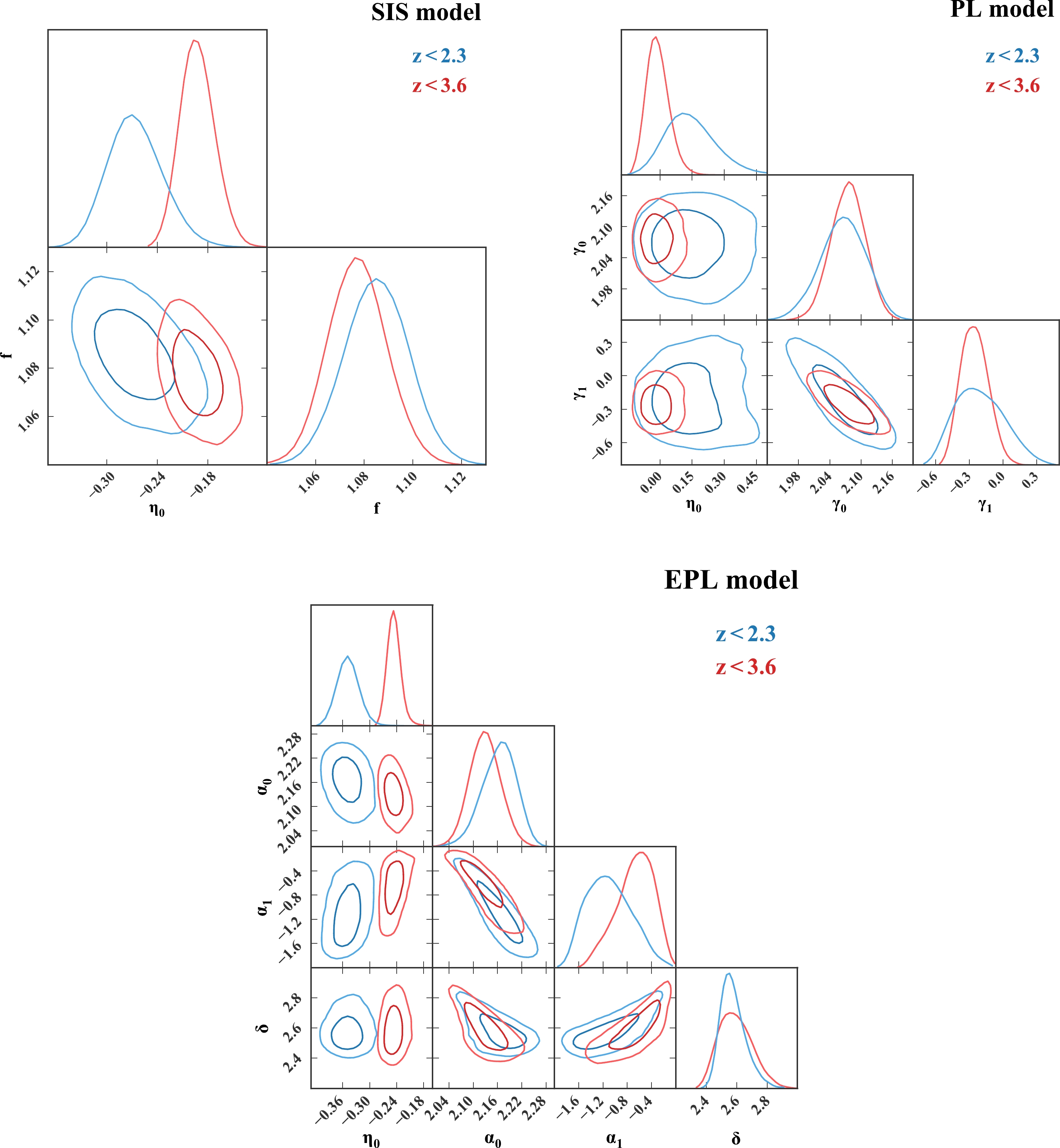
Figure 4. (color online) 2D confidence contours and one-dimensional PDFs for the parameters in three types of lens models.
In the framework of the SIS model, the DDR violation parameters are constrained as
$ \eta_0=-0.268^{+0.033}_{-0.029} $ with Sample I and$ \eta_0=-0.193^{+0.021}_{-0.019} $ with Sample II, which both deviate from zero at a$ >8\sigma $ confidence level. In the framework of the PL model, the constraint of the violation parameter is$ \eta_0=0.134^{+0.125}_{-0.100} $ with Sample I, deviating from the standard DDR at a$ 1\sigma $ confidence level. Conversely, the violation parameter is constrained as$ \eta_0=-0.014^{+0.053}_{-0.045} $ with Sample II, consistent with zero at a$ 1\sigma $ confidence level. In the EPL model, the violation parameters are$ \eta_0=-0.349^{+0.021}_{-0.020} $ with Sample I and$ \eta_0=-0.247^{+0.014}_{-0.013} $ with Sample II, which suggest that the DDR deviates at a$ >16\sigma $ confidence level. As the results show, the inclusion of high-redshift SGL systems can more tightly constrain the DDR violation parameter. Additionally, the model of the lens mass profile has a significant impact on the constraint of the parameter$ \eta_0 $ . On the premise of the exact lens model, the DDR can be constrained at a precision of$ O(10^{-2}) $ using deep learning. The accuracy is significantly improved compared with previous results [8, 9, 15, 16].As for the lens mass profile, all parameters are tightly constrained in the three lens models. In the SIS model, the parameters are constrained as
$ f=1.085^{+0.013}_{-0.013} $ with Sample I and$ f=1.077^{+0.012}_{-0.011} $ with Sample II, slightly deviating from unity but with high significance. In the PL model, the parameters are constrained as$ (\gamma_0,\gamma_1)= (2.066^{+0.042}_{-0.044}, -0.219^{+0.239}_{-0.205}) $ with Sample I and$ (\gamma_0,\gamma_1)= (2.076^{+0.032}_{-0.032}, -0.257^{+0.125}_{-0.116}) $ with Sample II. The slope parameter indicates no evidence of redshift-evolution with Sample I, whereas with Sample II, the slope parameter is negatively correlated with redshift at a$ 2\sigma $ confidence level, which is consistent with the results of Chen et al. [36]. For the parameters of the EPL model, the constraints are$ (\alpha_0,\alpha_1,\delta)=(2.166^{+0.037}_{-0.044},-1.117^{+0.408}_{-0.358}, 2.566^{+0.091}_{-0.066}) $ with Sample I and$ (\alpha_0,\alpha_1,\delta)=(2.129^{+0.037}_{-0.037}, -0.642^{+0.274}_{-0.346}, 2.586^{+0.117}_{-0.100}) $ with Sample II. The results demonstrate a non-negligible redshift-evolution of the mass-density slope α, which is consistent with the results of Cao et al. [52]. None of the three lens models can be reduced to the standard SIS model within a 1σ confidence level. In other words,$ f=1 $ is excluded in the SIS model,$ (\gamma_0,\gamma_1)=(2,0) $ is excluded in the PL model, and$ (\alpha_0,\alpha_1,\delta)=(2,0,2) $ is excluded in the EPL model. -
We investigate the DDR with SGL and SNe Ia using a model-independent deep learning method. With the RNN+BNN network, we reconstruct the apparent magnitude m from the Pantheon compilation up to a redshift
$ z\sim4 $ . The magnitudes at the redshifts of the lens and source in SGL systems can be determined with the reconstructed$ m(z) $ relation one-to-one. In contrast to previous studies [5–7, 13], we reconstruct data without any assumption on the cosmological model or a specific parametric form. Compared with the GP method [17, 39], our method can reconstruct data up to a higher redshift range but with a lower uncertainty. Taking the advantages of all SGL systems and considering the influence of the lens mass profile, we tightly constrain the parameter$ \eta_0 $ in three lens models. We find that the constraints on the DDR strongly depend on the lens mass model. In the framework of the SIS and EPL models, the DDR deviated at a high confidence level, whereas in the framework of the PL model, no strong evidence for the violation of the DDR was found. In other studies, if one requires the DDR to be valid, the SIS and EPL models are strongly excluded. The inclusion of high-redshift SGL data does not affect the main conclusions but can reduce the uncertainty on the DDR violation parameter. In both the SIS and EPL models, the DDR violation parameter η favors a negative value, which implies that$ D_L>(1+z)^2D_A $ . This may be caused by the dust extinction of SNe, making SNe fainter (with a longer luminosity distance) than expected. Once the lens mass model is clear, the DDR can be constrained at a precision of$ O(10^{-2}) $ with deep learning, which improves the accuracy by one order of magnitude compared with that from a previous study [15].The mass profiles of lens galaxies should be properly considered in cosmological research. We analyze the lens model with the DDR and find that the three types of lens models cannot be reduced to the standard SIS model. With the full SGL sample, the constraining result in the SIS model is
$ f=1.077^{+0.012}_{-0.011} $ , which slightly (but with high significance) deviates from the standard SIS model ($ f=1 $ ). In the PL model,$ (\gamma_0,\gamma_1)=(2.076^{+0.032}_{-0.032}, -0.257^{+0.125}_{-0.116}) $ excludes the standard SIS model$ (\gamma_0,\gamma_1)=(2,0) $ at a$ 2\sigma $ confidence level. Similar to the results of Ref. [36], the redshift dependence of the slope parameter γ in the PL model is verified at a 2σ confidence level. In the EPL model, the constraining results are$ (\alpha_0,\alpha_1,\delta) =(2.129^{+0.037}_{-0.037}, -0.642^{+0.274}_{-0.346}, 2.586^{+0.117}_{-0.100}) $ . As shown, the total mass profile and luminosity profile are different owing to the influence of dark matter. The slope of the mass profile α is clearly redshift-independent, with a trend of$ \partial \alpha/\partial z_l=-0.642^{+0.274}_{-0.346} $ . To correctly constrain the DDR, the mass profile of lens galaxies must be accurately modeled.
Deep learning method for testing the cosmic distance duality relation
- Received Date: 2022-07-19
- Available Online: 2023-01-15
Abstract: The cosmic distance duality relation (DDR) is constrained by a combination of type-Ia supernovae (SNe Ia) and strong gravitational lensing (SGL) systems using the deep learning method. To make use of the full SGL data, we reconstruct the luminosity distance from SNe Ia up to the highest redshift of SGL using deep learning, and then, this luminosity distance is compared with the angular diameter distance obtained from SGL. Considering the influence of the lens mass profile, we constrain the possible violation of the DDR in three lens mass models. The results show that, in the singular isothermal sphere and extended power-law models, the DDR is violated at a high confidence level, with the violation parameter





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: