Dependence of the tidal deformability of neutron stars on the nuclear equation of state

Understanding the nature and constraining the equation of state (EOS) of asymmetric nuclear matter have jointly been a major science goal shared by many astrophysical observations and nuclear experiments [1–8]. They also drive the construction of many radioactive beam facilities [9–15], X-ray observatories, and gravitational wave detectors [16–21] around the world. A basic input in calculating the EOS of nuclear matter is the specific energy $E(\rho, \delta)$, with ρ representing the nucleon density and $\delta=(\rho_n-\rho_p)/\rho$ being the isospin asymmetry, where $\rho_n$ and $\rho_p$ are the densities of neutrons and protons, respectively. Based on studies on existing nuclear many-body theories, $E(\rho, \delta)$ can be well approximated by [22]

where $E_0(\rho)$denotes the energy per nucleon in symmetric nuclear matter (SNM) having equal numbers of neutrons and protons, and $E_{\rm{sym}}(\rho)$ represents the symmetry energy.

Numerous constraints have been obtained on the nuclear EOS and bulk neutron star (NS) properties, such as radii and tidal deformabilities, after the observation of gravitational wave event GW170817 [23–28]. The dependence of NS EOS on the observed gravitational waves (GWs) has been widely investigated by using tidal deformabilities during the last orbits before merger [29–33] and the spectra of the gravitational radiation after merger [34–36]. The tidal deformabilities experienced by the two NSs in a binary-neutron-star (BNS) system modify the phase of the gravitational wave and determine crucial properties of the NS EOS.

Despite the NS tidal deformability is strongly correlated with the NS EOS, it has been claimed that the first detection by GW170817, i.e., $\Lambda_{1.4}=190^{+390}_{-190}$ at 90% confidence level (CFL), did not provide new insights into the EOS [27, 37, 38]. This is probably because the uncertainty on the tidal deformability remained large. The current constraints provided by diverse theoretical approaches are mostly model dependent [24, 26, 27, 39–41] or detector dependent [42]. Furthermore, the phase transition inside NSs, which is still an open question, plays an important role in constraining tidal deformabilities [43–46]. A sharp phase transition leads to a smaller value for tidal deformability.

In the present study, assuming nonrotating and charge-neutral neutron stars consisting of only neutrons, protons, electrons, and muons ( $npe\mu$) particles at β equilibrium, we employed a Bayesian inference approach coupled to a Markov-Chain Monte-Carlo (MCMC) with the Metropolis-Hastings algorithm to explore the EOS parameter space and confront our model predictions of tidal deformabilities to several constraints in the literature. We did not aim at constraining the tidal deformabilities and nuclear EOS. We focused on the dependence of NS tidal deformabilities on the high-density behavior of both the isospin-dependent and isospin-independent parts of the EOS of NS matter, especially mass-dependent tidal deformabilities. We also put emphasis on the correlations among $\Lambda_{1.4}$, $R_{1.4}$, $p(2\rho_0)$, $E_{\mathrm{sym}}(2\rho_0)$, $E_{\mathrm{sym}}(3\rho_0)$ and $M_{\mathrm{max}}$, where $M_{\mathrm{max}}$, $p(2\rho_0)$, and $E_{\mathrm{sym}}(2\rho_0)$ respectively denote the maximum mass of an NS, the pressure in an NS, and the symmetry energy at two times the saturation density $\rho_0$.

The paper is organized as follows. We summarize our theoretical framework in Section II. In Section III, we present the constraining range of the NS EOS by taking different tidal deformabilities and the correlations among NS observations and EOS parameters. Finally, a summary is provided in Section IV.

Most details of the theoretical approach used in the present study can be found in earlier publications [37, 47, 48]. For completeness and ease of discussion, here we briefly describe the main features of the model we used. The NS in our model consists of $npe\mu$ at β equilibrium, and the pressure inside an NS is expressed in terms of nucleon density ρ and isospin asymmetry δ as

where $\epsilon(\rho, \delta)=\epsilon_n(\rho, \delta)+\epsilon_l(\rho, \delta)$ denotes the energy density with $\epsilon_n(\rho, \delta)$ and $\epsilon_l(\rho, \delta)$ being respectively the energy densities of nucleons and leptons. $\epsilon_n(\rho, \delta)$ is obtained by the nucleon specific energy $E(\rho, \delta)$ and average mass of nucleons $M_N$ via

Both parts of $E(\rho,\delta)$ in Eq. (1) can be further parameterized as

Here, $E_0(\rho_0)$= –15.9 MeV. Moreover, K₀ = $9\rho_0^2[\partial^2 E_0(\rho)/\partial\rho^2]|_{\rho=\rho_0}$ and $J_0=27\rho_0^3[\partial^3 E_0(\rho)/\partial\rho^3]|_{\rho=\rho_0}$ are the incompressibility and skewness of SNM at $\rho_0$, respectively. The four parameters involved in $E_{\rm{sym}}(\rho)$ denote the magnitude $E_{\rm{sym}}(\rho_0)$, slope L = 3ρ₀× $[\partial E_{\rm{sym}}(\rho) / \partial\rho]|_{\rho=\rho_0}$, curvature $K_{\rm{sym}} = 9\rho_0^2[\partial^2 E_{\rm{sym}}(\rho) / \partial\rho^2]|_{\rho=\rho_0}$, and skewness $J_{\rm{sym}}= 27\rho_0^3[\partial^3 E_{\rm{sym}}(\rho)/\partial\rho^3]|_{\rho=\rho_0}$ of the nuclear symmetry energy at $\rho_0$, respectively. The isospin asymmetry δ in Eq. (1) is calculated according to the charge neutrality condition $\rho_p=\rho_e+\rho_{\mu}$ and β-equilibrium condition $\mu_n-\mu_p=\mu_e= \mu_{\mu}\approx 4\delta E_{\mathrm{sym}}(\rho)$, where μ represents the chemical potential and can be calculated by the expression $\mu_i = \partial \epsilon(\rho, \delta)/\partial \rho_i$ for the ith particle.

As discussed in detail in Refs. [37, 47, 48], above expressions (4) and (5) have a dual meaning. They are Taylor expansions around $\rho_0$ and can still be used to simulate the nuclear matter at densities far away from $\rho_0$ when we regard these parameters as free coefficients to be determined by observations and experiments. Based on the systematics of terrestrial nuclear experiments and predictions of various nuclear theories, $K_0$, $E_{\rm{sym}}(\rho_0)$, and L have been constrained to relatively narrow ranges [1, 3, 49–51], i.e., 220 MeV$\leq K_0 \leq$ 260 MeV, 28.5 MeV$\leq E_{\rm{sym}}(\rho_0) \leq$ 34.9 MeV, and 30 MeV $\leq L \leq$ 90 MeV. The parameters $J_0$, $K_{\rm{sym}}$, and $J_{\rm{sym}}$measuring the nuclear EOS at high densities are loosely constrained within the ranges of -800 MeV$\leq J_0 \leq 400$ MeV, -400 MeV$\leq K_{\rm sym}\leq100$ MeV, and -200 MeV$\leq J_{\rm sym}\leq800$ MeV) [52, 53]. In the Bayesian inference approach, these ranges are used as the prior limits of the six EOS parameters. The uniform form for prior probability distribution functions (PDFs) can be adopted because there is no known physical preference for the values of these parameters within their ranges.

Combining expressions (2)–(5), one can construct pressure as a function of density under the condition that the density profile of the isospin asymmetry or the proton fraction is obtained from the β-equilibrium and charge neutrality conditions, namely the EOS for the core of NSs. For the EOS of NS crust, we used the NV EOS [54] for the inner crust and the BPS EOS [55] for the outer crust of NSs, as done in Refs. [37, 47, 48].

The dimensionless tidal deformability Λ is calculated by the expression [29, 56]

where R is the radius and M the mass of NSs; $k_2$is the second Love number, controlled by the EOS through several complicated equations (see Eqs. (3)–(6) in Ref. [40]) coupled to the Tolman-Oppenheimer-Volkov (TOV) equation with some boundary conditions [23].

As in a recent study of ours [47, 48], we set the six parameters in Eqs. (4) and (5) as free parameters, and the dependence between these parameters and the NS properties was established within the Bayesian inference analysis. The key of the Bayesian analysis is Bayes theorem, which can be formulated as

where the denominator is a normalization constant. In particular, $P({\cal M}|D)$ represents the posterior PDF of the model $\cal M$ given the data set D, $P(D|{\cal M})$ is the likelihood function obtained through the comparison between theoretical results given by the model $\cal M$ and the data set D, and $P({\cal M})$ is the prior probability of the model $\cal M$ representing the knowledge on the theoretical parameters of $\cal M$ before being confronted with the data set D.

The six parameters in Eqs. (4) and (5) are assumed to be uniformly distributed and we randomly sample them between their minimum and maximum values summarized above. After generating the EOS parameters, $p_{i=1,2,\cdots, 6}$, one can construct the model $\cal M$ as described above and obtain the NS EOS. Using the NS EOS as the input of the TOV and tidal deformability equations, we can obtain the theoretical values of mass-dependent NS tidal deformabilities and subsequently compare them with the various constraints from other models or observed data to obtain the likelihood of this set of EOS parameters.

The likelihood function measures the ability of the model $\cal M$ to reproduce the data. In the present study, it is defined as

where $P_{\mathrm{filter}}$ is a filter that selects the parameter sets satisfying the following conditions: (i) the crust-core transition pressure stays positive; (ii) at all densities, the thermaldynamical stability condition, ${\rm d}P/{\rm d}\varepsilon\geq0$, and the causality condition, $0\leq v_s^2\leq c^2$, are satisfied. $P_{\mathrm{mass},\mathrm{max}}$denotes the probability associated with NS maximum masses, and a sharp cut-off at 1.97 M $_{\odot}$ was used in the present analysis. $P_{\mathrm{tial}}$ represents the probability measuring the compatibility between theoretical values of NS tidal deformability given by our model and observed data or constraints from other theoretical models; it can be expressed as

where $\Lambda_{\mathrm{th}}$ represents the theoretical values calculated from the NS model we used. $\Lambda'$ and $\sigma'$ represent the $data$ and its $1\sigma$ error bar used in the present study. We employed four types of $data$ at 90% CFL as follows: (i) $\Lambda_{1.4}=320\pm120$ deduced by analyzing the mass-radius data of 14 NSs using a deep neural network with supervised learning [41]; (ii) $\Lambda_{1.4}=320\pm250$, which is artificial and used to explore the effect of $\Lambda_{1.4}$ measurement accuracy; (iii) $\Lambda_{1.4}=196\pm90$, which was manually modified from $\Lambda_{1.4}=196^{+92}_{-63}$ based on GW170817 and existing observations of six thermonuclear bursters in low-mass X-ray binaries described in Ref. [57] to explore the effect of the lower boundary of $\Lambda_{1.4}$; and (iv) $\Lambda_{1.4}=320\pm120$ [41], $\Lambda_{1.8}=170\pm 100$, and $\Lambda_{2.0}=90\pm60$ from the prediction of ten realistic models that can accurately describe the properties of finite nuclei and support neutron stars of two solar masses [58]. These constraints on the tidal deformability are completely consistent with the results reported by the GW170817 measurement within the error bar [17].

An MCMC approach with the Metropolis-Hastings algorithm was used to simulate the posterior PDFs of the model parameters. The PDFs of all individual EOS parameters and the two-parameter correlations were calculated by integrating over all other parameters, i.e., the PDF for the ith parameter $p_i$ is expressed as

Numerically, we had to discard the initial samples in the so-called burn-in period because the MCMC process does not initially sample from the equilibrium distribution [59]. It was found that 40000 steps in the burn-in period for the six model parameters are enough, as reported in recent studies of ours [47, 48]. Therefore, we set 40000 steps for burn-in progress and the rest one million steps for calculating the PDFs of the six parameters in the present analysis.

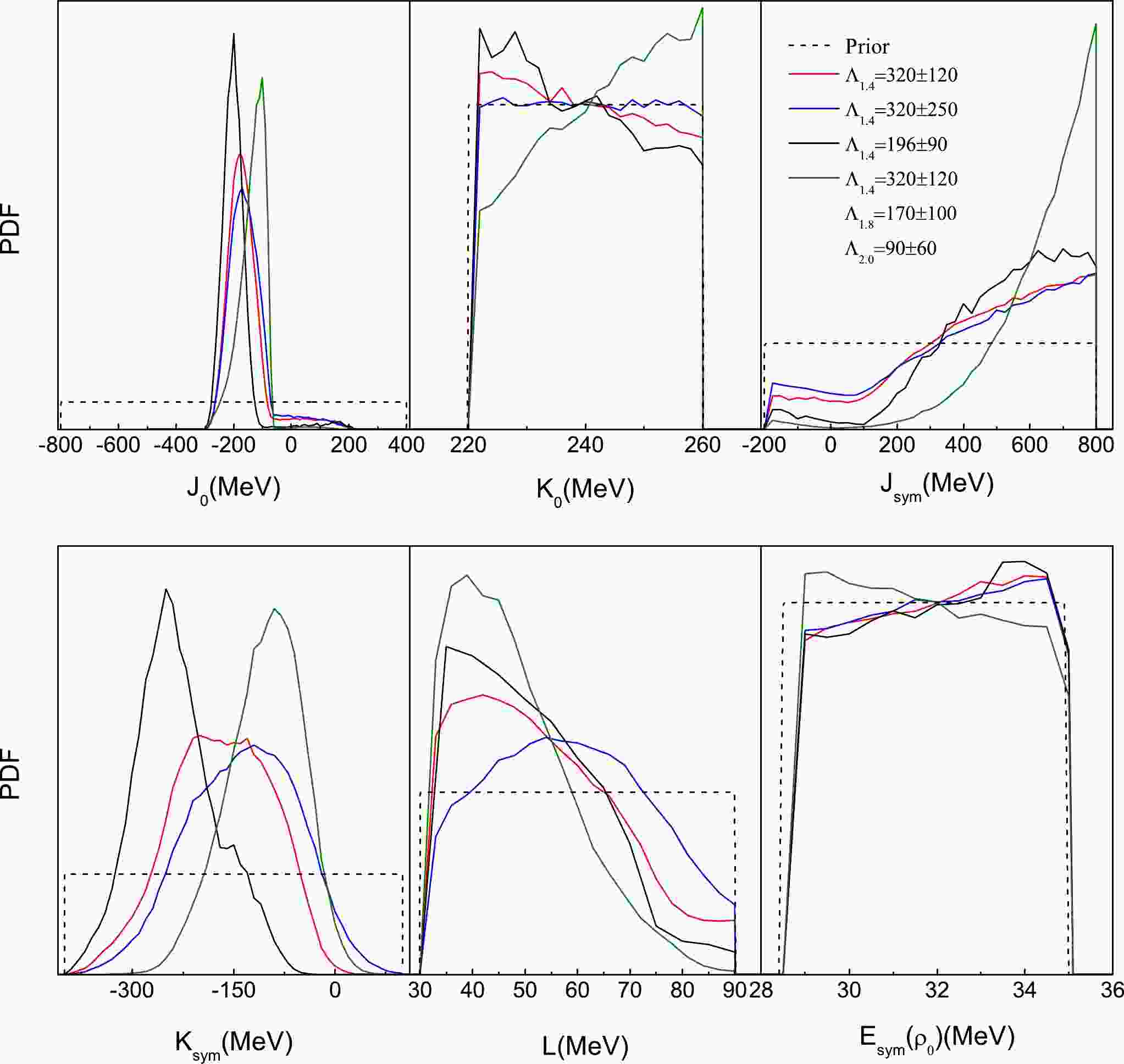
We first performed the calculations of the posterior PDFs of the six parameters in Eqs. (4) and (5); the results are represented in Fig. 1. The dashed and solid curves denote the prior and posterior PDFs of the parameters, respectively. Similar to NS radius data reported in previous studies of ours [47, 48], the NS tidal deformability can also improve our knowledge about the EOS parameters, except for $K_0$ and $E_{\rm{sym}}(\rho_0)$. How much better can we infer the EOS parameters by improving the measurement accuracy of NS tidal deformability in the future? The answer to this question can be found by comparing the posterior PDFs inferred from $\Lambda_{1.4}=320\pm120$ (represented by red curves) with those from $\Lambda_{1.4}=320\pm250$ (represented by blue curves). There are two observations we can make at this point. (i) The NS EOS becomes stiffer as the error of $\Lambda_{1.4}$ is increased; this is understandable because a larger tidal deformability corresponds to a stiffer EOS [7, 60]. (ii) Decreasing the error can better constrain the lower-order parameter L than other coefficients; it implies that a more precise measurement of $\Lambda_{1.4}$ can only improve the constraint on the symmetry energy at lower densities.

Figure 1.  (color online) Prior and posterior probability distribution functions of the six EOS parameters inferred from various tidal deformability constraints as indicated.

It was reported that the lower limit of the tidal deformability has a significant impact on the high-density behaviors of the NS EOS [25, 27, 40]. This effect is clearly illustrated by the posterior PDFs from $\Lambda_{1.4}=320\pm120$ and those from $\Lambda_{1.4}=196\pm90$ (represented by black curves). Decreasing the mean tidal deformability from approximately 320 to 196 requires a softer EOS representing the decreasing values of the SNM parameters as well as those of the symmetry energy. Note also from the figure that the $K_{\rm{sym}}$ and $J_0$ parameters that mainly characterize the high-density behavior of the EOS are more sensitive to this decrease than the parameter L. This means that determining the lower limit of tidal deformability notably affects the constraint on the NS EOS in the high-density region, especially the isospin-dependent part. What is more, this effect does not suffer from uncertainty in the low density region.

After we confront the EOS parameters to the tidal deformabilities of the massive NSs, i.e., not only $\Lambda_{1.4}=320\pm 120$ but also $\Lambda_{1.8}=170\pm100$ and $\Lambda_{2.0}=90\pm60$, there are two distinct observations we can make: (i) all EOS parameters are narrowed down except for $E_{\rm{sym}}(\rho_0)$, and a smaller L is preferred; (ii) a stiffer EOS is required that is mainly presented by the higher-order parameters $J_0, K_{\rm{sym}}$, and $J_{\rm{sym}}$. Observations of massive NSs can be used to probe the behavior of nuclear EOS in the regions at high densities, which is consistent with previous findings reported in Ref. [61].

The confidence bands of $E_0(\rho)$ and $E_{\rm{sym}}(\rho)$can be constructed after obtaining the confidence intervals of the parameters according to expressions (4) and (5). Figure 2 shows $E_0(\rho)$ and $E_{\rm{sym}}(\rho)$ as a function of the reduced density based on the tidal deformability data of $\Lambda_{1.4}=196\pm90$ and $\Lambda_{1.4}=320\pm120$ as well as the mass-dependent one at 68% CFL. For comparison, the figure also includes the results adopting the radius data of the canonical NS $R_{1.4}$ from previous calculations [47]. Increasing the lower limit of the tidal deformability lifts the lower bound of both $E_0(\rho)$ and $E_{\rm{sym}}(\rho)$ at high densities. The results from $\Lambda_{1.4}=196\pm90$ are almost the same as those from the radius data. Corresponding to the inferred posterior PDFs of the six EOS parameters according to the mass-dependent tidal deformabilities shown in Fig. 1, both the isoscalar and isovector parts of the nuclear EOS are significantly raised and constrained. These findings are also verified by the results shown in Table 1, in which we summarize the most probable values and their 68% confidence intervals for $E_{\rm{sym}}(2\rho_0)$ and $E_{\rm{sym}}(3\rho_0)$ calculated on the basis of these neutron-star observations.

Figure 2.  (color online) $E_0(\rho)$ and $E_{\rm{sym}}(\rho)$ bands at 68% confidence level calculated by using the tidal deformabilities of $\Lambda_{1.4}=196\pm90$, $\Lambda_{1.4}=320\pm120$, and the mass-dependent one as indicated. For comparison, the results from the radius data of the canonical NS extracted from Ref. [47] are included.

	$\Lambda_{1.4}=196\pm90$	$\Lambda_{1.4}=320\pm120$	$R_{1.4}$	mass-dependent Λ data
$E_{\rm{sym}}(2\rho_0)$	$38.4_{-8.6}^{+11.4}$	$41.8_{-9.9}^{+15.6}$	$39.2_{-8.2}^{+12.1}$	$45.9_{-9.0}^{+7.7}$
$E_{\rm{sym}}(3\rho_0)$	$44.6_{-31.5}^{+33.4}$	$57.1_{-34.0}^{+46.3}$	$48.4_{-32.1}^{+33.5}$	$78.5_{-29.0}^{+18.4}$

Table 1.  Most probable values and their 68% credible intervals of $E_{\rm{sym}}(2\rho_0)$ and $E_{\rm{sym}}(3\rho_0)$ in units of MeV by adopting $\Lambda_{1.4}=196\pm90$, $\Lambda_{1.4}=320\pm120$, $R_{1.4}$, and the mass-dependent tidal deformabilities mentioned in the context, respectively. The results concerning $R_{1.4}$ are extracted from Ref. [47].

To further explore the dependence of the tidal deformability on the nuclear EOS, we performed calculations on the correlations among the six EOS parameters, $\Lambda_{1.4}$, $\Lambda_{2.0}$, and $R_{1.4}$. The tidal deformability of $\Lambda_{1.4}=320\pm 120$ was adopted. The results are depicted in Fig. 3. We can see that $E_{\mathrm{sym}}(\rho_0)$ and $K_0$ are insensitive to these neutron-star observations. As thoroughly discussed in Refs. [47, 48], this is because they characterize the EOS behavior in lower density regions, whereas these observations are usually used to probe the NS EOS around 2$\rho_0$[62]. The correlation between $R_{1.4}$ and L is stronger than those between $R_{1.4}$ and $K_{\rm{sym}}$. By contrast, $\Lambda_{1.4}$ is more strongly correlated with $K_{\rm{sym}}$ with respect to L. This reflects the fact that $\Lambda_{1.4}$ carries more high-density information of the nuclear EOS than $R_{1.4}$. This is proven by the correlation between $\Lambda_{1.4}$ and $J_0$. The latter mainly characterizes the high-density behavior of symmetric nuclear matter.

Figure 3.  (color online) Posterior probability distribution functions of $\Lambda_{1.4}$, $\Lambda_{2.0}$, and $R_{1.4}$ and their correlations with the EOS parameters.

To support massive NSs, the larger pressure inside an NS is needed. Thus, it is easy to understand that $\Lambda_{2.0}$ is strongly (weakly) correlated with $J_{\mathrm{sym}}$ and $J_0$ ($K_{\rm{sym}}$) given that they dominate the pressure in high-density regions, whereas $\Lambda_{1.4}$ and $R_{1.4}$ are uncorrelated with $J_{\mathrm{sym}}$ but highly correlate with $K_{\rm{sym}}$ and L. More interestingly, a weak anticorrelation is found between $\Lambda_{2.0}$ and L. It demonstrates that $\Lambda_{2.0}$ is more sensitive to the higher-order parameters and the behavior of the nuclear EOS at higher densities than these observations with 1.4 times the solar mass. This is why the parameters $K_{\rm{sym}}$, $J_{\rm{sym}}$, and $J_0$ are limited notably better when we incorporate the tidal deformabilities of massive NSs into the Bayesian calculations, as shown in Fig. 1.

The relation between $\Lambda_{1.4}$ and $R_{1.4}$ has been studied in the framework of the relativistic mean field theory [23, 40, 63, 64], Skyrme Hartree-Fock theory [65, 66], microscopic theories [27], and parameterized approach [67, 68]. An approximate linear relation between $\Lambda_{1.4}$ and $R_{1.4}$ is predicted by these forward approaches. In particular, it has been reported that L is a key factor in determining the relation between $\Lambda_{1.4}$ and $R_{1.4}$ [67]. In the present study, the six EOS parameters were randomly selected within their specified ranges instead of being fixed at some values, as done in Ref. [67]. It was found that the posterior PDF for the correlation between $\Lambda_{1.4}$ and $R_{1.4}$ is consistent with the findings by the theories mentioned above. In addition, we also found that positive correlations exist between $\Lambda_{2.0}$ and $\Lambda_{1.4}$ and between $\Lambda_{2.0}$ and $R_{1.4}$.

The aforementioned findings were further confirmed by the results shown in Fig. 4. The correlation between $R_{1.4}$ and $E_{\rm{sym}}(3\rho_0)$ is weaker than that between $\Lambda_{1.4}$ and $E_{\rm{sym}}(3\rho_0)$. This shows that $\Lambda_{1.4}$ is more competent for exploring the behavior of the symmetry energy around 3$\rho_0$ than $R_{1.4}$. A stronger (weaker) correlation between $\Lambda_{2.0}$ and $E_{\rm{sym}}(3\rho_0)$ ($E_{\rm{sym}}(2\rho_0)$) demonstrates that $\Lambda_{2.0}$ can be used to constrain the symmetry energy around 3$\rho_0$ without suffering from that around 2 $\rho_0$.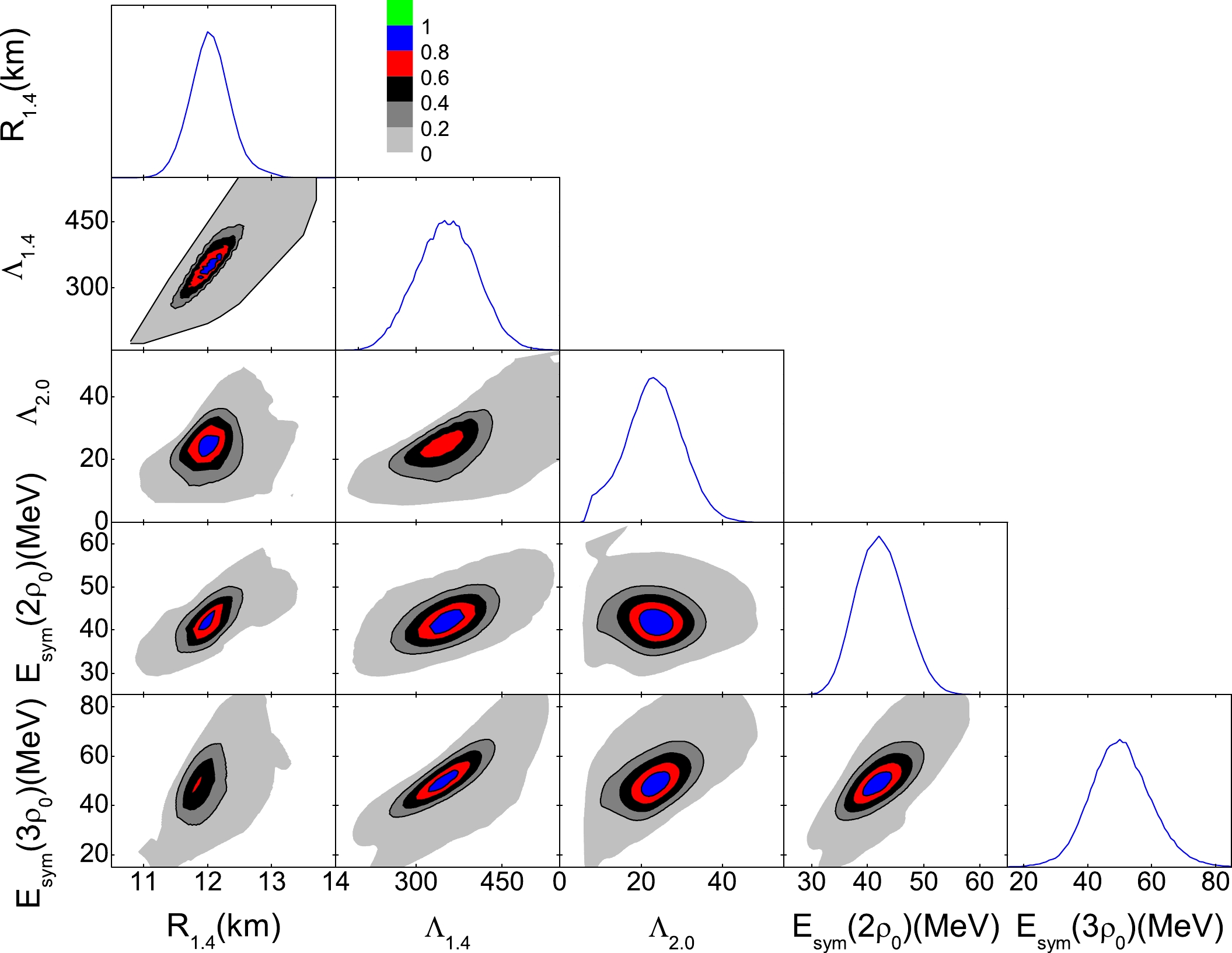

Figure 4.  (color online) Posterior probability distribution functions of $R_{1.4}$, $\Lambda_{1.4}$, $\Lambda_{2.0}$, $E_{\rm{sym}}(2\rho_0)$, and $E_{\rm{sym}}(3\rho_0)$ and their correlations.

In Fig. 5, we present the posterior PDFs of the correlations among $R_{1.4}$, $\Lambda_{1.4}$, $M_{\mathrm{max}}$, and $p(2\rho_0)$. For comparison, the posterior PDFs for these observations extracted from Ref. [69] are included. It has been reported that $R_{1.4}$ is most sensitive to the pressure around 2$\rho_0$ [62]. This point was verified by the correlation between $R_{1.4}$ and $p(2\rho_0)$, as indicated in the figure. It is not surprising that $\Lambda_{1.4}$ is positively correlated to $p(2\rho_0)$, and $M_{\mathrm{max}}$ has no relation with the other quantities. Our intervals for $R_{1.4}$, $\Lambda_{1.4}$, $M_{\mathrm{max}}$, and $p(2\rho_0)$ fall into those reported in Ref. [69]. There is a small peak for $M_{\mathrm{max}}$ around 2$M_{\mathrm{sun}}$ resulting from the sharp cut of 1.97 $M_{\mathrm{sun}}$ used in the calculations.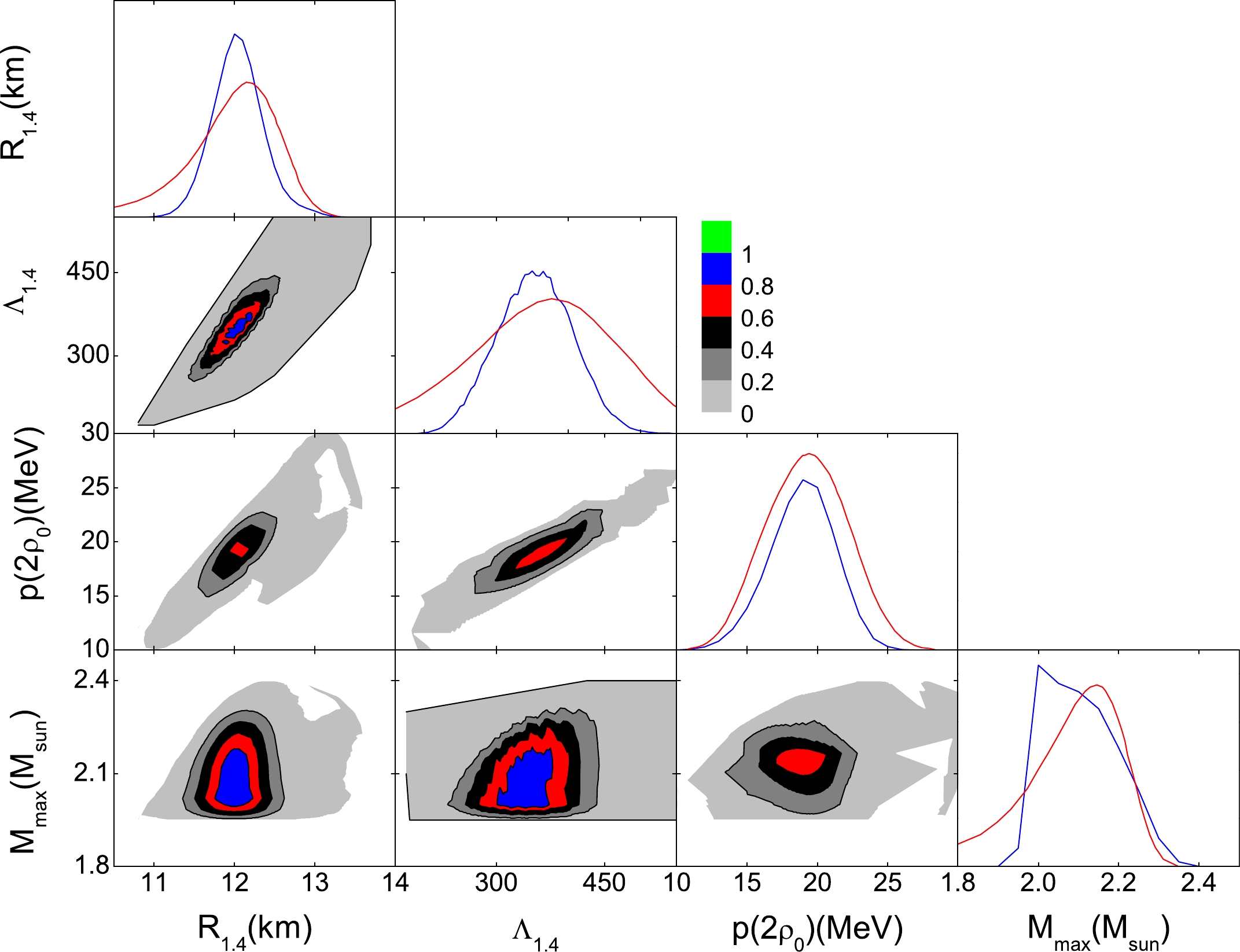

Figure 5.  (color online) Posterior probability distribution functions of the correlations among $R_{1.4}$, $\Lambda_{1.4}$, $M_{\mathrm{max}}$, and $p(2\rho_0)$. For comparison, results extracted from Ref. [69], represented by red curves, are included.

Using an explicitly isospin-dependent parametric EOS of nucleonic matter within the minimum NS model, Bayesian inference of both the specific energy in SNM and nuclear symmetry energy using the tidal deformabilities of NSs inferred by several theories was performed. The main conclusions from this study are as follows.

1. More accurate measurement of $\Lambda_{1.4}$ only has an important role in narrowing down the lower-order parameter L of the symmetry energy. Determining the lower boundaries of $\Lambda_{1.4}$ is significantly useful for constraining the NS EOS in high-density regions.

2. The nuclear EOS is highly limited and raised if the tidal deformabilities of more massive NSs is taken into account.

3. In comparison with the dependence of $R_{1.4}$ on the nuclear EOS, $\Lambda_{1.4}$ can be used to probe the EOS behavior at higher densities.

4. $\Lambda_{2.0}$ is a useful observation to constrain the higher-order parameter $J_{\mathrm{sym}}$ of the symmetry energy without suffering from the uncertainty of $K_{\rm{sym}}$. This cannot be the case for $R_{1.4}$ and $\Lambda_{1.4}$.

5. Stronger positive correlations among $R_{1.4}$, $\Lambda_{1.4}$, $\Lambda_{2.0}$, $E_{\rm{sym}}(2\rho_0)$, $E_{\rm{sym}}(3\rho_0)$, and $p(2\rho_0)$ were found, except for the weaker correlation between $\Lambda_{2.0}$ and $E_{\rm{sym}}(2\rho_0)$ and the correlation between $\Lambda_{2.0}$ and $p(2\rho_0)$, which is not shown here.

We would like to thank Professor Bao-An Li for helpful discussions.