-
In April 2021, a new result for the muon anomalous magnetic moment (
$ {{\rm{muon}}}\; g - 2 $ or$ \delta a_\mu $ ) was reported at Fermilab [1], revealing an exciting disparity compared to the standard model (SM) prediction. Combined with the previous result at Brookhaven [2], the discrepancy can be$ 4.2\; \sigma $ [1],$ \begin{eqnarray} \delta a_\mu \equiv a_\mu^{ {{\rm{ex}}}} - a_\mu^{ {{\rm{SM}}}} \;= (25.1 \pm 5.9) \times 10^{-10} \;, \end{eqnarray} $

(1) where the combined experimental result
$ a_\mu^{\rm ex} $ [1] and SM prediction$ a_\mu^{\rm SM} $ [3–25] are given by$ a_\mu^{ {{\rm{ex}}}} = (11659206.1 \pm 4.1) \times 10^{-10} \;, $

(2) $ \begin{eqnarray} a_\mu^{ {{\rm{SM}}}} = (11659181.0 \pm 4.3) \times 10^{-10} \;. \end{eqnarray} $

(3) It is widely believed that the SM is not a complete description of nature. Besides the
$ {{\rm{muon}}}\; g - 2 $ anomaly, the SM also cannot interpret problems such as hierarchy, grand unification, dark matter (DM), and baryogenesis. To interpret these problems, researchers have proposed many theories beyond the SM (BSM), among which supersymmetry (SUSY) is the most fascinating [26–29]. SUSY assumes that every SM particle has a SUSY partner whose spin differs from that of the corresponding SM particle by half. These extra SUSY particles can significantly contribute to solving problems and anomalies, including$ {{\rm{muon}}}\; g - 2 $ . The SUSY effects on$ {{\rm{muon}}}\; g - 2 $ were first calculated in the 1980s [30–34] and comprehensively described in Refs. [35–37]. In recent years, especially after the new result released at Fermilab, there have been numerous papers on interpreting the$ {{\rm{muon}}}\; g - 2 $ anomaly in the minimal supersymmetric SM (MSSM) and its extensions, such as the next-to MSSM (NMSSM) [38–69]. In the MSSM and NMSSM, the main contributions to$ \delta a_\mu $ originate from chargino-sneutrino loops and neutralino-smuon loops. Thus, light SUSY particles, such as smuons, sneutrinos, charginos, and neutralinos, are generally required to interpret the distinct$ {{\rm{muon}}}\; g - 2 $ anomaly.However, the null results from the search for SUSY at the LHC in recent years have set strong constraints on SUSY particles. For gluino and the first two-generation squarks, the low mass bounds can be over 2 TeV [70–72]. Even for colorless charginos and sleptons, including smuons, the low mass bounds can be hundreds of GeV in simple models, except for compressed-spectrum scenarios [73–78]. Recent searches for smuons by the ATLAS collaboration with
$139~{\rm{f}}{{\rm{b}}^{ - 1}}$ of data have demonstrated that the mass bound can be approximately 600 GeV, assuming that a smuon decays100% into a muon plus the lightest neutralino [77]. Thus, for constraints to SUSY models, the direct SUSY searches at the LHC and the$ {{\rm{muon}}}\; g - 2 $ anomaly may be at odds with each other. In this study, we consider the status of smuons in the NMSSM confronted with$ {{\rm{muon}}}\; g - 2 $ and SUSY searches and investigate their implications for DM.The added singlet scalar in the NMSSM and its partner singlino can introduce different phenomenology from those in the MSSM. In the Higgs sector, mixing between light singlet and doublet scalars can change the production and decay of the SM-like Higgs boson. In the neutralino sector, a light singlino-like neutralino can be a good candidate for DM and can change the decay of SUSY particles. Thus, the additional parts in the NMSSM can change the status of MSSM confronting Higgs data, DM detection, and SUSY searches and indirectly affect its
$ {{\rm{muon}}}\; g - 2 $ . Moreover, the lightest neutralino with a gaugino or higgsino component can get into neutralino-smuon loops and affect$ {{\rm{muon}}}\; g - 2 $ directly. In this study on the NMSSM, to obtain a more general result, we take the SUSY scale as the input scale of parameters, which differs from our former studies on the semi-constrained NMSSM [53–55]. To ensure that surviving samples satisfy all types of experimental constraints, we impose them one by one (with the entire Higgs data as one), different from the likelihood method in most NMSSM references (e.g., Refs. [42–45]).The rest of this paper is organized as follows. In Sec. II, we introduce the NMSSM, briefly presenting relevant analytic calculations on
$ {{\rm{muon}}}\; g - 2 $ . In Sec. III, we present the numerical calculations and discussions. Finally, we summarize and draw our principal conclusions in Sec. IV. -
In contrast to the manual and large μ parameter used in the MSSM, the μ parameter in the NMSSM is effective and generated naturally when the additional singlet superfield
$ \hat{S} $ obtains a vacuum expected value (VEV) [79–81]. In the NMSSM of$ \mathbb{Z}_3 $ -invariant vision, the superpotential can be expressed as$ \begin{eqnarray} W^ {{\rm{NMSSM}}} = W^ {{\rm{MSSM}}}_{\mu\to\lambda \hat{S}} + \frac{\kappa}{3} \hat{S}^3, \end{eqnarray} $

(4) where λ and κ are dimensionless couplings,
$ W^ {{\rm{MSSM}}} $ is the superpotential in the MSSM,$ \begin{eqnarray} W^ {{\rm{MSSM}}} = \mu \hat{H}_u \cdot \hat{H}_d + {\bf y _u} \hat{u} \hat{Q} \cdot \hat{H}_{ u} - {\bf y _d} \hat{d} \hat{Q} \cdot \hat{H}_{ d} - {\bf y _e} \hat{e} \hat{L} \cdot \hat{H}_{ d}, \; \; \; \; \; \; \end{eqnarray} $

(5) and in terms including quarks or leptons, the generation indexes being summed over are omitted.
After electroweak symmetry breaking, several SUSY particles with the same quantum numbers mix, generating an equal number of mass eigenstates. The SUSY partners of left- and right-handed muon leptons have spin 0, denoted by
$ \tilde{\mu}_L $ and$ \tilde{\mu}_R $ , both known as smuons. In the$ \{ \tilde{\mu}_L, \tilde{\mu}_R \} $ basis, the smuon-mass matrix can be written as$ \begin{eqnarray} M^2_{ \tilde{\mu}} = \left( \begin{array}{cc} M_{L_2}^2 + (\sin^2 \theta_{W} - \dfrac{1}{2}) m_Z^2 \cos 2\beta & m_\mu (A_{E_2} - \mu\tan\beta) \\ m_\mu (A_{E_2} - \mu\tan\beta) & M_{E_2}^2 - m_Z^2\sin^2 \theta_{W} \cos 2\beta \end{array}\right) , \; \; \; \; \end{eqnarray} $

(6) where
$ M_{L_2, E_2} $ and$ A_{E_2} $ are the soft masses of left- and right-handed smuons and the trilinear couplings of smuons, respectively, and when$ M_{L_2, E_2}\gg m_Z, \sqrt{m_\mu A_{E_2}} $ and$ \sqrt{m_\mu \mu \tan \beta} $ , the mixing between$ \tilde{\mu}_L $ and$ \tilde{\mu}_R $ is negligible. Because neutrinos are left-handed and massless in the NMSSM, the mass of the muon neutrino's partner muon sneutrino$ m_{\tilde{\nu}} $ is related to the left-handed smuon mass by$ \begin{eqnarray} m^2_{ \tilde{\nu}} = M_L^2 + \frac{1}{2}m^2_Z\cos 2\beta \;. \end{eqnarray} $

(7) When
$ M_L\gg m_Z $ , the masses are approximately equal.The SUSY partners of the gauge bosons
$ W_{1,2,3}, \; B^0 $ , doublet Higgs, and singlet scalars are called winos, binos, higgsinos, and singlinos, respectively, and all have spin$ 1/2 $ and are written with a tilde. Among them, the charged ones mix into two pairs of charginos, and the neutral ones mix to form five neutralinos. In the$ \{ \tilde{W}^\pm, \tilde{H}^\pm \} $ base, the chargino-mass matrix can be written as$ \begin{eqnarray} M_{ \tilde{\chi}^\pm} = \left( \begin{array}{cc} M_2 & \sqrt{2}\,m_W \sin \beta \\ \sqrt{2}\,m_W \cos \beta & \mu \end{array} \right). \end{eqnarray} $

(8) In the
$ \{ \tilde{B}^0, \tilde{W}^0, \tilde{H}_u^0, \tilde{H}_d^0, \tilde{S} \} $ base, the neutralino-mass matrix can be written as$ \begin{eqnarray} M_{ \tilde{\chi}^0} = \left( \begin{array}{ccccc} M_{1} & 0 & -m_Z \cos \beta \sin \theta_W & m_Z \sin \beta\sin \theta_W & 0 \\ 0 & M_{2} & m_Z \cos \beta \cos \theta_W & -m_Z \sin \beta\cos \theta_W & 0 \\ -m_Z \cos \beta\sin \theta_W & m_Z \cos \beta\cos \theta_W & 0 & -\mu & -\lambda v_{d} \\ m_Z \sin \beta\sin \theta_W & -m_Z \sin \beta\cos \theta_W & -\mu & 0 & -\lambda v_{u} \\ 0 & 0 & -\lambda v_d & -\lambda v_u & 2\kappa \mu/\lambda \\ \end{array} \right) \,, \; \; \; \end{eqnarray} $

(9) where
$ v_u $ and$ v_d $ are the VEVs of$ H_u $ and$ H_d $ , respectively, with$ v_u/v_d=\tan\beta $ .The SUSY effects on
$ {{\rm{muon}}}\; g - 2 $ at the one-loop level are mainly from chargino-sneutrino loops and neutralino-smuon loops, with summations performed over all corresponding mass eigenstates. The contributions of these two types of loops can be written as [35]$ \begin{aligned}[b] \delta_n = & \frac{m_\mu}{16\pi^2} \sum_{i,m} \left[ -\frac{m_\mu}{12m^2_{ \tilde{\mu}_m}} \left( |n_{im}^L|^2 + |n^R_{im}|^2\right) F^N_1(x_{im}) \right.\\&\left. +\frac{m_{ \tilde{\chi}^0_i}}{3 m^2_{ \tilde{\mu}_m}} {{\rm{Re}}}\left(n^L_{im}n^R_{im}\right) F^N_2(x_{im}) \right], \end{aligned} $

(10) $ \begin{aligned}[b] \delta_c = & \frac{m_\mu}{16\pi^2}\sum_k \left[ \frac{m_\mu}{ 12 m^2_{ \tilde{\nu}_\mu}} \left(|c^L_k|^2 + |c^R_k|^2 \right) F^C_1(x_k) \right.\\&\left.+\frac{2m_{ \tilde{\chi}^\pm_k}}{3m^2_{ \tilde{\nu}_\mu}} {{\rm{Re}}} \left(c^L_kc^R_k\right) F^C_2(x_k) \right], \phantom{deltac} \end{aligned} $

(11) respectively, where the variables
$ x_{im}=m_{ \tilde{\chi}^0_i}^2/m_{ \tilde{\mu}_m}^2 $ and$ x_k=m_{ \tilde{\chi}^\pm_k}^2/m_{ \tilde{\nu}_\mu}^2 $ , with$i=1,2,3,4,5$ denoting five mass-eigenstate neutralino labels, and$ k=1,2 $ and$ m=1,2 $ denoting two mass-eigenstate chargino and smuon labels, respectively. Functions depending on$ x_{im}, x_k $ , which originate from loop integrals and are normalized, can be written as [35]$ \begin{eqnarray} F^N_1(x)= \frac{2}{(1-x)^4} \left( 1-6x+3x^2+2x^3-6x^2\ln x \right) \,, \end{eqnarray} $

(12) $ \begin{eqnarray} F^N_2(x)= \frac{3}{(1-x)^3} \left( 1-x^2+2x\ln x \right) \,, \end{eqnarray} $

(13) $ \begin{eqnarray} F^C_1(x)= \frac{2}{(1-x)^4} \left( 2+ 3x - 6x^2 + x^3 +6x\ln x\right) \,, \end{eqnarray} $

(14) $ \begin{eqnarray} F^C_2(x)=-\frac{3}{2(1-x)^3} \left( 3-4x+x^2 +2\ln x \right) \; . \end{eqnarray} $

(15) With these functions,
$ F_{1,2}^{N,C}(1) = 1 $ corresponds to the case in which SUSY particles degenerate. In addition, the corresponding coefficients are written as$ \begin{eqnarray} n^R_{im} = \sqrt{2} g_1 N_{i1} X_{m2} + y_\mu N_{i3} X_{m1}, \end{eqnarray} $

(16) $ \begin{eqnarray} n^L_{im} = \frac{1}{\sqrt{2}} \left(g_2 N_{i2} + g_1 N_{i1} \right) X_{m1}^* - y_\mu N_{i3} X^*_{m2}, \end{eqnarray} $

(17) $ \begin{eqnarray} c^R_k = y_\mu U_{k2}, \end{eqnarray} $

(18) $ \begin{eqnarray} c^L_k = -g_2V_{k1}, \end{eqnarray} $

(19) where
$ N_{ij} $ ,$ \{U_{kl}, V_{kl}\} $ , and$ X_{mn} $ are the mixing matrix of neutralinos, charginos, and smuons, respectively, defined as$ \begin{eqnarray} N^* M_{ \tilde{\chi}^0} N^\dagger = {{\rm{Diag}}} \left\{ m_{ \tilde{\chi}^0_1}, m_{ \tilde{\chi}^0_2}, m_{ \tilde{\chi}^0_3}, m_{ \tilde{\chi}^0_4} \right\}, \end{eqnarray} $

(20) $ \begin{eqnarray} U^* {M}_{ \tilde{\chi}^\pm} V^\dagger = {{\rm{Diag}}} \left\{ m_{ \tilde{\chi}^\pm_1}, m_{ \tilde{\chi}^\pm_2} \right\} \end{eqnarray}, $

(21) $ \begin{eqnarray} X M^2_{ \tilde{\mu}}\, X^\dagger = {{\rm{Diag}}} \left\{ m^2_{ \tilde{\mu}_1}, m^2_{ \tilde{\mu}_2} \right\} \;. \end{eqnarray} $

(22) Finally,
$ g_2 \simeq 0.66 $ and$ g_1 \simeq 0.36 $ are the${{SU(2)_L}}$ and${{U(1)_Y}}$ gauge couplings, respectively, and$ y_\mu \ll g_{1,2} $ is the muon Yukawa coupling.Considering that the SUSY particles in the loops, which are the neutralinos
$ \tilde{\chi}^0_{1,2,3,4,5} $ and smuons$ \tilde{\mu}_{1,2} $ , or the charginos$ \tilde{\chi}^\pm_{1,2} $ and muon sneutrino$ \tilde{\nu}_{\mu} $ , approximately have the same masses,$ \sqrt{m_{ \tilde{\chi}^0} m_{ \tilde{\mu}}} $ or$ \sqrt{m_{ \tilde{\chi}^\pm} m_{ \tilde{\nu}_\mu}} $ , their contributions to$ {{\rm{muon}}}\; g - 2 $ can be approximately written as [36]$ \begin{eqnarray} \delta_n \simeq \frac{1}{192\pi^2} \frac{ m_\mu^2}{m_{ \tilde{\chi}^0} m_{ \tilde{\mu}}}(g_1^2 - g_2^2) \tan \beta \,, \end{eqnarray} $

(23) $ \begin{eqnarray} \delta_c \simeq \frac{1}{32\pi^2} \frac{ m_\mu^2}{m_{ \tilde{\chi}^\pm} m_{ \tilde{\nu}_{\mu}}}g_2^2 \tan \beta \;. \end{eqnarray} $

(24) -
In this study, we first scan the parameter space of the NMSSM with
$ \mathbb{Z}_3 $ -symmetry to obtain surviving samples under corresponding theoretical and experimental constraints. To focus on the light smuon, a light colorless SUSY particle preferred by the$ {{\rm{muon}}}\; g - 2 $ anomaly, we assume colored SUSY particles and heavy Higgs to be heavy and fix them to 5 TeV :$ \begin{eqnarray} M_A,M_3,M_{Q_i},M_{U_i},M_{D_i} = 5~{\rm{TeV}} \,, \quad A_{U_i},A_{D_i} = 0 ~{\rm{TeV}} \,, \end{eqnarray} $

(25) where
$ M_A,M_3,M_{Q_i},M_{U_i},M_{D_i} $ are the soft masses of the heavy Higgs, gluino, left-handed squarks, right-handed up-type squarks, and right-handed down-type squarks, respectively, and$ A_{U_i},A_{D_i} $ are the trilinear couplings of up- and down-type squarks, respectively, with the generation index$ i=1,2,3 $ . The other required parameters correlated with light and colorless SUSY particles are set as$ \begin{aligned}[b] & 0<\lambda, |\kappa|<0.8, \quad 1<\tan\beta <100 \,, \\ & 0<\mu, M_1, M_2, M_P<1~{\rm{TeV}} \,, \\ & 0<M_{L_i},M_{E_i},|A_{E_i}|<10~{\rm{TeV}} \,. \end{aligned} $

(26) To considerably differ from former studies that used
$ \tilde{\tau}_1 $ as the lightest slepton, we also manually require$ m_{\tilde{\tau}_1} > m_{ \tilde{\mu}_1} $ .The model spectrum, including masses and decay information, is calculated with
$\textsf{NMSSMTools-5.5.4}$ [82–84]. The corresponding constraints we consider in our scan are listed briefly as follows:● Theoretical constraints from a stable vacuum (the effective scalar potential gets its least value when all scalar fields equal to their VEVs) and the inexistent Landau pole below the GUT scale [82, 83, 85].
● LEP constraints on chargino and slepton masses heavier than approximately 100 GeV.
● Flavor constraints, such as rare B-meson decays and the mass differences
$ \Delta m_d $ and$ \Delta m_s $ [86–89].● A Higgs boson of
$ 122 \sim 128$ GeV with signal predictions consistent with Higgs data at the LHC [90–92]①.● Constraints from searches for additional Higgs and exotic decays of SM-like Higgs, imposed with
$\textsf{HiggsBounds-5.10.1}$ [95–99].● Upper bounds of the DM relic density
$ \Omega h^2 \le 0.131 $ from WMAP/Planck [100, 101], with the relevant quantities calculated using$\textsf{micrOMEGAs 5.0}$ [102–105].● Constraints on direct searches for DM, the spin-independent case by XENON1T [106], and the spin-dependent case by LUX [107], XENON1T [108], and PICO-60 [109], where the original values are rescaled by
$ \Omega/\Omega_0 $ accordingly.● The constraints from
$ {{\rm{muon}}}\; g - 2 $ at the$ 2\sigma $ level, where we use the combined experimental value$a_\mu^{ {{\rm{ex}}}} = (11659206.1 \pm 4.1) \times 10^{-10}$ [1] and calculate the SM value$ a_\mu^{ {{\rm{SM}}}} $ without the Higgs contribution, considering that the NMSSM contains a SM-like Higgs. Including the theoretical error on SUSY contributions, we obtain the range of$ \delta a_\mu\equiv a_\mu^{ {{\rm{ex}}}} -a_\mu^{ {{\rm{SM}}}} $ as$ (6.1 \sim 45.0) \times 10^{-10} $ at the$ 2\sigma $ level.Moreover, in imposing constraints from SUSY searches, we exploit
$\textsf{SModelS 2.1.1}$ [110–118] with official database version$\textsf{2.1.0}$ [119]. To focus on the status of the smuon, we pay special attention to the constraints on smuon searches in Refs. ATLAS-SUSY-2018-32 [77] and CMS-SUS-17-009 [78]. In these analyses of smuons, they were assumed to be produced in pairs and$ 100\ $ % decay into a muon lepton and the lightest neutralino; thus, the final state is composed of two opposite-charge and same-flavor leptons (dimuon) and a large missing transverse momentum$\overrightarrow {\not {p}} _T$ . However, no significant excess over the SM background was recorded in either report. The ATLAS analysis was based on$139~{\rm{f}}{{\rm{b}}^{ - 1}}$ of data at the 13 TeV LHC, and smuon masses up to approximately 600 GeV were excluded with the massless lightest neutralino. For consistency with these analyses, we employ$\textsf{Resummino 3.0}$ [120–126] to calculate the smuon production at the 13-TeV LHC at the next-to leading order (NLO).$ \begin{equation} p p \to \tilde{\mu}^+_L \tilde{\mu}^-_L,\qquad p p \to \tilde{\mu}^+_R \tilde{\mu}^-_R \, , \end{equation} $

(27) where
$ \tilde{\mu}_L $ and$ \tilde{\mu}_R $ are the SUSY partners of the left- and right-handed muon leptons, respectively, and the cross-section of the former is times larger than the latter. Thus,$ \tilde{\mu}_L $ is more constrained than$ \tilde{\mu}_R $ , and we mainly study$ \tilde{\mu}_L $ , denoting it as a muon or$ \tilde{\mu} $ in this paper. Because this is a real model NMSSM, we calculate the real branching ratios, including smuon decay into a muon lepton and the lightest neutralino, that is,$ Br(\tilde{\mu}^- \to \tilde{\chi}^0_1 + \mu^-) $ . We constrain our samples by requiring the cross-section timing branching ratio to be below the corresponding exclusion curves from the ATLAS and CMS collaborations.Finally, we obtain the surviving samples that satisfy all the above constraints and present them in the following figures.
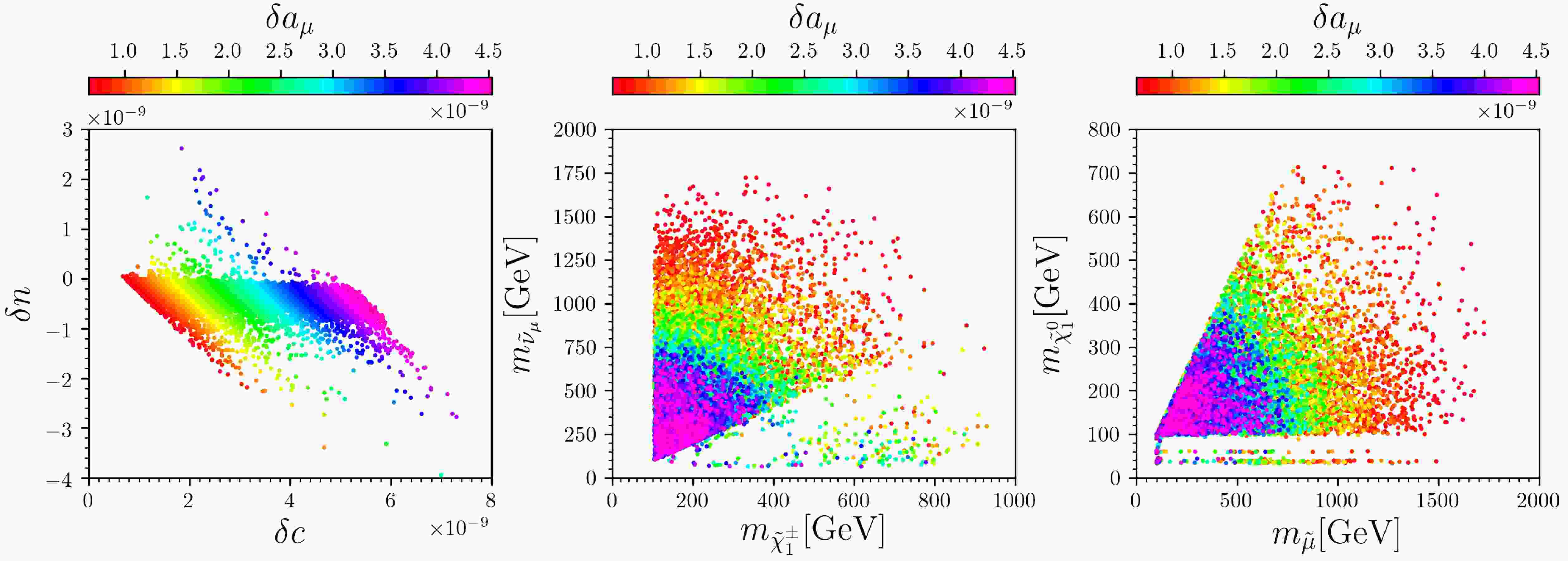
To study the dependence of
$ {{\rm{muon}}}\; g - 2 $ on smuon mass, we display the surviving samples in Fig. 1, from which we determine the following facts:
Figure 1. (color online) Surviving samples projected in the
$ \delta_n $ versus$ \delta_c $ (left),$ m_{ \tilde{\mu}_\mu} $ versus$ m_{ \tilde{\chi}^\pm_1} $ (middle), and$ m_{ \tilde{\chi}^0_1} $ versus$ m_{ \tilde{\mu}} $ (right) planes, where$ \tilde{\mu} $ is the SUSY partner of the left-handed muon lepton,$ \delta a_\mu $ is the SUSY contribution to$ {{\rm{muon}}}\; g - 2 $ , and$ \delta_c $ and$ \delta_n $ are the chargino-sneutrino and neutralino-smuon contributions to$ \delta a_\mu $ , respectively. In all the planes, colors indicate$ \delta a_\mu $ , and samples with larger$ \delta a_\mu $ are projected on top of smaller ones.● The
$ {{\rm{muon}}}\; g - 2 $ anomaly can be interpreted within$ 1\sigma $ . For$ 1 \sigma $ samples, muon sneutrinos and left-handed smuons are lighter than 1000 GeV , the light charginos are lighter than 900 GeV, and the lightest neutralinos are lighter than 600 GeV.● For most surviving samples,
$ m_{ \tilde{\chi}^\pm_1} \approx m_{ \tilde{\chi}^0_1} $ and$ m_{ \tilde{\mu}} \approx m_{ \tilde{\nu}_\mu} $ ; thus, their distributions in the middle and right planes have almost the same shapes. We verify that for most of these samples, the lightest neutralinos are wino- or higgsino-dominated, the same as the light chargino. For the other samples,$ m_{ \tilde{\chi}^\pm_1} > m_{ \tilde{\chi}^0_1} $ , and the lightest neutralinos are bino- or singlino-dominated.● The SUSY contribution to
$ {{\rm{muon}}}\; g - 2 $ is approximately equal to the sum of chargino-sneutrino and neutralino-smuon loops ($ \delta a_\mu \approx \delta_c + \delta_n $ ), and for most samples, the former dominates ($ \delta_c > \delta_n $ ), even when the lightest neutralinos and smuons are very light. From Eqs. (23) and (24), we know that this makes sense because$ g_2^2/32 \gg (g_1^2 - g_2^2)/192 $ . Furthermore, we check that the contributions are both proportional to$ \tan \beta $ and verify that$ \delta_n $ can be both positive and negative because of the different masses of the five neutralinos and two smuons.To study the constraints on smuon searches at the LHC, we display the surviving samples in Fig. 2, where the solid and dotted curves denote the corresponding exclusion limits at the 95% confidence level from the ATLAS [77] and CMS collaborations [78]. From this figure we can find that

Figure 2. (color online) Surviving samples projected in the
$ m_{ \tilde{\chi}^0_1} $ versus$ m_{ \tilde{\mu}} $ planes, where$ \tilde{\mu} $ is the SUSY partner of the left-handed muon lepton. Colors indicate the branching ratios$ Br(\tilde{\mu}^- \to \tilde{\chi}^0_1 + \mu^-) $ (left), the μ (middle), and$ M_2 $ parameters (right). The dashed line of$ m_{ \tilde{\chi}^0_1} = m_{ \tilde{\mu}} $ indicates that the smuon and$ \tilde{\chi}^0_1 $ are mass-degenerate, and the solid and dotted curves are the exclusion limits at the$ 95\ $ % CL from direct searches for smuons given by the ATLAS [77] and CMS collaborations [78], respectively. Samples with larger$ Br(\tilde{\mu}^- \to \tilde{\chi}^0_1 + \mu^-) $ are projected on top of smaller ones.● For surviving samples below the exclusion curve by ATLAS, all the branching ratios of
$ Br(\tilde{\mu}^- \to \tilde{\chi}^0_1 + \mu^-) $ are lower than$ 50\ $ % because the large values are excluded in the experiments. We check that for these surviving samples, the lightest neutralinos are either higgsino-dominated, with masses approximating to the μ parameter, or wino-dominated, with masses approximating to the$ M_2 $ parameter. Thus,$ m_{ \tilde{\chi}^\pm_1} \approx m_{ \tilde{\chi}^0_1} \approx \min\{\mu, M_2\} $ , and the smuon also decays with a sizable branching ratio to a light chargino plus muon sneutrino.● For surviving samples with a mass-degenerate smuon and
$ \tilde{\chi}^0_1 $ , all the branching ratios$ Br(\tilde{\mu}^- \to \tilde{\chi}^0_1 + \mu^-) $ are nearly$ 100\ $ % because the current experimental results of direct searches are powerless in the compressed SUSY spectrum.To illustrate the implication of light smuons for DM, we display the surviving samples in Fig. 3, where
$ N_{11}^2 $ denotes the bino component in the LSP dark matter$ \tilde{\chi}^0_1 $ , and$ N_{12}^2 $ denotes the corresponding wino component. From this figure, we can learn the following:
Figure 3. (color online) Surviving samples projected in the
$ m_{ \tilde{\chi}^0_1} $ versus$ m_{ \tilde{\mu}} $ planes, where$ \tilde{\mu} $ is the SUSY partner of the left-handed muon lepton. Colors indicate$ N_{11}^2 $ (left),$ N_{12}^2 $ (middle), and$ \Omega h^2 $ (right), where$ N_{11}^2 $ and$ N_{12}^2 $ indicate the ratios of the bino and wino components in$ \tilde{\chi}^0_1 $ , respectively, and$ \Omega h^2 $ indicates the relic density of the LSP dark matter$ \tilde{\chi}^0_1 $ . Samples with larger$ \Omega h^2 $ are projected on top of smaller ones.● For most of the surviving samples with right relic density or Z- or
$ h_1 $ -funnel annihilation, the LSP DM$ \tilde{\chi}^0_1 $ is bino-dominated. Some others are singlino-dominated.● For most of the surviving samples with a mass-degenerate smuon and
$ \tilde{\chi}^0_1 $ , the LSP DM$ \tilde{\chi}^0_1 $ is bino-dominated, and we check that the dominating annihilation mechanism is slepton annihilation. These samples constitute a large part of samples with right relic density only with the LSP$ \tilde{\chi}^0_1 $ .● For all the surviving samples with wino-dominated
$ \tilde{\chi}^0_1 $ , the relic density is insufficient because of mass-degenerate charginos; however, it is larger than that of higgsino-dominated-$ \tilde{\chi}^0_1 $ samples (in all three planes, samples with larger$ \Omega h^2 $ are projected on top of smaller ones, and in the middle plane, wino-dominated-$ \tilde{\chi}^0_1 $ samples are covered by higgsino-dominated-$ \tilde{\chi}^0_1 $ samples).In addition, we also list detailed information on six benchmark points for further study in Table 1.
BP1 BP2 BP3 BP4 BP5 BP6 λ 0.0803 0.0015 0.0367 0.0260 0.187 0.0363 κ 0.667 –0.663 0.553 –0.0047 –0.606 –0.630 $ \tan \beta $ 

70 69 46 13 55 43 μ 796 567 440 310 699 479 $ M_1 $ 

464 34 60 931 340 198 $ M_2 $ 

689 448 941 150 337 890 $ M_{L2} $ 

471 709 119 143 638 217 $ M_{E2} $ 

640 1480 1250 368 2160 575 $ A_{E2} $ 

77 –1190 –1500 32 –524 5.0 $ m_{ \tilde{\chi}^0_1} $ /GeV

461 34 59 115 336 196 $ m_{ \tilde{\chi}^0_2} $ /GeV

712 463 449 150 361 489 $ m_{ \tilde{\chi}^\pm_1} $ /GeV

712 463 449 151 361 488 $ m_{ \tilde{\chi}^\pm_2} $ /GeV

846 610 1010 346 727 957 $ N_{11}^2 $ 

0.99 0.99 0.99 0.00 0.98 0.99 $ N_{12}^2 $ 

0.00 0.00 0.00 0.00 0.01 0.00 $ N_{13}^2 + N_{14}^2 $ 

0.01 0.01 0.01 0.00 0.01 0.01 $ N_{15}^2 $ 

0.00 0.00 0.00 1.00 0.00 0.00 $ N_{21}^2 $ 

0.00 0.00 0.01 0.00 0.02 0.01 $ N_{22}^2 $ 

0.76 0.81 0.01 0.87 0.96 0.02 $ N_{23}^2 + N_{24}^2 $ 

0.24 0.19 0.98 0.13 0.02 0.97 $ m_{ \tilde{\mu}_L} $ /GeV

470 709 119 143 638 217 $ m_{ \tilde{\mu}_R} $ /GeV

640 1480 1250 368 2160 575 $ m_{ \tilde{\nu}_\mu} $ /GeV

464 705 92 121 633 203 ${\rm Br}(\tilde{\mu}^- \to \tilde{\chi}^0_1 + \mu^-)$ 

1.00 0.28 1.00 1.00 0.07 1.00 ${\rm Br}(\tilde{\mu}^- \to \tilde{\chi}^0_2 + \mu^-)$ 

0.00 0.24 0.00 0.00 0.34 0.00 ${\rm Br}(\tilde{\mu}^- \to \tilde{\chi}^\pm_1 + \nu_\mu)$ 

0.00 0.44 0.00 0.00 0.59 0.00 $ \delta a_\mu [\times 10^{-10}] $ 

21.8 22.8 28.2 41.7 20.5 24.3 $ \Omega h^2 $ 

0.126 0.120 0.115 0.120 0.109 0.117 $ p_h $ 

0.923 0.928 0.849 0.928 0.920 0.920 Table 1. Detailed information on six benchmark points, where
$ N_{i1}^2 $ ,$ N_{i2}^2 $ ,$ N_{i3}^2 + N_{i4}^2 $ , and$ N_{i5}^2 $ indicate the ratios of the bino, wino, higgsino, and singlino components in the neutralinos$ \tilde{\chi}^0_i $ , respectively. Moreover,$ \tilde{\mu}_L $ ($ \tilde{\mu}_R $ ) is the SUSY partner of the left-handed (right-handed) muon lepton, and$ \tilde{\mu}_L $ is the smuon that we investigate in this study. -
In this study, motivated by recent SUSY search results, which prefer most SUSY particles to be heavy, and the
$ {{\rm{muon}}}\; g - 2 $ anomaly, which prefers colorless SUSY particles to be light, we explore the status of the smuon (the SUSY partner of the left-handed muon lepton) in the NMSSM. Assuming that colored SUSY particles are heavy, and considering numerous experimental constraints, including the$ {{\rm{muon}}}\; g - 2 $ , SUSY searches, and DM, we scan the parameter space in the NMSSM with$ \mathbb{Z}_3 $ -symmetry and check the status of colorless SUSY particles and their possible mass order, paying special attention to the status of a smuon confronted with$ {{\rm{muon}}}\; g - 2 $ and direct SUSY searches. We also investigate their implication for DM.We draw the following conclusions regarding the smuon,
$ {{\rm{muon}}}\; g - 2 $ , SUSY searches, and DM in the NMSSM:● The dominated SUSY contributions to
$ {{\rm{muon}}}\; g - 2 $ originate from chargino-sneutrino loops; however, the$ {{\rm{muon}}}\; g - 2 $ anomaly can also constrain the mass of smuons seriously because of the mass-degenerate relationship between smuons and muon sneutrinos. To interpret the$ {{\rm{muon}}}\; g - 2 $ anomaly at the$ 1\sigma $ ($ 2\sigma $ ) level, the smuon must be lighter than 1 TeV (1.8 TeV).● When
$ \tilde{\chi}^0_1 $ is wino- or higgsino-dominated, the smuon and muon sneutrino,$ \tilde{\chi}^\pm_1 $ and$ \tilde{\chi}^0_1 $ , respectively, are usually mass-degenerate. Thus, the branching ratio$ Br(\tilde{\mu}^- \to \tilde{\chi}^0_1 + \mu^-) $ is suppressed to lower than$ 50\ $ %, and the smuon can escape from direct searches with low mass, e.g., 300 GeV.● When the smuon and
$ \tilde{\chi}^0_1 $ are mass-degenerate, the smuon can be as light as 200 GeV, whereas the$ \tilde{\chi}^0_1 $ is usually bino-dominated or sometimes singlino-dominated, and its relic density can most likely reach the observed value. The dominating annihilation mechanism is slepton annihilation.Moreover, we emphasize again that this study is performed in the NMSSM with
$ \mathbb{Z}_3 $ symmetry, which includes no large free parameters in the superpotential but may cause the so-called 'domain wall' problem in cosmology. This problem can be solved by introducing$ \mathbb{Z}_3 $ -breaking terms, such as$ \xi m_s^3 S $ [127]. This term may have an effect on the singlino sector and DM phenomenology when it is singlino-dominated. Because the chargino-sneutrino contribution to$ {{\rm{muon}}}\; g - 2 $ dominates in our study, and$ \kappa/\lambda $ is arbitrary in the singlino or DM sector, the$ \mathbb{Z}_3 $ -breaking terms from the singlet field have little effect on the mass region of the smuon.Note added: The uncertainty on the SM theoretical value of
$ {{\rm{muon}}}\; g - 2 $ is dominated by hadronic vacuum polarization (HVP), which can be calculated using the data-driven method, as quoted in the experimental report of the$ {{\rm{muon}}}\; g - 2 $ collaboration [1] and this paper, or the lattice method. In 2020, the BMW collaboration released their lattice result for the HVP contribution [128], which was considerably different from the quoted data-driven result. Recently, another group released a new lattice result [129], independently showing agreement with the 2020 BMW value. Employing the two lattice results for the HVP contribution, the$ {{\rm{muon}}}\; g - 2 $ anomaly can change to$ \delta a_{\mu} = 10.4\pm 7.0 \times 10^{-10} $ , with the significance changing to$ 1.5\sigma $ . We verified that there are still samples in the smuon mass region as low as 0.1 TeV that can satisfy this$ \delta a_{\mu} $ value at the$ 2\sigma $ level, and the surviving samples can have smuon masses higher than 1.8 TeV.
Smuon in the NMSSM confronted with the muon g–2 anomaly and SUSY searches
- Received Date: 2022-08-15
- Available Online: 2023-01-15
Abstract: Motivated by recent supersymmetry (SUSY) search results, which prefer most SUSY particles to be heavy, and the muon g–2 anomaly, which prefers colorless SUSY particles to be light, we explore the status of a light smuon (the SUSY partner of a left-handed muon lepton) in the next-to-minimal supersymmetric standard model (NMSSM). Assuming colored SUSY particles to be heavy, and considering numerous experimental constraints, including muon g-2, SUSY searches, and dark matter, we scan the parameter space in the NMSSM with






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: