-
Heavy-ion collision experiments conducted at the BNL Relativistic Heavy-Ion Collider (RHIC) and the CERN Large Hadron Collider (LHC) provide a unique opportunity to study the color deconfined state of nuclear matter, known as quark-gluon plasma (QGP) [1]. Heavy quarks serve as a clean probe that reveals QGP properties at different energy scales [2, 3]. Owing to the large mass of heavy quarks, they are mainly produced from the very early hard scatterings of high-energy nuclear collisions, prior to the formation of QGP. They then propagate through the medium and observe the entire evolution history of QGP before they hadronize. Therefore, the difference in heavy flavor observables between proton-proton (p+p) and nucleus-nucleus (A+A) collisions characterizes the transport properties of QGP [4, 5].
Considerable effort has been devoted to developing transport models for heavy quarks to understand their dynamics inside hot nuclear matter. It is now generally accepted that at high transverse momentum (
$p_{T}$ ), perturbative calculations that involve both elastic and inelastic scatterings between heavy quarks and QGP provide a successful description of the nuclear modification factor ($R_{AA}$ ) of heavy flavor hadrons [6–12]. At intermediate$p_{T}$ , a combination of fragmentation and coalescence mechanisms is essential in understanding the hadronization process of heavy quarks and thus describing the heavy flavor hadron chemistry observed at the RHIC and LHC [13–16]. At low$p_{T}$ , modeling the non-perturbative scatterings between heavy quarks and the medium becomes inevitable to understand their strong interactions, as revealed by the large elliptic flow coefficients of D mesons [17–21]. In addition to$R_{AA}$ and$ v_2 $ , novel observables have also been proposed to place more stringent constraints on the heavy quark dynamics inside QGP, such as the momentum imbalance and angular correlation between heavy meson pairs [22, 23], correlation of the higher-order harmonic flow coefficients between heavy and light flavor hadrons [24], and inner structures of heavy-flavor tagged jets [25, 26].The directed flow coefficient (
$ v_1 $ ) of heavy quarks is another observable of great interest owing to the copious information of the medium properties it encodes. It was proposed that due to the asymmetric distribution of nuclear matter along the longitudinal direction, the heavy meson$ v_1 $ could be more than an order of magnitude larger than the light flavor hadrons emitted from QGP [27–29]. This was soon confirmed by the STAR measurement [30] and attracted many further studies [31–33] that couple various transport models to a tilted QGP fireball in the reaction plane [34]. Meanwhile, the splitting of$ v_1 $ ($ \Delta v_{1} $ ) between heavy quarks and their anti-particles is also considered an effective tool to probe the extremely strong electromagnetic field generated by non-central heavy-ion collisions because of the opposite Lorentz forces exerted on them [27, 28, 31, 33, 35, 36]. Interestingly, while a decreasing$ v_1 $ with respect to rapidity (y) was observed for both$ D^{0} $ and$ \bar{D}^{0} $ at STAR [30] with small difference between them, apparent splitting of$ v_1 $ was seen by ALICE [37] with$ D^{0} $ increasing but$ \bar{D}^{0} $ decreasing with respect to pseudorapidity (η). This puzzling observation implies competing effects between the longitudinally tilted medium geometry and the electromagnetic field on the heavy flavor$ v_1 $ at the RHIC and LHC.In our previous study [33], we found that while the formation of heavy flavor
$ v_1 $ is dominated by the deformed medium profile at the RHIC energy, it is mainly determined by the electromagnetic field at the LHC. As a follow-up study, we focus here on 200 A GeV Au+Au collisions at the RHIC and conduct a systematic exploration of how heavy quarks can be utilized to probe the initial energy density distribution of QGP. In addition to D mesons,$R_{AA}$ ,$ v_1 $ , and$ v_2 $ are also calculated for B mesons and their decayed electrons. We study the transverse momentum dependence of the heavy flavor$ v_1 $ and extract the slope parameter of the$ v_1(y) $ function, which can be tested by more precise future measurements and will help quantify the tilt of QGP in its initial state. Finally, the difference in the heavy flavor$R_{AA}$ between different angular regions is also investigated as an alternative tool to characterize the asymmetry of the medium along different directions.This paper is organized as follows. In Sec. II, we provide a brief overview of our model setup, including a tilted initial condition of the bulk medium with respect to the longitudinal direction and its evolution via the CLVisc hydrodynamic model in Sec. II.A, and a modified Langevin approach that describes the heavy quark interaction with QGP is presented in Sec. II.B. In Sec. III, we present our numerical results on the heavy flavor
$R_{AA}$ ,$ v_{1} $ , and$ v_{2} $ and study how they depend on the heavy quark mass, transverse momentum, and medium geometry. Finally, we summarize the study and discuss future developments in Sec. IV. -
In this study, the spacetime evolution profile of QGP is calculated using the (3+1)-dimensional viscous hydrodynamic model CLVisc [38–41]. The initial energy density distribution is modeled with a parameterization that takes into account a tilt of the medium produced by non-central heavy-ion collisions [42, 43]. Its dependence on the transverse coordinates
$ (x,y) $ and spacetime rapidity$(\eta_{s})$ is given by$ \begin{aligned}[b] \varepsilon(x,\;y,\eta_{s})=& K \cdot \frac{0.95W_{N}(x,y,\eta_{s})+0.05 n_\text{BC}(x,y)}{\left[0.95W_{N}(0,0,0)+0.05 n_\text{BC}(0,0)\right]|_{\boldsymbol{b}=0}}\\ &\times \exp\left[-\frac{(|\eta_{s}|-\eta_{w})^{2}}{2\sigma^{2}_{\eta}}\theta(|\eta_{s}|-\eta_{w}) \right], \end{aligned} $

(1) where K is an overall normalization factor that is fixed by the multiplicity distribution of the final charged particles (
${\rm d} N_{ \rm{ch}}/{\rm d}\eta$ ) observed in experiments,$ n_\text{BC} $ is the distribution of binary collision points from the Glauber model,$\boldsymbol{b}$ represents the impact parameter, and$W_{N}$ is the distribution of wounded nucleons, parameterized as$ \begin{aligned}[b] W_{N}(x,y,\eta_{s})=&[T_{1}(x,y)+T_{2}(x,y)]\\ &+H_{t}[T_{1}(x,y)-T_{2}(x,y)]\tan\left(\frac{\eta_{s}}{\eta_{t}}\right). \end{aligned} $

(2) Here,
$ T_1(x,y) $ and$ T_2(x,y) $ are the density distributions of participant nucleons from the projectile and target nuclei propagating along the positive and negative longitudinal (z) directions, respectively, and$H_{t}\tan (\eta_{s}/\eta_{t})$ is introduced to model the imbalance of hadron emission between forward and backward rapidities. In addition, at the end of Eq. (1), an envelope function in the Gaussian form is used to describe the plateau structure of the hadron yield observed at mid-rapidity, in which$\eta_{w}$ is the width of the central rapidity plateau, and$ \sigma_{\eta} $ controls the speed of decay away from the plateau region [39]. In Table 1, we summarize all related model parameters introduced above. These values have been adjusted from Ref. [43] for a satisfactory description of the light hadron yield${\rm d} N_{\mathrm{ch}}/{\rm d}\eta$ and the directed flow coefficient$ v_{1} $ measured at the RHIC and LHC.$ \tau_{0} $ /(fm/c)

K/(GeV/fm $ ^{3} $ )

$\eta_{w}$ 

$ \sigma_{\eta} $ 

$\eta_{t}$ 

$T_{ \rm{frz} }/\rm{MeV}$ 

0.6 35.5 1.3 1.5 8.0 137 Table 1. Model parameters of the initial condition and hydrodynamic evolution for Au+Au collisions at
$\sqrt{s_{NN}}$ = 200 GeV. The tilted parameter$ H_\mathrm{t} $ for centrality bins 0–10% ($ b = 3.4 $ fm), 10%–40% ($ b = 7.6 $ fm), and 10%–80% ($ b=8.5 $ fm) are 1.3, 3.0, and 3.9, respectively. Here, b is the impact parameter.The initial fluid velocity is assumed to follow the Bjorken approximation, where
$ v_{x} = v_{y} =0 $ , and$ v_{z} = z/t $ [42]. The initial transverse expansion and asymmetric distribution of$ v_z $ along the impact parameter (x) direction are neglected in the present study, although the latter will become crucial when discussing the development of global polarization in heavy-ion collisions [44].With these setups, we present a three-dimensional profile of nuclear matter at the initial time of hydrodynamic evolution
$ \tau_0=0.6 $ fm/c in Fig. 1; the upper panel shows a side view ($ \eta_\mathrm{s} $ -x plane) of the energy density distribution, and the lower panel shows a top view (x-y plane) of the temperature distribution. In the figure, a clear counter-clockwise tilt of the medium in the$ \eta_\mathrm{s} $ -x with respect to the longitudinal direction ($ \eta_\mathrm{s} $ ) can be observed, which has been shown to be essential for understanding the non-zero directed flow of soft hadrons emitted from QGP [43]. However, because heavy quarks are produced in the initial hard scatterings of nuclear collisions, they are expected to distribute symmetrically around the center$ (0,0) $ of the overlapping region between the two colliding nuclei. As a result, they propagate through different path length, and thus experience different amounts of energy loss, toward different directions at finite rapidity. For instance, at forward rapidity ($ y>0 $ ), heavy quarks traverse longer path length toward$ +x $ (right) than$ -x $ (left), resulting in a negative x-component of the average heavy quark momentum ($ \langle p_x\rangle $ ) in the end.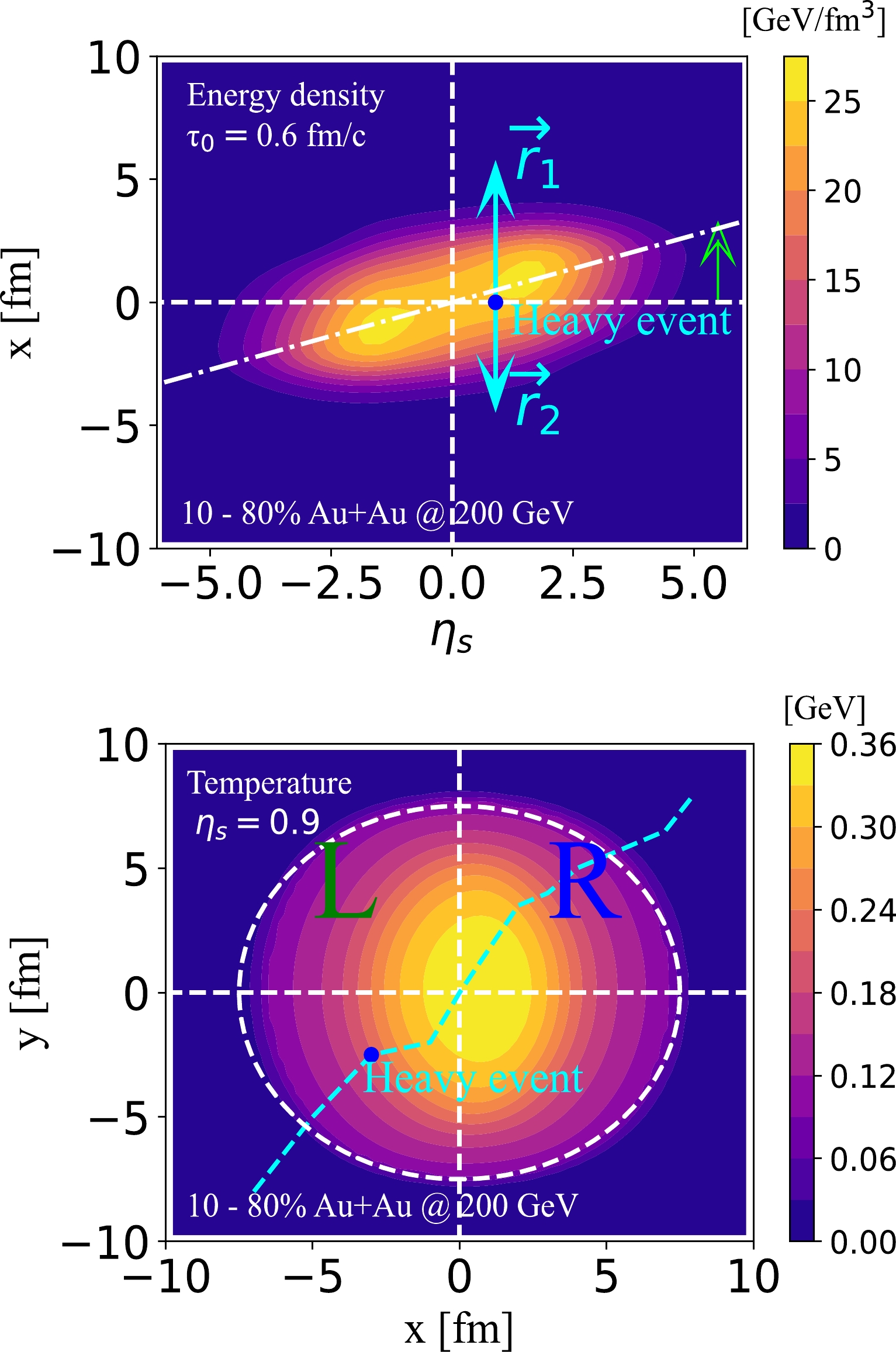
Figure 1. (color online) Initial profile of QGP at
$ \tau_0 = 0.6 $ fm/c for 10%–80% ($ b = 8.5 $ fm) Au+Au collisions at$\sqrt{s_{NN}}=200$ GeV; upper panel for a side view of the energy density distribution, and lower panel for a top view of the temperature distribution. The solid arrows$ \vec{r}_{1} $ and$ \vec{r}_{2} $ (aqua color) indicate the heavy quark propagation, and the empty arrow (limes color) denotes the counter-clockwise tilt of the medium in the$ \eta_\mathrm{s} $ -x plane.With the tilted initial condition above, we use the CLVisc hydrodynamic model to evolve the QGP profile. The hydrodynamic equation reads as
$ \begin{equation} \partial_{\mu}T^{\mu\nu}=0, \end{equation} $

(3) where the energy-momentum tensor
$ T^{\mu\nu} $ is given by$ \begin{equation} T^{\mu\nu}=\varepsilon u^{\mu}u^{\nu}-(P+\Pi)\Delta^{\mu\nu} + \pi^{\mu\nu}, \end{equation} $

(4) where ε is the local energy density,
$ u^{\mu} $ is the fluid four velocity, P is the pressure, Π is the bulk viscosity pressure, and$ \pi^{\mu\nu} $ is the shear viscosity tensor. In addition,$ \Delta^{\mu\nu} = g^{\mu\nu}-u^{\mu}u^{\nu} $ is the projection operator with the metric tensor$ g^{\mu\nu} = \text{diag} (1,-1,-1,-1) $ . In this study, the shear-viscosity-to-entropy-density-ratio is set as$\eta_{v}/s = 0.08$ ($\eta_{v}$ for the shear viscosity), whereas the bulk viscosity and net baryon density are ignored. The equation of state (EoS) is taken from the Wuppertal-Budapest study [45]. After hydrodynamic evolution, the QGP medium is converted to light flavor hadrons according to the Cooper-Frye mechanism, with the isothermal freeze-out condition determined with a constant temperature$ T_{ \rm{frz}}=137 $ MeV. These setups allow a reasonable description of the soft hadron spectra and their directed and elliptic flow coefficients observed at the RHIC and LHC [39, 42, 43]. -
The interactions between heavy quarks and the QGP medium are described using our modified Langevin approach [9, 46] that includes both elastic and inelastic scattering processes. The modified Langevin equation reads as
$ \frac{{\rm d}\vec{p}}{{\rm d} t}=-\eta_{D}(\vec{p})\vec{p}+\vec{\xi}+\vec{f}_{g}, $

(5) where
$-\eta_{D}(\vec{p})\vec{p}$ provides the drag force, and$ \vec{\xi} $ gives the thermal random force on heavy quarks inside a thermal medium. The third term$ \vec{f}_{g} $ is introduced to describe the recoil force experienced by heavy quarks when they emit medium-induced gluons.For quasielastic scatterings, we assume that
$ \vec{\xi} $ is independent of momentum ($ \vec{p} $ ) in the present study. Its strength is determined by the white noise$\big\langle \xi^i (t) \xi^j(t') \big\rangle = \kappa \delta^{ij} \delta(t-t')$ , where κ is the momentum space diffusion coefficient of heavy quarks. Here, κ is further related to the drag coefficient via the fluctuation-dissipation relation$ \eta_\mathrm{D}(p)=\kappa/(2TE) $ , with T and E being the medium temperature and heavy quark energy, respectively. The spatial diffusion coefficient of heavy quarks can then be extracted as$ D_\mathrm{s}\equiv T/[M\eta_\mathrm{D}(0)]=2T^2/\kappa $ , in which M is the heavy quark mass. This$D_{s}$ is treated as the only model parameter for our modified Langevin approach [23, 46]. For a minimal model, a constant value of$D_{s}(2\pi T)$ is used in this study, which is determined by the$R_{AA}$ of heavy mesons and their decayed electrons, as shown in the next section. A more elaborate dynamical calculation of this diffusion coefficient was developed in our recent investigation based on a non-perturbative potential scattering approach [21], which can also be implemented in this Langevin model in future studies.The recoil force in Eq. (5) is given by
$\vec{f_g}=-{\rm d}\vec{p}_g/{\rm d}t$ , where$ \vec{p}_g $ denotes the momentum of medium-induced gluons, whose spectrum can be taken from the higher-twist energy loss calculation [47–49]. The strength of this term is characterized by the jet quenching parameter$ \hat{q} $ , which can be directly related to the momentum space diffusion coefficient of heavy quarks via a dimension factor –$ \hat{q}=2\kappa $ [9] – and is further connected to the$D_{s}$ parameter discussed earlier. Details on the balance between gluon radiation and absorption are not rigorously included in our current study owing to the lack of the latter process; however, a lower cutoff$ \omega_{0} $ =$ \pi T $ is imposed for the gluon energy to exclude net gluon emission below the thermal scale. The mass effects of quark energy loss are included in both the mass dependence of the medium-induced gluon spectrum and heavy quark transport coefficients.For heavy quark production and evolution in realistic heavy-ion collisions, we initialize the spatial distributions of heavy quarks using the Monte-Carlo Glauber model, and their momentum spectra using the Fixed-Order-Next-to-Leading-Log (FONLL) perturbative QCD calculation [50–52] that includes both pair production and flavor excitation processes. In this study, the FONLL calculation is coupled to the CT14NLO parton distribution function (PDF) [53] and the EPPS16 parameterization [54] of nuclei to consider the nuclear shadowing effect in heavy-ion collisions. We assume that the interactions between heavy quarks and QGP start from the initial time (
$ \tau_0=0.6 $ fm/c) of the hydrodynamic evolution of nuclear matter. During the QGP stage, the energy-momentum of heavy quarks is updated according to Eq. (5) in the local rest frame of QGP. The local temperature and flow velocity information of QGP are provided by the CLVisc hydrodynamic model described in the previous subsection. When heavy quarks travel across the QGP boundary, defined by a hypersurface at a fixed decoupling temperature$T_{d} = 165$ MeV, they are converted into heavy flavor hadrons via a hybrid fragmentation and coalescence model [16], which includes both s and p-wave hadron states and their decay contributions and is well constrained by the heavy flavor hadron chemistry measured at the RHIC and LHC. The B-decayed D mesons are not considered. We ignore the further evolution of heavy flavor hadrons inside the hadron gas, that is, between the chemical freezeout temperature 165 MeV and the kinetic freezeout temperature 137 MeV, considering that the interactions between heavy flavor hadrons and the hadron gas are significantly weaker than those between heavy quarks and QGP [9]. Finally, the heavy flavor hadrons decay into electrons via Pythia simulation [55]. For a summary of the systematic uncertainties contributed by various components of our model, see Ref. [56]. -
In this section, we provide calculations on the nuclear modification factors and collective flow coefficients of heavy flavor mesons and their decayed electrons and discuss how they are affected by a tilted QGP fireball. The nuclear modification factor (
$R_{AA}$ ) is defined as the ratio of particle spectra between A+A and p+p collisions, normalized with the average number of binary collisions ($ \mathcal{N}_\mathrm{coll} $ ) per A+A collision.$ R_{ {AA}}(y,p_{T},\phi_p)=\frac{1}{\mathcal{N}_\mathrm{coll}}\frac{{\rm d} N_{ {AA}}/{\rm d}y{\rm d}p_{ {T}}{\rm d}\phi_p}{{\rm d}N_{ {pp}}/{\rm d}y{\rm d}p_{ {T}}{\rm d}\phi_p}. $

(6) For collective flow coefficients, we focus on the directed flow
$ v_{1}=\langle \cos(\phi-\Psi_1)\rangle=\left\langle\frac{p_{x}}{ p_\text{T}}\right\rangle, $

(7) and the elliptic flow
$ v_{2}=\langle \cos(2(\phi-\Psi_2))\rangle=\left\langle\frac{p_{x}^{2}-p_{y}^{2}}{p_{x}^{2}+p_{y}^{2}}\right\rangle, $

(8) which can be viewed as the first and second order Fourier coefficients of the angular distribution of the particle spectra, respectively. In the above equations,
$ \Psi_1 $ and$ \Psi_2 $ represent the first- and second-order event plane angles, respectively, and$ \langle...\rangle $ denotes the average over both the final-state particles and different collision events. Because we use the modified optical Glauber model to calculate the initial energy density distribution of QGP (as described in Sec. II), the event-by-event fluctuations are not taken into account [23, 33]. Therefore, the event plane in the final state is the same as the participant plane in the initial state and also the spectator plane that can be measured from the deflected neutrons in experiments [33]. -
We start with the nuclear modification factor and elliptic and directed flow coefficients of heavy mesons in 200 A GeV Au+Au collisions at the RHIC.
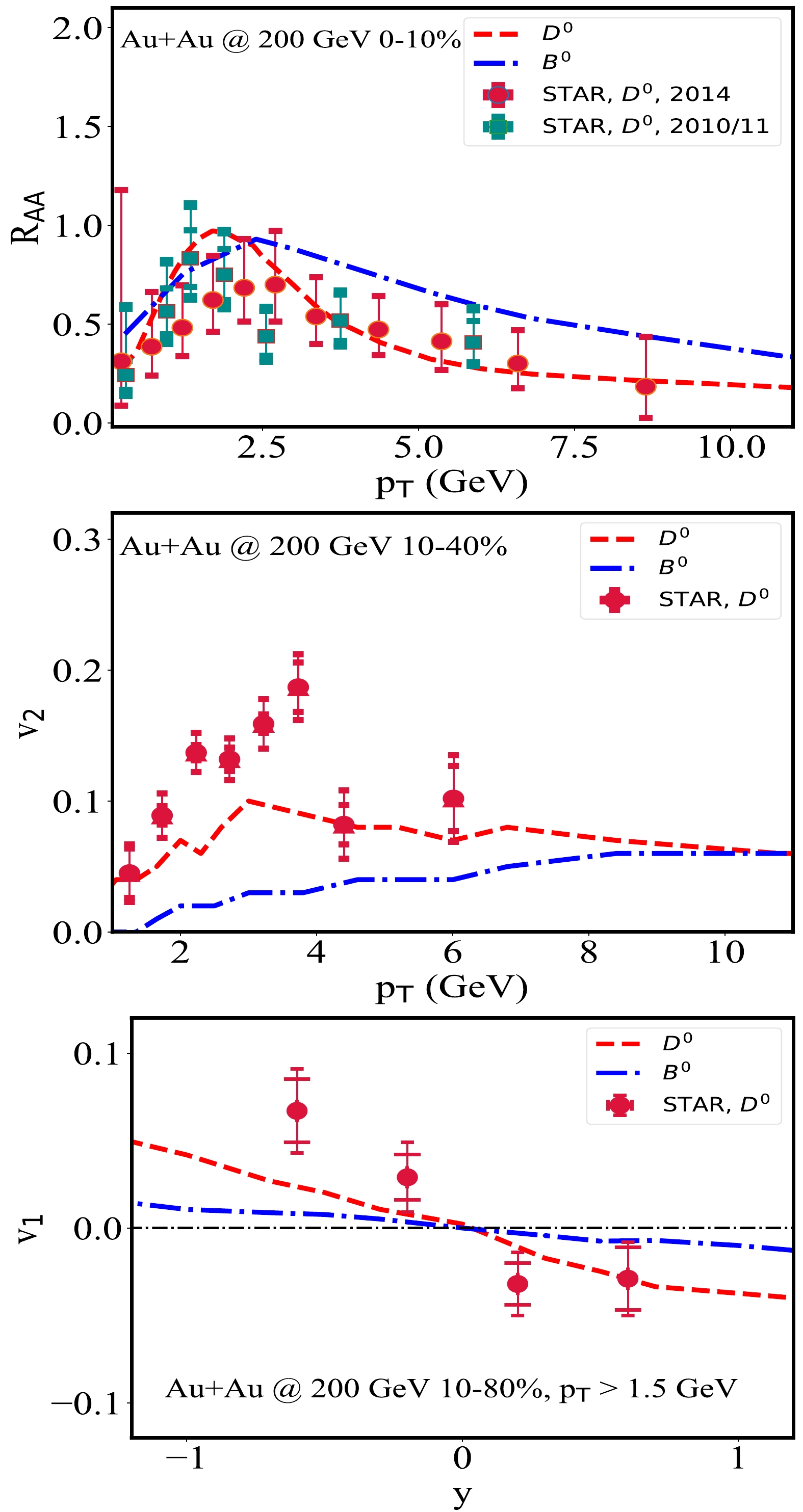
In the upper panel of Fig. 2, we present the
$R_{AA}$ of D and B mesons in 0–10% Au+Au collisions in the mid-rapidity region ($ |y|<1 $ ). Using the spatial diffusion coefficient$D_{s}(2\pi T)=4$ for c-quarks, our calculation provides a reasonable description of the D meson$R_{AA}$ measured by STAR [57, 59]. For B mesons, a slightly smaller diffusion coefficient$ D_{s}(2\pi T)=3 $ is used here, which is extracted from the$ R_{AA} $ of b-decay electrons [60]. As discussed in the previous section,$ D_{s}(2\pi T) $ is treated as a model parameter, whose detailed dependence on the heavy quark mass will be explored in a separate study. The peak structures of the D and B meson$ R_{AA} $ arise from the coalescence process that combines low$ p_{T} $ heavy and thermal light partons into medium$ p_{T} $ hadrons [9]. Above the peak region ($ p_{T} \gtrsim 2.5 $ GeV), B mesons exhibit a larger$ R_{AA} $ than D mesons owing to the lower energy loss of heavier partons through QGP.In the middle panel of Fig. 2, we present the elliptic flow
$ v_{2} $ of D and B mesons in 10%–40% Au+Au collisions as a function of$p_{T}$ at mid-rapidity ($ |y|<1 $ ). Within the Langevin model using a constant$D_{s}(2\pi T)$ value, our calculation underestimates the D meson$ v_2 $ at its peak value ($p_{T}$ between 2 and 4 GeV) measured by STAR [58, 59]. This indicates non-trivial dependences of the diffusion coefficient on the heavy quark momentum and medium temperature, which can be improved with a more delicate calculation of the non-perturbative interactions between heavy quarks and QGP at low$ p_{T} $ [21]. As discussed in Ref. [61], while the heavy flavor$ R_{AA} $ is more sensitive to the earlier evolution stage of QGP,$ v_2 $ is more sensitive to the later stage when the QGP flow has been developed. Therefore, a simultaneous description of$ R_{AA} $ and$ v_2 $ requires a correct dependence of the interaction strength on the medium temperature. Here, we also present the$ v_2 $ of B mesons, which is non-zero but significantly smaller than that of the D mesons. This is consistent with the findings observed for their$ R_{AA} $ , suggesting a smaller energy loss of b-quarks than c-quarks owing to the larger mass of the former.With the same diffusion coefficients as used above, we present the rapidity dependence of the D meson
$ v_1 $ and predict the B meson$ v_1 $ in 10%–80% Au+Au collisions in the lower panel of Fig. 2. Our calculation qualitatively describes the trend of the D meson$ v_{1} $ observed at STAR [30]. Both D and B mesons exhibit negative slopes of$ v_1 $ with respect to rapidity owing to the longer (shorter) path length of heavy quarks along the$ +x $ -direction than the$ -x $ -direction in the positive (negative) rapidity region, as illustrated in Fig. 1. This is a direct feature from a tilted QGP fireball. Because b-quarks are heavier than c-quarks, the unbalanced energy loss of b-quarks is smaller than that of c quarks between the$ + $ and$ -x $ directions, resulting in a smaller slope of the B meson$ v_1 $ than that of the D meson$ v_1 $ . The slope parameters we extract around the$ y=\pm 1 $ regions are${\rm d} v_{1}/{\rm d} y=-0.045\pm0.005$ for D mesons and${\rm d} v_{1}/{\rm d} y=-0.010\pm0.002$ for B mesons. -
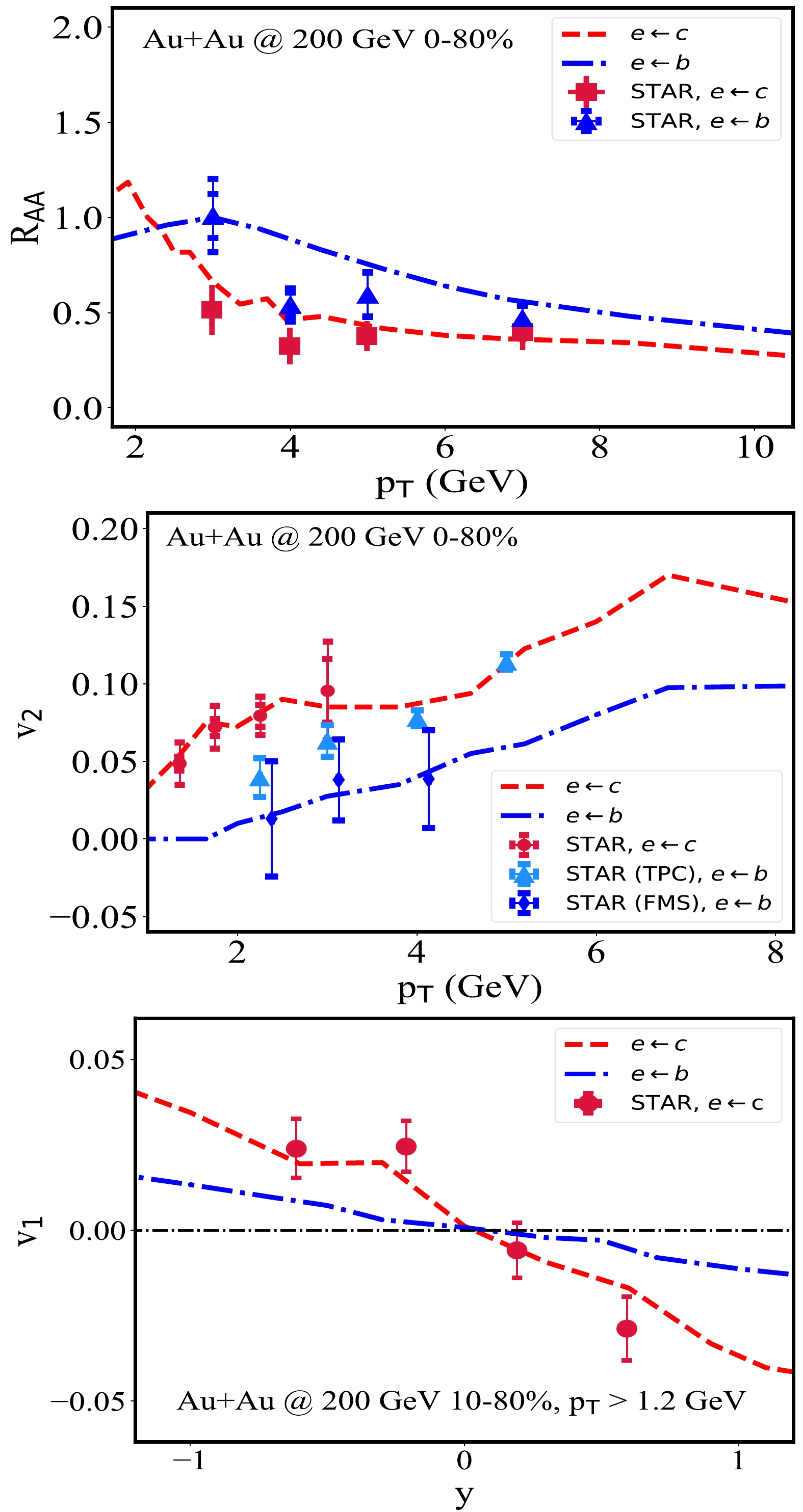
The Heavy Flavor Tracker (HFT) at the RHIC-STAR is able to measure single electrons from charm and beauty semi-leptonic decays [62], providing a complementary tool to investigate the properties of heavy quarks with particular species, considering the challenges in reconstructing D and B mesons in experiments. In this subsection, we present model calculations for
$R_{AA}$ ,$ v_1 $ , and$ v_2 $ of charm and beauty decayed electrons and study how they depend on the medium geometry.We start with the nuclear modification factors of c and b-decayed electrons at mid-rapidity in the upper panel of Fig. 3. With the same diffusion coefficients used in the previous subsection for heavy mesons (
$ D^{0} $ and$ B^{0} $ ), our model calculation provides a reasonable description of the c and b-decayed electron$R_{AA}$ observed by STAR [60] in 0–80% Au+Au collisions at$\sqrt{s_{NN}}=200$ GeV. Note that although the flavor (or mass) hierarchy of parton energy loss is not obvious at high$p_{T}$ [11], a clear difference between the charm and beauty quark energy loss can be observed in the kinematic region focused by the RHIC experiment.After fixing the diffusion coefficients with the heavy flavor
$ R_{AA} $ , we calculate their$ v_2 $ in the middle panel of Fig. 3. Our model results for both$ v_{2}(e\leftarrow c)(p_{T}) $ and$ v_{2}(e\leftarrow b)(p_{T}) $ are in good agreement with the STAR measurement [60] for 0–80% Au+Au collisions. A larger$ v_2 $ of charm decayed electrons than beauty decayed electrons is observed in both our model calculation and experimental data, which is consistent with the hierarchy in their$ R_{AA} $ (the upper panel) and also that in the heavy meson$ R_{AA} $ and$ v_2 $ (Fig. 2). Note that the discrepancy in the D meson$ v_2 $ between our model result and STAR data (middle panel of Fig. 2) is not shown here for the electron$ v_2 $ , indicating that certain features of heavy flavor dynamics may be shadowed by the momentum shift during the decay process. This smearing could depend on both the heavy quark spectra and the magnitude of their$ v_2 $ . At the LHC energy, we still underestimate the$ v_2 $ of heavy-flavor decayed leptons when a constant value of$ D_{s}(2\pi T) $ is used. Similar effects can also be expected for the heavy flavor$ v_1 $ between hadron and lepton levels.The directed flow coefficient
$ v_{1} $ of c and b-decayed electrons is shown in the lower panel of Fig. 3 as a function of rapidity. Our calculation provides a good description of the c-decayed electron$ v_1 $ measured by STAR [64, 65] in 10%–80% Au+Au collisions at$ \sqrt{s_{NN}}= $ 200 GeV, with a slope parameter extracted as${\rm d}v_{1} /{\rm d}y = - 0.043\pm 0.005$ around the$ y=\pm 1 $ regions. The$ v_{1}(y) $ of b-decayed electrons is also predicted, with its slope parameter extracted as$ {\rm d}v_{1}/{\rm d}y=-0.013\pm0.003 $ around$ y=\pm1 $ , which can be tested via future measurement at the RHIC. The rapidity dependence of the heavy flavor decayed electrons here further confirms the longitudinally tilted geometry of the QGP fireball produced at the RHIC energy. -
While it is now generally accepted that the tilted geometry of QGP generates the observed rapidity dependence of
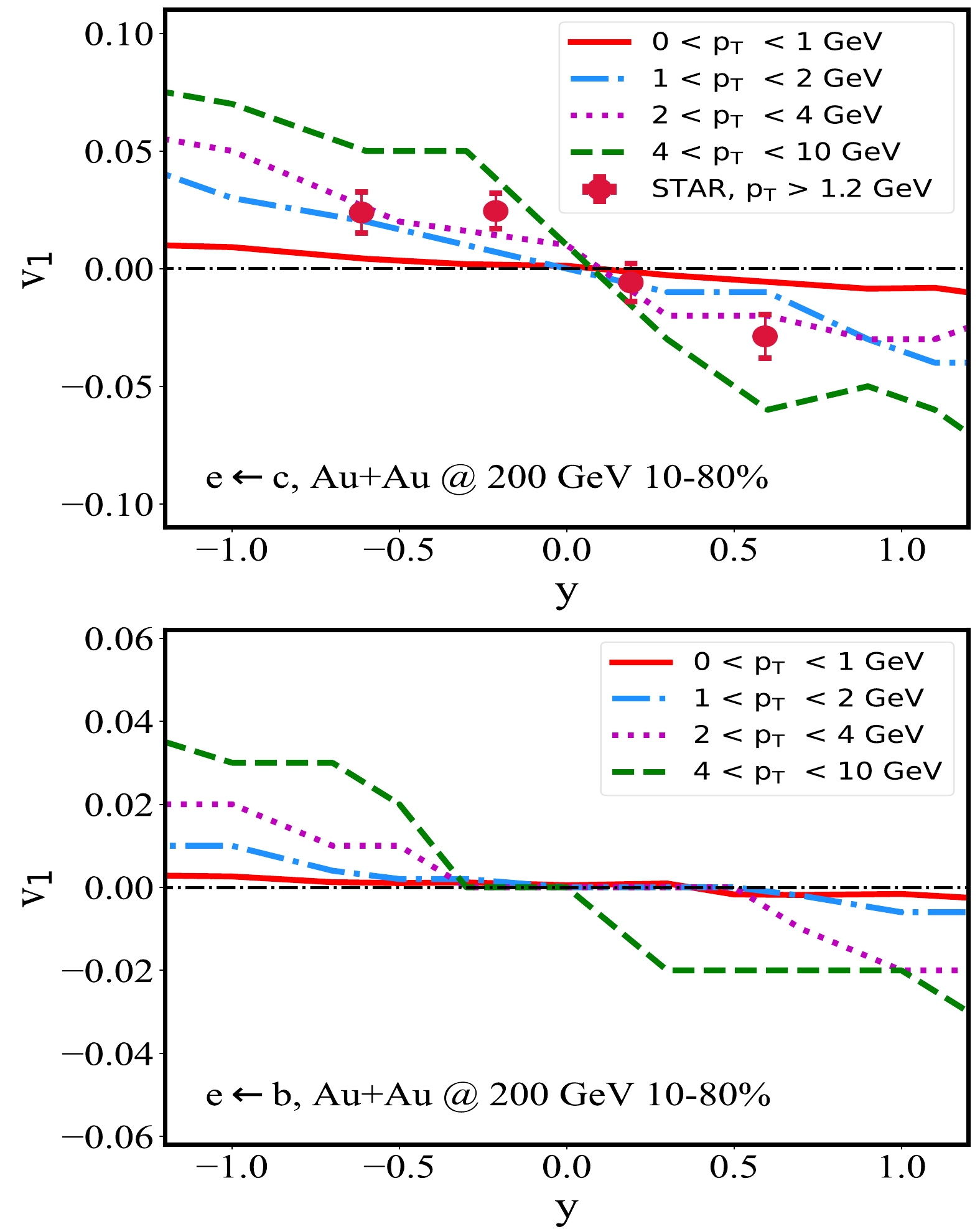
$ v_1 $ of D mesons and their decayed electrons at the RHIC, its$p_{T}$ dependence has not yet been sufficiently discussed. This is the focus of this subsection.Shown in Fig. 4 is the
$ v_{1} $ of D mesons (upper panel) and B mesons (lower panel) for different$p_{T}$ regions in 10%–80% Au+Au collisions at$\sqrt{s_{NN}} = 200$ GeV. It is interesting to see that with increasing$p_{T}$ , the heavy meson$ v_1 $ becomes larger. This can be understood with the different origins of the heavy flavor$ v_1 $ at different$p_{T}$ scales. At very low$p_{T}$ , heavy quarks tend to thermalize with the medium and thus encode the thermal properties of QGP. Because the$ v_1 $ of soft hadrons emitted from QGP is small [43], one can also expect a small$ v_1 $ of heavy quarks. Within the kinematic regions explored here, the maximum slope parameter we obtain is for the$ 4< p_{T}<10 \rm{\; GeV} $ bin, whose value is extracted as${\rm d}v_{1}/{\rm d}y= -0.050\pm 0.005\; (-0.025\pm0.005)$ for D (B) mesons around$ y=\pm1 $ , which can be tested by future measurements.
Figure 4. (color online) Directed flow coefficients of D (upper panel) and B (lower panel) mesons in different
$ p_\text{T} $ bins in 10%–80% Au+Au collisions at$\sqrt{s_{NN}}=200$ GeV.A similar study is also conducted for heavy flavor decayed electrons in Fig. 5, with the upper panel for charm and the lower panel for beauty decayed electrons in different
$ p_{T} $ bins of 10%–80% Au+Au collisions. Consistent with the previous results for D and B mesons, we find that the slope of$ v_{1}(y) $ increases for higher$ p_{T} $ bins. For$ 4< p_{T}<10 $ GeV, the slope parameter is extracted as$ {\rm d}v_{1}/{\rm d}y=-0.065\pm0.005\; (-0.025\pm0.005) $ for c (b)-decayed electrons around$ y=\pm1 $ . However, the statistics of high$ p_\mathrm{T} $ electrons are not as good as those of heavy mesons after the decay process. -
In addition to the directed flow coefficient, an alternative way to quantify the asymmetry of energy loss along different directions is by studying the angular dependence of
$R_{AA}$ [66–68]. In this subsection, we conclude our study by comparing the heavy flavor$R_{AA}$ in different angular regions.As previously illustrated in Fig. 1, in the positive rapidity region of a tilted QGP medium, heavy quarks that are initially produced symmetrically around the origin (0,0) propagate through a longer and hotter medium toward the
$ +x $ (right) direction than toward the$ -x $ (left) direction and thus lose more energy in the right hemisphere than in the left. Therefore, the azimuthal angle dependence of the heavy flavor$R_{AA}$ can be utilized to investigate the violation of longitudinal boost invariance in nuclear collisions. We measure the azimuthal angle counter-clockwise from the$ +x $ direction and refer to the$ -\pi/2<\phi<\pi/2 $ region as the "right" region and$ \pi/2<\phi<3\pi/2 $ as the "left". In the upper panel of Fig. 6, we present the D meson$ R_{AA} $ as a function of its$ p_{T} $ in the forward rapidity region of 10%–80% Au+Au collisions at$\sqrt{s_{NN}}=200$ GeV, analyzed within the left and right regions separately. Indeed, at high$ p_{T} $ ($ \gtrsim 4 $ GeV), we observe a smaller$ R_{AA} $ (right) than$ R_{AA} $ (left) of D mesons in the$ 0<y<1 $ region. This could be viewed as an alternative signal of the longitudinal tilted fireball produced at the RHIC energy. At lower$ p_{T} $ ($ \lesssim4 $ GeV), the heavy meson$ R_{AA} $ is also strongly affected by the coalescence process, which is sensitive to the radial flow of QGP, and thus may not directly reflect the energy loss asymmetry of heavy quarks toward different directions. This could be viewed as an alternative signal of the longitudinal tilted fireball produced at the RHIC energy, although the small difference shown here could be easily hidden by statistical fluctuations in both theoretical calculations and experimental measurements.
Figure 6. (color online) Heavy flavor
$ R_{AA} $ in the$ + $ /$ -x $ (right/ left) hemispheres (upper panel) and the ratios between them (lower panel) in 10%–80% Au+Au collisions at$ \sqrt{s_{NN}}=200 $ GeV.To better illustrate the heavy flavor
$ R_{AA} $ in different angular regions, we present the ratio between$ R_{AA} $ (left) and$ R_{AA} $ (right) in the lower panel of Fig. 6. Results are shown for D and B mesons as well as their decayed electrons. Above$ p_{T}\sim 4 $ GeV, these$ R_{AA} $ ratios are all consistently above one in the forward rapidity region. -
In this paper, a systematic investigation on the heavy flavor nuclear modification factor (
$R_{AA}$ ), directed flow ($ v_{1} $ ), and elliptic flow ($ v_{2} $ ) is presented. Effects from a longitudinally tilted bulk medium on these observables are explored within a modified Langevin transport model coupled to a (3+1)-D viscous hydrodynamic model CLVisc.Within this framework, our calculation provides a reasonable description of the
$ R_{AA} $ ,$ v_1 $ , and$ v_2 $ of heavy mesons and their decayed electrons compared to data currently available at the RHIC. A clear mass hierarchy of parton energy loss can be observed within the$ p_{T} $ range focused by RHIC experiments, where D mesons exhibit smaller$ R_{AA} $ but larger$ v_1 $ and$ v_2 $ than those of B mesons. The same hierarchy remains between charm and beauty decayed electrons. We demonstrate that$ v_{1} $ and the angular-dependent$ R_{AA} $ of heavy mesons and their decayed electrons encode information on the initial longitudinal deformation of the QGP energy distribution. An initially counter-clockwise tilted QGP fireball in the$ \eta_{s} $ -x plane results in a positive (negative)$ v_1 $ of heavy quarks in the backward (forward) rapidity regions. In addition, at high$ p_{T} $ , a smaller heavy flavor$ R_{AA} $ in the$ +x $ (right) hemisphere than in the$ -x $ (left) one is proposed at forward rapidity, which serves as an alternative observable to help constrain the 3D geometry of the QGP profile. The opposite conclusion is expected at backward rapidity. Furthermore, dependence of the directed flow on the heavy flavor$ p_{T} $ is studied at the RHIC energy. As$ p_{T} $ increases, heavy quarks become less thermalized, and their observables are more dominated by their energy loss through QGP. Within the kinematic range under investigation, the heavy flavor$ v_1 $ increases as a higher$ p_{T} $ region is applied. Our conclusions consistently hold across D and B mesons and their decayed electrons and await verification from future experimental observations.While this study contributes to a more comprehensive understanding of how heavy flavor probes can be utilized to constrain the initial geometry of nuclear matter, it can be further extended in several directions. For instance, the recent isobar experiments at the RHIC provide a novel environment to study the properties of QGP produced by colliding nuclei with the same number of nucleons but different geometries [69–72]. It would be interesting to investigate whether this difference in nuclear structure can also be probed using heavy flavor observables within our framework. In addition, although the effect of the electromagnetic field on heavy quarks is weak at the RHIC energy, it becomes a dominating factor generating the heavy flavor
$ v_1 $ at the LHC energy [33]. However, it still remains a challenge to establish an ideal spacetime evolution profile of the electromagnetic field for a precise description of the heavy meson$ v_1 $ observed at the LHC [28, 31, 35, 73]. These will be explored in our follow-up efforts. -
We are grateful for helpful discussions with Jiaxing Zhao, Xiang-Yu Wu, and Guang-You Qin.
Interactions between heavy quarks and tilted QGP fireballs in 200 A GeV Au+Au collisions
- Received Date: 2022-09-27
- Available Online: 2023-02-15
Abstract: Heavy quark observables are applied to probe the initial energy density distribution with violation of longitudinal boost invariance produced in relativistic heavy-ion collisions. Using an improved Langevin model coupled to a (3+1)-dimensional viscous hydrodynamic model, we study the nuclear modification factor (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: