-
The classification of the statistical nature of neutrinos as either Majorana or Dirac particles is an unresolved issue in neutrino physics.
The flavor neutrino mass matrix of Majorana-type neutrinos is symmetric. However, the flavor neutrino mass matrix of Dirac-type neutrinos is not symmetric. Therefore, the texture of the Dirac flavor neutrino mass matrix has a more complicated structure than that of the Majorana flavor neutrino mass matrix. Moreover, it is relatively difficult to find symmetry for the Dirac neutrino mass matrix. Thus, exploring the Majorana flavor mass matrix immanent in the Dirac flavor mass matrix appears sensible. This immanence provides a clue for solving the problem of the statistical nature of neutrinos.
In this study, we focus on magic texture, which is a known successful texture of the Majorana flavor neutrino mass matrix [1–8]. Accordingly, we investigate the relationship between the Dirac flavor neutrino mass and Majorana flavor neutrino mass matrices.
Several types of magic textures have been reproduced in the results of neutrino oscillation experiments. The first discovered traditional magic texture of the Majorana flavor neutrino mass matrix is parameterized as follows [9]:
$ \begin{array}{*{20}{l}} \left( \begin{array}{ccc} a & b & c \\ b & d & a+c-d \\ c & a+c-d & b-c+d \end{array} \right) \begin{array}{c} \leftarrow a+b+c \\ \leftarrow a+b+c \\ \leftarrow a+b+c .\\ \end{array} \end{array} $

(1) The traditional magic texture is invariant under
$ Z_2 $ symmetry. Indeed, the traditional magic texture is independent of the neutrino mass eigenvalues$ (m_1,m_2,m_3) $ and is related only to the mixing matrix [10].The relationship between the texture of the flavor neutrino mass matrix for Dirac-type neutrinos and magic texture has been investigated in Ref. [11]. Here, we explain the difference between this previous study and the current study. The previous study involved no discussions on the magic texture of Majorana neutrinos immanent in the texture of the Dirac flavor mass matrix [11], whereas this immanence is the main topic of discussion in this study. Additionally, although the elements of the Dirac flavor neutrino mass matrix are complex, the elements of the mass matrix are assumed to be real in Ref. [11]. In this study, the elements of the mass matrix are considered complex.
In addition to the magic texture, numerous possible textures of the flavor mass matrix for Majorana-type neutrinos have been proposed in the literature; these include a tri-bi maximal texture [9, 12–14], texture zeros [15–55],
$ \mu-\tau $ symmetric texture [56–81], and textures under discrete symmetries, for example,$ A_n $ and$ S_n $ [82].The remainder of this paper is organized as follows: In Sec. II, we review magic textures of the neutrino mass matrix for Majorana-type neutrinos. In Sec. III, we estimate the magic textures of the Majorana-type neutrino mass matrix immanent in the Dirac-type neutrino mass matrix. Section IV provides a summary.
-
We review the magic textures of the mass matrix for Majorana-type neutrinos [1–3].
Because the Majorana neutrino flavor mass matrix is symmetric, the following five independent sums exist:
$ \{S_{\rm M1}, S_{\rm M2}, S_{\rm M3}, S_{\rm M4}, S_{\rm M5}\} $ . Schematically,$ \begin{array}{*{20}{l}} \quad\;\; \quad \quad M_{\rm M}= \left( \begin{array}{ccc} \ a\ & \ b \ & \ c \ \\ b & d & e \\ c & e & f \\ \end{array} \right) \begin{array}{c} \leftarrow S_{\rm M1}\\ \leftarrow S_{\rm M2}\\ \leftarrow S_{\rm M3}\\ \end{array} \\ \begin{array}{ccccccc} &\nearrow & \; \uparrow & \; \uparrow & \; \uparrow & \nwarrow & \\ S_{\rm M5}&&S_{\rm M1} & S_{\rm M2}& S_{\rm M3} &&S_{\rm M4}\\ \end{array} \end{array} $

(2) where
$ \begin{array}{*{20}{l}} S_{\rm M1}= a+b+c, \quad S_{\rm M2}= b+d+e, \quad S_{\rm M3}= c+e+f \end{array} $

(3) for the ith raw (ith column), and
$ \begin{array}{*{20}{l}} S_{\rm M4}= a+d+f, \quad S_{\rm M5}= 2c + d,\end{array} $

(4) for diagonal elements.
The above five sums,
$ \{S_{\rm M1}, S_{\rm M2}, S_{\rm M3}, S_{\rm M4}, S_{\rm M5}\} $ , have been used to classify the types of magic textures for the Majorana neutrino flavor mass matrix [1]. Based on the success of the first discovered magic texture, presented in Eq. (1), it appears that three of the five sums must be the same in the Majorana neutrino mass matrix for other magic textures. Under this requirement, we have$ _5C_3=10 $ types of magic textures. These ten textures are referred to as type M1, type M2,$ \cdots $ , and type M10, with the following definitions①:$ \begin{aligned}[b] & {\bf M1:} \ S_{\rm M1}=S_{\rm M2}=S_{\rm M3}, \quad {\bf M2:} \ S_{\rm M1}=S_{\rm M2}=S_{\rm M4}, \\ & {\bf M3:} \ S_{\rm M1}=S_{\rm M3}=S_{\rm M4}, \quad{\bf M4:} \ S_{\rm M2}=S_{\rm M3}=S_{\rm M4}, \\ & {\bf M5:} \ S_{\rm M1}=S_{\rm M2}=S_{\rm M5} , \quad {\bf M6:} \ S_{\rm M1}=S_{\rm M3}=S_{\rm M5}, \\ &{\bf M7:} \ S_{\rm M2}=S_{\rm M3}=S_{\rm M5}, \quad {\bf M8:} \ S_{\rm M1}=S_{\rm M4}=S_{\rm M5}, \\ & {\bf M9:} \ S_{\rm M2}=S_{\rm M4}=S_{\rm M5}, \quad {\bf M10:} \ S_{\rm M3}=S_{\rm M4}=S_{\rm M5}. \end{aligned} $

(5) We have the following ten types for the flavor neutrino mass matrix:
$ \begin{array}{*{20}{l}} M_{\rm M1}=\left( \begin{array}{ccc} a & b & c \\ b & e & a+c-e \\ c & a+c-e & b-c+e \end{array} \right),\end{array} $

(6) $ \begin{array}{*{20}{l}} M_{\rm M2} =\left( \begin{array}{ccc} a & b & c \\ b & e & a+c-e \\ c & a+c-e & b+c-e \end{array} \right),\end{array} $

(7) $ \begin{array}{*{20}{l}} M_{\rm M3} =\left( \begin{array}{ccc} a & b & c \\ b & e & a-c+e \\ c & a-c+e & b+c-e \end{array} \right),\end{array} $

(8) $ \begin{array}{*{20}{l}} M_{\rm M4} =\left( \begin{array}{ccc} a & b & c \\ b & e & a-c+e \\ c & a-c+e & b-c+e \end{array} \right),\end{array} $

(9) $ \begin{array}{*{20}{l}} M_{\rm M5} =\left( \begin{array}{ccc} a & b & c \\ b & a+b-c & -b+2c \\ c & -b+2c & i \end{array} \right),\end{array} $

(10) $ \begin{array}{*{20}{l}} M_{\rm M6} =\left( \begin{array}{ccc} a & b & c \\ b & a+b-c & f\\ c & f & a+b-f \end{array} \right),\end{array} $

(11) $ \begin{array}{*{20}{l}} M_{\rm M7} =\left( \begin{array}{ccc} a & b & c \\ b & e & -b+2c \\ c & -b+2c & b-c+e \end{array} \right),\end{array} $

(12) $ \begin{array}{*{20}{l}} M_{\rm M8} =\left( \begin{array}{ccc} a & b & c \\ b & a+b-c & f \\ c & f & -a+2c \end{array} \right),\end{array} $

(13) $ \begin{array}{*{20}{l}} M_{\rm M9} =\left( \begin{array}{ccc} a & b & c \\ b & e & -b+2c \\ c & -b+2c & -a+2c \end{array} \right),\end{array} $

(14) $ \begin{array}{*{20}{l}} M_{\rm M10} =\left( \begin{array}{ccc} a & b & c \\ b & e & a-c+e \\ c & a-c+e & -a+2c \end{array} \right). \end{array} $

(15) According to previous studies [1–3], types M1, M4, and M9 can be satisfied by observations. Type M1 is a traditional magic texture, represented in Eq. (1).
-
This study aims to investigate the relationship between the Dirac flavor neutrino mass matrix and magic textures for Majorana-type neutrinos.
We assume that the mass matrix of charged leptons is diagonal and real. In this case, the Dirac flavor neutrino mass matrix is written as
$ \begin{aligned}[b] M_{\rm D} & = \left ( \begin{array}{ccc} a & b & c \\ d & e & f \\ g& h & i \\ \end{array} \right) \\ & = {\rm diag.}({\rm e}^{{\rm i}\phi_e}, {\rm e}^{{\rm i}\phi_\mu}, {\rm e}^{{\rm i}\phi_\tau}) U {\rm diag.}(m_1,m_2, m_3) V^\dagger,\end{aligned} $

(16) where
$ \phi_e,\phi_\mu,\phi_\tau \in (-\pi, \pi) $ denote the phases of left-handed neutrinos;$ m_1,m_2 $ , and$ m_3 $ denote neutrino mass eigenstates; and U denotes the Pontecorvo-Maki-Nakagawa-Sakata mixing matrix [83–86]:$ U = \left ( \begin{array}{ccc} c_{12}c_{13} & s_{12}c_{13} & s_{13} {\rm e}^{{\rm -i}\delta} \\ - s_{12}c_{23} - c_{12}s_{23}s_{13} {\rm e}^{{\rm i}\delta} & c_{12}c_{23} - s_{12}s_{23}s_{13} {\rm e}^{{\rm i}\delta} & s_{23}c_{13} \\ s_{12}s_{23} - c_{12}c_{23}s_{13} {\rm e}^{{\rm i}\delta} & - c_{12}s_{23} - s_{12}c_{23}s_{13} {\rm e}^{{\rm i}\delta} & c_{23}c_{13} \\ \end{array} \right), $

(17) where
$ c_{ij}=\cos\theta_{ij} $ ,$ s_{ij}=\sin\theta_{ij} $ ($ i,j $ =1,2,3),$ \theta_{ij} $ is the mixing angle, and δ is the Dirac CP-violating phase.The matrix V is the transformation matrix of three right-handed neutrinos [87], which can be parameterized with three rotation angles
$ \phi_{ij} \in (0, \pi/2) ~(ij=12, 23,13) $ , six phases$ \omega_i \in (-\pi, \pi) $ ($ i=1,2,\cdots,5 $ ), and$ \delta_V \in (-\pi, \pi) $ . The matrix V can be written as [87, 88]$ \begin{array}{*{20}{l}} V = {\rm diag.}({\rm e}^{{\rm i}\omega_1}, {\rm e}^{{\rm i}\omega_2}, {\rm e}^{{\rm i}\omega_3}) \tilde V (\phi_{ij}, \delta_V) {\rm diag.}({\rm e}^{{\rm i}\omega_4}, {\rm e}^{{\rm i}\omega_5}, 1) ,\end{array} $

(18) where
$ \tilde V = \left ( \begin{array}{ccc} \tilde c_{12}\tilde c_{13} & \tilde s_{12}\tilde c_{13} & \tilde s_{13} {\rm e}^{-{\rm i}\delta_V} \\ - \tilde s_{12}\tilde c_{23} - \tilde c_{12}\tilde s_{23}\tilde s_{13} {\rm e}^{{\rm i}\delta_V} & \tilde c_{12}\tilde c_{23} - \tilde s_{12}\tilde s_{23}\tilde s_{13}{\rm e}^{{\rm i}\delta_V} & \tilde s_{23}\tilde c_{13} \\ \tilde s_{12}\tilde s_{23} - \tilde c_{12}\tilde c_{23}\tilde s_{13}{\rm e}^{{\rm i}\delta_V} & - \tilde c_{12}\tilde s_{23} - \tilde s_{12}\tilde c_{23}\tilde s_{13}{\rm e}^{{\rm i}\delta_V} & \tilde c_{23}\tilde c_{13} \\ \end{array} \right). $

(19) Here,
$ \tilde c_{ij}=\cos\phi_{ij} $ , and$ \tilde s_{ij}=\sin\phi_{ij} $ .With the magic texture of the Majorana-type mass matrix
$ M_{\rm Mi} $ , the Dirac flavor neutrino mass matrix$ M_{\rm D} $ can be decomposed into$ \begin{aligned}[b] M_{\rm D}&=M_{\rm{M}i}+\Delta M_{\rm{i}} \\ &= M_{\rm{Mi}} + \left( \begin{array}{ccc} \ 0 \ & \ 0 \ & \ 0 \ \\ \delta_{1}& 0 & \delta_{1}^{\rm{Mi}} \\ \delta_{2} &\delta_{2}^{\rm{Mi}}& \delta_{3}^{\rm{Mi}}\\ \end{array} \right) \; \; (\rm{i}=1,2,3,4,7,9,10),\end{aligned} $

(20) $ M_{\rm D} = M_{\rm{M5}}+\Delta M_{\rm{5}} = M_{\rm{M5}}+ \left( \begin{array}{ccc} \ 0 \ &\ 0 \ & \ 0 \ \\ \delta_{1} & \delta_{1}^{\rm{M5}} &\delta_{3}^{\rm{M5}}\\ \delta_{2} &\delta_{2}^{\rm{M5}}& 0 \\ \end{array} \right), $

(21) and
$ \begin{aligned}[b] M_{\rm D}& = M_{\rm{Mi}}+\Delta M_{\rm{i}} \\ &= M_{\rm{Mi}} + \left( \begin{array}{ccc} \ 0 \ & \ 0 \ & \ 0 \ \\ \delta_{1} & \delta_{1}^{\rm{Mi}} &0 \\ \delta_{2} & \delta_{2}^{\rm{Mi}}& \delta_{3}^{\rm{Mi}} \\ \end{array} \right) \; \; (\rm{i}=6,8).\end{aligned} $

(22) Based on Ref. [89], we define dimensionless parameters to quantify the strength of the violations of the magic texture feature as follows:
$ \begin{array}{*{20}{l}} \epsilon_1=\dfrac{d-b}{d+b},\quad \epsilon_2=\dfrac{g-c}{g+c},\end{array} $

(23) and
$ \begin{aligned}[b] &\epsilon_{1}^{\rm{M1}}=\dfrac{f-(a+c-e)}{f+(a+c-e)},\quad \epsilon_{2}^{\rm{M1}}=\dfrac{h-(a+c-e)}{h+(a+c-e)}, \\ &\epsilon_{3}^{\rm{M1}}=\dfrac{i-(b-c-e)}{i+(b-c+e)}, \quad \epsilon_{1}^{\rm{M2}}=\dfrac{f-(a+c-e)}{f+(a+c-e)},\\ &\epsilon_{2}^{\rm{M2}}=\dfrac{h-(a+c-e)}{h+(a+c-e)}, \quad \epsilon_{3}^{\rm{M2}}=\dfrac{i-(b+c-e)}{i+(b+c-e)},\\ &\epsilon_{1}^{\rm{M3}}=\dfrac{f-(a-c+e)}{f+(a-c+e)},\quad \epsilon_{2}^{\rm{M3}}=\dfrac{h-(a-c+e)}{h+(a-c+e)}, \\ &\epsilon_{3}^{\rm{M3}}=\dfrac{i-(b+c-e)}{i+(b+c-e)}, \quad\epsilon_{1}^{\rm{M4}}=\dfrac{f-(a-c+e)}{f+(a-c+e)},\\ &\epsilon_{2}^{\rm{M4}}=\dfrac{h-(a-c+e)}{h+(a-c+e)}, \quad \epsilon_{3}^{\rm{M4}}=\dfrac{i-(b-c+e)}{i+(b-c+e)},\\ &\epsilon_{1}^{\rm{M5}}=\dfrac{e-(a+b-c)}{e+(a+b-c)},\quad \epsilon_{2}^{\rm{M5}}=\dfrac{h-(-b+2c)}{h+(-b+2c)}, \\ &\epsilon_{3}^{\rm{M5}}=\dfrac{f-(a+b-c)}{f+(a+b-c)}, \quad\epsilon_{1}^{\rm{M6}}=\dfrac{e-(a+b-c)}{e+(a+b-c)},\\ &\epsilon_{2}^{\rm{M6}}=\dfrac{h-f}{h+f}, \quad\quad\quad\quad\;\;\epsilon_{3}^{\rm{M6}}=\dfrac{i-(a+b-f)}{i+(a+b-f)},\\ &\epsilon_{1}^{\rm{M7}}=\dfrac{f-(-b+2c)}{f+(-b+2c)},\quad \epsilon_{2}^{\rm{M7}}=\dfrac{h-(-b+2c)}{h+(-b+2c)}, \\ &\epsilon_{3}^{\rm{M7}}=\dfrac{i-(b-c+e)}{i+(b-c+e)}, \quad\epsilon_{1}^{\rm{M8}}=\dfrac{e-(a+b-c)}{e+(a+b-c)},\\ &\epsilon_{2}^{\rm{M8}}=\dfrac{h-f}{h+f}, \quad\quad\quad\quad\;\;\epsilon_{3}^{\rm{M8}}=\dfrac{i-(-a+2c)}{i+(-a+2c)}, \\ &\epsilon_{1}^{\rm{M9}}=\dfrac{f-(-b+2c)}{f+(-b+2c)},\quad \; \epsilon_{2}^{\rm{M9}}=\dfrac{h-(-b+2c)}{h+(-b+2c)},\\ &\epsilon_{3}^{\rm{M9}}=\dfrac{i-(-a+2c)}{i+(-a+2c)}, \;\;\quad\epsilon_{1}^{\rm{M10}}=\dfrac{f-(a-c+e)}{f+(a-c+e)},\\ &\epsilon_{2}^{\rm{M10}}=\dfrac{h-(a-c+e)}{h+(a-c+e)},\quad \epsilon_{3}^{\rm{M10}}=\dfrac{i-(-a+2c)}{i+(-a+2c)}.\end{aligned} $

(24) Using Eqs. (23) and (24),
$ \delta_{i} $ and$ \delta_{i}^{\rm{Mi}} $ can be written as$ \begin{array}{*{20}{l}} \delta_{1}=\epsilon_1(b+c), \quad \delta_{2}=\epsilon_2(g+c),\end{array} $

(25) and
$ \begin{aligned}[b] &\delta_{1}^{\rm{M1}}=\epsilon_{1}^{\rm{M1}}\{f+(a+c-e)\}, \quad \delta_{2}^{\rm{M1}}=\epsilon_{2}^{\rm{M1}}\{h+(a+c-e)\},\\ &\delta_{3}^{\rm{M1}}=\epsilon_{3}^{\rm{M1}}\{i+(b-c-e)\}, \quad \delta_{1}^{\rm{M2}}=\epsilon_{1}^{\rm{M2}}\{f+(a+c-e)\}, \\ &\delta_{2}^{\rm{M2}}=\epsilon_{2}^{\rm{M2}}\{h+(a+c-e)\}, \quad \delta_{3}^{\rm{M2}}=\epsilon_{3}^{\rm{M2}}\{i+(b+c-e)\}, \\ &\delta_{1}^{\rm{M3}}=\epsilon_{1}^{\rm{M3}}\{f+(a-c+e)\}, \quad \delta_{2}^{\rm{M3}}=\epsilon_{2}^{\rm{M3}}\{h+(a-c+e)\}, \\ &\delta_{3}^{\rm{M3}}=\epsilon_{3}^{\rm{M3}}\{i+(b+c-e)\}, \quad \delta_{1}^{\rm{M4}}=\epsilon_{1}^{\rm{M4}}\{f+(a-c+e)\}, \\ &\delta_{2}^{\rm{M4}}=\epsilon_{2}^{\rm{M4}}\{h+(a-c+e)\}, \quad \delta_{3}^{\rm{M4}}=\epsilon_{3}^{\rm{M4}}\{i+(b-c+e)\}, \\ & \delta_{1}^{\rm{M5}}=\epsilon_{1}^{\rm{M5}}\{e+(a+b-c)\}, \quad \delta_{2}^{\rm{M5}}=\epsilon_{2}^{\rm{M5}}\{h+(-b+2c)\}, \\ &\delta_{3}^{\rm{M5}}=\epsilon_{2}^{\rm{M5}}\{f+(a+b-c)\}, \quad \delta_{1}^{\rm{M6}}=\epsilon_{1}^{\rm{M6}}\{e+(a+b-c)\}, \\ &\delta_{2}^{\rm{M6}}=\epsilon_{2}^{\rm{M6}}\{h+f\}, \quad\quad\quad\quad \delta_{3}^{\rm{M6}}=\epsilon_{3}^{\rm{M6}}\{i+(a+b-f)\}, \\ &\delta_{1}^{\rm{M7}}=\epsilon_{1}^{\rm{M7}}\{f+(-b+2c)\}, \quad\delta_{2}^{\rm{M7}}=\epsilon_{2}^{\rm{M7}}\{h+(-b+2c)\}, \\ &\delta_{3}^{\rm{M7}}=\epsilon_{3}^{\rm{M7}}\{i+(b-c+e)\}, \quad \delta_{1}^{\rm{M8}}=\epsilon_{1}^{\rm{M8}}\{e+(a+b-c)\}, \\ &\delta_{2}^{\rm{M8}}=\epsilon_{2}^{\rm{M8}}\{h+f\}, \quad\quad\quad\quad \delta_{3}^{\rm{M8}}=\epsilon_{3}^{\rm{M8}}\{i+(-a+2c)\}, \\ & \delta_{1}^{\rm{M9}}=\epsilon_{1}^{\rm{M9}}\{f+(-b+2c)\}, \quad\delta_{2}^{\rm{M9}}=\epsilon_{2}^{\rm{M9}}\{h+(-b+2c)\}, \\ &\delta_{3}^{\rm{M9}}=\epsilon_{3}^{\rm{M9}}\{i+(-a+2c)\}, \quad \delta_{1}^{\rm{M10}}=\epsilon_{1}^{\rm{M10}}\{f+(a-c+e)\}, \\ &\delta_{2}^{\rm{M10}}=\epsilon_{2}^{\rm{M10}}\{h+(a-c+e)\}, \quad \delta_{3}^{\rm{M10}}=\epsilon_{3}^{\rm{M10}}\{i+(-a+2c)\}.\end{aligned} $

(26) Moreover, we define
$ \begin{array}{*{20}{l}} |\epsilon|=|\epsilon_{1}|+|\epsilon_{2}|, \quad |\epsilon_{\rm{Mi}}|=|\epsilon_{1}^{\rm{Mi}}|+|\epsilon_{2}^{\rm{Mi}}|+|\epsilon_{3}^{\rm{Mi}}|,\end{array} $

(27) and
$ \begin{array}{*{20}{l}} |E_{\rm{Mi}}|=|\epsilon|+|\epsilon_{\rm{Mi}}|.\end{array} $

(28) If
$ |E_{\rm{Mi}}|\ll 1 $ (in other words,$ \Delta M_{\rm{i}} $ is small),$ M_{\rm{D}} $ is approximately the same as type Mi magic texture.A global analysis of current data results in the following best-fit values for the squared mass differences
$ \Delta m_{ij}^2=m_i^2-m_j^2 $ and the mixing angles for normal mass ordering (NO),$ m_1<m_2<m_3 $ [90]:$ \begin{aligned}[b] &\frac{\Delta m^2_{21}}{10^{-5} {\rm eV}^2} = 7.42^{+0.21}_{-0.20} \quad (6.82 \sim 8.04), \\ &\frac{\Delta m^2_{31}}{10^{-3}{\rm eV}^2} = 2.510^{+0.027}_{-0.027} \quad (2.430 \sim 2.593), \\ &\theta_{12}/(^{\circ}) = 33.45^{+0.77}_{-0.75} \quad (31.27 \sim 35.87), \\ &\theta_{23}/(^{\circ}) = 42.1^{+1.1}_{-0.9} \quad (39.7 \sim 50.9), \\ &\theta_{13}/(^{\circ}) = 8.62^{+0.12}_{-0.12} \quad (8.25 \sim 8.98), \\ &\delta/(^{\circ}) = 230^{+36}_{-25} \quad (144 \sim 350),\end{aligned} $

(29) where
$ \pm $ denotes the$ 1 \sigma $ region, and the parentheses denote the$ 3 \sigma $ region. For inverted mass ordering (IO),$ m_3 < m_1<m_2 $ , we have$ \begin{aligned}[b] & \frac{\Delta m^2_{21}}{10^{-5} {\rm eV}^2} = 7.42^{+0.21}_{-0.20} \quad (6.82 \sim 8.04), \\ & \frac{\Delta m^2_{32}}{10^{-3}{\rm eV}^2} = -2.490^{+0.026}_{-0.028} \quad (-2.574 \sim -2.410), \\ & \theta_{12}/(^{\circ}) = 33.45^{+0.78}_{-0.75} \quad (31.27 \sim 35.87), \\ & \theta_{23}/(^{\circ}) = 49.0^{+0.9}_{-1.3} \quad (39.8 \sim 51.6), \\ & \theta_{13}/(^{\circ}) = 8.61^{+0.14}_{-0.12} \quad (8.24 \sim 9.02), \\ & \delta/(^{\circ}) = 278^{+22}_{-30} \quad (194 \sim 345). \end{aligned} $

(30) Moreover, we have the following constraint:
$ \begin{array}{*{20}{l}} \displaystyle\sum m_i < 0.12 - 0.69 \; {\rm eV},\end{array} $

(31) from cosmological observations of cosmic microwave background radiation [52, 91–94].
In our numerical calculations, we require that the square mass differences
$ \Delta m_{ij}^{2} $ , mixing angles$ \theta_{ij} $ , and Dirac CP-violating phase δ vary within the$ 3\sigma $ region, and the lightest neutrino mass$ m_{\rm{lightest}} $ ($ m_{\rm{lightest}}=m_1 $ for NO and$ m_{\rm{lightest}}=m_3 $ for IO) varies within$ 0-0.12 $ eV. We also require that the constraint$ \sum m_i < 0.12 \; {\rm eV} $ is satisfied.Table 1 lists the magnitudes of
$ |\epsilon| $ ,$ |\epsilon_1|,~ |\epsilon_2| $ ,$ |\epsilon_{\rm{Mi}}| $ ,$ |\epsilon_{1}^{\rm{Mi}}| $ ,$ |\epsilon_{2}^{\rm{Mi}}| $ , and$ |\epsilon_{3}^{\rm{Mi}}| $ for the smallest$ |E_{\rm{Mi}}|_{\rm min} $ . The parameter sets for the smallest$ |E_{\rm{Mi}}|_{\rm min} $ are indicated in bold fonts for the NO and IO cases. In Table 1, we observe the following:NO type $ |E_{\rm{Mi}}|_{\rm{min}} $ 

$ |\epsilon| $ 

$ |\epsilon_1| $ 

$ |\epsilon_2| $ 

$ |\epsilon_{\rm{Mi}}| $ 

$ |\epsilon_{1}^{\rm{Mi}}| $ 

$ |\epsilon_{2}^{\rm{Mi}}| $ 

$ |\epsilon_{3}^{\rm{Mi}}| $ 

1 0.461 0.207 0.112 0.0953 0.254 0.0753 0.114 0.0642 2 0.613 0.270 0.0850 0.185 0.343 0.0974 0.121 0.125 3 0.648 0.178 0.0830 0.0948 0.471 0.254 0.143 0.0732 4 0.395 0.0960 0.0769 0.0192 0.299 0.147 0.0373 0.115 5 0.726 0.141 0.0843 0.0563 0.586 0.327 0.197 0.0624 6 0.634 0.365 0.123 0.242 0.269 0.167 0.0363 0.0653 7 0.534 0.365 0.123 0.242 0.169 0.0524 0.0180 0.0986 8 0.377 0.147 0.0549 0.0923 0.230 0.0696 0.156 0.00412 9 0.532 0.221 0.0874 0.134 0.311 0.206 0.00777 0.0968 10 0.545 0.220 0.0720 0.148 0.324 0.0577 0.185 0.0818 IO type $ |E_{\rm{Mi}}|_{\rm{min}} $ 

$ |\epsilon| $ 

$ |\epsilon_1| $ 

$ |\epsilon_2| $ 

$ |\epsilon_{\rm{Mi}}| $ 

$ |\epsilon_{1}^{\rm{Mi}}| $ 

$ |\epsilon_{2}^{\rm{Mi}}| $ 

$ |\epsilon_{3}^{\rm{Mi}}| $ 

1 0.386 0.201 0.0940 0.107 0.185 0.108 0.0601 0.0167 2 0.720 0.124 0.0709 0.0532 0.596 0.071 0.0734 0.451 3 0.485 0.141 0.0593 0.0814 0.344 0.196 0.0998 0.0481 4 0.502 0.229 0.139 0.0896 0.273 0.177 0.0311 0.0648 5 0.695 0.363 0.144 0.219 0.332 0.120 0.0873 0.124 6 0.602 0.217 0.146 0.0707 0.386 0.127 0.0574 0.201 7 0.532 0.242 0.0661 0.176 0.290 0.0388 0.0858 0.166 8 0.731 0.397 0.240 0.157 0.334 0.165 0.0153 0.153 9 0.887 0.167 0.0642 0.103 0.720 0.277 0.211 0.232 10 0.815 0.357 0.100 0.257 0.459 0.281 0.0952 0.0823 Table 1.
$ |\epsilon| $ ,$|\epsilon_1|,~ |\epsilon_2|$ ,$ |\epsilon_{\rm{Mi}}| $ ,$ |\epsilon_{1}^{\rm{Mi}}| $ ,$ |\epsilon_{2}^{\rm{Mi}}| $ , and$ |\epsilon_{3}^{\rm{Mi}}| $ for the smallest$ |E_{\rm{Mi}}|_{\rm min} $ .● The smallest value of
$ |E_{\rm{Mi}}|_{\rm min} $ is obtained in type M8 (M1) for NO (IO).●
$ |\epsilon_2| $ in type M1 for IO is one order of magnitude greater than that in type M8 for the NO case.●
$ |\epsilon_{1}^{\rm{M8}}| $ and$ |\epsilon_{3}^{\rm{M8}}| $ in the NO case are lower than$ |\epsilon_{1}^{\rm{M1}}| $ and$ |\epsilon_{3}^{\rm{M1}}| $ in the IO case.Therefore, we can expect that the flavor neutrino mass matrix for Dirac neutrinos approximately obeys type M8 (M1) magic texture for the NO (IO) case. Moreover, because
$ |E_{M8}|_{\rm{min}} $ for NO is smaller than$ |E_{M1}|_{\rm{min}} $ for IO, NO is slightly preferable to IO in the context of magic textures. In addition, by comparing$ |\epsilon_n| $ and$ |\epsilon_{n}^{\rm{M8}}| $ in type M8 for the NO case,$ |\epsilon_n| $ ,$ |\epsilon_{1}^{\rm{Mi8}}| $ , and$ |\epsilon_{3}^{\rm{M8}}| $ appear to be lower than$ |\epsilon_{2}^{\rm{M8}}| $ , suggesting that the violation of type M8 magic texture is related to$ \tau \mu $ mixing. Similarly, by comparing$ |\epsilon_n| $ and$ |\epsilon_{n}^{\rm{M1}}| $ in type M1 for the IO case,$ |\epsilon_1| $ ,$ |\epsilon_{2}^{\rm{M1}}| $ , and$ |\epsilon_{3 }^{\rm{M1}}| $ appear to be less than$ |\epsilon_2| $ and$ |\epsilon_{1}^{\rm{M1}}| $ , suggesting that the violation of type M1 magic texture is related to the$ \tau e $ and$ \mu \tau $ mixings.Table 2 presents the neutrino parameters
$ \{m_1,m_2,m_3, \theta_{12},\theta_{23},\theta_{13},\delta\} $ for$ |E_{\rm{Mi}}|_{\rm min} $ . Regardless of mass ordering, we observe that$ \theta_{23}>45^\circ $ and$ \delta>180^\circ $ are favorable in the context of magic texture. A disagreement can be noted between T2K and NOvA [95, 96]. Both experiments favor the upper octant of$ \theta_{23} $ . However, NOvA and T2K report extremely different best fit values of δ for the NO case. In fact,$ \delta \sim 145^\circ $ was reported by NOvA [95]. Meanwhile, a value of$ \delta \sim 250^\circ $ was reported by T2K [96]. The predicted value$ \delta=288^\circ $ for type M8 is similar to the T2K best-fit value. Therefore, it appears that the T2K result is more favorable than the NOvA result in the context of magic textures.NO type $ |E_{\rm{Mi}}|_{\rm{min}} $ 

$ m_1 $ 

$ m_2 $ 

$ m_3 $ 

$ \theta_{12} $ 

$ \theta_{23} $ 

$ \theta_{13} $ 

δ 1 0.461 0.00671 0.0110 0.0498 35.5 50.3 8.55 307 2 0.613 0.0238 0.0254 0.0550 35.6 49.8 8.76 163 3 0.648 0.0187 0.0205 0.0531 34.1 47.4 8.84 303 4 0.395 0.0224 0.0240 0.0542 34.0 40.6 8.82 228 5 0.726 0.0236 0.0251 0.0558 32.8 43.5 8.81 300 6 0.634 0.0296 0.0308 0.0575 34.4 46.4 8.65 338 7 0.534 0.0296 0.0308 0.0575 34.4 46.4 8.65 338 8 0.377 0.0178 0.0197 0.0532 33.0 48.1 8.47 288 9 0.532 0.0127 0.0154 0.0514 33.2 48.1 8.62 175 10 0.545 0.0285 0.0297 0.0580 35.3 40.4 8.89 219 IO type $ |E_{\rm{Mi}}|_{\rm{min}} $ 

$ m_1 $ 

$ m_2 $ 

$ m_3 $ 

$ \theta_{12} $ 

$ \theta_{23} $ 

$ \theta_{13} $ 

δ 1 0.386 0.0513 0.0521 0.0120 35.1 48.5 8.75 218 2 0.720 0.0501 0.0509 0.0121 35.1 51.0 8.98 330 3 0.485 0.0499 0.0506 0.0100 31.8 39.8 8.79 295 4 0.502 0.0493 0.0500 0.000524 34.2 43.6 8.35 194 5 0.695 0.0514 0.0521 0.0146 34.0 41.1 8.41 268 6 0.602 0.0503 0.0510 0.00664 34.9 43.3 8.48 302 7 0.532 0.0509 0.0515 0.0127 34.4 40.3 8.79 198 8 0.731 0.0500 0.0508 0.00930 35.9 42.4 9.01 200 9 0.887 0.0495 0.0503 0.00607 33.0 42.8 8.28 329 10 0.815 0.0518 0.0525 0.0146 33.6 45.0 8.26 306 Table 2. Neutrino parameters
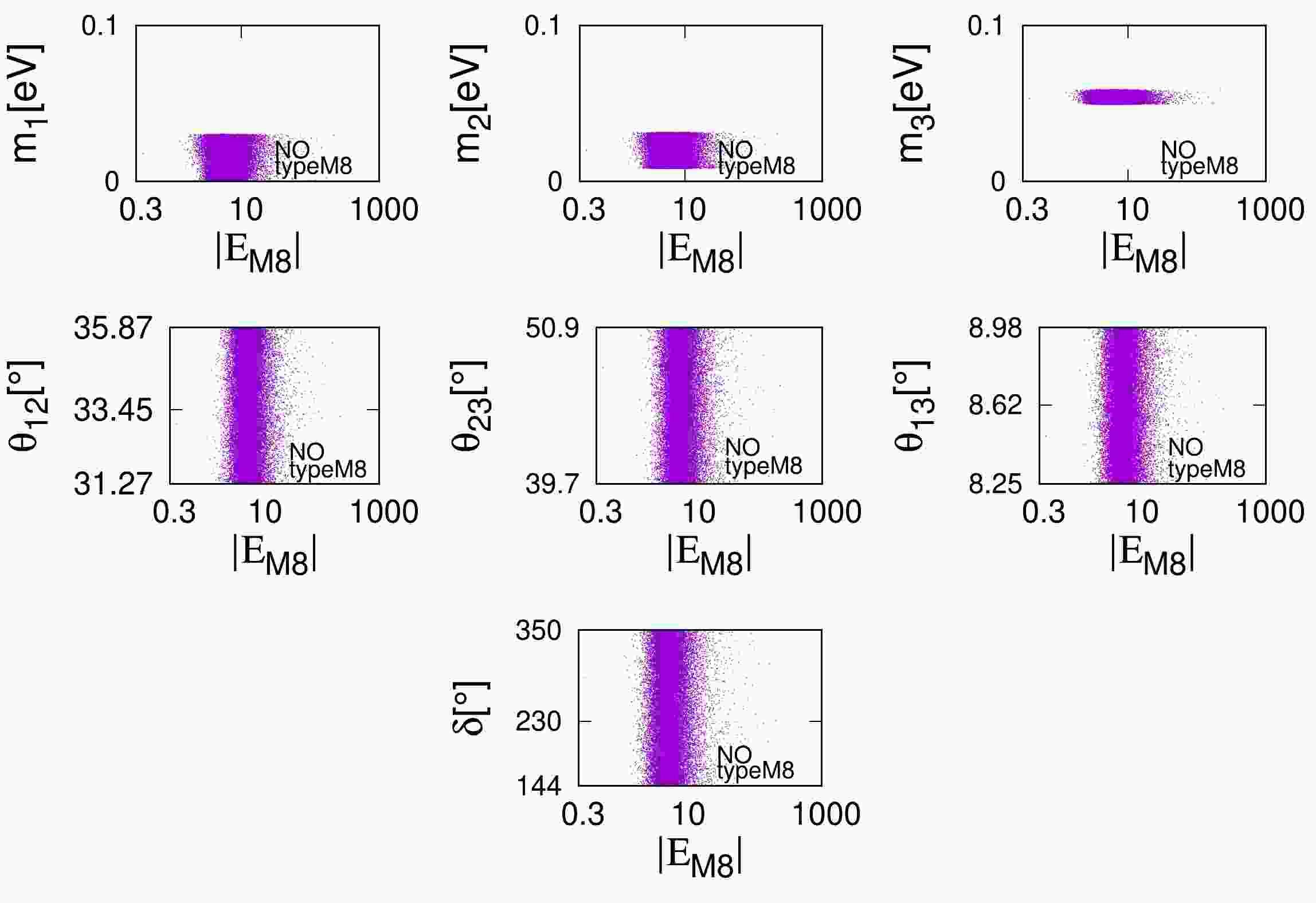
$ m_i $ in eV,$ \theta_{ij} $ , and δ for the smallest$ |E_{\rm{Mi}}|_{\rm min} $ .Figure 1 (Fig. 2) presents the dependence of the neutrino parameters
$ \{m_{i},\theta_{ij},\delta\} $ on$ |E_{\rm{M8}}| (|E_{\rm{M1}}|) $ for the NO (IO) case.$ |E_{\rm{M8}}| $ does not correlate with the neutrino masses$ m_1,m_2,m_3 $ ; mixing angles$ \theta_{ij} $ ; and Dirac CP-violating phase δ. Therefore, the smallest values of$ |E_{\rm{M8}}|_{\rm min} $ and$ |E_{\rm{M1}}|_{\rm min} $ are obtained for very specific neutrino parameters. -
Magic texture is known to be a successful texture of the flavor neutrino mass matrix for Majorana neutrinos.
In this study, we estimate the relationship between the Dirac flavor neutrino mass matrix and magic texture for Majorana-type neutrinos. Consequently, we demonstrate that several types of magic textures for Majorana neutrinos may be approximately immanent in the Dirac flavor neutrino mass matrix. More concretely, in type M8 for NO (
$ |E_{\rm{M8}}|_{\rm{min}}=0.377 $ ) and type M1 for IO ($ |E_{\rm{M1}}|_{\rm{min}} = 0.386 $ ), the Dirac mass matrices approximately obey the magic texture. Because$ |E_{\rm{M8}}|_{\rm{min}} $ for NO is smaller than$ |E_{\rm{M8}}|_{\rm{min}} $ for IO, NO is slightly preferable to IO in the context of magic textures.
Is the magic texture of Majorana neutrinos immanent in Dirac nature?
- Received Date: 2022-08-26
- Available Online: 2023-04-15
Abstract: Magic textures are successful candidates of the correct texture for Majorana neutrinos. In this study, we demonstrate that several types of magic textures of Majorana neutrinos are approximately immanent in the flavor mass matrix of Dirac neutrinos. In addition, the normal mass ordering of Dirac neutrino masses is slightly preferable to inverted mass ordering in the context of magic textures.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: