-
The P-wave
$ 0^{++} $ charmonium state$ \chi_{c0} $ cannot be created by the colorless current$ \bar c\gamma^\mu(1-\gamma_5)c $ . Its production in B meson decays is suppressed in the factorization approximation because of charge conjugation invariance, spin-parity, and vector current conservation [1–4]. Thus, it is not surprising that the reported branching fraction$ \mathcal{B}(B^+\to K^+\chi_{c0})=(6.0^{+2.1}_{-1.8} ({\rm stat.}) \pm1.1({\rm syst.}))\times10^{-4} $ [5] from the Belle Collaboration triggered many studies on this two-body decay mode involving$ \chi_{c0} $ and the relevant decay processes. The measurement by the BaBar Collaboration in 2004 confirmed Belle's result for$ B^+\to K^+\chi_{c0} $ and presented the value$ (2.7\pm0.7)\times10^{-4} $ for its branching fraction [6]. The recent value in Review of Particle Physics for this two-body decay process is$ 1.51^{+0.15}_{-0.13}\times 10^{-4} $ [7], which is only approximately$ 1/4 $ of its first appearance [5]; however, it is still relatively comparable to that of the factorization-allowed decay$ B^+\to K^+J/\psi $ , which has a branching fraction of$ (1.020\pm0.019)\times 10^{-3} $ , as shown in Ref. [7].Since Belle's measurement [5], numerous theoretical studies have been conducted to investigate large nonfactorizable contributions, the decay characteristic in
$ B^+\to K^+\chi_{c0} $ , and other relevant decay modes. Using the light-cone QCD sum rules approach, the nonfactorizable soft contributions in$ B\to K\eta_c, K\chi_{c0} $ decays were analyzed in Ref. [8]. Within the perturbative QCD (PQCD) approach, the nonfactorizable contributions to B meson decays into charmonia, including$ B^{0,+}\to K^{(\ast)0,+} \chi_{c0} $ , were calculated in Refs. [9, 10]. In the framework of QCD factorization (QCDF), exclusive decays, including$ B \to \chi_{c0}K $ , were studied in Refs. [11–16]. From these studies, it was observed that infrared divergences resulting from nonfactorizable vertex corrections could not be eliminated [11, 12]. Non-zero gluon mass was then employed to regularize the infrared divergences in the vertex corrections [13]. Conversely, the authors of [16] found that these infrared divergences can be subtracted consistently into the matrix elements of colour-octet operators in exclusive B to P-wave charmonia decays. In Ref. [15],$ B\to K\chi_{c0,2} $ decays were investigated in QCDF by introducing a non-zero binding energy to regularize the infrared divergence of the vertex part and adopting model dependent parameterization to remove the logarithmic and linear infrared divergences in the spectator diagrams. The rescattering effects mediated by intermediate charmed mesons were studied in Refs. [17, 18], and the authors concluded that such effects could produce a large branching ratio for the decay$ B^+\to K^+\chi_{c0} $ .Unlike the
$ 2P $ state$ \chi_{c0}^\prime $ , which mainly decays into$ D\bar D $ in an S-wave [19–21], the state$ \chi_{c0} $ , with its mass below the threshold of$ D\bar D $ [7], can decay into light hadronic states via gluon-rich processes [22–24]. Although the branching fractions for$ \chi_{c0}\to\pi^+\pi^- $ and$ \chi_{c0}\to K^+K^- $ are small, in the order of$ 10^{-3} $ [7], the resonance contributions from$ \chi_{c0} $ are not negligible in the three-body decays$ B\to h\pi^+\pi^- (K^+K^-) $ because of the enhancements originating from the Cabibbo-Kobayashi-Maskawa (CKM) matrix elements when compared with the resonant states$ \rho(770) $ or$ \phi(1020) $ [25, 26], where h is a light pseudoscalar π and K, the B meson is$ B^{+,0} $ and$ B^0_s $ , and the inclusion of charge-conjugate processes are implied throughout this study. Taking$ B^+\to K^+K^-K^- $ as an example, the branching fraction is$ (1.12\pm0.15\pm0.06)\times10^{-6} $ for the quasi-two-body decay process$ B^+\to K^+\chi_{c0}\to K^+K^+K^- $ in [27], which is approximately$ 1/4 $ of the value for the process$B^+\to $ $ K^+\phi(1020)\to K^+K^+K^-$ and is approximately$ 3.24 $ % of the total branching fraction for$ B^+\to K^+K^+K^- $ [27]. The fit fraction for the quasi-two-body decay$ B^+\to K^+\chi_{c0}\to K^+\pi^+\pi^- $ is$(1.12\pm 0.12^{+0.24}_{-0.08}) $ % in [28] and$ (3.56\pm0.93)%\ $ % (the model$ A_0 $ ) in [29]. Therefore, it is important to study the resonance contributions from$ \chi_{c0} $ in charmless three-body hadronic B meson decays, and this research will improve our understanding of three-body decays.In this study, we systematically analyze the contributions from
$ \chi_{c0} $ in the decays$ B\to h\pi^+\pi^- (K^+K^-) $ using the PQCD approach [30–33], which has previously been adopted to study three-body B meson decays [34–38]. With the help of experimental inputs for time-like pion form factors [39] and two-pion distribution amplitudes [40–42], the decays$B\to K\rho(770),~~ K\rho^\prime(1450)\to K\pi\pi$ [43],$B\to K^{\ast}_0(1430)h, ~~ K^{\ast}_0(1950)h \to K\pi h$ [44],$B\to D^{\ast}(2007)^0h,~~ D^{\ast}(2010)^{\pm}h\to D\pi h$ [45], and$B^0_{(s)}\to \eta_c(2s) \pi^+\pi^-$ [46] are analyzed in the quasi-two-body framework. The method used in [43] have been adopted for other quasi-two-body B meson decays in Refs. [47–53] over recent years. For detailed discussions on the quasi-two-body framework based on the PQCD approach, refer to Refs. [43, 53]. -
Under the factorization hypothesis, the decay amplitude for
$ B\to h \chi_{c0} \to hK^+K^- $ is given by$ \begin{aligned}[b] \langle h(K^+K^-)_{\chi_{c0}} | \mathcal{H}_{\rm eff}| B \rangle \simeq& \langle K^+K^-|\chi_{c0}\rangle\frac{1}{\mathcal{D}_{\rm BW}} \langle h\chi_{c0} | \mathcal{H}_{\rm eff}| B \rangle \\ =&\frac{g_{\chi_{c0}K^+K^-}}{\mathcal{D}_{\rm BW}}\langle h\chi_{c0} | \mathcal{H}_{\rm eff}| B \rangle \\ =& C_{KK}(s)\cdot \mathcal{A}(s)\;, \end{aligned} $

(1) where the denominator
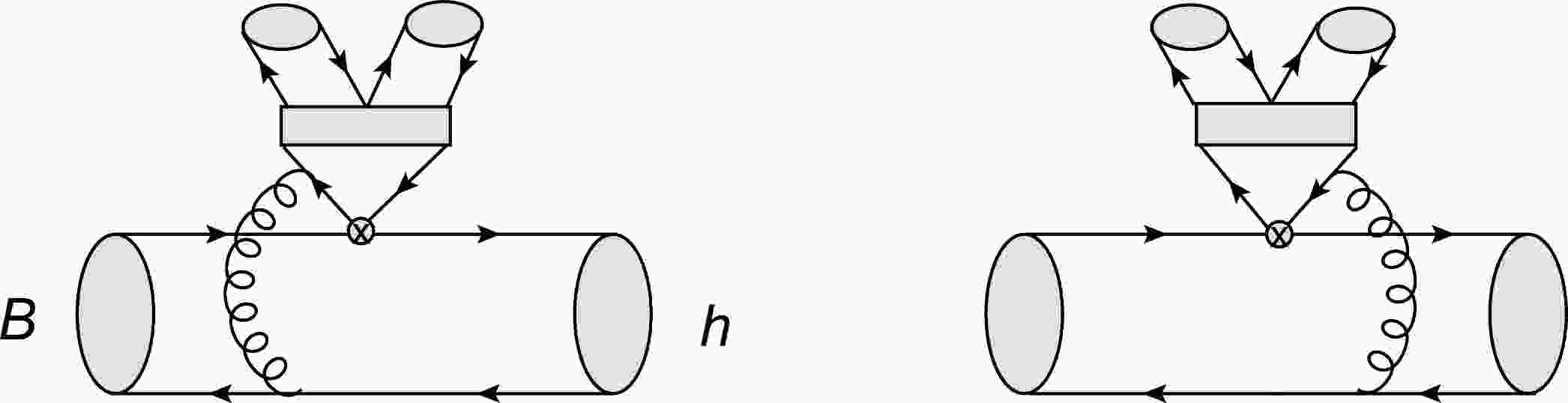
${\mathcal{D}_{\rm BW}}=m^2_0-s-{\rm i} m_0\Gamma(s)$ , the mass-dependent decay width$ \Gamma(s) $ is defined as$\Gamma(s)= \Gamma_0\dfrac{m_0}{\sqrt s}\left(\dfrac{q}{q_0}\right)^{2L_R+1}$ ,$ m_0=(3414.71\pm0.30) $ MeV and$\Gamma_0= (10.8\pm 0.6)$ MeV [7] are the pole mass and full width of the resonant state$ \chi_{c0} $ , respectively, and s is the invariant mass square for the$ K^+K^- $ pair in the final decay state.$ L_R $ denotes the spin of the resonances [27, 29]. In the rest frame of the resonant state$ \chi_{c0} $ , its daughter$ K^+ $ or$ K^- $ has the magnitude of the momentum,$q=\dfrac{1}{2}\sqrt{s-4m_K^2}$ , and$ q_0 $ in$ \Gamma(s) $ is the value of q at$ s=m^2_0 $ . By combining various contributions from relevant Feynman diagrams, as shown in Fig. 1, the amplitude$ \mathcal{A}(s)=\langle h\chi_{c0} | \mathcal{H}_{\rm eff}| B \rangle $ for the quasi-two-body decays considered in this study can be found, as presented in the Appendix. The mass-dependent coefficient$ C_{KK}(s) $ is$ g_{\chi_{c0}K^+K^-}/\mathcal{D}_{\rm BW} $ . We obtain the coupling constant$ g_{\chi_{c0}K^+K^-} $ from the relation [54, 55]
Figure 1. Feynman diagrams for the spectator figure to
$ B_{(s)}\rightarrow h \chi_{c0}\rightarrow h\pi^+\pi^- $ and$ B_{(s)}\rightarrow h \chi_{c0}\rightarrow hK^+K^- $ .$ g_{\chi_{c0}K^+K^-}=\sqrt{\frac{8\pi m^2_0 \Gamma_{\chi_{c0}\to K^+K^-}}{q_0}}\;, $

(2) where
$ \Gamma_{\chi_{c0}\to K^+K^-} $ is the partial width for$ \chi_{c0}\to K^+K^- $ . For the process$ B\to h \chi_{c0} \to h\pi^+\pi^- $ , we must apply the replacement$ K\to \pi $ for Eqs. (1) and (2) and the relevant parameters. The effective Hamiltonian$ \mathcal{H}_{\rm eff} $ with four-fermion operators is the same as in Ref. [9].In the rest frame of the B meson, we choose its momentum
$ p_B $ and the momenta$ p_3 $ and p for the bachelor states h and$ \chi_{c0} $ as$ \begin{aligned}[b] p_B=&\frac{m_B}{\sqrt{2}}(1,1,{ 0_{\rm T}}), \quad\quad\;\; p_3=\frac{m_B}{\sqrt{2}}(0,1-\eta,{ 0_{\rm T}}), \\ p=&\frac{m_B}{\sqrt{2}}(1,\eta,{ 0_{\rm T}}),\quad\quad k_B=\left(0,\frac{m_B}{\sqrt{2}}x_B,k_{\rm BT}\right),\\ k_3=&\left(0,\frac{m_B}{\sqrt{2}}(1-\eta)x_3,k_{\rm 3T}\right),\quad k=\left(\frac{m_B}{\sqrt{2}}z,\frac{m_B}{\sqrt{2}}z\eta,k_{\rm T}\right), \end{aligned} $

(3) where
$ x_B $ ,$ x_3 $ , and z are the corresponding momentum fractions,$ m_B $ is the mass of the B meson, and the variable η is defined as$ \eta=s/m_B^2 $ , with the invariant mass square$ s=p^2 $ . For$ B^{+,0} $ and$ B^0_s $ in this study, we employ the same distribution amplitudes$ \phi_{B/B_s} $ as in Refs. [36, 56]. The wave functions for the bachelor states π and K in this study are written as$ \Phi_{h}(p,z)=\frac{1}{\sqrt{2N_c}}\gamma_5[\not p\phi^{A}(z)+ m_0^h\phi^{P}(z)+ m_0^h({\not n}{\not v}-1)\phi^{T}(z)], $

(4) where
$ m_0^h $ is the chiral mass, p and z are the momentum and corresponding momentum fraction, respectively, of π and k. The distribution amplitudes$ \phi^{A}(z) $ ,$ \phi^{P}(z) $ , and$ \phi^{T}(z) $ can be written as [57–60]$ \begin{aligned}[b] \phi^{A}(z)=&\frac{f_h}{2\sqrt{2N_c}}6z(1-z)[1+a_1^hC_1^{3/2}(t)\\&+a_2^hC_2^{3/2}(t)+a_4^hC_4^{3/2}(t)],\\ \phi^{P}(z)=&\frac{f_h}{2\sqrt{2N_c}}\bigg[1+\left(30\eta_3-\frac{5}{2}\rho_h^2\right)C_1^{1/2}(t)\\&-3\left[\eta_3\omega_3+\frac{9}{20}\rho_h^2(1+6a_2^h)\right]C_4^{1/2}(t)\bigg],\\ \phi^{T}(z)=&\frac{f_h}{2\sqrt{2N_c}}(1-2z)\bigg[1+6 \bigg(5\eta_3-\frac{1}{2}\eta_3\omega_3\\&-\frac{7}{20}\rho_h^2-\frac{3}{5}\rho_h^2a_2^h\bigg)(1-10z+10z^2)\bigg], \end{aligned} $

(5) where the Gegenbauer moments are chosen as
$ a_1^{\pi}=0 $ ,$ a_1^K=0.06 $ ,$ a_2^{\pi,K}=0.25\pm0.15 $ , and$ a_4^{\pi}=-0.015 $ , and the parameters follow$ \rho_{\pi}= m_{\pi}/m_{0}^{\pi} $ ,$ \rho_{K}= m_{K}/m_{0}^{K} $ ,$ \eta_3^{\pi,K}=0.015 $ , and$ \omega_3^{\pi,K}=-3 $ . We adopt$m_{0}^{\pi}=(1.4\pm0.1)\rm\;{GeV}$ and$m_{0}^{K}=(1.6\pm 0.1)\rm\;{GeV}$ in the numerical calculations. The Gegenbauer polynomials are defined as$ \begin{aligned}[b] C_1^{\frac{3}{2}}(t)=&3t,\quad C_2^{\frac{1}{2}}(t)=\frac{1}{2}(3t^{2}-1),\quad C_2^{\frac{3}{2}}(t)=\frac{3}{2}(5t^{2}-1),\\ C_4^{\frac{1}{2}}(t)=&\frac{1}{8}(3-30t^2+35t^4),\quad C_4^{\frac{3}{2}}(t)=\frac{15}{8}(3-30t^2+35t^4), \end{aligned} $

(6) where the variable
$ t=2z-1 $ . The mass-dependent$ \pi\pi $ or$ KK $ system, which comes from$ \chi_{c0} $ , has the distribution amplitude [9]$ \Phi_{\pi\pi(KK)}=\frac{1}{\sqrt{2N_c}}({\not p}\phi_{\pi\pi(KK)}^v(z)+\sqrt{s}\phi_{\pi\pi(KK)}^s(z)), $

(7) with the twist-2 and twist-3 distribution amplitudes
$ \phi_{\pi\pi(KK)}^v(z,s) $ and$ \phi_{\pi\pi(KK)}^s(z,s) $ $ \begin{aligned}[b] \phi_{\pi\pi(KK)}^v(z,s)=&\frac{F_{\chi_{c0}}(s)}{2\sqrt{2N_c}}27.46(1 - 2z)\left\{\frac{z(1 - z)[1-4z(1 - z)]}{[1-2.8z(1-z)]^2}\right\}^{0.7},\\ \phi_{\pi\pi(KK)}^s(z,s)=&\frac{F_{\chi_{c0}}(s)}{2\sqrt{2N_c}}4.73\left\{\frac{z(1-z)[1-4z(1-z)]}{[1-2.8z(1-z)]^2}\right\}^{0.7}. \end{aligned} $

(8) The timelike form factor
$ F_{\chi_{c0}}(z,s) $ is parameterized with the RBW line shape [61] and can be expressed as follows [62–64]:$ F_{\chi_{c0}}(s)=\frac{m^2_{0}}{m^2_{0}-s-{\rm i} m_{0}\Gamma_{(s)}}, $

(9) where
$ m_{0} $ is the pole mass. The mass-dependent decay width$ \Gamma_{(s)} $ is defined as$ \Gamma(s)=\Gamma_0\frac{m_0}{\sqrt s} (\frac{q}{q_0} )^{2L_R+1}. $

(10) $ L_R $ is the spin of the resonances, and$ L_R=0 $ for the scalar intermediate state$ \chi_{c0} $ . -
The differential branching ratios (
$ \mathcal B $ ) for the decay processes$ B\to h\pi^+\pi^-(K^+K^-) $ are$ \frac{{\rm d}\mathcal{B}}{{\rm d} s}=\tau_B\frac{q_h q }{64\pi^3m^3_B }{\overline{|C_{\pi\pi(KK)}\cdot\mathcal{A}}|^2}, $

(11) where
$ \tau_B $ is the lifetime of the B meson, and$ q_h $ is the magnitude momentum for the bachelor h in the rest frame of$ \chi_{c0} $ ,$ q_h=\frac{1}{2}\sqrt{\left[ (m_B^2-m_h^2)^2-2(m_B^2+m_h^2)s+s^2 \right]/s}\; , $

(12) with
$ m_h $ as the mass of h. The central values (in units of GeV) of the relevant mesons and quark masses are adopted as [7]$ \begin{aligned}[b]& m_{B}=5.279, \quad m_{B_s}=5.367,\quad m_{\pi^{\pm}}=0.140,\quad m_{\pi^0}=0.135,\\& m_{K^{\pm}}=0.494,\quad m_{K^0}=0.498,\quad m_{b}(pole)=4.8,\quad m_{c}=1.275. \end{aligned} $

(13) For the decay constants (in units of GeV) and lifetimes (in units of ps) of the relevant mesons, we use [7]
$ \begin{aligned}[b] f_{B}=&0.19, \quad f_{B_s}=0.227,\quad f_{\chi_{c0}}=0.36, \quad f_{\pi}=0.131,\\ f_{K}=&0.156, \quad\tau_{B^\pm}=1.638,\quad \tau_{B^0}=1.52,\quad \tau_{B_s}=1.51. \end{aligned} $

(14) The QCD scale follows
$ \Lambda_{\overline{MS}}^{(f=4)}=0.25{\rm GeV} $ . We adopt the Wolfenstein parameters$ (A,\overline{\lambda},\overline{\rho},\overline{\eta}) $ of the CKM mixing matrix,$ A=0.836\pm0.015 $ ,$ \overline{\lambda}=0.22453\pm0.00044 $ ,$ \overline{\rho}= 0.122^{+0.018}_{-0.017} $ , and$ \overline{\eta}=0.335^{+0.012}_{-0.011} $ [7]. For the shape parameter uncertainty of the$ B_{(s)} $ meson, we use$ \omega_B=0.4\pm0.04\,{\rm GeV} $ and$ \omega_{B_s}=0.5\pm0.05\,{\rm GeV} $ , which contribute the largest error for the branching fractions. The latter is from the Gegenbauer moments$ a_2^{h} $ in the bachelor meson distribution amplitudes. Two other errors originate from the decay width of the resonance$ \chi_{c0} $ and the chiral mass$ m_0^{h} $ of the bachelor meson, which have a smaller impact on the uncertainties in our approach. There are further errors that are small and can be safely ignored, such as minor and disregarded parameters in the bachelor meson$ (\pi/K) $ distribution amplitudes and Wolfenstein parameters.We calculate the branching ratios for the decays
$ B \rightarrow h\chi_{c0} \rightarrow h\pi^+\pi^-(K^+K^-) $ , as shown in Table 1, using the differential branching ratios in Eq. (4) and the decay amplitudes in the Appendix. We then compare and analyze our numerical results with current world average values from the PDG [7] and various theoretical predictions in PQCD, LCSR, and QCDF in Table 2.Mode Unit Branching ratios Data [7] $ B^+\rightarrow K^+\chi_{c0}\rightarrow K^+\pi^+\pi^- $ 

$ (10^{-6}) $ 

$ 0.81_{-0.22}^{+0.21}(\omega_B)_{-0.21}^{+0.12}(a_2)_{-0.05}^{+0.11}(\Gamma_{\chi_{c0}})_{-0.06}^{+0.06}(m_0^K) $ 

$ - $ 

$ B^+\rightarrow K^+\chi_{c0}\rightarrow K^+K^+K^- $ 

$ (10^{-6}) $ 

$ 0.84_{-0.24}^{+0.22}(\omega_B)_{-0.12}^{+0.08}(a_2)_{-0.08}^{+0.07}(\Gamma_{\chi_{c0}})_{-0.02}^{+0.02}(m_0^K) $ 

$ - $ 

$ B^0\rightarrow K^0\chi_{c0}\rightarrow K^0\pi^+\pi^- $ 

$ (10^{-6}) $ 

$ 1.21_{-0.32}^{+0.55}(\omega_B)_{-0.13}^{+0.27}(a_2)_{-0.10}^{+0.12}(\Gamma_{\chi_{c0}})_{-0.05}^{+0.01}(m_0^K) $ 

$ - $ 

$ B^0\rightarrow K^0\chi_{c0}\rightarrow K^0 K^+K^- $ 

$ (10^{-6}) $ 

$ 1.30_{-0.27}^{+0.32}(\omega_B)_{-0.16}^{+0.22}(a_2)_{-0.02}^{+0.01}(\Gamma_{\chi_{c0}})_{-0.04}^{+0.01}(m_0^K) $ 

$ - $ 

$ B_s^0\rightarrow \bar{K}^0\chi_{c0}\rightarrow \bar{K}^0\pi^+\pi^- $ 

$ (10^{-7}) $ 

$ 1.86_{-0.28}^{+0.41}(\omega_B)_{-0.22}^{+0.38}(a_2)_{-0.12}^{+0.14}(\Gamma_{\chi_{c0}})_{-0.04}^{+0.03}(m_0^K) $ 

- $ B_s^0\rightarrow \bar{K}^0\chi_{c0}\rightarrow \bar{K}^0 K^+K^- $ 

$ (10^{-7}) $ 

$ 2.45_{-0.61}^{+0.33}(\omega_B)_{-0.26}^{+0.39}(a_2)_{-0.23}^{+0.45}(\Gamma_{\chi_{c0}})_{-0.02}^{+0.02}(m_0^K) $ 

- $ B^+\rightarrow \pi^+\chi_{c0}\rightarrow \pi^+\pi^+\pi^- $ 

$ (10^{-8}) $ 

$ 3.93_{-0.70}^{+0.65}(\omega_B)_{-0.54}^{+0.40}(a_2)_{-0.21}^{+0.18}(\Gamma_{\chi_{c0}})_{-0.01}^{+0.01}(m_0^{\pi}) $ 

$<10 $ 

$ B^+\rightarrow \pi^+\chi_{c0}\rightarrow \pi^+K^+K^- $ 

$ (10^{-8}) $ 

$ 4.15_{-1.01}^{+0.89}(\omega_B)_{-0.60}^{+0.63}(a_2)_{-0.23}^{+0.24}(\Gamma_{\chi_{c0}})_{-0.02}^{+0.01}(m_0^{\pi}) $ 

$ - $ 

$ B^0\rightarrow \pi^0\chi_{c0}\rightarrow \pi^0\pi^+\pi^- $ 

$ (10^{-8}) $ 

$ 1.96_{-0.13}^{+0.32}(\omega_B)_{-0.28}^{+0.26}(a_2)_{-0.13}^{+0.16}(\Gamma_{\chi_{c0}})_{-0.00}^{+0.02}(m_0^{\pi}) $ 

$ - $ 

$ B^0\rightarrow \pi^0\chi_{c0}\rightarrow \pi^0 K^+K^- $ 

$ (10^{-8}) $ 

$ 2.06_{-0.36}^{+0.45}(\omega_B)_{-0.32}^{+0.30}(a_2)_{-0.10}^{+0.12}(\Gamma_{\chi_{c0}})_{-0.04}^{+0.01}(m_0^{\pi}) $ 

$ - $ 

Table 1. PQCD predictions of branching ratios for the quasi-two-body decays
$ B_{(s)}\rightarrow h\chi_{c0}\rightarrow h\pi^+\pi^-(K^+K^-) $ .Mode Unit This study Data [7] PQCD LCSR QCDF $ B^+\rightarrow K^+\chi_{c0} $ 

$ (10^{-4}) $ 

$ 1.42_{-0.92}^{+0.78} $ 

$ 1.51_{-0.13}^{+0.15} $ 

$ 1.4^{+1.3}_{-0.9} $ [10]

$ 1.0\pm0.6 $ [8]

$ 1.05 $ [14]

5.61[9] $ 0.78_{-0.35}^{+0.46} $ [15]

$ B^0\rightarrow K^0\chi_{c0} $ 

$ (10^{-4}) $ 

$ 2.13_{-1.01}^{+1.54} $ 

$ 1.9\pm0.4 $ 

$ 1.3_{-0.8}^{+1.2} $ [10]

- $ 1.13\sim5.19 $ [16]

5.24[9] $ B_s^0\rightarrow \bar{K}^0\chi_{c0} $ 

$ (10^{-5}) $ 

$ 3.28_{-1.08}^{+1.51} $ 

$ - $ 

$ 4.3_{-3.0}^{+4.4}$ [10]

$ - $ 

$ - $ 

$ B^+\rightarrow \pi^+\chi_{c0} $ 

$ (10^{-5}) $ 

$ 0.69_{-0.26}^{+0.22} $ 

$ - $ 

$ 0.36_{-0.24}^{+0.37} $ [10]

$ - $ 

$ - $ 

$ B^0\rightarrow \pi^0\chi_{c0} $ 

$ (10^{-5}) $ 

$ 0.34_{-0.10}^{+0.13} $ 

$ - $ 

$ - $ 

$ - $ 

$ - $ 

Table 2. PQCD predictions of branching ratios for the two-body decays
$ B_{(s)}\rightarrow h\chi_{c0}[\chi_{c0} \rightarrow \pi^+\pi^-(K^+K^-)] $ .With the assumption that the reaction between the branching ratio of the quasi-two-body decay and the two-body framework satisfies
$ \mathcal{B}(B^+\rightarrow h\chi_{c0}\rightarrow h\pi^+\pi^-)= \mathcal{B}(B^+\rightarrow h\chi_{c0})\cdot\mathcal{B}(\chi_{c0}\rightarrow \pi^+\pi^-) $ , we find the PQCD prediction of the branching ratio$\mathcal{B}(B^+\rightarrow K^+\chi_{c0})= $ $\dfrac{\mathcal{B}(B^+\rightarrow K^+\chi_{c0}\rightarrow K^+\pi^+\pi^-)}{\mathcal{B}(\chi_{c0}\rightarrow \pi^+\pi^-)}= (1.42_{-0.92}^{+0.78})\times10^{-4},$ and$\mathcal{B}(B^+\rightarrow K^+\chi_{c0})=\dfrac{\mathcal{B}(B^+ \rightarrow K^+\chi_{c0} \rightarrow K^+K^+K^-)}{\mathcal{B}(\chi_{c0}\rightarrow K^+K^-)}=(1.39_{-0.73}^{+0.54})\times 10^{-4},$ where the branching ratio$ \mathcal{B}(\chi_{c0}\rightarrow \pi^+\pi^-)= \dfrac{2}{3}\mathcal{B}(\chi_{c0}\rightarrow \pi\pi)= (5.67\pm0.22)\times10^{-3} $ , and$ \mathcal{B}(\chi_{c0}\rightarrow K^+K^-)= (6.05\pm 0.31)\times 10^{-3} $ [7]. The above two results predicted by PQCD agree well with the branching fractions$ (1.51_{-0.13}^{+0.15})\times10^{-4} $ for the two-body decays$ B^+\rightarrow K^+\chi_{c0} $ in Review of Particle Physics [7]. Our prediction for$\mathcal{B}(B^0\rightarrow K^0\chi_{c0})=(2.13_{-1.01}^{+1.54})\times 10^{-4}$ agrees with data, ($1.9\pm0.4)\times 10^{-4}$ , for the two-body decays$ B^0\rightarrow K^0\chi_{c0} $ [7].We compare the various theoretical predictions for the
$ B\rightarrow K\chi_{c0} $ cases of the investigated quasi-two-body and two-body decays. The LCSR calculations mainly focus on$ B^+\rightarrow K^+\chi_{c0} $ , and the prediction value is$ (1.0\pm0.6)\times 10^{-4} $ [8]. Compared with previous PQCD calculations [9, 10], we update the charmonium distribution amplitudes and several input parameters in this study. Our predictions are smaller than those of [9] and closer to those of [10]. QCDF suffers endpoint divergences caused by spectator amplitudes and infrared divergences resulting from vertex diagrams. The different treatment of these divergences, as mentioned in the Introduction, in [14–16] leads to different numerical results. Both our results in this study and the computations above are in excellent agreement with the available data for$ B^+\rightarrow K^+\chi_{c0} $ and$ B^0\rightarrow K^0\chi_{c0} $ .Now, we turn our attention to
$ B\rightarrow h\chi_{c0}\rightarrow h\pi^+\pi^- (K^+K^-) $ with$ h=\pi,\bar{K}^0 $ decay models. These decays, which proceed via a$ b \rightarrow dc\bar{c} $ quark transition, are Cabibbo-suppressed decays. The influence of$ SU(3) $ breaking on the distribution amplitudes offers a negative contribution to the decay, causing the branching ratio to be small. Experimentally, only the BaBar Collaboration reported the upper bound$ 0.1\times 10^{-6} $ on the branching ratio for$ B^+\rightarrow \pi^+\chi_{c0}\rightarrow \pi^+\pi^+\pi^- $ [65]. Our result is$ 3.93_{-1.46}^{+1.69}\times10^{-8} $ , which is inconsistent with the scope of the measured data by BaBar. The data for the decay modes$ B^+\rightarrow \pi^+\chi_{c0}\rightarrow \pi^+K^+K^- $ ,$ \sqrt{2}B^0\rightarrow \pi^0\chi_{c0}\rightarrow \pi^0\pi^+\pi^- $ , and$ \sqrt{2}B^0\rightarrow \pi^0\chi_{c0}\rightarrow \pi^0 K^+K^- $ are approximately$ 10^{-8} $ , which can be examined in forthcoming experiments. Because these Cabibbo-suppressed decays still receive less attention in other approaches, we await future comparisons.For the quasi-two-body processes
$ B^+\rightarrow \pi^+\chi_{c0}\rightarrow \pi^+\pi^+\pi^- $ and$ B^+\rightarrow K^+\chi_{c0}\rightarrow K^+\pi^+\pi^- $ , which have an identical step,$ \chi_{c0}\rightarrow \pi^+\pi^- $ , the difference of these two decay modes originates from the bachelor particles pions and kaons. Assuming factorization and flavor-$ SU(3) $ symmetry, the ratio$ R_{\chi_{c0}} $ for the branching fractions of these two processes is$ R_{\chi_{c0}}=\frac{\mathcal{B}(B^+\rightarrow \pi^+\chi_{c0}\rightarrow \pi^+\pi^+\pi^-)}{\mathcal{B}(B^+\rightarrow K^+\chi_{c0}\rightarrow K^+\pi^+\pi^-)}\approx \mid\frac{V_{cd}}{V_{cs}}\mid^2 \cdot \frac{f_{\pi}^2}{f_k^2}. $

(15) With the result
$ \mid \frac{V_{cd}}{V_{cs}}\mid \cdot \frac{f_{\pi}}{f_k}=0.189, $

(16) in Review of Particle Physics [7],
$ R_{\chi_{c0}}\approx 0.036 $ . This still meets the expectations from our PQCD anticipated ratio$ R_{\chi_{c0}}=\frac{\mathcal{B}(B^+\rightarrow \pi^+\chi_{c0}\rightarrow \pi^+\pi^+\pi^-)}{\mathcal{B}(B^+\rightarrow K^+\chi_{c0}\rightarrow K^+\pi^+\pi^-)}=0.049_{-0.009}^{+0.020}. $

(17) In Fig. 2, we show the distribution of branching ratios for the decays modes
$ B^+\rightarrow K^+\chi_{c0} \rightarrow K^+K^+K^- $ . The mass of$ \chi_{c0} $ is visible as a narrow peak near$ 3.414\,{\rm GeV} $ . We find that the central portion of the branching ratios lies in the region around the pole mass of the$ \chi_{c0} $ resonance, as shown by the distribution of the branching ratios in the$ \pi\pi $ invariant mass. -
We study the nonfactorizable contributions to the factorization-forbidden quasi-two-body decays
$ B \to K\chi_{c0} \to K\pi\pi(KK) $ ,$ B_s \to \bar{K}^0\chi_{c0} \to \bar{K}^0\pi\pi(KK) $ , and$ B_s \to \pi\chi_{c0} \to \pi\pi\pi(KK) $ using the PQCD approach. Our predictions for the branching ratios are summarized in Table 1 and compared with other theoretical results. The obtained branching ratios of the$ B\rightarrow K\chi_{c0} $ decay are essentially consistent with current data. For the decay involving π or$ \bar{K} $ in the final state, which is not yet measured, the calculated branching ratios will be further tested by experiments in the near future. By utilizing flavor-$ SU(3) $ symmetry to examine quasi-two-body decays with the same intermediate step, we are able to establish the ratio$ R_{\chi_{c0}} $ for the processes$ B^+\rightarrow \pi^+\chi_{c0}\rightarrow \pi^+\pi^+\pi^- $ and$ B^+\rightarrow K^+\chi_{c0}\rightarrow K^+\pi^+\pi^- $ . The ratio$ R_{\chi_{c0}} $ is predicted via PQCD to be$ 0.049 $ , which is close to the value$ 0.036 $ reported in Review of Particle Physics. We also show the distribution of branching ratios for various decay modes in invariant mass and discover that the majority of the branching ratios are located in the vicinity of the pole mass of$ \chi_{c0} $ resonance. -
Many thanks to Wen-Fei Wang, Da-Cheng Yan, and Jun Hua for valuable discussions.
-
The considered quasi-two-body decay amplitudes are given in the PQCD approach by
$ \mathcal{A}\left(B^+\rightarrow \pi^+[\chi_{c0}\rightarrow ]\pi^+\pi^-\right)=\frac{G_F}{\sqrt{2}}\left\{V_{cb}^*V_{cd} c_2 M_{e\pi}^{LL}-V_{tb}^*V_{td}\left[(c_4+c_{10})M_{e\pi}^{LL}+(c_6+c_8)M_{e\pi}^{SP}\right]\right\}, \tag{A1} $ 
$ \mathcal{A}\left(B^+\rightarrow K^+[\chi_{c0}\rightarrow ]\pi^+\pi^-\right)=\frac{G_F}{\sqrt{2}}\left\{V_{cb}^*V_{cs} c_2 M_{eK}^{LL}-V_{tb}^*V_{ts}\left[(c_4+c_{10})M_{eK}^{LL}+(c_6+c_8)M_{eK}^{SP}\right]\right\},\tag{A2} $

$ \mathcal{A}\left(B^0\rightarrow \pi^0[\chi_{c0}\rightarrow ]\pi^+\pi^-\right)=\frac{G_F}{\sqrt{2}}\left\{V_{cb}^*V_{cd} c_2 M_{e\pi}^{LL}-V_{tb}^*V_{td}\left[(c_4+c_{10})M_{e\pi}^{LL}+(c_6+c_8)M_{e\pi}^{SP}\right]\right\}, \tag{A3} $

$ \mathcal{A}\left(B^0\rightarrow K^0[\chi_{c0}\rightarrow ]\pi^+\pi^-\right)=\frac{G_F}{\sqrt{2}}\left\{V_{cb}^*V_{cs} c_2 M_{eK}^{LL} -V_{tb}^*V_{ts}\left[(c_4+c_{10})M_{eK}^{LL}+(c_6+c_8)M_{eK}^{SP}\right]\right\}, \tag{A4} $

$ \mathcal{A}\left(B_s^0\rightarrow \bar{K}^0[\chi_{c0}\rightarrow ]\pi^+\pi^-\right)=\frac{G_F}{\sqrt{2}}\left\{V_{cb}^*V_{cd} c_2 M_{eK}^{LL} -V_{tb}^*V_{td}\left[(c_4+c_{10})M_{eK}^{LL}+(c_6+c_8)M_{eK}^{SP}\right]\right\}, \tag{A5} $

where
$ G_F $ is the Fermi coupling constant,$ V^{,}\text{s} $ are the CKM matrix elements, and$ c_i $ are the Wilson coefficients. The amplitudes in the above equations are written as$ \begin{aligned}[b] M_{eK(\pi)}^{LL}=&-16\sqrt{\frac{2}{3}}\pi C_F m_B^4\int_0^1 {\rm d} x_B {\rm d} z {\rm d} x_3\int_0^\infty b_B {\rm d} b_B b_3 {\rm d} b_3\phi_B(x_B,b_B) \\ &\{[(\eta-1)(\sqrt{\eta}r\phi_{\pi\pi}^s(z)-(\eta+1)(x_B+z-1)\phi_{\pi\pi}^v(z))\phi^A(x_3)\\ &+r_3(4\sqrt{\eta}r\phi_{\pi\pi}^s(z)+(x_3-\eta(x_3+x_B+2z-2))\phi_{\pi\pi}^v(z))\phi^P(x_3)\\ &+r_3((\eta-1)x_3-\eta x_B)\phi_{\pi\pi}^v(z)\phi^T(x_3)]E_a(t_a)h_a(x_B,z,x_3;b_B,b_3)\\ &+[(\eta-1)(\sqrt{\eta}r\phi_{\pi\pi}^s(z)+((\eta-1)x_3+x_B-(\eta+1)z)\phi_{\pi\pi}^v(z))\phi^A(x_3)\\ &+r_3(4\sqrt{\eta}r\phi_{\pi\pi}^s(z)+(\eta(x_3+x_B-2z)-x_3)\phi_{\pi\pi}^v(z))\phi^P(x_3)\\ &+r_3((\eta-1)x_3-\eta x_B)\phi_{\pi\pi}^v(z)\phi^T(x_3)]E_b(t_b)h_b(x_B,z,x_3;b_B,b_3)\}, \end{aligned}\tag{A6} $

$ \begin{aligned}[b] M_{eK(\pi)}^{SP}=&-16\sqrt{\frac{2}{3}}\pi C_F m_B^4\int_0^1 {\rm d} x_B {\rm d} z {\rm d} x_3\int_0^\infty b_B {\rm d} b_B b_3 {\rm d} b_3\phi_B(x_B,b_B) \\ &\{[(\eta-1)(\sqrt{\eta}r\phi_{\pi\pi}^s(z)-((\eta-1)x_3+x_B+(\eta+1)(z-1))\phi_{\pi\pi}^v(z))\phi^A(x_3)\\ &+r_3(4\sqrt{\eta}r\phi_{\pi\pi}^s(z)+(x_3-\eta(x_3+x_B+2z-2))\phi_{\pi\pi}^v(z))\phi^P(x_3)\\ &-r_3((\eta-1)x_3-\eta x_B)\phi_{\pi\pi}^v(z)\phi^T(x_3)]E_a(t_a)h_a(x_B,z,x_3;b_B,b_3)\\ &+[(\eta-1)(\sqrt{\eta}r\phi_{\pi\pi}^s(z)+(\eta+1)(x_B-z)\phi_{\pi\pi}^v(z))\phi^A(x_3)\\ &+r_3(4\sqrt{\eta}r\phi_{\pi\pi}^s(z)+(\eta(x_3+x_B-2z)-x_3)\phi_{\pi\pi}^v(z))\phi^P(x_3)\\ &-r_3((\eta-1)x_3-\eta x_B)\phi_{\pi\pi}^v(z)\phi^T(x_3)]E_b(t_b)h_b(x_B,z,x_3;b_B,b_3)\}, \end{aligned}\tag{A7} $

with
$ r_c=m_c/m_B $ , and$ r_3=m_{0}^{h}/m_B $ . The evolution factors in the above formulas are given by$ \begin{array}{*{20}{l}} E_{a(b)}(t)=\alpha_s(t)\exp[-S_{ab}(t)]. \end{array} \tag{A8}$

The explicit expressions of the hard functions
$ h_{a(b)} $ , hard scales$ t_{a(b)} $ , and factor$ S_{ab}(t) $ are shown in the appendix of [66].
Resonance contributions from χc0 in charmless three-body hadronic B meson decays
- Received Date: 2022-11-01
- Available Online: 2023-04-15
Abstract: Within the framework of perturbative QCD factorization, we investigate the nonfactorizable contributions to the factorization-forbidden quasi-two-body decays






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
























 DownLoad:
DownLoad: