-
Clustering is one of the fundamental phenomena in nuclear structures. It occurs not only in α-conjugate nuclei, for example,
$ ^{12} $ C,$ ^{16} $ O,$ ^{20} $ Ne$ etc. $ , but also in neutron-proton asymmetric nuclei-forming molecule-like structures [1−4]. In recent years, cluster-structure studies have also been extended to systems with a hole in one of the cluster cores, such as the α + α + t configuration in$ ^{11} $ B, α +$ ^{15} $ N or t +$ ^{16} $ O configurations in$ ^{19} $ F, and α +$ ^{15} $ O or$ ^3 $ He +$ ^{16} $ O configurations in$ ^{19} $ Ne ([5, 6] and references therein).Clustering with a hole configuration is useful not only for nuclear structures but also for the synthesis of nuclei in stars during the hydrogen-burning initiated processes [6, 7]. For instance, the α-cluster structure in
$ ^{19} $ Ne would largely affect the$ ^{15} $ O($ \alpha, \gamma $ )$ ^{19} $ Ne reaction rate, which is closely related to the breakout of the hot-CNO cycles and the ignition of the rapid-proton ($ rp $ ) process [8−11]. Another important reaction is$ ^{18} $ F(p, α)$ ^{15} $ O, which determines the destruction of$ ^{18} $ F in stars. Notably, in the first few hours of novae explosion and before the optical light becomes observable, telescope-detected γ rays provide unique information for novae explosion, such as the temperature, density, and timescale. This is based on the assumption of sufficient knowledge about γ-ray sources, which are believed to be dominated by positron annihilation associated with the$ \beta^+ $ decay of$ ^{18} $ F [7, 12].However, after years of studies, there still exist large uncertainties in the reaction
$ ^{18} $ F(p, α)$ ^{15} $ O , which destroy the$ ^{18} $ F system, although the production mechanisms for$ ^{18} $ F have been studied wel [6, 7]. This is mostly attributed to the limited knowledge about the resonances in$ ^{19} $ Ne around its proton-decay threshold. Various reaction tools have been applied to investigate these resonances, particularly those with a low spin (3/2 or 1/2), which may have a large impact on the$ ^{18} $ F-related reaction rate during the novae explosion ([7] and references therein). We note that Dufour and Deuscouvemont have predicted two broad 1/2$ ^+ $ resonances at about 7.9 MeV and 6.0 MeV in$ ^{19} $ Ne [13]. Although substantially above and below the proton threshold, these two broad states may significantly change the astrophysical reaction rate (or S-factor) via interference with the narrow low-spin resonances at energies very close to the threshold and are well overlapped with the effective proton energy at a star temperature below 1 GK [7, 12, 14]. Since 2009, these broad 1/2$ ^+ $ resonances have been studied by several experiments [7, 14−17], but the results are still inconsistent and have large uncertainties [7] (see more details in Sec. IV). We note that the cross section for resonant reaction$ ^{18} $ F(p, α)$ ^{15} $ O is proportional to the product of the partial decay widths$ \Gamma_{\alpha} \times \Gamma_p $ related to$ ^{19} $ Ne resonance decay [18]. Hence, the study of the reaction cross section is equivalent to the study of the resonance-decay property of$ ^{19} $ Ne, with the latter being produced from any reaction.In the present work, we have performed a new multi-nucleon transfer-reaction experiment to acquire further information about cluster formation in
$ ^{19} $ Ne with a one-hole configuration and to analyze the associated effects on astrophysical processes. As numerous studies have investigated the resonances at relatively lower excitation energies near the proton threshold, we have extended this study to higher excitation energies to observe the possible persistence of the exotic cluster structure. Special attention has been paid to the astrophysically important state at about 7.9 MeV. -
The experiment was carried out at the HI-13 tandem accelerator facility at the China Institute of Atomic Energy, Beijing. A
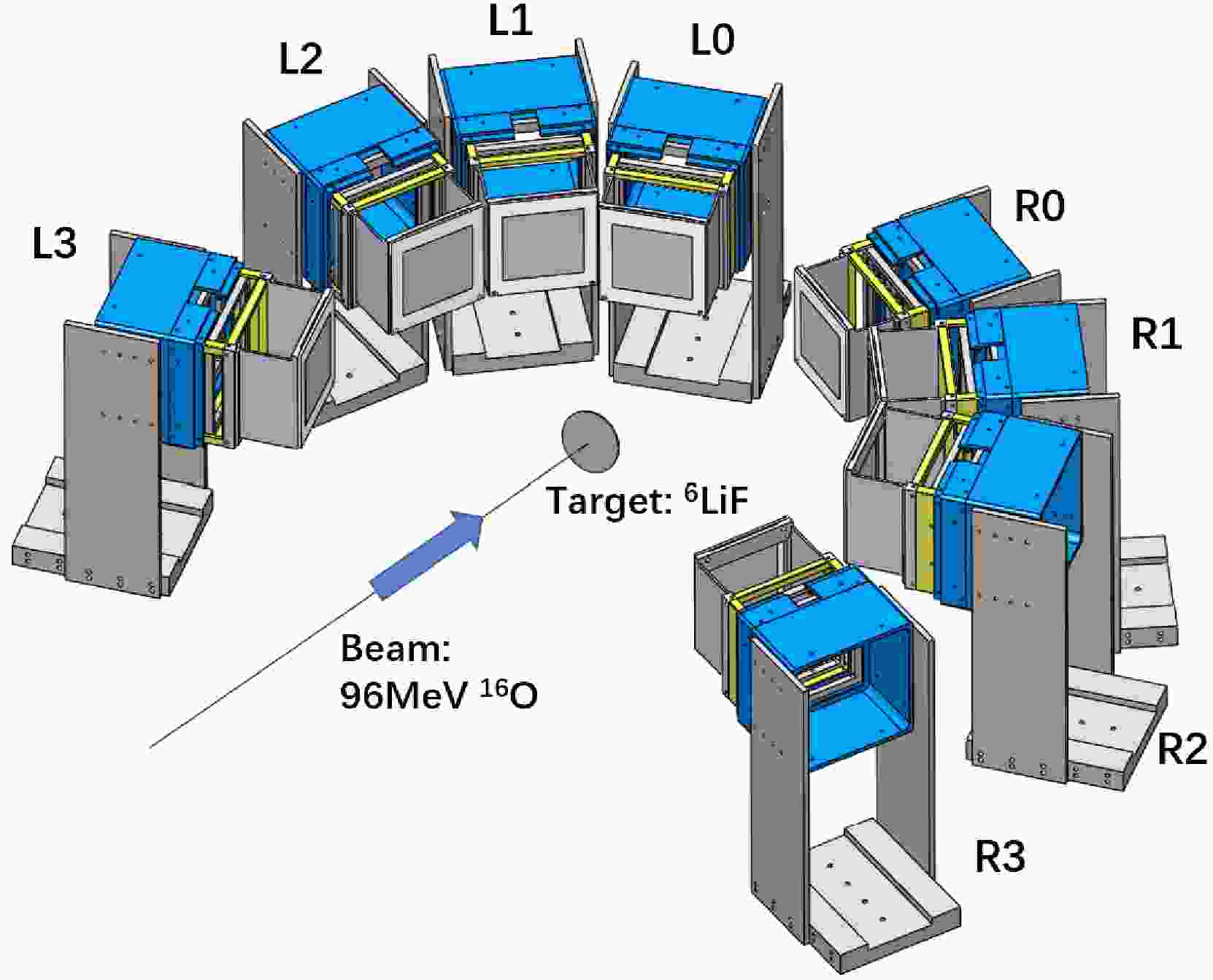
$ ^{16} $ O beam at an energy of 96 MeV and with an intensity of about 4 enA was impinged onto a self-supporting$ ^6 $ LiF target (275 μg/cm$ ^2 $ ). A$ ^6 $ Li($ ^{16} $ O,$ ^{19} $ Ne$ ^* $ )$ ^3 $ H transfer reaction was conducted, followed by cluster decay from the$ ^{19} $ Ne resonant states.As shown in Fig. 1, a total of eight position-sensitive charged-particle telescopes (L0-L3 and R0-R3 detector arrays; L and R denote the left and right sides of the beam line, respectively) were symmetrically installed on both sides of the beam line. The two forward telescopes (L0 and R0), located at a distance of 160 mm from the target and centered at
$ \pm 24° $ with respect to the beam line, were composed of two layers of double-sided silicon-strip detectors (DSSDs) with thicknesses of about 40 μm (W1-40) and 500 μm (BB7-500), respectively, and one large size silicon detector (SSD) with a thickness of 1500 μm (MSX40-1500). The active areas are$ 50\; \rm{mm} \times 50 \; \rm{mm} $ for W1-40 and$ 64\; \rm{mm} \times 64\; \rm{mm} $ for BB7-500 and MSX40-1500. Each side of W1-40 (BB7-500) is divided into 16 (32) strips, providing good two-dimensional position resolution. The L1 and R1 telescopes were located at 180 mm from the target and centered at$ \pm 47° $ , and the detector composition was the same as that for L0 and R0. The L2 and R2 telescopes, each composed of a W1-40 and a MSX40-1500, were located at 180 mm from the target and centered at$ \pm 70 ° $ . The L3 and R3 telescopes, each composed of a BB7-40 and a MSX40-1500, were located at 180 mm from the target and centered at$ \pm 110 ° $ .The
$ ^3 $ H particles, recoiled from the$ ^6 $ Li($ ^{16} $ O,$ ^{19} $ Ne$ ^* $ )$ ^3 $ H transfer reaction, can be detected by the large angle telescopes (L1-3 and R1-3). The α particle or proton, emitted from the$ ^{19} $ Ne-resonance decay ($ ^{19}\rm{Ne} \to \alpha + ^{15}\rm{O} $ and$ ^{19}{\rm Ne} \to p + ^{18}\rm{F} $ ), were mostly measured by the forward telescopes L0 and R0. According to the reaction kinematics, all these light particles could penetrate the first layer but stopped in the last layers of the telescopes and, therefore, can be well identified through the standard energy loss versus residual energy ($ \Delta E - E $ ) method [19−24]. The particle identification (PID) performances of the L0 and L1 telescopes are shown in Fig. 2 (a) and (b), respectively.
Figure 2. (color online) PID spectra measured by (a) the first two layers of L0 telescope and (b) the last two layers of L1 telescope.
Using the information of the detected recoil particle
$ ^3 $ H and decay particle α (or p), together with the beam information, the momentum and energy of the remaining decay fragment$ ^{15} $ O (or$ ^{18} $ F) can be deduced according to the momentum conservation law [20, 25]. The reaction energy, namely the Q value, can then be calculated by subtracting the beam energy from the total kinematic energy of the final three particles [19−23, 26]:$ \begin{equation} Q=E_{\rm tot}-E_{\rm beam}=\sum_{i} E_i - E_{\rm beam}, \end{equation} $

(1) where
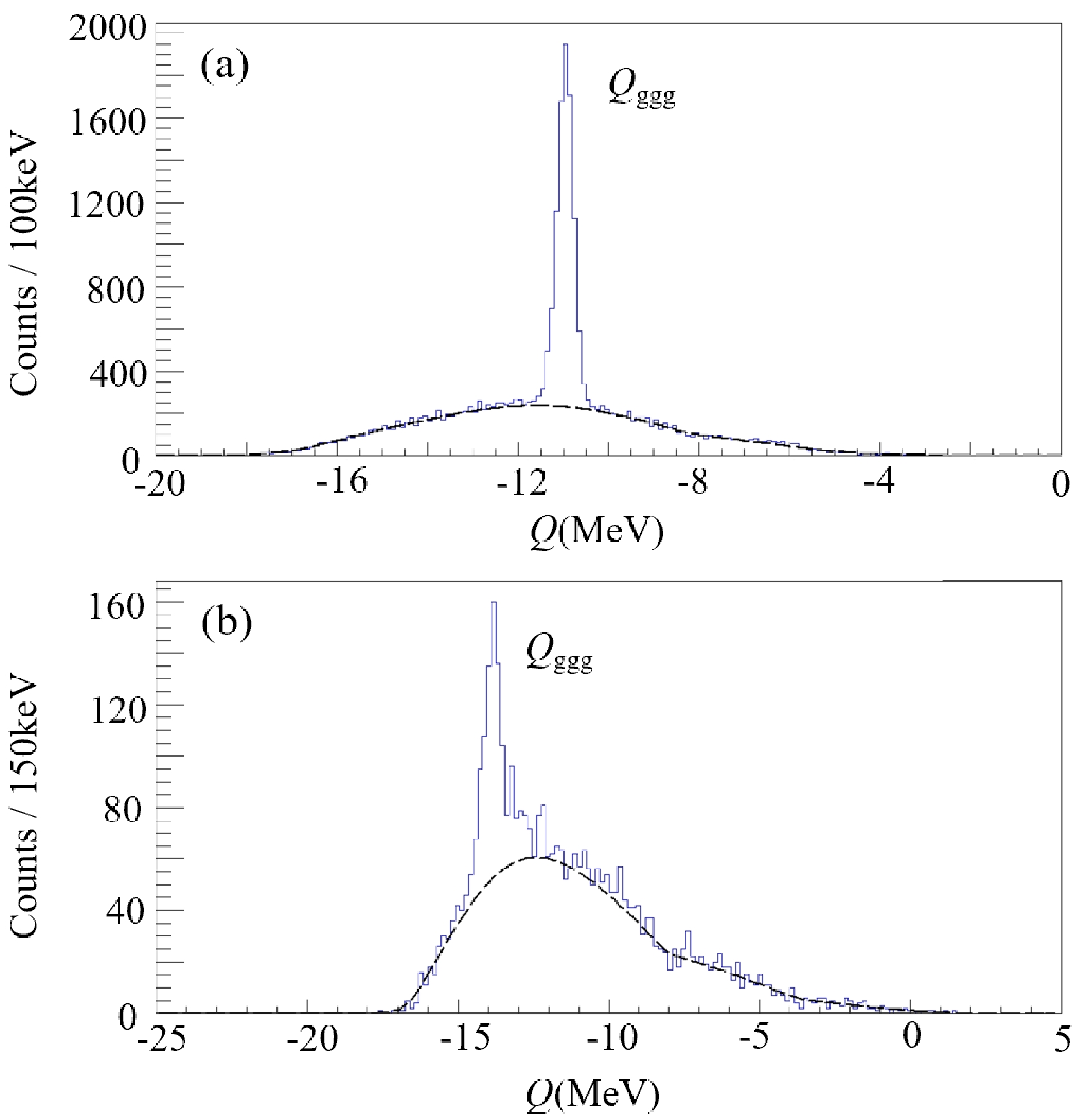
$E_{\rm beam}$ and$ E_i $ ($ i = 1\; \rm{to}\; 3 $ ) are the kinetic energies of the incident beam particle and the final three particles. Figure 3 shows the Q-value spectra for the two reaction-decay channels, respectively, as exhibited by the corresponding peaks. In the spectra, we see also quite intense and broadly distributed background beneath the expected Q-value peaks. This should be attributed to the misidentified particles in the PID spectra and the undetected particles that do not belong to the assumed decay channels. By gating on the specific Q-value peak, the mass combination of the reaction channel can be selected [19, 20, 24]. The Q-value analysis also demonstrated the negligible contribution from the$ ^{19} $ F content of the target material to the present measurement, which was also verified by the EP-plot analysis [21, 27]. -
The excitation energy spectra of
$ ^{19} $ Ne in the α decay channel as well as the proton decay channel can be obtained by the standard invariant mass (IM) method [19−24, 26, 28−30]. The invariant mass M of the residual nucleus, the relative energy of its decay fragments ($ E_{\rm{rel}} $ ) and the excitation energy ($ E_{x} $ ) of the mother nucleus (residual nucleus) are defined according to [24, 26, 28−31]$ \begin{align} &M^2=(\sum_i E_i)^2-(\sum_i \boldsymbol{p}_i)^2, \end{align} $

(2) $ \begin{align} &E_{\rm{rel}}=M-\sum_i m_i ,\end{align} $

(3) $ \begin{align} &E_{\rm{x}}=E_{\rm{rel}}+E_{\rm{thres}}, \end{align} $

(4) where
$ E_i $ ,$ p_i $ , and$ m_i $ (i = 1, 2) are the kinetic energy, momentum, and mass, respectively, of the decay fragment, and$ E_{\rm{thres}} $ is the threshold energy for separating the residual nucleus into the corresponding two fragments.Figure 4 (a) and (b) represent the excitation energy spectra of
$ ^{19} $ Ne obtained from the IM reconstruction using the detected α particle plus the deduced$ ^{15} $ O fragment and that obtained using the detected proton plus the deduced$ ^{18} $ F fragment, respectively [20]. Each spectrum is fitted with several peak functions plus a smoothly varying background curve [32]. Each peak function is a convolution of the Breit-Wigner (BW) form and the energy-resolution Gaussian function [20, 25, 32]. The initial values for the peak central positions were set according to the previously reported results in the literature or the actual spectrum shape. The widths (Γ) of the BW forms were fixed according to values available from the literature (Table 1) or otherwise used as free fitting parameters. The experimental energy resolutions, as well as the detection efficiencies (black-dotted lines in Fig. 4), as a function of the relative energy$ E_{\rm{rel}} $ were obtained by Monte Carlo simulation, taking into account the realistic detector setup and performances. The obtained peak positions are listed in Table 1. The statistical errors for the peak positions obtained from the fitting are very small in comparison to the typical systematic uncertainty. The latter is estimated to be about 100 keV, and the main contribution is from the energy calibration of the silicon detectors [19]. Since the widths of the observed peaks are essentially dominated by the resolution function, which is about 300−350 keV (FWHM) in the considered energy range, the Γ parameters extracted from the fitting procedure are mostly very small and with large uncertainties. We therefore do not list them in Table 1.
Figure 4. (color online) Excitation energy spectra of
$^{19}$ Ne based on the reconstructions from (a) the detected α particle and the deduced$^{15}$ O fragment; (b) the detected proton and the deduced$^{18}$ F fragment. Each spectrum is fitted by the sum (red-solid line) of a number of resonant peaks (blue-solid lines) and a smoothly varying background (black-dashed line). The black-dotted lines represent the detection efficiencies with the corresponding highest values indicated. Each vertical black-dashed line is used to collect the same resonant state but decaying to both α and p channels.$^{19}$ Ne, this work

$^{19}$ Ne, literature

$E_{x}$ /MeV

BR $_\alpha$ 

$^\dagger$ (%)

$\Gamma_p/\Gamma_\alpha$ 

$^\dagger$ 

$ \theta_\alpha^2$ 

$^\dagger$ 

$E_{x}$ /MeV

$J^\pi$ 

Γ /keV $\Gamma_p/\Gamma_\alpha$ 

$\theta_\alpha^2$ 

4.74 4.712(10)f (5/2 $^-$ )f

5.44 5.424(7)f (7/2 $^+$ )f

6.02 6.100(1)g (7/2 $^+$ )g

6.26 6.2916(9)g (11/2 $^+$ )g

6.50 6.423(3)g (3/2 $^+$ )g

6.441(3)g (3/2 $^+$ )g

6.89 6.853(3)g (7/2 $^-$ )g

7.22 7.203(31)c (3/2 $^+$ )c

35(12)c 0.67(0.23)a 7.61 63.7(4.1) 0.57(0.10) $7.3(3.5)\times10^{-3}$ 

7.616(5)c (3/2 $^+$ )c

21(10)c 1.2(0.4)a 7.85 54.1(2.9) 0.85(0.10) 0.073(0.027) 7.863(39)c (1/2 $^+$ )c

292(107)c 1.754(14)d 0.159(54)h 8.14 45.5(2.5) 1.20(0.12) $7.8(5.7)\times 10^{-3}$ 

7.974(10)c (5/2 $^-$ )c

11(8)c 15.2(1.2)d 8.51 62.9(2.4) 0.59(0.06) 0.46(0.12) 8.428(2)b (13/2 $^-$ )b

4(1)b 0.31(4)b 8.89 29.7(2.0) 2.37(0.23) 0.12(0.03) (8.790)b (11/2 $^{+/-}$ )b

4(1)b 0.10(3)b 9.25 1.31(0.23) 9.77 9.788(13)e 10.23 $^\star$ The statistical errors are very small, but a systematic uncertainty of about 100 keV can be estimated considering mostly the energy calibration of the silicon detectors [19].

$^\dagger$ Only the statistical errors (1 s.d.) are shown here. In addition, a systematic error of about

$15%$ is estimated, considering the possible variation of the background function. a Calculated from

$\Gamma_p$ and

$\Gamma_\alpha$ results obtained in Reference [16]

b Reference [11]
c Reference [14]
d Reference [15]
e Reference [36]
f Reference [10]
g Reference [34]
h Reference [16]Table 1. Summary of the excited states of
$^{19}$ Ne, observed in the present$^6$ Li($^{16}$ O,$^{19}$ Ne$^* \to \alpha$ +$^{15}$ O)$^3$ H reaction and$^6$ Li($^{16}$ O,$^{19}$ Ne$^* \to $ p +$^{18}$ F)$^3$ H reaction. For comparison, results from previous experimental measurements are also presented.Six resonant peaks between 7.5 MeV and 9.5 MeV can be identified simultaneously in both α- and p-decay channels, as can be seen in Fig. 4 (a) and (b), respectively. For each of these states, the BW function parameters (central position and width) were maintained exactly the same for both decay channels during the above fitting procedure. The relative decay strengths (the ratios of the partial widths) can then be obtained by comparing the areas (N) of the corresponding peaks corrected by the detection efficiencies (
$ \epsilon $ ) [15]:$ \begin{align} &\Gamma_p/\Gamma_\alpha=\frac{N_p/\epsilon_p}{N_\alpha/\epsilon_\alpha}, \end{align} $

(5) The results are also listed in Table 1. In addition to the statistical errors (1 s.d.) listed in the table, a systematic uncertainty of about
$ 15% $ can be estimated, which is most likely due to the uncertainties in background modeling [20, 32] as adopted in Fig. 4.The α branch ratios (BR
$ _\alpha $ ) and the α-decay partial width$ \Gamma_\alpha $ (not listed in Table 1) above 7.6 MeV are all deduced from the measured$ \Gamma_p/\Gamma_\alpha $ ratios and the referenced total widths by neglecting the contribution of γ decay [33, 34]. Only the statistical errors are presented in Table 1. Based on the obtained$ \Gamma_\alpha $ , the dimensionless reduced α width$ \theta^2_\alpha $ can be deduced according to$ \Gamma_\alpha = 2P_L(a)\gamma_W^2(a)\theta_\alpha^2(a) $ , where$ P_L $ is the Coulomb penetration factor,$ \gamma_W^2 $ is the Wigner limit value, and a is the channel radius [23, 31, 35].$ \theta^2_\alpha $ is usually regarded as the probability of finding the α-structure in the nucleus. The obtained$ \theta^2_\alpha $ values are also listed in Table 1.It should be noted that, for the α-decay channel, there may be an accompanying background reaction-decay channel
$ ^6 $ Li($ ^{16} $ O,$ ^{15} $ O)$ ^7 $ Li$ \to \alpha \; + \; ^3 $ H, which has the same final mass combination as the$ ^{19} $ Ne-decay channel and thus cannot be excluded by the Q-value selection. However, this background channel tends to emit$ ^3 $ H- and α-particles to the same side of the beam line, whereas for the targeted physics channel, namely$ ^6 $ Li($ ^{16} $ O,$ ^{19}{\rm Ne} \to $ $ \alpha \; + \; ^{15} $ O)$ ^3 $ H, those two light particles would move to either side of the beam line. By applying the latter as a requirement, the background channel can be effectively eliminated. This has been proven by a Dalitz-plot analysis which allows to check the possible existence of the events with$ ^7 $ Li$ \to \alpha \; + \; ^3 $ H decay. This has also been checked for the p-decay channel. -
In early years, a number of
$ ^{16} $ O($ ^6 $ Li,$ ^3 $ H) inclusive experiments had been performed to examine the direct three-nucleon transfer-reaction mechanism and to investigate the excited states in$ ^{19} $ Ne [37−40]. It was proven that this kind of multi-nucleon transfer reaction is in favor of populating the three-particle cluster structure, such as the$ ^3 $ He +$ ^{16} $ O configuration, and the four-particle one-hole cluster structure, such as the$ ^4 $ He +$ ^{15} $ O configuration, in the intermediate nucleus$ ^{19} $ Ne. This configuration mixing has been well described within the microscopic generator-coordinate-method (GCM) approach [5]. In the following, we discuss the physics relevance of the observed resonant states in$ ^{19} $ Ne, which decay into the α +$ ^{15} $ O or (and) p +$ ^{18} $ F channels. -
According to the threshold rule (or the Ikeda diagram) [41], the cluster structure tends to be formed in a nucleus in the vicinity of the corresponding separation threshold. In the case of
$ ^{19} $ Ne, the threshold energies for the separation (breakup) of$ ^{19} $ Ne into α +$ ^{15} $ O, p +$ ^{18} $ F,$ ^3 $ He +$ ^{16} $ O, and n +$ ^{18} $ Ne are 3.528, 6.411, 8.442, and 11.64 MeV, respectively. Therefore, the observed resonant states between 4.7 and 6.9 MeV, which are well above the α-decay threshold and slightly above the p-decay threshold, are dominated by the α-decay channel and associated with a strong α cluster structure [7, 8], considering the effect of the Coulomb penetration factor. These resonances actually affect the fusion reaction$ ^{15} $ O($ \alpha, \gamma $ )$ ^{19} $ Ne, which is one of key pathways for the breakout from the hot-CNO cycles and the commencement of the$ rp $ process to yield heavier nuclei in stars [8−11]. The lowest two states, observed at 4.74 and 5.44 MeV, were reported previously ([10] and references therein). In particular, the sharp peak at 5.44 MeV [Fig. 4 (a)] is in excellent agreement with the value reported in the literature [10, 37−40], demonstrating the accuracy of the present measurement and reconstruction data analysis. The next few resonances up to 6.89 MeV are also in agreement with the previously reported values obtained from precise γ-ray measurements [34]. Note that three close resonances (6.02, 6.26, 6.50 MeV) are incorporated into one strong peak at about 6.3 MeV due to the limited energy resolution. -
The present work focuses on the
$ ^{19} $ Ne-resonances above 7.0 MeV, where both α- and p-decays become significant. As indicated in the introduction section, these resonances are directly related to the destruction of$ ^{18} $ F via the$ ^{18} $ F($p,~ \alpha$ )$ ^{15} $ O reaction [6, 7, 14, 16, 34, 42, 43]. Dufour and Descouvemont [13] had predicted a broad 1/2$ ^+ $ resonance at about 1.49 MeV above the proton threshold ($ E_{x} \sim $ 7.9 MeV). The existence of this resonant state would significantly influence the astrophysical$ ^{18} $ F(p, α)$ ^{15} $ O process due to the interference of this state with the low-spin (1/2$ ^{\pm} $ or 3/2$ ^{\pm} $ ) states around the proton-decay threshold (6.41 MeV) [14, 44]. In 2009, Dalouzy$ et \; al. $ pioneered the observation of this state via an inelastic scattering experiment$ ^1 $ H($ ^{19} $ Ne,$ ^{19} $ Ne$ ^* \to p + ^{18} $ F)p in inverse kinematics. The resonance energy and total width were reported as 7.863 (39) MeV and 292 (107) keV, respectively (Table 1 and [14]). However, this experiment involved measurements of only the decay proton, providing no information of the α-decay channel. In 2012, Adekola$ et \; al. $ reported the measurement of both the proton- and α-decays from$ ^{19} $ Ne resonances within an energy range of 7$ \sim $ 8 MeV (Table 1 and [15]). Among them, the ratios of the decay widths$ \Gamma_p/\Gamma_\alpha $ were calculated as 1.754 (14) and 15.2 (1.2) for two close states at 7.879 (26) and 8.072 (30) MeV, respectively, corresponding to the 7.863 (39) and 7.974(10) MeV states, respectively, measured by Dalouzy$ et \; al. $ (Table 1 and [14]), respectively. It should be noted that these two states were not well resolved in Adekola's work [15], and the obtained$ \Gamma_p/\Gamma_\alpha $ ratios were very different from those reported in [16] (see Table 1). In the present work, two resonances at 7.85 and 8.14 MeV were identified (Fig. 4 and Table 1) with stringent constraints from the p-decay spectrum [Fig. 4 (b)], corresponding to the two states discussed above (Table 1). We note that the inclusion of the 7.85 MeV peak in the spectrum clearly improved the fitting performance ($ \chi^2/ $ ndf values improved from 4.57 to 3.22), supporting its real existence. From the fitting, we obtained the$ \Gamma_p/\Gamma_\alpha $ values of 0.85 (0.10) and 1.20 (0.12), respectively, for the two states discussed above. These results for the$ \Gamma_p/\Gamma_\alpha $ ratio are very different from previously reported ones (Table 1 and [15, 16]). Particularly, the new branching ratio values for the broad resonance at about 7.85 MeV should have a significant impact on the astrophysically important$ ^{18} $ F(p, α)$ ^{15} $ O reaction according to the interference effect [14, 44]. For the 8.14 MeV state, the estimated$ \Gamma_p/\Gamma_\alpha $ value of about 1.20 is much smaller than the previous one of 15.2, indicating a larger probability of α formation in this state.We also note the observation of 7.22 MeV resonance in the α-decay channel, which is in good agreement with the previously reported state at this energy value [14, 15]. Unfortunately, we were unable to extract its p-decay strength due to the very low statistics [Fig. 4 (b)].
-
Thus far, there exists only limited information about α-clustering structures in
$ ^{19} $ Ne for$ E_{x} > $ 8.4 MeV [36], except infomation obtained from some inclusive resonant scattering measurements together with R-matrix analysis [6, 11]. The resonances at 8.51 MeV and 8.89 MeV (Fig. 4 and Table 1) observed in this study may correspond to 8.428 and 8.790 MeV states reported by Torresi$ et \; al. $ [11], with spin-parity assignments of 13/2$ ^- $ and 11/2$ ^{+/-} $ , respectively (tentative). For the first time, we have measured the$ \Gamma_p/\Gamma_\alpha $ ratios for these two states (Fig. 4 and Table 1) based on the strong constraint from the p-decay spectrum [Fig. 4 (b)]. Combining this with a total width of 4 keV for both states, as extracted by Torresi$ et \; al $ . [11], we can deduce the α-decay branching ratios of 62.9 (2.4) % and 29.7 (2.0) %, repsectively, and hence the corresponding α spectroscopic factors ($ \theta^2_\alpha $ ) of 0.46(0.12) and 0.12(0.03), respectively. These results are comparable with those of Torresi$ et \; al. $ [11], which imply the existence of a strong α +$ ^{15} $ O cluster configuration in$ ^{19} $ Ne at high excitation energies. We note that the strong clustering at these energies has been predicted by Otani$ et \; al. $ [5, 45] under the context of one hole in a cluster core, which is related to the$ N = 8 $ cluster rotational band of$ ^{20} $ Ne.Three higher-lying states at 9.25, 9.77, and 10.23 MeV were also observed in the α-decay channel of the present measurement, wherein the first one corresponded with the p-decay channel as well [Fig. 4 and Table 1]. Although there are some hints from previous experiments [36] about the α-cluster structure in this high energy range [36], the currently observed resonances with significant α-decay strengths would encourage further investigation of their spins and resonance widths
$ etc. $ to clarify the exotic structure in$ ^{19} $ Ne at high excitation energies. -
In summary, we performed a new multi-nucleon transfer experiment to populate the highly excited states of
$ ^{19} $ Ne. Owing to the application of an array of many position-sensitive particle telescopes, the decayed light particles, namely proton and α, were detected in coincidence with the recoiled triton-particles. The invariant mass spectra of$ ^{19} $ Ne were then reconstructed from the detected proton or α and the deduced$ ^{18} $ F or$ ^{15} $ O, respectively. The relatively low-lying states, dominated by the α-decay channel, are in good agreement with those observed in previous measurements, demonstrating the accuracy of the present measurement and analysis. The broad resonance at about 7.9 MeV (1/2$ ^+ $ ) has a crucial effect on the destruction of$ ^{18} $ F via the$ ^{18} $ F(p, α)$ ^{15} $ O reaction. The obtained value of the ratio of the partial decay widths is quite different from the previously reported ones, providing new and important insights into the astrophysical analysis. For the first time, a few resonant states at energies higher than 9 MeV have been observed in the α-decay channel, encouraging further studies on the exotic structures in$ ^{19} $ Ne at very high excitation energies. -
The authors thank the staff of the HI-13 tandem accelerator at CIAE for providing excellent technical and operational support during the experiment.
New measurement of 4He and proton decays from resonant states in 19Ne
- Received Date: 2023-01-10
- Available Online: 2023-11-15
Abstract: A





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF























 DownLoad:
DownLoad: