Toward a description of the centrality dependence of the charge balance function in the HYDJET++ model

With the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC) in operation, a number of exquisite and intriguing phenomena have been revealed that could have never been systematically studied with the previous generation of accelerators. Among these, anisotropic flow, the energy loss of high transverse momentum particles, and the charge balance function may be used as sensitive probes of the collective properties of a new state of matter, quark-gluon plasma (QGP); see, e.g., [1, 2]. The large number of these physical observables measured in heavy-ion collisions during RHIC and LHC operation can be successfully described within the framework of the popular HYDJET++ model [3]. Calculations applying this model, such as the transverse momentum spectra, pseudorapidity and centrality dependence of inclusive charged particle multiplicity, and $ \pi^\pm \pi^\pm $ correlation radii in central Pb+Pb collisions [4], the centrality and momentum dependence of second and higher-order harmonic coefficients [5], flow fluctuations [6], jet quenching effects [7, 8], and angular dihadron correlations [9] are in fair agreement with the experimental data.

Some of the experimental measurements proposed as indicators of QGP creation involve an implicit understanding of quark production dependence on time. While, for example, the fact of strangeness enhancement has been well established indeed, it remains unclear whether the arbitrary mechanism is dominant during early ($ \tau < 1 $ fm/c) or late stages of the QGP fireball expansion. The charge balance function (CBF) was proposed in [10] as a means of pinpointing the time of quark production by quantifying the separation of balancing charges. Connections between the CBFs and charge fluctuations and correlations were discussed in [11], whereas in [12] the possibility was demonstrated of applying species-binned CBFs as constraints on the diffusivity. Emergence of the charge balance functions has been studied, e.g., in hydrodynamics [13], in a thermal model with resonances [14], and in a coalescence model [15], as well as in other dynamic and statistical models [16]. Experimentally, the charge balance function has been measured at RHIC [17−19] in pp, d+Au, and Au+Au collisions and at LHC [20−22] in pp, p+Pb, and Pb+Pb collisions. The charge balance function dependence on the collision centrality and beam energy are presented in these studies alongside some experimental techniques. An extensive overview of the CBF from both theoretical and experimental perspectives can be found in [23]. In the present paper we focus on the charge balance function as a source of valuable insights into the charge creation mechanism as well.

The width of the balance function reported by the STAR Collaboration in [17] and by the ALICE Collaboration in [21] decreases with increasing centrality of the collisions. This centrality dependence is not reproduced by many event generators, e.g., HIJING [24, 25] and AMPT [26−28], and poses a challenge for HYDJET++ as well since a majority of soft particles is produced in the grand canonical ensemble approach, where charge conservation holds in the mean only. Nevertheless, a reasonable simple modification of the current version of the HYDJET++ model allows us to reproduce the experimentally observed nontrivial centrality dependence of the balance function widths qualitatively due to the different charge creation mechanisms in soft and hard processes. Further essential modernizations have also been suggested within the canonical ensemble approach to describe the charge balance function quantitatively.

The paper is organized as follows. Basic characteristics of the model are sketched in Sec. II. Section III presents a comparison of model results calculated within the default version of HYDJET++ with the experimental data. The widths of the CBFs in the model are broader than the experimental ones. Possible variations in the partial contributions of soft and hard processes to the CBFs are studied. A modification procedure that takes into account exact charge conservation in a single event without changing its bulk characteristics is introduced in Sec. IV. Implementation of this procedure in HYDJET++ allows us to reproduce both the widths and the centrality dependence of the charge balance functions fairly well compared to the data. Conclusions are drawn in Sec. V.

It should be noted that currently there are many competing Monte Carlo event generators successfully describing the soft and hard momentum components of particle production in ultrarelativistic nuclear collisions separately. The HYDJET++ model is one of the few, such as EPOS [29], QGSJET [30], PACIAE [31, 32], ANGANTYR [33], that aim to treat the soft and hard physics of the collisions simultaneously. For instance, the presence of both soft and hard processes "in one package" has recently allowed the model to reproduce [34] the experimentally observed [35] nontrivial centrality dependence of elliptic flow correlations at low and high transverse momenta in Pb+Pb collisions at LHC energies. The origin of the correlations between the low and high-$ p_T $ flow components in (semi)peripheral Pb+Pb collisions was traced to the correlations of particles in jets. As we will see below, these correlations are also important for the description of the charge balance function. Details of the model can be found in the HYDJET++ manual [3]. Here we stress and recall briefly only the main features crucial for the present study.

The HYDJET++ is a Monte Carlo event generator for the simulation of relativistic heavy-ion collisions considered as a superposition of two independent components, namely, the soft hydro-type state and the hard state arising from in-medium multiparton fragmentation. It is based on the adapted version of the event generator FASTMC [36, 37] and the PYQUEN partonic energy loss model [38].

In the hard part the partons propagate through the expanding quark-gluon plasma and lose energy due to parton rescattering and gluon radiation. A number of jets is generated in accordance with a binomial distribution. The mean number of jets produced in an A+A event is a product of the number of nucleon-nucleon (NN) binary subcollisions at a given impact parameter b and the integral cross section of the hard subprocess in these subcollisions with the minimum transverse momentum transfer $ p_T^{\rm min} $. Its value is one of the input key parameters of the model, because partons produced in (semi)hard processes with the momentum transfer lower than $ p_T^{\rm min} $ are excluded from the hard process treatment. Their hadronization products are automatically added to the soft component of the particle spectrum.

The soft part of the model is represented by the thermalized hadronic state generated on the chemical and thermal freeze-out hypersurfaces prescribed by the parametrization of relativistic hydrodynamics with preset freeze-out conditions. Particle multiplicities are calculated within the effective thermal volume using a statistical model approach. The effective volume absorbs the collective velocity profile and the hypersurface shape and cancels out in all particle number ratios. Therefore, the latter do not depend on the freeze-out details so long as the local thermodynamic parameters are independent of spatial coordinates [36, 37]. The concept of the effective volume is applied to calculate the hadronic composition at both chemical and thermal freeze-outs. The number of particles in an event is calculated according to a Poisson distribution around its mean value, which is supposed to be proportional to the number of participating nucleons for a given impact parameter of A+A collision. To simulate the elliptic and triangular flow effects, a hydro-inspired parametrization [39] for the momentum and spatial anisotropy of soft hadron emission source is implemented; see [3, 40, 41] for details. In the following we refer to HYDJET++ version 2.4, freely available for download at [42], as the default version.

The charge balance function has been proposed as a convenient measure of the correlation between oppositely charged particles [10]. It provides valuable insight into the charge creation mechanism and can address the fundamental question concerning the hadronization process in nuclear collisions at relativistic energies. The final degree of correlations is reflected in the balance function and consequently in its width. It is defined as

where $ \langle N_{+-}(\Delta \eta) \rangle $ is the average number of opposite-charge pairs with particles separated by the relative pseudorapidity $ \Delta \eta =\eta_{+}-\eta_{-} $, and similarly for $ \langle N_{-+}(\Delta \eta) \rangle $, $ \langle N_{++}(\Delta \eta) \rangle $ and $ \langle N_{–}(\Delta \eta) \rangle $. Both particles of the pair have to fall within a certain pseudorapidity interval, for instance $ |\eta|< 0.8 $, in accordance with the ALICE analysis conditions [21]. $ \langle N_{+} \rangle $ (and $ \langle N_{-} \rangle $) is the number of positive (negative) charge particles in the pseudorapidity interval $ |\eta|< 0.8 $ averaged over all events. The charge balance function $ B(\Delta\varphi) $ as a function of the relative azimuthal angle $ \Delta\varphi $ is defined similarly. Each term $ N(\Delta\eta) $ is corrected for the acceptance limitation, reflecting the fact that the number of pairs in the limited acceptance has a maximum at $ \Delta\eta = 0 $.

The width of the balance function distribution is defined as

where $ B(\Delta \eta_{i}) $ is the balance function value for each bin $ \Delta\eta_{i} $ , with the sum running over all k bins.

Figure 1 shows the charge balance function in terms of the pseudorapidity $ \Delta\eta $ calculated in the HYDJET++ model separately for each component, soft and hard, together with the resulting total value. Calculations are done for Pb+Pb collisions at center-of-mass energy per nucleon pair $ \sqrt{s_{{{{NN}}}}} = 2.76 $ TeV with centrality 0–5%. One can see that the resulting total balance function is mainly dominated by the balance function of the soft component. This is not surprising, because in the momentum range $ 0.3 < p_T < 1.5~~ {{\rm{GeV}}}/{c} $ chosen for ALICE analysis [21], the majority of particles is soft. It is worth noting that the balance function of the soft component has already been studied [43] in the framework of the FASTMC event generator [36, 37] and has been compared to the STAR measurements [18]. The main results and conclusions of this study are the following.

Figure 1.  (color online) Balance function as a function of $ \Delta\eta $ in Pb+Pb collisions at $ \sqrt{s_{{{{NN}}}}} = 2.76 $ TeV with centrality 0−5% calculated in HYDJET++ for each component, soft (crosses) and hard (triangles), together with the resulting total values (circles).

In the statistical model, directly produced particles, called "primordial," are generated independently, and there are no balancing charge correlations. As a result, the FASTMC balance function vanishes for the "primordial" particles. In this approach, the phase-space correlations between the final state particles arise only from the decays of hadronic resonances. Therefore, these correlations are determined merely by the kinematics of the decays. All charged particles falling into the considered pseudorapidity interval contribute to the denominator of Eq. (1), whereas only those from the resonance decays, i.e., correlated pairs, contribute to the numerator when one calculates the balance function for the soft component. At RHIC energies, for instance, about a quarter of the observed pions at the freeze-out are primordial ones, while the remainder are produced via resonance decays.

The balance functions for the soft component in terms of relative pseudorapidity, $ \Delta\eta $, depend on the maximum transverse flow velocity and the thermal freeze-out temperature. The option with large transverse flow and low thermal freeze-out temperature generally produces a relatively smaller width of the balance function than does the higher thermal freeze-out temperature option. The width of the balance function is inversely proportional to the strength of the transverse flow. The balance functions calculated in the framework of the FASTMC generator are usually lower than those measured in central Au+Au collisions at center-of-mass energy 200 GeV per nucleon pair [43], indicating that there are other sources of charge correlations besides resonance decays. However, the widths of FASTMC balance function are rather close to those measured in central Au+Au collisions, indicating that an important source of the correlation between the opposite-charge particles is the decay of resonances.

The balance function in Fig. 1 for the soft hadrons coming from the hard component (for $ 0.3< p_T < 1.5~ {{\rm{GeV}}}/{c} $) is higher than that for the soft component, and its width is broader than that of the soft component. This means that the charge correlations of the jet particles are weaker than those from the decay of resonances, which can be explained by the fact that the number of parton decays in the parton cascade during the jet fragmentation is larger than the number of consecutive resonance decays. Each subsequent decay makes the charge correlations weaker. The visible difference between the widths of soft and hard components opens some room for effectively reproducing the experimentally observed centrality dependence of the balance function widths. As a matter of fact, at the default parameters of HYDJET++ model the widths of the balance function reveal practically no centrality dependence, as shown in Fig. 2. The widths are calculated in the entire interval where the balance function is measured, i.e., $ |\Delta\eta| < 1.6 $ and $ -\pi/2 <\Delta\varphi < 3\pi/2 $. The applicability of the HYDJET++ generator to very peripheral collisions with centrality greater than 60% is doubtful due to a number of physical assumptions and approximations made in the model.

Figure 2.  (color online) Centrality dependence of the width of the balance function of charged hadrons in Pb+Pb collisions at $ \sqrt{s_{{{{NN}}}}} = 2.76 $ TeV for the correlations studied in terms of (a) relative pseudorapidity $ \langle \Delta\eta\rangle $ and (b) relative angle $ \langle\Delta\phi\rangle $, respectively. The model calculations with default (full circles) and modified (triangles) versions of HYDJET++ are compared to the ALICE data (open circles) from [21]. Lines are drawn to guide the eye.

The centrality independence of the default model calculations indicates that some enhancement of the relative contribution from the jet part to the balance function is needed to reproduce the experimentally observed increase of the balance function widths in peripheral Pb+Pb collisions. Indeed, the mean "soft" and "hard" multiplicities depend on the centrality in different ways: They are roughly proportional to the mean number of participant nucleons $ \langle N_{\rm part}(b) \rangle $ and the mean number of binary $ NN $ subcollisions $ \langle N_{\rm bin}(b) \rangle $ at a given impact parameter b, respectively. The relative contribution of the soft and hard parts to the total event multiplicity is fixed through the centrality dependence of the pseudorapidity hadron spectra $ {\rm d}N/{\rm d}\eta $. The corresponding contributions from the hydro and jet parts are mainly determined by the two input parameters: $ \mu_{\pi}^{\rm eff th} $, which is the (effective) chemical potential of positively charged pions at thermal freeze-out, and the minimum transverse momentum transfer of hard parton-parton scattering, $ p_T^{\rm min} $.

Besides, with the enhancement of the hard part for more peripheral collisions we decrease the contribution of the soft component. The contribution of the soft part to the total multiplicity varies with centrality because of its dependence on $ \langle N_{\rm part}(b) \rangle $. We additionally decrease it by the factor $ f_s $. The values of $ p_T^{\rm min} $ and $ f_s $, listed in Table 1, are adjusted in such a way that the total spectra ${\rm d}N/{\rm d}p_T$ remains similar to that calculated with the default parameters $ p_T^{\rm min} = 8.2~ {\rm GeV}/c $ and $ f_s=1 $ for a given centrality. Note that the contribution of the hard component to the total particle multiplicity increases with event centrality in the HYDJET++ model. However, for the procedure described above such an increase is less pronounced than in the default HYDJET++ version. This is because the introduced additional enhancement of the hard part for more peripheral collisions is accompanied by a corresponding decrease in the contribution of the soft component in order to keep the total multiplicity for each event centrality the same as in the default version of HYDJET++.

Centrality	$ p_T^{\rm min} $, ${ {\rm{GeV} } }/{ c}$	$ f_s $
0−5%	8.2	1
20%−30%	6.7	0.75
50%−60%	5.15	0.395

Table 1.  Parameters of the modified version of HYDJET++. See text for details.

The widths for the modified version show the desired centrality dependence. However, our calculations are systematically higher than the experimental data. Moreover, the amplitudes of the modified balance functions shown in Fig. 3 demonstrate a centrality dependence opposite that of the default model calculations. These amplitudes increase with increasing impact parameter for calculations within the modified version, unlike the default model results, in which the amplitudes decrease as in the experimental data [21]. This discrepancy requires explanation.

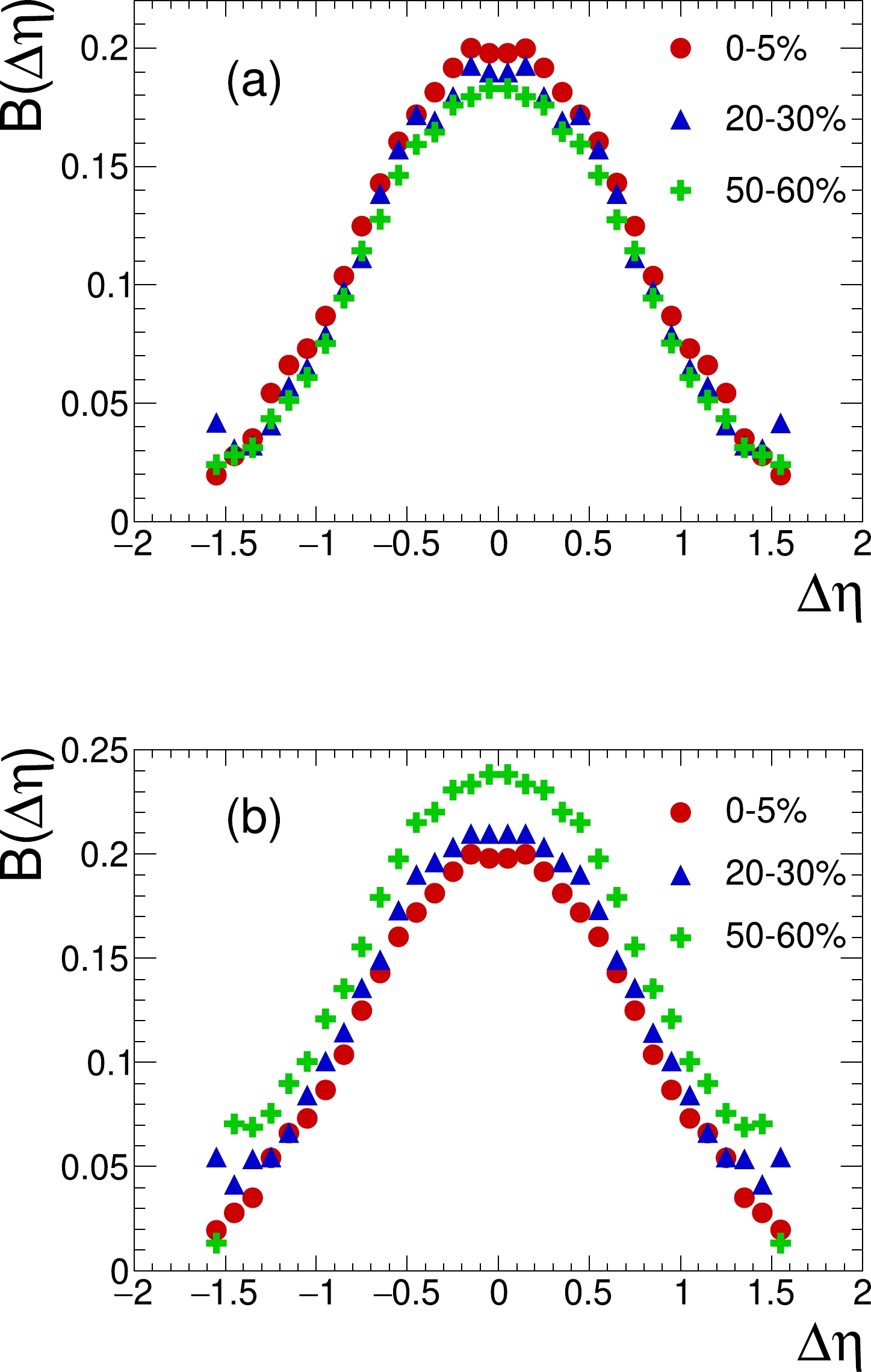
Figure 3.  (color online) Balance function $ B(\Delta\eta) $ of charged hadrons in Pb+Pb collisions at $ \sqrt{s_{{{{NN}}}}} = 2.76 $ TeV calculated with (a) HYDJET++ with the default parameters and (b) HYDJET++ with increased hard part and decreased soft part for three centralities, 0–5% (circles), 20%–30% (triangles), and 50%–60% (crosses).

Since the relative contribution of the hard part increases in particular with the growth of the impact factor in the modified version, the width and amplitude of the total BF increase, because these values for the hard part are initially larger than those for the soft part. Somewhat unexpectedly, though only at first glance, there appears to be a simultaneous increase in both width and amplitude. This behavior is due to the fact that the BF normalization is not unique and is determined by hard, soft, and full multiplicity. In the case of Gaussian distributions with the same fixed normalization, the amplitudes always decrease with increasing width, in contrast to our situation with its own normalization for each centrality class. In the HYDJET++ model we have two independent sources of charge correlations, namely, the resonances with the width $ \langle \Delta\eta\rangle _{\rm res} $ and the jets with $ \langle \Delta\eta\rangle_{\rm jet} $. Note that $ \langle \Delta\eta\rangle _{\rm res} $ is less than $ \langle \Delta\eta\rangle_{\rm jet} $. The resulting width has some intermediate value between $ \langle \Delta\eta\rangle _{\rm res} $ and $ \langle \Delta\eta\rangle_{\rm jet} $ depending on the relative contributions from these sources. The widths $ \langle \Delta\eta\rangle _{\rm res} $ and $ \langle \Delta\eta\rangle_{\rm jet} $ are initially larger than $ \langle \Delta\eta\rangle_{\rm exp} $; therefore, any resulting width from these sources will be larger than $ \langle \Delta\eta\rangle_{\rm exp} $ as well. Our observation indicates that some additional source of charge correlation with a width less than $ \langle \Delta\eta\rangle _{\rm res} $ is needed to reproduce the experimentally observed values in the interval of relatively low transverse momenta.

For higher transverse momentum regions it was found [20] that the balance function is increasingly narrow, thus indicating that the correlations become stronger. Moreover, the centrality dependence of the widths practically vanishes. We compare the widths calculated at the high transverse momenta in the intervals

(1) $ 2.0 < p_{T,\rm assoc} < 3.0 < p_{T,\rm trig} < 4.0~~ {{\rm{GeV}}}/{ c} $ and

(2) $ 3.0 < p_{T,\rm assoc} < 8.0 < p_{T,\rm trig} < 15.0~~ {{\rm{GeV}}}/{ c} $

with the data [20]. Here the widths were calculated in accordance with experimental calculations, not in the entire intervals of $ \Delta\eta $, $ \Delta\varphi $, but in the narrow interval. The balance function distributions are fitted to a sum of a Gaussian and a constant. The width is then calculated within $ 3 \sigma_{\rm Gauss} $. The comparison is displayed in Fig. 4. One can see in this figure that with increasing transverse momentum the default model results describe the experimental data much better, since in these transverse momentum intervals the contribution from the soft component is weaker. In practical terms we observe a transition to a single source of charge correlations, namely, charge correlations in jets for which exact charge conservation holds at each stage. The decrease of the width with increasing transverse momentum can also be explained as due to particles with higher transverse momenta being created closer to the beginning of parton cascade, where the charge correlations are stronger.

Figure 4.  (color online) The same as Fig. 2 but for two transverse momentum intervals labeled in the text as (1) and (2). For interval (1) HYDJET++ calculations and the data from [21] are denoted as full and open circles, respectively, whereas for interval (2) the calculations and the data are indicated as full and open triangles. Lines are drawn to guide the eye.

Our investigation reveals that the interval of relatively low transverse momenta remains problematic in descriptions of the charge balance function despite the attempts that have been made to address it. It is a long-standing conceptual problem that the majority of soft particles are generated independently in the statistical model approach, and the charge correlations emerge merely as a result of the resonance decays. The widths $ \langle \Delta\eta\rangle _{\rm res} $ are larger than $ \langle \Delta\eta\rangle_{\rm exp} $, and in accordance with the consideration above another source of charge correlation with width less than $ \langle \Delta\eta\rangle _{\rm res} $ should be introduced to reproduce the experimentally observed values in the interval of relatively low $ p_T $.

In order to take exact charge conservation into account, we modified the generation procedure of soft direct hadrons. In the default model version a number N of particles with specified coordinates and momenta are generated in each event. In the modified version the following procedure is realized. For the sake of simplicity, we consider here the electrically neutral system similar to the midrapidity part of the fireball produced in heavy-ion collisions at LHC energies. First, half of all charged particles are removed randomly in every event, whereas all neutral particles remain unaffected. Then, for each particle with a given charge, an antiparticle with opposite charge is added to the particle spectrum. For instance, $ \pi^- $ should be added to $ \pi^+ $, and vice versa. The coordinates and transverse momentum of each new particle are assigned the same values as the corresponding original particle, ensuring local charge conservation. The pseudorapidities and the azimuthal angles of these new particles are distributed around the pseudorapidities and the azimuthal angles of the corresponding original particles. The Gaussian distributions are used

Here $ x = \{\eta; \varphi \} $, and the dispersions $ \sigma_x $ of the distributions are new parameters of the model. They should yield widths of the charge balance function less than $ \langle \Delta\eta\rangle _{\rm res} $ and $ \langle \Delta\varphi\rangle _{\rm res} $ to reproduce the experimental data in the most central collisions. As a result, equal numbers of particles with positive and negative charges will be obtained in each newly generated event. (As a matter of fact, the pairs of particles and antiparticles with correlated pseudorapidity and azimuthal angle are generated in a similar way in other models.) Finally, the spectra of the newly generated direct hadrons remain almost unchanged, but their balance function will be nonzero with a some finite width, in contrast to the original procedure with the formally infinite width of soft direct hadrons, because we have no charge correlations at all due to the independent generation of particles. The dispersion of Gaussian distributions should be fitted to reproduce the centrality dependence of widths in the intervals of relatively low transverse momenta.

The results of our fitting procedure are shown in Fig. 5. The model calculations reproduce the experimentally observed centrality dependence of widths rather well if the dispersions of Gaussian distributions increase with the growth of the impact parameter. This indicates that the charge correlations of direct hadrons become weaker in more peripheral collisions than central ones.

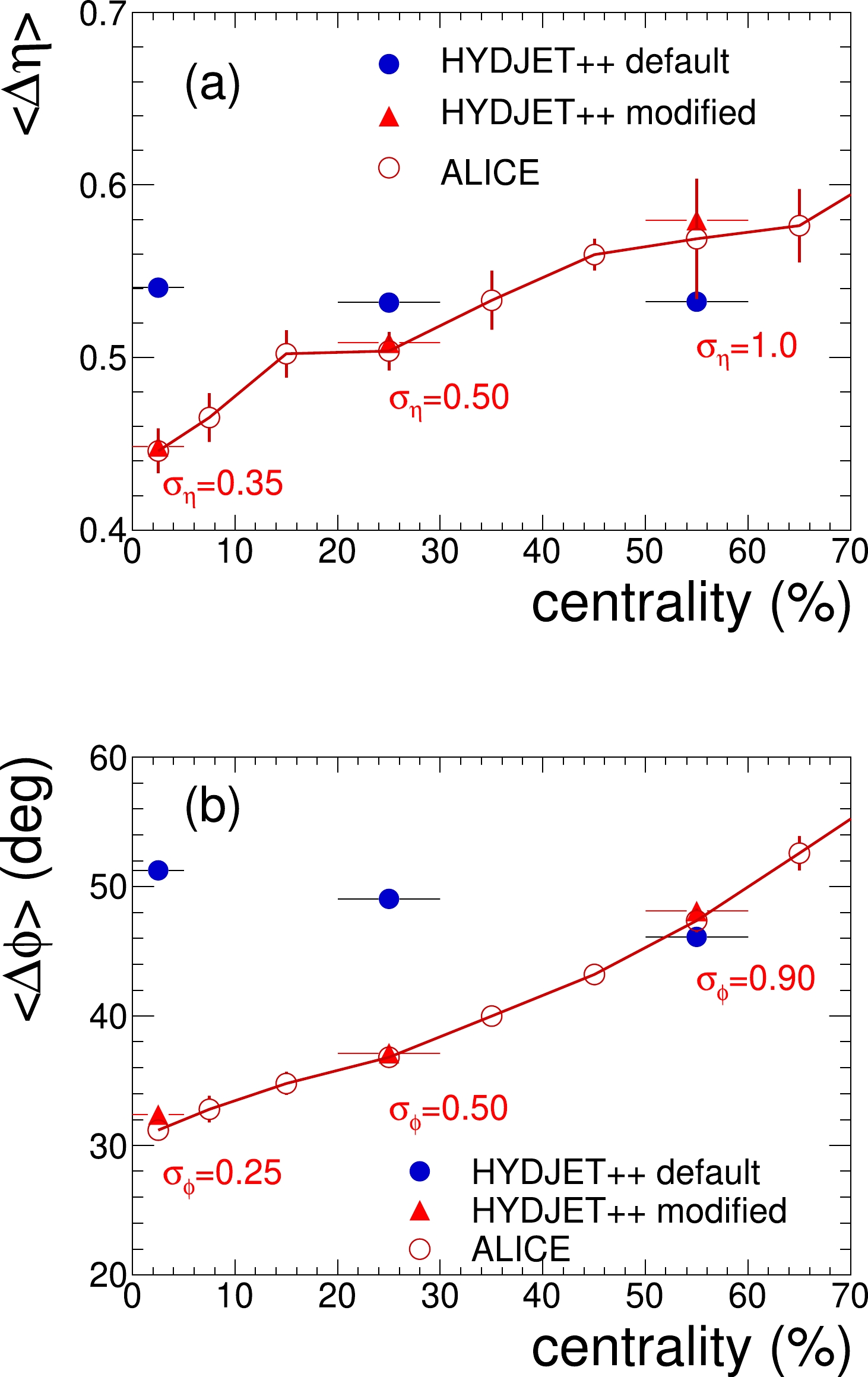
Figure 5.  (color online) The same as Fig. 2 but for calculations with a modified version of HYDJET++ (triangles) incorporating exact charge conservation. Full circles denote the default version calculations and open circles indicate the experimental data. Lines are drawn to guide the eye.

To reveal the physical mechanism that provides a shorter correlation length than that given by resonance decays and jet fragmentation at the freeze-out stage, a full description of system evolution is necessary. In the statistical and hydrodynamical models, particles are produced at the freeze-out hypersurfaces. In these models part of the information about early system dynamics is encoded in the parameters of the emission source of soft hadrons; for example, the strength and direction of the elliptic flow are governed by two parameters characterizing the momentum and spatial anisotropy of the emission source. Similarly, the charge correlations of the hadrons directly produced at the freeze-out stage are encoded using the dispersions of Gaussian distributions. An explanation why these dispersions should increase with an increase of the impact parameter is as follows. The number of characteristic elementary volumes, i.e., the independent particle sources, within which the charge is explicitly conserved, decreases with increasing impact parameter, since the area of the nuclear overlap region becomes smaller. This means that the fluctuations become stronger [44], thus destroying the charge correlation in general. The fluctuation centrality dependence [44] of the dispersions can be presented in a form

where $ \sigma_x (C_0) $ should be fixed at some centrality $ C_0 $, e.g., for the most central collisions $ C_0=0 $ and $ \sigma_{\eta} (0)= 0.35 $, as follows from our fitting procedure. After that, other dispersions can be calculated. Their values are very close to the fitting values presented in Fig. 5. Thus, the simple fluctuation formula given by Eq. (4) can be used as a good approximation instead of the fitting procedure in every centrality bin.

The total energy-momentum of the new system and the original are slightly different in each single event, but in the statistical approach, the total energy-momentum, together with the number of particles, varies (fluctuates) from event to event; only their averages and moments make sense. The large number of particles in each event during the random selection procedure ensures that the average of the considered values remain unchanged in case of large statistics of generated events. To demonstrate this explicitly, we provide in Fig. 6 the multiplicity distributions of charged particles versus pseudorapidity [Fig. 6(a), (b)], azimuthal angle [Fig. 6(c), (d)], and transverse momentum [Fig. 6(e), (f)], calculated in the default and modified versions of HYDJET++ for one event (left column) and for one thousand events (right column). It is clear that despite some differences between the spectra for a single event, the ${\rm d}N/{\rm d} \eta$, ${\rm d}N/{\rm d} \phi$, and ${\rm d}N/{\rm d} p_T$ distributions calculated for 1000 events with the modified and default versions coincide.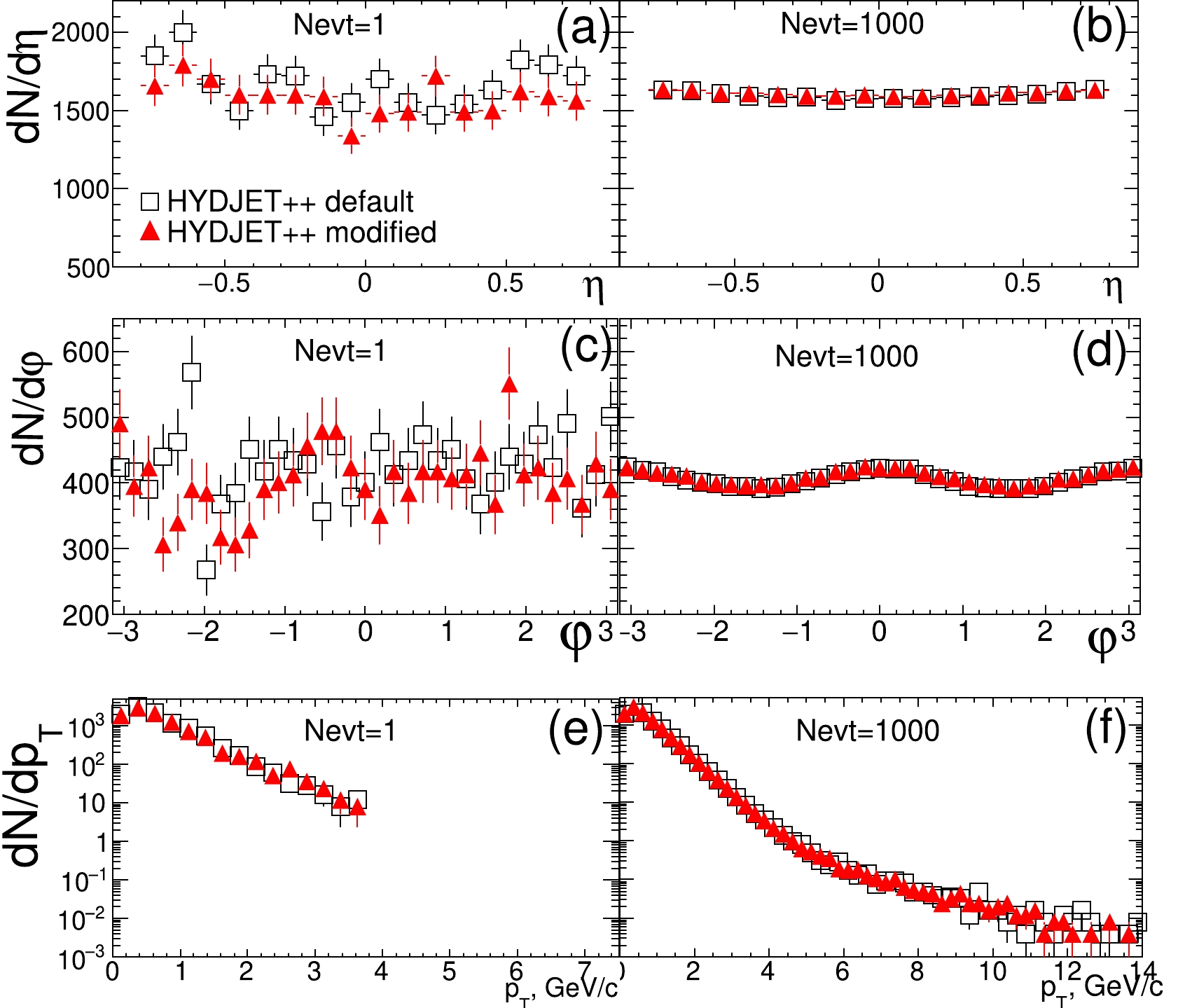

Figure 6.  (color online) Charged particle multiplicity versus pseudorapidity (a), (b), azimuthal angle (c), (d), and transverse momentum (e), (f) calculated in the default (open squares) and modified (full triangles) versions of HYDJET++ for one event (left column) and one thousand events (right column).

Here it is worth mentioning a recently developed method [45] to ensure conservation laws for each sampled configuration in spatially compact regions, or patches, at the freeze-out stage. This method allows one also to study the correlation effects sensitive to the patch size as a fitting parameter. Our procedure is considerably simpler for the realization in Monte Carlo event generators and does not imply any modification of single particle spectra or any additional tuning of other free parameters of the model.

The phenomenological analysis of the charge balance function in Pb+Pb collisions at center-of-mass energy 2.76 TeV per nucleon pair has been performed within the two-component HYDJET++ model. It is shown that the experimentally observed increase of the balance function width with increasing impact parameter in the relatively low transverse momentum interval can be qualitatively reproduced by the relative enhancement of the contribution from the hard component in peripheral Pb+Pb collisions. However, the centrality dependence of the CBF magnitude shows an opposite tendency to the experimental one. A fully adequate description of the balance function in this interval assumes modification of the essential model through the explicit inclusion of charge conservation in a statistical approach. This procedure has been implemented for the first time in Monte Carlo event generators of such a kind. With increasing transverse momentum the default model results describe the experimental data much better, because in these transverse momentum intervals the contribution from the soft component of the model is weakened. In practical terms, we find a transition to a single source of charge correlations, namely, the charge correlations in jets for which exact charge conservation holds at each stage.

Fruitful discussions with A.V. Belyaev, L.V. Bravina, and A.I. Demyanov are gratefully acknowledged.