-
Nonrelativistic QCD (NRQCD) [1] is widely used in the study of heavy quarkonium physics. In this framework, a quarkonium production process can be factorized as the multiplication of short-distance coefficients (SDCs) and long-distance NRQCD matrix elements (LDMEs). The SDCs can be calculated perturbatively and the LDMEs are strongly ordered by the relative velocity v between the quark and anti-quark inside of the quarkonium. This factorization has been applied in single quarkonium production and tested in various experiments [2−13].
Besides single quarkonium production, multi-quarkonuim production complements our understanding of the quarkonium production mechanism. At the LHC, the LHCb Collaboration measured
$ J/\psi $ pair production for the first time at the center-of-mass energy$ \sqrt{s}=7\; \mathrm{TeV} $ with an integrated luminosity of$ 35.2\; \mathrm{pb}^{-1} $ in 2011 [14]. In 2013, the CMS Collaboration released further data on$ J/\psi $ pair production [15] with a considerably larger transverse moment range, providing a good platform for testing the validity of NRQCD in quarkonium pair production. In addition, the ATLAS Collaboration has also provided a measurement of$ J/\psi $ pair production [16], and a large transverse momentum cut is imposed on both$ J/\psi $ .In Refs. [17−19], the leading order (LO) in the
$ \alpha_s $ calculation of$ J/\psi $ pair production in the color singlet model (CSM) was performed. Relativistic correction to$ J/\psi $ pair production was conducted in Ref. [20], which helped significant dilute the discrepancy between the LO results and experimental data. Furthermore, partial next-to-leading order ($ \mathrm{NLO}^{\star} $ ) correction for$ J/\psi $ pair production was calculated by Lansberg and Shao [21, 22]. They argued that the$ \mathrm{NLO}^{\star} $ yield can approach the full NLO result at large$ p_T $ , which is the transverse momentum of one of the two$ J/\psi $ , and thus the$ \mathrm{NLO}^{\star} $ results give a more precise theoretical prediction than the LO results in this region. The full NLO predictions for the color singlet (CS) channel were obtained in our previous study [23]. Moreover, the complete LO predictions within NRQCD were obtained by Kniehl and He [24]. All the above studies were performed under the single parton scattering (SPS) mechanism. The contribution of double parton scattering (DPS) was assessed in Refs. [22, 25−27], which is expected to be important, and the color evaporation model has also been used to interpret the production of a$ J/\psi $ pair [28, 29]. Because predictions for DPS and the color evaporation model are highly model-dependent, accurate calculation of the SPS contribution is required before one can extract the DPS contribution.To further study multi-quarkonium production, it is necessary to evaluate
$ J/\psi $ pair production to NLO for more channels, including$ {}^{1}S_0^{[8]} $ ,$ {}^{3}S_1^{[8]} $ , and$ {}^{3}P_J^{[8]} $ . Because$ {}^{1}S_0^{[8]} $ is found to give the most important contribution for single$ J/\psi $ production [30], we focus on the$ {}^{1}S_0^{[8]} $ channel and evaluate each$ J/\psi $ in the$ {}^{3}S_1^{[1]} $ and$ {}^{1}S_0^{[8]} $ fock states to the NLO. The calculations of the$ {}^{3}S_1^{[8]} $ and$ {}^{3}P_J^{[8]} $ channels will be performed in the future. Compared with the LO result, the NLO result can not only decrease theoretical uncertainties but also open new kinematic enhanced topologies, which dominate at large$ p_T $ . More precisely, we find that the differential cross section${\rm d}\sigma/{\rm d}p_T^2$ at large$ p_T $ acts as$ p_T^{-8} $ at LO, whereas it acts as$ p_T^{-6} $ at NLO owing to double parton fragmentation contributions [31]. -
In NRQCD factorization, the cross section of
$ J/\psi $ pair production at the LHC can be expressed as [1]$ \begin{aligned}[b] {\rm d}\sigma_{p+p \to J/\psi+J/\psi}=&\sum_{i,j,n_1,n_2}{\int}{\rm d} x_1 {\rm d} x_2{f_{i/p}(x_1)}{f_{j/p}(x_2)} \\& \times\; {{\rm d}\hat{\sigma}^{n_1,n_2}_{i,j}}\langle\mathcal{O}_{n_1}\rangle^{J/\psi} \langle\mathcal{O}_{n_2}\rangle^{J/\psi}, \end{aligned} $

(1) where
$ f_{i/p}(x_{1,2}) $ are the parton distribution functions (PDFs),$ x_1 $ and$ x_2 $ represent the momentum fraction of initial state partons from protons,$ \langle\mathcal{O}_{n}\rangle^{J/\psi} $ are the LDMEs of$ J/\psi $ with$ n = {}^{2S+1}L_J^{[c]} $ in standard spectroscopic notation for the quantum numbers of the produced intermediate heavy quark pairs, and$ d\hat{\sigma} $ are partonic short-distance coefficients. In this study, we set either$ n_1=n_2={}^{3}S_1^{[1]} $ or$ n_1=n_2={}^{1}S_0^{[8]} $ in Eq. (1).In the LO calculation, there are two subprocesses:
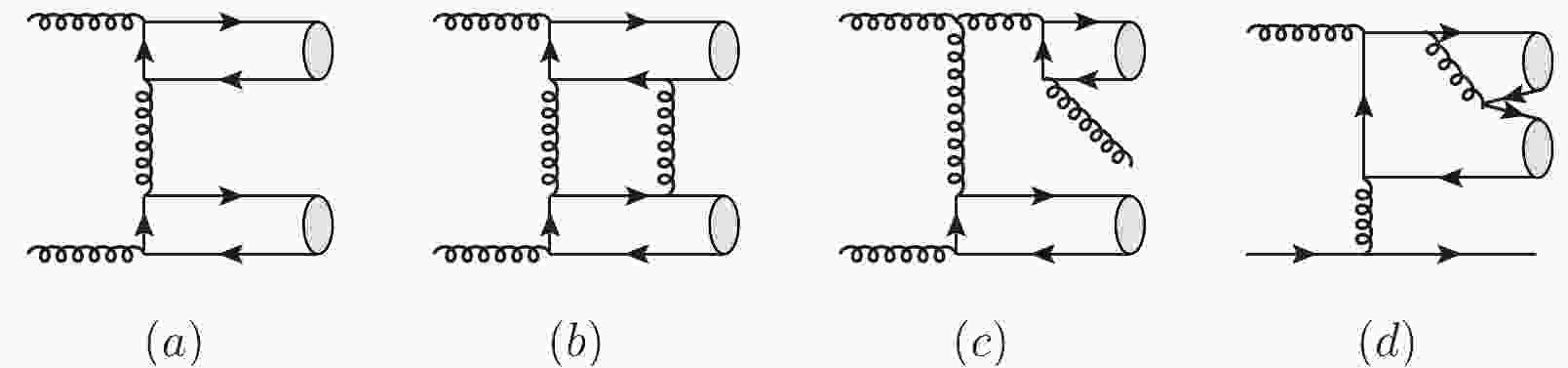
$ g+g{\rightarrow }J/\psi+J/\psi $ and$ q+\bar{q}{\rightarrow }J/\psi+J/\psi $ . However, only the former is considered because the contribution of the latter process is highly suppressed by the quark PDFs. In the NLO case, besides the gluon fusion process, the quark gluon process$ q+g\rightarrow 2J/\psi+q $ should also be considered because it can offer a non-negligible contribution. Typical Feynman diagrams at LO and NLO are shown in Fig. 1.
Figure 1. Typical Feynman diagrams for
$ J/\psi $ pair production in the$ {}^{3}S_1^{[1]} $ and$ {}^{1}S_0^{[8]} $ channels, including LO and NLO.To address the infrared (IR) divergences in real corrections, the two-cutoff phase space slicing method [32] is employed. After isolating the soft and collinear divergences, the cross sections for
$ J/\psi $ pair production at NLO can be expressed as$ \begin{eqnarray} \sigma_{\rm NLO}=\sigma_{\rm Born}+\sigma_{\rm Virtual}+\sigma_{\rm Real}^{\rm soft}+ \sigma_{\rm Real}^{HC}+\sigma_{\rm Real}^{\overline{HC}}, \end{eqnarray} $

(2) where
$ HC $ and$ \overline{HC} $ represent hard collinear and hard non-collinear contributions, respectively. The soft and collinear divergences from real corrections will cancel the divergences from virtual corrections, and thus the final NLO contributions are IR safe.Because there are two
$ J/\psi $ states in the final state, the LO contributions act as$ p_T^{-8} $ when$ p_T $ is large. However, at the NLO level, there are contributions which exhibit$ p_T^{-6} $ behavior [31] [Fig. 1 (c) and (d)]. Thus, we expect that the NLO contribution will dominate at large$ p_T $ , especially for the CMS and ATLAS data, where a relatively large lower$ p_T $ cutoff is taken [15, 16]. This expectation is confirmed by our numerical results shown below. -
Because of the complexity of
$ J/\psi $ pair production, in our calculation, the FeynArts package [33] is used to generate the Feynman diagrams and amplitudes. The phase space integration is evaluated by employing the package Vegas [34].In numerical calculation, the CTEQ6L1 and CTEQ6M PDFs [35, 36] are used. The renormalization scale
$ \mu_r $ and factorization scale$ \mu_f $ are chosen as$ \mu_r=\mu_f=m_T $ , with$ m_T=\sqrt{p_T^2+16m_c^2} $ and the charm quark mass$ m_c=M_{J/\psi}/2=1.55\; \mathrm{GeV} $ . In the two-cutoff method, there are soft and collinear cutoffs,$ \delta_s $ and$ \delta_c $ , which we set as$ \delta_s=10^{-2} $ and$ \delta_c=10^{-4} $ . Theoretical uncertainties are estimated by varying$ \mu_r=\mu_f $ from$ m_T/2 $ to$ 2m_T $ .The CS LDME
$\langle\mathcal{O}(^3 S_1^{[1]})\rangle^{J/\psi}=1.16 \;\rm{GeV}^3$ is estimated using the$ \mathrm{B-T} $ potential model [37], and the color octet (CO) LDME$\langle\mathcal{O}(^1 S_0^{[8]})\rangle^{J/\psi}=0.089~ \rm{GeV}^3$ is taken from [38], which is determined by fitting experimental data. -
In the following, we present our results for
$ J/\psi $ pair production. Under the CMS conditions [15]$ \begin{aligned} &|y(J/\psi)|<1.2,\; \;\mathrm{for}\;\; p_T>6.5\; \mathrm{GeV},\;\; \mathrm{or}\nonumber\\ &1.2<|y(J/\psi)|<1.43,\; \mathrm{for}\;\; p_T>6.5\rightarrow 4.5\; \mathrm{GeV}, \;\;\mathrm{or}\nonumber\\ &1.43<|y(J/\psi)|<2.2,\; \;\mathrm{for}\;\; p_T>4.5\; \mathrm{GeV}, \end{aligned} $

with
$ \sqrt{s}=7\; \mathrm{TeV} $ , the total cross section is measured as$ \begin{eqnarray} \sigma_{\rm Exp.}=1.49\pm0.07\pm0.14\; \mathrm{nb}, \end{eqnarray} $

(3) whereas our LO and NLO calculations for the total cross section give
$ \begin{aligned}[b] \sigma_{\mathrm{LO}}=&(0.048+0.014)\; \pm0.02\; \mathrm{nb},\\ \sigma_{\mathrm{NLO}}=&(0.18+0.03)\pm0.10\; \mathrm{nb}. \end{aligned} $

(4) Here, the first value in the brackets represents the CS contribution, whereas the second value represents the CO contribution, and the uncertainties originate from
$ \mu_r=\mu_f $ varying from$ m_T/2 $ to$ 2m_T $ . As expected, we find the NLO calculation gives the dominant contribution. In Eq. (4) the contributions of the feeddown processes$ p+p\rightarrow J/\psi+\psi(2S)+X\rightarrow 2J/\psi+X $ and$p+p\rightarrow J/\psi+ \chi_{cJ}+X\rightarrow 2J/\psi+X$ are also included, which are estimated to be$ 30$ % of the direct production [19]. Comparing Eq. (3) with Eq. (4), we can see the cross section measured by CMS cannot be described by the NRQCD calculation at NLO.We then compare our prediction for the transverse momentum
$ p_{T J/\psi J/\psi} $ distribution of the$ J/\psi $ pair with the CMS data and$ \mathrm{NLO^{\star}} $ [21] yields. The result is shown in Fig. 2. At LO,$ p_{T J/\psi J/\psi} $ is always zero because it is a two-body final state process. At NLO, we first find that the contribution of the$ {}^{1}S_0^{[8]} $ channel is small even at large$ p_{T J/\psi J/\psi} $ . We believe this to be normal because the dominant contribution at large$ p_{T J/\psi J/\psi} $ may originate from the$ {}^{3}S_1^{[8]} $ channel, which will be explored in our subsequent study. We also find that the behavior of the NRQCD result is similar to but smaller than the experimental data by an order of magnitude. For$ \mathrm{NLO^{\star}} $ , the result is consistent with our NLO prediction at large$ p_{T J/\psi J/\psi} $ . The data evidently overshoots our NLO prediction in the entire$ p_{T J/\psi J/\psi} $ region. Because both the CS and dominant CO contributions are considered, we concluded that NRQCD factorization cannot describe the CMS data even after NLO correction. Therefore, another mechanism must be included besides the SPS contribution in the NRQCD framework to explain experimental data.
Figure 2. (color online) Differential cross sections in bins of the transverse momentum of the
$ J/\psi $ pair at the CMS. The data are taken from Ref. [15], and the$ \mathrm{NLO^{\star}} $ results are taken from Ref. [21]. The dashed and dot dashed lines denote the NLO$ {}^{3}S_1^{[1]} $ and$ {}^{1}S_0^{[8]} $ results, respectively, and the band denotes the NLO total result, where the uncertainties are due to the scale choices mentioned in the text.The invariant mass distribution (denoted as
$ M_{J/\psi J/\psi} $ ) for the CMS is shown in Fig. 3. The$ {}^{1}S_0^{[8]} $ channel has a large contribution in the medium and large$ M_{J/\psi J/\psi} $ regions, which is important to compare with the$ {}^{3}S_1^{[1]} $ channel. The sum of the$ {}^{3}S_1^{[1]} $ and$ {}^{1}S_0^{[8]} $ channels again indicates that the NLO result cannot describe the CMS data. Similar to the$ p_{T J/\psi J/\psi} $ distribution, the NLO prediction for the$ M_{J/\psi J/\psi} $ distribution is smaller than the experimental data by at least one order of magnitude for each bin, which also reflects the fact that the NRQCD prediction contributes little in$ J/\psi $ pair production.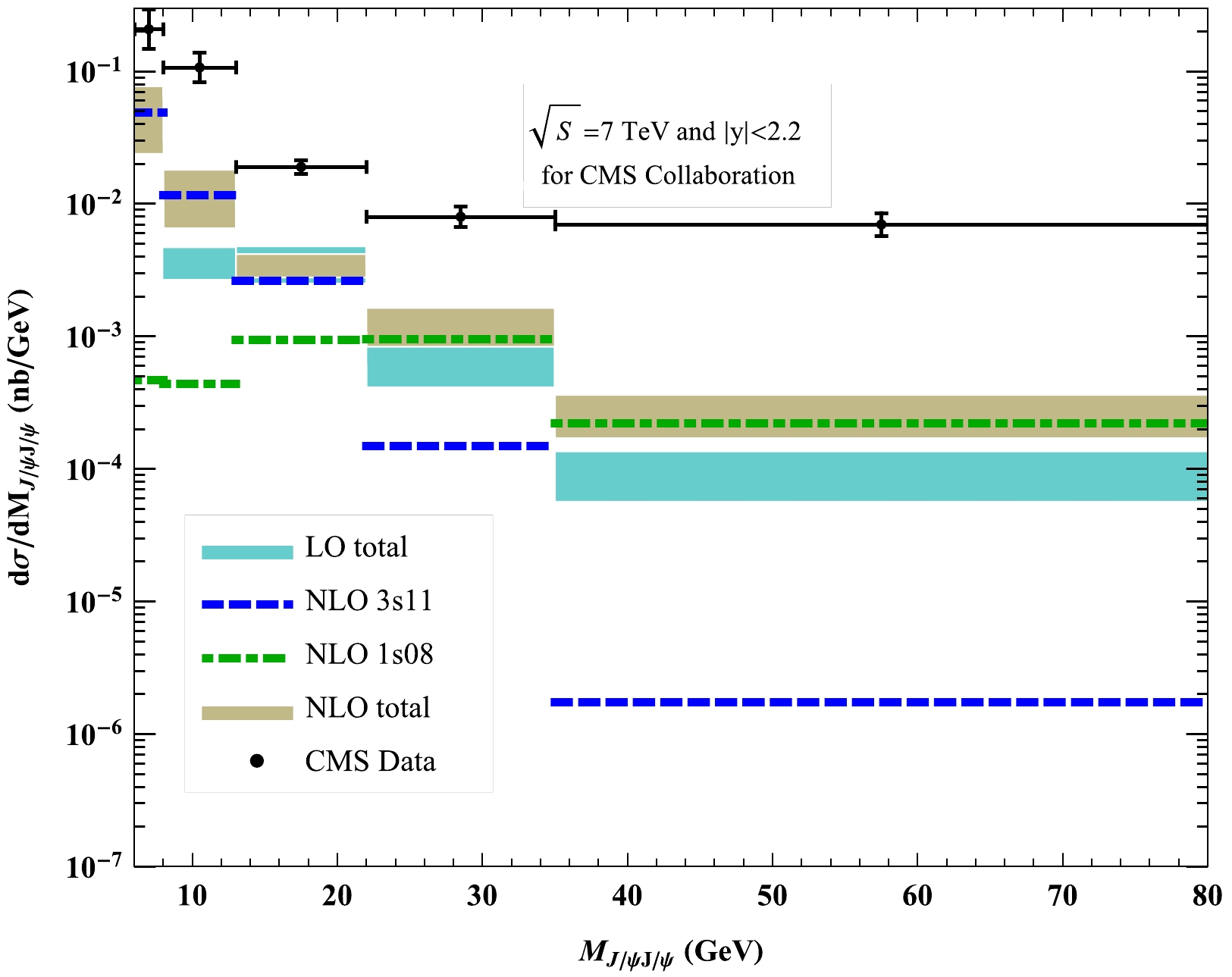
Figure 3. (color online) Differential cross sections in bins of the
$ J/\psi $ pair invariant mass at the CMS. The data are taken from Ref. [15], and the$ \mathrm{NLO^{\star}} $ results are taken from Ref. [21]. The dotted, dashed, and dot dashed lines denote the NLO$ {}^{3}S_1^{[1]} $ , LO$ {}^{1}S_0^{[8]} $ , and NLO$ {}^{1}S_0^{[8]} $ results, respectively, and the two bands denote the total LO and NLO results, where the uncertainties are due to the scale choices mentioned in the text.The
$ J/\psi $ pair rapidity difference$ |\Delta y| $ distribution for the CMS is shown in Fig. 4. The$ {}^{1}S_0^{[8]} $ channel also has a large contribution in the medium and large$ |\Delta y| $ regions, and at large$ |\Delta y| $ , the$ {}^{1}S_0^{[8]} $ channel is dominant. Despite this, the sum of the$ {}^{3}S_1^{[1]} $ and$ {}^{1}S_0^{[8]} $ channels cannot describe the CMS data, similar to the above two distributions.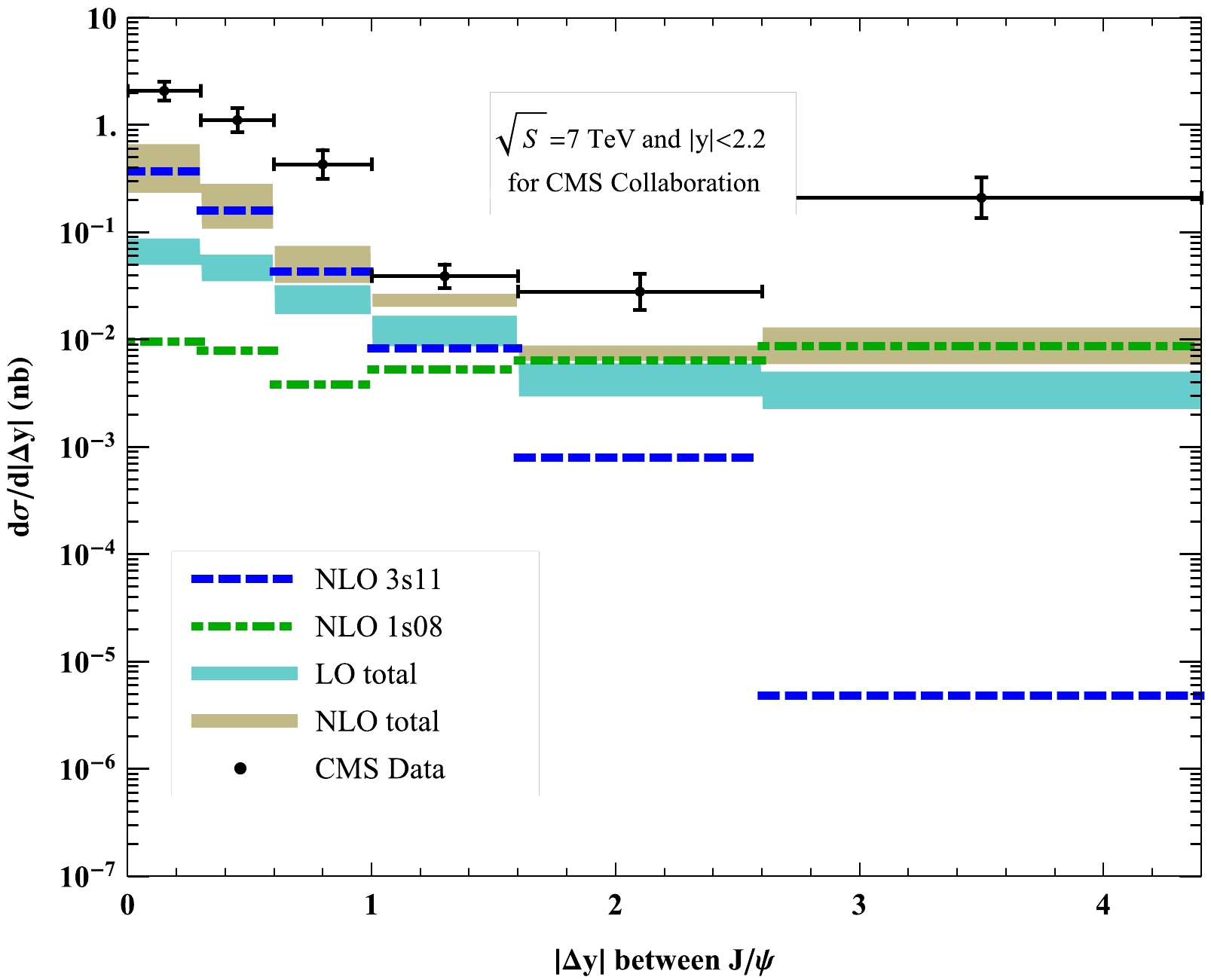
Figure 4. (color online) Differential cross sections in bins of the
$ J/\psi $ pair$ |\Delta y| $ at the CMS. The data are taken from Ref. [15], and the$ \mathrm{NLO^{\star}} $ results are taken from Ref. [21]. The dotted, dashed, and dot dashed lines denote the NLO$ {}^{3}S_1^{[1]} $ , LO$ {}^{1}S_0^{[8]} $ , and NLO$ {}^{1}S_0^{[8]} $ results, respectively, and the two bands denote the total LO and NLO results, where the uncertainties are due to the scale choices mentioned in the text. -
In the framework of NRQCD factorization, we evaluate full NLO
$ J/\psi $ pair production via the$ {}^{3}S_1^{[1]} $ and$ {}^{1}S_0^{[8]} $ channels. We find that NLO corrections are essential for$ J/\psi $ pair production, in contrast with the LO results. For the CMS, the NLO predictions of the total cross section,$ p_{T J/\psi J/\psi} $ distribution, invariant mass distribution of the$ J/\psi $ pair, and rapidity difference distribution of the$ J/\psi $ pair are considerably smaller than CMS data by approximately an order of magnitude. This reveals that in the$ J/\psi $ pair production process, the NRQCD NLO result is not the dominant contribution, and there must be some new schemes dominating the process if the CMS data are confirmed. -
We thank Y. Q. Ma and C. Meng for valuable discussions and suggestions.
J/ψ pair hadroproduction at next-to-leading order in nonrelativistic-QCD at CMS
- Received Date: 2023-05-05
- Available Online: 2023-09-15
Abstract: We perform a complete study of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: