-
Neutron skin is an interesting phenomenon in the domain of nuclear physics. In particular, for neutron-rich systems, owing to the large asymmetry between the proton (p) and neutron (n) numbers (denoted as Z and N, respectively), these two types of fermions tend to be decoupled around the surface region of a nucleus, providing valuable information to study the nuclear force [1], including the symmetry energy regarding the equation of state (EOS) of nuclear matter [2−7]. Moreover, neutron skin thickness is a direct observation of the nuclear structure, which is strongly associated with the difference in radii between mirror nuclei across the nuclear landscape. To this end, we aim to investigate the correlation between neutron skin thickness and various physical quantities by studying the region of light and mid-heavy nuclei and gain more insight into the connection between nuclear structure and matter.
Neutron-skin thickness is defined as the difference between the root-mean-square (rms) radius of the neutron and that of the proton:
$ S_{n} \equiv \langle r_{n}^{2}\rangle^{1/2}-\langle r_{p}^{2}\rangle^{1/2} \equiv R_{n}-R_{p} $ . The proton radius of a nucleus can be extracted with relatively high accuracy via the electromagnetic interaction [8]; however, it is difficult to obtain precise neutron radii using strong or weak interaction probes. Consequently, the extracted results of neutron-skin thickness are usually model-dependent and vary greatly between different experimental methods [9]. Therefore, high-precision data on neutron-skin thickness are anticipated and will play a significant role in nuclear physics and astrophysics.According to the EOS, the energy per nucleon of nuclear matter can be approximately expressed as
$ \begin{equation} E(\rho,\delta) = E_0(\rho) + E_\text{sym}(\rho)\delta^2 + O(\delta^4), \end{equation} $

(1) where
$ \rho_{n} $ ,$ \rho_{p} $ , and$ \rho = \rho_{n} + \rho_{p} $ are the neutron, proton, and total nucleon densities, respectively,$ \delta=(\rho_{n}-\rho_{p})/\rho $ is the isospin asymmetry,$ E_0(\rho) = E(\rho, \delta=0) $ is the energy per nucleon of symmetric nuclear matter, and$ E_\text{sym}(\rho) $ is the nuclear symmetry energy described as$ \begin{equation} E_\text{sym}(\rho) \equiv \left. \frac{1}{2!} \frac{\partial ^{2}E(\rho,\delta)}{\partial \delta^{2}}\right|_{\delta=0}. \end{equation} $

(2) The properties of symmetric nuclear matter are relatively well-determined; however, the isovector part remains largely uncertain and attracts significant attention because it may offer more information on dripline nuclei, astrophysics, and heavy-ion collisions [10−15]. Around the saturation density
$ \rho_0 $ ,$ E_\text{sym}(\rho) $ can be expanded as$ \begin{aligned}[b] E_\text{sym}(\rho) =& E_\text{sym}(\rho_0)+\frac{L}{3} \left( \frac{\rho-\rho_0}{\rho_0}\right) \\& + \frac{K_\text{sym}}{18}\left( \frac{\rho-\rho_0}{\rho_0}\right)^2+\cdots, \end{aligned} $

(3) where L and
$ K_\text{sym} $ are the slope and curvature of the symmetry energy at the saturation density, respectively, defined as$ \begin{equation} L \equiv 3\rho_0\left. \frac{\partial E_\text{sym}(\rho)}{\partial \rho}\right|_{\rho=\rho_0}, \end{equation} $

(4) $ \begin{equation} K_\text{sym} \equiv 9\rho_0^2\left. \frac{\partial ^{2}E_\text{sym}(\rho)}{\partial \rho^{2}}\right|_{\rho=\rho_0}. \end{equation} $

(5) These two characteristic parameters govern the behavior of the symmetry energy at the subsaturation and oversaturation densities [16−23]. Similarly, the coefficient of the third-order term, known as the incompressibility of symmetric nuclear matter, can be written as
$ \begin{equation} K_0 \equiv 9\rho_0^2\left. \frac{\partial ^{2}E_0(\rho)}{\partial \rho^{2}}\right|_{\rho=\rho_0}. \end{equation} $

(6) A larger
$ K_0 $ indicates that it is harder to compress nuclear matter, corresponding to a stiff EOS, whereas the opposite is regarded as a soft EOS [16, 24−30]. According to various studies on density functional theory [18, 31−37], there is a strong linear correlation between$ S_{n} $ and L for the heavy nucleus$ ^{208}\text{Pb} $ . It has also been shown that these properties can be constrained by the scattering phase shift related to nuclear force [38].Supposing perfect charge symmetry, the neutron radius of a given nucleus (
$ ^{A}_{Z}X $ ) is strictly equal to the proton radius of the corresponding mirror nucleus ($ ^{A}_{N}Y $ ), where$ A=N+Z $ is the mass number. Therefore, the thickness of neutron skin can be evaluated through the difference in the proton rms radius of mirror nuclei [39−42], that is,$ \begin{equation} S_{n}(^{A}_{Z}X) = R_{p}(^{A}_{N}Y) - R_{p}(^{A}_{Z}X) \equiv R_{p}^{\rm mir}(^{A}_{Z}X). \end{equation} $

(7) Although, in reality, charge symmetry is slight broken mainly due to the presence of the Coulomb interaction between protons, it has been shown that there is a linear correlation between the difference in the rms charge radii of mirror nuclei (
$ R_{\rm ch}^{\rm mir} $ ) and$ |N-Z| \times L $ [39, 40]. In addition,$ S_{n} $ is related to both$ |N-Z| \times L $ and$E_\text{sym} (\rho = 0.10\ \rm fm^{-3})$ [39]. When$ |N-Z| $ is large, the L dependence in$ S_{n} $ dominates. It is worth noting that the above research results are based on neutron-deficient nickel isotopes and their corresponding mirror nuclei. The lack of experimental data on the charge radii of most nickel isotopes makes it impossible to predict$ S_{n} $ through their relationship with$ R_{\rm ch}^{\rm mir} $ . Moreover, for nuclei far from doubly magic nuclei, deformation and pairing effects play a significant role but are not fully considered in the above studies. Refs. [43, 44] proposed that pairing effects weaken the correlation between$ R_{\rm ch}^{\rm mir} $ and L. Therefore, further study on the dependence of$ R_{\rm ch}^{\rm mir} $ on isovector sensitive observables is required.In this study, we adopt the density-functional solver HFBTHO [45], in which the axially deformed solutions of the Skyrme-Hartree-Fock-Bogoliubov (HFB) equations are considered to investigate the neutron and proton rms radii of different nuclei. To investigate the pairing and deformation effect, the results of the Skyrme-Hartree-Fock (SHF) method are also shown. Using various sets of Skyrme interaction parameters, different neutron skin sizes are obtained and the correlations between
$ S_{n} $ , L, and$ R_{p}^{\rm mir} $ are investigated. By extracting the neutron-skin thickness of certain neutron-rich nuclei, the constraints on the characteristic parameters of the EOS – such as L – are studied. -
The SHF methodology [46] has been successfully applied to study the structure of finite nuclei across the nuclear landscape, including deformed nuclei near drip lines, superheavy elements, and heavy-ion collisions [47−51]. In the Hartree-Fock framework, a nucleon of a system is regarded as moving in the mean field of other nucleons. The total wave function of the system can be constructed using the Slater determinant of the single-particle ones, which is obtained through the single-particle Hamiltonian generated by the mean field [52−54]. Consequently, the total energy functional of the nucleus can be separated as
$ \begin{equation} E = E_\text{Skyrme} +E_\text{Coulomb} + E_\text{pair} - E_\text{cm}. \end{equation} $

(8) A widely used Skyrme energy functional can be written in the following form [46]:
$ \begin{aligned}[b] E_\text{Skyrme} =& 4\pi\int_{0}^{\infty}{\rm d} r\,r^2\left\{\frac{\hbar^2}{2m}\tau\right. \\ & + \frac{1}{2}t_0(1+\frac{1}{2}x_0)\rho^2 - \frac{1}{2}t_0(\frac{1}{2}+x_0)\sum_{\rm q}\rho_{\rm q}^2 \end{aligned} $

$ \begin{aligned}[b] & + \frac{1}{12}t_3(1+\frac{1}{2}x_3)\rho^{\alpha+2} - \frac{1}{12}t_3(\frac{1}{2}+x_3)\rho^{\alpha}\sum_{\rm q}\rho_{\rm q}^2 \\ & + \frac{1}{4}[t_1(1+\frac{1}{2}x_1)+t_2(1+\frac{1}{2}x_2)]\rho\tau \\ & - \frac{1}{4}[t_1(\frac{1}{2}+x_1)-t_2(\frac{1}{2}+x_2)]\sum_{\rm q}\rho_{\rm q}\tau_{\rm q} \\ & - \frac{1}{16}[3t_1(1+\frac{1}{2}x_1)-t_2(1+\frac{1}{2}x_2)]\rho\nabla^2\rho \\ & + \frac{1}{16}[3t_1(1+\frac{1}{2}x_1)+t_2(1+\frac{1}{2}x_2)]\sum_{\rm q}\rho_{\rm q}\nabla^2\rho_{\rm q} \\ &\left. - \frac{1}{2}W_0[\rho\nabla\cdot\boldsymbol{J}+\sum_{\rm q}\rho_{\rm q}\nabla\cdot\boldsymbol{J}_{\rm q}] \right\}, \end{aligned} $

(9) where
$ \nabla^2=\dfrac{\partial^2}{\partial r^2}+\dfrac{2}{r}\dfrac{\partial}{\partial r} $ is the Laplacian operator,$q \in \{n, p\}$ (n = neutron and p = proton) is the isospin label, and$ \rho=\rho_{n}+\rho_{p} $ ,$ \tau=\tau_{n}+\tau_{p} $ , and$ \boldsymbol{J}=\boldsymbol{J}_{n}+\boldsymbol{J}_{p} $ are the total density of the nucleon, kinetic energy, and spin-orbit coupling, respectively. Eq. (9) contains ten Skyrme interaction parameters:$ t_0 $ ,$ t_1 $ ,$ t_2 $ ,$ t_3 $ ,$ x_0 $ ,$ x_1 $ ,$ x_2 $ ,$ x_3 $ , α, and$ W_0 $ . Additionally, α is also known as the density-dependent coefficient of the Skyrme interaction potential and commonly ranges from 1/6 to 1. When$ \alpha<1 $ , the potential is soft with a comparatively small$ K_0 $ , whereas when$ \alpha=1 $ , the potential is stiff.To date, many Skyrme parameter sets have been proposed by fitting experimental data on the properties of the ground state of finite nuclei and several observables of infinite nuclear matter near the saturation density [55]. Each set of parameters has its own macroscopic quantities, such as
$ \rho_0 $ , L,$ E_{\rm sym} $ , and$ K_0 $ . Near the β-stability line, most Skyrme energy functionals provide similar results. However, the theoretical predictions for the properties of asymmetric nuclear matter or finite nuclei far from the stability line generally vary significantly, which strongly depends on the selected set of parameters [56]. Therefore, we attempt to investigate the impact of density functionals on the neutron skin, in which the Coulomb energy$ E_{\rm Coulomb} $ , including the Coulomb-exchange part which is treated in the Slater approximation, and a correction for the spurious center-of-mass (CoM) motion of the mean field$ E_{\rm cm} $ [46, 57] are considered. Except for SLy6 and SLy7, which use the simplified version of the two-body CoM correction [58], the one-body CoM motion is considered in this study.Moreover, nucleon-nucleon correlation is widely exhibited in the nuclear landscape and plays a significant role in the bulk properties. To investigate the pairing and deformation effects, the HFB solver is utilized, in which the axial transformed harmonic oscillator single-particle basis is used to expand quasi-particle wave functions. The pairing channel is parameterized by a density-dependent delta-pairing force with mixed volume and surface features:
$ \begin{equation} V_{ pair,\rm q}(\boldsymbol{r}) = V_{0,q}\left(1-\frac{1}{2}\frac{\rho_c(\boldsymbol{r})}{\rho_0}\right)\delta(\boldsymbol{r}-\boldsymbol{r}'), \end{equation} $

(10) where
$V_{0,q}$ is the pairing strength,$ \rho_c(\boldsymbol{r}) $ is the isoscalar local density, and$ \rho_0 $ is the saturation density fixed at 0.16 fm$ ^{-3} $ . A general review of the HFBTHO solver can be found in Ref. [45]. In the case of the UNEDF parameterizations, the pairing strengths should not be adjusted by the user because they are fitted together with the Skyrme coupling constants. For UNEDF0, UNEDF1, and UNEDF2 [59], the recommended values of$V_{0,n}$ are$ -170.374 $ MeV,$ -186.065 $ MeV, and$ -208.889 $ MeV, respectively, and the recommended values of$V_{0,p}$ are$ -199.202 $ MeV,$ -206.580 $ MeV, and$ -230.330 $ MeV, respectively. For other Skyrme interactions,$V_{0,n}$ and$V_{0,p}$ are chosen as$ -300 $ MeV, which results in a binding energy approximately consistent with experimental data, as verified in this study.In this study, we consider 128 sets of Skyrme interaction parameters out of 240 available in literature [55] to obtain the density distributions of neutron/proton and calculate the corresponding rms radii and
$ S_{n} $ . These 128 Skyrme interactions are selected by considering two aspects:1. The range of L (the slope of the symmetry energy at the saturation density) is limited to 0 – 130 MeV, as previous research recommends [12, 60−62].
2. The calculated binding energy per nucleon should approximately match the experimental data for all nuclei involved in this study.
Furthermore, we want to emphasize that the value of L is yet to be determined (this requires further study), and our paper mainly focuses on the correlations between the the neutron skin thickness and various physical quantities. Removing a small number of Skyrme interactions has little effect on the overall results and conclusions.
Both the SHF and HFB frameworks are used to make comparisons and investigate the influence of the pairing and deformation effects. The 132 parameter sets give a relatively wide range of nuclear-matter quantities regarding the EOS, including
$0.145\;\rm fm^{-3}\leqslant \rho_0 \leqslant0.175\ \rm fm^{-3}$ ,$0.13\ {\rm MeV}\leqslant\; L \;\leqslant129.33 \ \rm MeV$ ,$22.83\ {\rm MeV}\leqslant\; E_\text{sym}(\rho_0) \; \leqslant 37.40\ \rm MeV$ , and$200.97\ {\rm MeV}\leqslant\; K_0 \; \leqslant370.38\ \rm MeV$ . The correlations between$ S_{n} $ ,$ R_{p}^{\rm mir} $ , and L are studied. Based on the experimental data [41, 42, 63], we investigate 12 pairs of mirror nuclei that have available charge radii data. By considering the electromagnetic spin-orbit effects, the conversion formula between the charge and point-proton radius can be expressed approximately as [64]$ \begin{equation} R_{p} = \sqrt{R_{\rm ch}^2-\langle \tilde{R}_{p}^2\rangle-\frac{N}{Z}\langle \tilde{R}_{n}^2\rangle-\frac{3}{4M^2}-\langle r^2\rangle_{\rm so}}. \end{equation} $

(11) Here,
$\langle r^2\rangle_{\rm so}$ is the spin-orbit contribution [65],$ \langle \tilde{R}_{p}^2\rangle = 0.769(12)\rm \ fm^2 $ and$ \langle \tilde{R}_{n}^2\rangle = -0.1161(22)\rm \ fm^2 $ are the mean-square charge radii of the proton and neutron, respectively, and the term$ \dfrac{3}{4M^2} = 0.033\rm \ fm^2 $ is known as the Darwin-Foldy term [66]. Consequently, the experimental value of the difference in proton radii and the corresponding error from the error propagation formula can be obtained. In this way, we can not only forecast the$ S_{n} $ of several neutron-rich nuclei but also discover which sets of Skyrme parameters are more reasonable for constraining the range of L. Moreover, we explore correlation strength based on the linearity between$ S_{n} $ and$ R_{p}^{\rm mir} $ for the$ N=20 $ and$ N=28 $ isotone chains [40]. -
First, we take
$ ^{48}\text{Ca} $ as an example and calculate the correlations of$ S_{n} $ –L,$ S_{n} $ –$ R_{p}^{\rm mir} $ , and$ R_{p}^{\rm mir} $ –L (see Fig. 1). Although either$ R_{p}^{\rm mir} $ or$ R_{\rm ch}^{\rm mir} $ can be used in these analyses, the results will be nearly identical. For the sake of consistency, we use$ R_{p}^{\rm mir} $ in our discussions. Each point in Fig. 1 corresponds to the results of individual Skyrme energy functional. We label the results of the HFB9, UNEDF0, UNEDF1, and UNEDF2 parameterizations using black crosses.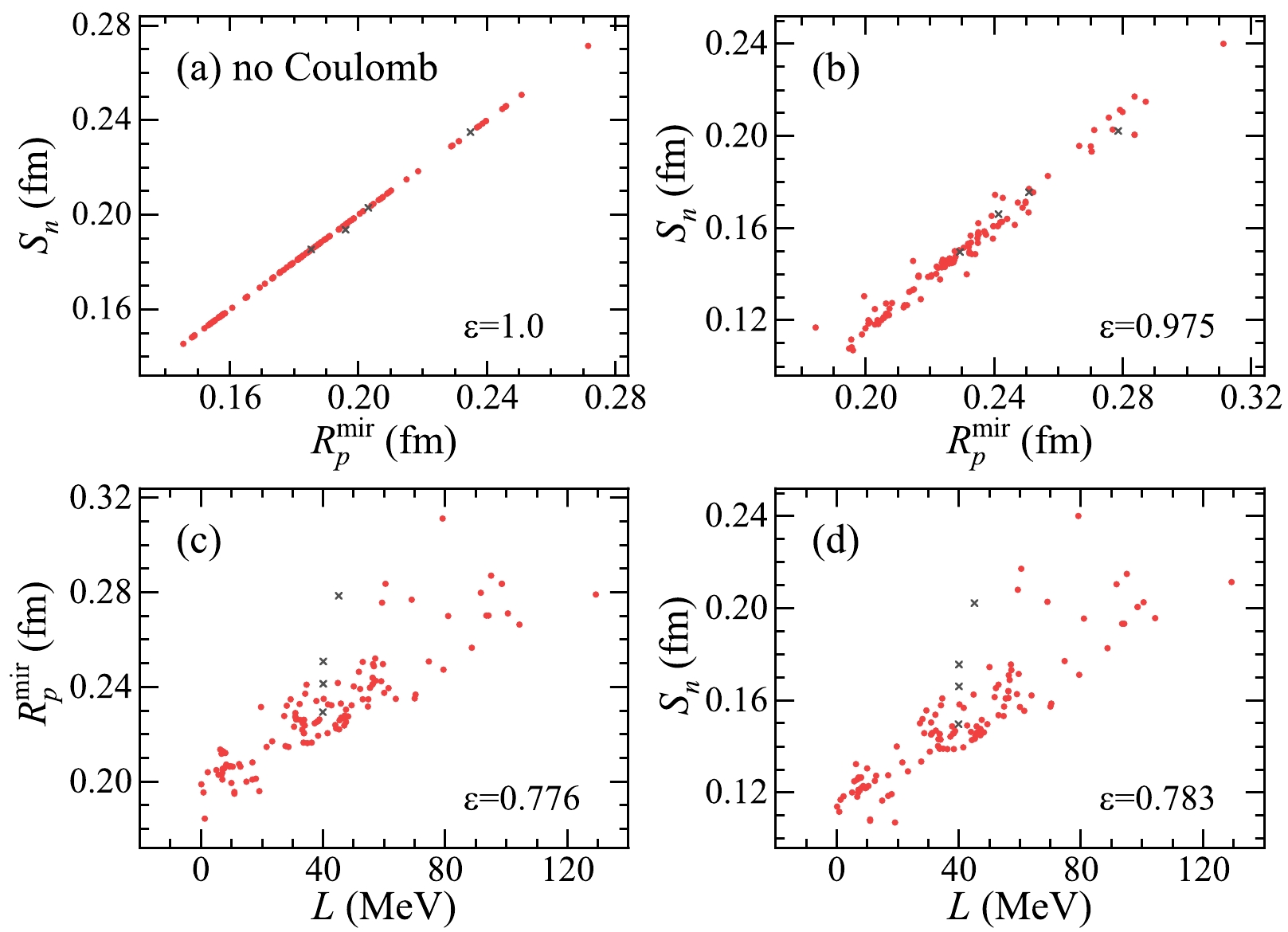
Figure 1. (color online) Correlation between two physical quantities of
$ ^{48}\text{Ca} $ calculated with HFBTHO using 132 sets of Skyrme interaction parameters.$ S_{n} $ and$ R_{p}^{\rm mir} $ (a),$ S_{n} $ and$ R_{p}^{\rm mir} $ (b),$ R_{p}^{\rm mir} $ and L (c), and$ S_{n} $ and L (d). (a) and (b-d) represent the results obtained without and with the Coulomb interaction, respectively. Each point corresponds to a set of parameters, and the black crosses denote the results of the HFB9, UNEDF0, UNEDF1, and UNEDF2 parameterizations. ε is the coefficient of determination of linear fit.As shown in Fig. 1(a), a perfect linear relationship is exhibited between neutron-skin thickness and the difference in the proton radii of mirror nuclei when the Coulomb interaction is not considered due to Eq. (7). In reality, the Coulomb interaction should be considered, as shown in Fig. 1(b)−(d). It is interesting to note that a roughly linear correlation remains even in the presence of the Coulomb interaction, especially in Fig. 1(b). Therefore, we perform the statistical analysis approach as follows: If two physical quantities (x and y) have a linear statistical correlation, we can establish the linear regression equation as
$ \begin{equation} \hat{y} = C_0 + C_1x, \end{equation} $

(12) where the constants
$ C_0 $ and$ C_1 $ are the linear regression intercept and slope, respectively. To signify the degree of linear relation, the coefficient of determination (ε) is defined as$ \begin{equation} \varepsilon = \frac{\displaystyle\sum\limits_{i=1}^{n}(\hat{y}_{\rm i}-\bar{y})^2}{\displaystyle\sum\limits_{i=1}^{n}(y_{\rm i}-\bar{y})^2} = 1 - \frac{\displaystyle\sum\limits_{i=1}^{n}(y_{\rm i}-\hat{y}_{\rm i})^2}{\displaystyle\sum\limits_{i=1}^{n}(y_{\rm i}-\bar{y})^2}, \end{equation} $

(13) where
$ \begin{equation} \hat{y}_{\rm i}=C_0+C_1x_i,\ \bar{y}=\sum\limits_{i=1}^{n}y_i/n. \end{equation} $

(14) In the above,
$ (x_{\rm i},y_{\rm i}) $ is the ith observed value of$ (x,y) $ , which corresponds to each calculation result, and n is the total number of samples. ε ranges from zero to one, and the closer it gets to one, the stronger the linear correlation.According to our calculation (see Fig. 1), the difference in radii between mirror nuclei has a considerably better correlation with neutron-skin thickness than the slope of the symmetry energy. This is because the correlation between neutron-skin thickness and the slope of the symmetry energy becomes weaker with decreasing nucleus mass. A strong correlation only exists for heavier nuclei such as
$ ^{208}\text{Pb} $ ,$ ^{132}\text{Sn} $ , and$ ^{124}\text{Sn} $ , as found in Ref. [31] using the SHF model with 21 sets of Skyrme interaction parameters. This indicates that, as one of the characteristic parameters of the EOS of nuclear matter, the slope of the symmetry energy only has an obvious linear correlation with$ S_{n} $ or$ R_{p}^{\rm mir} $ in heavy nuclei near nuclear matter. However, neutron-skin thickness is a direct observation of the nuclear structure; hence, it would strongly associate with mirror proton radii due to Eq. (7) for both light and heavy nuclei. The mirror nuclei pairs investigated in this study are systems with relatively light masses. Therefore, we will focus on the correlation between neutron-skin thickness and the difference in proton radii in the presence of the Coulomb interaction in our subsequent study. Using the good linear correlations,$ S_{n} $ or$ R_{p}^{\rm mir} $ can be deduced through the other's experimental value.Nuclear charge radii can be extracted through different experimental methods, such as elastic electron scattering, muonic atom X-rays,
$ K_{\alpha} $ isotope shifts, and optical isotope shifts. Currently, there are 12 pairs of mirror nuclei with known information on their charge radii:$ ^{18}\text{O} $ –$ ^{18}\text{Ne} $ ,$ ^{19}\text{F} $ –$ ^{19}\text{Ne} $ ,$ ^{21}\text{Ne} $ –$ ^{21}\text{Na} $ ,$ ^{22}\text{Ne} $ –$ ^{22}\text{Mg} $ ,$ ^{23}\text{Na} $ –$ ^{23}\text{Mg} $ ,$ ^{34}\text{S} $ –$ ^{34}\text{Ar} $ ,$ ^{36}\text{S} $ –$ ^{36}\text{Ca} $ ,$ ^{35}\text{Cl} $ –$ ^{35}\text{Ar} $ ,$ ^{37}\text{Cl} $ –$ ^{37}\text{Ca} $ ,$ ^{37}\text{Ar} $ –$ ^{37}\text{K} $ ,$ ^{38}\text{Ar} $ –$ ^{38}\text{Ca} $ , and$ ^{54}\text{Fe} $ –$ ^{54}\text{Ni} $ . It is noted that$ R_{\rm ch} $ of$ ^{54}\text{Fe} $ –$ ^{54}\text{Ni} $ and$ ^{36,38}\text{Ca} $ were evaluated in Ref. [63] and Ref. [41], respectively, and$ R_{\rm ch} $ of other nuclei are listed in Ref. [42]. Consequently, we can deduce the information on the difference in proton radii using Eq. (11) and the corresponding error using the error propagation formula. The estimated experimental proton radii are listed in Table 1. Based on the HFB framework with 132 sets of Skyrme parameters, the predicted correlations between neutron-skin thickness and the difference in proton radii from oxygen to iron isotopes are shown in Fig. 2(a)−(l), respectively. The solid blue lines are the results of the linear fit, which can be expressed as$ S_{n}=C_0+C_1R_{p}^{\rm mir} $ . This indicates that the resulting correlations vary for different nuclei. Roughly, the linear correlation is stronger when the neutron-rich nucleus has a larger neutron-proton ratio ($ N/Z $ ). Moreover, except for$ ^{37}\text{Ar} $ –$ ^{37}\text{K} $ and$ ^{54}\text{Fe} $ –$ ^{54}\text{Ni} $ with small$ N/Z $ , the coefficients of determination of the other pairs are larger than 0.7, making it possible to estimate$ S_n $ from experimental$ R_{p}^{\rm mir} $ . In particular, the coefficient of determination of the$ ^{18}\text{O} $ –$ ^{18}\text{Ne} $ mirror pair is extremely close to 1, as shown in Fig. 2(a), making it possible to predict the neutron-skin thickness of$ ^{18}\text{O} $ with a moderate neutron-proton ratio ($ N/Z=1.25 $ ). As a result, the linear expression isMirror nuclei $ |N-Z| $ 

$ R_{p}^{\rm mir} ({\rm{Exp}})$ 

$ ^{18}_{ 8} $ O

$ _{10} $ -

$ ^{18}_{10} $ Ne

$ _{8} $ 

2 0.183 ± 0.009 $ ^{19}_{ 9} $ F

$ _{10} $ -

$ ^{19}_{10} $ Ne

$ _{9} $ 

1 0.104 ± 0.005 $ ^{21}_{10} $ Ne

$ _{11} $ -

$ ^{21}_{11} $ Na

$ _{10} $ 

1 0.036 ± 0.029 $ ^{22}_{10} $ Ne

$ _{12} $ -

$ ^{22}_{12} $ Mg

$ _{10} $ 

2 0.103 ± 0.010 $ ^{23}_{11} $ Na

$ _{12} $ -

$ ^{23}_{12} $ Mg

$ _{11} $ 

1 0.042 ± 0.007 $ ^{34}_{16} $ S

$ _{18} $ -

$ ^{34}_{18} $ Ar

$ _{16} $ 

2 0.100 ± 0.005 $ ^{36}_{16} $ S

$ _{20} $ -

$ ^{36}_{20} $ Ca

$ _{16} $ 

4 0.167 ± 0.005 $ ^{35}_{17} $ Cl

$ _{18} $ -

$ ^{35}_{18} $ Ar

$ _{17} $ 

1 0.016 ± 0.020 $ ^{37}_{17} $ Cl

$ _{20} $ -

$ ^{37}_{20} $ Ca

$ _{17} $ 

3 0.079 ± 0.017 $ ^{37}_{18} $ Ar

$ _{19} $ -

$ ^{37}_{19} $ K

$ _{18} $ 

1 0.032 ± 0.011 $ ^{38}_{18} $ Ar

$ _{20} $ -

$ ^{38}_{20} $ Ca

$ _{18} $ 

2 0.062 ± 0.003 $ ^{54}_{26}{\rm{Fe}}_{28} $ -

$ ^{54}_{28}{\rm{Ni}}_{26} $ 

2 0.042 ± 0.004 Table 1. Experimental proton radii for mirror pairs.
$ R_{p}^{\rm mir} $ (Exp) is the experimental value of the difference in proton rms radii with the uncertainty including both experimental and systematic errors (all in fm).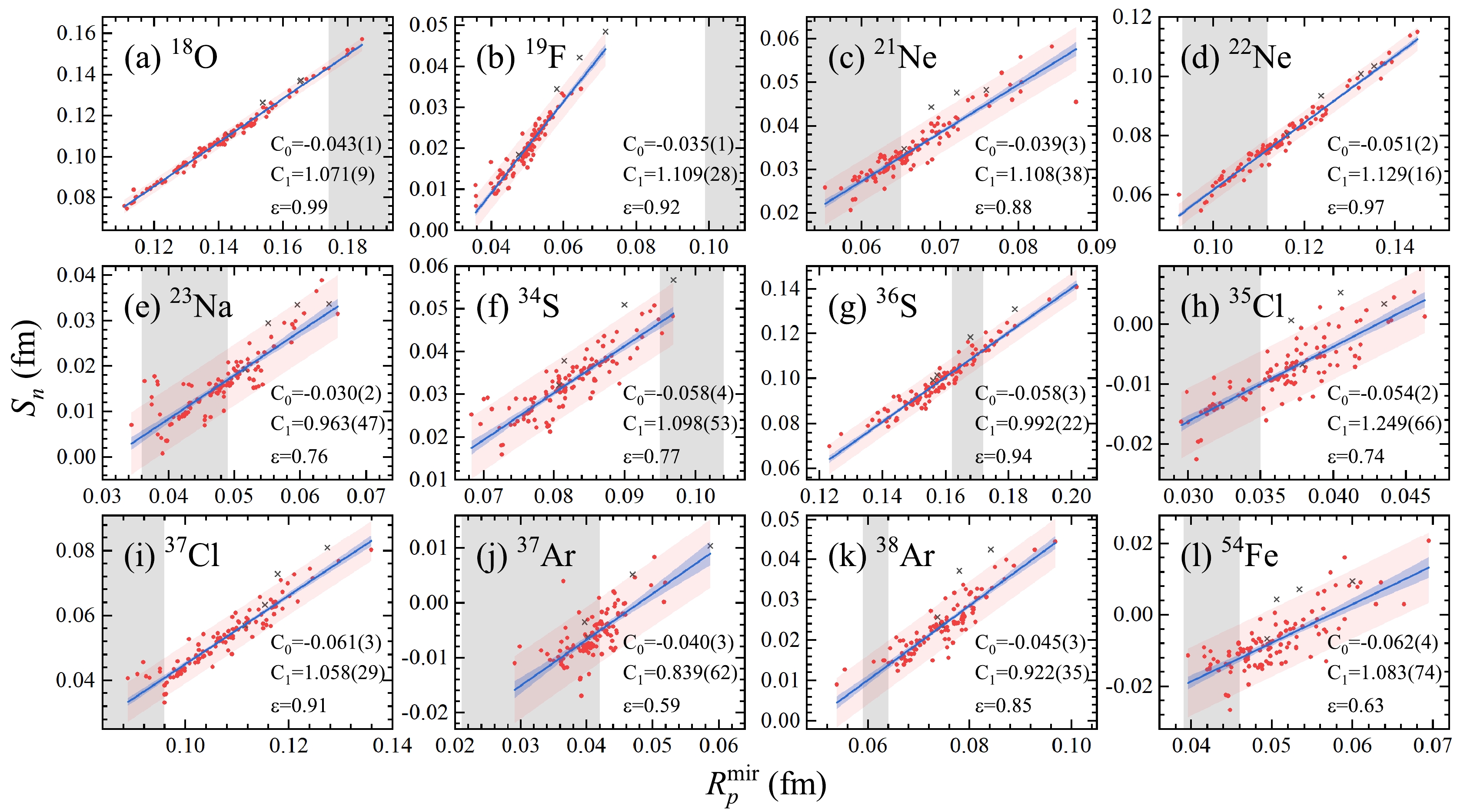
Figure 2. (color online) Correlation between
$ S_{n} $ and$ R_{p}^{\rm mir} $ for the neutron-rich nuclei$ ^{18}\text{O} $ (a),$ ^{19}\text{F} $ (b),$ ^{21}\text{Ne} $ (c),$ ^{22}\text{Ne} $ (d),$ ^{23}\text{Na} $ (e),$ ^{34}\text{S} $ (f),$ ^{36}\text{S} $ (g),$ ^{35}\text{Cl} $ (h),$ ^{37}\text{Cl} $ (i),$ ^{37}\text{Ar} $ (j),$ ^{38}\text{Ar} $ (k), and$ ^{54}\text{Fe} $ (l) calculated via the HFBTHO (including the Coulomb interaction) using 132 sets of Skyrme interaction parameters. Each point represents the result of an individual set, and the black crosses denote the results of the HFB9, UNEDF0, UNEDF1, and UNEDF2 parameterizations. The solid blue lines are the results of the linear fit. The coefficients of determination (ε), linear regression intercepts ($ C_0 $ ), and slopes ($ C_1 $ ) are also presented, and the corresponding errors are given in parentheses. The blue and red shadows are the 95$ \% $ confidence bands and 95$ \% $ prediction bands, respectively. The vertical gray shadows represent the range of experimental$ R_{p}^{\rm mir} $ .$ \begin{equation} S_{n}(^{18}\text{O}) = -0.043 + 1.071 R_{p}^{\rm mir}(^{18}\text{O}). \end{equation} $

(15) According to
$ R_{p}^{\rm mir}(^{18}\text{O}) = 0.183 \pm 0.009 \rm \ fm $ in Table 1, we can deduce$ S_{n}(^{18}\text{O}) $ to be 0.153$ \pm $ 0.010 fm, which is close to the 0.17 fm measured via$ \pi^{-} $ and$ \pi^{+} $ elastic scattering at 180 MeV in Ref. [67] and the 0.179 fm obtained at the Swiss Institute of Nuclear Research (SIN) using 163 MeV pions in Ref. [68]. Additionally, there are six sets of Skyrme parameters that give the predicted$ R_{p}^{\rm mir} $ within experimental uncertainty, namely, SKI3 [69], SKT4 [69], SKI5 [69], SKI6 [70], SK255 [71], and SK272 [71]. The corresponding L values are 100.53 MeV, 60.39 MeV, 129.33 MeV, 59.24 MeV, 95.05 MeV, and 91.67 MeV, respectively, which limits the value of L to the range 59–101 MeV.Furthermore, Figure 3 displays the range of the slope of the symmetry energy at the saturation density restricted by experimental
$ R_{p}^{\rm mir} $ for each mirror pair. The horizontal gray band shows the results from Ref. [62]. This is based on 24 new analyses of neutron star observables since GW170817, which gives a range of L of 38.7–76.7 MeV at a 68$\% $ confidence level. In addition, this is consistent with its fiducial value from surveys of over 50 earlier analyses of both terrestrial and astrophysical data within error bars. Except for the mirror pairs$ ^{19}\text{F} $ –$ ^{19}\text{Ne} $ and$ ^{37}\text{Cl} $ –$ ^{37}\text{Ca} $ , the constraints on L of the other ten pairs overlap with the gray band to some extent. As for the$ ^{19}\text{F} $ –$ ^{19}\text{Ne} $ pair, none of the 132 Skyrme parameter sets provides predictions that match the experimental data. In terms of the$ ^{37}\text{Cl} $ –$ ^{37}\text{Ca} $ pair, its constraint on L is relatively lower than the deductions in Refs. [62, 72] because Ref. [41] has noted that its experimental uncertainty is large and the combined analysis cannot be used for the evaluation of$ R_{\rm ch}(^{37}\text{Cl}) $ owing to the lack of muonic atom data and no reliable value of$ R_{\rm ch} $ . This may be why the data of$ ^{37}\text{Cl} $ –$ ^{37}\text{Ca} $ are different from the other data.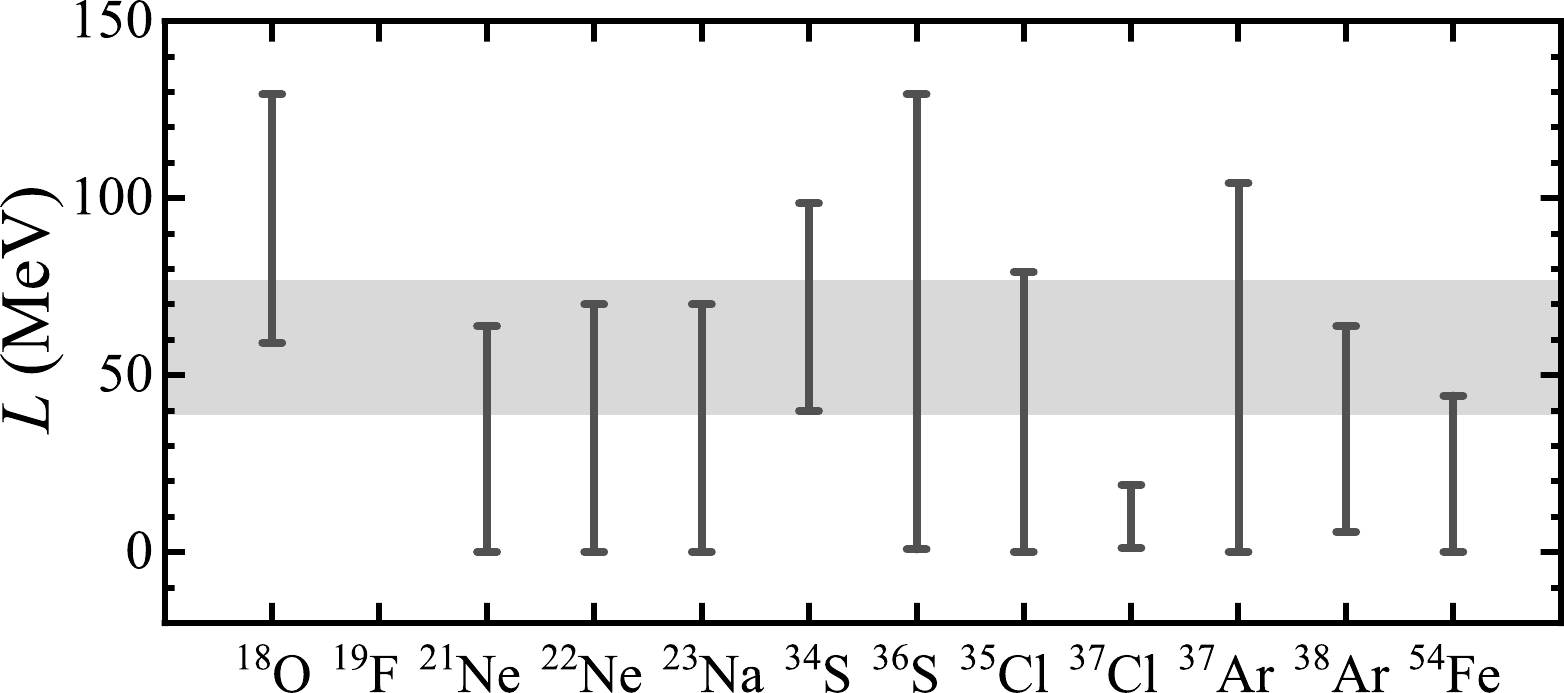
Figure 3. Constraints on the slope of the symmetry energy at the saturation density for each mirror pair. The results extracted from neutron star observables [62] are shown as a horizontal gray band.
To investigate the effects of pairing correlations and deformation, we also compare the results of the SHF model on the correlation between
$ R_{p}^{\rm mir} $ and$ S_n $ with 128 sets of Skyrme interaction parameters (without HFB9, UNEDF0, UNEDF1, and UNEDF2), as shown in Fig. 2. We summarize the values of$ C_0 $ ,$ C_1 $ , and ε with the HFBTHO and SHF solver in Table 2 to simplify the comparison. For the mirror pairs$ ^{18}\text{O} $ –$ ^{18}\text{Ne} $ and$ ^{22}\text{Ne} $ –$ ^{22}\text{Mg} $ , their linear correlations computed from SHF are as good as the previous calculations by HFBTHO. In addition, with the inclusion of pairing correlations and deformation, the correlations become stronger for most of the investigated mirror nuclei ($ ^{34}\text{S} $ –$ ^{34}\text{Ar} $ ,$ ^{36}\text{S} $ –$ ^{36}\text{Ca} $ ,$ ^{35}\text{Cl} $ –$ ^{35}\text{Ar} $ ,$ ^{37}\text{Cl} $ –$ ^{37}\text{Ca} $ ,$ ^{37}\text{Ar} $ –$ ^{37}\text{K} $ , and$ ^{38}\text{Ar} $ –$ ^{38}\text{Ca} $ ). Among them, the correlations of$ ^{35}\text{Cl} $ –$ ^{35}\text{Ar} $ ,$ ^{37}\text{Ar} $ –$ ^{37}\text{K} $ , and$ ^{38}\text{Ar} $ –$ ^{38}\text{Ca} $ are significantly enhanced. However, for the remaining pairs with small$ N/Z $ and hence small neutron-skin structure, the correlations between$ R_{p}^{\rm mir} $ and$ S_n $ are weakened to some extent after considering pairing and deformation effects. More specifically, the ε values of$ ^{19}\text{F} $ –$ ^{19}\text{Ne} $ and$ ^{21}\text{Ne} $ –$ ^{21}\text{Na} $ decrease slightly by approximately 0.05, whereas for$ ^{23}\text{Na} $ –$ ^{23}\text{Mg} $ and$ ^{54}\text{Fe} $ –$ ^{54}\text{Ni} $ , the dependence of$ S_n $ on$ R_{p}^{\rm mir} $ becomes significantly weaker, and therefore the ε obtained by HFBTHO is approximately 0.15 less than that obtained by SHF. In the case of the$ ^{19}\text{F} $ –$ ^{19}\text{Ne} $ pair, compared to the HFBTHO calculations, some SHF results have better agreement with the experimental$ R_{p}^{\rm mir} $ , as shown in Fig. 4(b). However, for most of the other mirror pairs, the HFBTHO code, with proper consideration of pairing and deformation effects, is able to provide a more appropriate description, which is evidently reflected in the mirror pairs of$ ^{21}\text{Ne} $ ,$ ^{22}\text{Ne} $ ,$ ^{23}\text{Na} $ , and$ ^{35}\text{Cl} $ . In general, both the SHF and HFBTHO solvers can give reliable descriptions of nuclei with closed shells. Nevertheless, for nuclei away from doubly magic nuclei, the HFBTHO framework, which properly considers the pairing and deformation effects through the Bogoliubov transformation, is more reasonable. Furthermore, we set the values of$V_{0,q}$ in Eq. (10) to zero to eliminate pairing energy and explore the influence of deformation separately. Most nuclei investigated in this study are around the β-stability line near the closed shell and are therefore spherical or nearly spherical. Therefore, we choose the$ ^{37}\text{Ar} $ –$ ^{37}\text{K} $ pair as an example with a relatively large deformation. As shown in Fig. 5, deformation effects may weaken the correlation between$ R_{p}^{\rm mir} $ and$ S_n $ . One possible reason is because deformation enhances the coupling of orbitals with high angular-momenta, which makes the nuclear structure more complicated.HFBTHO SHF $C_0$ 

$C_1$ 

ε $C_0$ 

$C_1$ 

ε $^{18}\text{O}$ 

$-0.043(1)$ 

1.071(9) 0.99 $-0.048(2)$ 

0.972(8) 0.99 $^{19}\text{F}$ 

$-0.035(1)$ 

1.109(28) 0.92 $-0.040(2)$ 

0.959(16) 0.96 $^{21}\text{Ne}$ 

$-0.039(3)$ 

1.108(38) 0.88 $-0.037(2)$ 

0.916(21) 0.93 $^{22}\text{Ne}$ 

$-0.051(2)$ 

1.129(16) 0.97 $-0.048(2)$ 

0.968(13) 0.97 $^{23}\text{Na}$ 

$-0.030(2)$ 

0.963(47) 0.76 $-0.043(2)$ 

0.991(29) 0.90 $^{34}\text{S}$ 

$-0.058(4)$ 

1.098(53) 0.77 $-0.047(4)$ 

0.902(47) 0.75 $^{36}\text{S}$ 

$-0.058(3)$ 

0.992(22) 0.94 $-0.055(5)$ 

0.928(29) 0.89 $^{35}\text{Cl}$ 

$-0.054(2)$ 

1.249(66) 0.74 $-0.042(4)$ 

0.819(87) 0.42 $^{37}\text{Cl}$ 

$-0.061(3)$ 

1.058(29) 0.91 $-0.049(4)$ 

0.898(35) 0.84 $^{37}\text{Ar}$ 

$-0.040(3)$ 

0.839(62) 0.59 $-0.042(4)$ 

0.785(93) 0.36 $^{38}\text{Ar}$ 

$-0.045(3)$ 

0.922(35) 0.85 $-0.048(4)$ 

0.898(57) 0.66 $^{54}\text{Fe}$ 

$-0.062(4)$ 

1.083(74) 0.63 $-0.061(2)$ 

0.993(45) 0.79 Table 2. Comparisons of the values of linear regression intercepts (
$C_0$ ), slopes ($C_1$ ), and coefficients of determination (ε) between the HFBTHO and SHF solvers. The corresponding uncertainties are given in parentheses.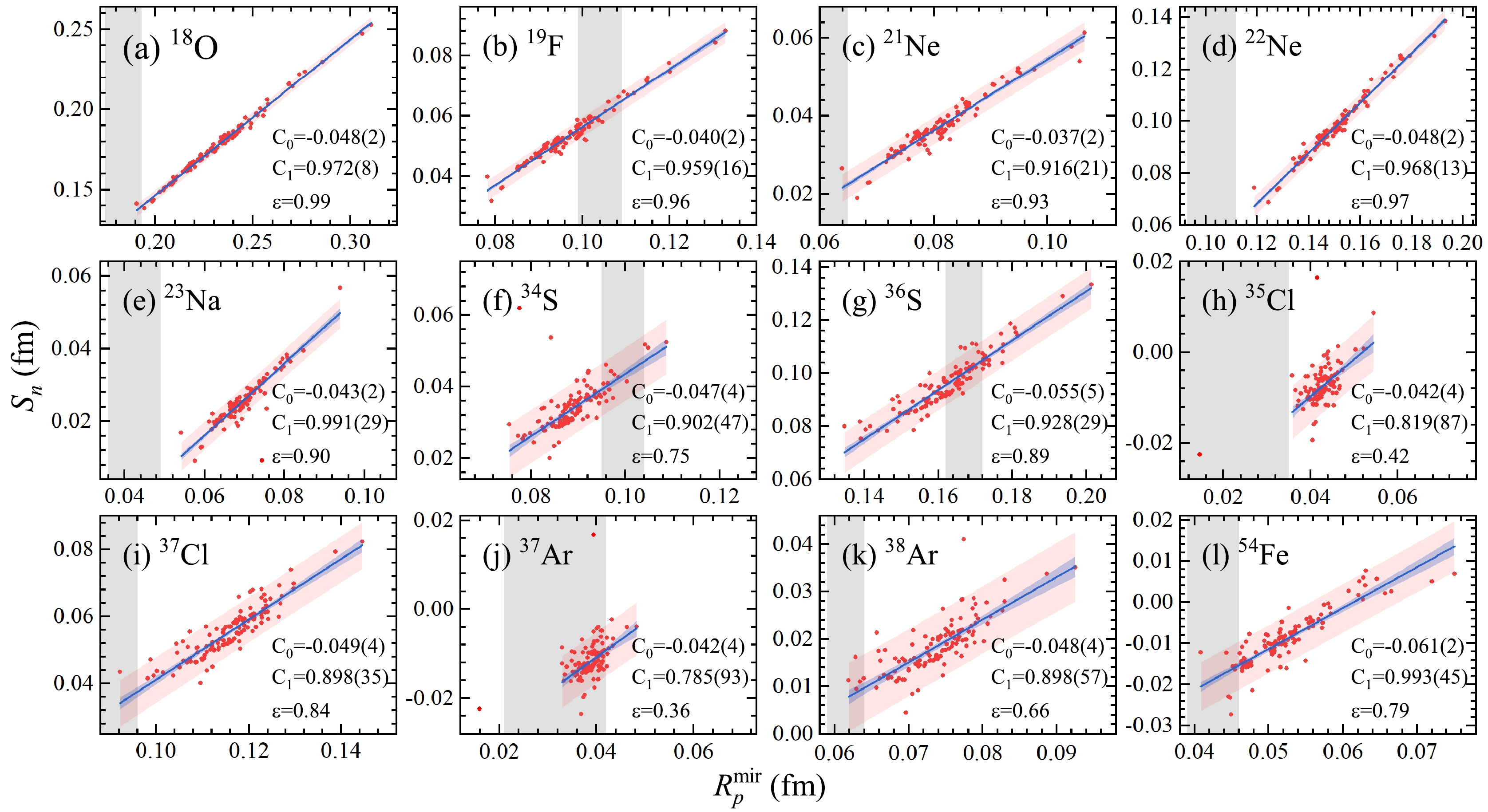
Figure 4. (color online) Same as Fig. 2, but calculated using the SHF model with 128 sets of Skyrme interaction parameters.
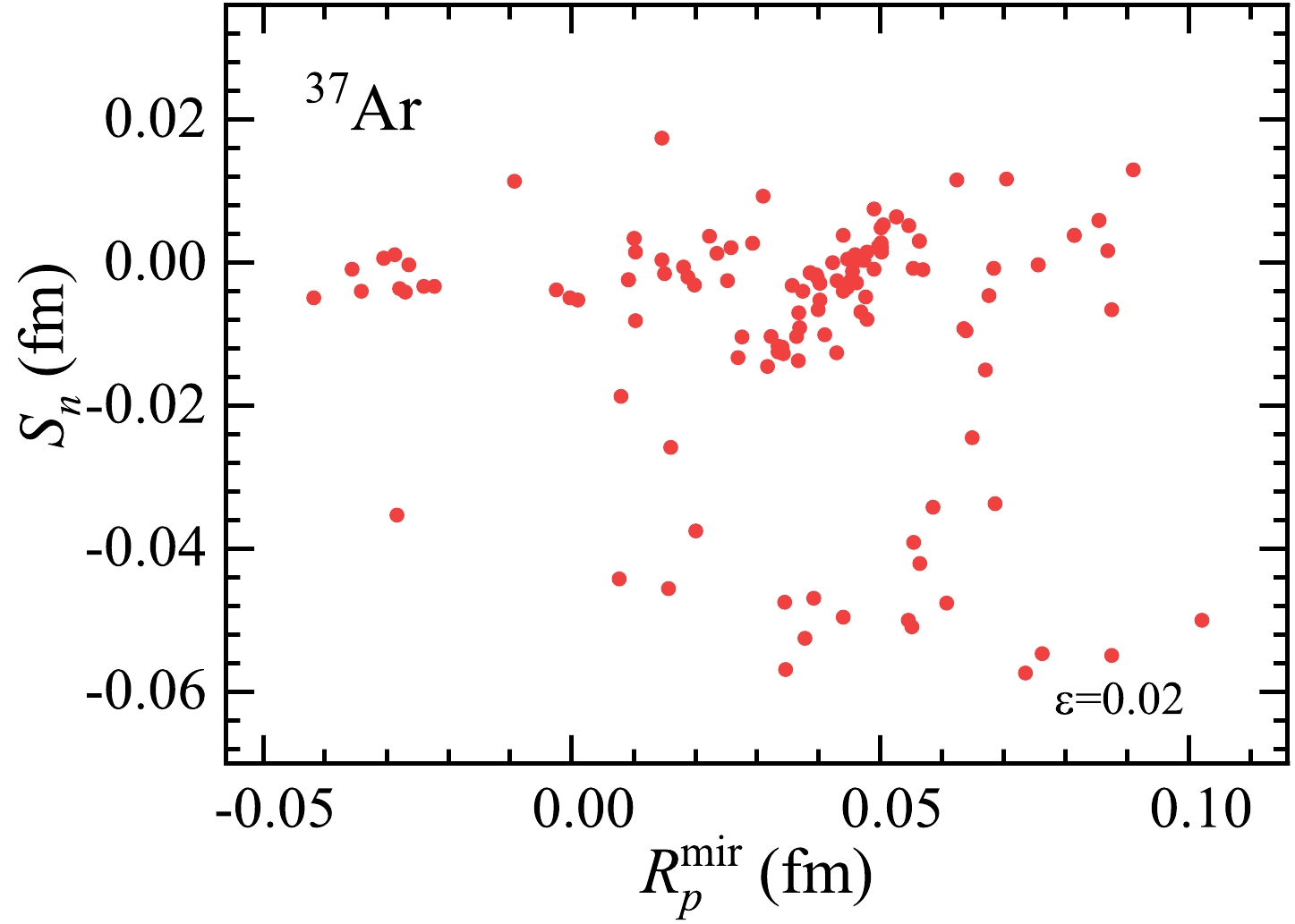
Figure 5. (color online) Correlation between
$ S_{n} $ and$ R_{p}^{\rm mir} $ of$ ^{37}\text{Ar} $ calculated via the HFBTHO (including the Coulomb interaction but without the pairing interaction) using 128 sets of Skyrme interaction parameters. Each point corresponds to a set of parameters. The coefficient of determination (ε) is also presented.The above discussion is based on nuclei with experimental
$ R_{p}^{\rm mir} $ . However, a neutron-rich nucleus with a large value of$ |N-Z| $ is more unstable, and it is difficult to measure its radius in experiments. Consequently, because of the lack of experimental data, it is difficult to extract$ S_{n} $ from the linear correlation between the neutron-skin thickness and the difference in mirror proton radii. To resolve this situation, we investigate the dependence of$ S_n $ and$ R_{p}^{\rm mir} $ for the$ N=20 $ and$ N=28 $ isotonic chains (see Fig. 6). From left to right, the mass number decreases but$ |N-Z| $ increases. This indicates that$ S_n $ of a neutron-rich nucleus is also roughly proportional to$ R_{p}^{\rm mir} $ of its isotopes. In Fig. 6, we label the values of ε next to the fitting lines and show the dependence of linear regression slopes$ C_1 $ on$ \ln(|N-Z|) $ for the isotone chains in the inserts. As$ |N-Z| $ decreases, the linear correlation becomes weaker and the value of the linear regression slope becomes larger. This indicates that the experimental data of charge radii must be more accurate to obtain the neutron-skin thickness within a certain precision. Furthermore, the linear regression slope$ C_1 $ is proportional to$ -\ln(|N-Z|) $ , as shown in inserts of Fig. 6, which can be quantitatively expressed as$C_1(N=20) = 3.324 - 1.104 \times \ln(|N-Z|)$ and$ C_1(N=28) = 5.289 - 2.065 \ln(|N-Z|) $ . The above conclusion offers the possibility of estimating$ S_n $ of a neutron-rich nucleus using$ R_{p}^{\rm mir} $ of another nucleus with the same N but a larger Z. For example, as shown in Fig. 6(a), even if there are no experimental data on the charge radii of$ ^{32}\text{Mg} $ and$ ^{32}\text{Ca} $ , the neutron-skin thickness of$ ^{32}\text{Mg} $ can be evaluated using the mirror nucleus pair$ ^{36}\text{S} $ –$ ^{36}\text{Ca} $ with the relatively good linear relation. Using$R_{p}^{\rm mir}(^{36}\text{S}) = 0.167 \pm 0.005 \rm \ fm$ in Table 1 and the result of the linear fit,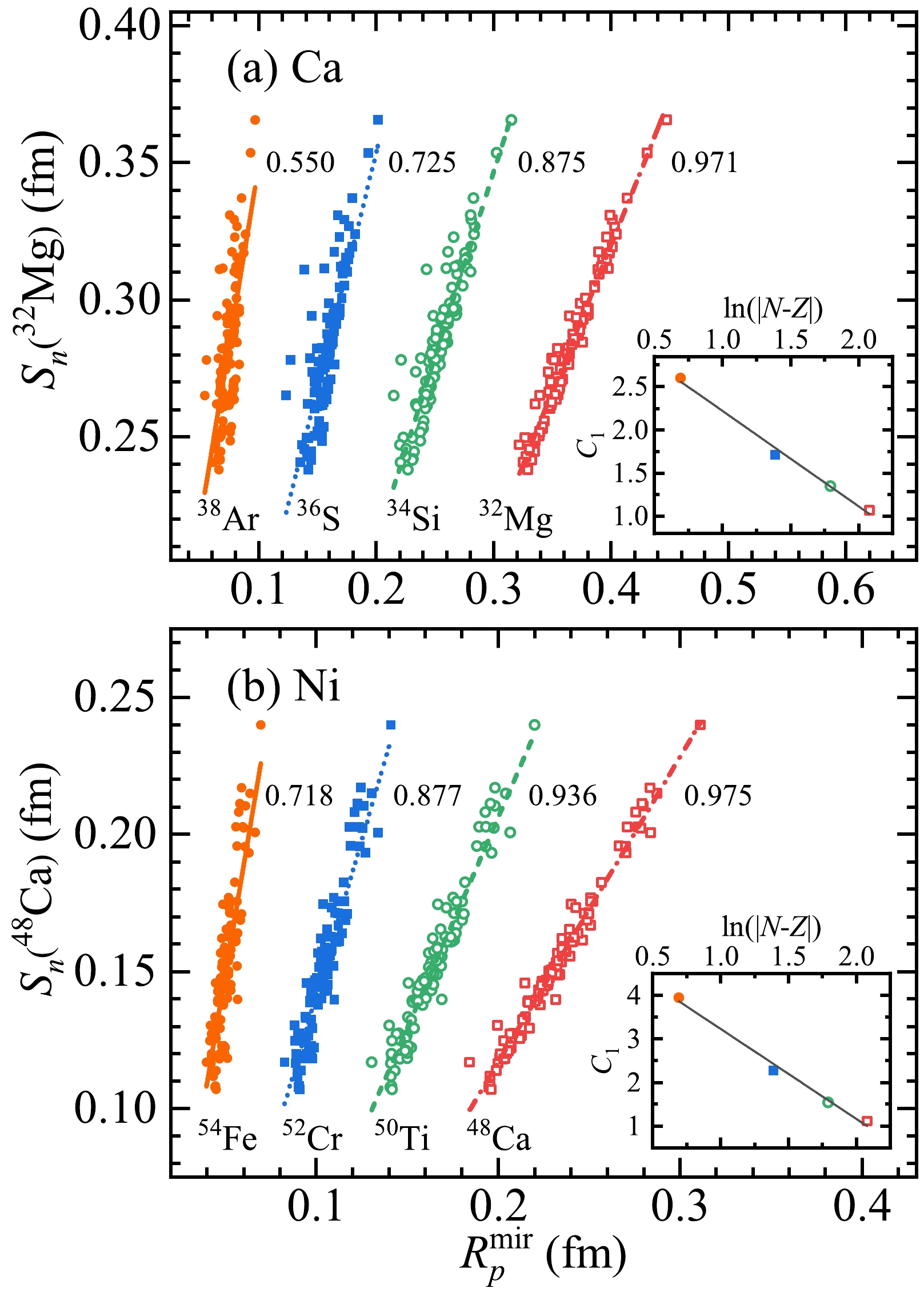
Figure 6. (color online) Correlation between the neutron-skin thickness of
$ ^{32}\text{Mg} $ and the difference in proton radii between$ N=20 $ isotones ($ A= $ 32−38) and their corresponding mirror nuclei (neutron-deficient calcium isotopes) (a). Correlation between the neutron-skin thickness of$ ^{48}\text{Ca} $ and the difference in proton radii between$ N=28 $ isotones ($ A= $ 48−54) and their corresponding mirror nuclei (neutron-deficient nickel isotopes) (b). Calculation is computed from the HFBTHO (including the Coulomb interaction) using 132 sets of Skyrme interaction parameters. The lines are the results of linear fit. The numbers next to the lines represent the coefficients of determination (ε). The inserts show the correlations between the linear regression slopes$ C_1 $ and$ \ln(|N-Z|) $ for isotone chains.$ \begin{equation} S_{n}(^{32}\text{Mg}) = 0.012 + 1.708 R_{p}^{\rm mir}(^{36}\text{S}), \end{equation} $

(16) we find that the value of
$ S_{n}(^{32}\text{Mg}) $ is 0.297$ \pm $ 0.009 fm. Similarly, using$ R_{p}^{\rm mir} $ of$ ^{54}\text{Fe} $ –$ ^{54}\text{Ni} $ ,$ S_{n}(^{48}\text{Ca}) $ = 0.119$ \pm $ 0.014 fm, which agrees with the latest measurement of the calcium radius experiments CREX giving$ S_{n}(^{48}\text{Ca}) $ = 0.121$ \pm $ 0.026(exp)$ \pm $ 0.024(model) fm [73]. It also coincides with the results from both Ref. [74] with 104 MeV α particle scattering ($ S_{\rm n}(^{48}\text{Ca}) $ = 0.17$ \pm $ 0.05 fm) and Ref. [75] with pion scattering analyzed using model densities in which the neutron matter distributions are considered to have two components corresponding to core and valence neutrons ($ S_{n}(^{48}\text{Ca}) $ = 0.11$ \pm $ 0.04 fm). -
Based on the framework of the axially deformed solutions of the Skyrme-Hartree-Fock-Bogoliubov equations with 132 sets of interaction parameters, we systematically study the neutron and proton rms radii of different nuclei to investigate the correlation between
$ S_{n} $ , L, and$ R_{p}^{\rm mir} $ . It has been confirmed that neutron-skin thickness is proportional to the difference in the proton radii of mirror nuclei, especially when not considering the Coulomb interaction. To explore the effects of pairing and deformation, we compare the results with the calculations from the SHF model with 128 sets of Skyrme interaction parameters (without HFB9, UNEDF0, UNEDF1, and UNEDF2). With the inclusion of pairing effects, the correlation between$ R_{p}^{\rm mir} $ and$ S_{n} $ become stronger for most mirror pairs, whereas deformation effects seems to weaken this correlation.By studying 12 pairs of mirror nuclei with available experimental data on charge radii, the
$ ^{18}\text{O} $ –$ ^{18}\text{Ne} $ mirror pair shows an almost ideal linear correlation between these two quantities. The neutron-skin thickness of$ ^{18}\text{O} $ is deduced to be 0.153$ \pm $ 0.010 fm, which is consistent with the experimental data. The constraints on the characteristic parameters of the EOS are also studied.Furthermore, the correlations between
$ R_{p}^{\rm mir} $ of isotones with$ N=20 $ and$ N=28 $ and$ S_{n} $ of the neutron-rich nucleus with the smallest Z are studied. With increasing$ |N-Z| $ , the linear correlation becomes stronger and the value of the linear regression slope becomes smaller, which offers a possible way of determining$ S_{n} $ of the unstable nucleus without experimental data on$ R_{p}^{\rm mir} $ . Based on this relation,$ S_{n}(^{32}\text{Mg}) $ is deduced to be 0.297$ \pm $ 0.009 fm from$ R_{p}^{\rm mir} $ of the$ ^{36}\text{S} $ –$ ^{36}\text{Ca} $ pair and$ S_{n}(^{48}\text{Ca}) $ is deduced to be 0.119$ \pm $ 0.014 fm from$ R_{p}^{\rm mir} $ of the$ ^{54}\text{Fe} $ –$ ^{54}\text{Ni} $ pair. This study reveals that the proton radii of mirror nuclei may be a good observable to extract the neutron-skin thickness of certain neutron-rich nuclei. To obtain more precise$ S_{n} $ for unstable nuclei, further theoretical study and more experimental data on the proton radii of mirror nuclei are necessary.
Investigation of the relationship between mirror proton radii and neutron-skin thickness
- Received Date: 2023-05-24
- Available Online: 2023-09-15
Abstract: Through systematic investigations using the axially deformed solutions of the Skyrme-Hartree-Fock-Bogoliubov equations with 132 sets of Skyrme interaction parameters, it is confirmed that the neutron-skin thickness (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: