-
As a strong-weak duality, the anti-de Sitter/conform field theory (AdS/CFT) correspondence reveals that certain strongly coupled theories can be described by an extra-dimensional dual theory that contains weak gravitational interactions [1−4]. In recent years, this correspondence has been proven to be an extremely useful approach to holographically study the properties of the phase transition in high temperature superconductors [5−8]. The physical picture considers an Einstein-Maxwell-scalar field theory with a negative cosmological constant. A Reissner-Norstr
$\rm \ddot{o} $ m-AdS (RN-AdS) black hole will become unstable to form scalar "hair" as the temperature of the black hole decreases. This condensation of the "hair" induces spontaneous$ U(1) $ symmetry breaking [6], which leads to a finite vacuum expectation value of the dual operator on the field theory side.On the other hand, entanglement entropy is expected to be a key quantity to characterize difficult phases and the associated phase transition in quantum many-body physics [9, 10]. Nevertheless, the investigation of entanglement entropy is extremely difficult, except for the case in
$ 1+1 $ dimensions. According to the AdS/CFT correspondence, Refs. [11, 12] present a holographic proposal for computing the entanglement entropy of a strongly interacting system from a weekly coupled gravity dual. Specifically, considering a subsystem$ \mathcal{A} $ of the total boundary system, the entanglement entropy of$ \mathcal{A} $ with its complement can be calculated from the minimal area surface$ \gamma_{\mathcal{A}} $ in the bulk with the same boundary$ \partial \mathcal{A} $ of$ \mathcal{A} $ [13, 14].$ \begin{equation} S_{\mathcal{A}}=\frac{{\rm Area}(\gamma_{\mathcal{A}})}{4G^{d+1}_N}, \end{equation} $

(1) where
$ \gamma_A $ is the d–1 dimensional static minimal surface in$ {\rm AdS}_d+1 $ , whose boundary is given by$ \partial\mathcal{A} $ , and$ G^{d+1}_N $ is the$ d+1 $ dimensional Newton constant in Einstein gravity in the AdS space. In this novel way, holographic entanglement entropy has been widely applied to explore the properties of phase transition in various aspects of holographic superconductor models with a linear Maxwell gauge field [15−28].Generalized to nonlinear electrodynamics, we first studied holographic entanglement entropy in the insulator/superconductor phase transition with Born-Infeld electrodynamics [29] and found that the the critical width of confinement/deconfinement is dependent on the Born-Infeld parameter. Interestingly, in the metal/superconductor phase transition, holographic entanglement entropy with respect to the Born-Infeld factor is not monotonic in the superconductor phase [30]. In this paper, we focus on holographic entanglement entropy with Power-Maxwell electrodynamics. The Lagrangian of the Power-Maxwell field is
$ (-F_{\mu\nu}F^{\mu\nu})^q $ . Interestingly, this Lagrangian is under the conformal transformation$ g_{\mu\nu}\rightarrow \Omega^2g_{\mu\nu} $ and$ A_\mu\rightarrow A_\mu $ . Another attractive property of Power-Maxwell electrodynamics is its conformal invariance in d-dimensional space-time as the power of the Power-Maxwell field$ q=d/4 $ . In the context of the AdS/CFT correspondence, the Power-Maxwell field has been considered as electrodynamics sours in various holographic superconductor models [31−36].Motivated by string theory, which contains gravity and requires more than four dimensions [37], the authors in Ref. [38] considered the case in a higher dimensional AdS black hole background and found that the slope of holographic entanglement entropy at the phase transition point is discontinuous and corresponds to the second order transition. The aim of this paper is to extend the exploration of holographic entanglement entropy with Power-Maxwell electrodynamics in a higher dimensional AdS black hole background and observe how the Power-Maxwell field affects the properties of the phase transition in this study.
This paper is organized as follows. In the next section, we introduce the basic field equations and boundary conditions of the Power-Maxwell holographic superconductor in n-dimension AdS black hole spacetime. In Sec. III. we study the condensation of the scalar operator and the temperature of the phase transition in the full back-reaction system. In Sec. IV, we explore the behaviors of entanglement entropy via the holographic approach. The final section is devoted to the conclusion.
-
The action of the holographic superconductor model with Power-Maxwell electrodynamics in d-dimensional AdS spacetime reads as
$ \begin{aligned}[b] S=&\int {\rm d}^{d} x\sqrt{-g}\Bigg[\frac{1}{16\pi G_N}\left(R+\frac{(d-1)(d-2)}{L^2}\right)\\&-|\nabla_\mu\psi-{\rm i}A_\mu\psi |^2-m^2|\psi|^2+b(-F_{\mu\nu}F^{\mu\nu})^q\Bigg], \end{aligned} $

(2) where g and
$ G_N $ are the determinant of the metric and the gravitational constant, respectively, R is the Ricci scalar curvature,$ -(d-1)(d-2)/2L^2 $ is the negative cosmological constant of d-dimensional AdS spacetime, where L is the AdS radius, which will be scaled to unity in our exploration, ψ represents a scalar field with mass m,$ A_\mu $ is the electromagnetic four-potential in general relativity, and$ F_{\mu\nu}=\partial_\mu A_\nu-\partial_\nu A_\mu $ . The factor b is a coupling factor and q is the power parameter of the Power-Maxwell field. In the case where$ b\rightarrow1/4 $ and$ q\rightarrow1 $ , the Power-Maxwell Lagrangian will reduce to the Maxwell case.Taking the full backreaction into consideration, the metric ansatz for the d-dimensional planar black hole is
$ \begin{eqnarray} {\rm d}s^2=-f(r){\rm e}^{-\chi(r)}{\rm d}t^{2}+\frac{{\rm d}r^2}{f(r)}+r^{2}h_{ij}{\rm d}x^{i}{\rm d}x^{j}, \end{eqnarray} $

(3) where
$ f(r) $ is the metric function and asymptotically becomes the metric of the AdS space,$ \chi(r) $ is the backreaction effect, and$h_{ij}{\rm d}x^{i}{\rm d}x^{j}$ is the line element of the (d-2)-dimensional hypersurface. Then, the Hawking temperature of the black hole is$ \begin{eqnarray} T_{H}=\frac{f^{\prime}(r_+){\rm e}^{-\chi(r_+)/2}}{4\pi}, \end{eqnarray} $

(4) where
$ r_{+} $ is the horizon of the black hole, satisfying$ f(r_+)=0 $ . For the purpose of obtaining the equations of motion of the Power-Maxwell holographic superconductor model in d-dimensional AdS black hole spacetime, we consider the matter fields in the forms [5]$ \begin{eqnarray} A_\mu {\rm d}x^\mu=\phi(r){\rm d}t,\; \; \psi=\psi(r), \end{eqnarray} $

(5) Based on the above ansatz of the gravitational field
$ g_{\mu\nu} $ , scalar field ψ, and gauge field$ A_\mu $ , the field equations can be written as$ \begin{eqnarray} && \psi^{\prime\prime}+\left(\frac{d-2}{r}-\frac{\chi^{\prime}}{2}+ \frac{f^\prime}{f}\right)\psi^\prime+ \frac{1}{f}\left(\frac{{\rm e}^{\chi}\phi^2}{f}-m^2\right) \psi=0, \end{eqnarray} $

(6) $ \begin{eqnarray} && \phi^{\prime\prime}+\left(\frac{d-2}{r(2q-1)} +\frac{\chi^{\prime}}{2}\right)\phi^\prime- \frac{(-2)^{-q}{\rm e}^{\chi(1-q)}}{bq(1-2q)}\frac{\psi^{2}\phi^{\prime(2-2q)}}{f}\phi =0, \end{eqnarray} $

(7) $ \begin{eqnarray} && \chi^{\prime}+\frac{2r}{d-2}\left(\psi^{\prime 2}+\frac{{\rm e}^{\chi}\phi^{2}\psi^{2}}{f^{2}}\right)=0, \end{eqnarray} $

(8) $ \begin{aligned}[b] & f^{\prime}-\left((d-1)r-\frac{(d-3)f}{r}\right) +\frac{r}{d-2}\Bigg[ m^{2}\psi^{2} \\&+f\left(\psi^{\prime2}+\frac{{\rm e}^{\chi}\phi^{2}\psi^{2}}{f^2}\right) +b(-2)^{q}(1-2q){\rm e}^{q\chi}\phi^{\prime2q} \Bigg]=0, \end{aligned} $

(9) where a prime denotes the derivative with respect to r, and
$ 16\pi G=1 $ is used, imposing the boundary conditions below [39]. At the horizon$ r_+ $ , one must have$ \begin{eqnarray} \phi(r)=\phi_1(r-r_+)+\phi_2(r-r_+)^2+... , \end{eqnarray} $

(10) $ \begin{eqnarray} \psi(r)=\psi_0+\psi_1(r-r_+)+\psi_2(r-r_+)^2+... , \end{eqnarray} $

(11) $ \begin{eqnarray} \chi(r)=\chi_0+\chi_1(r-r_+)+\chi_2(r-r_+)^2+... , \end{eqnarray} $

(12) $ \begin{eqnarray} f(r)=f_1(r-r_+)+f_2(r-r_+)^2+... . \end{eqnarray} $

(13) At the asymptotic AdS boundary (
$ r\rightarrow \infty $ ), the asymptotic behaviors of the solutions are$ \begin{eqnarray} \chi\rightarrow0\,, \quad f\sim r^2\, \quad \phi\sim\mu-\frac{\rho^{1/2q-1}}{r^{d-2q-1/2q-1}}\, \quad \psi\sim\frac{\psi_-}{r^{\Delta_-}}+\frac{\psi_+}{r^{\Delta_+}}\, \end{eqnarray} $

(14) with
$ \begin{equation} \Delta_\pm=\frac{1}{2}\big[(d-1)\pm\sqrt{(d-1)^2+4m^{2}}\big], \end{equation} $

(15) where μ and ρ are interpreted as the chemical potential and charge density in the dual field theory. According to AdS/CFT duality,
$ \psi_{-}=<\mathcal{O}_{-}> $ ,$ \psi_{+}=<\mathcal{O}_{+}> $ correspond to the vacuum expectation values of the dual operator$ \mathcal{O} $ . Taking the Breitenlohner-Freedman bound [40] into consideration, the mass of the scalar field must be restricted as$ m^2>-(d-1)^2/4 $ . On the other hand, requiring a finite value for the gauge field at the asymptotic boundary, the range for the factor should be$ 1/2<q<(d-1)/2 $ . -
In this section, our aim is to study the condensation of the scalar operator
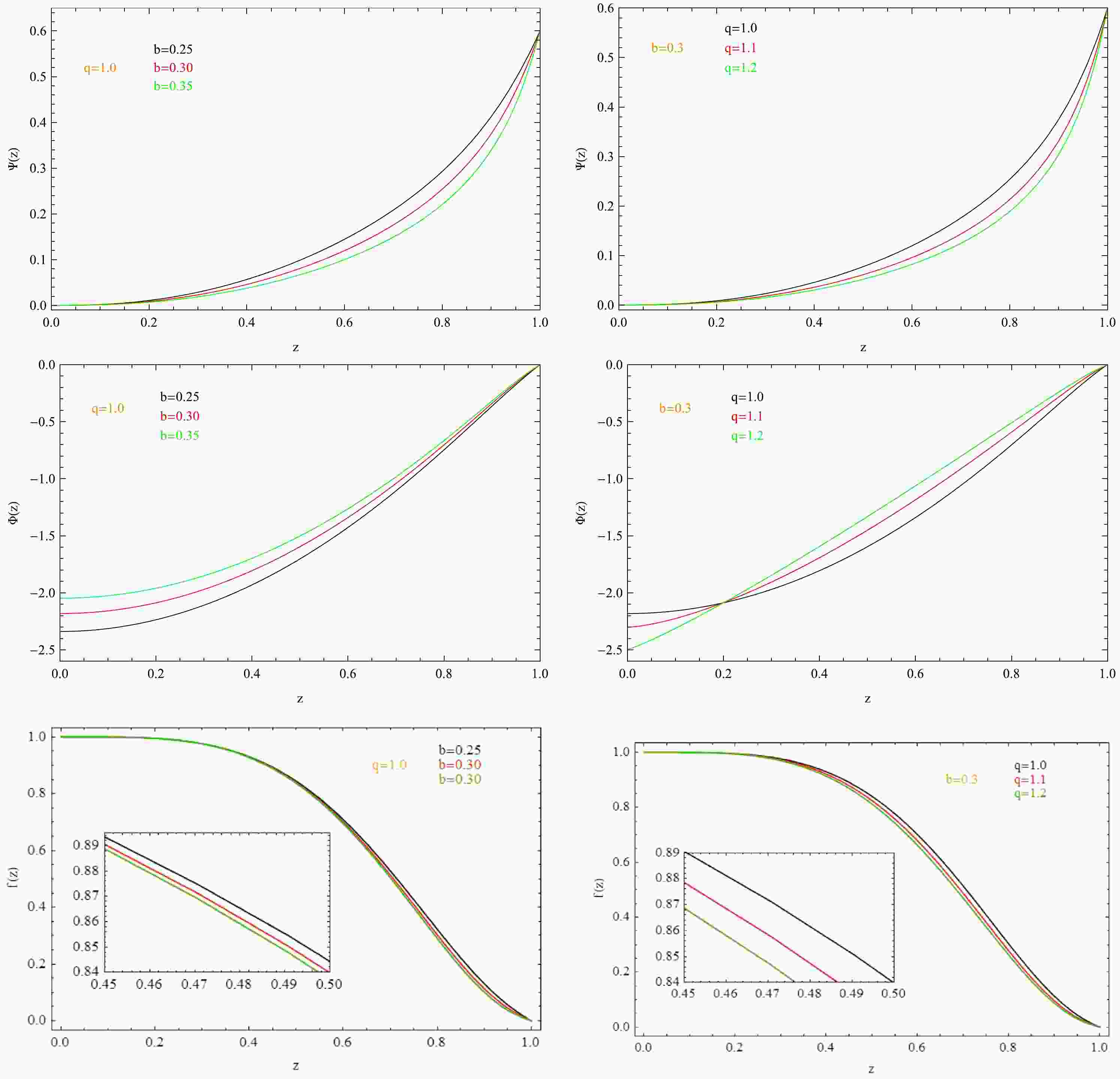
$ <\mathcal{O}_{+}> $ with the Power-Maxwell field in higher dimensional spacetime. Substituting the above boundary conditions (Eqs. (10)−(15)) into the field equations (Eqs. (6)−(9)), we can obtain the solution of the holographic superconductor using the shooting method. For concreteness, we focus on the case of$ d=5 $ ,$ m^2=-15/4 $ . To obtain a stable theory, we set$ <\mathcal{O}_{-}>=0 $ and use the scalar operator$ <\mathcal{O}_{+}> $ to describe the properties of phase transitions in the dual CFT. A typical solution with nonvanishing scalar hair for different values of the parameters b and q is presented in Fig. 1. As shown in the figure, both b and q have an influence on the scalar field$ \psi(z) $ , static electric potential$ \phi(z) $ , and metric function$ f(z) $ . The parameter b has a stronger effect on the functions$ \psi(z) $ and$ \phi(z) $ than parameter b. However, the effect of factor b on the function$ f(z) $ is weaker than that of factor q. Therefore, it is of interest to study the effect of the factors b and q on the phase transition in this system.
Figure 1. (color online) Effects of the factors b and q on the functions
$ \psi(z) $ ,$ \; \phi(z) $ , and$ f(z) $ . Here, the value of the scalar at the horizon is$ \psi_0=3/5 $ and$ z=1/r $ .In Fig. 2, we plot the property of phase transition for this physical system with different factor b values in the dimensionless quantities
$ <\mathcal{O}_{+}>^{2/5}/\rho^{1/3} $ and$ T/\rho^{1/3} $ . From the left panel, we observe that when the temperature is below a critical value$ T_c $ for a given factor b, condensation of the operator emerges, which can be identified as a superconductor phase. However, when$ T>T_c $ , the scalar field is vanishing, which indicates the metal phase. The behavior of the scalar operator$ <\mathcal{O}_{+}> $ at the phase transition point$ T_c $ is$ <\mathcal{O}_{+}>\propto (1-T/T_c)^{1/2} $ , which shows that the phase transition is second order. It is worth noting that the condensate tends to a constant as$ T\rightarrow0 $ , which is similar to BCS theory, and this behavior is also present for different parameter b values. Furthermore, the effect of the factor b on the critical temperature$ T_c $ of the phase transition is shown in the right panel. With the increase in the factor b, the critical temperature decreases, which indicates that a larger parameter b makes condensation more difficult. Interestingly, the critical temperature decreases more slowly as the factor b increases.
Figure 2. (color online) Operator
$ \langle \mathcal{O}_{+}\rangle $ as a function of the temperature T for different b (left plot). The right plot presents the behavior of the critical temperature$ T_c $ as a function of the factor b. The lines from top to bottom correspond to$b=0.25$ (black),$b=0.30$ (red), and$b=0.35$ (green).The behavior of the condensation for this physical system with different factor q values is depicted in Fig. 3. We find that the behavior of the operator
$ <\mathcal{O}_{+}> $ with respect to the temperature T for each q is similar to that of the parameter b, and the phase transition is a second-order phase transition, which is shown on the left side of Fig. 3. In the right plot, it is interesting to note that increasing q decreases the critical temperature$ T_c $ , and the critical temperature decreases more slowly. More importantly, compared with the influence of parameter b on the critical temperature, we find that parameter q has less influence on the critical temperature of the phase transition.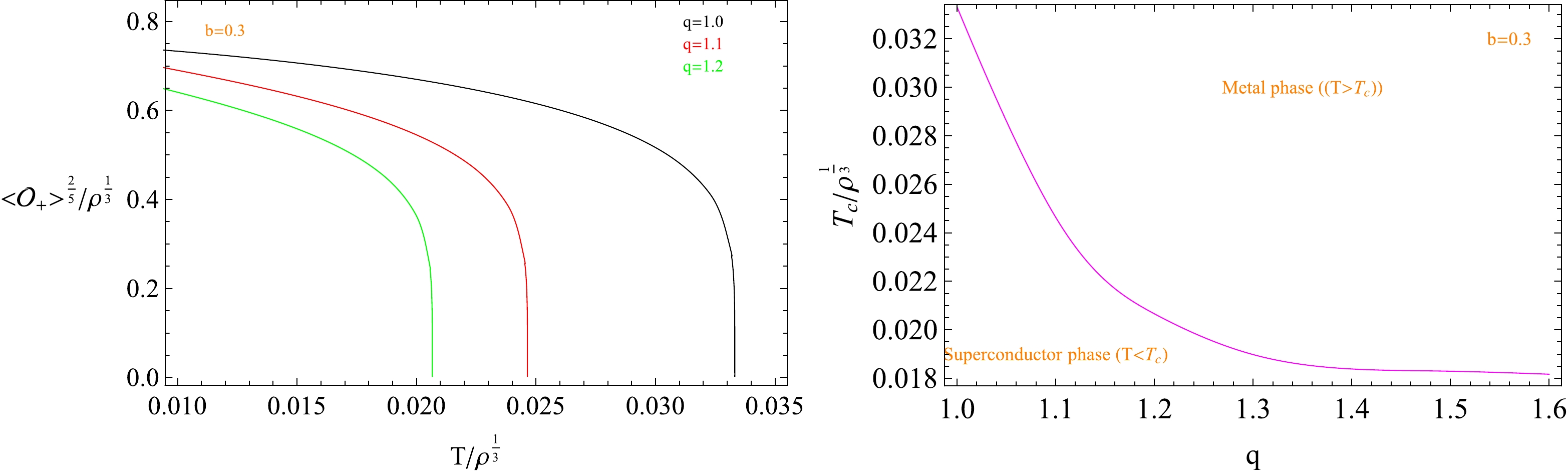
Figure 3. (color online) Operator
$ \langle \mathcal{O}_{+}\rangle $ as a function of the temperature T for different q (left plot). The right plot presents the behavior of the critical temperature$ T_c $ as a function of the factor q. The lines from top to bottom correspond to$ q=1.0 $ (black),$ q=1.1 $ (red), and$ q=1.2 $ (green). -
In this section, we further investigate the properties of the phase transition via holographic entanglement entropy in the physical holographic model. We consider a straight geometry
$ \mathcal{A} $ with a finite width$ \ell $ along the x direction and infinitely extending in the y and τ directions. The holographic dual surface$ \gamma_{\mathcal{A}} $ is defined as a three-dimensional surface,$ \begin{equation} t=0, \ \ x=x(r),\ \ -\frac{R}{2}<y< \frac{R}{2}(R\rightarrow \infty), \ \ -\frac{W}{2}< \tau < \frac{W}{2}(W\rightarrow \infty), \end{equation} $

(16) and the holographic surface
$ \gamma_{\mathcal{A}} $ in this direction starts from$ x=\dfrac{\ell}{2} $ at$ r=\dfrac{1}{\epsilon} $ , extends into the bulk until it reaches$ r=r_* $ , then returns back to the AdS boundary$ r=\dfrac{1}{\epsilon} $ at$ x=-\dfrac{\ell}{2} $ . The induced metric on the hypersurface$ \gamma_{\mathcal{A}} $ is$ \begin{equation} {\rm d}s^2 =h_{ij}{\rm d}x^i {\rm d}x^j=\left (\frac{1}{f(r)}+r^2\left (\frac{{\rm d}x}{{\rm d}r}\right )^2\right ){\rm d}r^2+r^2 {\rm d}y^2+r^2{\rm d}\tau^2. \end{equation} $

(17) According to the RT formula, Eq. (1), the entanglement entropy in the strip geometry can be obtained as
$ \begin{equation} S_\mathcal{A}[x]=\frac{RW}{2G_5}\int_{r_*}^{\frac{1}{\epsilon}} r^2\sqrt{\frac{1}{f(r)}+r^2({\rm d}x/{\rm d}r)^2}{\rm d}r, \end{equation} $

(18) where
$ r=\dfrac{1}{\epsilon} $ is the UV cutoff. Noting that the above expression can be treated as a Lagrangian with the x direction thought of as time, the equation of motion for the minimal surface from Eq. (18) is given by$ \begin{equation} \frac{r^4({\rm d}x/{\rm d}r)\sqrt{f(r)}}{\sqrt{1+r^2f(r)({\rm d}x/{\rm d}r)^2}}=r_*^3 . \end{equation} $

(19) Considering that the surface is smooth at
$ r=r_* $ ,${\rm d}x/{\rm d}r|_{r=r_*}=0$ . Using the variable$ z=1/r $ , the width of the belt geometry$ \ell $ in terms of z is$ \begin{eqnarray} \frac{\ell}{2}=\int^{z_{*}}_{\epsilon}{\rm d}z\frac{z^{3}}{\sqrt{(z^{6}_{*}-z^{6})z^{2}f(z)}}, \end{eqnarray} $

(20) and the holographic entanglement entropy in the z-coordinate can be rewritten as
$ \begin{eqnarray} S_\mathcal{A}=\frac{R W}{2G_5}\int^{z_{*}}_{\epsilon}{\rm d}z\frac{z_{*}^{3}}{z^{2}} \frac{1}{\sqrt{(z^{6}_{*}-z^{6})z^{2}f(z)}} =\frac{R W}{4G_5}\left(\frac{1}{\epsilon^2}+s\right). \end{eqnarray} $

(21) Note that the divergent part of
$ S_\mathcal{A} $ , known as the area law, will not change because this part is only sensitive to UV quantities [11, 12]. The second term s is independent of the cutoff and is finite; hence, it is a physical quantity. Notice that the result in Eq. (21) does not include a subleading divergent term. This is because the subsystem A has straight belt geometry [12]. In this study, we focus on the holographic entanglement entropy s in the holographic superconductor model and explore its dependence on the temperature T, coupling parameter b, Power-Maxwell factor b, and belt width$ \ell $ .The behaviors of s with respect to the temperature for various factors b and q with the dimensionless quantities
$ s/ \rho^{\frac{1}{3}},\ \ell \rho^{\frac{1}{3}}, \ T/\rho^{\frac{1}{3}} $ are presented in Fig. 4. From the left-hand plot, we observe that the values of the critical point$ T_c $ at the phase transition for different b, represented by vertical dashed lines, are the same as the values obtained by the scalar operator. The entanglement entropy at the phase transition point is continuous, but its slope has a jump, which means that the phase transition here is of the second order. With the increase in the parameter b, the entanglement entropy at$ T_c $ increases. Note that the entanglement entropy in the superconductor phase, represented by solid lines in the figure, is smaller than that in the metal phase, which is represented by dotted solid lines. This implies some type of new degree of freedom similar to that a Cooper pair would form after the phase transition. As shown on the right of Fig. 4, the influence of the factor q on the holographic entanglement entropy s is similar to the case of the factor b. Interestingly, the effect of the factor q on the holographic entanglement entropy is weaker than that of the parameter b.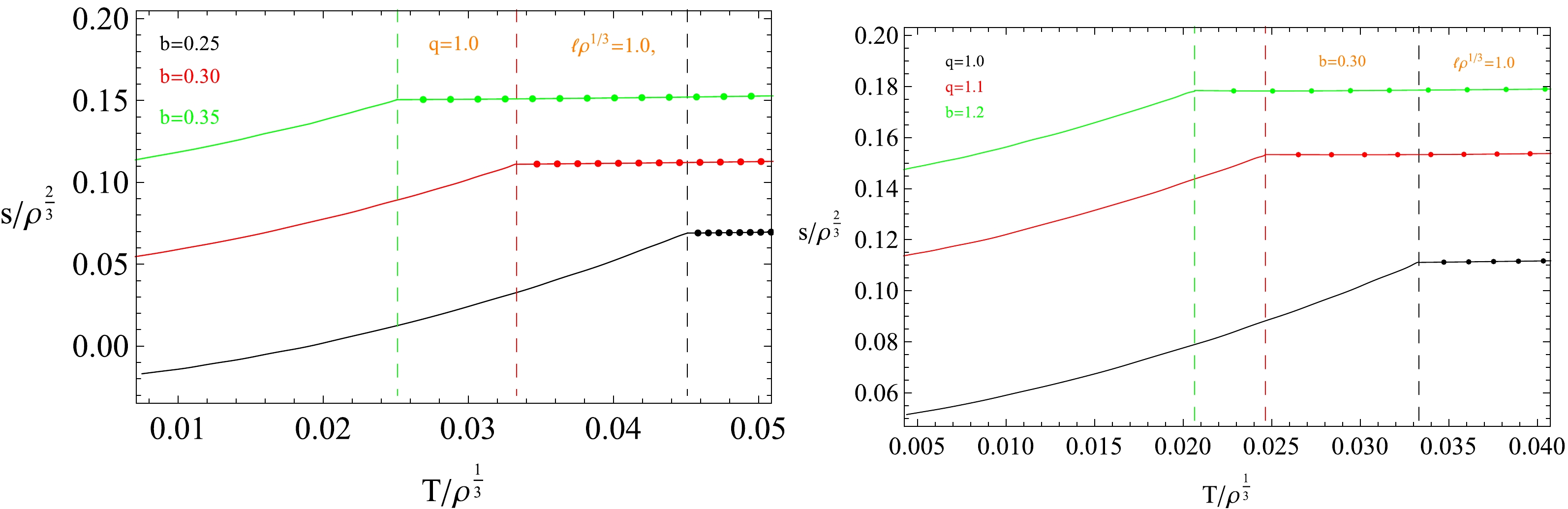
Figure 4. (color online) Holographic entanglement entropy s as a function of the temperature T for different factors.
By comparing the critical temperature of the scalar operator with that of holographic entanglement entropy in Table 1, we find that the values of the critical temperature
$ T_c $ calculated from the condensation of the scalar operators are equal to the results obtained from the behaviors of holographic entanglement entropy. In other words, entanglement entropy is a good probe for studying the phase transition point.$ b \Big\backslash T_c $ 

$ q=1.0 $ 

$ b=0.3 $ 

$ q \Big\backslash T_c $ 

$<\mathcal{O}_{+}> $ 

$\rm HEE$ 

$<\mathcal{O}_{+}> $ 

$\rm HEE$ 

$ 0.25 $ 

0.04510 $ \rho^{\frac{1}{3}} $ 

0.04510 $ \rho^{\frac{1}{3}} $ 

0.03332 $ \rho^{\frac{1}{3}} $ 

0.03332 $ \rho^{\frac{1}{3}} $ 

$ 1.0 $ 

$ 0.3 $ 

0.03332 $ \rho^{\frac{1}{3}} $ 

0.03332 $ \rho^{\frac{1}{3}} $ 

0.020464 $ \rho^{\frac{1}{3}} $ 

0.02464 $ \rho^{\frac{1}{3}} $ 

$ 1.1 $ 

$ 0.4 $ 

0.01935 $ \rho^{\frac{1}{3}} $ 

0.01935 $ \rho^{\frac{1}{3}} $ 

0.02066 $ \rho^{\frac{1}{3}} $ 

0.02066 $ \rho^{\frac{1}{3}} $ 

$ 1.2 $ 

$ 0.5 $ 

0.012298 $ \rho^{\frac{1}{3}} $ 

0.012298 $ \rho^{\frac{1}{3}} $ 

0.01898 $ \rho^{\frac{1}{3}} $ 

0.01898 $ \rho^{\frac{1}{3}} $ 

$ 1.3 $ 

$ 0.6 $ 

0.008449 $ \rho^{\frac{1}{3}} $ 

0.008449 $ \rho^{\frac{1}{3}} $ 

0.01838 $ \rho^{\frac{1}{3}} $ 

0.01838 $ \rho^{\frac{1}{3}} $ 

$ 1.4 $ 

Table 1. Critical temperature
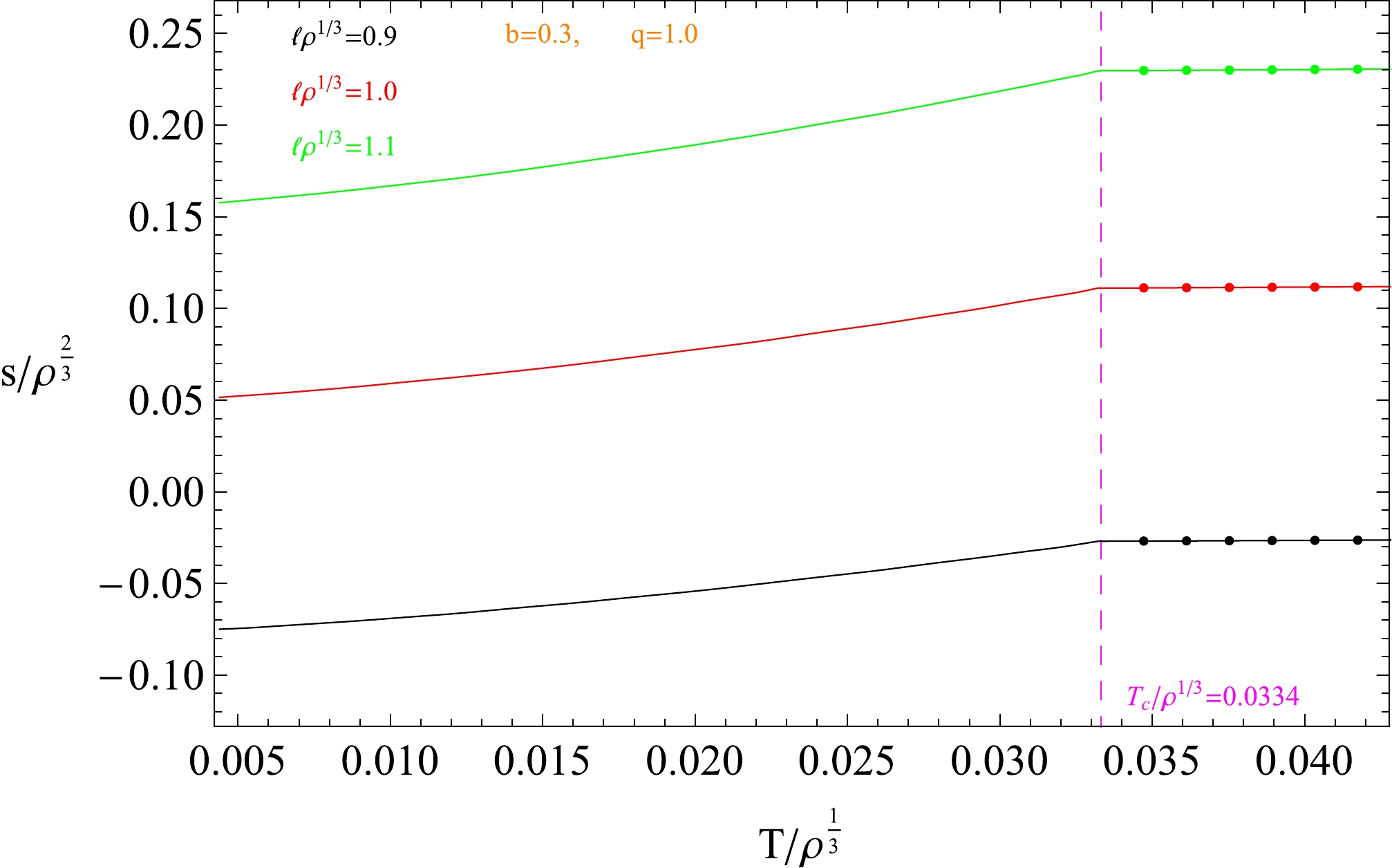
$ T_c $ obtained via the condensation of the scalar operator ($ <\mathcal{O}_{+}> $ ) and from the behaviors of holographic entanglement entropy (HEE) for different parameters b and q.Furthermore, the effect of the belt on the entanglement entropy is shown in Fig. 5. The entanglement entropy in the superconductor and metal phases increases as the width of the geometry
$ \ell $ increases. Clearly, the value of the temperature at the phase transition point is independent of the width$ \ell $ of the geometric model. -
In this study, we investigate a holographic superconductor with Power-Maxwell electrodynamics in higher dimensional AdS black hole spacetime using the scalar operator and entanglement entropy. According to the behavior of the scalar operator in this physical model, the scalar operator condensates at the critical temperature point
$ T_c $ , which indicates that phase transition occurs. Furthermore, the phase transition is of a second order. With the increase in the factors b and q, the critical temperature decreases. In other words, larger values of the parameters b and q make the phase transition more difficult. We also find that the critical temperature decreases more slowly as the parameters increase. From the holographic study of entanglement entropy, we note that entanglement entropy at the critical point is continuous, but its slope is discontinuous for various factors, and the value of the critical point is consistent with the phase transition temperature obtained by the scalar operator. In other words, entanglement entropy is a powerful tool to search for the phase transition point and the order of phase transition. Considering the effect of the coupling parameter b, Power-Maxwell factor q, and belt width$ \ell $ on entanglement entropy, both in the superconductor and metal phases, the entanglement entropy increases as the parameters increase.
Holographic entanglement entropy with Power-Maxwell electrodynamics in higher dimensional AdS black hole spacetime
- Received Date: 2023-05-09
- Available Online: 2023-11-15
Abstract: We investigate the behaviors of the scalar operator and holographic entanglement entropy in the metal/superconductor phase transition with Power-Maxwell electrodynamics in a higher dimensional background away from the probe limit. We observe that the larger parameters b and q make the condensation of the scalar operator more difficult, and the critical temperature decreases more slowly as the factors increase. In the belt geometry, the value of the entanglement entropy in the metal and superconductor phases is not only related to the the strength of the Power-Maxwell field but also to the width of the strip geometry. At the phase transition point, the discontinuous slope of entanglement entropy is universal for different model factors. It turns out that holographic entanglement entropy is a powerful tool to probe the properties of the phase transition in this holographic superconductor model.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: