Gauss-Bonnet solution with a cloud of strings in de Sitter and anti-de Sitter space

General relativity (GR) [1] is the simplest and most successful theory of gravitation. It was proposed over a century ago and has been confirmed by many experiments [2]. However, there are still several unknown issues such as dark energy and dark matter, which indicate that GR may not yet be perfect. These issues strongly motivate us to consider the possibility of a modified gravity theory beyond GR. Moreover, as demanded by string theory [3], black holes in higher dimensions must have higher curvature corrections. In the last decades, many possible modified gravity schemes have been proposed [4]; however, in most of these theories, higher derivative equations must usually be solved. One solution is to consider a specific combination of the higher-order polynomial of the Riemann tensor such that the equation of motion remains as two derivatives. The simplest choice of this type of theory is the famous Gauss-Bonnet gravity [5]. In addition, a quadratic Gauss-Bonnet term also appears as the one-loop correction of heterotic string theory [6].

A recent theoretical study proposed a scenario in which the fundamental building blocks of our Universe are extended objects rather than point objects [7]. The most natural and popular candidate is the one-dimensional string object [8, 9]. A cloud of strings behaves like a pressureless perfect fluid, and its one-dimensional character means that the energy-momentum tensor only has a spacial component. With this, many exact black hole solutions have been obtained. Letelier [8] first presented a cloud of strings model extension of the Schwarzschild black hole. In this solution, the Schwarzschild radius of the black hole is thereby enlarged as $ r_h=\dfrac{2M}{1-a} $, where a is the string cloud parameter. This solution may have several astrophysical consequences [10]. Recently, many related studies have considered the string cloud as a fluid in the spacetime background and constructed relevant exact solutions. For example, except in GR, a black hole solution with a cloud of strings in four-dimensional Einstein-Gauss-Bonnet gravity was constructed in [11]. Ghosh et al. [12] discussed radiating black holes with a cloud of strings in second and third-order Lovelock gravity. Later, Rodrigues and Vieira constructed the Bardeen solution with a cloud of strings and studied its thermodynamic properties [13].

However, in most of these studies, only black hole solutions without the cosmological constant were considered. Note that our current Universe is undergoing accelerating expansion, which is known as the dark energy issue. The simplest explanation for current cosmic acceleration is a nonzero positive cosmological constant [14, 15]. Moreover, the AdS/CFT correspondence usually requires us to consider a black hole solution with a negative cosmological constant. In addition, AdS black holes usually possess a considerably richer thermodynamical phase structure; for instance, the well known Hawking-Page phase transition can occur for AdS black holes [16]. Given the above motivations, we investigate a black hole in a cloud of strings background with a cosmological constant in Gauss-Bonnet gravity in higher dimensions. Both the uncharged and charged cases are considered, and we investigate the thermodynamic properties of these black holes in the presence of a cloud of strings. To enhance the readability of the paper, we only consider the positive cosmological constant (dS) solutions in the main text and present the negative cosmological constant (AdS) solutions in the appendix.

The remainder of this paper is organized as follows. In Sec. II, we solve the field equation and obtain (charged) black hole solutions coupled with a cloud of strings and the cosmological constant. In Sec. III, we explore the thermodynamic properties, such as phase transitions and critical phenomena, of black holes with and without charge in dS space. Finally, we summarize our results in Sec. IV. In addition, in the appendix, we briefly discuss the black hole solutions in AdS space. We adopt the units $ 8 \pi G=1 $ and $ \hbar = c = 1 $.

In this section, we derive Gauss-Bonnet charged black hole solutions in dS spacetime surrounded by a cloud of strings (SC). The action of Gauss-Bonnet gravity with the cosmological constant Λ coupled to the Maxwell electrodynamics (ME) and a cloud of strings reads as

where g is the metric determinant, R denotes the Einstein term, and $ L_e(F^2) $ represents the ME Lagrangian with the scalar $ F = F_{\mu\nu}F^{\mu\nu} $, where $ F_{\mu\nu}=A_{\mu;\nu}-A_{\nu;\mu} $. Moreover, α is the Gauss-Bonnet coefficient, and $ L_{\rm GB} $ denotes the second-order Lovelock (Gauss-Bonnet) term, which is generally written as

and $S_{\rm SC}$ is the action of a cloud of strings. The equations of motion can be obtained using $ \dfrac{\delta S}{\delta g_{\mu\nu}} = 0 $ and $ \dfrac{\delta S}{\delta A_\mu} = 0 $, which in our case are

where $ G_{\mu\nu} $ is the Einstein tensor, and $ H_{\mu\nu} $ is the tensor related to the Gauss-Bonnet term, defined as

$ T_{\mu\nu} $ is the total energy-momentum tensor. Hence, Eq. (3) reads as

Consider the following spherically symmetric metric ansatz in the D dimension:

where $ \gamma_{ij} $ is the metric of a $ D-2 $ dimensional constant curvature space $ k = 1 $. For the sake of convenience, we use $ n = D-2 $ instead of the dimension D and define

The cosmological constant is positive, which indicates that the space is de Sitter. Now, Eq. (3) can be expressed as

This differential equation is integrable, which can be written as

By integrating the differential equation, we obtain the general metric function of a Gauss-Bonnet black hole [17]:

The sign $ \pm $ before the square root refers to the two different branches of metric solutions, and [18] proves that the positive branch is unstable and the corresponding graviton has negative mass. Therefore, we only consider the negative branch. μ is a integration constant related to the ADM mass via

where $ V_n $ is the volume of the n-dimensional unit sphere. $ {\cal{T}} $ is associated with the total energy-momentum tensor via

where an arbitrary constant c leads to the integration constant μ. Next, we discuss the energy-momentum tensor of the electromagnetic field and a cloud of strings.

Following the theory of a cloud of strings, the action of a cloud of strings is called Nambu-Goto action, which is given by [8, 11, 13, 19]

where m is a positive constant related to the string, and $ \lambda^0 $ and $ \lambda^1 $ are timelike and spacelike parameters, respectively. The string world sheet Σ is determined using

Here, we introduce the bivector associated with the string world sheet:

where $ \epsilon^{AB} $ is the two-dimensional Levi-Civita symbol normalized as $ \epsilon^{01} = -\epsilon^{10} = 1 $. Within this setup, the Lagrangian density can be written as

Therefore, the energy-momentum tensor for one string is

Replacing m with the proper density ρ, the energy-momentum tensor for a cloud of strings reads as [8, 11, 13, 19]

The quantities $ \rho(-\gamma)^{1/2} $, $ \rho\Sigma^{\mu\nu} $, and $ \Sigma^{\mu\nu}/(-\gamma)^{1/2} $ are manifestly gauge-invariant. The conditions for $ \Sigma^{\mu\nu} $ to be a surface forming bivector are

where the square bracket $ [\alpha\beta\gamma] $ indicates anti-symmetrization of the indices. In conjunction with definition of the bivector (17), we get

The combination the above identity with the conservation of energy-momentum tensor $ T^{\mu\nu}_{;\nu} = 0 $ leads to

Under the static spherically symmetric condition, the only nonzero component of the bivector Σ is $ \Sigma^{01} = -\Sigma^{10} $, and hence $T^0_0({\rm SC}) = T^1_1({\rm SC}) = -\rho\Sigma^{01}$. Together with Eq. (24), we obtain $ \partial_r(\sqrt{r^{n}T^0_0}) = 0 $, which implies

where a is the string parameter, a positive integration constant that satisfies $ (-\gamma)^{1/2}\rho = a/r^{n} $. In addition, a should be less than one for the model to have a clear meaning [11, 19]. From (13) and (6), we have

As for the electric term, the gauge field is $ A_\mu = \phi(r)\delta_\mu^t $ under the static condition [20, 21], where $ \phi(r) $ denotes the electric potential, and the electric field is $ E(r) = -\phi'(r) $, with ' denoting the derivative with respect to r. According to ME, the field-strength is

Simple calculation shows that $ F^2 = -2E^2 $, and from Eq. (4), we get

which results in the generalized Gauss law

where q is a parameter associated with charge via $ Q^2 = 8V_n^2q^2 $ [22]. Based on the Maxwell electric Lagrangian $ {\cal{L}} = -F^2 $, the Maxwell electric energy-momentum tensor takes the form

Now, from Eq. (29), we can obtain

The energy-momentum tensor then reads as

Therefore,

Now, we are able to obtain the metric of Gauss-Bonnet charged black holes with the cosmological constant in the presence of a cloud of strings:

In this study, we keep to the common case $ k = 1 $ in dS space; thus, the sign before $ l^2 $ is positive, and we briefly discuss the AdS space case in the appendix.

In this section, we first discuss the event horizons and thermodynamics of dS black holes without charge [23, 24]. We consider the case with charge in the second part. In the case without charge, the metric function (34) reads as

Here, $ \tilde{\alpha} = \alpha(n-1)(n-2) $. Note that the event horizon is located at $ f(r_+)=0 $. Although we are not able to obtain an analytical expression for $ r_+ $, we can show the behavior of $ f(r) $ as a function of r in Fig. 1 and search for zero points.

Figure 1.  (color online) Plots of the metric function $ f(r) $ as a function of radius, with the values: $ \alpha=1 $, $ l = 1 $, and $ \mu=1 $. Left: Case in the absence of a cloud of strings, $ a=0 $; Right: Case in the presence of a cloud of strings and $ a=0.4 $.

As shown in Fig. 1, in five dimensions, there is one zero point in the case without strings. When there are string clouds involved, there are two zero points. In other dimensions, two horizons exist if strings are not considered; however, when string clouds exist, the event horizons disappear. That is, the involvement of the strings in space-time may cause black holes to disappear. In the following, we consider the presence of black holes and discuss the thermodynamic properties of black holes. We can express the ADM mass of a black hole in terms of the horizon radius $ r_+ $ as

Evidently, a cloud of strings provides a source of negative mass, which may lead to instability of the system. Based on black hole thermodynamics, the Hawking temperature T is

This expression is complicated and hence analytical studies are rarely performed. In the following, we use numerical analysis to explore the thermodynamic properties of dS black holes. First, we plot a $ T-r_+ $ diagram.

Note that negative temperature indicates an unstable state. From Fig. 2, we can see that strings may cause the temperature to change from positive to negative in the extremely small radius region. In other words, the cloud of strings makes the region partially unstable. Moreover, the first law of thermodynamics of the black hole ${\rm d} M = T{\rm d}S$ indicates that the entropy S is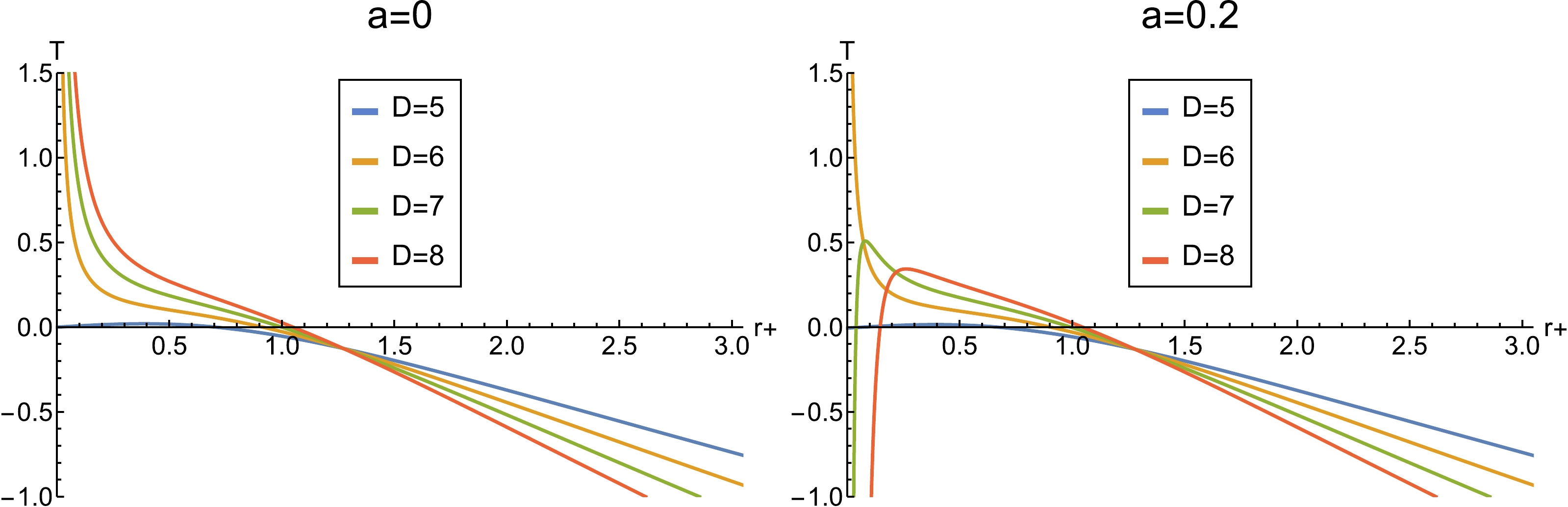

Figure 2.  (color online) Graphic representation of Hawking temperature vs horizon radius with the values $ \alpha=1 $ and $ l = 1 $. Left: Case in the absence of a cloud of strings, $ a=0 $; Right: Case in the presence of a cloud of strings and $ a=0.2 $.

which is independent of the string parameter a.

Thermodynamical stability includes local and global stability [25, 26], mainly determined by the behavior of the heat capacity and free energy, respectively. A negative heat capacity indicates that the black hole is locally unstable. Divergence with a change in sign in the heat capacity represents a second order phase transition, in which the system changes from instability (stability) to stability (instability). The heat capacity of a black hole is given by

With the help of Eqs. (36) and (37), in our case, it reads as

where

and

Then, we plot a $ C-r_+ $ diagram with different dimensions and parameter values.

As shown in Fig. 3, there is initially no phase transition in seven and eight dimensions; however, with the interference of the strings, new phase transitions occur. We can simply conclude that the cloud of strings has a significant impact on the heat capacity, that is, it increases the number of phase transitions. Moreover, we are interested in the global stability in dS space-time, and a positive free energy indicates that the black hole is globally unstable. Free energy is given by

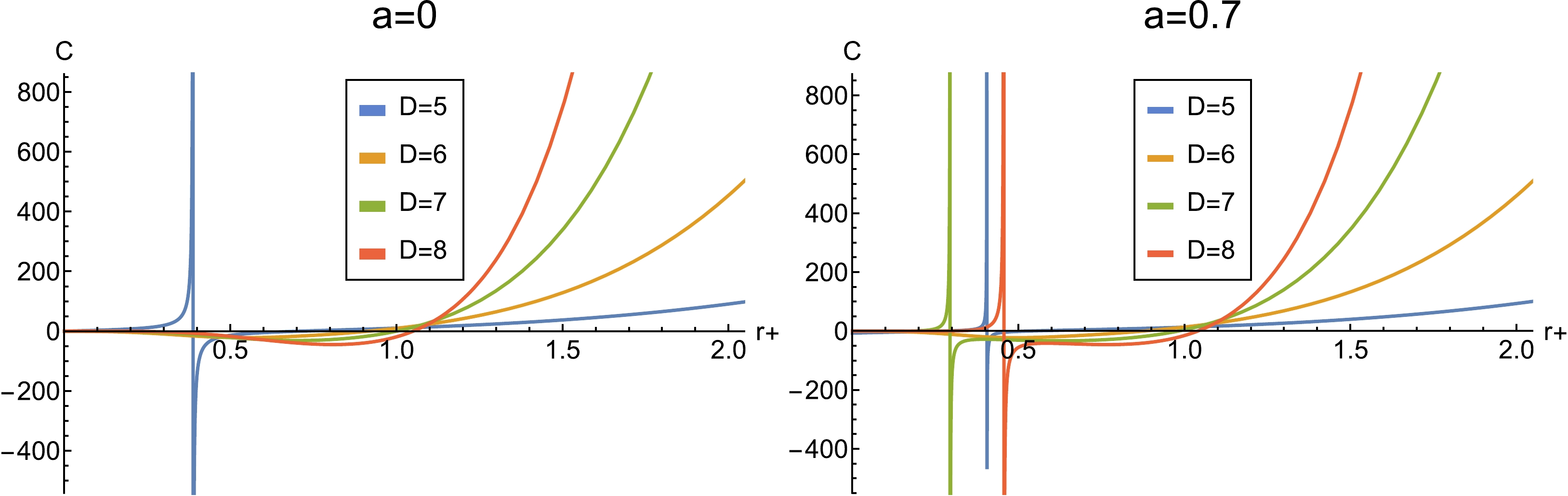
Figure 3.  (color online) Graphic representation of heat capacity C vs horizon radius $ r_+ $ with the values $ \alpha=1 $ and $ l = 1 $. Left: Case in the absence of a cloud of strings, $ a=0 $; Right: Case in the presence of a cloud of strings and $ a=0.5 $.

Here,

We plot the $ F-r_+ $ diagram as follows:

As shown in Fig. 4, the black hole is always globally unstable, with or without a cloud of strings.

Figure 4.  (color online) Graphic representation of free energy vs horizon radius with the values $ \alpha=1 $ and $ l = 1 $. Left: Case in the absence of a cloud of strings, $ a=0 $; Right: Case in the presence of a cloud of strings and $ a=0.6 $.

Thermodynamic pressure P is thought to be associated with the cosmological constant via [27, 28]

and the volume reads as

This is the exact thermodynamic volume of the system; thus, it is different from the geometric volume of the black hole. From Eqs. (42) and (37), we can write the equation of state as

The phase transitions occur at critical points, and the critical points occur at the inflection points of the isothermal process that satisfies

Or equivalently,

Solving Eq. (46), we can obtain the critical radius $ r_c $ using

Taking $ n=3 $ as a simple example, we can analytically solve the rational critical radius $ r_c $ as

Note that if the Gauss-Bonnet coefficient is negative and the string parameter a is zero, the solution of $ r_c $ is imaginary, which indicates no critical phenomena in the system. However, when the string parameter $ a\neq 0 $, the solution of $ r_c $ may be real and the phase transition can occur. In other words, similar to the phase transition of heat capacity, a cloud of strings may increase the number of phase transitions. Using the critical radius $ r_c $, we can obtain other critical values such as temperature $ T_c $, pressure $ P_c $, and volume $ V_c $.

In the next part, we succinctly discuss the thermodynamic properties of a black hole with charge. The method is consistent with the previous treatment. We plot the behavior of $ f(r) $ as a function of r in Fig. 5.

Figure 5.  (color online) Plot of the metric function $ f(r) $ as a function of radius with the values $ \alpha=1 $, $ l = 1 $, $ \mu=1 $, $ a=0.4 $, and $ Q=0.1 $.

As shown in Fig. 5, whether the strings exist or not, there is always a zero point at extremely small radii. Unlike the uncharged case, the charge guarantees the existence of a black hole. The thermodynamic quantities are given by

(1) Entropy

This is the same as (38), and the entropy is also independent of charge.

(2) Mass

Here, in contrast with the string parameter a, the charge Q provides a source of positive mass.

(3) Hawking temperature

We plot a $ T-r_+ $ diagram below.

As shown in Fig. 6, the charge behaves like strings; it may also cause the temperature to change from positive to negative in the small radius region.

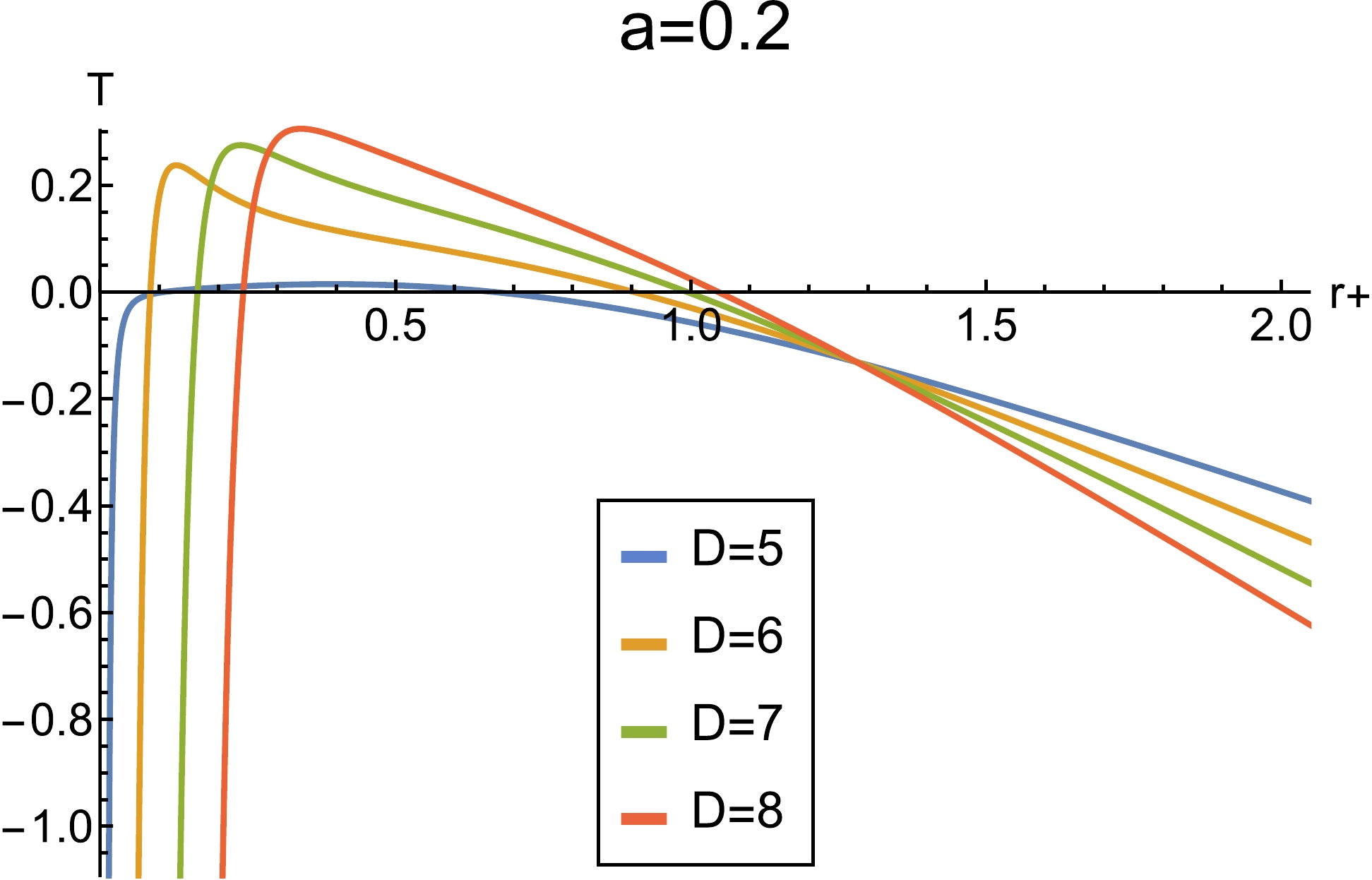
Figure 6.  (color online) Plot of Hawking temperature with respect to horizon radius with the values $ \alpha=1 $, $ l = 1 $, $ a=0.2 $, and $ Q=0.01 $.

(4) Heat capacity: The form of heat capacity is identical to (40), but now

A $ C-r_+ $ diagram is shown in Fig. 7.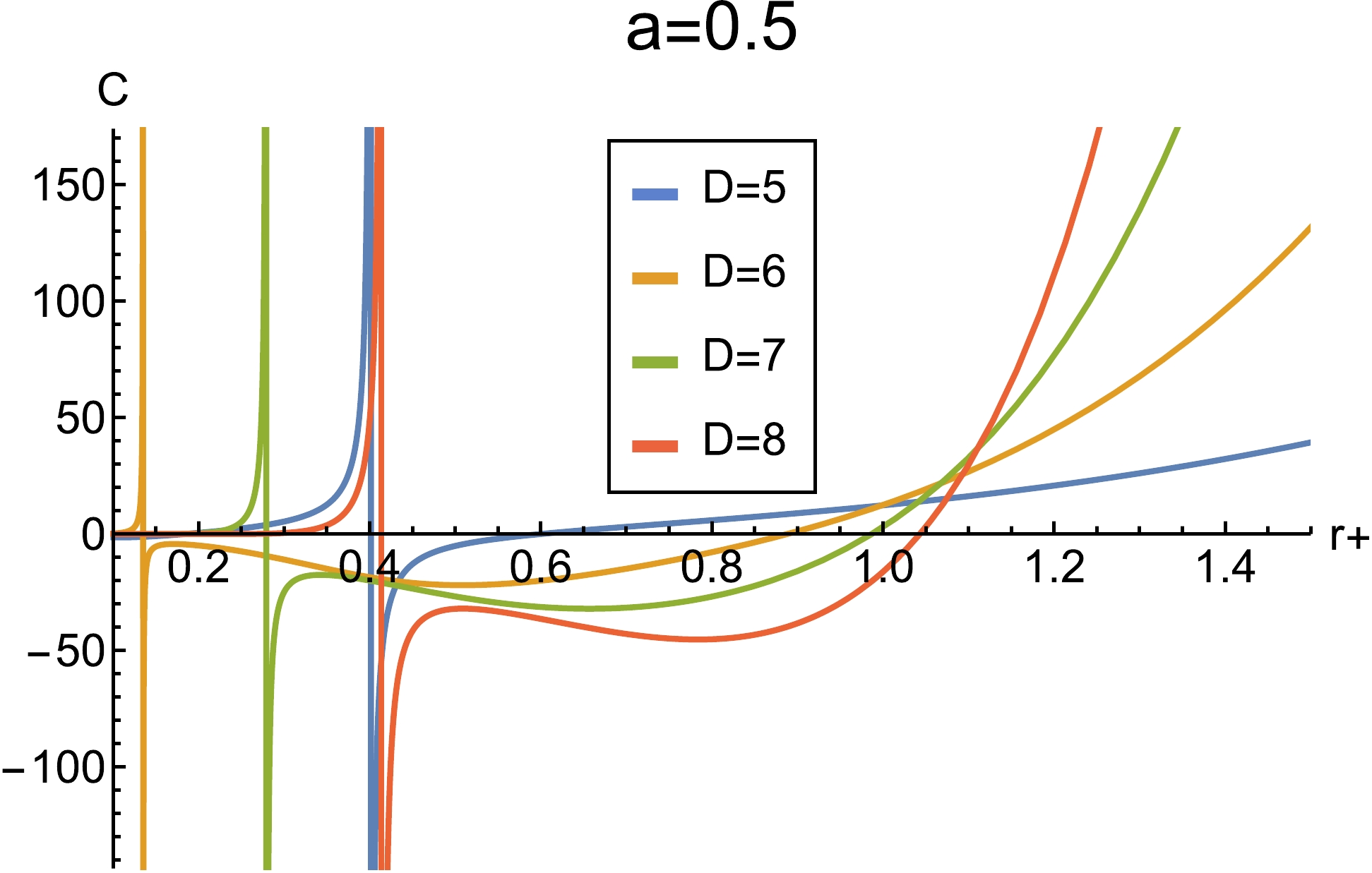

Figure 7.  (color online) Plot of heat capacity with respect to horizon radius with the values $ \alpha=1 $, $ l = 1 $, $ a=0.5 $, and $ Q=0.01 $.

Again, we can see that the effect of charge on the heat capacity is similar to that of a cloud of strings. With charge involved, six dimensions that have not phase transitioned before have a phase transition.

(5) Free energy: The form of free energy is identical to (41), but with different $ F_1 $ and $ F_2 $:

An $ F-r_+ $ diagram is shown in Fig. 8.

Figure 8.  (color online) Plot of free energy with respect to horizon radius with the values $ \alpha=1 $, $ l = 1 $, $ a=0.6 $, and $ Q=0.01 $.

Charge makes the free energy at small radii tend to infinity; however, it does not affect the sign of the free energy. Hence, charge has only a numerical effect on the free energy. Charge also increases the area of negative temperature and the number of phase transitions, and the black hole is still globally unstable. The difference is that the charge provides a source of positive mass whereas strings provide a negative source for mass. The equation of state for the charged case reads as

Moreover, the equation of critical radius $ r_c $ is given by

and

In this study, we obtain the Gauss-Bonnet black hole solution with a cloud of strings in the de-Sitter space. Both the uncharged and charged cases are considered. By using the Einstein equation and static spherical ansatz, an exact black hole solution is obtained. When the string parameter $ a=0 $, our solution is reduced to the Gauss-Bonnet black hole solution in the dS space [24]. Then, we focus on the effect of a cloud of strings on the thermodynamic properties and event horizons of the black hole. We use the numerical method to calculate thermodynamic quantities and analyze them. Interestingly, we find that a cloud of strings provides a negative source for the black hole mass, whereas it has only a quantitative influence on temperature.

We also study thermodynamic stability based on heat capacity and free energy. We find that the existence of a cloud of strings has a significant impact on the stability of the system. The strings can increase the number of phase transitions owing to the heat capacity related to the strings. However, globally unstable black holes are still retained even with the existence of strings.

Moreover, we present the equation of state and discuss the critical phenomena. We express the conditions for the phase transitions, and these conditions can be used to find critical points. We take the five-dimension as an example and discover that the critical points correlate with the strings, which indicates that the existence of phase transitions due to thermodynamic pressure is dependent on strings. The question of whether strings have any effect on other types of phase transitions will be left for future studies.

Charged spherical symmetric Gauss-Bonnet black holes with a cloud of strings in AdS space have been studied in [29, 30]; however, they only discussed the thermodynamic properties in five dimensions. Here, we extend this solution with general topology and briefly discuss the thermodynamic properties in higher dimensions. Now, the metric function f reads as

For AdS space, the constant curvature space $ k=1 $, –1, or 0, corresponding to spherical, hyperbolic, and flat geometries, respectively. For the sake of comparison with the dS space, we only discuss $ k=1 $. Here, we plot the function$ f(r) $ with respect to r in Fig. A1, and Hawking temperature T, heat capacity C, and free energy F with respect to horizon radius $ r_+ $ in Fig. A2 .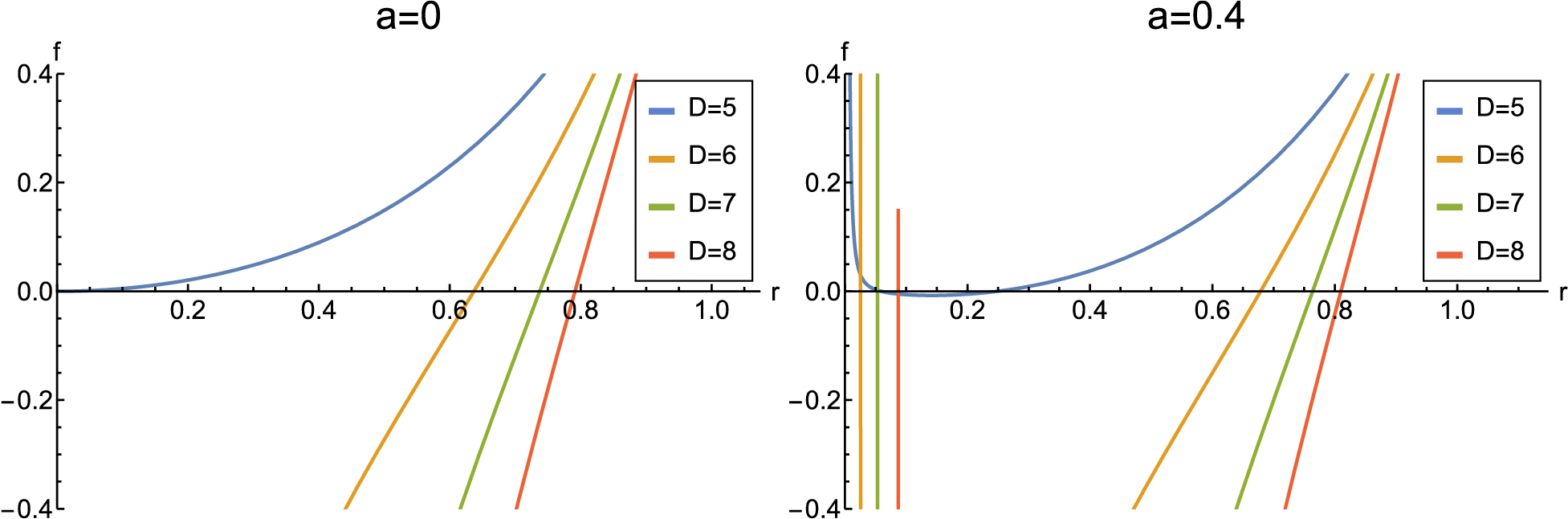

Figure A1.  (color online) Plot of the metric function $ f(r) $ against radius with the values: Left: $ \alpha=1,l=1,\mu=0,a=0,Q=0 $; Right:$ \alpha=1,l=1,a=0.4,Q=0.1 $.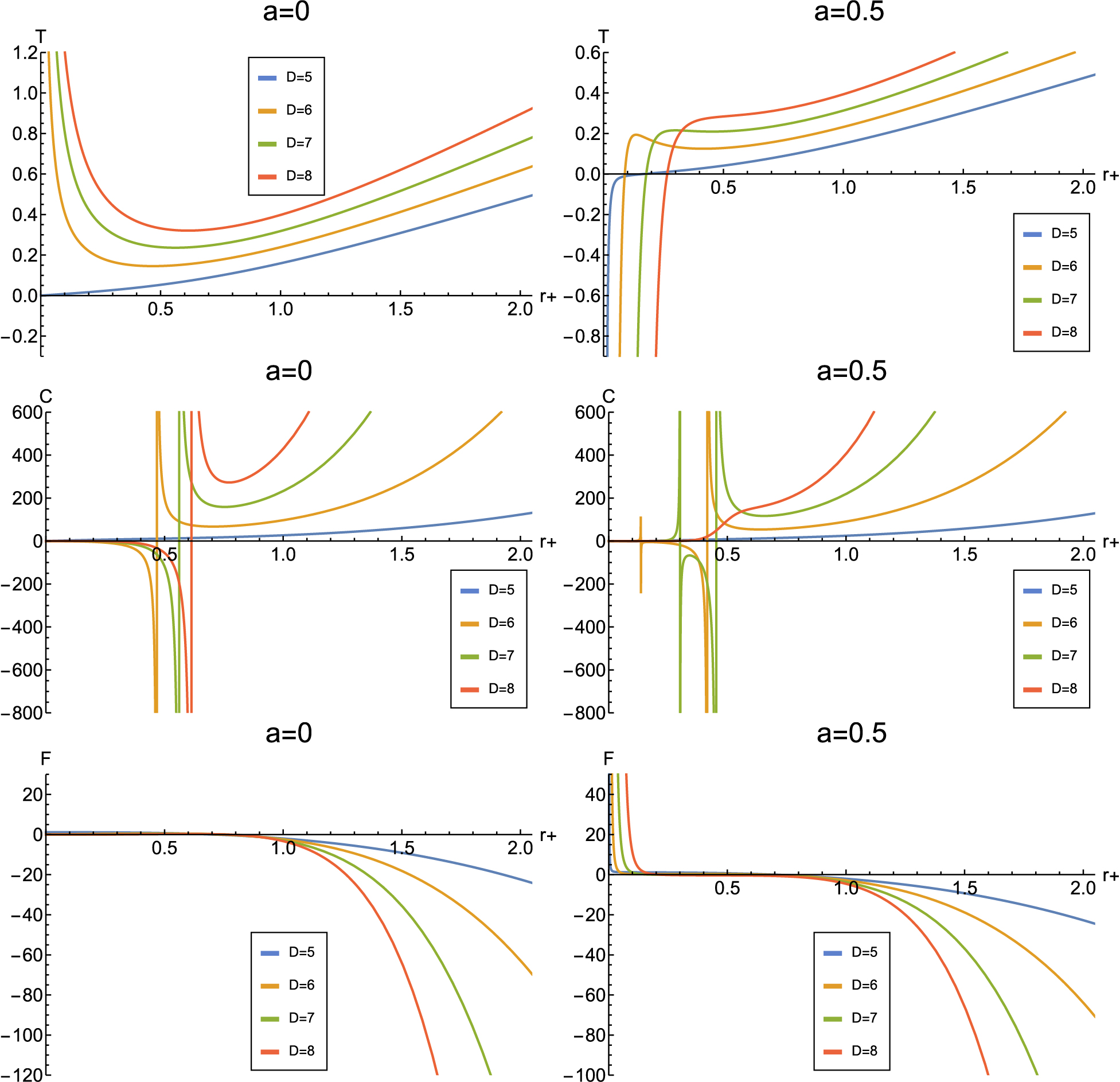

Figure A2.  (color online) Plot of Hawking temperature, heat capacity, and free energy (from top to bottom) vs horizon radius with the values: Left: $ \alpha=1,l=1,a=0,Q=0 $; Right:$ \alpha=1,l=1,a=0.5,Q=0.01 $.

Here, we find that in the AdS space, the charge still guarantees the existence of a small black hole in six, seven, and eight dimensions. Moreover, charge and clouds of strings have an influence on the number of transitions, as in the dS space.