Study of bending angle and shadow in a new Schwarzschild-like black hole affected by plasma and non-plasma mediums

Black holes (BHs), as predicted by Einstein's theory of general relativity (GR), are significant objects that are thought to originate as a result of the gravitational collapse of enormous astronomical objects. Numerous experimental and observational studies support GR [1]. These investigations have revealed that experimental data, including those on gravity waves, wormholes, and gravitational lensing on BHs, are consistent with the theoretical predictions of this theory. Gravitational waves are ripples in the structure of the universe, which are created by the collision of enormous objects such as BHs. Gravitational waves are induced by the curvature of space-time. A distribution of matter between a source and an observer that can bend light from the source to the observer is known as the deflection angle (DA). The DA is useful in studying the universe's dark matter distribution and imaging the furthest galaxies. In GR, the expectation that light will bend as it approaches big objects is met. The DA phenomenon is highly useful for detecting BHs in the cosmos because it implies that light beams are bent owing to the curvature of spacetime. The DA is classified as a weak field in literature and helps determine the position of BH geometry.

Gibbon and Werner [2] adopted the Gauss-Bonnet theorem (GBT) to derive the DA of light beams. The integral in a finite domain defined by a light ray was calculated using this method. Werner then developed this formalism further by applying Nazim's method with the Randers-Finsler metric [3] to determine the DA by a Kerr-Newman BH. Recently, the DA in a static, spherical, symmetrical, and asymptotically flat region [4–7] was calculated using the finite distance between an observer and a light source. Moreover, the GBT has topological implications when applied to the geometries of wormholes and non-asymptotically flat spacetime [8, 9]. Jusufi and Övgün [10] recently made a significant contribution by discussing the quantum correction effects on light deflection caused by quantum-expanding Kerr BHs in a cosmic string. The DA in spacetimes with topological defects was calculated using both cosmic strings and global monopoles [11–14]. This strategy has been used in several studies for various spacetimes [15, 16].

Javed et al. [17] employed the light DA resulting from a Brane-Dicke wormhole in the weak field limit approximation and examined the effect of the Brane-Dicke coupling parameter on weak gravitational lensing. Their findings offer a useful tool for immediately identifying the wormhole and naked singularity types and searching for evidence supporting the Brane-Dicke theory. They also used the GBT to determine the weak DA of light in the frame of an Einstein-Maxwell-Dilaton-axion BH [18] and investigated the effect of a plasma medium when light is deflected around a particular BH.

BHs are massive objects that are studied by GR at the center of our galaxy. It is commonly known that photons from a light source behind a BH cause the observer's sky in the dark area to appear as the "BH shadow." The BH shadow, which is an impose of the BH, provides essential information about the BH. To illustrate, from the BH shadow, one may extract the charge and spin of the BH [19–24] and limit certain additional parameters produced by changing gravities for the BH shadow [25–29]. Synge [30] and Luminet [31] investigated the shadow cast by an ideal circle, or BH, with spherical symmetry. They also provided formulas for the shadow's size and angular radius. Bardeen [32] was the first to investigate the shadow generated by a Kerr BH, and the dragging effect was found to distort the shape of the shadow. The BH shadow has been widely studied in literature. For instance, the BH shadow and photon sphere were investigated in dynamically shifting spacetimes in Ref. [33], and in Ref. [34], the implications of the cosmological constant on the BH shadow were examined. The shadow of a normal rotating BH was studied in Ref. [35], the shadow of a model-independent parameterized axisymmetric BH was computed in Ref. [36], and the quasinormal modes in the eikonal limit and the radius of the BH shadow were found to be related in [37, 38]. Additional important examinations of the BH shadow and DA were performed in [39–41]. The shadow cast by a dyon BH, also known as Kerr-Newman-Kasuya spacetime, was studied in [42], where it was concluded that the shadow image is affected by both its rotational momentum and dyon charge. Övgün et al. studied [43, 44] the DA for spacetime solutions, such as the generalized Einstein-Cartan-Kibble-Sciama and null aether theories, using the GBT and verified that weak deflection of BHs is effected in these theories. An extensive review of quasinormal modes, analytic greybody factors, and gravitational lensing in rotating BH spacetime, such as bumblebees, is presented in [45]. Using GR combined with the bumblebee theory, the investigation produced impressive results in four dimensions. This was demonstrated to be the more physically accurate metric form of a rotating bumblebee-like BH after presenting some of its physical characteristics. The light deflection in the spacetime of a rotating BH that is electrically charged was examined in [46] and considered in terms of its impact on the cosmological constant. The deflection for a Kerr-Newman anti-Sitter BH was also computed by exploiting the Rindler-Ishak technique extension.

A significant astrophysical BH is produced with BH mass and algebraic thermodynamic parameters. Furthermore, to obtain a thorough understanding of the features of a modified BH, the BH geometry under the impacts of the DA and BH shadow modifications must be analyzed. In addition, a BH is typically surrounded by plasma; therefore, the effects of plasma, BH mass, and algebraic thermodynamic parameters on the BH DA and shadow must also be investigated.

This paper is organized as follows. In Sec. II, we explore the DA of light for a new type of Schwarzschild BH in a non-plasma medium. In Section III, we investigate the DA for the new type of Schwarzschild BH in a plasma medium. In Sec. IV, we verify our results using the Keeton and Petter technique, Section V comprises the equation of motion for light rays under the influence of non-magnetized plasma to compute the shadow of the corresponding BH, and in Sec. VI, we discuss the results of our study.

The study of the DA in a non-plasma medium for a novel type of Schwarzschild BH forms the basis of this section. For this purpose, we consider the four-dimensional space-time metric of this new Schwarzschild BH, given as [47, 48]

where ${\rm d}\Omega^{2}={\rm d}\theta^{2}+\sin^{2}\theta {\rm d}\phi$ and $ G(r)=\dfrac{1}{U(r)}= \Big(1-\dfrac{\mu}{r}+ \dfrac{p^{2}}{r^{2}}\Big) $. Moreover, the parameters M and p represent the BH mass and algebraic thermodynamic parameters, respectively. The parameter μ is associated with the BH mass defined by the relation $ M=\dfrac{\mu}{2} $. By considering the metric function $ G(r)=0 $, we can obtain the inner ($ r_{-} $) and outer ($ r_{+} $) horizons via

Figure 1 shows the behavior of the metric function $ G(r_+) $. The left plot indicates this behavior for different choices of the algebraic parameter, whereas the right plot represents this behavior for different μ. In both plots, the metric function negatively increases and decreases, which indicates an unstable form.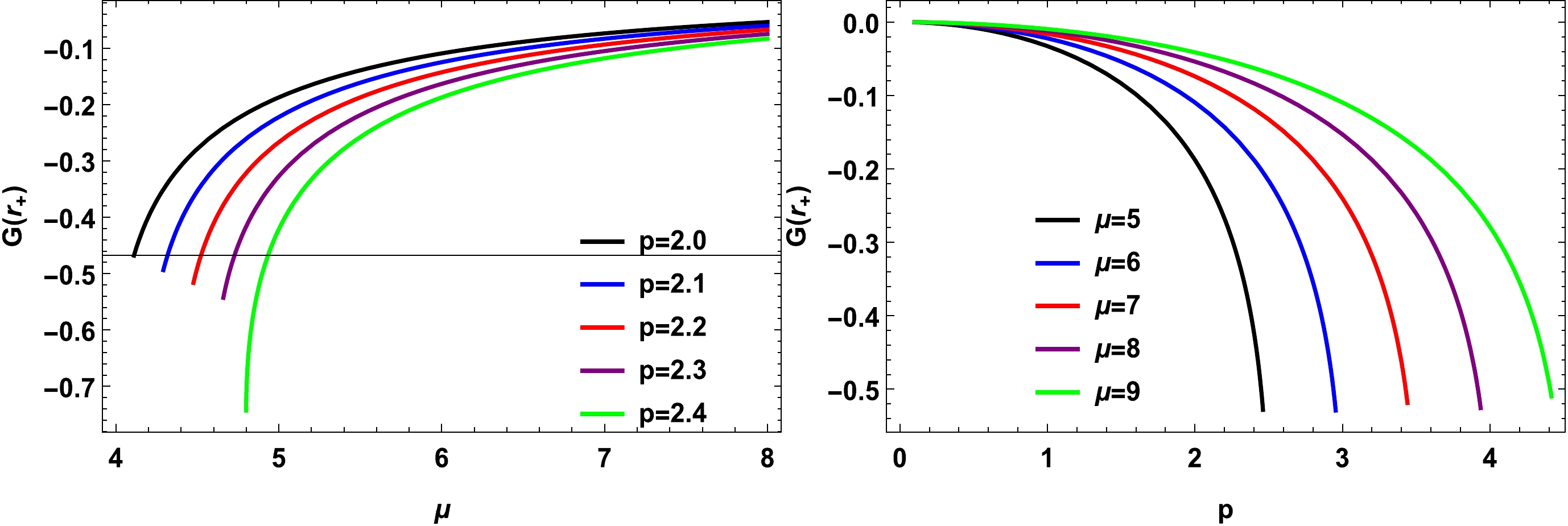

Figure 1.  (color online) Metric function $ G(r_+) $ with respect to the ADM mass μ and algebraic parameter p.

The BH becomes an extreme BH at the condition $ r_{+}=r_{-} $. The relationship between the algebraic parameters and μ and the horizons is given as follows:

The condition $ p^2\leqslant\dfrac{\mu^{2}}{4} $ is always satisfied, except for the naked singularity at $ r=0 $. Here, we investigate the BH bending angle in a non-plasma medium using the GBT. In the event that the tropical region is linked to the observer, source, and null photon, we can investigate ($ \theta=\dfrac{\pi}{2} $). By setting ${\rm d}s^2=0$ in Eq. (1), we derive the optical metric via

The following formula yields the non-zero Christoffel symbols for the given metric:

where 1 and 2 indicate the r and ϕ coordinates, respectively, and the Ricci scalar for the given metric is computed as follows:

To calculate the Gaussian curvature, we use the formula

Inserting Eq. (6) into Eq. (7), the Gaussian curvature can be computed via

This formula is helpful in calculating the DA for a new type of Schwarzschild BH solution utilizing the GBT in the region of the non-singular domain $ M_e $ :

In the above expression, $ k=\bar{g}(\nabla_{\dot{\zeta}}\dot{\zeta}, \ddot{\zeta}) $ denotes the geodesic curvature. The unit acceleration vector $ \ddot{\zeta} $ is denoted by $ \bar{g}(\dot{\zeta}, \dot{\zeta})=1 $, whereas the exterior angle of the $ ith $ vertex is expressed as $ \epsilon_{i} i $. The associated jump angles decrease to $ \dfrac{\pi}{2} $ as $ e\rightarrow \infty $, yielding $ \theta_{O}+\theta_{s}\rightarrow \pi $ , and $ \zeta(\mathbb{K}) = 1 $ is the Euler characteristic. Therefore, the above equation can be rewritten as

To obtain the geodesic curvature, we use the following relation:

The radial component of geodesic curvature can be defined as

Therefore, following result can be computed for a large value of e, such that $ W_{e}:= r(\phi)=e=\text{constant} $ as

Because there is no topological flaw in the geodesic curvature, $ k(W_{e})\rightarrow e^{-1} $. Nevertheless, it can be stated as $ {\rm d}t = e {\rm d}\phi $ by applying the optical metric Eq. (4). Consequently, we have

Now, the following equation may be obtained by utilizing the previous expression:

In the weak field limitations, the $ 0th $ order light ray is computed as $ r(t)=\dfrac{b}{\sin\phi} $. Equations (9) and (15) can be used to obtain the bending angle as

where$\sqrt{{\rm det}\vec{g}}$ is computed as

The DA is computed using the Gaussian curvature up to the leading order terms:

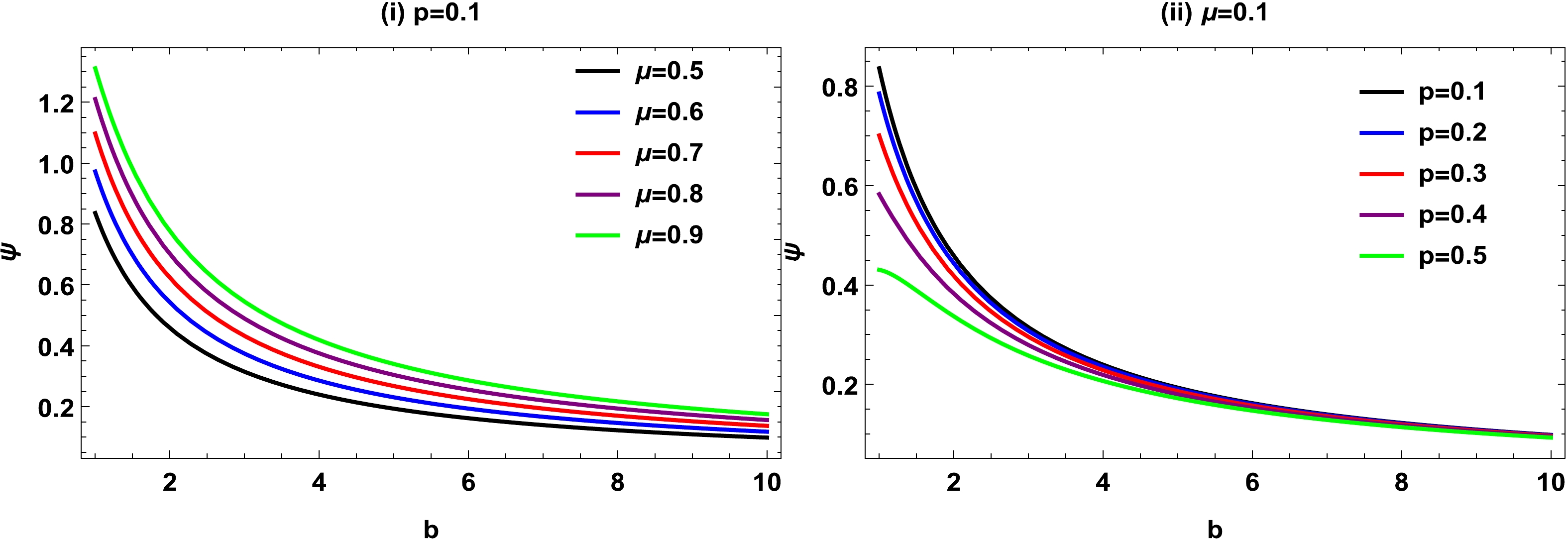
The above DA depends on the impact parameter b, algebraic parameter p, and ADM mass μ. We can also observe that the impact parameter has an inverse relationship with the DA. It is important to note that our results are similar to the Reissner–Nordström BH given in [49, 50] without higher order magnetic correction terms. Moreover, by setting $ \mu=2M $ and $ p=0 $, that is, an improved relationship for the trajectory of a light ray in the integration domain, our expected first-order DAs are reduced to the standard Schwarzschild BH DA, $ \psi_{Sch}=\dfrac{4M}{b} $ , found in [51].

Figure 2 indicates the behavior of the DA ψ with the impact parameter b for different choices of μ and p. From both plots, we graphically observe that the impact parameter has an inverse relationship with the DA. The DA decreases as the impact parameter increases in the region $ 1\leqslant b\leqslant10 $. Moreover, the ADM mass has a direct relationship with the angle, whereas the algebraic parameter has an inverse relationship. We can also conclude that the light bends with a maximum angle for small values of the impact parameter.

Figure 2.  (color online) Deflection angle ψ with respect to the impact parameter b. The left plot shows the behavior for various μ with fixed $ p=0.1 $ , and the right plot shows the behavior for different p with fixed $ \mu=0.1 $.

Next, the DA in a plasma medium is calculated. Let v be the speed of light through hot ionized gas, representing the effects of plasma. The refractive index, $ n(r) = c/v $, for the given BH is defined as [52]

where $ \omega^{2}_{e} $ represents electron plasma frequency, and $ \omega^{2}_{\infty} $ represents the photon frequency determined at infinity by the observer. The associated optical metric is defined as

The optical Gaussian curvature for the new type of Schwarzschild BH can be calculated as

We calculate the bending angle using the GBT. To achieve this, we use the approximation $ r(t)=\dfrac{b}{\sin\phi} $ at the $ 0th $ order, and the DA is obtained as

For the leading order terms of the new form of Schwarzschild BH under the impacts of a plasma medium and using the values of Gaussian curvature obtained by inserting Eq. (21) into Eq. (22), the DA is computed as

The above expression for the DA in a plasma medium is dependent on the impact parameter b, ADM mass μ, algebraic parameter p, and electron and photon frequencies $ \omega_{e} $ and $ \omega_{\infty} $, respectively. It is important to note that when $ \dfrac{\omega_{e}}{\omega_{\infty}}\rightarrow 0 $, the above equation reduces to Eq. (18).

Figure 3 represents the graphical behavior of the DA ψ with b for different choices of μ and p. From both plots, we note that the impact parameter also has a inverse relationship with the angle in the presence of a plasma medium. The DA decreases when the impact parameter increases in the region $ 1\leqslant b\leqslant15 $. Moreover, the algebraic parameter has an inverse relationship with the angle, whereas the ADM mass has a direct relationship with the angle in the presence of plasma. We observe a strong deflection at small values of the impact parameter.

Figure 3.  (color online) Deflection angle ψ with respect to the impact parameter b. The left plot shows the behavior for various μ, and the right plot shows the behavior for different p.

The DA of the novel Schwarzschild BH solution is determined using the Keeton and Petters approach. Keeton and Petters modified the original approach to make it more in line with their methodology and obtain outcomes [53, 54]. Post-post Newtonian (PPN) theory provides a straightforward method for handling any gravity theories, where the weak deflection limit is expressed as a single variable m series expansion. For this purpose, we can take space-time in the form

The metric functions Y and Z can be written in a PPN series as

where γ represents the Newtonian potential in three-dimensions and can be defined as

The DA $ \psi_{2} $ is expressed in a series expansion form as follows:

Here,

Now, we compare Y with $ G(r) $ and Z with $ U(r) $ given in Eq. (1) and compute the PPN coefficients as follows:

After inserting all of the above co-efficients into Eqs. (28) and (29), we obtain

After substituting the values from Eq. (27) into Eq. (31), we obtain the DA as

The values of m, p, b, and μ have an impact on the required DA.

To obtain the conditions of null geodesics, we can derive the equations of motion and consider the impact of an electron plasma frequency $ \omega_{e}(r) $ on a non-magnetized cold plasma through the Hamiltonian [55] of the moving photon to study the shadow of the new type of Schwarzschild BH:

The Hamiltonian in Eq. (33) for a two-fluid source is derived from Maxwell's equations, and the quantities of continuous motion $ f_t $ and $ f_{\phi} $ connected to the energy $ -f_t=E $ and angular momentum $ f_{\phi}=L $ can be defined to obtain the equations of motion for photons:

which imply that

where $ f_{r} $ gives the radial momentum and can be defined as

Moreover,

with $ H=0 $, such that

In this case, the prime denotes differentiation with respect to r, whereas the dot denotes differentiation with respect to an affine parameter λ.

It is evident from Eqs. (35) and (36) that $ f_{t} $ and $ f_{\phi} $ are motion constants. The formula converts the frequency ω observed by a static observer into a function of r as follows:

We use Eqs. (40) and (41) to obtain the orbit equation

After substituting for $ f_{r} $ in Eq. (43),

where $ \omega_{0} $ denotes the frequency measured by a static observer, and we define the function

Given that X denotes the turning point of the trajectory, $\dfrac{{\rm d}r}{{\rm d}\phi|_{X}} = 0$ must hold. This formula connects X to the constant of motion $ \dfrac{f_{\phi}}{\omega_{0}} $ as

It is anticipated that a stationary observer at point $ r_0 $ will release light beams into the past with an angular radius β [55] relative to the radial direction:

Equation (45) can be used to rewrite the orbit equation (Eq. (47)) in the event that the light beam disappears after reaching a minimal radius R:

For the angle β, we obtain

By utilizing the identity, we have

Inserting Eq. (51) into Eq. (50), we obtain

Light rays traveling asymptotically toward a circular light orbit at radius $ r_{ph} $ define the boundary of the shadow β. For this reason, $ R\rightarrow r_{ph} $ in Eq. (52) yields the angular radius of the shadow as follows:

where $ p(r) $ is obtained using Eq. (46). In numerous instances, it is possible to presume that the observer is located in an area with a negligibly small plasma density. Therefore, Eq. (46) gives

and Eq. (54) implies that

After substituting all values, we obtain

The shadow β depends on the algebraic parameter p, ADM mass μ, plasma frequencies $ \omega_{0} $ & $ \omega_{e} $, photon radius $ r_{ph} $, and observer radius $ r_0 $.

Figure 4 illustrates the variations in the shadow β in terms of the photon $ r_{ph} $ and observer $ r_{0} $ radii. In plot (i), the shadow exponentially increases with variations in $ r_{0} $ with fixed $ p=0.1, \; \mu=10, \; \omega_e=0.2 $ , and $ \omega_0=0.3 $ in the region $ 0\leqslant r_{ph}\leqslant 2.5 $. The shadow is noticeably smaller for larger values of $ r_{0} $. This inverse proportionality between the shadow and photon radius can account for the reduction in the shadow β as $ r_{0} $ increases.

Figure 4.  (color online) Shadow in terms of the radii $ r_{ph} $ and $ r_{0} $. The left plot shows the behavior for various $ r_{0} $ , and the right plot shows the behavior for different $ r_{ph} $.

Plot (ii) illustrates the behavior of the shadow β in terms of the observer radius $ r_{0} $ with variations in $ r_{ph} $ with fixed $ p=5, \; \mu=10, \; \omega_e=0.2 $ , and $ \omega_0=0.3 $ in the region $ 3\leqslant r_{0}\leqslant 7 $. Symmetry can be observed in the shadow, along with a sharp edge at $ \beta=0 $.

The contour plots of the new type of Schwarzschild BH shadow can be plotted in the form of the celestial coordinates α and β.

Figure 5 (i) shows the contour plots of the shadow for different choices of photon radius, that is, $ r_{ph}=1 $ (purple), 2 (yellow), 3 (green), 4 (orange), 5 (blue), and 6 (red). The size of shadow radius increases with increasing photon radius.

Figure 5.  (color online) Shadow of the new type of Schwarzschild BH for different choices of radius $ r_{ph} $ and $ r_{0} $ and fixed values of $ \mu=5, p=0.5, \omega_e=0.1 $ , and $ \omega_0=0.5 $.

Figure 5 (ii) shows the contour plots of the shadow with variations in radius $ r_{0}=5 $(purple), 5.5 (yellow), 6 (green), 6.5 (orange), 7 (blue), and 7.5 (red). The shadow radius increases with increasing observer radius$ r_{0} $ and is larger than the photon radius. Figure 6 (i) depicts the contour plots of the shadow for different choices of ADM mass $ \mu=1 $(purple), 1.5 (yellow), 2 (green), 2.5 (orange), 3 (blue), and 3.5 (red). The inverse relationship between the shadow radius and ADM mass μ suggests that the radius decreases with increasing mass influence.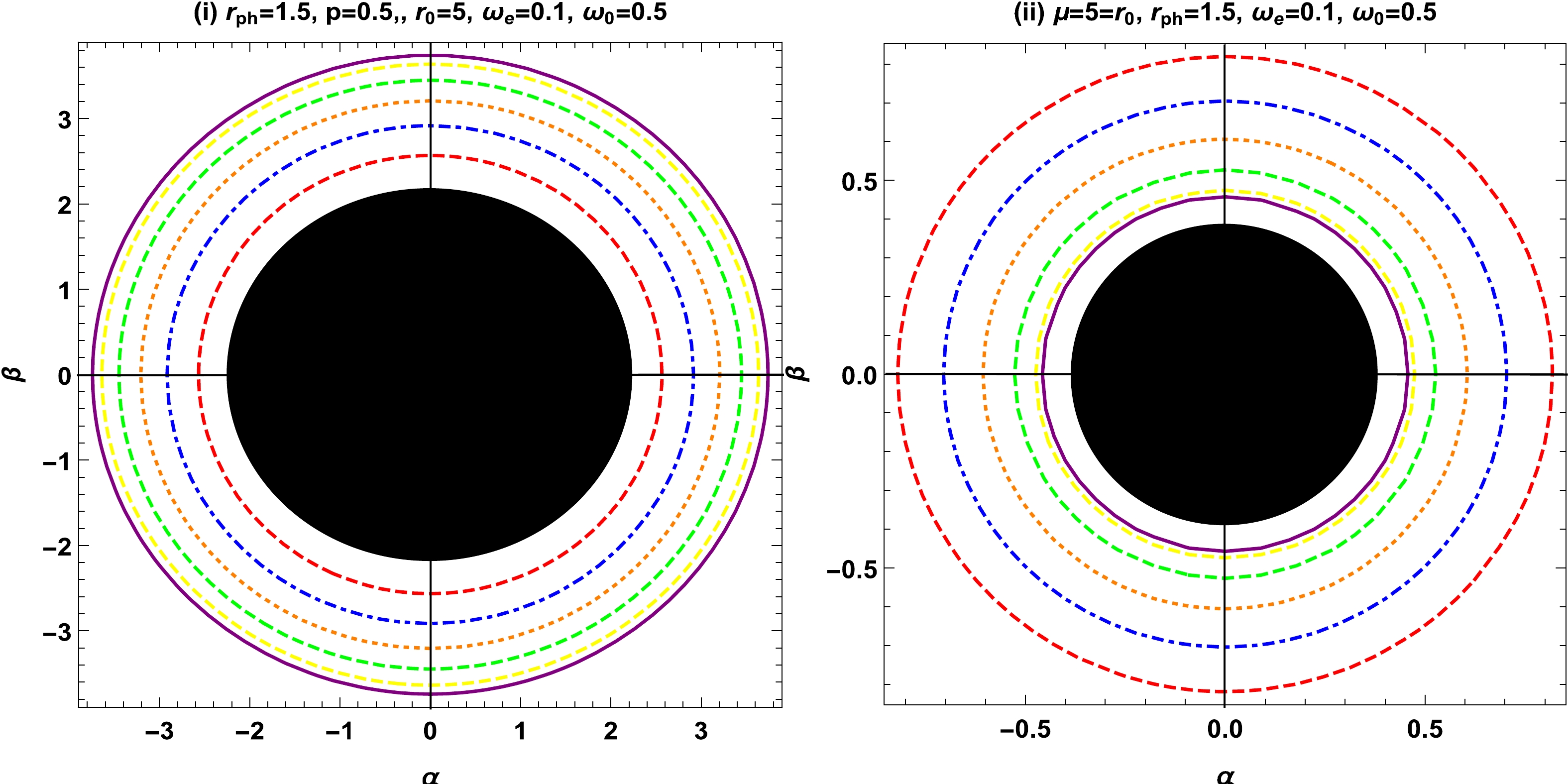

Figure 6.  (color online) Shadow of the new type of Schwarzschild BH for different choices of the ADM mass μ and algebraic parameter p and fixed values of $r_{0}=5,\; r_{ph}=1.5,\; \omega_e=0.1$ , and $ \omega_0=0.5 $.

Figure 6 (ii) represents the contour plots of the shadow with variations in the algebraic parameter $ p=0.1 $ (purple), 0.5 (yellow), 1 (green), 1.5 (orange), 2 (blue), and 2.5 (red). The size of shadow radius increases with increasing p.

This study uses mathematical calculations to analyze the weak DA and shadow of a novel type of Schwarzschild BH in the background of a non-plasma/plasma framework. The weak DA of this BH is then obtained using the GBT and Gibbons and Werner method to investigate the gravitational field of the BH and its fundamental properties, including the mass and algebraic parameters, the type of light bending, and the underlying validity of Einstein's theory. These help us understand the dynamics of BHs and guide observational astronomers in terms of what and what not to expect. The DA for the new type of Schwarzschild BH is found to vary greatly, with an increase caused by its regulating parameters.

First, we investigate the new type of Schwarzschild BH solution in a non-plasma frame and determine that the DA depends on the impact parameter b, ADM mass μ, and algebraic parameter p. It is worth noting that our result in Eq. (18) is similar to the Reissner–Nordström BH result given in [49, 50], without higher order magnetic correction terms. Moreover, by setting $ \mu=2M $ and $ p=0 $ in Eq. (18), our result for the DA is reduced to the DA of the standard Schwarzschild BH, $ \psi_{Sch}=\dfrac{4M}{b} $.

We also graphically conclude that the impact parameter has an inverse relationship with the DA. Moreover, the ADM mass has a direct relationship with the angle, whereas the algebraic parameter has an inverse relationship. We also conclude that for small values of the impact parameter, the light bends with a maximum angle.

Furthermore, we investigate the DA in a plasma frame and find that it is dependent on the impact parameter b, ADM mass μ, algebraic parameter p, and plasma frequencies $ \omega_{\infty} $ and $ \omega_e $. We also conclude that when $ \dfrac{\omega_e}{\omega_{\infty}}\rightarrow0 $, the results of the DA in a plasma medium (Eq. (23)) reduce to the results in a non-plasma medium (Eq. (18)). From our graphical analysis in the plasma medium, the ADM mass has an inverse relationship with the angle, whereas the algebraic parameter has a direct relationship with the angle. We observe a strong deflection in the plasma frame compared to the non-plasma medium.

Additionally, we apply the Keeton and Petters method to calculate and verify the results of the DA. We examine the dependence of the DA of the Keeton and Petters technique on the impact parameter, algebraic parameter, and ADM mass.

Finally, we study the shadow of the new type of Schwarzschild BH using an equation of motion for light rays under the impact of non-magnetized plasma. The magnitude of the shadow is dependent on a variety of parameters. The shadow β depends on the algebraic parameter p, ADM mass μ, plasma frequencies $ \omega_0 $ & $ \omega_{e} $, photon radius $ r_{ph} $, and observer radius $ r_{0} $. We also plot contour graphs for the shadow of the new type of Schwarzschild BH and analyze the effects of the photon and observer radii, algebraic parameter, and ADM mass on the BH shadow. We conclude that the size of the shadow increases with increasing algebraic parameter and photon and observer radii. Moreover, we observe the inverse relationship between the shadow radius and ADM mass μ, suggesting that the radius decreases with increasing mass influence.

The authors declare no conflicts of interest.

The data that support the findings of this study are available from the corresponding author upon reasonable request.